Preparatory co-activation of the ankle muscles may prevent ankle inversion injuries

Abstract

Ankle inversion sprains are the most frequent acute musculoskeletal injuries occurring in physical activity. Interventions that retrain muscle coordination have helped rehabilitate injured ankles, but it is unclear which muscle coordination strategies, if any, can prevent ankle sprains. The purpose of this study was to determine whether coordinated activity of the ankle muscles could prevent excessive ankle inversion during a simulated landing on a 30-degree incline. We used a set of musculoskeletal simulations to evaluate the efficacy of two strategies for coordinating the ankle evertor and invertor muscles during simulated landing scenarios: planned co-activation and stretch reflex activation with physiologic latency (60-millisecond delay). A full-body musculoskeletal model of landing was used to generate simulations of a subject dropping onto an inclined surface with each coordination condition. Within each condition, the intensity of evertor and invertor co-activity or stretch reflexes were varied systematically. The simulations revealed that strong preparatory co-activation of the ankle evertors and invertors prior to ground contact prevented ankle inversion from exceeding injury thresholds by rapidly generating eversion moments after initial contact. Conversely, stretch reflexes were too slow to generate eversion moments before the simulations reached the threshold for inversion injury. These results suggest that training interventions to protect the ankle should focus on stiffening the ankle with muscle co-activation prior to landing. The musculoskeletal models, controllers, software, and simulation results are freely available online at http://simtk.org/home/ankle-sprains, enabling others to reproduce the results and explore new injury scenarios and interventions.

INTRODUCTION

Ankle sprains are the most common of all acute musculoskeletal injuries that occur during physical activity (Fong et al., 2009, 2007). Roughly 80% of acute ankle injuries involve excessive inversion, with 77% resulting in lateral ligament sprains (Fong et al., 2009). These injuries often occur during landing, especially on irregular or unexpected surfaces, such as a competitor’s foot (Bahr et al., 1997, 1994). High impact forces directed medially to the subtalar joint induce rapid inversion (Fuller, 1999; Wright et al., 2000a, 2000b). Injury occurs when excessive inversion stretches the lateral ligaments that cross the talocrural and subtalar joints, causing plastic strains or ligament rupture (Hertel, 2002). Approximately 70% of patients experience incomplete recoveries that leave the ankle prone to recurring injuries (Anandacoomarasamy and Barnsley, 2005; Braun, 1999).

Load–deflection studies on cadavers have quantified the passive mechanics of the ankle (Chen et al., 1988; Lapointe et al., 1997; Siegler et al., 1990). Passive ankle stiffness decreases due to ligament sprains, reducing resistance to excessive ankle inversion (Lapointe et al., 1997; Siegler et al., 1990). Computer simulations of ankle inversion scenarios predicted that decreased passive ankle stiffness could increase the probability of inversion injuries (Wright et al., 2000a). Observations from large cohorts of athletes corroborate this finding, showing that ankles with previous inversion injuries are more susceptible to future injury than uninjured ankles (McGuine and Keene, 2006; Surve et al., 1994). Athletic tape and braces can stiffen ankles with previous injuries and decrease rates of recurring injuries (Kamiya et al., 2009); however, tape and braces have not been shown to decrease injury rates in uninjured ankles (Calatayud et al., 2014; Verhagen and Bay, 2010).

Posture and muscle coordination also affect ankle stability, but the relationships between muscle activity, landing pose, and the risk of inversion injury have not been adequately characterized. Landing with a plantarflexed or inverted ankle increased the rate of injury in musculoskeletal simulations (Wright et al., 2000b). Retraining trunk and leg posture has decreased the rate of ankle injuries in volleyball players (Bahr et al., 1997). Neuromotor interventions, which retrain muscle coordination, can protect the ankle. For example, balance training on unstable surfaces has decreased the rates of recurring ankle injuries in previously injured ankles (Bahr et al., 1997; Verhagen et al., 2004). Similarly, interventions combining balance, strength, and plyometric training have decreased the rates of recurring ankle injuries (Emery and Meeuwisse, 2010). However, according to multiple reviews (Calatayud et al., 2014; van der Wees et al., 2006; Verhagen and Bay, 2010), the majority of studies have found no effect of neuromotor retraining on preventing first-time ankle sprains.

While studies of neuromotor retraining are promising, outcomes are mixed and the mechanisms behind the protective effects are unknown, largely because the role of the ankle muscles in resisting inversion sprains is unclear. Some hypothesize that improved ankle proprioception (Arnold et al., 2009a; Hertel, 2002, 2000; Munn et al., 2010) and increased strength of the evertor muscles (Arnold et al., 2009b) are responsible. However, experiments exploring the effects of balance interventions have shown that neuromuscular retraining does not improve ankle proprioception (Gauffin et al., 1988; Kiers et al., 2012), and patients with recurring ankle sprains (Hiller et al., 2011) or functional ankle instability (Munn et al., 2003) do not demonstrate deficits in evertor strength. These findings suggest that changes in muscle coordination may be the primary protective mechanism of neuromuscular retraining. The capacity for the ankle muscles to prevent inversion injuries under various coordination strategies remains largely unexplored, and it is unclear if even healthy ankle reflexes with normal delays are sufficient to prevent injuries. Computer simulations provide a powerful tool to disentangle the contributions of reflexes and muscle preparatory activity to injury, but there are no publicly available models with physiological ankle joints or stretch reflex controllers that represent delays in muscle responses.

The purpose of this study was to determine whether coordinated activity of the ankle muscles could prevent excessive ankle inversion during an inversion-inducing landing scenario. We used musculoskeletal simulations to avoid the risk of injuring human subjects and enable systematic manipulation of muscle coordination. We used a musculoskeletal model (Delp et al., 1990) augmented with muscle excitation controllers, a foot–floor contact model, and passive mechanics of the ankle. We tested the model against experimental data and then used the model to generate muscle-driven simulations of a single-leg landing under a variety of muscle control strategies. The first goal was to quantify how co-activating the evertor and invertor muscles affects maximum inversion angles for a range of co-activation levels. The second goal was to quantify ankle inversion when the evertor and invertor muscles were coordinated with stretch reflexes. Thus, we were able to compare the efficacy of a planned muscle co-activation strategy to that of a purely reflexive strategy during an inversion-inducing landing.

METHODS

A musculoskeletal model for simulating inversion injuries

We developed a model (Figure 1) for simulating single-leg landings in OpenSim (Delp et al., 2007) by augmenting a well-established full-body musculoskeletal model. The model used the musculoskeletal geometry of the legs defined by Delp et al. (1990) with an articulating patella and quadriceps (DeMers et al., 2014). The torso–head segment connected to the pelvis by a ball- and-socket joint. The arms connected to the torso with ball-and-socket shoulder joints (Hamner et al., 2010). Forty-nine muscle–tendon units (muscles) actuated the legs and the lumbar joint (21 degrees of freedom in total). All muscles incorporated force–length, force–velocity, and activation dynamics behavior described by Thelen (2003) and reimplemented by Millard et al. (2013). The ankle complex was defined by Delp et al. (1990), which included one revolute joint for talocrural motion and a second revolute joint for the subtalar motion (Isman and Inman, 1969). Distal to the subtalar joint, the foot was modeled as a rigid segment with no joint between the forefoot and toes. The evertor muscles included the three peronei and extensor digitorum muscles. The ankle invertor muscles included the tibialis anterior, tibialis posterior, flexor digitorum, flexor hallucis, and extensor hallucis. Excitations of the model’s muscles were determined either by feedforward controllers or stretch feedback controllers, as described below.

Figure 1.

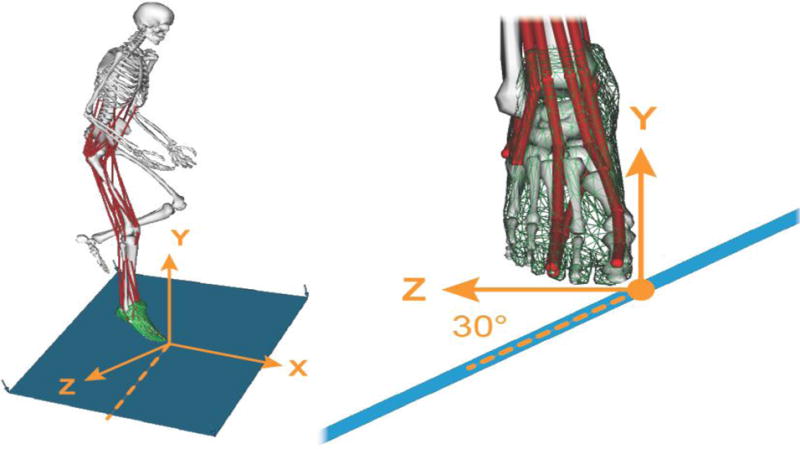
Musculoskeletal model used to simulate single-leg landings. 49 muscles (red) actuated the model’s 21 degrees of freedom in the right leg, the pelvis, and a lumped torso/head segment. The left leg was locked in the flexed pose shown. The arms were fixed in a posture anterior to the chest by locking the shoulder and elbow joints. Forces between the feet and floor were modeled as elastic foundation forces between a mesh fixed to the foot (green) and the plane of the floor (blue). We simulated landing from a 0.3 meter fall onto the floor, which was tilted at 30 degrees in the coronal plane to induce rapid ankle inversion.

To represent the landing surface, the simulation included a contact plane fixed to a platform, which could be configured to any height and orientation below the musculoskeletal model. This contact plane interacted with the feet, which were defined by a three dimensional mesh digitized from computed tomography of a cadaver foot (Erdemir et al., 2009). An elastic foundation contact model (Blankevoort et al., 1991; Sherman, 2014; Sherman et al., 2011) between the contact plane and the foot mesh generated reaction forces between the foot and floor. Contact material parameters were selected to represent rubber contacting rubber, with a shoe sole thickness of 2 centimeters. Estimated stiffness in unconstrained compression, E* (50 MPa/m), was determined from the division of the Young’s modulus of shoe blown rubber (1 MPa, Nakamura et al., 1981) by the shoe sole thickness (0.02 meters). The coefficient of friction (0.9) was the minimum required to maintain stiction between the forefoot and floor during landing. The dissipation (5 s/m) was the minimum required to maintain continuous contact without bouncing after the foot contacted the floor.

The passive mechanics measured in cadaver ankles (Chen et al., 1988; Lapointe et al., 1997; Siegler et al., 1990) were represented in the model as a three-dimensional torsional bushing. The bushing acted like a set of three uncoupled, nonlinear torsional springs between the distal tibia and the calcaneus, crossing the talocrural and subtalar joints. Cubic polynomials represented the nonlinear torque–deflection behavior about the x, y, and z axes (Figure 2). To determine the polynomial coefficients, we minimized the root-mean-squared error between the polynomials and the passive torque–angle behavior measured in cadavers (Chen et al., 1988). The bushing captured the passive response of all ligaments and soft structures that cross the ankle, excluding musculature. The root-mean-squared errors between the bushing moments and the measured moments were 0.2 N-m about the x-axis, 0.6 N-m about the y-axis, and 0.2 N-m about the z-axis.

Figure 2.

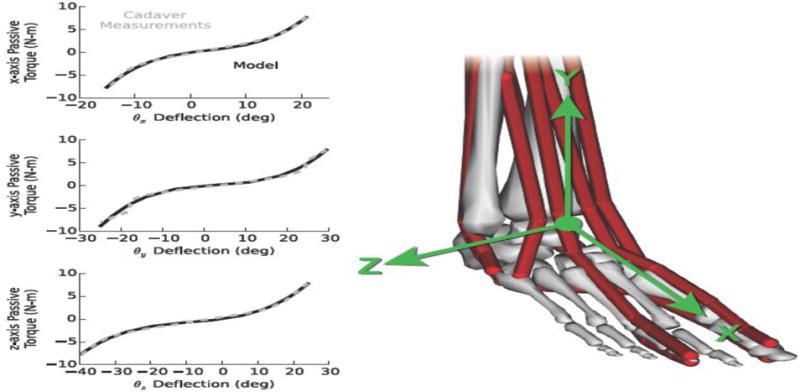
Load–deflection mechanics of passive ankle structures in the model compared to soft tissue mechanics measured in cadavers (Chen et al., 1988). The model lumped all ligament and other soft tissue loads—excluding the muscles—into a three-directional torsional bushing crossing the talocrural and subtalar joints. Load–deflection profiles about the x, y, and z axes were modeled with uncoupled, cubic polynomials and were fit to the average experimental data using least-squares error minimization.

Generating a nominal simulation of landing on level ground

We generated a nominal simulation of single-leg landing on level ground based on experimental measurements (Shultz et al., 2015). We used three-dimensional kinematics and ground reaction force data of a single subject (19-year-old female, 68 kg mass, 1.8 m height) performing five landing trials onto her right leg. Each trial began with the subject standing on a block 0.4 meters above the ground, followed by a voluntary drop onto a flat, level surface after which she landed and balanced on her right foot. All bone segments and muscle attachments of the landing model were scaled to match the segment lengths of the subject based on distances measured between markers placed on anatomical landmarks. Specifically, the three-dimensional contact mesh on the landing foot was scaled based on the distance from the most posterior point on the calcaneus to the most distal point on the first metatarsal.

We generated simulations of single-leg landing using the Forward Dynamics Tool in OpenSim (Delp et al., 2007). Simulations began at the first foot-floor contact time. Initial conditions for the joint angles and velocities were determined from the average values of the five experimental trials measured at the time of first foot–floor contact. Excitations of the torso, hip, knee, ankle plantarflexor, and ankle dorsiflexor muscles (Supplementary Table 1) were modeled with muscle stretch feedback controllers. The stretch feedback controllers excited the leg muscles prior to and during landing. The ankle evertor and invertor muscles were omitted from the stretch feedback controllers so that their control could serve as the experimental parameter that was systematically varied across the experimental conditions.

Each muscle’s stretch feedback controller computed the instantaneous muscle excitation, x_m, according to Equation 1.

$$x_m(t)=k_p{\left({\tilde{l}}_m(t)-{\tilde{l}}_m^d\right)}_{+}+k_v{\left({\tilde{\dot{l}}}_m(t)\right)}_{+}$$ (1)

The stretch feedback controllers behave like a proportional-derivative controller of the muscle’s length, where k_p is the gain on normalized muscle stretch and k_v is the gain on normalized muscle stretch velocity. Normalized muscle stretch was computed as the difference between the current normalized muscle fiber length, ${\tilde{l}}_m$, and the desired normalized muscle fiber length, ${\tilde{l}}_m^d$. Both were normalized by the optimal muscle fiber length. Normalized muscle stretch velocity, ${\tilde{\dot{l}}}_m$, was computed as the ratio of current muscle fiber lengthening velocity, ${\dot{l}}_m$, to the maximum contractile velocity of the muscle, ${\dot{l}}_m^{\mathit{max}}$. Only positive muscle stretch and velocity were considered, as indicated by the parentheses, ()₊, in Equation 1. Each muscle was assigned to one of five functional groups in which all controller parameters (k_p, k_v, ${\tilde{l}}_m^d$) were the same (Supplementary Table 1). These five groups were the torso, hip, knee, ankle plantarflexor, and ankle dorsiflexor muscles. Multiarticular muscles were assigned to the functional group corresponding to the largest average moment arm for any joints they crossed. Excitations of the ankle evertor and invertor muscles were constrained to be zero during the nominal simulation. We chose stretch feedback controller parameters with an optimization that minimized the integral of error between the simulated and experimentally measured kinematics for the first 100 milliseconds of landing after initial foot-floor contact (Supplementary Methods). The stretch feedback controller produced muscle activations that allowed the leg to flex under the influence of gravity and muscles, and reproduced the experimentally measured landing kinematics (Figure 3, average error 1.1 degrees, Supplementary Video 1). The optimization did not consider errors between simulated and measured ground reaction forces; a comparison showed that the simulated forces were larger and developed faster that experimental forces and indicate that the experimental subject and model had begun to settle towards but not yet reached static equilibrium by 100 milliseconds (Figure 3). Ground reaction forces in the transverse plane (not shown) were less than 10% of the magnitude of vertical ground reaction forces in both the simulation and the experiments.

Figure 3.

Simulated kinematics and ground reaction forces after foot contact for a 0.3-meter landing onto level ground compared to those measured from a subject executing the same landing. Hip, knee, and ankle plantar flexion kinematics of the model (black lines) evolved due to simple stretch reflexes in the torso and landing leg (right leg) and are similar to the range of kinematics measured during five experimental landing trials (gray lines). Simulated ground reaction forces were larger and peaked earlier than measured forces, indicating that the model experienced greater forces than the subject experienced.

Inducing ankle inversion in simulated landings

We perturbed the landing conditions of the nominal simulation of landing on level ground to induce rapid ankle inversion upon impact. Firstly, the subtalar joint angle and velocity at landing were set to 0 degrees and 0 degrees/second. This removed the effect of non-neutral subtalar pose at impact, which has been previously studied (Wright et al., 2000b), and isolated the current study to the effect of muscle coordination alone. The ankle angle at landing was 34 degrees of plantarflexion as observed in the experimental landing trials. Secondly, we inclined the floor to 30 degrees in the coronal plane such that the medial aspect of the landing foot impacted first, inducing a moment about the subtalar joint that rapidly inverted the ankle. This simulation scenario served as the basis for exploring coordination of the ankle evertor and invertor muscles.

Quantifying the effect of planned co-activation

We quantified the effect of planned co-activation by varying the level of co-activation of the ankle evertor and invertor muscles (Supplementary Table 1) during the 30-degree incline landing scenario. Co-activation was modeled as constant, feedforward activation of the opposing ankle evertor and invertor muscles groups, which generated zero net subtalar moment at initial ground contact. For a given co-activation level, all evertor muscles received the same activation. All invertor muscles received 93% of the evertor activations to guarantee that the net subtalar moment was zero at the neutral pose, regardless of co-activation level. We generated eleven simulations varying the level of constant, planned co-activation from 0% (no active contraction) to 100% (maximal evertor contraction and 93% invertor contraction) in 10% increments. All other parameters were held constant. The simulation began when the foot impacted the ground and proceeded for 150 milliseconds. To quantify the effects of co-activation level on ankle inversion, we observed whether the subtalar angle exceeded an injury threshold of 30 degrees based on Aydogan et al., 2006, which reported that repaired lateral ankle ligaments failed at 35±6 degrees of inversion (Figure 4, gray area).

Figure 4.

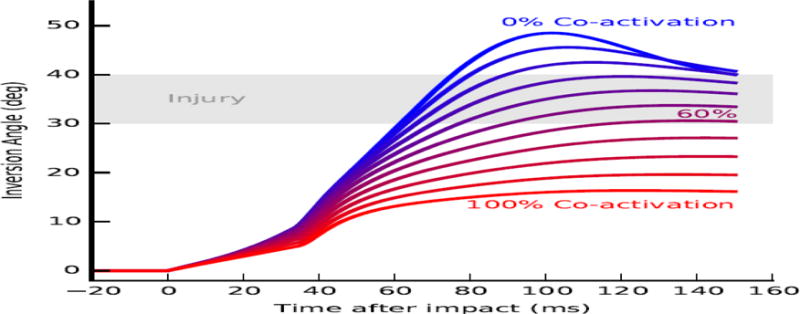
Ankle inversion trajectories immediately after impact for various levels of evertor and invertor muscle co-activation. Each contour represents excursion of the subtalar joint during a single simulation in which the evertor and invertor muscles generated force due to constant activation. Co- activation level was varied from 0% (blue) to 100% (red). Impact occurs at zero milliseconds (ms). An approximate injury threshold of 30 to 40 degrees inversion (Aydogan et al., 2006) is shown for reference (gray area).

Quantifying the effect of ankle stretch reflexes

We quantified the effect of stretch reflexes by varying the intensities of ankle evertor and invertor muscular responses to stretch during the 30-degree incline landing scenario. Evertor and invertor muscle stretch reflexes were modeled as muscle velocity controllers with a response delay. The delay represented the latency due to neural transmission delay between muscle stretch and muscle excitation, which has been measured as 60–120 milliseconds in the human peroneal muscles (Beckman and Buchanan, 1995; Karlsson and Andreasson, 1992; Konradsen and Bohsen Ravn, 1991; Vaes et al., 2002). We chose a constant delay of 60 milliseconds to test whether the fastest human evertor reflex could prevent injurious inversion angles in our simulation scenario. Each muscle’s stretch reflex controller computed the instantaneous muscle excitation according to Equation 2.

$$x_m=k_v{\left({\tilde{\dot{l}}}_m(t-0.060)\right)}_{+}$$ (2)

The stretch reflex controller behaves like a delayed derivative controller of a muscle’s normalized stretch velocity, ${\tilde{\dot{l}}}_m$, in which k_v is the gain on stretch velocity 60 milliseconds in the past. To determine the effect of reflex intensity on ankle inversion, we generated six simulations of landing on a 30-degree incline, varying only the gain, k_v. For the six simulations, k_v was set to 0.0, 0.1, 0.5, 1, 5, and 10; results for k_v > 10 are not reported since simulations with k_v = 10 and k_v = 100 generated the same kinematics. To quantify the effects of reflex intensity on ankle inversion, we observed whether the subtalar angle exceeded the injury threshold of 30 degrees based on Aydogan et al. (2006) (Figure 5, gray region).

Figure 5.

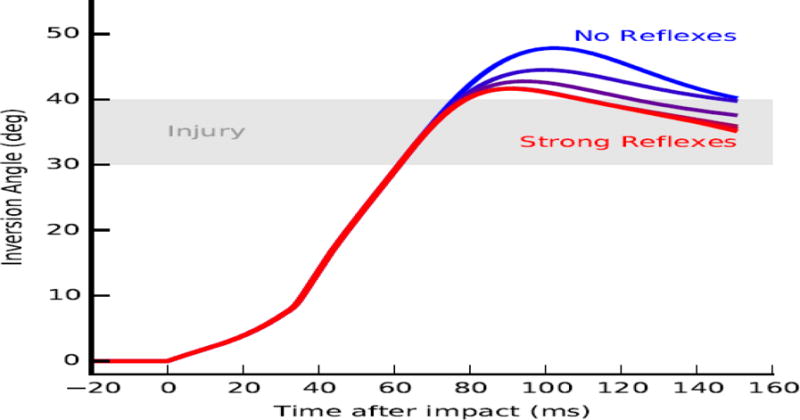
Ankle inversion trajectories immediately after impact with ankle evertor and invertor stretch reflexes of various intensities. Reflexes were modeled as feedback from the muscle lengthening speed to muscle excitations, with reflex intensity modulated using a feedback gain. Each contour represents ankle inversion angle during a single simulation in which the evertor and invertor muscles generated force with a constant reflex gain. Reflex gains were varied from 0.0 (blue) to 10 (red). Impact occurs at zero milliseconds (ms). An approximate injury threshold of 30 to 40 degrees inversion (Aydogan et al., 2006) is shown for reference (gray area).

RESULTS

Strong co-activation of the ankle evertors and invertors prior to landing prevented ankle inversion angles (positive rotations about the subtalar axis) from exceeding the injury threshold (Figure 4). Increasing co-activation level from 0% (blue) to 100% (red) decreased peak inversion angle from 49 degrees to 17 degrees. Increasing co-activation also decreased peak inversion velocity from 950 degrees/second to 550 degrees/second. Increasing simulated co-activation up to 60% increased the time to exceeding the injury threshold (gray area) from 62 to 120 milliseconds. Co-activation levels of 62% and above prevented ankle inversion from exceeding the injury threshold altogether.

Stretch reflexes of the evertors in response to landing failed to prevent excessive ankle inversion (Figure 5). For all values of the reflex gain, k_v, ranging from 0 (blue) to 10 (red), ankle inversion angles exceeded the injury threshold (grey area). Also for all values of k_v, ankle inversion angle exceeded the injury threshold quickly, within 62 milliseconds of impact. Prior to 60 milliseconds, the ankle inversion trajectories under all conditions were identical, due to the 60 millisecond reflex delay, and exhibited a peak inversion velocity of 950 degrees/second.

Co-activating the ankle evertors and invertors resulted in higher net eversion moments (Figure 6A) compared to the moments resulting from stretch reflexes in the same muscles (Figure 6B) during the first 150 milliseconds of landing. For both cases, the soleus and gastrocnemius muscles, plantarflexors that also cross the subtalar joint, generated a net inversion moment immediately after initial ground contact (Figure 6A and 6B, dashed gray lines). Co-activating the evertors and invertors at levels that protected the ankle generated large eversion moments. For example, co-activation of 70% resulted in a maximum moment of 29 Newton-meters (Figure 6A, dark gray region). Passive forces from the ankle ligaments generated small eversion moments compared to the muscle-generated moments (Figure 6A, light grey region). The superposition of muscle and ligament loads resulted in net eversion moments throughout the landing simulations for the co-activation case. Conversely, for the case of strong stretch reflexes in the ankle evertors and invertors (Figure 6B), the superposition of all muscles and ligaments generated net inversion moments until 38 milliseconds after initial ground contact. Regardless of the gain of the stretch reflex controllers, the ankle evertors and invertors produced less than 10 Newton-meter of eversion moment (Figure 6B, dark grey area) before the time of injury.

Figure 6.

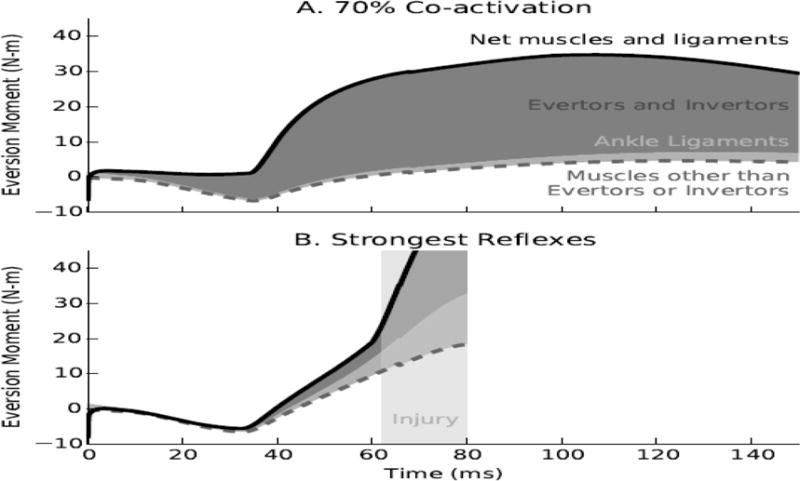
Examples of the contributions of muscles and ligaments to the protective eversion moment when adopting planned co-activation or strong stretch reflexes in the ankle evertor and invertor muscles. Co-activating the evertors and invertors at the level of 70% (panel A) generated large eversion moments (dark gray region, max. 29 Newton-meters) compared to all other muscles (dashed gray line) and the ankle ligaments (light gray region), resulting in a net eversion moment (solid black line) throughout the landing simulation. Conversely, strong reflexes in the ankle evertors and invertors (panel B, stretch velocity gain of 10, delay 60 ms) failed to generate a net eversion moment until 38 ms after landing and produced less than 10 N-m of eversion moment at the time of injury.

DISCUSSION

Our simulations suggest that co-activation of the ankle muscles prior to landing can prevent excessive inversion during an inversion-inducing landing scenario. Conversely, stretch reflexes of the evertor and invertor muscles failed to prevent excessive inversion angles because the injury occurs within 62 milliseconds in our simulated landing scenario, before reflexes generate stabilizing forces. This suggests that interventions aimed at retraining muscle coordination should target feedforward co-activation to prevent lateral ankle sprains.

Feedforward co-activation of the ankle evertor and invertor muscles protects the ankle from unanticipated inversion insults in our simulated landings. With planned co-activation of the evertors and invertors, the muscles are generating force to stiffen the ankle in preparation for the large inversion moment induced at landing. As the ankle inverts, the actively lengthening evertors and shortening invertors generate a net eversion moment that immediately resists inversion. This occurs because of the force–length–velocity property of muscle, which has a stabilizing influence (John et al., 2013), and has been called a ‘preflex’ to refer to the pre-reflex response of muscle to disturbances (Loeb et al., 1999). Experimental electromyography recordings show that individuals co-activate the ankle muscles in midair during landing tasks (Caulfield et al., 2004; Grüneberg et al., 2003). Higher co-activation generated higher joint stiffness and reduced the maximum inversion angles during our landing simulations. Wright et al. (2000a) found that passively stiffening the ankle, for example with orthoses or tape, reduced the incidence of simulated inversion injuries. Our simulations support the protective effect of ankle stiffening and demonstrate that the evertor and invertor muscles can achieve this stiffness without assistance from orthoses or tape.

Stretch reflexes, regardless of their intensity, show little capacity to protect the ankle from unanticipated inversion insults upon landing, especially when injury occurs within 60 milliseconds, as in our simulations. Our simulations demonstrate that the fastest stretch reflexes consistently recorded in healthy human evertor muscles (Calatayud et al., 2014; Vaes et al., 2002) are too slow to prevent the inversion injury posed in this study. This finding contradicts research that suggests improving peroneal reflex latency may prevent inversion injuries (Akhbari et al., 2007; Clark and Burden, 2005; Delahunt, 2007; Osborne et al., 2001; Sheth et al., 1997). Fong et al., (2013, 2012) demonstrated that a device with injury detection and external electrical stimulation could provide artificially fast peroneal contractions in under 10 milliseconds. However, our findings show that, lacking advanced feedback control devices such as Fong’s, interventions to reduce evertor latency are unlikely to prevent rapid inversion injuries.

Our simulation approach for exploring ankle inversion injuries has limitations. First, we defined an injury threshold of 30 degrees of inversion based on an experiment on repaired lateral ligaments (Aydogan et al., 2006). We chose a conservative injury threshold of 30 degrees such that a simulated injury represents the limit at which injury would likely occur in the highest-risk individuals. The injury threshold could vary in non-injured ankles and between individuals. Second, we lumped all 47 muscles of the landing leg and torso into only five groups of stretch feedback controllers (torso, hip, knee, plantarflexor, and dorsiflexor muscles). Supplementary to this study, we developed landing models using up to nine functional groups coordinating the landing leg. For both level and inclined landing conditions, adding this complexity did not affect our findings; thus, we present the simplest model here. Rigorously exploring the effects of control complexity and relative timing between muscles on ankle injuries could be a productive area of future research. Third, by using the same torso, hip, knee, and plantarflexion muscle controllers in all simulation conditions, we assumed that the landing model could not alter whole-body coordination. This assumption corresponds to rapid injury scenarios, in which the individual would not have sufficient time to change her landing posture or leg stiffness. However, altering landing posture and leg stiffness may mitigate ankle inversion injuries and could be explored in future studies. Fourth, while ankle inversion injuries occur during landing, running, change of direction, and collision, we only simulated injuries during landing on a surface inclined at 30 degrees. Other scenarios, which allow more time to adjust, may allow for reflexes to make a significant contribution to protecting the joint. It should be noted, however, that the mechanisms allowing co-activated evertors to resist inversion moments more rapidly than evertor reflexes would apply to any ankle inversion scenario. Future studies should explore the protective capacity of co-activation in a variety of ankle injury scenarios. Fifth, we could not compare our simulations to humans landing on inclined surfaces because of the risk of injuring the experimental subjects; thus, there is uncertainty in how well the simulations represent inclined landings. Finally, the model simplified the foot and toes into a single rigid mesh. The model’s rigid foot and toes likely decrease the compliance of the model and increase ground reaction forces compared to the experimental subject. Although simulated and experimental ground forces imparted similar net impulses on the foot (2% error up to the time of injury, 11% error over total simulation time), simulated forces were larger and peaked earlier than measured forces (Figure 3). Larger, earlier simulated forces are characteristic of a faster landing velocity from a higher drop compared to the experimental jumps. Therefore, the simulated landings were more severe than landings performed by the subject, supporting our finding that planned co- activation can resist intense and rapid injury scenarios. Conversely, physiologic stretch reflexes, which were too slow to prevent inversion injuries in this scenario, may be sufficient to prevent injury in slower, less intense scenarios.

Through development of a contact-based landing model and implementation of novel muscle controllers this study provides a rich platform for investigating ankle injuries and strategies for mitigating them. All models, software, and data for this study are publicly available (http://simtk.org/home/ankle-sprains) along with tutorials on their use. We encourage others to use these tools to explore other injury scenarios and protective mechanisms.