Separation of cancer cells using vortical microfluidic flows

Abstract

Label-free separation of viable cancer cells using vortical microfluidic flows has been introduced as a feasible cell collection method in oncological studies. Besides the clinical importance, the physics of particle interactions with the vortex that forms in a wall-confined geometry of a microchannel is a relatively new area of fluid dynamics. In our previous work [Haddadi and Di Carlo, J. Fluid. Mech. 811, 436–467 (2017)], we have introduced distinct aspects of inertial flow of dilute suspensions over cavities in a microchannel such as breakdown of the separatrix and formation of stable limit cycle orbits for finite size polystyrene particles. In this work, we extend our experiments to address the engineering-physics of cancer cell entrapment in microfluidic cavities. We begin by studying the effects of the channel width and device height on the morphology of the vortex, which has not been discussed in our previous work. The stable limit cycle orbits of finite size cancer cells are then presented. We demonstrate effects of the separatrix breakdown and the limit cycle formation on the operation of the cancer cell separation platform. By studying the flow of dilute cell suspensions over the cavities, we further develop the notion of the cavity capacity and the relative rate of cell accumulation as optimization criteria which connect the device geometry with the flow. Finally, we discuss the proper placement of multiple cavities inside a microchannel for improved cell entrapment.

I. INTRODUCTION

In this work, we discuss parameters that affect the performance of the microfluidic vortical flow cell separation platform. After demonstrating the feasibility of cell separation using vortices in microchannels,¹ the microfluidic vortex method has shown promising results in high efficiency,² high purity,⁴ and high throughput³ separation of viable cancer cells from healthy blood cells. In addition to clinical utility, the interaction of particles with vortices in the wall-confined geometry of microchannels is a relatively new problem in fluid dynamics. In our previous work on the inertial flow of dilute suspensions over cavities,⁵ we explained the exchange of fluid and polystyrene particles with an isolated cavity in a microchannel. Here, we study flow of cancer cell suspensions.

Circulating tumor cells, or CTCs, which detach from the tumor tissue, extravasate into blood or lymphatic vessels, disseminate and colonize in distant sites of the body, are considered the primary cause of metastasis.⁹ CTCs were observed in the blood more than a century ago.⁶ However, employing CTCs as biomarkers for cancer diagnosis, monitoring of disease progression, prediction of metastatic relapse, and drug discovery has accelerated after the development of CTC collection technologies such as CellSearch by Veridex.⁷ Collection of CTCs from a blood draw may serve as a minimally invasive replacement for direct surgical biopsy from the tumor tissue. Considering their short lifetime in the blood stream,⁸ CTCs contain real-time information about the tumor. Various methods have been developed for non-invasive collection of CTCs from blood samples. All these methods address the challenging question of rare cell separation from billions of healthy blood cells. Cote presents a thorough review of existing technologies.¹⁰ The majority of methods either use epithelial cell adhesion molecules (Ep-CAMs)⁹ or rely on physical and mechanical properties of cancer cells such as size,^1,11 density,¹² or electrical properties.¹³ The former methods are categorized as “affinity-based” and the latter as “non-affinity based” (also called “passive”) cell capture methods. Each technology, including the method we explain in this study, has advantages and disadvantages in CTC separation. For instance, affinity-based capture provides high selectivity by labeling and targeting specific cells. However, cancer cells may lose traditional epithelial markers via Epithelial-Mesenchymal Transition (EMT), which leads to low efficiency of affinity-based technologies.¹⁴ On the other hand, passive methods may not yield high purity due to the similarity of the physical and mechanical properties of cancer cells to white blood cells. Regardless, passive methods are advantageous for label-free separation of cells.

The capability of microfluidics in cell enrichment, single cell analysis, and quantitative measurement of biomarkers expanded the application of microfluidic systems to cancer diagnosis.^1,15,16 Both affinity-based and passive methods have been incorporated in microfluidic platforms. Microfluidic devices that employ filtering,¹⁷ acoustic waves,¹⁸ and hydrodynamic force^1,19 have been utilized in the liquid biopsy of cancer cells. However, the complex physics of cell separation in the wall-confined geometry of microchannels, in which the cell size can be a large fraction of the channel characteristic dimensions, has been a challenge in gaining a comprehensive engineering command of device performance. Here, we address the engineering details that govern the performance of the vortical flow CTC separation device. The platform has been previously developed and enhanced by our group.^1–4 Here, we extensively describe the engineering-physics of the vortical flow cell separation and present the details on the hydrodynamics of cell entrapment.

The remarkable feature of vortical flow CTC isolation is the entrapment of cancer cells using hydrodynamic forces alone. In general, hydrodynamic-based CTC separation methods either rely on “excluded volume” of particles in Stokes flow²¹ or inertial forces.^1,19 The trajectory of a rigid object is deflected after collision with an obstacle, primarily due to the excluded volume of objects during collision.²⁰ The trajectory deflection in Stokes flow is used for engineering the particle path by intelligent placement of micro-pillars.²¹ The separation performance of arrays can also be enhanced by surface-modification of micro-pillars with EpCAM anti-bodies to improve purity.¹⁵ Inertial microfluidic platforms use hydrodynamic lift force to direct particles to certain equilibrium locations inside the channel. Formation of the lateral lift force on particles, first observed by Segré and Silberberg in tubes, leads to margination of particles close to walls,^22,23 which also occurs in rectangular microchannels.^26,27 In a tube, the inertial migration phenomenon forms concentrated ring-like zones of particles.²⁴ In microchannels with a rectangular channel cross-section, particles migrate towards inertial equilibrium points.²⁶ Although the mechanistic details of the inertial migration phenomenon are still not clearly known, the scaling arguments relate the lateral force to the fluid velocity, channel width, and particle size.^25,26 The method of inertial focusing has been used for various microfluidic applications such as particle separation,²⁹ cell deformability analysis,³⁰ cell imaging,³¹ and fabrication of micro-particles.³² In addition to the formation of lateral lift force on particles, the vortices and wakes behind bluff bodies and surface indentations are classical features of inertial flow.³³ In the vortical flow cell separation platform, laminar vortices are the auxiliary tools for particle entrapment.

The geometrical simplicity of the vortical flow cell separation is an appealing feature for clinical translation. Despite the simple geometry, the inertial flow of “finite size” particles with diameters comparable to the channel size is a challenging problem. Even at moderate flow rates, the particle inertia is significantly large, leading to pronounced deviation of particles from flow streamlines. In our previous contribution,⁵ we discussed essential hydrodynamic aspects of the particle interaction with vortices. Using our previous explanations, here we examine the entrapment of cancer cells in the vortex. After demonstrating the feasibility of particle separation using vortices by Hur et al.,¹ the configuration and performance of the device have been improved for high-purity separation by Che⁴ and for the high-efficiency separation by Dhar.² Additionally, the clinical utility of the device for collecting CTCs from patient samples has been demonstrated by Sollier.³ The mentioned contributions elaborately discuss the practical aspects of the work such as device performance and cell viability for various cancer cell lines. However, many physical aspects of cell trapping in a size-selective manner still remain an open question. Here, we discuss the underlying physics and engineering details that govern the separation purity, efficiency, and throughput based on the fluid dynamics of cell separation. Section II outlines the scope of the work in more detail.

II. PROBLEM DESCRIPTION

We briefly explain the proposed mechanism of the particle entrapment in the vortex. We refer to our previous contribution, abbreviated as H&D hereafter, for a more detailed description of the separation mechanism. Figure 1 shows the schematics of the device geometry and directions of the coordinate system. In a more fundamental fluid dynamical representation, the cavity geometry can be considered a forward-facing step followed by a backward-facing step. The inertial flow passes through a flow expansion-contraction geometry. The abrupt deceleration of flow at the leading wall results in separation of the momentum boundary layer and formation of a vortex. At large enough Re, the longitudinal size of the vortex increases to span the entire cavity length from the leading to trailing walls. The first proposed mechanism of particle entrapment was based on the imbalance of wall-induced and velocity gradient lift forces on the particle.^1,3 The particles migrate to inertial focusing locations of the channel and equilibrate close to the walls due to the balance between the velocity gradient lift f_L and the wall lift f_W forces. Both f_L and f_W depend on the particle size. The velocity gradient and the wall lift scale with the particle diameters d as $f_L\sim d^{3–5}$^25,26 and $f_w\sim d^6$,²⁶ respectively. In the cavity expansion region, the wall lift abruptly decreases and stronger velocity gradient lift directs the particles into the vortical traps. Although this explanation can partially explain the vortical entrapment of particles, the particle acceleration is not solely affected by lateral lift forces. Due to abrupt changes in particle trajectory, the particle acceleration is affected by added mass and drag forces as well. Besides, the effect of fluid exchange with the vortex was not included in the proposed mechanism. Considering the particle inertia, one would expect that larger size particles are more likely to enter the vortical flow. Further explanation of the effect of particle acceleration on entrapment is presented in H&D.

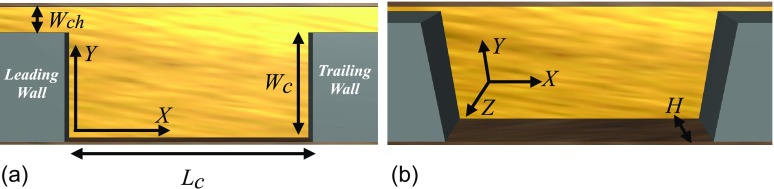
FIG. 1.

The cavity and channel configurations and directions of the coordinate system. Two views of the same device are exhibited for more clarity. The cavity length, width, and height are denoted by L_c, W_c, and H, respectively. W_ch indicates the channel width. X, Y, and Z designate the direction of the coordinate system in the flow, primary, and secondary directions of the velocity gradient, respectively. The device is bounded by walls in Y and Z directions. (a) Side view. (b) Angled view.

The main component of the vortical flow cell separation device is thus a rectangular cavity placed in a rectangular channel. In fluid dynamics, the vortex inside the cavity is termed the “flow cell” and flow over cavities is categorized as “cellular flow.” The laminar vortex inside the cavity or the “flow cell” entraps cells from a dilute suspension of cancer cells suspended in the blood or a similar suspending fluid such as Phosphate-buffer Saline (PBS). We first examine the dynamics of an isolated cell inside the flow cell. Then, we study flow of dilute cancer cell suspensions over the cavity to discuss the effect of cavity geometry, including the effects of cavity length L_c, width W_c, width of the channel connected to the cavity W_ch, and height of the device H (see Fig. 1) on the entrapment of cells. In H&D, we presented the effect of the cavity length and width, or the cavity aspect ratio $\lambda =\frac{L_c}{W_c}$, on the exchange of fluid and polystyrene particles with the flow cell. Here, we present more extended discussions on the influence of device geometry on entrapment. In addition to intrinsic properties of cells such as size, shape, and deformability, the hydrodynamic force on a cell depends on the cavity and channel size and the infusion rate of cell suspension. The effects of the device geometry and infusion flow rate (denoted by q) are represented by Reynolds number Re. We choose the average inlet velocity of the fluid $\overline{u}$ and the hydraulic diameter $h_d=\frac{2W_{c}H}{(W_c+H)}$ to define Re as $Re=\frac{\overline{u}{h}_d}{\nu }$, where ν is the kinematic viscosity of the suspending fluid.

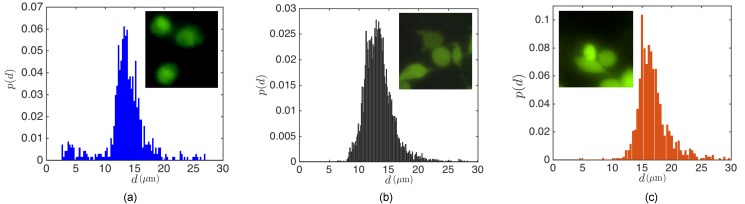
It is commonly stated that cancer cells are normally larger than other blood components. However, cell populations usually comprise a wide range of cell diameters. In Fig. 2, we demonstrate the size distributions of MDA-MB-231 GFP expressing cells (MDA) (breast cancer), human promyelocytic leukemia cells (HL60), and human prostate cancer cells (PC3) used in our study. As opposed to uniform sized polystyrene beads, the cell diameter d ranges from small $d=5\hspace{0.17em}\mu$m to large $d=30\hspace{0.17em}\mu$m cells. The size distribution and the similarity between the size of cancer cells and white blood cells lead to a trade-off between high efficiency and high purity separation. We chose MDA, PC3, and HL60 cell lines due to their nearly spherical shape. However, the morphological diversity of cells can also alter the particle dynamics and entrapment. We also point out that the size distribution of the cultured cells might be different than actual tumor cells circulating in the blood, which can vary specially during treatment of patients.²⁸

FIG. 2.

The size distribution of three cancer cell lines discussed in our study: (a) HL60, (b) MDA, and (c) PC3. It should be noted that HL60 cells normally grow in suspension and are nearly spherical in shape. However, MDA and PC3 cells grow in adhering layers but become spherical when brought into suspension.

We present our results in the following order: In Sec. IV, we discuss the breakdown of the separatrix. Then, we address the stable motion of cancer cells inside the flow cell. We explain the effect of separatrix breakdown on the entry of red blood cells and provide details of the importance of stable orbits for collecting the cancer cells. In Sec. V, we address the flow of dilute cell suspensions over cavities in order to introduce an engineering path for improving the device performance. Parameters affecting the efficiency and purity of cell separation, which have not been discussed in prior contributions, will be explained. In Sec. VI, we discuss the placement of cavities in serial configurations. We summarize our work by concluding remarks in Sec. VII.

III. EXPERIMENTAL-COMPUTATIONAL APPROACH

The microfluidic devices in this study are composed of rectangular cavities located along a straight microchannel fabricated by a standard soft lithography procedure.³⁴ We fabricated the master molds by spin coating the SU-8 photoresist (MicroChem) on a silicon substrate. The patterns are then generated by exposure through a transparency mask. The microfluidic device is produced by casting Sylgard polydimethylsiloxane (PDMS) elastomers into the master molds and curing the elastomer for 24 h in $65°$. After punching the inlets and outlets on the device using a biopsy punch, the device is enclosed by bonding on a glass slide using oxygen plasma. The device is ready to use after about 24 h of annealing.

We explain the effects of cavity length L_c using devices with the constant width and height of W_c = 310 and $H=70\hspace{0.17em}\mu$m and lengths of L_c = 930 and $1550\hspace{0.17em}\mu$m. Similar to our previous work, we denote these cavities by L₃ and L₅ (see Table I in H&D). Both L₃ and L₅ cavities are connected to a $W_{ch}=40\hspace{0.17em}\mu$m channel. By fabricating the L₃ cavity connected to W_ch = 30, 40, and $50\hspace{0.17em}\mu$m channels, we study the effect of the channel width. We fabricate the master molds of the standard L₃ cavity with two heights of H = 45 and $70\hspace{0.17em}\mu$m to study the effect of the device height.

In this work, we examine the entrapment of MDA (breast cancer), PC3 (prostate), and HL60 (leukemia) cell lines from a cell suspension. The operational procedure of the device is based on initial infusion of PBS to generate vortices, followed by infusing the cell suspension. The cell suspensions are prepared by dispersing $75–20\hspace{0.17em}000$ cells in 1 ml of PBS. The initial number of dispersed cells, denoted as $\varphi$, depends on the type of experiments. We use Harvard PHD2000 syringe pumps for liquid infusion. The cells are counted using a hemocytometer before dispersion in PBS. We monitor the cell entrapment using high-speed video-microscopy using a Phantom V2010 high-speed camera. The streamline visualizations of $d=1\hspace{0.17em}\mu$m tracers are performed using a Nikon TS100 eclipse microscope and a Phantom V2010 camera.

Here, we present a brief description of the computational parameters for lattice-Boltzmann simulations of particle flow in the system. The details of the computational method have been explained in our previous works.^5,35 The majority of the fluid flow simulations has been performed in a $X\times Y\times Z=L_c\times W_c\times H=768\times 176\times 35$ lattice unit (l.u) computational box. The box is wall-bounded in Y and Z directions and periodic in the X direction. The cavity-channel geometry is implemented by placing rectangular blocks 150 l.u away from the inlet and outlet.

IV. FLOW INSIDE THE CAVITY

First, we briefly restate the fluid flow and dynamics of isolated particles inside the flow cell presented by H&D. A characteristic feature of the cavity flow in a wall-confined geometry associated with microfluidics is exchange of fluid with the channel or separatrix breakdown. Fluid from the channel continuously spirals into the cavity, swirls inside the flow cell, and leaves towards downstream. Spiraling fluid flow does not occur for unconfined cavities at steady-state. The mass exchange mechanism with an unconfined cavity is either molecular diffusion or the “lobe-turnstile” dynamics.³³ Based on the lobe-turnstile mechanism, unsteady flow over the cavity results in fluid exchange by forming lobes on the separatrix, which is the limiting streamline on the boundary of the flow cell and the free stream. H&D demonstrated that in the wall-confined geometry of microchannels, the planar recirculating flow cell is replaced by a three-dimensional vortex. The exchange of fluid with the vortex leads to the entry and exit of small particles which follow the fluid streamlines. As opposed to tracers, large particles deviate from streamlines due to hydrodynamic forces of disturbance flow. Large particles are usually termed “finite size” considering their comparable size with the flow length scales (the channel width W_ch for instance). After entrapment in the flow cell, the finite size particles spiral toward a stable orbit close to cavity boundaries. To explain the hydrodynamic contributions on finite size particles, we used the Basset-Boussinesq-Oseen (BBO) equation of motion³⁶

$$\begin{array}{c}{m}_p\frac{d\mathit{V}}{dt}=m_f\frac{D\mathit{u}}{Dt}{|}_{\mathit{Y}(t)}-\frac{1}{2}{m}_f\frac{d}{dt}(\mathit{V}(t)-\mathit{u}[\mathit{Y}(t),t]-\frac{1}{10}{a}^2{▽}^2\mathit{u}{|}_{\mathit{Y}(t)})\\ +\mathit{f}-6\pi a\eta (\mathit{V}(t)-\mathit{u}[\mathit{Y}(t),t]-\frac{1}{6}{a}^2{▽}^2\mathit{u}{|}_{Y(t)}),\end{array}$$ (1)

where V represents the center of mass velocity of a particle located at $\mathit{Y}(t)$ at time t, and u is the undisturbed fluid velocity. The mass of the suspending fluid, the mass of the particle, and the fluid viscosity are denoted as m_f, m_p, and η, respectively. In the BBO equation, particle motion is affected by the force of the undisturbed flow and additional hydrodynamic contributions from the disturbance flow generated by the finite particle size and rigidity. The force of the undisturbed flow $m_f\frac{D\mathit{u}}{Dt}{|}_{\mathit{Y}(t)}$ would also act on a fluid element of the same size. Replacing the particle with a (deformable) fluid element at $\mathit{Y}(t)$ does not alter this force. Other terms of the BBO equation represent forces arising from the disturbance flow. An accelerating particle accelerates the fluid in the vicinity of the particle surface, which applies the “added mass” force on the particle. The second term on the right hand side of the BBO equation represents the added mass forces. The contribution of body forces f, which can be of gravitational or magnetic type in microfluidic systems, is described by the third term. The hydrodynamic stress on the surface of an object generates a drag force, which is represented by the last term on the right hand side of the BBO equation. The hydrodynamic drag appears in all examples of particle motion in fluids. The drag force depends on the difference between the particle center of mass velocity and velocity of the undisturbed flow at the particle center of mass $\mathit{V}(t)-\mathit{u}[\mathit{Y}(t),t]$. The Faxèn corrections, denoted by the Laplacian of the fluid velocity field ${▽}^2\mathit{u}$, include the hydrodynamic force generated by curvature of the fluid velocity. We mention that the Basset history force is not included in the equation considering that particle motion does not start from rest in flow over cavities. Further details of the BBO equation are explained by Maxey and Riley³⁶ and in H&D.

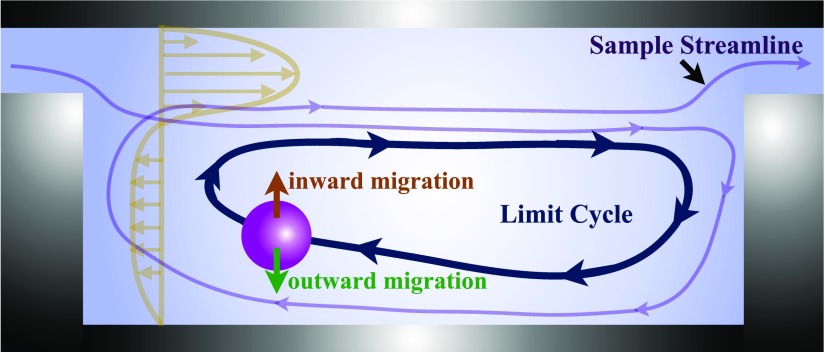
We explained that all inertial contributions to the hydrodynamic force are incorporated by a single $\frac{d\mathbf{V}}{dt}$ term in the BBO equation. The inertial forces include the lateral lift and all other contributions to the particle acceleration. For instance, in flow of particles over confined cavities, the particle acceleration is affected by the abrupt variations in the magnitude and direction of the background flow. A quantitative explanation of the separate effect of each inertial contribution is thus not possible. As a baseline description, however, we explained that the stable limit cycle trajectory forms due to the hydrodynamic forces on a finite size particle. While fluid continuously enters and leaves the cavity, the finite size particle spirals towards the flow cell boundaries. The inertial migration of particles towards the flow cell boundary is opposed by inward migration generated by the shear gradient lift force. A particle reaches the steady limit cycle orbit due to the balance between inward and outward migrations. Figure 3 schematically exhibits the continuous fluid exchange with the cavity and formation of the stable limit cycle orbit for a finite size particle.

FIG. 3.

Schematic of the continuous fluid exchange with the cavity and formation of a stable limit cycle trajectory for finite size particles. The sample streamline depicts the entry and exit of fluid from the flow cell. As opposed to the fluid, a finite size particle forms a sable limit cycle trajectory and remains inside the cavity. According to the baseline description presented by H&D, the outward migration of particles towards the flow cell boundaries is opposed by inward migration generated by the shear gradient lift force. The profile of the axial fluid velocity at an arbitrary axial location is shown in the figure.

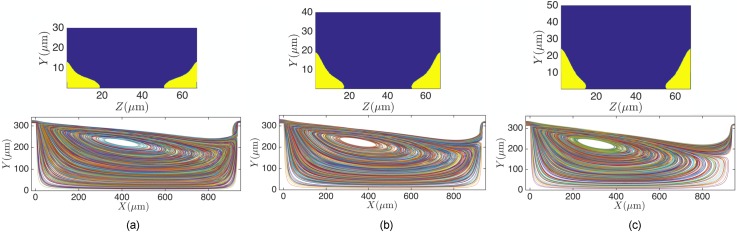
We start our discussion of fluid flow and isolated particle dynamics by presenting the effect of channel width W_ch and device height H on the vortex morphology. In H&D, we addressed the effects of cavity length L_c and width W_c on the morphology of the flow cell. At low Re, a triangular vortex forms close to the leading cavity wall and partially fills the cavity (the “incomplete” flow cell). With increasing Re, the vortex covers the entire cavity and a “complete” flow cell is generated. Here, we study variations of the vortex morphology with Re for cavities which are connected to W_ch = 30, 40, and $50\hspace{0.17em}\mu$m microchannels. Figure 4 shows streamlines visualized by fluorescent imaging of $d=1\hspace{0.17em}\mu$m tracers. We compare the vortex size at Re = 63, 123, and 216. We remind that due to the difference in the hydraulic diameter at identical Re, the flow rate q in a channel with larger W_ch is higher. Figure 4 shows that the longitudinal vortex size is invariant of W_ch for the values examined in our study. At Re = 63 and for all channel widths, an incomplete triangular vortex forms inside the cavities. Increasing Re generates a complete flow cell extending from the leading to the trailing cavity walls. With a further increase in Re, the vortex core approaches the trailing cavity wall. The longitudinal vortex size directly affects the particle entrapment. The particle capture is low inside an incomplete vortex and increases upon formation of a complete flow cell. After generation of the complete flow cell at high Re, a further increase in Re results in the reduction of the particle capture considering that inertial particles follow the stronger forward flow in the channel and pass the cavity without entrapment (extended discussion provided in Fig. 14 of H&D).

FIG. 4.

Fluorescent imaging of flow inside the L₃ cavity connected to channels with $W_{ch}=30\hspace{0.17em}\mu$m (a)–(c), $40\mu$ m (d)–(f), and $50\hspace{0.17em}\mu$m (g)–(i) at different Re using $d=1\hspace{0.17em}\mu$m tracers. Considering the difference in hydraulic diameter, the flow rates required to generate a specific Re in a wider channel is larger. Regardless of the difference between W_ch, the morphology of vortices is almost similar at identical Re. (a) W_ch = 30 μm, Re = 63, (b) W_ch = 30 μm, Re = 123, (c) W_ch = 30 μm, Re = 216, (d) W_ch = 40 μm, Re = 63, (e) W_ch = 40 μm, Re = 123, (f) W_ch = 40 μm, Re = 216, (g) W_ch = 50 μm, Re = 63, (h) W_ch = 50 μm, Re = 123, and (i) W_ch = 50 μm, Re = 216.

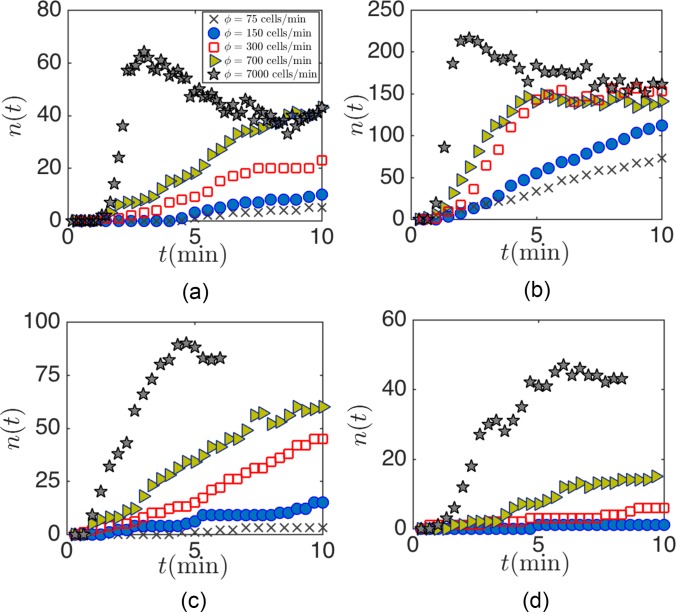
FIG. 14.

Flow of extremely dilute suspension of PC3 cells over (a) L₃, (b) L₅, (c) $W_c=460\hspace{0.17em}\mu$m, and $W_{ch}=30\hspace{0.17em}\mu$m cavities. The loading time of the cavity increases with the reduction of the number of dispersed cells $\varphi$ in the cell suspension. The cell suspensions are infused at Re_max for both cavities, i.e., Re_max = 123 and 253 for L₃ and L₅ cavities, respectively. Cavities do not reach their full capacity by infusing a very dilute $\varphi \le 300$ cells/ml suspension.

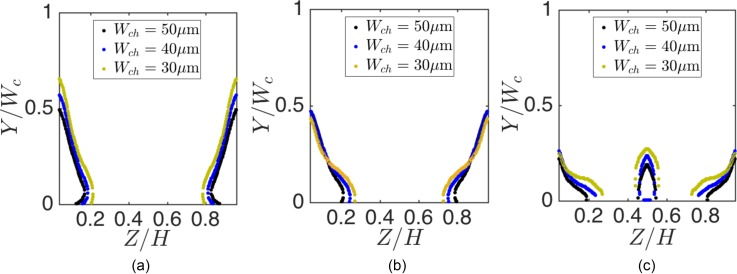
Besides the longitudinal vortex size, which is an observable morphological feature of the flow cell, continuous fluid exchange with the flow cell or the separatrix breakdown emerges in confined cellular flows. We demonstrate the separatrix breakdown for different channel widths W_ch of the L₃ cavity. In order to quantify the fluid entry, we compute the size of the streamline entry basins inside the channel using lattice-Boltzmann method (LBM) simulations. The basin size of streamlines entering the cavity is a measure of fluid exchange with the vortex. Figure 5 shows the location and size of entry basins inside W_ch = 30, 40, and $50\hspace{0.17em}\mu$m channels at Re = 123. We also show sample streamlines that spiral into the vortex. At lower Re, the entry basins appear in the vicinity of Z = 0 and $Z=H_c$ walls. With increasing Re, a secondary entry region forms around $Z=\frac{H}{2}$. Formation of the secondary basin at high Re can influence the entry of particles that are equilibrated at inertial focusing locations in the middle of the channel. In Fig. 6, we compare the size of basins for different W_ch at Re = 64, 123, and 216. With increasing W_ch, the size of streamline entry regions (as a fraction of the channel width W_ch) decreases. For all values of W_ch, increasing Re augments the entry of fluid into the flow cell.

FIG. 5.

The streamline entry basins for (a) $W_{ch}=30\hspace{0.17em}\mu$m, (b) $W_{ch}=40\hspace{0.17em}\mu$m, and (c) $W_{ch}=50\hspace{0.17em}\mu$m channels at Re = 123. The sample streamlines entering the cavity are also illustrated in the figures.

FIG. 6.

Comparing the size of entry basins at (a) Re = 64, (b) Re = 123, and (c) Re = 216. We normalized Z and Y axes using the channel height ($H=70\hspace{0.17em}\mu$m) and width, respectively. With increasing the channel width W_ch, the size of the streamline entry region reduces.

It is known that wall-confinement dissipates the momentum and injects vorticity. Decreasing the device height H generates more confinement in the channels and consequently changes the morphology of the flow cell. In Fig. 7, we present the morphologies of the flow cell for $H=45\hspace{0.17em}\mu$m cavities. Other dimensions are identical to the L₃ cavity connected to a $W_{ch}=40\hspace{0.17em}\mu$m channel. For reference, Figs. 7(d)–7(f) also display the vortex inside the $H=70\hspace{0.17em}\mu$m L₃ cavity at q = 100, 200, and $450\hspace{0.17em}\mu$l/min, corresponding to Re = 30, 63, and 123, respectively. Due to the difference in the hydraulic diameter h_d between H = 45 and $70\hspace{0.17em}\mu$m cavities, we compare the flow cells at identical flow rates q [Figs. (a)–(c)] and identical Re [Figs. (g)–(i)] with the vortices in the reference $H=70\hspace{0.17em}\mu$m cavity [Figs. (d)–(f)]. Comparisons based on the flow rate q show that the longitudinal vortex size inside the $H=45\hspace{0.17em}\mu$m is smaller; indicating that the formation of the vortex inside the $H=45\hspace{0.17em}\mu$m cavity requires higher flow rates. Similar results are observed when comparing the vortex morphologies based on Re. Therefore, the momentum dissipation of the nearby walls results in a smaller vortex size inside a cavity with lower height at a specific Re and q. Formation of the complete flow cell in a device with a lower height thus requires larger flow rates, which in turn generates large pressure drops and stress on the channel walls. Wall stress can lead to device failure and flow induced deformations in elastomeric channels,³⁷ particularly for a device with multiple serial cavities. Therefore, reducing the device height for a high-throughput process is not the preferred approach. In Sec. V, we present more details on the effect of device height H on particle entrapment.

FIG. 7.

The longitudinal flow cell size inside $H=45\hspace{0.17em}\mu$m (a)–(c); (g)–(i) and $H=70\hspace{0.17em}\mu$m (d)–(f) cavities. At identical flow rates [compare (a)–(c) and (d)–(f)] and Re [compare (g)–(i) and (d)–(f)], the longitudinal vortex size in the $H=45\hspace{0.17em}\mu$m cavity is smaller than $H=70\hspace{0.17em}\mu$m. (a) q = 100 μl/min, Re = 39, (b) q = 200 μl/min, Re = 78.

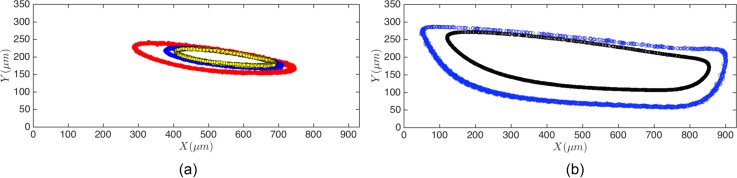
Here, we explain the dynamics of finite size cancer cells inside the vortex. The average diameter of all cell lines examined in our study is above $d\ge 10\hspace{0.17em}\mu$m, which is comparable to the channel width $\frac{d}{W_{ch}}\ge 0.3$. Due to the finite size of cells, the hydrodynamic force on cells is not negligible. The hydrodynamic force leads to migration of cancer cells towards the stable limit cycle orbits inside the cavity. Figure 8(a) displays trajectories of isolated leukemia (HL60) cells inside the flow cell. Each trajectory is obtained by isolating a single cell inside the cavity and monitoring the stable motion over a 10 min time span. We also illustrate the limit cycle orbits of d = 10 and $20\hspace{0.17em}\mu$m polystyrene particles in Fig. 8(b). We have studied the limit cycle of polystyrene particles in H&D and demonstrated that the topology of the limit cycle in a flow cell depends on the particle size and Re. Studies of the limit cycle topology at higher values of Re confirm our results for a wider range of Re.³⁸ Due to size variations in a cell population, the limit cycle topologies are not the same. For $d\ge 25\hspace{0.17em}\mu$m HL60 cells in Fig. 8(a), the limit cycle forms closer to the vortex core. Smaller cells migrate further toward a stable orbit close to the cavity walls.

FIG. 8.

The stable limit cycle trajectories of (a) HL60 leukemia cells and (b) polystyrene beads of d = 10 and $20\hspace{0.17em}\mu$m diameter at Re = 151 inside the L₃ cavity. We display the limit cycle orbit of multiple cells in a cell population. Considering that the diameter of entrapped HL60 cells is $d\ge 25\hspace{0.17em}\mu$m, the limit cycle orbits form closer to the vortex core.

We state that due to the deformability of cancer cells and irregularity in shape, the motion of cancer cells is affected by center of mass $\mathit{\alpha }$, centrifugal $\mathit{\omega }\times \mathit{\omega }\times \mathit{r}$, and azimuthal $\Omega \times \mathit{r}$ accelerations. For a non-deformable spherical object with symmetric distribution of the material around the centroid, the center of mass acceleration $\mathit{\alpha }$ represents the particle acceleration, and other contributions to the acceleration are zero. Although we observe the effect of the cell size on the limit cycle topology, we do not address the effect of the cell shape and deformability on the limit cycle topology. The effect of deformability on dynamics of particles has been computationally addressed by using the lattice-Boltzmann,^39,40 immersed boundary,⁴¹ and boundary integral⁴² methods.

Both the fluid exchange and the limit cycle formation affect the performance of the cell isolation platform. We display the effect of separatrix breakdown on the entry of small blood components and describe the practical importance of limit cycle formation. According to an inertial description for cell capture which does not consider the complexities of cell deformability, the inertial entrapment of particles is directly proportional to the particle size. The red blood cells are therefore less likely to be captured by the vortex considering that inertial forces (the lateral lift force for example) are reduced for small blood components. However, we still observe the significant entry of red cells into the cavities. Even with dilution of the blood suspension, which reduces the probability of collision-induced particle entry, red cells are still present inside the flow cell. The red blood cell entry can be attributed to the continuous fluid entry into the vortex due to separatrix breakdown. Figure 9 displays flow of a 20× dilute blood suspension over the L₅ cavity. At Re = 123 [Fig. 9(a)] and for an incomplete flow cell inside L₅ cavities, the entry of fluid is negligible, and the flow cell is depleted of small blood cells. By enhancing the fluid exchange at Re = 151 and 216, more blood components enter the flow cell. The entry of red cells can be detrimental to the device performance. Collision of captured cancer cells with red blood cells can result in particle exit and low capture efficiency.

FIG. 9.

(a)–(c) The effect of fluid mass exchange with the cavity. The consequence of fluid exchange between the flow cell and channel is the entry of red blood cells and other small components. With increasing Re, stronger swirling flow enhances the convective mass exchange between the flow cell and the channel, which leads to a more significant entry of small blood components into the cavity. The importance of the limit cycle formation for finite size particles is manifested in stable entrapment of “finite size” cancer cells inside the cavity. We utilize the stable limit cycle orbits of cancer cells to wash the cavities from smaller blood components, such as red cells and platelets, while retaining the cancer cells. In (d)–(f), we demonstrate the depletion of red cells from the device using the PBS buffer solution within less than 10 s, while maintaining prostate cells inside the flow cell for later release. Considering that the limit cycle formation ensures the stable entrapment, cancer cells remain inside the cavity as long as vortex morphology is preserved by flow of buffer solution. (a) Re = 123, (b) Re = 151, (c) Re = 216, (d) buffer wash-snapshot 1, (e) buffer wash-snapshot 2, and (f) buffer wash-snapshot 3.

Formation of the limit cycle orbit is necessary for collection of cells after entrapment. It is reminded that the limit cycle orbit forms due to particle inertia and depends on the particle size and Re. At Re = 216, the cancer cells ($d\gtrsim 10\hspace{0.17em}\mu$m) form stable orbits, while smaller red cells and platelets ($d\lesssim 10\hspace{0.17em}\mu$m) exit the cavity. The stable orbits are utilized to remove the small cells without losing the captured cancer cells. After infusing the blood suspension spiked with cancer cells, we infuse the buffer solution at an identical flow rate (the wash step). Figure 9 demonstrates that after stoppage of the suspension flow at Re = 216, small red cells and platelets leave the cavity due to continuous flow of buffer solution and larger cancer cells maintain their stable motion on the limit cycle orbit. The cancer cells are later collected by reduction of the flow rate and releasing the cells from the vortex.

V. CELL ENTRAPMENT AND THE CAVITY CAPACITY

In H&D, we introduced the notion of capacity for flow of dilute suspensions over cavities in a microchannel. We showed that after infusing the suspension, the number of particles inside the cavity increases to reach a steady-state. After the steady-state, the cavity is saturated by particles. A temporary reduction in the number of entrapped particles, which is likely caused by collision between particles, is compensated by the particle entry from the channel. Therefore, the number of particles inside the cavity fluctuates around an average value. We used the term cavity capacity for the average number of entrapped particles after saturation. We denote the cavity capacity by N_p. The cavity capacity N_p depends on the cavity size, Re, and the size of particles. The number of entrapped particles of a certain size can be maximized by changing the cavity and channel width, the cavity length, and the device height. This pool of geometric variables, combined with the infusion rate of the cell suspension, usually yields a vast parameter space for optimization. The cavity capacity can thus be used as a tool to seek the best combination of device geometry and flow rates. We observed that for a cavity with a certain size, N_p reaches a maximum at $Re=R{e}_{max}$, i.e., $N_p=n_{max}$. So, by adjusting the flow rate to yield Re_max, the particle entrapment is maximized. H&D provides an explanation for the formation of Re_max based on the collective effects of flow cell morphology and particle inertia.

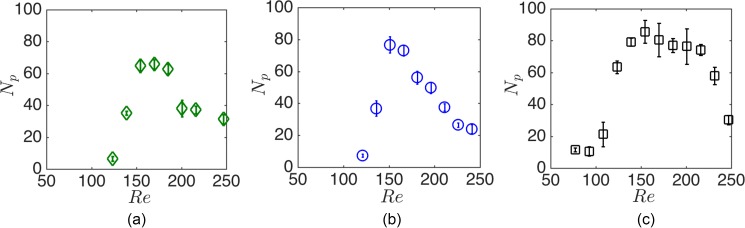
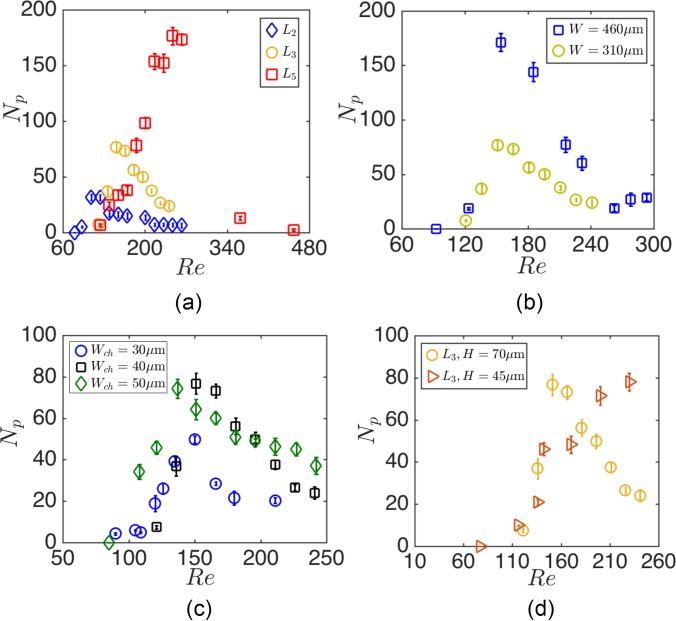
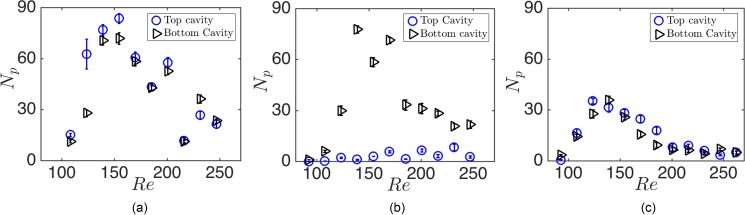
Here, we explain the cavity capacity of cancer cells and study the effects of the cavity geometry and infusion rate on maximum cell entrapment. First, we demonstrate the presence of Re_max for the entrapment of cancer cells in Fig. 10 in $100\le Re\le 310$. Due to poly-dispersity of cells, Re_max forms in a wider range of Re compared with mono-disperse polystyrene beads exhibited in H&D. The effect of the cavity and channel geometry on the capacity can thus be examined from the variations of Re_max and n_max.

FIG. 10.

The capacity of $L_c\times W_c\times H=930\times 310\times 70\hspace{0.17em}\mu$m cavities for (a) HL60 leukemia, (b) MDA-breast, and (c) PC3 prostate cancer cells lines. The average cell sizes are $⟨d⟩=13.8$, 13.4, and $16.8\hspace{0.17em}\mu$m for HL60, MDA, and PC3 cell lines, respectively. The range of maximized entrapment, i.e., Re_max, is wider for cancer cells. For larger PC3 cells, the entrapment begins at lower Re. The error bars indicate the fluctuation of the number of cells around the average value after reaching the steady state.

Figure 11 shows the effects of L_c, W_c, W_ch, and H on Re_max and n_max of MDA cells. Cell suspensions of $\varphi =20\hspace{0.17em}000$ (cells/ml) are infused, and the loading of cavities with cancer cells is monitored by high-speed video-microscopy. Experiments are performed for each cavity, and N_p at each Re is extracted from the analysis of readouts. Figure 11(a) exhibits that with increasing the cavity length L_c, both Re_max and n_max increase. We demonstrate the effect of cavity width W_c in Fig. 11(b). Increasing W_c leads to enhanced cell entrapment without a significant change of Re_max. As it is observed in Fig. 11(c), both Re_max and n_max are invariant of the channel width W_ch for W_ch = 30, 40, and $50\hspace{0.17em}\mu$m channels examined. Figure 11(d) shows the Re_max and n_max for H = 45 and $70\hspace{0.17em}\mu$m devices. Reducing the device height does not significantly change n_max. However, entrapment of an equivalent number of particles in a lower height device requires higher Re. Increasing Re inside the wall-confined channel generates large hydrodynamic stress on channel walls, which in turn resulted in repeated device failures. In our experiments, we did not increase the flow rate for the $H=45\hspace{0.17em}\mu$m device beyond $q=590\hspace{0.17em}\mu$l/min, corresponding to Re = 230.

FIG. 11.

The effect of (a) cavity length, (b) width, (c) channel width, and (d) device height on the cavity capacity at various Re. The Re is computed using the hydraulic diameter of the channel h_d and the average inlet velocity. The cavity length and width are the same ($L_c=930\hspace{0.17em}\mu$m and $W_c=310\hspace{0.17em}\mu$m) for devices with different channel width W_ch (c) and device height H (d). We also remind that L₂, L₃, and L₅ correspond to L_c = 620, 930, and $1550\hspace{0.17em}\mu$m cavities with identical widths and heights $W_c\times H=310\times 70\hspace{0.17em}\mu$m.

It should be mentioned that consideration of the cavity capacity is not enough to improve entrapment efficiency. In addition to the steady-state number of entrapped particles N_p after saturation, the time of loading to reach saturation should also be considered for improved efficiency. Slow loading is detrimental to efficient capture considering that a significant number of cells pass over the cavity without entrapment. We will discuss the entrapment of cells from extremely dilute cell suspensions later.

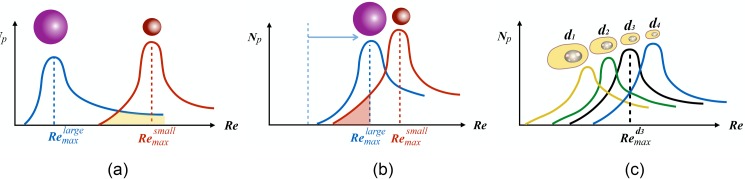
In addition to the maximum capture, the purity or the size-selectivity is an expected functionality in a cell isolation platform. Although low purity is an intrinsic feature of cell isolation systems that are based on cell size, H&D showed that vortical flow in microfluidic cavities enables size-selective entrapment of large particles in flow of a bimodal mixture of d = 10 and $20\hspace{0.17em}\mu$m polystyrene particles. The size-selectivity of particle capture is attributed to the formation of distinct Re_max for particles with different diameters. As an example for the L₃ cavities, $R{e}_{max}^{\mathit{\text{large}}}=151$ for $d=20\hspace{0.17em}\mu$m and $R{e}_{max}^{\mathit{\text{small}}}=245$ for $10\hspace{0.17em}\mu$m particles. Considering that at $R{e}_{max}^{\mathit{\text{large}}}=151$ the entry of $d=10\hspace{0.17em}\mu$m particles into the cavity is zero, only $d=20\hspace{0.17em}\mu$m particles are captured without the entry of smaller particles into the cavity. Therefore, using the L₃ cavities and by infusing the bimodal suspensions at $R{e}_{max}^{\mathit{\text{large}}}=151$, we could selectively isolate $d=20\hspace{0.17em}\mu$m particles from a bimodal mixture. Although the entry of large $d=20\hspace{0.17em}\mu$m particles diminishes at higher $Re>R{e}_{max}^{\mathit{\text{large}}}=151$, the entry of large particles does not cease. Therefore, a similar level of purity cannot be achieved if separation of $d=10\hspace{0.17em}\mu$m from the bimodal suspension is intended. At $R{e}_{max}^{\mathit{\text{small}}}$, both small and large particles are captured even though the entrapment of smaller cells is more probable at higher Re.³⁸ The schematic of Fig. 12 illustrates that the purity of small particle separation diminishes due to the overlap between the cavity capacities for small and large particles. Despite the increase in the number of entrapped particles in a long cavity, H&D showed that the larger overlap between capacities results in the reduction of entrapment purity in cavities with longer L_c [Fig. 12(b)]. Figure 12(c) schematically illustrates that due to the overlap between the capacities of large and small cells in a cell population, adjusting the infusion Re at R_max for a certain size also results in the entrapment of other cells with different diameters.

FIG. 12.

Schematic of how entrapment purity for inertial flow of suspensions over cavities can be estimated from cavity capacity curves: (a) based on the formation of distinct Re_max for small and large particles; the separation of large particles from a bimodal mixture is easily achievable. The overlap between capacities indicates that purity of entrapment may diminish for separation of small particles. (b) With the increasing cavity length, the overlap between capacities increases, which would suggest a reduction of capture purity. However, the number of entrapped particles in a long cavity is larger than a cavity with smaller length; (c) the purity of cell separation is negatively affected by poly-dispersity considering the significance of overlap between capacities for each cell present in the cell population.

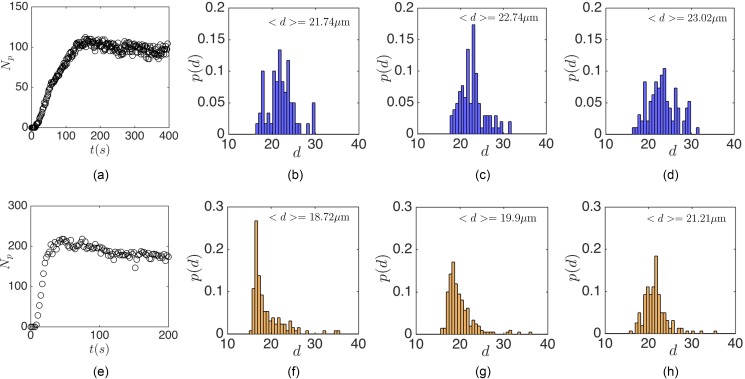
Figures 13(b)–13(d) plot the size distribution of entrapped MDA cells inside the L₃ cavity at three time points of $t_1=71,\hspace{0.17em}{t}_2=150$, and $t_3=393$(s) after infusing the cell suspension at Re_max = 151. Time points are arbitrarily chosen to indicate different stages of the cell loading. So, $t_1=71$(s) corresponds to the early stages of infusion, $t_2=150$(s) to the time of reaching the maximum capacity, and $t_3=393$(s) to long times after reaching the steady-state. Considering that at early stages the number of entrapped cells is low, $t_1=71$ is chosen after entrapment of at least N_p = 50 cells in order to obtain accurate histograms for size distributions. To attribute t to the stages of cell loading, Fig. 13(a) shows the time-dependent number of cells N_p inside the flow cell. Although the average size of MDA cells in a population is $⟨d⟩\simeq 13\hspace{0.17em}\mu$m, the average diameter of entrapped cells is larger than the average population size $⟨d{⟩}^{\mathit{\text{captured}}}\ge 21.74\hspace{0.17em}\mu$m. The capture in L₃ cavities always favors larger cells. The capture of large cells inside the cavity can be explained based on the non-zero probability of large particle capture in all flow rates [see Fig. 12(a)]. By adjusting the device operating Re at Re_o = Re_max for a specific cell size, larger cells with $R{e}^{max}<R{e}_o$ also enter the cavity. The entrapment of large cells may prevent smaller cells from entry by occupying the cavity to the maximum loading capacity. Besides, the collision-induced deviation from the limit cycle results in depletion of the cavity from smaller cells. Depletion of the cavity of smaller cells in long infusion times can be more clearly observed in the L₅ cavity. We show the size distribution of entrapped cells by infusing MDA cells over the L₅ cavity at Re_max = 290. Similarly, Fig. 13(e) shows that at t = 19(s) and due to the presence of small cells, the average diameter of captured cells is $⟨d⟩=18.72\hspace{0.17em}\mu$m. At later stages of infusion, the cavity is occupied only by $d\gtrsim 20\hspace{0.17em}\mu$m cells. It can be concluded that entrapment inside the cavity favors the larger cells in a cell population. Even if smaller cells are captured at initial stages, larger cells occupy the cavity at longer infusion times.

FIG. 13.

The size distribution of MDA cells entrapped inside (a)–(d) L₃ and (e)–(h) L₅ cavities. (a) and (e) display the loading stage of cavities until reaching the steady-state. Cell suspensions are infused at Re_max. At the early stages of infusion and due to the presence of cells with various sizes in the suspension, both small and large cells are entrapped inside the cavities. However, large cells occupy the cavity at later stages. (a) N_p-time, (b) t = 71 (s), (c) t = 150 (s), (d) t = 393 (s), (e) N_p-time, (f) t = 19 (s), (g) t = 46 (s), and (h) t = 198 (s).

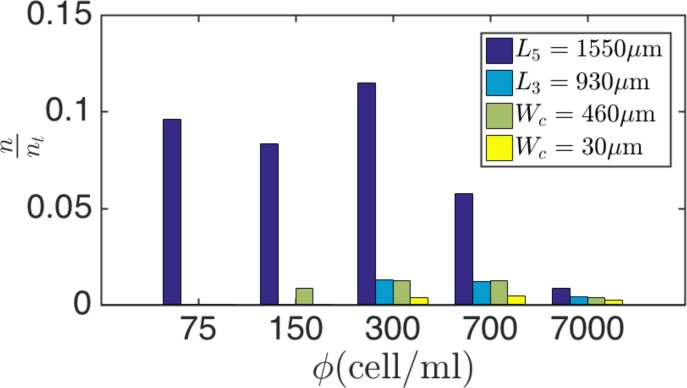
Our studies of the cavity capacity are based on infusion of a relatively dilute cell suspension of $\varphi =20\hspace{0.17em}000$ cells/ml. Although the precise number of CTCs in a background of healthy blood cells is not clearly known, tumor cells are rare compared to billions of red and millions of white blood cells. It is expected that cavities operate under the “starved” condition without reaching n_max in a practical time span. Here, we examine the performance of cavities for extremely dilute cell suspensions ($\varphi <1000$ cells/ml) and explain the consequence of CTC rarity on entrapment. We begin by studying the loading rate of cavities for dilute cell suspensions of $\varphi =75$, 150, 300, 700, and 7000 cells/ml at Re_max. The high rate of cavity loading is particularly important for efficient capture before cells pass the cavity and flow downstream.

Figure 14 exhibits loading of the L₃ (a), L₅ (b), $W_c=460\hspace{0.17em}\mu$m (c), and $W_{ch}=30\hspace{0.17em}\mu$m (d) cavities after infusing dilute PC3 cell suspensions. The cell suspensions are infused at Re_max of each cavity. The rate of cavity loading is lower for smaller $\varphi$. To compare the effects of cavity length L_c on capture from a dilute suspension, we study the percentage of captured cells for $\varphi \le 7000$ cells/ml within t = 4 min of suspension infusion. It is reminded that Re_max is different for each cavity. For instance, Re_max = 145 and 216 for L₃ and L₅ cavities mean higher infusion rates of 450 and $800\hspace{0.17em}\mu$l/min to reach Re_max for L₃ and L₅ cavities, respectively. The larger infusion rate consequently leads to an increase in the total infused cells and possible cell waste. To add more details, Fig. 15 exhibits the fraction of captured cells with respect to the total number of infused cells at Re_max. Regardless, the L₅ cavity captures a significantly larger percentage of cells. We also point out that reaching the maximum capacity is detrimental to the overall efficiency. After reaching the capacity, the average number of cells inside the cavity does not increase and the infused cells leave the device without entrapment. Based on our discussion and using the cavity loading rates and capacity, increasing the length is one possible way of reaching the enhanced entrapment.

FIG. 15.

Ratio of entrapped PC3 cells to the total cells infused after t = 4 min of cell infusion. Increasing the cavity length significantly enhances the entrapment. Although the higher flow rate of cell infusion for L₅ cavities leads to higher possibility of cell waste, the high rate of entrapment improves the overall entrapment.

VI. SERIALIZING CAVITIES

The overall device throughput can be increased by placing multiple cavities along each microchannel. However, serial placement of multiple cavities in close proximity to one another can result in non-uniform capture in the cavities. Repeated expansion and contraction of the flow above the cavities modulates the profile of fluid velocity away from the parabolic flow in a long straight channel. This in turn reduces the shear-gradient lift forces that direct particles toward the channel walls and maintain stable limit cycles inside the flow cell. Serial placement therefore necessitates considering sufficient length for restoration of the fluid velocity profile and positioning of particles near basins of entry into the flow cell before flowing over other downstream cavities. Here, we study the serial placement of cavities in each microchannel to address the effect of the distance between cavities on cell entrapment. To obtain the best distance between cavities, we observe the flow streamlines and measure the cavity capacities for three possible configurations. The configurations are designed based on the axial distance $\Delta x$ between two $L_3=930\hspace{0.17em}\mu$m cavities. We define $\Delta x$ as the axial distance between cavity centers. Therefore, ${\Delta }_x=0$ specifies the mirrored placement of cavities in the channel. Figure 16 exhibits the cavity placement possibilities. The first configuration is actually a rectangular expansion in the channel generated by placing two cavities with $\Delta x=0$. In the second configuration, the centers of cavities are $\Delta x=L_c$ apart. In the third configuration, the cavities are located with $\Delta x=2L_c$ axial separation.

FIG. 16.

Visualization of the flow in (a)–(c) $\Delta x=0$, (d)–(f) $\Delta x=L_c$, and (g)–(i) $\Delta x=2L_c$ configurations. The streamlines are visualized using fluorescent imaging of $d=1\mu$m fluorescent particles at Re = 63, 154, and 216. Considering that the morphology of the flow cells in each cavity for $\Delta x=2L_c$ configuration is identical to an isolated L₃ cavity, we demonstrate the flow cell inside one cavity. (a) Re = 63, (b) Re = 154, (c) Re = 216, (d) Re = 63, (e) Re = 154, (f) Re = 216, (g) Re = 63, (h) Re = 154, and (i) Re = 216.

First, we study the flow streamlines for different configurations. For $\Delta x=0$ and $\Delta x=2L_c$, the streamlines are symmetric and similar to an isolated cavity at identical Re. At Re = 61, an incomplete flow cell forms in both cavities and the longitudinal vortex size is identical to an isolated cavity at Re = 61. Similarly, the vortices at Re = 154 and 216 are morphologically similar to an isolated cavity. As opposed to $\Delta x=0$ and $\Delta x=2L_c$, the vortex morphologies are not similar in the first and second cavities of the $\Delta x=L_c$ configuration. We study the entrapment of cells by infusing a $\varphi =20\hspace{0.17em}000$ cells/ml PC3 cell suspension. The results are shown in Fig. 16. For the $\Delta x=0$ configuration, the number of entrapped particles in both cavities is equal. However, the cell entrapment in the $\Delta x=0$ configuration is lower than the actual capacity of an isolated L₃ cavity ($n_{max}\simeq 30$ versus $n_{max}\simeq 80$). The lower entrapment in the cavities of the $\Delta x=0$ configuration can be attributed to the reduction of the shear-gradient velocity gradient in a wider symmetric expansion of the $\Delta x=0$ configuration, compared to an isolated cavity. For the $\Delta x=L_c$ configuration, the first cavity captures more cells, and the second cavity remains depleted. The low entrapment in the second cavity may arise from asymmetry of vortices and the absence of enough restoration length between the cavities. The restoration distance is required to re-establish a parabolic profile in the channel, which leads to a maximal shear-gradient in the velocity field yielding shear-gradient lift forces that direct particles towards the wall and maintain them within limit cycles in the cavity. The cavities that are placed $\Delta x=2L_c$ apart entrap particles symmetrically, and the number of captured cells in each cavity is identical to an isolated cavity. The length of $\Delta x=2L_c$ between cavities provides enough distance for restoration of the fluid velocity profile and also the particle trajectory (Fig. 17).

FIG. 17.

The number of PC3 cells entrapped in each cavity for $\Delta x=2L_c$ (a), $\Delta x=0$, (b) and $\Delta x=L_c$ (c) configurations at Re_max. Considering a trajectory restoration distance is required to improve the efficiency in cavities placed serially inside the straight channel.

VII. CONCLUDING REMARKS

In this work, we used microfluidic experiments and LBM simulations to address the entrapment of cancer cells in the vortical flows inside microfluidic cavities. Based on the previous insights we obtained by studying flow of dilute suspensions of polystyrene beads over the cavities,⁵ we developed guidelines for improving the efficiency of vortical flow cell separation platforms. We summarize our observations in the following:

• (a)The distinction between a cavity in the wall-bounded geometry of a microchannel and an open cavity in unbounded flows is the absence of the separatrix. The flow cell in a confined cavity is not an isolated zone of “recirculating” flow. Rather, spiraling flow streams continuously convey the fluid into a three-dimensional vortex. The separatrix breakdown provides an answer to previous observations of the entry of red blood cells into the cavity. Knowing that the red cells are small and almost unaffected by the lateral lift forces and other contributions to particle acceleration, the entry of red blood cells even at significant blood dilution is caused by the fluid entry and breakdown of the separatrix.
• (b)Finite size cancer cells are affected by hydrodynamic forces of disturbance flow. Besides hydrodynamic drag, the inertial flow generates additional acceleration forces on the particle. However, the inertial accelerations, such as inertial lift or forces due to the change in the magnitude or direction of the background flow, are not included in the Basset-Boussinesq-Oseen equation of motion. A single $\frac{d\mathbf{V}}{dt}$ term represents the collective effects of particle accelerations. Therefore, by considering the collective effect of inertial accelerations, we showed that a finite size cancer cell forms a stable limit cycle orbit inside the flow cell. The formation of the stable orbit is an inertial phenomenon and depends on Re and particle size (or particle scale inertia Re_p as discussed in H&D⁵). The limit cycle formation is crucial for the stable entrapment of particles. Without a limit cycle, which is actually a trajectory attractor, particles exit the cavity.
• (c)Regardless of the geometrical simplicity of the vortical flow cell isolation platform, the combinatorial space of geometry and flow comprises various parameters. We introduced the notion of cavity capacity: a cavity can only entrap a certain number of particles. The main feature of the cavity capacity is the formation of a maximum at Re_max, at which the number of entrapped cells is maximized, which then can be used to explore the combination of flow and geometric variations of the cavity for reaching the best design.
• (d)The particle entrapment in a cavity always favors the larger particles in a cell population. In that sense, the cavity is actually size selective. Although the purity of the capture might be low for capturing cells with diameters close to white blood cells ($d\simeq 15\hspace{0.17em}\mu$m), the size-selective capture of large cells ($d\ge 20\hspace{0.17em}\mu$m) is accurately feasible.
• (e)Generally, all CTC separation platforms collect rare cancer cells from a background of blood cells. We demonstrated that increasing the cavity length provides a significant improvement in capture efficiency for dilute cell suspensions.
• (f)Increasing throughput by placing cavities in serial or parallel configurations has been utilized in prior works on this subject.^2–4 For serial placements, uniform entrapment in each cavity can be achieved by considering a fluid velocity and trajectory restoration distance between the cavities.

Finally, we emphasize that the vortical flow cell separation is an appealing platform for clinical translation of microfluidic systems. We examined key parameters affecting the cell entrapment in flow cells. However, the path for devising further optimization methods is open.