Unsupervised trajectory analysis of single-cell RNA-seq and imaging data reveals alternate tuft cell origins in the gut

Summary

Modern single-cell technologies allow multiplexed sampling of cellular states within a tissue. However, computational tools that can infer developmental cell-state transitions reproducibly from such single-cell data are lacking. Here, we introduce p-Creode, an unsupervised algorithm that produces multi-branching graphs from single-cell data, compares graphs with differing topologies, and infers a statistically robust hierarchy of cell-state transitions that define developmental trajectories. We have applied p-Creode to mass cytometry, multiplex immunofluorescence, and single-cell RNA-seq data. As a test case, we validate cell state-transition trajectories predicted by p-Creode for intestinal tuft cells, a rare, chemosensory cell type. We clarify that tuft cells are specified outside of the Atoh1-dependent secretory lineage in the small intestine. However, p-Creode also predicts, and we confirm, that tuft cells arise from an alternative, Atoh1-driven developmental program in the colon. These studies introduce p-Creode as a reliable method for analyzing large datasets that depict branching transition trajectories. p-Creode is publicly available for download here: https://github.com/KenLauLab/pCreode.

eTOC Blurb

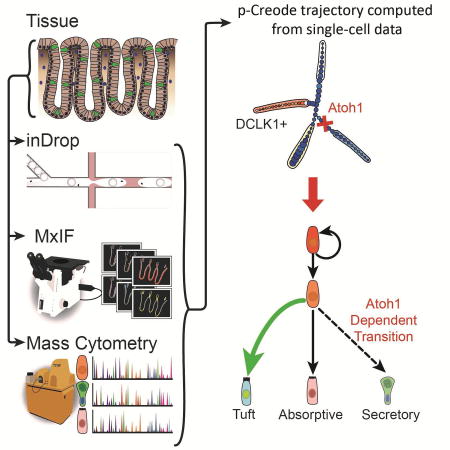
Herring et al. developed an unsupervised algorithm to map single-cell RNA-seq, imaging, and mass cytometry onto multi-branching transitional trajectories. This approach identified alternative origins of tuft cells, a specialized chemosensory cell in the gut, between the small intestine and the colon.

Introduction

Multi-cellular organ function emerges from heterogeneous collectives of individual cells with distinct phenotypes and behaviors. Integral to understanding organ function are the different routes from which distinct cell types arise. Multipotent cells transition towards mature states through continuous, intermediary steps with increasingly restricted access to other cell states (Waddington, 1957). A stem cell can be identified by lineage tracing, a method whereby continuous generation and differentiation of cells from a labeled source results in permanently labeled organ units (Barker et al., 2007). Seminal studies have determined the relationship between stem and differentiated cells by focusing on the effects of genetic and epigenetic perturbations on terminal cell states (Noah et al., 2011). While the behaviors of intermediate states such as progenitor cells remain to be fully elucidated, modern single-cell technologies have enabled the interrogation of transitional cell states that contain information regarding branching cell fate decisions across entire developmental continuums (Gerdes et al., 2013; Giesen et al., 2014; Grün et al., 2015; Klein et al., 2015; Paul et al., 2015; Simmons et al., 2016; Treutlein et al., 2014). Despite experimental tools to generate data at single-cell resolution, resolving cellular relationships from large volumes of data remains a challenge.

Various computational approaches have been developed for tracking cell transition trajectories when temporal datasets are available (Marco et al., 2014; Zunder et al., 2015). However, for most adult and human tissues, in vivo cell transitions have to be inferred from data collected at a snapshot in time. A major push in the field of single-cell biology is to enable data-driven arrangement of cell states into pseudo-progression trajectories to infer cellular transitions. These algorithms fall broadly into two categories: Minimum Spanning Tree (MST)-based approaches (Anchang et al., 2016; Ji and Ji, 2016; Qiu et al., 2011; Shin et al., 2015; Trapnell et al., 2014) and non-linear data-embedding approaches (Haghverdi et al., 2015; Welch et al., 2016). MST algorithms are widely known to be unstable with large datasets, such that multiple distinct solutions are obtained given the same dataset (Giecold et al., 2016). MST algorithms also tend to overfit smaller datasets, producing topologies with superfluous branches (Setty et al., 2016; Zunder et al., 2015). While MST-based tools have shown utility when applied to well-defined systems such as hematopoiesis, they do not provide a direct means to assess solutions for determining the correct topologies of less-defined systems. Non-linear embedding algorithms, such as Diffusion Map, are sensitive to the distribution of data such that local resolution may be gained or lost. Thus, they are largely used for depicting simple topologies that can be derived from the largest variation in the data, with less emphasis on sub-branches (Haghverdi et al., 2015; Setty et al., 2016; Welch et al., 2016). While a large amount of effort has focused on visualization strategies (Zunder et al., 2015), solutions to statistically assess computed results remain to be developed and formalized. A class of algorithms developed by Dana Pe’er’s group using supervised-random walk over a cellular network produce robust results that can be statistically scored (Bendall et al., 2014; Setty et al., 2016). The most recent advance, named Wishbone, can identify bifurcations in a topology, but is limited to cases with a single, known branch point (Setty et al., 2016). There is a paucity of data-driven, unsupervised approaches that generate cell transition hierarchies de novo to map multiple branching decisions in a statistically verifiable way.

Tuft cells, also known as brush or caveolated cells, in the gut are a rare population of chemosensory cells that remains poorly understood (Gerbe and Jay, 2016). They originate from epithelial stem cells (Gerbe et al., 2011), and express taste receptors such as α-gustducin (Höfer et al., 1996) and TRPM5 (Bezençon et al., 2007, 2008; Höfer et al., 1996), which implicate their function in chemoreception similar to lingual taste cells. Recently, a number of important studies have demonstrated their role in immune responses against helminth infection by establishing an IL25-IL13 circuit with innate lymphoid cells type 2 (ILC2s) (Gerbe et al., 2016; Howitt et al., 2016; von Moltke et al., 2015). Thus, understanding the development of tuft cells is important in intestinal disease contexts. Tuft cells are commonly thought to be specified from the secretory lineage (Gerbe et al., 2011) along with goblet, Paneth, and enteroendocrine cells (VanDussen et al., 2012), although their origins have recently been disputed (Bjerknes et al., 2012).

We sought to clarify the lineage origin of tuft cells with single-cell analysis. We present p-Creode, a novel algorithm to derive multi-branching transition trajectories with a unique method to statistically score each result. After rigorous validation of p-Creode, we used this tool, along with validation experiments in the mouse, to demonstrate that tuft cells may be specified outside the Atoh1-dependent secretory lineage in the small intestine, but are regulated by Atoh1 in the colon. Our findings highlight important physiological differences between the small intestine and the colon, which directly impact the development and function of tuft cells in these two anatomically distinct regions.

Results

p-Creode maps synthetic single-cell data into the correct trajectories

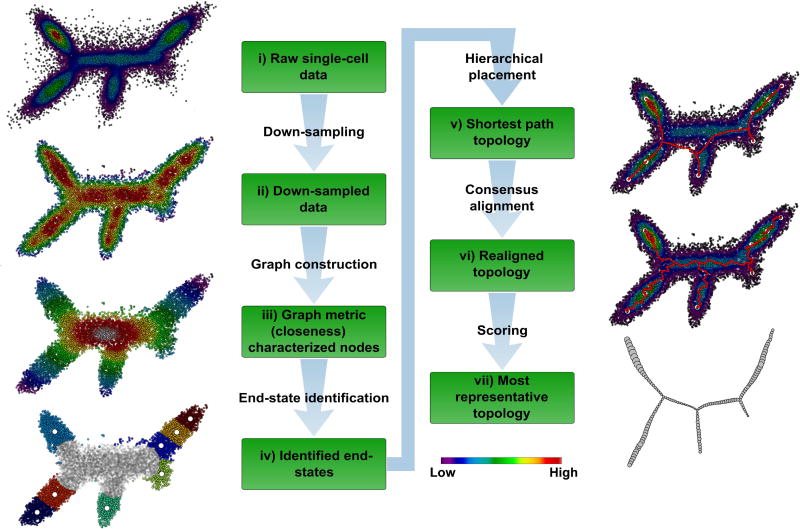
The term creode was coined by C.H. Waddington, combining the Greek words for “necessary” and “path” (Waddington, 1957) to describe the transition trajectories that define cell fate specification. Our algorithm aims to identify consensus routes from relatively noisy single-cell data and thus we named this algorithm p- (putative) Creode. Conceptually, p-Creode determines the geometric shape of a collection of dense data points (i.e., a data cloud) in order to reveal the underlying structure of transitional routes. Similar to other pseudo-progression analyses, this algorithm assumes a continuous transition process. In addition, a dense dataset (on the order of thousands of cells) is required to capture switch-like transitions. We created a synthetic, single-cell dataset in two-dimensional space that recapitulates a multi-branch hierarchy (five end-states, three branch-points) with realistic noise (Figure 1). We then developed and applied p-Creode on this visually and analytically tractable dataset to identify the five end-states and three branch-points.

Figure 1. The p-Creode algorithm for analyzing single-cell data.

(i) Synthetic dataset representing single cells in two-dimensional expression space with five end-states and three branch points. Overlay represents density of cells. (ii) Density-normalized representation of the original dataset from down-sampling. Overlay represents the density after down-sampling. (iii) Density-based k-nearest neighbor (d-kNN) network constructed from down-sampled data. Overlay represents the graph measure of closeness centrality derived from the d-kNN network, which is a surrogate for cell state (low – end-state, high – transition state). (iv) End-states identified by K-means clustering and silhouette scoring of cells with low closeness values (<mean). The number of end-state clusters is doubled to allow for rare cell types. End-state clusters are colored, and open circles represent the centroid per cluster. (v) Topology constructed with a hierarchical placement strategy of cells on path nodes between end-states (red), which allows for the placement of data points along an ancestral continuum. Overlay represents the original density of cells. (vi) Aligned topology (red) with maximal consensus though iterative assignment and repositioning of path nodes using neighborhood cell densities. (vii) Representative topology extracted using p-Creode scoring from an ensemble of N topologies. Node size in the output graph represents the original density of cells. See also Figure S1–S3.

The p-Creode algorithm consists of six steps (Figure 1, for details of each step, see STAR Methods). Specifically novel are: a) our strategy to automatically identify end-states (stem or differentiated cell states) using the graph attribute closeness centrality, b) our hierarchical placement strategy to place data points on branches instead of leaves of a tree to depict ancestral relationships, and c) our strategy to leverage ensembles of N resampled topologies with a Gromov–Hausdorff-inspired scoring metric, called the p-Creode score, to depict the relative robustness of data in supporting the final computed topology (Figure S2). This newly developed metric has general applicability outside of p-Creode to assess graphs with simultaneously differing node positions and connections. The validity of the p-Creode score is demonstrated in Figure S3. The topology most representative of the ensemble is selected based on this metric.

p-Creode produces accurate and precise multi-branching trajectories of hematopoiesis

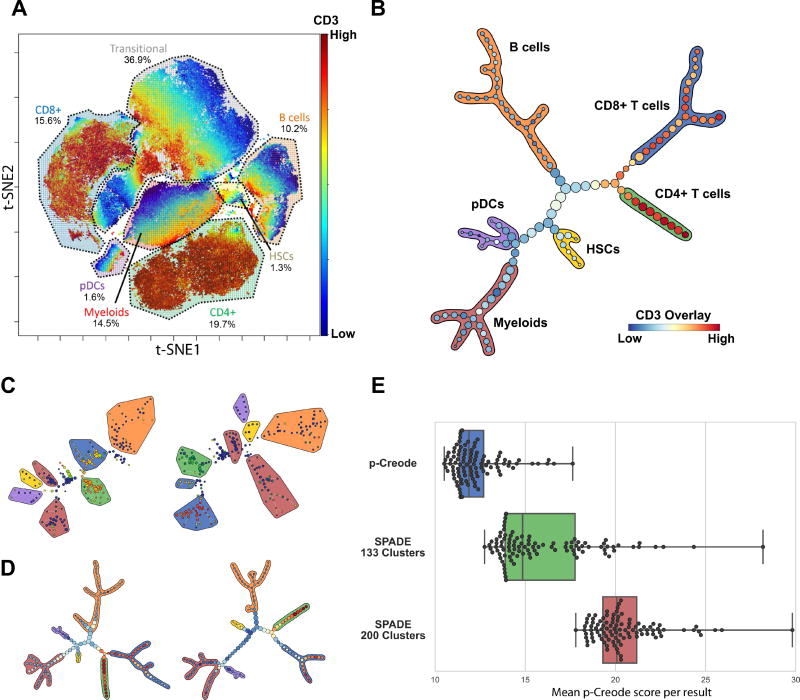
We applied p-Creode to publicly available mass cytometry data generated from normal human bone marrow (Bendall et al., 2011), as the well-defined process of hematopoiesis usually serves as a first litmus test for pseudo-progression analysis algorithms. The mass cytometry dataset is composed of approximately 240,000 cells evaluated by a reagent panel of 13 cell-surface markers that describes hematopoietic differentiation (CD45, CD45RA, CD19, CD11b, CD4, CD8, CD34, CD20, CD33, CD123, CD38, CD90, CD3). t-Distributed Stochastic Neighbor Embedding (t-SNE) (van der Maaten et al., 2011) and manual gating revealed several groupings of well-known cell types (Figure 2A). A large portion of cells remained unidentified, as previously described (Amir et al., 2013), which we considered to be potential transitional cell states.

Figure 2. p-Creode analysis of single-cell mass cytometry data identifies the hematopoietic differentiation hierarchy.

(A) t-SNE analysis of a 13-marker panel mass cytometry dataset from Bendall et al. Cell types, as defined by clusters on the t-SNE map, were manually annotated. Overlay represents CD3 levels. (B) p-Creode analysis of the same dataset in A. The most representative graph over N=100 runs, as defined by the graph with the minimum p-Creode score when compared to all graphs in the analysis, is represented. Colored outlines indicate cell types defined in A, and overlay indicates CD3 levels. (C) Two random runs of the same dataset in A using SPADE (200 nodes), with the same color scheme for cell types and overlay in B. (D) Two random runs (N=100) of the same dataset in A using p-Creode, with the same color scheme for cell types and overlay in B. (E) Comparison of the robustness of p-Creode, SPADE run with 133 nodes, and SPADE run with 200 nodes. Each data point represents the mean p-Creode score calculated for each resulting graph (N=100). Boxes show the quartiles while whiskers show the minimum and maximum scores. See also Figure S4–S5.

Application of p-Creode on this dataset (N=100) generated topologies that correctly delineated the known hematopoietic differentiation hierarchy (Miyazaki et al., 2014), with HSCs giving rise to myeloid and lymphoid progenitor trajectories, lymphoid cells transitioning into CD3+ T cells and CD19+ B cells, and CD3+ T cells further branching into CD4+ helper T cells and CD8+ cytotoxic T cells (Figure 2B, Figure S4). We then compared our results to a MST-based algorithm, SPADE, which grouped similar cells into populations, but the transitions inferred by the MST connecting these populations were inconsistent with known hematopoietic differentiation (Figure 2C, Figure S5A). For example, MST-defined topologies placed CD8+ T cells as a transitional cell type in the B cell trajectory (Figure 2C - left), and, in another instance, T lymphocytes and myeloid cells shared a common trajectory (Figure 2C - right). These results demonstrate the utility of p-Creode in generating accurate results for inferring cellular hierarchies from single-cell data.

To assess the precision of the p-Creode algorithm, we evaluated whether resampled runs generate quantitatively similar topologies. Hematopoietic differentiation in the normal bone marrow is a relatively well-regulated process, and thus we expect to extract a conserved topology with multiple runs on the same dataset. We leveraged data down-sampling to produce resampled runs on both SPADE and p-Creode (Figure 2C–D, Figure S5). In general, p-Creode generated topologies consisting of 133 nodes, and we compared its performance with SPADE, first also at 133 nodes (clusters), and then at 200 nodes corresponding to the default SPADE setting at Cytobank.org and the published number of nodes used in the original analysis (Bendall et al., 2011). Resampled topologies generated by p-Creode were notably more similar than those produced by SPADE (Figure 2C–D, Figure S5).

To quantitatively and statistically assess this similarity, we used a Gromov–Hausdorff-inspired metric, the p-Creode score, to capture the dissimilarity of one topology to another given changing node positions and connections (Figure S2, S3). At either node number, p-Creode topologies had both lower mean p-Creode scores and lower variances compared to SPADE (Figure 2E), demonstrating p-Creode to be a more robust method that generates a lower number of outlier topologies. These results demonstrate the ability of p-Creode to derive well-established cell transition relationships from single-cell data in an unsupervised and robust manner.

p-Creode analysis of differentiating thymic T cells reveals protein expression dynamics

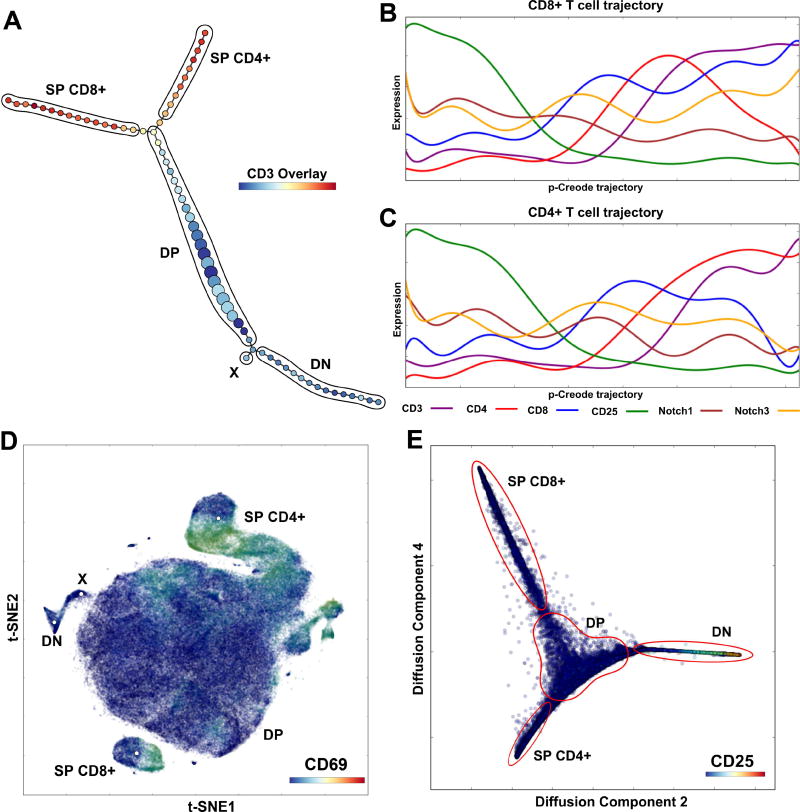
Wishbone is a novel non-linear embedding algorithm for analyzing single bifurcation events given a user-defined “starting cell” (Setty et al., 2016). We aimed to compare results generated by p-Creode, which is capable of producing multi-branching hierarchies, to Wishbone, which is designed to analyze protein dynamics over a process containing a single branch point. Wishbone requires prior knowledge of an existing, single branch point, and thus, it differs from p-Creode, which is an unsupervised tool. In the original Wishbone manuscript, mass cytometry datasets of mouse thymus were used for reconstructing T cell development where lymphoid progenitor cells bifurcate into CD4+ helper T cells and CD8+ cytotoxic T cells. These datasets were also used for benchmarking Wishbone to existing trajectory reconstruction algorithms, such as Diffusion Map, SCUBA, and Monocle (Haghverdi et al., 2015; Marco et al., 2014; Trapnell et al., 2014). In line with these comparisons, we applied p-Creode to analyze the same mouse thymus mass cytometry datasets from the Wishbone manuscript (Figure 3, Figure S6), using as input the same 14 cell-surface markers (CD27, CD4, CD5, CD127, CD44, CD69, CD117, CD62L, CD24, CD3, CD8, CD25, TCRb, CD90).

Figure 3. p-Creode analysis of single-cell mass cytometry data generates topologies that reflect thymic T cell development.

(A) p-Creode analysis of the first replicate 14-marker mass cytometry dataset from Setty et al. with PCA preprocessing, representative of N=100 runs. Cell populations were manually labeled. Overlay represents CD3 levels. (B, C) Marker trends along p-Creode trajectories with Diffusion Map preprocessing for CD8+ SP (B) and CD4+ SP (C) trajectories. Trends are similar to results obtained by Wishbone analysis and consistent with established stages of T cell differentiation. (D) t-SNE analysis of the Setty et al. dataset with manual annotation of clusters, including population X identified by p-Creode. (E) Diffusion Map of the dataset depicting T cell maturation. See also Figure S6–S7.

p-Creode generated topologies that reflected canonical T cell development with CD4-/CD8-double negative (DN) (1–4) cell states progressing through CD4+/CD8+ double positive (DP) cell states before finally bifurcating into the CD4+ and CD8+ single positive (SP) cell types (Figure 3A–C, Figure S6) (Koch and Radtke, 2011), a result that was also obtained by Wishbone. However, unlike Wishbone, p-Creode does not require user knowledge of a single branch point in the hierarchy, thus allowing for the discovery of uncharacterized branches. Based on this feature, p-Creode identified a T cell population branching from the DN to DP transition area (Figure 3A, Figure S6A), which was also identified by t-SNE (Figure 3D – population X), but not by Wishbone. This population, marked by the expression of CD24 and CD27, may represent progenitors developing towards gamma delta T cells (Fahl et al., 2014; Ribot et al., 2009).

We next focused on the dynamics of marker expression as a function of cell-state transition. In this example, p-Creode generated the correct topology for cell specification and also identified the macroscopic dynamics of marker fluctuation (Figure S7A–B). However, due to the increased sparseness of cell states in multi-dimensional space, the resolution of marker dynamics, a function of the number of cell states within a trajectory, was lower. Diffusion Map is a non-linear embedding tool to fold multi-dimensional data into elongated and compressed shapes (Coifman et al., 2005). Wishbone relies on Diffusion Map as a preprocessing step, and thus we hypothesized that the decreased number of dimensions resulting from this step would lead to a higher resolution of protein marker dynamics by reducing data sparseness. Without additional downstream analysis, Diffusion Map itself was able to capture the branching structure of differentiation, as well as the associated protein expression dynamics (Figure 3E), as previously noted for another Diffusion Map-based algorithm (Haghverdi et al., 2015). Application of p-Creode downstream of Diffusion Map enhanced the resolution of protein marker dynamics to a level comparable to Wishbone (Figure 3B–C, Figure S6B–C) (Setty et al., 2016).

We then tested whether Diffusion Map by itself can be used to analyze more complex, multi-branching hierarchies. Application of Diffusion Map to the Bendall et al. hematopoietic dataset resulted in convoluted trajectories with illogical transitions between the major differentiated cell types (Figure S7C), such as a direct transition between CD4+ T cells and myeloid cells. These results suggest that Diffusion Maps may not scale well with data depicting multi-branching transitions, while p-Creode is capable of analyzing such data.

p-Creode analysis of MxIF data generates robust topologies depicting intestinal cell specification

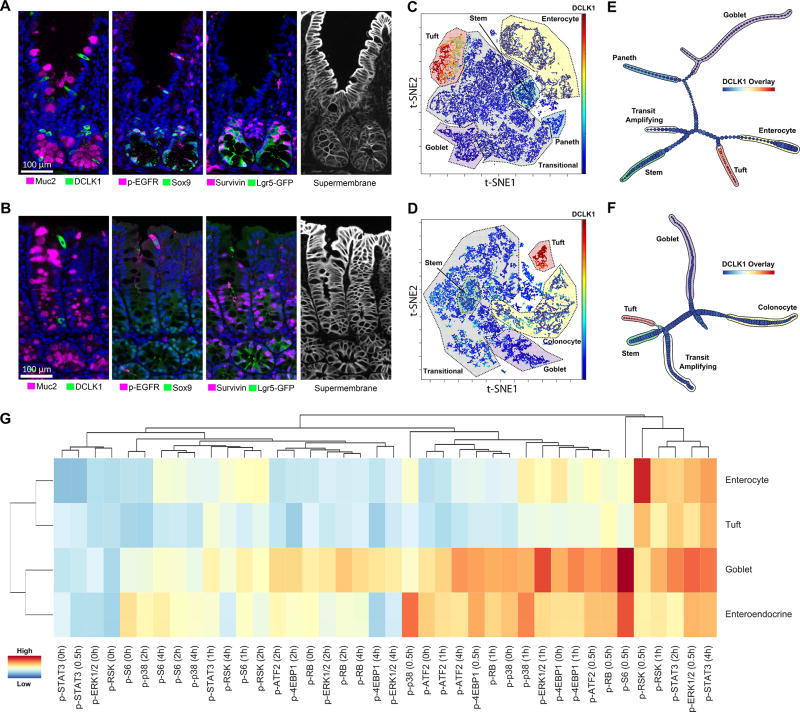
An unresolved issue in single-cell data analysis is the applicability of various algorithms across experimental platforms, such as flow-based or imaging-based methods, that generate data with different distributions. Therefore, we applied p-Creode to derive biological insights from data generated on a different technological platform, MxIF, to analyze intestinal cell transition relationships using single-cell data. MxIF is an iterative fluorescence staining procedure that dramatically increases the number of protein analytes that can be analyzed in a single tissue section (Gerdes et al., 2013). We applied MxIF to generate single-cell data depicting cell specification at homeostasis of the murine intestinal and colonic epithelia, which are continuously renewing tissues fueled by a stem cell-driven process (van der Flier and Clevers, 2009). Similar to hematopoiesis in the bone marrow, transitioning cell states (known as transit-amplifying or TA cells in the gut) are present at any snapshot in time, but they are poorly characterized and lack specific markers (Buczacki et al., 2013; van Es et al., 2012; Tetteh et al., 2016). We used MxIF with a 18-marker panel that broadly covers the stem-to-differentiated cell spectrum (Hopx, PCNA, Lgr5(GFP), Sox9, Survivin, CK20, Chromogranin A, DCLK1, Lysozyme, Muc2, p-EGFR(Y1068), Ki67, Villin, β-Catenin, NaKATPase, pan-Cytokeratin-PCK26, CD44v6, S6), with the assumption that multiple marker combinations can delineate transitioning cell states.

Mature cell types can be identified by canonical markers, such as Muc2 marking goblet cells, DCLK1 marking tuft cells, Villin marking enterocytes, Chromogranin A marking enteroendocrine cells, and Lysozyme marking Paneth cells. Combinations of p-EGFR, Hopx, and Sox9 marked distinct TA cells (Figure 4A–B). More importantly, the spatial resolution afforded by MxIF allowed the direct visualization of transitioning cells above the bottom of the crypt. For example, Lgr5(GFP) from a reporter mouse marked thin, wedge-shaped stem cells (crypt-based columnar cells or CBCs) (Barker et al., 2007) intercalating Paneth and Paneth-like cells at the crypt base, while Survivin marked CBCs and also transitioning cells in the mid-crypt (Figure 4A–B). A full depiction of all markers throughout the crypt-luminal axis of the small intestine and colon is presented in Figures S8 and S9, respectively. Object segmentation with a super-membrane mask (β-Catenin, NaKATPase, PCK26, CD44v6), preprocessing to remove non-cells, and quantification of single cells were performed as previously described (McKinley et al., 2017). We also applied an additional filter to remove data points (cells) that were gated negative for all markers and, therefore, uninformative to the analysis. Overall, data from 39,000 and 17,000 individual cells acquired from the small intestine and colon, respectively, were analyzed.

Figure 4. p-Creode analysis of single-cell multiplex immunofluorescence (MxIF) data reveals an alternate origin for tuft cells in small intestine versus colon.

(A, B) MxIF images where quantitative single-cell data are derived by extracting segmented cell objects using a combined, “supermembrane” mask. Example staining for differentiated, transit-amplifying (TA), and stem cell markers in the small intestinal (A) and the colonic epithelium (B). (C, D) t-SNE analysis on 19-marker MxIF datasets of the small intestinal (C) and the colonic epithelium (D). Cell types, as defined by clusters on the t-SNE map, were manually annotated. Overlay represents DCLK1 levels. (E, F) p-Creode analysis of datasets in E and F with the most representative graphs over N=100 runs, for small intestine (E) and colon (F). Overlay represents DCLK1 levels. (G) Hierarchical clustering of major epithelial cell types by their response to in vivo stimulation by TNF. Clustering on all normalized signals (indicated by heat map) measured by DISSECT-CyTOF. See also Figure S8–S14.

t-SNE and manual gating applied to the small intestine and colon datasets revealed several groupings of well-known intestinal epithelial cell types, as well as a large portion of unidentified, potentially transitioning cell states in both tissues (Figure 4C–D). p-Creode analysis of these datasets with N=100 resampled runs generated topologies with the same terminal cell types identified by t-SNE analysis (Figure 4E–F). Furthermore, the topologies connecting these terminal cell types through transitional cells largely resembled the known differentiation hierarchy of the small intestinal and colonic epithelium (Kim et al., 2014). At N=100 runs, robust results were obtained with most of the individual runs generating similar topologies (Figure S10). In the small intestine, Lgr5(GFP)+ stem cells were depicted to transit through cell states with variable expression of Survivin, Ki67, PCNA, Sox9, p-EGFR, and Hopx in cells largely residing outside the stem cell zone, as indicated by imaging (Figure S11, S12). The topology implied a decision between secretory and absorptive lineages in this transitioning zone with secretory progenitors biased towards Hopx and Sox9 (Paneth and goblet progenitors), and absorptive progenitors biased towards proliferative markers (Ki67 and Survivin) (Figure S11, S12). This bias is supported by studies of Notch activation and inhibition, which controls secretory versus absorptive cell specification associated with proliferation (Fre et al., 2005; Tsai et al., 2014). Secretory progenitors further branched into goblet and Paneth cells in the intestine, which are known to share a common origin.

Two possible abnormalities were identified from these topologies. First, Chromogranin A+ enteroendocrine cells were not identified, stemming from the extreme rarity of this cell type in our dataset (<0.2%), which makes them indistinguishable from technical noise in down-sampling. The rarity of Chromogranin A+ endocrine cells is supported by a recent study using a Chromogranin A-GFP reporter mouse (Engelstoft et al., 2015). Tuft cells, also relatively rare, make up ~ 1% of all epithelial cells in our datasets and thus were differentiated from noise. Second, cycling cells (Ki67/PCNA+) were identified as an end-state with its own branch, although the location of the branch in the topology was correct (in the TA population close to stem cells) (Figure 4E–F). Appearance of additional branches can result from using markers denoting cells in other states (such as in the cell cycle) distinct from the process of interest (cell specification). When we eliminated proliferative markers from the analysis, p-Creode was able to align TA cells, which express Survivin, Ki67, and PCNA, into the correct transition trajectory between stem cells and differentiated cells (Figure S13). Thus, markers selected for the analysis of a specific cell transition process must be considered since a complex biological system engages multiple processes simultaneously. Overall, p-Creode analysis on single-cell MxIF data was able to generate cell transition topologies of the gut that are supported by the literature.

Tuft cells are specified outside the Atoh1-dependent secretory lineage in the small intestine in contrast to the colon

Tuft cells are luminal-sensing epithelial cells recognized as a secretory cell type akin to goblet and Paneth cells. In the p-Creode analysis, tuft cells in the small intestine appeared distinct from the secretory lineage consisting of goblet and Paneth cells, and instead shared a common trajectory with enterocytes (Figure 4E). In the colon, however, tuft cells exhibited an alternative trajectory close to stem cells (Figure 4F). These results suggest alternate routes for tuft cell development between the small intestine and the colon.

To determine if tuft cells in the small intestine behave more similarly to secretory or absorptive cells, we evaluated epithelial cell type-specific responses to tumor necrosis factor (TNF) stimulation. Using the DISSECT approach (Simmons et al., 2015), intestinal epithelial tissues were collected over specific time points over a four-hour time course after systemic administration of TNF, disaggregated, evaluated by mass cytometry, and data were gated into different villus cell populations (Figure S14A). From these populations, 8 signaling proteins previously determined to respond to TNF were measured. As previously shown (Simmons et al., 2016), TNF elicited stronger signaling responses in secretory cells compared to enterocytes (p-S6, p-ATF2, p-RB, p-p38, p-4EBP1, p-ERK1/2) (Figure S14B). Tuft cells shared low signaling amplitudes with enterocytes, as well as similar transient p-ERK and p-RSK dynamics (Figure S14B). Summarizing these observations, we used hierarchical clustering on all signaling parameters to determine similarities among cell types. Secretory cells clustered together, as expected, whereas enterocytes and tuft cells clustered together in contrast to their established lineages (Figure 4G). These results demonstrate that the signaling behaviors of small intestinal tuft cells over multiple pathways do not resemble secretory cells, consistent with p-Creode results of their origins.

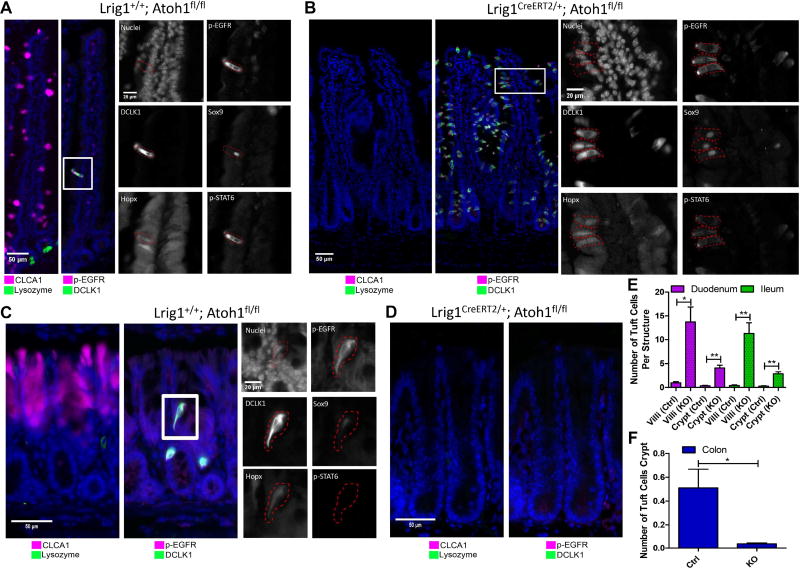
To further validate p-Creode-generated results, we selectively ablated Atoh1, a master transcription factor that regulates the secretory lineage in the intestinal epithelium (VanDussen and Samuelson, 2010). We used the Lrig1^CreERT2/+ driver to induce excision of the Atoh1 floxed allele in intestinal epithelial stem and progenitor cells (Powell et al., 2012), generating Lrig1^CreERT2/+;Atoh1^flox/flox mice. Tamoxifen administration in adult mice resulted in complete ablation of CLCA1+ goblet and Lysozyme+ Paneth cells in the small intestine and CLCA1+ goblet cells in the colon (Figure 5A–D, Figure S15A–B). In contrast to previous findings (Gerbe et al., 2011), tuft cells, as marked by DCLK1, increased in the small intestine, rather than being suppressed (Figures 5A–B, 5E, S15A–C). These DCLK1 cells are bona fide tuft cells and not stem-like cells, as evidenced by their villus localization, candle-like “tufted” morphologies, and multi-marker protein signature (McKinley et al., 2017) (Figures 5B, 5E, S15B).

Figure 5. Tuft cells have alternative specification requirements in small intestine versus the colon.

(A) Control (Lrig1^+/+;Atoh1^fl/fl + tamoxifen) and (B) epithelial-specific Atoh1 ablated (Lrig1^CreERT2/+;Atoh1^fl/fl + tamoxifen) duodenum, with acute ablation of Atoh1 at 8 weeks of age and analysis performed 2 weeks later. Analysis of Paneth (Lysozyme+), goblet (CLCA1+), and tuft (DCLK1+; p-EGFR+) cells. Inset represents a multi-marker tuft cell signature of cells on the villi with certain markers (p-STAT6, p-EGFR) demonstrating an apical tuft staining pattern. (C) Control and (D) epithelial-specific Atoh1 ablated colon, analyzed the same way as A,B. (E,F) Quantitative analysis of DCLK1+ cells from images per crypt or villus in the small intestine (E) and colon (F). Error bars represent SEM from n=3 animals. **P<0.01, *P<0.05 by t-test. See also Figure S15.

Because previous work has used a Villin^CreERT2/+ driver to induce recombination, we repeated our experiment using Villin^CreERT2/+;Atoh1^flox/flox tissue, which again resulted in the increase of DCLK1+ cells (Fig. S15D). In contrast, dibenzazepine (DBZ), a γ-secretase inhibitor known to inhibit Notch signaling, resulted in complete conversion of the epithelium into secretory cells, yet showed only a slight increase in numbers of tuft cells (Fig. S15E) (VanDussen et al., 2012). Since Atoh1 is the most proximal inducer of intestinal secretory progenitors (Buczacki et al., 2013; Kim et al., 2014, 2016; Li et al., 2016; Shroyer et al., 2005), these results again suggest that tuft cells do not descend from the established secretory lineage in the small intestine.

Contrary to the small intestine, tuft cells in the colon, marked by DCLK1 expression, were absent when Atoh1 was ablated, responding to Atoh1 loss in a similar fashion to CLCA1+ goblet cells (Figures 5C–D, 5F). This result suggested that colonic tuft cell specification was indeed controlled by the master secretory cell transcription factor Atoh1, whereas this was not the case in the small intestine. These experiments corroborated our p-Creode assessment of tuft cell specification differences between the small intestine and colon.

Application of p-Creode on published single-cell RNA-seq (scRNA-seq) data recapitulates complex differentiation processes

In contrast to candidate-based approaches such as mass cytometry and MxIF, scRNA-seq enables unbiased characterization of cells using thousands of transcript analytes. We assessed the performance of p-Creode on scRNA-seq data, using two publicly available datasets that describe (1) lung alveolar epithelial cell differentiation (Treutlein et al., 2014), and (2) blood cell differentiation from myeloid progenitors (Paul et al., 2015). These two datasets were generated using different analytical strategies, and thus, allowed for the evaluation of the general applicability of p-Creode. The former used Fluidigm C1 to analyze hundreds of data points by FPKM, while the latter used a plate-based MARS-seq platform to analyze thousands of data points by transcript counting.

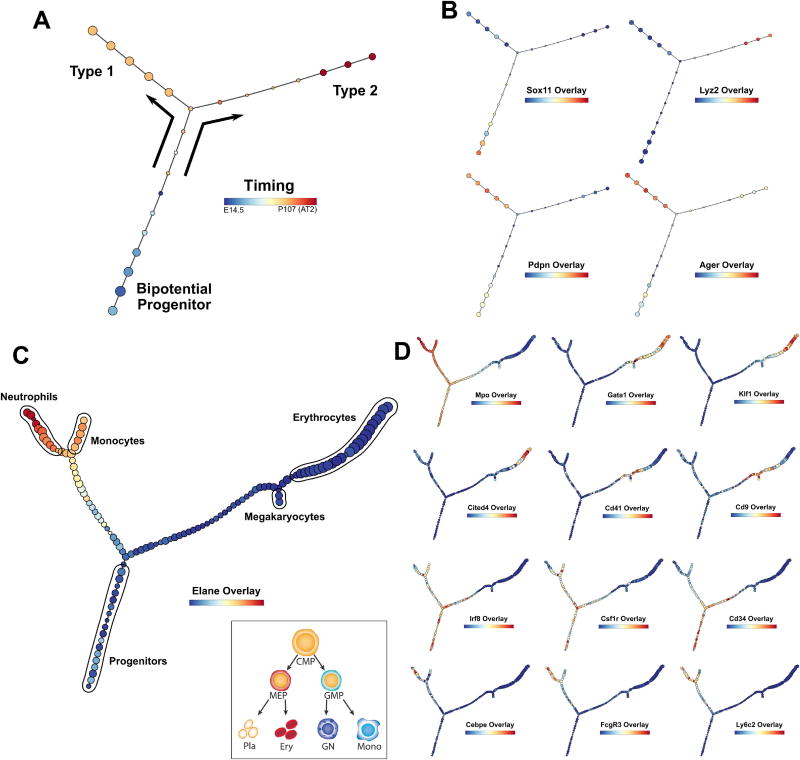
For the alveolar differentiation analysis, we combined separate datasets collected at E14.5, E16.5, E18.5 and P107 (AT2), which covers the progression of development from bipotential progenitors (BPs) to alveolar type 1 and type 2 cells. Data were processed with a neighborhood variance gene selection procedure as described previously (see STAR Methods). p-Creode analysis, modified for sparse datasets (see STAR Methods), resulted in a characteristic T-shaped topology with a single branch point, depicting the differentiation of BP (Sox11+) into type 1 (Pdpn/Ager+) and type 2 (Lyz2+) cells, consistent with previous analyses (Figure 6A–B)(Treutlein et al., 2014; Welch et al., 2016). Importantly, the timing of differentiation from E14.5 to P107 was recapitulated on differentiation trajectories constructed solely from expression data (Figure 6A). While p-Creode’s design was not intended to run on small datasets (<500 cells), these results demonstrate that it is possible to adapt this algorithm to perform adequately on sparse scRNA-seq data.

Figure 6. Application of p-Creode on published scRNA-seq data reveals multi-branching topologies.

(A) p-Creode analysis of the scRNA-seq dataset generated from alveolar cells by Treutlein et al. Cells collected over multiple developmental time points were mixed and analyzed together. Overlay represents developmental time that was recovered. (B) Overlay of selected transcripts depicting alveolar cell differentiation on the p-Creode topology generated in A. (C) p-Creode analysis of the scRNA-seq dataset generated from myeloid progenitor cells by Paul et al., most representative graphs over N=100 runs. Overlay represents Elane transcript levels. Inset represents an accepted model of myeloid differentiation. (D) Overlay of selected transcripts depicting myeloid cell differentiation on the p-Creode topology generated in C. Overlays represent ArcSinh-scaled gene expression data. See also Figure S16.

In contrast, the myeloid progenitor dataset contains a large number of data points and thus, it is well-suited for p-Creode analysis. After data processing as above, p-Creode analysis resulted in highly reproducible, multi-branching trajectories (Figure S16). In the original paper, multiple cell populations primed for megakaryocyte, erythrocyte, monocyte, and granulocyte development were identified (Figure 6C - inset) (Paul et al., 2015). However, previous lineage reconstruction algorithms were not able to place these sub-branches, and only identified the two major branches, the megakaryocyte-erythrocyte (ME) and granulocyte-monocyte (GM) branches, arising from the Cd34+ common myeloid progenitor (CMP) cells (Campbell and Yau, 2017; Setty et al., 2016). p-Creode, because of its ability to map multi-branching trajectories, generated a more complex topology with further sub-branches arising from the major ME (Gata1+/Car2+) and GM (Elane+/Mpo+) branches, including the neutrophil (Cebpe+/FcgR3+), monocyte (Irf8+/Csf1r+), erythrocyte (Klf1+/Cited4+), and megakaryocyte (Cd41+/Cd9+) sub-branches (Figure 6C–D). In line with the down-sampling issue of distinguishing rare cells from noise, eosinophils and basophils, which makes up 0.3% and 0.8% of the cells, respectively, were not identified as end-states. These results highlight the ability of p-Creode for generating multi-branching trajectories from high-resolution scRNA-seq data.

p-Creode application on scRNA-seq data generated from mouse colon reveals additional cell transition relationships

We then generated scRNA-seq data on the mouse colon with the inDrop platform, which uses droplet-based encapsulation in conjunction with a barcoding strategy to query thousands of cells (Klein et al., 2015). Using an epithelial enrichment procedure (Sato et al., 2011), single cells were isolated with at least 85% viability (Leelatian et al., 2017). After additional viability enrichment (see STAR Methods) to >99% viability, ~1900 and ~700 colonic cells from two replicates were encapsulated and sequenced. After sequence mapping, barcode deconvolution, and filtering by reads (Klein et al., 2015), 2402 (92%) colonic cells with an average of 49,680 reads per cell were recovered. In line with previous results with inDrop, the doublet rate appeared close to 0% (Figure 7A). We then performed t-SNE analysis and observed that the data from the two replicates were largely interspersed within each other, signifying minimal batch effects (Figure 7B). t-SNE analysis on these data revealed the presence of progenitor cells, secretory cells, absorptive cells, and immune cells identified by lineage-specific markers (Figure 7C–D, Figure S17). Immune cells, presumably intraepithelial lymphocytes, were gated out such that only epithelial cells were further analyzed.

Figure 7. inDrop scRNA-seq reveals the developmental trajectory of Reg4+ secretory cells in the murine colon.

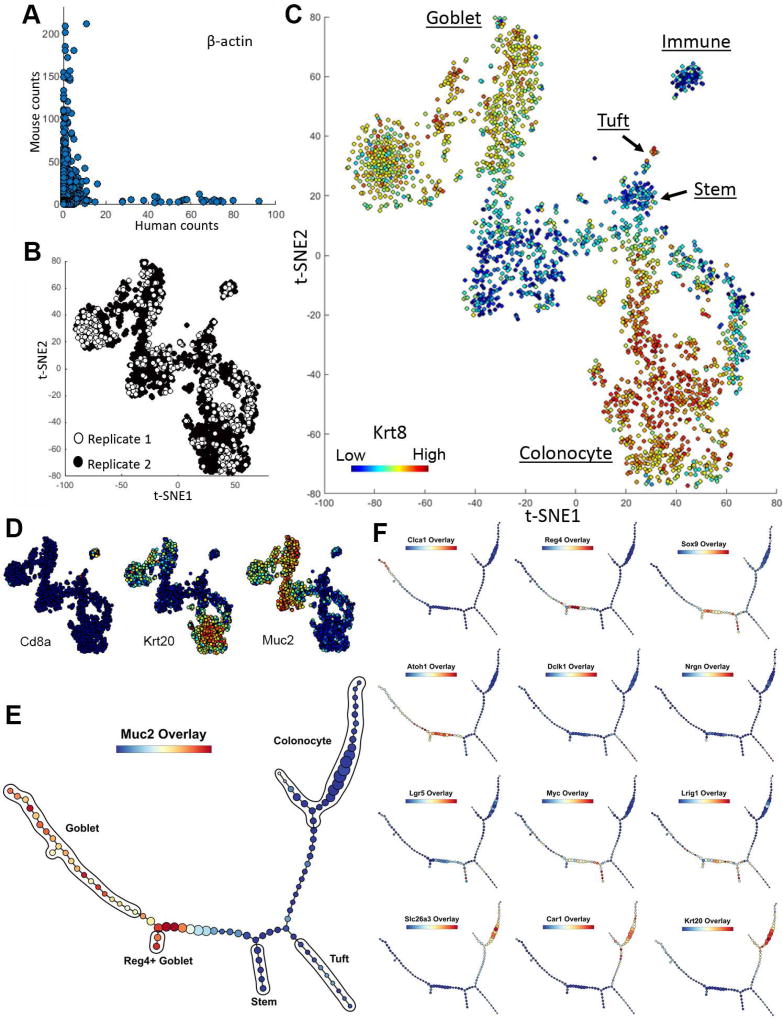
(A) Human versus mouse β-actin transcript count by mapping to human and mouse reference genomes, respectively. Each data point represents a single cell. (B) t-SNE analysis of scRNA-seq data demonstrating the absence of segregation of data points from 2 replicates. (C) t-SNE analysis of murine colonic cells using scRNA-seq data. Cell types, as defined by clusters corresponding to specific cell type markers on the t-SNE map, were manually annotated. Overlay represents Krt8 transcript levels. (D) Overlay of selected transcripts depicting colonic cell lineages on the t-SNE map generated in C. (E) p-Creode analysis of scRNA-seq data generated by inDrop from colonic epithelial cells, most representative graph over N=100 runs. Overlay represents Muc2 transcript levels. (F) Overlay of selected transcripts depicting colonic epithelial cell differentiation on the p-Creode topology generated in E. Overlays represent ArcSinh-scaled gene expression data. See also Figure S17.

p-Creode analysis on colonic scRNA-seq data revealed a characteristic cell transition pattern with a stem/progenitor branch (Lgr5+/Lrig1+/Sox9+), an absorptive colonocyte branch (Slc26a3+/ Car1+), and a secretory goblet cell branch (Muc2+/Clca1+) (Figure 7E–F). Progenitor to differentiated cell relationships can be clearly delineated with the pan-differentiation marker Krt20 (CK20). Unlike MxIF which is candidate-based, scRNA-seq afforded additional details regarding cell trajectories. For instance, a Reg4+ goblet cell branch can be seen arising from the secretory lineage (Figure 7F). Reg4+ goblet cells were recently identified as deep crypt secretory cells that exhibit niche roles in the colon analogous to Paneth cells in the small intestine (Rothenberg et al., 2012; Sasaki et al., 2016). Similar to Paneth cells, they share a trajectory with goblet cells in the colon in our analysis. These cells appear to arise from a Sox9+ progenitor, and Sox9 is a known transcription factor required for Paneth cell differentiation (Mori-Akiyama et al., 2007). In addition, Atoh1, the master transcription factor for the secretory lineage, was also mapped to secretory cell progenitors.

While p-Creode has the potential to contribute to the ongoing debate on the existence of multiple reserve stem cell populations or whether reserve stem cells are dedifferentiated committed cells (Buczacki et al., 2013; Li et al., 2016; Yan et al., 2017), our limited dataset does not allow us to reach a definitive conclusion. Because of the overrepresentation of committed cell states, the resolution required to depict the more nuanced relationships among rare populations of reserve stem cells (~5 cells in a set of >2000 cells) was lacking. To refine these relationships, it will be necessary to enrich these populations prior to encapsulation in a more targeted analysis. Similar to stem cells, tuft cells were also underrepresented in our dataset (Figure 7B). They expressed tuft cell markers, including Dclk1 and Nrgn (Middelhoff et al., 2017), and also Il25 (data not shown), a cytokine recently identified to be expressed in tuft cells to modulate type 2 immune responses (Gerbe et al., 2016; von Moltke et al., 2015) (Figure 7F). Similar to analysis derived from MxIF data, both t-SNE and p-Creode analysis placed the tuft cell lineage close to the stem cell lineage in the colon (Figure 7B, E). These results reveal the global structure of cell-state transitions from unbiased scRNA-seq data of the colonic epithelium.

Discussion

We have developed a new single-cell data analysis platform, called p-Creode, for the unsupervised mapping of multi-branching topologies from high-dimensional single-cell data. Importantly, a metric for scoring graph structures comprised of both changing nodes and edges was derived to statistically evaluate the quality of computed results. To the authors’ knowledge, this metric is the first of its kind in the field of graph theory, and can be applied to a variety of graphs such as signal transduction networks or phylogenetic trees. We have assessed p-Creode’s performance against current MST-based and non-linear embedding-based algorithms, and applied p-Creode on a variety of datasets from mass cytometry, MxIF, and scRNA-seq, both publicly available and those generated by our group. Specifically important is the ability of p-Creode to generate multi-branching trajectories in each of these cases to recapitulate the complexity of cell-state transitions, which is a significant step forward in the single-cell biology field.

We uncovered alternative routes of tuft cell ontogeny between the small intestine and the colon from our analysis. Tuft cells were originally found to be specified in the secretory lineage (Gerbe et al., 2011), but their origins have since been contested (Bjerknes et al., 2012; Westphalen et al., 2014). Both our computational and experimental analyses indicate an Atoh1-independent, and possibly, non-secretory cell origin of tuft cells in the small intestine, and an alternative origin of tuft cells in the colon. These observations support recent speculations by Gerbe and Jay regarding the potential functional differences among tuft cells at different anatomical sites (Gerbe and Jay, 2016), as well as our previous observations of different tuft cell distributions between the small intestine and the colon (McKinley et al., 2017). The discrepancies in phenotypes among studies and organ systems may arise due to the secondary effects of the microbiome. It has been shown that tuft cells can be regulated by luminal parasites, such as helminths (Gerbe et al., 2016; Howitt et al., 2016; von Moltke et al., 2015), and commensal bacteria (McKinley et al., 2017). As such, knockout of Atoh1 ablates microbiome-regulating goblet and Paneth cells, which can subsequently affect tuft cells as a secondary effect. It should be noted that the small intestine and colon are characterized by large differences in microbial content and load, and we observe differential dependence of Atoh1 on tuft cell development between the two regions. A recent study also suggested that tuft cells may share a common progenitor with subsets of enteroendocrine cells in the small intestine (Yan et al., 2017). Because of the importance of the microbiome in various ailments, modulating luminal-sensing tuft cell may be important in controlling allergic and inflammatory diseases.

One of the features of p-Creode is its use of an ensemble approach that allows for delineation of alternative routes of specification (see STAR Methods for explanation). Statistical ensemble representation of p-Creode can allow greater depth of analysis, including the assessment of the level of regulation of a transitional process and representation of loops. Another key feature of p-Creode is the ability to manage large numbers of cells, which facilitates the tracking of less continuous, switchlike processes. A number of newer algorithms, such as SLICE (Guo et al. 2016), are largely designed for sparse scRNA-seq datasets, and they produce rudimentary trajectories (with single branch points) that may not scale to more complex multi-branching processes. However, scRNA-seq technologies that can query thousands of cells are emerging (Klein et al., 2015; Macosko et al., 2015), and the datasets generated, such as those here, will require scalable algorithms such as p-Creode.

A specific point of consideration is the selection of markers or principal components to include in the analysis; these should be related to the cell transition process of interest. Unrefined selection of markers will result in ectopic identification of terminal states that depict unrelated cellular behaviors, for instance, cell cycle states in a differentiation hierarchy. The selection of markers is especially crucial for candidate-based approaches such as MxIF and CyTOF, since a larger emphasis is placed on each marker due to the relatively small number of markers evaluated. This problem may be somewhat alleviated in large-scale scRNA-seq studies, where cell-state transitions are driven by massive epigenetic changes reflected in gene expression programs, and genes with coordinated changes can be selected without bias. A recent Bayesian approach used the pattern of gene expression fluctuation at branch and transition points to systematically identify small sets of transcripts important for such transitions (Furchtgott et al., 2017). Future developments into unbiased feature selection from highly multiplexed gene expression data can further improve the stability of cell-state transition trajectory analysis such as p-Creode.

Another issue with single-cell analysis algorithms is the discrimination of rare cell populations from technical noise. Even in well-controlled single-cell experiments, misidentified data points (doublets/mis-segmented cells) exist and will appear as sparse data points with unique profiles distributed similarly to rare cells. p-Creode limits the effects of technical noise by 1) removing outliers at down-sampling, 2) consensus alignment of pathway nodes, and 3) selecting representative topologies using dissimilarity scoring. Improvements in rare cell detection can be achieved by having less noisy data and by developing better down-sampling algorithms that can distinguish technical noise from rare cells. These approaches may leverage current strategies for rare cell detection, such as raceID (Grün et al., 2015) and GiniClust (Jiang et al., 2016).

p-Creode analysis on single-cell, tissue-level data generates hypotheses regarding cellular transitions. Specifically, p-Creode can be used to provide insights as to how the structures of transitional topologies change upon external perturbations such as in disease or wound repair. Our scoring metric provides a rigorous way to quantify the probabilistic nature of cell transitions where we expect a diverse ensemble of computed topologies in more stochastic transition processes. Overall, broad advances in single-cell data analysis, such as p-Creode, may have significant potential in a range of biomedical applications.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Ken S. Lau (ken.s.lau@vanderbilt.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mouse Experiments

Animal experiments were performed under protocols approved by the Vanderbilt University Animal Care and Use Committee and in accordance with NIH guidelines. Mice were stimulated with TNF-α as a time course, and their duodena (proximal small intestine) were collected for analysis as previously described (Lau et al., 2012; Lau et al., 2013). Briefly, TNF-α (0.4 mg/kg in PBS) was injected retro-orbitally into mice, and mice were sacrificed at various time points for tissue collection. For DISSECT, a previously published protocol was used (Simmons et al., 2015). Collected tissues were fixed in 4% paraformaldehyde with protease and phosphatase inhibitors for 30 minutes, exposed to −20°C acetone briefly, then incubated in a detergent solution (1% saponin, 0.05% Triton X-100, 0.01% SDS) for 30 min. Samples were then stained with antibodies, re-fixed, and disaggregated with collagenase type I and dispase at 37°C for 1 h. Tissues were then dissociated gently into single cells with a needle, and filtered for cytometry analysis. For FFPE embedding for MxIF imaging, tissues were fixed in 4% formaldehyde for 24 hours and then were subjected to standard embedding procedures. For Cre-induced recombination experiments, 2 mg of tamoxifen (Sigma) was administered intraperitoneally at 2 months of age for 4 consecutive days, and animals were sacrificed and their tissues harvested 14 days after the first injection. Both Cre and wildtype mice were administered tamoxifen to control for its effects. Lrig1^CreERT2 and Atoh1^fl strains were purchased from the Jackson Laboratory in a C57BL/6 background. DBZ experiments were performed as previously described (Kim et al., 2014). Briefly, DBZ was suspended in the appropriate vehicle and injected intraperitoneally into animals (100µmol/kg).

Subject Details

Male animals about 2 months of age were used for all experiments. All subjects were treatment naïve, and animals were housed in a SPF barrier facility fed on standard chow. Independent biological replicates on different animals were performed, and comparisons were made on littermates when possible. Replicate experiments were performed on different days to ensure independence. We used empirical data from our previous single-cell and cell counting experiments to estimate sample size with 90% power and 5% type 1 error in a comparison between two groups of animals. No blinding, normalization, or exclusion criterion was used in the study design.

METHOD DETAILS

Mass Cytometry Analysis

Mass cytometry was performed on a Fluidigm-DVS CyTOFI instrument with elemental calibration bead spike-ins (Finck et al., 2013). Cells were gated using intercalator (Iridium) following established procedures to identify intact single cells and eliminate cell doublets and clusters from analysis (Simmons et al., 2015). Single cells were then analyzed for intensity of multiple antibody conjugates (Key Resources Table).

MxlF Analysis

FFPE tissues were sectioned at 4 µn and processed using standard immunohistological and antigen-retrieval techniques. MxIF was performed by using a sequential staining and fluorescence-inactivation protocol, as previously described (Gerdes et al., 2013). Briefly, directly labeled antibodies (with Cy3, Cy5, or Cy7) were applied on tissue sections overnight at 4°C. Microscopy was performed on the whole tissue section, and the sample was then photo-inactivated with an alkaline peroxide solution. Cycles of staining and imaging were then performed until the entire set of analytes was analyzed. Imaging was performed on an Olympus X81 inverted microscope with a motorized stage and acquired at 20x magnification. Antibody (Key Resources Table) staining was performed overnight at 4°C. At each round, images were computationally registered, and corrected for illumination and autofluorescence. Processed images were then segmented using a multi-marker supermembrane mask, and individual cells were quantified, as described (Gerdes et al., 2013). Partial and poorly segmented cells were removed. The mean, standard deviation, median, and maximum staining intensity for each protein was quantified with respect to the whole cell, cell membrane, cytoplasm, and nucleus, as well as cell location, area, and shape. Image processing was performed on the Amazon Cloud through the KNIME parallel architecture.

Single-cell RNA-sequencing

Colonic epithelium was enriched by incubating colonic issues in a 2mM EDTA/EGTA chelation buffer at 4°C for 45 minutes and then shaking for 30 seconds (Sato et al., 2011). The epithelium was then dissociated into single cells with a collagenase/DNAse enzyme cocktail (2mg/ml Collagenase I, 2.5mg/ml DNAse1) in a modified protocol that maintains high cell viability (Leelatian et al., 2017). Cell viability was determined by counting Trypan Blue positive cells. The cell suspension was further enriched with a MACS dead cell removal kit (Miltenyi) prior to encapsulation, and the density of cells were calculated by counting. Before encapsulation ~10% human K562 cells were spiked into the suspension to evaluate the doublet rate. Single cells were encapsulated and barcoded using the inDrop platform (1CellBio) with an in vitro transcription library preparation protocol (Klein et al., 2015). As per Klein et al., the CEL-Seq work flow is summarized: 1) RT, 2) ExoI, 3) SPRI purification (SPRIP), 4) SSS, 5) SPRIP, 6) T7 in vitro transcription linear Amplification, 7) SPRIP, 8) RNA Fragmentation, 9) SPRIP, 10) primer ligation, 11) RT, 12) library enrichment PCR. The number of cells encapsulated was calculated by the density of cells arriving at the device multiplied by the duration of encapsulation. After library preparation, the samples were sequenced using Nextseq 500 (Illumina) using a 150bp paired-end sequencing kit in a customized sequencing run (50 cycles read 2, 6 for the index read, rest for read 1). The two replicates were multiplexed in a single sequencing run. After sequencing, reads were filtered, sorted by their barcode of origin and aligned to the reference transcriptome using inDrops pipeline (https://github.com/indrops/indrops). Mapped reads were quantified into UMI-filtered counts per gene, and barcodes that correspond to cells were retrieved based on previously established methods (Klein et al., 2015). Overall, out of ~2600 cells encapsulated, 2402 cells (92%) were retrieved.

scRNA-seq Data Analysis

For the alveolar data obtained using the Fludigm C1 system, previous criteria of selecting cells with >= 1000 genes detected at >= 1 FPKM with control ERCC > 0 were used (Welch et al., 2016). For the myeloid data obtained using MARS-seq, previous criteria of filtering out cells with < 250 molecules was used (Setty et al., 2016). For both MARS-seq and inDrop data, which consisted of raw transcript count, mitochondrial genes and genes where the maximal counts are one (noise) were filtered out, resulting in ~15,000 genes remaining. Transcript counts for each gene were normalized to the total transcript count per cell to obtain a fraction gene expressed and then multiplied by a constant (the median total transcript count across all cells) (Setty et al., 2016). Data generated for all 3 approaches C1, MARS-seq, and inDrop were then ArcSinh normalized to stabilize the variance with a cofactor of 5, noting that the outcomes were not sensitive to the cofactor being used. From these normalized data table, the select gene procedure was applied (https://github.com/jw156605/SLICER) (Welch et al., 2016), which selects monotonically changing genes using a neighborhood variance approach over a graph. These data were then analyzed by p-Creode.

p-Creode Overview

The purpose of p-Creode is take inherently noisy single cell data and reveal the robust, underlying structure under such data with n cells in N dimensional analyte space. The inherent technical variabilities generated by single-cell approaches conceal this structure to varying degrees. This is dependent on the process of study and the technology applied. Each of p-Creode algorithm’s 6 steps is geared towards managing this issue: i) Down-sampling, ii) Graph construction, iii) End-state identification, iv) Topology reconstruction, v) Consensus alignment, vi) Scoring.

i) Down-sampling

As a first step p-Creode performs a density-dependent down-sampling to normalize the representation of rare and overrepresented cell states. Our approach to down-sampling is similar to the approach outlined in (Qiu et al., 2011). To start, a radius (rad) must be calculated to serve as a limiting factor in calculating the local density (LD_i) of each data point (or cell) i. rad for each dataset is determined by taking the product of a user defined scaling factor (SF) and the median minimum distance (MMD), where MMD is the median Euclidean distance of 5,000 randomly-selected data points (or all data points if sum total is less than 5,000) to their closest neighbors in the complete dataset. The LD_i for each cell is then calculated by counting the number of data points contained in an N dimensional sphere defined by the rad. Next, a probability (P_i) of inclusion is established for each data point based on LD_i and its relationship to the user provided target density (TD) and outlier density (OD). If a cell has LD_i lower than or equal to OD, the cell is considered noise and not selected. If LD_i is higher than OD and less than or equal to TD then the cell is automatically selected for inclusion. Finally, if the LD_i is greater than TD, P_i is equal to LD_i divided by TD.

$$\begin{array}{cc}\mathit{\text{if }}{\mathit{\text{LD}}}_i\le \mathit{\text{OD}}\hfill & P_i=0\hfill \\ \mathit{\text{if }}{\mathit{\text{OD}}}_i<{\mathit{\text{LD}}}_i\le \mathit{\text{TD}}\hfill & \hfill P_i=1\\ \mathit{\text{if }}L{D}_i>\mathit{\text{TD}}\hfill & P_i=\frac{\mathit{\text{TD}}}{{\mathit{\text{LD}}}_i}\hfill \end{array}$$

Three user defined input variables are required for performing the down-sampling procedure. The SF is used to scale rad, effectively shrinking or growing the volume of the sphere surrounding each data point. Care must be taken to insure that the selected SF parameter sufficiently maps the different pockets of density that represent each cell type. Due to biological and technical differences that exist among individual datasets, the distribution of data points will differ between each, causing the value SF to differ as well. When available, we used prior knowledge to aid in SF determination. For instance, in the bone marrow dataset (Bendall et al., 2011), we knew that myeloids, CD4+ T, cells and CD8+ T cells were in abundance, which allowed us to check our density calculations by ensuring that each population was adequately represented after down-sampling. When prior knowledge was not available, a histogram of cellular densities was used to visualize the range and abundances of densities, where SF parameters producing a large range of populated densities were preferred over values producing a low range of densities or a large range of densities with regions of near-zero densities. The next user-defined parameters, OD and TD, are responsible for adjusting the probabilities of inclusion, and like SF, will vary dataset to dataset. The OD is essentially a noise threshold for inclusion; anything with a density below OD is considered noise and uninformative. The last user-defined parameter, TD, was largely used to control the size of the downsampled dataset. In our case, we selected values of TD to produce down-sampled datasets that contained ~14,000 cells to allow efficient computational processing.

ii) Graph Construction

As has been previously reported (Bendall et al., 2014; Setty et al., 2016), spurious relations (edges) between cells (nodes) that are farther apart in development space but closer in analyte data space (“short circuits”) is a serious issue when attempting to order cellular trajectories. To combat this issue and as noted before (Setty et al., 2016), we leveraged graph distances derived from undirected k-nearest neighbor (kNN) graphs between cells instead of depending on simple distances in analyte data space depicting expression similarities. This process ensures that relationships are specified in regions of data space occupied by data points, instead of “short-circuiting” between points simply due to lowest pairwise distances. In p-Creode, we have made additions to typical kNN graph construction by incorporating density into k selection and into how edge weights are calculated. In place of a typical kNN, we use a density based k-nearest neighbor (d-kNN). Similar to a traditional kNN graph, the d-kNN graph is built by connecting each node in the down-sampled dataset with its k nearest neighbors, ranked by Euclidean distance, but the value of k in a d-kNN graph is set according to the density of that node, as calculated before being down-sampled. The value of k ranges from 10, for the densest nodes, to 2, for the least dense. These values were chosen as a balance between increasing the risk of “short circuits” on the high end and limiting the amount of unconnected graph components on the low end. To complete graph construction, isolated graph components are connected by closest inter-node distances, in order to ensure that the final d-kNN graph is one fully connected graph. After graph construction, edges are weighted with a cellular similarity component in the form of Euclidean distance and a cellular transitional likelihood in the form of a density weight. More specifically, weighted edge (E_i,j) connecting nodes i and j is defined as the product of the Euclidean distance (dist) between the two nodes and a density weight (dens):

$$E_{i,j}=\mathit{\text{dist}}(i,j)\times \mathit{\text{dens}}(i,j)$$

where dens(i,j) is defined as:

$$\mathit{\text{dens}}(i,j)=1.1-\mathit{\text{minimum}}({\mathit{\text{nLD}}}_i,{\mathit{\text{nLD}}}_j)$$

Here, nLD_i refers to the densities calculated before down-sampling, but normalized (min=0, max=1) over all down-sampled data points to limit the effects of density outliers on the normalization process.

iii) End-state identification

A requirement in creating lineage trajectories in some algorithms is the identification of end-states from which to start and end trajectory construction. This process can be performed manually, but is made harder when multiple end-states in multiple dimensions exist. Another strategy to identify cell states is by clustering, but this is inadequate for continuous data, when data points are artificially forced into clusters even if no identifiable clusters exist. To identify end-states automatically in multi-dimensional data space, we use a graph-theoretical metric from our d-kNN graphs, called closeness centrality, to separate end-states from transition states. Closeness (cls_i) measures the inverse mean graph distance from a node i to all other nodes in a graph, where the graph distance (gdist) is the shortest weighted edge path connecting node i to node j as determined by Dijkstra’s algorithm (Dijkstra, 1959).

$${\mathit{\text{cls}}}_i=\frac{n}{{\sum }_j^n\mathit{\text{ gdist}}(i,j)}$$

Nodes with high closeness are more interconnected within a graph and nodes with low closeness are less interconnected. In our graphs, end-states are characterized by low values of closeness, representing geometric fringes in data space similar to (Korem et al., 2015). These data points are less interconnected, having connections with other cell states in a single or few geometric directions. Transitional cell states, on the other hand, are more interconnected in the d-kNN graph from being completely flanked by other transiting cell states, thus, having high closeness. Nodes with low closeness (end-states with less than mean closeness over all cells) are clustered using K-means clustering. The number of end-states is determined by silhouette scoring (Rousseeuw, 1987) over varying values of K, where K is the number of clusters. The optimal K is then doubled to allow for the possibility of underrepresented cell states. From each cluster, a most representative node is selected by finding the data point in the dataset closest to the centroid of the cluster.

iv) Topology reconstruction using hierarchical placement

Next, p-Creode constructs a representative topology from the identified end-states and selected transition states with a hierarchical placement strategy. Unlike hierarchical clustering where all data points appear on the leaves of a dendrogram, this method places data points on branches to allow depiction of ancestral relationships. p-Creode starts by connecting the two closest end-states (Figure S1 – step 1 - orange nodes), as measured by graph distance through the d-kNN graph. The connection consists of transition states selected along the shortest path, now defined as path nodes, connecting the end-states. The now connected end-states and any connecting path nodes form a graph component (Figure S1 – step 2 – green nodes) that is added back to the pool of possible connections for the remaining end-states. Connections between nodes in the same graph component are disregarded but all other connections are possible whether they be between an end-state and another end-state (connected or unconnected) (Figure S1 – Step 2–3), a connected path node from one component to another connected path node from another component (Figure S1 – Step 4–5), or an end-state and a connected path node (Figure S1 – Step 5–6). Following these rules the remaining end-states are iteratively connected until all the end-states form one complete graph containing only end-states and path-connecting nodes. Specifically, bifurcation points will be contained with the set of transition states selected to be path nodes.

v) Consensus alignment

As an additional step to alleviate “short circuiting” due to noise and sparse data, we add a consensus alignment step that reassigns the locations of path nodes in the constructed topology in a way that more accurately reflects the paths observed in the data. The consensus alignment starts by taking each of the path nodes from the constructed topology in step iv and iteratively assigns random data points from the original dataset (1000 at a time minus noisy data points) to one of the path nodes based on Euclidean distance, while updating the position of the path node by taking the median between assigned data points and the path node. This process functions similar to a relaxation, where the relative abundance of the data points serves as a “potential energy” function, pulling path nodes into basins defined by density. After reassignment, the new path nodes are reconnected using our hierarchical placement strategy, creating a new multi-branching topology. Following this step, lineages leading to nodes not identified as end-states are removed and a final topology is produced.

Because consensus alignment employs a sequence of cells for mapping the most consensus routes, we systematically tested whether randomizing this sequence will alter the final results generated by p-Creode. Starting from the same graph generated by hierarchical placement, we ran consensus alignment 100 times with a randomized sequence of cells each time. The results were then evaluated by clustering on p-Creode scoring to determine whether this type of randomization will result in different clusters of graph topologies. Having a single cluster of graphs with few outliers reflects that the sequence by which consensus alignment is performed has minimal effect on p-Creode results.

As a detailed illustration, we used the Setty et al. thymic dataset as an example. Performing the above procedure resulted in 96% of the resulting topologies placed in the major cluster with 4% as outliers (Figure S18A). The outlier topologies consisted of graphs without the gamma delta T cell population (X), which for the most part, has been gated out of the dataset aside from a small precursor remnant (Figure S18B). The major branches consisting of progenitor, CD4+, and CD8+ T cells remained intact. Graphs sampled from different subclusters of the main cluster consisted of very similar topologies to Figure 3A and Figure S6A (Figure S18C–E). We also performed the same procedure on the Bendall et al. bone marrow mass cytometry dataset and Paul et al. myeloid scRNA-seq dataset, with similar results (Figure S18F–G). These results demonstrate that the order by which cells are used for consensus alignment has minimal effect on the final outcome of p-Creode.

vi) Scoring

Due to random down-sampling, multiple independent runs will produce an ensemble of N final topologies. We leveraged an ensemble approach to account for the possibility of alternative routes reflected in the data. For example, in dysregulated processes such as cancer, we envision that increased plasticity leads to multiple alternative routes of cell transitions that reflect real biological differences. For well-controlled processes in healthy tissue though, we expect p-Creode to mostly produce a single cell transition trajectory from the data (with outliers due to technical noise). In this report, we are dealing with the latter and not the former, and representation of dysregulated transition processes will be addressed in future studies. To standardize our ensemble approach, we used N=100 runs. The reasons behind this number are as of follows:

1. If we use a small number for N (e.g., N=10), alternate topologies may appear only once, which may not allow us to distinguish between technical noise versus biological variations.

2. For N>100, we begin to see a diminishing rate of return. That is, we do not get added value in seeing different classes of graphs while the computation costs increase. We performed an additional study varying N (Paul et al. dataset), and we observed that changing N (from 10 to 1000) in this well-controlled process has minimal effect on the final p-Creode output (Figure S19).

In this report, it appears that p-Creode is robust to changing N values given that we are analyzing homeostatic processes. Having N=100 allows for an ensemble approach that captures different alternative topologies by providing a high enough N to enable statistically significant clustering of these alternative graphs, if they exist. This ensemble aspect will be useful for modeling dysregulated processes in future investigations.

To come to a consensus on a final topology and to measure the robustness of the generated topologies, we developed a scoring metric (called p-Creode score) to compare the dissimilarity between topologies - a non-trivial problem given that each computed graph has different edges and nodes. Each topology can be viewed as a metric space where a distance matrix can be defined by the graph distance between all nodes. This definition allows us to leverage a version of the Gromov-Hausdorff distance, previously used to compare the distance between metric spaces (Edwards, 1975). While inspired by the Gromov-Hausdorff distance, our approach is tailored to the task of measuring the dissimilarity of graph ensembles generated from a common pool of data points. Specifically, our metric is uniquely built to comparing graphs generated by p-Creode and other similar lineage reconstruction algorithms, being that they are acyclic, undirected, and asymmetric in architecture.

Our approach is composed of two scoring components, a graph distance component and a topological component, to capture changes in the position of and connection between nodes, respectively. More formally, we wish to compare two graphs A and B defined as a pair of sets (V,E), where V refers to a set of nodes and E is a set of weighted edges. If graph A contains x number of nodes and graph B y number of nodes. Then the nodes sets are defined as V_A = {a₁, a₂,……., a_x} and Vb = {b₁, b₂,……., b_y}respectively. The p-Creode score (Score_AB) of comparing graph A to graph B is the sum of the graph distance component (GD_AB) and the topological component (TP_AB),

$${\mathit{\text{Score}}}_{\mathit{\text{AB}}}={\mathit{\text{GD}}}_{\mathit{\text{AB}}}+{\mathit{\text{TB}}}_{\mathit{\text{AB}}}$$

GD_AB is the per comparison average difference in pairwise Euclidean weighted graph distance (gdist) plus a transformation distance or

$${\mathit{\text{GD}}}_{\mathit{\text{AB}}}={(\underset{2}{\overset{x}{}})}^{-1}\sum _{\{a,a\prime \}\in V_a}{\delta }_{\mathit{\text{AB}}}(a,a\prime )$$

where

$${\delta }_{AB}(a,a\prime )=\mathit{\text{abs}}({\mathit{\text{gdist}}}_A(a,a\prime )-[{\mathit{\text{trans}}}_{\mathit{\text{AB}}}(a)+{\mathit{\text{trans}}}_{\mathit{\text{AB}}}(a\prime )+{\mathit{\text{gdist}}}_B(T_B(a),T_B(a\prime ))])$$

trans_AB (a) is the Euclidean distance between node a in graph A and its closest neighboring node in graph B or T_B(a),

$${\mathit{\text{trans}}}_{\mathit{\text{AB}}}(a)=\mathit{\text{dist}}(a,T_B(a))$$

The TP_AB is the per comparison average difference in summed degree of path nodes with degree over 2 (pdeg), where the degree of a node in an undirected graph is equal to the number of edges connected to it, and any node with a degree over 2 signifies a branch point in the topology. More specifically,

$${\mathit{\text{TP}}}_{\mathit{\text{AB}}}=\sum _{\{a,a\prime \}\in V_a}\beta (a,a\prime )$$

where

$$\beta (a,a\prime )=\mathit{\text{abs}}([{\mathit{\text{pdeg}}}_A(a,a\prime )-2\times |{\mathit{\text{pdeg}}}_A(a,a\prime )|]-[{\mathit{\text{pdeg}}}_B(T_B(a),T_B(a\prime ))-(2\times |{\mathit{\text{pdeg}}}_B(T_B(a),T_B(a\prime ))\left|\right])$$

and |pathdeg| is the number of nodes in the shortest path with degree greater than two. Since p-Creode scoring function is not inherently symmetric (Score_AB ≠ Score_BA) the maximum of the comparisons is taken,

$$\mathit{\text{pScore}}(A,B)=\mathit{\text{max}}({\mathit{\text{Score}}}_{\mathit{\text{AB}}},{\mathit{\text{Score}}}_{\mathit{\text{AB}}})$$

For a given set of computed graphs, a score matrix is created by comparing each graph to all other graphs. The most representative topology is the graph with the lowest overall mean p-Creode score.

Figure S2 demonstrates a single comparison on a toy graph. Two graphs are constructed from nodes selected from a common pool of 8 data points in 2-dimensional analyte space (Figure S2A, B). These two graphs are comprised of different numbers and identities of nodes with different connections. For the single comparison, we are comparing the difference in the graph relationship between nodes 1 and 8. For the distance component of the metric, the graph distance between nodes 1 and 8 in graph A is calculated as before, but since neither 1 or 8 are in graph B a node transformation is performed by finding nodes in graph A that are closest in Euclidean distance to 1 and 8 in graph B (nodes 2 and 7, respectively) (Figure S2C, D). The transformation constitutes a penalty for subsequent calculations (Figure S2D - dashed lines). The distance between nodes 1 and 8 in graph B is calculated by summing the total transformation penalty and the graph distance between nodes 2 and 7 in graph B. For the topological component, the number of branches points (Figure S2C and 2D - red centered nodes) are counted along shortest path length between nodes being compared (Figure 2C, D - dashed outlined nodes). The difference between these counts is the topological component.

There are two applications of the p-Creode score to the overall algorithm. First, over an ensemble of N iterations, we can use the p-Creode score to gauge the similarity of each graph to each other in a run, with a low score describing a highly robust result (i.e., getting the same or similar graphs over multiple runs). This would provide a glimpse on how regulated a process is in terms of biological variation or how noisy the data are in terms of technical variation. Secondly, we use the p-Creode score to select the most representative graph for visualization purposes. If the data describes a homeostatic process that is well-regulated producing one major population of graphs via p-Creode, the graph with the lowest average score (most similar to all other graphs) is chosen to be visualized. We envision that the p-Creode score has application beyond the p-Creode algorithm for comparing graph structures in other data science problems. However, because this scoring metric is new, we sought to verify its utility in graph comparisons independent of the p-Creode algorithm, as detailed below.

Independent Validation of the p-Creode Score

To empirically demonstrate the validity of the p-Creode score, we compared and contrasted its utility with other common metrics in a toy graph optimization problem representing a large random cohort of graph comparisons. We ran this stochastic optimization problem 100 times to sample the performance of this metric over a search space of over 10²⁰⁰ graphs (Cayley) to obtain a comprehensive variety of graph comparison situations. We compared the performance of our metric to two other common metrics, the Euclidean distance between matching (nearest) nodes (positional scoring) and the difference in average path lengths between graphs (path scoring). These two metrics capture aspects of the changing positions of and connections (graph structure) between nodes.

To describe the optimization problem briefly, the goal is to match a starting graph to a target graph using a progressive search function that guided by a metric (either the p-Creode score or the common metrics). Our search space is composed of all graphs (~10²⁰⁰) that can possibly be constructed by 100 nodes (points) distributed in 2 dimensional space. The starting graph is chosen randomly and can comprise any number of nodes connected in any way into a single graph, on which an iteration of perturbation and scoring is performed. The most similar graph according to scoring using the p-Creode score, positional scoring, or path scoring is kept after each iteration until convergence is reached. Examples of this problem are shown in Figure S3A and B, with a simple and complex initial graph, respectively. The details of this algorithm is described in the pseudocode below. The p-Creode score was the only scoring metric used that was able to consistently return the target graph with matching nodes and connections. As expected, position scoring by Euclidean distance returned graphs with mostly matching nodes but with edges randomly oriented. Path scoring by average path length returned graphs with rudimentary structure and node positions not matching the target graph. When guided by p-Creode scoring, tracking of the other scoring metrics during iterative optimization shows a similar downward trend, reflecting increasing similarity (over both positional and structural aspects of graph comparisons) as the target graph (Figure S3 E, F).

Because the data points exist in two-dimensional space, it is possible to visually compare the graphs. As an unbiased way to “visually” compare graphs, we used image processing to quantify graphical differences between the selected graphs and the target graph (Figure S3G). Over 100 simulations using the p-Creode score, position score, and path score were conducted and the selected graphs from each were compared to the target graph by image processing. Similar to our qualitative assessment, graphical comparisons revealed that only when guided by p-Creode scoring does the final selected graphs closely resemble the target graph.

Pseudo-code for scoring optimization routine

1.	best_graph = randomly initialized starting graph
2.	best_score = starting graph score (scored by position, path, or p-Creode)
3.	unsuccessful_attempts = 0
4.
5.	for ( 100,000 attempts ):
6.	randomly perturb best graph by selecting from the following
	a. add a new node (or datapoint) to the graph
	b. delete a node from the graph
	c. swap a node ID (or position in dimensional space) with ID of node already in the graph
	d. swap a node ID with ID of node not currently in graph
7.
8.	run_score = mutated graph score
9.	unsuccessful attempts += 1
10.
11.	if ( run_score<best_score ):
12.	best_score = run_score
13.	best_graph = perturbed graph
14.	unsuccessful_attempts = 0
15.	if ( best_score == 0 ):
16.	break
17.
18.	elif ( unsuccessful attempts >= 2,000 ):
19.	best_score = run_score
20.	best_graph = perturbed graph
21.	unsuccessful_attempts = 0

p-Creode modifications for sparse datasets

p-Creode was originally designed to run on large datasets consisting of thousands of data points in order to ensure that transition states required for connecting a graph are adequately represented. For instance, for samples where terminal states are overrepresented and transition states are underrepresented, end-state selection, hierarchical placement, and consensus alignment would fail since there will be an infinite number of ways to connect cell states. Down-sampling equalizes the distribution of data points across all cell states to ensure adequate representation. With that said, p-Creode can theoretically run on small datasets (hundreds of cells) where data points are originally well-distributed across cell states. This is the case with alveolar dataset. The following modifications were made to p-Creode for running sparse datasets:

1. No noise was removed, so all data points were viewed as informative.

2. We did not double the number of clusters identified as end-states due to the sparseness of the dataset. Performing this procedure in such a small dataset will artificially split cell populations.

3. The closeness threshold was raised from 0 to 1, given the sparseness of transitional cell states overinflates the closeness values of denser end-states.

QUANTIFICATION AND STATISTICAL ANALYSIS

Data Analysis

t-SNE analysis was performed using the Barnes-Hut’s algorithm (van der Maaten et al., 2011). Unpaired t-tests and 1-way ANOVA tests were performed using Prism (Graphpad). p-Creode was written in Python. Hierarchical clustering was performed in MATLAB (Mathworks). Villus and crypt cell quantification was performed with custom scripts in ImageJ with manual annotation using multiple fields of view per animal. For fully automated analysis, segmentation using nuclear markers (DAPI, Sox9, IL33, etc.) and membrane markers (PCK26, β-Catenin, etc.) was used to generate epithelial nuclear masks and count total epithelial cells. p-Creode was written in Python and analysis was performed on an Intel(R) Core(TM) i7-4790 CPU @ 3.60GHz with 32GB of RAM with Ubuntu 16.04.3 LTS. Down-sampled datasets with up to 14,000 datapoints can be analyzed with p-Creode with each independent iteration taking between 3–4 minutes each.

Statistical Considerations

For animal experiments, n refers to the number of animals used as independent biological replicates. For computational analyses, N refers to the number of resampled runs on the same data consisting of hundreds to thousands of cells. ANOVA and t-test were used based on previous data to quantify that the tuft cell distribution in the gut follows a Gaussian distribution over multiple samples (McKinley et al., 2017).

DATA AND SOFTWARE AVAILABILITY

Data Accessibility

The raw sequencing data for the colon is available in the Gene Expression Omnibus (GEO) database, accession number GSE102698, whereas the processed data are available on www.flowrepository.org (FR-FCM-ZYAG). MxIF data (small intestine and colon) are available on wsww.flowrepository.org (FR-FCM-ZY9Q).

Software Accessibility

p-Creode and its accompanying tutorial is available at https://github.com/KenLauLab/pCreode.

ADDITIONAL RESOURCES

Reprocessed Data

Previously generated data were reprocessed for this paper. Reprocessed scRNA-seq data for the lung (Treutlein et al., 2014), myeloid differentiation (Paul et al., 2015), and bone marrow mass cytometry data (Bendall et al., 2011) are available on www.flowrepository.org, accession numbers FR-FCM-ZYAW, FR-FCM-ZYAH, FR-FCM-ZY9R, respectively. Thymic datasets (Setty et al., 2016) were directly applied to p-Creode without changes and can be downloaded from the original manuscript.

Highlights.

• The p-Creode algorithm derives multi-branching trajectories from single-cell data

• p-Creode quantitatively assesses result quality by graph comparisons

• p-Creode reveals alternate origins of tuft cells between the intestine and colon

• Differential dependence of tuft cell specification on Atoh1 between the two regions