Abstract
The tumor microenvironment is an integral component in promoting tumor development. Cancer-associated fibroblasts (CAFs), which reside in the tumor stroma, produce Hepatocyte Growth Factor (HGF), an important trigger for invasive and metastatic tumor behavior. HGF contributes to a pro-tumorigenic environment by activating its cognate receptor, c-Met, on tumor cells. Tumor cells, in turn, secrete growth factors that upregulate HGF production in CAFs, thereby establishing a dynamic tumor-host signaling program. Using a spatiotemporal multispecies model of tumor growth, we investigate how the development and spread of a tumor is impacted by the initiation of a dynamic interaction between tumor-derived growth factors and CAF-derived HGF. We show that establishment of such an interaction results in increased tumor growth and morphological instability, the latter due in part to increased cell species heterogeneity at the tumor-host boundary. Invasive behavior is further increased if the tumor lowers responsiveness to paracrine pro-differentiation signals, which is a hallmark of neoplastic development. By modeling anti-HGF and anti-c-Met therapy, we show how disruption of the HGF/c-Met axis can reduce tumor invasiveness and growth, thereby providing theoretical evidence that targeting tumor-microenvironment interactions is a promising avenue for therapeutic development.
Keywords: cancer, stem cell, microenvironment, multiscale, computational model, feedback regulation, cancer therapy
Graphical abstract
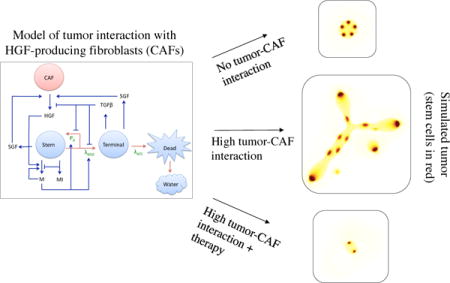
1. Introduction
The tumor microenvironment consists of vascular endothelial cells, pericytes, immune inflammatory cells, and cancer associated fibroblasts (CAFs), all which contribute to the hallmarks of cancer (Hanahan and Weinberg, 2011; Hanahan and Coussens, 2012). CAFs include both tissue-derived fibroblasts and recruited myofibroblasts, and promote tumor invasion and metastasis via secretion of growth factors and extracellular matrix (ECM) components (Kalluri and Zeisberg, 2006; Bhowmick et al., 2004). CAF-derived Hepatocyte Growth Factor, HGF, contributes to a pro-tumorigenic environment by activating its cognate receptor, c-Met. High HGF/c-Met activity has been identified in a large number of cancers and is correlated with more severe tumor grade and poor patient survival (Christensen et al., 2005; Matsumoto and Nakamura, 2006; Organ and Tsao, 2011). The signaling cascades triggered by c-Met include the PI3K/AKT, ERK/MAPK, NF-κB, Wnt/β-catenin, and STAT/JNK pathways, among others. These and other cascades contribute to a complex phenotypic response to HGF, which also depends on the cell type and culture conditions. Nevertheless, common responses of tumor cells include increased anchorage-independent growth, motility, and proliferation. Indeed, HGF was first termed Scatter Factor for its scattering effect on epithelial cells (Stoker and Perryman, 1985). Moreover, epithelial tubulogenesis is also observed in some cell types (Birchmeier et al., 2003; Trusolino et al., 2010; Organ and Tsao, 2011). Tumor cells secrete growth factors, including PDGF, TNFα, bFGF, and others (depending on tumor-type) that upregulate HGF production in CAFs (De Luca et al., 2010; Matsumoto and Nakamura, 2006), thereby establishing a dynamic tumor-host signaling program.
An additional heterogeneity in tumors results from intratumoral cell hierarchies, which are generally less robustly controlled and more heterogeneous than in normal tissues (Schatton et al., 2009; Medema, 2013). In vitro research on both primary tumor cells and established cancer cell lines has resulted in emergence of cancer stem cells (CSCs) as potential targets of new cancer therapeutics (Jordan et al., 2006). CSCs are currently regarded as a highly dynamic population, whose behavior is determined by both genetic and environmental factors, and may be, instead of a specific cell type amenable to therapeutic targeting, a phenotype that a large population of cancer cells can achieve in the appropriate environmental conditions (Zeuner et al., 2014; Kreso and Dick, 2014).
Mathematical models of tumor growth now compose several classes, including continuous, discrete, and hybrid; single compartment and multi-compartment (see (Byrne, 2010; Lowengrub et al., 2010; Deisboeck et al., 2011; Wang et al., 2015), for comprehensive reviews of the aforementioned model types). Incorporation of the microenvironment into these models involves adding an extra layer of complexity to an underlying model structure. Angiogenesis, macrophage infiltration, and stromal-mechanical perturbations have all been modeled by one or more of the previous model classes (Anderson et al., 2006; Eikenberry et al., 2009; Rejniak and McCawley, 2010; Eftimie et al., 2011; Katira et al., 2013; Frieboes et al., 2013; Welter and Rieger, 2013; Yan et al., 2016, 2017). Many of these modeling studies also include simulation of drug action in the complex milieu of the microenvironment. For example, Eikenberry et al. (2009) developed a partial differential equation model to investigate how surgical resection of a primary melanoma, along with its associated immune cells, would impact the stability of local metastases by disrupting the immune suppression induced by the primary tumor-resident immune cells. The model incorporated tumor-immune interactions into a spatially explicit system that could elucidate how therapy would impact the complex interplay of primary and satellite tumor cells with the immune response.
Despite the prevalence of tumor and tumor-microenvironment models, based on our current knowledge, no tissue-level models of CAF-tumor interactions have been developed that specifically addresses the HGF/c-Met and tumor-derived growth-factor signaling pathway dynamics. Using, as a starting point, a spatiotemporal, multispecies model of tumor growth that accounts for feedback signaling between CSCs and non-CSCs (Youssefpour et al., 2012; Yan et al., 2016, 2017), we investigate how the development and spread of a tumor is impacted by a dynamic interaction between tumor-derived growth factors and CAF-derived HGF, and the physiological effect of therapies directed at reducing the strength of this feedback mechanism.
2. The Mathematical Model
2.1. Overview
A multispecies continuum model of tumor growth with lineage dynamics and feedback regulation was developed by Youssefpour et al. (2012), who investigated two-stage lineages primarily in two dimensions and Yan et al. (2016), who investigated three-stage lineages in three dimensons. One-way coupling of HGF to tumor dynamics was investigated by Yan et al. (2017), where a non-monotonic effect of external HGF treatment on tumor shape was shown: a low dose increased morphological asymmetry, whereas a higher dose resulted in a larger, but more morphologically stable tumor. In this work, we extend the investigation of HGF-mediated tumor growth by developing a model that incorporates a dynamic, two-way coupling between the tumor and HGF-producing CAFs (Figure 1). The tumor tissue is modeled to be composed of three cell types: stem, terminal, and dead. While many cell lineage models also include committed progenitor cells as an intermediate phenotype between stem and terminal cells, our model classifies both committed progenitor and cancer stem cells in the stem cell category. We do this in order to lower the parameter burden and to simplify the model. In future work, we will consider these two compartments separately.
Figure 1.
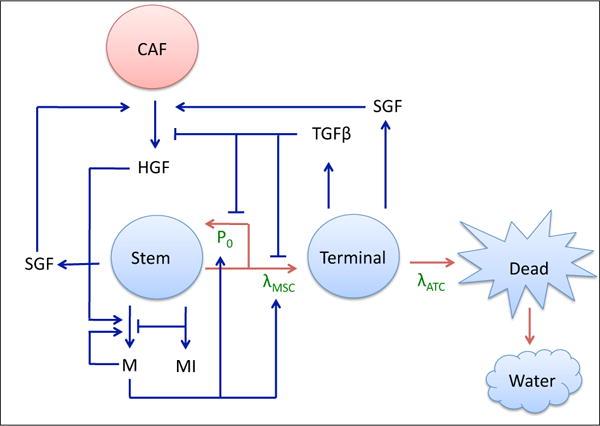
Tumor-CAF interaction model. Tumor components (water and stem, terminal, and dead cells) are in blue, the host component (CAF) is in red, and associated growth factors and proteins (c-Met (M), c-Met inhibitors (MI), HGF, SGF, TGFβ, and SGF) are in black. Critical parameters are in green, red arrows represent tumor species interconversion, and blue arrows represent chemical production and action. Stem cells renew with probability P0 and divide with rate λMSC. Terminal cells die at a rate λATC and dead cells are converted to water. P0 is promoted by products of the c-Met signaling cascade (M) and HGF, and lowered by TGFβ, which is produced by the terminal cells. c-Met production, in turn, is promoted by itself and HGF, and lowered by c-Met inhibitors (MI). HGF production by CAFs is promoted by SGF, which are produced by stem and terminal cells.
Stem cells have a probability of self-renewal, P0, and a division rate, λMSC, that are dependent upon negative feedback from TGFβ family members produced by terminal cells and positive feedback from products of the c-Met signaling cascade. Stem cell scatter and motility are also increased by c-Met (not shown in Figure 1). Additionally, c-Met is inhibited by stem-cell produced c-Met inhibitors. Cancer-associated fibroblasts, CAFs, reside in the host tissue, and interact with the tumor by secreting HGF, which is stimulated by release of stroma-acting growth factors (SGF) by the stem and terminal cells. HGF, in turn, promotes production of c-Met products. Terminal cells die at a rate λATC, and dead cells are eventually converted to water (Figure 1).
2.2. Cell species conservation, HGF-induced cell spread, and cell velocity
Local area fractions of the cell species (ϕCSC,TC,DC), host (ϕH), and water (ϕW) make up the dependent variables, which sum to 1. Assuming that that the total solid and water fractions are constant allows us to determine the water component via solid component dynamics. A conservation equation of the form
| (1) |
is assumed for each cell type, where ∗ denotes tumor cell species. A Helmholtz free energy of global adhesion is given by (Wise et al., 2008; Youssefpour et al., 2012)
| (2) |
where Ω is the domain occupied by the tumor and host, ϕT = ϕCSC + ϕTC + ϕDC is the total solid tumor area fraction, F(ϕT) models energy from local adhesion, ε models longer range component interactions, and γ is a global measure of cell-cell adhesion (incorporating both local and longer-range contributions to adhesion). Generalized diffusion for tumor components is represented by −∇·J*, where J* = −Mbϕ*∇μ. For the host, we have JH = MbϕT∇μ. Here, Mb is mobility and μ is the chemical potential,
| (3) |
Since the first discovery of HGF as a scatter factor for epithelial cells, HGF has been shown to have a pro-migratory effect on cells in the contexts of development, wound healing, and cancer (Birchmeier et al., 2003). The pro-migratory effect is mediated by several pleiotropic effects of activated c-Met on cell physiology. The c-Met-activated Ras cascade has been shown to be critical for disassembly of adherens junctions between tumor cells (Potempa and Ridley, 1998; Ueoka et al., 2000). Additionally, activated c-Met results in increased production of the proteolytic enzyme urokinase-type plasminogen activator (uPA) and its receptor (uPAR) (Jeffers et al., 1996; Nishimura et al., 2003). uPA catalyzes ECM degradation and remodeling, and is correlated with increased malignancy in several cancers (Sidenius and Blasi, 2003; Duffy, 2004; Ulisse et al., 2009). In MDCK cells, HGF-activated c-Met was found to further promote cell dispersal by enhancing cell-ECM interactions via modification of cellular transmembrane integrin protein activity (Trusolino et al., 2000).
We model the effect of c-Met on cell spread by having it act on the local interaction energy, F(ϕT), as follows. First, we model F as a double-well potential and represent it as a sum of its convex and concave parts, which model cell-cell repulsion (and attraction to ECM), and cell-cell attraction, respectively, with cell-cell adhesion arising from a balance between the two (Wise et al., 2008). We can model the effect of HGF as shifting this balance via its effect on c-Met. Accordingly, we introduce a weighting function g(CM) and modify F as follows,
| (4) |
| (5) |
| (6) |
where Ẽ > 0 is an energy scale and CM is the concentration of c-Met. When Ẽ(CM) = g(CM) = 1, the original F is recovered. As g(CM) decreases, F tends towards a single-well potential at ϕT = 1/2. By taking g(CM) as in (6), where δ1 is the strength of c-Met effect on g, we can obtain a shift towards the single-well potential with increasing c-Met. This allows us to model the breakdown of cell-cell adhesion and increase in cell-matrix adhesion promoted by c-Met. Additionally, by taking Ẽ as in (5), where δ2 indicates strength of c-Met action on Ẽ, we can model the local effect of c-Met on ECM remodeling, since an increased Ẽ increases the driving force of the components independently of whether F is a single- or double-well potential.
The cell velocity, us, is assumed to satisfy the generalized Darcy’s law, which is a constitutive equation that models fluid flow through a porous media (Wise et al., 2008; Lowengrub et al., 2010),
| (7) |
where κ reflects combined effects of cell-cell and cell-matrix adhesion, p is the solid pressure generated by cell proliferation, and μ is the chemical potential (3). We can sum the conservation equations to obtain an equation for velocity
| (8) |
with the assumption that the host is under homeostatic conditions (SrcH = 0). The pressure p can be obtained by solving Equations (7) and (8).
At the far-field boundary, Σ∞, of the domain, Ω, we impose no-flux, homogeneous Neumann boundary conditions: ∇ϕT,CSC,TC = ω∞ = 0, where ω∞ is the outwards-pointing normal vector on Σ∞. Chemical potential, μ, and pressure, p, have homogeneous Dirichlet conditions μ = p = 0 on Σ∞, allowing the tumor to move across the outer boundary (Wise et al., 2008).
2.3. The mass-exchange equations
Src* represents the mass-exchange terms, which incorporate mitosis, differentiation, death, and species conversion. The self-renewal rate of the CSCs is P0, and both the self-renewal and mitosis rates are proportional to the concentration of oxygen and nutrients, represented by a single variable CO. The source terms are as follows:
| (9) |
| (10) |
| (11) |
where mitosis, cell death, and lysis rates are denoted by λM*, λA, and λL, respectively, where ∗ indicates cell type. Proliferation is cut off at sufficiently low concentration by G(ϕ*), specifically, we take (Wise et al., 2008; Youssefpour et al., 2012)
| (12) |
2.4. Stem cell self-renewal and division
HGF/c-Met induces cellular proliferation via multiple signaling cascades, including Ras/Raf, PI3K/Akt, NF-κB, and Wnt/β-catenin (Birchmeier et al., 2003; Trusolino et al., 2010; Organ and Tsao, 2011; Muller et al., 2002; Li et al., 2015). Moreover, HGF/c-Met has been implicated in CSC development and maintenance in colon cancer (Vermeulen et al., 2010), glioblastoma (Li et al., 2011; Joo et al., 2012) and head and neck squamous cell carcinoma (HNSCC) (Lim et al., 2014). For example, Vermeulen et al. (2010) showed that HGF-induced β-catenin nuclear localization and activation of canonical Wnt signal was associated with increased cellular clonogenicity in primary colon cancer spheroid cultures, implicating the cascade in promoting the CSC phenotype. Similarly, Lim et al. (2014) have shown that in HNSCC HGF/c-Met promoted HNCSCC CSC marker expression and cell sphere-forming capacity. When c-Met was knocked down, the cells showed increased radiosensitivity and decreased ability to form tumors in a mouse xenograft model. HGF has also been shown to have an effect on reducing cell death rates (Xiao et al., 2001).
TGFβ is a potent growth inhibitor (Huang and Huang, 2005) and differentiation promoter (Watabe and Miyazono, 2009) for many cell types and early-stage tumors. We model the effect of c-Met and TGFβ on stem cell self-renewal and proliferation below. To lower the parameter burden, we maintain a low, and constant, apoptotic rate in the Src* equations that is not dependent on the growth factors. We take
| (13) |
| (14) |
where CTGFβ is the concentration of TGFβ, and Pmin,max and are the minimum and maximum rates of self-renewal and CSC division rates, respectively. The strength of the c-Met effect on P0 and λMSC is represented by ξ0 and ξ1, respectively, while the strength of the inhibitory TGFβ action on P0 and λMSC is represented by ψ0 and ψ1, respectively.
2.5. Chemical Species
2.5.1. Oxygen/Nutrients
The combined effect of oxygen and nutrients is denoted as O. Uptake is assumed to be negligible in the host in comparison to the tumor species, and diffusion rapid in comparison to the rate of cell proliferation (Wise et al., 2008; Youssefpour et al., 2012). Hence, the corresponding concentration CO can be modeled using a quasi-steady state equation,
| (15) |
where νUOCSC, νUOTC are the uptake rates by the CSCs and TCs, respectively, and DO is the diffusion coefficient. The rate of O entering the microenvironment is modeled by νPO, and the concentration of O in the medium sufficiently far from the tumor is given by , which is also taken to be the boundary condition on Σ∞, . The host domain is approximated by Q(c), an interpolating function from the tumor (Q = 0) to the host (Q = 1), and is taken to be (Wise et al., 2008)
| (16) |
where c = 1 − ϕT.
2.5.2. TGFβ
A diffusible differentiation promoter, produced by the terminal cells, is modeled by the variable TGFβ, which represents the TGFβ superfamily (Moses and Serra, 1996; Lombardo et al., 2011). Although in later stages of cancer TGFβ may be produced by other cells (namely stroma and immune), we do not model that here since this progression coincides with inactivation of certain TGFβ downstream signaling components and results in a phenotypically distinct role of TGFβ from its tumor-suppressing effects (Massagué, 2008). We model the loss of responsiveness to TGFβ in Section 3.3 and discuss approaches to modeling the ‘TGFβ paradox’ (i.e. its tumor-promoting actions) in Section 4.
Rapid diffusion is assumed for TGFβ due to the long-range action of some of its family members, such as Activin (Jones et al., 1996), which is directly involved in regulating epithelial tumorigenesis (Le Bras et al., 2014), or BMP4, which can have an effective long-range gradient due to long-range diffusion of its inhibitors (Jones and Smith, 1998; Dale and Wardle, 1999). Hence, we use a quasi-steady reaction-diffusion equation for CTGFβ,
| (17) |
where νUTGFβ is the uptake rate by CSCs, νDTGFβ is the decay rate, νPTGFβ is the production rate by TCs, and DTGFβ is the TGFβ diffusion coefficient. The boundary condition for CTGFβ is taken to be Dirichlet (CTGFβ = 0) on Σ∞.
2.5.3. c-Met and c-Met inhibitors
A generalized Geirer-Meinhardt-Turing system is used to model the interaction of the activator c-Met and its downstream products with their inhibitors (Turing, 1952; Gierer and Meinhardt, 1972). Such a system, with Wnt/Dkk as the activator/inhibitor pair has been suggested in hair follicle development (Sick et al., 2006), crypt generation (Zhang et al., 2012), and tumor development (Youssefpour et al., 2012). The large number of cross-activating downstream signaling components of c-Met, some of which include positive feedback loops amongst themselves (Verma et al., 2015; Syed et al., 2011), motivate a nonlinear c-Met activation term. Inhibitors of c-Met and the downstream effectors activated by induced c-Met include the autocrine-acting c-CBL (Petrelli et al., 2002), paracrine-acting Delta (Stella et al., 2005), and the secreted factor Dkk. Since c-Met products are autocrine or paracrine effectors, we take c-Met products to have a short-range, and c-Met inhibitors a long-range, diffusion coefficient. The functional correlation between cancer stem cells and enhanced c-Met activity has been discussed in Section 2.4, hence we model c-Met and c-Met inhibitor production to be limited primarily to CSCs. We also include low-level background production of c-Met by all viable tumor cell types. Since HGF activates c-Met products and induces c-Met production, we model the effect of HGF on c-Met by its positive effect on the production rate of c-Met. Finally, production is made dependent on nutrient (O) levels (in this model, we do not consider hypoxia-dependent c-Met upregulation (Trusolino et al., 2010)). We take
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
where CM and CMI are the concentrations of c-Met products and c-Met inhibitors, respectively, DM is the diffusion coefficient for downstream c-Met effectors, which is assumed to be small relative to the diffusion coefficient for c-Met inhibitors, DMI. The strength of positive feedback of HGF on c-Met is represented by , ηM represents background production of c-Met products, νPM, νDM are the respective production and decay rates of c-Met-activated proteins and νPMI, νDMI are the respective production and decay rates of c-Met inhibitor proteins. The production rate of c-Met-activated proteins, νPM, is taken to be the sum of ν0, the auto-activation rate of M, and .
We note that we have two HGF-dependent actions on c-Met production, with respective strengths and , due to the multi-modality of HGF action on c-Met and its downstream effectors. In order to better understand how each HGF-dependent action on c-Met affects c-Met product levels and tumor phenotype, we developed a reduced, homogenous model of the system and performed a Turing analysis on it in Appendix A.
We assume no flux, homogeneous Neumann, boundary conditions for c-Met and c-Met inhibitor chemical fields, hence we take ω∞·∇CM = ω∞·∇CMI = 0 on Σ∞.
2.5.4. HGF and stroma-acting growth factors (SGF)
Cancer cells secrete growth factors and cytokines such as TNFα, bFGF, and PDGF, which induce upregulation of HGF production in stroma-resident fibroblast cells (Gohda et al., 1994; Roletto et al., 1996; De Luca et al., 2010; Matsumoto and Nakamura, 2006). Because of the lack of definitive data, we cannot currently specify whether the CSCs preferentially release these growth factors, and if increased c-Met signal results in an increased release of these factors, thus we model a positive effect of the growth factors from all viable tumor tissue on HGF production by fibroblasts in the stroma. The fibroblasts are considered to be homogeneously, and densely, distributed within the stroma (Karagiannis et al., 2012), although there is evidence that ECM remodeling occurs at the tumor-host boundary to allow for tumor spread (Friedl and Wolf, 2008), we account for this phenomenon not via changing the host phenotype but by making tumor cells more motile (see Section 2.2)).
Additionally, there is substantial evidence that TGFβ is a negative regulator of HGF production in stroma-resident fibroblasts, and thus we include its inhibitory effect in the model (Gohda et al., 1992; Harrison et al., 2000; Matsumoto and Nakamura, 2006):
| (23) |
| (24) |
where CHGF is the concentration of HGF, νPHGF and νDHGF are the respective production and decay rates of HGF, and ζ is a value close to zero added to regularize the equation. The interpolation function Q(ϕT) ≈ 1 − ϕT is given by Equation (16), and DHGF is the diffusion coefficient for HGF. DHGF is taken to be smaller than the diffusion coefficients for the other growth factors due to its high molecular weight (Nakamura et al., 1989). The production rates of SGF by the stem and terminal cell fractions are νSGFS and νSGFT, respectively. The decay rate is νDSGF and DSGF is the diffusion rate of the growth factors. In the main text, we let νSGFS = νSGFT, and test the cases where SGF production is significantly higher for the CSC or terminal cell compartment in the Supplementary Material, Section S3.
2.6. Nondimensionalized Equations
The equations are nondimensionalized following (Wise et al., 2008; Youssefpour et al., 2012): we take the O diffusion scale, , and the mitosis time scale , where represents the mean of and . The diffusion length scale, l, is estimated to be l ≈ 150μm and the mitosis time scale to be τ ≈ 1 day following (Frieboes et al., 2006). The nondimensionalization procedure and parameters are described in Supplementary Material, Section S1 and Section 2.7, respectively. Below we show the equations that change after nondimensionalization, where the others are identical with the dimensional forms, except that variables and parameters are redefined, as explained in the Supplementary Material Section S1 and Section 2.7.
The nondimensionalized equations for O and TGFβ, respectively, are
| (25) |
| (26) |
The nondimensionalized equations for c-Met and c-Met inhibitors are
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
2.7. Nondimensionalized Model Parameters
The nondimensional parameter values used in the model are presented in Tables 1–2, for brevity, c-Met is shortened to M and c-Met inhibitors to MI. Since this model is an extension of the Youssefpour et al. (2012) model, with earlier versions published in Konstorum et al. (2013a,b), a majority are derived from these references, as identified by (*) for Youssepour et al. (2012) and (**) for Konstorum et al. (2013b), in the References column of Tables 1 – 2. Choices of other parameters are discussed in the main text. The reader is referred to the part of the text that address the specific parameter under the References column of Tables 1 – 2.
Table 1.
Nondimensionalized cell-level parameters (Sections 2.2 – 2.4, 2.6).
| Parameter | Description | Value | Reference | |
|---|---|---|---|---|
| γ | Global adhesion | −0.1 | (*) | |
| ε | Diffuse interface thickness | 0.05 | (*) | |
| Mb | Mobility | 10.0 | (*) | |
| δ1 | Strength of M effect on F(ϕT), measure of cell scatter | 0.02 | Section 3.2 | |
| δ2 | Strength of M effect on Ẽ, the energy scale | 0.02 | Section 3.2 | |
| κ | Pressure-dependent cell motility | 1.0 | (*) | |
| λMTC | TC mitosis rate | 0.1 | (*) | |
| λATC | TC death rate | 0.1 | (*) | |
| λL | DC lysis rate | 1.0 | (*) | |
| Pmin | Min. CSC self-renewal rate | 0.2 | (*) | |
| Pmax | Max. CSC self-renewal rate | 1.0 | (*) | |
| ξ0 | Strength of M action on P0 | 1.0 | (*) | |
| ψ0 | Strength of TGFβ action on P0 | 1.0 | Section 3.1 | |
|
|
Min. CSC mitosis rate | 0.5 | Estimated, (Frank, 2007, Chapter 12) | |
|
|
Max. CSC mitosis rate | 1.5 | Estimated, (Frank, 2007, Chapter 12) | |
| ξ1 | Strength of M action on λMSC | 0.5 | Estimated by simulation | |
| ψ1 | Strength of TGFβ action on λMSC | 0.5 | (**) |
Table 2.
Nondimensionalized chemical species parameters (Sections 2.5, 2.6).
| Parameter | Description | Value | Reference | |
|---|---|---|---|---|
| νUOTC | Oxygen uptake rate by TCs | 1.0 | (*) | |
| νPO | Oxygen transfer rate | 0.5 | (*) | |
| νUTGFβ | TGFβ uptake rate by CSCs | 0.05 | (*) | |
| νTGFβ | TGFβ decay rate | 0.0 | (*) | |
| νPTGFβ | TGFβ production rate by TCs | 0.1 | (*) | |
| DM | Diffusion of M effectors | 1.0 | (*) | |
| DMI | Diffusion of MI effectors | 25.0 | (*) | |
| ν0 | Strength of HGF-independent M activation | 1.0 | (*) | |
|
|
Strength of HGF-induced M activation | 0.5 | Section 3.2 | |
| νDM | M decay rate | 1.0 | (*) | |
| ηM | Background M production rate | 0.2 | (*) | |
| νDMI | MI Decay rate | 1.0 | (*) | |
| R | Reaction rate | 50.0 | (*) | |
| νPHGF | Strength of SGF on HGF activation | {5,10,15} | Sections 3.1, S3 | |
| νDHGF | HGF decay rate | 1.0 | (**) | |
| DHGF | HGF diffusion rate | 0.1 | (**) | |
| νSGFS | SGF production rate by CSCs | {5,10,15} | Section 3.1, S3 | |
| νSGFT | SGF production rate by TCs | {5,10,15} | Section 3.1, S3 | |
| νDSGF | SGF decay rate | 1.0 | (**) | |
| DSGF | SGF diffusion rate | 1.0 | (**) |
3. Results
An adaptive finite difference nonlinear multigrid method (Wise et al., 2008, 2011; Youssefpour et al., 2012) is used to solve the governing equations efficiently on a computational domain of [−20, 20]2. We solve for ϕT = ϕCSC + ϕTC + ϕDC, then we can calculate ϕTC = ϕT − (ϕCSC + ϕDC). To remove the high-order time step constraint incurred by an explicit method, we use an implicit 2nd order accurate time discretization of Crank-Nicholson type, and spatial derivatives are discretized using 2nd order accurate central difference approximations. In regions of large gradients, block structured Cartesian refinement is used to provide enhanced local resolution. For further details, see Wise et al. (2011) or Youssefpour et al. (2012).
We initialize the tumor with an asymmetrical shape and a 45/50/5 homogenous fractional distribution of SCs, TCs, and DCs (respectively). We note that changing the initial fractional distribution of cell compartments does not have a qualitative effect on the simulations. The initialized asymmetrical shape can be visualized in the inset in Figure 2(a), its mathematical formulation is described in the Supplementary Material, Section S2. This initial condition provides a diffuse interface representation of an asymmetrical tumor centered at the origin with maximum radius of . Choice of a different asymmetrical initial shape does not influence the results in a qualitative manner.
Figure 2.
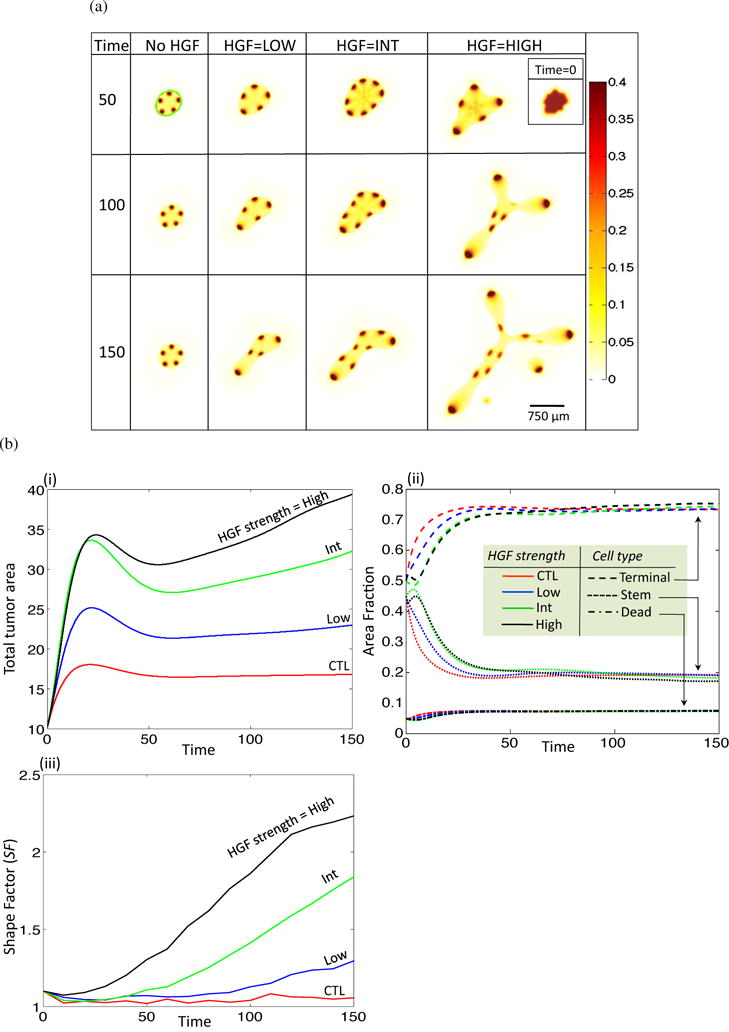
HGF feedback increases tumor growth rates and enhances invasiveness. (a) Stem cell fractions for increasing HGF dynamics and T = 50, 100, 150. Inset in top right corner shows initial tumor shape via visualization of the stem cell fraction for all HGF dynamics at T = 0. (b) Area, area fraction, and shape factor. (i) Total area and (ii) area fraction for no (red), low (blue), int (green) and high (black) HGF. Area fraction is shown for different cell types: terminal, dash; stem, dot; dead, dash-dot). (iii) Shape factor (SF) results for the four treatment types.
We take initial conditions for CM and CMI, the concentrations of c-Met and c-Met inhibitor, as identical to those for CW and CWI, the concentrations for Wnt and Wnt inhibitors, respectively, in Youssefpour et al. (2012) in order to maintain continuity with the former model in the sense that we want the control condition to be qualitatively similar to the model presented therein. We elaborate on our choice of initial conditions for CM, CMI, as well as for CSGF and CHGF in the Supplementary Material, Section S2. We note that other initial conditions for c-Met, c-Met inhibitor, HGF, and SGF produce qualitatively similar results. Since CO and CTGFβ satisfy quasi-steady diffusion equations, we need not take initial conditions for these fields.
3.1. Tumor progression with varying HGF feedback
We begin by simulating HGF dynamics in a tumor in its early stages, when response to inhibitory growth feedback is relatively strong. We do this by setting the TGFβ self-renewal feedback parameter, ψ0, to ψ0 = 1. In Youssefpour et al. (2012), the authors showed that a growing tumor with no HGF feedback and ψ0 = 1 grows slower and is more stable than a tumor with ψ0 = 0.5. In Section 3.3, we will show how HGF feedback alters tumor behavior with lowered response to TGFβ. We incorporate different strengths of HGF feedback (see below) at time T = 10 (recall T is measured in CSC cell cycles) in the simulation. We do this since we expect a delay between tumor initialization and microenvironmental recruitment, although there is evidence that in certain cases, mutations in microenvironmental components may drive tumorigenesis (Trimboli et al., 2009). In our system we consider the tumor as the initiator of the microenvironment-tumor interaction. We note that we do not observe qualitative differences between the choice of early T at which to start the HGF dynamics and the resulting tumor phenotype1.
Since the strength of the dynamic relationship between HGF and SGF feedback is unknown, we simulate growth of the tumor in four distinct conditions: none, low, intermediate (int), and high HGF feedback. To change the strength of feedback, we focus on three parameters found in equations (23) and (24), νPHGF, νSGFS, and νSGFT. The strength of SGF action on HGF is represented by νPHGF, and νSGFS,T are the respective production rates of SGF by the stem and terminal tissue fractions. For low (respectively, int, high) HGF, we set νPHGF = νSGFS = νSGFT = 5 (respectively 10, 15). With HGF dynamics initiated at T = 10, the stem cell fractions from the resulting simulations for T = 50, 100, and 150 are shown in Figure 2(a). The outline of the tumor body is clearly visible in all simulations, and is highlighted in green for the no HGF, T = 50 case. We see that as HGF dynamics increase from none to int, the number of stem cell spots increases, and there is a change to a more asymmetrical morphology. As HGF dynamics further increase to the high mode, the number of spots decreases, but the spot size increases, and there is a large change in the morphology with an increase in invasive fingering and tumor fragmentation (T = 150).
We observe that the rate of increase of total tumor area is positively correlated with increasing HGF strength (Figure 2(b)(i)), whereas the different cell fractions remain similar over all HGF strengths (Figure 2(b)(ii)). Indeed, it has been observed that cancer stem cells constitute a stable fraction of the tumor population (Dalerba et al., 2007). In order to measure the changes in morphology induced by HGF dynamics, we consider the shape factor, SF, for an object, which is calculated by
| (32) |
where P and A are the object perimeter and area, respectively. The shape factor for a circle is SF = 1, and increases as the shape of the object deviates from a circle. The shape factor tends to increase over time in all cases, but increases more drastically as HGF dynamics increase (Figure 2(b)(iii)), supporting the experimental results that HGF can induce branching and invasive morphology in exposed tissues and tumors, respectively (Brinkmann et al., 1995; Ikari et al., 2003; Wong et al., 2000).
We fix T = 100 in order to more closely observe other variables associated with the simulations, namely concentrations of c-Met, HGF, and SGF (Figure 3(a)) and total tumor, terminal cell, and dead cell fractions (Figure 3(b)). c-Met levels in the spots increase with increasing HGF dynamics, and there is an increase in HGF concentration at the tumor-host boundary and SGF concentration within the tumor (Figure 3(a)). A large fraction of all the cases contain terminal cells, with a smaller co-localized percentage of dead cells, and with both cell types concentrated outside of the areas with stem cell spots (Figure 3(b)).
Figure 3.
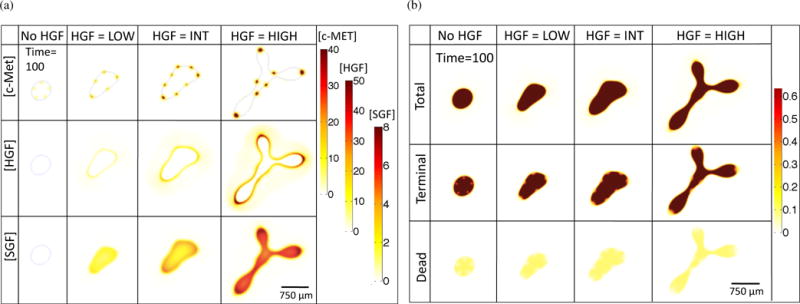
Chemical species (a) and cell species (b) concentrations for increasing HGF dynamics at T = 100.
3.2. HGF, cell scatter, and pattern formation
In order to better understand how HGF dynamics influence spot formation, we examine the early and late-time dynamics of the simulations with and without c-Met-induced cell scatter (the latter case is simulated by setting δ1,2 = 0 in Equations (5) and (6)). For brevity, we call the case with δ1,2 = 0, ‘ScOff’, and the case with δ1,2 = 0.02, ‘ScOn’. The values for δ1,2 were chosen to simulate a moderate, but observable effect, of HGF on cell-cell and cell-ECM interactions. We observe that c-Met-induced cell scatter results in loss of stem cell spots and an increase in invasive fingering (Figure 4(a)). We can quantify these effects by measuring the shape factor (SF, Equation (32)) and the stem scatter fraction (SSF) of the ScOn and ScOff simulations during the simulation runtime. We calculate the SSF by first measuring the concentration of stem cells in the host tissue, which is taken to be the area of stem cells in the host region normalized to the area of stem cells in the entire domain,
| (33) |
We find SSF and SF are increased for the ScOn compared to the ScOff case (Figure 4). This increase in SSF is due to the increased cell scatter, whereas the increase in SF is due to the increased heterogeneity of cell types and behavior at the tumor-host boundary.
Figure 4.
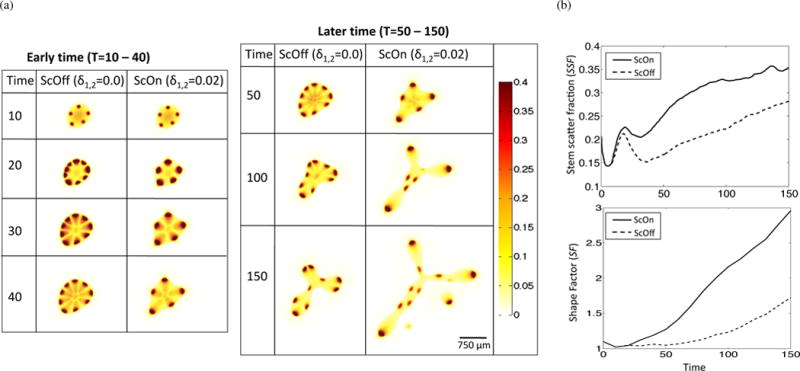
Effect of c-Met-mediated cell scatter on spot formation, tumor growth, and invasive morphology in high HGF conditions. (a) Stem cell distributions in HGF high conditions and without (ScOff, δ1,2 = 0.0) or with (ScOn, δ1,2 = 0.02) HGF-induced effect on cell scatter. (b) Quantification of stem scatter fraction (SSF) and shape factor (SF) for ScOff and ScOn simulations. Time-course data was smoothed using Moving Average Filtering in Matlab R2014b.
Pattern formation is also impacted by the respective strengths of in Equations (18), (20), and (21). In Figure 5, we observe that if , then as increases, we eventually see a continuous strip of stem cells at the tumor host boundary. Alternatively, setting and increasing does not result in the increase in spot number, but each spot is bigger, has higher c-Met and c-Met inhibitor concentrations, and gives rise to larger tumor fingers.
Figure 5.
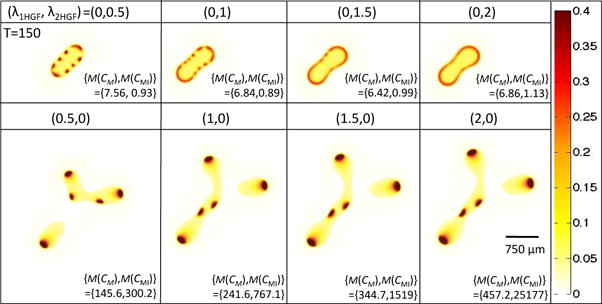
Isolating the effects of and in Equations (18), (20), and (21) on stem cell distributions and concentrations of c-Met and c-Met inhibitors. Stem cell distribution is shown for T = 150 and ( , ) as indicated. The bottom right-hand corner of each simulation shows the maximum concentration of c-Met and c-Met inhibitor that is reached (the short-hand M(X) = max(X) is used). Note that δ1 and δ2 in Equations (5) and (6) are set to 0 to control for the HGF-induced effect on cell scatter.
To obtain an analytical understanding of the effect of HGF action with respect to these two parameters, we performed a Turing Analysis on a reduced system of two equations modeling a nonlinear reaction-diffusion system with a forcing term (Appendix A). In the reduced system (A1), we find that an increase in the term νa, which is linearly proportional to , results in increased steady state ā and , which correspond to CM and CMI, respectively, in the original system, and no effect on the critical wavenumber, qmin, (Equation A6) or maximum eigenvalues (Equation A8) of Aq, as defined in Equation (A7). This system corresponds to the simulations with , where x is positive, as shown in the bottom row of Figure 5, where we indeed see no change in the number of stem cell spots, but do see an increase in both CM and CMI. Alternatively, the Turing Analysis on system (A9) shows that increasing the term Ea, which corresponds to in the original system, leads to a decrease in the critical wavenumber qmin and maximal eigenvalues of Aq (Figure A1). We would expect such a system to eventually become more stable with increasing Ea, especially at low νa, since the decrease in maximal eigenvalues indicates that the growth rates of the perturbations will decrease with increasing Ea. Although qmin is decreasing, which signals that we may find more unstable wave numbers, a very low perturbation growth rate suggests that pattern formation will not occur. In the original system, when we take , with x positive, we indeed see a uniform band of stem cells forming when is large enough (Figure 5).
3.3. Effect of negative feedback on tumor growth
A common characteristic of tumors that progress from pre-neoplastic lesions to neoplasms is that they lose the ability to respond to negative growth feedback signals (Hanahan and Weinberg, 2011). For example, in colorectal cancer, resistance to TGFβ by mutation of a cognate receptor is associated with progression from adenoma to malignant carcinoma (Grady et al., 1998). The TGFβ pathway can also be inactivated by a mutation of the TGFβ receptor TGFβR2 or by inactivation of downstream signaling components SMAD2, SMAD3, or SMAD4 (Markowitz and Bertagnolli, 2009).
Loss of response to members of the TGFβ family is correlated with poorer prognosis in a clinical setting (Pickup et al., 2013). Therefore, to model the effect of HGF dynamics in a tumor that has progressed beyond the initial stages, we reduce the strength of TGFβ feedback on stem cell self-renewal from ψ0 = 1.0 to ψ0 = 0.5. When compared to the the case with ψ0 = 1.0, the simulation results with reduced response to negative feedback have a greater total area and shape factor, indicating the enhanced invasive potential of such tumors (Figure 6).
Figure 6.
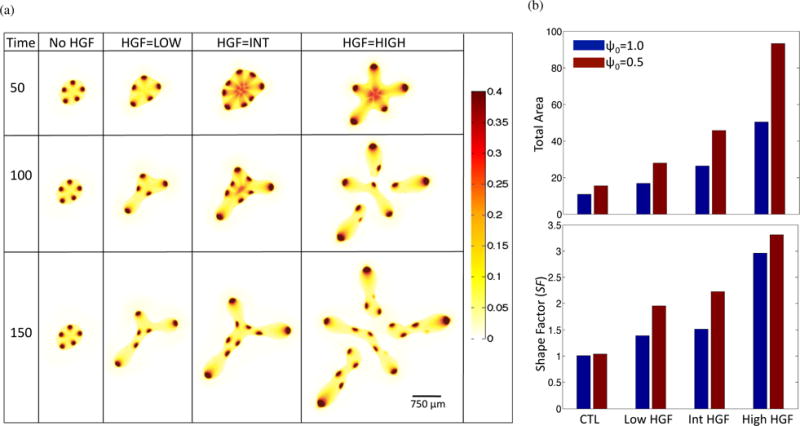
Tumor evolution under decreased negative feedback. From the baseline simulation, ψ0 in Equation (13) is lowered from 1.0 to 0.5. (a) Stem cell distributions for increasing HGF dynamics. (b) Comparison of total area (top panel) and shape factor (SF) (bottom panel) between ψ0 = 1 (blue) and ψ0 = 0.5 (red) simulations at T = 150.
3.4. Therapy
Therapies targeting various aspects of the HGF/c-Met axis, including antibodies against HGF and c-Met, HGF-competitive analogs, tyrosine kinase inhibitors (TKIs) targeting c-Met, and downstream pathway inhibitors are currently in development (Knudsen and Vande Woude, 2008; Blumenschein et al., 2012). Over 20 drugs are currently in Phase I–III clinical trials (Cecchi et al., 2012), indicating strong interest by the biomedical community in translating the accumulated knowledge of the HGF/c-Met axis into cancer therapeutics. We model targeted therapy by changing ν0, the strength of c-Met auto-activation, and , the strength of HGF-induced c-Met activation, in Equations (20) and (21). Lowering and models drugs that act by inhibiting HGF (class T1), while lowering ν0 represents drugs that specifically disrupt c-Met auto-catalysis. Drugs that inhibit c-Met or its downstream effectors lower both auto-catalysis rates and the ability of HGF to upregulate c-Met products (class T2). Therefore, activity of such drugs should be modeled by lowering all three parameters. We model class T1 and T2 drugs as follows, at T = 50 we apply either therapy T1, which lowers and from 0.5 to 0.05 or therapy T2, which lowers and to 0.005 and ν0 from 1.0 to 0.1 (Figure 7). We choose these two therapies as they represent two different classes of drugs as described above, and they also represent the two classes of therapy results that were observed when both parameters were systematically lowered for high HGF (Figure S2). Therapy is applied until the last time point, T = 150. We find that therapy class T1 results in decreased total area and shape factor, but it is the T2 class that results in a shape factor close to 1, indicating that the invasive morphology has been significantly reduced along with total tumor size. It has been shown that very strong inhibition of c-Met phosphorylation (> 90%) is required for significant inhibition of tumor growth (> 50%) in a tumor xenograft mouse model (Yamazaki et al., 2008), which is consistent with our simulation results. Additionally, we find that when therapy is terminated prematurely, the tumor grows back rapidly (Figure S2), indicating that ultimate tumor eradication requires combination therapy and/or surgical resection alongside anti-HGF/c-Met drugs. We note that in Yamazaki et al. (2008), mice were euthanized maximally 24 hours after the last therapy dose, which lasted between 9-11 days, hence it is not known what the tumor behavior would have been for a longer period after therapy cessation.
Figure 7.
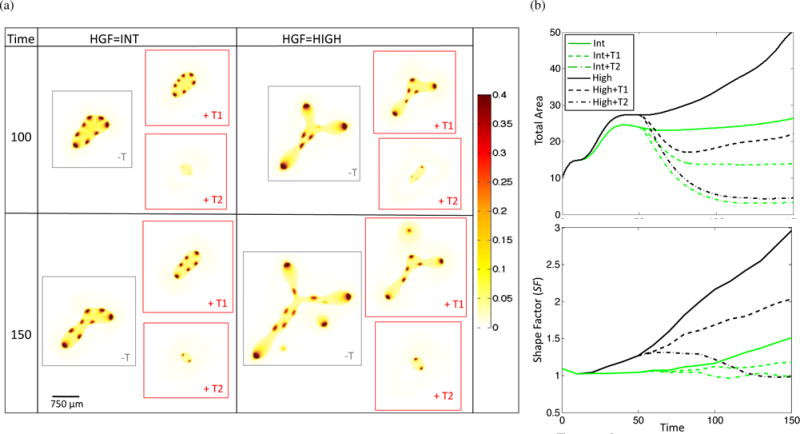
Response of tumor to anti-HGF (T1, and lowered from 0.5 to 0.05) and anti-c-Met (T2, and lowered from 0.5 to 0.005 and ν0 lowered from 1.0 to 0.1) therapy applied at T = 50. (a) Representative stem cell fraction and (b) total area and shape factor for no therapy, T1, and T2 applied to int and high HGF tumors.
4. Discussion
By incorporating tumor-produced SGF and the HGF/c-Met axis into a multispecies model of tumor growth, we have shown that establishment of a dynamic interaction between the tumor and its microenvironment results in increased tumor growth and morphological instability, the latter due in part to increased cell-species heterogeneity at the tumor-host boundary. Indeed, such a phenomenon has been investigated by Cristini et al. (2005). Using both experimental and simulation results, Cristini et al. (2005) showed that spatially heterogeneous cell proliferation, alongside disruption of cell-cell adhesion, results in invasive fingering and migration of cell clusters. In their model, the heterogeneity occurred due to heterogeneous distribution of oxygen, nutrients, and pH levels caused by atypical tumor vasculature and other disruptions to diffusion in the tumor. Similarly, in a hybrid cellular automata and PDE tumor growth model, Sottoriva et al. (2010) showed that a tumor that has a 100% CSC fraction yields a sphere-like morphology whereas tumors with low CSC fractions (in this model, CSCs differ from differentiated cells, DCs, in that CSCs have unlimited replicative potential, can migrate and mutate unlike the DCs), show invasive fingering with highly irregular shape. In our model, the heterogeneity occurs due to formation of stem cell spots at the tumor-host boundary via a Turing mechanism of c-Met and c-Met inhibitors. This heterogeneity is exacerbated by the presence of HGF-SGF signaling cross-talk since the effect of HGF on cell scatter results in a more irregular spot distribution at the tumor-host boundary, and the effect of HGF on proliferation/self-renewal increases the size of the remaining spots. Thus, when the effect of HGF on cell scatter is removed from the model, the tumor becomes more stable due to a more uniform distribution of stem cell spots at the tumor-host boundary, even though there are more such spots than in the original model (Figure 4). Cristini et al. (2005) propose that suppression of morphologic instability via homogenization of cell proliferation and increase in cell-cell adhesion will result in a more compact, noninvasive tumor morphology. Our therapy results support their conclusions: when we block the HGF/c-Met axis sufficiently enough to reduce the highly proliferative spot size, the tumor does not only grow more slowly, but it grows in a more compact manner (Figure 7).
We find that invasive behavior is further increased if the tumor lowers responsiveness to tumor-derived pro-differentiation signals, which is a traditional hallmark of neoplastic development (Hanahan and Weinberg, 2000). We have not addressed a portion of the pleiotropic effects of TGFβ that constitute the ‘TGFβ paradox’. Namely, our model does not consider that in certain cases, TGFβ can increase cellular motility, as well as hasten the Epithelial-to-Mesenchymal Transition (EMT) of tumorigenic epithelial cells (Pickup et al., 2013). Moreover, it has been found that in advanced cancers, immune components and fibroblasts can produce TGFβ, which has tumor-promoting effects (Massagué, 2008). In this study, we only model the anti-proliferative effects of TGFβ, with its production localized to terminal cells. Incorporation of the tumor-promoting action of TGFβ may be best done using a specific cancer model and data, since such effects show greater diversity among different cancers than the other growth factors modeled in this study.
By modeling anti-HGF and anti-c-Met therapy, we show how disruption of the HGF/c-Met cascade can lower tumor invasiveness and growth, thereby providing theoretical evidence that targeting tumor-microenvironment dynamics is a promising avenue for therapeutic development. An important consideration in clinical development of anti-HGF/c-Met therapies is patient selection and stratification. Studies on efficacy of HGF/c-Met targeted therapies have consistently shown that patients with high c-Met expression levels respond best to these therapies (Graveel et al., 2013), indicating that patient pre-selection based on tumor biomarkers of HGF/c-Met axis activation can improve therapy outcomes (Blumenschein et al., 2012). As our model assumes c-Met as a main driver in stem cell self-renewal and division rate, it is most directly applicable to patients with high c-Met activity.
Many of our assumptions and results are based upon quantification of specific features of the tumor and its microenvironment, including the spatially-distributed stem cell fraction of the tumor, and chemical diffusion, uptake, and activity coefficients. In order to better align our model with experimental observations, it is necessary to use an experimental system that is capable of recapitulating and capturing some of the complexities of the tumor microenvironment. In their review of emerging technologies in this field, Guldner and Zhang (2015) noted that new technology is necessary to explore the tumor microenvironment that incorporates spatial and temporal dynamics of tumor-microenvironmental interactions, and can measure cell-type specific behavior. They discuss emerging technologies that can aide in this goal, including deep tissue optical sectioning, intravital microscopy (IVM, the imaging of live animal tissue), and in situ cell-type specific genetic isolation. For example, Tanaka et al. (2012) used IVM in a liver metastatic xenograft system where RFP-labeled human colorectal cells were injected into GFP-expressing nude mice to obtain a time-series of of the phenotypic changes in tumor and host during liver metastasis and with and without chemotherapy. In addition, development of sophisticated 3D-culture systems where protein and drug diffusion and uptake rates can be measured via techniques such as FRAP or FLIM-FRET, which are already in use (Conway et al., 2014; Talukdar and Kundu, 2012). Therefore, it is possible to construct an appropriate experimental system to test the hypotheses generated by our model regarding quantifiable tumor behavior with an activated HGF/c-Met axis, such as increased invasiveness and formation of areas with high stem-cell concentration at the tumor-host boundary.
Supplementary Material
Highlights.
A multispecies continuum model is developed to investigate tumor-stroma interactions.
HGF, produced by stroma in response to tumor signals, promotes tumor instability.
Tumor instability occurs due to tumor cell species heterogeneity at the boundary.
Simulated therapies targeting this interaction can stabilize the tumor.
Appendix A Turing Analysis of Nonlinear Activator-Inhibitor dynamics with additional forcing term
A.1 Simplifed nonlinear activator-inhibitor model
In Equations (18) – (22) (nondimensionalized in Equations (27) – (31)), we model the effect of HGF on c-Met activation using two parameters, and . To better understand how each parameter affects pattern formation, we develop a simplified nonlinear model of activator-inhibitor dynamics and perform a Turing analysis on it. We begin with the system
| (A1) |
where a is the activator and b is the inhibitor, νa and νb are the respective production rates of a and b, and da and db are the respective decay rates of a and b. This system represents and νa as linearly proportional to . Taking and f2(a, b) = νba2−dbb, we find a stationary state without diffusion for (A1), i.e. we identify such that (f1, f2) = (0, 0). There is one solution,
| (A2) |
We note that ā is proportional to νa. Thus, we expect that if is negligible in the original system, then an increase in should result in higher steady state c-Met concentration.
In order to simplify stability analysis of the system, we take Da = 1 and Db = 25, analogous to nondimensionalized values for the parameters DM and DMI, respectively. The Jacobian of the system is
| (A3) |
Then, taking , we have
| (A4) |
In order for a and b to be stable in the absence of diffusion, we must have
a11 + a22 < 0,
a11a22 − a12a21 > 0,
which occurs if da − db < 0 and −dadb + 2dadb = dadb > 0. Diffusion will destabilize the system when the wavenumber, q, is near
| (A5) |
In our case, we obtain
| (A6) |
We find that qmin does not depend on νa. Moreover, the growth rate of perturbations to the steady state is given by the eigenvalues of the matrix
| (A7) |
The eigenvalues of Aq are
| (A8) |
Importantly, the eigenvalues also do not depend on νa.
We can thus conclude that in an activator-inhibitor reaction of this type, the steady state of a will be directly proportional to νa, but pattern formation will not be influenced.
A.2 Simplified nonlinear activator-inhibitor model with an additional forcing term
We now introduce the additional term Ea to system (A1) to represent non-trivial as follows:
| (A9) |
Taking and f2(a, b) = νba2−dbb, there is one real solution to the system (f1, f2) = (0, 0), but it is unwieldy analytically. Therefore, we find , A, qmin, and eiqenvalues of Aq for specific values of νa and Ea. We take νa = {5, 10, 15, 20} and Ea = {5, 10, 15, 20}. We also take da = db = νb = 1. We find the real-valued using the ‘solve’ function in Matlab for (f1, f2) = (0, 0).
In Figure A1(a,b), we observe that while increasing νa leads to an increase in both ā and , the effect of Ea on ā and is much less pronounced.
As before, we find A = (aij), the Jacobian of the system (f1(a, b), f2(a, b)) at and νb = da = db = 1,
| (A10) |
We note that for the values of νa and Ea considered, the conditions for stability of the system without diffusion (∗) are satisfied.
We use equation (A5) to calculate qmin for discrete values of νa and Ea (Figure A1c). We note that qmin decreases as Ea increases, and this decrease is stronger at lower values of νa. Moreover, taking Aq as in Equation (A7), with q = qmin, the maximum eigenvalue decreases with increasing Ea and decreasing νa (Figure A1(d)).
Figure A1.
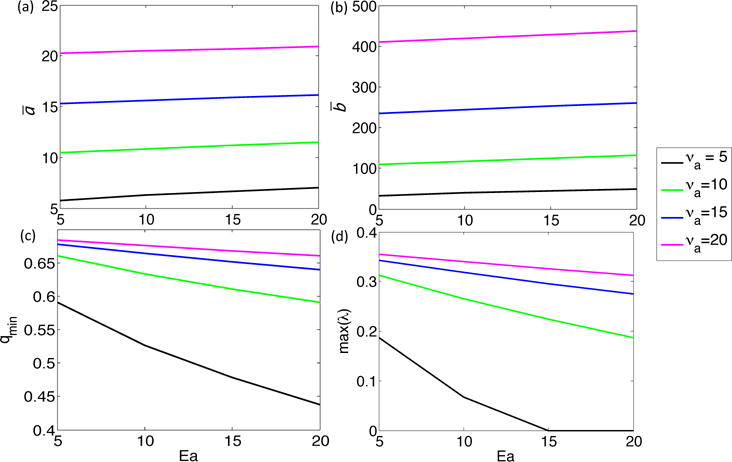
Effect of increasing νa and Ea in System A1 on (a) ā, (b) , (c) qmin, and (d) max(λ), where ā and give stationary states for the system without diffusion, qmin is the critical wavenumber for the system, and max(λ) is the maximum eigenvalue of Aq, where Aq is taken as in Equation (A7) with q = qmin.
Footnotes
An exception to this statement occurs if we include HGF dynamics at T < 2. During very early time, initial pattern formation occurs, and we have observed that the resulting phenotype becomes highly sensitive to parameter values and specific time of HGF dynamic initialization, whereas the system is much more robust if HGF dynamics are incorporated at T ≥ 2. Since we hypothesize that a time delay does occur between tumor initiation and formation of the HGF feedback loop, we present results of simulations when the HGF dynamic is initialized at T ≥ 2.
References
- Anderson ARA, Weaver AM, Cummings PT, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006 Dec;127(5):905–15. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- Bhowmick NA, Neilson EG, Moses HL. Stromal fibroblasts in cancer initiation and progression. Nature. 2004 Nov;432(7015):332–7. doi: 10.1038/nature03096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birchmeier C, Birchmeier W, Gherardi E, Vande Woude GF. Met, metastasis, motility and more. Nat Rev Mol Cell Biol. 2003 Dec;4(12):915–25. doi: 10.1038/nrm1261. [DOI] [PubMed] [Google Scholar]
- Blumenschein GR, Jr, Mills GB, Gonzalez-Angulo AM. Targeting the hepatocyte growth factor-cmet axis in cancer therapy. J Clin Oncol. 2012 Sep;30(26):3287–96. doi: 10.1200/JCO.2011.40.3774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinkmann V, Foroutan H, Sachs M, Weidner K, Birchmeier W. Hepatocyte growth factor/scatter factor induces a variety of tissue-specific morphogenic progrmas in epithelial cells. J Cell Biol. 1995;131(6 Pt 1):1573–86. doi: 10.1083/jcb.131.6.1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne HM. Dissecting cancer through mathematics: from the cell to the animal model. Nat Rev Cancer. 2010 Mar;10(3):221–30. doi: 10.1038/nrc2808. [DOI] [PubMed] [Google Scholar]
- Cecchi F, Rabe DC, Bottaro DP. Targeting the hgf/met signaling pathway in cancer therapy. Expert Opin Ther Targets. 2012 Jun;16(6):553–72. doi: 10.1517/14728222.2012.680957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen JG, Burrows J, Salgia R. c-met as a target for human cancer and characterization of inhibitors for therapeutic intervention. Cancer Lett. 2005 Jul;225(1):1–26. doi: 10.1016/j.canlet.2004.09.044. [DOI] [PubMed] [Google Scholar]
- Conway JRW, Carragher NO, Timpson P. Developments in preclinical cancer imaging: innovating the discovery of therapeutics. Nat Rev Cancer. 2014 May;14(5):314–28. doi: 10.1038/nrc3724. [DOI] [PubMed] [Google Scholar]
- Cristini V, Frieboes HB, Gatenby R, Caserta S, Ferrari M, Sinek J. Morphologic instability and cancer invasion. Clin Cancer Res. 2005 Oct;11(19 Pt 1):6772–9. doi: 10.1158/1078-0432.CCR-05-0852. [DOI] [PubMed] [Google Scholar]
- Dale L, Wardle FC. A gradient of bmp activity specifies dorsal-ventral fates in early xenopus embryos. Semin Cell Dev Biol. 1999 Jun;10(3):319–26. doi: 10.1006/scdb.1999.0308. [DOI] [PubMed] [Google Scholar]
- Dalerba P, Cho RW, Clarke MF. Cancer stem cells: models and concepts. Annu Rev Med. 2007;58:267–84. doi: 10.1146/annurev.med.58.062105.204854. [DOI] [PubMed] [Google Scholar]
- De Luca A, Gallo M, Aldinucci D, Ribatti D, Lamura L, D’Alessio A, De Filippi R, Pinto A, Normanno N. The role of the egfr ligand/receptor system in the secretion of angiogenic factors in mesenchymal stem cells. J Cell Physiol. 2010 Dec; doi: 10.1002/jcp.22548. [DOI] [PubMed] [Google Scholar]
- Deisboeck TS, Wang Z, Macklin P, Cristini V. Multiscale cancer modeling. Annu Rev Biomed Eng. 2011 Aug;13:127–55. doi: 10.1146/annurev-bioeng-071910-124729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy MJ. The urokinase plasminogen activator system: role in malignancy. Curr Pharm Des. 2004;10(1):39–49. doi: 10.2174/1381612043453559. [DOI] [PubMed] [Google Scholar]
- Eftimie R, Bramson JL, Earn DJD. Interactions between the immune system and cancer: a brief review of non-spatial mathematical models. Bull Math Biol. 2011 Jan;73(1):2–32. doi: 10.1007/s11538-010-9526-3. [DOI] [PubMed] [Google Scholar]
- Eikenberry S, Thalhauser C, Kuang Y. Tumor-immune interaction, surgical treatment, and cancer recurrence in a mathematical model of melanoma. PLoS Comput Biol. 2009 Apr;5(4):e1000362. doi: 10.1371/journal.pcbi.1000362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank S. Dynamics of Cancer: Incidence, Inheritence, and Evolution. Princeton University Press; 2007. [PubMed] [Google Scholar]
- Frieboes HB, Wu M, Lowengrub J, Decuzzi P, Cristini V. A computational model for predicting nanoparticle accumulation in tumor vasculature. PLoS One. 2013;8(2):e56876. doi: 10.1371/journal.pone.0056876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frieboes HB, Zheng X, Sun CH, Tromberg B, Gatenby R, Cristini V. An integrated computational/experimental model of tumor invasion. Cancer Res. 2006 Feb;66(3):1597–604. doi: 10.1158/0008-5472.CAN-05-3166. [DOI] [PubMed] [Google Scholar]
- Friedl P, Wolf K. Tube travel: the role of proteases in individual and collective cancer cell invasion. Cancer Res. 2008 Sep;68(18):7247–9. doi: 10.1158/0008-5472.CAN-08-0784. [DOI] [PubMed] [Google Scholar]
- Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik. 1972 Dec;12(1):30–39. doi: 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
- Gohda E, Matsunaga T, Kataoka H, Takebe T, Yamamoto I. Induction of hepatocyte growth factor in human skin fibroblasts by epidermal growth factor, platelet-derived growth factor and fibroblast growth factor. Cytokine. 1994 Nov;6(6):633–40. doi: 10.1016/1043-4666(94)90051-5. [DOI] [PubMed] [Google Scholar]
- Gohda E, Matsunaga T, Kataoka H, Yamamoto I. Tgf-beta is a potent inhibitor of hepatocyte growth factor secretion by human fibroblasts. Cell Biol Int Rep. 1992 Sep;16(9):917–26. doi: 10.1016/s0309-1651(06)80171-2. [DOI] [PubMed] [Google Scholar]
- Grady WM, Rajput A, Myeroff L, Liu DF, Kwon K, Willis J, Markowitz S. Mutation of the type ii transforming growth factor-beta receptor is coincident with the transformation of human colon adenomas to malignant carcinomas. Cancer Res. 1998 Jul;58(14):3101–4. [PubMed] [Google Scholar]
- Graveel CR, Tolbert D, Vande Woude GF. Met: a critical player in tumorigenesis and therapeutic target. Cold Spring Harb Perspect Biol. 2013 Jul;5(7) doi: 10.1101/cshperspect.a009209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guldner IH, Zhang S. A journey to uncharted territory: new technical frontiers in studying tumor-stromal cell interactions. Integr Biol (Camb) 2015 Feb;7(2):153–61. doi: 10.1039/c4ib00192c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D, Coussens LM. Accessories to the crime: functions of cells recruited to the tumor microenvironment. Cancer Cell. 2012 Mar;21(3):309–22. doi: 10.1016/j.ccr.2012.02.022. [DOI] [PubMed] [Google Scholar]
- Hanahan D, Weinberg R. The hallmarks of cancer. Cell. 2000;100(1):57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell. 2011 Mar;144(5):646–74. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- Harrison P, Bradley L, Bomford A. Mechanism of regulation of hgf/sf gene expression in fibroblasts by tgf-beta1. Biochem Biophys Res Commun. 2000 Apr;271(1):203–11. doi: 10.1006/bbrc.2000.2612. [DOI] [PubMed] [Google Scholar]
- Huang SS, Huang JS. Tgf-beta control of cell proliferation. J Cell Biochem. 2005 Oct;96(3):447–62. doi: 10.1002/jcb.20558. [DOI] [PubMed] [Google Scholar]
- Ikari T, Hiraki A, Seki K, Sugiura T, Matsumoto K, Shirasuna K. Involvement of hepatocyte growth factor in branching morphogenesis of murine salivary gland. Dev Dyn. 2003;228(2):173–84. doi: 10.1002/dvdy.10377. [DOI] [PubMed] [Google Scholar]
- Jeffers M, Rong S, Vande Woude GF. Enhanced tumorigenicity and invasion-metastasis by hepatocyte growth factor/scatter factor-met signalling in human cells concomitant with induction of the urokinase proteolysis network. Mol Cell Biol. 1996 Mar;16(3):1115–25. doi: 10.1128/mcb.16.3.1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones CM, Armes N, Smith JC. Signalling by tgf-beta family members: short-range effects of xnr-2 and bmp-4 contrast with the long-range effects of activin. Curr Biol. 1996 Nov;6(11):1468–75. doi: 10.1016/s0960-9822(96)00751-8. [DOI] [PubMed] [Google Scholar]
- Jones CM, Smith JC. Establishment of a bmp-4 morphogen gradient by long-range inhibition. Dev Biol. 1998 Feb;194(1):12–7. doi: 10.1006/dbio.1997.8752. [DOI] [PubMed] [Google Scholar]
- Joo KM, Jin J, Kim E, Ho Kim K, Kim Y, Gu Kang B, Kang YJ, Lathia JD, Cheong KH, Song PH, Kim H, Seol HJ, Kong DS, Lee JI, Rich JN, Lee J, Nam DH. Met signaling regulates glioblastoma stem cells. Cancer Res. 2012 Aug;72(15):3828–38. doi: 10.1158/0008-5472.CAN-11-3760. [DOI] [PubMed] [Google Scholar]
- Jordan CT, Guzman ML, Noble M. Cancer stem cells. N Engl J Med. 2006 Sep;355(12):1253–61. doi: 10.1056/NEJMra061808. [DOI] [PubMed] [Google Scholar]
- Kalluri R, Zeisberg M. Fibroblasts in cancer. Nat Rev Cancer. 2006 May;6(5):392–401. doi: 10.1038/nrc1877. [DOI] [PubMed] [Google Scholar]
- Karagiannis GS, Poutahidis T, Erdman SE, Kirsch R, Riddell RH, Diamandis EP. Cancer-associated fibroblasts drive the progression of metastasis through both paracrine and mechanical pressure on cancer tissue. Mol Cancer Res. 2012 Nov;10(11):1403–18. doi: 10.1158/1541-7786.MCR-12-0307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katira P, Bonnecaze RT, Zaman MH. Modeling the mechanics of cancer: effect of changes in cellular and extra-cellular mechanical properties. Front Oncol. 2013;3:145. doi: 10.3389/fonc.2013.00145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knudsen BS, Vande Woude G. Showering c-met-dependent cancers with drugs. Curr Opin Genet Dev. 2008 Feb;18(1):87–96. doi: 10.1016/j.gde.2008.02.001. [DOI] [PubMed] [Google Scholar]
- Konstorum A, Sprowl SA, Lander AD, Waterman ML, Lowengrub JS. Elaboration of a multispecies model of solid tumor growth with tumor-host interactions. Proc 3rd Int Conf Appl Nonlinear Dynamics. 2013a:295–303. [Google Scholar]
- Konstorum A, Sprowl SA, Waterman ML, Lander AD, Lowengrub JS. Predicting mechanism of biphasic growth factor action on tumor growth using a multi-species model with feedback control. J Coupled Syst Multiscale Dyn. 2013b Dec;1(4):459–467. doi: 10.1166/jcsmd.2013.1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreso A, Dick JE. Evolution of the cancer stem cell model. Cell Stem Cell. 2014 Mar;14(3):275–91. doi: 10.1016/j.stem.2014.02.006. [DOI] [PubMed] [Google Scholar]
- Le Bras GF, Loomans HA, Taylor CJ, Revetta FL, Andl CD. Activin a balance regulates epithelial invasiveness and tumorigenesis. Lab Invest. 2014 Oct;94(10):1134–46. doi: 10.1038/labinvest.2014.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Xin X, Wu T, Hua T, Wang H, Wang H. Stromal cells of endometrial carcinoma promotes proliferation of epithelial cells through the hgf/c-met/akt signaling pathway. Tumour Biol. 2015 Mar; doi: 10.1007/s13277-015-3309-2. [DOI] [PubMed] [Google Scholar]
- Li Y, Li A, Glas M, Lal B, Ying M, Sang Y, Xia S, Trageser D, Guerrero-Cázares H, Eberhart CG, Quiñones-Hinojosa A, Scheffler B, Laterra J. c-met signaling induces a reprogramming network and supports the glioblastoma stem-like phenotype. Proc Natl Acad Sci U S A. 2011 Jun;108(24):9951–6. doi: 10.1073/pnas.1016912108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim YC, Kang HJ, Moon JH. C-met pathway promotes self-renewal and tumorigenecity of head and neck squamous cell carcinoma stem-like cell. Oral Oncol. 2014 Jul;50(7):633–9. doi: 10.1016/j.oraloncology.2014.04.004. [DOI] [PubMed] [Google Scholar]
- Lombardo Y, Scopelliti A, Cammareri P, Todaro M, Iovino F, Ricci-Vitiani L, Gulotta G, Dieli F, de Maria R, Stassi G. Bone morphogenetic protein 4 induces differentiation of colorectal cancer stem cells and increases their response to chemotherapy in mice. Gastroenterology. 2011 Jan;140(1):297–309. doi: 10.1053/j.gastro.2010.10.005. [DOI] [PubMed] [Google Scholar]
- Lowengrub JS, Frieboes HB, Jin F, Chuang YL, Li X, Macklin P, Wise SM, Cristini V. Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity. 2010;23(1):R1–R9. doi: 10.1088/0951-7715/23/1/r01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz SD, Bertagnolli MM. Molecular origins of cancer: Molecular basis of colorectal cancer. N Engl J Med. 2009 Dec;361(25):2449–60. doi: 10.1056/NEJMra0804588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massagué J. Tgfbeta in cancer. Cell. 2008 Jul;134(2):215–30. doi: 10.1016/j.cell.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto K, Nakamura T. Hepatocyte growth factor and the met system as a mediator of tumor-stromal interactions. Int J Cancer. 2006 Aug;119(3):477–483. doi: 10.1002/ijc.21808. [DOI] [PubMed] [Google Scholar]
- Medema JP. Cancer stem cells: the challenges ahead. Nat Cell Biol. 2013 Apr;15(4):338–44. doi: 10.1038/ncb2717. [DOI] [PubMed] [Google Scholar]
- Moses HL, Serra R. Regulation of differentiation by tgf-beta. Curr Opin Genet Dev. 1996 Oct;6(5):581–6. doi: 10.1016/s0959-437x(96)80087-6. [DOI] [PubMed] [Google Scholar]
- Muller T, Bain G, Wang X, Papkoff J. Regulation of epithelial cell migration and tumor formation by beta-catenin signaling. Exp Cell Res. 2002 Oct;280(1):119–133. doi: 10.1006/excr.2002.5630. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Nishizawa T, Hagiya M, Seki T, Shimonishi M, Sugimura A, Tashiro K, Shimizu S. Molecular cloning and expression of human hepatocyte growth factor. Nature. 1989 Nov;342(6248):440–3. doi: 10.1038/342440a0. [DOI] [PubMed] [Google Scholar]
- Nishimura K, Matsumiya K, Miura H, Tsujimura A, Nonomura N, Matsumoto K, Nakamura T, Okuyama A. Effects of hepatocyte growth factor on urokinase-type plasminogen activator (upa) and upa receptor in du145 prostate cancer cells. Int J Androl. 2003 Jun;26(3):175–9. doi: 10.1046/j.1365-2605.2003.00413.x. [DOI] [PubMed] [Google Scholar]
- Organ SL, Tsao MS. An overview of the c-met signaling pathway. Ther Adv Med Oncol. 2011 Nov;3(1 Suppl):S7–S19. doi: 10.1177/1758834011422556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrelli A, Gilestro GF, Lanzardo S, Comoglio PM, Migone N, Giordano S. The endophilin-cin85-cbl complex mediates ligand-dependent downregulation of c-met. Nature. 2002 Mar;416(6877):187–90. doi: 10.1038/416187a. [DOI] [PubMed] [Google Scholar]
- Pickup M, Novit S, Moses H. The roles of tgf-beta in the tumour microenvironment. Nat Rev Cancer. 2013;13(11):788–99. doi: 10.1038/nrc3603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potempa S, Ridley AJ. Activation of both map kinase and phosphatidylinositide 3-kinase by ras is required for hepatocyte growth factor/scatter factor-induced adherens junction disassembly. Mol Biol Cell. 1998 Aug;9(8):2185–200. doi: 10.1091/mbc.9.8.2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejniak KA, McCawley LJ. Current trends in mathematical modeling of tumor-microenvironment interactions: a survey of tools and applications. Exp Biol Med (Maywood) 2010 Apr;235(4):411–23. doi: 10.1258/ebm.2009.009230. [DOI] [PubMed] [Google Scholar]
- Roletto F, Galvani AP, Cristiani C, Valsasina B, Landonio A, Bertolero F. Basic fibroblast growth factor stimulates hepatocyte growth factor/scatter factor secretion by human mesenchymal cells. J Cell Physiol. 1996 Jan;166(1):105–11. doi: 10.1002/(SICI)1097-4652(199601)166:1<105::AID-JCP12>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Schatton T, Frank NY, Frank MH. Identification and targeting of cancer stem cells. Bioessays. 2009 Oct;31(10):1038–49. doi: 10.1002/bies.200900058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sick S, Reinker S, Timmer J, Schlake T. Wnt and dkk determine hair follicle spacing through a reaction-diffusion mechanism. Science. 2006 Dec;314(5804):1447–50. doi: 10.1126/science.1130088. [DOI] [PubMed] [Google Scholar]
- Sidenius N, Blasi F. The urokinase plasminogen activator system in cancer: recent advances and implication for prognosis and therapy. Cancer Metastasis Rev. 2003;22(2-3):205–22. doi: 10.1023/a:1023099415940. [DOI] [PubMed] [Google Scholar]
- Sottoriva A, Verhoeff JJC, Borovski T, McWeeney SK, Naumov L, Medema JP, Sloot PMA, Vermeulen L. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 2010 Jan;70(1):46–56. doi: 10.1158/0008-5472.CAN-09-3663. [DOI] [PubMed] [Google Scholar]
- Stella MC, Trusolino L, Pennacchietti S, Comoglio PM. Negative feedback regulation of met-dependent invasive growth by notch. Mol Cell Biol. 2005 May;25(10):3982–96. doi: 10.1128/MCB.25.10.3982-3996.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoker M, Perryman M. An epithelial scatter factor released by embryo fibroblasts. J Cell Sci. 1985 Aug;77:209–23. doi: 10.1242/jcs.77.1.209. [DOI] [PubMed] [Google Scholar]
- Syed ZA, Yin W, Hughes K, Gill JN, Shi R, Clifford JL. Hgf/c-met/stat3 signaling during skin tumor cell invasion: indications for a positive feedback loop. BMC Cancer. 2011;11:180. doi: 10.1186/1471-2407-11-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talukdar S, Kundu SC. A non-mulberry silk fibroin proten based 3d in vitro tumor model for evaluation of anticancer drug activity. ADvanced Functional Materials. 2012;22(22):4778–4788. [Google Scholar]
- Tanaka K, Okigami M, Toiyama Y, Morimoto Y, Matsushita K, Kawamura M, Hashimoto K, Saigusa S, Okugawa Y, Inoue Y, Uchida K, Araki T, Mohri Y, Mizoguchi A, Kusunoki M. In vivo real-time imaging of chemotherapy response on the liver metastatic tumor microenvironment using multiphoton microscopy. Oncol Rep. 2012 Nov;28(5):1822–30. doi: 10.3892/or.2012.1983. [DOI] [PubMed] [Google Scholar]
- Trimboli AJ, Cantemir-Stone CZ, Li F, Wallace JA, Merchant A, Creasap N, Thompson JC, Caserta E, Wang H, Chong JL, Naidu S, Wei G, Sharma SM, Stephens JA, Fernandez SA, Gurcan MN, Weinstein MB, Barsky SH, Yee L, Rosol TJ, Stromberg PC, Robinson ML, Pepin F, Hallett M, Park M, Ostrowski MC, Leone G. Pten in stromal fibroblasts suppresses mammary epithelial tumours. Nature. 2009 Oct;461(7267):1084–91. doi: 10.1038/nature08486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trusolino L, Bertotti A, Comoglio PM. Met signalling: principles and functions in development, organ regeneration and cancer. Nat Rev Mol Cell Biol. 2010 Dec;11(12):834–48. doi: 10.1038/nrm3012. [DOI] [PubMed] [Google Scholar]
- Trusolino L, Cavassa S, Angelini P, Andó M, Bertotti A, Comoglio PM, Boccaccio C. Hgf/scatter factor selectively promotes cell invasion by increasing integrin avidity. FASEB J. 2000 Aug;14(11):1629–40. doi: 10.1096/fj.14.11.1629. [DOI] [PubMed] [Google Scholar]
- Turing AM. The chemical basis of morphogenesis. j-PHILOS-TRANS-R-SOC-LOND-SER-B-BIO-SCI B. 1952 Aug;237(641):37–72. [Google Scholar]
- Ueoka Y, Kato K, Kuriaki Y, Horiuchi S, Terao Y, Nishida J, Ueno H, Wake N. Hepatocyte growth factor modulates motility and invasiveness of ovarian carcinomas via ras-mediated pathway. Br J Cancer. 2000 Feb;82(4):891–9. doi: 10.1054/bjoc.1999.1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulisse S, Baldini E, Sorrenti S, D’Armiento M. The urokinase plasminogen activator system: a target for anti-cancer therapy. Curr Cancer Drug Targets. 2009 Feb;9(1):32–71. doi: 10.2174/156800909787314002. [DOI] [PubMed] [Google Scholar]
- Verma N, Keinan O, Selitrennik M, Karn T, Filipits M, Lev S. Pyk2 sustains endosomal-derived receptor signalling and enhances epithelial-to-mesenchymal transition. Nat Commun. 2015;6:6064. doi: 10.1038/ncomms7064. [DOI] [PubMed] [Google Scholar]
- Vermeulen L, De Sousa E Melo F, van der Heijden M, Cameron K, de Jong JH, Borovski T, Tuynman JB, Todaro M, Merz C, Rodermond H, Sprick MR, Kemper K, Richel DJ, Stassi G, Medema JP. Wnt activity defines colon cancer stem cells and is regulated by the microenvironment. Nat Cell Biol. 2010 May;12(5):468–476. doi: 10.1038/ncb2048. [DOI] [PubMed] [Google Scholar]
- Wang Z, Butner JD, Kerketta R, Cristini V, Deisboeck TS. Simulating cancer growth with multiscale agent-based modeling. Semin Cancer Biol. 2015 Feb;30:70–8. doi: 10.1016/j.semcancer.2014.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watabe T, Miyazono K. Roles of tgf-beta family signaling in stem cell renewal and differentiation. Cell Res. 2009 Jan;19(1):103–15. doi: 10.1038/cr.2008.323. [DOI] [PubMed] [Google Scholar]
- Welter M, Rieger H. Interstitial fluid flow and drug delivery in vascularized tumors: a computational model. PLoS One. 2013;8(8):e70395. doi: 10.1371/journal.pone.0070395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise S, Lowengrub J, Cristini V. An adaptive multigrid algorithm for simulating solid tumor growth using mixture models. Mathematical and Computer Modelling. 2011 Jan;53(1-2):1–20. doi: 10.1016/j.mcm.2010.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise SM, Lowengrub JS, Frieboes HB, Cristini V. Three-dimensional multispecies nonlinear tumor growth–i model and numerical method. J Theor Biol. 2008 Aug;253(3):524–43. doi: 10.1016/j.jtbi.2008.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong A, Leung P, Auersperg N. Hepatocyte growth factor promotes in vitro scattering and morphogenesis of humanc cervical carcinomal cells. Gynocel Oncol. 2000;78(2):158–65. doi: 10.1006/gyno.2000.5877. [DOI] [PubMed] [Google Scholar]
- Xiao GH, Jeffers M, Bellacosa A, Mitsuuchi Y, Vande Woude GF, Testa JR. Anti-apoptotic signaling by hepatocyte growth factor/met via the phosphatidylinositol 3-kinase/akt and mitogen-activated protein kinase pathways. Proc Natl Acad Sci U S A. 2001 Jan;98(1):247–52. doi: 10.1073/pnas.011532898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki S, Skaptason J, Romero D, Lee JH, Zou HY, Christensen JG, Koup JR, Smith BJ, Koudriakova T. Pharmacokinetic-pharmacodynamic modeling of biomarker response and tumor growth inhibition to an orally available cmet kinase inhibitor in human tumor xenograft mouse models. Drug Metab Dispos. 2008 Jul;36(7):1267–74. doi: 10.1124/dmd.107.019711. [DOI] [PubMed] [Google Scholar]
- Yan H, Konstorum A, Lowengrub J. Three-dimensional spatiotemporal modeling of colon cancer organoids reveals that multimodal control of stem cell self-renewal is a critical determinant of size and shape in early stages of tumor growth. Bulletin of Mathematical Biology. 2017 doi: 10.1007/s11538-017-0294-1. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan H, Romero-Lopez M, Frieboes HB, Hughes CCW, Lowengrub JS. Multiscale modeling of glioblastoma suggests that the partial disruption of vessel/cancer stem cell crosstalk can promote tumor regression without increasing invasiveness. IEEE Trans Biomed Eng. 2016 Oct; doi: 10.1109/TBME.2016.2615566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Youssefpour H, Li X, Lander AD, Lowengrub JS. Multispecies model of cell lineages and feedback control in solid tumors. J Theor Biol. 2012 Jul;304:39–59. doi: 10.1016/j.jtbi.2012.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuner A, Todaro M, Stassi G, De Maria R. Colorectal cancer stem cells: From the crypt to the clinic. Cell Stem Cell. 2014 Dec;15(6):692–705. doi: 10.1016/j.stem.2014.11.012. [DOI] [PubMed] [Google Scholar]
- Zhang L, Lander AD, Nie Q. A reaction-diffusion mechanism influences cell lineage progression as a basis for formation, regeneration, and stability of intestinal crypts. BMC Syst Biol. 2012;6:93. doi: 10.1186/1752-0509-6-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


