Abstract
The magnitude of diffusive carbon dioxide (CO2) and methane (CH4) emission from man-made reservoirs is uncertain because the spatial variability generally is not well-represented. Here, we examine the spatial variability and its drivers for partial pressure, gas-exchange velocity (k), and diffusive flux of CO2 and CH4 in three tropical reservoirs using spatially resolved measurements of both gas concentrations and k. We observed high spatial variability in CO2 and CH4 concentrations and flux within all three reservoirs, with river inflow areas generally displaying elevated CH4 concentrations. Conversely, areas close to the dam are generally characterized by low concentrations and are therefore not likely to be representative for the whole system. A large share (44–83%) of the within-reservoir variability of gas concentration was explained by dissolved oxygen, pH, chlorophyll, water depth, and within-reservoir location. High spatial variability in k was observed, and kCH4 was persistently higher (on average, 2.5 times more) than kCO2. Not accounting for the within-reservoir variability in concentrations and k may lead to up to 80% underestimation of whole-system diffusive emission of CO2 and CH4. Our findings provide valuable information on how to develop field-sampling strategies to reliably capture the spatial heterogeneity of diffusive carbon fluxes from reservoirs.
Introduction
Reservoirs, or artificial lakes formed by river damming, are sites of intense carbon (C) processing, with substantial influence on the global C budget.1−3 Globally, reservoirs emit 51 Tg of C year–1 to the atmosphere, of which 36.8 Tg year–1 is emitted as carbon dioxide (CO2) and 13.3 Tg year–1 as methane (CH4).3 If global-warming potential is taken into account, CH4 (28 times higher global warming potential than CO2 over a 100 year time period)4 is responsible for reservoirs impact on global greenhouse gas emissions. CO2 and CH4 emissions from reservoirs vary greatly in both space and time,5 but the variability of fluxes and their drivers remain poorly understood. Consequently, there is high uncertainty in global estimates of C emissions from reservoirs.6,7
Part of the CH4 emission (∼40% of total) and most of the CO2 emission (>90% of the total) from reservoirs occur via molecular diffusion at the air–water interface (the remainder being emitted through ebullition).3 Gas diffusion rates are controlled by the product of the difference in concentration between a gas in water and air and the gas-exchange velocity (k).8−10 Typically, gas concentration measurements are performed in fewer than 10 sites per reservoir, and a single value of k, estimated from wind speed, is assumed to calculate diffusive emission for an entire reservoir.3 The simplicity of such approach, however, may be deceptive, because C dynamics, and CO2 and CH4 fluxes, in freshwaters are results from complex interactions between local hydrological and biogeochemical processes and may, thus, vary greatly in space.11 Different regions of a reservoir may show different C dynamics in the water column,12 as a result of large heterogeneity in the type of the flooded biomass and sediment, organic and inorganic material inputs from rivers, primary production rates, bacterial respiration rates, and dam operation regime.5,13 For example, high particulate organic carbon (OC) import from the catchment in river inflow areas may lead to high sediment deposition and CO2 and CH4 production.13−16 However, while the large spatial variability of CO2 diffusive fluxes from reservoirs has been demonstrated in a few systems,5 there has been no assessments of the overall spatial variability in CH4 emissions from reservoirs that we know.
The k is a function of water turbulence, which is largely dependent on wind speed and driven by convective mixing only at low wind speed.17 Therefore, k is commonly scaled from wind speed,8,18 but the scaling relationships are highly uncertain.8 Wind speed measurements are often done at only one or a few sites or are obtained from nearby meteorological stations and are therefore unlikely to represent site-specific patterns. Alternatively, floating chambers (FC) are frequently used to measure emission directly, but they are only capable of covering a small window in space and time. Whereas high water turbulence and high k can be expected at river inflow areas or in open, wind-exposed areas, low water turbulence, and low k are expected in narrow, wind-protected bays. Such variabilities are unaccounted for at present, and the resulting diffusion estimates are consequently uncertain. To account for the complex dynamics of the parameters that modify the rate of GHG emission for large impoundments, good spatial coverage needs to be performed by sampling.5,19
Here, we test the hypothesis that the diffusive emission of CO2 and CH4 from tropical reservoirs is characterized by strong spatial variability and the fact that emissions are underestimated if measurements are only made close to the dam, which we consider to be cold spots of emission. We studied three tropical reservoirs located in different biomes of Brazil (Amazon, Cerrado (Savannah), and Atlantic Forest) because tropical reservoirs are important sources of C emission2 but still poorly represented in the most recent global estimate.3 This is particularly problematic given the large number of existing reservoirs in the tropics and the projected increase in hydropower production in tropical countries.20 We used spatially resolved concentration measurements (1 measurement every 2 m) with an online equilibration system in combination with spatially resolved measurements of k with FC. We investigate how spatial resolution of C concentration and k measurements can affect the whole-reservoir C flux estimates.
Experimental Section
Study Sites
We studied three tropical reservoirs located in different biomes in Brazil: Chapéu D’Uvas (CDU), Curuá-Una (CUN), and Furnas (FNS) (Table 1). CDU is a 12 km2 oligotrophic water supply reservoir located in the Atlantic Forest biome. CUN is a 72 km2 oligotrophic hydroelectric reservoir located in the Amazon. FNS is a 1342 km2 hydroelectric reservoir located in the Cerrado (Savannah) biome, with two different arms that exhibit distinct trophic states: the northern arm is mesotrophic, whereas the southern arm is eutrophic (Figure S1). The climate in all reservoirs is characterized by rainy summers and dry winters.21
Table 1. Location and Features of the Three Reservoirs.
| CDU | CUN | FNS | |
|---|---|---|---|
| coordinates | 21°33′ S 43°35′ W | 2°50′ S 54°18′W | 20°39′ S 46°18′ W |
| biome | Atlantic Forest | Amazonia | Cerrado (Savannah) |
| year of operation | 1994 | 1977 | 1963 |
| reservoir use | water supply | hydroelectricity | hydroelectricity |
| area (km2) | 12 | 72 | 1342 |
| volume (km3) | 0.146 | 0.472 | 20.7 |
| watershed area (km2) | 309 | 15300 | 51773 |
| maximum depth (m) | 41 | 36 | 89 |
| mean depth (m) | 19 | 6 | 15 |
| residence time (years) | 29 | 1.38 | |
| elevation (m) | 682 | 68 | 755 |
| mean total phosphorus (μg L−1) | 12 | 19 | 39 |
| mean total nitrogen (μg L−1) | 452 | 661 | 1204 |
| annual mean air temperature (°C) | 18 | 28 | 20 |
| annual precipitation (mm) | 1600 | 2200 | 1260 |
Measurements
A single field campaign was conducted in each reservoir during low-water season. In CDU, this was in September 2015; in CUN, March 2016; and in FNS, June and July 2015 (Figure S2).
Equilibrator-Based CO2 and CH4 Concentrations (pCO2 and pCH4)
We used an online equilibration system connected to an ultraportable greenhouse gas analyzer (UGGA, Los Gatos Research) to perform continuous measurements of CO2 and CH4 partial pressure (pCO2 and pCH4) in the water as the boat moved in a zigzag pattern (7 km h–1) through the reservoirs (Figure S3). Water from a ∼0.5 m depth was pumped continuously (3 L min–1) through a prefilter and a cartridge filter (10 μm pore size, Eaton Lofwind) and was further led to a membrane-based equilibrator (Permselect module PDMS-XA 1.0, Medarray Inc.), composed of an array of silicone hollow fibers with a total exchange area of 1 m2. In this membrane-based equilibrator, the water flows outside the hollow fibers, while the gas flows inside the hollow fibers toward the UGGA (a similar setup was described by Gonzalez-Valencia et al.).22 The gas flow is open so that the gas is not sent back to the equilibrator after passing the UGGA. The UGGA output data were logged with 1 Hz frequency and combined with geographic coordinates from a USB-GPS device (Navilock 6002U) running with the software Coolterm 1.4.7, and other geographic coordinates were recorded concomitantly using a hand-held GPS device (Garmin, eTrex 30x), for the discrete samples measurements (see later discussion). Each measured point was corrected by the response time of the online equilibration system, which was 3 min for CO2 and 5 min for CH4. Accounting for boat speed, every data point represents a moving average integrating over 350 m for CO2, and 580 m for CH4. Equilibration efficiency was 84% (SD: ± 14) for CO2 and 87% for CH4 (SD: ± 12), determined by comparing equilibrator-derived CO2 and CH4 concentrations with concentrations derived from manual samples (see later discussion).
Discrete Samples of pCO2 and pCH4
In addition to equilibrator-based measurements, we measured pCO2 and pCH4 manually, applying the headspace equilibration technique,8 at approximately every kilometer along the length of each reservoir (a total of 13 sites in CDU, 30 in CUN, and 33 in FNS, with triplicate measurements at each site). The discrete measurements were performed to (i) calculate the equilibration efficiency of the online equilibration system; (ii) calculate the k values in conjunction with floating chamber measurements of diffusive flux, as further described below (eq 2). At each measurement site, we filled 3 60 mL syringes with 30 mL of surface water and 10 mL of atmospheric air. The syringes were then vigorously shaken for 60 s to allow the gas and water phases to equilibrate. Then, the 10 mL headspace was transferred to a second syringe and injected in the UGGA. For this purpose, the UGGA was equipped with a custom-made inlet port connected to a carrier gas flow consisting of CO2-free air (ambient air passing through a soda-lime cartridge) and driven by its internal pump. The resulting baselines were zero for CO2, and atmospheric concentration for CH4 (∼1.8 ± 0.1 ppm). The peaks recorded by the UGGA were integrated in an in-house R script (R version 3.3.2) and compared to an in-house calibration curve to determine the pCO2 and pCH4. We used the solubility coefficients of Weiss23 and Yamamoto et al.24 to compute the water surface concentrations of CO2 and CH4, respectively. Detection limits for manual injection into the UGGA were 1.5 × 10–7 and 2.76 × 10–10 mol L–1 for dissolved CO2 and CH4 concentration, respectively.
Calculation of the Gas-Exchange Coefficient (k)
We performed FC measurements, which give direct estimates of CO2 and CH4 flux across the air–water interface, and discrete gas concentration measurements at the same sites to allow for the determination of k.25 FCs were deployed approximately every 1 km, including sites of open water, flooded forests, land–water boundaries, and river inflow areas (a total of 13 sites in CDU, 30 in CUN, and 33 in FNS, with triplicate measurements at each site). Transparent acrylic FC with a total volume of 17 L, a 0.07 m2 surface area, and a circular design were used. The chamber walls extended 4–5 cm into the water column. Transparent material was used to not affect photosynthesis and, therefore, CO2 flux during incubation. We deployed our FC three times at each sampling spot. The FC was left drifting during measurement to avoid creation of artificial turbulence. It was connected to the UGGA with a closed gas loop to quantify changes in CO2 and CH4 concentration inside the chamber over about 5 min per deployment. Real-time display of concentrations inside the chamber via the UGGA allowed the keeping of each chamber deployment as short as possible, which, in turn, minimized any temperature change inside the chamber. Chamber deployments were discarded if a linear regression between concentration increase and time rendered r2 < 0.9, indicating nonlinear behavior that is probably related to gas bubbles enriched in CH4 and CO2 (ebullition) entering the chamber.26
The diffusive gas flux depends on two main factors: the concentration gradient over the air–water interface and the k for a given gas at a given temperature. This gradient is expressed as the difference between the actual concentration of gas in the water and the concentration that water should have if it was in equilibrium with the atmosphere. Thus, the flux across the air–water interface can be calculated following the equation proposed by Cole and Caraco:8
| 1 |
where Fg,T is the flux at the air–water interface for a given gas (g) at a given temperature (T) (mmol m–2 day–1), k is the gas-exchange coefficient for the given gas (m day–1), Cw is the concentration of the given gas in water (mmol m–3), and Ceq is the theoretical concentration of the given gas in water if the water phase was in equilibrium with the atmosphere (mmol m–3).
The k values were derived from concomitant measurements of gas flux (by FC measurements) and of the measured pCO2 and pCH4 as follows and are called kFC hereafter:
| 2 |
To compare kFC for CO2 and CH4, the kFC was normalized to a Schmidt number of 600 for both CO2 and CH4 at 20 °C according to Jähne et al.:27
| 3 |
where Scg,T is the Schmidt number for a given gas at a given temperature.28 We used n = 2/3 for wind speed at 10 m < 3.7 m s–1 and n = 1/2 for wind speed at 10 m > 3.7 m s–1.26,29,30 The k600 was calculated for both gases, i.e., from CO2 flux and CO2 concentrations (termed k600CO2) and from CH4 flux and CH4 concentrations (termed k600CH4).
To assess the influence of assuming single k values for the calculation of gas fluxes across the entire reservoir, we computed gas fluxes using two different scenarios of fixed k values. The first scenario assumes a single k value (one for CO2 and one for CH4) derived from FC measurements at the dam of each reservoir (kd). The second scenario was derived from the average wind speed (equation from Cole and Caraco)8 at each reservoir (kws).
Bathymetry Analysis
Bathymetric surveys were performed in each reservoir using a parametric sub-bottom profiler (Innomar SES-2000) detecting the sediment-water interface at 100 kHz frequency. Shore-to-shore zigzag transects were made at 10 km h–1 along the entire length of each of the reservoirs, and the output data were geo-referenced using an on-board GPS receiver.
Environmental and Limnological Variables
We measured air temperature and wind speed at 2 m above the water surface with a portable anemometer (Skymaster Speedtech SM-28, accuracy: 3%) every 1 km of distance. Wind speed measurements were normalized to wind speed at 10 m above water level.31 Surface water temperature, conductivity, turbidity, pH, chlorophyll a, and dissolved oxygen (O2) concentrations were determined using a multi-parameter probe (YSI 6600 V2) logging at 30 s intervals.
Surface-water samples were collected using polypropylene bottles (300 mL) at each point of discrete samples. The samples were analyzed for total phosphorus (TP), total nitrogen (TN), and total organic carbon (TOC) in the laboratory at the Federal University of Juiz de Fora. TP and TN samples were analyzed by spectrophotometry (Beckman Coulter, DU - 640) following potassium persulfate digestion (TP) and alkaline persulfate digestion (TN). TOC samples were analyzed by high-temperature combustion on a total carbon analyzer (Shimadzu, TOC-L CPH/ASI-L).
Data Analysis and Statistical Procedures
Data interpolation to create maps of pCO2 and pCH4, kFC, and bathymetry was performed using the inverse distance weighted algorithm (IDW, cell size of approximately 37 m × 37 m)32 using the software ArcGIS (v10.2, ESRI). We preferred IDW to another interpolation algorithm (Kriging) because the root-mean squares of the interpolated maps were lower for IDW. Maps of interpolated diffusive fluxes of CO2 and CH4 were created by combining each grid cell (pixel) of partial pressure maps of CO2 and CH4 (air and water) with the corresponding grid cell of kFC maps, following eq 1. This computation was performed using the Map Algebra tool of ArcGIS. Finally, we extracted the cell values from all maps (partial pressure, k, diffusive fluxes, and bathymetry) to obtain data from all reservoirs with the same spatial resolution (∼37 m × 37 m), which were then used in the analysis. The CO2 and CH4 flux measurements derived from FCs were not used in this study as the relatively small number of measurements leads to higher uncertainty in comparison with the equilibrator-derived measurements. To test the differences between kFC, kws, and kd, we performed an ANOVA grouping the values from the three reservoirs.
The potential predictors of variability in pCO2 and pCH4 concentrations within reservoirs were investigated using partial least-squares regression (PLS) performed for each gas and each reservoir separately.33 The potential predictor variables included in the PLS were measurements of date and time, latitude and longitude, water depth, water temperature, pH, conductivity, chlorophyll a, turbidity, dissolved O2 concentration, and dissolved O2 saturation.
We estimated the minimum sampling effort required to produce a representative spatial coverage for each reservoir with high confidence (95% probability) of reaching ±20% of the mean diffusive flux, assuming that the high spatial resolution of our sampling effort was sufficient to capture the entire spatial variation of carbon fluxes in each reservoir. These simulations were not carried out using the interpolated flux values shown on the maps (Figures 1, S5, and S6) but using the “boat track flux”, which was calculated from measured gas concentrations along the boat track and the discrete measurements of k along the boat track, which were assumed to be valid until the next site of discrete k measurement. This “boat track flux” directly reflects the maximum sampling effort conducted in this study (n = 21827, 106373, and 87824 boat track flux values at CDU, CUN, and FNS, respectively). We then simulated hypothetical sampling scenarios by down-sampling, as described in detail by Wik et al.34 For each reservoir, we generated two data sets (one for CO2 flux and one for CH4 flux) that were structured in bins. The first bin in each data set represents the outcome of randomly selecting one data point out of the entire data set 100 times, and the nth bin represents the outcome of randomly selecting n data points out of the entire data set 100 times. This down-sampling simulation procedure allowed us to determine the minimum sampling effort per square kilometer in each reservoir. Statistical analyses were performed using the software JMP (Version 12.1.0). For PLS analyses, we used the software SIMCA 13 (Umetrics, Umeå Sweden). For all statistical tests, we assumed p < 0.05 as the threshold level of acceptance. The down-sampling simulations to predict the minimum sampling effort and the ANOVA to test the differences between different calculated k values were performed in the R Statistical Software (version 3.3.2).
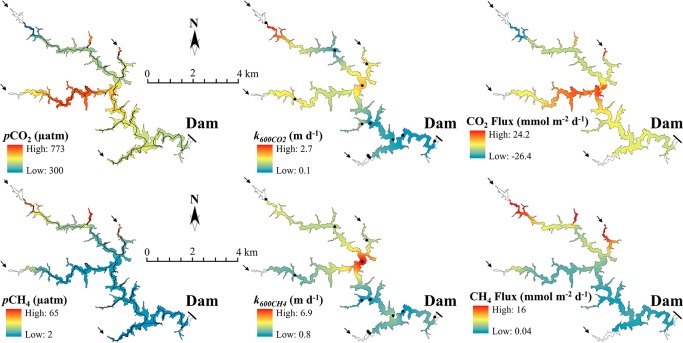
Figure 1.
pCO2 and pCH4 (μatm), k600CO2, k600CH4 (m day–1), and diffusive flux of CO2 and CH4 (mmol m–2 day–1) from IDW interpolation in CDU. The black arrows on the maps indicate river entrances. The black lines represent the equilibrator transects, and each black dot represents three measurements of floating chambers and discrete samples.
Results
Variability of pCO2 and pCH4
The pCO2 varied from 300 to 773 μatm in CDU (mean ± SD: 439 ± 63 μatm), from 387 to 1478 μatm in CUN (664 ± 221 μatm), and from 7 to 3090 μatm in FNS (400 ± 299 μatm) (Figure S4). The pCH4 varied from 2 to 65 μatm in CDU (11 ± 9 μatm), from 1.8 to 50 μatm in CUN (9 ± 5 μatm), and from 1.8 to 217 μatm in FNS (30 ± 20 μatm) (Figure S4). Expressed as the coefficient of variation, the range of variability within the reservoirs varied between 0.1 (CDU) and 0.8 (FNS) for pCO2, and between 0.5 (CUN) and 0.8 (CDU) for pCH4 (Table S1). There was a trend toward higher pCO2 and pCH4 in river inflow areas and decreasing values toward the dam (Figures 1, S5, and S6). The exception was pCO2 in FNS, which increased close to the dam (Figure S6). All of the reservoirs were consistently supersaturated in both CO2 and CH4 with respect to the atmosphere; the overall mean pCO2 and pCH4 considering all reservoirs together were 4.5 times and 9 times higher than atmospheric equilibrium, respectively.
Gas-Exchange Coefficient (k600)
The k600 for CO2 ranged from 0.1 to 2.7 m day–1 (0.9 ± 0.6 m day–1) in CDU, 0.1 to 4.7 m day–1 (0.5 ± 0.6 m day–1) in CUN, and 0.1 to 7.9 m day–1 (1.1 ± 1.2 m day–1) in FNS. The k600 for CH4 ranged from 0.8 to 6.9 m day–1 in CDU (2.8 ± 1.6 m day–1), 0.2 to 6.1 m day–1 in CUN (1.4 ± 1.0 m day–1), and 0.3 to 19.1 m day–1 in FNS (3.0 ± 3.3 m day–1). While we have not observed a clear, distinct pattern of spatial variation, we found some high k600 values in large open waters and river inflow areas (e.g., in CDU, Figure 1). The k600CH4 and k600CO2 values were significantly correlated (r2 = 0.519 p < 0.0001) but deviated strongly from the 1:1 line. The k600 values derived from CH4 were higher than the k600 derived from CO2 in more than 98% of the measurements (Figure S7). The k600CH4-to-k600CO2 ratio was similar in all reservoirs, with averages ranging from 2.7 to 3.1 (Table S1).
We compared our k values derived from all FC measurements (kFC) with k values derived from average wind speed (kws) and with k values derived from FC measurements near the dam (kd). We found that kFC are generally higher but not significantly different (p > 0.05) than kd and kws (Table S2).
Diffusive Fluxes of CO2 and CH4
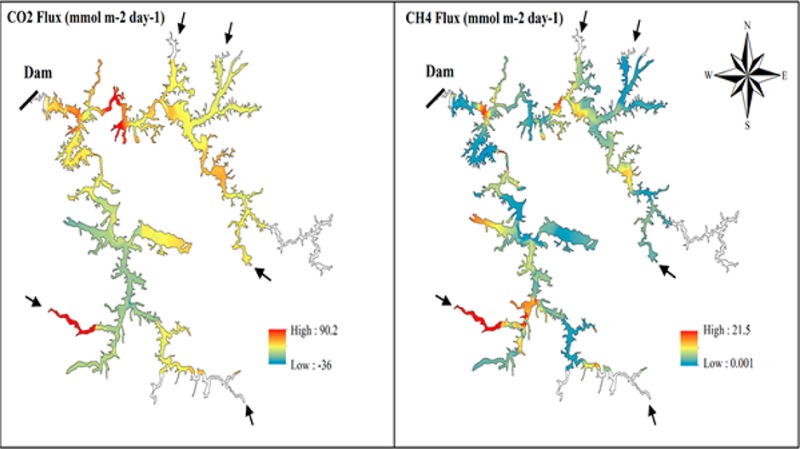
The diffusive flux of CO2 calculated from gridded data varied from −26.4 to 24.2 mmol m–2 day–1 (4.8 ± 6 mmol m–2 day–1) in CDU, 0.6 to 82.8 mmol m–2 day–1 (7.7 ± 9.5 mmol m–2 day–1) in CUN, and −36 to 90.2 mmol m–2 day–1 (7.1 ± 15.8 mmol m–2 day–1) in FNS (Table S2). For CH4, the diffusive flux calculated from gridded data ranged from 0.04 to 16 mmol m–2 day–1 (1.6 ± 1.7 mmol m–2 day–1) in CDU, 0.09 to 6.9 mmol m–2 day–1 (0.6 ± 0.8 mmol m–2 day–1) in CUN, and 0.001 to 21.5 mmol m–2 day–1 (2.5 ± 2.5 mmol m–2 day–1) in FNS (Table S2). The CO2 and CH4 diffusive fluxes observed in all reservoirs show large variability, resulting from high variability in both concentrations and k values (Figures 1, S5 and S6).
The gas fluxes computed from k values as derived from various FC measurements (kFC) were consistently higher than those derived from a single FC measurement at the dam site (kd) or the average wind speed on the reservoir (kws). The average, standard deviation, and range of k values and the respective diffusive fluxes of CO2 and CH4 as calculated from kFC, kd, and kws are shown in Table S2.
Limnological Parameters
The average water temperature ranged from 21.3 ± 0.8 °C (average ± SD) in FNS to 30.1 ± 1.4 °C in CUN (Table S2). The pH was slightly acidic in the Amazonian reservoir (CUN, 6.1 ± 0.7) and alkaline in the others (7.8 ± 0.1 and 8.4 ± 0.9 in CDU and FNS, respectively). CUN also showed lower conductivity (16 ± 11 μS cm–1) and dissolved oxygen concentrations (6.7 ± 1.9 mg L–1) in comparison to CDU (26.7 ± 0.6 μS cm–1; 8.5 ± 0.4 mg L–1) and FNS (32 ± 16 μS cm–1; 7.1 ± 3.4 mg L–1). Chlorophyll a concentration and turbidity were measured in CUN and FNS only. The average chlorophyll a concentration was 11.5 ± 15 μg L–1 in CDU and 7 ± 30.2 μg L–1 in FNS, while the average turbidity was 19.7 ± 10.3 NTU in CDU and 24.6 ± 12.6 NTU in FNS (Table S2).
Drivers of Within-Reservoir Variability
Our PLS models explained the variability in pCO2 well in all reservoirs (r2Y of 0.65 for CDU, 0.83 for CUN, 0.77 for FNS). In all reservoirs, we detected strong negative relationships of pCO2 with dissolved O2 (Table S3). Negative relationships with pH were observed also in all reservoirs (Table S3), and relationships with date and time were apparent in some of the reservoirs. The variability in pCH4 could also be well explained in each reservoir by the PLS model (r2Y of 0.44–0.79), and the geographic coordinates were strongly connected to the variability in pCH4 in all reservoirs. pH as well as depth, date and time were important for explaining variability in pCH4, albeit not consistently in all reservoirs. The Q2 values of all PLS models were similar to the r2Y values, indicating high predictive power (Table S3).
We additionally looked for statistical drivers of within-reservoir variability in k600, but the resulting statistical models were weak (data not shown). In most cases, either PLS models did not converge or permutation tests showed that random data generated models of similar explanatory power. While there were positive relationships between k600 (determined from FC) and wind speed, the great spread in these relationships makes wind speed a poor predictor of k600 (Figure S8).
Sampling Effort
We performed downsampling simulations to predict how many flux measurements would have been enough to reach total flux estimates within ±20% of our observed mean, provided that the flux measurements are randomly distributed across the reservoir. For CDU (total number of boat track flux values of 21 827 or 1819 measurements per square kilometer), the simulations indicated that the minimum sampling effort needed to meet the ±20% criteria would be ∼6 flux measurements per square kilometer for CO2 and ∼10 flux measurements per square kilometer for CH4. For CUN (total number of boat track flux values of 10 6373, or 1477 measurements per square kilometer), the minimum sampling effort would be ∼2 flux measurements per square kilometer for both CO2 and CH4. For FNS (total number of boat track flux values of 87 274 or 65 measurements per square kilometer), the minimum sampling effort would be ∼1 flux measurement per square kilometer for CO2 and ∼0.1 flux measurement per square kilometer for CH4 (Figure S9).
Discussion
This study shows large within-reservoir variability in pCO2, pCH4, and k values (Figures 1, S5, and S6), which results in large spatial variability of CO2 and CH4 diffusive emissions (Figures 1, S5, and S6). Our results also corroborate the hypothesis that taking k measurements exclusively close to the dam will result in underestimation of diffusive CO2 and CH4 emissions from reservoirs.
Within-Reservoir Variability in pCO2 and pCH4
The three reservoirs were predominantly supersaturated in CO2 and CH4 (Table S1). Therefore, they were overall sources of CO2 and CH4 to the atmosphere, even though uptake of CO2 from the atmosphere was observed in some areas. The magnitude and variability of pCO2 and pCH4 reported here (Table S1) are in accordance with previous results reported for tropical and temperate reservoirs.5,9,12,19 To our knowledge, this is the first study demonstrating that riverine inflow areas are likely to have higher pCO2 and pCH4 than the main river channel close to the dam. The only case in which this pattern was not evident for pCO2 was in FNS, in which not all of the river inflow areas had elevated pCO2, while the dam area had comparatively higher pCO2 (Figure S6).
In the PLS regression models, the geographic location within a reservoir was an important variable (variable importance in projection, VIP > 1; Table S3) explaining pCH4 (r2Y of 0.44–0.79), with a smaller importance for date and time (most VIP < 1; Table S3). This implies that there are significant spatial gradients of pCH4 along the main longitudinal axis of the reservoirs as a result of the dam areas being cold spots of pCH4 and the river inflows being prone to be pCH4 hot spots (Figures 1, S5, and S6). It is noteworthy that the areas considered as hot spots showed pCH4 values 5 to 7 times higher than the whole-reservoir averages (which also include the hot spots, making it a conservative comparison). Although we have not measured sedimentation and anaerobic metabolism, the literature suggests that the higher pCH4 at river inflows may be attributable to the fact that in these areas water slows down and sediment is deposited, often leading to the formation of deltas.15,35 The deposition of fluvial organic matter supports degradation via methanogenic microbes, increasing CH4 production.15 Accordingly, water depth, a proxy of the connectivity between sediment and surface water, was an important variable in two of the reservoirs (VIP > 1; Table S3). Additionally, CH4 imported from the catchment may further contribute to the observed pattern at river inflow areas.14,36
Aquatic metabolism is another factor that may explain within-reservoir variability of pCO2 and pCH4. In all reservoirs, pCO2 correlated negatively with O2 concentration and not strongly with geographic location (Table S3), indicating that internal patterns in planktonic metabolism are important modulators of pCO2. For example, pCO2 was undersaturated in a large part of the southern arm of FNS (Figure S6), where the eutrophic Sapucaí River (average TN: 1340 μg L–1, average TP: 41 μg L–1) enters the reservoir. Chlorophyll a concentrations in the southern arm of FNS are high (21.2 ± 14.0 μg L–1), and two times larger than in the northern arm (9.8 ± 9.0 μg L–1). Intense CO2 uptake during phytoplankton primary production is likely causing CO2 undersaturation in the eutrophic southern arm.5,12 In CUN, geographic location was an important predictor of pCO2 (VIP > 1; Table S3), and the high pCO2 in the river inflows may be attributed to sediment organic matter degradation and riverine input of terrestrially respired CO2.12,13
In contrast to low pCO2 in the eutrophic southern arm of FNS, pCH4 was high. This suggests that anaerobic decomposition of phytoplankton debris in the sediments increases CH4 production. Indeed, eutrophication has recently been pointed out as a key driver of CH4 fluxes in reservoirs on a global scale.3 Similarly, organic matter-rich effluent from local settlements may also result in high pCH4, such as close to the village ∼12 km upstream the dam in CUN (Figure S5). We cannot exclude the possibility that the variability of pCO2 and pCH4 is due to different types of flooded organic matter and the reservoir’s morphometry.5,12,19
Within-Reservoir Variability in Gas-Exchange Velocity
While our values of k600 (averages of discrete measurements: 0.9 ± 1.0 m day–1 for k600CO2 and 2.3 ± 2.4 m day–1 for k600CH4) were in the range of earlier studies,29,37,38 we observed a pronounced spatial variability of k600 in all reservoirs. There were positive but rather weak relationships between k600 and wind speed (Figure S8), and the PLS regression models were overall weak, indicating that k600 was not very predictable from the variables collected in this study. In some instances, we observed high k600 values in river inflow areas (Figures 1, S5, and S6). In these areas, turbulence may be stronger than in the reservoir main body due to the higher flow velocity of water,39 enhancing the gas exchange with the atmosphere. We also found higher k600 in some larger open areas (e.g., in CUN’s reservoir main stem; Figure S5). These areas have more wind exposure, which also may increase turbulence in the water surface. Because k is largely driven by water turbulence, it varies in space and time even at short time scales and depends on water flow and the speed and direction of wind.8,18,26,40 Evidently, this creates pronounced spatial and temporal patterns in k600 (Figures 1, S5, and S6), which are highly variable, not readily predictable, and not adequately represented by estimations of average k600 from wind speed.
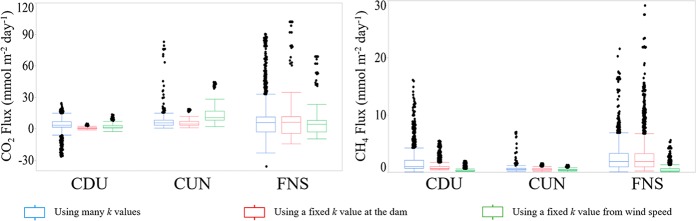
The diffusive fluxes of CO2 and CH4 were computed through three different k calculation approaches as described above. Using the interpolated k derived from spatially distributed floating chamber measurements (kFC), the resulting fluxes of CO2 showed expectedly higher spatial variability than other approaches that use fixed values of k (Figure 2). The same pattern was observed for diffusive fluxes of CH4 from CDU and CUN but not FNS, where the use of kd-CH4 returned more variable flux (Figure 2). We, then, argue that despite there being no statistical difference among the mean values of kFC, kws, and kd, the use of the spatially resolved kFC results in a better representation of the spatial variability of diffusive fluxes of CO2 and CH4.
Figure 2.
Box plot of CO2 and CH4 fluxes, calculated from spatially resolved concentration as measured in combination with three different approaches of determining the gas-exchange velocity k.
Compared to using kFC, using kd-CO2 underestimated the diffusive flux of CO2 by ∼86% in CDU, ∼ 26% in CUN, and ∼11% in FNS. For the diffusive flux of CH4, the use of kd-CH4 instead of kFC underestimated the flux by ∼44% for CDU and ∼17% for CUN but overestimated the flux by ∼8% for FNS.
Using a fixed k value scaled from average wind speed (kws)8 for each reservoir, the diffusive flux of CO2 as calculated from kFC was underestimated by ∼57% for CDU and ∼41% for FNS, but it was overestimated by ∼70% in CUN. The diffusive flux of CH4, calculated using kws-CH4, underestimated the kFC-derived flux by ∼82% for CDU, ∼34% for CUN, and ∼80% for FNS. Our results strongly suggest that spatially resolved measurements are necessary to derive accurate estimates of diffusive emission.
Persistence of Higher k600CH4 Values Compared to k600CO2
We found that k600CH4 was persistently higher than k600CO2 for all reservoirs (Figure S7). On average, k600CH4 was 2.8 times higher than k600CO2, and there were no differences among reservoirs. According to the Fickian transport, k600CO2 values should be similar to k600CH4 values because the speed of diffusion for these gases is similar.41 However, the persistently higher k600CH4 values indicate that the two gases behave differently. The k600CH4-to-k600CO2 ratio found in this study is in agreement with observations by recent studies29,30 suggesting that the presence of CH4 microbubbles may explain why k600CH4 is constantly higher than k600CO2. It is important to note that the k values reported here are derived from continuous measurements of linear concentration increase inside FCs over short time intervals (<5 min). Hence, if the elevated k600CH4 were driven by microbubbles, the microbubble flux into the FC would need to be close to constant across time and ubiquitous in space to produce the pattern observed here (Figure S7). More research on k is clearly needed.
Within-Reservoir Variability in Diffusive CO2 and CH4 Fluxes
Because of the variability in concentrations and k, CO2 diffusive fluxes varied between −36 and 90.2 mmol m–2 day–1 (6.1 ± 12.2, median: 4.5 mmol m–2 day–1) and diffusive flux of CH4 varied between 0.001 and 21.5 mmol m–2 day–1 (2 ± 2.2, median: 1.3 mmol m–2 day–1) (Table S2). Diffusive CH4 emission was higher in most river inflow areas in comparison to the respective dam area (Figures 1, S5, and S6). Also, several river inflow areas showed high diffusive fluxes of CO2, similar to the observations by Pacheco et al.12 Evidently, patterns of diffusive gas emission were not entirely congruent with patterns in gas concentrations because the k was regulated by other factors than gas concentrations. It is important to consider that the observed within-reservoir patterns of diffusive CO2 and CH4 emission are snapshots in space and time: the k600 maps are the result of instantaneous and very local measurements, which are subject to rapid change depending on the water column and meteorological conditions, as well as the location of measurement. However, we consider the maps of gas concentration to reflect largely prevailing spatial patterns driven by inflow and internal productivity during the dry season. While the high-resolution mapping of surface water gas concentrations of this study represents an important advance toward improved estimates of diffusive emission from reservoirs, more research needs to be done on the variability and regulation of the k in these large and morphologically complex systems. While this paper focused on representing spatial variability, seasonal variability is not included in our estimates even though it can be substantial.12 Hence, we do not recommend using the fluxes reported here to calculate yearly emissions.
Minimum Sampling Effort
Both the coefficient of variation (CV) of boat track diffusive flux and the down-sampling simulations (Figure S9) give congruent indications on the minimum number of sampling points needed to reach within ±20% of our known mean flux with 95% probability. In CDU, the coefficients of variation (CV) for boat track diffusive flux of CO2 and CH4 were similar (1.2 and 1.0, respectively), and so was the minimum sampling effort (∼6 and ∼10 km–2, respectively). Also in CUN, the CV for CO2 and CH4 were similar (both 1.2), and so was the minimum sampling effort (both ∼2 km–2). In FNS, the CV for CO2 was two times higher than the CV for CH4 (2.2 and 1.0, respectively), and accordingly, the minimum sampling effort for CO2 (∼1 km–2) was higher than that for CH4 (∼0.1 km–2) (Figure S9).
These results suggest that small systems require higher sampling densities, even though we cannot statistically support this observation because only three reservoirs were studied. Our findings are in agreement with a previous study that reported a negative but not strong relationship between pCO2 spatial variability and reservoir area in five tropical reservoirs.5 For instance, the down-sampling simulations indicated that 0.1 flux measurements per square kilometer randomly distributed across the reservoir are sufficient to capture the spatial variability of CH4 fluxes for FNS, the largest reservoir (area = 1342 km2), whereas for CDU, the smallest reservoir (area = 12 km2), the simulated minimum sampling effort is 10 flux measurements per km2. This means that the influence of sediments and land on water quality of marginal areas may be higher in small systems. Furthermore, the heterogeneity of other local factors such as primary production, trophic state, depth, morphometry, or river entrances may exert greater influence on the variability of fluxes from small systems. Finally, our results indicate that sampling only one or a few sites to scale gas fluxes across the entire reservoir may result in substantial errors (Figure S10). Our simulations indicate that the probability of getting the actual flux when gas fluxes are scaled from one or a few measurements to represent the entire reservoir is less than 25% (Figure S10).
Implications
Through conducting spatially resolved measurements of both CO2 and CH4 concentrations, as well as gas-exchange velocities, this study documents pronounced spatial variability in diffusive C emission from tropical reservoirs, which to a large extent is linked to river inflows, sedimentation and in-system metabolism. Accordingly, river inflows and eutrophic areas were identified as hot spots of diffusive C gas flux. To produce representative estimates of C emission from reservoirs, spatially resolved measurements must be conducted. Not accounting for the spatial variability in concentrations, or assuming a fixed gas-exchange velocity, may underestimate the diffusive C emission by ∼10% to 80%.
Acknowledgments
We are grateful to Carlos H. E. Duque-Estrada, Roseilson do Vale, Felipe Rust, and Gladson R. Marques who were greatly helpful during all fieldwork and sample analyses in the laboratory in Juiz de Fora. We are also grateful to Eletronorte S/A for logistic support during the field work in the Curuá-Una reservoir. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 336642 and from the Fundação de Amparo à Pesquisa de Minas Gerais/FAPEMIG (CRA APQ 03045/16). We are grateful for the support from the Pesquisador Visitante Especial Ciência sem Fronteiras program no. 401384/2014-4. J.R.P. was additionally supported by FAPEMIG (scholarship no. 11178). F.R. has been supported by the Brazilian National Council of Research and Development (CNPq; grant no. 401384/2014-4).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.7b05138.
Figures showing a map of the study sites, reservoir water level, sampling strategy, box plots, IDW interpolation results, the relationship between gas-exchange velocities, the relationship between wind speed and gas-exchange coefficients, down-sampling simulations, and the chance of reaching a whole-system mean flux. Tables showing descriptive statistics, an average of k values, and the parameters of PLS models. (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- St Louis V. L.; Kelly C. A.; Duchemin É.; Rudd J. W.; Rosenberg D. M. Reservoir Surfaces as Sources of Greenhouse Gases to the Atmosphere: A Global Estimate: Reservoirs are sources of greenhouse gases to the atmosphere, and their surface areas have increased to the point where they should be included in global inventories of anthropogenic emissions of greenhouse gases. BioScience 2000, 50 (9), 766–775. 10.1641/0006-3568(2000)050[0766:RSASOG]2.0.CO;2. [DOI] [Google Scholar]
- Barros N.; Cole J. J.; Tranvik L. J.; Prairie Y. T.; Bastviken D.; Huszar V. L.; Del Giorgio P.; Roland F. Carbon emission from hydroelectric reservoirs linked to reservoir age and latitude. Nat. Geosci. 2011, 4 (9), 593–596. 10.1038/ngeo1211. [DOI] [Google Scholar]
- Deemer B. R.; Harrison J. A.; Li S.; Beaulieu J. J.; DelSontro T.; Barros N.; Bezerra-Neto J. F.; Powers S. M.; dos Santos M. A.; Vonk J. A. Greenhouse gas emissions from reservoir water surfaces: a new global synthesis. BioScience 2016, 66 (11), 949–964. 10.1093/biosci/biw117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myhre G.; Shindell D.; Bréon F.-M.; Collins W.; Fuglestvedt J.; Huang J.; Koch D.; Lamarque J.-F.; Lee D.; Mendoza B. Anthropogenic and natural radiative forcing. Climate change 2013, 423, 658–740. [Google Scholar]
- Roland F.; Vidal L. O.; Pacheco F. S.; Barros N. O.; Assireu A.; Ometto J. P.; Cimbleris A. C.; Cole J. J. Variability of carbon dioxide flux from tropical (Cerrado) hydroelectric reservoirs. Aquat. Sci. 2010, 72 (3), 283–293. 10.1007/s00027-010-0140-0. [DOI] [Google Scholar]
- Bastviken D.; Tranvik L. J.; Downing J. A.; Crill P. M.; Enrich-Prast A. Freshwater methane emissions offset the continental carbon sink. Science 2011, 331 (6013), 50–50. 10.1126/science.1196808. [DOI] [PubMed] [Google Scholar]
- Raymond P. A.; Hartmann J.; Lauerwald R.; Sobek S.; McDonald C.; Hoover M.; Butman D.; Striegl R.; Mayorga E.; Humborg C. Global carbon dioxide emissions from inland waters. Nature 2013, 503 (7476), 355–359. 10.1038/nature12760. [DOI] [PubMed] [Google Scholar]
- Cole J. J.; Caraco N. F. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF6. Limnol. Oceanogr. 1998, 43 (4), 647–656. 10.4319/lo.1998.43.4.0647. [DOI] [Google Scholar]
- Abril G.; Richard S.; Guérin F. In situ measurements of dissolved gases (CO2 and CH4) in a wide range of concentrations in a tropical reservoir using an equilibrator. Sci. Total Environ. 2006, 354 (2), 246–251. 10.1016/j.scitotenv.2004.12.051. [DOI] [PubMed] [Google Scholar]
- Sobek S.; Tranvik L. J.; Cole J. J. Temperature independence of carbon dioxide supersaturation in global lakes. Global Biogeochemical Cycles 2005, 19 (2), 1–10. 10.1029/2004GB002264. [DOI] [Google Scholar]
- Borges A. V.; Darchambeau F.; Teodoru C. R.; Marwick T. R.; Tamooh F.; Geeraert N.; Omengo F. O.; Guérin F.; Lambert T.; Morana C. Globally significant greenhouse-gas emissions from African inland waters. Nat. Geosci. 2015, 8 (8), 637–642. 10.1038/ngeo2486. [DOI] [Google Scholar]
- Pacheco F.; Soares M.; Assireu A.; Curtarelli M.; Abril G.; Stech J.; Alvalá P.; Ometto J. The effects of river inflow and retention time on the spatial heterogeneity of chlorophyll and water-air CO2 fluxes in a tropical hydropower reservoir. Biogeosciences 2015, 12 (1), 147. 10.5194/bg-12-147-2015. [DOI] [Google Scholar]
- Cardoso S. J.; Vidal L. O.; Mendonça R. F.; Tranvik L. J.; Sobek S.; Fábio R. Spatial variation of sediment mineralization supports differential CO2 emissions from a tropical hydroelectric reservoir. Front. Microbiol. 2013, 4, 1–8. 10.3389/fmicb.2013.00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DelSontro T.; Kunz M. J.; Kempter T.; Wüest A.; Wehrli B.; Senn D. B. Spatial heterogeneity of methane ebullition in a large tropical reservoir. Environ. Sci. Technol. 2011, 45 (23), 9866–9873. 10.1021/es2005545. [DOI] [PubMed] [Google Scholar]
- Sobek S.; DelSontro T.; Wongfun N.; Wehrli B. Extreme organic carbon burial fuels intense methane bubbling in a temperate reservoir. Geophys. Res. Lett. 2012, 39 (1), 1–4. 10.1029/2011GL050144. [DOI] [Google Scholar]
- Maeck A.; Hofmann H.; Lorke A. Pumping methane out of aquatic sediments: Ebullition forcing mechanisms in an impounded river. Biogeosciences 2014, 11 (11), 2925–2938. 10.5194/bg-11-2925-2014. [DOI] [Google Scholar]
- MacIntyre S.; Jonsson A.; Jansson M.; Aberg J.; Turney D. E.; Miller S. D. Buoyancy flux, turbulence, and the gas transfer coefficient in a stratified lake. Geophys. Res. Lett. 2010, 37 (24), 1–5. 10.1029/2010GL044164. [DOI] [Google Scholar]
- Vachon D.; Prairie Y. T. The ecosystem size and shape dependence of gas transfer velocity versus wind speed relationships in lakes. Can. J. Fish. Aquat. Sci. 2013, 70 (12), 1757–1764. 10.1139/cjfas-2013-0241. [DOI] [Google Scholar]
- Teodoru C. R.; Prairie Y. T.; Del Giorgio P. A. Spatial heterogeneity of surface CO2 fluxes in a newly created Eastmain-1 reservoir in northern Quebec, Canada. Ecosystems 2011, 14 (1), 28–46. 10.1007/s10021-010-9393-7. [DOI] [Google Scholar]
- Zarfl C.; Lumsdon A. E.; Berlekamp J.; Tydecks L.; Tockner K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77 (1), 161–170. 10.1007/s00027-014-0377-0. [DOI] [Google Scholar]
- IBGE D. d. P. Coordenação de Agropecuária. Produção Pecuária Municipal 2012, 43, 1–55. [Google Scholar]
- Gonzalez-Valencia R.; Magana-Rodriguez F.; Gerardo-Nieto O.; Sepulveda-Jauregui A.; Martinez-Cruz K.; Walter Anthony K.; Baer D.; Thalasso F. In situ measurement of dissolved methane and carbon dioxide in freshwater ecosystems by off-axis integrated cavity output spectroscopy. Environ. Sci. Technol. 2014, 48 (19), 11421–11428. 10.1021/es500987j. [DOI] [PubMed] [Google Scholar]
- Weiss R. F. Carbon dioxide in water and seawater: the solubility of a non-ideal gas. Mar. Chem. 1974, 2 (3), 203–215. 10.1016/0304-4203(74)90015-2. [DOI] [Google Scholar]
- Yamamoto S.; Alcauskas J. B.; Crozier T. E. Solubility of methane in distilled water and seawater. J. Chem. Eng. Data 1976, 21 (1), 78–80. 10.1021/je60068a029. [DOI] [Google Scholar]
- Cole J. J.; Bade D. L.; Bastviken D.; Pace M. L.; Van de Bogert M. Multiple approaches to estimating air-water gas exchange in small lakes. Limnol. Oceanogr.: Methods 2010, 8 (6), 285–293. 10.4319/lom.2010.8.285. [DOI] [Google Scholar]
- Guérin F.; Abril G.; Serça D.; Delon C.; Richard S.; Delmas R.; Tremblay A.; Varfalvy L. Gas transfer velocities of CO2 and CH4 in a tropical reservoir and its river downstream. Journal of Marine Systems 2007, 66 (1), 161–172. 10.1016/j.jmarsys.2006.03.019. [DOI] [Google Scholar]
- Jähne B.; Münnich K. O.; Bösinger R.; Dutzi A.; Huber W.; Libner P. On the parameters influencing air-water gas exchange. J. Geophys. Res. 1987, 92 (C2), 1937–1949. 10.1029/JC092iC02p01937. [DOI] [Google Scholar]
- Wanninkhof R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 1992, 97 (C5), 7373–7382. 10.1029/92JC00188. [DOI] [Google Scholar]
- Prairie Y. T.; del Giorgio P. A. A new pathway of freshwater methane emissions and the putative importance of microbubbles. Inland Waters 2013, 3 (3), 311–320. 10.5268/IW-3.3.542. [DOI] [Google Scholar]
- McGinnis D. F.; Kirillin G.; Tang K. W.; Flury S.; Bodmer P.; Engelhardt C.; Casper P.; Grossart H.-P. Enhancing surface methane fluxes from an oligotrophic lake: exploring the microbubble hypothesis. Environ. Sci. Technol. 2015, 49 (2), 873–880. 10.1021/es503385d. [DOI] [PubMed] [Google Scholar]
- Smith S. Physical, chemical and biological characteristics of CO2 gas flux across the air-water interface. Plant, Cell Environ. 1985, 8 (6), 387–398. 10.1111/j.1365-3040.1985.tb01674.x. [DOI] [Google Scholar]
- Xiong W.; Holman I.; Lin E.; Conway D.; Li Y.; Wu W. Untangling relative contributions of recent climate and CO2 trends to national cereal production in China. Environ. Res. Lett. 2012, 7 (4), 044014. 10.1088/1748-9326/7/4/044014. [DOI] [Google Scholar]
- Höskuldsson A. PLS regression methods. J. Chemom. 1988, 2 (3), 211–228. 10.1002/cem.1180020306. [DOI] [Google Scholar]
- Wik M.; Thornton B. F.; Bastviken D.; Uhlbäck J.; Crill P. M. Biased sampling of methane release from northern lakes: A problem for extrapolation. Geophys. Res. Lett. 2016, 43 (3), 1256–1262. 10.1002/2015GL066501. [DOI] [Google Scholar]
- Stevens M. A. Reservoir Sedimentation Handbook—Design and Management of Dams, Reservoirs, and Watershed for Sustainable Use. Journal of Hydraulic Engineering 2000, 126 (6), 481–482. 10.1061/(ASCE)0733-9429(2000)126:6(481). [DOI] [Google Scholar]
- Mendonça R.; Kosten S.; Sobek S.; Cole J. J.; Bastos A. C.; Albuquerque A. L.; Cardoso S. J.; Roland F. Carbon sequestration in a large hydroelectric reservoir: an integrative seismic approach. Ecosystems 2014, 17 (3), 430–441. 10.1007/s10021-013-9735-3. [DOI] [Google Scholar]
- Vachon D.; Prairie Y. T.; Cole J. J. The relationship between near-surface turbulence and gas transfer velocity in freshwater systems and its implications for floating chamber measurements of gas exchange. Limnol. Oceanogr. 2010, 55 (4), 1723–1732. 10.4319/lo.2010.55.4.1723. [DOI] [Google Scholar]
- Rantakari M.; Heiskanen J.; Mammarella I.; Tulonen T.; Linnaluoma J.; Kankaala P.; Ojala A. Different apparent gas exchange coefficients for CO2 and CH4: Comparing a brown-water and a clear-water lake in the boreal zone during the whole growing season. Environ. Sci. Technol. 2015, 49 (19), 11388–11394. 10.1021/acs.est.5b01261. [DOI] [PubMed] [Google Scholar]
- Long H.; Vihermaa L.; Waldron S.; Hoey T.; Quemin S.; Newton J. Hydraulics are a first-order control on CO2 efflux from fluvial systems. J. Geophys. Res.: Biogeosci. 2015, 120 (10), 1912–1922. 10.1002/2015JG002955. [DOI] [Google Scholar]
- Zappa C. J.; McGillis W. R.; Raymond P. A.; Edson J. B.; Hintsa E. J.; Zemmelink H. J.; Dacey J. W.; Ho D. T.. Environmental turbulent mixing controls on air-water gas exchange in marine and aquatic systems. Geophys. Res. Lett. 2007, 34, ( (10), ). 10.1029/2006GL028790 [DOI] [Google Scholar]
- Jähne B.; Heinz G.; Dietrich W. Measurement of the diffusion coefficients of sparingly soluble gases in water. J. Geophys. Res. 1987, 92 (C10), 10767–10776. 10.1029/JC092iC10p10767. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.