Abstract
The evolution and diversification of cell types is a key means by which animal complexity evolves. Recently, hierarchical clustering and phylogenetic methods have been applied to RNA-seq data to infer cell type evolutionary history and homology. A major challenge for interpreting this data is that cell type transcriptomes may not evolve independently due to correlated changes in gene expression. This nonindependence can arise for several reasons, such as common regulatory sequences for genes expressed in multiple tissues, that is, pleiotropic effects of mutations. We develop a model to estimate the level of correlated transcriptome evolution (LCE) and apply it to different data sets. The results reveal pervasive correlated transcriptome evolution among different cell and tissue types. In general, tissues related by morphology or developmental lineage exhibit higher LCE than more distantly related tissues. Analyzing new data collected from bird skin appendages suggests that LCE decreases with the phylogenetic age of tissues compared, with recently evolved tissues exhibiting the highest LCE. Furthermore, we show correlated evolution can alter patterns of hierarchical clustering, causing different tissue types from the same species to cluster together. To identify genes that most strongly contribute to the correlated evolution signal, we performed a gene-wise estimation of LCE on a data set with ten species. Removing genes with high LCE allows for accurate reconstruction of evolutionary relationships among tissue types. Our study provides a statistical method to measure and account for correlated gene expression evolution when interpreting comparative transcriptome data.
Keywords: comparative transcriptomincs, cell type evolution, gene expression evolution, correlated evolution
Introduction
Complex organisms, such as birds and mammals, generally have a much higher number of cell types than anatomically “simple” organisms, like sponges and Trichoplax. For example, there are >400 cell types recognized in humans (Vickaryous and Hall 2006). In contrast, Trichoplax, the morphologically simplest free-living animal, has five to six cell types (Grell and Ruthmann 1991; Syed and Schierwater 2002), and in sponges only ∼10–18 cell types have been recognized (Simpson 1984; Valentine et al. 1994; Ereskovsky 2010). Viewed through the lens of animal phylogeny, this observation suggests that animal complexity increased, in part, via the evolution of new cell types (Arendt 2008; Wagner 2014; Arendt et al. 2016). Thus, understanding the evolution of animal complexity requires investigating cell type evolutionary history and homology.
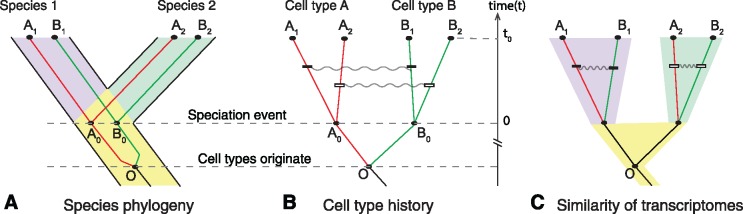
A promising approach for inferring cell or tissue type homology and evolutionary history is the use of hierarchical clustering or phylogenetic methods with RNA-seq data to reconstruct cell type trees (fig. 1A and B; we used cell types and tissue types interchangeably in this figure, to represent the samples that were frequently collected in comparative RNA-seq studies) (Pu and Brady 2010; Wang et al. 2011; Pankey et al. 2014; Tschopp et al. 2014; Achim et al. 2015; Kin et al. 2015; Musser and Wagner 2015). These are analogous to a gene or species trees, but depict relationships among different cell or tissue types. Homologous cell and tissue types are expected to be more closely related to each other than to other tissues (fig. 1A and B). This pattern has been observed in analyses of mature tissues with distinct functions (Brawand et al. 2011; Merkin et al. 2012; Sudmant et al. 2015). However, the opposite pattern has also been documented (Pankey et al. 2014; Tschopp et al. 2014), in which distinct cell/tissue types cluster according to species of origin, rather than by homology, even when the tissue types are phylogenetically older than the species (fig. 1C). Recent analyses of this phenomenon have suggested the clustering pattern is related to both tissue similarity and the divergence times between the species under comparison (Sudmant et al. 2015; Gu 2016). However, how and why these factors are related to the shape of reconstructed trees are currently unclear.
Fig. 1.—
Correlated evolution of cell transcriptomes. (A) Cell type history embedded within species history. Cell types A and B originate from ancestral cell type O prior to split of species 1 and 2. Cell type lineages show homology relationships for the two cell types in the descendant species (subscripts indicate species). (B) Cell type history without species phylogeny illustrates cell type homology. Gray squiggly lines indicate nonindependence of transcriptome change. Correlated transcriptome evolution leads to an increase of transcriptome similarities in cell types of the same species relative to their homologous counterparts in other species. (C) Correlated evolution causes the accumulation of species-specific gene expression similarities between tissues in the same organism, potentially resulting in different tissues within a species being more similar to each other than to their homologous counterparts in another species.
Phylogenetic inference using tree-building methods assumes that the individuals under comparison (in this case cell or tissue types) evolve independently of each other, thus forming distinct historical lineages. Cell and tissue types maintain distinct gene expression programs, and thus may evolve cell and tissue specific gene expression independently. However, many RNA-seq studies find that most genes are not uniquely expressed in a single cell or tissue type. For instance, different neuronal cell types express synaptic genes (Sieburth et al. 2005; Ruvinsky et al. 2007; Stefanakis et al. 2015), different muscle cell types share expression of contractile genes (Steinmetz et al. 2012; Brunet et al. 2016), and all tissues employ “housekeeping genes” (Eisenberg and Levanon 2013). Thus, it is likely that some evolutionary changes will alter the expression of some genes simultaneously across multiple tissues, resulting in correlated patterns of gene expression evolution. This has the potential to influence the relationships inferred in cell type trees by generating similarities among cell types from the same species, causing them to cluster by species, rather than homologous tissue type (fig. 1B and C) (Musser and Wagner 2015). Correlated evolution of gene expression was recently shown to be important in understanding transcriptome structure using phylogenetic networks (Gu et al. 2017).
To address the issue discussed earlier, the level of correlated gene expression (transcriptome) evolution (LCE), and its influence on tree reconstruction, needs to be evaluated. Estimating correlations among quantitative phenotypic traits along a known phylogeny has been extensively studied (Felsenstein 1985; Felsenstein 1988; Martins and Garland 1991; Pagel 1994; Diaz-Uriarte and Garland 1996; Felsenstein 2004; Pagel and Meade 2006). These approaches analyze the evolution of a few traits over a large number of species. In contrast, transcriptomic studies deal with many traits (expression levels of genes or transcripts) over comparatively fewer species, where traditional methods do not directly apply. For this reason, we focus on estimating the average correlation over all genes to obtain an estimate for the overall strength of correlated evolution affecting transcriptomes.
In this study, we propose a statistical method to measure LCE by incorporating a parameter for correlated evolution in both Brownian and Ornstein–Uhlenbeck (OU) models of gene expression evolution. Using simulations of gene expression evolution, we show that our method accurately estimates the level of correlated evolution among transcriptomes. Applying this method to published data, we find that correlated evolution is pervasive, and varies in accordance with developmental and evolutionary relatedness. We show that tissues of more recent origin display higher LCE compared with more distantly related tissues, suggesting that the evolutionary independence, or transcriptomic individuation, of tissues may increase over time. Further, a theoretical study of our stochastic model of gene expression reveals how LCE and species divergence time influence transcriptome similarities, and thus affect the hierarchical clustering patterns. Using a data set with sufficient species sampling, we quantify LCE for individual genes. By excluding genes with high LCE, we were able to reconstruct trees that recover expected patterns of tissue type homology.
Materials and Methods
Publicly Available Transcriptome Data Processing
Transcript read counts in Merkin et al. (2012) were downloaded from GSE41637 (http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE41637; last accessed January 25, 2018). Nine tissues (brain, colon, heart, kidney, liver, lung, muscle, spleen, and testes) in five species (chicken, cow, mouse, rat, and rhesus macaque) are profiled in this work. We followed methods in Merkin et al. (2012) to map each transcript to respective genomes (musmus9, rhemac2, ratnor4, bostau4, galgal3) and extract FPKM values for each gene. We then normalized FPKM to TPM (Transcript per million mapped transcripts) by the sum (Wagner et al. 2012).
Normalized gene expression RPKM from Brawand et al. (2011) was downloaded from the supplementary tables of the original publication. According to Brawand et al., RPKM were normalized using the median value of the most conserved a thousand genes among samples. Six tissues (cerebellum, brain without cerebellum, heart, kidney, liver, and testis) in nine mammalian species and chicken are profiled in this work.
Transcript read counts from Tschopp et al. (2014) was downloaded from GSE60373 (http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE60373; last accessed January 25, 2018). Tail bud, forelimb bud, hindlimb bud, and genital bud in early development stage from mouse and anolis were profiled in this work. Read counts were also normalized to TPM values.
Skin Appendage at Placode Stage Transcriptome Data
To collect skin appendage placode transcriptome data, we dissected developing skin from embryos of single comb white leghorn chicken and emu. Fertile chicken eggs, obtained from the University of Connecticut Poultry Farm, and emu eggs, obtained from Songline Emu Farm in Gill, MA, were incubated in a standard egg incubator at 37.8 and 35.5 °C, respectively. Skin appendages in birds develop at different times across the embryo. We dissected embryonic placode skin from dorsal tract feathers between Hamburger and Hamilton (1951; H&H) stages 33 and 34, asymmetric (scutate) scales from the dorsal hindlimb tarsometatarsus at H&H stage 37, symmetric (reticulate) scales from the hindlimb ventral metatarsal footpad at H&H stage 39, and claws from the tips of the hindlimb digits at H&H stage 36. Dissected skin was treated with 10 mg/ml dispase for ∼12 h at 4 °C to allow for complete separation of epidermis and dermis. RNA was extracted from epidermal tissue using a Qiagen Rneasy kit. Stand-specific polyadenylated RNA libraries were prepared for sequencing by the Yale Center for Genome Analysis using an in-house protocol. For each individual tissue sample, we sequenced ∼50 million reads (one-quarter of a lane) on an Illumina Hiseq 2000. We sequenced two biological replicates for each tissue, with the exception of emu symmetric scales and claws, for which we were only able to obtain one replicate due to limitations in the number of eggs we could acquire.
Reads were mapped to the respective species genome available at the time: WASHUC2 for chicken (Ensembl release 68 downloaded October 4, 2012) and a preliminary version of the Emu genome generated by the laboratory of Allan Baker at the Royal Ontario Museum and University of Toronto (mapped on December 5, 2012). Reads were mapped with Tophat2 v2.0.6 using the –GTF option. Mapped reads were assigned to genes using the program HTSeq, requiring that reads map to the correct strand, and using the “intersection-nonempty” option for dealing with reads that mapped to more than one feature.
Estimating the Level of Correlated Transcriptome Evolution
For all data sets, we calculated TPM (transcripts per million transcripts) as the measure of gene expression level (Wagner et al. 2012). We also used normalized RPKM from Brawand et al. (2011) to compare the effect of different quantification methods. All transcriptome data were further processed to facilitate cross-species comparison, with the exception of the normalized RPKM of Brawand data set which was already normalized between species using a median-scaling procedure on highly conserved genes. For the other data sets, we followed the normalization method of Musser and Wagner (2015), using one-to-one orthologs. We then used the square root transformation to correct for the heteroscedasticity of transcriptome data (Musser and Wagner 2015). However, even after the square root transformation, we found some very highly expressed genes, such as mitochondrial genes, that still exhibited high variance relative to other genes. These were removed to prevent overestimation of correlated evolution. Finally, we averaged sqrt(TPM) values across replicates to generate a representative transcriptome for each tissue in each species.
We estimated LCE () for all combinations of tissue and species in all data sets by calculating the Pearson correlation of their contrast vectors. We tested the significance of correlated evolution by calculating a P value from a null distribution of randomly permutated gene expression contrast vectors (described below). We conducted 1, 000 permutations to generate a null distribution of the LCE . Actual estimates of correlated evolution were considered significantly higher than expected by chance if they fell in the top 5% of the null distribution. We conducted ANOVA tests in R to determine whether correlated evolution values varied depending on time since the last common ancestor of the species used for comparisons. The Welch’s t-test was used to determine whether the mean values estimated from the Brawand and Merkin data sets for the same tissue pairs were significantly different.
One challenge of estimating the permutation P value is that the degree of freedom would be overestimated using the whole transcriptome, because gene expression evolution between genes is not independent (Oakley et al. 2005; Ghanbarian and Hurst 2015), for instance because genes can be coregulated by the same transcription factors (Pavlicev and Widder 2015). Thus, a low P value is always achieved if a whole transcriptome permutation test is performed. To account for this, we subsampled 50 genes for each permutation, which represents a lower bound for the number of independently varying gene clusters identified in single cell transcriptome data. The lower bound of independently varying gene clusters is estimated using the approach of Wagner et al. (2008). We randomly sampled different sets of n genes. For each set of n genes, we calculated a correlation matrix using gene expression values from the single-cell transcriptome data set of Pavlicev et al. (2017). We then calculated the eigenvalues of the correlation matrix, and the variance of the eigenvalues. According to (Wagner et al. 2008), the effective number of independent genes equals to n minus the variance of eigenvalues of the correlation matrix. We observed that the variance of eigenvalues is always <1 when . That is to say, if we randomly draw 50 genes, their gene expression can be considered as independent events. Further, we estimated the theoretical P value for a . Based on the characteristic of Pearson correlation coefficient, the test statistic is distributed as a t-distribution with n−2 degrees of freedom. According to the discussion above, the lower bound of n is 50 for the whole transcriptome. Thus, we find the minimal to get a theoretical P value <0.05 is 0.235 (fig. 4, dashed line).
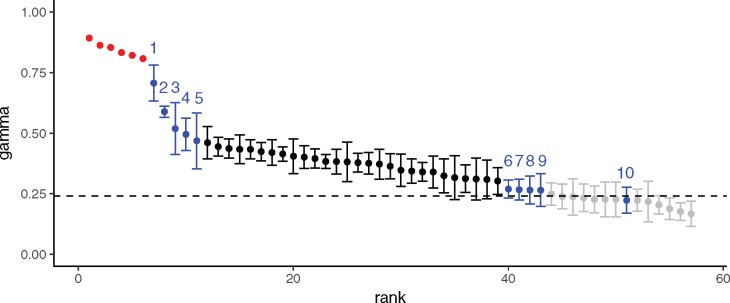
Fig. 4.—
Estimates of LCE in various tissue pairs. LCE estimates for Tschopp, Merkin, and Brawand data sets. Tschopp estimates (; points in red) are for early forelimb-, hindlimb-, genital-, and tail buds from mouse and Anolis. Merkin and Brawand estimates () are from 10 different mature tissues in 12 species of mammal and chicken. Estimates of LCE range from 0 to 1, with higher values indicating stronger correlated evolution. Dotted line indicates cutoff for estimates of significantly greater than expected by chance under a model without correlated evolution (see Materials and Methods). Gray colors identify LCE estimates with testes. Numbers identify LCE estimates for other tissues with highest and lowest LCE (points in blue): 1) cerebellum and forebrain, 2) spleen and lung, 3) spleen and colon, 4) colon and lung, 5) heart and skeletal muscle, 6) brain and liver (Brawand data set), 7) heart and liver, 8) cerebellum and liver, 9) brain and liver (Merkin data set), and 10) liver and skeletal muscle. Black data points are the remaining tissue comparisons from Merkin and Brawand data set (supplementary table S4, Supplementary Material online). Of note, brain and liver comparison were tested in both Merkin and Brawand data set, and LCE estimates from two data sets do not significantly differ from each other (t-test P value > 0.5).
We estimated the per-gene LCE () using the correlation between phylogenetic independent contrasts (Felsenstein 1985) for all tissue pairs in the Brawand data set. We tested its significance using the test statistic . According to the property of the sample correlation coefficient, is distributed as a t-distribution with degrees of freedom under the null hypothesis . Here, n is the number of independent contrasts. We calculated the P value of per-gene LCE using the probability of under the null hypothesis. We calculated the FDR and the fraction of genes under the true null hypothesis (, i.e., the proportion of genes do not have correlated evolution between two tissues) using Bioconductor package “qvalue” (Benjamini–Hochberg procedure). We performed gene ontology (GO) analysis using DAVID bioinformatics tools (v6.8).
Results
Stochastic Modeling of Correlated Transcriptome Evolution
To model correlated transcriptome evolution, we initially consider two cell types, A and B, in two species, 1 and 2 (fig. 1A and B). We assume that the two cell types are more ancient than the last common ancestor of species 1 and 2, which we refer to as species 0. We use vectors , , , to represent the transcriptome profiles of cell types A and B in species 1 and 2, respectively. Similarly, we use vectors , to represent the unknown transcriptome profiles in species 0. For each gene i, we model the evolution of its expression level in the four cell types as a stochastic process:
| (1) |
Here, ’s are multivariate random variables indexed by the continuous time variable t, representing the expression level of gene i in cell types A and B from two species. We consider the time interval from the speciation event () to present (). The initial state of the stochastic process is . Gene expression values are only measured at the present time . We studied the stochastic process with the Brownian model and the Ornstein–Uhlenbeck (OU) model, and developed an estimator of LCE (eqs. 6 and 8).
Brownian Model
We first study the case when is a Brownian process, a model for neutral transcriptome evolution. The Brownian model is adequate when gene expression changes can be sufficiently explained by random drift (Khaitovich et al. 2004; Yanai et al. 2004; Yang et al. 2017). The accumulated variances in gene expression are proportional to the divergence time in this model. We describe the multivariate Brownian process with the following stochastic differential equation:
| (2) |
Here, is a vector of four independent Brownian processes (Here, we use D for Brownian processes to avoid the confusion with cell type B). At time t, they are independent and identically normally distributed with mean 0 and variance . is the variance in gene expression that is expected to accumulate per unit time in each cell type. LCE is modeled by parameter in the correlation matrix of this process:
| (3) |
, ranging in [−1, 1], is the correlation between the gene expression changes in the two cell types: and . If , cell types A and B will undergo correlated gene expression evolution. We generally expect that , although negative correlations are also mathematically possible. This is because gene expression levels may change toward the same direction if they are coregulated in two cell types. On the other hand, if , gene expression changes are uncorrelated in tissues A and B, and no correlated evolution is happening.
We developed a method to estimate LCE parameter using data from current time, t. For Brownian models, it is known that gene expression vector, , is distributed as a multivariate normal random vector with mean , and covariance matrix: . Its gene expression contrast vector,
| (4) |
is a linear transformation of :
| (5) |
Because a linear transformation of a normally distributed random variable is still normally distributed, is distributed as bivariate normal distribution with mean and covariance matrix: , regardless of the initial state of the Brownian process. Thus, we find that is the Pearson correlation coefficient of the gene expression contrasts between cell types A and B. As a result, we estimate using the correlation coefficient of the observed transcriptome contrasts:
| (6) |
Although we assumed a universal parameter for all genes in the derivation above, our simulation analysis (see below) showed that when varies among genes, estimated the average LCE among all genes.
Ornstein–Uhlenbeck Model
We also studied when gene expression evolution is subject to stabilizing selection (Gilad et al. 2006; Fay and Wittkopp 2008; Bedford and Hartl 2009; Metzger et al. 2017). In this case, is a multivariate Ornstein–Uhlenbeck process. This process is described by the following stochastic differential equation:
| (7) |
Here, S and are defined as the same as in the Brownian model (eq. 3). represents the strength of stabilizing selection and is always positive. (Brownian model is the limiting case when .) is the fitness optimum. For a gene i, gene expression optima are the same in homologous tissues, whereas they may differ between tissues in the same species. Assuming that tissues A and B have evolved long before the speciation event, we study the stationary solution for the OU process.
We took an analogous approach to that we utilized for the Brownian model to estimate LCE parameter using data from current time. First, as shown in (Meucci 2009), the stationary solution for equation (7) is a multivariate normal distribution with mean and covariance matrix . Second, we got the gene expression contrast vector through the linear transformation (eqs. 4 and 5), and found that is distributed as bivariate normal distribution with mean 0 and covariance matrix , regardless of the evolutionary optimum. Again, we find that is the Pearson correlation coefficient of the gene expression contrasts between cell type A and B. As a result, we arrived at the same estimator of LCE parameter as in the Brownian model:
| (8) |
This formula indicates that our estimation of LCE is invariant to some transformations of gene expression measures. For example, if gene expression measure increases by an additive constant c in one species, remains unchanged. In fact the measure is invariant under any affine transformation: y = ax + c.
Estimation of Correlated Evolution Is Accurate in Simulated Data
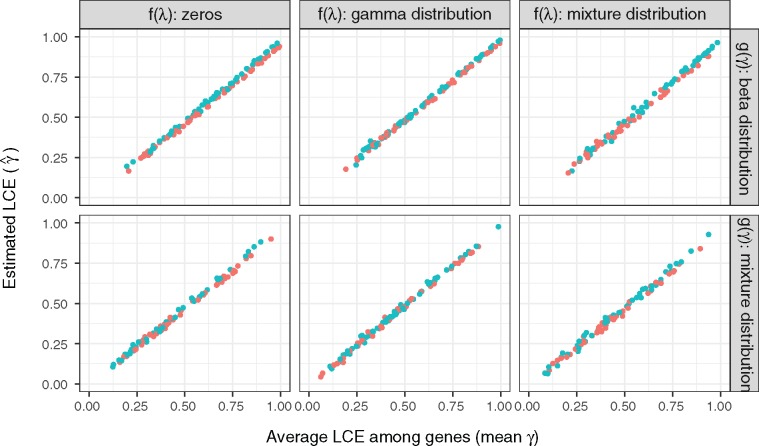
We simulated transcriptome evolution data to evaluate our LCE estimator under various conditions. A total of 6,119 one-to-one ortholog genes among four mammals and chicken are considered as in Merkin et. al (2012). For each gene, we simulated its gene expression evolutionary trajectory by iteratively updating for a short time period according to equation (7) ( for Brownian model; for OU model). Negative were suppressed to zero in each iteration to avoid negative expression values in the simulation. We used square root transformed gene expression TPMs from Merkin et al. as selective optima and their initial states (see Materials and Methods). TPMs from two pairs of tissues were used to represent both highly correlated transcriptome profiles (, fig. 2 blue points) and lowly correlated transcriptome profiles (, fig. 2 orange points). We generated LCE parameter and stabilizing selection parameter from various distributions to simulate different evolutionary conditions. were drawn from two distributions: 1) a beta distribution, and 2) a mixture distribution of beta distribution and zeros. The mixture distribution simulates the scenario that a fraction of the genes experience varied levels of correlated evolution, whereas the rest of the genes evolve independently. Similarly, were drawn from three distributions: 1) zeros (Brownian model), 2) a gamma distribution, and 3) a mixture distribution of gamma distribution and zeros. The mixture distribution simulates the scenario where genes are constrained by varied levels of stabilizing selection with a fraction of genes evolves neutrally. We find that our estimates of LCE are robust to various model parameters. We observed a high correlation () between estimated LCE () and the mean of true among genes in all cases (fig. 2). Meanwhile, as predicted by the theoretical analysis, the correlation in gene expression optima and the initial state of the stochastic process does not influence the estimation of LCE, (different colors in fig. 2). In summary, estimated from phylogenetic contrasts accurately estimates the average LCE among all genes under the Brownian and OU process.
Fig. 2.—
Estimation of LCE in simulated transcriptome data. We simulated 1, 000 transcriptome evolutionary trajectories with varied distributions of stabilizing force and LCE paratmer . The distributions of are: (Brownian model), a gamma distribution (Ornstein–Uhlenbeck model), and a mixture distribution of zeros and gamma distribution (mixture of Brownian and OU model). The distributions of are: a beta distribution, and a mixture distribution of beta distribution and zeros. In all conditions, we observed a high correlation between the estimated LCE () and the mean of true among genes (). Blue and orange colors are simulations with highly (lung–spleen) and lowly (brain–testes) correlated gene expression optima, respectively. We find that estimation of LCE are not influenced by the correlation between gene expression optima or the initial state of the stochastic process. We used square root transformed TPMs from Merkin data as gene expression optima and the initial states in the simulation. A total of 600 data points are randomly sampled to be plotted in this figure.
Correlated Evolution Estimates Are Consistent across Data Sets
To document LCE among various tissues, we applied our model to three previously published comparative transcriptome data sets: 1) Merkin et al. (2012), containing nine mature tissues from four mammals and chicken (fig. 3A), 2) Brawand et al. (2011), containing six mature tissues in ten species of mammals and chicken (fig. 3B), and 3) Tschopp et al. (2014), reporting data on limb, genital-, and tail buds at early developmental stages in mouse and Anolis. These data sets have three advantages. First, all samples for each data set were generated in the same lab and with the same protocol, reducing batch effects. Second, these data sets include a diverse set of both mature and developing tissues, enabling us to determine the extent to which correlated evolution varies depending on tissue relationships. Third, the Brawand and Merkin data sets sampled five tissues in common (“brain”, heart, liver, kidney, and testes), allowing us to determine whether estimates of LCE are consistent across data sets and species.
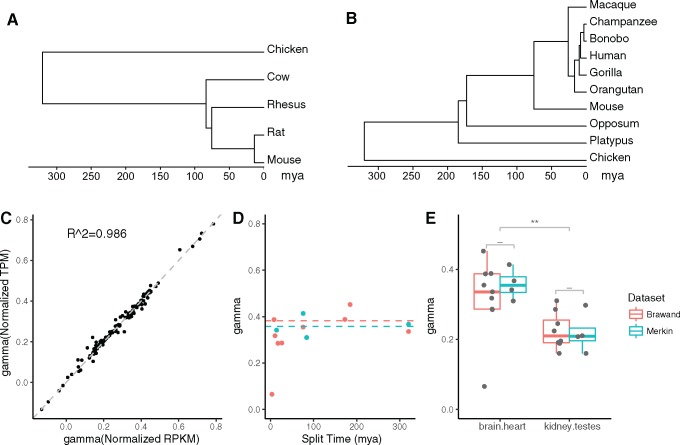
Fig. 3.—
Effect of normalization methods, species divergence time, and data set on estimates of LCE. (A) The time tree for species analyzed in Merkin data set. (B) The time tree for species analyzed in Brawand data set. All tissues considered here are much older than the species compared in these two data sets. (C) The scatterplot of estimated LCE using two normalization methods for Brawand data set: normalized RPKM according to most consistently expressed genes as in Brawand et al. (2011), and normalized TPM according to one-to-one orthologs as in Musser et al. (2015). The normalization methods of gene expression levels do not affect the estimation of LCE (R2 = 0.986). (D) Estimates of LCE ( from brain and heart sampled in both Merkin and Brawand data sets using independent contrasts. The horizontal axis is the species divergence time in million years at internal nodes as shown in (A) and (B). The vertical axis is the estimated LCE, . The estimated LCE ( is not influenced by species divergence time (ANOVA P value > 0.1). The dashed lines indicate the mean value of with divergence time > 50 Ma (blue for Merkin data, orange for Brawand data). (E) Boxplot of estimated LCE for two shared tissue comparisons between Brawand and Merkin data set (see all shared tissue comparisons in supplementary fig. S1, Supplementary Material online). Estimates from two data sets do not statistically differ (Welch’s t-test, “-“: P > 0.05, “*”: P < 0.05; “**” P < 0.01). We conclude that our estimates of LCE are consistent if estimated from data sets produced by different laboratories.
We explored the extent to which our estimates of LCE, , depends on the normalization method of gene expression measures, the species compared, and data set used. To ensure that observations are independent, we calculated using the correlation between phylogenetic independent contrast vectors (Felsenstein 1985) of gene expression levels in Merkin and Brawand data sets. We found that is consistent with different gene expression normalization methods: normalized RPKM as in Brawand et al. (2011), or normalized TPM as proposed in Musser and Wagner (2015) (fig. 3C, , supplementary fig. S1A, Supplementary Material online). We found consistent regardless of the divergence time based on estimates by Hedges et al. (2006) for mature tissues studied in both Brawand and Merkin (fig. 3D, for all tissue pairs ANOVA P values for dependence of on divergence time > 0.1). However, estimated from recently diverged species pairs (< 50 Myr) tended to be lower than from more distantly related species for the same tissues, contributing to relatively large SD for some tissue pairs (supplementary tables S1–S3, Supplementary Material online). One possible explanation of this finding is that recently diverged species have not accumulated enough gene expression changes to allow for accurate estimation of correlated evolution. Thus, comparisons from recently diverged species may be dominated by observational noise which likely is uncorrelated, resulting in underestimation of
Notably, we found consistent for the same tissue pairs across different data sets (fig. 3E and supplementary fig. 1B, Supplementary Material online). The average values for the same tissue pair, calculated for Merkin and Brawand data sets separately do not differ statistically (Welch’s t-test P values > 0.1), indicating that estimates of the relative LCE are robust to variations in data acquisition. As a result, the fact that our estimation of LCE is consistent with different normalization methods, species, as well as data sets suggests our results reflect biological properties of these tissues, rather than technical artifacts introduced by data acquisition or manipulation.
Correlated Evolution Is Pervasive and Varies in Degree across Diverse Tissues
Our results show that correlated evolution is pervasive and strong, and varies in degree depending on the tissues under comparison (fig. 4 andsupplementary tables S1 and S2, Supplementary Material online). The highest estimates of LCE were from embryonic appendage buds (fig. 4; points in red), where ranged from 0.81 (early hindlimb and tail buds) to 0.89 (early hindlimb and genital buds) consistent with the conclusion of the authors that genital and limb buds are developmentally highly related. Correlated evolution estimates among the differentiated tissues of the Brawand and Merkin data sets were lower. For each pair of tissues in the Brawand and Merkin data sets, we calculated , the mean value of from independent contrasts with split time > 50 Myr (supplementary tables S1 and S2, Supplementary Material online). Mean estimates ranged from 0.17 (liver and testes) to 0.71 (forebrain and cerebellum), indicating substantial variation in correlated evolution among differentiated tissues (fig. 4). Most tissues exhibited at least some degree of correlated evolution, with ∼71% of individual significantly greater than expected by chance (permutation P value < 0.05). Notable exceptions were tissue comparisons with testes, which dominated the lower end of LCE estimates (fig. 4, data points in gray), and could not be statistically distinguished from a model in which gene expression evolved independently between tissues.
Level of Correlated Evolution Differs with Phylogenetic Age of Tissues
The observation that tissues exhibit different LCE indicates that tissues’ evolutionary independence may itself evolve. For instance, do cell and tissue types of recent origin exhibit higher LCE relative to other tissues? To address this question, we collected transcriptomes from developing bird feathers, two different avian scale types, and claws from two avian species, chicken and emu. Feathers are an evolutionary innovation that evolved in the bird stem lineage, replacing scales across much of the body (Prum and Brush 2002). Scales are found in all reptiles, and also on the feet of birds. Bird scales include large, asymmetric “scutate” scales, found on the top of the foot, and small, symmetric “reticulate” scales on the sides and plantar surface. Birds also have claws, which develop from distal toe skin, immediately adjacent to both avian scale types. Claws are shared by reptiles and mammals, indicating that they are phylogenetically older than feathers and scales.
We sampled epidermis during early development of these skin appendages in chicken and emu. LCE estimates (table 1 and supplementary table S5, Supplementary Material online) ranged from 0.71 (feathers and claws) to 0.88 (feathers and scutate scales). Claws, the phylogenetically most ancient skin appendage in this sample, have a lower LCE compared with other skin appendages. Feathers, which evolved most recently, are highly correlated with scutate scales (), but exhibit less correlated evolution with reticulate scales (, t-test on bootstrapping P = 9×10−4) or claws (, t-test on bootstrapping P = 3×10−4). Notably, feathers and scutate scales undergo more correlated evolution than is found between the two avian scale types, which existed prior to the origin of feathers (). These results indicate that LCE is not determined by the shared anatomical location of scales and claws on the distal hindlimb. Rather, our data show that the more recently evolved tissue, feathers, evolves in concert with its sister tissue type, scutate scales. This is consistent with the hypotheses that feathers and scutate scales are serially homologous in early development, and are both derived from ancestral archosaur scales (Prum and Williamson 2001; Harris et al. 2002; Musser et al. 2015; Di-Poï and Milinkovitch 2016). Thus, our results suggest that the degree of genetic individuation may increase over evolutionary time, with tissues of more recent origin undergoing relatively higher LCE.
Table 1.
Estimated LCE among Avian Skin Appendages
| Feather | Scutate Scale | Reticulate Scale | Claw | |
|---|---|---|---|---|
| Feather | 1 | 0.88 | 0.79 | 0.71 |
| Scutate Scale | 1 | 0.86 | 0.72 | |
| Reticulate Scale | 1 | 0.71 | ||
| Claw | 1 |
Note.—Estimates were obtained from transcriptomes of early skin appendage development (placodes) in chicken and emu embryos. For each skin appendage type in each species, we averaged gene expression across replicates, and calculated using gene expression contrasts <10 to avoid the influence of highly expressed structural genes.
Theoretical Analysis of Transcriptome Clustering Patterns
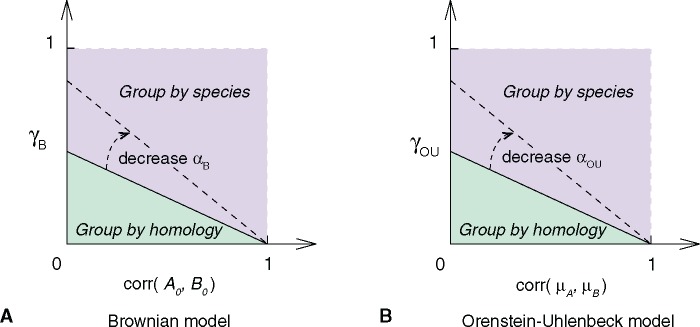
Hierarchical clustering of transcriptomes has been utilized as a discovery tool for cell and tissue type homologies across species (Tschopp et al. 2014), and for reconstructing the phylogeny of cell type diversification (Arendt 2008; Kin et al. 2015). However, it is unclear how correlated evolution may influence the result of hierarchical clustering. To explore this, we first conducted a theoretical analysis of how LCE influences the hierarchical clustering pattern of two tissues in two species using our stochastic models of transcriptome evolution. Using Pearson correlation as the similarity measure, samples group by tissue type when the correlation between the same tissue ( and ) is higher than the correlation between tissues from the same species ( and ). Otherwise they group by species. We studied the formula of their transcriptome correlation matrix to predict the hierarchical clustering pattern under various conditions (fig. 5).
Fig. 5.—
Theoretical hierarchical clustering pattern varies with model parameters. (A) Brownian model. (B) Ornstein–Uhlenbeck model. The hierarchical clustering pattern of four cell types, A1, A2, B1, and B2, is determined by the correlation matrix of their transcriptome profiles (supplementary eq. S2, Supplementary Material online). Homology signal (horizontal axis; or )) and correlated evolution signal (vertical axis; ) shape cell type transcriptome similarities together. The phase transition condition between clustering by homology and clustering by species is a straight line (supplementary eqs. S4 and S5, Supplementary Material online). In both models, no clustering by species pattern is observed without correlated evolution (). and are parameters that are related to the random walk variance, , in Brownian and OU model, respectively (see supplementary methods, Supplementary Material online). The dashed arrow indicates how the phase transition boundary changes with parameters and . If the random walk variance decreases, there is higher chance to see group-by-homology pattern.
Under the Brownian model, the correlation matrix of the four samples is determined by three parameters (supplementary methods, eqs. S1–S4, Supplementary Material online): LCE (), the correlation of gene expression profiles between the ancestral cell types (), and the ratio of accumulated random walk variances and the variances in gene expression levels in the ancestral cell types (). In the parameter space of and , the phase transition boundary between clustering by species and clustering by tissue is a straight line with positive intersections on both axis (fig. 5A and supplementary methods, eqs. S1–S4, Supplementary Material online). We find that samples cluster by tissue type with small and , whereas samples cluster by species when two tissue types are similar to each other ancestrally (large ) and have high LCE (large ).
We arrived at a similar conclusion under the OU model. The correlation matrix of four cell types is determined by LCE (), the correlation of gene expression optima in two tissues (), and the ratio of stochastic variances and the variances in the expression optima () (supplementary methods, eq. S5, Supplementary Material online). The phase transition boundary between two hierarchical clustering patterns in the parameter space of and is also a straight line as in the Brownian model (fig. 5B). We find again that samples cluster by species when two tissue types are similar to each other (large ) and experience high LCE (large ). In both models, when there is no correlated evolution (), it is expected that samples group by tissue type.
As a result, the hierarchical clustering pattern is shaped by evolutionary changes as well as historical residuals (fig. 5). In both models, the correlation between the same tissues from two species reflects, in part, the residual historical signature of homology. However, this historical signal decreases over time due to the variation introduced by gene expression evolution. On the other hand, the correlation between tissues from the same species is influenced by LCE, as well as their correlation in the ancestor (Brownian model) or correlation in their fitness optima (OU model). It is worthwhile to note that LCE (value on y axis) and the correlation in the ancestor or fitness optima (value on x axis) may be positively related. As a result, the biological observations are likely near the diagonal of figure 5. Together, these factors affect the hierarchical clustering pattern of cell type transcriptomes and need to be considered when using comparative transcriptomes in cell type evolutionary study.
Correlated Evolution Shapes Transcriptome Similarities
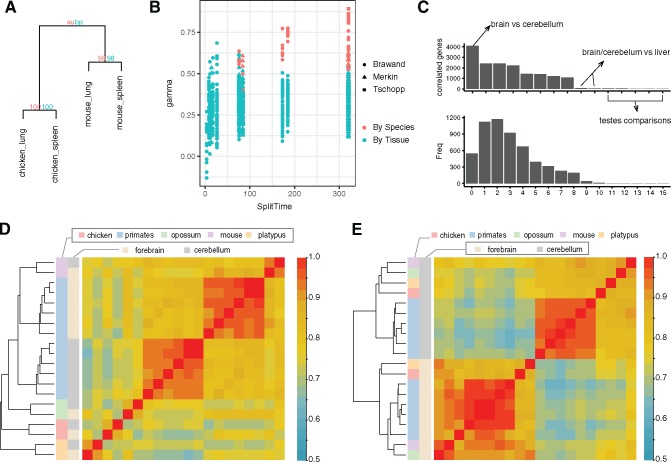
Our transcriptome evolution model suggests that LCE affects the hierarchical clustering pattern to various extents (fig. 5). This is consistent with the previous observation that tissue transcriptomes can cluster by species or by tissue homology under different conditions (Sudmant et al. 2015; Gu 2016). Clustering by species can occur even when the tissues are more ancient than the tissues under comparison, as has been shown in a number of cases (Lin et al. 2014; Tschopp et al. 2014; Sudmant et al. 2015; Gu 2016). Similarly, we observed the species clustering pattern in the reanalysis of three data sets described earlier, and the pattern persists with different gene expression metrics, including with both normalized TPM and RPKM relative expression values. For example, lung and spleen evolved prior to the common ancestor of birds and mammals, yet we found lung and spleen samples from chicken and mouse clustered by species, rather than tissue identity (fig. 6A).
Fig. 6.—
Clustering by homology can be recovered by excluding genes with high LCE. (A) Hierarchical clustering of mouse and chicken lung and spleen illustrating examples of tissues clustering by species. Numbers at nodes are confidence values (%) calculated by the package using two different methods. (B) LCE versus clustering pattern of tetrads with samples from two species and two homologous tissue types. Higher LCE are associated with larger chance of clustering by species, as is the age of the lineage split. With higher LCE and long evolution, correlated evolution leads to the accumulation of species specific similarities among tissues and thus to clustering by species. (C) Upper: Bar-plot of the number of correlated (high LCE) genes identified in all tissue comparisons in Brawand data set. The criteria for highly correlated genes are: q value < 0.05 (BH correction) and . The x-axis represents different tissue comparisons. Lower: Histogram of how many times each one-to-one orthologs are identified as correlated genes in all tissue pairs of Brawand data set. Only a minority of genes have high LCE in a majority of tissue pairs. (D) Heatmap and hierarchical clustering of forebrain and cerebellum samples from Brawand data using all one-to-one orthologs. Outside the primates samples cluster by species. (E) Samples cluster by tissue types when genes with high LCE are excluded in the hierarchical clustering analysis.
To explore the prevalence of clustering by species, and its association with LCE in real data, we determined the clustering pattern for every pair of tissue and species in the Brawand, Merkin, and Tschopp data sets. We found that the majority of mature tissues cluster by tissue type, whereas tissues with high LCE cluster by species (fig. 6B; symbols in red, supplementary table S4, Supplementary Material online). Further, the more distantly related the species, the more likely tissues clustered by species rather than homology. Tissues collected from species with divergence times <50 Myr always clustered by tissue homology. However, with >50 Myr of divergence, nearly all tissue pairs with > 0.5 clustered by species, rather than homologous tissue. Phylogenetic divergence time also affects clustering because greater divergence time allows for the accumulation of more species-specific similarities via correlated evolution, whereas similarity due to homology decays. Thus, transcriptomes reflect both the homology of cell and tissue types, as well as the effect of correlated evolution within each lineage.
Clustering by Tissue Type Is Recovered by Excluding Genes with High Correlated Evolution
The observation above suggest that the effect of correlated evolution needs to be carefully considered when using hierarchical clustering or phylogenetic reconstruction methods with comparative RNA-seq data. To dissect the contribution of each gene to correlated transcriptome evolution, we estimated per-gene LCE () for each one-to-one ortholog i, by calculating the correlation between its expression contrasts in two tissues along the phylogenetic tree (Felsenstein 1985). A limitation for estimating per-gene LCE is species number. As a result, we calculated per-gene LCE estimates only for the Brawand data set, which contained the largest number of species (fig. 3B). However, we only included gene expression contrasts outside the primate group to avoid biases from dense sampling in one clade and short branch lengths, which could result in inaccurate estimation of variance between species gene expression (Garland et al. 1992; Ackerly 2000).
We then tested whether our estimate of per-gene LCE is significant for all tissue pairs (see Materials and Methods). We estimated the portion of genes that belong to the true null hypothesis (), that is, do not show correlated evolution, using the P value distribution of all analyzed genes. In Brawand data, varies from 0.08 (forebrain–cerebellum) to 0.64 (liver–testes) (supplementary table S6, Supplementary Material online), indicating that in this analysis, a large fraction of one-to-one orthologous genes are influenced by correlated evolution. This included 36% of the genes in the liver–testes comparison and 92% in the forebrain–cerebellum comparison. We then identified individual genes with high LCE for each tissue pair using FDR < 0.05 (Benjamini–Hochberg procedure) and with effect size . The comparison of forebrain and cerebellum yielded the largest number of highly correlated genes (), whereas tissue comparisons with testes yielded limited number of highly correlated genes (average ; fig. 6C). The top enriched GO terms in forebrain–cerebellum specific correlated genes () are related to pan-neuronal functions such as ion transmembrane transport and chemical synaptic transmission (supplementary table S7, Supplementary Material online). We also identified 1,190 genes were highly correlated in at least five tissue comparisons. GO analysis of these genes showed enrichment for cell cycle, metabolic, and RNA processing related GO terms (supplementary table S8, Supplementary Material online). Finally, we refined the hierarchical clustering analysis of cell type transcriptomes by excluding genes with high LCE. Whereas forebrain and cerebellum samples cluster by species outside the primates using all one-to-one orthologous genes (fig. 6D), their clustering pattern reveals tissue homology after removing genes with high LCE (fig. 6E). Hence, identification and elimination of genes with high LCE can be used to recover the phylogenetic history of cell and tissue types.
Discussion
In this study, we analyzed patterns of transcriptome variation among different cell and tissue types and species using stochastic models of gene expression evolution. We found strong signals of correlated gene expression variation among different cell and tissue types. This pattern can arise for a number of reasons. The principal ones are: 1) Artifacts in measuring gene expression in different species causing species specific differences in estimated expression level (Gilad 2015; Sudmant et al. 2015); 2) mechanistic reasons, where either gene regulatory communalities among cell types leads to “concerted” evolution of gene expression due to pleiotropic effects of mutations (Musser and Wagner 2015) or species specific physiological differences affecting gene expression (Lin et al. 2014) (anonymous reviewer). We address these possible causes of correlated gene expression variation below.
As with any quantitative method, RNA-seq can be subject to artifacts, and some sources of artifacts have been identified (Marioni et al. 2008; Seqc Maqc-Iii Consortium 2014; Gilad 2015). For instance, batch effects can lead to systematic differences between data sets and thus affect downstream analysis. However, we consider it unlikely that the main result of this study, pervasive and strong correlated variation in gene expression, is caused solely by known artifacts. There are a number of features of our results that are hard to explain as artifacts. One is that the same tissues from different species and data from different laboratories leads to statistically indistinguishable results with respect to the estimated LCE (fig. 3D and E). Secondly, artifacts due to different genome quality and transcript annotations should affect estimates of different cell and tissues in the same way, resulting in statistically indistinguishable estimates of LCE between different tissue pairs. In contrast, we find that the LCE estimates varied across different tissue pairs, and is generally higher between tissues with similar cell biology (fig. 4). For instance, our highest estimates were among early developing limb, genital, and tail bud tissue. At this early stage of development, these anlagen largely consist of undifferentiated mesenchymal cells. Moreover, two of the highest measures of correlated evolution were for forebrain and cerebellum (=0.71), and heart and skeletal muscle (=0.47). Both tissue pairs express common sets of pan-neuronal and contractile genes, respectively. Furthermore, we found evidence that developmental origin influences the degree of correlated variation in differentiated tissue. Lung and colon (=0.50), both endodermal derivatives, were highly correlated relative to other differentiated tissues despite their very distinct functions. These findings along with the fact that our estimates are consistent across various data sets and consistent with respect to gene expression normalization methods (fig. 3) suggest that estimated LCE reflect the biological nature of the tissues under comparison, rather than artifacts of genome quality, transcripts annotation, or batch effects. The overall pattern of gene expression correlations described here would require a quite peculiar set of artifacts to generate the biologically plausible differences.
The second possible explanation for the correlated gene expression variation is what has been called “concerted” evolution of gene expression (Musser and Wagner 2015). Concerted gene expression evolution occurs when cell types share parts of their gene regulatory networks. Thus, mutations in certain cis- or trans-regulatory factors can affect gene expression in more than one cell type. This is a special case of pleiotropic effects, a widely recognized pattern for all kinds of characters (Stearns 2010; Wagner and Zhang 2011) and thus plausibly also for gene expression in different cell types. A related explanation is that correlated evolution is expected if species differ in their physiological states in a way that affects gene expression in the two cell types studied. For instance, differences in hormone levels, diet, or preferred temperature can lead to species-specific differences in gene expression affecting multiple cells. Correlated evolutionary changes caused by any of these molecular and physiological factors can be called concerted evolution. The term “concerted evolution” originated in the study of nucleotide sequence evolution (Dover 1993; Elder and Turner 1995; Liao 1999), but more generally we use the term here for the “sharing” of mutational effects among different cell types, tissues, and organs (Musser and Wagner 2015). This interpretation predicts that tissue specific genes do not contribute to correlated evolution. Consistent with this, we observed significantly decreased LCE when analyzing tissue specific genes only (supplementary fig. S2, Supplementary Material online, Welch’s t-test P value < 10−6).
One obvious reason for correlated evolution is the fact that nearly all cell types share certain metabolic and structural “housekeeping” genes, and thus evolutionary changes in their expression would contribute to correlated gene expression variation. However, our finding that different tissue types from the same set of species (e.g., human and mouse) can have very different LCE (figs. 3E and 4) suggests that correlated evolution does not solely originate from globally shared “housekeeping” genes. Instead, the correlated evolution signals are heavily influenced by the nature of the tissues and cells compared, suggesting that the structure of the gene regulatory networks active in these cells affects the strength of correlated evolution. For instance, our finding of relatively high LCE between forebrain and cerebellum is consistent with findings in other animals that common transcription factors regulate pan-neuronal gene expression across different neuronal cell types (Ruvinsky et al. 2007; Stefanakis et al. 2015). Previous studies have shown that gene expression in testes has a high degree of tissue-specificity (Lin et al. 2014; Yue et al. 2014), is highly divergent among mammals relative to other tissues (Brawand et al. 2011), and is under directional selection (Khaitovich et al. 2005, 2006). Our results suggest that a key factor in explaining the distinct evolutionary history of testes is its ability to evolve gene expression independently of other organs, that is, gene regulatory individuality.
Here, we acknowledge that most samples in our analysis contain more than one cell type, and cell types may be shared among different tissues. These may contribute to LCE estimated for tissue types. Never the less, tissue transcriptomes can still serve as a surrogate of gene expression profile of major cell types in that tissue type. Particularly, although testes share epithelial and mesenchymal cell types with other tissues, no significant LCE was observed between testes and other tissues. In addition, genes with strongest LCE signal between cerebellum and forebrain are highly enriched for synaptic functions rather than structural or supportive functions by sharing some glial cells.
Overall, it is important to note that the empirical results we report here identify a statistical pattern, correlated gene expression variation between cell and tissue types, which can have a variety of explanations. In this study, we did not specifically investigate the actual cause for these patterns, which needs to be done on a case by case basis. However, our results indicate that this pattern is less likely to be caused by artifacts or some global biological factor. Further empirical investigations are needed to reveal the mechanistic basis for this phenomenon.
Modeling Correlated Evolution Is Essential for Reconstructing Cell Type Phylogeny
Our study raises several issues of practical importance for comparative transcriptomics. It is clear that many evolutionary changes in gene expression are not limited to a single cell type, making cross species comparisons difficult. This fact has hampered attempts to use gene expression data to assess the homology of cells and tissues across species, because straight forward clustering of gene expression profiles from different species can lead to obviously wrong results. For example, Tschopp et al. (2014) showed that clustering of transcriptomes is unable to reproduce the fact that limb buds of mice and lizards are homologous and thus also prevented the assessment of the hypothesized serial homology of limbs and external genitalia (penis/clitoris). Hence, it would be desirable to correct for the effects of correlated variation when attempting to reconstruct the evolutionary history of cell and tissue types from comparative transcriptome data.
Correcting for correlated gene expression evolution is challenging because correlated evolution is occurring at different levels in different tissues. In this study, we outline a potential solution to this problem. We show that correlations of phylogenetic contrasts (Felsenstein 1985), with large enough taxon samples, can identify genes with high contributions to the correlated evolution signal. Excluding those genes from a hierarchical clustering analysis leads to a result reflecting tissue homology (fig. 6D and E). This highlights the importance of sampling more taxa in evolutionary studies of cell or tissue types. Genes that are less vulnerable to correlated evolution in tissues of interest can be identified from a group of species with known tissue homology. These genes allow for the classification of tissues with uncertain homology using unsupervised learning methods, such as PCA and hierarchical clustering (fig. 6D and E), thus facilitating the study of the origination of novel cell and tissue types. It will be of value to develop analytical tools to systematically correct for the effects of correlated gene expression evolution and thus enable the broad application of the comparative method with respect to cell and tissue transcriptomes.
It will also be useful to extend phylogenetic independent contrasts (PIC) to models other than Brownian motion. Previous simulation results suggest that PIC outperforms other methods under OU model but show decreased accuracy (Martins and Garland 1991; Diaz-Uriarte and Garland 1996). Moreover, there is currently a debate regarding whether Brownian motion is adequate for modeling gene expression evolution (Gilad et al. 2006; Fay and Wittkopp 2008). Recently diverged taxa, such as primates, may obey assumptions in the Brownian motion model (Khaitovich et al. 2004; Khaitovich et al. 2006; Yang et al. 2017). In other cases, transcriptome divergence has been observed to saturate (Bedford and Hartl 2009; Kin et al. 2016; Metzger et al. 2017) (Brawand data, supplementary fig. S3, Supplementary Material online), which may be adequately modeled with an OU model (supplementary methods, eqs. S6 and S7, Supplementary Material online). Thus, a theoretical study of comparative methods under the OU model may advance our understanding of correlated evolution.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Supplementary Material
Acknowledgments
We are thankful for the contributions of Allan Baker, principal investigator of the Emu Genome Project, who died unexpectedly in November 2014. Allan leaves behind a long legacy in the fields of ornithology, evolutionary biology, and avian conservation. He will be greatly missed. We would like to thank Thomas A. Stewart, Oliver W. Griffith, and Arun R. Chavan for their thoughtful and helpful review of the manuscript. CL gratefully acknowledges the receipt of a graduate fellowship from China Scholarship Council and the support of the Raymond and Beverly Sackler Institute. JM gratefully acknowledges funding from the Dillon and Mary Ripley Graduate Fellowship Fund at Yale University and the National Science Foundation Graduate Research Fellowship under grant No. DGE-1122492. The research was supported by the W. R. Coe Fund at Yale University, the John Templeton Foundation grant #54860, NSF grant # 14-001273, and the Yale University Science Development Fund. The opinions expressed in this article are not those of the John Templeton Foundation. RNAseq data for bird skin appendages was produced in the Yale Center of Genome Analysis.
Literature Cited
- Achim K, et al. 2015. High-throughput spatial mapping of single-cell RNA-seq data to tissue of origin. Nat Biotechnol. 33(5):503–509.http://dx.doi.org/10.1038/nbt.3209 [DOI] [PubMed] [Google Scholar]
- Ackerly DD. 2000. Taxon sampling, correlated evolution, and independent contrasts. Evolution 54(5):1480–1492.http://dx.doi.org/10.1111/j.0014-3820.2000.tb00694.x [DOI] [PubMed] [Google Scholar]
- Arendt D. 2008. The evolution of cell types in animals: emerging principles from molecular studies. Nat Rev Genet. 9(11):868–882.http://dx.doi.org/10.1038/nrg2416 [DOI] [PubMed] [Google Scholar]
- Arendt D, et al. 2016. The origin and evolution of cell types. Nat Rev Genet. 17:744–757. [DOI] [PubMed] [Google Scholar]
- Bedford T, Hartl DL.. 2009. Optimization of gene expression by natural selection. Proc Natl Acad Sci U S A. 106(4):1133–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brawand D, et al. 2011. The evolution of gene expression levels in mammalian organs. Nature 478(7369):343–348.http://dx.doi.org/10.1038/nature10532 [DOI] [PubMed] [Google Scholar]
- Brunet T, et al. 2016. The evolutionary origin of bilaterian smooth and striated myocytes. Elife 5. doi: 10.7554/eLife.19607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz-Uriarte R, Garland T.. 1996. Testing hypotheses of correlated evolution using phylogenetically independent contrasts: sensitivity to deviations from Brownian motion. Syst Biol. 45:27–47.http://dx.doi.org/10.1093/sysbio/45.1.27 [Google Scholar]
- Di-Poï N, Milinkovitch MC.. 2016. The anatomical placode in reptile scale morphogenesis indicates shared ancestry among skin appendages in amniotes. Sci Adv. 2:e1600708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dover GA. 1993. Evolution of genetic redundancy for advanced players. Curr Opin Genet Dev. 3(6):902–910.http://dx.doi.org/10.1016/0959-437X(93)90012-E [DOI] [PubMed] [Google Scholar]
- Eisenberg E, Levanon EY.. 2013. Human housekeeping genes, revisited. Trends Genet. 29(10):569–574.http://dx.doi.org/10.1016/j.tig.2013.05.010 [DOI] [PubMed] [Google Scholar]
- Elder JF Jr, Turner BJ.. 1995. Concerted evolution of repetitive DNA sequences in eukaryotes. Q Rev Biol. 70(3):297–320.http://dx.doi.org/10.1086/419073 [DOI] [PubMed] [Google Scholar]
- Ereskovsky AV. 2010. Comparative Embryology of Sponges. New York: Springer Publishing. [Google Scholar]
- Fay JC, Wittkopp PJ.. 2008. Evaluating the role of natural selection in the evolution of gene regulation. Heredity 100(2):191–199.http://dx.doi.org/10.1038/sj.hdy.6801000 [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1985. Phylogenies and the comparative method. Am Nat. 125(1):1–15. [Google Scholar]
- Felsenstein J. 1988. Phylogenies and quantitative characters. Annu Rev Ecol Syst. 19(1):445–471.http://dx.doi.org/10.1146/annurev.es.19.110188.002305 [Google Scholar]
- Felsenstein J. 2004. Inferring phylogenies. Sunderland (MA: ): Sinauer Associates. [Google Scholar]
- Garland T, Harvey PH, Ives AR.. 1992. Procedures for the analysis of comparative data using phylogenetically independent contrasts. Syst Biol. 41(1):18–32.http://dx.doi.org/10.1093/sysbio/41.1.18 [Google Scholar]
- Ghanbarian AT, Hurst LD.. 2015. Neighboring genes show correlated evolution in gene expression. Mol Biol Evol. 32(7):1748–1766.http://dx.doi.org/10.1093/molbev/msv053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilad Y, Oshlack A, Rifkin SA.. 2006. Natural selection on gene expression. Trends Genet. 22(8):456–461.http://dx.doi.org/10.1016/j.tig.2006.06.002 [DOI] [PubMed] [Google Scholar]
- Gilad YM-MO. 2015. A reanalysis of mouse ENCODE comparative gene expression data. F1000Res. 4:121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grell KG, Ruthmann A.. 1991. Placozoa In: Harrison FW, Ruppert EE, editors. Microscopic anatomy of invertebrates. New York: Wiley-Liss. p. 1–5, 7, 9, 10, 12–15. [Google Scholar]
- Gu X. 2016. Understanding tissue expression evolution: from expression phylogeny to phylogenetic network. Brief Bioinform 17(2):249–254.http://dx.doi.org/10.1093/bib/bbv041 [DOI] [PubMed] [Google Scholar]
- Gu X, Ruan H, Su Z, Zou Y.. 2017. Brownian model of transcriptome evolution and phylogenetic network visualization between tissues. Mol Phylogenet Evol. 114:34–39. [DOI] [PubMed] [Google Scholar]
- Hamburger V, Hamilton HL. 1951. A series of normal stages in the development of the chick embryo. J Morphol. 88:49–92. [PubMed] [Google Scholar]
- Harris MP, Fallon JF, Prum RO.. 2002. Shh-Bmp2 signaling module and the evolutionary origin and diversification of feathers. J Exp Zool. 294(2):160–176. [DOI] [PubMed] [Google Scholar]
- Hedges SB, Dudley J, Kumar S.. 2006. TimeTree: a public knowledge-base of divergence times among organisms. Bioinformatics 22(23):2971–2972.http://dx.doi.org/10.1093/bioinformatics/btl505 [DOI] [PubMed] [Google Scholar]
- Khaitovich P, Enard W, Lachmann M, Paabo S.. 2006. Evolution of primate gene expression. Nat Rev Genet. 7(9):693–702.http://dx.doi.org/10.1038/nrg1940 [DOI] [PubMed] [Google Scholar]
- Khaitovich P, et al. 2004. A neutral model of transcriptome evolution. PLoS Biol. 2(5):E132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaitovich P, et al. 2005. Parallel patterns of evolution in the genomes and transcriptomes of humans and chimpanzees. Science 309(5742):1850–1854.http://dx.doi.org/10.1126/science.1108296 [DOI] [PubMed] [Google Scholar]
- Kin K, et al. 2016. The transcriptomic evolution of mammalian pregnancy: gene expression innovations in endometrial stromal fibroblasts. Genome Biol Evol. 8:2459–2473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kin K, Nnamani MC, Lynch VJ, Michaelides E, Wagner GP.. 2015. Cell-type phylogenetics and the origin of endometrial stromal cells. Cell Rep. 10(8):1398–1409. [DOI] [PubMed] [Google Scholar]
- Liao D. 1999. Concerted evolution: molecular mechanism and biological implications. Am J Hum Genet. 64(1):24–30.http://dx.doi.org/10.1086/302221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin S, et al. 2014. Comparison of the transcriptional landscapes between human and mouse tissues. Proc Natl Acad Sci U S A. 111(48):17224–17229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marioni JC, Mason CE, Mane SM, Stephens M, Gilad Y.. 2008. RNA-seq: an assessment of technical reproducibility and comparison with gene expression arrays. Genome Res. 18(9):1509–1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins EP, Garland T.. 1991. Phylogenetic analyses of the correlated evolution of continuous characters – a simulation study. Evolution 45(3):534–557.http://dx.doi.org/10.1111/j.1558-5646.1991.tb04328.x [DOI] [PubMed] [Google Scholar]
- Merkin J, Russell C, Chen P, Burge CB.. 2012. Evolutionary dynamics of gene and isoform regulation in Mammalian tissues. Science 338(6114):1593–1599.http://dx.doi.org/10.1126/science.1228186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger BPH, Wittkopp PJ, Coolon JD.. 2017. Evolutionary dynamics of regulatory changes underlying gene expression divergence among Saccharomyces species. Genome Biol Evol. 9(4):843–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meucci A. 2009. Review of statistical arbitrage, cointegration, and multivariate Ornstein-Uhlenbeck. Available at SSRN: https://ssrn.com/abstract=1404905. or http://dx.doi.org/10.2139/ssrn.1404905; last accessed January 24, 2018.
- Musser JM, Wagner GP.. 2015. Character trees from transcriptome data: origin and individuation of morphological characters and the so-called “species signal”. J Exp Zool B Mol Dev Evol. 324:588–604. [DOI] [PubMed] [Google Scholar]
- Musser JM, Wagner GP, Prum RO.. 2015. Nuclear beta-catenin localization supports homology of feathers, avian scutate scales, and alligator scales in early development. Evol Dev. 17(3):185–194.http://dx.doi.org/10.1111/ede.12123 [DOI] [PubMed] [Google Scholar]
- Oakley TH, Gu Z, Abouheif E, Patel NH, Li WH.. 2005. Comparative methods for the analysis of gene-expression evolution: an example using yeast functional genomic data. Mol Biol Evol. 22(1):40–50.http://dx.doi.org/10.1093/molbev/msh257 [DOI] [PubMed] [Google Scholar]
- Pagel M. 1994. Detecting correlated evolution on phylogenies – a general-method for the comparative-analysis of discrete characters. Proc R Soc B Biol Sci. 255(1342):37–45. [Google Scholar]
- Pagel M, Meade A.. 2006. Bayesian analysis of correlated evolution of discrete characters by reversible-jump Markov chain Monte Carlo. Am Nat. 167(6):808–825. [DOI] [PubMed] [Google Scholar]
- Pankey MS, Minin VN, Imholte GC, Suchard MA, Oakley TH.. 2014. Predictable transcriptome evolution in the convergent and complex bioluminescent organs of squid. Proc Natl Acad Sci U S A. 111(44):E4736–E4742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M, et al. 2017. Single-cell transcriptomics of the human placenta: inferring the cell communication network of the maternal-fetal interface. Genome Res. 27(3):349–361.http://dx.doi.org/10.1101/gr.207597.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M, Widder S.. 2015. Wiring for independence: positive feedback motifs facilitate individuation of traits in development and evolution. J Exp Zool B Mol Dev Evol. 324(2):104–113. [DOI] [PubMed] [Google Scholar]
- Prum RO, Brush AH.. 2002. The evolutionary origin and diversification of feathers. Q Rev Biol. 77(3):261–295.http://dx.doi.org/10.1086/341993 [DOI] [PubMed] [Google Scholar]
- Prum RO, Williamson S.. 2001. Theory of the growth and evolution of feather shape. J Exp Zool 291(1):30–57.http://dx.doi.org/10.1002/jez.4 [DOI] [PubMed] [Google Scholar]
- Pu L, Brady S.. 2010. Systems biology update: cell type-specific transcriptional regulatory networks. Plant Physiol. 152(2):411–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruvinsky I, Ohler U, Burge CB, Ruvkun G.. 2007. Detection of broadly expressed neuronal genes in C. elegans. Dev Biol. 302(2):617–626. [DOI] [PubMed] [Google Scholar]
- Seqc Maqc-Iii Consortium 2014. A comprehensive assessment of RNA-seq accuracy, reproducibility and information content by the Sequencing Quality Control Consortium. Nat Biotechnol. 32(9):903–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sieburth D, et al. 2005. Systematic analysis of genes required for synapse structure and function. Nature 436(7050):510–517.http://dx.doi.org/10.1038/nature03809 [DOI] [PubMed] [Google Scholar]
- Simpson TL. 1984. The cell biology of sponges. New York: Springer New York. p. 1 online resource. [Google Scholar]
- Stearns FW. 2010. One hundred years of pleiotropy: a retrospective. Genetics 186(3):767–773.http://dx.doi.org/10.1534/genetics.110.122549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanakis N, Carrera I, Hobert O.. 2015. Regulatory logic of Pan-neuronal gene expression in C. elegans. Neuron 87(4):733–750.http://dx.doi.org/10.1016/j.neuron.2015.07.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz PR, et al. 2012. Independent evolution of striated muscles in cnidarians and bilaterians. Nature 487(7406):231–234.http://dx.doi.org/10.1038/nature11180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudmant PH, Alexis MS, Burge CB.. 2015. Meta-analysis of RNA-seq expression data across species, tissues and studies. Genome Biol. 16:287.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syed T, Schierwater B.. 2002. Trichoplax adhaerens: discovered as a missing link, forgotten as a hydrozoan, re-discovered as a key to metazoan evolution. Vie Milieu-Life Environ. 52:177–187. [Google Scholar]
- Tschopp P, et al. 2014. A relative shift in cloacal location repositions external genitalia in amniote evolution. Nature 516(7531):391–394.http://dx.doi.org/10.1038/nature13819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine JW, Collins AG, Meyer CP.. 1994. Morphological complexity increase in metazoans. Paleobiology 20(02):131–142.http://dx.doi.org/10.1017/S0094837300012641 [Google Scholar]
- Vickaryous MK, Hall BK.. 2006. Human cell type diversity, evolution, development, and classification with special reference to cells derived from the neural crest. Biol Rev Camb Philos Soc. 81(3):425–455.http://dx.doi.org/10.1017/S1464793106007068 [DOI] [PubMed] [Google Scholar]
- Wagner GP. 2014. Homology, genes, and evolutionary innovation. Princeton, New Jersey: Princeton University Press. [Google Scholar]
- Wagner GP, et al. 2008. Pleiotropic scaling of gene effects and the ‘cost of complexity’. Nature 452(7186):470–472. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Kin K, Lynch VJ.. 2012. Measurement of mRNA abundance using RNA-seq data: RPKM measure is inconsistent among samples. Theory Biosci. 131(4):281–285. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Zhang J.. 2011. The pleiotropic structure of the genotype-phenotype map: the evolvability of complex organisms. Nat Rev Genet. 12(3):204–213.http://dx.doi.org/10.1038/nrg2949 [DOI] [PubMed] [Google Scholar]
- Wang Z, Young RL, Xue H, Wagner GP.. 2011. Transcriptomic analysis of avian digits reveals conserved and derived digit identities in birds. Nature 477(7366):583–586.http://dx.doi.org/10.1038/nature10391 [DOI] [PubMed] [Google Scholar]
- Yanai I, Graur D, Ophir R.. 2004. Incongruent expression profiles between human and mouse orthologous genes suggest widespread neutral evolution of transcription control. Omics 8(1):15–24.http://dx.doi.org/10.1089/153623104773547462 [DOI] [PubMed] [Google Scholar]
- Yang JR, Maclean CJ, Park C, Zhao H, Zhang J.. 2017. Intra- and inter-specific variations of gene expression levels in yeast are largely neutral: (Nei Lecture, SMBE 2016, Gold Coast). Mol Biol Evol. 34:2125–2139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yue F, et al. 2014. A comparative encyclopedia of DNA elements in the mouse genome. Nature 515(7527):355–364.http://dx.doi.org/10.1038/nature13992 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.