Coherent Nanotwins and Dynamic Disorder in Cesium Lead Halide Perovskite Nanocrystals

Abstract

Crystal defects in highy luminescent colloidal nanocrystals (NCs) of CsPbX₃ perovskites (X = Cl, Br, I) are investigated. Here, using X-ray total scattering techniques and the Debye scattering equation (DSE), we provide evidence that the local structure of these NCs always exhibits orthorhombic tilting of PbX₆ octahedra within locally ordered subdomains. These subdomains are hinged through a two-/three-dimensional (2D/3D) network of twin boundaries through which the coherent arrangement of the Pb ions throughout the whole NC is preserved. The density of these twin boundaries determines the size of the subdomains and results in an apparent higher-symmetry structure on average in the high-temperature modification. Dynamic cooperative rotations of PbX₆ octahedra are likely at work at the twin boundaries, causing the rearrangement of the 2D or 3D network, particularly effective in the pseudocubic phases. An orthorhombic, 3D γ-phase, isostructural to that of CsPbBr₃ is found here in as-synthesized CsPbI₃ NCs.

The wide interest in semiconducting lead halide perovskites originated initially from the outstanding photovoltaic performance of hybrid organic–inorganic [CH₃NH₃]PbX₃ or [CH(NH₂)₂]PbX₃ (CH₃NH₃⁺ = methylammonium (MA), [CH(NH₂)₂]⁺ = formamidinium (FA), X = Cl, Br, I or mixture thereof) exhibiting power conversion efficiencies above 22%.¹⁻⁴ More recently, fully inorganic CsPbX₃ in the form of colloidal nanocrystals (NCs) or supported nanostructures has demonstrated bright room-temperature photoluminescence (PL) and potential for applications in light-emitting devices,⁵⁻¹¹ PL down-conversion in display technologies, and remote phosphors^12,13 as well as in photovoltaics.¹⁴⁻¹⁸ The PL is characterized by narrow emission line widths (full width at half maxima, fwhm = 12–42 nm, smaller for blue, larger for red NCs), high PL quantum yields (QY, 50–90%), and short radiative lifetimes (1–29 ns),^5,19 making these NCs a viable alternative to well-established CdSe- and InP-based semiconductor NCs.²⁰⁻²³ The latter NCs, also known as colloidal quantum dots, are wavelength-tuned primarily through quantum-size effect that is via ultraprecise size- and shape-controlled synthesis. In CsPbX₃ NCs quantum confinement is also strongly pronounced,^24,25 but apparently plays a rather minor practical role for controlling the band gap energy and thus the emission color. Instead, compositional tuning via inexpensive one-pot synthetic processes—through the formation of Cl/Br and Br/I solid solutions—enables highly accurate adjustment of their band gap energies through the whole visible spectral region (410–700 nm).^19,26 Another fundamental asset of perovskite NCs stems from the so-called defect tolerance, shared by all Pb-halide perovskites: common defects such as vacancies, grain boundaries and surfaces do not introduce midgap trap states.²⁷⁻³⁰ Hence, bright PL is achievable without the necessity for the electronic surface passivation needed with wider-gap materials, as usually required for conventional, defect-intolerant CdSe, InAs, or InP NCs, typically coated with epitaxial shells of CdS or ZnS.^20,22

In spite of this exciting scenario, there is still a lack of knowledge of the important structural aspects of the crystal defects.³¹⁻³⁴ The recent “renaissance” of halide perovskites has stimulated extensive experimental and theoretical studies,^35,36 mostly on bulk samples (single crystals and microcrystalline powders of CsPbX₃ and of their hybrids),³⁷⁻⁴⁰ aiming at clarifying the crystal structure of the different (cubic, tetragonal, orthorhombic) polymorphs, their stability ranges and transition conditions from one another upon external stimuli (temperature and pressure),³⁴ and the role of the structural disorder, either static (vacancies, nanodomains or twin defects) or dynamic (thermal vibrations and fluctuations of octahedra) on the electronic properties.⁴¹⁻⁴⁵

In small NCs, with sizes down to just a few nm, the inherently reduced extension of the coherent domains results in very broad Bragg peaks and a large amount of diffuse scattering, which makes the structural analysis of NCs by diffraction techniques far more complex than in the bulk. In the case of CsPbX₃, this limitation also makes challenging the correct identification of the stable crystal modification, even at ambient (or operational) conditions, and has resulted in conflicting conclusions in the recent literature.^5,6,46−48 Another factor is the similarity of the atomic arrangements in the various polymorphs of the CsPbX₃ family, which result in very small differences of the X-ray diffraction patterns and are practically indistinguishable by the other common characterization techniques such as high-resolution transmission electron microscopy (HRTEM) unless special in-line holography techniques are used.⁴⁹ Indeed, the cubic polymorph was initially assigned to all CsPbX₃ colloidal NCs, on the basis of a qualitative inspection of laboratory powder diffraction patterns and HRTEM analysis, resulting in a size-dependent structural stabilization of this polymorph being proposed.⁵ Presently, to the best of our knowledge, quantitative structural investigations on as-synthesized perovskite CsPbCl₃ and CsPbI₃ NCs are missing, whereas there is a general consensus on assigning the orthorhombic phase to CsPbBr₃ NCs at room temperature (RT), at least to describe the average crystal structure.⁴⁷ However, a more intricate and exciting picture is indeed taking shape. Very recent low-frequency Raman spectroscopy and inelastic X-ray scattering experiments (both requiring single crystals), providing evidence of polar fluctuations in the high-temperature (HT) cubic phase of CsPbBr₃ and MAPbBr₃, suggest that these structures are highly dynamic and appear cubic on average while fluctuating among (locally) noncubic structures.^44,45

Overall, this scenario suggests that defining the atomic arrangement, including crystal defects, is not trivial in this important class of perovskite NCs; extensive diffraction-based studies specifically addressed to investigate these aspects at the nanoscale are missing, and the potential impact of these defects on the peculiar functionalities of these materials is not fully understood.

In this work we present a precise investigation of the structural defectiveness of highly luminescent CsPbX₃ NCs prepared following the synthesis of Protesescu et al.,⁵ using a joint Debye scattering equation (DSE)/atomic pair distribution function (PDF) approach.^50,51 Through an advanced atomistic modeling of synchrotron wide-angle X-ray total scattering data relying on the DSE, we here provide clear evidence that such defectiveness results from the formation of orthorhombic subdomains (occurring both in the room and high-temperature phases) hinged through a two-dimensional (2D) or three-dimensional (3D) network of twin boundaries across which the coherence of the Pb sublattice is preserved throughout the whole NC. We also show here that the as-synthesized CsPbI₃ NCs studied in this work, highly luminescent in red and commonly assumed to be ideal cubic,⁵ are isostructural with the well-known orthorhombic γ-CsPbBr₃ phase.⁴⁷

The DSE-based method yields information about crystal structure, defects, size distribution, and morphology from polycrystalline samples, within a unifying, physically based and quantitative modeling framework. Through a real-space atomistic model of NCs, it provides a simulation of the diffraction pattern, which can be further optimized against the experimental data (details are provided in the Supporting Information). The method utilizes the information from the entire scattering signal, properly modeling non-Gaussian line-shapes and diffuse scattering effects, and goes well beyond the conventional Rietveld-based method that focuses only on information from Bragg peaks. It is suitable for studying short-range (nanoscale) structural correlations, either in an ordered or disordered state. The PDF method also utilizes both Bragg and diffuse scattering to yield information about the local structure, but the data are Fourier transformed to, and modeled directly in, real-space.⁵¹ Data suitable for a PDF analysis are collected over a wide range of momentum transfer, Q, and often are of low resolution in reciprocal space and as such provide complementary data to the high Q-resolution, limited Q-range data used for the reciprocal-space DSE methods. Both DSE-based and PDF analyses have been successfully applied in the past decade for the structural and microstructural characterization of nanoparticles and nanostructured materials, including lead chalcogenides and hybrid halide perovskites.^52,53

Our total scattering DSE-based structural characterization of CsPbX₃ NCs presented hereafter, performed both in their pristine colloidal and dry states (powders or gels), also includes the analysis of the NCs size and morphology and is further supported by Rietveld, PDF and small angle X-ray scattering (SAXS) analysis.

Results and Discussion

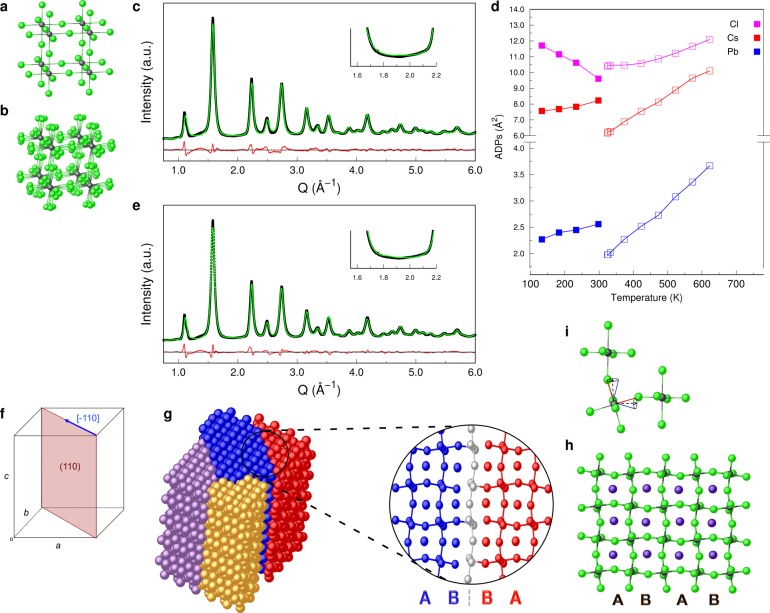
In CsPbX₃ perovskites, Pb atoms lie at the nodes of a (pseudo)cubic lattice and are octahedrally coordinated by the halides, whereas Cs ions rattle near the center of the cube. Owing to the high flexibility of the PbX₆ octahedra-based framework in 3D and depending on the size of the halide, CsPbX₃ perovskites may exhibit the archetypal cubic structure or lower symmetries, mainly resulting from the tilting of the octahedra implying bending of the Pb-X-Pb angles from the ideal 180° value. As schematically summarized in Figure 1, tilts may involve halides in the equatorial plane only (X_eq, leading to a tetragonal modification, P4/mbm) or simultaneously in the equatorial plane and along the normal axial direction (X_ax, leading to an orthorhombic modification, Pbnm or, equivalently, Pnma). We here refer to the nomenclature adopted in previous studies, indicating the cubic, tetragonal, and orthorhombic structures as the αβ and γ-phase, respectively.³⁴ At ambient conditions in the bulk, the thermodynamically stable polymorphs are perovskite structures (3D connectivity of corner-sharing PbX₆ octahedra), with cubic (though debated) for X = Cl and orthorhombic for X = Br symmetries, and for X = I a nonperovskite orthorhombic polymorph (δ-phase, 1D connectivity of edge-sharing PbX₆ octahedra, with a wider energy bandgap; PL inactive). Transitions from the α forms to the lower symmetry modifications are observed progressively upon cooling;³⁴ the ensuing distortion of the 3D framework through octahedral tilting is reported also to induce fragmentation of the crystals into several domains and formation of twin boundaries.⁵⁴ Considering that CsPbX₃ NCs are synthesized at T > 100 °C, the occurrence of these kinds of defects may be possible and can influence the NCs optical and electronic properties;⁵⁴ nevertheless, their detection and investigation by electron microscopy are not trivial, also due to the samples instability under the electron beam.⁴⁹

Figure 1.

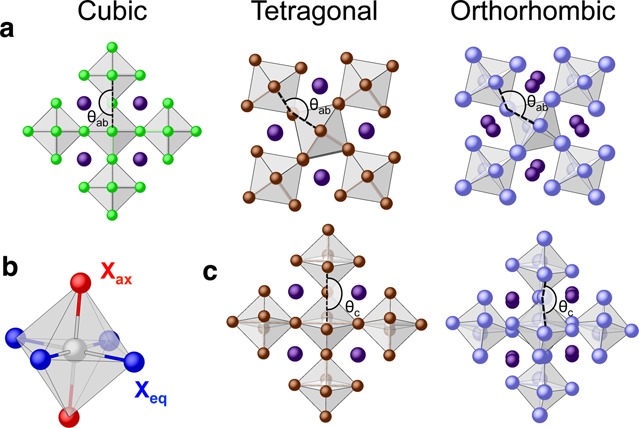
(a) Sketch of the 3D arrangement of the PbX₆ octahedra in CsPbX₃ perovskites exhibiting a cubic (C), tetragonal (T), or orthorhombic (O) structure; the symmetry descent is related to small coherent displacements of halides, leading to bending of Pb–X–Pb angles with θ_ab= θ_c = 180° (C), θ_ab< 180° and θ_c = 180° (T), and θ_ab= θ_c < 180° (O). Atomic species in the top (a) and side (c) views are Cs = violet, Pb = gray, X = green, brown, cyan. (b) Equatorial (X_eq) and axial (X_ax) halides in the PbX₆ octahedron are highlighted in blue and red, respectively.

Analysis of the Average Crystal Structure in CsPbX₃ NCs: Evidence of Multiple Anomalies

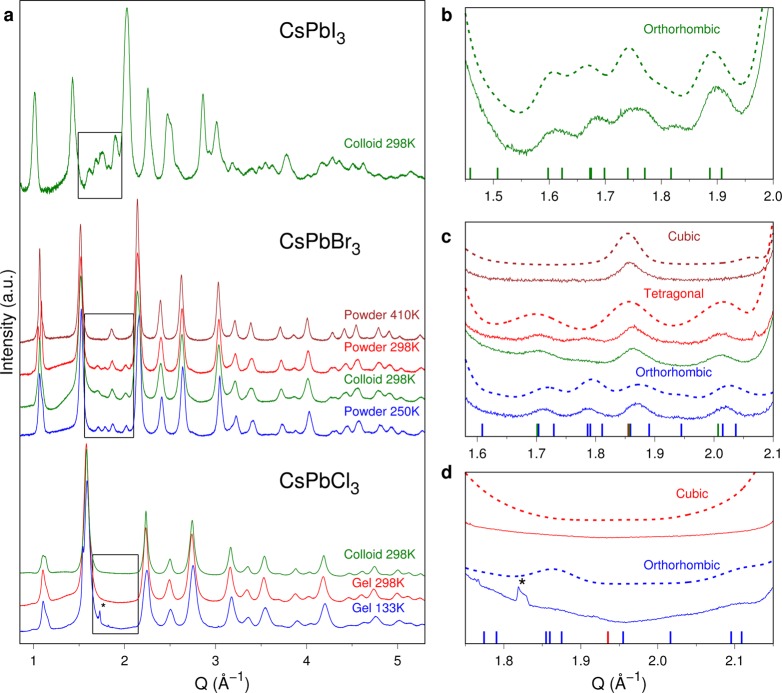
In order to clarify the proposed model, we first focus on some peculiar experimental evidence of the diffraction patterns observed at RT and upon heating or cooling. High-resolution synchrotron X-ray diffraction patterns of CsPbX₃ NCs (Figure 2) were collected at 298 K either on colloidal solutions (green lines, in hexane or toluene, the scattering signal of the solvent is here subtracted), for each halide or on dry samples (red lines, powders or gels). Dry samples of CsPbCl₃ and CsPbBr₃ were also measured at low- and high-temperatures (LT, blue lines; HT, brown line), below and above the reported phase transition values, and data were fruitfully used for the comprehension of their structure defectiveness, which remains the main focus of this work.

Figure 2.

(a) X-ray synchrotron total scattering data showing changes of superstructure peaks in CsPbX₃ NCs at RT and upon phase transitions; simulations (dashed lines) vs experimental traces (solid lines) in the 1.5–2.2 Å^–1Q range for (b) CsPbI₃, (c) CsPbBr₃, and (d) CsPbCl₃. The starred (narrow) peak in panels (a) and (d) corresponds to the 101 reflection of contaminant ice (I_h phase).

The diffraction traces underwent a data-reduction procedure, mandatory for a reliable total scattering DSE-based analysis, aiming at subtracting all extra sample scattering contributions and applying absorption corrections (details are given in the SI). These data have been used for both Rietveld and DSE analyses. Such a strict control of all experimental conditions makes the determination of isotropic atomic displacement parameters (ADPs) more reliable than from conventional powder diffraction measurements, their detailed analysis suggesting the manifestation of subtle structural effects. Note that the anisotropic ADP model was not considered, as diffraction data from nanosized materials (particularly with X-rays) do not provide robust information; therefore in the following, ADPs refer to isotropic values (in the form of Debye–Waller factors), even when not specifically said.

Significantly, Figure 2a shows (for some of the measured data) that the most intense diffraction peaks match the nominal Bragg positions of the cubic polymorphs in all CsPbX₃, but that a few weak superstructure peaks, the most representative appearing in the 1.5–2.2 Å^–1Q region (within boxes), are present, providing a fingerprint of PbX₆ octahedral tilts taking place in both CsPbBr₃ and CsPbI₃ at RT. A visual inspection of these peaks (Figure 2b–d) and their qualitative comparison with the pattern simulations of the expected polymorphs (dashed lines) in the same 1.5–2.2 Å^–1Q region, apparently pinpoints the cubic phase in RT CsPbCl₃ and HT CsPbBr₃ (Figure 2c,d) and also displays some unexpected deviations in CsPbBr₃ at 298 K (both dry and colloidal NCs). Rietveld analysis, performed on LT, RT, and HT data in analogy with that reported for RT CsPbBr₃ nanopowders,⁴⁷ did not provide any significant improvement in terms of average crystal structure(s) (the solely accessible by conventional crystallographic methods) compared to those available in the current literature for the corresponding bulk materials (numerical results appear in Tables 1 and S1–S3). However, subtle anomalies emerged therefrom, which were also observed in a parallel analysis by the DSE approach upon using the same ordered structural models provided by the Rietveld method (see Methods and Supporting Information for details). In most cases, pattern matching was partially unsatisfactory, resulting in unexpected misfits both in position and intensity of many peaks, particularly evident for the RT CsPbCl₃ and HT CsPbBr₃ NCs with the cubic model (Figures S1 and S3). In both cases, the 100 peak (Q ∼ 1.1 Å^–1) exhibits an asymmetric shape suggesting a low-symmetry splitting; moreover, an accurate analysis of the peak positions for these two samples (Figure S2), obtained by unconstrained profile fitting procedures, showed that reflections with even (h² + k² + l²) values are distributed around a well-defined cell parameter (5.618 Å for CsPbCl₃ and 5.866 Å for CsPbBr₃, respectively), whereas the odd ones are significantly shifted away with an unphysical cell parameter inflation of up to 0.07 Å. These findings clearly suggest, independently of the adoption of any structural model and refinement (Rietveld/DSE) technique, a noncubic lattice metric for both samples. These results all point to a lower-than-cubic symmetry for the NC structures, despite of the lacking of the superstructure peaks commented above.

Table 1. Isotropic Atomic Displacement Parameters (ADPs, Ų) for the Different Models of CsPbX₃ As Derived by Rietveld Analysis of Synchrotron X-ray Diffraction Data.

	CsPbCl3		CsPbBr3				CsPbI3
	RT		RT		HT (410 K)		RTb
	Ca	S	T	O	Ca	S	O
Pb	2.34(2)	2.44(1)	3.19(3)	2.99(3)	3.03(3)	3.60(3)	3.12(4)
Cs	7.43(4)	7.50(3)	9.34(6)	8.90(6)	10.00(7)	10.11(5)	8.54(13)
Xax	10.13(9)	1.89(8)	7.54(23)	1.721(12)	10.07(6)	2.06(5)	5.21(13)
Xeq	= Xax	= Xax	3.76(7)	2.85(9)	= Xax	= Xax	3.75(6)

^aC (cubic), S (split), T (tetragonal), and O (orthorhombic). Anomalous values, mitigated by atom splitting (C to S) or symmetry lowering (T to O), are highlighted in bold characters.

^bColloidal sample.

In this regard, very interesting is the analysis of the isotropic ADPs reported in Table 1. Anomalous high ADPs of Cl (10.13 Ų) and axial Br (7.14 Ų) and I (5.21 Ų) ions (i.e., those connecting the PbX₆ octahedra along the c-axis) were obtained in the cubic, tetragonal, and orthorhombic phases, respectively, indicating high structural disorder. These values, derived by Rietveld refinement, were confirmed by the DSE analysis based on the same ordered structural models. The anomalous behavior of the ADPs of Cl at RT is indeed nearly ubiquitously reported for the bulk material and interpreted as local displacements in the cubic structure (or by a strongly anharmonic potential well).⁵⁵ Resorting to a disordered cubic model with the Cl position refined to ∼0.5 Å away from the original one (Figure 3a,b) resulted in more physically reasonable ADPs (Table 1) with a marginal improvement in the fit (Figure 3c). Note that the Cs⁺ values are not affected. Indeed, the high ADP value(s) for Cs⁺ is attributed (in the NCs and in the bulk) to rattling of the cations within the cuboctahedral cavities, being Cs⁺ slightly too small than the ideal value (the Goldschmidt tolerance factors are 0.85 < τ < 0.87 for the I/Br/Cl CsPbX₃ NCs).⁵⁶ The split-Cl cubic model (with four equivalent displaced sites, each contributing with 25% probability) suggests a severe distortion of the PbCl₆ octahedra, which can be mitigated by lowering the crystal symmetry. In this view, there are numerous spectroscopic (NMR, NQR, and EPR) studies addressing the inequivalence of Cl ions in RT bulk CsPbCl₃, consistent with an orthorhombic disposition of PbCl₆ octahedra.^57,58 However, such a low symmetry modification, were it ordered over long-range, would conflict with our experimental data which clearly do not show any extra peaks in the 1.5–2.2 Å^–1Q region. This is clearly visible in Figure S3, where the DSE best fits based on ideal defect-free NC populations are shown. Moreover, this phase modification and even lower symmetry structures were unable to recover the 100 peak splitting (Figure S3). Therefore, a different explanation for the apparent cubic structure in our RT CsPbCl₃ NCs is needed. Interestingly, the HT cubic phase in our CsPbBr₃ NCs behaves in a similar way than the Cl-based cubic perovskite (isotropic ADPs of Br are 11.0 Ų and 2.06 Ų in the cubic and split-cubic models, respectively, Table 1 and Figure S3); this finding is in line with the highly dynamic distorted local structure reported for the HT bulk phase.⁴⁵

Figure 3.

(a) Cubic and (b) cubic-split model for CsPbCl₃. (c) DSE best fit of RT X-ray synchrotron data (λ = 0.565468 Å) corresponding to the cubic-split model. The 1.8–2.2 Å^–1Q region (inset) matches the cubic phase diffraction features. (d) ADPs behavior of Cl, Cs and Pb ions vs temperature as provided by Rietveld analysis (filled squares) in the 133–298 K range on NCs and by neutron diffraction (empty squares) on single crystal in the 325–623 K range from Sakata et al.⁵⁵ The discontinuity near 320 K is explained by markedly different experimental conditions and methods of analysis. (e) DSE best fit corresponding to orthorhombic coherent subdomains; the 1.8–2.2 Å^–1Q region (inset) well matches the cubic phase diffraction features: (f) schematic representation of a single 1/2[−110](110) twin boundary; (g) atomistic representation of nanotwins within a NC; the twin boundary highlighted in the circle shows the discontinuity of the halides lattice and the coherence of the Pb sublattice; (h) 2D projections of the undistorted orthorhombic structure; and (i) sketch of the cooperative rotations of PbCl₆ octahedra at the twin boundaries as a viable mechanism of the dynamically changing twins network.

Our low- and high-temperature synchrotron X-ray scattering measurements of CsPbCl₃ and CsPbBr₃ NCs provide the clue for a viable interpretation, which is fully supported by a DSE modeling based on defective (polytwinned) NCs and reinforced by the systematic comparison of this with the corresponding defect-free DSE model (Table S4). Since the size of the halide influences the temperature at which the apparent cubic structure is observed, we first illustrate our interpretation and the ensuing modeling for CsPbCl₃ NCs.

Toward a Model of Coherent Nanotwins. The Case of CsPbCl₃ NCs

We were inspired by a thorough single-crystal neutron diffraction study in which an anomalous (but not understood) rise of Cl ADPs was found upon cooling below 400 K, whereas a linear increase is restored in the HT regime (i.e., >400 K, well above the claimed tetragonal-to-cubic transition temperature, T_C, of 320 K).⁵⁹ Rietveld analysis of data collected on our powdered CsPbCl₃ at four different temperatures down to 133 K (performed upon adopting the ordered cubic model to make meaningful comparisons with the above-mentioned study, see Table S2) showed the same anomalous LT rise of Cl, whereas Cs and Pb ADPs lower, as they should, upon cooling (Figure 3d, filled symbols). As increasing ADPs at LT do not come from harmonic thermal vibrational effects, the peculiar temperature dependence of atomic thermal vibrations in CsPbCl₃ indicates that, already at T > T_C, and below T_C, deviation from the cubic symmetry progressively increases, boosting the “orthorhombic character”. Altogether these findings suggest that “orthorhombic” subdomains may form in our NCs, giving rise to a multiply twinned structure, as already theoretically proposed and experimentally confirmed by optical microscopy and ¹³³Cs NMR studies on bulk CsPbCl₃.⁶⁰⁻⁶²

In order to investigate such a possibility by DSE-based diffraction methods, we studied the effects of twin boundaries on the diffraction pattern of halide perovskite NCs, assuming the RT orthorhombic structure (isostructural to the γ-CsPbBr₃)⁴⁷ for the nanodomains. We considered the case of coherent twins that maintains unperturbed the Pb sublattice of the orthorhombic phase. Indeed, owing to the fact that we are playing with randomly oriented powder-like materials, incoherent twin boundaries (as those reported in the single crystals case)⁵⁴ are expected to influence the size distribution of coherent domains (discussed later on) without introducing other diffraction features. With reference to the appropriate terminology, we investigated the combination of different {hkl} slip planes, ⟨hkl⟩ slip directions and magnitudes of the shift (k) (summarized by the k ⟨hkl⟩ {hkl} formalism, including symmetry equivalencies, in the orthorhombic frame). As detailed in the SI, through these combinations, a selective control of the intensity of the orthorhombic superstructure peaks is achieved, depending also on the hkl reflection indices (Figure S4). Figure 3f exemplifies the location of a single (110) slip plane (as observed in a number of oxide perovskites),⁶³ acting along the [−110] slip direction (blue arrows) with k = 1/2 (a magnitude of half the lattice vector along the same direction is required). When a network of 1/2⟨110⟩{110} twin boundaries is inserted in a single NC (with the slip direction always lying within the slip plane), the corresponding atomistic model results in the arrangement of multiple coherent subdomains, as shown in Figure 3g. Using the DSE approach implemented in the Debussy Suite,⁶⁴ we generated a population of twinned NCs of prismatic shape and increasing size (as detailed in the Methods) that results in an apparently cubic diffraction pattern (Figure 3e and inset) with an improved matching of the experimental data compared to the (DSE-based) split-cubic model (GoF = 10.1 vs 12.1). The enlarged portion of the NC in Figure 3g shows the 2D atomistic details at the twin boundary in comparison to the untwinned orthorhombic structure (Figure 3h). A large density of twin boundaries is necessary to obtain this effect, suggesting that the density of defects increases upon temperature increase (in CsPbCl₃ from LT to RT), whereas a self-healing process, enlarging the orthorhombic subdomains, should happen upon cooling. A viable mechanism of formation and dynamic migration of these boundaries is sketched in Figure 3i, which locally modifies the arrangement of (ideally undistorted) PbX₆ octahedra through cooperative (in and out-of phase) rotations.⁶⁵ These synchronized movements may flip (part of) the domains modifying their relative sizes and orientations (by 90° one to each other).

Nanotwins in Room- And High-Temperature Phases of CsPbBr₃ NCs

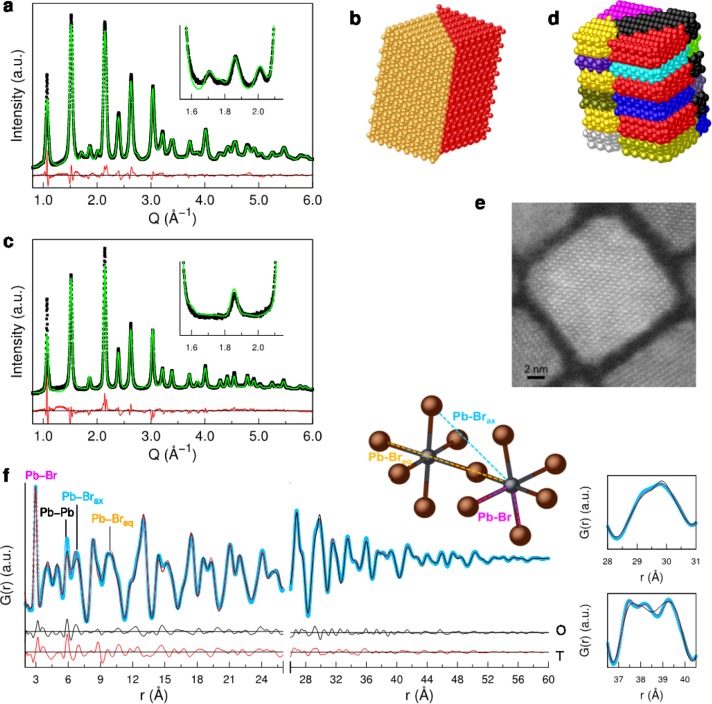
Inspired by the case of CsPbCl₃, we investigated the existence of orthorhombic subdomains in CsPbBr₃ NCs, aiming at explaining the apparent cubic (HT) and tetragonal (RT) phases observed in the X-ray synchrotron data (Figure 2c). The results of this modeling are graphically summarized in Figure 4. The slip plane still belongs to the {110} family in all cases;⁶³ a single twin boundary per NC along the ⟨001⟩ slip direction with k = 1/2 (Figure 4b) is sufficient to obtain the features of the tetragonal pattern (Figure 4a), suggesting that our experimental observation can be interpreted as a slight deviation from the plain orthorhombic structure. In contrast, polydomain NCs combining 1/2⟨110⟩{110} and 1/2⟨110⟩{001} (Figure 4d) are necessary for obtaining a “cubic-like” pattern (Figure 4c), in which the orthorhombic superstructure peaks vanish. Again, upon increasing the temperature, the number of defects increases, and the twinned orthorhombic model very well matches the experimental data, as witnessed also by the statistical indices: GoF = 2.26 compared to 3.07 for the cubic model. In contrast, the low density of defects in the RT data makes the two models (orthorhombic, defectless, and twinned) rather competitive in terms of numerical statistical indicators (GoF = 2.08 vs 1.99, respectively). We have collected a number of HRTEM images, but owing to the sub-Å scale of the (rotation-induced) halide offset at the domain interface, twin boundaries cannot be observed (Figure 4e). To further support the hypothesis of nanotwins in RT CsPbBr₃ NCs, we performed PDF analysis.

Figure 4.

X-ray synchrotron data (λ = 0.564960 Å) collected on CsPbBr₃ NCs at 298 K (a) and at 410 K (c); the green traces draw the DSE best fits corresponding to the poly twinned orthorhombic models shown in (b) and (d), respectively. These models cause the vanishing of many peaks resulting into an apparent tetragonal (a) or cubic pattern (c). (e) BF-STEM image of CsPbBr₃ NCs (scale bar 2 nm); (f) G(r) fits of RT CsPbBr₃ QDs: the black (red) solid lines show the residuals of the orthorhombic (tetragonal) model(s) in the low and medium r sections. The assignment of the marked peaks (Pb–Br, Pb···Br_ax, and Pb···Br_eq) is sketched in the inset (Pb, black; Br, brown).

High-energy (67 keV) scattering data were collected at 28-ID-2 beamline at NSLS-II (Brookhaven National Laboratory) on the powdered sample and targeted to the investigation of the short vs medium order range through the atomic PDF (Figure 4f).⁴⁴ We found that the proposed orthorhombic structure fits reasonably well the low r region up to 26 Å (R_w = 12.9% vs R_w = 18.5% obtained with the tetragonal structure), whereas a tetragonal description has to be preferred in the 26–70 Å range (R_w = 10.9% vs 12.4%, details in SI). Interestingly, interoctahedra Pb–Pb peaks in Figure 4f are much narrower than expected, whereas Pb–Br peaks are broader, indicating a more ordered arrangement of the Pb network and the discontinuity of halide sublattice at the twin boundaries. More details about the PDF analysis, including the separate partial contribution of the different pairs to the total PDF signal, are provided in Figure S5.

The Crystal Structure of CsPbI₃ γ-Phase in NCs

We here report on the 3D perovskite structure of the as-synthesized colloidal CsPbI₃ NCs studied in this work. These CsPbI₃ NCs do not belong to the known thermodynamically stable (but PL inactive) 1D-, δ-phase, yellow in color.³⁴ Instead, they share very similar structural features with the distorted perovskite phases discussed above, at least for the RT phase. As the bulk single crystals and thin films, our NCs synthesized at higher temperatures in a 3D-, red-luminescent phase are metastable, eventually turning into the 1D-phase. This transition takes from several days to several months, depending upon the surface treatment and storage conditions.³⁴

In contrast to recent reports on the stabilization of the cubic α-phase at RT,⁶⁶ X-ray synchrotron data collected on our colloidal CsPbI₃ NCs show four distinct peaks not compatible with either the α- (Figure 5b) or the δ-phases (Figure 5c). The occurrence of a new orthorhombic polymorph is established here, which is isostructural with the well-known γ-CsPbBr₃ phase. The refined coordinates are given in the SI. The DSE best fit shown in Figure 5a corresponds to the untwinned orthorhombic structure. For the newly identified γ-phase, neither (apparent) cubic- nor tetragonal-like X-ray diffraction patterns were ever observed in repeated syntheses, therefore we consider the formation of multiple twinning in CsPbI₃ NCs at RT a much less severe occurrence, easily explained by the larger ionic radius of I. Nevertheless, the presence of residual misfits in the superstructure peaks (Figure 5a), and the relatively high value of I_ax ADPs (see Table 1) suggest that, also in this case, a minor fraction of NCs may not be single domain. Needless to say, the proposed defective model holds also for cubic CsPbI₃ NCs (Figure S6), of which experimental data on HT phases could not be collected.

Figure 5.

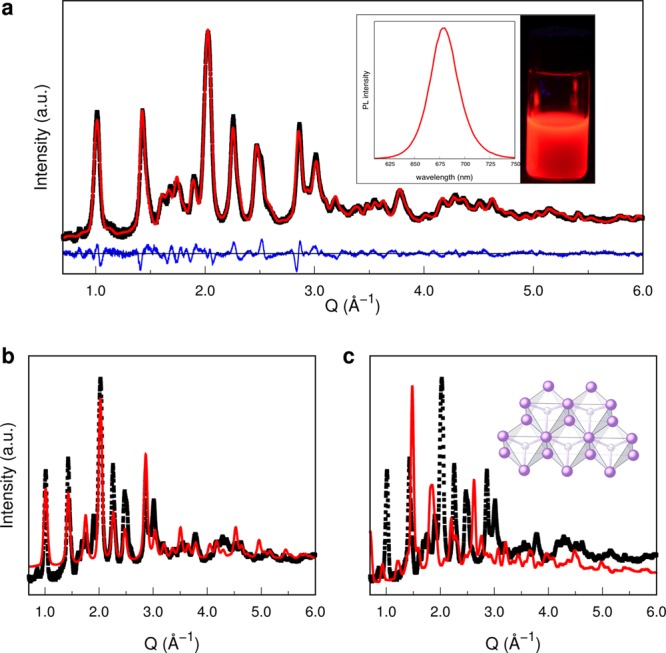
(a) DSE best fit of X-ray synchrotron data (λ = 0.49544310 Å) collected on as-synthesized CsPbI₃ NCs corresponding to the orthorhombic γ-phase. DSE simulations of the α-phase (b) and δ-phase (c) are shown for comparison.

A Generalized Model of Coherent Nanotwins in CsPbX₃ NCs

Altogether, we envisage that CsPbX₃ NCs contain nearly ordered γ-phase subdomains, separated by a network of twin boundaries, denser at high temperatures and maintaining unchanged Pb locations. Their mutual orientation may lead to an “apparent” higher-symmetry (tetragonal or cubic) structure on average, while keeping the tilted “orthorhombic” arrangement of PbX₆ octahedra at the length scale of the subdomains.

Why this occurs can be explained by a simplified model, in which N domains (of volume V_i) hinge about 2D interfaces of area A_ij (i,j running on the domain sequence), with ΔH_o and ΔH_c being the molar formation energies of the orthorhombic and cubic phases, respectively. As evidenced by DSC measurements, ΔH_o < ΔH_c, the orthorhombic structure being favored at low temperatures.⁶⁷ By introducing the surface tension γ_ij relative to the ij interface,⁶⁸ the (practically identical) crystal densities ρ_o and ρ_c, and the pertinent formula weight (fw), the overall enthalpy of a polytwinned NC can be approximated by

which, if γ_ij values are low enough, may be lower than the single cubic domain value of V_NC volume:

However, since the creation of boundaries contributes to increase the overall free energy by a positive term proportional to N^1/3 (see SI for details), entropic contributions (proportional to N and different in sign) may result in temperature-dependent stabilization. Accordingly, the progressive subdivision into ordered subdomains becomes entropically favored at HT. The formation enthalpy of the boundary network creation reduces the network at LT and increases the sizes of the orthorhombic domains; differently, at higher T, the negative term associated with the entropy increase (∝N) more than compensates the energy needed to create many new boundaries. Therefore, within this model, the presence of truly cubic domains becomes unnecessary.

As reorientation of the PbX₆ octahedra may be very easy (with practically no activation energy), the “phase transitions” at the nanoscale are here interpreted by the insurgence of networks of twin boundaries of different density and dimensionality rather than changes of the symmetry of the average crystal structure. Lowering the temperature from the HT phase would therefore appear as a progressive lowering of the interfacial energy, very much as it occurs in the foam coarsening process.

This finding may have important implications on understanding the optical and electronic properties of halide perovskite NCs (Figure S7). In contrast to the reported observation of the lack of change in the PL peak position of CsPbBr₃ NCs upon temperature-induced phase transitions,²¹ we found that the PL of polymer-encapsulated CsPbBr₃ NC films monotonically decreases with heating from RT up to 100 °C (Figure S8). During heating, the wavelength blue-shifts, with an increase in the band gap in line with the values of other lead-based semiconductor materials.⁶⁹ The smooth changes in the PL intensity and maximum position with temperature are almost reversible, exhibiting a behavior consistent with a temperature-induced lattice expansion. This finding goes well with the persistence of tilted octahedra in an orthorhombic-like arrangement within the subdomains above the expected “phase transitions” and with the ∼1% in volume lattice expansion (in the 298–410 K range) found for the CsPbBr₃ NCs of this work.

The disappearance/appearance of weak superstructure peaks upon heating/cooling further suggests the dynamic (rising and self-healing) processes within twin-boundary modifications. Since our diffraction methods cannot catch transformations on a picosecond time scale, no direct observation of the dynamic rearrangement of the nanotwins is possible. Nevertheless, our findings are well in agreement with the very recent report on the intrinsic dynamic disorder in lead halide perovskites (in the high temperature cubic modification), as emerged from inelastic X-ray scattering on hybrid (CH₃NH₃PbX₃) and from the compared study of hybrid and full-inorganic CsPbBr₃ crystals through Raman scattering and first-principles molecular dynamics.⁴⁵ Of relevance is the suggestion that the low charge carrier mobility and recombination in these materials may be influenced by such strong dynamic disorder.

Within the more general theme of correlated disorder, emerging as one of the most exciting challenges of modern crystallography,⁷⁰ the dynamic rearrangement of the nanotwins leading to an apparent higher symmetry on average also suggests similarities with the nondisplacive phase transition model recently proposed for BaTiO₃.⁷¹ However, in BaTiO₃, an equivalent effect emerges from correlations of the local symmetry-breaking distortions related to the off-centering of Ti ions (leading to a rhombohedral local structure), whereas halide perovskites NCs feature the tilts of PbX₆ octahedra (resulting in an orthorhombic local structure). Despite of these analogies, the two models are clearly material dependent and not interchangeable. With reference to the ABX₃ general formula of perovskites and according to a classification based on the purely geometric Goldschmidt tolerance factor, the distortions in CsPbX₃ and BaTiO₃ differ in that they are B-site (τ > 1) and A-site (τ < 1) driven,⁷² respectively, the tolerance factors being all below 1 for CsPbX₃ and τ = 1.06 for BaTiO_3.^56,72 Moreover, A-site driven lattice distortions are prevalently observed in nonferroelectric perovskites, which is also the case of CsPbX₃ NCs. Indeed, differently from ferroelectric BaTiO₃, dielectric measurements show that CsPbCl₃ is neither ferroelectric nor antiferroelectric;⁷³ electric polarization has been detected in hybrid halide perovskites, owing to the presence of the polar molecule in the cuboctahedral cages, whereas a spherical cation like Cs⁺ in the highly isotropic environment of the A- site will not.³²

As a final remark, the nanotwin model proposed for CsPbX₃ NCs does not account for the asymmetry of the lowest-Q peak (100 in the cubic notation), which is observed in most measured data (visible in Figures 3e and 4a,c). This finding suggests the possible occurrence of additional defectiveness, of second order with respect to the one here discussed, requiring further investigations.

Morphology and self-assembly of CsPbX₃ NCs

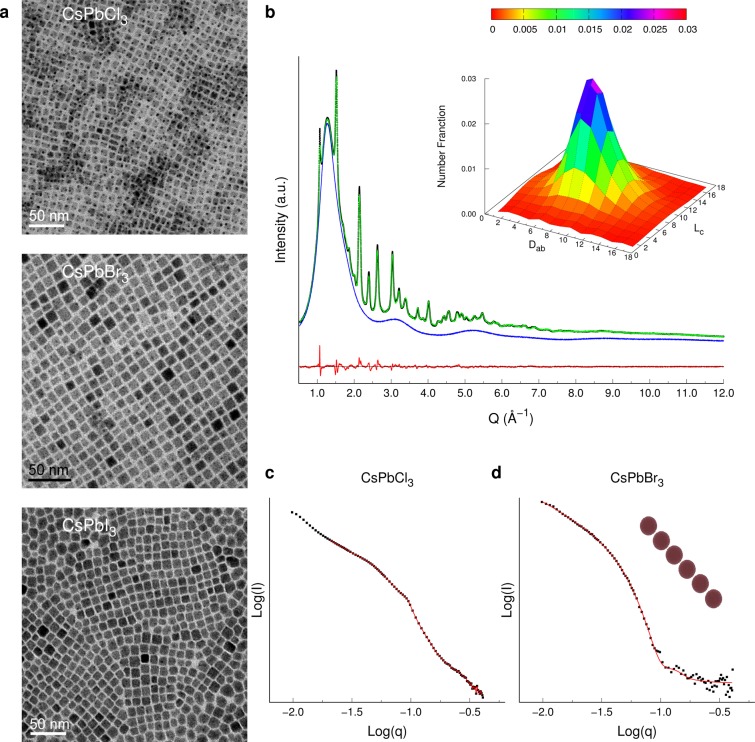
The morphological characterization of the CsPbX₃ NCs investigated here by the DSE analysis (in their colloidal state, using the 298 K data) provided a more detailed and variegated picture compared to the simplified cubic representation emerging from the 2D projections in TEM images (Figure 6a). Although morphological details on NCs facets are not introduced in the DSE modeling (such a level of shape information being lost in the experimental wide-angle X-ray data), the capability of the DSE approach of combining atomic-scale details of the crystal structure with the NCs shape description enables the identification of the longest and shortest sizes with reference to the crystallographic axes. This is a relevant issue in anisotropically elongated (nanorods) or flattened (nanoplate) particles. Such information is typically achieved by TEM analysis, as long as an appropriate orientation of the crystals is possible. However, distinguishing nearly identical interatomic distances in the cubic, tetragonal, and orthorhombic polymorphs of CsPbX₃ NCs by HRTEM is beyond the spatial resolution and sensitivity of the technique, making the method inapplicable in this case.⁴⁹ We further consider that even SAXS analysis, that does not possess atomic-scale resolution, cannot provide such information, which definitely makes the DSE approach an extremely useful tool for the morphological characterization (in terms of a quantitative statistical distribution) for this class of materials at the nanosized regime. A bivariate growth model was applied here for characterizing all the CsPbX₃ NCs; in the orthorhombic case this approach is a good approximation of the much more complex but more appropriate triaxial model. The graphical outcome of the DSE best fit for CsPbBr₃ and its bivariate log-normal size distribution are shown in Figure 6b. Average sizes and size dispersions along the two growth directions are provided in Table 2 for the three colloids. Being number-based values, they are directly comparable to TEM-based average sizes. For CsPbBr₃, we performed a statistical analysis of the two edge sizes in the faces exposed in TEM images, which included ca. 100 particles. The averages over the longest (10.8 Å) and the shortest (8.9 Å) edges cannot be directly compared with the DSE sizes (in the absence of oriented NCs and knowledge of the third dimension); however they can be reasonably taken as limiting values. The single average of all edge lengths from TEM is indeed in very good agreement with the diameter (D_eq) of the sphere of equivalent volume of the prismatic particles used in the DSE model (9.87 Å vs 9.84 Å). This also indicates how reliable are the DSE estimates given in Table 2. CsPbBr₃ and CsPbI₃ exhibit comparable size and monodispersity (<20%), whereas smaller particles are found in CsPbCl₃ with relatively large size dispersion. On the morphological side, CsPbCl₃ and CsPbBr₃ NCs appear slightly elongated in the c-axis (aspect ratios are 1.4 and 1.2, respectively), whereas CsPbI₃ is slightly flattened along the same crystallographic direction.

Figure 6.

(a) TEM images of CsPbX₃ NCs. (b) DSE best fit of synchrotron X-ray data of CsPbBr₃ colloidal NCs in toluene with the 3D representation of the bivariate log-normal size distribution function. SAXS modeling of (c) CsPbCl₃ and (d) CsPbBr₃.

Table 2. DSE-Based Size and Shape Analysis of CsPbX₃ Colloidal NCs Resulting from the Assumption of a Bivariate Lognormal Distribution with Average Diameter ⟨D⟩ and Standard Deviation σ^a.

	CsPbCl3	CsPbBr3	CsPbI3
⟨Dab⟩, σab/⟨Dab⟩	5.34, 0.60	8.19, 0.24	9.86, 0.21
⟨Lc⟩, σc/⟨Lc⟩	7.62, 0.45	9.79, 0.20	8.01, 0.21
aspect ratio	1.41	1.19	0.81
⟨Deq⟩, σ/⟨Deq⟩	6.50, 0.41	9.84, 0.17	10.43, 0.15
⟨DSAXS⟩, σ/⟨DSAXS⟩	5.62(7), 0.20(1)	7.65(4), 0.16(2)	–

^aNumber-based values refer to average size (nm) and size dispersion along the two growth directions of prismatic NCs (⟨D_ab⟩, σ_ab/⟨D_ab⟩, ⟨L_c⟩, σ_c/⟨L_c⟩) and of the sphere of equivalent volume (⟨D_eq⟩, σ/⟨D_eq⟩) and relative aspect ratio (⟨L_c⟩/⟨D_ab⟩). Number-based average values provided by SAXS analysis are quoted in the last line. SAXS-based values are also provided.

SAXS analysis of colloidal CsPbCl₃ and CsPbBr₃, performed in diluted solutions, showed the interesting and unexpected tendency of NCs to self-assemble in a stacked sequence, as often observed in nanoplates in concentrated solutions.⁷⁴ The model (see details in SI) provides the size of the chain cross-section (quoted in Table 2) and the number of stacked beads, with much longer strings formed in CsPbCl₃ (>50 spheres) than in CsPbBr₃ (6 ± 0.8). Interestingly, the cross section of the string nicely matches the base size of the prism in the DSE model, suggesting that the particle alignment might occur through the {001} facets. Whether, and how, ligands drive this assembly needs further investigation.

Conclusions

We have proposed an original depiction of the structural defectiveness in CsPbX₃ NCs that goes beyond the classical vision of the average crystal structure and better complies with the flexibility of halide perovskites NCs upon halide changes and temperature variations. This characterization was possible through high-resolution synchrotron X-ray total scattering data and an advanced modeling performed through the DSE. The DSE enables the crystal structure and the NC morphology to be simultaneously treated within a coherent approach, providing a powerful tool for characterizing these complex materials. Future work will be addressed to other systems, such as hybrid organic–inorganics and mixed halides, in view of better understanding the structural features behind the outstanding properties of this class of perovskite NCs.

Methods

Synthesis of CsPbX₃ (X = Cl, Br, I) NCs

The CsPbX₃ NCs were prepared according to our previous report.¹ A 25 mL 3-neck flask was loaded with octadecene (ODE, 5 mL) and PbX₂ (0.188 mmol) such as PbI₂ (0.087g, ABCR, 99.999%), PbBr₂ (0.069g, ABCR, 98%), and PbCl₂ (0.052g, ABCR, 99.999%), and the mixture was dried under vacuum for 1 h at 120 °C. Dried oleylamine (0.5 mL, OLA, Acros 80–90%) and dried oleic acid (OA, 0.5 mL) were injected at 120 °C under N₂. After complete solubilization of a PbX₂ salt, the temperature was raised to 180 °C, and Cs-oleate solution (0.4 mL, 0.125 M in ODE, prepared from 0.814 g Cs₂CO₃ (Aldrich, 99.9%), 40 mL ODE, 2.5 mL oleic acid, under vacuum, at 120 °C) was quickly injected, and 5 s later, the reaction mixture was cooled by the ice–water bath. For CsPbCl₃, a higher temperature of 150 °C and 1 mL of trioctylphosphine (TOP, Strem, 97%) are required to solubilize PbCl₂. The obtained crude solutions were centrifuged for 4 min at 12 krpm, and the precipitate was redispersed in 3 mL of toluene. The solution was further centrifuged at low speed (4 krpm), and the supernatant was filtered and concentrated under vacuum for the measurements.

Characterization of CsPbX₃ NCs

CsPbX₃ NCs were characterized by a combination of: scanning transmission electron microscopy (STEM), steady-state PL, and wide (WAXS) and small angle (SAXS) X-ray scattering techniques. STEM was performed on a JEOL 2200FS TEM/STEM microscope. A Fluorolog iHR 320 Horiba Jobin Yvon spectrofluorimeter equipped with a PMT detector was used to acquire the steady-state PL spectra from solutions. The SAXS data were collected using a NanoSTAR instrument from Bruker AXS,⁷⁵ equipped with a liquid metal jet source from Excillum AB, Sweden, and with home-built scatterless slits.⁷⁶ A home-built flow-through quartz capillary sample cell was used for the measurements. Details on the SAXS data modeling are provided in the Supporting Information. WAXS synchrotron data were collected on colloidal and dry samples at the X04SA-MS Powder Diffraction Beamline of the Swiss Light Source of the Paul Scherrer Institut (Villigen, CH) with 25 and 22 keV beam energies in the 0.5–130 2θ range, using a single-photon counting silicon microstrip detector (MYTHEN II).⁷⁷ LT and HT measurements were performed through a temperature controller N₂ stream fluxing over the capillaries.

The high-energy X-ray WAXS data of CsPbBr₃ (as dry powder) for PDF analysis were collected at the 28-ID-2 XPD beamline at National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory (Upton, NY, USA). The measurements were performed at RT using a X-ray energy of 67 keV. Details on atomic PDF data analysis are supplied in the Supporting Information.

The DSE Method

According to the DSE-based approach implemented in the DebUsSy program suite,⁶⁴ atomistic models of prismatic NCs were built by stacking a building block (the atoms of the unit cell of the appropriate polymorph) along two independent growth directions, one lying in the ab-plane and the second one parallel to the c-axis (details can be found in the Supporting Information, section 3). In the case of defective clusters, the proper slip system was added to the orthorhombic model, by shifting the atoms according to the required twin law: k ⟨hkl⟩ {hkl}, where k is the magnitude of the shift, ⟨hkl⟩ is the direction (including all the symmetry equivalent ones), and {hkl} is all the equivalent family of the planes of the twin boundary (see Supporting Information, section 4). In order to speed up the calculation of the total scattering pattern through the DSE, sampled interatomic distances, instead of the true ones, were computed from the population of NCs of different sizes.⁷⁸

Model parameters were then optimized against the experimental data. These include structural (isotropic atomic thermal displacement parameters, ADPs) and microstructural parameters (according to a bivariate log-normal distribution function with four adjustable parameters, namely average sizes and standard deviations along the two independent growth directions) to properly describe the NCs size and shape distribution.

Preparation of Polymer-Encapsulated CsPbBr₃ NC Films

Twenty μL of toluene solution of CsPbBr₃ NCs (10 mg/mL) were mixed with 200 μL of toluene solution of poly(methyl methacrylate) (PMMA, molecular weight: 350 kDa, concentration 5%) and drop casted on a precleaned glass slide.

Temperature-Dependent PL Measurements of Polymer-Encapsulated CsPbBr₃ NC Films

The optical emission was recorded by an optical fiber coupled CCD spectrometer (LR1-T from ASEQ-instruments, 1 nm spectral resolution). A CW laser diode with a wavelength of 405 nm and a power of 3 mW was used as the excitation source. The emitted light was measured using long-pass filters (FEL450, Thorlabs). In order to avoid photodegradation effects, the sample was exposed to the laser beam only during 200 ms per each measurement, while during the remaining time it was kept in the dark. The temperature was controlled by a custom-built setup consistent of a heater with Arduino microcontroller board. The speed of heating up and cooling down was set to be 5 °C per minute. Spectra were smoothed in order to avoid noise impact before taking the maximum position.

Code Availability

The DebUsSy program suite is freely available a http://debussy.sourceforge.net.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b00017.

• Information on experiments, DSE, PDF and SAXS data reduction and modeling, and Rietveld analysis (PDF)

The authors declare no competing financial interest.