A novel DTI-QA tool: Automated metric extraction exploiting the sphericity of an agar filled phantom

Abstract

Purpose

To develop a quality assurance (QA) tool (acquisition guidelines and automated processing) for diffusion tensor imaging (DTI) data using a common agar-based phantom used for fMRI QA. The goal is to produce a comprehensive set of automated, sensitive and robust QA metrics.

Methods

A readily available agar phantom was scanned with and without parallel imaging reconstruction. Other scanning parameters were matched to the human scans. A central slab made up of either a thick slice or an average of a few slices, was extracted and all processing was performed on that image. The proposed QA relies on the creation of two ROIs for processing: (i) a preset central circular region of interest (ccROI) and (ii) a signal mask for all images in the dataset. The ccROI enables computation of average signal for SNR calculations as well as average FA values. The production of the signal masks enables automated measurements of eddy current and B0 inhomogeneity induced distortions by exploiting the sphericity of the phantom. Also, the signal masks allow automated background localization to assess levels of Nyquist ghosting.

Results

The proposed DTI-QA was shown to produce eleven metrics which are robust yet sensitive to image quality changes within site and differences across sites. It can be performed in a reasonable amount of scan time (~15 min) and the code for automated processing has been made publicly available.

Conclusions

A novel DTI-QA tool has been proposed. It has been applied successfully on data from several scanners/platforms. The novelty lies in the exploitation of the sphericity of the phantom for distortion measurements. Other novel contributions are: the computation of an SNR value per gradient direction for the diffusion weighted images (DWIs) and an SNR value per non-DWI, an automated background detection for the Nyquist ghosting measurement and an error metric reflecting the contribution of EPI instability to the eddy current induced shape changes observed for DWIs.

1. Introduction

Diffusion tensor imaging (DTI) is demanding on MRI scanner hardware due to fast switching gradients required for fast imaging (i.e., echo-planar imaging, EPI) combined with strong diffusion sensitizing gradients to produce diffusion-weighted images (DWIs). As with all quantitative methods, the accuracy and sensitivity of the DTI metrics rely on good image quality. Furthermore, a large dataset is produced, made up of more than one non-diffusion weighted image, nDWI, and a large number of gradient directions (typically ≥30). This precludes visual inspection as a reliable form of monitoring the scanner performance. For these reasons, an automated, DTI-specific, phantom-based quality assurance protocol (QA) is of upmost importance both to track changes in performance at a given site as well as to assess inter-site differences in performance for multisite studies.

Due to the high incidence of image quality issues, it has become common practice to manually inspect and discard “bad” DTI images before computing DTI metrics, such as fractional anisotropy (FA) and apparent diffusion coefficient (ADC). However, the sporadic nature of many artifacts and the DTI data redundancy make such manual inspection tedious and unreliable. To mitigate these inconsistent practices, some DTI processing tools incorporate automated image rejection and distortion correction [1–3]. Because distortions are inevitable in EPI-based DTI data, all processing pipelines involve some form of distortion correction which can be accomplished using a variety of tools such as FUGUE and eddy [4] in FSL (FMRIB Software Library, Oxford, UK) [5]. Although necessary, these distortion correction tools may mask artifacts and hide scanner issues as they arise. Most quality control efforts focus on subject-specific in vivo effects and in many cases, the quality assurance/control is integrated with the DTI processing pipelines such as DTI studio [2], DTIprep [6], TORTOISE [1] and the work of Lauzon et al. [7]. However, the variable effectiveness of these methods at correcting image quality issues introduces another source of variability in DTI data [8]. Previous automated phantom-based QA approaches have focused primarily on the ability of the diffusion sensitizing gradients to perform as expected, measuring accuracy, repeatability and precision of ADC/FA measurements in a variety of isotropic phantoms. These methods offer gradient calibration routines [9] and other calibration metrics for multicentre studies [10–12]. Here, we present a phantom-based, automated quality assurance (QA) tool which incorporates both the assessment of artifacts and distortions present in DTI data, while measuring the performance of the diffusion sensitizing gradients as well. It is fast and simple and it can be used on a standardized spherical agar phantom.

To the best of our knowledge, only two similar DTI-QA protocols have been previously proposed [13,14]. Our approach is novel in three ways: (i) we produce similar DTI-QA metrics as previous studies but all are computed in a different way. In particular, our approach to distortion measurements is very different from that used in either previous DTI-QA protocol. We use a different phantom than Wang et al. [13] and hence do not have internal structures. Although we use the same agar phantom as Zhou et al. [14], we measure the distortions due to eddy currents and B0 inhomogeneity (not measured by ref. [14]) by exploiting the sphericity of the phantom. (ii) The image processing required to compute the metrics is fully automated and made publicly available. (iii) We expand the outcome metrics to capture the effects of parallel imaging (PAR) by scanning the phantom with and without PAR, as well as scanner stability within DTI scan time (e.g., SNR across nDWIs and SNR across DWIs) which indirectly measures the gradient performance; these were not available in either previous DTI-QA. This QA produces eleven relevant metrics that represent a comprehensive assessment of DTI data quality.

The focus of ref. [14] is on longitudinal HARDI (high angular resolution diffusion imaging) data quality for a multicentre trial. The metrics we propose can also be tracked in time, across sites and within site, following the criteria presented by Zhou et al. [14]. Therefore, this paper does not focus on the longitudinal aspect of the QA but rather on how the expanded set of metrics are computed, and what those metrics reflect, at a given time point, across scanners. The goal is to produce automated, sensitive and robust QA metrics. The code for the required processing is available for general use at https://github.com/josephdviviano/qa-dti. The output of the code is described in more details in the discussion.

2. Materials and methods

This DTI-QA was developed for purposes of intra- and inter-site monitoring in a multisite study called ‘SPINS’ which comprises three sites with different 3 T MRI scanners of different vendors/models. The sites are the Centre for Addiction and Mental Health (CMH, Toronto, CA), the Maryland Psychiatric Research Centre (MRC, Maryland) and the Zucker-Hillside Hospital (ZHH, NY) with the following 3T MRI scanners respectively: GE MR750 (GE Healthcare, WI), Siemens Trio (Siemens Medical Solutions, Erlangen, Germany) and GE HDx. For the GE sites, the ‘dual spin echo’ option was used [15] to minimize eddy currents as per human scans and the 8-channel head coil was used. For the Siemens site, a 12-channel head coil was used.

2.1. Phantom and image acquisition

The FBIRN (Function Biomedical Informatics Research Network) agar-filled phantom [16,17] is used for several reasons: (i) it is smaller (diameter = 17.5 cm) and more manageable than the ACR phantom so it fits in more head coils (ii) it allows for better consistency because of the agar; there is no need to wait for the liquid to settle, there will be no moving air bubbles and it is less prone to vibrational effects (iii) the diffusion in agar as well as the relaxation parameters (T1, T2) and RF load mimic the brain better than an aqueous phantom. Although the agar phantom diffusivity is expected to be a little higher than that in brain tissue (1.5 × 10⁻³ mm²/s vs 0.5–1.4 × 10⁻³ mm²/s) [14], we propose the use of this standard phantom because it has been used for many years in fMRI QA protocols [17] and has been shown to be temporally stable in diffusion measures (FA) as well spatially uniform [14]. It can be ordered from FBIRN so it is made in one location, following a consistent recipe and protocol, minimizing variability in production across sites. As for all phantom-based diffusion acquisitions, temperature is a possible source of contrast change because some scan parameters and diffusion are temperature dependent. For this reason, the temperature of the phantom is tracked and it is stored in a place with consistent temperature to ensure minimal variation within a given site; temperature may be a common source of inter-site differences which can be monitored.

The image acquisition parameters should match what is being run on subjects at the site to best capture the hardware/software performance at the given site. In particular, the b-value, the set of diffusion sensitizing gradient directions as well as the number of phase encode (PE) steps should match that used on brain scans because these values determine the size of the diffusion-sensitizing gradients and how they are played out. We can reduce the repetition time (TR) because a large value (≫T1) is used for DTI in order to fit the number of slices required to cover the entire brain within one TR. For the purpose of this QA, we do not require full phantom coverage so we reduce the number of slices and shorten TR to the minimum. Although some signal loss is expected, we balance the need for good SNR with the need for a short scan time.

Due to the rather large b-value required for human scanning and the decrease in TR, a single central phantom slice may not have sufficient signal to perform the following QA reliably. In particular, the measurements that require well-defined edges of the phantom relative to the surrounding may be compromised, depending on the coil. The signal loss can be compensated for by either increasing the slice thickness or averaging over a few central slices. These operations will increase the absolute value of the signal without altering distortions or any other relative measures of interest: e.g., SNR of DWI relative to nDWI. As long as the same number of slices and slice thickness is used across different sites, the resulting values will be comparable across sites as well. The following calculations will be done on this central average slab, herein referred to as “the image”. All QA metrics presented are derived from a set of such images, each one representing either a nDWI or the DWI for a particular diffusion direction. The number of nDWIs and DWIs will be denoted by N₀ and N_DWI respectively. For the SPINS multisite study, the following scan parameters were consistent across sites: TE/TR = Minimum Full/2000 ms, slice thickness 4 mm, 2 mm in-plane resolution (FOV = 25.6 cm, Nx × Ny = 128 × 128), 7 slices, N₀ = 5, N_DWI = 60 (same directions at all sites) and b = 1000 s/mm². The total scan time is kept below 15 min at all sites.

We propose to run the DTI-QA scan twice, once with no parallel imaging reconstruction (nPAR) and once with PAR (ASSET/iPAT factor 2). The changes in SNR and distortions can be used to assess the effectiveness of the PAR setting which is commonly used on all subject scans due to possible improvements to both of these measures. It is noteworthy to mention that there is a discrepancy across vendors in the implementation of PAR acquisitions: only for some cases PAR allows a reduction in minimum TE which results in signal recovery that can compensate for the reduction of data collection [18]. For other platforms, the PAR option does not allow a reduction in the minimum TE (e.g., GE, ASSET = 2 has same minimum TE as no ASSET). Here we use the minimum TE allowed for each case and make a note of the TE when interpreting the results.

2.2. Image processing

In contrast to what is suggested by Wang et al. [13], we propose to not register the DWIs to each other nor to the nDWIs as a first step. We do not believe that this is a necessary step for a phantom QA as long as the phantom is fixed in a given position within the bore because in that case, discrepancy between nDWIs and DWIs is not due to motion but rather differences in scanner performance which we do not wish to mask by performing a coregistration. In the case of ref. [13], the coregistration step used built-in scanner functions which could differ across vendors/sites, introducing yet another source of variability.

2.2.1. Making the ccROI

A central, circular ROI (ccROI) is used to compute metrics that capture average values (such as SNR and FA) throughout most of the image while avoiding the edges. It is defined such that its size is maximized while ensuring that no edge effects are included across all images in the dataset (nDWIs + DWIs). For our parameters, the ccROI is defined as a central circle of radius equal to 30 voxels (=6 cm) because the phantom has a radius of approximately 8.5 cm.

2.2.2. Signal mask making

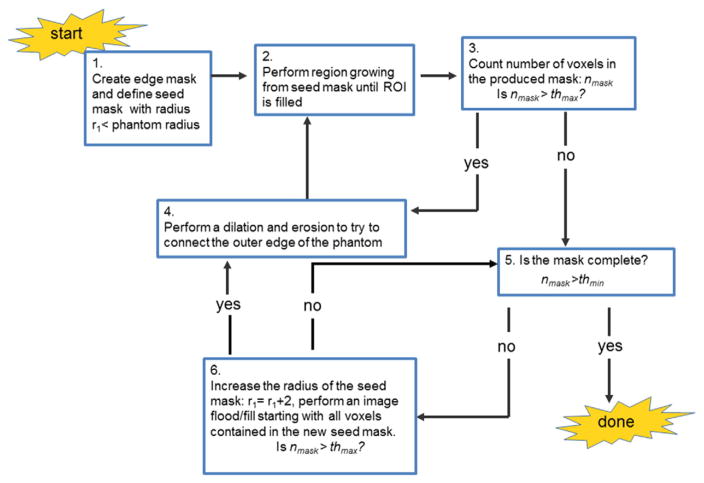
The first critical step for computing several outcome metrics (particularly those related to distortions) is to determine the signal mask for each image in the dataset. Here, we use an iterative edge-detection region-filling algorithm because this was found to be more robust than a simple thresholding algorithm for DWIs which often have low signal in the central region. Ideally, the first step will result in a closed loop outlining the circular border of the phantom. The second step involves region filling/flooding the edge mask from a central seed. The signal mask-making step was accomplished with built-in functions in Matlab (The MathWorks Inc., Natick, MA).

A single pass of edge detection and region filling is sufficient for a good mask detection if the SNR of the images is high (e.g. nDWIs). However, there are a few situations when the above does not work on the first pass and more iterations are required. There are two main causes for failure on the first pass: (i) inhomogeneity of the signal within the agar phantom results in closed loop edges within the phantom, containg the region flooding seed (ii) the outer edge is incomplete at the first pass so the entire image is filled with the region-filling algorithm. Case (i) can be corrected by using a seed mask rather than a single voxel seed. A seed mask is defined as a circular mask, well within the phantom (radius < phantom radius). Every voxel contained in the seed mask is used as a filling seed. This last step is performed iteratively: the central seed mask grows at each iteration until the image filling step entirely fills the phantom mask. A good starting radius value for the seed mask, r₁, is the radius of the ccROI (e.g., r₁ = 30). Case (ii) can be corrected by iterative dilation and erosion steps until the phantom outer edge mask is closed. The incidence of case (ii) can also be reduced by the use of a very sensitive algorithm for edge detection at the expense of increasing the incidence of case (i). Both cases can be reduced by performing an edge-preserving median filtering of the image before edge detection.

Cases (i) and (ii) can be automatically detected by checking the number of voxels in the resulting signal mask, n_mask, against thresholds of minimum and maximum values: th_min and th_max. Given that a single pass of edge detection and region filling is usually enough for good signal masking for the nDWIs, the initial threshold values can be preset to reasonable values, based on the size of the phantom and the resolution of the images, without any negative impact. For an N × N image and a phantom with radius = r (cm) and image resolution = x (cm), we have found reasonable thresholds to be: th_max = 0.9·N² and th_min = (N_r · 0.95)²π where N_r = floor(r/x) is the approximate number of voxels that make up the radius of the phantom. After the nDWI signal masks are formed, the average n_mask value resulting for those, ave(n_mask)₀, can be used to define a minimal threshold value for n_mask for the DWI signal masks: th_min = 0.95 ave(n_mask)₀. A flowchart for the algorithm for this process is given in Fig. 1. A negative response to Step 5 corresponds to case (i) whereas an affirmative response to Step 3 corresponds to case (ii). Steps 4 and 6 correspond to the iterative steps. The final result is a signal mask, SMask_i, for each image i = 1:N₀ + N_DWI.

Fig. 1.

Mask making algorithm flowchart. The main steps for the mask making algorithm are given. There are three steps that require a yes/no response to decide how to proceed. Steps 3 to 4 represent the iterative process for closing the outer edge of the phantom. Steps 5 to 6 represent the iterative process for filling the mask. The first step requires a selection of a radius r₁ such that it is much smaller than the radius of the phantom (r₁ = 30 voxels as per ccROI). The threshold values, th_min and th_max, consist of minimum and maximum expected number of voxels in the mask (see text to compute these). The number of voxels in the mask, n_mask, is computed at Steps 3 and 6.

2.3. Computation of outcome metrics

For each subsection below, a particular artifact/effect is measured. Within each subsection, several intermediate measures are computed which can be used to identify sources of changes/differences and to troubleshoot problems. The cumulative outcome metrics presented for each subsection are the values that we recommend for tracking in time as an overall measure of image quality. They are listed in the subsection heading and italicized in the text for clarity.

2.3.1. The signal-to-noise ratio (SNR): AVE(SNR)₀, CV(SNR)₀, AVE(SNR)_DWI, CV(SNR)_DWI, ADC

SNR is not computed pixel-wise but rather using the average signal over the ccROI. This value combines the effect of signal intensity due to TE and diffusion as well as signal inhomogeneity within the homogenous phantom resulting from B1 and coil sensitivity effects. Also, the noise level is not uniform across the images as a result of multi-channel data combination and in some cases, PAR reconstruction. However, we found that most spatial dependencies of the noise can be removed by subtracting two nDWIs. This is consistent with previous findings [19]. A plot of the histograms of the resulting “noise map” within the ccROI can be used to confirm that it follows a Gaussian distribution and thus computing the standard deviation, STD(noise), within the ccROI is a good measure of noise for the SNR calculation. The noise maps computed by taking the difference between any two images, where both are nDWI or DWIs, should produce the same result, as long as there are enough data points, because the noise is not dependent on the diffusion sensitization. Once we determine STD(noise), we use the same value to compute SNR for each image in the dataset and then compute four cumulative metrics: average and standard deviation SNR across nDWIs: AVE(SNR)₀ and STD(SNR)₀, and the same two values across DWIs: AVE(SNR)_DWI and STD(SNR)_DWI. Cumulative metrics are AVE(SNR) and coefficient of variation, CV(SNR) = STD(SNR) * 100/AVE(SNR) for both nDWIs and DWIs.

A ratio R_SNR = AVE(SNR)_DWI/AVE(SNR)₀ is directly related to the mean diffusivity of the phantom (also known as the apparent diffusion coefficient, ADC) through the relation:

$$\mathrm{S}={\mathrm{S}}_{0}exp(-\text{ADC}·\mathrm{b})$$ (1)

where S and S₀ are the signal magnitude values for DWIs and nDWIs respectively. R_SNR is used to compute ADC = −ln(R_SNR)/b and ADC is tracked longitudinally within a site along with the temperature of the phantom. For inter-site comparisons, ADC may reflect differences in effective b-values, noise floor of DWIs or phantom temperature if we assume negligible agar variability across sites.

The STD(SNR)_DWI reflects the consistency of diffusion sensitization across gradient directions. Inconsistencies across gradient directions can result from gradient nonlinearities/miscalibrations. Comparisons between STD(SNR)_DWI and STD(SNR)₀ can isolate the contribution of the diffusion sensitizing gradients to the instability.

2.3.2. B0 inhomogeneity image distortion: Ratio_B0

The B0 field inhomogeneity (ΔB0) is known to distort EPI-based images through stretches/compression, with possible signal pileup/loss, in the PE direction only (i.e., the readout direction, RO, remains undistorted). We can thus exploit the sphericity of the phantom to assess the extent of this type of asymmetrical distortion by comparing phantom dimensions along both the PE and RO directions. We will assume that the image is oriented so that the PE and RO directions are vertical and horizontal respectively. Although the ΔB0 distortion is along the PE direction (vertical), it may not be centred horizontally, i.e., there may be a shear. Furthermore, the distortion may be a stretching or compression, depending on the direction of the PE data collection with respect to the sign of ΔB0. However, the sphericity of the phantom results in a convex image border despite the distortion, making it simple to produce a metric that captures the amount of distortion.

A comparison of PE and RO dimensions along the centre of the phantom may not be the most sensitive measure to assess the amount of ΔB0-induced distortion in cases where there is shear. Instead, we propose to use the following. Using the signal mask made from the nDWIs as described in Section 2.2.2, we take the average location of the ten voxels of the mask that have smallest row index values (i.e., closest to the top) and do the same for ten voxels with the highest row index values and compute the PE diameter, dia_PE, as a difference between these. Although not necessarily a true phantom diameter, this measure will capture the extent to which the phantom was distorted along the PE dimension and allow for sub-voxel sensitivity. Similarly, we average the location of the ten voxels of the mask that have smallest column index values, do the same for ten voxels with largest column index values and compute dia_RO from the difference. In this case, we expect the ten voxels to lie in a central position on the phantom because there is no distortion in this dimension. Thus, dia_RO is expected to correspond to the true phantom diameter. We then compute the Ratio_B0:

$${\mathit{Ratio}}_{BO}={\text{dia}}_{\text{PE}}/{\text{dia}}_{\text{RO}}$$ (2)

The amount of stretch/compression is captured by the extent to which B0_Ratio differs from unity. Values for Ratio_B0 < 1 and > 1 indicate compressions and stretches respectively. While only the amount by which Ratio_B0 deviates from 1 is indicative of the amount of distortion, we track the value Ratio_B0 for a given site so as maintain sensitivity to any change in scanner performance.

2.3.3. Eddy current induced distortions: avevoxelshift, %∈_vshifit

Large diffusion sensitizing gradients are required to produce DWIs. These gradients can interfere with other scanner components/hardware, resulting in the production of unwanted eddy currents. These unpredictable currents result in unexpected gradients in the imaging system which in turn, cause image distortions due to the low effective bandwidth in the PE direction. These distortions consist primarily of affine distortions which include three distinct types, depending on which spatial dimension is affected: shift of centre of image, stretch/compression along the PE direction or a shear across the RO direction. All effects change the shape/location of the object along the PE dimension. To capture the effect of eddy currents in a DTI dataset, one can compare the shape of the images between nDWIs and DWIs. Furthermore, the eddy currents produced will depend on the particular gradient direction as the gradient amplitude along each of the three orthogonal (i.e., x, y and z) directions varies. Thus, each DWI has a unique distortion with respect to the nDWIs. We propose to quantify the amount of distortion associated with each DWI as follows.

We use the first nDWI mask, SMask_1, from a dataset as the reference. We subtract it from each DWI mask and take an absolute value to produce a difference mask associated with each gradient direction, j:

$${\text{DiffMask}}_{\mathrm{j}}=\mid {\text{SMask}}_{\mathrm{j}}-{\text{SMask}}_1\mid \mathit{where}j=N_0+1:N_0+N_{\mathit{DWI}}$$ (3)

These difference masks consist of incomplete phantom contours which capture the small shape differences. To quantify the amount of shape difference, we perform a column-wise calculation. We split the difference mask into top and bottom halves along a central horizontal axis and compute a column-wise average edge thickness: for column, c, and image j, we determine the thickness across the top hemisphere, ${\mathit{voxelshift}}_{cj}^{\mathit{top}}$, and for the bottom hemisphere, ${\mathit{voxelshift}}_{cj}^{\mathit{bottom}}$ and average these values to produce a single value for a given column. We perform this for all columns contained within SMask_j and compute an average across all columns as our final metric, vshift_j, for each gradient direction j. We can use this same procedure to obtain differences across nDWI which do not reflect eddy current distortions but rather instabilities in the EPI acquisition and/or masking algorithm. We can use those values as an estimate of the error in the vshift_j metric (i.e., the contribution from other instabilities that are not associated with eddy currents):

$$\begin{gathered} {\text{vshift}}_{\mathrm{j}}={\sum }_c\frac{\left(\frac{{\mathit{voxelshift}}_{cj}^{\mathit{top}}+{\mathit{voxelshift}}_{cj}^{\mathit{bottom}}}{2}\right)}{N_c} \\ ={\sum }_c\left(\frac{{\mathit{voxelshift}}_{cj}}{2N_c}\right)c\in {\text{SMask}}_1 \end{gathered}$$ (4)

where N_c is the number of columns within the mask minus four (i.e., two edge columns on each side are omitted) and voxelshift_cj indicates the total voxel count in DiffMask_j at column, c. The error in the eddy current distortion metric can be given as the average of the vshift_j value computed over DiffMask_j for j = 2:N₀ (since DWI₁ is used as the reference):

$${\in }_{\text{vshifit}}=\text{ave}{({\text{vshift}}_{\mathrm{j}})}_{\text{nDWI}}=\sum _{i=2}^{N_0}{\mathit{vshift}}_i/(N_0-1)$$ (5)

The cumulative metrics used to capture the amount of eddy current distortions in a DTI dataset is then given by the average vshift_j across all DWIs:

$$\mathit{avevoxelshift}={\text{avevshift}}_{\mathrm{j}}\text{DWI}=\frac{{\sum }_j{\mathit{vshift}}_j}{N_{\mathit{DWI}}}\mathit{where}j=N_0+1:N_0+N_{\mathit{DWI}}$$ (6)

with relative error: %∈_vshifit = ∈_vshifit * 100%/avevoxelshift.

2.3.4. Nyquist ghosting: Ratio_Nyq

The EPI readout can result in a so-called N/2 Nyquist ghost due to inconsistent phase errors across alternate PE lines due to the change in direction of the readout gradient for even and odd echoes. This ghost is a replica of the image, usually of much lower intensity, centred at the uppermost edge of the image and wrapping back into the bottom half. Most scanners have some form of Nyquist ghost adjustment/compensation techniques which may include calibration of hardware components and the acquisition of a pair of zero phase-encoded reference scans for phase correction. However, hardware components are known to deteriorate in time, thus changes in the ability to produce ghost-free EPIs must be monitored. Also, differences across scanner platforms result in a large variation in the level of ghosting across sites making it an important QA metric.

The level of Nyquist ghosting is often reported as a percentage ghost intensity relative to the main image. However, there is no consensus as to how/where the ghost and signal intensity are measured. Here, we propose an automated method that extracts all background values from an image in both the PE and RO direction. Nyquist ghosting will only contaminate the PE background signal thus a ratio of average background values along the PE relative to the RO direction will be an adequate metric for level of ghost assessment:

$${\mathit{Ratio}}_{\mathit{Nyq}}=\frac{\text{AVE}({\text{background}}_{\text{PE}})}{\text{AVE}({\text{background}}_{\text{RO}})}$$ (7)

The automated background detection is obtained by use of the signal masks of the nDWIs and an image frame that includes all zero-valued image voxels around the borders of the image. Both background ROIs are made up of two separated regions, one on either side of the phantom. The background_PE ROI is defined as two horizontal strips that avoid the signal mask and exclude the image frame. Similarly, the background_RO ROI is defined as two vertical strips that avoid the signal mask and exclude the image frame. To maximize our accuracy, we aim to make these regions as large as possible. However, to maximize our sensitivity to the ghost artifact, we restrict the possible ghost-containing background (i.e., background_PE) region to include only columns which may contain the ghost: both horizontal strips are confined, in the left-right direction, by the outermost columns that contain the phantom as the Nyquist ghost cannot extend beyond the phantom borders in the RO direction. The voxel values contained in both strips that make up each ROI are concatenated and an average value is computed to yield AVE(background_PE) and AVE(background_RO) and ultimately, Ratio_Nyq given in Eq. (7). Here, the mean is used because we want the measurement to be sensitive to outliers as the Nyquist ghost in the background often consists of only a few voxels associated with the edges of the phantom.

A larger value of Ratio_Nyq indicates a poorer image quality as more contamination of ghosting in present in the image.

2.3.5. FA maps: AVE(FA), STD(FA)

Fractional anisotropy (FA) maps are produced using FSL (FMRIB Software Library, Oxford, UK) with no eddy current correction, resulting in some edge effects but it should not affect the signal in the ccROI. The amount of noise and consistency of diffusion sensitization across gradient directions is captured by how much the average FA within the ccROI differs from zero in this homogeneous phantom. Increases in noise as well as any discrepancy across gradient directions will result in an artifactual increase in FA. The inhomogeneity of FA, due to both noise and spatially dependent signal variations, is captured by the standard deviation of FA within the ccROI: STD(FA). We expect AVE(FA) to be close to zero for this homogeneous phantom. For this reason, we use propose to track the STD(FA) rather than use the relative measure given by the coefficient of variation.

3. Results

The proposed DTI-QA was implemented at the three aforementioned sites: CMH, MRC and ZHH. In the following, we show the intermediate results at various stages of the DTI-QA for one time point, at two contrasting sites to demonstrate the contrast in data quality across vendors and scanners. We show that both image-based and cumulative metrics correspond to observable data quality differences. We recommend producing several figures when running the DTI-QA as those will help troubleshoot issues when a cumulative metric deviates from the expected range at a site. Finally, we show examples of how the resulting DTI-QA cumulative metrics can be used to track changes in data quality within a site and/or compare and track data quality differences across sites. At the GE sites, CMH and ZHH, the TE was constant across PAR and NPAR acquisitions (TE = 85 ms). For the Siemens site, MRC, the TE was shorter for the PAR (TE = 85 ms) than for the NPAR (TE = 97 ms) acquisition. This will only be a factor when comparing SNR changes across PAR and NPAR acquisitions.

3.1. Phantom and image acquisition

Sample images, nDWI and DWI, across the three sites, for PAR and NPAR are shown in Fig. 2. It is clear that there are large image quality variations across sites. Decrease in SNR and distortions are also evident in the PAR acquisitions.

Fig. 2.

Sample Images used for DTI-QA metrics calculations across sites and across NPAR/PAR. Each row shows representative data for one of the SPINS sites. Representative images (nDWI and DWI) without PAR (NPAR) and with PAR are shown on the left and right, respectively. The nDWIs are scaled the same across NPAR/PAR, the same is true for the DWIs (but scales for nDWI and DWIs are different). The change in background is apparent for the GE sites: CMH and ZHH (top and bottom rows).

3.2. Image processing: mask results

Despite the obvious reduction in contrast between the phantom signal and background for DWIs relative to nDWIs (notice different scaling in Fig. 2), and the variability in the image inhomogeneities across sites, the proposed mask algorithm was successful in producing signal masks for nDWIs at all sites. The result of a Canny edge detection, method available in Matlab (The MathWorks Inc., Natick, MA), is shown in Fig. 3. The image frame (zero-valued voxels) can be seen to differ across nDWI and DWI, as well as across sites. Fig. 3 demonstrates the result for two different scanners. In one case (CMH-nDWI), an almost closed inner edge loop can be seen (grey arrow) and in the other case (ZHH-DWI), an incomplete phantom border is shown (grey arrow). The proposed method with r1 = 30 voxels (same rationale as for the ccROI, this ensures the circle is within the phantom), successfully created signal masks for all nDWIs as well as DWIs at all three sites.

Fig. 3.

Signal mask making examples. Intermediate steps of the mask making algorithm are shown for two cases, different sites, across nDWI and DWI images (all are NPAR scans here). Here, the nDWIs and DWIs are scaled the same within site to emphasize the SNR challenge presented by the DWIs. The ‘edges’ step shows all the edges found on the first pass; image frame (zero-values border) differences are apparent across sites and nDWI/DWI. The top row (CMH-nDWI) shows an example where a central loop edge is found. Although it is not closed, it demonstrates how it could happen. The bottom row shows an example where the outer phantom edge is incomplete at the first pass. A single application of Step 4 was sufficient to close it in this case.

3.3. Computing the DTI-QA metrics

3.3.1. The signal-to-noise ratio: AVE(SNR)₀, CV(SNR)₀, AVE(SNR)_DWI, CV(SNR)_DWI, ADC

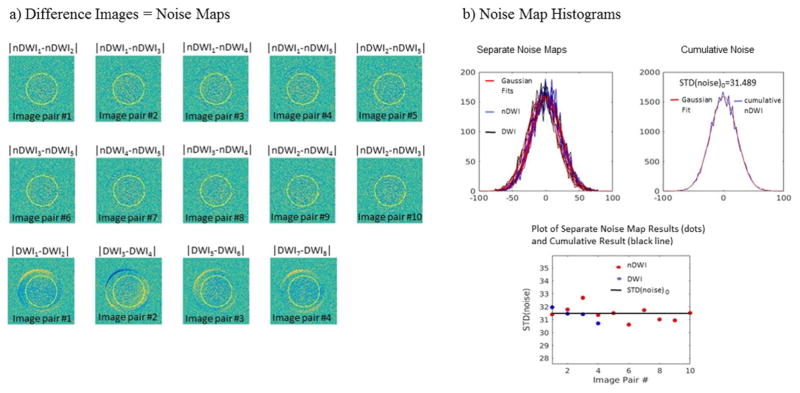
Noise maps were produced by taking the difference between pairwise nDWIs as well as for four pairs of DWIs (i.e., pairwise across the first eight DWIs, using each DWI only once). Noise values within the ccROI were then obtained and a histogram was plotted to check for Gaussian distribution. If the fit to a Gaussian was good, we computed STD(noise) for each noise map, as well as for the cumulative noise values obtained by concatenating all noise map values. Fig. 4 shows sample noise maps as well as histograms of the values with Gaussian fits and resulting STD(noise). It was found that although the STD(noise) did not vary much across noise maps, the noise maps produced by the DWIs did show some unwanted signal intensity variations across gradient sensitization directions at some sites (bottom row of Fig. 4a). These could interfere with the STD(noise) measurement. Thus, we propose to use the STD(noise) obtained by combining noise values across nDWI noise maps in cases when there are more than two nDWIs: N₀ > 2. In order to include all nDWIs in the calculation with equal weighting to avoid a bias in the result, we propose to produce noise maps for pairwise nDWIs where each possible pair is used; this will result in N₀(N₀ − 1)/2 pairs. Then, all noise values are concatenated and an overall STD(noise)₀ is estimated (Fig. 4b). We use this result in the denominator of all SNR computations in that dataset.

Fig. 4.

Calculation of STD(noise) for SNR measurements. a) Sample noise map images resulting from taking image differences: subtracting all possible nDWI pairs (top and central row) and also subtracting the first four pairs of DWIs (bottom row). Some gradation of signal is apparent in the DWIs noise maps that is not there for the nDWIs noise maps. b) Noise map histograms resulting for each noise map in a), as well as the cumulative noise histogram that results when all nDWI noise maps are combined. Gaussian fits are show over each histogram to demonstrate the Gaussian nature of the noise when computed in this manner. STD(noise) resulting from the Gaussian fits are plotted for each nDWIs and DWI pair shown in a), as well as for the cumulative nDWI noise histogram which we propose to use for all SNR calculations.

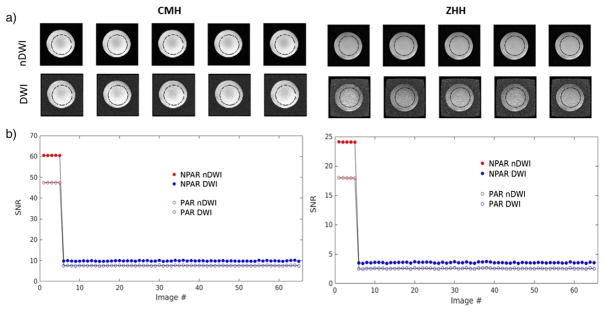
In all cases, the noise distribution was Gaussian as expected. A plot of SNR across all images reflects more variability across DWIs than nDWIs, reflecting gradient nonlinearities and/or gradient calibration differences [20] which may result in varying effective b-values across different gradient directions (Fig. 5). The cumulative SNR metrics shown in Table 1: AVE(SNR)₀, CV(SNR)₀, AVE(SNR)_DWI, CV(SNR)_DWI, were in concordance with the visible differences in image quality across sites (Fig. 1).

Fig. 5.

SNR results. Sample images are shown along with SNR plots across nDWIs and DWIs, for two sites. Plots show NPAR and PAR results overlaid for comparison. The images in a) show sample images (nDWI and DWIs) for the NPAR case with the position of the ccROI used to compute average signal for SNR computations; this ROI enables the exclusion of edge effects. The increased stability of SNR_DWI and overall decrease in SNR with PAR is apparent in the plots in b).

Table 1.

DTI-QA outcome metrics. Eleven cumulative metrics are indicated with a * in front.

Metric\site	NPAR			PAR
	CMH	MRC	ZHH	CMH	MRC	ZHH
SNR
*AVE(SNR)0	60.55	19.29	24.10	47.45	19.12	17.96
STD(SNR)0	0.0202	0.0162	0.0202	0.00565	0.0153	0.0222
*CV(SNR)0	0.03%	0.08%	0.08%	0.01%	0.08%	0.12%
*AVE(SNR)DWI	9.87	3.39	3.57	7.62	2.84	2.57
STD(SNR)DWI	0.1455	0.0459	0.0768	0.0758	0.0532	0.0518
*CV(SNR)DWI	1.47%	1.35%	2.15%	0.99%	1.87%	2.02%
*ADC (×10−3 s/mm2)	1.81	1.74	1.91	1.83	1.91	1.94
ΔB0 distortion
diaRO (voxels)	84.4	83.9	85.4	84.5	83.9	85.6
diaPE (voxels)	82.0	81.6	83.7	83.0	82.0	84.5
*RatioB0	0.972	0.973	0.980	0.982	0.977	0.987
Eddy current distortions
*avevoxelshift (voxels)	0.262	0.336	0.446	0.161	0.187	0.187
∈vshift	0.009	0.027	0.018	0.018	0.032	0.032
*%∈vshift	3.4%	8.0%	4.0%	11.2%	17.1%	17.1%
Nyquist ghosting
*RatioNyq	1.051	1.368	1.047	–	–	–
FA
*AVE(FA)	0.0222	0.0454	0.0530	0.0266	0.0551	0.0771
*STD(FA)	0.0223	0.0251	0.0353	0.0248	0.0303	0.0759

In particular, Table 1 indicates that CV(SNR)₀ was insignificant (<0.02%) across sites relative to CV(SNR)_DWI (> 1% in most cases). A general reduction in CV(SNR)_DWI can be seen across the GE sites (CMH and ZHH) for PAR relative to NPAR (Fig. 5) but this is not the case for the Siemens site (MRC). The value of ADC varied across sites but it remained almost constant between PAR and NPAR acquisitions (<2% difference) at CMH and ZHH while a significant increase in ADC (9.8%) was observed for PAR relative to NPAR acquisitions at MRC.

3.3.2. B0 inhomogeneity image distortion: Ratio_B0

The B0 inhomogeneity induced image distortion, captured by Ratio_B0, was easily computed at all sites because the signal masks were easily obtained for nDWIs. A sample for each site is shown on the top row of Fig. 6. In general, we obtained Ratio_B0 < 1 which reflects an image compression rather than a stretch. This value usually indicated less than a 3% shape change and it was slightly reduced (closer to 1) for PAR relative to NPAR in all cases (Table 1).

Fig. 6.

B0 distortion and Nyquist ghost results. Sample nDWIs are shown for all three sites of the SPINS study (one in each column). The top row indicates the B0 distortion results per image, with measurements overlaid on images which are scaled to emphasize the background; the Nyquist ghosting of MRC is evident. The bottom row indicates the Nyquist ghosting metric results per image, while demonstrating the localization of the automated background ROIs used to compute Ratio_Nyq.

3.3.3. Eddy current induced distortions: avevoxelshift, %∈_vshifit

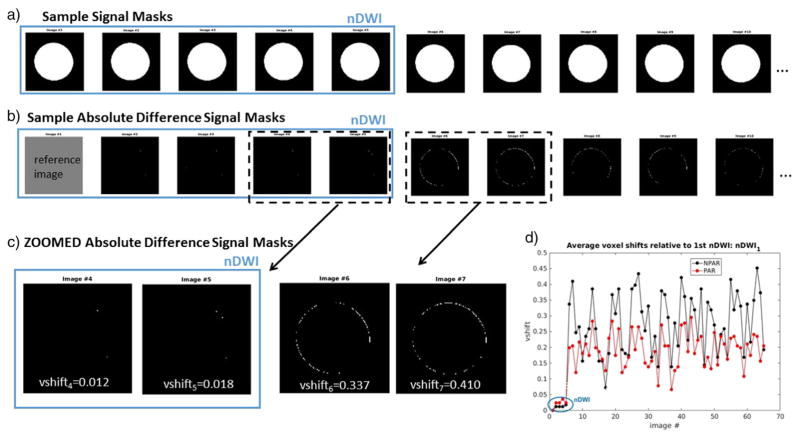
Difference masks were obtained for all images using nDWI₁ as the reference. Based on the results across sites, the EPI instability is in general negligible relative to the eddy current distortions as can be seen by only a few random voxels in the Difference Masks for nDWIs, in contrast to those for DWIs which often reflect a contour of the phantom. Also, the value for vshift_i is in concordance with the visible amount of difference mask detected for a given image (Fig. 7c). The cumulative metrics, avevoxelshift and %∈_vshifit, are quite variable across sites and there is an obvious reduction in the amount of detectable eddy current distortions (decrease in avevoxelshift) across DWIs with the use of parallel imaging (PAR vs NPAR) at the expense of an increase in EPI-induced shape instability, reflected by %∈_vshifit, across all sites (see Table 1 and Fig. 7d).

Fig. 7.

Eddy current distortion measurements. a) Sample signal masks are shown for nDWIs and DWIs along the top row at a given site (CMH-NPAR). b) Difference signal masks resulting when the first nDWI signal mask is used as a reference. c) Zoomed difference signal masks are shown for two nDWIs and two DWIs along with the corresponding vshift value; it is evident that this value captures the amount of shape difference well. d) Plots of vshift values resulting for all images in the dataset (nDWI and DWI). Here, NPAR and PAR results are overlaid for comparison. It is obvious that for this case, the EPI-based instability, given by the shifts across nDWIs, is much less significant than the eddy current induced shifts which exclusively affect the DWIs. Furthermore, it is evident that PAR reduces the amount of shift present in the DWIs (i.e., the eddy current shift) while increasing it slightly for the nDWIs (i.e., the EPI-based instability).

3.3.4. Nyquist ghosting: Ratio_Nyq

The automated Nyquist ghosting detection was able to effectively capture the amount of ghosting visible in the background of the nDWIs images. A comparison across three sites is shown in Fig. 6 where the images are scaled to maximize the ghost contrast. The only site with appreciable ghosting is MRC and the values for Ratio_Nyq are consistent with this: Ratio_Nyq = 1.368 for MRC, whereas Ratio_Nyq = 1.051 and 1.047 for CMH and ZHH, respectively. This metric, Ratio_Nyq, is particularly sensitive to any contamination from phantom signal as the background values are much lower than those in the phantom signal and we compute the mean. For this reason, we dilate the signal masks (3 × 3 kernel) before excluding these mask voxels. The background detection proposed here performs much better than the common use of fixed background regions defined a priori because it ensures that regions belonging to the signal masks are excluded, regardless of phantom placement or distortion, and it adapts to the differences in image frame seen across scanners (see Fig. 6 bottom row). The success of this automated background detection relies on the fact that we have an accurate and robust method to produce nDWI signal masks.

3.3.5. FA maps: AVE(FA), STD(FA)

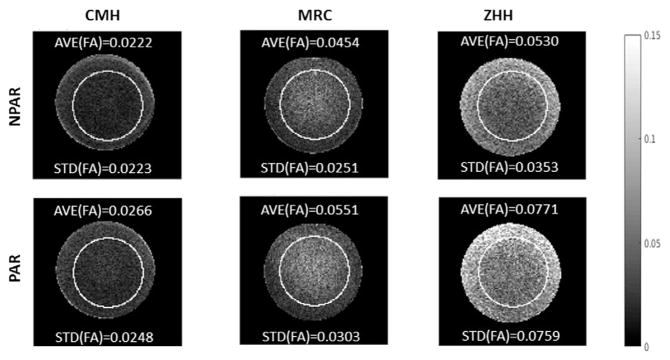
FA maps show some variation in FA within the homogeneous phantom which is related to gradient nonlinearities/miscalibrations as well as image artifacts and noise (Fig. 8). In all cases, the use of PAR slightly increased the AVE(FA) of this homogeneous phantom and the effect was more pronounced for the site for which the SNR was very low (ZHH) where it increased from 0.0530 to 0.0771 (+45%).

Fig. 8.

FA results. Sample FA maps are shown (with ccROI overlaid) across sites, for NPAR and PAR. It is clear that FA is not constant throughout the homogeneous phantom, in particular around edges, but the amount of variation is site-dependent. Also, PAR tends to increase the FA in all cases. AVE(FA) and STD(FA) values are given along with each image to demonstrate how well the metric reflects the observable data quality.

3.4. Multisite studies

We have implemented the above DTI-QA for the SPINS multisite study presented here as well as for another larger multisite study, as part of Brain-CODE, funded by the Ontario Brain Institute, OBI (http://www.braininstitute.ca/brain-code) with a total of ten sites with varying scanning platforms [21]. Across all sites, there is only one metric (avevoxelshift) that the proposed approach could not compute at one site due to the low SNR of the phantom signal near the edges of the phantom for the DWIs at that site (attributed to the age of the scanner). For these studies, we perform the DTI-QA on a weekly or monthly basis at all sites and results will be published elsewhere.

4. Discussion

It is clear that the data quality is not homogeneous across vendors and/or scanner/software versions; the SNR and image artifacts vary considerably. This is most relevant when performing a multisite study as these factors are rarely consistent across sites. The DTI-QA metrics we have presented represent a comprehensive assessment of DTI image quality and scanner performance; they are sensitive and robust measures and their computation is fully automated. The most novel contributions are the distortion measurements based on phantom sphericity, automated ROI detection for Nyquist ghost measurements and the extensive SNR measurements that allow an assessment of gradient nonlinearities/calibrations and scanner EPI stability within scan time i.e., CV(SNR)₀ and CV(SNR)_DWI and %∈_vshift. The code made available through github (https://github.com/josephdviviano/qa-dti) will output the proposed cumulative metrics as text files in csv format. Several figures (in jpeg format) capturing other intermediate values (similar to the figures shown in this manuscript) are also produced by the code for troubleshooting purposes. It is recommended to use the text files to temporally append cumulative metrics while keeping the figures in date-specific folders for easy access in cases where the cumulative metrics are not as expected. This can be customized in a site-specific manner.

All metrics presented in this DTI-QA protocol rely on the creation of one of the two masks: ccROI and SigMasks. Although ccROI is placed in the centre of the FOV which may not be the exact centre of the phantom image, metrics that use this mask in the computation were found to not depend on small discrepancies between the two centres. The important purpose of this ROI is to exclude edge effects. The SigMasks were created from the images themselves and thus the choice of edge detection method used (with varying sensitivity), may affect the signal masking results and in turn, the metrics that depend on these. The extent to which a very sensitive method should be used depends on the data quality (i.e., SNR) of the images in the dataset. While a more sensitive method is more likely to find the border of the phantom, it is also more likely to find closed loops within the phantom. The iterative process can be optimized for the given data by performing several variations of edge-detection methods and edge-preserving filtering. For all images tested, the Canny edge-detection performed after a 3 × 3 median filter resulted in good signal mask detection except in one case where, for some DWIs, the edges of the phantom blended into the background due to very poor SNR.

The SNR was found to decrease for PAR scans relative to NPAR scans as expected, at the GE sites (CMH and ZHH) where a fixed TE value was used. The cumulative metrics thus isolate the effects of increased relative noise that come from PAR reconstruction artifacts and a reduction in the number of k-space lines of data. However, this reduction in SNR for PAR may be overcome to some extent by the signal gain associated with a reduction in TE [18] available on some platforms, such as for MRC. In our case, a 16% decrease in SNR (3.39 to 2.84) across PAR and NPAR scans is observed for the DWIs at MRC despite the relatively constant SNR achieved for nDWIs, resulting from the decrease in TE. This indicates an increase in relative noise associated with the PAR that is not overcome by decreased TE. Nevertheless, significant decreases in avevoxelshift and Ratio_B0 can be attributed to using PAR as expected [18], supporting the use of PAR for DTI human scanning.

We get average ADC (〈ADC〉) values within the expected range for this phantom at all sites: 1.81 · 10⁻³ s/mm² (NPAR) and 1.83 · 10⁻³ s/mm² (PAR) for CMH, 1.74 · 10⁻³ s/mm² (NPAR) and 1.90 · 10⁻³ s/mm² (PAR) for MRC and 1.91 · 10⁻³ s/mm² (NPAR) and 1.94 · 10⁻³ s/mm² (PAR) for ZHH. The GE sites produce more consistent 〈ADC〉 values across NPAR/PAR (<2% difference). Some of the discrepancy in 〈ADC〉 across sites may be due to phantom temperature although the large variation in 〈ADC〉 (8.4%) across NPAR/PAR within site (for MRC) is larger than the across site differences. The source of this discrepancy is not clear as an increased noise floor with PAR would result in an underestimation of 〈ADC〉 but the opposite is observed. Furthermore, the values of AVE(SNR)₀ change very little for PAR vs NPAR for this site (less than for the other two GE sites) while the CV(SNR)_DWI increases only for this site. This indicates a very different behaviour in SNR across volumes with the introduction of PAR at this site, which could be the result of a vendor-specific reconstruction algorithm. Comparisons in behaviour with other Siemens sites would be necessary to further investigate this.

The Nyquist ghost measurement relies on the background values of the image. For most scanners, the background is suppressed when PAR is used to do the reconstruction which is why we propose to compute Ratio_Nyq only on the NPAR scans. However, there are cases when the background is suppressed even for NPAR if filters are used on the images. It is important to acquire filter-free images for this DTI-QA. In general, for phantom-based QA procedures, if a filter is deemed necessary to enhance a particular feature of the images, it can be applied as long as it is not done on the scanner, using a scanner-specific implementation that will only add to the variability across sites/vendors. Instead, a standard filter can be chosen and applied equally off-line to all images from all sites, preserving the ability to compare across sites.

We propose to use voxel-wise FA computations (i.e. FA map), later taking AVE and STD values within the ccROI as this way the FA metrics capture both noise effects and gradient nonlinearities/miscalibrations simultaneously. In contrast, Wang et al. propose to use ROI-based FA where a single FA value is computed based on average signal values within an ROI, i.e., one value for each gradient direction, to isolate gradient nonlinearities/miscalibrations as the random noise is “averaged out” [13]. In our case, we compute SNR for each DWI separately and thus any signal variation due to gradient nonlinearities/miscalibrations will be reflected in a variation of SNR across DWIs i.e., STD(SNR)_DWI. Therefore, we are more interested in capturing both the effects of noise and gradient nonlinearities/miscalibrations on our FA maps. The fact that FA increases for all PAR vs NPAR scans (see Table 1) despite the apparent decrease in STD(SNR)_DWI for the two GE sites (CMH and ZHH) indicates that, in agreement with ref. [13], noise and PAR-induced artifacts dominate the voxel-based FA metric; gradient based effects are secondary. This is also confirmed by computing Pearson’s correlation coefficients for AVE(SNR) vs AVE(FA), combining across NPAR/PAR scans. We find significant negative correlations for both nDWI (r = −0.86, p = 0.027) and DWIs (r = −0.89, p = 0.019) and a much less significant positive correlation between STD(SNR)_DWI and AVE(FA) (r = 0.77, p = 0.075).

Of note, in contrast to ref. [14], we have chosen not to incorporate a spike noise detection method [22] as part of our phantom-based DTI-QA as spike noise is very sporadic in nature; in our experience, the lack of spike noise in a single phantom scan does not guarantee a spike-free image when human data is acquired. We think phantom-based spike noise detection may lead to false positives and/or false negatives so we believe it is best to check all human data for the possible presence of this artifact.

Both aforementioned multisite studies have been using the proposed DTI-QA to track data quality consistency within a site and to compare data quality across sites for over one year. We do not present longitudinal data here as it is the focus of several other works in progress. Although scanner performance has improved over recent years, reducing the incidence and magnitude of most DTI-related image artifacts, the metrics we propose have been shown to be sensitive and reliable in tracking scanner performance and detecting scanner issues. Both studies have benefited from such a tool: it has enabled timely identification of scanner performance issues within sites. Currently, efforts are underway to incorporate some of these cumulative outcome metrics, particularly those that differ most across sites, in a modified mega-analytical homogenization approach to improve statistical power of multisite human DTI data analysis [23].

5. Conclusions

A novel DTI-QA tool has been proposed. It has been applied successfully on data from several scanners/platforms. The novelty lies in the exploitation of the sphericity of the phantom. Other novel contributions are the determination of STD(noise) that can be used to compute SNR values across all images (nDWIs and DWIs), as well as a relative error metric reflecting the contribution of EPI instability to the total shape changes observed for DWIs, enabling an isolation of eddy current induced effects. The metrics are computed in a fully automated manner and the code has been made publicly. The hope is that this will facilitate homogenization of DTI-QA efforts across sites/studies.