Restoration of Monotonicity Respecting in Dynamic Regression

Abstract

Dynamic regression models, including the quantile regression model and Aalen’s additive hazards model, are widely adopted to investigate evolving covariate effects. Yet lack of monotonicity respecting with standard estimation procedures remains an outstanding issue. Advances have recently been made, but none provides a complete resolution. In this article, we propose a novel adaptive interpolation method to restore monotonicity respecting, by successively identifying and then interpolating nearest monotonicity-respecting points of an original estimator. Under mild regularity conditions, the resulting regression coefficient estimator is shown to be asymptotically equivalent to the original. Our numerical studies have demonstrated that the proposed estimator is much more smooth and may have better finite-sample efficiency than the original as well as, when available as only in special cases, other competing monotonicity-respecting estimators. Illustration with a clinical study is provided.

1. Introduction

Quantile regression (Koenker and Bassett 1978) models and estimates potentially dynamic covariate effects on quantiles. As popular as it has become, lack of monotonicity respecting remains an outstanding issue (e.g., He 1997). For example, an estimated 90th percentile may actually exceed its 95th counterpart. Although it may not have received as much attention elsewhere, this issue is general with linear dynamic regression models that relate a response variable Y with covariate vector X through

$$D_{\mathbf{x}}(t)={\mathbf{x}}^{\top }\mathit{\beta }(t)(t\in 𝕋,\mathbf{x}\in 𝕏).$$ (1)

Above, D_x(·) is a functional that has a one-to-one mapping with the distribution function of Y given X = x, β(·) is a regression coefficient that quantifies the dynamic covariate effects, $𝕋$ is an interval index set on the real line, and $𝕏$ is a covariate space. In the case of quantile regression, D_x(·) is the quantile function, possibly upon a transformation. One sub-class, due to Peng and Huang (2007), takes a transformation of the survival function as D_x(·); the additive hazards model (Aalen 1980) and the additive complementary log-log survival model (Peng and Huang 2007) are special cases. With all these models, D_x(t) is a monotone function of $t\in 𝕋$ for all $\mathbf{x}\in 𝕏$. However, a standard regression procedure, with coefficient estimator $\widehat{\mathit{\beta }}(·)$, may not respect the monotonicity in the sense that ${\widehat{D}}_{\mathbf{x}}(t)={\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(t)$ is not monotone over $t\in 𝕋$ at least for some $\mathbf{x}\in 𝕏$. Without loss of generality, monotonicity is taken to be monotonically increasing throughout.

To elaborate, consider the typical circumstance that ${\inf }_{\mathbf{x}\in 𝕏}{\mathbf{x}}^{\top }\{\mathit{\beta }(t)-\mathit{\beta }(s)\}>0$ for any given s < t and $\widehat{\mathit{\beta }}(·)$ is uniformly consistent for β(·). Then, with respect to discrete points in $𝕋$ and in large sample, lack of monotonicity respecting can be lesser of an issue. Between a fixed point and any other one outside a fixed neighborhood, $\widehat{\mathit{\beta }}(·)$ is monotonicity-respecting with respect to them with probability tending to 1 as sample size n increases. So is for any finite set of fixed points. Nevertheless, ${\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(t)$ may not be monotone over all $t\in 𝕋$ for most $\mathbf{x}\in 𝕏$ even in large sample. With standard quantile regression of Koenker and Bassett (1978), ${\widehat{D}}_{\mathbf{x}}(·)$ is monotone when x is the covariate sample average and by continuity in a neighborhood thereof. Neocleous and Portnoy (2008) argued that the neighborhood, however, is quite small and generally tends to zero in size as n increases. This might also explain the roughness of $\widehat{\mathit{\beta }}(·)$ as typically observed.

There are several notable recent developments to tackle this issue with quantile regression. Neocleous and Portnoy (2008) suggested to linearly interpolate the points of an imposed grid, and showed that the resulting estimator is asymptotically monotonicity-respecting and equivalent to the original Koenker–Bassett estimator if the mesh approaches 0 at an appropriate rate. However, monotonicity respecting is not guaranteed in finite sample. Wu and Liu (2009) and Bondell et al. (2010) investigated a somewhat different problem to target the estimation at discrete points only. Moreover, their methods may not adapt easily for other dynamic regression procedures.

As a related problem, curve monotonization has a much longer history in the literature. Many well-known methods, including isotonic regression (e.g., Barlow et al. 1972; Mammen 1991) and monotone regression splines (e.g., Ramsay 1988), were mostly developed for nonparametric regression. Even though they might be adapted, their statistical properties are largely unknown in our context (e.g., Chernozhukov et al. 2010), where the curve of concern ${\widehat{D}}_{\mathbf{x}}(t)$ is dependent across $t\in 𝕋$. Only a few are more relevant. For a baseline cumulative hazard function, Lin and Ying (1994) suggested to monotonize their original estimator by maximizing over the range below, and argued that the asymptotic properties are preserved. Recently, Chernozhukov et al. (2009, 2010) proposed and investigated the rearrangement method to monotonize an estimated curve. The rearranged curve is closer to the estimand in common metrics, and is asymptotically equivalent to the original under regularity conditions. Clearly, a curve monotonization method may be used to monotonize a fitted curve in a dynamic regression, i.e., ${\widehat{D}}_{\mathbf{x}}(t)$ for a given x, or curves. However, these monotonized curves typically no longer respect the linearity in model (1). Thus, they may not correspond to a monotonicity-respecting regression coefficient estimator, which is of primary interest as a direct and meaningful measure of covariate effect. If the covariate space is of a special type, we later devise a procedure for monotonicity-respecting regression using a generic curve monotonization method. Nevertheless, this is not a general resolution.

In this article, we propose a novel adaptive interpolation method for monotonicity-respecting estimation of β(·) with a general covariate space $𝕏$. Starting from a standard estimator, the approach restores monotonicity respecting by construction. This general method applies across various dynamic regressions. As a byproduct, it also reduces to a new curve monotonization method. Section 2 presents the proposed method along with an asymptotic study. Simulations are reported in Section 3, and an illustration given in Section 4. Final remarks are provided in Section 5. Technical details are deferred to the Appendix.

2. The adaptive interpolation method

Standard dynamic regression procedures typically yield estimators that are cadlag step functions, such as cadlag version of the Koenker–Bassett estimator (Huang 2010, Section 3.4) for quantile regression, the estimator of Huang (2010) of censored quantile regression, the generalized Nelson–Aalen estimator under the additive hazards model, and the estimator of Peng and Huang (2007) under their dynamic survival regression models. These estimators are natural, being invariant to a monotonically increasing transformation of the index scale. We shall thus focus on such an original estimator $\widehat{\mathit{\beta }}(·)$; see related discussion later in Remark 3.

For generality, the monotonicity respecting will be restored with respect to an arbitrary covariate sub-space, ${𝕏}_S\subseteq 𝕏$. As such, the proposal also accommodates the usual practical situation with unknown $𝕏$, where a natural replacement is the convex hull of observed covariate values, or the empirical covariate space $\widehat{𝕏}$. Moreover, the proposal reduces to a curve monotonization method when ${𝕏}_S$ is singleton. Thus, ${𝕏}_S$ can be random, and the linear space spanned by ${𝕏}_S$ may have a lower dimension than that by $𝕏$.

2·1 The proposed estimator

Without loss of generality, suppose that the interval set $𝕋$ is closed; a boundary point can always be included whereby a cadlag function at the boundary point may be set as an appropriate limit. Denote the interior and boundary of a set by circle superscript and ∂, respectively. Write

$$𝔻=\{t\in 𝕋°:\widehat{\mathit{\beta }}(t-)\ne \widehat{\mathit{\beta }}(t)\}\cup \partial 𝕋,$$

which contains all the breakpoints of $\widehat{\mathit{\beta }}(·)$ along with the boundary points of $𝕋$. From a starting point $\tau \in 𝔻$,

$$max\left[t\in 𝔻:t<\tau ,\underset{\mathbf{x}\in {𝕏}_S}{\sup }\{{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(t)-{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(\tau )\}\le 0\right],$$ (2)

is the left nearest monotonicity-respecting neighbor, in the sense that $\widehat{\mathit{\beta }}(·)$ respects the monotonicity at these two points. Recursively each identified point then has its own left nearest monotonicity-respecting neighbor determined, until such a neighbor no longer exists. In the other direction, right neighbors can be similarly obtained; the right nearest monotonicity-respecting neighbor to τ is

$$min\left[t\in 𝔻:t>\tau ,\underset{\mathbf{x}\in {𝕏}_S}{\inf }\{{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(t)-{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(\tau )\}\ge 0\right].$$ (3)

Denote the collection of all these points, including the starting one τ, by $𝕄$. Note that ${𝕏}_S$ may be replaced with the vertex set of its convex hull in these neighbor definitions. Also, such nearest monotonicity-respecting neighbors are not necessarily mutual: That point A is the left one to point B does not imply that B is the right one to A.

Interpolating $\widehat{\mathit{\beta }}(·)$ linearly between adjacent points in $𝕄$ then yields a monotonicity-respecting estimator $\stackrel{\sim }{\mathit{\beta }}(·)$. for any t within two adjacent points in $𝕄$, say τ_l < τ_r,

$$\stackrel{\sim }{\mathit{\beta }}(t)=\frac{{\tau }_r-t}{{\tau }_r-{\tau }_l}\widehat{\mathit{\beta }}({\tau }_l)+\frac{t-{\tau }_l}{{\tau }_r-{\tau }_l}\widehat{\mathit{\beta }}({\tau }_r).$$ (4)

Moreover, set $\stackrel{\sim }{\mathit{\beta }}(t)=\widehat{\mathit{\beta }}(min𝕄)$ for $t<min𝕄$ and $\stackrel{\sim }{\mathit{\beta }}(t)=\widehat{\mathit{\beta }}(max𝕄)$ for $t>max𝕄$. Unlike $\widehat{\mathit{\beta }}(·)$, $\stackrel{\sim }{\mathit{\beta }}(·)$ is a piecewise-linear continuous function.

The proposed adaptive interpolation method is invariant to linear transformation of the covariates in ${𝕏}_S$. In the case that ${𝕏}_S$ is a singleton, say {x}, the dynamic regression model (1) therefore becomes irrelevant and the proposal reduces to a curve monotonization procedure, for ${\widehat{D}}_{\mathbf{x}}(t)$, just like Lin and Ying (1994) and Chernozhukov et al. (2009, 2010). Figure 1 illustrates the procedure in this special case. As an appealing characteristic, the monotonicity respecting is induced locally. For the large part, the proposed estimator is thus insensitive to potential tail instability of the original estimator so long as the starting point τ is positioned away from such a tail or tails. In contrast, the Lin–Ying and rearranged estimators are subject to influence by one tail and both tails, respectively. The proposed estimator has no more knots than breakpoints of the original estimator, and is always more smooth. However, unlike the rearranged estimator, the adaptive interpolation estimator is not necessarily closer to the estimand than the original. Nevertheless, it might be so on average as suggested by our numerical studies shown later.

Figure 1.

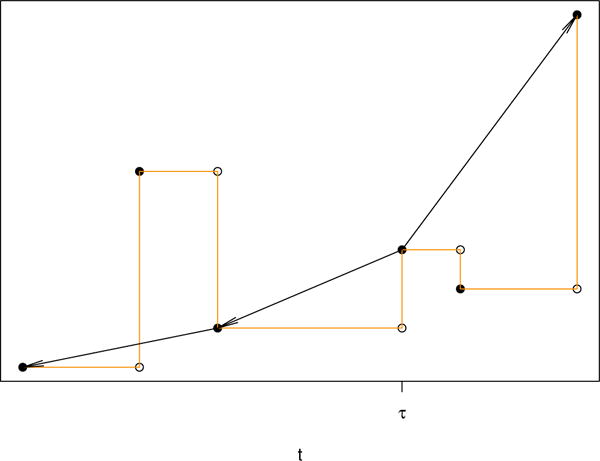
An illustration of the proposed adaptive interpolation method in the case that ${𝕏}_S$ is a singleton, {x}. The light line is the original ${\widehat{D}}_{\mathbf{x}}(t)$. The dark line is the adaptive interpolation estimate, where each arrow points to a nearest monotonicity-respecting neighbor.

This proposal requires a choice of the starting point, τ. Our asymptotic analysis and numerical studies will later show that a wide range of choices would make little difference in the resulting estimator. Nevertheless, a starting point at which the original estimator is most reliable seems natural; such a point depends on the specific regression model under consideration.

2·2 An asymptotic analysis

Mild regularity conditions are imposed for this purpose.

Condition 1

(Original estimator) $\widehat{\mathit{\beta }}(·)$ is consistent for β(·) uniformly on some interval $[a,b]\subseteq 𝕋$. Furthermore, $n^{1/2}\{\widehat{\mathit{\beta }}(·)-\mathit{\beta }(·)\}$ on [a, b] converges weakly to a tight mean-zero Gaussian process with a continuous covariance function.

Condition 2

(Covariates) $𝕏$ is bounded.

Condition 3

(Estimand) The derivative β′(t) exists for all t ∈ [a, b], and ${\inf }_{\mathbf{x}\in 𝕏,t\in [a,b]}{\mathbf{x}}^{\top }{\mathit{\beta }}^{\prime }(t)>0$ strictly.

Condition 4

(Starting point) τ is in [a, b] with probability tending to 1.

Uniform consistency and asymptotic normality as in Condition 1 hold in general for standard dynamic regression estimators. See Koenker (2005) for quantile regression, Peng and Huang (2008) and Huang (2010) for censored quantile regression, McKeague (1988) for the additive hazards model, and Peng and Huang (2007) for their dynamic survival regression models, among others.

We first characterize the distance between adjacent points in $𝔻$ and $𝕄$, within interval [a, b]. Write the points in $(𝔻\cap [a,b])\cup \{a,b\}$ as a ≡ ν₁ < ⋯ < ν_J ≡ b and those in $(𝕄\cap [a,b])\cup \{a,b\}$ as a ≡ τ₁ < ⋯ < τ_K ≡ b.

Lemma 1

Under Conditions 1, 2, and 3,

$$\underset{1<j\le J}{max}({\nu }_j-{\nu }_{j-1})=o_p(n^{-1/2}).$$ (5)

With Condition 4 in addition,

$$\underset{1<k\le K}{max}({\tau }_k-{\tau }_{k-1})=O_p(n^{-1/2}).$$ (6)

This result paves the way for establishing the statistical properties of $\stackrel{\sim }{\mathit{\beta }}(·)$. Denote the L^p norm, p ≥ 1, by ‖ · ‖_p.

Theorem 1

Suppose that Conditions 1, 2, 3, and 4 hold. Then,

$$\underset{t\in [a+\iota ,b-\iota ]}{\sup }\Vert \stackrel{\sim }{\mathit{\beta }}(t)-\widehat{\mathit{\beta }}(t){\Vert }_2=o_p(n^{-1/2})$$ (7)

for any small ι > 0. If τ = a or τ = b, the asymptotic equivalence of $\stackrel{\sim }{\mathit{\beta }}(·)$ and $\widehat{\mathit{\beta }}(·)$ as above holds over an extended interval [a, b − ι] or [a + ι, b], respectively.

Since ι can be made arbitrarily small, $\stackrel{\sim }{\mathit{\beta }}(·)$ is asymptotically equivalent to $\widehat{\mathit{\beta }}(·)$ over essentially the same interval where the latter is consistent and asymptotically normal. Accordingly, for inference with the monotonicity-respecting $\stackrel{\sim }{\mathit{\beta }}(·)$, both interval estimation and hypothesis testing using the original $\widehat{\mathit{\beta }}(·)$, based on either asymptotic distribution theory or re-sampling methods, can be easily adapted. Specifically, the same standard error may be used for $\stackrel{\sim }{\mathit{\beta }}(·)$, and a pointwise confidence interval or simultaneous confidence band with $\stackrel{\sim }{\mathit{\beta }}(·)$ can be obtained by re-centering the interval or band with $\widehat{\mathit{\beta }}(·)$ around $\stackrel{\sim }{\mathit{\beta }}(·)$. Furthermore, a test statistic with $\stackrel{\sim }{\mathit{\beta }}(·)$ in place of $\widehat{\mathit{\beta }}(·)$ would typically remain asymptotically equivalent. This inference strategy was used in the numerical studies presented later.

As a result of selecting monotonicity-respecting points, the maximum distance between adjacent points increases from o_p(n^−1/2) in $𝔻$ to O_p(n^−1/2) in $𝕄$. if a step function instead is used to connect the points in $𝕄$, the resulting monotonicity-respecting estimator then has a bias of O_p(n^−1/2), which is not sufficient for an asymptotic equivalence result like (7). The linear interpolation in the proposal ensures a negligible bias of o_p(n^−1/2).

Remark 1

A restricted parameter space is typically associated with improved estimation efficiency. It is not so for the monotonicity-respecting estimation in terms of first-order asymptotic efficiency, although finite-sample improvement might still be possible.

Remark 2

Although β(·) is introduced through the dynamic regression model (1), the model is nonessential whereby β(·) can be interpreted merely as the limit of $\widehat{\mathit{\beta }}(·)$. However, the strict monotonicity of x^⊤β(t) over t for all x, given by Condition 3, is critical, so as to bound the distance between adjacent points in $𝕄$ and in turn give rise to the asymptotic equivalence of $\stackrel{\sim }{\mathit{\beta }}(·)$ and $\widehat{\mathit{\beta }}(·)$.

Remark 3

Monotonicity respecting may be restored for a general original estimator without much additional difficulty. Approximation by a step function is one approach. Alternatively, the proposal may be adapted to include all points in $𝕋$ as candidates in the nearest monotonicity-respecting neighbor identification. When the original is actually a cadlag step function, the adaptation is not the same as the proposal, however, and our proposed estimator tends to be more smooth.

Remark 4

The proposal shares one ingredient, linear interpolation, with the approach of Neocleous and Portnoy (2008). However, an important distinction is that ours is adaptive so as to guarantee monotonicity respecting in finite sample. Moreover, their results are specific to quantile regression and implicitly require existence of the second derivative of β(·). Finally, our gap between knots, as given by (6), is tighter than their grid mesh in order.

3. Simulations

Simulations were conducted to investigate the performance of our proposal under practical sample size with various dynamic regressions. Overall precision was assessed using maximum absolute error and root mean integrated squared error; for example, in the case of estimator $\stackrel{\sim }{\mathit{\beta }}(·)$ over interval [c₁, c₂], these measures are given by

$$\underset{t\in [c_1,c_2]}{max}{\Vert \stackrel{\sim }{\mathit{\beta }}(t)-\mathit{\beta }(t)\Vert }_{\infty },{\left\{{\displaystyle {\int }_{c_1}^{c_2}{\Vert \stackrel{\sim }{\mathit{\beta }}(t)-\mathit{\beta }(t)\Vert }_2^{2}dt}\right\}}^{1/2},$$

respectively.

3·1 Quantile regression models

The first model contained an intercept and two non-constant covariates. The response Y followed an extreme value distribution conditionally. The two covariates were independent and identically distributed as uniform between 0 and 1. Under formulation (1), D_x(t) was the conditional t-th quantile of Y and β(·) consisted of an intercept and two slopes:

$$\mathit{\beta }(t)={[\log \{-\log (1-t)\},t,t^2]}^{\top }.$$

Cadlag version of the Koenker–Bassett estimator was taken as the original, and its standard error was obtained from the multiplier bootstrap of size 200 as in Huang (2010). With the proposed adaptive interpolation method, we considered the covariate space $𝕏$ or its empirical counterpart $\widehat{𝕏}$. So far as τ is concerned, it might not take 0 or 1 since β(·) was not even bounded at the extremes. Instead, any value in the middle would be viable. A natural choice was the left breakpoint of the original estimator closest to 0.5, denoted by τ ≏ 0.5, and we also considered τ ≏ 0.8. Meanwhile, two additional estimators were also studied, each involving a single component of the two in the adaptive interpolation method. One was the linearly interpolated original estimator, and the other was the stairwise monotonicity-respecting estimator that jumps only at the points in $𝕄$ as obtained with $\widehat{𝕏}$ and τ ≏ 0.5. Sample sizes of 200 and 400 were studied.

Table 1 reports the results on the regression coefficient estimators from 1000 replications. Not surprisingly, the interpolated original estimator behaved similarly to the original one; asymptotically the interpolation is negligible since the adjacent points in $𝔻$ are sufficiently close to each other, as given by (5). However, the stairwise monotonicity-respecting estimator showed notable bias, highlighting the role of interpolation in the proposed adaptive interpolation method. Among the adaptive interpolation estimators, empirical $\widehat{𝕏}$ versus theoretical $𝕏$ and τ ≏ 0.5 versus τ ≏ 0.8 made little difference. They all had considerably smaller maximum absolute error on average than the original estimator, although the magnitude was more modest in terms of root mean integrated squared error; these improvements were larger with smaller sample size. Meanwhile, they had roughly 10% as many knots on average as the breakpoints of the original estimator; the average numbers of breakpoints were 257 and 517 for the original estimator for sample sizes 200 and 400, respectively. At given probability indices, the proposed adaptive interpolation estimators had smaller standard deviation than the original estimator, especially in the circumstance of smaller sample size, but behaved similarly in bias and coverage of Wald confidence interval.

Table 1.

Regression coefficient estimation under a quantile regression model

				t = 0.2			t = 0.5			t = 0.8
sample size: 200
Orig			B	−40	47	17	−27	28	9	−17	13	−3
			SD	466	631	611	343	470	480	308	440	435
			SE	485	659	657	347	491	493	314	448	451
			CI	93.4	95.1	95.9	94.3	94.7	94.8	94.3	94.6	95.2
IO	MAE	0.99	B	−30	49	19	−22	31	11	−11	15	1
	RMISE	1.00	SD	466	630	609	341	467	479	307	438	436
SW	MAE	1.02	B	−181	26	−2	−120	−5	−14	−62	−41	−63
	RMISE	1.05	SD	516	668	653	353	480	482	314	337	439
$\text{AI-}\widehat{𝕏}$	MAE	0.87	B	−45	60	26	−26	32	12	7	−1	−12
	RMISE	0.96	SD	440	598	578	339	464	478	299	422	421
	BRK	0.11	CI	94.9	95.8	97.3	94.5	94.8	94.7	95.0	94.9	95.2
$\text{AI-}𝕏$	MAE	0.86	B	−48	60	28	−26	32	12	13	−4	−20
	RMISE	0.95	SD	438	593	573	339	464	478	298	422	416
	BRK	0.10	CI	95.1	95.7	97.1	94.4	94.8	94.7	95.6	94.9	95.9
$\text{AI-}\widehat{𝕏}$	MAE	0.87	B	−46	61	26	−37	41	31	−14	15	0
τ ≏ 0.8	RMISE	0.96	SD	440	598	578	333	457	465	306	437	435
	BRK	0.11	CI	94.9	95.8	97.3	95.3	94.7	95.2	94.8	95.0	94.8
sample size: 400
Orig			B	2	8	−5	−4	8	7	−1	−1	−2
			SD	330	429	446	241	338	320	215	314	304
			SE	338	456	457	242	345	343	219	314	313
			CI	94.2	95.0	94.2	92.9	94.5	96.1	94.2	93.9	94.1
IO	MAE	0.99	B	8	8	−5	−1	9	7	2	1	−1
	RMISE	1.00	SD	330	429	445	240	338	320	214	314	302
SW	MAE	0.99	B	−68	−7	−9	−51	−9	−3	−25	−30	−43
	RMISE	1.03	SD	346	437	458	246	344	320	217	314	310
$\text{AI-}\widehat{𝕏}$	MAE	0.90	B	1	12	0	−3	9	7	11	−6	−12
	RMISE	0.98	SD	324	420	434	240	339	320	210	307	299
	BRK	0.10	CI	94.8	95.1	94.4	92.8	94.5	96.0	94.3	94.7	95.0
$\text{AI-}𝕏$	MAE	0.90	B	1	14	−1	−3	9	7	12	−7	−13
	RMISE	0.97	SD	322	419	432	240	339	319	210	307	298
	BRK	0.10	CI	94.9	95.2	94.5	92.8	94.5	96.1	94.3	95.1	95.2
$\text{AI-}\widehat{𝕏}$	MAE	0.91	B	1	12	0	−11	19	18	0	1	−1
τ ≏ 0.8	RMISE	0.97	SD	324	420	434	239	335	316	213	313	301
	BRK	0.10	CI	94.8	95.1	94.4	93.3	94.7	96.0	94.2	93.6	94.6

Orig: the original estimator; IO: the interpolated original estimator; SW: the stairwise monotonicity-respecting estimator; $\text{AI-}{𝕏}_S$: the proposed adaptive interpolation estimator with ${𝕏}_S$ and, unless otherwise specified, τ ≏ 0.5.

MAE: maximum absolute error over [0.1, 0.9]; RMISE: root mean integrated squared error over [0.1, 0.9]; BRK: number of knots or breakpoints. All are average measures, reported as relative to the original estimator. B: Empirical bias (×1000); SD: Empirical standard deviation (×1000); SE: Average standard error (×1000); CI: Empirical coverage (%) of 95% Wald confidence interval.

Three columns under each t value correspond to the estimated intercept and two slopes.

We also investigated estimated conditional quantile functions. The proposed adaptive interpolation method with ${𝕏}_S=𝕏$ yields a monotone estimated conditional quantile function for a given covariate x. Meanwhile, a curve monotonization method may also be used to monotonize ${\mathbf{x}}^T\widehat{\mathit{\beta }}(·)$. Such methods include the adaptive interpolation with ${𝕏}_S=\left\{\mathbf{x}\right\}$ and the rearrangement of Chernozhukov et al. (2009, 2010). From the same simulations as for Table 1, Table 2 show the estimated conditional quantile functions corresponding to non-constant covariate values of (1, 0)^⊤, (0, 1)^⊤, and (1, 1)^⊤, three out of the four vertices of $𝕏$; the other vertex takes (0, 0)^⊤ and the conditional quantile function is the intercept. Note that the lack of monotonicity with the original estimator ${\mathbf{x}}^T\widehat{\mathit{\beta }}(·)$ might be more serious when x is farther away from the covariate sample average; see Section 1. Overall, all these different estimated conditional quantile functions had comparable performance at given probability indices. This is expected since they are all first-order asymptotically equivalent. Nevertheless, the adaptive interpolation estimator with ${𝕏}_S=𝕏$ typically had better average maximum absolute error and average root mean integrated squared error, as well as far fewer knots on average. This suggests that the stronger constraint as imposed helps improve finite-sample estimation efficiency.

Table 2.

Estimation of conditional quantile functions

						t = 0.2			t = 0.5			t = 0.8
sample size: 200
Orig					B	7	−23	24	1	−18	10	−4	−20	−7
					SD	472	466	488	364	359	388	333	344	356
					SE	508	496	510	378	374	396	337	347	368
					CI	93.9	94.0	94.9	93.6	94.2	93.9	93.8	93.7	94.7
$\text{AI-}𝕏$	MAE	0.84	0.84	0.84	B	13	−20	41	6	−14	17	9	−7	−11
	RMISE	0.95	0.95	0.95	SD	449	439	462	364	354	385	316	328	344
	BRK		0.10		CI	94.5	95.7	95.6	93.7	94.3	94.1	95.1	94.2	95.1
AI-{x}	MAE	0.91	0.91	0.91	B	−45	−74	−19	2	−18	14	49	33	40
	RMISE	0.98	0.98	0.98	SD	462	452	478	364	356	386	325	338	352
	BRK	0.41	0.41	0.47	CI	94.9	94.9	95.5	93.6	94.4	93.9	93.9	93.7	94.7
RA	MAE	0.91	0.91	0.93	B	10	−14	30	0	−16	12	−4	−19	−9
	RMISE	0.97	0.97	0.98	SD	463	455	480	360	352	385	321	334	352
	BRK	1.00	1.00	1.00	CI	94.5	94.7	95.2	94.0	94.5	94.5	94.7	94.4	94.8
sample size: 400
Orig					B	10	−3	5	4	3	12	−2	−3	−4
					SD	335	323	342	252	250	268	236	240	255
					SE	348	342	359	263	261	279	235	244	256
					CI	94.5	95.1	95.3	95.0	94.4	94.6	92.8	93.7	93.4
$\text{AI-}𝕏$	MAE	0.88	0.88	0.88	B	15	0	14	6	4	13	5	−1	−8
	RMISE	0.97	0.97	0.97	SD	326	314	334	252	250	267	231	237	250
	BRK		0.10		CI	94.9	95.9	95.8	94.9	94.7	94.8	92.8	94.4	94.1
AI-{x}	MAE	0.93	0.94	0.94	B	−14	−31	−17	5	3	12	26	22	21
	RMISE	0.99	0.99	0.99	SD	332	318	342	252	250	267	233	237	254
	BRK	0.40	0.41	0.46	CI	94.9	95.7	95.7	94.9	94.4	94.9	92.3	94.2	93.5
RA	MAE	0.94	0.94	0.95	B	10	−3	6	4	3	12	−2	−4	−4
	RMISE	0.99	0.99	0.99	SD	333	319	340	251	248	268	233	238	253
	BRK	1.00	1.00	1.00	CI	94.7	95.6	95.4	94.9	94.3	94.7	93.3	93.9	93.5

Orig: the original estimator; $\text{AI-}{𝕏}_S$: the adaptive interpolation estimator with ${𝕏}_S$ and τ ≏ 0.5; RA: the rearranged estimator.

MAE: maximum absolute error over [0.1, 0.9]; RMISE: root mean integrated squared error over [0.1, 0.9]; BRK: number of knots or breakpoints. All are average measures, reported as relative to the original estimator. B: Empirical bias (×1000); SD: Empirical standard deviation (×1000); SE: Average standard error (×1000); CI: Empirical coverage (%) of 95% Wald confidence interval.

Three columns as grouped correspond to the estimated conditional quantile functions with non-constant covariate vectors (1, 0)^⊤, (0, 1)^⊤, and (1, 1)^⊤.

To evaluate the sensitivity to covariate dimension, seven additional covariates were incorporated to the previous model. All these non-constant covariates were independent and identically distributed as uniform between 0 and 1, and the seven additional coefficients were set to 0 for model comparability. Table 3 shows the simulation results of the original Koenker–Bassett estimator versus the proposed adaptive interpolation estimator, using empirical $\widehat{𝕏}$ and τ ≏ 0.5, with sample size of 400 and from 1000 replications. In comparison with Table 1, b the most notable change in the performance of the proposed estimator was the reduced average number of knots relative to that of breakpoints of the original estimator; the average numbers of breakpoints for the proposed and original were 8.4 and 831, respectively. This reduction was partly attributable to the stronger monotonicity-respecting constraint associated with the increase of covariate dimension. Other summary statistics remained largely comparable, and the performance of the proposed method was satisfactory.

Table 3.

Regression coefficient estimation under a quantile regression model with ten coefficients

				t = 0.2				t = 0.5				t = 0.8
Orig			B	25	1	−13	−8	8	−9	−15	−8	−18	−13	−8	−11
			SD	620	442	450	448	493	344	347	330	460	307	310	312
			SE	701	466	465	463	536	360	358	357	477	318	321	319
			CI	96.8	96.6	96.2	95.3	96.2	95.0	95.6	96.4	95.2	94.3	94.6	95.6
$\text{AI-}\widehat{𝕏}$	MAE	0.87	B	−27	14	−9	−4	7	−9	−15	−8	4	−22	−21	−6
	RMISE	0.95	SD	593	414	434	431	493	343	347	329	431	287	297	287
	BRK	0.01	CI	97.8	97.1	96.4	95.9	96.2	95.2	95.5	96.3	96.1	96.1	95.9	96.6

Orig: the original estimator; $\text{AI-}\widehat{𝕏}$: the proposed adaptive interpolation estimator with $\widehat{𝕏}$ and τ ≏ 0.5.

MAE: maximum absolute error over [0.1, 0.9]; RMISE: root mean integrated squared error over [0.1, 0.9]; BRK: number of knots or breakpoints. All are average measures, reported as relative to the original estimator. B: Empirical bias (×1000); SD: Empirical standard deviation (×1000); SE: Average standard error (×1000); CI: Empirical coverage (%) of 95% Wald confidence interval.

Under each t value are the first four estimated coefficients; the fourth is representative of the last seven.

3·2 Additive hazards model with simplex covariate space

A curve monotonization method may be used to attain monotonicity-respecting regression when the covariate space has a simplex convex hull with the same number of affinely independent vertices as the coefficient dimension. In this circumstance, the curves of D_x(·) corresponding to those vertices have a one-to-one linear mapping with the regression coefficient β(·). Accordingly, once these estimated curves are monotonized, they uniquely determine a monotonicity-respecting estimator of β(·). This simplex condition is automatically satisfied in a model with an intercept and a single non-constant covariate. We simulated such an additive hazards model and compared so adapted monotonicity-respecting regression methods with our proposal. Note that the simplex condition, of course, is restrictive in general; for example, it is not satisfied by the covariate spaces of the foregoing quantile regression models.

For the additive hazards model, D_x(t) in (1) was the conditional cumulative hazard function and

$$\mathit{\beta }(t)={(0.1t^2,0.5t)}^{\top }.$$

The covariate followed the uniform distribution between 0 and 1. Response Y was subject to right censoring, with the censoring time being uniformly distributed between 0 and 8 and independent of Y and the covariate. The response and censoring time were not directly observed but only through their minimum and the censoring indicator. The censoring rate was approximately 24.5%. The generalized Nelson–Aalen estimator was used as the original. Four methods were investigated to restore monotonicity respecting with respect to the empirical covariate space $\widehat{𝕏}$. The first was the adaptive interpolation method taking ${𝕏}_S=\widehat{𝕏}$, and the others were adapted from three curve monotonization procedures: the adaptive interpolation method taking ${𝕏}_S=\left\{\mathbf{x}\right\}$, i.e., the singleton of a given covariate, the Lin–Ying method, and the rearrangement method. For the adaptive interpolation in both methods, the starting point τ = 0 was a natural choice for this model and it also guaranteed respecting for nonnegative cumulative hazard. The adapted Lin–Ying method ensured this additional property as well, but the adapted rearrangement might not. The martingale-based standard error was adopted for the original estimator, and also used for inference with all the monotonicity-respecting estimators.

Table 4 reports the simulation results with sample size 400 from 1000 replications. On average, the proposed adaptive interpolation estimator with ${𝕏}_S=\widehat{𝕏}$ had the smallest maximum absolute error and root mean integrated squared error, and far fewer knots than breakpoints of other estimators. Its performance was otherwise similar to that of the original, the adaptive interpolation with ${𝕏}_S=\left\{\mathbf{x}\right\}$, and adapted Lin–Ying estimators. The adapted rearrangement estimator, however, performed poorly, with serious bias, larger standard deviation, and confidence interval under-coverage particularly at small t. Apparently, right tail instability in the original estimator had a substantial impact on the rearrangement method; see the discussion in Section 2. This was verified by the improved performance of a limited rearrangement where the original estimator beyond t = 5 was curtailed. As a note, t = 1, 2, 3, 4, 5 correspond to the 29, 58, 79, 91, 97-th percentiles, respectively, of the marginal Y distribution.

Table 4.

Regression coefficient estimation under an additive hazards model

				t = 1		t = 2		t = 3		t = 4
Orig			B	1	−6	3	−13	5	−15	−12	−4
			SD	52	119	104	232	187	444	354	863
			SE	52	116	104	231	186	426	340	824
			CI	93.8	94.2	95.0	94.2	95.4	94.8	94.0	94.9
$\text{AI-}\widehat{𝕏}$	MAE	0.83	B	9	−19	11	−22	15	−20	1	36
	RMISE	0.94	SD	48	112	101	224	179	417	326	772
	BRK	0.31	CI	96.3	94.8	95.0	95.2	96.6	95.5	95.5	96.9
Adapted estimators from curve monotonization
AI-{x}	MAE	0.92	B	10	−10	14	−14	27	−7	44	49
	RMISE	0.99	SD	49	116	102	230	184	438	352	847
	BRK	0.94	CI	96.2	94.7	95.2	94.8	96.5	94.8	95.2	95.5
LY	MAE	0.92	B	9	−12	11	−17	19	−14	18	32
	RMISE	0.97	SD	49	115	101	228	183	434	344	834
	BRK	0.94	CI	96.3	94.8	95.5	94.8	96.3	95.0	94.8	95.9
RA	MAE	5.75	B	−29	−329	−5	−73	−16	−86	−64	−147
	RMISE	4.05	SD	607	4819	109	356	197	479	349	799
	BRK	1.96	CI	95.0	86.9	93.5	89.2	93.3	91.8	92.8	94.9
RA, limited	MAE	0.87	B	2	−7	3	−14	2	−17	−25	−34
	RMISE	0.96	SD	49	116	102	230	183	431	337	776
	BRK	1.93	CI	95.5	94.5	95.4	94.4	95.7	95.4	94.9	96.3

Orig: the original estimator; $\text{AI-}\widehat{𝕏}$: the proposed adaptive interpolation estimator with $\widehat{𝕏}$; AI-{x}: the adaptive interpolation method with $𝕏S$ taking the singleton of a given covariate; LY: the Lin–Ying method; RA: the rearrangement method; RA, limited: the rearrangement limited to interval [0, 5].

MAE: maximum absolute error over [0, 4]; RMISE: root mean integrated squared error over [0, 4]; BRK: number of knots or breakpoints. All are average measures, reported as relative to the original estimator. B: Empirical bias (×1000); SD: Empirical standard deviation (×1000); SE: Average standard error (×1000); CI: Empirical coverage (%) of 95% Wald confidence interval.

Two columns under each t value correspond to the estimated intercept and slope.

3·3 Remark on computation

All these numerical studies and others exhibited high computational efficiency of the proposed adaptive interpolation method, despite that our implementation was seemingly primitive. Particularly in the case that the empirical covariate space $\widehat{𝕏}$ was adopted, each and every observation in a sample was assessed for the purpose of identifying nearest monotonicity-respecting neighbors as in (2) and (3). Nevertheless, the computation time was only a small fraction of that for the original estimator. Taking quantile regression as an example, the adaptive interpolation method took only about 3% of the computation time for point estimation of the Koenker–Bassett estimator over a wide range of sample size and covariate dimension; the efficient algorithm of Huang (2010) was used for the latter. This provided little impetus for an obvious and more sophisticated implementation that takes the vertex set of the empirical $\widehat{𝕏}$ instead in the nearest neighbor identification. The vertex set size could be much smaller than the sample size when the covariate dimension is small, say, 2 or 3. However, the difference reduces fast with a higher covariate dimension. Meanwhile, the cost of computing the vertex set escalates tremendously. Therefore, such an implementation may not always fare well and we have not pursued it further beyond the initial exploration.

4. Illustration with a clinical study

Huang (2010) analyzed the Mayo primary biliary cirrhosis study (Fleming and Harrington 1991, Appendix D) using his censored quantile regression procedure. The data consisted of 416 primary biliary cirrhosis patients, with a median follow-up time of 4.74 years and a censoring rate of 61.5%. The survival time, on the logarithmic scale, was regressed over five covariates: age, edema, log(bilirubin), log(albumin), and log(prothrombin time). We applied our proposal to obtain monotonicity-respecting regression.

With censored quantile regression, choice of the starting point τ is not obvious. Typically, β(t) becomes non-identifiable as t approaches 1 but the identifiability upper bound is unknown. Huang (2013) suggested an estimate that is less than the identifiability bound with probability tending to 1, yet with its limit reasonably close to the bound nevertheless. For this data set, we obtained such an identifiability bound surrogate, 0.828, corresponding to Huang (2013, Equation 12) with κ = 0.05^dim(X); dim(X) is the dimension of covariate vector X including the unity element. Our starting point τ was taken to be the left breakpoint of the original estimator closest to half of the identifiability bound surrogate. The monotonicity respecting was restored with respect to the empirical covariate space $\widehat{𝕏}$.

Figure 2 displays both the original estimate of Huang (2010) and our proposed adaptive interpolation estimate for the regression coefficients. The former is fairly rugged, with 267 breakpoints, a large part of which results presumably from random noise. In contrast, the latter is much more smooth, and has only 9 knots with $min𝕄$ and $max𝕄$ being 0.0397 and 0.856, respectively. Nevertheless, the latter tracks the former quite well, except for the tails as expected. Thus, the monotonicity-respecting estimation might help prevent an over-interpretation of the dynamic effects. Figure 3 shows that estimated conditional quantile functions have their monotonicity restored by the proposed method.

Figure 2.

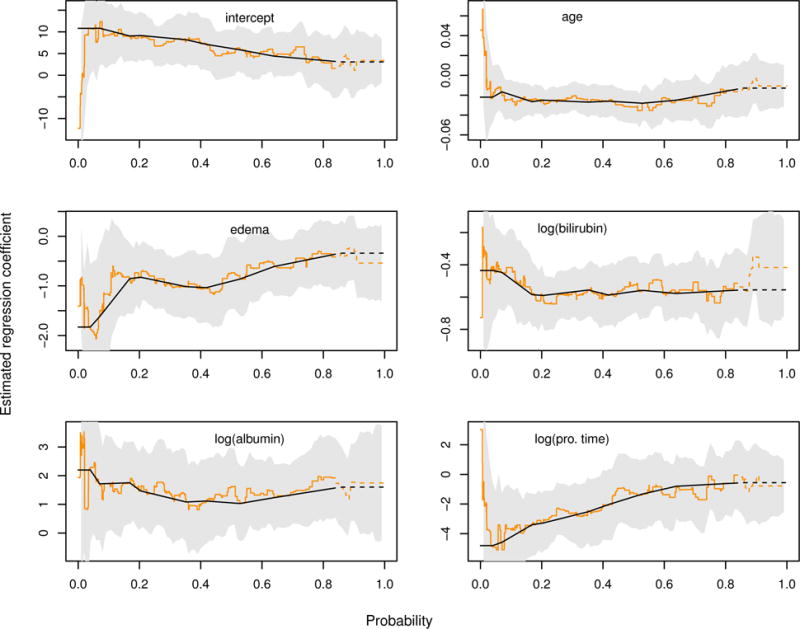
Estimated regression coefficients from the Mayo primary biliary cirrhosis study. The light lines are the original regression coefficient estimate, $\widehat{\mathit{\beta }}(·)$, with their pointwise Wald 95% confidence intervals in shaded areas, from censored quantile regression (Huang 2010). The dark lines correspond to the proposed adaptive interpolation estimate $\stackrel{\sim }{\mathit{\beta }}(·)$. Portions of these estimates beyond the identifiability bound surrogate, 0.828, are denoted with dashed lines.

Figure 3.

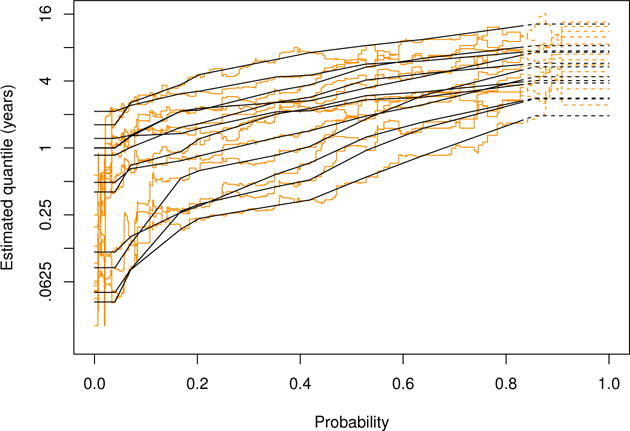
Estimated conditional quantile functions from the Mayo primary biliary cirrhosis study. The original estimates, in light, and those from the adaptive interpolation method, in dark, are shown for 12 covariate values as chosen from the 102 vertices of $\widehat{𝕏}$. Portions of these estimators beyond the identifiability bound surrogate, 0.828, are denoted with dashed lines.

5. Discussion

The proposed method can be applied more generally. Additional pertinent models include those with a mixture of constant and varying effects (e.g., Qian and Peng 2010) and for recurrent events (Fine et al. 2004; Huang and Peng 2009). The proposal may also accommodate time-dependent covariates in, e.g., the additive hazards model, provided that the covariate space across $t\in 𝕋$ remains the same. In fact, it suffices to consider time-independent covariates only in the monotonicity respecting induction, since monotonicity of the estimated D_x(·) corresponding to any time-dependent covariate process then would also be guaranteed.

Alternative definition for the nearest monotonicity-respecting neighbor was explored. A more stringent left neighbor to starting point $\tau \in 𝔻$ is given by

$$max\left[t\in 𝔻:t<\tau ,\underset{\mathbf{x}\in 𝕏,s\in 𝔻:s\le t}{\sup }\{{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(s)-{\mathbf{x}}^{\top }\widehat{\mathit{\beta }}(\tau )\}\le 0\right],$$

and the right counterpart can be accordingly defined. As such, the monotonicity respecting is also required with respect to the current point and every point beyond the neighbor. Fewer knots would thus be involved in the interpolation. Despite that the asymptotic results remain largely the same, finite-sample performance can be inferior since the estimator might become sensitive to tail behavior of the original estimator; see related discussion in Section 2.

As a small price to pay, our monotonicity-respecting estimator is not invariant to a monotonically increasing transformation of the index scale in the dynamic regression model (1). By the same token, the interpolation of our proposal may be generalized since the linear interpolation on a nonlinearly transformed index scale is no longer linear on the original scale. To be slightly more general, the interpolated value given by (4) at t between adjacent points τ_l and τ_r can be extended to

$$\frac{h_{{\tau }_l,{\tau }_r}({\tau }_r)-h_{{\tau }_l,{\tau }_r}(t)}{h_{{\tau }_l,{\tau }_r}({\tau }_r)-h_{{\tau }_l,{\tau }_r}({\tau }_l)}\widehat{\mathit{\beta }}({\tau }_l)+\frac{h_{{\tau }_l,{\tau }_r}(t)-h_{{\tau }_l,{\tau }_r}({\tau }_l)}{h_{{\tau }_l,{\tau }_r}({\tau }_r)-h_{{\tau }_l,{\tau }_r}({\tau }_l)}\widehat{\mathit{\beta }}({\tau }_r),$$

for a given monotonically increasing function $h_{{\tau }_l,{\tau }_r}(·)$ specific to the interval [τ_l, τ_r]. If $h_{{\tau }_l,{\tau }_r}(·)$ is differentiable and its derivative is bounded away from both 0 and ∞ uniformly for all τ_l and τ_r, then the resulting estimator has the same asymptotic equivalence result as $\stackrel{\sim }{\mathit{\beta }}(·)$ given by Theorem 1. This generalization offers the possibility to further subject a monotonicity-respecting estimator to, e.g., certain smoothness, which merits further investigation.

Throughout, we have focused on the linear dynamic regression model (1). Its restoration of monotonicity respecting is distinct from that of a nonparametric dynamic regression model, which imposes little structure on the covariate effects. For the latter, it is a matter of curve monotonization only, for estimated D_x(·) with given x. Dette and Volgushev (2008) and Qu and Yoon (2015), among others, recently developed monotone estimation for nonparametric quantile regression. These methods share similar ideas with Chernozhukov et al. (2009, 2010) and Neocleous and Portnoy (2008) to exploit rearrangement and interpolation for monotonization. Our proposed adaptive interpolation as a curve monotonization procedure might also be applicable, and in-depth analytical and numerical studies are warranted.

Appendix: Proofs of Lemma 1 and Theorem 1

We first establish a result on $\widehat{\mathit{\beta }}(·)$ that will be used repeatedly in the proofs. Write ϕ(·) as the limit of $n^{1/2}\{\widehat{\mathit{\beta }}(·)-\mathit{\beta }(·)\}$, on [a, b]. Denote the first elements of ϕ(·), $\widehat{\mathit{\beta }}(·)$, and β(·) by ϕ⁽¹⁾(·), ${\widehat{\mathit{\beta }}}^{(1)}(·)$, and β⁽¹⁾(·), respectively. Since $n^{1/2}\{{\widehat{\mathit{\beta }}}^{(1)}(·)-{\mathit{\beta }}^{(1)}(·)\}$ converges weakly to the tight Gaussian process ϕ⁽¹⁾(·) by Condition 1, it is implied that, for every ε > 0,

$$\underset{\delta \downarrow 0}{\lim }\underset{n\to \infty }{\lim \sup }{\mathrm{Pr}}^{\ast }\left\{\underset{s,t\in [a,b]:\rho (s,t)<\delta }{\sup }{n}^{1/2}\left|\{{\widehat{\mathit{\beta }}}^{(1)}(s)-{\mathit{\beta }}^{(1)}(s)\}-\{{\widehat{\mathit{\beta }}}^{(1)}(t)-{\mathit{\beta }}^{(1)}(t)\}\right|>\epsilon \right\}=0$$

where Pr* denotes outer probability and ρ(s, t) = [var{ϕ⁽¹⁾(s) − ϕ⁽¹⁾(t)}]^1/2 (Kosorok 2008, Theorem 2.1). Meanwhile, the covariance function of ϕ⁽¹⁾(·) is continuous by Condition 1, and hence uniformly continuous by the Heine–Cantor theorem. Therefore, for any δ > 0, there exists η > 0 such that |s − t| < η implies ρ(s, t) < δ for all s, t ∈ [a, b]. Consequently, ρ(s, t) in the above equation can be replaced with |s − t|. Furthermore, the same result applies to each and every other element of $\widehat{\mathit{\beta }}(·)-\mathit{\beta }(·)$. Thus, for every ε > 0,

$$\underset{\delta \downarrow 0}{\lim }\underset{n\to \infty }{\lim \sup }{\mathrm{Pr}}^{\ast }\left\{\underset{s,t\in [a,b]:|s-t|<\delta }{\sup }{n}^{1/2}{\Vert \{\widehat{\mathit{\beta }}(s)-\mathit{\beta }(s)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}\Vert }_2>\epsilon \right\}=0.$$ (A.1)

In words, $n^{1/2}\{\widehat{\mathit{\beta }}(·)-\mathit{\beta }(·)\}$ is asymptotically uniformly equicontinuous in probability.

Proof of Lemma 1

Write $c={\inf }_{\mathbf{x}\in {𝕏}_S,t\in [a,b]}{\mathbf{x}}^{\top }{\mathit{\beta }}^{\prime }(t)$, where c > 0 by Condition 3. Then, for any $\mathbf{x}\in {𝕏}_S$ and 1 < j ≤ J,

$$c({\nu }_j-{\nu }_{j-1})\le {\mathbf{x}}^{\top }\{\mathit{\beta }({\nu }_j)-\mathit{\beta }({\nu }_{j-1})\}\le \Vert \mathbf{x}{\Vert }_2\Vert \mathit{\beta }({\nu }_j)-\mathit{\beta }({\nu }_{j-1}){\Vert }_2=O(\Vert \mathit{\beta }({\nu }_j)-\mathit{\beta }({\nu }_{j-1}){\Vert }_2)$$

by Cauchy–Schwarz inequality and Condition 2. Meanwhile,

$$\underset{1<j\le J}{max}\Vert \mathit{\beta }({\nu }_j)-\mathit{\beta }({\nu }_{j-1}){\Vert }_2=\underset{1<j\le J}{max}\underset{s,t\in [{\nu }_{j-1},{\nu }_j)}{\sup }{\Vert \{\widehat{\mathit{\beta }}(s)-\mathit{\beta }(s)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}\Vert }_2\le 2\underset{t\in [a,b]}{\sup }\Vert \widehat{\mathit{\beta }}(t)-\mathit{\beta }(t){\Vert }_2=O_p(n^{-1/2})$$ (A.2)

by Condition 1. Therefore,

$$\underset{1<j\le J}{max}({\nu }_j-{\nu }_{j-1})=O_p(n^{-1/2}).$$

In light of (A.1), the above result implies that the right-hand side of (A.2) is actually o_p(n^−1/2). Accordingly, the refinement (5) is obtained.

For any $\mathbf{x}\in {𝕏}_S$ and any s, t ∈ [a, b] such that t − s = n^−1/2,

$${\mathbf{x}}^{\top }\{\widehat{\mathit{\beta }}(t)-\widehat{\mathit{\beta }}(s)\}={\mathbf{x}}^{\top }\{\mathit{\beta }(t)-\mathit{\beta }(s)\}+{\mathbf{x}}^{\top }[\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}-\{\widehat{\mathit{\beta }}(s)-\mathit{\beta }(s)\}]\ge c{n}^{-1/2}-\Vert x{\Vert }_2\Vert \{\widehat{\mathit{\beta }}(s)-\mathit{\beta }(s)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}{\Vert }_2.$$

From (A.1),

$$\underset{s,t\in [a,b]:t-s=n^{-1/2}}{\sup }{\Vert \{\widehat{\mathit{\beta }}(s)-\mathit{\beta }(s)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}\Vert }_2=o_p(n^{-1/2}).$$

Therefore, with probability tending to 1,

$$\underset{\mathbf{x}\in {𝕏}_S,s,t\in [a,b]:t-s=n^{-1/2}}{min}{\mathbf{x}}^{\top }\{\widehat{\mathit{\beta }}(t)-\widehat{\mathit{\beta }}(s)\}>0$$

and subsequently

$$\underset{1<k\le K}{max}({\tau }_k-{\tau }_{k-1})\le n^{-1/2}+\underset{1<j\le J}{max}({\nu }_j-{\nu }_{j-1})$$

under Condition 4. Thus, equation (6) is obtained.

Proof of Theorem 1

By definition (4), for t ∈ [τ_l, τ_r],

$$\stackrel{\sim }{\mathit{\beta }}(t)-\widehat{\mathit{\beta }}(t)=\frac{{\tau }_r-t}{{\tau }_r-{\tau }_l}[\{\widehat{\mathit{\beta }}({\tau }_l)-\mathit{\beta }({\tau }_l)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}]+\frac{t-{\tau }_l}{{\tau }_r-{\tau }_l}[\{\widehat{\mathit{\beta }}({\tau }_r)-\mathit{\beta }({\tau }_r)\}-\{\widehat{\mathit{\beta }}(t)-\mathit{\beta }(t)\}]+\frac{{\tau }_r-t}{{\tau }_r-{\tau }_l}\mathit{\beta }({\tau }_l)+\frac{t-{\tau }_l}{{\tau }_r-{\tau }_l}\mathit{\beta }({\tau }_r)-\mathit{\beta }(t).$$

Lemma 1 implies that, with probability tending to 1, each and every point in [a + ι, b − ι] is within two adjacent points in $𝕄\cap [a,b]$. Given bound (6) on the gap, result (A.1) implies that the supremum over t ∈ [a + ι, b − ι] of the first line on the right-hand side above is o_p(n^−1/2). Moreover, by Taylor expansion, the second line above is o(τ_r − τ_l). Combining them yields (7).

If the starting point τ is equal to a or b, each and every point in [a, b − ι] or [a + ι, b], respectively, then lies within adjacent points in $𝕄\cap [a,b]$ with probability tending to 1. Thus, the asymptotic equivalence of $\stackrel{\sim }{\mathit{\beta }}(·)$ and $\widehat{\mathit{\beta }}(·)$ holds on the extended interval.