A Recipe for inferference: Start with Causal Inference. Add Interference. Mix Well with R

Abstract

In causal inference, interference occurs when the treatment of one subject affects the outcome of other subjects. Interference can distort research conclusions about causal effects when not accounted for properly. In the absence of interference, inverse probability weighted (IPW) estimators are commonly used to estimate causal effects from observational data. Recently, IPW estimators have been extended to handle interference. Tchetgen Tchetgen and VanderWeele (2012) proposed IPW methods to estimate direct and indirect (or spillover) effects that allow for interference between individuals within groups. In this paper, we present inferference, an R package that computes these IPW causal effect estimates when interference may be present within groups. We illustrate use of the package with examples from political science and infectious disease.

1. Introduction

Interference occurs when the treatment (or exposure) of one subject affects the outcome of other subjects (Cox 1958). Without accounting for interference, measuring only a treatment’s direct effect may be misleading. For example, a vaccine’s direct effect on an individual in a group with a large proportion of vaccinated individuals can be small. However, the protective, indirect effect from other group members’ vaccinations may be large. In this case the vaccine may be judged to be ineffective based on the direct effect despite possibly having great public health utility due to the indirect effect (Clemens et al. 2011). Other areas where interference may be present include criminology (e.g., Sampson 2010; Verbitsky-Savitz and Raudenbush 2012), developmental psychology (e.g., Duncan et al. 2005; Foster 2010), econometrics (e.g., Sobel 2006; Manski 2013), education (e.g., Hong and Raudenbush 2006; VanderWeele et al. 2013), imaging (e.g., Luo et al. 2012), political science (e.g., Sinclair et al. 2012; Bowers et al. 2013), social media and network analysis (e.g., VanderWeele and An 2013; Toulis and Kao 2013; Eckles et al. 2014; Kramer et al. 2014), sociology (e.g., Aronow and Samii 2013), and spatial analyses (e.g., Zigler et al. 2012; Graham et al. 2013).

Inverse probability weighted (IPW) methods are often used to estimate causal effects when interference is absent (Rosenbaum 1987; Robins et al. 2000; Lunceford and Davidian 2004; Cole and Hernan 2008). Recent developments have extended IPW estimators to estimate causal effects when interference may be present in either randomized or observational studies. Tchetgen Tchetgen and VanderWeele (2012) proposed estimators for observational studies assuming partial interference (Sobel 2006), i.e., individuals can be partitioned into groups where there may be interference between individuals in the same group but not between individuals in different groups. Partial interference could be reasonable, for example, in study of bovine disease where physical separation of herds precludes pathogen transmission between herds. On the other hand, if birds or farm workers could spread the pathogen between herds, then partial interference may be questionable. The Tchetgen Tchetgen and VanderWeele (2012) IPW estimators require a model for the group-level propensity score (i.e., the probability of a group’s observed treatment allocation). The large sample properties of these estimators were derived by Perez-Heydrich et al. (2014).

To date, software for analysis of causal effects in the presence of interference is limited. Without interference, the R (R Core Team 2014) package ipw provides tools to compute IPW estimators (van der Wal and Geskus 2011). Existing interference-related R packages, including interferenceCI (Rigdon 2015) and blockTools (Moore 2015), were designed for analysis of randomized experiments. In this paper, we present the R package inferference which computes the Tchetgen Tchetgen and VanderWeele (2012) IPW estimators and the large sample variance estimators developed by Perez-Heydrich et al. (2014).

The outline for the remainder of this paper is as follows. The next section provides background on interference and an overview of the mathematical concepts and notation. Section 3 describes the package’s main features. Sections 4 and 5 demonstrate the software with examples from public health and political science. The example in Section 5 shows advanced features of the package. We discuss computational issues with IPW estimators when groups have large numbers of individuals in Section 6. We conclude with a brief discussion and future directions in Section 7.

2. Preliminaries

2.1. A brief history of interference

Much of causal inference assumes that the exposure of one individual does not affect the outcomes of other individuals, i.e., there is no interference between individuals. Rubin (1980) bundled no interference with the assumption that treatments for all units are comparable (no hidden forms of treatment) into the “Stable Unit Treatment Value Assumption” (SUTVA). Despite sporadic efforts, the research community gave little attention to this assumption until the early 2000s. One approach to relaxing the no interference assumption is to assume partial interference. Under this assumption, space, time, and/or social network groupings preclude interference between individuals in different groups, but interference may occur within a group.

Sobel (2006), Hudgens and Halloran (2008), and Tchetgen Tchetgen and VanderWeele (2012) developed methods based on the assumption of partial interference to estimate causal effects in the presence of interference. When an experimenter randomizes units – by design – at the group and individual levels, Hudgens and Halloran (2008) defined estimators that, under certain assumptions, are unbiased for a treatment’s direct and indirect (or spillover) effects.

Observational studies complicate estimation of interference effects. Tchetgen Tchetgen and VanderWeele (2012) proposed IPW estimators of causal effects based on group-level propensity scores for non-randomized treatment allocation. They showed these estimators to be unbiased when the propensity score is known. Perez-Heydrich et al. (2014) derived the large sample properties of these estimators when the propensity scores are unknown but correctly modeled. They applied these results to draw inference about the direct and indirect effects of cholera vaccination in Matlab, Bangladesh.

2.2. Basic partial interference setup

Consider N individuals partitioned into m groups, each with n_i individuals for i = 1, …, m. The triplet (Y_ij, A_ij, X_ij) represents the observed outcome, treatment, and baseline covariate vector, respectively, for individual j in group i. We let capitalized letters denote random variables, and lowercase letters (e.g., (y_ij, a_ij, x_ij)) denote observed or realized values. Let X_i and A_i be the matrix of baseline covariates and vector of treatment allocations for members of group i. Let A_i,−j = (A_i1, …, A_ij−1, A_ij+1, …, A_ini) represent a group’s treatment allocation excluding the jth subject. Let Y_ij(a_ij, a_i,−j) = Y_ij(a_i) be the potential outcome for individual j in group i if, possibly contrary to fact, group i received a_i. By causal consistency, Y_ij = Y_ij(A_i) (Pearl 2010). Let Y_i be the vector of potential outcomes for group i. By assuming no interference between groups, an individual’s potential outcome may depend only on the treatment allocation of its group. The set 𝒜(n_i) contains all of group i’s possible treatment vectors. With a binary treatment, A_ij ∈ {a₁, a₂}, this set has 2^n_i elements.

Estimands

Without interference, researchers often estimate an average treatment effect, which contrasts the average outcome for two treatment allocations: the entire population treated versus the entire population untreated. With interference, causal estimands may be defined in terms of the continuum of treatment allocation strategies between those extremes. In inferference, we consider Bernoulli-type allocation strategies proposed by Tchetgen Tchetgen and VanderWeele (2012), where individuals independently receive treatment with probability α. For this allocation strategy, the probability of a group’s treatment vector is denoted as ${\pi }_i({\mathbf{A}}_i;\alpha )={\prod }_{j=1}^{n_i}{\alpha }^{A_{ij}}{(1-\alpha )}^{1-A_{ij}}$ and, excluding the jth subject, ${\pi }_i({\mathbf{A}}_{i,-j};\alpha )={\prod }_{k=1,k\ne j}^{n_i}{\alpha }^{A_{ik}}{(1-\alpha )}^{1-A_{ik}}$. The analyst may compute the estimators described below over a range of α’s to explore hypothetical underlying treatment allocations. In their analysis of a cholera vaccine study, Perez-Heydrich et al. (2014) examined strategies between α = 0.3 and α = 0.6 because 75% of the groups had observed vaccine coverages in that range.

Define an individual’s average potential outcome when assigned treatment a under strategy α by

$${Ȳ}_{ij}(a;\alpha )=\sum _{{\mathbf{a}}_{i,-j}\in 𝒜(n_i-1)}{Y}_{ij}(a,{\mathbf{a}}_{i,-j}){\pi }_i({\mathbf{a}}_{i,-j};\alpha ).$$

In words, Ȳ_ij(a; α) is a weighted average of individual j’s potential outcomes under possible treatment vectors of the other n_i − 1 subjects in group i weighted by the probability of each treatment vector. Similarly, define the marginal individual average potential outcome by

$${Ȳ}_{ij}(\alpha )=\sum _{{\mathbf{a}}_i\in 𝒜(n_i)}{Y}_{ij}({\mathbf{a}}_i){\pi }_i({\mathbf{a}}_i;\alpha ).$$

Here, the weighted average of individual j’s potential outcomes is across all group treatment vectors in 𝒜(n_i).

A simple mean of individual average potential outcomes within a cluster defines group average potential outcomes. Then group-level estimands are averaged to make population-level estimands. For example, $Ȳ(a;\alpha )={\sum }_{i=1}^m\{{\sum }_{j=1}^{n_i}{Ȳ}_{ij}(a;\alpha )/n_i\}/m$ is the population-level average outcome when individuals receive treatment a and their group adopts allocation strategy α. Likewise, $Ȳ(\alpha )={\sum }_{i=1}^m\{{\sum }_{j=1}^{n_i}{Ȳ}_{ij}(\alpha )/n_i\}/m$ is the population-level average outcome when groups adopt allocation strategy α.

Contrasts of the population average potential outcomes define causal effects. Hudgens and Halloran (2008) describe four causal effects: direct, indirect, total, and overall (see also Tchetgen Tchetgen and VanderWeele 2012). The direct (or unit-level treatment) effect compares average potential outcomes within a single allocation strategy:

$$\overline{DE}(\alpha )=Ȳ(a_1;\alpha )-Ȳ(a_2;\alpha ).$$

An indirect effect compares a treatment’s average potential outcomes under different allocation strategies:

$$\overline{IE}(\alpha ,\alpha \prime )=Ȳ(a_1;\alpha )-Ȳ(a_1;\alpha \prime ).$$

For a binary treatment, there are two indirect effects for a fixed (α, α′) pair: one for a₁ and one for a₂. If interference is not present, then the indirect effect equals zero. The total effect accounts for both the direct and indirect effects:

$$\overline{TE}(\alpha ,\alpha \prime )=Ȳ(a_1;\alpha )-Ȳ(a_2;\alpha \prime ).$$

The overall effect contrasts the marginal average potential outcomes for two allocation strategies:

$$\overline{OE}(\alpha ,\alpha \prime )=Ȳ(\alpha )-Ȳ(\alpha \prime ).$$

See Hudgens and Halloran (2008) and Tchetgen Tchetgen and VanderWeele (2012) for further discussion of these causal estimands.

2.3. IPW estimation

Tchetgen Tchetgen and VanderWeele (2012) proposed IPW estimators of the causal estimands defined above assuming partial interference. Their estimator weights an individual’s outcome by the inverse of the group-level propensity score, Pr(A_i|X_i), the probability of a group’s treatment allocation given the covariates of the group’s individuals. Tchetgen Tchetgen and VanderWeele (2012) showed the IPW estimators to be unbiased when the group-level propensities are known, under the following assumptions:

1. Conditional independence: Pr(A_i = a_i|X_i, Y_i) = Pr(A_i = a_i|X_i)

2. Positivity: Pr(A_i = a_i|X_i) > 0 ∀a_i ∈ 𝒜(n_i)

The true propensity scores are not generally known in observational studies and must be estimated. Tchetgen Tchetgen and VanderWeele (2012) suggested estimating Pr(A_i|X_i) using a generalized mixed effects model. We denote these models as f_Ai|Xi(A_i|X_i; θ_x, θ_s), where θ_x represents fixed effects parameters and θ_s a group random effect parameter. Model parameters may be estimated by maximum likelihood methods, which we denote θ̂ = (θ̂_x, θ̂_s). For a binary treatment, a model for the group’s propensity score might be:

$$f_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;{\mathit{\theta }}_x,{\theta }_s)=\int \prod _{j=1}^{n_i}{h}_{ij}{(b_i;{\mathit{\theta }}_x)}^{A_{ij}}{\{1-h_{ij}(b_i;{\mathit{\theta }}_x)\}}^{1-A_{ij}}{f}_b(b_i;{\theta }_s)d{b}_i$$ (1)

where h_ij(b_i; θ_x) = Pr(A_ij = 1|X_ij, b_i, θ_x) = logit⁻¹(X_ijθ_x + b_i) and f_b(·; θ_s) is the density of a Normal random variable with mean 0 and variance θ_s. This is the default group-level propensity score model in inferference; the examples below show how the user can modify the default group propensity score model. Validity of inferences drawn using the methods described below requires correct specification of the group propensity score model. Therefore, it is important in practice to conduct diagnostics to assess the fit of the model employed. For example, if (1) is assumed, then the Tchetgen Tchetgen and Coull (2006) diagnostic test can be used to assess whether the random effects are Normally distributed.

The IPW estimator for the group-level average potential outcomes is a straightforward weighted sum,

$${Ŷ}_i^{ipw}(a,\alpha )=\frac{{\sum }_{j=1}^{n_i}{\pi }_i({\mathbf{A}}_{i,-j};\alpha )I(A_{ij}=a)Y_{ij}}{n_i{f}_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;\hat{\mathit{\theta }})},$$ (2)

as is the estimator for group-level marginal potential outcomes,

$${Ŷ}_i^{ipw}(\alpha )=\frac{{\sum }_{j=1}^{n_i}{\pi }_i({\mathbf{A}}_i;\alpha )Y_{ij}}{n_i{f}_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;\hat{\mathit{\theta }})}.$$ (3)

From (2) and (3), one constructs population-level average potential outcome and marginal population-level average potential outcome estimators by ${Ŷ}^{ipw}(a;\alpha )={\sum }_{i=1}^m{Ŷ}_i^{ipw}(a;\alpha )/m$ and ${Ŷ}^{ipw}(\alpha )={\sum }_{i=1}^m{Ŷ}_i^{ipw}(\alpha )/m$. Estimators for direct, indirect, total, and overall effects simply contrast population-level estimators,

$$\widehat{DE}(\alpha )={Ŷ}^{ipw}(a_1;\alpha )-{Ŷ}^{ipw}(a_2;\alpha )$$

$$\widehat{IE}(\alpha ,\alpha \prime )={Ŷ}^{ipw}(a_1;\alpha )-{Ŷ}^{ipw}(a_1;\alpha \prime )$$

$$\widehat{TE}(\alpha ,\alpha \prime )={Ŷ}^{ipw}(a_1;\alpha )-{Ŷ}^{ipw}(a_2;\alpha \prime )$$

$$\widehat{OE}(\alpha ,\alpha \prime )={Ŷ}^{ipw}(\alpha )-{Ŷ}^{ipw}(\alpha \prime ).$$

IPW variance estimation

Perez-Heydrich et al. (2014) derived asymptotic distributions of the IPW estimators using standard estimating equation theory. Briefly, the IPW estimators above are consistent and asymptotically Normal as the number of groups m tends to infinity. When the group-level propensity scores are known (as in the case of simulation or randomized studies), a large sample estimator of the variance of $\widehat{DE}(\alpha )$ is

$$\frac{1}{m^2}\sum _{i=1}^m{\{{\widehat{DE}}_i(\alpha )-\widehat{DE}(\alpha )\}}^2.$$

Results for $\widehat{IE},\widehat{TE}$, and $\widehat{OE}$ are analogous. As explained below, when variance_estimation = ‘naive’ in the interference function, this formula is used to compute standard errors and Wald-type confidence intervals.

When the propensity scores are unknown and instead estimated using a parametric model, computing variance estimators is more complicated and involves derivatives of the group propensity with respect to each parameter and derivatives of the propensity model’s log likelihood. The supplementary materials in Perez-Heydrich et al. (2014) contain the mathematical details, and this method is available with the variance_estimation = ‘robust’ option. The robust option computes consistent variance estimates which account for the estimation of the weights, whereas the naive option computes variance estimates described in the preceding paragraph which ignore estimation of the weights and are conservative (i.e., tend to be too large).

3. Using inferference

3.1. User’s guide

To start, install the package from CRAN using install.packages(‘inferference’). The list below details the arguments for interference, the primary function in inferference. Special attention should be given to the propensity_integrand and formula arguments.

• formula: formula used to define the causal model. formula has a minimum of 4 parts, separated by | and ~ in a specific structure: outcome | exposure ~ covariates | group. The order matters, and the pipes (|) split the data frame into corresponding pieces (Zeileis and Croissant 2010). The exposure ~ covariates piece is passed as a single formula to the chosen model_method (defined below) used to estimate or fix propensity parameters.

  • –
    The following includes a random effect for the group: outcome | exposure ~ covariates + (1|group) | group. In this instance, the group variable appears twice.
  • –
    If the study design includes a ‘participation’ variable (as in both examples below), this is easily added to the formula: outcome | exposure | participation ~ covariates | group.
• propensity_integrand: a function, which may be created by the user, used to compute the IP weights. This defaults to the function logit_integrand(), which calculates the product of inverse logits for individuals in a group: ${\prod }_{j=1}^{n_i}{\{r{h}_{ij}(b_i)\}}^{A_{ij}}{\{1-r{h}_{ij}(b_i)\}}^{1-A_{ij}}{f}_b(b_i;{\theta }_s)$, where h_ij(b_i) = logit⁻¹(X_ijθ_x + b_i), b_i is a group-level random effect, f_b is a N(0, θ_s) density, and r is a known constant. In an observational study typically r = 1. The examples below include individual randomized experiments in which case r denotes the randomization probability among trial participants. logit_integrand() is the integrand of (1) where h_ij(b_i) is scaled by a constant r term. If no random effect is included in the formula, logit_integrand() ignores the random effect. IP weights are computed by numerically integrating propensity_integrand over the random effect distribution using stats::integrate() to which arguments may be passed via … (see below). The default logit_integrand() also takes the following argument that can be passed via the … argument in interference():

  • –
    randomization: a scalar. This is the r in the formula just above. It defaults to 1 in the case that a participation vector is not included. The vaccine study example in Section 4 demonstrates use of this argument.

• loglihood_integrand: a function, which may be created by the user, that defines the log likelihood of the propensity score model. This should generally be the same function as propensity_integrand, which is the default.

• allocations: a vector of values in [0, 1]. These are the α’s defined in Section 2.2. Increasing the number of elements of the allocation vector increases computation time; however, a larger number of allocations will make plotted effect estimates smoother. A minimum of two allocations is required.

• data: the analysis data frame. This must include all the variables defined in the formula.

• model_method: the method used to estimate or set the propensity model parameters. Must be one of ‘glm’, ‘glmer’, or ‘oracle’. For a fixed effects only model use ‘glm’, or to include random effects use lme4’s ‘glmer’ (Bates et al. 2014). logit_integrand only supports a single random effect for the grouping variable, corresponding to b_i. When the propensity parameters are known (as in simulations) or if estimating parameters for the propensity model outside of interference, use the ‘oracle’ option. See model_options for details on how to pass the oracle parameters. Defaults to ‘glmer’.

• model_options: a list of options passed to the function in model_method. Defaults to list(family = binomial(link = ‘logit’)). When model_method = ‘oracle’, the list must have two elements, fixed.effects and random.effects. If the model does not include random effects, set random.effects = NULL.

• causal_estimation_method: currently only supports and defaults to ‘ipw’.

• causal_estmation_options: a list with a single item variance_estimation, which is either ‘naive’ or ‘robust’. See Section 2.3 for details. Defaults to ‘robust’.

• conf.level: level for confidence intervals. Defaults to 0.95.

• rescale.factor: a scalar multiplication factor by which to rescale outcomes and effects. Defaults to 1.

• integrate_allocation: indicator of whether the integrand function uses the allocation parameter. Defaults to TRUE.

• …: used to pass additional arguments to internal functions such as numDeriv::grad() or stats::integrate(). Arguments can also be passed to the propensity_integrand and loglihood_integrand functions.

3.2. The interference object

An interference() call results in an S3 object of class interference which contains:

• estimates: a data frame of causal effect estimates;

• models$propensity_model: the glm or glmer object;

• summary: a list of objects summarizing the causal model such as the number of groups, number of allocations, and the formula used in the interference call;

• weights: (# of groups) × (# of allocations) matrix of group-level weights:

  $$w_{i,k}=\frac{{\pi }_i({\mathbf{A}}_i;{\alpha }_k)}{f_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;\hat{\mathit{\theta }})}.$$

If variance_estimation = ‘robust’, then the object also includes:

• weightd: (# of groups) × (# of allocations) × (# of parameters) array of weights computed using derivatives of the propensity function with respect to each parameter;

• scores: (# of groups) × (# of parameters) matrix of derivatives of the log likelihood.

3.3. Utility functions

The package includes tools to extract effect estimates of interest from the S3 object. The functions direct_effect, indirect_effect (or ie), total_effect (or te), and overall_effect (or oe) select appropriate records from the estimates data frame in the interference object. Section 4 shows an example.

4. Example: vaccine study

This section illustrates the use of inferference with an example drawn from vaccine research. The package includes a single dataset based on the same set of parameters used in the simulation study by Perez-Heydrich et al. (2014). The vaccinesim dataset consists of 3000 units in 250 groups and contains two covariates (X1 = age in decades and X2 = distance to river), a vaccination indicator (A), a participation indicator (B), a binary outcome (Y) indicating cholera infection (1 yes, 0 no), and the unit’s group.

R> library("inferference")
R> head(vaccinesim)

  Y        X1       X2 A B group
1 1 5.3607405 1.715527 0 0     1
2 0 0.1964597 1.730802 0 1     1
3 0 0.4846243 1.769546 1 1     1
4 0 0.8012977 1.715527 0 1     1
5 0 2.1426629 1.772158 1 1     1
6 0 1.2861017 1.715527 0 1     1

>

Like the original study (Ali et al. 2005) that inspired the simulation, individuals were randomized to vaccine with a known probability of 2/3, but subjects could opt to not participate in the trial. In essence, there are both experimental and observational aspects to the data. The interference function handles this design when logit_integrand’s randomization argument is used and a participation variable is included in the formula.

R> example1 <- interference(
+     formula = Y | A | B ~ X1 + X2 + (1|group) | group,
+     allocations = c(.3, .45,  .6),
+     data = vaccinesim,
+     randomization = 2/3,
+     method = 'simple')

>

The only arguments required for interference to run are formula, allocations, and data. When using the ‘robust’ method (the default) to compute the variance, the internal workings call numDeriv::grad (Gilbert and Varadhan 2012) and stats::integrate frequently. The option method = ‘simple’ greatly speeds up the numDeriv::grad function. For more accurate derivatives, leave out this option. See ?numDeriv::grad for more options.

The print.interference function provides an overview of the causal effect estimates, estimated standard errors, and Wald-type confidence intervals. In the output, alpha1 and alpha2 refer to α and α′, while trt1 and trt2 refer to a₁ and a₂, respectively.

R> print(example1)


 --------------------------------------------------------------------------
                               Model Summary
 --------------------------------------------------------------------------
 Formula: Y | A | B ~ X1 + X2 + (1 | group) | group
 Number of groups:  250
 3 allocations were used from 0.3 (min) to 0.6 (max)
 --------------------------------------------------------------------------
                          Causal Effect Summary
                         Confidence level: 0.95
                         Variance method: robust
 --------------------------------------------------------------------------


 Direct Effects
 alpha1 trt1 alpha2 trt2 estimate std.error conf.low conf.high
   0.30    0   0.30    1   0.1605   0.02474  0.11202    0.2090
   0.60    0   0.60    1   0.1086   0.01857  0.07219    0.1450
   0.45    0   0.45    1   0.1339   0.01778  0.09904    0.1687


 Indirect Effects
 alpha1 trt1 alpha2 trt2 estimate std.error conf.low conf.high
   0.30    0   0.60    0  0.15907   0.02617  0.10777    0.2104
   0.30    0   0.45    0  0.08657   0.01732  0.05263    0.1205
   0.45    0   0.60    0  0.07250   0.01408  0.04490    0.1001


 Total Effects
 alpha1 trt1 alpha2 trt2 estimate std.error conf.low conf.high
   0.30    0   0.60    1   0.2677   0.02435   0.2199    0.3154
   0.30    0   0.45    1   0.2205   0.02469   0.1721    0.2688
   0.45    0   0.60    1   0.1811   0.01841   0.1450    0.2172


 Overall Effects
 alpha1 trt1 alpha2 trt2 estimate std.error conf.low conf.high
   0.30   NA   0.60   NA  0.17607  0.019247  0.13835    0.2138
   0.30   NA   0.45   NA  0.09867  0.014207  0.07083    0.1265
   0.45   NA   0.60   NA  0.07740  0.008981  0.05980    0.0950

 --------------------------------------------------------------------------

>

The utility functions return selected effect estimates.

R> direct_effect(example1, .3)

  alpha1 trt1 alpha2 trt2  estimate  std.error  conf.low conf.high
1    0.3    0    0.3    1 0.1605036 0.02473782 0.1120184 0.2089888

R> ie(example1, .3)

  alpha1 trt1 alpha2 trt2   estimate  std.error   conf.low conf.high
1    0.3    0   0.30    0 0.00000000 0.00000000 0.00000000 0.0000000
2    0.3    0   0.45    0 0.08656992 0.01731878 0.05262574 0.1205141
3    0.3    0   0.60    0 0.15906887 0.02617398 0.10776882 0.2103689

>

4.1. Plotting effect estimates

Plots of effect estimates over a range of α levels may be helpful in summarizing results. Perez-Heydrich et al. (2014) present several such graphical displays. Here we demonstrate how to generate similar plots of effect estimates using inferference.

First, we estimate the effects over a dense sequence of allocations so that lines will be smooth.

R> example2 <- interference( formula = Y | A | B ~ X1 + X2 + (1|group) | group,
+     allocations = seq(.2, .8, by = .01),
+     data = vaccinesim, randomization = 2/3, method = 'simple')

>

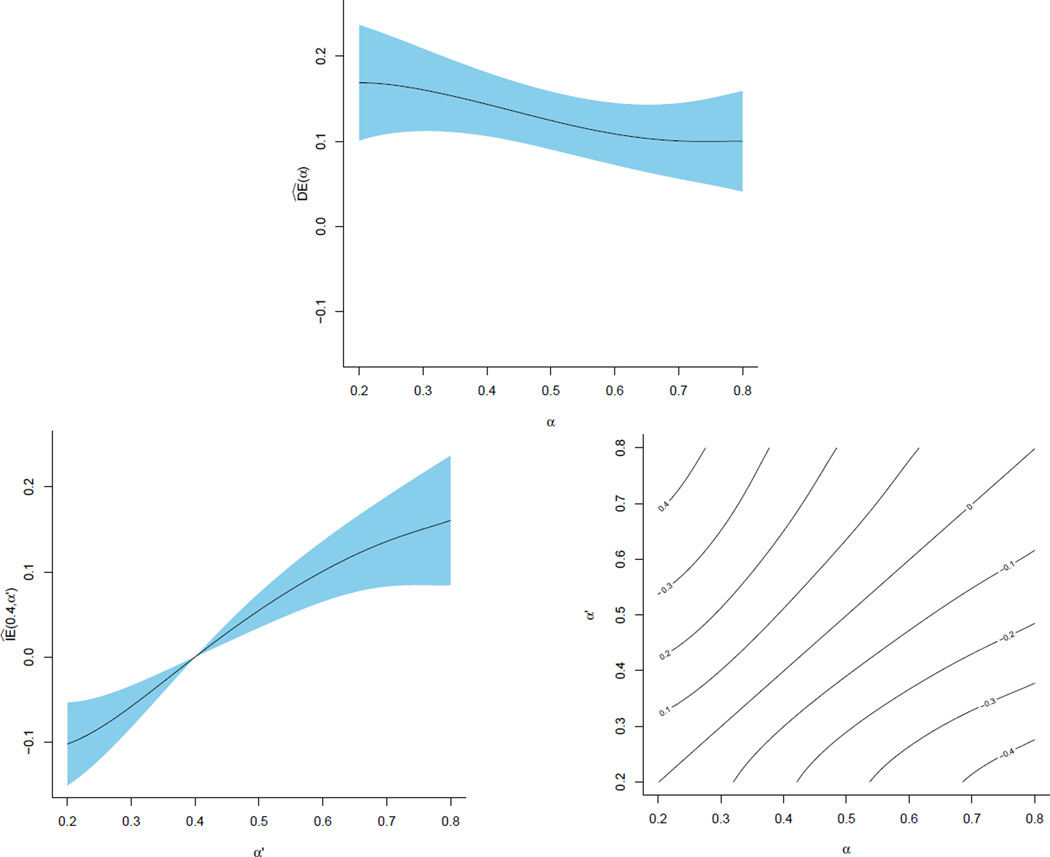
In Figure 1, we present the direct and indirect effect estimates over this range of allocations. For direct effects, a simple scatterplot showing the point-wise confidence intervals suffices. One approach with indirect effects fixes α and plots estimates over a range of α′, whereas a contour plot displays all pairwise (α, α′) comparisons over a range of allocation strategies.

R> deff <- direct_effect(example2)
R> x <- deff$alpha1
R> y <- as.numeric(deff$estimate)
R> u <- as.numeric(deff$conf.high)
R> l <- as.numeric(deff$conf.low)
R> plot(c(min(x), max(x)), c(−.15, .25), type = 'n', bty = 'l',
+      xlab = expression(alpha), ylab = " )
R> title(ylab = expression(widehat(DE) * "(" * alpha  * ")"),
+       line = 2)
R> polygon(c(x, rev(x)), c(u, rev(l)), col = 'skyblue', border = NA)
R> lines(x, y, cex = 2)

R> ieff.4 <- ie(example2, allocation1 = .4)
R> x <- ieff.4$alpha2
R> y <- as.numeric(ieff.4$estimate)
R> u <- as.numeric(ieff.4$conf.high)
R> l <- as.numeric(ieff.4$conf.low)
R> plot(c(min(x), max(x)),c(−.15, .25), type = 'n', bty = 'l',
+      xlab = expression(alpha * "'"), ylab = ")
R> title(ylab = expression(widehat(IE) * "(" * 0.4 * "," * alpha * "'" * ")"),
+       line = 2)
R> polygon(c(x, rev(x)), c(u, rev(l)), col = 'skyblue', border = NA)
R> lines(x, y, cex = 2)

R> ieff <- subset(example2[["estimates"]], effect == 'indirect')
R> x <- sort(unique(ieff$alpha1))
R> y <- sort(unique(ieff$alpha2))
R> z <- xtabs(estimate ~ alpha1 + alpha2, data= ieff)
R> contour(x, y, z, xlab = expression(alpha),
+         ylab = expression(alpha * "'"), bty = 'l')

>

Figure 1.

Plots of the estimates from example2. The top plot shows the direct effect estimates. The bottom two plots demonstrate different ways of viewing the indirect effect estimates. The shaded regions show the point-wise 95% confidence intervals.

4.2. Diagnostics

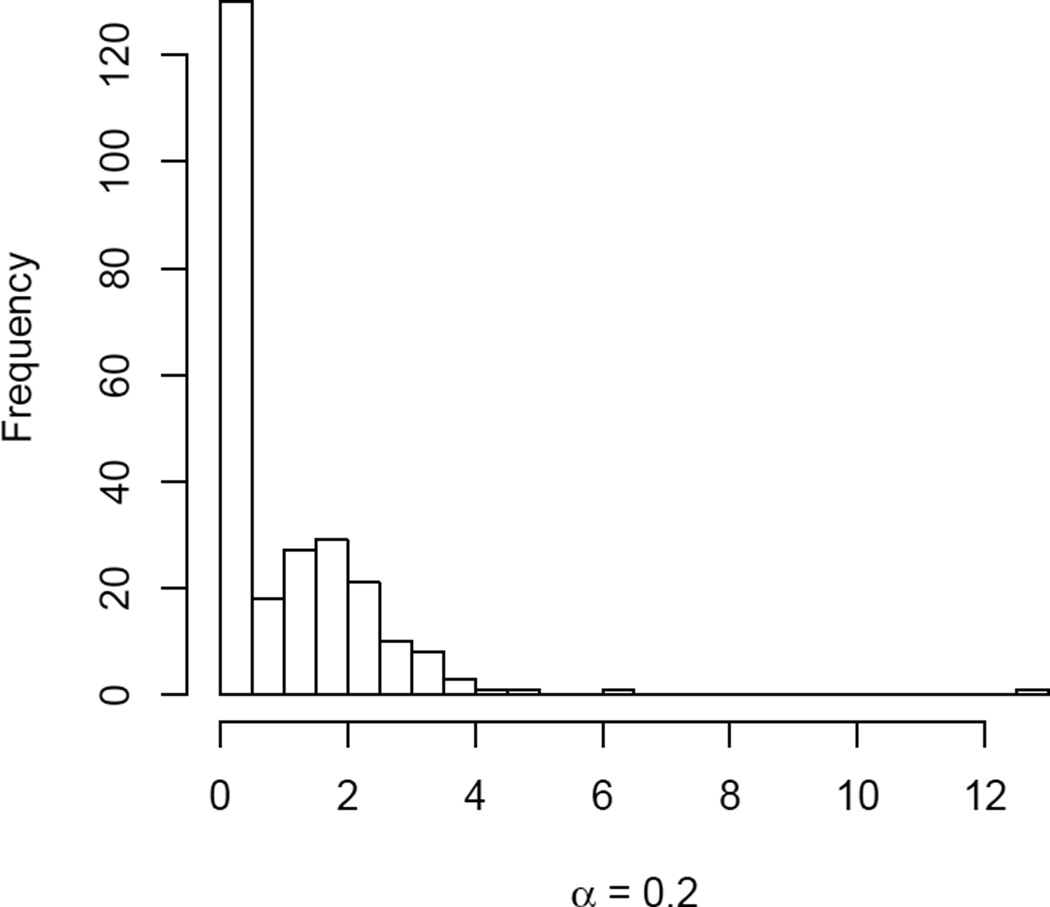
IPW estimators are known to be unstable if the weights range greatly. The package includes a basic utility to check the performance of the group-level weights, w_i,k, for multiple allocations. The function diagnose_weights plots histograms of weights for chosen allocation levels. If the allocations argument is left NULL, the function plots histograms for five allocation levels used in the interference call. Figure 2 shows the resulting histogram for a single allocation. The analyst should examine groups with extreme weights, which may unduly influence population-level estimates.

R> diagnose_weights(example2, allocations = .5, breaks = 30)

>

Figure 2.

A histogram of group-level weights, w_i,k, for α_k = 0.2.

5. Example: voting experiment

The preceding example used the default logit_integrand function to define the group-level propensities. The following example demonstrates how to customize the propensity score function.

Nickerson (2008) reported an experiment on voter behavior to examine peer-to-peer indirect effects on voting participation. The experiment randomized households with only two registered voters in Denver and Minneapolis to receive one of three assignments: voting encouragement, recycling encouragement, or nothing. Canvassers knocked on doors of households randomized to the voting or recycling groups a week before the 2002 primary. If a registered voter answered the door, the canvassers delivered a scripted message about voting (treatment) or recycling (control). The researchers used voter turnout records to determine if each member of the household then voted in the election. Nickerson was interested in the potential spillover effect of the voting encouragement to the untreated individual via the treated individual. From analysis of the observed data, he concluded there was a “secondary effect” where the household members not contacted by the canvassers voted more often in the treatment groups compared to the control groups.

The dataset voters contains information for 3861 households, 2549 in Denver and 1312 in Minneapolis, including covariates such as age, gender, previous voting history, and party affiliation. Our estimand of interest involves average voting outcomes when households receive voting encouragement compared to when household receive the recycling message, hence we exclude households not contacted by canvassers. We also exclude the single household where a canvasser appears to have contacted both registered voters.

R> voters <-  within(voters, {
+     treated     = (treatment == 1 & reached == 1) * 1
+     c_age       = (age - mean(age))/10
+    })
R> reach_cnt <- tapply(voters$reached, voters$family, sum)
R> voters <- voters[!(voters$family %in% names(reach_cnt[reach_cnt > 1])), ]
R> voters <- voters[voters$hsecontact == 1, ]

>

5.1. Household-level propensity

Unlike the vaccine study example, in this data set randomization occurred at the group level but individual level treatment was not randomized. With only two subjects, A_i = (A_i1, A_i2) is the treatment allocation for group i and X_i = (X_i1, X_i2) is the matrix of individuals’ covariate matrices for group i. Let B_i = (B_i1, B_i2) be indicators of being reached by a canvasser in group i. Since we only consider households where someone answered the door, B_i ∈ {(1, 0), (0, 1)} and Pr(B_i1 = 1|X_i) + Pr(B_i2 = 1|X_i) = 1. Let h_ij = Pr(B_ij = 1|X_i; θ) = logit⁻¹(X_iθ_x). Let G_i ∈ {0, 1} be the indicator that group i is randomized to treatment (1) or control (0). By design, Pr(G_i = 1) = 0.5. Since Pr(A_i1|X_i; θ) = 1 − Pr(A_i2|X_i; θ), Pr(A_i|X_i; θ) can arbitrarily be defined in terms of either household member. By convention we use the first subject (subject one) of each group found in the dataset. Among treated groups, the probability of subject one being treated is the probability that a canvasser reached subject one. That is, $\text{Pr}(A_{i1}|G_i=1,{\mathbf{X}}_i;\theta )=h_{i1}^{A_{i1}}{(1-h_{i1})}^{1-A_{i1}}$. Thus, the group-level propensity can be expressed:

$$\text{Pr}({\mathbf{A}}_i|{\mathbf{X}}_i;\theta )=\text{Pr}({\mathbf{A}}_i|G_i=1,{\mathbf{X}}_i;\theta )\text{ Pr}(G_i=1)+\text{Pr}({\mathbf{A}}_i|G_i=0,{\mathbf{X}}_i;\theta )\text{ Pr}(G_i=0)=0.5\{\text{Pr}({\mathbf{A}}_i|G_i=1,{\mathbf{X}}_i;\theta )+\text{Pr}({\mathbf{A}}_i|G_i=0,{\mathbf{X}}_i;\theta )\}=\{\begin{array}{cc}.5\hfill & \text{if }{A}_{i1}=0,A_{i2}=0\text{ and }{G}_i=0\hfill \\ .5h_{i1}^{A_{i1}}{(1-h_{i1})}^{1-A_{i1}}\hfill & \text{if }(A_{i1}=0,A_{i2}=0\text{ or }{A}_{i1}=1,A_{i2}=0)\text{ and }{G}_i=1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

Thus, h_i1 is sufficient to determine the group-level propensity. If we know whether or not the first subject was reached by a canvasser, then we know if the second was. Therefore, we can estimate parameters for h_i1 with a dataset that includes only subject one from each group. To do this, we must estimate the parameters outside of inferference and use model_method = ‘oracle’. We include centered age (in decades) in the propensity model for demonstration purposes.

R> voters1 <- do.call(rbind, by(voters, voters[, 'family'], function(x) x[1, ]))
R> coef.voters <- coef(glm(reached ~ c_age, data = voters1,
+                      family = binomial(link = 'logit')))

>

5.2. Coding the propensity function

Custom propensity_integrand and loglihood_integrand functions must have at least one argument:

• b: the first argument is the variable for which the integrate function computes the integral. As in this example, the function can be written so that the integral evaluates to 1 and has no effect.

For example, the following function will fix the group-level propensity to 0.5 for all groups when variance_estimation = ‘naive’:

R> fixed_propensity <- function(b){
R>  return(0.5 * dnorm(b))
R> }

>

For more realistic models, additional arguments may be passed to the custom function:

• X: the covariate matrix (determined by the formula) for the ith group

• A: the vector of treatment indicators for the ith group

• parameters: vector of estimated parameters from the model_method

• allocation: the allocation level for which the propensity is currently being estimated

• …: other arguments can be passed via the ellipsis in interference

Now we have the pieces to write the propensity function for the voting example.

R> household_propensity <- function(b, X, A,
+                                  parameters,
+                                  group.randomization = .5){
+   if(!is.matrix(X)){
+     X <- as.matrix(X)
+   }
+   if(sum(A) == 0){
+     pr <-  group.randomization
+   } else {
+     X.1 <- X[1 ,]; A.1 <- A[1]
+     h   <- plogis(X.1 %*% parameters)
+     pr  <-  group.randomization * dbinom(A.1, 1, h)
+   }
+   out <- pr * dnorm(b)
+   out
+ }

>

5.3. Evidence of a peer influence effect

The influence of the door opener on the non-door opener’s voting behavior corresponds to an indirect effect. Though the Bernoulli-type parametrization of the estimands allows us to look at a range of allocations, $\widehat{IE}(0.5,0)$ makes the sensible comparison between a world where individuals receive a voting message with probability 0.5 to a world where individuals have zero probability of receiving the voting message.

R> example3 <- interference(
+   formula = voted02p | treated | reached ~ c_age | family,
+   propensity_integrand = 'household_propensity',
+   data = voters,
+   model_method = 'oracle',
+   model_options =  list(fixed.effects = coef.voters, random.effects = NULL),
+   allocations   =  c(0, .5),
+   integrate_allocation  = FALSE,
+   causal_estimation_options  = list(variance_estimation = 'robust'),
+   conf.level = .9)

R> ie(example3, .5, 0)[ , c('estimate', 'conf.low', 'conf.high')]

    estimate    conf.low  conf.high
1 0.03151501 0.002290586 0.06073944

>

The point estimate suggests an individual receiving the voting encouragement increases the voting likelihood of the other household member by 3.2%. The 90% confidence interval excludes zero, indicating a significant indirect effect corroborating the analysis in Nickerson (2008).

For comparison, suppose that a flip of a fair coin determined which registered voter opened the door. We exclude age as a covariate and instead set h_i1 = 0.5. Here we assume to know the propensity score, so we use variance_estimation = ‘naive’.

R> example4 <- interference(
+   formula = voted02p | treated | reached ~ 1 | family,
+   propensity_integrand = 'household_propensity',
+   data = voters,
+   model_method = 'oracle',
+   model_options =  list(fixed.effects = 0, random.effects = NULL),
+   allocations   =  c(0, .5),
+   integrate_allocation  = FALSE,
+   causal_estimation_options  = list(variance_estimation = 'naive'),
+   conf.level = .9)

R> ie(example4, .5, 0)[ , c('estimate', 'conf.low', 'conf.high')]

    estimate    conf.low  conf.high
1 0.03144654 0.002209019 0.06068406

>

Examining the group-level weights may help diagnose coding errors in the propensity score function. In the case of a fixed probability as in example4, the propensity weights are easily computed by hand. For example, for α = 0.5,

$$w_i=\frac{\pi ({\mathbf{A}}_i;0.5)}{f_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;\theta =0)}=\{\begin{array}{cc}\frac{{0.5}^2}{.5}=.5\hfill & \text{if }{G}_i=0\hfill \\ \frac{{0.5}^2}{{.5}^2}=1\hfill & \text{if }{G}_i=1\hfill \end{array},$$

which we can confirm the software computed.

R> G <- tapply(voters[1:12, 'treated'], voters[1:12, 'family'], sum)
R> W <- head(example4[["weights"]]) [, 2]
R> cbind(G, W)

   G   W
2  1 1.0
4  0 0.5
5  0 0.5
6  0 0.5
9  1 1.0
10 0 0.5

>

6. Computational issues with IPW estimators

We show in this section how computation of the group-level weights may affect estimation as the number of individuals in groups grows. To illustrate, consider the IPW estimator of the overall effect, which weights individual outcomes in group i with:

$$w_{1i}=\frac{\pi ({\mathbf{A}}_i;\alpha )}{f_{{\mathbf{A}}_i|{\mathbf{X}}_i}({\mathbf{A}}_i|{\mathbf{X}}_i;\hat{\mathit{\theta }})}=\frac{{\prod }_{j=1}^{n_i}{\alpha }^{A_{ij}}{(1-\alpha )}^{1-A_{ij}}}{\int {\prod }_{j=1}^{n_i}{h}_{ij}^{A_{ij}}{(1-h_{ij})}^{1-A_{ij}}{f}_b(b_i;{\hat{\theta }}_s)d{b}_i}$$

or equivalently,

$$w_{2i}={\{\int \prod _{j=1}^{n_i}{\left(\frac{h_{ij}}{\alpha }\right)}^{A_{ij}}{\left(\frac{1-h_{ij}}{1-\alpha }\right)}^{1-A_{ij}}{f}_b(b_i;{\hat{\theta }}_s)d{b}_i\}}^{-1}$$

or,

$$w_{3i}={\{\int \text{ exp }[\sum _{j=1}^{n_i}\left\{A_{ij}\text{ log }\right(\frac{h_{ij}}{\alpha })+(1-A_{ij})\text{ log }(\frac{1-h_{ij}}{1-\alpha }\left)\right\}]f_b(b_i;{\hat{\theta }}_s)d{b}_i\}}^{-1}.$$

While mathematically equivalent, these weights may be computationally dissimilar. In the case of w_1i, the product term within the integral entails multiplying probabilities and thus will tend to 0 as n_i increases, causing the denominator of w_1i to get arbitrarily large. In contrast, the product term in w_2i entails multiplying values which may be less than or greater than 1 and thus tends to be less susceptible to numerical instability. Summing log(h_ij/α) or log(1 − h_ij)/(1 − α)) and then exponentiating the result may provide greater numerical stability. Internally, inferference uses w_3i.

When group sizes are small, the differences between these weights tend to be infinitesimal, but as group sizes grow the differences become important. To be specific, consider the code below comparing w_1i, w_2i, and w_3i for increasing group sizes where α = 0.5, all units are treated, there is no random effect, and h_ij is fixed at 0.5.

R> compare_weights <- function(n, alpha = .5, h = .5){
+   pi  <- rep(alpha, n)
+   PrA <- rep(h, n)
+   c(w1 = prod(pi)/prod(PrA),
+     w2 = 1/prod(PrA/pi),
+     w3 = 1/exp(sum(log(PrA/pi))))
+ }
R>
R> n <- c(50, 100, 500, 1074, 1075, 10000)
R> cbind(n, t(sapply(n, FUN = compare_weights)))

         n  w1 w2 w3
[1,]    50   1  1  1
[2,]   100   1  1  1
[3,]   500   1  1  1
[4,]  1074   1  1  1
[5,]  1075 NaN  1  1
[6,] 10000 NaN  1  1

>

For group sizes up to 1074 there is no difference, but when n reaches 1075, w_1i returns NaN while w_2i and w_3i correctly return 1.

Perez-Heydrich et al. (2014) used w_1i to calculate weights, but 15 groups in their analysis had over 1000 subjects. These groups had missing values for weights for all the values of α considered and were excluded from computing the average IPW estimate. Rather than computing the average IPW across 700 groups, they inadvertently took the average across 685 groups. Correcting the estimates by using w_2i or w_3i did not alter the conclusions in this case, but analysts should be aware of this issue when dealing with large groups.

7. Discussion

The R package inferference computes inverse probability weighted estimators of causal effects in the presence of interference. The package currently supports the IPW methods of Tchetgen Tchetgen and VanderWeele (2012) and Perez-Heydrich et al. (2014). These methods require a model for the group-level propensity scores. The package provides useful defaults for the propensity models but allows for non-standard models.

Development and application of statistical methods for inferring causal effects in the presence of interference is an active area of research. Future versions of inferference may incorporate other estimation methods, such as doubly robust methods and stratification. Also, additional methods for estimating variances and effect bounds may be incorporated into the software.