Abstract
Sound onsets dominate spatial judgments of many types of periodic sound. Conversely, ongoing cues often dominate in spatial judgments of aperiodic noise. This study quantified onset dominance as a function of both the bandwidth and the temporal regularity of stimuli by measuring temporal weighting functions (TWF) from Stecker, Ostreicher, and Brown [(2013) J. Acoust. Soc. Am. 134, 1242–1252] for lateralization of periodic and aperiodic noise-burst trains. Stimuli consisted of 16 noise bursts (1 ms each) repeating at an interval of 2 or 5 ms. TWFs were calculated by multiple regression of lateralization judgments onto interaural time and level differences, which varied independently (, ±2 dB) across bursts. Noise tokens were either refreshed on each burst (aperiodic) or repeated across sets of 2, 4, 8, or 16 bursts. TWFs revealed strong onset dominance for periodic noise-burst trains (16 repeats per token), which was markedly reduced in aperiodic trains. A second experiment measured TWFs for periodic but sinusoidally amplitude-modulated noise burst trains, revealing greater weight on the earliest and least intense bursts of the rising envelope slope. The results support the view that envelope fluctuations drive access to binaural information in both periodic and aperiodic sounds.
I. INTRODUCTION
In natural listening, competing sources, echoes, and reverberation cause auditory spatial cues—for example, interaural time differences (ITD) and interaural level differences (ILD)—to fluctuate over time. Yet the processing of auditory spatial cues by human and animal listeners is remarkably robust to such fluctuations, in part because spatial hearing strongly weights the most reliable cues (e.g., those carried by sound onsets) and discounts the least reliable (Brown et al., 2015). These patterns of cue weighting can even be observed in controlled laboratory settings lacking reverberant effects, and are thought to reflect basic mechanisms of auditory spatial processing.
Previous publications in this series (Brown and Stecker, 2010, 2011; Stecker et al., 2013; Stecker, 2014) characterized temporal variation in cue weighting by measuring temporal weighting functions (TWF) for lateralization and discrimination of ITD and ILD in brief narrowband stimuli. The current study extends this work to consider periodic and aperiodic trains of broadband noise bursts in an effort to understand the impacts of (a) spectral bandwidth and (b) temporal regularity on binaural cue weighting.
A. Review of key TWF features
The TWF approach (Saberi, 1996; Stecker and Hafter, 2002, 2009) introduces temporally random variation on spatial cues (e.g., ITD and/or ILD) in each temporal segment of a brief sound. Multiple regression is used to relate spatial judgments to cue variation; regression weights characterize the relative influence of cues in each temporal segment and comprise the TWF. Our earlier work focused on measuring TWFs for ITD and ILD discrimination (Brown and Stecker, 2010, 2011) and lateralization (Stecker et al., 2013; Stecker, 2014) in Gabor click trains, which are modulated high-frequency sounds that convey salient ILD and envelope-ITD cues. The chief results can be summarized as follows:
-
(1)
Onset dominance. For high-rate stimuli—i.e., when the interclick interval (ICI) is shorter than about 5 ms—judgments are strongly dominated by the ITD and ILD of the first, or onset, click. Weights on the second and later clicks are substantially lower, and that reduction in weights is immediate, not gradual (Saberi, 1996; Stecker and Hafter, 2002; see also Zurek, 1980; Akeroyd and Bernstein, 2001).
-
(2)
Rate dependence. Onset dominance is strongly dependent on the click rate or ICI. In general, onset dominance is greatest at the shortest ICIs (1–3 ms) and weakens with longer ICI. At ICI ms, TWFs are approximately flat, consistent with integration of ITD and ILD across the entire stimulus. The results are consistent with rate-dependent binaural adaptation (Hafter and Dye, 1983; Hafter et al., 1983).
-
(3)
Greater onset dominance for ITD than ILD. Several studies noted greater weight on ILD of post-onset clicks than in equivalent ITD conditions (e.g., Brown and Stecker, 2010). That result suggests a greater role, or longer window, of temporal integration for ILD than ITD processing.
-
(4)
Recency effects. Stecker and Hafter (2002, 2009) noted recency effects in TWFs measured for free-field localization, whereby larger weights were observed near the end of the stimulus than in the middle. Stecker et al. (2013) replicated that result for headphone-based lateralization, where recency effects were observed for ILD- but not ITD-based lateralization.
-
(5)
Effects of carrier frequency. A major contributor to onset dominance at low carrier frequencies is hypothesized to be the temporal overlap between auditory filter responses to successive clicks (Tollin, 1998). That view is supported by exaggerated onset- and offset-weighting in TWFs measured at 1–2 kHz compared to higher carrier frequencies (Stecker, 2014).
Although this series of papers has focused on periodically modulated high-frequency sounds, other studies have used alternative approaches to also demonstrate correlates of onset dominance at lower frequencies and in pure tones (Dietz et al., 2013; Stecker and Bibee, 2014; Diedesch and Stecker, 2015). Together, results suggest that onset dominance is a general phenomenon of binaural hearing, impacting a wide range of frequencies and cue types, including fine-structure ITD, envelope ITD, and ILD (Stecker, 2016b).
B. Temporal weighting of binaural cues in noise
In contrast to the case for tones and other narrowband periodic stimuli, previous studies suggest little to no onset dominance for noise. Rather, the ongoing cues appear to dominate (e.g., Tobias and Schubert, 1959), perhaps due to the natural agreement of cues across frequency (cf. Trahiotis and Stern, 1989) or the greater temporal irregularity (cf. Goupell et al., 2009) of noise. To date, no published study has directly measured TWFs for aperiodic stimuli, although some studies have measured onset dominance with noise carriers (e.g., Tobias and Schubert, 1959; Freyman et al., 1997). Freyman et al. (1997) asked listeners to lateralize trains of noise bursts (ICI = 2 ms) with ITD that alternated between favoring the left or the right ear by . When identical noise samples were used for all bursts (i.e., periodic noise-burst trains), listeners lateralized consistently in the direction of the initial burst, consistent with onset dominance as observed for periodic narrowband sounds. Aperiodic trains, with new samples of noise on each burst, were lateralized inconsistently to the left or right.
The results of Freyman et al. (1997) suggest that temporal regularity—rather than overall bandwidth—may be responsible for reduced onset dominance in noise. In a subsequent study (Freyman et al., 2010), the noise token was fixed within each pair of opposing binaural bursts, but not across pairs. In that case, judgments favored the initial location of each pair even when it opposed the overall onset burst. This “ongoing precedence effect” suggests that binaural processing is capable of tracking similarities in temporal fine structure across bursts, or that brief envelope fluctuations are capable of triggering onset dominance at short temporal scales (cf. Hafter and Buell, 1990). The current study adapted the stimulus of Freyman et al. (2010) to the TWF approach, with the aim to (a) replicate these results across approaches, (b) characterize the temporal profile of the ongoing precedence effect, and (c) test the hypothesis that envelope fluctuations drive these effects.
II. EXPERIMENT 1: TWF FOR TRAINS OF REPEATED AND NON-REPEATED BROADBAND NOISE BURSTS
Experiment 1 utilized broadband noise carriers to investigate the effects of spectral bandwidth and stimulus regularity on TWFs for binaural lateralization. The stimuli were adopted from Freyman et al. (1997), and the method from Stecker et al. (2013).
A. Methods
Experiment 1 was conducted at the University of Washington. It adopted the procedure and analytical approach of Stecker et al. (2013, Experiment 3) to measure TWFs for noise-burst trains. As in that study, which employed narrowband Gabor click trains, stimuli were presented with independent variation in the ITD and ILD applied to each of 16 noise bursts. Listeners judged the lateral positions of each stimulus (i.e., each train of noise bursts), and multiple regression was used to relate judgment position to the ITD and ILD cues carried by each burst. For 16 bursts, the result is 32 regression weights: 16 for ILD and 16 for ITD. These comprise the TWFs for ITD and ILD in such stimuli.
All procedures, including recruitment, consenting, and testing of human subjects, followed the guidelines of the University of Washington Human Subjects Division and were reviewed and approved by the cognizant Institutional Review Board.
1. Participants
Eight normal-hearing adult listeners participated in the experiment. All were paid participants naive to the purpose of the experiment. All participants reported normal hearing, which was confirmed by pure-tone detection thresholds dB hearing level (HL) over the range 250–8000 Hz. Two participants (1005 and 1210) completed testing only at ICI = 2 ms.
2. Stimuli
As depicted in Fig. 1, stimuli were trains of broadband Gaussian white noise bursts (clicks), each 1 ms in duration. Each train presented 16 bursts at an inter-click interval (ICI) of 2 or 5 ms. Sounds were computed in matlab (Mathworks, Natick, MA), synthesized at 48.828 kHz (Tucker-Davis Technologies RX6, Alachua, FL), and presented via headphones (Sennheiser HD 485, Hannover, Germany) at 70 dB sound pressure level (SPL) (peak equivalent).
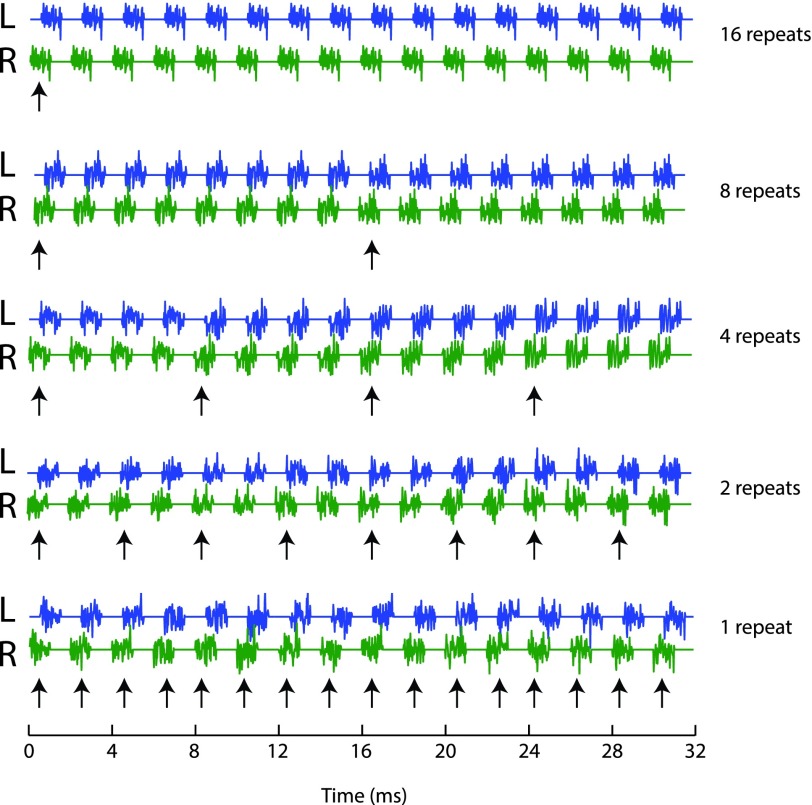
FIG. 1.
(Color online) Example stimulus waveforms in Experiment 1. Each row plots left (L) and right (R) ear waveforms for a single train of 16 noise bursts. Bursts are 1 ms in duration and repeat at 2-ms ICI. Noise tokens were repeated across a number of successive bursts that varied across conditions. In the “16 repeats” condition (top), a single token was presented on all 16 bursts; in the “1 repeat” condition (bottom), a new token was generated for each burst. Intermediate conditions presented new tokens after 8, 4, or 2 repeats. Vertical arrows indicate the timing of new noise tokens in each case.
Noise waveforms were either computed independently across bursts in a train (i.e., fresh tokens were generated with independent waveforms), or were repeated from burst to burst. Conditions varied in the number of times a token was repeated before a fresh token was generated. In one extreme condition, identical tokens were used for all 16 bursts. We designated that condition “16 repeats.” The other extreme consisted of a fresh token for each burst (“1 repeat”). Intermediate conditions presented fresh bursts after 8, 4, or 2 repeats. The first presentation of each token (i.e., the “local onset”) is indicated by arrows in Fig. 1 and by filled symbols in TWFs plotted in Fig. 2; open symbols indicate repeats of the preceding token.
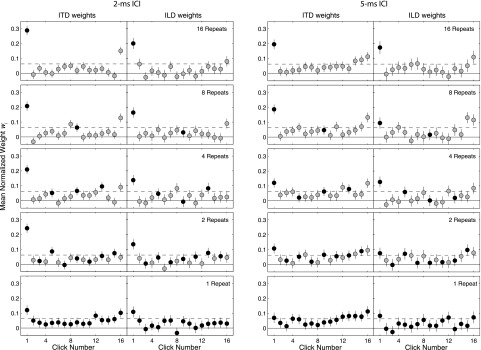
FIG. 2.
The TWFs for noise-burst trains (Experiment 1). Each panel plots mean normalized weight wi (y-axis), as a function of the temporal order of the clicks (x-axis) with ITD and ILD weights in separate panels (left/right column in each group). Error bars indicate bootstrapped 95% confidence intervals. The dashed horizontal line in each panel indicates the value that would be obtained if all clicks were equally weighted (1/16), while the solid line indicates zero. From top to bottom, panels plot TWFs for noise-burst trains with noise tokens repeating across 16 (top), 8, 4, 2, or 1 (bottom) sequential bursts. The initial presentation of each new noise token is indicated by a filled symbol; subsequent repeat presentations are indicated by open (gray) symbols. Two columns at left plot TWFs for lateralization at 2-ms ICI; columns at right plot TWFs obtained at 5-ms ICI.
Each stimulus was presented at a “base” ILD value, , of −5, −3, −1, +1, +3, or +5 dB. By convention, negative values favor the left ear and positive values favor the right. The base ITD value, , was calculated to match at a ratio of dB (e.g., was paired with + 3 dB). Thus, each stimulus was presented with a pair of base ITD and ILD values that agreed in sign and were correlated from trial to trial, as in Experiment 3 of Stecker et al. (2013). Base values were presented an equal number of times (15 per run), in random order. For each noise burst i within a stimulus, the ILD of that burst was perturbed by a random value drawn from a uniform distribution spanning ±2 dB. Thus, the ILD of each burst, , ranged from to dB. The ITD of each noise burst, , was perturbed by a random value drawn from an independent uniform distribution spanning . Note that the two cues (ILD and ITD) were perturbed independently of each other and independently across noise bursts. Thus, the binaural configuration of each stimulus was characterized by 32 binaural cue values: and for each of the 16 noise bursts.
3. Procedure
Testing took place in a double-walled sound-attenuating booth (IAC, Bronx, NY), with subject seated in a swivel chair and facing an 80-cm (diagonal) touch-sensitive display (Elo Touchsystems 3200L, Tyco Electronics, Bermuda) at a distance of 50 cm. Head position was monitored continuously (Polhemus Fastrak, Colchester, VT) to ensure stable head position during stimulus presentations.
On each trial, a single stimulus was presented, and listeners indicated the perceived lateral position of the stimulus by touching along a 55-cm horizontal bar displayed on the touch screen. Listeners were instructed to make an immediate eye movement to the judged position on the bar, and to maintain gaze while touching the foveated location with a finger. This instruction was intended to encourage listeners to rapidly orient to the sound's location and not perseverate on the scaling judgment. Following each response, the listener returned to initial position (within azimuth and elevation) before the next trial began. Listeners completed 90 trials per run (15 trials per base ITD or ILD value) and repeated eight runs per condition (combination of ICI and repeat number). Conditions were tested in random order within each of the eight replicate blocks.
4. Analysis
Response data were transformed to ranks (i.e., ranked according to lateral position) within each run prior to weighting analysis. This step minimized response nonlinearities and distributional differences across runs and subjects. Perceptual weights for each of the 16 clicks in a train were then estimated by multiple linear regression of the rank-transformed response θR onto the binaural cues applied to individual clicks ( and ), using matlab:
| (1) |
For comparison across subjects and conditions, regression coefficients βi were then normalized so that absolute values sum to 1 over the 16-click stimulus duration. Normalization was done separately for ITD and ILD:
| (2) |
| (3) |
The normalized weights wLi and wti comprise the TWF, and indicate each click's relative influence on a listener's judgments. Weights vary generally between 0 (no influence) and 1 (a perfect linear relationship). Strongly negative values would indicate a biasing of judgments away from the click location. TWFs were estimated separately for each combination of listener, ICI, and repeat condition using data obtained in all runs for that combination; 95% confidence intervals on wLi and wti were computed by normalizing the upper and lower confidence limits on βi by the denominator of Eq. (2) or (3).
Dominance of onset and offset cues was quantified, as in our previous studies (Stecker et al., 2013; Stecker, 2014), by the average ratio (AR, Saberi, 1996). AR was defined as the ratio of onset (first click) or offset (final click) weight to the mean of intermediate weights (i.e., the mean excluding onset and offset clicks)
| (4) |
or
| (5) |
where N () indicates the total number of clicks in each train. ARonset quantifies the dominance of binaural cues carried by the initial/onset burst. ARoffset similarly indicates the relative influence of the final, offset, burst.
Bootstrapped confidence intervals on mean AR were computed by 2000-fold resampling across subjects (Fox, 2008). Bootstrap tests were also used for post hoc tests of AR across pairs of conditions. Specifically, a set of 2000 bootstrapped mean AR values were generated for each condition (denoted A and B for illustration): ARAi and ARBi. For each bootstrapped replicate i, the difference between conditions () was then computed, resulting in 2000 bootstrapped difference scores. The proportion of difference scores greater than or equal to zero gave the raw p value for A > B. A two-tailed p value was generated for each comparison by taking the minimum of p or . This procedure was followed to conduct 120 post hoc tests. These included three types of pairings. First, for each combination of cue (ITD or ILD), ICI, and measure (ARonset and ARoffset), each repeat value was compared to each other repeat value (80 tests). Second, for each combination of cue, measure, and repeat value, AR was compared across ICI (20 tests). Third, for each combination of ICI, measure, and repeat value, AR was compared across cues (20 tests). False discovery rate (FDR) was controlled at Q = 0.05 across the 120 possible comparisons using the procedure of Benjamini and Hochberg (1995).
B. Results and discussion
Figure 2 plots group-average TWFs for each condition tested in Experiment 1. Corresponding data for individual subjects appear in Fig. 3. A number of important features are apparent from Fig. 2, and further quantified in Fig. 4.
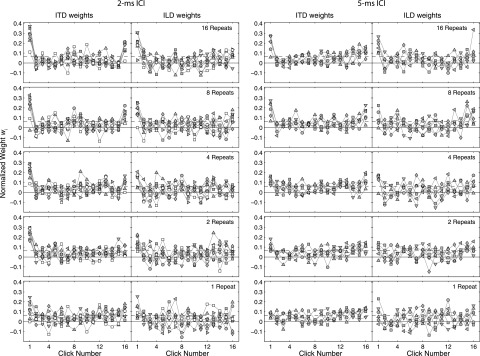
FIG. 3.
TWFs for noise-burst trains, individual data. Panels plot separate TWFs for each listener (symbols). Other formatting is identical to Fig. 2.
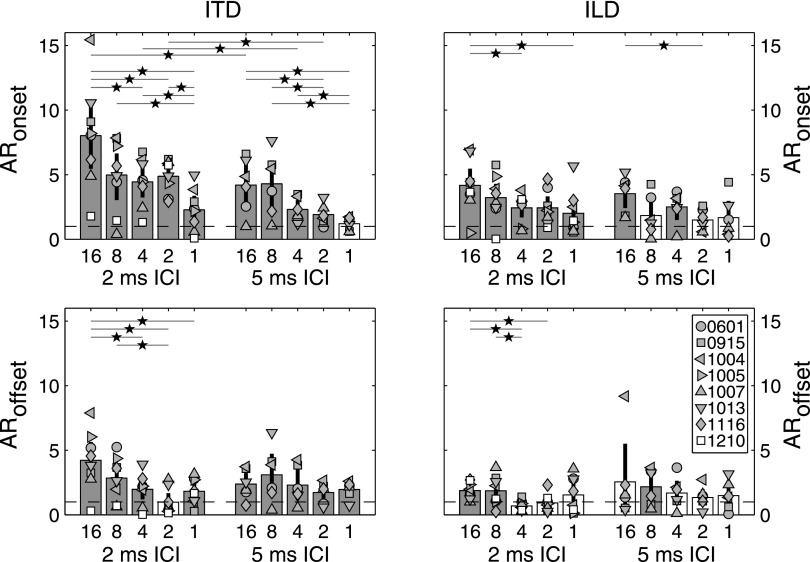
FIG. 4.
Quantification of onset- and offset-dominance. Upper panels plot values of ARonset, and lower panels plot ARoffset, for ITD (left panels) and ILD (right panels). Within each panel, bars plot mean AR across subjects and symbols plot individual-subject values. Shaded bars indicate AR values significantly greater than 1.0 (p < 0.02). Vertical error bars indicate bootstrapped 95% confidence intervals on each mean. Separate bars indicate AR for each combination of ICI and repeat value. Dashed lines mark 1.0, corresponding to the null hypothesis of onset or offset clicks weighted equally to the mean of other clicks. Starred horizontal lines at top of each panel indicate significant pairwise comparisons (p < 0.02, FDR controlled at Q < 0.05).
1. Weighting of the overall onset and offset
Strong ICI-dependent onset dominance was observed for both ITD and ILD cues, in the form of significantly elevated click-1 weights. Click-1 weights were larger, and ARonset greater, for 2-ms than for 5-ms ICI in a majority of conditions. Consistent with previous TWF measurements (Stecker et al., 2013) and with temporary binaural insensitivity following sound onsets (Akeroyd and Bernstein, 2001; Zurek, 1980), weights on clicks 2–3 tended to be among the lowest in each function.
Onset dominance was stronger for periodic stimuli (16-repeats condition) than for aperiodic stimuli (1-repeat condition), consistent with a greater influence of ongoing cues with noise (Freyman et al., 1997). The magnitude of onset dominance tended to decrease with fewer repeats of each noise sample (i.e., as the stimulus became less periodic). That trend is quantified by measures of ARonset plotted in Fig. 4.
One previous study (Freyman and Zurek, 2017) measured onset weighting in the lateralization of noise burst trains similar to the current 2-repeat condition at 2-ms ICI. Onset weights were roughly 0.3 when the duration was similar to the current study (17 total bursts), onset ITD was fixed at , and ongoing ITD at . That value is very consistent with the current result of 0.24 in the corresponding condition (2-ms ICI, 2 repeats) despite stimulus differences such as the lack of ILD variation and the larger discrepancy between onset and ongoing ITD values. When the ongoing ITD alternated between from burst to burst, Freyman and Zurek (2017) noted onset weights greater than 0.6, suggesting that inconsistency and/or ambiguity in the ongoing ITD can produce even greater onset dominance than observed for compact stimuli as in the current study.
Elevated offset weights were observed in most conditions, often in a monotonically increasing pattern consistent with recency effects described by Stecker and Hafter (2009). Prominent click-16 weights (i.e., relative to click 15), consistent with a role of “ringing” peripheral filters (Tollin and Henning, 1999; Stecker, 2014), were observed in fewer conditions, and only at 2-ms ICI.
Figure 4 plots values of ARonset and ARoffset obtained in the various conditions. Individual subject data are indicated by symbols, whereas group means indicated by bar heights. Shaded bars indicate conditions in which AR significantly exceeded 1.0—that is, in which the onset or offset burst received significantly greater weight then other bursts. Mean values ranged from just below 1.0 to just over 8.0. The largest value, ARonset = 8.02, was obtained in the ITD condition at 2-ms ICI and a repeat value of 16. The corresponding value for ILD was ARonset = 4.16, significantly lower than for ITD (p < 0.008). Both values are in agreement with previous measurements using narrowband Gabor click trains at 2-ms ICI (Stecker et al., 2013; Stecker, 2014).
Pairwise testing of AR values across conditions resulted in 29 significant differences (all p < 0.02) when controlling false-discovery rate at Q < 0.05 across 120 post hoc tests (Benjamini and Hochberg, 1995). Excluding comparisons across ITD and ILD, the significant comparisons are indicated by starred lines in Fig. 4.
ARonset values were significantly greater for ITD than ILD for repeat values of 16, 4, and 2 at 2-ms ICI (p < 0.008). Similarly, ARoffset values were significantly greater for ITD than ILD at 2-ms ICI with repeat values of 16 and 4 (p < 0.008). In all other conditions, AR values were not significantly affected by cue type.
Effects of ICI on AR values were confined to ITD judgments of 16-, 4-, and 2-repeat stimuli. ARonset values in those conditions were significantly larger at 2-ms than 5-ms ICI ().
As suggested by the TWFs themselves, significant effects of repeat value were observed most clearly at 2-ms ICI, and particularly for ARonset with ITD as the judged cue. In that condition, ARonset values were significantly larger for 16-repeat stimuli, and smaller for 1-repeat stimuli than for other conditions (p < 0.02). Stimuli with 5-ms ICI, in contrast, exhibited few significant differences across repeat value.
2. Weighting of local “onsets” and the ongoing precedence effect
Finally, TWFs exhibited modest evidence for greater weight on cues carried by fresh noise tokens (filled symbols in Fig. 2), as expected due to the ongoing precedence effect (Freyman et al., 2010). For ITD at 2-ms ICI, we observed “local” onset dominance in the form of significantly greater weights on the first than the second repeat of each sample (most evident in the 4- and 8-repeats conditions). The trend is partly obscured by elevated weights on the burst immediately preceding each change. The mean TWFs thus suggest elevated weight on both the onsets and offsets within each group of repeating bursts, rather than a unique impact of the local onset.
The magnitude of local onset dominance was further quantified by calculating AR for fresh bursts rather than the overall onset. For this, the numerator of Eq. (4) was replaced with w9 in the 8-repeat condition or with the mean of w5, w9, and w13 in the 4-repeat condition. The denominator was the mean of weights excluding local and global onsets or offsets. Measured this way, local onset dominance was modest (8 repeats: ; 4 repeats: ) for ITD at 2-ms ICI and not apparent in other conditions. Local offset weights (quantified by replacing the numerator with w8 or the mean of w4, w8, and w12) were weakly but significantly elevated only for ILD in the 2-ms, 4-repeat condition (). While the direction of these effects is consistent with the ongoing precedence effect, the evidence is much less clear than in previous work (Freyman et al., 1997, 2010; Freyman and Zurek, 2017). However, it should be noted that the current study differed in key methodological aspects including the overall duration (32 ms vs 250 ms in Freyman et al., 2010) and the distribution of ITD variation from burst to burst (uniform vs alternating +500 and ). Both factors could plausibly have reduced local onset dominance in this case: the clearest evidence of ongoing precedence effects in Freyman et al. (2010) utilized slow gating to remove the overall onset, the influence of which can also be reduced by presenting longer durations (Tobias and Schubert, 1959; Freyman and Zurek, 2017), or by maintaining greater consistency among ongoing ITD cues (Freyman and Zurek, 2017).
3. The roles of bandwidth and temporal irregularity
A goal of Experiment 1 was to assess the impact of stimulus bandwidth on temporal weighting of ITD and ILD cues. It is well established that broadband sounds are more easily and accurately localized than narrowband sounds. In the domain of ITD processing, it is thought that cue agreement across frequency (i.e., “straightness” of binaural cross-correlation in different frequency channels; Trahiotis and Stern, 1989) plays a major role in acuity and in resolving ambiguous cues such as interaural coincidences that appear shifted by one or more periods of a narrowband waveform, particularly above 700 Hz (Zurek, 1980). Moreover, numerous studies have demonstrated the dominance of ongoing cues, rather than onset cues, in binaural processing of broadband noise (e.g., Tobias and Schubert, 1959; Hartmann and Rakerd, 1989). Such observations would suggest flatter TWFs for noise-burst stimuli than for narrowband stimuli. The results of this study suggest otherwise, in that some conditions resulted in onset dominance that was quantitatively similar to previous reports using narrowband stimulation (Stecker, 2014). That is, broad spectral bandwidth alone is not sufficient to significantly reduce onset dominance. In this regard, the results are in agreement with Freyman et al. (1997).
A second goal was to quantify the impact of temporal regularity on TWFs for ITD and ILD. This was accomplished by varying the degree of noise-burst repetition, and thus the periodicity, of the stimulus. The overall results of Experiment 1 demonstrate a clear effect of burst repetition. TWFs for periodic trains (16 repeats) were qualitatively similar, and AR values quantitatively so, to those reported previously using narrowband periodic stimulation (Stecker, 2014). In contrast, TWFs for aperiodic trains (1 repeat) were markedly flattened, and AR value reduced, relative to periodic trains. These results mirror the well-established discrepancy between strong onset dominance for periodic sounds and stronger ongoing-cue sensitivity for noise (Tobias and Schubert, 1959; Freyman et al., 1997, 2010).
In our view, the results also mirror those obtained using narrowband high-frequency stimuli with varying degrees of temporal irregularity. Brown and Stecker (2011) measured TWFs for ITD and ILD discrimination in Gabor click trains subject to varying amounts of binaurally synchronous temporal “jitter.” The authors noted a marked reduction in onset dominance—i.e., an increased influence of ongoing cues—as temporal jitter was increased. Better access to ongoing cues in such stimuli, they argued, could explain why better ITD sensitivity is often observed in jittered acoustical and electrical stimulation (Laback and Majdak, 2008; Goupell et al., 2009). Together, the current results and those of Brown and Stecker (2011) suggest that temporal irregularity—as opposed to spectral bandwidth—is the critical feature responsible for potent ongoing cues in noise targets.
How might temporal irregularity support binaural-cue sensitivity in noise stimuli? A number of recent studies have indicated the critical importance of envelope fluctuations for the processing of all types of binaural cues (see Stecker, 2016b, for a brief review). In particular, the rising slope of the amplitude envelope appears to dominate the processing of both envelope-based cues (Klein-Hennig et al., 2011) and fine-structure-based cues (Dietz et al., 2013; Stecker and Bibee, 2014). If so, fluctuations in the smoothed envelopes of temporally jittered stimuli (Brown and Stecker, 2011) could support potent ongoing cues by providing multiple rising-slope events (cf. Hafter and Buell, 1990). For broadband noise, the overall temporal envelope is flat; however, dramatic fluctuations may be observed in the local envelope at a given cochlear place. Similarly, the broadband envelopes of noise-burst trains used in Experiment 1 are dominated by the 2-ms ICI. Within-band envelopes, however, fluctuate with changes in the noise-burst token.
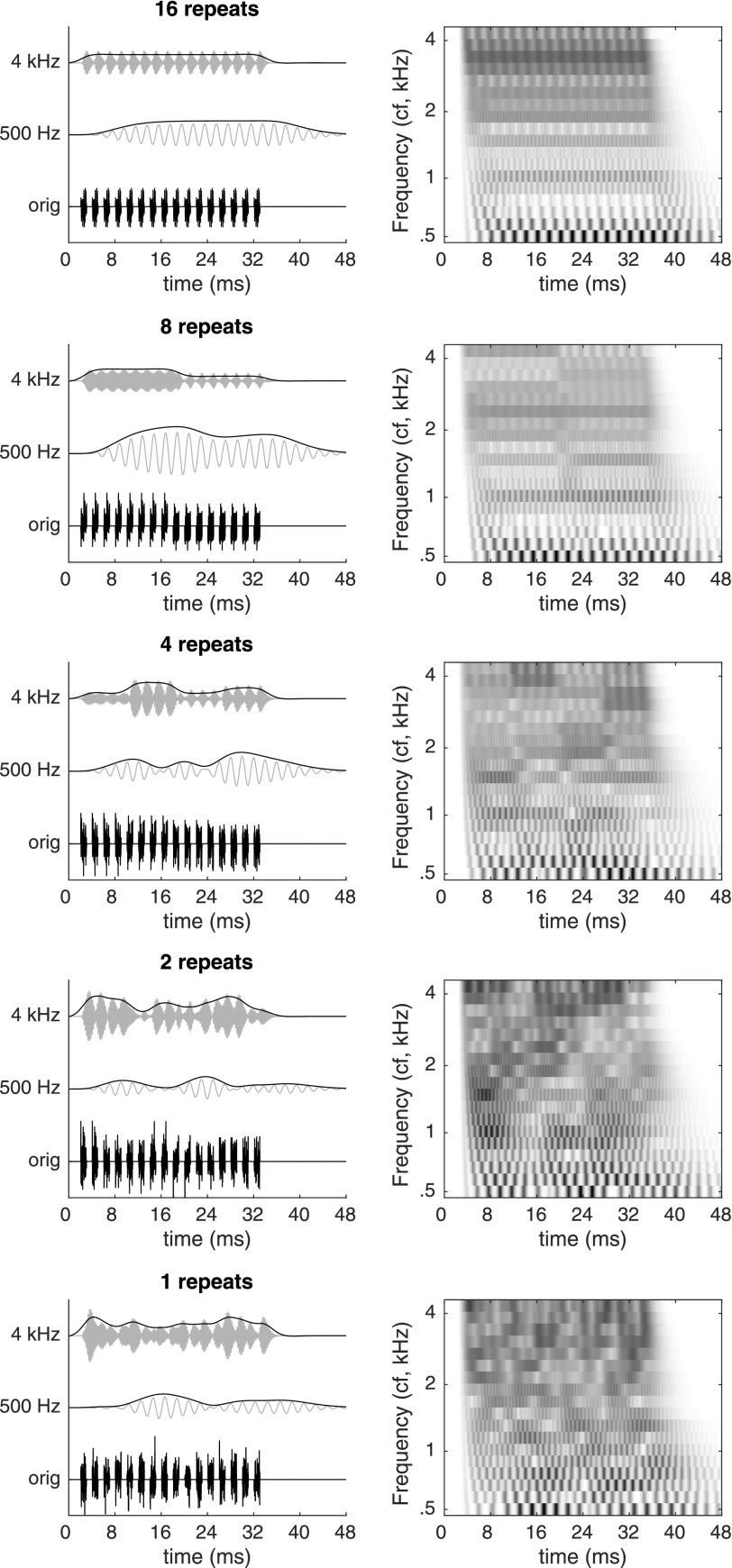
The effects of token change on within-band envelopes are illustrated in Fig. 5. For this analysis, we processed the experimental stimuli through a bank of 18 gammatone filters spanning 500–4325 Hz (Akeroyd, 2001) and computed the output envelopes. Examples of filter outputs at 500 and 3860 Hz are illustrated in the left-hand panels of Fig. 5. Pronounced fluctuations are apparent at both frequencies. Depending on the binaural system's sensitivity to fluctuations at these rates and depths, such features could be responsible for greater weighting of ongoing cues at small repeat values. The right-hand panels of Fig. 5 illustrate responses across the full set of modeled filters, following monaural transduction of the envelopes by compression (exponent = 0.23), halfwave rectification, expansion (exponent = 2.0), and 425-Hz lowpass filtering. Fluctuations associated with token-change events are clearly apparent, as are higher-rate fluctuations at the ICI and at of the low-frequency channels.
FIG. 5.
Illustration of within-band envelope fluctuations in noise-burst trains. Each pair of panels illustrates the result of gammatone filtering and envelope extraction (Akeroyd, 2001) at a different repeat value. Within each pair, the left panel plots the original stimulus waveform (“orig”) and the outputs of auditory filters centered at 500 Hz and 3860 Hz (“4 kHz”). Light gray lines plot the filtered waveform; black lines plot the corresponding envelope, obtained by full-wave rectification and low-pass filtering (second-order Butterworth at 150 Hz, applied using matlab command filtfilt). Right-hand panels illustrate the outputs of 18 gammatone filters spanning 500–4325 Hz. Filter outputs were further processed using an envelope-based monaural transduction model described by Bernstein and Trahiotis (1996). That model applied compression, half-wave rectification, expansion, and low-pass filtering at 425 Hz to each filter output prior to plotting.
III. EXPERIMENT 2: TWF FOR SINUSOIDALLY AMPLITUDE-MODULATED NOISE-BURST TRAINS
The results of Experiment 1 suggest that binaural sensitivity to ongoing cues in noise stimuli is driven by envelope fluctuations in auditory filter outputs. As an initial test of that hypothesis, Experiment 2 measured TWFs for noise-burst trains with sinusoidal amplitude modulation imposed. If binaural information is sampled during transient increases in the amplitude envelope (Klein-Hennig et al., 2011; Dietz et al., 2013; Stecker, 2016b), TWFs should reveal large weights during the rising slopes, rather than the most energetic portions, of the imposed envelope.
A. Methods
Experiment 2 was conducted at Vanderbilt University Medical Center (VUMC). All procedures, including recruitment, consenting, and testing of human subjects followed VUMC guidelines and were reviewed and approved by the cognizant Institutional Review Board.
1. Participants
Eight normal-hearing adult listeners participated in the experiment. One was the author, and two were research assistants working in the lab but not informed about the purpose of the experiment or nature of the stimuli. The remainder were paid participants naive to the purpose of the experiment. None had participated in Experiment 1. All reported normal hearing, which was confirmed by pure-tone detection thresholds dB HL over the range 250–8000 Hz.
2. Stimuli
As illustrated in Fig. 6(a), stimuli were periodic trains of 16 white-noise bursts, each 1 ms in duration and repeating at a rate of 500 Hz (i.e., 2-ms ICI). As in the “16 repeats” condition of Experiment 1, noise tokens were identical from burst to burst. Stimuli were delivered over headphones (Stax SR-307) at 70 dB SPL (peak equivalent). ITD and ILD varied from trial to trial across five base values of and dB. Within each trial, ITD and ILD varied randomly from click to click (uniform distribution spanning and ±2 dB). Unlike Experiment 1, however, ITD and ILD values were linked—as in Experiment 1 of Stecker et al. (2013)—such that a click carrying ITD also carried 1 dB ILD, etc.
FIG. 6.
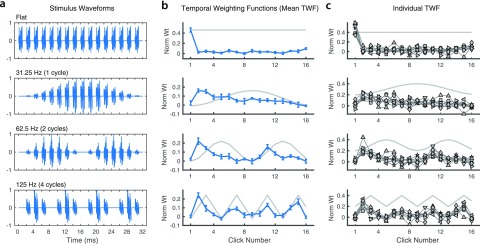
(Color online) TWFs with sinusoidal AM imposed (Experiment 2). (a) Example waveforms from each of the four conditions: unmodulated/flat envelope (top), 1, 2, or 4 AM cycles (bottom). Note that click 1 coincides with the initial envelope minimum for AM condition and thus has zero amplitude. (b) Mean TWF (±1 s.e.) in each condition. The overall AM envelope is illustrated for reference in each panel (gray line). (c) TWF plotted separately for each participant (symbols); data of the first author indicated by stars.
The parameter of interest in Experiment 2 was the temporal envelope. In one condition, stimuli were presented with a flat amplitude envelope (i.e., all noise bursts were presented at equal intensity). In other conditions, sinusoidal amplitude modulation (AM) was applied at three rates resulting in one, two, or four AM cycles over the stimulus duration. Modulation depth was 100% and modulation phase was configured to align the initial burst with an envelope minimum (i.e., “click 1” was silent in all AM conditions).
3. Procedure
Testing took place in a double-walled sound-treated room, with the subject seated in a swivel chair and facing an 80-cm (diagonal) touch-sensitive display (Elo Touchsystems 3200L, Tyco Electronics, Bermuda) at a distance of 50 cm. Although head tracking was not employed, other aspects of the procedure and instruction to participants were identical to Experiment 1. Participants completed four runs of 75 trials per AM condition. Conditions were tested in random order within each of the four replicate blocks.
Because ITD and ILD were manipulated together rather than independently as in Experiment 1, TWFs comprised 16 weights (one per click). Weights were calculated by regressing rank-transformed lateralization responses θR onto binaural cue values applied to each click,
| (6) |
where ΔLi indicates the ILD () applied to click i. Weights were normalized according to Eq. (3) prior to averaging across participants for plotting.
B. Results and discussion
Lines in Fig. 6(b) plot mean TWFs [±1 standard error (s.e.)] for each of the four AM conditions. These reveal clear onset dominance and modest recency effects in the flat-envelope condition (top), qualitatively consistent with Experiment 1 and with previous studies of TWF at 2-ms ICI (Stecker and Hafter, 2002, 2009). For this condition, mean ARonset was 15.95 (range across subjects: 9.3 to 29.3), significantly greater than mean values obtained for 2-ms ICI in Experiment 1: 8.0 for ITD; 4.2 for ILD. Note that the stimuli were identical except that ITD and ILD were manipulated in agreement, and with a larger range of ITD variation per burst, in Experiment 2. Neither factor seems likely to account for the difference. In particular, Stecker et al. (2013) directly compared TWF for ITD and ILD manipulated in isolation, in agreement, and independently, and found that ARonset, which ranged 6.0–8.2, did not differ significantly across conditions. One major difference between Experiments 1 and 2 is the experimental context: as in past studies, Experiment 1 measured TWF across a range of stimuli that all featured abrupt onsets. Listeners in Experiment 2 were exposed (on different runs) to AM sounds with a range of more gradual envelope slopes. It is possible that short-term experience induced different patterns of weighting, a possibility which should be addressed more directly in future research.
Mean ARoffset for the flat-envelope condition was 3.2, ranging 1.3 to 6.0 across subjects. That value is consistent with Experiment 1 and with previous studies (e.g., Stecker et al., 2013).
In all three AM conditions, the largest weights occurred during the earliest rising part of each modulation period. In each condition, the largest mean weight fell on click 2. Because “click 1” was actually silent, click 2 was both the earliest and the least intense of the non-silent clicks. In contrast, the most intense clicks received very low weights, as did clicks aligned with the falling phase of the envelope. These results are consistent with the dominance of the overall onset in sounds with flat envelopes, and with the importance of rising envelopes for ITD processing at high (Klein-Hennig et al., 2011) and low (Dietz et al., 2013) frequencies.
One apparent trend in the TWFs for two and four AM cycles is that in later cycles, the weight peak shifts toward alignment with the amplitude peak of the AM envelope. For example, the second TWF peak at 62.5 Hz [third row in Fig. 6(b)] occurs at click 11, which is two clicks (4 ms) after the envelope minimum at click 9. Had the pattern of weights simply repeated from the first to the second AM cycle, the peak should have occurred at click 10. Similarly, at 125 Hz (bottom row), local maxima shift from the first (click 2) toward the second (clicks 7, 11, and 15) click in each modulation cycle. The trend appears robust in the current data but will need to be replicated in future studies. It would suggest that weighting patterns might adapt to emphasize envelope peaks over slopes later in a sound's duration. Ongoing-cue sensitivity in longer-duration AM sounds might, then, reflect processing of envelope peaks. The observation could also relate to recent evidence that envelope peaks receive greater weight for slower pulse rates (200 Hz vs 600 Hz) where sensitivity to ongoing ITD is stronger (Hu et al., 2017).
IV. SUMMARY AND CONCLUSIONS
This study measured TWF for ITD and ILD carried by trains of broadband noise bursts. Stimuli varied from periodic (noise tokens repeated from burst to burst) to aperiodic (independent tokens on successive bursts).
-
(1)
Periodic noise-burst trains reveal TWF features (e.g., onset dominance at short ICI) that closely match those obtained with periodic narrowband sounds (Stecker, 2014).
-
(2)
TWFs for aperiodic noise-burst trains exhibit markedly reduced onset dominance, indicating greater potency of ongoing cues consistent with previous results with noise carriers (Tobias and Schubert, 1959).
-
(3)
These results support the importance of fluctuations in within-channel envelopes. Envelope-triggered sampling of binaural information (Hafter and Buell, 1990; Dietz et al., 2013; Stecker, 2016b) accounts for both onset dominance in periodic sounds and ongoing sensitivity in stochastic sounds.
-
(4)
Imposing a sinusoidal amplitude envelope on otherwise-periodic noise-burst trains reveals greatest weight during the earliest and least intense part of the rising envelope. Envelope peaks received less weight, but future work should assess whether that pattern adapts from cycle to cycle.
ACKNOWLEDGMENTS
This research was supported by Grant No. R01 DC011548 (to G.C.S.) from the National Institute on Deafness and Other Communication Disorders (NIDCD). The content is solely the responsibility of the author and does not necessarily represent the official views of the NIDCD or the National Institutes of Health. Portions of this work were presented to the International Congress on Acoustics (Montreal, Quebec, 2013; Buenos Aires, 2016) and published in the Proceedings of Meetings on Acoustics (Stecker, 2013, 2016a) and to the AES International Conference on Audio for Virtual and Augmented Reality (Stecker and Diedesch, 2016). Thanks to Julie Stecker for managing these studies and collecting the data, and to two anonymous reviewers who provided critical feedback on earlier versions of the manuscript.
References
- 1. Akeroyd, M. A. (2001). “ A binaural cross-correlogram toolbox for MATLAB,” Technical Report, University of Connecticut Health Center/University of Sussex, software downloadable from http://www.ihr.mrc.ac.uk/projects/matlab/binaural_toolbox (Last viewed 10 October 2014).
- 2. Akeroyd, M. A. , and Bernstein, L. R. (2001). “ The variation across time of sensitivity to interaural disparities: Behavioral measurements and quantitative analyses,” J. Acoust. Soc. Am. 110(5), 2516–2526. 10.1121/1.1412442 [DOI] [PubMed] [Google Scholar]
- 3. Benjamini, Y. , and Hochberg, Y. (1995). “ Controlling the false discovery rate: A practical and powerful approach to multiple testing,” J. R. Stat. Soc. Ser. B 57(1), 289–300. [Google Scholar]
- 4. Bernstein, L. R. , and Trahiotis, C. (1996). “ The normalized correlation: Accounting for binaural detection across center frequency,” J. Acoust. Soc. Am. 100(6), 3774–3784. 10.1121/1.417237 [DOI] [PubMed] [Google Scholar]
- 5. Brown, A. D. , and Stecker, G. C. (2010). “ Temporal weighting of interaural time and level differences in high-rate click trains,” J. Acoust. Soc. Am. 128(1), 332–341. 10.1121/1.3436540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Brown, A. D. , and Stecker, G. C. (2011). “ Temporal weighting functions for interaural time and level differences. II. The effect of binaurally synchronous temporal jitter,” J. Acoust. Soc. Am. 129(1), 293–300. 10.1121/1.3514422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Brown, A. D. , Stecker, G. C. , and Tollin, D. J. (2015). “ The precedence effect in sound localization,” J. Assoc. Res. Otolaryngol. 16(1), 1–28. 10.1007/s10162-014-0496-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Diedesch, A. C. , and Stecker, G. C. (2015). “ Temporal weighting of binaural information at low frequencies: Discrimination of dynamic interaural time and level differences,” J. Acoust. Soc. Am. 138(1), 125–133. 10.1121/1.4922327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Dietz, M. , Marquardt, T. , Salminen, N. H. , and McAlpine, D. (2013). “ Emphasis of spatial cues in the temporal fine structure during the rising segments of amplitude-modulated sounds,” Proc. Natl. Acad. Sci. U.S.A. 110(37), 15151–15156. 10.1073/pnas.1309712110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Fox, J. (2008). Applied Regression Analysis and Generalized Linear Models ( Sage Publications, Thousand Oaks, CA: ), Chap. 21, pp. 587–606. [Google Scholar]
- 11. Freyman, R. L. , Balakrishnan, U. , and Zurek, P. M. (2010). “ Lateralization of noise-burst trains based on onset and ongoing interaural delays,” J. Acoust. Soc. Am. 128(1), 320–331. 10.1121/1.3436560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Freyman, R. L. , and Zurek, P. M. (2017). “ Strength of onset and ongoing cues in judgments of lateral position,” J. Acoust. Soc. Am. 142(1), 206–214. 10.1121/1.4990020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Freyman, R. L. , Zurek, P. M. , Balakrishnan, U. , and Chiang, Y. C. (1997). “ Onset dominance in lateralization,” J. Acoust. Soc. Am. 101(3), 1649–1659. 10.1121/1.418149 [DOI] [PubMed] [Google Scholar]
- 14. Goupell, M. J. , Laback, B. , and Majdak, P. (2009). “ Enhancing sensitivity to interaural time differences at high modulation rates by introducing temporal jitter,” J. Acoust. Soc. Am. 126(5), 2511–2521. 10.1121/1.3206584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hafter, E. R. , and Buell, T. N. (1990). “ Restarting the adapted binaural system,” J. Acoust. Soc. Am. 88(2), 806–812. 10.1121/1.399730 [DOI] [PubMed] [Google Scholar]
- 16. Hafter, E. R. , and Dye, R. H. J. (1983). “ Detection of interaural differences of time in trains of high-frequency clicks as a function of interclick interval and number,” J. Acoust. Soc. Am. 73(2), 644–651. 10.1121/1.388956 [DOI] [PubMed] [Google Scholar]
- 17. Hafter, E. R. , Dye, R. H. J. , and Wenzel, E. M. (1983). “ Detection of interaural differences of intensity in trains of high-frequency clicks as a function of interclick interval and number,” J. Acoust. Soc. Am. 73, 1708–1713. 10.1121/1.389394 [DOI] [PubMed] [Google Scholar]
- 18. Hartmann, W. M. , and Rakerd, B. (1989). “ Localization of sound in rooms IV: The Franssen effect,” J. Acoust. Soc. Am. 86(4), 1366–1373. 10.1121/1.398696 [DOI] [PubMed] [Google Scholar]
- 19. Hu, H. , Ewert, S. D. , McAlpine, D. , and Dietz, M. (2017). “ Differences in the temporal course of interaural time difference sensitivity between acoustic and electric hearing in amplitude modulated stimuli,” J. Acoust. Soc. Am. 141(3), 1862–1873. 10.1121/1.4977014 [DOI] [PubMed] [Google Scholar]
- 20. Klein-Hennig, M. , Dietz, M. , Hohmann, V. , and Ewert, S. D. (2011). “ The influence of different segments of the ongoing envelope on sensitivity to interaural time delays,” J. Acoust. Soc. Am. 129(6), 3856–3872. 10.1121/1.3585847 [DOI] [PubMed] [Google Scholar]
- 21. Laback, B. , and Majdak, P. (2008). “ Binaural jitter improves interaural time-difference sensitivity of cochlear implantees at high pulse rates,” Proc. Natl. Acad. Sci. U.S.A. 105(2), 814–817. 10.1073/pnas.0709199105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Saberi, K. (1996). “ Observer weighting of interaural delays in filtered impulses,” Percept. Psychophys. 58(7), 1037–1046. 10.3758/BF03206831 [DOI] [PubMed] [Google Scholar]
- 23. Stecker, G. C. (2013). “ Effects of carrier frequency and bandwidth on temporal weighting of binaural differences,” Proc. Mtgs. Acoust. 19, 050166. 10.1121/1.4799585 [DOI] [Google Scholar]
- 24. Stecker, G. C. (2014). “ Temporal weighting functions for interaural time and level differences. IV. Effects of carrier frequency,” J. Acoust. Soc. Am. 136(6), 3221–3232. 10.1121/1.4900827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Stecker, G. C. (2016a). “ Exploiting envelope fluctuations to achieve robust extraction and intelligent integration of binaural cues,” in Proceedings of the International Congress on Acoustics, September 5–9, Buenos Aires, Argentina, Vol. 22, pp. 1–10. [Google Scholar]
- 26. Stecker, G. C. (2016b). “ Exploiting envelope fluctuations to enhance binaural perception,” in Proceedings of the Audio Engineering Society, June 4–7, Paris, France, Vol. 140. [Google Scholar]
- 27. Stecker, G. C. , and Bibee, J. M. (2014). “ Nonuniform temporal weighting of interaural time differences in 500 Hz tones,” J. Acoust. Soc. Am. 135(6), 3541–3547. 10.1121/1.4876179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Stecker, G. C. , and Diedesch, A. C. (2016). “ Perceptual weighting of binaural information: Toward an auditory perceptual ‘spatial codec’ for auditory augmented reality,” in Proceedings of the AES Conference on Audio for Virtual and Augmented Reality, September 30–October 1, Los Angeles, CA, pp. 107–114. [Google Scholar]
- 29. Stecker, G. C. , and Hafter, E. R. (2002). “ Temporal weighting in sound localization,” J. Acoust. Soc. Am. 112(3), 1046–1057. 10.1121/1.1497366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Stecker, G. C. , and Hafter, E. R. (2009). “ A recency effect in sound localization?,” J. Acoust. Soc. Am. 125(6), 3914–3924. 10.1121/1.3124776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Stecker, G. C. , Ostreicher, J. D. , and Brown, A. D. (2013). “ Temporal weighting functions for interaural time and level differences. III. Temporal weighting for lateral position judgments,” J. Acoust. Soc. Am. 134(2), 1242–1252. 10.1121/1.4812857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Tobias, J. V. , and Schubert, E. R. (1959). “ Effective onset duration of auditory stimuli,” J. Acoust. Soc. Am. 31, 1595–1605. 10.1121/1.1907665 [DOI] [Google Scholar]
- 33. Tollin, D. J. (1998). “ Computational model of the lateralization of clicks and their echoes,” in Proceedings of the NATO Advanced Study Institute on Computational Hearing, edited by Greenberg S. and Slaney M., July 1–12, Il Ciocco, Italy, pp. 77–82. [Google Scholar]
- 34. Tollin, D. J. , and Henning, G. B. (1999). “ Some aspects of the lateralization of echoed sound in man. II. The role of the stimulus spectrum,” J. Acoust. Soc. Am. 105(2), 838–849. 10.1121/1.426273 [DOI] [PubMed] [Google Scholar]
- 35. Trahiotis, C. , and Stern, R. M. (1989). “ Lateralization of bands of noise: Effects of bandwidth and differences of interaural time and phase,” J. Acoust. Soc. Am. 86(4), 1285–1293. 10.1121/1.398743 [DOI] [PubMed] [Google Scholar]
- 36. Zurek, P. M. (1980). “ The precedence effect and its possible role in the avoidance of interaural ambiguities,” J. Acoust. Soc. Am. 67(3), 952–964. 10.1121/1.383974 [DOI] [PubMed] [Google Scholar]