Human entorhinal cortex represents visual space using a boundary-anchored grid

Abstract

When participants performed a visual search task, fMRI responses in entorhinal cortex (EC) exhibited a 6-fold periodic modulation by gaze movement direction. The orientation of this modulation was determined by the shape and orientation of the bounded search space. These results indicate that human EC represents visual space using a boundary-anchored grid, analogous to that used to represent navigable space in rodents.

Main Text

During spatial navigation in rodents, grid cells fire when the body of the animal occupies a hexagonal lattice of spatial locations tiling the floor of the environment¹. These cells are believed to support a metric for navigational space that is anchored to environmental boundaries^{2, 3}. Recent work with monkeys has expanded the variety of spaces that might be represented by grid cells, by demonstrating the existence of neurons in EC that fire in a hexagonal lattice of positions on a screen while animals explore visual space⁴. However, it is currently unknown whether a similar grid-like coding of visual space exists in humans, or whether putative grid representations of visual space obey the same boundary-anchoring principles as grid representations of navigational space.

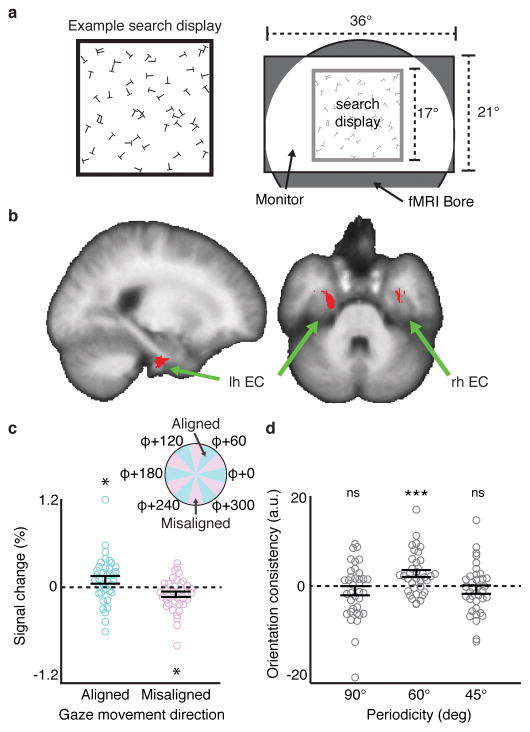
To address these issues, we used fMRI methods previously developed for identifying grid signals in humans during virtual navigation⁵. These methods are motivated by the observation that firing patterns for grid cells within an individual tend to have the same orientation^{1, 5}. Because of this common orientation, movements along a shared grid axis will yield a stronger grid-driven fMRI signal in EC than movements between grid axes, resulting in 60° periodic modulation by movement direction. We reasoned that if grid cells represent visual space in humans, then we should observe a similar 60° periodic fMRI signal as a function of gaze movement direction while participants visually explored the environment. To test this idea, participants (n=36) were scanned with fMRI and had their gaze tracked while they performed an unconstrained visual search task in which they had to find a target letter (‘L’) among numerous distractors letters (‘T’s) (Fig. 1A). A square border surrounded the search display for half the participants (n=18) and a rectangular border surrounded the display for the other half (n=18).

Figure 1. Visual grid-like representation in human entorhinal cortex (EC).

a) Left: example square visual search display (for display purposes, example display has fewer letters than actual displays and relative letter size is increased). Right: schematic of the scene visible during scanning. b) Reliable grid-like coding of visual space was observed in bilateral EC (t-test, p<0.05, SVC in bilateral EC; peak MNI coordinates: 40/−4/−38, peak Z=3.09). c) fMRI response in a 2mm sphere centered on the peak EC voxel from (b) for periods of gaze movement aligned to grid orientation φ (within ±15° of a φ axis) and misaligned (more than ± 15° from all φ axes) (aligned: t-test, t(35)=1.95, p=0.030, sign-test p=0.033; misaligned: t-test, t(35)=−2.60, p=0.014, sign-test p=0.029, two-tailed tests). d) Split-half orientation consistency (beta weight) in the spherical EC voxel ROI from (c) for 90° and 45° periodicities (magnitude of 60° plotted for scale). Neither 90° nor 45° showed significant orientation consistency (90°: t-test, t(35)=−1.15, p=0.87, sign-test p=0.56; 45°: t-test, t(35)=−1.02, p=0.84, sign-test p=0.93). Note that these null effects were not specific to the EC ROI based on the 60° periodicity analysis, as we saw no effect for 90° or 45° in the entire EC at p<0.05 (SVC). Throughout the figure, all statistical tests are one-tailed unless otherwise noted, and n=36 participants; error bars show ±1 SEM; *p<0.05; ***p<0.001; ns, not significant.

For each participant, we split the fMRI data into halves, identified the orientation of the 60° periodic signal as a function of gaze movement direction within EC in one half of the data, and tested the reliability of this visual grid orientation in the independent second half (Supplementary Fig. 1). Consistent with our prediction, we observed significant reliable 6-fold modulation of the fMRI signal as a function of gaze movement direction bilaterally in EC (Fig. 1B). This result reflects greater fMRI response when gaze movement directions were aligned with the three grid axes than misaligned (Fig. 1C; Supplementary Fig. 2). Conducting the same analyses for other rotational symmetries, we found no evidence of reliable 90° or 45° periodic signals across independent halves of the data in EC (Fig. 1D). Notably, across participants, the magnitude of the 60° periodic EC signal significantly correlated with self-reported navigational ability, suggesting that the same population of grid cells might support both vision and navigation (Supplementary Fig. 2). All gaze movement directions were sampled during the visual search task, and we detected no 6-fold biases in gaze behavior that could explain the presence of a 6-fold symmetric fMRI signal (Supplementary Fig. 3). Thus these results are evidence of a grid representation in human EC that codes for locations in visual space, complementing previous findings of grid representations in navigable space^{5, 6}. Grid-like coding of visual space was also observed in a medial prefrontal region of interest previously reported to exhibit a grid-like response during navigation⁵ (Supplementary Fig. 4).

We next explored the coordinate system that EC uses to encode visual space. For grid cells to provide useful information about environmental locations, grid cell firing patterns must be stably anchored to features of the external world, such as environmental boundaries. In previous work examining grid cells tiling visual space in monkey EC, the head of the animal was fixed relative to the visual display, making it difficult to determine whether these cells coded locations in egocentric (head-centered) or allocentric (world-centered) coordinates. To address this issue, we tested whether EC grid representations of visual space exhibit two signatures of boundary-anchored coding previously observed in rodent grid cells.

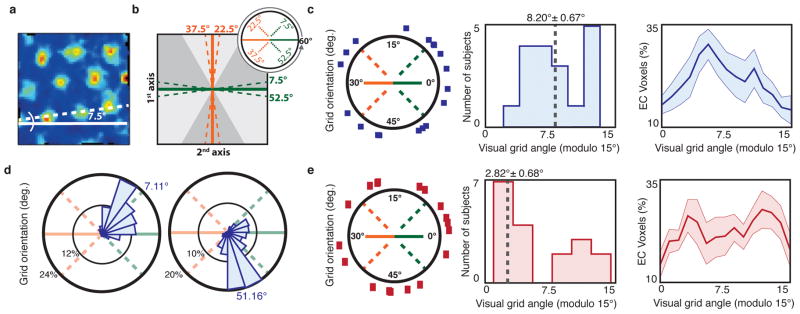
First, we asked whether grid orientations are reliably aligned by search display shape. When rodents explore square environments, the grid lattice aligns to ±7.5° from the cardinal axes of the borders^{2, 3} (Fig. 2A). We looked for a similar effect in the participants who searched square displays (Fig. 2B). Across these participants, the average EC visual grid orientations were significantly clustered around ±7.5° offset from the cardinal axes of the square display border (Fig. 2C). Moreover, of the 14/18 participants who showed significant clustering of grid angles across voxels in bilateral EC, 12/14 had grid angles significantly clustered across voxels 6°–9° offset from the display borders (Fig. 2D; Supplementary Fig. 5). By contrast, visual grid orientations for the rectangular display participants were not clustered around ±7.5° from the rectangular borders across participants (Fig. 2E). Indeed, grid orientations were closer to 7.5° offset from the display borders in the square display participants than in the rectangular display participants (t-test, t(34)=2.26, p=0.015, one-tailed). Because the shape of the display was the only stable environmental feature that differed between these participants, these results confirm that visual grid orientations were affected by the geometry of the visual environment.

Figure 2. Visual grid orientation is anchored to the search display geometry.

a) The grid orientations of rodents navigating through square environments align to an offset of 7.5° perpendicular to an environment wall (example cell shown is adapted with permission from ref. [3]). b) We tested whether the visual grid orientation φ was similarly offset 7.5° from the square display borders. Specifically, because the possible range of φ is between 0°–60°, we examined whether grid orientations cluster around 4 possible angles, each 7.5° from one of the two cardinal axes of the display borders. c) Grid orientations of the square display participants. Left: average grid angle in each participant (blue squares), on the range of 0°–60°; Middle: histogram of average grid orientations across participants modulo 15°, showing clustering around 7.5° (n=18; V-test, V=5.18, p=0.0421); Right: average percentage of grid orientations modulo 15° ±1 SEM across all bilateral EC voxels. The average grid angle and standard error reported above the middle histogram were computed in circular space. d) Polar histograms of all EC voxel grid orientations for two exemplary square display participants. Note clustering of grid orientations around ±7.5° from the display border (n=285, 289 voxels; V-test, V=180.42, 205.54, p=3x10⁻⁷, 5x10⁻⁹, Bonferonni corrected). e) Grid orientations of the rectangular display participants (red rectangles), organized as in (c). Across rectangular display participants, grid orientations were not clustered around 7.5° (n=18; V-test, V=−2.48, p=0.796).

Second, we examined whether rotation of the search display would induce a corresponding rotation of the visual grid. To address this question, each participant who performed the search task with the upright rectangular search displays also completed two additional scan runs in which the displays were rotated 30° clockwise (Fig. 3A). If the visual grid code is anchored to the borders of the search display, then rotation of the search display should yield a corresponding 30° rotation of the visual grid orientation, as observed in navigating rodents when chamber boundaries are rotated². We found that the fMRI signal in EC during rotated runs was better predicted by a grid angle that was rotated 30° relative to the upright-display-fit grid orientation than it was by a grid angle that was not rotated (Fig. 3B; Supplementary Fig. 6). Furthermore, the average grid orientation during rotated runs was offset 28.33°±2.87° (mean angle ± s.e.m.) relative to the grid orientation during upright runs (Fig. 3C). Interesting, 6 participants showed little grid angle rotation (Fig. 3D). Surprisingly, these non-rotating participants were faster at finding the target letter during the rotated-display runs than the participants whose grid orientations rotated (Fig. 3E). Thus, although visual grids were anchored to the borders of the search display on average, there were individual differences in which external reference frame was selected, and these differences had consequences for search behavior.

Figure 3. Visual grid orientation rotates in concert with rotation of the search display.

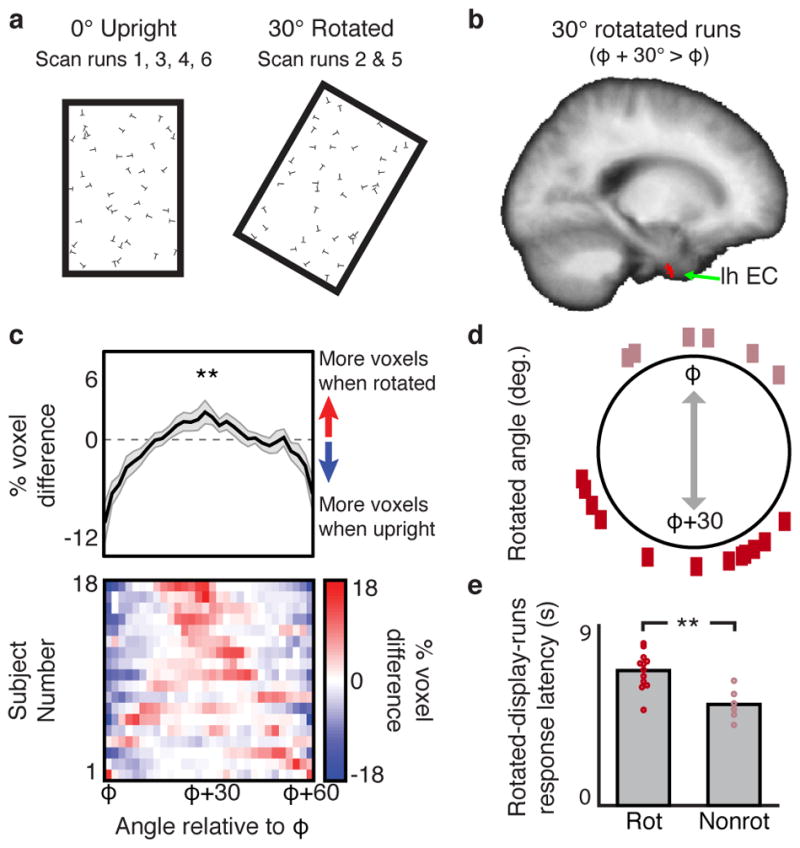
a) For the rectangular display participants, the search displays were rotated 30° clockwise during two scan runs. b) For the rotated-display-runs, we tested whether a 30° rotation of the grid orientation φ identified in the upright-display-runs (φ+30°) better predicted the fMRI signal than the original grid orientation (φ). In left EC, 60° periodic sinusoidal modulation of the fMRI signal was significantly greater when gaze movements were aligned to φ+30° than when they were aligned to φ (n=18 participants; t-test, p < 0.05 two-tailed, SVC in bilateral EC; peak MNI coordinates: −24/−5/−44, peak Z score = 3.32). No right hemisphere EC voxels survived SVC, and no EC voxels showed greater modulation for φ than for φ+30°. c) The percent difference in the distributions of grid orientations across all bilateral EC voxels during the rotated-display-runs compared to the upright-display-runs in each participant (bottom row) and on average ±1 SEM (top row). Across participants (n=18), there was a greater percentage of voxels with grid orientations around φ+30° when the display was rotated than upright (t-test, t(17)=2.89, p=0.005, one-tailed). d) Difference in average grid angles between the upright-display-runs and the rotated-display-runs in each participant. e) Comparison of response latency between subjects whose grid angles rotated with the display (Rot; n=12; dark rectangles in (d); >15° absolute upright vs. rotated difference) and those subjects whose grid angles remained fixed relative to an alternate reference frame (Nonrot; n=6; light rectangles in (d); <15° absolute difference) (t-test, t(16)=3.81, p=0.002, two-tailed). **p<0.01.

In sum, we report the first evidence that human EC represents locations in visual space using a grid code. This visual grid code exhibited two signatures of boundary-anchoring previously observed in rodent grid cells—alignment to boundaries based on the shape of the environment, and rotation when the environmental borders are rotated—indicating that similar computational principles anchor primate and rodent grid cells to the external world, even across different spatial domains. These results may illuminate a longstanding controversy over the representation of visual space. Previous evidence suggests that the mammalian visual system represents space in retinotopic coordinates^7–9, which are updated before each eye movement based on information about the intended direction of the upcoming saccade¹⁰. Although non-retinotopic spatial codes are observed under some circumstances^{11, 12}, it is often unclear whether these codes are egocentric (head-centered) or allocentric (world-centered), and evidence for an allocentric map that represents where a viewer is looking relative to stable visual environmental cues has remained sparse (although see refs. [^{13, 14}]). The current results provide evidence for such a map and suggest a mechanism by which it might be generated. During navigation, grid cells are thought to perform path integration by using self-motion inputs^{1, 15} to update allocentric representations of location^{2, 3}. We hypothesize that visual grid cells may use a similar path integration mechanism to update an allocentric representation of the current gaze position based on eye motion signals present in the hippocampus and EC^{16, 17}. Beyond navigation, recent work has also shown that a grid-like code is used to represent both imagined and conceptual spaces^18–20. Our data add to this growing body of work by showing that grid cells may provide the mechanism by which locations in visual space are coded, thus allowing us to form durable visuospatial representations that are stable across eye movements.

Online Methods

Participants

36 participants (14 male) took part in this experiment (mean age: 23; range: 18–32). All participants gave written consent and were paid for participating, in compliance with procedures approved by the University of Pennsylvania Internal Review Board. All had normal vision and reported to be in good health with no history of neurological disease. Data from 7 additional participants were collected but discarded before analysis of fMRI data due to poor eye tracking quality (6 because of inaccurate gaze reconstructions; one because of poor sampling of all gaze angles). Data from one additional participant was discarded due to excessive head motion during scanning (>3 mm average absolute head motion). Following scanning, each participant completed the Santa Barbara Sense of Direction (SBSOD) questionnaire²¹, which provides a standardized measure of self-reported navigational ability.

Visual search task

Participants completed a series of 6.5 min fMRI scan runs during which they performed a visual search task. Square display participants completed four runs and rectangular display participants completed six runs. Participants were randomly assigned to display shape groups. During each run, participants viewed visual search displays consisting of a single target letter ‘L’ shown amongst distractor letters ‘T’s (letter height = 0.74°). Participants were instructed to use their eyes to search for the target, and to press a button when they found the target letter. Each trial was self-paced, and lasted an average of 7.50±0.58 seconds (mean±s.e.m.). Stimuli were presented using Matlab (2016a, The MathWorks Inc., Massachusetts) and the Psychtoolbox²² (Version 3.0.11). A pseudo-random search display was generated on each trial, such that all letters had a random location within the borders of the search display shape, subject to the constraint that only partial overlap between the letters was permitted, and a random orientation. Note that this meant that the shape implied by the array of letters was the same as the shape defined by the drawn border. Each search display had one of three possible densities ([100, 144, 169] or [81, 100, 121] letters total in the square and rectangle conditions, respectively). The search display density was randomly selected on each trial, with the constraint that each of the three possible densities was presented once before repeating. Search displays subtended a visual angle of 17.0° × 17.0° (square participants) or 11.0° × 17.0° (rectangular participants), and the search display border line thickness was 0.21°. There was a variable inter-trial interval of 2–6 seconds, randomly selected on each trial, during which participants fixated on a centrally located fixation cross. The onset of each trial was time-locked to the onset of an fMRI acquisition.

For the rectangular display participants, four scan runs consisted of upright rectangular displays, and two runs consisted of rectangular displays rotated by 30° clockwise. For these participants, the presentation order of the displays was URUURU, where U and R correspond to upright and rotated displays, respectively. This ordering ensured that any effect of display rotation could not be due to general drift across runs.

Eye tracking methods and preprocessing

Participant’s gaze position during scanning was monitored and recorded using a LiveTrack AV MR-compatible eye tracking camera (Cambridge Research Systems, Rochester England). The gaze position of the right eye was recorded at 30 Hz. Prior to each scan run, gaze position was calibrated using a series of nine fixation points evenly spaced between −8° and +8° in the horizontal and vertical dimensions relative to screen center. The average calibration error across all runs was 0.332° ± 0.018° (mean ± s.e.m.). In order to separate periods of gaze movements from periods of fixations, periods of gaze movement were defined by a movement-velocity-thresholding procedure, as follows. To reduce misattribution of gaze movements to eye tracking noise, the gaze position time course was first temporally smoothed with a boxcar filter (half width = 0.185 seconds). Gaze movements were then identified based on a median split of the smoothed gaze movement instantaneous velocity. Gaze position measurements in the bottom half of gaze movement velocities were treated as no movement, as were samples during which participants blinked. Gaze movements with velocities in the upper median half tended to be long saccades relative to the size of the search displays, with an average ballistic gaze trajectory length of 1.60° ± 0.60° (mean ± standard deviation). Note that this velocity-thresholding procedure is conservative in that it excludes short gaze movements during which we would not expect to observe a strong grid-like fMRI signal, based on previous fMRI studies of human navigation^{5, 18}. Based on this method of classifying gaze movements, 7.1% ± 0.57% (mean ± s.e.m.) of all fMRI acquisitions contained no gaze movements whatsoever for the entire duration of the acquisition, which served as the implicit baseline relative to which fMRI signal change was measured.

fMRI acquisition

Scanning was performed at the Center for Functional Imaging at the University of Pennsylvania using a 3T Siemens Prisma scanner equipped with a 64-channel head coil. High-resolution T1-weighted images for anatomical localization were acquired using a 3-dimensional magnetization-prepared rapid-acquisition gradient-echo pulse sequence (repetition time [TR], 1620 ms; echo time [TE], 3.09 ms; inversion time, 950 ms; voxel size, 1x1x1 mm; matrix size, 192x256x160). T2*-weighted images sensitive to blood oxygenation level-dependent contrasts were acquired using a gradient-echo echoplanar pulse sequence (TR, 1000 ms; TE, 25 ms; flip angle 45°; voxel size, 2x2x2 mm; field of view, 192; matrix size, 96x96x78; multiband acceleration factor of 4). Ten additional fMRI volumes were also collected at the start of each scan run that were excluded from data analysis to account for signal steady-state transition. Visual stimuli were displayed at the rear bore face on an InVivo SensaVue Flat Panel Screen at 1920 × 1080 pixel resolution (diag = 80.0 cm, w × h = 69.7 × 39.2 cm). Participants viewed the stimuli through a mirror attached to the head coil. Behavioral responses were collected using a fiber-optic button box.

fMRI analysis – preprocessing

FMRI data analysis was carried out using FSL FEAT (FMRIB’s Software Library, version 6.00, www.fmrib.ox.ac.uk/fsl). The following standard data preprocessing was performed: motion correction using MCFLIRT²³, non-brain removal using BET²⁴; spatial smoothing using a Gaussian kernel of FWHM 8mm; grand-mean intensity normalization of the 4D dataset by a single multiplicative factor for each scan run; highpass temporal filtering (Gaussian-weighted least-squares straight line fitting, with sigma=50.0s). For second-level group analyses, EPI images were registered to the high-resolution anatomical image using boundary-based reconstruction and then normalized into standard space (MNI305) using non-linear registration. All data normalization was performed using Freesurfer (version 5.3.0, http://surfer.nmr.mgh.harvard.edu/).

fMRI analysis – Identifying grid-like coding of visual space

We performed a split-half analysis to estimate the orientation of the visual grid code during periods of gaze movement, following procedures used previously to identify grid-like codes during virtual navigation^{5, 18, 25, 26} (Supplementary Fig. 1). Data were first split into halves by run (runs [2,4] and [1,3] for square participants; runs [1,4] and [3,6] for rectangle participants, so that only the upright rectangle runs were used to identify grid-like coding in this initial analysis). For each half of the data, we identified the angular orientation of the putative visual grid axes in each participant’s bilateral EC. The grid orientation thus obtained was then subsequently used to predict a grid signal during the other independent half of the runs.

To fit the orientation of the 6-fold gaze movement direction-modulated signal within EC, we constructed a general linear model (GLM) with two parametric modulators (PMs) for periods of gaze movement. These two PMs were cos(6a(t)) and sin(6a(t)), where a(t) is the gaze movement direction sampled at time t (30 Hz). Each PM was down-sampled to the TR (1 Hz) by summing the values of the PM within each TR. The weights (b1 and b2) on these PMs were fitted to the fMRI time series for each voxel within the anatomically defined bilateral EC ROI. This EC ROI was constructed uniquely for each participant based on the automatic anatomical parcellation of the EC derived from FreeSurfer structural reconstruction. We then calculated the orientation of the 6-fold gaze movement direction-modulation from the mean weights across all voxels in the EC ROI as φ = [arctan(<b2>/<b1>)]/6, separately for each run, where arctan was mapped into 360° space, varying between 0° and 60°, according to signs of b2 and b1. Finally we computed the circular average orientation across runs for each separate half of the data. Grid orientations were quantitatively similar if we averaged the beta weights voxel-wise across runs before calculating the orientation instead of averaging the orientations across runs (circular correlation across participants: c=0.84, p<10⁻⁵).

To test whether the fit orientations predicted the analogous 6-fold periodic signal in the other independent half of the data, we constructed a GLM with a PM modeling the effect of gaze movement direction on the fMRI signal. The value of this PM at each timepoint was the cosine of gaze movement direction at that timepoint aligned to the orientation predicted by the first half of the data, cos(6(a(t)- φ)), where a(t) is the gaze movement direction sampled at time t (30 Hz). This PM was down sampled to the TR by summing the values of the PM within each TR. Each beta from this analysis reflects the extent of reliable split-half φ-oriented 6-fold gaze movement direction-modulated fMRI signal (which we call “orientation consistency”). The beta weights for this PM were averaged across all scan runs within each participant. The group-level test of the significance of these weights was small-volume FWE-corrected (SVC) within a group-level bilateral EC ROI, which was defined as the union of all individual-participant anatomically-defined EC ROIs projected into MNI space. To confirm that the gaze movement direction-modulated signal in EC exhibited a specifically 60° periodicity, we conducted this same split-half analysis for 90° (i.e., 4-fold) and 45° (i.e., 8-fold) periodicities.

Analyses were performed in FSL using FILM with local autocorrelation correction²⁷. Included in all GLMs was a binary boxcar regressor of no interest corresponding to periods of visual search and its temporal derivative, as well as six nuisance PMs to account for head motion-related artifacts. All regressors were convolved with double gamma hemodynamic response function and filtered by the same high pass filter as the fMRI data before entry into the GLM.

fMRI analysis – reliable offset of the grid-like representation orientation from the search display shape

To test whether grid orientations across participants consistently cluster around an offset of ±7.5° from the cardinal axes of the search display borders, we first computed the average of the grid orientations across all EC voxels and runs within each participant. We then folded the grid orientations of all participants by φ mod 15°, which would align all hypothesis-consistent alignments to 7.5° in a circular 0° to 15° space. Next we performed a V-test for nonuniformity centered around 7.5°. The V-test is similar to Rayleigh’s test for circular uniformity with the difference that under the alternative hypothesis the distribution is non-uniform centered at a particular hypothesized angle (in this case, 7.5°)^{28, 29}.

To test whether grid orientations in voxels within individual participants clustered around 7.5° offset from cardinal axes, we first evaluated whether EC voxels in each participant showed orientation clustering around any angle. To do so, we averaged the grid angle derived from each voxel across runs, yielding a distribution of voxel-wise grid orientations. Next we tested these voxel-wise grid orientations for non-uniformity using Rayleigh’s test for circular data. Note that because grid orientations were averaged voxel-wise across fMRI runs for this analysis, significant orientation clustering also requires temporal stability across runs of the grid orientation across voxels. This analysis identified participants who had significant nonuniformity, i.e. orientation clustering, of grid angles in EC (p<0.05, accounting for spatial smoothing). Finally, we tested whether the voxel-wise grid orientations in participants with significant clustering were specifically clustered around 6.0°–9.0° degrees in 0.5° increments (via folding and V-test, as described above; p-values were Bonferonni corrected for the seven grid angles tested).

fMRI analysis – rotation of the grid-like representation orientation with rotation of the search display

To test whether the visual grid orientations of rectangular-display participants rotated in concert with the rotated displays, we first computed the circular average of the grid orientation derived from each upright-display run. Next we rotated this average grid orientation, φ, by 30° and used this rotated orientation to predict the fMRI signal during rotated-display runs with a GLM. Specifically, a single PM to was used to model the effect of gaze movement direction on the fMRI signal during the rotated rectangle runs: a cosine of gaze movement angle aligned to the 30° rotated grid orientation, cos(6(a(t)-(φ+30°))). Positive weights from this analysis indicate that the 60° periodic fMRI signal is better predicted when the orientation of the grid axes is rotated 30° from φ during rotated-display runs, whereas negative weights indicate that rotated display runs are better predicted by the original grid orientation φ without rotation. The weights for this PM were first combined across both rotated-display runs in each participant, and then tested across participants with small-volume FWE-correction within the group-level bilateral EC ROI.

To examine the distribution of rotation effects across EC voxels, we first identified the grid orientation for each voxel during the rotated scan runs in the same fashion as we did for the upright scan runs. We then compared the distribution of grid orientations across all EC voxels when the display was upright to the distribution when the display was rotated. Specifically, for each participant, we subtracted φ from each EC voxel’s grid orientation, separately for the upright and rotated display runs, so that the average grid orientation across voxels were aligned relative to φ in each participant. We then calculated the distribution of voxels with grid orientations occurring from 0°–60° in 2° increments separately for the upright and rotated scan runs, and subtracted the upright distribution from the rotated distribution. If grid orientations across voxels rotate in concert with rotation of the search display, then there should be a higher percentage of voxels with grid angles around φ+30° when the display is rotated than upright.

Statistics

No statistical methods were used to pre-determine sample sizes, but our sample size was similar to those reported in previous publications^18–20. Parametric t-tests and non-parametric sign-tests were used throughout the paper. For each parametric test, unless otherwise noted, data values met normality assumptions (Lilliefors test, p>0.05). If data did not meet normality assumptions, only sign-tests are reported. Rayleigh’s tests and V-tests were also used, as described in detail in the two preceding fMRI analysis methods sections. Data collection and analysis were not performed blind to the conditions of the experiment. A Life Sciences Reporting Summary is available.

Code availability

The code that support the findings of this study are available from the corresponding authors upon request.

Data availability

The data that support the findings of this study are available from the corresponding authors upon request.