Measures of entropy and complexity in altered states of consciousness

Abstract

Quantification of complexity in neurophysiological signals has been studied using different methods, especially those from information or dynamical system theory. These studies have revealed a dependence on different states of consciousness, and in particular that wakefulness is characterized by a greater complexity of brain signals, perhaps due to the necessity for the brain to handle varied sensorimotor information. Thus, these frameworks are very useful in attempts to quantify cognitive states. We set out to analyze different types of signals obtained from scalp electroencephalography (EEG), intracranial EEG and magnetoencephalography recording in subjects during different states of consciousness: resting wakefulness, different sleep stages and epileptic seizures. The signals were analyzed using a statistical (permutation entropy) and a deterministic (permutation Lempel–Ziv complexity) analytical method. The results are presented in complexity versus entropy graphs, showing that the values of entropy and complexity of the signals tend to be greatest when the subjects are in fully alert states, falling in states with loss of awareness or consciousness. These findings were robust for all three types of recordings. We propose that the investigation of the structure of cognition using the frameworks of complexity will reveal mechanistic aspects of brain dynamics associated not only with altered states of consciousness but also with normal and pathological conditions.

Introduction

A multitude of studies have focused on the investigation of patterns of correlated activity among brain cell ensembles based on magnitudes of a variety of synchrony indices or similar measures. A prominent common aspect that is emerging from those studies is that of the importance of variability in the brain’s coordination dynamics. In general, neurophysiological signals associated with normal cognition demonstrate fluctuating patterns of activity that represent interactions among cell networks distributed in the brain (Guevara Erra et al. 2016). Similar result can be found in Werner (2009) and Pakhomov and Sudin (2013). This variability allows for a wide range of configurations of connections among those networks exchanging information, supporting the flexibility needed to process sensory inputs. Therefore, it has been argued that a certain degree of complexity in brain signals will be associated with healthy cognition, whereas low complexity may be a sign of pathologies (Garrett et al. 2013; Velazquez et al. 2003; Mateos et al. 2014; Dimitriadis et al. 2015). We sought to obtain evidence for the correlation between complexity in brain signals and conscious states, using brain electrophysiological recordings in conscious and unconscious states.

There exist a number of statistical measures to analyze electrophysiological recordings (Hlaváčková-Schindler et al. 2007). In our work we use two well known measures, one statistical—Shannon entropy, a measure of unpredictability of information content in a message (Shannon 1948), and the other deterministic—Lempel–Ziv complexity, based on the minimum information required to recreate the original signal (Lempel and Ziv 1976). For both measures, we use the quantifiers introduced by Bandt and Pompe (2002), called permutation vectors, which are based on the relationships of neighbor values belonging to a time series.

The Shannon entropy measure applied to the permutation vectors is known as permutation entropy (HPE) (Bandt and Pompe 2002). In a similar manner, the Lempel–Ziv complexity measure applied to the permutation vectors is called permutation Lempel–Ziv complexity (PLZC) (Zozor et al. 2014). We used these two methods to obtain information about the signal’s dynamics from two different perspectives, probabilistic (HPE) and deterministic (PLZC). The HPE and the LZC have been employed in previous studies analyzing electrophysiological recordings in epilepsy, coma or sleep stages (Olofsen et al. 2008; Ferlazzo et al. 2014; Nicolaou and Georgiou 2011; Casali et al. 2013; Zhang et al. 2001; Shalbaf et al. 2015). Moreover, there is an interesting relation, under certain restrictions, between Shannon entropy and Lempel–Ziv complexity that can naturally extend to HPE and PLZC (Cover and Thomas 2006; Zozor et al. 2014).

The results we obtain are shown in a complexity-entropy graphs. This kind of representation enables better visualization of the results giving a better understanding of the results especially for people who are not so familiar with these kind of analysis. A recent study on chaotic maps and random sequences, it showed that the complexity-entropy graph allows for the distinction of different dynamics that was impossible to discern using each analysis separately (Mateos et al. 2017). In our present work we analyze brain signals recorded using scalp electroencephalography (EEG), intracranial electroencephalography (iEEG) and magnetoencephalography (MEG), in fully alert states and in two conditions where consciousness is impaired: seizures and sleep. The hypothesis derived from the previous considerations on variability of brain activity is that the brain tends towards larger complexity and entropy in wakefulness as compared to the altered states of consciousness.

Method

Electrophysiological recordings

Recordings were analyzed from 27 subjects. Three patients with different epilepsy syndromes were studied with MEG; one patient with temporal lobe epilepsy was studied with iEEG; 3 patients with frontal or temporal lobe epilepsy were studied with simultaneous iEEG and scalp EEG; and 2 nonepileptic subjects were studied with scalp EEG.

For the study of seizures versus alert states, the 3 subjects with MEG recordings and the temporal lobe epilepsy patient investigated with iEEG were used. Details of these patients epilepsies, seizure types and recording specifics have been presented in previous studies (MEG patients in Garcia Dominguez et al. 2005; iEEG patient in Perez Velazquez et al. 2011). For the study of sleep versus alert states, recording from other 5 subject were used, with scalp EEG needed for accurate determination of sleep stages. The 3 patients with combined EEG–iEEG have been described previously (patients 1, 3, 4 in Wennberg 2010); the 2 subjects studied with scalp EEG alone were investigated because of a suspected history of epilepsy, but both were ultimately diagnosed with syncope, with no evidence of epilepsy found during prolonged EEG monitoring.

MEG recordings were obtained using a whole head CTF MEG system (Port Coquitlam, BC, Canada) with sensors covering the entire cerebral cortex, whereas iEEG subdural and depth electrodes were positioned in various locations in the frontal and temporal lobes depending on the clinical scenario, including the amygdala and hippocampal structures of both temporal lobes. EEG, iEEG and EEG–iEEG recordings were obtained using an XLTEK EEG system (Oakville, ON, Canada). Acquisition rates varied from 200 to 625 Hz and these differences were taken into consideration for the data analyses. The duration of the recordings varied as well: for the seizure study, MEG sample epochs were each of 2 min duration, with total recording times of 30–40 min per patient; the iEEG patient sample epoch selected for analysis from a continuous 24-h recording was of 55 min duration. The sleep study data segments were each 2–4 min in duration, selected from continuous 24-h recordings.

For the seizure analysis, we use 9 intracranial EEG (patient 10–18) from the European Epilepsy Database (Ihle et al. 2012). The database contains well-documented meta data, highly annotated raw data as well as several features. Acquisition rates varied from 254 to 1024 Hz and these differences were taken into consideration for the data analyses. For more information about the recordings and the setting see Ihle et al. (2012).

Finally we add 9 patient (scalp EEG) to the sleep analysis, belonged to physionet data bank The Sleep-EDF Database [Expanded] (Goldberger 2000; Kemp et al. 2000). This polysomnograms (PSGs) collection with accompanying hypnograms (expert annotations of sleep stages) comes from two studies (detail in Kemp et al. 2000, Mourtazaev et al. 1995). The recording are whole-night polysmnographic sleep recordings containing EEG (from Fpz-Cz electrode locations). The subjects included here, were 25–34 years old at the time of the recordings. The EEG signals were each sampled at 100 Hz. The sleep stages were classified based on a hypnogram in: Awake close eyes, REM, Sws 1, Sws 2, Sws 3, Sws 4.

Table 1 is shows all the subjects and recordings characteristics used in this work.

Table 1.

Subject and recording characteristics

Subject	Diagnosis	Electrophysiological recording	Setting
1	Primary generalized epilepsy	MEG	MEG unit
2	Symptomatic generalized epilepsy	MEG	MEG unit
3	Frontal lobe epilepsy	MEG	MEG unit
4	Temporal lobe epilepsy	iEEG	Epilepsy monitoring unit
5	Temporal lobe epilepsy	iEEG–EEG	Epilepsy monitoring unit
6	Frontal lobe epilepsy	iEEG–EEG	Epilepsy monitoring unit
7	Frontal lobe epilepsy	iEEG–EEG	Epilepsy monitoring unit
8	Syncope	EEG	Epilepsy monitoring unit
9	Syncope	EEG	Ambulatory
10	Temporal lobe epilepsy	iEEG	Epilepsy monitoring unit
11	Temporal frontal lobe epilepsy	iEEG	Epilepsy monitoring unit
12	Temporal lateral lobe epilepsy	iEEG	Epilepsy monitoring unit
13	Temporal lobe epilepsy	iEEG	Epilepsy monitoring unit
14	Temporal basal lobe epilepsy	iEEG	Epilepsy monitoring unit
15	Temporal mesial lobe epilepsy	iEEG	Epilepsy monitoring unit
16	Temporal lobe epilepsy	iEEG	Epilepsy monitoring unit
17	Temporal frontal lobe epilepsy	iEEG	Epilepsy monitoring unit
18	Temporal occipital lobe epilepsy	iEEG	Epilepsy monitoring unit
19	Normal	EEG	Polisomnography monitoring unit
20	Normal	EEG	Polisomnography monitoring unit
21	Normal	EEG	Polisomnography monitoring unit
22	Normal	EEG	Polisomnography monitoring unit
23	Normal	EEG	Polisomnography monitoring unit
24	Normal	EEG	Polisomnography monitoring unit
25	Normal	EEG	Polisomnography monitoring unit
26	Normal	EEG	Polisomnography monitoring unit
27	Normal	EEG	Polisomnography monitoring unit

Data analysis

Owing to the aforementioned relationship between HPE and PLZC results are depicted in the form of complexity-entropy graphs, so as to best extract information from the signals, either deterministic or statistical. In this section, we give a brief explanation of both methods and the relationship between them.

Permutation entropy (HPE)

HPE is a measure develop by Bandt and Pompe (2002), for time series based on comparing neighboring values. The continuous time series is mapped onto a sequence of symbols which describe the relationship between present values and a fixed number of equidistant values at a given past time.

To understand the idea let us consider a real-valued discrete-time series ${\{X_t\}}_{t\ge 0}$ , and let $d\ge 2$ and $\mathit{\tau }\ge 1$ be two integers. They will be called the embedding dimension and the time delay, respectively. From the original time series, we introduce a d-dimensional vector $Y_t^{(d,\mathit{\tau })}$:

$$\begin{array}{c}\hfill {\mathbf{Y}}_t^{(d,\mathit{\tau })}\to (X_{t-(d-1)\mathit{\tau }},\dots ,X_{t-\mathit{\tau }},X_t);t\ge (d-1)\mathit{\tau }\end{array}$$

There are conditions on d and in order that the vector ${\mathbf{Y}}_t^{(d,\mathit{\tau })}$ preserves the dynamical properties of the full dynamical system.1 The components of the phase space trajectory ${\mathbf{Y}}^{(d,\mathit{\tau })}$ are sorted in ascending order. Then, we can define a permutation vector, ${\mathit{\Pi }}_t^{d,\mathit{\tau }}$, with components given by the position of the sorted values of the component of ${\mathbf{Y}}_t^{(d,\mathit{\tau })}$. Each one of these vectors represents a pattern (or motif). There are d! possible patterns.

It is possible to calculate the frequencies of occurrence of any of the d! possible permutation vectors. From these frequencies, we can estimate the Shannon entropy associated with the probability distributions of permutation vector. If we denote the probability of occurrence of the i-th pattern by $P{({\mathit{\Pi }}^{d,\mathit{\tau }})}_i=P_i$ with $i\le d!$ then the (normalized) permutation entropy associated with the time series $\{X_t\}$ is (measured in bits):

$$\begin{array}{c}\hfill H_{PE}=\frac{-{\sum }_{i=1}^{d!}{P}_{i}lo{g}_2{P}_i}{lo{g}_{2}d!}\end{array}$$ 1

The fundamental assumption behind the definition of HPE is that the d! possible permutation vectors might not have the same probability of occurrence, and thus, this probability might unveil knowledge about the underlying system.

Permutation Lempel–Ziv complexity (PLZC)

Entropy is a statistical characterization of a random variable and/or sequence. An alternative characterization of time series is the deterministic notion of complexity of sequences due to Kolomogorof. In this view, complexity is defined as the size of the minimal (deterministic) program (or algorithm) allowing to generate the observed sequence (Cover and Thomas 2006, Chap. 14). Later on, Lempel and Ziv proposed to define such a complexity for the class of “programs” based on recursive copy-paste operators (Lempel and Ziv 1976).

To be more precise, let us consider a finite-size sequence $S_{1:T}=S_1\dots S_T$ of size T, of symbols $S_i$ that take their values in an alphabet $\mathcal{A}$ of finite size $\mathit{\alpha }=|\mathcal{A}|$. The definition of the Lempel–Ziv complexity lies in the two fundamental concepts of reproduction and production:

• Reproduction it consists of extending a sequence $S_{1:T}$ by a sequence $Q_{1:N}$ via recursive copy-paste operations, which leads to $S_{1{:}_T+N}=S_{1:T}{Q}_{1:N}$, i.e., where the first letter $Q_1$ is in $S_{1:T}$, let us say $Q_1=S_i$, the second one is the following one in the extended sequence of size $T+1$, i.e., $Q_1=S_{i+1}$ , etc.: $Q_{1:N}$ is a subsequence of $S_{1:T+N-1}$. In a sense, all of the “information” of the extended sequence $S_{1:T+N}$ is in $S_{1:T}$.

• Production the extended sequence $S_{1:T+N}$ is now such that $S_{1:T+N-1}$ can be reproduced by $S_{1:T}$, but the last symbol of the extension can either follow the recursive copy-paste operation (thus we face to a reproduction) or can be “new”. Note thus that a reproduction is a production, but the converse is false. Let us denote a production by $S_{1:T}\Rightarrow S_{1:N+T}$.

Any sequence can be viewed as constructed through a succession of productions, called a history $\mathcal{H}$. For instance, a history of $S_{1:T}$ can be $\mathcal{H}(S_{1:T}):\mathrm{\varnothing }\Rightarrow S_1\Rightarrow S_{1:2}\Rightarrow \cdots \Rightarrow S_{1:T}$. The number the productions used for the generation $C_{\mathcal{H}(S_{1:T})}$ is in this case equals to the size of the sequence. A given sequence does not have a unique history and in the spirit of the Kolmogorov complexity, Lempel and Ziv were interested in the optimal history, i.e., the minimal number of production necessary to generate the sequence. The size of the shortest history is the so-called Lempel–Ziv complexity, denoted as $C[S_{1:T}]={min}_{\mathcal{H}(S_{1:T})}{C}_{\mathcal{H}(S_{1:T})}$ (Lempel and Ziv 1976). In a sense, $C[S_{1:T}]$ describes the “minimal” information needed to generate the sequence $S_{1:T}$ by recursive copy-paste operations.

As explained above, the Lempel–Ziv complexity needed an alphabet of finite size to be used. In continuous time series such as EEG or MEG it is necessary to discretize the series before calculating the Lempel–Ziv. Using the same idea that in permutation entropy can be taken the alphabet as the set of permutation vectors $\mathcal{A}=\{{\mathit{\Pi }}^{(d,\mathit{\tau })}\}$ and the alphabet large $\mathit{\alpha }=|d!|$. This is called permutation Lempel–Ziv complexity (PLZC)2 (Zozor et al. 2014).

An interesting aspect is that although we are analyzing a sequence from a completely deterministic point of view, it appears that $C_{LZ}[S_{1:T}]$ sometimes contains the concept of information in a statistical sense. Indeed, it was shown in references Cover and Thomas (2006) and Lempel and Ziv (1976) that for a random stationary and ergodic process, when correctly normalized, the Lempel–Ziv complexity $C_{LZ}]$ of the sequence tends to the entropy rate of the process; theses results were extended to the PLZC and the HPE (Zozor et al. 2014); i.e.,

$$\begin{array}{c}\hfill \underset{T\to +\infty }{lim}{C}_{LZ}[S_{1:T}]\frac{log(T)}{T}=\underset{T\to +\infty }{lim}\frac{H_{PE}[S_{1:T}]}{T}\end{array}$$ 2

where $H_{PE}[S_{0:T-1}]$ is the joint permutation entropy of the T symbols, and the right hand side is the permutation entropy rate (entropy per symbol) of the process. Such a property gave rise to the use of the PLZC for HPE estimation purposes.

Results

The results obtained with recordings acquired during conscious states are compared with those acquired during unconscious states, which include sleep (all stages) and epileptic seizures. We note that while we work at the signal level, we made the reasonable assumption that the MEG and scalp EEG sensors record primarily cortical activity underlying those sensors, and thus throughout the text we used the term brain signals. On the other hand, iEEG obviously records signals at the source level. For all the signals the permutation vector parameters used were $d=3,\dots ,6$ and $\mathit{\tau }=1$.

Entropy-complexity analysis from epileptic recordings

To visualize the dynamics of entropy and complexity in time, we use a non-overlapping running window ($\mathit{\Delta }=625$) corresponding to 1s of MEG recording points. For each window the PLZC and HPE were calculated. Figure 1 shows the complexity (PLZC) and entropy (HPE) values corresponding to a MEG recording from a patient suffering primary generalized epilepsy (a, subject1), symptomatic generalized epilepsy (b, subject 2) and frontal lobe epilepsy (c, subject 3). For subject 1 and 2 the entropy and complexity values represent the average calculated over all 143 channels. For subject 3 the values in each plot correspond to a particular channel.

Fig. 1.

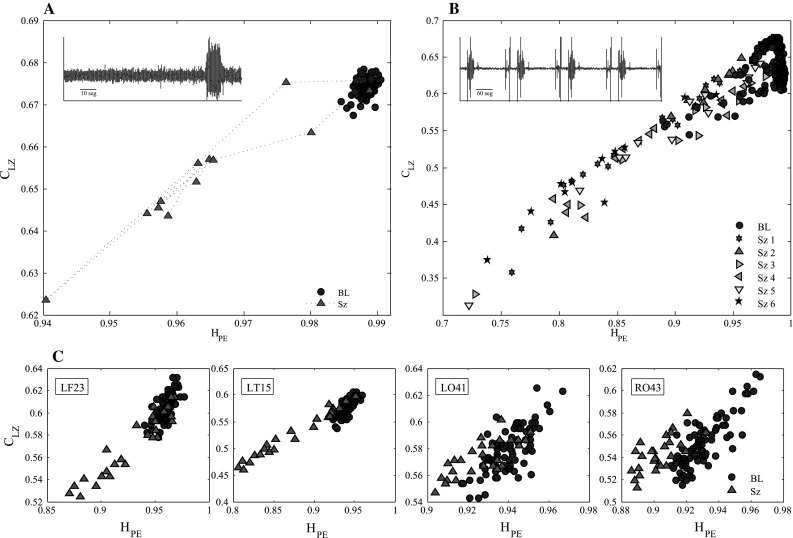
Represents the permutation Lempel Ziv complexity (PLZC) versus permutation entropy ($HPE$) (with parameter $d=4$ and $\mathit{\tau }=1$) time tracking values for MEG signal in epileptic patients during conscious, baseline (BL) and unconscious, seizure (Sz) states. a Subject 1, patient with primary generalized epilepsy; the MEG signal for one channel is plotted in the inset (the high amplitude change represents the absence seizure). We observe that before the seizure the entropy and complexity values remain very high, decreasing during the seizure and returning to the original values after the seizure. b Subject 2, patient with symptomatic generalized epilepsy, who had 7 generalized tonic seizures during the recording period, shown in the inset. When the patient is in the baseline inter-ictal (between seizure) state, entropy and complexity values are higher, decreasing during each ictal (seizure) state. c Subject 3, patient with frontal lobe epilepsy; 4 channels were analyzed separately, left frontal (LF23), left temporal (LT5), left occipital (LO41), right occipital (RO43). For the two recording areas most affected by the focal onset secondarily generalized tonic seizure (LF23 and LT5) entropy and complexity change in the ictal state, but for the areas which are not affected (LO41 and RO43), the $PLZC$ and $HPE$ values are the same as in the baseline state. The same results were obtained for the parameters $d=3,4,5,6$ and $\mathit{\tau }=1$

A single MEG channel from the recording of subject 1 shown in the inset of Fig. 1a, where the absence seizure is visible as a high amplitude change in the signal. The complexity-entropy graph depicts clearly the dynamics of the ictal event. During the conscious state the PLZC and HPE tend to maximum values, but as the patients experienced the absence seizure both values decreased markedly, returning to the original baseline values after the event.

Similar results can be seen in subject 2 who had 7 generalized tonic seizures during the recording epoch; the seizures are visible in the inset of Fig. 1b. We can see in the graph that the baseline interictal activity—the recording between seizures—reaches always the highest values in entropy and complexity, declining to values well below baseline in the ictal (seizure) state. This result is repeated for each of the seizures.

In Fig. 1c we show the analysis for 4 different MEG channels in subject 3, corresponding to: left frontal (LF23), left temporal (LT5), left occipital (LO41) and right occipital (RO43). The first two belong to the region where the focal onset frontal lobe seizure spread. For all channels the values of HPE and PLZC are higher in baseline, however the entropy and complexity decay in the most affected areas (LF23, LT5), while for the other areas (LO41, RO43) the complexity does not change, there being a small decrease in entropy. Similar result were found in the signals of the other epileptic patients, recorded with iEEG or EEG–iEEG.

In order to increase the number of recordings anlaysed, we took iEEG recordings of 9 subjects (subject 10–17) from the European Epilepsy Database (Ihle et al. 2012). The recordings were cut in two epochs, one belonging to the interictal state and the other to Seizure state. For each state PLZC and HPE were computed for all channels and then the mean value and the correlation error matrix were calculated. As we can see in the Fig. 2 for all subjects, the states are well distinguished: Seizure epoch shown a lower entropy and complexity than interictal states. These results are similar as those found in the MEG: recording analysis aforementioned. Table 2 is shows a summary of the HPE and PLZC mean value for all channels and patient (subject 1–4 and 10–18).

Fig. 2.

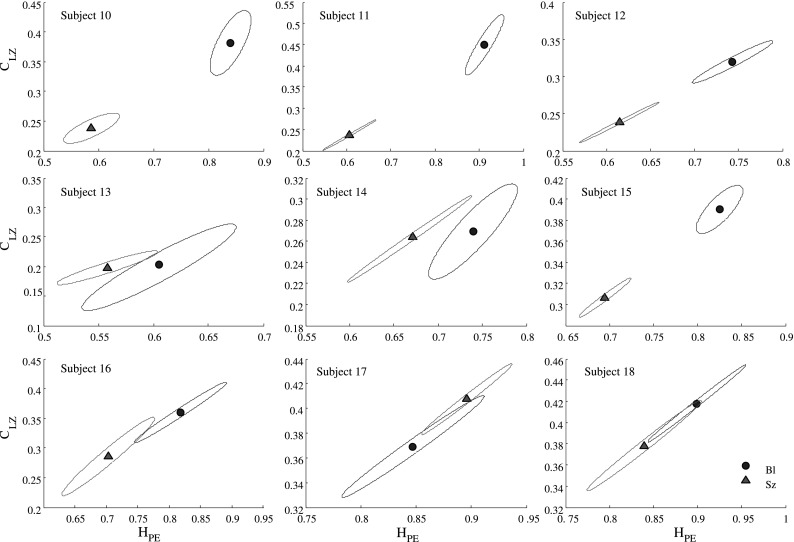
Permutation Lempel Ziv complexity (PLZC) versus permutation entropy ($HPE$) applied over 9 iEEG epileptic subject (subject 10–17). The blue point and red triangle, represent the mean value over all iEEG channels belong to the inter-ictal state and seizure state. The ellipses are the correlation error matrix. The two state are well distinguish for all the cases. The seizure state have lower entropy and complexity values than inter-Ictal state. The parameter used were $d=4$ and $\mathit{\tau }=1$, similar result were found for $d=5,6$. (Color figure online)

Table 2.

HPE and PLZC mean values over all recording channels, for the baseline and seizures epoch belong to the epileptic subject

Subject	Baseline		Seizure
	HPE	PLZC	HPE	PLZC
1	0.99	0.68	0.94	0.62
2	0.98	0.65	0.8	0.4
3 (A)	0.96	0.62	0.86	0.53
3 (N)	0.95	0.6	0.93	0.6
4	0.89	0.6	0.5	0.3
10	0.84	0.38	0.59	0.24
11	0.91	0.45	0.61	0.24
12	0.74	0.31	0.61	0.23
13	0.6	0.2	0.59	0.22
14	0.7	0.22	0.67	0.26
15	0.82	0.39	0.69	0.30
16	0.81	0.36	0.7	0.28
17	0.65	0.26	0.64	0.26
18	0.9	0.41	0.84	0.38

For the subject 3 are shown the values for the most affected (A) and the non-affected areas (N). The parameter used in all cases were $d=4$ and $\mathit{\tau }=1$

A possible reason for these decrease in complexity and entropy during seizures, is that there is higher synchrony during ictal periods (seizures), which therefore causes the recorded signals to become more stereotyped, with the number of permutation vectors used to quantize the signals smaller and more regular, resulting in lower entropy and complexity. This will be further commented on in the “Discussion” section.

Entropy-complexity analysis during sleep stages

Te recordings in these cases were of 2–4 min duration during wakefulness with eyes opened (’AwOe’) or closed, and in sleep stages slow-wave 2 (Sws 2), slow-wave 3–4 (Sws 3–4) and rapid eye movement (’REM’). Figure 3a shows entropy and complexity values applied to 4 subdural strip iEEG channels in subject 5: left frontal medial (LFM1), right frontal medial (RFM4), left temporal anterior (LTA1), right temporal anterior (RTA4). The various stages of sleep are remarkably differentiated in the graph. Note how during wakefulness entropy and complexity are in the higher region of the graph, whereas for the slow wave stages, the values stay in the lower region. The deepest sleep stage, slow wave 3–4 (Sws 3–4), has consistently the lowest entropy and complexity. Interestingly, entropy during REM sleep is very close, in most cases, to the normal, alert state. This result may not be as surprising as it appears, if we consider the mental activity during REM episodes that are normally associated with dreams. The results are in agreement with those reported in Nicolaou and Georgiou (2011) and Casali et al. (2013).

Fig. 3.

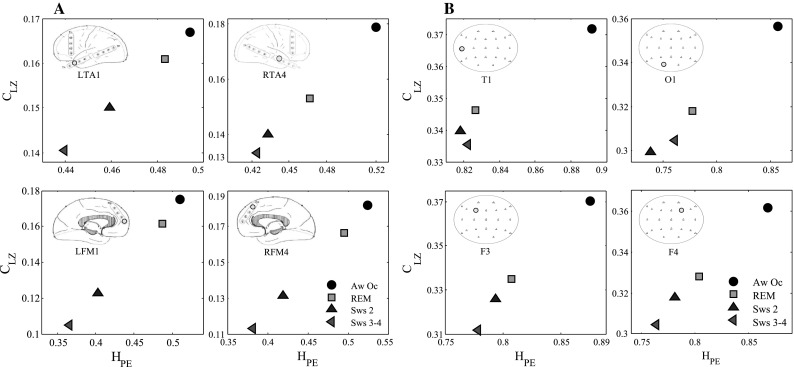
a Each window shows the iEEG recording channel and analyzisis result in ($PLZC$) versus ($HPE$) graph (with parameter $d=4$ and $\mathit{\tau }=1$), for subject 5 during wakefulness and sleep. Data samples were of 2–4 min duration during wakefulness with eyes open (‘Aw Oe’) , and sleep stages slow-wave 2 (Sws 2), slow-wave 3–4 (Sws 3–4) and rapid eye movement (‘REM’). The electrode localizations are: left frontal medial (LFM1), right frontal medial (RFM4), left temporal anterior (LTA1), right temporal anterior (RTA4), the yellow circle show the position of the channel on the surface of the brain. When the patient is in deeper sleep states, both PLZC and HPE decrease across all channels. b The same analysis as in A applied to another individual (subject 9, scalp EEG recording); as with the previous iEEG recording in subject 5, the awake state is associated with higher entropy and complexity and the values decrease for deeper states of sleep. For the REM sleep stage the values are between the slow-wave sleep stages and wakefulness. The same pattern of results was obtained for all subjects analyzed with the parameters $d=3,\dots ,6$ and $\mathit{\tau }=1$

The results obtained from 4 scalp EEG channels in subject 9, without epilepsy, are shown in Fig. 3b, where the same result was obtained: higher complexity and entropy for the awake state and lower complexity and entropy for the deep sleep state. In this case, during REM sleep, the values were situated between those of slow-wave sleep periods and wakefulness. In the analyses of EEG–iEEG signal from the other 2 epilepsy patient (subject 6 and 7) and scalp EEG from the other nonepileptic patient (subject 8) similar results were obtained.

Same analysis was performed on data from 9 patients taken from the physionet data bank The Sleep-EDF Database [Expanded] (Goldberger 2000; Kemp et al. 2000). In these cases we have (Fpz-Cz) channel recording. The recordings were divided into 6 different stages: Awake eyes close, REM , Sws1, Sws2, Sws3 and Sws4. For all stages, the mean value and the correlation matrix were calculated. Figure 4 depicts how the different stages can be differentiated, having the awake stage the higher values and decreasing as the subject goes into the deeper sleep states. Table 3 shows a summary of the HPE and PLZC mean value over all channels recording belong to the sleep subject (subject 5–9, and 19–27).

Fig. 4.

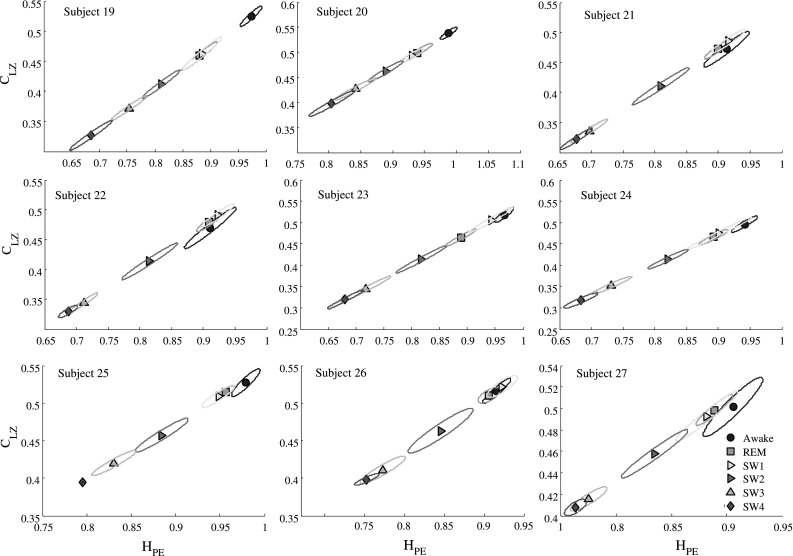
PLZC versus HPE analysis belong to 9 sleep subject in 6 different sleep stage (Awake, REM, Sws1, Sws2, Sws3, Sws4). The signal was recording in the Fpz-Cz channel over all night. The dots and the ellipses represent the mean values and the correlation error matrix over each state. The awake stage have the higher values and decreasing as that subject goes into the deeper sleep states. The parameter used were $d=4$ and $\mathit{\tau }=1$, same result were found for $d=3,5,6$

Table 3.

HPE and PLZC mean values over all recording channels, for the different sleep stages

Subject	Rec	Aw Eo		Aw Ec		REM		Sw 1		Sw 2		Sw 3–4
		HPE	PLZC	HPE	PLZC	HPE	PLZC	HPE	PLZC	HPE	PLZC	HPE	PLZC
5	iEEG	0.52	0.19	0.52	0.19	0.48	0.17	–	–	0.45	0.15	0.37	0.15
	EEG	0.73	0.31	–	–	0.71	0.30	–	–	0.69	0.29	0.67	0.20
6	iEEG	0.46	0.16	0.48	0.16	–	–	–	–	–	–	0.42	0.14
	EEG	0.59	0.23	0.59	0.23	–	–	–	–	–	–	0.60	0.19
7	iEEG	0.62	0.25	0.72	0.31	0.62	0.25	–	–	0.60	0.23	0.58	0.2
	EEG	0.76	0.33	0.76	0.33	0.77	0.34	–	–	0.73	0.31	0.75	0.30
8	EEG	–	–	0.89	0.41	0.83	0.30	–	–	0.82	0.37	0.70	0.30
9	EEG	0.68	0.28	0.8	0.35	0.75	0.33	0.74	0.34	0.68	0.29	0.27	0.12
19	EEG	–	–	0.97	0.52	0.88	0.46	0.88	0.46	0.81	0.41	0.68	0.33
20	EEG	–	–	0.99	0.54	0.94	0.5	0.93	0.49	0.89	0.46	0.8	0.4
21	EEG	–	–	0.91	0.47	0.9	0.47	0.92	0.49	0.81	0.41	0.68	0.32
22	EEG	–	–	0.91	0.47	0.9	0.48	0.92	0.49	0.82	0.41	0.69	0.33
23	EEG	–	–	0.97	0.51	0.89	0.47	0.94	0.5	0.81	0.41	0.68	0.32
24	EEG	–	–	0.94	0.50	0.89	0.47	0.90	0.47	0.82	0.41	0.68	0.31
25	EEG	–	–	0.98	0.53	0.96	0.51	0.95	0.5	0.88	0.46	0.79	0.39
26	EEG	–	–	0.96	0.51	0.96	0.51	0.97	0.52	0.89	0.46	0.80	0.4
27	EEG	–	–	0.95	0.5	0.93	0.5	0.93	0.49	0.88	0.46	0.81	0.40

Data samples were of 2–4 min duration during wakefulness with eyes open (‘Aw Oe’) , and sleep stages slow-wave 2 (Sws 2), slow-wave 3–4 (Sws 3–4) and rapid eye movement (‘REM’). The parameter used in all cases were $d=4$ and $\mathit{\tau }=1$

The fact that same qualitative result is obtained using different recording techniques indicates that this type of analysis is not influenced by the recording methodology.

Discussion

Our results indicate a pronounced loss of entropy and complexity in brain signals during unconscious states or in states that do not represent full alertness (eyes closed). This is consistent with what the signals represent: the coordinated collective activity of cell ensembles, which, in alert states, are responsible for optimal sensory processing. This optimality requires a certain variability in the interactions among those cell networks, which will be conceivably represented in greater complexity. Previous work has indicated a lesser variability in coordinated activity patterns in altered states of consciousness, finding mainly derived from the analysis of synchronization in patients in coma (Nenadovic et al. 2008, 2014), or during seizures (Garcia Dominguez et al. 2005; Perez Velazquez et al. 2007).

A common feature of several theories of consciousness is the notion of a broad distribution of cellular interactions in the brain that results in conscious awareness (reviewed in Klink et al. 2015). This requirement implies that a certain, high degree of variability in the formation and dissolution of functional cell ensembles should take place (Flohr 1995), and this variability will be reflected in higher complexity of the brain signals during alert states. Moreover, several computational studies have revealed as well a lower complexity associated with epilepsy and abnormal cognitive states, like schizophrenia (Steinke and Galán 2011).

In fully alert states, brain recordings exhibit higher frequencies of relatively low amplitude, and are less regular than during other states where alertness is perturbed, including closing the eyes (when a prominent periodic alpha rhythm appears in parieto-occipital areas, for instance). Brain cell ensembles need to integrate and segregate sensorimotor transformations while they receive rich sensory-motor inputs (Tononi 2004); it is then conceivable that these characteristics will be reflected in the high entropy and complexity values we observe. As consciousness is gradually lost, during sleep, the values of entropy and complexity decrease because brain networks do not need the richness in states needed to process the sensorium. The lack of arrival of multiple sensory inputs during unconscious states decreases the need for neurons to display many different firing frequencies, since there is not much integration/segregation being done at those stages and there is not much sensory load. One consequence of this change in firing patterns during unconscious states, particularly in sleep [for a comprehensive review of the neurophysiological mechanisms leading to slow-wave sleep and other thalamocortical phenomena see (Destexhe and Sejnowski 2001)] is that the high frequencies (gamma range) become less prominent and there is higher synchrony at lower frequencies. As well, the amplitude of the slow waves is now high since there are more synchronized cells. Thus, all these events result in the recording becoming more regular and exhibiting the typical slow wave frequencies, and therefore our complexity measures decrease as compared to alert states. These results are consistent with measures obtained from analysis of sleep EEG using permutation entropy (Nicolaou and Georgiou 2011) and other nonlinear measures, such as approximate entropy, correlation dimension, recurrence plots and Hurst exponent, amongst others (Röschke and Aldenhoff 1992; Acharya et al. 2005; Burioka et al. 2005).

In the case of the epileptic recordings we have observed that the complexity and entropy values are larger in the interictal stage (between seizures) and decline sharply in the ictal stage (seizures). This may be due to the fact that seizures are characterized by excessive synchronous neuronal activity, which generates predominance of large amplitude waveforms, the frequencies depending on the seizure type; e.g., the frequency is low in absence seizures (3–4 Hz), but varies substantially in temporal or frontal lobe seizures. However, the frequencies remain relatively constant for certain time periods (originating a distribution of periodic epochs, or laminar phases), that have been used in the characterization of dynamical regimes in epileptiform activity (Perez Velazquez et al. 1999), and therefore the complexity and entropy tend to decrease. During the slow wave sleep stages we also found decreased entropy and complexity as compared with alert states, a reflection of the aforementioned emergence of highly synchronous cell activity during slow wave sleep.

On the other hand, we found that complexity during REM sleep is similar to that of the awake state. This is conceivable since REM episodes are normally associated with dreaming, and there is certain cognitive activity going on in dreams, when there is partial awareness. This observation suggests that, in addition to processing sensory information, it is the complexity of the cognitive processes that results in more or less complexity in the brain signal. While there is not much external input during REM, the stored information becomes the internal sensory world. Previous work has shown decreases in HPE and LZC in patients under anesthesia effects (Zhang et al. 2001; Olofsen et al. 2008; Li et al. 2010), thus the decreased complexity of brain signals in unconscious states may be a common phenomenon.

Hence in the final analysis what we measure, at the macro(meso)scopic level (through the recording of collective cellular activity in EEG or MEG), is a reflection of the fact that the brain handles more information during wakefulness. It is important to note that handling of information in the nersvous system is associated with distinct waveforms and synchrony patterns, hence it is difficult disentangle neurophysiology and behavioural dispositions. For instance, upon closing of the eyes, the lack of visual sensory input result in an alteration of the neurophysiology, in this case the emergence of alpha wave. From this perspective it is therefore difficult to assert that the change in the complexity if the brain waves is due to the emergence of more synchronous wave or the diminution of inputs to the brain, for one leads to the other. A larger code is required to manipulate more information. The complexity/entropy of the signals used in this work have been quantified through the Bandt and Pompe method (Bandt and Pompe 2002), which focuses on the relative values of neighboring data points in a time series. Every embedding vector (or motif ${\mathit{\Pi }}_i^{d,\mathit{\tau }}$) gives an idea of how the waveform is, in a small section, of the original signal. As the original signal carries more variable information, the waveform tend to be more fluctuating, and the number of distinct motifs required to map it increases. Because of that the probability distribution of motifs $P({\mathit{\Pi }}^{d,\mathit{\tau }})$ tends to be uniform, and this causes entropy to increase. In addition, due to the waveform fluctuation, the PLZC increases too, since much more information is required to reconstruct the signal. In contrast, for monotonal repetitive signals that have little new information, just a limited number of motifs is required, e.g. for a sinusoidal signal the PLZC and HPE tend to be zero.

Through this analysis we have obtained evidence for the association between the behavioral dispositions of alert states and the brain signals that have larger number of patterns than those found in unconscious states. These patterns, the waveforms that are recorded using a variety of methods, display enough variability in their time course such that the complexity and entropy are high, similar to a white noise. Such growth in the number of different patterns is given by the variability that exists in the signal frequencies; many different frequencies allow cell ensembles to form a large variety of functional networks—having a large number of different frequencies would allow a heterogeneous synchronization among different brain areas—to improve information encoding/processing. On the other hand, in altered states of consciousness such as seizures, coma or slow wave sleep, the predominant frequencies in the brain are fewer. A signal with a constant frequency in time does not have much information to share, but if it has many different frequencies varying in time, the number of patterns (codes) it can handle is greater. In general, the temporal variability of the frequencies and the (transient) formation of cell networks allow brains to integrate and segregate the information. Hence, in order for the nervous system to manage and transmit large amount of internal and external information, the activity associated has to be complex enough to code it.

We note that our present results are complementary to those recently obtained using measures of coordinated activity, namely the number of configurations of connections derived from an index of phase synchronization (Guevara Erra et al. 2016); we should consider that the present analysis, done on the raw signals, also represents correlated activity as each local field potential (in the case of iEEG) or signal recorded in scalp EEG or MEG represents the collective activity in large cell ensembles, thus these signals are themselves a measure of coordinated cell activity, and therefore it is not surprising we obtain similar observations.

It can be concluded that in the awake state, when the information that has to be handled is larger, the complexity and entropy of the signals recorded from the brain tend to be higher than in the absence of consciousness, a result that stems from the distinct waveforms recorded in these mental states.