A Method for Identifying Prevalent Chemical Combinations in the U.S. Population

Abstract

Background:

Through the food and water they ingest, the air they breathe, and the consumer products with which they interact at home and at work, humans are exposed to tens of thousands of chemicals, many of which have not been evaluated to determine their potential toxicities. Furthermore, while current chemical testing tends to focus on individual chemicals, the exposures that people actually experience involve mixtures of chemicals. Unfortunately, the number of mixtures that can be formed from the thousands of environmental chemicals is enormous, and testing all of them would be impossible.

Objectives:

We seek to develop and demonstrate a method for identifying those mixtures that are most prevalent in humans.

Methods:

We applied frequent itemset mining, a technique traditionally used for market basket analysis, to biomonitoring data from the 2009–2010 cycle of the continuous National Health and Nutrition Examination Survey (NHANES) to identify combinations of chemicals that frequently co-occur in people.

Results:

We identified 90 chemical combinations consisting of relatively few chemicals that occur in at least 30% of the U.S. population, as well as three supercombinations consisting of relatively many chemicals that occur in a small but nonnegligible proportion of the U.S. population.

Conclusions:

We demonstrated how FIM can be used in conjunction with biomonitoring data to narrow a large number of possible chemical combinations down to a smaller set of prevalent chemical combinations. https://doi.org/10.1289/EHP1265

Introduction

The ubiquitous use of man-made chemicals in consumer products (Weschler 2009) and industrial processes (U.S. EPA 2014) leads to the potential for human exposure to large numbers of these substances starting from the earliest stages of life (Carpenter et al. 1998). In fact, the U.S. Environmental Protection Agency (EPA)’s Toxic Substances Control Act (TSCA) inventory now contains more than 84,000 chemical substances that may be in commercial use (Institute of Medicine 2014; U.S. Government Accountability Office 2013), and an estimated 30,000 of these substances are produced at rates greater than one metric ton per year (European Commission 2007). All humans, not just those inhabiting areas near major pollution centers, are now exposed to thousands of chemicals through the air they breathe, the water they drink, the food they eat, and the products they buy and use (Thornton et al. 2002). Furthermore, only a small fraction of the chemicals known to be present in our environment have been sufficiently characterized in terms of their potential to cause human or ecological toxicity to support regulatory action (Judson et al. 2009; National Research Council 1984). Exacerbating this problem of too many chemicals and insufficient data is the fact that people in the real world are not exposed to individual chemicals one at a time, but rather to mixtures of chemicals. The majority of toxicity assessments focus on single chemicals, but unfortunately, the effects of mixtures cannot always be determined using simple additive assumptions (Berenbaum 1989). Thus, the National Research Council has suggested the need to shift away from single chemical assessments in favor of mixtures testing (National Research Council 1994), and in response to this, the EPA has recommended that risk assessments be conducted using toxicity data on actual mixtures of concern or reasonably similar mixtures (U.S. EPA 2000).

At first glance, selecting mixtures to test seems an overwhelming prospect because of the sheer numbers. When considering a candidate pool of $n$ chemicals, there are $2^n-1$ possible combinations. Thus, for a universe of 20 chemicals, the number of possible combinations is over one million, and the number of combinations doubles with each chemical we add to the candidate pool. Fortunately, coexposure to environmental chemicals is not purely random, but is subject to various structuring processes (Tornero-Velez et al. 2012), so we expect that the number of combinations of $n$ chemicals that occur frequently in humans is likely much less than $2^n-1$. To focus our assessment efforts, we therefore need to develop tools that can identify prevalent chemical mixtures.

We suggest that the large number of mixtures that might be considered for toxicity testing be narrowed down to a relatively small number of mixtures of concern using a two-step process: first, identify combinations of chemicals that are most prevalent, and then identify the relative amounts (or concentrations) of the constituent chemicals to arrive at well-defined mixtures. Note that we make a distinction between chemical combinations and chemical mixtures. In particular, we define a combination to be a collection of chemicals that co-occur in an individual, whereas we define a mixture to be a collection of chemicals that co-occur in an individual in specific proportions as determined by their concentrations in blood or urine. In this manuscript, we focus on the first step in this process, identifying prevalent combinations of chemicals.

Our approach for identifying combinations of chemicals that are prevalent in humans relies on biomonitoring data, such as those collected in the National Health and Nutrition Examination Survey (NHANES). The National Center for Health Statistics (NCHS) of the Centers for Disease Control and Prevention conducts this ongoing survey of health metrics on a 2-y cycle, and part of each survey cycle involves the investigation of approximately 100 markers of chemical exposure in a representative sample of the U.S. population (CDC 2016a). Since the beginning of the continuous NHANES program in 1999 (CDC 2016b), 265 chemicals in total have been included in NHANES biomonitoring studies (Sobus et al. 2015). While these few hundred chemicals only account for a very small fraction of the aforementioned tens of thousands of chemicals to which we may be exposed, NHANES currently provides the most comprehensive source of internal human exposure data. Therefore, we chose to use NHANES biomonitoring data to explore methods for finding prevalent combinations of chemicals.

We propose that a market basket analysis technique known as frequent itemset mining (FIM) (Borgelt 2012) can be used to narrow down the large number of possible combinations that can be formed from a given pool of chemicals (such as the NHANES chemicals) by identifying those combinations that are most prevalent. While FIM has traditionally been applied to data sets describing consumer purchasing behavior (Agrawal and Srikant 1994), it has been used in a variety of other contexts (Borgelt 2012). Recently, (Bell and Edwards 2014; 2015) applied FIM to NHANES data sets, but in their case, they sought to find associations between chemicals and diseases through association rules mining. So, although the number of peer-reviewed publications utilizing NHANES biomarker data has increased steadily over the last 10 y (Sobus et al. 2015), to our knowledge, these data have not been used to isolate chemical combinations based upon their prevalence. Here, we demonstrate how FIM can be applied to NHANES biomarker data to identify combinations of chemicals that are present in a significant proportion of the U.S. population.

Methods

All data processing and analyses described herein were performed using Python 3.5 (version 3.5; Python Software Foundation) on a Dell Precision T7610 workstation running Red Hat Linux (version 6.8; Red Hat Enterprise). Scripts and relevant data files are available in the Supplemental Materials (as the compressed file EHP_Scripts_revised.zip).

Data Sets

We downloaded the NHANES 2009–2010 laboratory data (CDC 2016c), and from this, we used reported concentrations of environmental chemicals and their metabolites as measured in the urine and serum of subjects selected from the U.S. population. The 2009–2010 data set was selected because it was the most current complete data set available. We describe below the relevant features of this data set. Note that NHANES protocols were approved by the NCHS Research Ethics Review Board, and all NHANES participants provided informed consent before taking part in the survey.

Subsamples and chemical groups.

The NHANES 2009–2010 data set includes a sample of 10,537 total subjects; however, not all chemicals were measured in all subjects. NHANES divided the subjects into three disjoint subsamples, A, B, and C, each consisting of approximately one-third of the total sample and each designed to be a representative sample of the U.S. population (CDC 2016d). Individuals in Subsample A were tested for Group A chemicals, but not for Group B or Group C chemicals; similarly, Subsample B and Subsample C individuals were tested for chemicals from Group B or Group C, respectively, but not for chemicals from other groups (note that the terms Group A, Group B, and Group C do not appear in NHANES documentation; we use them here to simplify references to those chemicals analyzed in NHANES Subsamples A, B, and C, respectively.) Because of this block structuring, information about the co-occurrence of chemicals from different groups is not directly available from the NHANES data sets.

Each of the chemical groups in NHANES 2009–2010 included four subgroups of chemicals, and depending on the types of chemicals in a given subgroup, laboratory analyses were conducted using either urine or blood spot (i.e., one-time) samples. Group A included (A1) metals; (A2) arsenics; (A3) perchlorate, nitrate, and thiocyanate; and (A4) phytoestrogens, all of which were measured in spot urine samples. Group B included (B1) environmental phenols; (B2) environmental pesticides; (B3) phthalates; and (B4) polyaromatic hydrocarbons (PAHs), which were also all measured in urine. Finally, Group C included (C1) pyrethroids, herbicides, and organophosphate metabolites; (C2) polyfluoroalkyl chemicals; (C3) caffeine and metabolites; and (C4) diethyltoluamide (DEET) and metabolites. Most Group C chemicals were measured in urine, except for the 12 polyfluoroalkyl chemicals (Subgroup C2), which were measured in serum. We provide complete lists of the chemicals included in Groups A, B, and C in Tables 1, 2, and 3, respectively. More detailed information on these chemicals is presented in Tables S1, S2, and S3.

Table 1.

National Health and Nutrition Examination Survey (NHANES) 2009–2010 Group A chemicals.

NHANES code	Chemical name	NHANES file	Subgroup
URXUSB	Antimony	UHM_F	A1
URXUBA	Barium	UHM_F	A1
URXUBE	Beryllium	UHM_F	A1
URXUCD	Cadmium	UHM_F	A1
URXUCS	Cesium	UHM_F	A1
URXUCO	Cobalt	UHM_F	A1
URXUPB	Lead	UHM_F	A1
URXUMO	Molybdenum	UHM_F	A1
URXUPT	Platinum	UHM_F	A1
URXUTL	Thallium	UHM_F	A1
URXUTU	Tungsten	UHM_F	A1
URXUUR	Uranium	UHM_F	A1
URXUAS	Arsenic	UAS_F	A2
URXUAS5	Arsenic (V) acid	UAS_F	A2
URXUAB	Arsenobetaine	UAS_F	A2
URXUAC	Arsenocholine	UAS_F	A2
URXUAS3	Arsenous (III) acid	UAS_F	A2
URXUDMA	Dimethylarsinic acid	UAS_F	A2
URXUMMA	Monomethylarsonic acid	UAS_F	A2
URXUTM	Trimethylarsine oxide	UAS_F	A2
URXNO3	Nitrate	PERNT_F	A3
URXUP8	Perchlorate	PERNT_F	A3
URXSCN	Thiocyanate	PERNT_F	A3
URXDAZ	Daidzein	PHYTO_F	A4
URXETD	Enterodiol	PHYTO_F	A4
URXETL	Enterolactone	PHYTO_F	A4
URXEQU	Equol	PHYTO_F	A4
URXGNS	Genistein	PHYTO_F	A4
URXDMA	O-Desmethylangolensin	PHYTO_F	A4

Note: Subjects in Subsample A that met certain age and other requirements were tested for these chemicals (chemical groups and subgroups are described in the “Methods” section).

Table 2.

National Health and Nutrition Examination Survey (NHANES) 2009–2010 Group B chemicals.

NHANES code	Chemical name	NHANES file	Subgroup
URXBP3	Benzophenone-3	EPH_F	B1
URXBPH	Bisphenol A	EPH_F	B1
URX4TO	4-tert-Octylphenol	EPH_F	B1
URXTRS	Triclosan	EPH_F	B1
URXBUP	Butyl paraben	EPH_F	B1
URXEPB	Ethyl paraben	EPH_F	B1
URXMPB	Methyl paraben	EPH_F	B1
URXPPB	n-Propyl paraben	EPH_F	B1
URXOPP	ortho-Phenylphenol	PP_F	B2
URX1TB	2,4,5-Trichlorophenol	PP_F	B2
URX3TB	2,4,6-Trichlorophenol	PP_F	B2
URXDCB	2,4-Dichlorophenol	PP_F	B2
URX14D	2,5-Dichlorophenol	PP_F	B2
URXMZP	Monobenzyl phthalate	PHTHTE_F	B3
URXMIB	Monoisobutyl phthalate	PHTHTE_F	B3
URXMBP	Mono-n-butyl phthalate	PHTHTE_F	B3
URXMCP	Monocyclohexyl phthalate	PHTHTE_F	B3
URXMEP	Mono-ethyl phthalate	PHTHTE_F	B3
URXMHP	Mono(2-ethylhexyl) phthalate	PHTHTE_F	B3
URXMHH	Mono(2-ethyl-5-hydroxyhexyl) phthalate	PHTHTE_F	B3
URXMOH	Mono(2-ethyl-5-oxohexyl) phthalate	PHTHTE_F	B3
URXECP	Mono(2-ethyl-5-carboxypentyl) phthalate	PHTHTE_F	B3
URXCNP	Monocarboxynonyl phthalate	PHTHTE_F	B3
URXMNP	Monoisononyl phthalate	PHTHTE_F	B3
URXCOP	Monocarboxyoctyl phthalate	PHTHTE_F	B3
URXMNM	Mono-methyl phthalate	PHTHTE_F	B3
URXMC1	Mono(3-carboxypropyl) phthalate	PHTHTE_F	B3
URXMOP	Mono-n-octyl phthalate	PHTHTE_F	B3
URXP04	2-Hydroxyfluorene	PAH_F	B4
URXP03	3-Hydroxyfluorene	PAH_F	B4
URXP17	9-Hydroxyfluorene	PAH_F	B4
URXP06	1-Hydroxyphenanthrene	PAH_F	B4
URXP07	2-Hydroxyphenanthrene	PAH_F	B4
URXP05	3-Hydroxyphenanthrene	PAH_F	B4
URXP10	1-Hydroxypyrene	PAH_F	B4
URXP01	1-Hydroxynapthalene	PAH_F	B4
URXP02	2-Hydroxynapthalene	PAH_F	B4

Note: Subjects in Subsample B that met certain age and other requirements were tested for these chemicals (chemical groups and subgroups are described in the “Methods” section).

Table 3.

National Health and Nutrition Examination Survey (NHANES) 2009–2010 Group C chemicals.

NHANES code	Chemical name	NHANES file	Subgroup
URX24D	2,4-Dichlorophenoxyacetic acid	UPHOPM_F	C1
URX25T	2,4,5-Trichlorophenoxyacetic acid	UPHOPM_F	C1
URXMAL	Malathion dicarboxylic acid	UPHOPM_F	C1
URXOXY	2-Isopropyl-4-methyl-6-hydroxypyrimidine	UPHOPM_F	C1
URXPAR	para-Nitrophenol	UPHOPM_F	C1
URXCPM	3,5,6-Trichloro-2-pyridinol	UPHOPM_F	C1
URXTCC	trans-3-(2,2-Dichlorovinyl)-2,2-dimethylcyclopropane carboxylic acid	UPHOPM_F	C1
URXCB3	cis-3-(2,2-Dibromovinyl)-2,2-dimethylcyclopropane carboxylic acid	UPHOPM_F	C1
URX4FP	4-Fluoro-3-phenoxybenzoic acid	UPHOPM_F	C1
URXOPM	3-Phenoxybenzoic acid	UPHOPM_F	C1
LBXPFBS	Perfluorobutane sulfonic acid	PFC_F	C2
LBXPFDE	Perfluorodecanoic acid	PFC_F	C2
LBXPFDO	Perfluorododecanoic acid	PFC_F	C2
LBXPFHP	Perfluoroheptanoic acid	PFC_F	C2
LBXPFHS	Perfluorohexane sulfonic acid	PFC_F	C2
LBXPFNA	Perfluorononanoic acid	PFC_F	C2
LBXPFOA	Perfluorooctanoic acid	PFC_F	C2
LBXPFOS	Perfluorooctane sulfonic acid	PFC_F	C2
LBXPFSA	Perfluorooctane sulfonamide	PFC_F	C2
LBXEPAH	2-(N-Ethyl-perfluorooctane sulfonamido) acetic acid	PFC_F	C2
LBXMPAH	2-(N-Methyl-perfluorooctane sulfonamido) acetic acid	PFC_F	C2
LBXPFUA	Perfluoroundecanoic acid	PFC_F	C2
URXMU1	1-Methyluric acid	CAFE_F	C3
URXMU2	3-Methyluric acid	CAFE_F	C3
URXMU3	7-Methyluric acid	CAFE_F	C3
URXMU4	1,3-Dimethyluric acid	CAFE_F	C3
URXMU5	1,7-Dimethyluric acid	CAFE_F	C3
URXMU6	3,7-Dimethyluric acid	CAFE_F	C3
URXMU7	1,3,7-Trimethyluric acid	CAFE_F	C3
URXMX1	1-Methylxanthine	CAFE_F	C3
URXMX2	3-Methylxanthine	CAFE_F	C3
URXMX3	7-Methylxanthine	CAFE_F	C3
URXMX4	1,3-Dimethylxanthine	CAFE_F	C3
URXMX5	1,7-Dimethylxanthine	CAFE_F	C3
URXMX6	3,7-Dimethylxanthine	CAFE_F	C3
URXMX7	1,3,7-Trimethylxanthine	CAFE_F	C3
URXAMU	AAMU	CAFE_F	C3
URXDEE	N,N-diethyl-meta-toluamide	DEET_F	C4
URXDEA	3-diethyl-carbamoyl benzoic acid	DEET_F	C4
URXDHD	N,N-diethyl-3-hydroxymethylbenzamide	DEET_F	C4

Note: Subjects in Subsample C that met certain age and other requirements were tested for these chemicals (chemical groups and subgroups are described in the “Methods” section).

Age restrictions and excluded data.

NHANES 2009–2010 included subjects of all ages, but only subjects aged 6 and older were required to provide urine for laboratory analyses, and only subjects age 12 y and older were required to provide blood for analysis of polyfluoroalkyl chemicals (Subgroup C2). Analyses of some chemicals (e.g., cotinine in blood, and the metals mercury, lead, and cadmium in blood) were performed in subjects from all groups (also with age restrictions), but these chemicals were excluded from consideration to avoid issues related to the selection of appropriate subject weights (see “Sampling design and weights” below). Within subsamples, we also excluded individuals for which data on some chemicals was omitted. Thus, for our analysis, we only considered those subjects in each subsample for which blood or urine concentrations for all chemicals within the appropriate group were included.

Creatinine correction and fill values.

Because urine dilution can vary significantly due to fluid intake and other intra- and interindividual factors, NCHS recommends performing a creatinine correction when analyzing concentrations of chemicals in urine (CDC 2016e). Specifically, this entails computing the ratio of urinary chemical concentration to urinary creatinine concentration. We performed the NCHS recommended correction and used the resulting creatinine-adjusted chemical concentration for all chemicals measured in urine.

Each chemical analyzed in NHANES has a limit of detection (LOD) based on the laboratory method used for analysis (CDC 2016f). NHANES reports which measurements fall below this empirically derived LOD, and in the NHANES 2009–2010 data files, concentrations below the LOD are converted to fill values (typically, the LOD divided by the square root of two). When performing the creatinine correction, we set the creatinine-adjusted concentration to zero whenever the raw concentration was below the LOD. In this way, our creatinine correction preserves the homogeneity of all measurements below the LOD.

Note that we do not perform a creatinine correction for concentrations measured in serum. Thus, we work with raw serum concentrations and creatinine-adjusted urine concentrations in our analyses. For the sake of brevity, it is convenient to refer to both of these types of data as concentrations, and so hereafter, we use the term “concentration” in place of “creatinine-adjusted concentration” when describing an adjusted urine concentration.

Sampling design and weights.

NHANES employs a complex, multistage probability sampling design to select human subjects representative of the noninstitutionalized, civilian U.S. population (CDC 2016g). In using this approach, NHANES oversamples various subpopulations, allowing data analysts to achieve increased reliability and precision in estimates of health and nutrition indicators for these groups. Because the NHANES 2009–2010 data set was not constructed from a simple random sample of the U.S. population, NHANES assigned a different weight to each subject, that is, one may think of each subject as representing a fixed number of demographically similar U.S. residents, but this fixed number, or weight, is, in general, different for each subject.

Each subject included in NHANES 2009–2010 belongs not only to the total 2009–2010 sample, but also to one of the subsamples (A, B, or C). Therefore, NHANES assigns each subject two distinct weights: one to be used when analyzing the entire sample, and another when analyzing a subsample (CDC 2016g). Since we focus here on analyzing subsamples of individuals that have all been tested for the same group of chemicals, we utilize the NHANES subsample weights.

Table 4 provides summary information on each of the NHANES 2009–2010 subsamples. The subsample weight for a given NHANES subject can be interpreted as the number of U.S. residents represented by that subject, so the sum of the weights gives the size of the total population represented (CDC 2016h). Note that Table 4 implies that the population sizes represented by Subsamples A, B, and C differ. This is because NHANES omits some subjects from the biomarker analyses conducted for each of the subsamples, including those deemed too young to be included in certain laboratory tests, and because we further omit those subjects for which some relevant chemical concentrations were not available.

Table 4.

Summary information for each of the National Health and Nutrition Examination Survey (NHANES) 2009–2010 subsamples.

Category	Subsample A	Subsample B	Subsample C
Number of subjects	2,741	2,736	2,132
Number of chemicals	29	37	40
Maximum weight	476,883.0	426,061.1	413,068.1
Minimum weight	14,002.7	13,975.1	12,659.3
Sum of weights	258,281,689.4	272,911,664.0	226,021,580.6
Records needed	18,445.1	19,528.5	17,854.1

Note: The number of subjects and the summary statistics for the subsample weights only reflect those subjects that met the criteria described in “Methods” section. That is, some NHANES 2009–2010 subjects were omitted from consideration because they did not meet age requirements for certain laboratory analyses or because chemical concentration information was incomplete. As discussed in the text, we preprocessed the raw data to obtain subject-chemical databases before conducting frequent itemset mining (FIM). Part of this process entailed duplicating subject records to reflect subsample weights. The final row in this table gives the total number of records needed (after duplication) so that each record corresponding to a subject with the minimum weight would occur exactly once in the transaction database.

Procedure

We applied FIM to the NHANES 2009–2010 data set to identify the most prevalent combinations of chemicals present in U.S. residents. As described below, we first preprocessed the raw NHANES data to obtain information amenable to FIM. Then we identified prevalent combinations and supercombinations of NHANES chemicals.

Frequent itemset mining.

FIM is a popular data mining technique originally developed for market basket analysis (Borgelt 2012). Since this method was designed for analysis of consumer purchasing behavior, the FIM terminology established in the literature tends to focus on the following: items, which are typically goods or services that can be purchased; itemsets, which are collections of these items; and transactions, which are lists of items purchased, e.g., by a particular person at a particular place and time. This same technique can be applied, however, to any data set that can be organized as a list of transactions. For our purposes, we considered each NHANES subject to be a transaction and each chemical analyte to be an item. Thus, any combination of the chemicals analyzed constitutes an itemset, and prevalent combinations correspond to frequent itemsets.

We now define the chemical-centric FIM nomenclature used hereafter in this manuscript (which is distinct from the FIM terminology used elsewhere). To begin, we let $B=\left\{i_1,\dots ,i_m\right\}$ be a set of $m$ chemicals. We call this set the chemical base (which is analogous to an item base in traditional FIM terminology). For our purposes, this was the set of all chemicals in a given group (either A, B, or C). Now, call any subset $I$ of $B$ a combination of chemicals. Next, let $T=\left[t_1,\dots ,t_n\right]$ be a list of $n$ chemical combinations corresponding to $n$ NHANES subjects. In general, we call a list like $T$ a subject-chemical database (analogous to a transaction database). Note that $t_k$ is a subset of $B$, and $k\in \left\{1,\dots ,n\right\}$ is an index that identifies the specific NHANES subject in which the combination of chemicals $t_k$ occurs. That is, each record in $T$ consists of a list of the chemicals that are deemed to be present in a given subject. More will be said about determining the presence (or absence) of a chemical in an individual subject in the next subsection of this manuscript.

Next, we define the concept of support. First, note that a chemical combination $I$ is said to occur in subject $k$ if and only if the set $I$ is contained in the set $t_k$. So, the absolute support of $I$ with respect to $T$, denoted $s_T\left(I\right)$, is the number of occurrences of combination $I$ in the database $T$; that is, $s_T\left(I\right)$ denotes the number of subjects for which all the chemicals in $I$ are present. Furthermore, the relative support of $I$ with respect to $T$, denoted ${\mathrm{\sigma }}_T\left(I\right)$, is the proportion of subjects in $T$ for which all the chemicals in $I$ are present. Note that we use the term prevalence level as a synonym for relative support throughout this manuscript.

The following series of examples serves to illustrate the terminology established in the preceding paragraphs:

• •$B=\left\{a,b,c,d,e\right\}$ is a chemical base. For our purposes, $a$, $b$, $c$, $d$, and $e$ could represent five chemicals analyzed in a hypothetical NHANES subsample.
• •$I=\left\{a,b\right\}$ is an example of a combination. This could be a set of chemicals that occur together.
• •$T=\left[t_1,t_2,t_3,t_4\right]=\left[\left\{a,b,c\right\},\left\{a,b,d\right\},\left\{c,e\right\},\left\{a\right\}\right]$ is a subject-chemical database. This list could represent four subjects in the hypothetical NHANES subsample already referenced. In that case, each set in the list consists of the chemicals that are present in the corresponding subject. In particular, chemicals $a$, $b$, and $c$ are present in Subject 1; chemicals $a$, $b$, and $d$ are present in Subject 2; and so on. As shown below, this subject-chemical database can also be represented as a presence–absence matrix in which the rows and columns correspond to subjects and chemicals, respectively.

• •The combination $\left\{a,b\right\}$ occurs in Subject 1. We know this because $\left\{a,b\right\}$ is contained in $t_1=\left\{a,b,c\right\}$. Equivalently, we might state “Chemicals $a$ and $b$ are present in Subject 1.”
• •The absolute support of $\left\{a,b\right\}$ is 2. Equivalent: “Chemicals $a$ and $b$ co-occur in exactly 2 subjects.”
• •The prevalence level of $\left\{a,b\right\}$ is $2/4=0.5$. Equivalent: “Chemicals $a$ and $b$ co-occur in exactly 50% of the subjects.”

Using the concept of support, or prevalence level, we can now describe precisely what we mean by a prevalent chemical combination. Given a chemical base $B=\left\{i_1,\dots ,i_m\right\}$, a subject-chemical database $T=\left\{t_1,\dots ,t_n\right\}$, and a minimum prevalence level ${\mathrm{\sigma }}_{\min }\in \left[0,1\right]$, the set of prevalent combinations (analogous to frequent itemsets) is

$${\mathcal{F}}_T\left({\mathrm{\sigma }}_{\min }\right)=\left\{I\subseteq B\mathrm{\hspace{0.17em}}|{\mathrm{\hspace{0.17em}}\mathrm{\sigma }}_T\left(I\right)\ge {\mathrm{\sigma }}_{\min }\right\}.$$

In other words, the prevalent combinations are those that occur in at least the proportion ${\mathrm{\sigma }}_{\min }$ of the subjects represented in $T$. The following example assumes the same item base $B$ and transaction database $T$ described in the examples above:

• •${\mathcal{F}}_T\left(0.5\right)=\left\{\left\{a\right\},\left\{b\right\},\left\{c\right\},\left\{a,b\right\}\right\}$. That is, for minimum prevalence level 0.5, the prevalent chemical combinations are $\left\{a\right\}$, $\left\{b\right\}$, $\left\{c\right\}$, and $\left\{a,b\right\}$.

FIM, therefore, is any process or algorithm used to identify frequent itemsets, or in our case, prevalent chemical combinations. A number of FIM algorithms exist (Agrawal and Srikant 1994; Zaki et al. 1997), but we used the Frequent Pattern Growth (FP-Growth) algorithm (Han et al. 2000) as implemented in the PyFIM module (Borgelt 2016) for Python. Different FIM algorithms may be more efficient in processing different types of data sets, but all will yield the same results because FIM is a deterministic process. We chose to use FP-Growth because it is designed to efficiently identify maximal frequent itemsets (see “The Apriori property and maximal prevalent combinations” below). For our purposes, frequent itemset mining of NHANES data sets provides a means for identifying combinations of chemicals that co-occur in (at least) some specified proportion of the U.S. population.

Converting NHANES data sets into subject-chemical databases.

To apply FIM to the NHANES 2009–2010 data set, we first converted the data set into a subject-chemical database. This required two essential steps: converting information on chemical concentrations into presence–absence information, and accounting for differently weighted subjects.

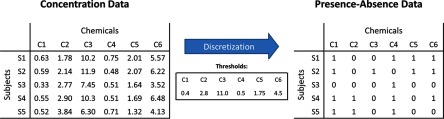
NHANES biomonitoring data consist of concentration information, whereas FIM as previously described operates on a subject-chemical database describing presence or absence of chemicals in various subjects. It is worth noting that here absence technically means probably present, but at a level below some prescribed threshold. Therefore, NHANES data must be discretized before applying an FIM algorithm. Figure 1 illustrates conceptually the conversion of a concentration matrix into a discretized presence–absence matrix. The presence–absence matrix is simply an array representation of the aforementioned subject-chemical database. In the discussion that follows, note that rows represent subjects and columns represent chemicals in both the concentration matrix and the presence–absence matrix. We used two essential approaches for performing the discretization, and each of these operates one column (or chemical) at a time. In the first, we used the LOD for each chemical as a threshold, setting values below the LOD for a given chemical to 0 (indicating absence) and setting all other values to 1 (indicating presence). In the second approach, we used a percentile threshold for each chemical. In this case, we utilized subsample weights to find the observed value corresponding to a given percentile concentration measurement. That is, for each chemical, we duplicated each concentration according to the weight of the corresponding subject and then computed a percentile in the usual way from the resulting list of concentration values. Each observed measurement over this value was translated to 1, and the remaining values were each set to 0. Because we considered the three NHANES 2009–2010 subsamples (A, B, and C) separately, note that we converted three concentration matrices into presence–absence matrices for any particular threshold or discretization method applied.

Figure 1.

Discretization of data for a hypothetical National Health and Nutrition Examination Survey (NHANES) subsample consisting of five subjects (S1–S5) that were each tested for six chemicals (C1–C6). The concentration data consist of real numbers representing concentrations, whereas the presence–absence data consist of binary digits, with 1 indicating presence and 0 indicating absence. For each chemical concentration, the appropriate discretization threshold was used to determine presence or absence. For example, the concentration in the top left cell of the concentration data matrix (0.63) was converted to a 1 in the presence–absence data matrix because 0.63 exceeds the chemical-specific threshold of 0.4.

As just described, applying the discretization step of the data conversion process results in a presence–absence matrix with the same dimensions as the concentration matrix. While FIM could be applied to this presence–absence matrix as is, the results would likely be biased because, in general, each row in the matrix represents a differently weighted subject. To state this another way, each row in the matrix represents a certain proportion of the U.S. population, and the proportion represented varies from row to row. To overcome this issue, we duplicated rows in each presence–absence matrix to create a new presence–absence matrix with an identical number of columns, but a larger number of rows. Using the summary statistics on subsample weights reported in Table 4, we determined the number of rows, or records, that should be created in this new matrix as duplicates of the $i$ th row, or subject, in the original presence–absence matrix as

$$R\left(\frac{w_i}{{\sum }_k{w}_k}\times N\right),$$

where $w_i$ denotes the weight of the $i$ th subject represented in the original presence–absence matrix, ${\sum }_k{w}_k$ denotes the sum of the weights of all subjects, $N$ denotes the desired total number of records in the final presence–absence matrix, and $R$ denotes the function that rounds a real number to the nearest integer. To determine a suitable value for $N$, we computed the number of records that would ensure a subject with the minimum weight would be represented exactly once (before rounding) in the new matrix; that is, we computed the sum of weights divided by the minimum subject weight. Note that this number of records needed is provided as the last row of Table 4. For each subsample, this value is close to, but does not exceed, 20,000, so we used $N=\mathrm{20,000}$ to create our presence–absence matrices. These presence–absence matrices were then used as the subject-chemical databases for FIM analysis. We reiterate that because a single NHANES subject can appear one or more times as a record in presence–absence matrices created as just described, many of the subjects, or records, in the subject-chemical databases we constructed for FIM are actually duplicates.

The Apriori property and maximal prevalent combinations.

One fairly obvious property of FIM support is that it decreases monotonically. In other words, if a chemical combination is extended (by adding one or more chemicals to it), its support will not increase. If we supply a minimum prevalence level ${\mathrm{\sigma }}_{\min }$, the Apriori property (Agrawal and Srikant 1994) follows immediately from this: a superset of a nonprevalent chemical combination cannot be prevalent. This property forms the basis for many of the aforementioned FIM algorithms [including the FP-Growth algorithm (Han et al. 2000)].

The contrapositive of the Apriori property (in the context of chemical-subject data) is that all subsets of a prevalent combination are also prevalent. This useful property leads us to the concept of a maximal prevalent combination (Bayardo 1998) (a maximal prevalent combination corresponds to a maximal frequent itemset in the FIM literature). A prevalent combination $I\in {\mathcal{F}}_T\left({\mathrm{\sigma }}_{\min }\right)$ is maximal if and only if all supersets of $I$ are nonprevalent. Using the Apriori property contraposition, the set of all prevalent combinations can easily be recovered from the set ${\mathcal{M}}_T\left({\mathrm{\sigma }}_{\min }\right)$ of maximal prevalent combinations (Borgelt 2012). In order to reduce the total number of chemical combinations we ultimately needed to manually examine, we focused on maximal prevalent combinations for our analysis. The FIM method of the PyFIM module (Borgelt 2016) can be set to return either all prevalent combinations or just the maximal prevalent combinations. Thus, we used this method to generate maximal prevalent combinations as needed.

Identification of supercombinations.

When we set discretization thresholds and minimum prevalence levels to relatively high values, the prevalent combinations (and maximal prevalent combinations) that emerged consisted of relatively few chemicals. We were also interested, however, in finding combinations that might have low prevalence, but which do nevertheless occur in U.S. residents and which consist of relatively many chemicals. We call such combinations of many chemicals that have low but nonzero prevalence levels supercombinations.

In order to find supercombinations of chemicals in each group, we applied FIM to subject-chemical databases in which subjects were not duplicated as described previously described. In particular, we searched for combinations that occurred in at least two NHANES subjects, but which also met some minimum size requirement (e.g., containing at least 20 chemicals). In this approach, we did not utilize subject weights in order to duplicate subjects in the transaction databases. Instead, we utilized the subject weights after applying FIM in order to determine prevalence levels of the supercombinations. The FIM method of the PyFIM module (Borgelt 2016) allows the user to specify absolute support and minimum combination size as parameters. Therefore, we used these parameters to specify an absolute support of two subjects and a relatively large minimum combination size (e.g., 25 in the case of Group A chemicals). This allowed us to find supercombinations efficiently without taxing computer memory resources.

Investigation of reproducibility of prevalent combinations and demographic considerations.

After identifying maximal prevalent combinations within each group of chemicals as described above, we investigated the robustness of the observed prevalence levels of these combinations by examining partitions of the NHANES subsamples. In particular, we randomly assigned each subject in a given subsample (e.g., Subsample A) to one of four partitions of approximately equal size. Utilizing the NHANES subsample weights of the subjects, we then calculated the observed prevalence of a given combination in the represented subpopulation as $\frac{S_1}{S_2}$, where $S_1$ denotes the sum of the weights of all subjects in the partition for which all chemicals in the combination were present (at a concentration above the threshold), and $S_2$ denotes the sum of the weights of all subjects in the partition.

To investigate the effects of demographics on the prevalence of identified combinations, we also assigned each subject in a given NHANES subsample to one or more classes using demographic information recorded by NHANES. In particular, we examined prevalence of combinations in the following demographic classes: male, female, persons age 6–11 y, persons age 12–19 y, persons age 20–65 y, persons age 66 or more years, and persons who self-identified “as having used nicotine and/or tobacco in the 5 d prior to completing the NHANES questionnaire” (CDC 2016b). As with the partitions, the observed prevalence in the represented subpopulation was calculated as $S_1/S_2$, but in this case, $S_1$ denotes the sum of the weights of all subjects in the demographic class (within the given subsample) for which all chemicals in the combination were present (at a concentration above the threshold), and $S_2$ denotes the sum of the weights of all subjects in the demographic class (within the given subsample).

Using the aforementioned partitions of the NHANES subsamples, we investigated the degree to which prevalent combinations are reproducible given variations in sampling. To do this, we reapplied FIM to NHANES biomonitoring data essentially as described above, but with several important modifications to our method. First, after constructing the presence–absence matrix for a given NHANES subsample (in which rows represent subjects and columns represent chemicals), we created a new presence–absence matrix by selecting only those rows of the complete matrix that corresponded to the subjects within the partition of interest. We then used this smaller presence–absence matrix to construct a subject-chemical database by duplicating rows based on subject weights (as described previously). Finally, we selected a minimum prevalence level and applied FIM to the subject-chemical database, but this time we set the fim method of the PyFIM module (Borgelt 2016) to return all prevalent combinations rather than just the maximal prevalent combinations.

As a measure of the degree of concordance in the prevalent combinations thus identified for two partitions, we computed a concordance percentage. That is, for two partitions $i$ and $j$ of a given subsample, we denoted the sets of prevalent combinations found in these partitions $c_i$ and $c_j$, respectively, and computed the concordance percentage as $P_{ij}=100·\left|c_i\cap c_j\right|/\left|c_i\right|$, where $\left|c_i\cap c_j\right|$ represents the number of combinations in both sets (i.e., in their intersection) and $\left|c_i\right|$ represents number of combinations in set $c_i$. We then computed the average concordance percentage as

$$P=\frac{1}{12}\sum _{i=1}^4\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^4{P}_{ij}.$$

Importantly, we did not include the components of the form $P_{ii}$, which are necessarily all equal to 100% in this average.

Results

Using FIM, we identified 90 maximal prevalent combinations and 3 supercombinations made up of chemicals analyzed in NHANES 2009–2010. Because of the block structure of the NHANES data, we focused exclusively on combinations made up of chemicals within the same group. We also analyzed the numbers of single chemicals from each group that tend to be present in individuals.

Numbers of Chemicals Present in Individuals

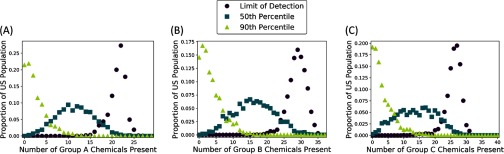
Figure 2 illustrates how the numbers of chemicals present in individuals change as we modify the discretization thresholds used to determine presence. In particular, Figure 2A shows that 95.0% of people have 18 or more of the 29 Group A chemicals, provided that exceeding the LOD constitutes presence of a chemical. On the other hand, 95.0% of people have 7 or fewer of the Group A chemicals when exceeding the 90th percentile indicates presence. When the threshold is set at the 50th percentile, 91.8% of people have 17 or fewer of the Group A chemicals. Similarly, Figure 2B reveals that 97.1% of people have 24 or more of the 37 Group B chemicals when the LOD is the discretization threshold; 93.6% of people have 9 or fewer Group B chemicals when using the 90th percentile as the discretization threshold; and 93.6% of people have 25 or fewer Group B chemicals when using the 50th percentile as the discretization threshold. Finally, Figure 2C shows that 95.6% of people have 22 or more of the 40 Group C chemicals when discretizing presence using the LOD; 94.2% of people have 9 or fewer Group C chemicals when discretizing using the 90th percentile; and 94.2% of people have 23 or fewer Group C chemicals when discretizing using the 50th percentile. In summary, the results illustrated in Figure 2 agree with expectations: As the threshold for presence of each individual chemical is increased, the number of chemicals present in the largest proportion of people decreases.

Figure 2.

Histograms indicating proportions of the U.S. population for which a given number of National Health and Nutrition Examination Survey (NHANES) chemicals from (A) Group A, (B) Group B, or (C) Group C are present. As indicated by the legend, three different discretization thresholds were applied to determine whether a chemical was present in a given person. Thus, there are three histograms in each panel: for the histogram indicated by circles, a chemical was considered to be present if the observed concentration was at or above the limit of detection (LOD); for the histogram indicated by squares, a chemical was considered to be present if the concentration was above the 50th percentile measurement; and for the histogram indicated by triangles, a chemical was considered to be present if the concentration was above the 90th percentile measurement.

General Findings for NHANES Chemical Combinations

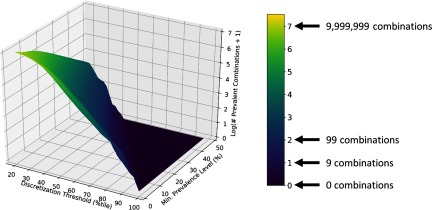
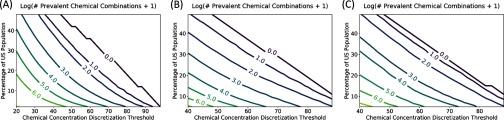
The total number of prevalent combinations that will be identified by an FIM algorithm depends on two tuning parameters: the discretization threshold (expressed as a percentile), and the minimum prevalence level. In Figure 3, we used the results of frequent itemset mining of NHANES 2009–2010 Group A chemical data to illustrate how the number of prevalent chemical combinations tends to vary with these two parameters. We emphasize that in this particular FIM application, minimum prevalence level (or minimum support) signifies a lower bound on the percentage of individuals in the U.S. population for which all the chemicals in a given chemical combination are present. Figure 3 uses a surface plot to convey information about numbers of prevalent chemical combinations from Group A, while Figure 4 uses contour plots to provide comparable information for all three groups (A, B, and C) of chemicals. The primary finding illustrated by Figure 3 and Figure 4 is that by increasing the values of either or both of the two aforementioned tuning parameters (the threshold for presence in an individual and the minimum prevalence in the population) we decrease the number of prevalent chemical combinations. Furthermore, if one wishes to prioritize a known fixed number of combinations for toxicity testing, surface or contour plots such as those shown in Figure 3 and Figure 4 can be used to select the tuning parameters and thus to establish the degree of prevalence of the combinations to be tested.

Figure 3.

Surface plot illustrating how the number of prevalent combinations of National Health and Nutrition Examination Survey (NHANES) 2009–2010 Group A chemicals decreases as the chemical concentration discretization threshold and the minimum prevalence level are increased. Here we have used the distributions (or more specifically, certain percentiles) of concentration measurements for individual chemicals to set thresholds for “significant” chemical exposure. For example, a value of 50 on the “discretization threshold” axis implies that a chemical was considered to be present in any subjects for which the concentration exceeded the median, or 50th percentile, concentration for that chemical. It is also important to note that the values for the surface plot were computed by a) computing the number (or count) of prevalent combinations containing at least two elements, b) adding one to this value, and then c) taking the base 10 logarithm of the result. Because of a), we exclude from consideration combinations of chemicals consisting of just one chemical. By performing b), we ensure that all counts are greater than zero so that c) will not fail. Importantly, due to the way we constructed the subject-chemical databases, we can interpret the minimum prevalence level as the minimum percentage of the U.S. population that will test positive for a given combination (a subject is considered to test positive for a combination when his/her concentrations of all chemicals in the combination exceed the chemical concentration discretization threshold). Note that Figure 4A gives a contour plot representation of the same information contained in this surface plot, while Figures 5B and 5C give contour plots corresponding to NHANES 2009–2010 Group B and Group C chemicals, respectively.

Figure 4.

Contour plots illustrating how the number of prevalent combinations of National Health and Nutrition Examination Survey (NHANES) 2009–2010 (A) Group A, (B) Group B, and (C) Group C chemicals decreases as the chemical concentration discretization threshold and the minimum percentage of the U.S. population required to test positive for a given combination are increased (cf. caption of Figure 3).

Figure 5, Figure 6, and Figure 7 depict maximal prevalent combinations and supercombinations for the NHANES 2009–2010 chemical groups A, B, and C, respectively. In all cases, we set the discretization thresholds at the 50th percentiles. This is a convenient threshold choice because median exposure estimates for many chemicals are readily available (Wambaugh et al. 2013; Wambaugh et al. 2014). To determine the maximal prevalent combinations, we chose different prevalence levels for each group such that the total number of these combinations fell between 20 and 40. This produced lists of prevalent combinations that could be represented at a reasonable resolution in the aforementioned figures. To identify supercombinations, we searched for the largest number of chemicals that occurred in at least two NHANES subjects.

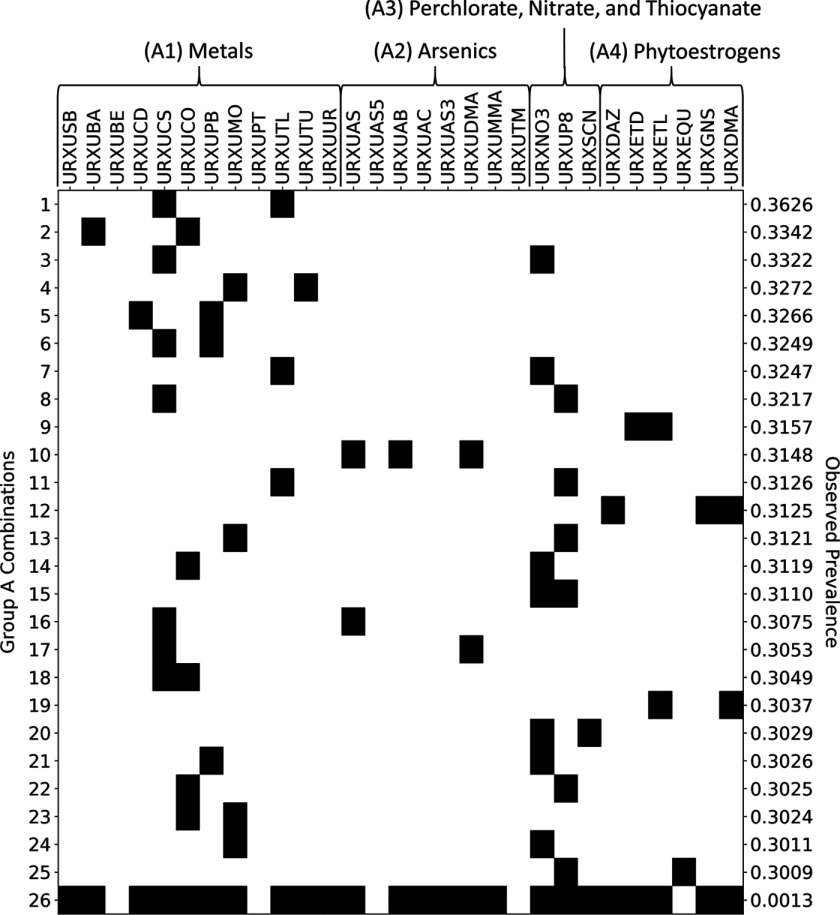
Figure 5.

Presence–absence map (black indicates present) illustrating 25 maximal prevalent combinations of Group A chemicals (rows 1 through 25) and one supercombination consisting of 24 of the 29 chemicals in Group A (row 26). The maximal prevalent combinations were identified using frequent item set mining (FIM) with discretization thresholds set at the 50th percentiles and a minimum prevalence level of 30%. The supercombination occurred in 3 Subsample A subjects, representing a total of 324,107 (or 0.13%) of 258,281,689 represented U.S. residents. National Health and Nutrition Examination Survey (NHANES) codes along the top of the figure indicate Group A chemicals, and these are organized into subgroups A1, A2, A3, and A4. The observed prevalence number at the right of each row indicates the proportion of U.S. residents in which the given combination was observed to occur.

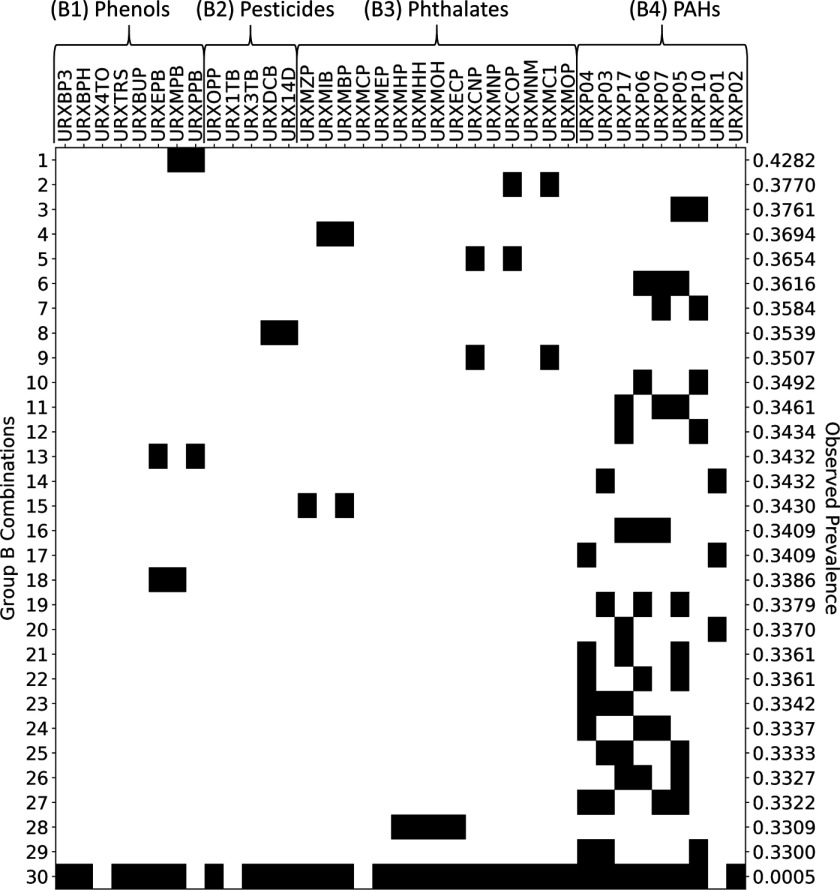
Figure 6.

Presence–absence map (black indicates present) illustrating 29 maximal prevalent combinations of Group B chemicals (rows 1 through 29) and one supercombination consisting of 32 of the 37 chemicals in Group B (row 30). The maximal prevalent combinations were identified using frequent item set mining (FIM) with discretization thresholds set at the 50th percentiles and a minimum prevalence level of 33%. The supercombination occurred in 2 Subsample B subjects, representing a total of 137,261 (or 0.05%) of 272,911,633 represented U.S. residents. National Health and Nutrition Examination Survey (NHANES) codes along the top of the figure indicate Group B chemicals, and these are organized into subgroups B1, B2, B3, and B4. The observed prevalence number at the right of each row indicates the proportion of U.S. residents in which the given combination was observed to occur.

Figure 7.

Presence–absence map (black indicates present) illustrating 36 maximal prevalent combinations of Group C chemicals (rows 1 through 36) and one supercombination consisting of 27 of the 40 chemicals in Group C (row 37). The maximal prevalent combinations were identified using frequent item set mining (FIM) with discretization thresholds set at the 50th percentiles and a minimum prevalence level of 40%. The supercombination occurred in 2 Subsample C subjects, representing a total of 479,033 (or 0.21%) of 226,021,580 represented U.S. residents. NHANES codes along the top of the figure indicate Group C chemicals, and these are organized into subgroups C1, C2, C3, and C4. The observed prevalence number at the right of each row indicates the proportion of U.S. residents in which the given combination was observed to occur.

Group A Combinations

For Group A, there are 25 maximal prevalent combinations when the minimum prevalence level is 30%. These combinations, which are represented in rows 1–25 of the presence–absence map in Figure 5, each contain two or three chemicals. Note that each column in the figure corresponds to one of the Group A chemicals, and a dark cell indicates the presence of a chemical in a given combination. Note also that the right label of each row gives the proportion of represented U.S. residents in which the combination occurs. The last row in the presence–absence map of Figure 5 depicts a supercombination consisting of 24 of the 29 Group A chemicals. This combination occurred in 3 Subsample A subjects, and based on the weights of those subjects, we concluded that it occurs in 324,107 (or 0.13%) of 258,281,689 represented U.S. residents.

Prevalent combinations of Group A chemicals included combinations of just metals, combinations of metals and polyatomic ions, and combinations of phytoestrogens. For example, several binary combinations of metals appear to occur in at least 30% of U.S. residents, including thallium and cesium (row 1 of Figure 5), barium and cobalt (row 2), tungsten and molybdenum (row 4), cadmium and lead (row 5), and lead and cesium (row 6). Several combinations consisting of one metal and one small polyatomic ion are also prevalent, including nitrate and cesium (row 3) and molybdenum and perchlorate (row 13). The combination of O-desmethylangolensin, genistein, and daidzein (row 12) occurs in about 31% of U.S. residents. Genistein and daidzein are both phytoestrogens found naturally in soybeans and other plants, whereas O-desmethylangolensin is a metabolite of daidzein (Frankenfeld 2011).

Group B Combinations

Using a minimum prevalence level of 33%, we found 29 maximal prevalent combinations of Group B chemicals. These combinations, which each contain 2 to 4 chemicals, are depicted in rows 1–29 of Figure 6. In its last row, this figure depicts a supercombination consisting of 32 of the 37 Group B chemicals. The supercombination occurred in two Subsample B subjects representing 137,261 (or 0.05%) of 272,911,633 U.S. residents.

Group B prevalent combinations included several assemblies of PAH metabolites. For example, a combination of three metabolites of fluorene (row 23 of Figure 6) occurs in at least one-third of U.S. residents, as does a combination of one pyrene metabolite and two fluorene metabolites (row 29), several combinations of fluorene and phenanthrene metabolites (rows 11, 16, 19, 21, 22, and 24–27), and a combination of one naphthalene and one fluorene metabolite (row 20). Another category of prevalent combinations of Group B chemicals involved parabens. For example, N-propyl paraben and methyl paraben (row 1 of Figure 6) co-occur in about 43% of people, and N-propyl paraben and ethyl paraben (row 13) co-occur in about 34% of people. Various binary combinations of phthalate metabolites also occur with high frequency (see rows 2, 4, and 5).

Group C Combinations

Finally, for Group C, there are 36 maximal prevalent combinations when the minimum prevalence level is 40%. The maximal prevalent combinations, which each contain 2 to 3 chemicals, are shown in the first 36 rows of the presence–absence map in Figure 7. The largest number of Group C chemicals occurring in at least 2 of the Subsample C subjects was 27 (out of 40), but we actually found 9 different combinations of 27 chemicals that met this requirement. The most prevalent of these (based on subject weights) occurs in an estimated 479,033 (or 0.21%) of 226,021,580 represented U.S. residents, and is depicted in the last row of Figure 7. Notably, all maximal prevalent combinations identified from Group C consisted of caffeine, caffeine homologs (e.g., theophylline and theobromine, which both occur naturally in chocolate), and metabolites of these (i.e., Subgroup C3). As human exposure to these particular chemicals is likely intentional, we reanalyzed Group C chemicals after omitting data on Subgroup C3. The results of this separate analysis are included in Figure S1.

Reproducibility of Prevalent Combinations and Demographic Considerations

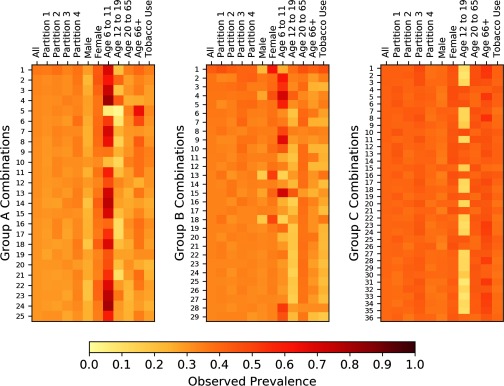
For each of the maximal prevalent combinations that we identified in Groups A, B, and C using FIM, we computed the observed prevalence in several groups, including the entire population represented by the corresponding NHANES subsample (generally, all U.S. residents over age 6 y), all represented males, all represented females, all represented persons in certain age categories, and all represented tobacco users (i.e., persons who would self-identify as having recently used tobacco). We estimated observed prevalence in the total represented population in two ways: a) considering the weights of all subjects in the relevant subsample; and b) considering the weights of all subjects in each of the four randomly generated partitions of the subsample. For each NHANES subsample, the number of subjects in each partition and each demographic group is listed in Table 5. The observed prevalence values for each chemical combination (cf. Figure 5, Figure 6, and Figure 7) from each chemical group (A, B, and C) are illustrated in the form of a heat map in Figure 8. Note that the demographic group “Age 6 to 11” is not included in the heat map for Group C chemical combinations. This is because NHANES excluded subjects under the age of 12 from blood collection used to measure serum concentrations of certain Group C chemicals (cf. subsections “Subsamples and chemical groups” and “Age restrictions and excluded data” of the “Methods” section).

Table 5.

Summary of information concerning partitioning and demographics for each of the National Health and Nutrition Examination Survey (NHANES) 2009–2010 subsamples.

Category	Subsample A	Subsample B	Subsample C
All	2,741	2,736	2,132
Partition 1	685	684	533
Partition 2	685	684	533
Partition 3	686	684	533
Partition 4	685	684	533
Male	1,359	1,392	1,026
Female	1,382	1,344	1,106
Age 6 to 11	363	411	0
Age 12 to 19	436	417	348
Age 20 to 65	1,507	1,501	1,387
Age 66 or more	316	295	282
Tobacco use	1,653	1,596	1,504

Note: The numbers of subjects listed only reflect those subjects which met the criteria described in “Methods” section. That is, some NHANES 2009–2010 subjects were omitted from consideration because they did not meet age requirements for certain laboratory analyses or because chemical concentration information was incomplete.

Figure 8.

Heat maps indicating the observed prevalence of chemical combinations within various partitions and demographic subpopulations. The enumerated combinations for Groups A, B, and C are identical to the enumerated prevalent combinations that are provided in Figure 5, Figure 6, and Figure 7, respectively.

The heat maps shown in Figure 8 indicate little variation in observed prevalence when considering an entire subsample or partitions thereof; i.e., the observed prevalence levels of the most prevalent combinations in a given subsample are approximately the same as those observed when considering a random subset of this subsample. In contrast, when considering only persons aged 6 to 11 y, many of the group A combinations are far more prevalent (with observed prevalence levels approaching 90% in some cases) than in the total population. Group A combination 5 is much more prevalent in individuals aged greater than 65 than in other demographic classes. Furthermore, all prevalent combinations in Group A are slightly more prevalent in women than in men.

Using minimum prevalence levels of 30%, 33%, and 40% for Groups A, B, and C, respectively, we applied FIM to identify prevalent combinations in each of the four partitions for each of the NHANES subsamples (A, B, and C). We found that the average concordance percentages for sets of prevalent combinations (identified in partitions of the subsamples) for Groups A, B, and C were 72.1%, 88.0%, and 83.9%, respectively. That is, on average, between 12.0% and 27.9% of combinations found to be prevalent when analyzing partition $i$ were not found to be prevalent when analyzing partition $j$. This typically occurred, however, when a combination had an observed prevalence in the second partition ($j$) that fell just below the nominal threshold (e.g., 30% minimum prevalence level for Group A combinations). When we relaxed the minimum prevalence level of the second partition ($j$) by two percentage points (e.g., to 28% for Group A combinations), we found that the average concordance percentages were 91.7%, 97.7%, and 97.7% for Groups A, B, and C, respectively. More detailed statistics concerning this reproducibility study are reported in Tables S4, S5, and S6.

Discussion

The 106 chemicals considered in the NHANES 2009–2010 biomonitoring data can be assembled to form nearly ${10}^{32}$ possible chemical combinations, and it is highly unlikely that any research entity could analyze such a large number of mixtures in a reasonable time frame. Fortunately, our FIM analyses illustrates that the number of prevalent combinations is much less than this. We conclude, therefore, that our approach can be used to identify relevant chemical combinations for bioactivity testing. That is, our FIM-based method could be applied as a first step in prioritizing chemical mixtures for further investigation. To apply the method described here, however, some important decisions must be made concerning the interpretation of biomonitoring data. In particular, one must choose discretization thresholds so that continuous measures of concentration can be converted into presence–absence information.

Other approaches for unsupervised machine learning (i.e., the identification of clusters within data) exist, such as ensemble learning methods based on random forests (Shi and Horvath 2006). In considering NHANES data, such methods would offer the ability to use continuous biomarker concentrations rather than discretized presence–absence information. One complication, however, is that many machine learning methods require synthesis of a data set from a reference distribution (Shi and Horvath 2006); given the large number of chemicals in each subset and the skewed population distributions, such a data set may be difficult to construct. FIM is particularly well suited for identifying chemical combinations for toxicity testing because it allows explicit specification of the desired prevalence of combinations. Other clustering methods, such as random forest classification, do not inherently consider whether a given cluster is common in the sample analyzed. FIM is also deterministic: regardless of the FIM algorithm, the combinations identified and prevalence of those combinations within the data is an objective feature of the data itself.

While it has some limitations, NHANES provides a rich source of information on actual chemical exposures and coexposures experienced by people. As evidence of this, we applied FIM to NHANES 2009–2010 data and discovered 90 chemical combinations prevalent in U.S. residents. We discuss several notable chemical combinations that were produced by our FIM analysis as case studies below.

Discretization Options

Most biomonitoring data consist of continuous quantitative measures of chemical concentrations that must be simplified to either present or absent at a significant level to be processed via FIM. To perform this discretization for NHANES data, we used percentiles from the observed chemical concentration distributions as thresholds, but these thresholds are somewhat arbitrary from the standpoint of risk. Ideally, the threshold for presence of a given chemical would be a critical concentration, or point of departure (POD), associated with potential toxicity. This approach would not provide a perfect solution, however, as PODs for individual chemicals do not take into account possible interactive effects of chemicals within mixtures (Carpenter et al. 1998). Furthermore, POD thresholds are typically determined in terms of in vivo doses (e.g., in animals such as rats) or in vitro concentrations (e.g., in high-throughput screening assays), rather than blood or urine concentrations. While it may make sense to compare analyte concentrations in blood directly with POD thresholds determined in vitro, additional work would be needed to compare such concentrations with in vivo doses. For example, one could use toxicokinetic models [see, e.g., the models of Pearce et al. (2016)] to convert POD oral doses into internal plasma concentrations, and then use the latter as discretization thresholds when examining blood analyte concentrations. Comparing urine analyte concentrations to POD thresholds is even more complicated. Toxicokinetic models can help again, perhaps, by allowing one to reverse engineer feasible doses based on known urine concentrations (Mage et al. 2004; Tan et al. 2007). Alternatively, one could derive concentration thresholds that are biomonitoring equivalents of existing reference doses or other screening criteria (Hays et al. 2007). In this case, too, toxicokinetic models are needed. Detailed toxicokinetic models based on extensive empirical data are limited to a relatively small number of chemicals [e.g., bisphenol A (Vandenberg et al. 2010)], and will therefore not completely address the current needs. New high-throughput toxicokinetic models based on fewer chemical specific parameters (e.g., hepatic clearance rate and plasma protein binding affinity) provide a solution for several hundred chemicals (Pearce et al. 2016; Rotroff et al. 2010; Wetmore et al. 2012; Wetmore et al. 2013; Wetmore et al. 2014), but such models are not yet available for all the chemicals included in NHANES biomonitoring. Thus, we emphasize the need to prioritize experimental work that provides toxicokinetic parameter values for NHANES chemicals.

Limitations and Strengths of NHANES Biomonitoring Data

NHANES provides the richest available data set for internal human chemical exposures; however, NHANES biomonitoring data do have a number of limitations. First of all, not all chemicals are measured in all people, and this makes it difficult to discover co-occurrence patterns for chemicals from different groups. Also, due to the age thresholds established for collecting urine and blood specimens, NHANES has very limited biomonitoring data for children, who tend to be especially susceptible to the toxic effects of chemicals (Wattigney et al. 2007). Another issue is that many chemicals measured in NHANES have short half-lives in humans, and thus, it may be difficult to draw conclusions about the true prevalence of chemical exposures based on the survey’s spot urine samples. In the context of chemical risk prioritization, one of the most important shortcomings of NHANES biomonitoring data is that they cover only a small fraction of the approximately 84,000 chemicals on the TSCA inventory (Institute of Medicine 2014; U.S. Government Accountability Office 2013) to which humans are potentially exposed (Carpenter et al. 1998; Weschler 2009). Because of this, the prevalent combinations we identified by applying FIM to currently available NHANES data are unlikely to represent the complete spectrum of chemical mixtures present in humans. Established NHANES laboratory analysis protocols only provide concentration measures for a relatively small, predefined list of targeted chemicals; nontargeted screening approaches (Rager et al. 2016), on the other hand, may eventually allow us to identify more of the chemical species that actually exist in human urine and blood samples. Closing the gap between the few hundred chemicals that have been included in NHANES and the tens of thousands of chemicals potentially present in humans will allow us to fully realize the prioritization potential of the FIM techniques described herein. Despite these various limitations, NHANES offers the best currently available source of data on human exposure to environmental chemicals. In particular, NHANES utilizes a large representative sample of U.S. residents and considers several hundred chemicals to provide information on actual internal exposures experienced by people.

Case Studies

Here we highlight several prevalent chemical combinations named in the “Results” section. Our FIM analysis of Group A chemicals, for example, identified cadmium and lead as a prevalent combination (cf. row 5 of Figure 5). These two metals have been found to co-occur in well water (Sanders et al. 2014), so drinking water might prove to be important exposure vehicles for mixtures of these metals. Using analyses of various municipal and private drinking water supplies, one might therefore derive relative proportions of cadmium and lead that form relevant mixtures.

The isoflavones daidzein and genistein, along with the daidzein metabolite O-desmethylangolensin, form another prevalent combination from Group A (cf. row 12 of Figure 5). The two parent isoflavones occur together in fruits and nuts (Liggins et al. 2000a) and in vegetables (Liggins et al. 2000b), and are both especially abundant in soybeans, which are a prominent ingredient in many foods consumed by Americans (Barrett 2006). Thus, it is not surprising that FIM identified daidzein and genistein as a prevalent chemical combination in U.S. residents. In order to identify a specific mixture of these isoflavones for bioactivity testing, one could use their relative proportions in commonly consumed soy-derived foods [see, e.g., USDA 2008 database for the isoflavone content] together with consumption rates for these foods to estimate human doses. High-throughput toxicokinetics could then be applied to arrive at relevant internal (blood plasma) mixture proportions.

FIM produces several prevalent combinations of PAHs, which make up one of the subgroups of Group B chemicals (cf. Subgroup B4 in Figure 6 and Table 2). Due to the high rate of co-occurrence of certain PAH metabolites in urine samples, we infer that fluorene frequently co-occurs with pyrene, phenanthrene, and naphthalene in humans. Being products of the incomplete combustion of organic materials, PAHs frequently occur together in tobacco smoke (International Agency for Research on Cancer 2004), but they may also co-occur in foods (Zelinkova and Wenzl 2015). Thus, it can be challenging to identify a definite exposure vehicle for combinations of PAHs; nevertheless, it may be possible by examining the specific PAHs that co-occur. For example, in one study researchers found that 1-, 2-, and 3-hydroxyfluorenes and 2-hydroxynaphthalene are more closely correlated with tobacco smoke exposure than 1-hydroxypyrene and hydroxyphenanthrenes (St. Helen et al. 2012).

From Combinations to Mixtures

FIM allows for the extraction of prevalent combinations of chemicals from biomonitoring data sets, but more work is required to explicitly define mixtures of concern that can be tested. One possible approach (as discussed in the case studies above) would be to perform exposure reconstruction; that is, by identifying likely exposure vehicles (e.g., water or food sources) for chemicals, one can examine the relative proportions of the chemicals in those exposure vehicles. Another approach is to use toxicokinetic models to infer the concentrations in target tissues that are implied by biomarker data (both urine and blood). Toxicokinetics can also inform exposure reconstruction, since biomarker concentrations will depend on chemical affinity for tissues (e.g., lipophilicity) and half-life within the body. Depending on the rate at which a given chemical is cleared from the body, the presence of a biomarker may be impacted by many different exposure events, different pathways of exposure (e.g., diet vs. product use), and even legacy concentrations inherited from one’s mother at birth (Tan et al. 2007).

Prevalence vs. Correlation

Other researchers have sought to identify correlations in chemical exposures (Patel and Manrai 2015), and even correlations between chemical exposures and adverse health outcomes (Bell and Edwards 2015; Patel et al. 2010), but here we have focused on developing a method for the identification of chemical combinations based on their prevalence in humans. To illustrate the distinction, consider hypothetical chemicals X and Y. Suppose that the exposure patterns (and consequently the biomarker levels) of X and Y are highly correlated for those subjects in which both chemicals occur, but that X and Y only co-occur in a small fraction of the population. In this case, the combination X and Y is not a prevalent combination, and it would not be identified by our method.

One might still wonder whether identified chemical combinations rise to a threshold prevalence level purely because of the high prevalence of their individual constituents or if the prevalence of a combination implies some degree of correlation in the levels of these constituents. We argue that because we have used discretization thresholds set at the 50th percentile concentrations and minimum prevalence levels of at least 30% in all of our analyses, the prevalent combinations identified herein suggest considerable correlations (or nonindependence) of the levels of the individual chemicals involved. Take, for example, any prevalent combination of two chemicals. Since both of the chemicals occur (above the 50th percentile level) in no more than 50% of the population, the maximum expected prevalence of the combination, assuming independence, would be ${0.5}^2=0.25$, i.e., if there is no correlation, we would expect that no more than 25% of people have the combination. Because this prevalent combination was identified by specifying a minimum prevalence level of 30% (or more), however, we know that the actual prevalence was more than 30%, which is substantially more than the 25% (or less) expected based on assumptions of independence. It therefore follows that prevalent combinations do indeed indicate correlations in the occurrence of their constituents.

An advantage of the exposome globe of Patel and Manrai (2015) is that it provides a powerful and compact visual of the correlations identified in NHANES. However, because this visual is constructed from pairwise correlations, it is difficult to discern co-occurrence patterns that go beyond binary associations. Our approach explicitly provides prevalence rates for combinations of varying order. Furthermore, while it is useful to mine exposure–effect relationships from NHANES data, we suggest that examining the toxicities of prevalent mixtures (such as those identified using FIM) using high-throughput screening assays and other toxicological assessments would provide more complete information on the effects of the most relevant mixtures.

Reproducibility of Prevalent Combinations

The first five columns of each heat map in Figure 8 provide a visual indication of the degree to which the FIM algorithm is robust in determining the prevalence level of chemical combinations in the NHANES biomonitoring data. The near uniformity of color (which represents observed prevalence) across these first five columns (which correspond to analysis of all subjects and just those subjects in each of the four partitions) in each case (A, B, and C) indicates that prevalence levels are approximately the same when analyzing the entire subsample or just a subset of the subsample. This provides evidence that the method is robust.

To quantify the reproducibility of the sets of prevalent combinations, we reapplied FIM to four randomly generated partitions of each NHANES subsample and found that, on average, between 72.1% and 88.0% of combinations identified as prevalent using one partition ($i$) are also identified as prevalent when using another partition ($j$) of the same subsample. These average concordance percentages increase to between 91.7% and 97.7% when the minimum prevalence level for the second partition ($j$) is decreased by two percentage points from that used in analyzing the first partition ($i$). This higher range for the average concordance percentages demonstrates that much of the discrepancy in the sets of prevalent combinations identified in two partitions within the same subsamples occurs when the actual prevalence of some combinations is quite close to (i.e., just above or just below) the nominal minimum prevalence level. In these cases, sampling variability will lead to a determination that the combination is prevalent when analyzing some partitions but not others.

Demographic Considerations

The right-most columns of each heat map in Figure 8 provide information about the prevalence within various demographic groups of those combinations identified as prevalent in the overall population. Using the left-most five columns (which, as described above, tend to have similar color/intensity in a given row) as a visual control reference point, one can identify demographic groups for which prevalence of the corresponding combination varies markedly from that observed the overall population. For example, combination 5 in Group A, which consists of cadmium and lead, appears to be considerably less prevalent in persons from 6 to 19 y of age than in the overall population; however, this same combination appears to be considerably more prevalent in persons aged 66 and older. With the exception of combinations 5 and 10, most of the Group A combinations tend to have higher prevalence in persons aged 6 to 11 y. This is also true for 9 of the 29 Group B combinations. It is important to note that NHANES measured all Group A and Group B chemical concentrations in urine, so fundamental differences in the clearance rates or urine chemistry of younger people could potentially confound the interpretation of apparent demographic differences implied by Figure 8.

Conclusions

In the real world, people are exposed to mixtures rather than individual chemicals, so there is a need to identify relevant mixtures that can be assessed for toxicity. To precisely describe such mixtures, we must first identify the specific combinations of chemicals of which they are composed. Although the number of possible combinations that can be formed from the tens of thousands of chemicals in the environment is practically infinite, the number of prevalent combinations of these chemicals is much smaller. We have presented here a novel application of FIM to NHANES biomonitoring data and demonstrated how this approach can be utilized to yield a manageable number of prevalent chemical combinations.