Validation of the Vectra H1 portable three-dimensional photogrammetry system for facial imaging

Abstract

Three-dimensional (3D) surface imaging using stereophotogrammetry has become increasingly popular in clinical settings, offering advantages for surgical planning and outcome evaluation. The handheld Vectra H1 is a low-cost, highly portable system that offers several advantages over larger stationary cameras, but independent technical validation is currently lacking. In this study, 3D facial images of 26 adult participants were captured with the Vectra H1 system and the previously validated 3dMDface system. Using error magnitude statistics, 136 linear distances were compared between cameras. In addition, 3D facial surfaces from each system were registered, heat maps generated, and global root mean square (RMS) error calculated. The 136 distances were highly comparable across the two cameras, with an average technical error of measurement (TEM) value of 0.84 mm (range 0.19–1.54 mm). The average RMS value of the 26 surface-to-surface comparisons was 0.43 mm (range 0.33–0.59 mm). In each case, the vast majority of the facial surface differences were within a ±1 mm threshold. Areas exceeding ±1 mm were generally limited to facial regions containing hair or subject to facial microexpressions. These results indicate that 3D facial surface images acquired with the Vectra H1 system are sufficiently accurate for most clinical applications.

Introduction

Soft tissue facial anthropometry plays a fundamental role in clinical practice by providing objective information on the craniofacial growth of patients and assisting in the surgical planning and outcome assessment process¹. Technological advances over the last several decades have replaced classic direct anthropometry (using rulers and calipers) and two-dimensional (2D) photography with non-invasive three-dimensional (3D) surface imaging methods. One of the most common techniques for 3D facial surface imaging today is digital stereophotogrammetry^2,3. This technique involves capturing images of the facial surface from multiple cameras with overlapping fields of view and then using software to merge these images into a single 3D model, with facial geometry represented as a dense point cloud and realistic facial skin texture⁴. Highly detailed measurements can then be collected on the resulting 3D facial models, including distances, curvatures, volumes, angles, and surface areas. A single 3D image can provide any desired view of the patient and can be taken in a fraction of the time needed for traditional multiview clinical photographs. Compared to direct anthropometry, measurements can be taken after the visit without spending added time with the patient, and the variability due to soft tissue deformation is minimized⁵.

Most digital stereophotogrammetry systems currently available on the market involve large stationary rigs with cameras set at specific angles to capture different views of the patient simultaneously. These have the disadvantage of being expensive, bulky set-ups that require frequent calibration⁶. More recently, ultra-portable low-cost systems have come onto the market, comprising little more than an SLR camera and a laptop computer. With larger stationary systems, multiple facial captures are obtained simultaneously. In contrast, with ultra-portable handheld SLR-type systems, the user must obtain multiple sequential captures from different angles. This raises the possibility of error being introduced into the process, as subjects may not maintain the same facial posture between successive captures. The independent validation of these newer systems is essential.

The current study compared landmark-based linear measurements and whole 3D surface geometry obtained using two facial stereophotogrammetry systems in a sample of adult participants: the portable SLR-type Vectra H1 system (Canfield Imaging, Parsippany, NJ, USA) and the widely used and extensively tested stationary 3dMDface system (3dMD Inc., Atlanta, GA, USA). The goal was to determine the concordance between these two systems, one new and one more established. The reproducibility of the Vectra H1 system was also assessed, by comparing multiple 3D images obtained on a single static mannequin head.

Materials and methods

A sample of 26 volunteer participants was recruited from the Pittsburgh region. The gender distribution was six male and 20 female. The mean age of the sample was 33.1 years (standard deviation 12.3 years, range 21–62 years). Both gender and age were self-reported.

After obtaining written informed consent, each participant was imaged with two different digital 3D stereophotogrammetry systems. Prior to 3D image capture, each participant was asked to remove jewelry and pull back any hair that was obstructing the forehead and ears to expose the full facial surface. Individuals with conspicuous facial hair were excluded. A series of 17 points were placed directly on each participant’s face using commercially available liquid eyeliner. Most of these points correspond to the locations of traditional facial surface landmarks⁷, with a handful of additional non-traditional points to ensure adequate facial surface coverage (Fig. 1). The purpose of placing these points was to minimize localization errors when placing landmarks on the 3D surface models (described below). All imaging was done in the same environment under standard ambient lighting conditions.

Fig. 1.

Example of a 3D facial surface indicating the 17 landmarks collected. The coordinate positions associated with these 17 landmarks were used to calculate 136 linear distances.

3D facial images were captured first using a 3dMDface system consisting of two multi-camera imaging pods positioned at a fixed distance and angle to ensure overlapping fields of view⁸. Following calibration according to the manufacturer’s instructions, each participant was seated and positioned symmetrically between the left and right camera pods. The participant’s head was tilted approximately 15° above the Frankfort horizontal to help ensure adequate coverage under the nose and chin. During the 3D capture process, participants were directed to keep a neutral facial expression with their lips gently closed and their eyes open gazing forward. The 3D facial surface capture is completed in 1.5 ms, with another 30 s of processing to automatically generate the final 3D model. The 3dMDface system is widely used in craniofacial clinics and research laboratories and has been tested extensively for accuracy and precision in facial applications^9–12.

Immediately following the imaging session with 3dMD, participants were imaged with the Vectra H1 3D camera system adhering to the manufacturer’s guidelines for image capture. The Vectra H1 system consists of a single handheld Canon SLR camera body fitted with a special lens and a range-finding apparatus to allow for 3D capture. Because the Vectra H1 system comprises a single camera, each individual capture is limited in surface coverage. Thus, three sequential captures are necessary to obtain the facial surface from ear to ear. Participants were seated and directed to keep a neutral facial expression through the capture process. For the first capture, the camera was positioned 45° to the participant’s right and approximately 30 cm below the participant’s face (at chest level), such that the camera was tilted slightly upwards. This position helps ensure that the underside of the chin and nose are adequately captured. The Vectra H1 system guides the user with visual prompts to ensure that the camera is the correct distance from the facial target, with two projected green dots functioning as a guide. When the dots converge on the facial surface the camera distance is correct. For the first capture, the participant is positioned properly when the converged green dot is located on the right cheek, at the level of the right nasal ala horizontally and the outer corner of the right eye vertically. The second capture is a frontal shot taken at face level, with the green dot positioning guide located on the participant’s philtrum. The third capture repeats the process for the first capture, but positioned to the participant’s left side. For each capture, the participant remains immobile and the camera user is required to move to the necessary position. According to the manufacturer, the speed of each capture is 2 ms. The minimum time between captures (allowing for the system’s flashes to recharge) is approximately 5 s, so the entire capture process takes about 20–30 s to be completed assuming a compliant participant and an experienced user. The Vectra H1 images were recorded on an internal SD memory card and then transferred to a PC containing the proprietary Vectra software to stitch together a full 3D facial model from the three sequential captures. By automatically identifying facial surface features that overlap between the right, center and left 3D captures, the stitching process is accomplished automatically.

The first set of tests involved comparing linear distances derived from the 3D models generated with each camera system. The facial landmarks indicated directly on the face with eyeliner were identified on each 3D facial model and the associated x,y,z coordinates saved. Care was taken to place the computerized landmarks exactly in the center of the pre-labeled points. Landmarking was done using either 3dMDpatient software (for 3dMDface surfaces) or VAM software (for the Vectra H1 surfaces). The 3D landmark coordinates for each participant were then incorporated into a single file and imported into the program WinEDMA v1.0.1¹³, where all possible unique inter-landmark linear distances (n = 136) were calculated. During the landmarking process, it was noted that three participants had missing landmarks near the ears in either the 3dMD or Vectra HI surface models or both. These three participants were excluded from the linear distance analysis, leaving 23 participants.

Several error magnitude statistics were calculated for each of the 136 measurements derived. The technical error of measurement (TEM), also known as the method error statistic, is widely used in anthropometric studies to compare measurements across different observers or acquisition methods^2,14–16. It is calculated using the following formula:

$$\text{TEM}=\sqrt{(\sum D^2)/2N},$$

where, in the current study, D represents the difference between the 3dMD and Vectra H1 measurement for each individual in the dataset and N represents the number of individuals measured. Similar to standard deviation, TEM is in the original units of measurement. In the context of this study, smaller TEM values indicate greater similarity of measurements produced by the two 3D imaging devices being compared. Because error magnitude statistics like TEM tend to increase as measurements become larger¹⁵, it is often helpful to express the error as a relative term. The relative technical error of measurement (rTEM) is simply calculated by dividing the TEM for a given variable by the grand mean for that variable and multiplying the result by 100¹⁶. Expressed as a percentage, the rTEM represents an estimate of error magnitude relative to the size of the measurement. To facilitate interpretation, rTEM values were divided into five agreement categories: <1% = excellent, 1–3.9% = very good, 4– 6.9% = good, 7–9.9% = moderate, and >10% = poor. The final error statistic was the mean signed difference (d) between 3dMD and Vectra H1 measurements. This was calculated by simply subtracting the Vectra H1 value from the 3dMD value for each participant for a given measurement. The mean of all the raw difference scores was then computed. The direction of the resulting d statistic can provide an indication of bias. For all error statistics (TEM, rTEM, and d), 95% bootstrap confidence intervals were calculated for each measurement using 10,000 resamples with replacement. The TEM, rTEM, and d statistics were calculated in Microsoft Excel (Microsoft Inc., Redmond, WA, USA). The bootstrapping procedure was performed in the R statistical programming environment (R Foundation for Statistical Computing, Vienna, Austria).

Because landmark-based linear distance approaches can only provide limited information about the face, a more comprehensive analysis of whole 3D facial surfaces was also performed. For this analysis, the 3D surface models for each participant (3dMD and Vectra H1) were registered, and measures of global error across the two surfaces were computed. First, the two 3D surfaces for each participant were converted to Wavefront object files (.obj) and loaded without texture maps into the 3dMDpatient software environment. Next, the two surfaces were manually aligned and trimmed to remove the neck, ears, and upper forehead. This process removed hair and other extraneous portions of the 3D meshes that could interfere with the analysis. A shape-based Levenberg–Marquardt curve-fitting algorithm was then applied to automatically register the two manually aligned and trimmed 3D facial surfaces^17–19. The purpose of the registration process was to establish a correspondence between the two 3D surfaces, ensuring that each point in the 3dMD-generated surface was paired with a corresponding point in the Vectra-generated surface. Surface-to-surface distances for each corresponding pair of points were then generated and color-coded to produce a heat map that represents visually the magnitude and direction of the differences between the two registered surfaces. This process was repeated for all 26 pairs of 3D facial surfaces. To quantify the magnitude of the difference between each pair of surfaces, the global root mean square (RMS) and signed mean difference (d) were calculated.

To assess repeatability of the Vectra H1 camera, an anatomically realistic male mannequin head was used. Textured matte paint was applied to the mannequin’s facial surface in order to simulate the skin pores and markings typically observed on human faces. The head was then imaged twice with the Vectra H1 system, using the same sequential right–center–left capture protocol as for live participants. The resulting 3D surfaces were then registered as described above for live participants and global surface-to-surface error statistics calculated.

The same mannequin head was also imaged once with the 3dMDface system for surface-to-surface comparison against the two Vectra H1 scans. This allowed a comparison between camera systems with facial expression effects eliminated. With possible motion effects removed, any remaining differences between the Vectra H1 and 3dMD facial surface models would have to be due to either surface registration artifacts or true discrepancies between the imaging systems.

Results

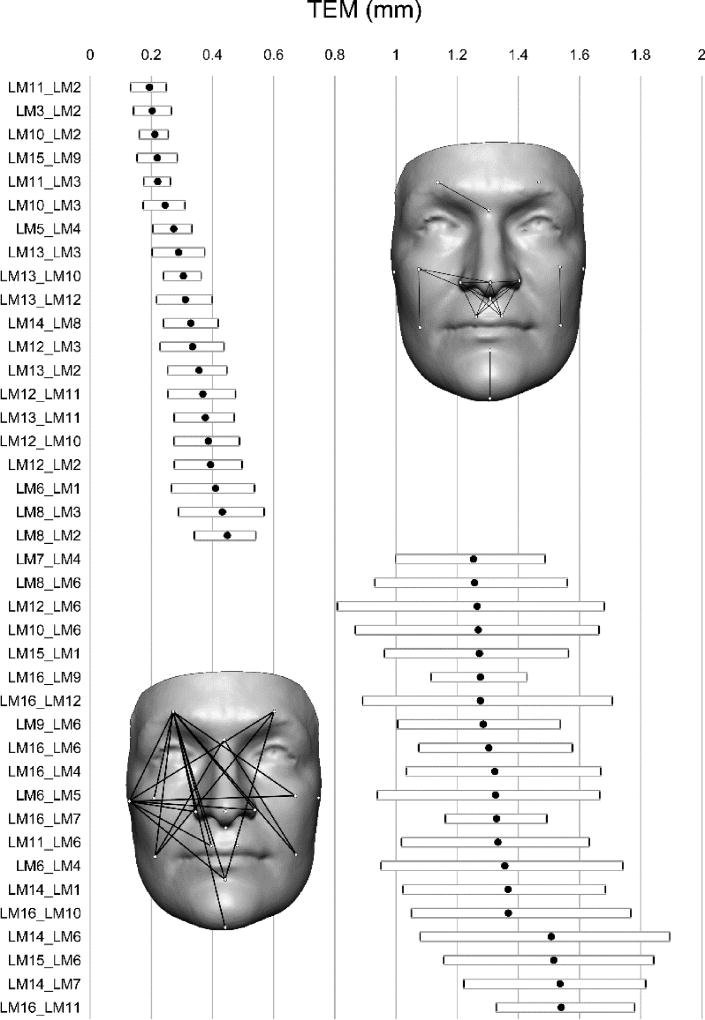
Across the 136 linear distances, the average TEM value was 0.84 mm (range 0.19–1.54 mm). In addition, none of the 136 confidence intervals exceeded 2 mm. The 20 distances with highest TEM values tended to involve landmarks located more laterally on the face; distances involving landmark 6 (right supraorbital arch) appeared 10 times and landmark 16 (right tragion) appeared seven times. In contrast, distances with the lowest TEM values tended to involve landmarks closer to the facial midline. The 20 measures with the highest and lowest TEM values are shown in Fig. 2. The average rTEM value across all 136 distances was 1.13% (range 0.44–2.48%). Fifty-five of the 136 distances (40.4%) fell within the ‘excellent’ category of less than 1%, while the remaining 81 distances (59.6%) fell within the ‘very good’ range. None of the 95% confidence intervals for rTEM exceeded 3.24%. Lastly, the grand average d value across the entire set of distances was 0.89 mm (range −0.35 mm to 2.07 mm). Only nine of the 95% confidence intervals exceeded 2 mm and none exceeded 2.36 mm. All but five of the 136 mean difference values had a positive sign, indicating that for the vast majority of measurements 3dMD was on average larger than Vectra H1. The values for these error magnitude statistics and their accompanying confidence intervals for all 136 linear distances are available in the Supplementary Material (Table S1).

Fig. 2.

Mean technical error of measurement (TEM) with 95% confidence intervals for the 20 distances, showing the lowest (upper half) and highest (lower half) error from inter-camera comparison. These distances are given along the y-axis. LM11_LM2, for example, indicates the distance between landmark 11 and landmark 2. See Fig. 1 for landmark numbers. For quick reference, the faces included show the location of the distances.

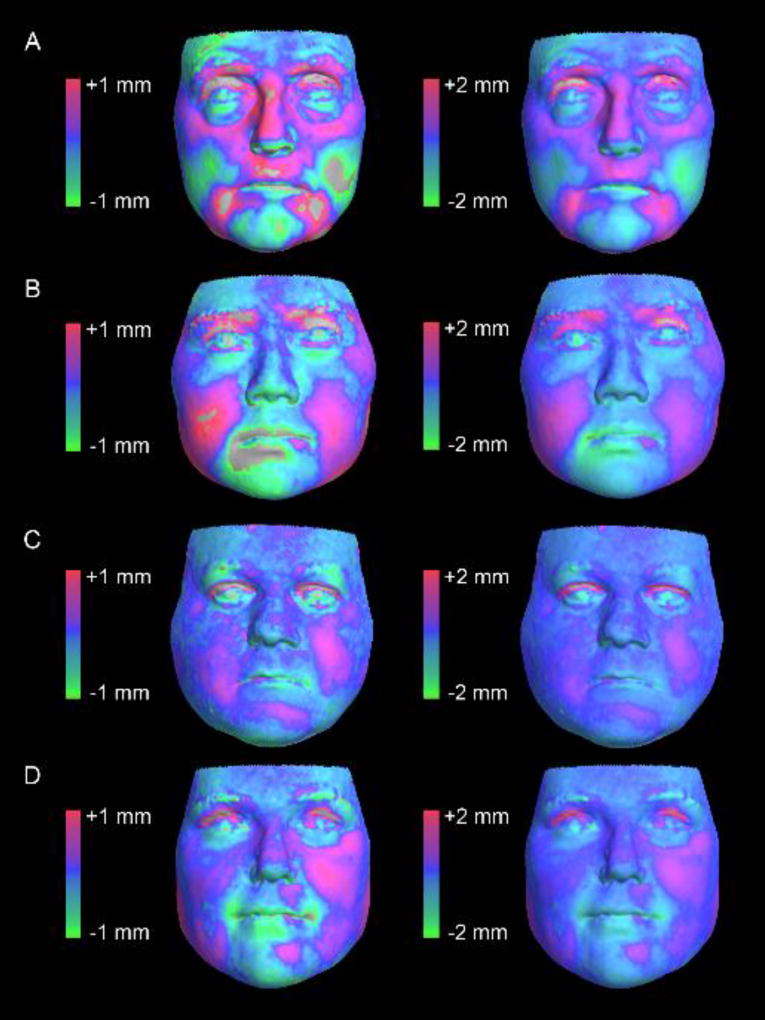
For the surface-based analysis, an average of 23,032 3D point-to-point correspondences were established between the 26 registered 3dMD and Vectra H1 facial surfaces (range 18,024–28,236 points). The average RMS value (global error) computed between corresponding points across the 26 registered surfaces was 0.43 mm (range 0.33–0.59 mm). The error showed little evidence of directionality, with an average d value across the 26 registered surfaces of −0.02 mm (range −0.12 mm to 0.05 mm). Examples of heat maps showing the direction and magnitude of the error across the registered facial surfaces with high and low RMS values are shown in Fig. 3. The error tended to be greatest around the mouth and eyes, consistent with the effects of minor facial expressions. However, this error rarely exceeded 1 mm. Heat maps for all 26 registered facial surfaces with RMS values are shown in the Supplementary Material (Figs. S1 and S2).

Fig. 3.

Heat maps showing surface-to-surface deviations following the registration of 3D models generated from the Vectra H1 and 3dMDface camera systems on four live participants. The faces at the top (A, B) had root mean square (RMS) values at the high end of those observed (0.59 mm and 0.54 mm, respectively). The faces at the bottom (C, D) had RMS values at the low end of those observed (0.33 mm and 0.33 mm, respectively). Faces in the first column show heat maps with a ±1 mm threshold. This threshold was relaxed to ±2 mm for faces in the second column. Colors at the red end of the spectrum indicate locations where the Vectra H1 surfaces show outward displacement relative to the 3dMDface surfaces. Colors at the green end of the spectrum show inward displacement. Blue tones indicate areas of no difference. Regions where surface-to-surface differences exceed the ±1 mm or ±2 mm thresholds are indicated in grey. Note that the vast majority of the surface differences fall within the upper and lower bounds of the error thresholds. Heat maps for all 26 participants are available in the Supplementary Material (Figs. S1 and S2).

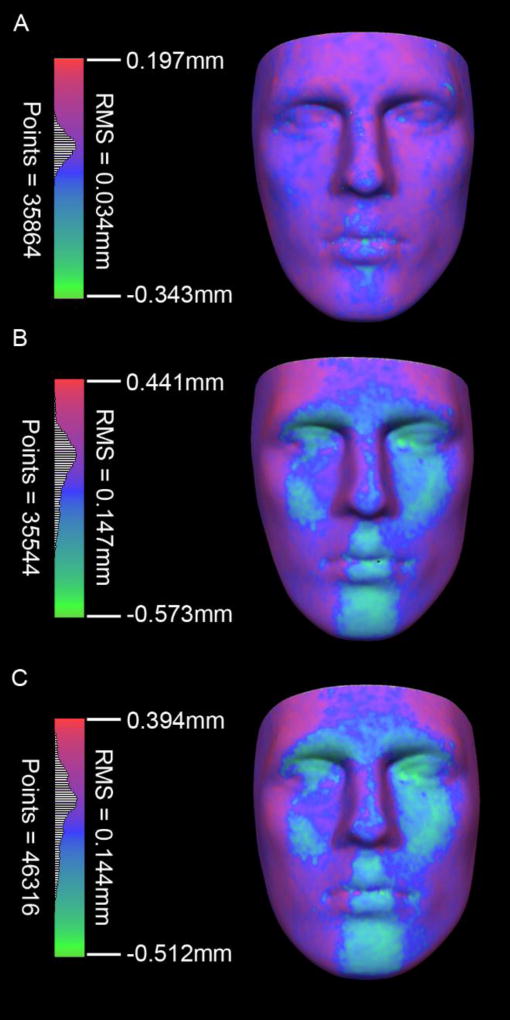
For the static object testing with a mannequin head, the Vectra H1 showed excellent repeatability. Comparing the two Vectra H1 3D surfaces, the global RMS error was 0.034 mm across over 35,000 points. The vast majority of the surface-to-surface distances were within ±0.1 mm (Fig. 4A). When each of the Vectra H1 surfaces was compared separately against the 3dMDface surface of the same mannequin head, RMS errors were 0.147 mm and 0.144 mm. The pattern of surface-to-surface distances apparent on the heat map (Fig. 4B, C) revealed that, relative to the Vectra H1, points on the 3dMDface surfaces tended to show greater displacement at the lateral parts of the face and sides of the nose and less displacement in parts of the face with a more frontal orientation. However, the magnitude of the discrepancies was still very small, with the vast majority of the surface-to-surface distances falling within ±0.25 mm.

Fig. 4.

Heat maps showing surface-to-surface deviations following the registration of 3D models generated from the Vectra H1 and 3dMDface camera systems on a static mannequin head. (A) As a test of repeatability, two separate 3D surfaces generated by the Vectra H1 camera were compared directly. (B, C) Each of the Vectra H1 surfaces was then compared to a surface generated by the 3dMDface system on the same mannequin head. For parts B and C, colors at the red end of the spectrum indicate locations where the 3dMDface surfaces show outward displacement relative to the Vectra H1surfaces. Colors at the green end of the spectrum show inward displacement.

Discussion

The goal of this study was to validate the Vectra H1 stereophotogrammetry system for facial imaging applications. Facial surface images obtained with the Vectra H1 system were quantitatively compared to images obtained with the more established 3dMDface system. This comparison was performed on both a sample of live participants and a static mannequin head. The 3dMDface system has been validated independently in terms of accuracy and precision by a number of investigators, with studies uniformly showing sub-millimeter global error margins and outstanding inter/intra-observer precision^6,9,10,20. 3dMD is also currently the most widely used digital stereophotogrammetry technology. Therefore, this system was treated as the reference standard in this analysis. In addition, the repeatability of the Vectra H1 system was evaluated by capturing a static mannequin head two times and comparing the resulting 3D surface models.

The results of the analyses indicate that facial images obtained with the Vectra H1 system are highly comparable to those obtained with the 3dMDface system. In this comparison of inter-landmark distances obtained from 3D facial images, it was found that the two systems were highly comparable. Among the 136 distances compared, an average TEM of 0.84 mm (range 0.19–1.54 mm), an average rTEM of 1.13% (range 0.44–2.48%), and an average d of 0.89 mm (range −0.35 mm to 2.07 mm) were observed. In a similar study design, Weinberg et al. compared the Genex FaceCam250 and 3dMDface systems using mannequin heads and found that differences in linear distance were consistently under 1 mm¹⁰. Some of the differences in the present study exceeded 1 mm, but the use of live participants would be expected to increase variability and error due to subtle changes in facial expression. The error values observed in the present study fell within the range of what constitutes acceptable measurement error when validating single 3D systems on live participants. For example, De Menezes et al. assessed the intra-operator random error of a stationary Vectra system and found that the TEM for repeated measures ranged from 0.13 mm to 1.19 mm³. This is similar to the TEM range observed in the current study, despite comparing two different technologies. Distances with the highest TEM in the present analysis involved landmarks near the tragus and right supraorbital arches, both of which classically constitute problem zones due to micro animation, hair interference, or extreme laterality of the landmark^2,3,11. Overall, error less than 2 mm has been considered appropriate for accuracy and precision in previous studies of 3D photogrammetric validation^2,10,11,21. However, a 1–2 mm discrepancy might become relevant when highly precise measurements are required, such as for cleft lip and nose surgery or other pediatric facial measurements^20,22.

The surface-to-surface comparisons similarly showed a high degree of correspondence across the two camera systems. The average error (RMS) between the registered 3dMD and Vectra H1 3D surfaces was 0.43 mm, with little evidence of directionality (average d = −0.02 mm). As evident from the facial heat maps, the greatest error tended to occur around the eyelids and the corners of the mouth, consistent with facial microexpression^3,23. When the 3D surfaces of the mannequin head obtained with the two systems were compared, the observed global RMS error dropped to approximately 0.14 mm. The slightly higher error observed in the live participants can probably be attributed to small differences in facial expression and posture between captures. Nevertheless, even in the live participants, differences rarely exceeded 1 mm, showing a very good correspondence between systems.

In terms of repeatability, the Vectra H1 system performed well. The global RMS error between the two Vectra H1 scans of the same mannequin head was only 0.034 mm. This is in line with a previous study by Winder et al., who used a similar approach to compare surfaces of mannequin heads taken repeatedly with the Di3D stereophotogrammetry system and found an average error of only 0.057 mm, with the largest error occurring at the outer margins of the surface²⁴. The present study results suggest that one can expect consistent results from scan to scan using the same Vectra H1 device. However, this study did not compare different Vectra H1 models to one another.

The 3D surface models from the two systems were also comparable in terms of overall texture and mesh quality. The facial skin produced by the 3dMDface system tended to have more shadows and the tone was slightly darker. The Vectra H1 skin surface textures displayed a more even hue and had higher contrast and greater detail; this was most apparent when the 3D model was enlarged. The underlying surface geometry in both systems suffered from common stereophotogrammetry problems, such as excess noise around the eyelids (slightly more pronounced with the Vectra H1), concave or flat eye surfaces due to reflectivity problems, and incomplete ear coverage due to hair obstruction. Several of the 3dMDface surfaces had small areas of missing data below the chin. These missing areas were low enough on the neck that they did not impact the placement of landmarks. A number of the Vectra H1 surfaces had minor artifacts resulting from the post-capture 3D stitching process. However, these defects were localized to the neck region and did not impact the facial surface. In general, scalp hair reproduced better with the 3dMDface system, whereas facial hair (e.g., eyebrows) tended to be similar with the two systems. Some of the above defects (e.g., missing data under the chin) can often be avoided with improved head positioning during the 3D capture process²⁵. Other problems, like excess noise around the eyelids, are unavoidable.

3dMDface is a stationary modular system that consists of six cameras positioned at a fixed distance and angle to ensure overlapping fields of view. Cameras simultaneously capture all images in 1.5 ms, limiting the risk of motion artifacts. In contrast, the Vectra H1 system consists of a single handheld Canon SLR camera body fitted with a special lens to allow for 3D captures. Because the Vectra H1 system comprises a single camera instead of six, each individual capture is limited in surface coverage, and three captures from different angles are necessary to obtain a complete facial surface. Although the individual speed of each shot is similarly quick to the 3dMD (2 ms), the photographer must change positions for each sequential shot, increasing the total time required for complete data capture. For optimal results, an individual being photographed must maintain a consistent facial position and expression throughout the entire capture process. Failing to do so may introduce motion artifacts and error into the final 3D model. Although ‘staying still’ might not be as challenging for an adult, this may not be possible for young children and individuals with certain disabilities. Because the Vectra H1 system was only tested on an adult sample, the suitability of this system for pediatric populations could not be determined. Despite these limitations, an outstanding advantage of the Vectra H1 system is its portability. It allows the use of the camera ‘on-the-go’ in a variety of settings that are not restricted to a specific office space, such as the operating room (with the patient asleep on the table), rotating patient rooms in clinic, mission trips abroad, etc. This feature makes it very appealing for clinicians or those working in field conditions.

In conclusion, 3D facial surfaces obtained with the portable Vectra H1 system were found to be highly comparable to the 3dMDface system. The sequential nature of the facial capture process did not result in significant additional error in a sample of adults. The Vectra H1 also showed high repeatability when multiple 3D models of a stable mannequin head were compared. These results suggest that the Vectra H1 camera system is accurate and reliable enough for most clinical and research applications, and that 3D facial surfaces collected from these two systems can be compared and/or combined in most circumstances.

Patient consent

Not required.