Abstract
Fluoroscopy and 2D/3D shape-matching has emerged as the standard for non-invasively quantifying kinematics. However, its accuracy has not been well established for the shoulder complex when using single-plane fluoroscopy. The purpose of this study was to determine the accuracy of single-plane fluoroscopy and 2D/3D shape-matching for quantifying full shoulder complex kinematics. Tantalum markers were implanted into the clavicle, humerus, and scapula of four cadaveric shoulders. Biplane radiographs were obtained with the shoulder in five humerothoracic elevation positions (arm at the side, 30°, 60°, 90°, maximum). Images from both systems were used to perform marker tracking, while only those images acquired with the primary fluoroscopy system were used to perform 2D/3D shape-matching. Kinematics errors due to shape-matching were calculated as the difference between marker tracking and 2D/3D shape-matching and expressed as root mean square (RMS) error, bias, and precision. Overall RMS errors for the glenohumeral joint ranged from 0.7–3.3° and 1.2–4.2 mm, while errors for the acromioclavicular joint ranged from 1.7–3.4°. Errors associated with shape-matching individual bones ranged from 1.2–3.2° for the humerus, 0.5–1.6° for the scapula, and 0.4–3.7° for the clavicle. The results of the study demonstrate that single-plane fluoroscopy and 2D/3D shape-matching can accurately quantify full shoulder complex motion.
Keywords: glenohumeral, acromioclavicular, shoulder, kinematics, fluoroscopy
1. Introduction
Quantifying shoulder kinematics is often fundamental to many clinical questions regarding the development and/or progression of orthopaedic conditions including rotator cuff disease and multidirectional instability. Traditional methods to non-invasively quantify kinematics include optical and electromagnetic motion capture. However, these methods are subject to skin motion artifact [1–3]. Other studies quantified kinematics by attaching motion sensors to pins inserted directly into bones [4, 5]. While these studies provide a more accurate description of joint motion, they are limited by small sample sizes due to the invasive nature of the methodology. Consequently, larger studies investigating clinically-focused research questions are not feasible.
More recently the use of fluoroscopy and model-based image registration (i.e. 2D/3D shape-matching) has become the standard for non-invasively quantifying joint motion [6–9]. Biplane fluoroscopy provides highly precise estimates of glenohumeral motion with errors less than 1.0° and 0.5 mm [10]. However, the use of two radiographic systems increases the dose to the subject compared to using a single plane. Further, the use of single plane fluoroscopy does not require specialized biplane radiographic systems but can be employed using common clinical c-arm systems.
In exchange for reduced radiation dose, single plane fluoroscopy generally results in lower kinematic accuracy [11]. However, its accuracy for quantifying shoulder kinematics is not well established despite its use in several studies [12–16]. Only two studies have investigated the accuracy for glenohumeral joint motion [15, 17]. Both studies utilized a single specimen which may limit the generalizability of the results given the substantial variation in shoulder anatomy that exists both between and within individuals [18–20], and the inherent dependency of shape-matching on anatomical morphologies. Furthermore, no study has investigated the accuracy of tracking clavicular kinematics. This hinders a comprehensive understanding of shoulder complex motion given the clavicle’s important role in shoulder complex function [4, 21, 22]. Therefore, the purpose of this study was to determine the accuracy of single plane fluoroscopy and 2D/3D shape-matching for quantifying full shoulder complex kinematics using biplane marker tracking (i.e. radiostereometric analysis, or RSA) as the criterion reference.
2. Methods
2.1. Instrumentation
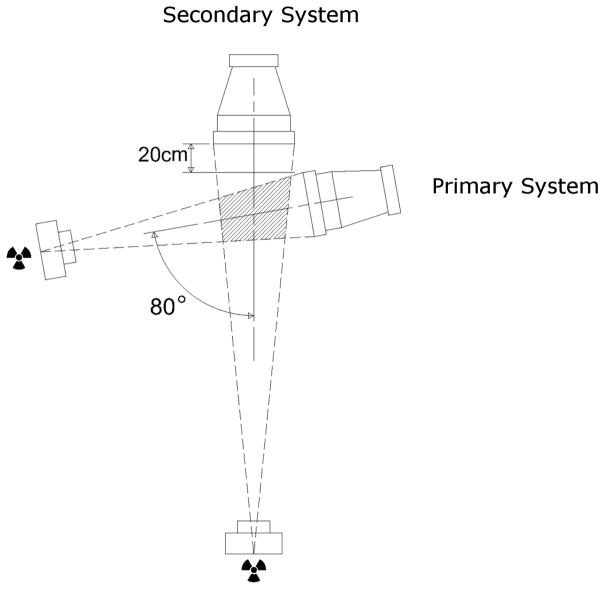
The primary imaging system utilized in this study was a Philips BV Pulsera mobile c-arm fluoroscopy unit (99.5 cm source-to-image distance (SID), 30 cm field-of-view (FOV), 1024×1024 image resolution). The secondary imaging system was a custom video-radiography system (152 cm SID, 40.6 cm FOV, 1080×1080 image resolution). The imaging systems were positioned with an 80 degree inter-beam angle and with the image intensifier of the primary system 20 cm off the face of the secondary system (FIGURE 1). This gap allowed for a larger imaging volume without decreasing the source-to-object distance (SOD) of the primary imaging system, and thus preventing unnecessary magnification and reduction of the functional FOV.
FIGURE 1.
Configuration of the biplane radiographic setup (top view). Marker tracking was performed using images acquired from both the primary and secondary systems in the biplane configuration, while 2D/3D shape-matching utilized images only from the primary fluoroscopy system.
2.2. Marker Tracking Validation
Prior to the in vitro validation experiment, the accuracy of tracking markers within the 3D imaging volume was verified using an acrylic validation object was precision milled with six 1-mm diameter tantalum markers positioned in two clusters of three markers. The distances between markers and marker clusters were chosen to simulate the approximate distances between markers placed into the clavicle and scapula during the in vitro experiments. Two orthogonal coordinate systems were constructed from the two sets of marker clusters using the known 3D marker coordinates.
Images of a distortion grid and calibration cube were acquired using both radiographic systems to correct for image distortion and to define the imaging geometry of the biplane system [23]. The validation object was positioned and imaged in 30 positions and orientations throughout the biplane imaging volume. Image distortion correction, 3D volume calibration, and biplane marker digitization were performed using XMALab 1.3.3 software [24]. Following digitization, the 3D coordinates of each marker were exported for data analysis using custom MATLAB codes (The Mathworks, Inc.; Natick, USA).
The Euclidean distance between marker pairs (i.e. inter-bead distance) was calculated from the 3D marker coordinates. The relative position and orientation of the two marker clusters were also determined. Errors in inter-bead distances and relative marker cluster position and orientation were determined based on the known marker coordinates and those estimated from digitization. Errors were expressed as RMS error (i.e. the square root of the mean squared error), bias (i.e. the mean error), and precision (i.e. the standard deviation of the mean error).
2.3. Single plane 2D/3D Shape-Matching Validation
Two cadaveric specimens consisting of the thorax and bilateral upper extremities (4 shoulders total) were acquired (1 male, age at death: 58 and 80 years). Tantalum markers (1 mm diameter) were inserted into the clavicle, scapula, and humerus through sharp dissection. Resected soft tissue was returned to its anatomical position and sutured following marker placement. The specimens were then secured to a chair in an upright seated position allowing for full shoulder complex motion.
The specimens were oriented in the biplane imaging volume such that the scapula was approximately parallel to the image intensifier of the primary imaging system. The arm was elevated and held passively using a pulley system at five static positions: arm at side (i.e. minimum), 30°, 60°, 90°, and maximum humerothoracic elevation. Humerothoracic elevation angles were verified using a clinical goniometer within ±5° of the target angle. Images were acquired using both radiographic systems with the shoulder at each elevated position. All images acquired with the primary imaging system used high definition fluoroscopy (continuous x-ray mode) and the system’s automatic kV/mA function (50–60 kV, 4.0–4.5 mA).
Computed topography (CT) scans of the entire shoulder complex were acquired for each specimen using a Siemens SOMATOM Sensation 64 CT scanner (140 kVp, 0.6 mm slice thickness, 315 mA, 512×512 resolution). Three-dimensional bone models of the humerus scapula, and clavicle were created using Mimics software (Materialise NV; Leuven, Belgium). The tantalum markers were included in the segmented bone masks such that when the 3D bone models were rendered the cortical surface of the bone did not have any evidence of discontinuity from the marker, thus masking bead placements which could create user bias during shape-matching.
Anatomical coordinate systems were constructed by digitizing landmarks on the 3D models per the recommendations of the International Society of Biomechanics [25] and expressed relative to the CT coordinate system. Due to the difficulty of consistently identifying three non-collinear points on the clavicle, the third clavicular point was defined 5 cm superior to the center of mass along the clavicle’s superior/inferior inertial axis. The geometric center of the humeral head was determined using a least-squares sphere fit to the articular surface. The origins of the humeral and scapular coordinate systems were placed at the geometric center of the humeral head, and the origin of the clavicular coordinate system was placed at the acromioclavicular joint. The locations of marker centroids were digitized on the CT images allowing for the definition of a temporary marker-based coordinate system for each bone. The transformation between the anatomical coordinate system and the temporary marker-based coordinate system was calculated for each bone segment using the CT scanner’s coordinate system as the common reference frame.
Radiographic image distortion correction, calibration, and biplane marker digitization were performed using XMALab software [24] as previously described. Temporary marker-based coordinate systems were constructed for each segment in each radiographic frame and transformed to anatomical coordinate system using the transformation previously calculated. This process assumes the markers remained rigidly fixed in the bone, which was verified by comparing the precision of the inter-bead distances to those obtained during the marker validation experiment. Model registration was performed using the undistorted images acquired from the primary fluoroscopy system using an open source model-image registration software (JointTrack, available at: https://sourceforge.net/projects/jointtrack/) (FIGURE 2).
FIGURE 2.

Example of shape-matched humerus, scapula, and clavicle at the minimum position of humerothoracic elevation. Figure demonstrates the crank shape of the clavicle can be visualized when the subject is placed such that the scapula is approximately parallel to the image intensifier. The image also shows an example of anatomical variability in that the specimen has an extremely sloped humeral greater tuberosity compared to the expected relatively flat superior surface.
A custom MATLAB code was used to process and analyze the kinematic data. Glenohumeral joint position and orientation were described as the humeral anatomical coordinate system relative to the scapular anatomical coordinate system using an X,Z′,Y″ rotation sequence [26]. Acromioclavicular joint orientation was described as the scapular anatomical coordinate system relative to the clavicular anatomical coordinate system using an Y,X′,Z″ rotation sequence [25]. The error in joint kinematics due to shape-matching was calculated at each humerothoracic position as the difference between marker tracking and 2D/3D shape-matching. All errors were expressed as RMS error, bias error, and precision. Overall RMS error, bias error, and precision were also calculated by pooling data from all humerothoracic positions. To investigate kinematics errors further, the error due to shape-matching individual bone segments was described by calculating the displacement between the segment’s anatomical coordinate systems as defined by marker tracking and 2D/3D shape-matching.
3. Results
3.1. Marker Tracking Validation
The RMS error for the inter-bead distance of the validation object across trials was 0.2 mm with a bias (± precision) of −0.1 mm (± 0.1 mm). This corresponded to relative orientation and position RMS errors between the two marker clusters of 0.2° and 0.3 mm, respectively. The bias error for relative marker cluster orientation and position was 0.0° (± 0.1°) and 0.1 mm (±0.2 mm), respectively.
3.2. 2D/3D Shape-Matching Validation
One frame was excluded in one specimen due to marker drop-out for the minimum humerothoracic elevation position. The average maximum angle of glenohumeral elevation was 82.3° (±5.0°), which corresponded to an average humerothoracic elevation of 109° ± 6.9°.
For the acromioclavicular joint, the overall RMS error across all humerothoracic elevation angles was 1.7° for internal rotation, 3.4° for upward rotation, and 2.0° for tilt. RMS error at each angle of humerothoracic elevation are shown in FIGURE 3A, and bias and precision are presented in TABLE 1.
FIGURE 3.
RMS errors (in degrees) for orientation of the (A) acromioclavicular and (B) glenohumeral joints across humerothoracic elevation angles. IR = internal rotation, ER = external rotation, UR = upward rotation, DR = downward rotation.
TABLE 1.
Bias ± precision (in degrees) for acromioclavicular and glenohumeral joint orientations across angles of humerothoracic elevation. IR = internal rotation, ER = external rotation, UR = upward rotation, DR = downward rotation. Bias represents systematic errors or offsets. Positive bias values for the acromioclavicular joint indicates shape-matching overestimated external rotation, upward rotation, and anterior tilt as compared to marker tracking, or underestimated internal rotation, downward rotation, and posterior tilt. Positive bias values for the glenohumeral joint indicates shape-matching overestimated abduction, posterior plane of elevation, and external rotation as compared to marker tracking, or underestimated adduction, anterior plane of elevation, and internal rotation.
| Acromioclavicular Joint | Glenohumeral Joint | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Position | IR/ER | UR/DR | Tilt | Elevation | Plane of Elevation | Axial Rotation |
| Min | 0.3 ± 1.7 | −0.3 ± 4.1 | −0.9 ± 0.5 | −0.3 ± 1.0 | −0.5 ± 0.9 | −0.3 ± 1.2 |
| 30° | 1.1 ± 1.4 | 1.5 ± 3.2 | −1.7 ± 2.1 | −0.3 ± 0.2 | −0.9 ± 2.4 | 1.0 ± 3.7 |
| 60° | 0.0 ± 1.6 | 1.2 ± 3.7 | −1.2 ± 0.7 | 0.1 ± 0.2 | −1.4 ± 3.5 | 1.2 ± 3.0 |
| 90° | 0.6 ± 1.8 | 0.5 ± 5.4 | −0.2 ± 3.2 | −0.4 ± 0.8 | −1.7 ± 2.4 | −1.3 ± 4.8 |
| Max | 0.1 ± 2.8 | 0.3 ± 1.9 | −0.8 ± 1.9 | 0.0 ± 1.0 | −0.9 ± 2.8 | −0.8 ± 4.1 |
|
| ||||||
| Overall | 0.4 ± 1.7 | 0.7 ± 3.4 | −0.9 ± 1.9 | −0.2 ± 0.7 | −1.1 ± 2.4 | 0.0 ± 3.4 |
For glenohumeral joint orientation, the overall RMS error across all humerothoracic elevation angles was 0.7° for elevation, 2.6° for plane of elevation, and 3.3° for axial rotation. RMS error at each angle of humerothoracic elevation are shown in FIGURE 3B, and bias and precision are presented in TABLE 1. The overall RMS error for glenohumeral geometric center position was 4.2 mm along the anterior/posterior axis, 1.2 mm along the superior/inferior axis, and 1.8 mm along the medial/lateral axis. RMS error, bias, and precision at each angle of humerothoracic elevation are presented in TABLE 2.
TABLE 2.
RMS error (bias ± precision) (in mm) for glenohumeral joint center position across angles of humerothoracic elevation. Positive bias indicates shape-matching resulted in a more posterior, inferior, and/or medial position of the humerus relative to the scapula as compared to marker tracking.
| Anterior/Posterior | Superior/Inferior | Medial/Lateral | |
|---|---|---|---|
| Min | 3.0 (1.0 ± 3.4) | 1.4 (1.2 ± 1.0) | 1.2 (−0.9 ± 0.9) |
| 30° | 3.8 (0.4 ± 4.4) | 1.2 (0.3 ± 1.3) | 1.7 (−1.5 ± 1.0) |
| 60° | 2.8 (2.2 ± 1.9) | 0.9 (0.1 ± 1.0) | 1.5 (−1.5 ± 0.3) |
| 90° | 5.6 (4.2 ± 4.3) | 1.1 (0.2 ± 1.3) | 2.1 (−1.7 ± 1.4) |
| Max | 4.8 (3.7 ± 3.6) | 1.2 (0.0 ± 1.3) | 2.1 (−1.8 ± 1.2) |
|
| |||
| Overall | 4.2 (2.4 ± 3.5) | 1.2 (0.3 ± 1.1) | 1.8 (−1.5 ± 1.0) |
RMS errors representing the angular error in shape-matching each individual bone segment are presented in FIGURE 4. RMS errors ranged between 1.2–3.2° for the humerus, 0.5–1.6° for the scapula, and 0.4–3.7° for the clavicle. Corresponding bias and precision values are presented in TABLE 3. Overall RMS errors representing the positional error in shape-matching ranged between 4.2–8.1 mm for the humerus and 1.6–9.3 mm for the scapula. RMS error, bias, and precision at each angle of humerothoracic elevation are presented in TABLE 4.
FIGURE 4.
RMS errors (in degrees) representing the angular difference between the anatomical coordinate system from marker tracking and shape-matching for the (A) humerus, (B) scapula, and (C) clavicle across humerothoracic elevation angles. IR = internal rotation, ER = external rotation, UR = upward rotation, DR = downward rotation, Prot = protraction, Ret = retraction, Elev = elevation, Dep = depression.
TABLE 3.
Bias ± precision (in degrees) for humeral, scapular, and clavicular bone angular error. IR = internal rotation, ER = external rotation, UR = upward rotation, DR = downward rotation. Positive bias values for the humerus indicates shape-matching overestimated abduction, posterior plane of elevation, and external rotation as compared to marker tracking, or underestimated adduction, anterior plane of elevation, and internal rotation. Positive bias values for the scapula indicates shape-matching overestimated external rotation, upward rotation, and anterior tilt as compared to marker tracking, or underestimated internal rotation, downward rotation, and posterior tilt. Positive bias values for the clavicle indicates shape-matching overestimated retraction, elevation, and anterior axial rotation as compared to marker tracking, or underestimated protraction, depression, and posterior axial rotation
| Humerus | |||
|---|---|---|---|
| Elevation | Plane | Axial Rotation | |
| Min | 0.5 ± 0.7 | 0.1 ± 0.4 | −0.4 ± 1.6 |
| 30° | 0.8 ± 2.1 | −0.2 ± 1.1 | −1.4 ± 2.8 |
| 60° | 1.3 ± 3.4 | 0.4 ± 0.7 | −1.1 ± 3.4 |
| 90° | 1.5 ± 1.3 | 0.4 ± 0.7 | 1.2 ± 5.0 |
| Max | 1.4 ± 2.4 | 0.0 ± 2.5 | 0.6 ± 3.8 |
|
| |||
| Overall | 1.1 ± 2.0 | 0.1 ± 1.2 | −0.2 ± 3.3 |
|
| |||
| Scapula | |||
| IR/ER | UR/DR | Tilt | |
|
| |||
| Min | −0.3 ± 1.9 | 0.2 ± 0.3 | 0.5 ± 1.3 |
| 30° | −0.5 ± 1.4 | −0.1 ± 0.4 | 0.0 ± 0.3 |
| 60° | 0.1 ± 1.6 | 0.2 ± 0.3 | 0.1 ± 1.0 |
| 90° | −0.3 ± 1.7 | −0.1 ± 0.3 | −0.1 ± 1.1 |
| Max | 0.0 ± 2.3 | 0.6 ± 0.6 | 0.3 ± 0.3 |
|
| |||
| Overall | −0.2 ± 1.6 | 0.2 ± 0.4 | 0.2 ± 0.8 |
|
| |||
| Clavicle | |||
| Retraction | Elevation | Axial Rotation | |
|
| |||
| Min | 0.0 ± 0.1 | −0.2 ± 1.0 | −0.3 ± 3.8 |
| 30° | 0.3 ± 0.6 | −0.2 ± 0.6 | −2.2 ± 3.5 |
| 60° | 0.0 ± 0.2 | 0.0 ± 0.7 | −1.8 ± 3.3 |
| 90° | 0.4 ± 0.5 | 0.1 ± 0.5 | −0.6 ± 6.0 |
| Max | 0.2 ± 0.4 | 0.2 ± 0.5 | −1.0 ± 2.3 |
|
| |||
| Overall | 0.2 ± 0.4 | 0.0 ± 0.6 | −1.2 ± 3.6 |
TABLE 4.
RMS error (bias ± precision) (in mm) for humeral and scapular bone position error position. Positive bias. X axis = anterior/posterior, Y axis = superior/inferior, Z axis = medial/lateral. Positive bias indicates shape-matching resulted in a more posterior, inferior, and/or medial position of the bone segment compared to marker tracking.
| Anterior/Posterior | Superior/Inferior | Medial/Lateral | |
|---|---|---|---|
| Humerus | |||
| Min | 2.7 (1.2 ± 3.0) | 1.2 (0.6 ± 1.3) | 4.8 (−3.4 ± 4.2) |
| 30° | 4.3 (−3.5 ± 3.0) | 4.0 (−2.5 ± 3.6) | 11.6 (9.8 ± 7.2) |
| 60° | 3.2 (−1.8 ± 3.1) | 4.1 (−2.7 ± 3.6) | 9.0 (7.1 ± 6.5) |
| 90° | 4.4 (−2.5 ± 4.1) | 3.2 (−2.6 ± 2.2) | 6.8 (5.6 ± 4.3) |
| Max | 5.5 (−2.3 ± 5.8) | 3.6 (−2.5 ± 2.9) | 5.7 (4.4 ± 4.2) |
|
| |||
| Overall | 4.2 (−1.9 ± 3.9) | 3.5 (−2.1 ± 2.9) | 8.1 (5.1 ± 6.4) |
|
| |||
| Scapula | |||
| Min | 5.9 (4.5 ± 4.7) | 2.9 (2.4 ± 2.0) | 1.9 (−1.6 ± 1.3) |
| 30° | 12.9 (−9.9 ± 9.5) | 3.8 (−1.3 ± 4.2) | 1.6 (0.0 ± 1.9) |
| 60° | 9.5 (−5.5 ± 9.0) | 2.8 (−0.5 ± 3.1) | 0.9 (−0.3 ± 1.0) |
| 90° | 7.2 (−2.5 ± 7.8) | 2.6 (0.0 ± 3.0) | 1.3 (−0.2 ± 1.4) |
| Max | 8.6 (−1.2 ± 9.9) | 3.5 (−0.2 ± 4.1) | 2.2 (−0.1 ± 2.6) |
|
| |||
| Overall | 9.3 (−3.3 ± 8.9) | 3.2 (0.0 ± 3.3) | 1.6(−0.4 ± 1.6) |
4. Discussion
This study provides a comprehensive analysis of the accuracy of using single plane fluoroscopy and 2D/3D shape-matching for quantifying static shoulder complex kinematics. Importantly, the study establishes the methodology as a viable option for quantifying static shoulder complex kinematics. This study also demonstrates the process can be accomplished using clinically available imaging technology, which strengthens the potential to successfully translate this methodology to clinical application of identifying movement disorders. Furthermore, by describing both joint and bone segment accuracy using multiple error metrics, the results of the study can help understand the implications of the errors when the methodology is used to describe shoulder complex kinematics in vivo.
Only two previous studies have investigated the accuracy of tracking glenohumeral kinematics using single plane fluoroscopy [15, 17]. In general, the results of these investigations are comparable to the current study. Specifically, Zhu [17] found glenohumeral RMS errors of 0.8–3.7° and 0.5–1.5 mm, while Matsuki [15] found bias errors for the humerus and scapula of 0.5–2.0° and 0.2–5.3 mm. However, both studies are limited by the use of only one cadaveric shoulder resulting in errors that may not be generalizable due to the variation in shoulder complex anatomy both between and within individuals [18–20] (FIGURE 2). Additionally, both studies investigated dynamic shoulder motion while static trials were utilized in the current study due to the inability to sync the primary and secondary radiographic systems in the biplane configuration. Although dynamic trials may introduce image blur that may affect shape-matching accuracy, the comparable results between the current study and previous work [15, 17] suggests dynamic motion may not significantly affect shape-matching accuracy compared to the error associated with having a single imaging plane.
Comparison of individual kinematic parameters between fluoroscopy validation studies is often complicated due to the use of “in-plane” and “out-of-plane” terminology. While use of these terms is common and accepted for the primarily uniaxial motion of the knee joint, they are an oversimplification of shoulder complex motion. When the image receptor is positioned parallel to the scapula and the humerus elevated in the scapular plane, glenohumeral elevation is often considered “in plane”. However, the humerus externally rotates considerably as it elevates [4], altering the degree to which a motion is considered in- or out-of-plane. Additionally, the complex geometry of the shoulder girdle makes this terminology even more difficult to interpret. For example, scapular upward/downward rotation could be considered an “in-plane” motion if positioned parallel to the image receptor. However, when it is described relative to the clavicle as is done for acromioclavicular joint motion, scapular upward rotation can no longer be considered “in plane” due to sternoclavicular retraction, which places the clavicle oblique to the imaging plane. These considerations emphasize the need for specific, anatomical descriptions of errors from validation studies.
Importantly, this study demonstrates the clavicle can be accurately tracked using single plane 2D/3D shape matching. With surface sensors, it is generally recommended to limit tracking to humeral elevation angles lower than 115° due to skin motion artifact affecting axial rotation [27]. Given axial rotation is the primary motion of the clavicle [4], accurately quantifying this rotation is critical to understanding the contribution of clavicular motion to overall shoulder complex function. Although it is unknown whether the accuracy for tracking the clavicle found in the current study will be similar for dynamic trials, this methodology looks promising for tracking clavicular motion throughout the range of motion because RMS errors did not appear to be influenced by humerothoracic elevation angle (FIGURE 4).
The current study also offered a more comprehensive analysis of shape-matching errors than previous works that report either bias and precision [17] or RMS error [15]. Although subtle, the differences between these error metrics have very important implications on interpreting validation studies. Specifically, RMS error describes the average magnitude of the error and therefore provides an estimate of accuracy. In contrast, bias error describes the mean error and can appear artificially small if errors are not consistently positive or negative (i.e. systematic error). For example, glenohumeral axial rotation bias error in the current study is 0.0°, while the RMS is 3.3°. This suggests glenohumeral axial rotation errors are not biased but are on average 3.3° from their true value. In comparison, the similar magnitude of the RMS and bias errors for glenohumeral medial/lateral position indicates a systematic error of approximately 1.5 mm resulting in a more medial position relative to the scapula than its true position. These examples highlight the need to report both metrics when describing the accuracy of measurement systems.
Calculating errors associated with both the joint and individual bone segments allows for investigation into potential sources of error, which has not been possible in reviewing the results of previous studies. For example, acromioclavicular upward rotation was found to have the highest overall rotation RMS error value (3.4°). According to the coupling theory [22], this acromioclavicular joint position is related to scapular upward/downward rotation and clavicular elevation/depression and axial rotation. Inspection of the RMS errors for scapular upward rotation error (0.5°) and clavicular elevation (0.6°) and axial rotation (3.7°) suggests the error in acromioclavicular upward rotation is likely due to error in shape-matching clavicle axial rotation. Likewise, the error associated with glenohumeral axial rotation appears to be due to shape- matching errors of humeral internal/external rotation as opposed to scapular internal/external rotation. Interpreting errors in this way is useful when working to improve the accuracy of shape-matching by identifying the specific bone motion responsible for the resulting description of joint error.
Inspection of the bone data also brings to light the complexities of shape-matching each bone segment. Angular errors for the scapula and clavicle were generally lower than that for the humerus. For the scapula, this is likely a reflection of anatomical uniqueness of the bone as it has many structures that provide valuable information for shape-matching. In comparison, the clavicle does not have as many unique anatomical structures, however obtaining the radiographic image in the scapular plane helps visualize the crank shape of the clavicle (FIGURE 2). This provides information about the degree to which the clavicle is rotated about its long axis, which is difficult to visualize on a more A-P view when the clavicle appears more cylindrical. In contrast, the humerus offers less anatomical information to assist in shape-matching due to its long symmetrical shape, which results in higher shape-matching errors (FIGURE 4).
The preliminary experiment validating marker tracking is critical when using RSA to validate 2D/3D shape-matching as it determines how accurately markers can be tracked in 3D space. The current study found higher errors relative to the results of previous studies [9, 23, 28]. These studies reported inter-bead distance bias errors up to ±0.02 mm and precision values up to 0.05 mm. However, expressing marker tracking accuracy in terms of inter-bead distance may be less meaningful because the metric is not in the units of our primary dependent variable (i.e. relative position and orientation). Developing coordinate systems from the marker clusters allowed marker tracking errors to be described in terms of relative orientation (degrees) and position (mm). This analysis demonstrated that the errors associated with the orientation/position of the marker clusters are very small and within an acceptable tolerance, despite higher inter-bead distance errors.
This study has limitations that should be considered. First, the use of RSA to validate shape-matching has inherent limitations. The same images are used for marker tracking and shape-matching. As such, they are subject to the same distortion correction and calibration and any inaccuracies with these processes will not be known. While the results of the marker validation experiment provide an estimate of the magnitude of this error, an optimal validation experiment would have separate sources of error. However, the use of other systems such as electromagnetic sensors or optical markers would introduce additional differences associated with the unique definition of the coordinate systems from two different methodologies. Second, the accuracy of RSA as the gold standard in describing rotations about anatomical axes is limited by the resolution of the CT scan and metal artifact from the tantalum markers. This is because error in identifying the marker centroids on the CT scan will result in errors in defining the “true” orientation/position of the temporary marker-based coordinate system. This error will affect the transformation between the temporary marker-based coordinate system and the anatomical coordinate system, resulting in a systematic error in describing anatomical bone orientation/position. Therefore, it is possible the errors in defining the marker centroids increased the errors attributed to the 2D/3D shape-matching. Finally, although the study included more specimens than previous validation studies using single plane fluoroscopy, additional specimens would likely improve the estimate of the error associated shape-matching.
Overall, the results of the study demonstrate that single-plane fluoroscopy and 2D/3D shape-matching can accurately quantify shoulder complex motion. Furthermore, the methodology can be performed using clinically available technology. Future research is needed to quantify how the errors affect the result of kinematic models used to estimate parameters such as acromiohumeral distance, cartilage deformation, and joint forces and net muscle moments.
Highlights.
Validation of single-plane fluoroscopy and 2D/3D shape-matching is performed
The methodology can accurately quantify full shoulder complex kinematics
Kinematic errors should be fully described using anatomical descriptions
Acknowledgments
We would like to thank Conrad Lindquist for his technical support, Theodore Lawrence for his technical drawings, and the donors and their families for their generous gift.
Funding: Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) under Award Numbers F31HD087069 and K12HD073945, and the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS) under Award Number T32AR050938. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This project was also supported by the Foundation for Physical Therapy, the Minnesota Partnership for Biotechnology and Medical Geonomics (MNP IF #14.02), and the University of Minnesota’s Office of Discovery and Translation (ODAT) Translational Grant Program. Study sponsors were not involved in the study design, data collection, analysis, or interpretation, or in the writing and submission of the manuscript.
Footnotes
Competing interests: None declared
Ethical approval: Not required
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Hamming D, Braman JP, Phadke V, LaPrade RF, Ludewig PM. The accuracy of measuring glenohumeral motion with a surface humeral cuff. J Biomech. 2012;45:1161–8. doi: 10.1016/j.jbiomech.2012.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Karduna AR, McClure PW, Michener LA, Sennett B. Dynamic Measurements of Three-Dimensional Scapular Kinematics: A Validation Study. Journal of Biomechanical Engineering. 2001:123. doi: 10.1115/1.1351892. [DOI] [PubMed] [Google Scholar]
- 3.Ludewig P, Cook TM, Shields RK. Comparison of surface sensor and bone-fixed measurement of humeral motion. Journal of Applied Biomechanics. 2002;18:163–70. [Google Scholar]
- 4.Ludewig PM, Phadke V, Braman JP, Hassett DR, Cieminski CJ, LaPrade RF. Motion of the shoulder complex during multiplanar humeral elevation. J Bone Joint Surg Am. 2009;91:378–89. doi: 10.2106/JBJS.G.01483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.McClure PW, Michener LA, Sennett BJ, Karduna AR. Direct 3-dimensional measurement of scapular kinematics during dynamic movements in vivo. J Shoulder Elbow Surg. 2001;10:269–77. doi: 10.1067/mse.2001.112954. [DOI] [PubMed] [Google Scholar]
- 6.Bey MJ, Kline SK, Zauel R, Lock TR, Kolowich PA. Measuring dynamic in-vivo glenohumeral joint kinematics: technique and preliminary results. J Biomech. 2008;41:711–4. doi: 10.1016/j.jbiomech.2007.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Giphart JE, Brunkhorst JP, Horn NH, Shelburne KB, Torry MR, Millett PJ. Effect of plane of arm elevation on glenohumeral kinematics: a normative biplane fluoroscopy study. J Bone Joint Surg Am. 2013;95:238–45. doi: 10.2106/JBJS.J.01875. [DOI] [PubMed] [Google Scholar]
- 8.Miranda DL, Schwartz JB, Loomis AC, Brainerd EL, Fleming BC, Crisco JJ. Static and dynamic error of a biplanar videoradiography system using marker-based and markerless tracking techniques. J Biomech Eng. 2011;133:121002. doi: 10.1115/1.4005471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tashman S, Anderst W. In-Vivo Measurement of Dynamic Joint Motion Using High Speed Biplane Radiography and CT: Application to Canine ACL Deficiency. Journal of Biomechanical Engineering. 2003:125. doi: 10.1115/1.1559896. [DOI] [PubMed] [Google Scholar]
- 10.Giphart JE, van der Meijden OA, Millett PJ. The effects of arm elevation on the 3-dimensional acromiohumeral distance: a biplane fluoroscopy study with normative data. J Shoulder Elbow Surg. 2012;21:1593–600. doi: 10.1016/j.jse.2011.11.023. [DOI] [PubMed] [Google Scholar]
- 11.You B-M, Siy P, Anderst W, Tashman S. In vivo measurement of 3-D skeletal kinematics from sequences of biplane radiographs: Application to knee kinematics. IEEE Trans Med Imaging. 2001;20:514–25. doi: 10.1109/42.929617. [DOI] [PubMed] [Google Scholar]
- 12.Kon Y, Nishinaka N, Gamada K, Tsutsui H, Banks SA. The influence of handheld weight on the scapulohumeral rhythm. J Shoulder Elbow Surg. 2008;17:943–6. doi: 10.1016/j.jse.2008.05.047. [DOI] [PubMed] [Google Scholar]
- 13.Matsuki K, Matsuki KO, Mu S, Yamaguchi S, Ochiai N, Sasho T, et al. In vivo 3- dimensional analysis of scapular kinematics: comparison of dominant and nondominant shoulders. J Shoulder Elbow Surg. 2011;20:659–65. doi: 10.1016/j.jse.2010.09.012. [DOI] [PubMed] [Google Scholar]
- 14.Matsuki K, Matsuki KO, Mu S, Kenmoku T, Yamaguchi S, Ochiai N, et al. In vivo 3D analysis of clavicular kinematics during scapular plane abduction: comparison of dominant and non-dominant shoulders. Gait Posture. 2014;39:625–7. doi: 10.1016/j.gaitpost.2013.06.021. [DOI] [PubMed] [Google Scholar]
- 15.Matsuki K, Matsuki KO, Yamaguchi S, Ochiai N, Sasho T, Sugaya H, et al. Dynamic in vivo glenohumeral kinematics during scapular plane abduction in healthy shoulders. J Orthop Sports Phys Ther. 2012;42:96–104. doi: 10.2519/jospt.2012.3584. [DOI] [PubMed] [Google Scholar]
- 16.Nishinaka N, Tsutsui H, Mihara K, Suzuki K, Makiuchi D, Kon Y, et al. Determination of in vivo glenohumeral translation using fluoroscopy and shape-matching techniques. J Shoulder Elbow Surg. 2008;17:319–22. doi: 10.1016/j.jse.2007.05.018. [DOI] [PubMed] [Google Scholar]
- 17.Zhu Z, Massimini DF, Wang G, Warner JJ, Li G. The accuracy and repeatability of an automatic 2D-3D fluoroscopic image-model registration technique for determining shoulder joint kinematics. Med Eng Phys. 2012;34:1303–9. doi: 10.1016/j.medengphy.2011.12.021. [DOI] [PubMed] [Google Scholar]
- 18.Auerbach BM, Raxter MH. Patterns of clavicular bilateral asymmetry in relation to the humerus: variation among humans. J Hum Evol. 2008;54:663–74. doi: 10.1016/j.jhevol.2007.10.002. [DOI] [PubMed] [Google Scholar]
- 19.Daruwalla ZJ, Courtis P, Fitzpatrick C, Fitzpatrick D, Mullett H. Anatomic variation of the clavicle: A novel three-dimensional study. Clin Anat. 2010;23:199–209. doi: 10.1002/ca.20924. [DOI] [PubMed] [Google Scholar]
- 20.Jacobson A, Gilot GJ, Hamilton MA, Greene A, Flurin P, Wright TW, et al. Glenohumeral anatomic study. A comparison of male and female shoulders with similar average age and BMI. Bull Hosp Jt Dis. 2013;73(Suppl 1):S68–S78. [PubMed] [Google Scholar]
- 21.Dvir Z, Berme N. The shoulder complex in elevation of the arm: a mechanism approach. J Biomech. 1978;11:219–25. doi: 10.1016/0021-9290(78)90047-7. [DOI] [PubMed] [Google Scholar]
- 22.Teece RM, Lunden JB, Lloyd AS, Kaiser AP, Cieminski CJ, Ludewig PM. Three-dimensional acromioclavicular joint motions during elevation of the arm. J Orthop Sports Phys Ther. 2008;38:181–90. doi: 10.2519/jospt.2008.2386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brainerd EL, Baier DB, Gatesy SM, Hedrick TL, Metzger KA, Gilbert SL, et al. X-ray reconstruction of moving morphology (XROMM): precision, accuracy and applications in comparative biomechanics research. J Exp Zool A Ecol Genet Physiol. 2010;313:262–79. doi: 10.1002/jez.589. [DOI] [PubMed] [Google Scholar]
- 24.Knorlein BJ, Baier DB, Gatesy SM, Laurence-Chasen JD, Brainerd EL. Validation of XMALab software for marker-based XROMM. J Exp Biol. 2016;219:3701–11. doi: 10.1242/jeb.145383. [DOI] [PubMed] [Google Scholar]
- 25.Wu G, van der Helm FCT, Veeger HEJ, Makhsous M, Van Roy P, Anglin C, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: shoulder, elbow, wrist and hand. Journal of Biomechanics. 2005;38:981–92. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]
- 26.Phadke V, Braman JP, LaPrade RF, Ludewig PM. Comparison of glenohumeral motion using different rotation sequences. J Biomech. 2011;44:700–5. doi: 10.1016/j.jbiomech.2010.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ludewig PM, Behrens SA, Meyer SM, Spoden SM, Wilson LA. Three-dimensional clavicular motion during arm elevation: reliability and descriptive data. J Orthop Sports Phys Ther. 2004;34:140–9. doi: 10.2519/jospt.2004.34.3.140. [DOI] [PubMed] [Google Scholar]
- 28.Anderst W, Zauel R, Bishop J, Demps E, Tashman S. Validation of three-dimensional model-based tibio-femoral tracking during running. Med Eng Phys. 2009;31:10–6. doi: 10.1016/j.medengphy.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]