Age and sex-related effects in children with mild traumatic brain injury on diffusion MRI properties: a comparison of voxelwise and tractography methods

Abstract

Although there are several techniques to analyze diffusion-weighted imaging, any technique must be sufficiently sensitive to detect clinical abnormalities. This is especially critical in disorders like mild traumatic brain injury (mTBI), where pathology is likely to be subtle. mTBI represents a major public health concern, especially for youth under 15 years of age. However, the developmental period from birth to 18 years is also a time of tremendous brain changes. Therefore, it is important to establish the degree of age- and sex-related differences. Participants were children aged 8–15 years with mTBI or mild orthopedic injuries (OI). Imaging was obtained within 10 days of injury. We performed tract-based spatial statistics (TBSS), deterministic tractography using AFQ (Automated Fiber Quantification), and probabilistic tractography using TRACULA (TRActs Constrained by UnderLying Anatomy) to evaluate whether any method provided improved sensitivity at identifying group, developmental, and/or sex-related differences. Although, there were no group differences from any of the three analyses, many of the tracts, but not all, revealed increases of fractional anisotropy (FA) and decreases of axial, radial, and mean diffusivity (AD, RD, and MD, respectively) with age. TBSS analyses resulted in age-related changes across all white matter tracts. AFQ and TRACULA revealed age-related changes within the corpus callosum, cingulum cingulate, corticospinal tract, inferior and superior longitudinal fasciculus, and uncinate fasciculus. The results are in many ways consistent across all three methods. However, results from the tractography methods provided improved sensitivity and better tract-specific results for identifying developmental and sex-related differences within the brain.

Graphical abstract

Although there are several techniques to analyze diffusion weighted imaging, any technique must be sufficiently sensitive to detect clinical abnormalities in children with mild traumatic brain injury. Results from tractography methods provide improved sensitivity and better tract-specific results for identifying developmental and sex-related differences within the brain.

1. Introduction

There are several different quantitative imaging analysis techniques that can be applied to diffusion-weighted imaging as measures of white matter integrity. As with all techniques, the goal of any neuroimaging outcome study is to generate quantifiable measurement of brain development, disease, damage, or degeneration that is not only sensitive in detecting clinically significant differences but can also account for non-injury or disease variables such as age and sex. In order to achieve this goal, any technique must be sufficiently sensitive at detecting clinical abnormalities. This is especially critical in populations like mild traumatic brain injury (mTBI), where pathology, when present, is likely to be subtle (Aoki and Inokuchi, 2016; Fink et al., 2016; Hulkower et al., 2013). mTBI represents a major public health concern, especially for youth under 15 years of age. However, the developmental period from birth to early adulthood is also a time period of tremendous developmental changes in the brain where diffusion tensor imaging (DTI) metrics reflect both dynamic age- (Drakesmith et al., 2016) and sex-dependent changes in the brain (van Hemmen et al., 2016; Schwehm et al., 2016; Kodiweera et al., 2016). Moderate to severe TBI alters age-typical developmental white matter (Johnson et al., 2015; Wu et al., 2010). Given potential developmental as well as injury-related DTI changes, a critical step in a pediatric mTBI study is to ascertain the role of age and sex differences in both injured children and controls and determine the quality of the DTI metrics to detect anticipated age and sex differences. Before embarking on a full examination of effects of injury on DTI metrics, it is important to establish age- and sex-related effects on imaging parameters and identify preferred approaches to DTI analysis.

Diffusion-weighted imaging measures the direction of water diffusion in brain tissue and is thought to be an indicator of the fiber tract integrity: reflecting coherence, organization and/or density of the fiber bundles. The most common standard diffusion measure is fractional anisotropy (FA). The value of FA, which ranges from 0 to 1, is highest in major white matter tracts (FA value approaches 1), lower in gray matter, and approaches 0 in cerebrospinal fluid. FA is considered a marker of white matter integrity, because variations reflect myelination, axon density, axonal membrane integrity, and axon diameter. Axial diffusivity (AD) represents diffusivity along the principal eigenvector. In contrast, radial diffusivity (RD) describes an average of the eigenvectors perpendicular to the principal direction. The interpretation of these DTI metrics is still being explored, but in general higher FA and lower MD values are interpreted as reflecting developmental increases in axon myelination and fiber organization in white matter pathways (Chen et al., 2016; Lebel et al., 2012; Westlye et al., 2010; Kochunov et al., 2012; Yeatman et al., 2012). Sex differences in DTI metrics are much less well understood (Herting et al., 2012; Wang et al., 2012; Schmithorst et al., 2008). In the context of mTBI alterations in DTI metrics are thought to reflect directly on white matter integrity and presence of traumatic axonal injury (Toth et al. PMID: 28249729).

In the current study, we compared several automated methods for measuring white matter integrity from DTI data. One diffusion-weighted imaging method is a tract-based spatial statistic (TBSS) approach (Smith et al., 2006, 2007). TBSS is an automated method that combines the strengths of both voxel-based morphometry (VBM) and tract-based spatial statistic methods. In VBM analyses, each participant’s FA image is registered to a template and then voxelwise statistics are computed to find brain areas that differ between groups. One major limitation to VBM methods is that coregistration algorithms are not able to accurately align fiber tracts across participants (Bookstein, 2001). This has been a long-standing issue with any VBM analysis. There is no way to ensure that a voxel in standard space contains data from the same portion of the brain across participants. Long projection white matter fiber tracts vary too much in size and shape and there is no method to be sure that registration of every participant’s FA image to a common space has been completely successful (Wassermann et al., 2011; Yeatman et al., 2011). TBSS aims to overcome these limitations of VBM but relies on registering participants to a common template space and only provides a modest improvement over traditional VBM methods. TBSS techniques also cannot ensure that any voxel corresponds to the same tract across participants. Notwithstanding these limitations, TBSS analyses remain the most common approach to analyzing diffusion-weighted images.

Another method is a tractography-based approach and these methods have complementary strengths and weakness with TBSS. Tractography uses the principal water diffusion direction to reconstruct the trajectories of the fiber tracts. Tractography overcomes the alignment problems by estimating diffusion properties in native participant space. Brain shape is variable and measuring white matter integrity in native brain space preserves individual differences. Tractography is considered the most accurate method for identifying white matter tracts in humans, but tractography has the limitation that it does not allow the whole brain to be investigated and, in some cases, requires some level of user interaction. Any method that is semi-automated can be a major hindrance for large-scale clinical research. Another potential limitation of tractography is the method of extracting diffusion measures from identified tracts. Standard tractography methods collapse tracts and allow for extraction of a single DTI mean value but are also a potential limitation. Due to anatomical factors like crossing fibers, nearness to cerebrospinal fluid and/or grey matter, or microstructural factors like axon density and/or diameter, diffusion measures can vary along tract trajectories (Xue et al., 1999). Averaging along the entire tract obscures potentially important information and may not be optimal for localization of group differences. If there is damage or change that occurs within a small portion of the tract, those differences may be missed when the whole tract is averaged. Given reports emphasizing the utility of analyzing diffusion properties along the tract in healthy brain anatomy (Gong et al., 2005; O’Donnell et al., 2009) and variations in relation to development (Geng et al., 2012), aging (Davis et al., 2009), and clinical conditions (Berman et al., 2005; Colby et al., 2012; Concha et al., 2012; Lin et al., 2006; Myall et al., 2013), it is important to consider diffusion measures along the tract and not average across the entire tract. Fortunately, more recently developed methods are fully automated. These techniques rapidly and reliably identify and measure white matter fiber tracts and allow analysis of diffusion properties along the tract trajectory, thus avoiding the need for user intervention to define the tracts.

There are multiple tractography methods that can be used to determine the pathway between distant brain regions. When determining diffusion orientation at each voxel, there are two options: deterministic and probabilistic tractography. Deterministic (streamline) tractography models paths as a one-dimensional curve. Deterministic tractography uses the principal direction of diffusion to propagate trajectories from the defined anchor point until termination criterion are met (i.e., excessive angular deviation, minimum FA voxel threshold, and/or endpoint(s)). Probabilistic tractography generates a range of possible diffusion directions for each voxel instead of a single diffusion direction; therefore, probabilistic tractography actually models the uncertainty along the tract. Tractography, whether you are using deterministic or probabilistic methods, can be completed either locally or globally. Local tractography reconstructs the path step-by-step using only the local orientation at each voxel. Local tractography is best suited for exploratory studies of brain connectivity. Tracts are reconstructed starting from a single seed region and are not constrained to any given target region, therefore, endpoints can occur anywhere within the brain. In contrast, global tractography fits the entire path at once, using diffusion orientation of all voxels along the path length. Global tractography is best suited for reconstructing known white-matter pathways. Tracts are constrained to connections of two specific end points and symmetric between beginning seed and end target regions.

To date, most published DTI studies contain relatively small samples sizes and limited age ranges that often exclude adolescents. Another limitation has been the use a single DTI method of voxelwise analyses, as opposed to a priori defined and anatomically validated white matter tracts. Therefore, these studies have been limited in their ability to detect subtle changes in white matter integrity. To overcome these challenges, the current investigation addresses these developmental issues within a pediatric mTBI study, the Mild Injury Outcome Study (MIOS) involving children 8 to 15 years of age who have sustained mTBI or orthopedic injury (OI). The aim of the current study was to establish which DTI analysis is preferable for assessing potential effects of mTBI since preliminary analyses show no gross differences between white matter integrity between the OI and mTBI groups. In the present study, we performed TBSS, global deterministic, and probabilistic tractography in children with mTBI and age-matched OI controls to compare methods in terms of sensitivity in identifying developmental and/or sex-related differences within the brain. As proof of concept, we demonstrate that automated tractography methods for reconstructing white matter fasciculi do not require user intervention and can provide a reliable way to investigate subtle changes in white matter integrity in mTBI populations.

2. Methods

2.1 Participants

Participants were recruited through a multi-site (Columbus, OH; Cleveland, OH) study of outcomes in children with mTBI. The study was conducted in accordance with established guidelines and received institutional ethics approval from the two data collection sites (The Research Institute at Nationwide Children’s Hospital in Columbus, OH and Rainbow Babies and Children’s Hospital in Cleveland, OH); written informed consent and/or assent was obtained from all participants. Participants were 153 children aged 8 to 17 years. The mTBI group consisted of 94 children (63 boys and 31 girls) who experienced head trauma resulting in hospitalization and who had a recorded day of injury post-resuscitation Glasgow Coma Scale (GCS) score of 12 or less. The OI group comprised 59 children (43 boys, 16 girls) with fractures not accompanied by symptoms of head injury and with GCS scores, if recorded, of 15. Descriptive statistics of scanner site, age, sex, and Wechsler Abbreviated Scale of Intelligence ® Second Edition Full Scale IQ scores are reported in Table 1.

Table 1.

Participant descriptive statistics.

	Columbus		Cleveland
	OI	TBI	OI	TBI
n (male : female)	42 (30:12)	63 (40:23)	17 (13:4)	31 (23:8)
Age (± SE)	12.59±0.40	12.81±0.33	12.14±0.57	12.42±0.53
FSIQ (± SE)	99.24±2.27	99.44±1.81	98.12±3.76	95.59±2.55

2.2 MRI Acquisition

2.2.1 Columbus

Magnetic resonance images of the participants were obtained using a Siemens Trio 3T scanner with a 32-channel head coil at the Research Institute at Nationwide Children’s Hospital in Columbus. High-resolution T1-weighted images were acquired using a 3D magnetization-prepared rapid gradient echo (MPRAGE) pulse sequence. The 3D MPRAGE T1-weighted sequence parameters were as follows: 192 contiguous sagittal slices with TR (repetition time) = 2200 ms; TE (echo time) = 4.37 ms; in-plane resolution = 0.90 × 0.90 mm; slice thickness = 0.90 mm; flip angle = 7°; and a field of view of 230 mm and an acquisition matrix of 256 × 256 mm. Diffusion MRI images were acquired using a diffusion-weighted spin-echo echo-planar imaging (EPI) pulse sequence with the following parameters: 64 interleaved axial slices with TR (repetition time) = 6600 ms; TE (echo time) = 72.4 ms; in-plane resolution = 1.8 × 1.8 mm; slice thickness = 1.8 mm; bandwidth = 1860 Hz/Px; and a field of view of 230 mm and an acquisition matrix of 128 × 128 mm. Diffusion gradients were applied in 30 directions with b = 700 s/mm².

2.2.2 Cleveland

Magnetic resonance images of the participants were obtained using a Philips 3.0T Achieva scanner with an 8-channel head coil at the University Hospitals Case Medical Center in Cleveland. High-resolution T1- weighted images were acquired using a 3D magnetization-prepared rapid gradient echo (T1 3D TFE) pulse sequence. The 3D TFE T1-weighted sequence parameters were as follows: 170 contiguous sagittal slices with TR (repetition time) = 8.9 ms; TE (echo time) = 4.1 ms; in-plane resolution = 0.90 × 0.90 mm; slice thickness = 0.90 mm; flip angle = 8°; and a field of view of 240 mm and an acquisition matrix of 256 × 256 mm. Diffusion MRI images were acquired using a diffusion-weighted spin-echo echo-planar imaging (EPI) pulse sequence with the following parameters: 60 interleaved axial slices with TR (repetition time) = 6634 ms; TE (echo time) = 76 ms; in-plane resolution = 2 × 2 mm; slice thickness = 2 mm; bandwidth = 1786.9 Hz/Px in EPI freq direction; and a field of view of 224 mm and an acquisition matrix of 128 × 128 mm. Diffusion gradients were applied in 32 directions with b = 800 s/mm².

2.3 MRI Preprocessing

The detailed protocol is available in Supplemental Materials. Briefly, preprocessing and brain extraction procedures were completed on a remote Linux computing cluster. T1- and diffusion-weighted DICOM images were converted into NIfTI format using the dcm2niix tool in MRIcron, publicly available software (https://github.com/rordenlab/dcm2niix) and the bval and bvec files were automatically created from the raw diffusion-weighted DICOM headers. During conversion to NIfTI format, T1 images were automatically reoriented to canonical space and auto-cropped. Using the Automatic Registration Toolbox (ART) acpcdetect tool, freely downloadable here (https://www.nitrc.org/frs/?group_id=90), the T1 images were put into standard alignment. Using the Convert3D Medical Image Processing Tool, freely downloadable here (http://www.itksnap.org/pmwiki/pmwiki.php?n=Downloads.C3D), T1 images were resampled with an isotropic voxel resolution of 1-mm. Skull-stripped T1 images were acquired using the Advanced Normalization Tools version 2.1.0 (ANTs; Avants et al., 2014) volume-based cortical thickness estimation pipeline (antsCorticalThickness.sh), freely downloadable here (https://github.com/stnava/ANTs/releases/tag/v2.1.0).

2.4 Head Motion

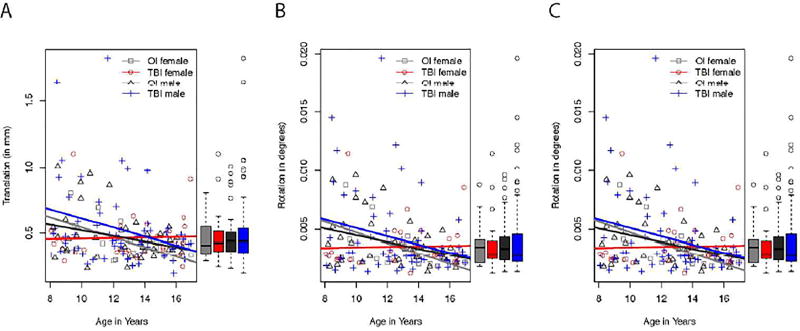
Since diffusion-weighted imaging analyses are designed to detect the motion of water molecules, this makes diffusion MR images particularly sensitive to head motion. Head motion results in not only misalignment between consecutive diffusion-weighted images, but also intensity changes. Misalignment can be corrected by registering the diffusion-weighted images to each other; however, intensity alterations cannot be corrected. There are three measures of head motion outputted from the TRACULA pipeline (see below): the average volume-by-volume translation and rotation, and the percent of slices with excessive intensity drop-out. We used the average volumeby- volume translation and rotation as covariates in our analyses.

2.5 Tract-Based Spatial Statistics (TBSS)

Diffusion-weighted images were preprocessed using FMRIB’s Diffusion Toolbox within FSL version 5.0.7 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation). Preprocessing included eddy current correction, motion correction, and brain masking. FDT (FMRIBs Diffusion Toolbox) was used to fit the tensor model to every voxel of the brain mask and compute the FA, MD, RD, and AD maps. Voxel-wise analysis was performed using TBSS toolbox of FSL (Smith et al., 2007, 2006). FA maps were aligned to FMRIB58 FA template and affine transformed into MNI standard space using the nonlinear registration tool FNIRT. The mean FA-image was created following registration and thinned to FA > 0.2 to represent the mean FA skeleton. Individual FA volumes were then projected onto this common skeleton. Similarly, the MD, RD, and AD maps were also projected onto the mean FA skeleton.

Analyses were carried out using FSL randomise program with 5000 permutations (Nichols and Holmes, 2002). Using a nonparametric permutation test, we performed voxelwise statistical analysis of individual FA, RD, MD, and AD skeleton images of OI and mTBI groups for both contrasts (OI > mTBI; OI < mTBI and boys and girls for both contrasts (boys > girls; boys < girls) with age and the average volume-by-volume translation and rotation as covariates. To avoid artifacts caused by inappropriate thresholds, the threshold-free cluster enhancement method (Smith and Nichols, 2009) was used for all statistical analyses. The resulting statistical maps were superimposed on the MNI152 template supplied by FSL. FSLView and its atlas tools (ICBM-DTI-81 white-matter labels atlas; JHU white-matter tractography atlas) as well as general neuroanatomical handbooks were used to allocate FA changes detected by TBSS to the different anatomical structures in the MNI152 space (Hua et al., 2008; Wakana et al., 2004).

2.6 Automated Fiber Quantification (AFQ)

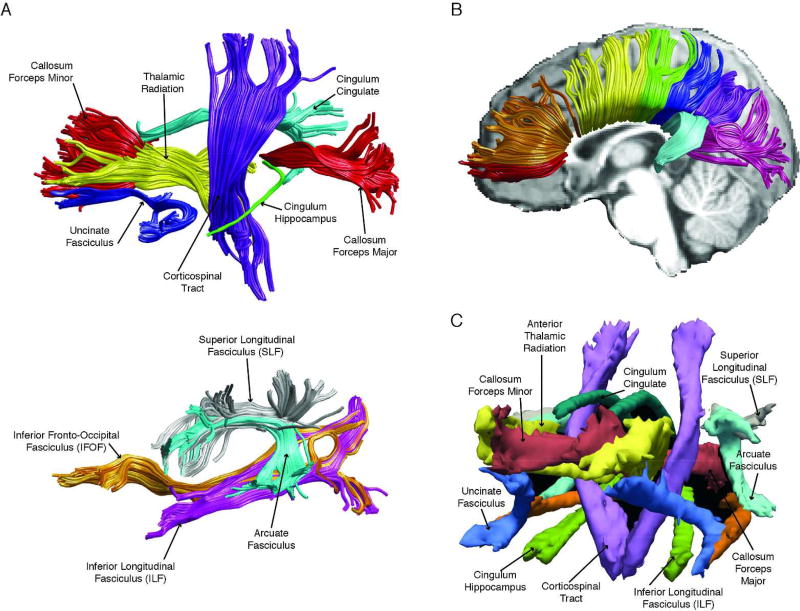
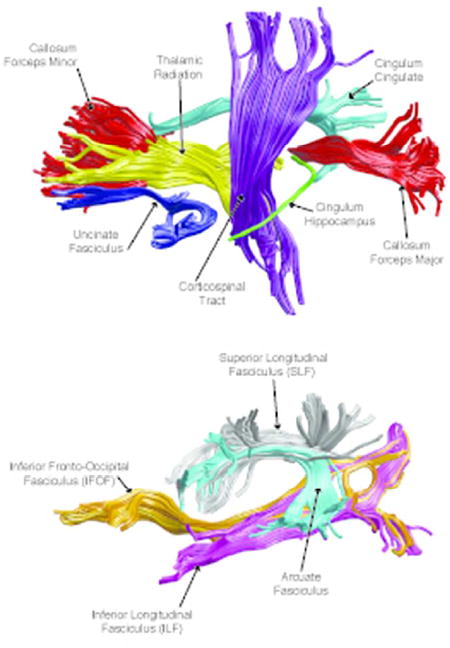
Automated global deterministic tractography was performed according to standard protocols. First, diffusion-weighted images were preprocessed using the dtiInit preprocessing pipeline wrapper from Stanford open-source VISTASOFT package version 1.0 (https://github.com/vistalab/vistasoft) running on MATLAB version R2015b (MATLAB, 2015). The diffusion-weighted images were corrected for eddy currents and head motion, skull-stripped, and tensor fitted. White matter pathways were automatically identified using an open-source, freely available software package, Automated Fiber Quantification (AFQ) version 1.2 (https://github.com/yeatmanlab/AFQ). AFQ (Yeatman et al., 2012) identifies twenty major fiber tracts (see Figure 1) and additionally segments the corpus callosum into eight sections. The twenty major pathways include the corticospinal tract, inferior longitudinal fasciculus, inferior fronto-occipital fasciculus, uncinate fasciculus, anterior thalamic radiation, cingulum cingulate gyrus and hippocampal bundles, superior longitudinal fasciculus, arcuate fasciculus, and forceps major and forceps minor of the corpus callosum. Furthermore, the corpus callosum was segmented into eight different sections (see Figure 2). The eight segments are roughly associated with the following regions: orbitofrontal, anterior frontal, superior frontal, motor, superior parietal, posterior parietal, occipital, and temporal.

Figure 1.

(A) Automated Fiber Quantification (AFQ) pipeline identifies 20 major fiber tracts including: corticospinal tract, uncinate fasciculus, anterior thalamic radiation, cingulum cingulate gyrus and hippocampal bundles, corpus callosum forceps major and forceps minor, inferior longitudinal fasciculus, inferior fronto-occipital fasciculus, arcuate fasciculus, and superior longitudinal fasciculus. (B) AFQ pipeline also segments the corpus callosum (anterior to posterior): orbital frontal (red), anterior frontal (orange), superior frontal (yellow), motor (green), superior parietal (blue), posterior parietal (purple), occipital (pink), and temporal (cyan). (C) TRActs Constrained by UnderLying Anatomy (TRACULA) identifies the probability distribution of 18 major tracts including: corticospinal tract, inferior longitudinal fasciculus, uncinate fasciculus, anterior thalamic radiation, cingulum cingulate gyrus and hippocampal bundles, superior longitudinal fasciculus, arcuate fasciculus, and corpus callosum’s forceps major and forceps minor. The tracts are displayed at 20% of their maximum threshold.

Figure 2.

We used three measures to evaluate head motion: the average volume-by-volume translation and rotation and the percent of slices with excessive intensity drop-out. There was no significant interaction between the effects of gender and group across the three measures. Moreover, there was no significant difference between boys and girls or between mild orthopedic injury and mild traumatic brain injury groups. However, compared to older participants, younger participants had greater average volume-to-volume translation and rotation, but no difference in slices removed because of intensity drop-out.

For each identified pathway, FA, MD, RD, and AD were extracted along the tract. Statistical analyses were performed on the diffusion metrics across 100 segments of each tract. We performed two-way analyses of covariance (ANCOVAs) to examine differences between the OI and mTBI groups and between boys and girls on each diffusion metric at each location along each of the twenty tracts and each of the 8 corpus callosum segments using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate for multiple comparisons.

2.7 TRActs Constrained by UnderLying Anatomy (TRACULA)

Probabilistic tractography was performed according to standard protocols. Diffusion-weighted images were analyzed with TRACULA package (Yendiki et al., 2011), implemented in FreeSurfer version 5.3.0 (http://surfer.nmr.mgh.harvard.edu/fswiki/Download). TRACULA uses the prior anatomical information derived from the cortical parcellation and subcortical segmentation obtained from FreeSurfer. First, we performed the automated reconstruction and labeling of cortical and subcortical regions as performed by FreeSurfer on the T1-weighted images. The technical details of these procedures are described in prior publications (Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 2002; Fischl, 2004; Fischl et al., 2004, 2001, 1999; Han et al., 2006; Jovicich et al., 2006; Reuter et al., 2010, 2012; Ségonne et al., 2004). FreeSurfer cortical labels were visually inspected by a reliable rater (G.B.) prior to analyses.

The processing workflow of TRACULA is based on a standardized routine that utilizes tools available in the software library of FSL. Once diffusion-weighted images were preprocessed, TRACULA then uses the individual participant’s local diffusion orientations, as well as the participant’s cortical and subcortical segmentation labels, combined with prior information of each tract’s to estimate the probability distributions of each tract. Eighteen major pathways were reconstructed (see Figure 3). The eighteen major pathways include the corticospinal tract, inferior longitudinal fasciculus, uncinate fasciculus, anterior thalamic radiation, cingulum-cingulate gyrus bundle, cingulum-angular bundle, superior longitudinal fasciculus-parietal bundle, superior longitudinal fasciculus-temporal bundle, and forceps major and forceps minor of the corpus callosum.

Figure 3.

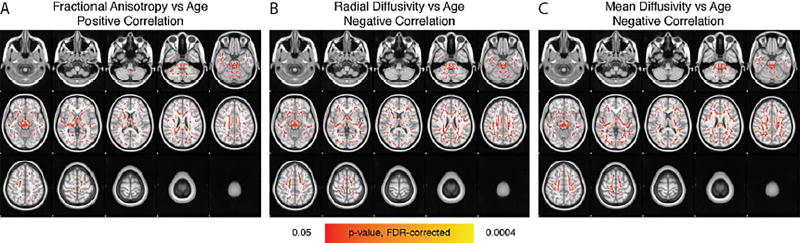
Shown are the summarized results from the Tract-Based Spatial Statistics (TBSS) analysis. The p-value, FWE-corrected, shown in red-yellow is overlaid onto the MNI152 template. (A) Fractional anisotropy increases with age within every major white matter tract. (B) Radial diffusivity decreases with age within every major white matter tract. (C) Mean diffusivity decreases with age within every major white matter tract. Age did not relate axial diffusivity.

For each identified pathway, FA, MD, RD, and AD were extracted along the tract. Statistical analyses were performed on each DTI metric along each fiber pathway. We performed two-way analyses of covariance (ANCOVAs) to examine differences between the OI and mTBI groups and between boys and girls on each DTI metric at each location along each of the eighteen tracts using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate for multiple comparisons.

3. Results

Descriptive statistics of age and Wechsler Abbreviated Scale of Intelligence ® Second Addition Full Scale IQ scores are reported in Table 1. The OI and mTBI groups did not differ in age (t (151) = 0.49, p = 0.49) or Full-Scale IQ (t (149) = 1.48, p = 0.23). There were two participants who did not have a Full-Scale IQ score.

3.1 Head Motion

Shown in Figure 4 is the average volume-by-volume translation, rotation, and percent of slices with excessive intensity drop-out as related to age. We performed a two-way ANCOVA to determine if head motion was statistically different between mTBI and OI groups and boys and girls whilst controlling for age. There was no significant interaction between the effects of gender and group on translation (F (1, 148) = 0.14, p = 0.71). Simple main effects analysis showed that there were no differences between boys and girls (F (1, 148) = 0.64, p = 0.42) or between OI and mTBI groups (F (1, 148) = 0.95, p = 0.33). The covariate, age, was significantly related to translation (F (1, 148) = 9.58, p = 0.002). There was no significant interaction between the effects of gender and group on rotation (F (1, 148) = 0.15, p = 0.70). Simple main effects analysis showed that there were no differences between boys and girls (F (1, 148) = 0.57, p = 0.45) or between OI and mTBI groups (F (1, 148) = 0.27, p = 0.60). The covariate, age, was significantly related to rotation (F (1, 148) = 9.25, p = 0.003). There was no significant interaction between the effects of gender and group on percent of slices with excessive intensity drop-out (F (1, 148) = 0.68, p = 0.41). Simple main effects analysis showed that there were no differences between boys and girls (F (1, 148) = 1.32, p = 0.25) or between OI and mTBI groups (F (1, 148) = 0.68, p = 0.41). The covariate, age, was not significantly related to percent of slices with excessive intensity drop-out (F (1, 148) = 2.00, p = 0.41).

Figure 4.

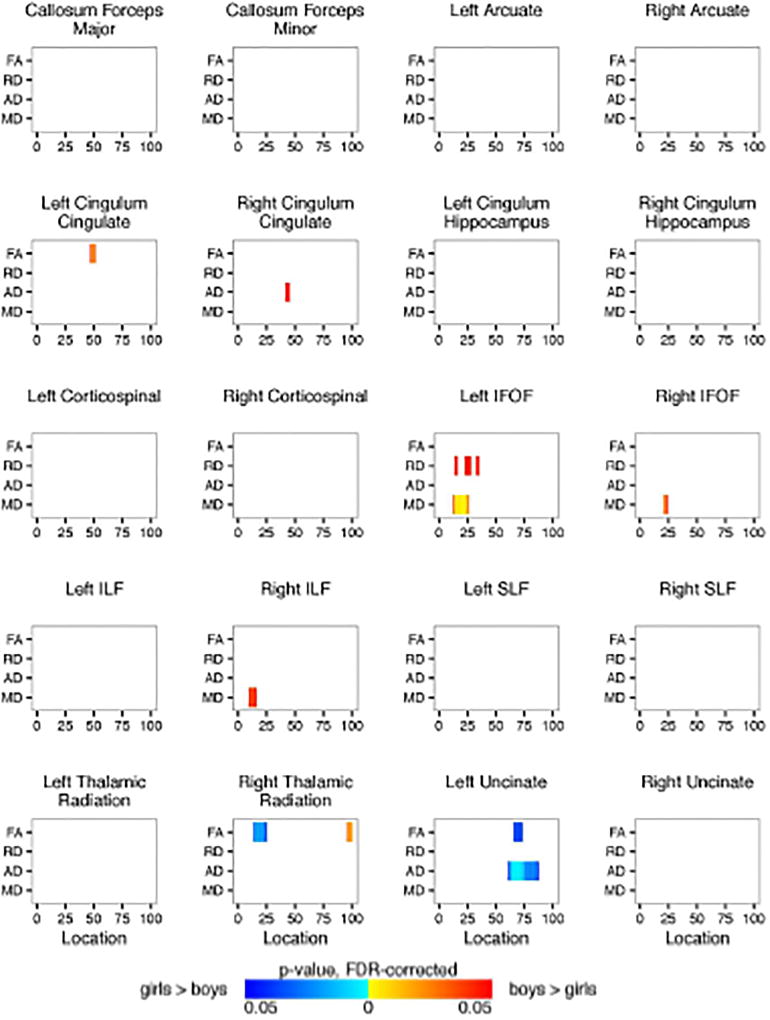
Shown are the Automated Fiber Quantification (AFQ) summarized results for each of the 20 identified fiber tracts comparing the girl and boy participants. Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent girls > boys. Red regions represent boys > girls.

3.2 Tract-Based Spatial Statistics (TBSS)

There were no significant differences between the OI and mTBI groups or between boys and girls. However, age was significantly related to FA, MD, and RD. FA was positively correlated with age within every major white matter tract (see Figure 6), whereas RD (see Figure 7) and MD (see Figure 8) were negatively correlated. Age was not significantly correlated with AD.

Figure 6.

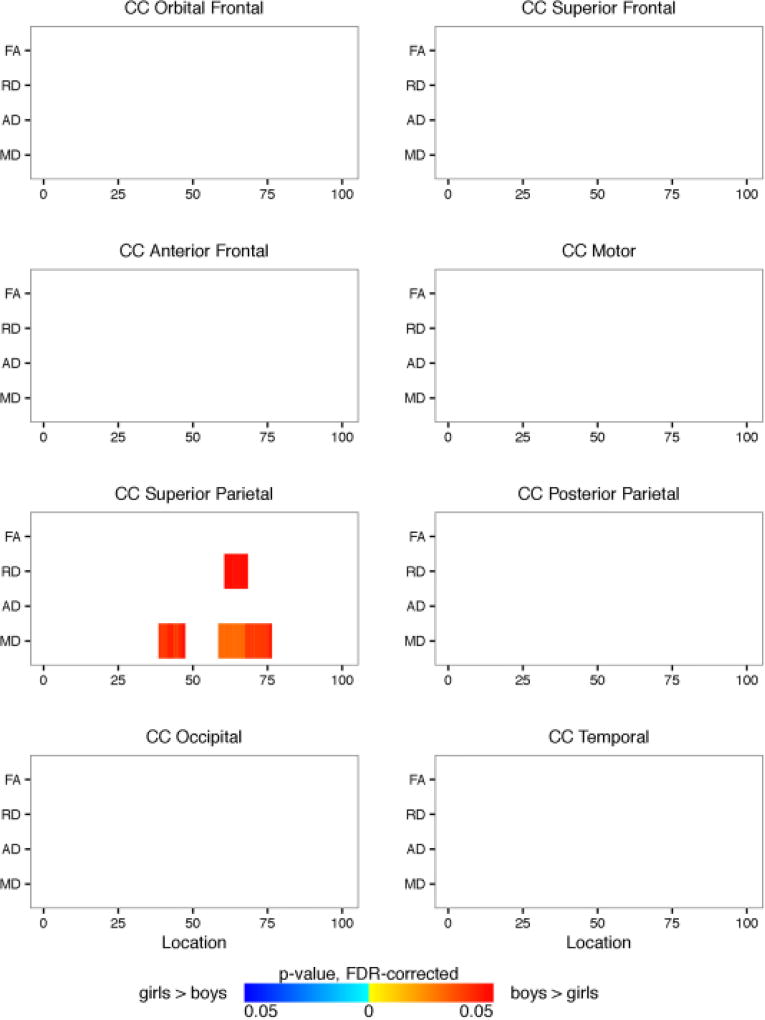
Shown are the Automated Fiber Quantification (AFQ) summarized results from the 8 corpus callosum segments comparing the girl and boy participants. Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent girls > boys. Red regions represent boys > girls.

Figure 7.

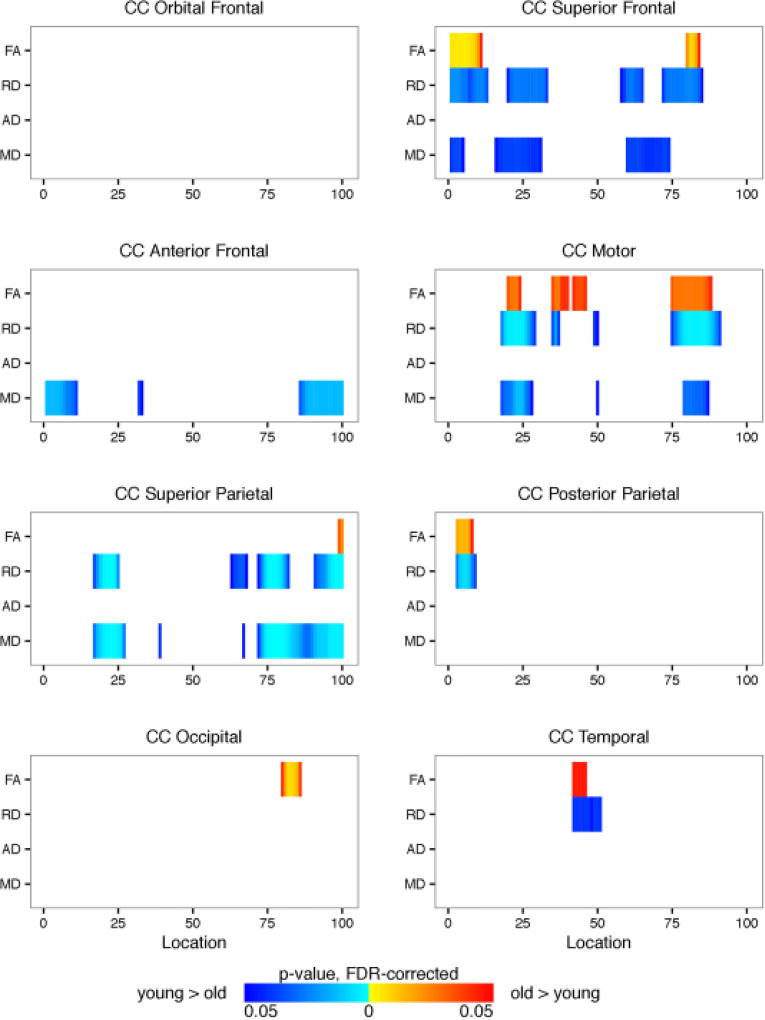
Shown are the Automated Fiber Quantification (AFQ) summarized results from the 8 corpus callosum segments related to age. For visualization purposes only, age was collapsed into two groups, young (age <= 13.0 years) and old (age > 13 years). Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent negative correlation with age. Red regions represent positive correlation with age.

Figure 8.

Shown are the TRACULA results for each of the 18 identified fiber tracts comparing the girl and boy participants. Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent girls > boys. Red regions represent boys > girls.

3.3 Automated Fiber Quantification (AFQ)

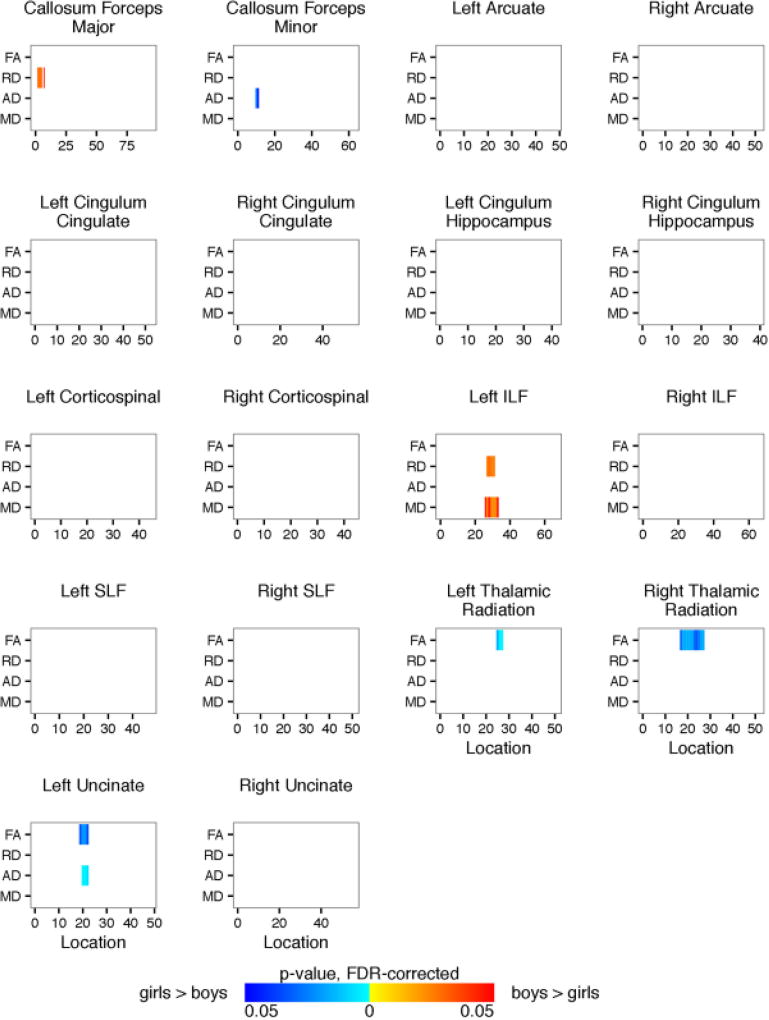
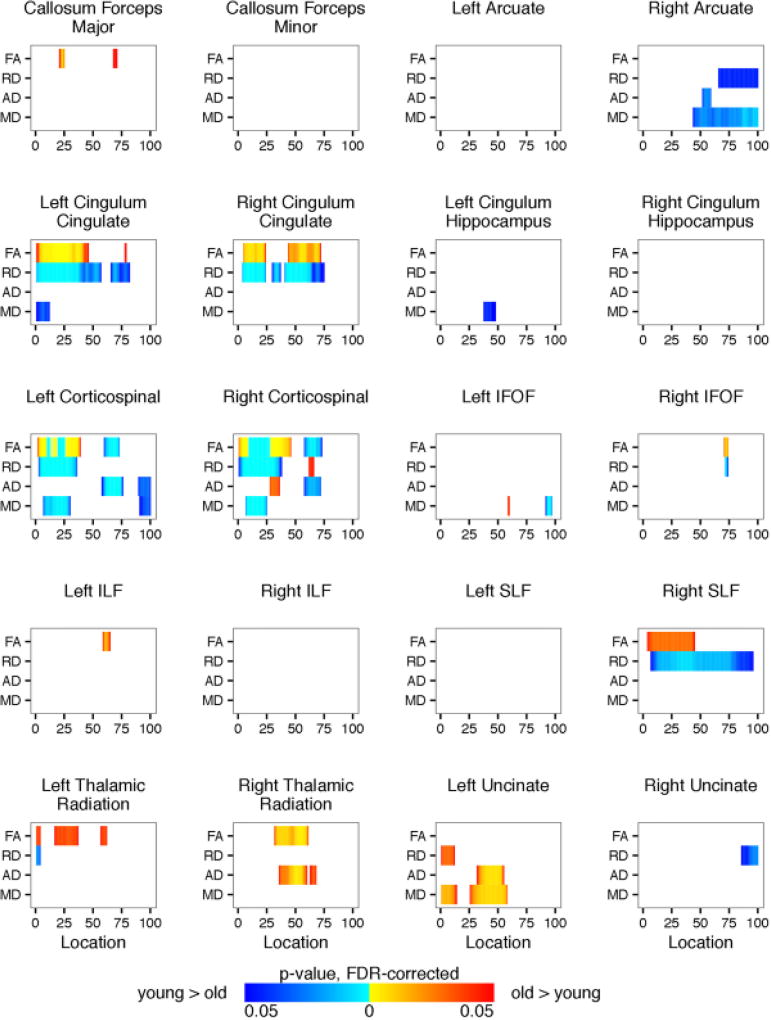
We performed two-way ANCOVAs to examine differences between the OI and mTBI groups and between boys and girls on each diffusion metric (FA, RD, MD, and AD) at each location along each of the twenty fiber tracts using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate for multiple comparisons. There was no significant interaction between the effects of gender and group. Simple main effects analysis showed that there were no differences between the OI and mTBI groups either. There were a few areas within the left and right cingulum cingulate and inferior fronto-occipital fasciculus, right inferior longitudinal fasciculus, right thalamic radiation, and left uncinate fasciculus in which there were significant differences between boys and girls. Figure 9 shows the summarized results for each of the 20 identified fiber tracts. Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017a).

Figure 9.

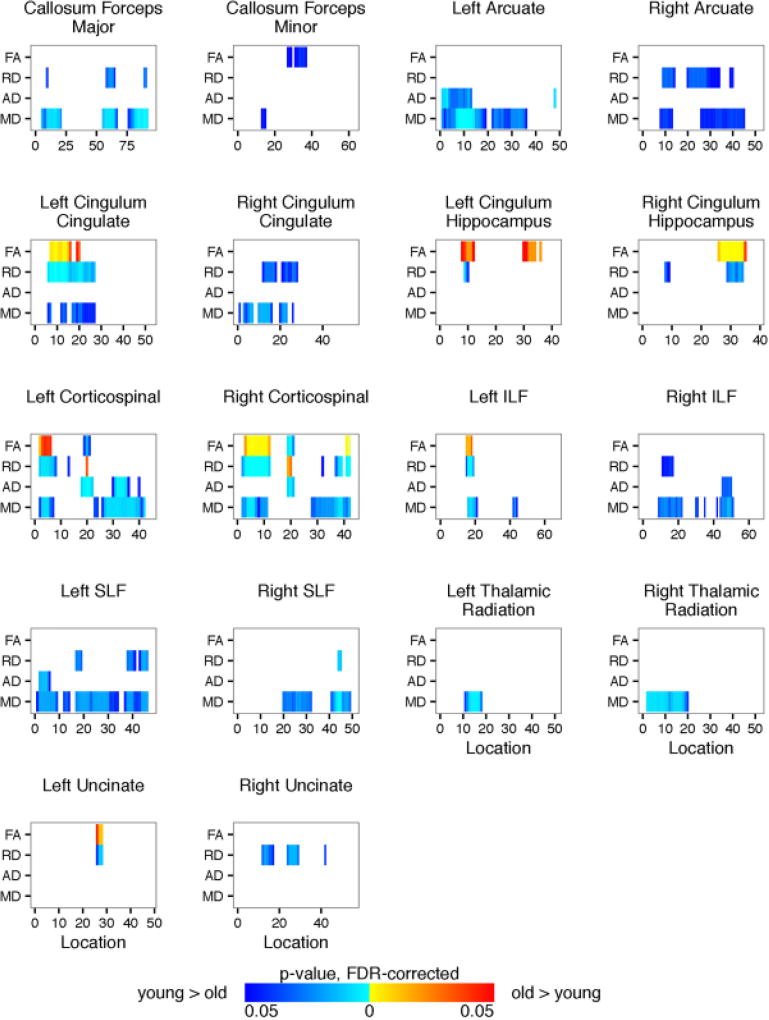
Shown are the TRACULA results for each of the 18 identified fiber tracts related to age. For visualization purposes only, age was collapsed into two groups, young (age <= 13.0 years) and old (age > 13 years). Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent negative correlation with age. Red regions represent positive correlation with age.

Age was significantly related to diffusion metrics (see Figure 10). For visualization purposes only, we classified participants into young and old groups based upon the median age of 13.0 years old to show age-related differences in tract profiles, p-values reported are from the two-way ANCOVA performed (see above). Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017b). Compared to younger participants, older participants had higher FA and lower RD, AD, and MD within portions of the corpus callosum forceps major and minor; left and right cingulum cingulate, corticospinal tract, inferior fronto-occipital fasciculus, thalamic radiation, and uncinate fasciculus; right arcuate fasciculus; left inferior longitudinal fasciculus; and right superior longitudinal fasciculus.

We performed two-way ANCOVAs to examine differences between the OI and mTBI groups and between boys and girls on each diffusion metric at each location along each of the eight segments of the corpus callosum using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate for multiple comparisons. There was no significant interaction between the effects of gender and group. Simple main effect analysis showed that there were no differences between the OI and mTBI groups either. Girls and boys did not show differences in FA or AD within any of the eight corpus callosum segments (see Figure 11). However, compared to girls, boys had higher RD and MD within the superior parietal section of the corpus callosum. Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017c)

Figure 12 shows that FA was significantly higher in older participants within the superior frontal, motor, superior parietal, posterior parietal, occipital, and temporal segments of the corpus callosum. Older participants also had lower RD, AD, and MD within these corpus callosum segments. Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017d).

3.4 TRActs Constrained by UnderLying Anatomy (TRACULA)

We performed two-way ANCOVAs to examine differences between the OI and mTBI groups and between boys and girls on each diffusion metric at each location along each of the eighteen tracts using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate for multiple comparisons. There was no significant interaction between the effects of gender and group. Simple main effects analysis showed that there were no differences between the OI and mTBI groups either. Compared to girls, boys had higher RD within the corpus callosum forceps major, higher RD and MD within the left inferior longitudinal fasciculus, and lower FA within the right and left thalamic radiation and left uncinate fasciculus. Figure 13 shows the summarized results for each of the 18 identified fiber tracts. Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017e).

Age was significantly related to the diffusion metrics (see Figure 14). Results for full tract profiles can be found on FigShare (Goodrich-Hunsaker, 2017f). Compared to younger participants, older participants had higher FA within the left cingulum cingulate, left inferior longitudinal fasciculus, left uncinate fasciculus, and corticospinal tract in both hemispheres. Older participants had lower RD, AD, and MD throughout the 18 fiber tracts.

4. Discussion

Diffusion-weighted images were collected as part of a project examining outcomes of pediatric mTBI and analyzed using three different automated methods. Our goal was to identify DTI analytic methods that would be useful in assessing white matter integrity in subsequent investigation of the effects on mTBI on brain structure since preliminary analyses show no differences between white matter integrity between the mild OI and mTBI groups. The current study focused on age- and sex-related effects, as justified by the need to take these sources of variation into account in examining injury effects and because the effects of mTBI on brain structure are likely to be subtle (Aoki and Inokuchi, 2016; Fink et al., 2016; Hulkower et al., 2013). The three automated methods included: TBSS, deterministic tractography using AFQ, and probabilistic tractography using TRACULA. Each of these methods have different strengths and weaknesses. The results were in many ways consistent across all three methods, although results from the TBSS method were less anatomically specific compared to those obtained from AFQ and TRACULA.

Only minor sex differences were evident. The results from the TBSS method suggest that boys and girls did not significantly differ in fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD). Previous studies have reported subtle sex differences but included additional covariates besides age in their statistical models (Herting et al., 2012), had small sample sizes, or examined a more limited age range (Wang et al., 2012). No previous study has examined sex differences in children 8 to 15 years of age using tractography methods. Our findings indicating that tractography methods may be more sensitive to DTI integrity given some sex differences were found using AFQ and TRACULA, but not with TBSS methods.

Across all three methods, many of the tracts revealed increases of FA and decreases of RD and MD with age. TBSS analyses resulted in age-related changes across the all the white matter tracts to such a degree that no specific cluster could be delineated. AFQ and TRACULA provided more anatomically precise, tract-specific results. Consistent with previous studies (Walker et al., 2016; Uda et al., 2015), age-related changes occurred within the corpus callosum, cingulum cingulate, corticospinal tract, inferior and superior longitudinal fasciculus, and uncinate fasciculus. In a recent longitudinal study, changes in FA across time were related to age at onset of more severe traumatic brain injury. Younger children with mTBI sustained greater loss of FA because of their injury but also greater increase in FA across time from 3 to 24 months post injury, whereas older children with mTBI did not display as great of FA reduction, though there was limited FA increase post injury within the superior and inferior longitudinal fasciculi and the uncinate fasciculi (Ewing-Cobbs et al., 2016). Unfortunately, sex differences were not evaluated in these studies. In summary, future studies would be well-advised to consider age at time of injury and to use methods to detect subtle changes within specific fiber tracts not limited to voxelwise analyses.

While this is the first study to investigate developmental and sex-related differences within the brain comparing three DTI methods, several limitations should be acknowledged. First, because sample sizes for boys and girls were unbalanced, our analyses may not have been adequately powered to detect statistically significant sex differences. Secondly, the scans come from multiple scanning sites, a difference that may alter DTI measurements. In the current study, we did not find any site differences and therefore combined data from both scanning sites. In future analyses, we will continue to explore various methods that reduce inter-site variability (Mirzaalian et al., 2016). For the current analyses, using data from multiple sites may make our results more generalizable to clinical settings in which DTI sequence parameters are not strictly controlled.

Despite these limitations the current findings highlight the usefulness of using tractography methods, as they provide improved sensitivity in accounting for developmental and sex-related differences in brain structure and in controlling for these factors in examining injury effects in white matter integrity. Furthermore, tractography methods can be applied to larger datasets because they do not require user intervention. We will use tractography methods for future analyses because these methods provide maximal sensitivity in detecting subtle changes in white matter integrity. Future findings using these methods may serve as biomarkers for prediction of outcomes of pediatric mTBI.

Figure 5.

Shown are the Automated Fiber Quantification (AFQ) summarized results for each of the 20 identified fiber tracts related to age. For visualization purposes only, age was collapsed into two groups, young (age <= 13.0 years) and old (age > 13 years). Plotted is significant p-values (FDR-corrected) for fractional anisotropy and radial, axial, and mean diffusivity (y-axis) along the length of the fiber tract (x-axis). Blue regions represent negative correlation with age. Red regions represent positive correlation with age.

Significance.

The results reported in this manuscript provide the first direct comparison between voxelwise and deterministic and probabilistic tractography methods to evaluate diffusion-weighted MR properties in mild traumatic brain injury (mTBI). These converging methods both identified previously characterized age-related changes in fractional anisotropy and diffusivity measures; however, the tractography methods were able to provide anatomically precise localizations of these age-related changes. The anatomical localization of effects identified by both tractography methods provide valuable data points that can be used to train algorithms to detect potential neuroanatomic biomarkers within white matter in mild TBI.

Appendix

Software Setup and Commands

Because most of the programs used for the current study offer a range of flexible options, the following commands can be used to replicate our analyses. Unless otherwise noted, all imaging procedures were completed on the Fulton Supercomputing Lab (FSL; https://marylou.byu.edu/), a high performance computing resource at Brigham Young University. All compute nodes have Red Hat Enterprise Linux 6.6. T1- and diffusion-weighted DICOM images were converted into NIfTI format using the dcm2niix tool in MRIcron (hhttps://github.com/rordenlab/dcm2niix). All T1 DICOM images were automatically reoriented to canonical space. The following terminal bash command was used to convert the T1 images:

The following terminal bash command was used to convert the diffusion weighted images:

Output NIfTI images were named, t1.nii and dwi.nii.gz, respectively. The bvec and bval files were automatically generated and files were renamed accordingly.

T1-Weighted Imaging

The T1-weighted images were automatically aligned, resampled, and skull-stripped. Using the Automatic Registration Toolbox (ART) acpcdetect module (https://www.nitrc.org/frs/?group_id=90), the scans were put into standard alignment so that the anterior commissure (AC) and posterior commissure (PC) were along a horizontal plane and the mid-sagittal plane passed through both landmarks. The acpcdetect module is a model-based program that locates and makes adjustments to the image based on those landmarks: (1) the anterior commissure (AC), (2) the posterior commissure (PC), and (3) the vertex of the superior pontine sulcus (VSPS). This initial alignment, often referred to as AC-PC alignment, is a rigid-body (i.e., three-translation and three-rotation) transformation. The input IMAGE was the T1-weighted NIfTI image from the previous step (e.g., t1.nii). The name for the OUTPUT file (e.g., acpc.nii) and the path to the default MODEL (e.g., $ARTHOME/T1acpc.mdl) was set.

Using the Convert3D Medical Image Processing Tool (http://www.itksnap.org/pmwiki/pmwiki.php?n=Downloads.C3D), images were cropped and resampled to an isotropic voxel resolution of 1-mm using the default linear algorithm. The input IMAGE was the AC-PC aligned, T1-weighted image from the previous step (e.g., acpc.nii). The name for the OUTPUT file was set (e.g., resampled.nii.gz):

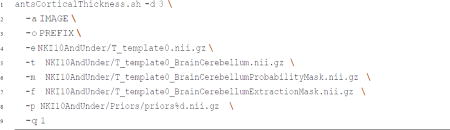
Skull-striped images were automatically acquired using the Advanced Normalization Tools (ANTs; Avants, Tustison, & Song, 2014) volume-based cortical thickness estimation pipeline, antsCorticalThickness.sh, downloadable here (https://github.com/stnava/ANTs/releases/tag/v2.1.0). The shell script, antsCorticalThickness.sh, provides brain volume extraction, segmentation, and registration-based labeling. The workflow consisted of (1) correcting the signal intensity inhomogeneities using the N4 bias field algorithm, (2) initial template-based brain extraction, (3) prior-based 6-tissue (cerebrospinal fluid, cortical gray matter, white matter, deep gray matter, brain stem, and cerebellum) segmentation, (4) and DiReCT-based cortical thickness estimation. The input IMAGE was the resampled T1-weighted image from the previous step (e.g., resampled.nii.gz) and the OUTPUT prefix was set (e.g., antsCorticalThickness/). For this step, we used an age-matched template, NKI10AndUnder template (Avants & Tustison, 2014), to improve brain extraction success. Ultimately, we will generate our own population template using either ANTs antsMultivariateTemplateConstruction.sh or buildtemplateparallel.sh scripts, but did not for the current study because we were only interested in acquiring a rough brain mask for each participant.

Although the pipeline outputs many files, the only file used in the current study was the brain extracted T1 image (e.g., ExtractedBrain0N4.nii.gz). We could have also used ANTs antsBrainExtraction.sh script to generate a brain extracted T1 image.

Tract-Based Spatial Statistics (TBSS)

Diffusion-weighted images were corrected for eddy current and head motion, skull-stripped, and tensor fitted. Using FMRIB’s Diffusion Toolbox within FSL version 5.0.7 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation), image distortions induced by eddy currents and head motion were corrected by aligning each image to the mean non-diffusion-weighted (b=0) using linear image registration. The eddy_correct module was run with the diffusion weighted IMAGE file (e.g., dwi.nii.gz) and the OUTPUT file was set (e.g., dti.nii.gz).

After correction, diffusion weighted images were skull-stripped in order to exclude non-brain voxels from all analyses. The bet module was run with the corrected IMAGE file prefix (e.g. dti) and the OUTPUT prefix was set (e.g., dti_brain).

Once skull-stripped, a diffusion tensor model was fit at each voxel, generating fractional anisotropy (FA), axial diffusivity (AD), radial diffusivity (RD), and mean diffusivity (MD) maps. The DTIfit module was run with the corrected diffusion weighted IMAGE file (e.g., dti.nii.gz), brain MASK file (e.g., dti_brain_mask.nii.gz), BVECS file (e.g., dwi.bvec), and BVALS file (e.g., dwi.bval) and the OUTPUT file was set (e.g., dti).

Besides analyzing FA, we also wanted to compare the other diffusion measures: MD, AD, and RD. The output files from DTIfit are as follows: MD file (e.g., dti_MD.nii.gz), AD file (e.g., dti_L1.nii.gz), and RD file (e.g., mean of dti_L2.nii.gz and dti_L3.nii.gz). Since RD is not an output of DTIfit, this file must be calculated for each participant:

Next, all participants’ FA volumes were skeletonized and transformed into common space as employed in TBSS (Smith et al., 2006; Smith et al., 2007). Volumes were nonlinearly warped to the FMRIB58_FA template, which is supplied with FSL, by use of local deformation procedures performed by FNIRT (Andersson, Jenkinson, & Smith, 2007), a nonlinear registration toolkit using a b-spline representation of the registration warp field (Rueckert et al., 1999). All warped FA volumes were visually inspected for accuracy. Each participants’ FA image was moved into a single directory for the TBSS pipeline. Within the directory that contains all the FA images, the following was run:

Next tbss_3_postreg was run to generate a mean FA volume of all participants. This mean FA volume was thinned to create a mean FA skeleton representing the centers of all common tracts. We thresholded and binarized the mean skeleton at FA > 0.20 to reduce the likelihood of partial voluming along the borders between tissue classes (i.e., tbss_4_prestats). Participant FA images were then warped onto this mean skeleton mask. The resulting skeletons for each participant were fed into voxelwise permutation based cross-subject statistics. First the design matrix was created (i.e., design_ttest2) and finally the analysis was run (i.e., randomise).

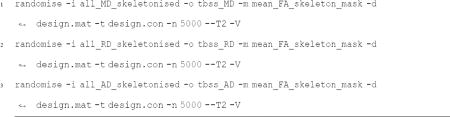
Luckily there is a straightforward way to analyze other diffusion measures besides FA. After completing the full TBSS analyses with the FA images, we analyzed the other diffusion measures: MD, AD, and RD. Each participants’ MD, AD, and RD image was moved into a single directory, respectively, for the TBSS pipeline. In other words, we created three new directories called MD, AD, and RD in the TBSS analysis directory (the one that contains the existing origdata, FA and stats directories from the FA analysis). Each participant’s MD image was moved into the MD directory, making sure that the MD file was named exactly the same as the original FA image. Each participant’s AD image was moved into the AD directory and RD image moved into the RD directory, making sure that the AD and RD files were named exactly the same as the original FA image. With the data organized, the original nonlinear registration was applied to the MD, AD, and RD data, mean MD, AD, and RD volume and skeleton was generated, and finally participant MD, RD, and AD images were then warped onto the mean MD, RD, and AD skeleton masks. The follow code was run within the top working TBSS directory (the one that contains FA, stats, etc.):

The resulting skeletons for each participant were fed into voxelwise permutation based cross-subject statistics.

Automated Fiber Quantification (AFQ)

For the AFQ analyses, diffusion weighted images were preprocessed using the dtiInit preprocessing pipeline wrapper from Stanford open-source VISTASOFT package version 1.0 (https://github.com/vistalab/vistasoft) running on MATLAB version R2015b (MATLAB, 2015). First, the skull-stripped T1-weighted images were reformatted to be compatible with the current pipeline. In MATLAB, the final preprocessed T1-weighted IMAGE (e.g., brain.nii.gz) was reformatted. Finally, the OUTPUT file was set (e.g., afq.nii.gz).

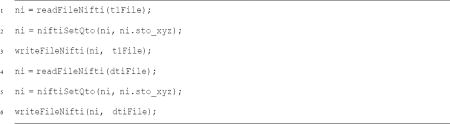
Next, the qto on both the T1- and diffusion-weighted images were set:

Because the diffusion-weighted images were acquired on a Siemens Trio Tim scanner the following parameters had to be set for the dtiInit pipeline and the dtiInit pipeline was run for each participant using their T1- and diffusion-weighted file from the previous step. As part of the pipeline, the diffusion-weighted images were corrected for eddy currents and head motion, skull-stripped, and tensor fitted. Eddy current distortions and participant motion artifacts were removed using the algorithm described in Rohde, Barnett, Basser, Marenco, and Pierpaoli, 2004. The algorithm combines a rigid-body 3D motion correction (6-parameters) with a constrained non-linear warping (8-parameters) based on the expected pattern of eddy-current distortions given the phase-encode direction of the acquired data. Each diffusion-weighted image was registered to the non-diffusion-weighted (b=0) image using a two-stage coarse-to-fine approach that maximized the normalized mutual information. The mean of the non-diffusion-weighted images was automatically aligned to the skull-stripped T1 image using a rigid-body transformation. Next, diffusion-weighted images were resampled to 2-mm using a 7th-order b-spline algorithm. An eddy-current intensity correction was applied to the diffusion-weighted images at the resampling stage. The rotation component of the omnibus coordinate transform was applied to the diffusion-weighting gradient directions to preserve their orientation with respect to the resampled diffusion images. The tensors were then fit using a robust least-squares algorithm designed to remove outliers from the tensor estimation step. We computed the eigenvalue decomposition of the diffusion tensor and the resulting eigenvalues were used to compute FA:

Once preprocessing was completed, white matter pathways were automatically identified using an open-source, freely available software package, Automated Fiber Quantification version 1.2 (https://github.com/yeatmanlab/AFQ). AFQ (Yeatman, Dougherty, Myall, Wandell, & Feldman, 2012) identifies twenty major fiber tracts in an individual’s brain. First, whole-brain tractography was estimated using a deterministic streamline tracking algorithm (STT). Individual fibers were assigned to a fiber tract if they passed through two waypoint ROIs that were used to define the trajectory of the pathway. ROIs were automatically placed in equivalent anatomical locations across each participant. Identified fiber tracts were validated by comparing each tract to a fiber tract probability map. Fibers within the identified fiber tract of low probability were discarded, because they did not conform to the shape of the fiber tract as defined by the fiber probability map. Finally, a mat file containing a list of the participant’s directories was created (e.g., sub_dirs.mat), as well as a file demarcating which group each participant belonged (e.g., sub_group.mat).

In addition to the default pathways, several additional tracts were identified, specifically the entire corpus callosum was segmented into 8 regions. The output mat file (e.g., afq.mat) was used as the input AFQ file:

Because the endpoints vary tremendously across participants, identified fiber pathways in each hemisphere were clipped at each waypoint ROI. With just the central portion of the fiber tracts, we further aligned and resampled individual fiber tracts into 100 equal segments, the default, then extracted the diffusion properties from each segment along the trajectory using a weighted-average approach.

Statistical analyses were performed using R version 3.2.4. We performed one-way analyses of covariance (ANCOVAs) to examine group differences between males and females on each DTI metric at each location along each of the twenty tracts and each of the 8 corpus callosum segments using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate (FDR) for multiple comparisons.

TRActs Constrained by UnderLying Anatomy (TRACULA)

Probabilistic tractography was performed according to standard protocols. Diffusion-weighted images were analyzed with TRACULA package (Yendiki et al., 2011), implemented in FreeSurfer version 5.3.0 (http://surfer.nmr.mgh.harvard.edu/fswiki/Download). TRACULA uses the prior anatomical information derived from the cortical parcellation and subcortical segmentation obtained for each subject by processing the individual T1-weighted images from FreeSurfer. First, we performed the automated reconstruction and labeling of cortical and subcortical regions as performed by FreeSurfer on the T1-weighted images. The technical details of these procedures are described in prior publications (Dale, Fischl, & Sereno, 1999; Fischl, 2004; Fischl & Dale, 2000; Fischl, Liu, & Dale, 2001; Fischl et al., 2002; Fischl et al., 2004; Fischl, Sereno, Tootell, & Dale, 1999; Han et al., 2006; Jovicich et al., 2006; Reuter, Rosas, & Fischl, 2010; Reuter, Schmansky, Rosas, & Fischl, 2012; Ségonne et al., 2004).

FreeSurfer cortical labels were visually inspected by a reliable rater (G.B.) prior to analysis. Next, a configuration file was generated using the DTI image (i.e., dwi.nii.gz), bvec (i.e., dwi.bvec) and bval (i.e., dwi.bval) files output from dcm2niix module. Default options were used for the rest of the configuration file. Preprocessing of the diffusion image data was automatically completed. The processing workflow of TRACULA is based on a standardized routine that utilizes tools available in the software library of FSL. The automatic preprocessing steps include: eddy-current compensation, computing measures of head motion, intra-subject registration of individual diffusion-weighted image to individual T1-weighted image, inter-subject registration of individual T1-weighted image to common space, creation of cortical and white-matter masks from FreeSufer reconstructions, tensor fitting, and computing anatomical priors for white-matter pathways from the TRACULA atlas. The argument of the -c command-line option is the configuration file, where preferences for these preprocessing steps can be specified.

FSL’s bedpostX (Behrens, Berg, Jbabdi, Rushworth, & Woolrich, 2007) was used to apply the ball-and-stick model of diffusion. TRACULA uses the ball-and-stick model of diffusion to reconstruct the pathways from the diffusion-weighted imaging data. The following command runs bedpostX on the preprocessed data of all the participants specified in the configuration file:

The final step of TRACULA is to generate the probability distributions for each white-matter bundles specified in the configuration file. This is done by simultaneously fitting the shape of each pathway to the results of the ball-and-stick model of diffusion from above and to the prior knowledge of the pathway anatomy given by the set of manually labeled training subjects in the TRACULA atlas. The following command reconstructs the probabilistic distribution of the pathways:

For each identified pathway, fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD) were extracted along the tract at the maximum position on the a posteriori path, as well averaged over all sample paths. Because tracts were reconstructed in each participant’s native diffusion space and not on a template, diffusion measures must be interpolated to corresponding positions along the tract for all participants. Once interpolated, some participants’ endpoints contained NA values. Because the endpoints vary tremendously across participants, fiber tracts were clipped; the NA values were removed.

Statistical analyses were performed using R version 3.2.4. We performed one-way analyses of covariance (ANCOVAs) to examine group differences between males and females on each DTI metric at each location along each of the eighteen tracts using age and the average volume-by-volume translation and rotation as covariates. Significance levels for the F-statistic were controlled for by the false discovery rate (FDR) for multiple comparisons.