WRIST - A WRist Image Segmentation Toolkit for Carpal Bone Delineation from MRI

Abstract

Segmentation of the carpal bones from 3D imaging modalities, such as magnetic resonance imaging (MRI), is commonly performed for in vivo analysis of wrist morphology, kinematics, and biomechanics. This crucial task, however, is typically carried out manually and is labor intensive, time consuming, subject to high inter- and intra-observer variability, and may result in topologically incorrect surfaces. We present a method, WRist Image Segmentation Toolkit (WRIST), for 3D semi-automated, rapid segmentation of the carpal bones of the wrist from MRI. In our method, the boundary of the bones were iteratively found using prior known anatomical constraints and a shape-detection level set. The parameters of the method were optimized using a training dataset of 48 manually segmented carpal bones and evaluated on 112 carpal bones which included both healthy participants without known wrist condition and participants with thumb basilar osteoarthritis (OA). Manual segmentation by two expert human observers was considered as a reference. On the healthy subject dataset we obtained a Dice overlap of 93.0 ± 3.8, Jaccard Index of 87.3 ± 6.2, and a Hausdorff distance of 2.7 ± 3.4 mm, while on the OA dataset we obtained a Dice overlap of 90.7 ± 8.6, Jaccard Index of 83.0 ± 10.6, and a Hausdorff distance of 4.0 ± 4.4 mm. The short computational time of 20.8 seconds per bone (or 5.1 seconds per bone in the parallelized version) and the high agreement with the expert observers gives WRIST the potential to be utilized in musculoskeletal research.

1. Introduction

The human wrist is a complex anatomical structure consisting of eight independently moving bones that enable sophisticated maneuvers and motion. Carpal bone shape plays an important role in musculoskeletal research, such as for characterizing wrist biomechanics [32], developing joint replacement methods [41], and quantifying the role of sex [14, 17], skeletal maturation [11, 48] or other factors on disease processes such as osteoarthritis (OA) or rheumatoid arthritis [7, 19].

Magnetic resonance imaging (MRI), a three-dimensional in vivo imaging modality, is commonly employed for assessing wrist injuries and conditions (such as ligament tears, articular cartilage damage, and arthritis) and provides contrast for the carpal bones (see Figure 1). A critical step needed for utilizing MRI scans for studies involving analysis of carpal bone shape is their accurate segmentation from the images. Segmentation is the process of finding the boundaries of some object within the image, i.e. the carpal bones, and consists of two steps: (1) recognition (approximately finding the bones within the 3D image), and (2) delineation which finds the exact object boundaries using the approximate locations from step (1). Given that an MRI volumetric image may have tens if not hundreds of slices, manual delineation of the carpal bone outlines is labor intensive, time consuming (up to 4 hours), and susceptible to high inter- and intra-observer variability [7]. Additionally, there is currently a paucity of computational tools to accurately delineate carpal bone from wrist MRI scans efficiently [30].

Figure 1.

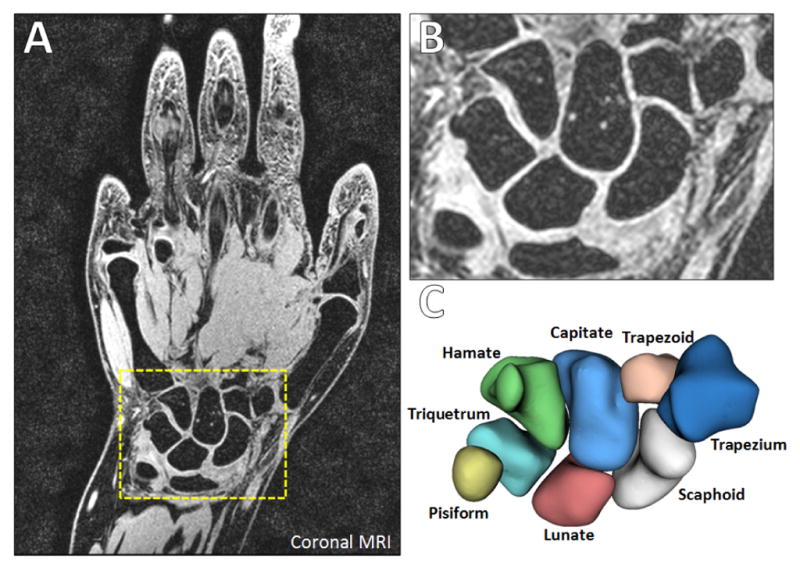
Wrist MRI (from our work). (A) Coronal section with the carpal bones in the dashed yellow box. (B) Zoomed image of the carpal bones. (C) Labeled rendered surfaces of the eight carpal bones.

In this study we propose WRIST, a WRist Image Segmentation Toolkit: a new computational toolbox for rapid, semiautomated delineation of carpal bones from wrist MRI. We optimized the method and assessed its merits considering manual segmentations by two human observers as a reference. The approach was validated on a healthy cohort of men and women and a symptomatic cohort of advanced OA participants and performed parameter optimization and initial seed location sensitivity analysis to gauge the tool’s robustness and accuracy. The manual segmentations were used for the validation and were compared for inter- and intra-observer variability. Our work aimed at providing improved segmentation accuracy compared to existing methods while also having significantly decreased computational time. It was implemented as an open-source module for the popular image analysis tool, 3D Slicer. The tool will be made available in the 3D Slicer module library at www.Slicer.org and posted to GitHub at www.GitHub.com/AJChaudhari/WRIST-Segmentation upon the acceptance of this manuscript.

2. Methods

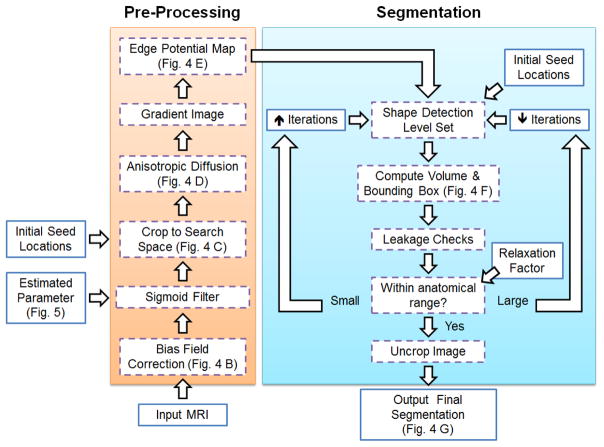
The method consists of the following steps, as outlined in Figure 2.

Figure 2.

Flowchart of the proposed method. Inputs, e.g. MRI scans, and manually selected parameters, are given in the solid lined boxes while the processing and segmentation steps are given in dashed boxes.

1. The user defines one seed location in each carpal bone which initializes the method by constraining the search space and giving an initial location for the segmentation.

2. Pre-processing steps are used to enhance edges, reduce noise and MRI specific artifacts while preserving edges.

3. A shape based level set approach [25] grows a region in three dimensions from the single user defined seed location per bone on the pre-processed image.

4. After convergence of the level set, volume based measures are derived and utilized to detect potential leakage areas or no change of the level set.

5. If the check fails, the parameters of the level set or the initial seed location are automatically adjusted and the level set is repeated iteratively.

The iterative aspect of the method aimed to increase the robustness of the method against image noise, partial volume effect, and broken boundaries of the image segmentation [1, 37]. Please see Figure 3 for example challenges of wrist MR images. The following subsections describe the MRI acquisition, method development, parameter optimization, reference segmentation creation, and validation in further detail.

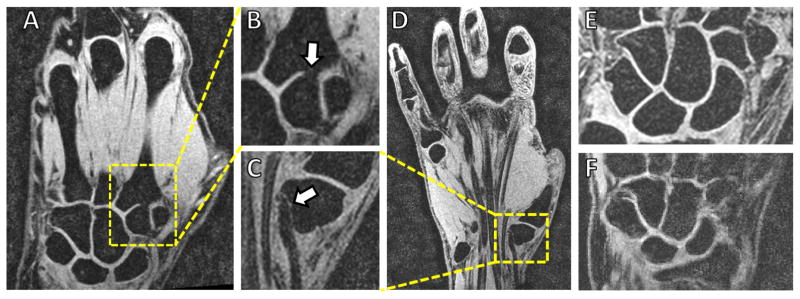
Figure 3.

Examples of the challenges for carpal bone segmentation from MRI. (A–B) Missing boundaries between the trapezoid and the second metacarpal bones, due to partial volume, are not uncommon. (C–D) Tendons and bones (in this case the trapezium) may map to similar intensity values and contours estimated from region growing-based methods may leak into the background. Noise is seen in the images such as in a relatively lower noise image (E) or high noise image such as (F) which makes finding the boundaries difficult.

2.1. MRI Scanning

We obtained Institutional Review Board approval and informed consent from 20 participants before acquiring wrist MR images from each participant using a 3D T₁-weighted VIBE (volumetric interpolated breath-hold examination) pulse sequence with water excitation. The VIBE sequence is a common clinically-used pulse sequence. The 20 MRI exams were split randomly into 6 training exams (for developing the proposed method consisting of 48 carpal bones) and 14 evaluation exams (for evaluating the accuracy of the method consisting of 112 carpal bones). Often times image segmentation methods use a single image spatial resolution for training and evaluation, but in our work we used several different resolutions that make the proposed method more generalizable to a wider variety of MRI exams. See Table 1 for the number of scans at each resolution. The training set consisted of participants with no known wrist conditions, and the evaluation set included 10 healthy subjects (5 men and 5 women, 80 bones) and 4 participants with thumb basilar OA (32 bones). The ages for the healthy subjects was 31.4±8.2 years while the ages for the OA subjects was 62.8 ±10.3 years.

Table 1.

MRI Voxel Dimensions

Training Set	Evaluation Set	Resolution
2	6	0.24 × 0.24 × 0.29 mm
4	5	0.47 × 0.47 × 0.50 mm
0	3	0.47 × 0.47 × 1.00 mm

2.2. Image Segmentation: Method development and optimization using training data

Image Pre-Processing

We conducted the following image processing steps to increase the accuracy and robustness of the segmentation result.

1. The N4ITK bias correction field filter [43], as implemented in SimpleITK [24], was applied to the images in order to reduce the bias of the magnetic field.

2. An anisotropic diffusion filter, an implementation from [31], was used to reduce noise while preserving edges with empirically chosen parameters including time step of 0.01, 5 iterations, and a conductance level of 2.

3. A sigmoid filter was then applied to reduce the image noise which required an upper threshold parameter. We automatically determined the sigmoid filter upper threshold parameter based on the mean and standard deviation of the MRI exam, i.e. a simple estimation of the image noise and mean intensity, by using the following linear model

   $$t(x)=0.825x-26.26$$ (1)

   where x is the mean intensity of the image added to the standard deviation of the image and t(x) is the sigmoid threshold parameter. This simple model was created by fitting a line between the mean plus standard deviation of the six training MRI exams and manually selected sigmoid parameters for each exam, see Figure 5 for a plot of the data and the linear fit.

4. Lastly, an edge potential map was computed by

   $$g(I(x,y,z))=e^{-\mid (\nabla \ast G)(I(x,y,z))\mid }$$ (2)

   using the image intensity I(x, y, z) and the derivative of Gaussian operator (∇ * G) [24]. Essentially, the edge potential map estimates the probability of an edge being at each image position. Specifically, the areas of the image which are estimated to be bone have a value close to 1 while image areas which are estimated to be an edge have a value close to 0. Please see Figure 4(E) for an example of an edge potential map of the hamate bone.

Figure 5.

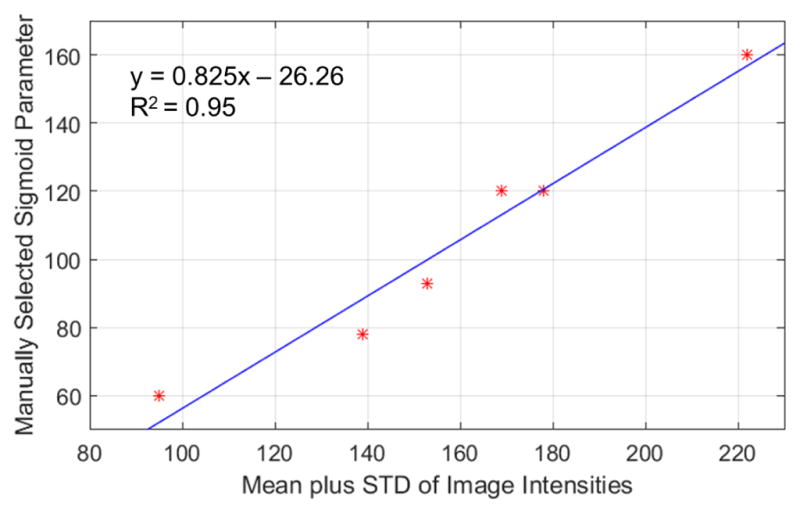
The sigmoid filter upper threshold parameter was selected based on fitting a curve between manually selected parameters against the mean image intensity plus the standard deviation (STD) of the image.

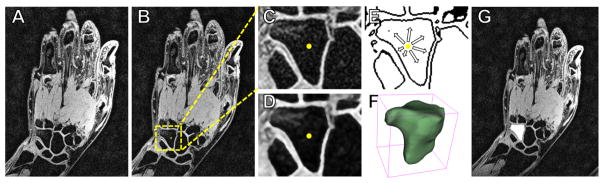
Figure 4.

Example of the segmentation steps. (A) Original MRI exam of the hand and wrist. (B) The user selects an initial seed location on the hamate bone (yellow dot) and a search space is automatically determined (yellow dashed box). (C) Image is cropped to include only the search space. (D) Anisotropic diffusion filtering is applied to reduce noise. (E) An edge potential map is created using the found sigmoid parameter, and the shape detection level set grows from the seed point on this image. (F) A bounding box is created around the segmentation to estimate the convergence using anatomical prior knowledge. (G) The segmentation (white area) is then placed back into the coordinate system of the original MRI scan.

Segmentation

A shape detection 3D level set approach based on [25], as implemented in the “ShapeDetectionLevelSetImageFilter” in SimpleITK, was used to perform the segmentation on the postprocessed images. The segmentation contour grew in 3D from a single user-defined initial seed point somewhere within the bone boundary. This level set approach has fast computational time (a large advantage for this application), robustness to image noise and missing edges (commonly encountered in MRI), and flexibility by modifying or choosing just a few parameters. Broadly, due to these desirable properties, level sets have been demonstrated as being superior compared to other methods for segmenting various tissues on MR images such as brain tumors as well as whole organs such as the liver [12, 13, 33, 35]. The level set is described by

$${\mathrm{\Psi }}_t+k(x,y,z)\ast (F_A+F_G)\mid \nabla \mathrm{\Psi }\mid =0$$

where this scaling factor k is defined by

$$k(x,y,z)=e^{-\mid (\nabla \ast G)(I(x,y,z))\mid }$$

from the edge potential map, Ψ_t is the current level set, F_A is the propagation term, and F_G is the diffusion term which depends on the local curvature for regularization. ∇Ψ was calculated based on a signed Maurer distance map [27] filter in SimpleITK. The parameters used with the level set were the maximum root mean square error, propagation scale, shape curvature scale, and maximum iteration number. These were selected based on a machine learning optimization strategy as is outlined below. Please see Figure 4 for an example of the image segmentation steps.

Convergence Check

A check was automatically performed on the bone segmentation result to assess if it corresponded to a significantly different overall bone volume or bounding box size from prior anatomical knowledge, as we describe below. The prior knowledge we used was from Crisco et al., [6], where the volume of each carpal bone and the sex of the subject are provided. If the sex of the subject was unknown, then the mean between men and women for each bone was used instead. The bone volumes range from the smallest bone, i.e. pisiform, with 854 ± 203 mm³ in men and 570 ± 122 mm³ in women to the largest bone, i.e. capitate, with a volume of 3701 ± 564 mm³ in men and 2547 ± 345 mm³ in women [6].

If the convergence check failed, the segmentation was automatically repeated using either a smaller or larger number of iterations (by a random percentage between 5% and 15%, with an average of 10%) to attempt to improve the level set convergence. Additionally, if the volume was too small, a new initial seed location was automatically chosen by selecting a nearby randomly chosen voxel within a 3×3×3 cube of the first location. This convergence check allowed for improved robustness of the segmentation result if the level set grew into the background regions (due to a missing or weak boundary), if the level set failed to grow from the initial seed location (perhaps due to large image noise around the initial seed location), or if the maximum iteration parameter chosen was too small to allow the level set to converge onto the boundary of the bone.

Parameter Selection and Sensitivity

Selection of suitable parameters of the shape detection level set to use as default settings in the tool was done in two steps. First, an optimization procedure was used to find the best parameter values on the training dataset. Next, a sensitivity analysis of the parameters around the values found from the optimization procedure was done to see how changes in these values influence the resulting segmentation.

The machine learning procedure used for optimizing the parameters was the differential evolution (DE) method [39] as implemented in SciPy (a Python toolkit) [18]. DE is a multivariate stochastic optimization method which optimizes by utilizing a population of candidate solutions and creating new candidate solutions by combining existing ones [18]. The optimization provides a measure of quality of a candidate solution such that a gradient is not needed. The method was primarily chosen due to its ability to optimize several variables simultaneously without the need of computing a gradient. The method requires a user-defined search space for each parameter as a range of values. The search space was empirically chosen as the following: maximum iteration number 100–2000, level set curvature scale 0–6, level set propagation scale 0–6, and maximum root mean square (RMS) error 0.001–0.05. The measure of quality for the candidate solution was the Dice overlap of the resulting segmentation as compared with a manual segmentation on a training set of 48 bones from the 6 training MR images.

The machine learning considered all parameters at once so the sensitivity of any one parameter on the segmentation result was found by varying only one parameter at a time while keeping all others at the default values found previously. This was important information because a parameter with little influence on the segmentation result will not need to be changed for a variety of images while a more sensitive parameter may need slight adjustment for different image characteristics. The same interval as was used for the DE optimization was chosen and each parameter was linearly varied within this interval by 40 equally spaced steps.

Initial Seed Sensitivity

We quantified the sensitivity of the initial seed selection on the segmentation accuracy. First, the manual segmentations for each bone were eroded by 3 voxels to prevent the randomly selected seed from being exactly on the bone boundary while still allowing it to be quite close, a fair assumption given that the module instructions will advise users not to click on the boundary of the bone for the initial seed selection. Next, 30 voxels were randomly chosen within the eroded manual segmentation regions to avoid any selection bias of the seed locations. Finally, the segmentation result of the first seed was compared with the other 29 seeds to calculate the Dice overlap coefficient to quantify the overlap of all the resulting segmentations with each other. This process was repeated for all bones, and the seed sensitivity was evaluated on both the training (N=1,440 seeds) and the healthy subject evaluation datasets (N=2,400 seeds) of expert manual segmentations with randomly chosen seed locations. If the segmentation was not sensitive at all to the initial seed location the Dice overlap would be 100%, while if it was sensitive to seed location the Dice would be lower.

Parallelization

Multiple logical cores, either in the same computer or over a cluster of computational nodes, can be used to significantly speed up the computational time. Parallelizing computations is made fairly straightforward with recent advances in software tools. The free open-source SCOOP (Scalable COncurrent Operations in Python) module for Python was used for distributing the computations across CPU nodes [16]. The segmentation of each carpal bone is independent of the other segmentations so this, in principle, is done efficiently at the same time. The preprocessed image and user defined seed for each bone were fed into separate logical cores of the computer, and the segmentation step was done concurrently. Since the bones are segmented one at a time, this should lead to up to N times faster computation for a computer with N logical cores. While the number of logical cores was automatically determined for this study, users have the option to specify a number. The method can easily be run in either a serial mode (one bone at a time on one core) or in a parallelized mode (several bones being segmented at the same time).

3D Slicer Module

WRIST was implemented as an open-source module for a popular image analysis tool, 3D Slicer [9] found at www.slicer.org, to allow for easy sharing and installation. Please see Figure 6 for the layout of the module within 3D Slicer. 3D Slicer is advantageous due to its excellent ability to load, save, and display images and renderings of segmentations. It also allows the user to input the initial seed locations needed (manually using the visualization interface, or via a script) and comes with Python built in so the user does not need to configure or build anything from source code. The installation of WRIST consists of simply copying and pasting the code into a particular 3D Slicer folder. After installation, WRIST will automatically load with 3D Slicer. After opening and loading an MRI exam, the user simply adds a fiducial marker to each bone of interest and corresponding label of the bone within the module so that the anatomical prior knowledge of each particular bone can be utilized. Upon acceptance of this paper, the tool will be released on the Slicer module library for even easier installation (just an install button within Slicer) as well as on GitHub at www.GitHub.com/AJChaudhari/WRIST-Segmentation.

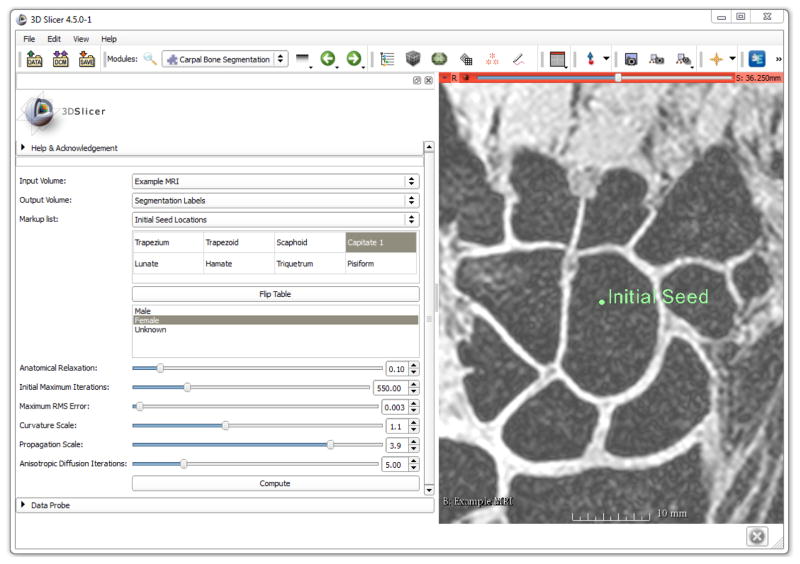
Figure 6.

Layout of the 3D Slicer WRIST module with one of the training MR images shown with an initial seed location on the capitate. The table on the left is used to select the bone(s) of interest and the order of seed locations. The optimized parameter values are the default parameters of the module.

In the GitHub repository, there is also a command line tool which may be useful for processing a large number of images by reading in a text file of initial seed locations and MRI file-names. The command line tool incorporates both the serial and parallelized modes.

2.3. Segmentation Method Evaluation

Several commonly used statistics of segmentation accuracy were calculated, including the Dice overlap coefficient, Jaccard index, and the Hausdorff distance [26]. The Dice coefficient and Jaccard index are measures of the volume overlap while the Hausdorff distance measures the maximum distance between the two segmentations and is especially useful for evaluating local deviations which do not take up much volume. The Dice overlap coefficient in percentage was defined as

$$D(S,G)=\frac{2\mid S\cap G\mid }{\mid S\mid +\mid G\mid }\times 100,$$ (3)

and the Jaccard Index in percentage was defined as

$$J(S,G)=\frac{\mid S\cap G\mid }{\mid S\cup G\mid }\times 100,$$ (4)

where S is the segmented image and G is the ground truth image [42]. Both the Dice coefficient and Jaccard index were expressed as percentages. They range from 0% (no overlap) to 100% (perfect agreement). The Hausdorff distance was defined in a two stage manner using the following equations, where

$$H_{SG}=max\{d_i^{SG}\},i=\{1\dots n_S\}$$

is the maximum value of the minimum distance from all points in S to G,

$$H_{GS}=max\{d_i^{GS}\},i=\{1\dots n_G\}$$

is the maximum value of the minimum distance from all points in G to S, and

$$H=max\{H_{SG},H_{GS}\}$$ (5)

is the Hausdorff distance which is the maximum of H_SG and H_GS [2].

2.4. MRI datasets

The training set of exams from healthy participants was used for optimizing the parameters, evaluating the parameter sensitivity, developing the 3D Slicer module, and evaluating the initial seed location sensitivity. The evaluation set was manually segmented by two independent expert observers using the manual delineation tools in the ITK-SNAP [47] software and compared with segmentations from the same images generated via the proposed method. The training set was manually segmented by a different expert observer also using ITK-SNAP for manual delineation.

3. Results

3.1. Parameter Optimization

The DE optimization approach was used with the proposed method to optimize the various parameters on the training images, see Figure 7. The convergence is rather noisy due to its stochastic approach for selecting the parameter values in the next iteration, but eventually suitable parameter values were found with a maximum Dice overlap of 96% on the training dataset. The resulting values found for each parameter were 550 maximum iterations, curvature scale of 1.10, propagation scale of 3.90, and RMS error of 0.003. These were made the default values (Figure 6) for our method.

Figure 7.

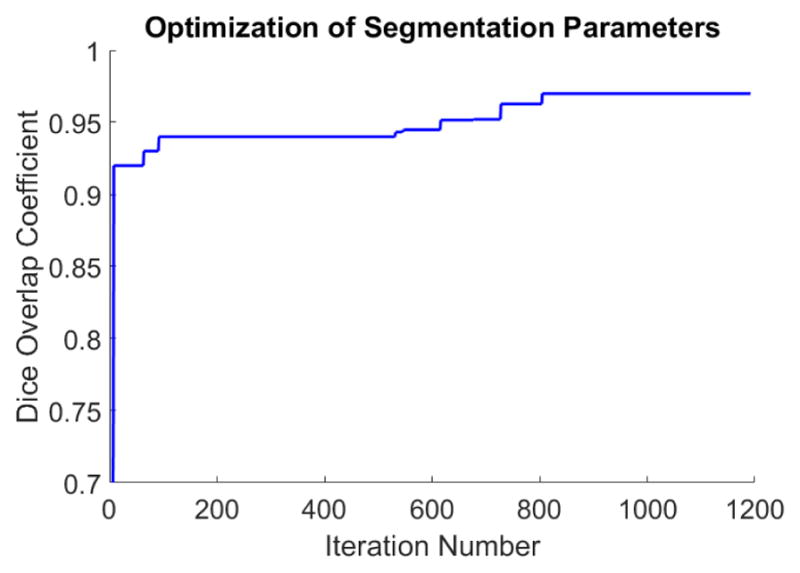
Optimization of the segmentation parameters using the DE optimization approach is plotted. The Dice overlap coefficient of the training dataset was the objective function used, and is plotted against the iteration number. The blue line represents the cumulative maximum Dice coefficient found so far with a maximum Dice overlap of 96%. These parameters were then used on the training and evaluation dataset.

3.2. Parameter Sensitivity

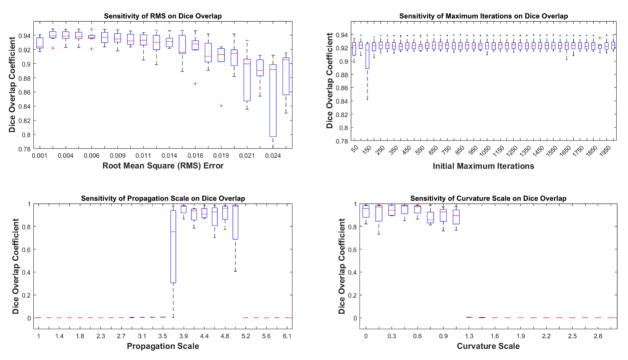
The RMS error parameter did not significantly affect the Dice overlap for the training images for values between 0 and around 0.015, see Figure 8. Values larger than this caused a decrease in the accuracy of the segmentation result likely due to failure of the level set to converge. The initial maximum iteration number did not affect the Dice overlap for any values over 200 which is likely due to the leakage check of the method which uses anatomical knowledge to determine convergence. When convergence is estimated to not have been achieved, the maximum iteration number is automatically increased. The propagation scale was required to be between 3.9 and 4.6 for a good segmentation result. Values outside of this range caused the level set to either not grow at all, i.e. values less than 3.5, or grow past the boundaries into the background, i.e. values larger than 5, which led eventually to a Dice overlap of close to 0. Lastly, the curvature scale was only mildly sensitive for values less than 1.2 while the level set failed to grow for values larger than 1.2.

Figure 8.

Sensitivity of the Dice overlap coefficient to a range of parameters values. Parameters included the RMS error, initial maximum iterations, level set propagation scale, and the level set curvature scale.

3.3. Comparison with Manual Segmentations

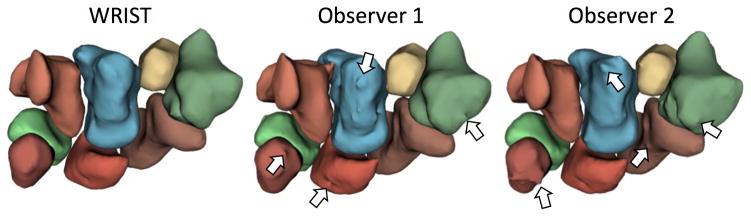
Our results are from the evaluation dataset of 112 carpal bones. First, the proposed method was compared to expert manual delineation. Next, observer 1 was compared with observer 2 to quantify normal variance in manual segmentation definition. Please see Table 2 for the measures by carpal bone for the healthy participants and Table 3 for the measures by carpal bone for the OA participants. In general, the proposed method provided smoother segmentations than the individual observers (Figure 9), which may be important for bone shape analysis [3, 19]. Please see Figure 10 which shows segmentation examples from the proposed method on a less noisy and noisy MRI scans.

Table 2.

Segmentation Comparison for Healthy Subjects (N=80 bones)

	WRIST vs. Observer 1			WRIST vs. Observer 2			Observer 1 vs. Observer 2
Bone	Dice	Jaccard	Hausdorff	Dice	Jaccard	Hausdorff	Dice	Jaccard	Hausdorff
Scaphoid	93.7 ± 4.9	88.4 ± 8.1	3.6 ± 3.8	93.7 ± 5.0	88.6 ± 8.3	3.6 ± 3.8	98.0 ± 1.4	96.0 ± 2.6	0.9 ± 0.3
Lunate	93.7 ± 2.8	88.4 ± 5.0	1.4 ± 0.8	93.8 ± 3.4	88.5 ± 6.0	1.5 ± 0.9	97.6 ± 1.4	95.4 ± 2.7	0.9 ± 0.3
Triquetrum	93.3 ± 3.6	88.9 ± 4.3	3.1 ± 5.8	93.2 ± 3.7	88.8 ± 4.5	3.0 ± 5.9	97.6 ± 1.5	95.3 ± 2.8	1.3 ± 0.5
Pisiform	91.4 ± 3.7	84.3 ± 6.2	1.2 ± 0.5	91.1 ± 3.6	83.9 ± 6.1	1.4 ± 0.6	96.3 ± 2.4	93.0 ± 4.4	1.1 ± 0.6
Trapezium	93.1 ± 2.6	87.1 ± 4.5	2.3 ± 0.4	92.6 ± 2.9	86.3 ± 4.8	2.3 ± 0.6	96.4 ± 2.6	93.1 ± 4.7	1.7 ± 0.8
Trapezoid	92.1 ± 3.5	85.5 ± 5.9	1.9 ± 0.6	92.0 ± 3.9	85.3 ± 6.4	1.9 ± 0.5	96.2 ± 2.3	92.6 ± 4.1	1.5 ± 0.6
Capitate	94.5 ± 2.0	90.3 ± 3.0	2.8 ± 2.7	94.5 ± 2.6	90.3 ± 4.0	2.6 ± 2.9	97.3 ± 1.4	94.8 ± 2.6	1.8 ± 0.8
Hamate	92.1 ± 4.3	85.6 ± 7.2	5.1 ± 4.8	92.2 ± 4.1	85.7 ± 7.0	5.3 ± 4.7	96.9 ± 1.6	94.0 ± 3.0	1.9 ± 0.8
Overall	93.0 ± 3.7	87.3 ± 6.0	2.7 ± 3.4	92.9 ± 3.9	87.2 ± 6.4	2.7 ± 3.4	97.1 ± 2.0	94.3 ± 3.7	1.4 ± 0.7

Table 3.

Segmentation Comparison for OA Subjects (N=32 bones)

	WRIST vs. Observer 1			WRIST vs. Observer 2			Observer 1 vs. Observer 2
Bone	Dice	Jaccard	Hausdorff	Dice	Jaccard	Hausdorff	Dice	Jaccard	Hausdorff
Scaphoid	92.7 ± 3.5	86.4 ± 6.1	3.7 ± 1.3	92.1 ± 3.7	85.3 ± 6.2	3.6 ± 1.3	97.8 ± 1.4	95.7 ± 2.6	1.3 ± 0.2
Lunate	93.4 ± 4.3	87.7 ± 7.0	3.4 ± 6.7	91.9 ± 4.6	87.1 ± 8.0	3.4 ± 6.7	97.4 ± 1.6	94.8 ± 2.9	1.0 ± 0.2
Triquetrum	93.9 ± 11.3	88.4 ± 10.1	1.8 ± 1.1	93.1 ± 9.4	87.2 ± 9.5	1.6 ± 1.3	96.9 ± 3.2	94.0 ± 5.7	1.2 ± 0.4
Pisiform	92.2 ± 7.3	85.7 ± 11.2	1.4 ± 0.1	92.2 ± 7.3	85.6 ± 9.7	1.4 ± 1.3	96.0 ± 3.6	92.3 ± 6.3	0.9 ± 0.2
Trapezium	80.5 ± 10.5	63.2 ± 5.0	6.1 ± 0.9	77.7 ± 8.6	61.8 ± 6.9	6.1 ± 1.2	84.5 ± 2.6	72.7 ± 4.1	3.1 ± 1.8
Trapezoid	91.5 ± 2.9	84.3 ± 5.0	2.6 ± 0.9	90.1 ± 4.8	82.1 ± 7.5	2.5 ± 1.0	96.2 ± 3.8	92.7 ± 6.5	1.2 ± 0.3
Capitate	93.0 ± 4.2	86.9 ± 6.7	3.9 ± 2.8	92.8 ± 5.4	86.7 ± 8.5	4.2 ± 2.9	96.8 ± 1.9	93.9 ± 3.5	1.6 ± 0.3
Hamate	92.7 ± 6.7	86.1 ± 5.4	9.0 ± 6.6	92.0 ± 6.8	85.3 ± 7.1	8.5 ± 6.9	96.8 ± 2.3	93.8 ± 2.3	2.0 ± 0.5
Overall	91.2 ± 8.6	83.6 ± 10.3	4.0 ± 4.4	90.2 ± 8.5	82.6 ± 10.8	3.9 ± 4.4	95.3 ± 4.6	91.2 ± 7.8	1.5 ± 1.1

Figure 9.

Example renderings of the eight carpal bones from WRIST, observer 1, and observer 2. Note that WRIST gives a smoother surface as compared with the manual segmentations which is important for shape analysis and may be more reproducible over manual segmentations. Arrows point to segmentation artifacts on the rendered surfaces by non-smooth manual segmentations.

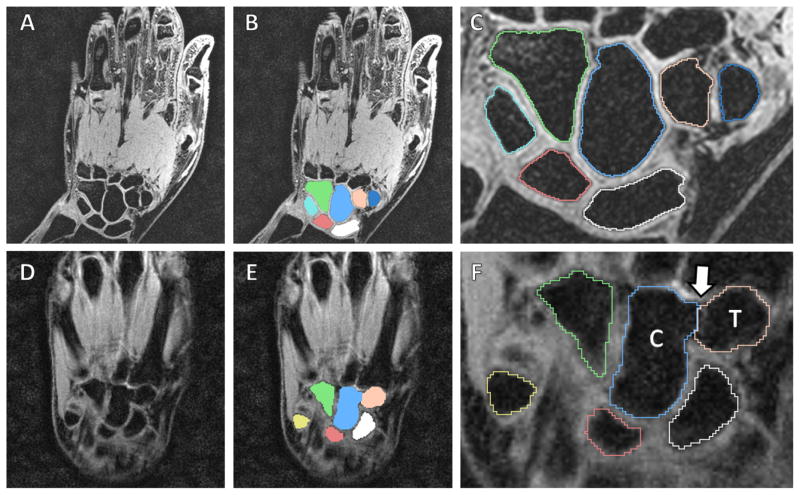
Figure 10.

Segmentation example of a lower noise/higher resolution MRI (A–C) and a higher noise/lower resolution MRI (D–F). Note the shape detection level set correctly found the separation between the trapezoid (“T”) and capitate (“C”) despite the missing boundary between them (white arrow).

3.4. Seed Location Sensitivity

Overall, we found a Dice overlap of 92.9 ± 6.0%, see the evaluation dataset results in Table 4 which suggests that picking random seeds within the bones will overlap by 92.9%. The capitate had the highest agreement between the various seed locations while the trapezium had a marginally lower agreement. Choosing an appropriate seed location is more important for some bones, such as the trapezium and hamate, while being less important for others such as the capitate and pisiform.

Table 4.

Dice Overlap (%) of 30 Seed Locations per Bone (N=80 bones)

Scaphoid	Lunate	Triquetrum	Pisiform	Trapezium	Trapezoid	Capitate	Hamate	Overall
92.8 ± 6.3	93.4 ± 5.1	92.1 ± 4.2	93.9 ± 9.3	91.1 ± 5.0	92.5 ± 7.2	95.9 ± 3.5	91.8 ± 3.2	92.9 ± 6.0

3.5. Computation Time

While conducting the seed sensitivity test for 2,400 segmentations, the computation time for each segmentation was noted on an 8 core, i7 CPU, 3.50 GHz, 64-bit, and 32 GB RAM computer running Windows 7. When running the method in its serial mode, the mean time for segmenting one carpal bone was 20.8 ± 8.3 seconds. When running the method in its parallelized format, the time was reduced to 5.1 ± 3.2 seconds per bone, i.e. 40.8 seconds for all eight carpal bones in one MRI exam. The time reduction was less than 20.8/8 seconds for the 8 logical cores likely due to the overhead of running it in parallel or not enough RAM memory, but the computational time improvement was on average a factor of 4.1 times faster then in serial mode. In comparison, the expert observers reported spending an average of 4 hours per MRI to manually segment the eight carpal bones due to the anatomical complexity and high number of slices (mean of 170 slices per evaluation MRI scan).

4. Discussion

Precise carpal bone segmentations can be utilized for applications, such as biomechanical modeling [32], quantifying sex-based differences (a possible predisposition for OA) [3, 14, 17, 19], skeletal maturity and development models [11, 48], bone erosion quantification in rheumatoid arthritis [7, 19], and quantification of treatment effects on wrist joints. Segmentations from volumetric images during active motion, e.g. radio-ulnar deviation, are needed to compute the wrist kinematics which is crucial for better understanding scapholunate advanced collapse [15, 22], and sex-based motion differences [21]. In this approach, MRIs of the wrist in multiple static orientations would be acquired and the bone surfaces derived from each image. A small study may image both wrists of 20 volunteers at 5 static positions per wrist, i.e. 200 MR images. Manual segmentation of these 200 high-resolution MRI volumes would be impractical and could take months. This problem worsens with larger sample sizes such as MRIs of 50 volunteers. The proposed method utilizes properties of level sets, such as their high computational speed and robustness to missing edges, to fill in the gap of a lack of an accurate and fast segmentation tool for the carpal bones, and provides an efficient solution.

Surface models may also be potentially beneficial in the development of medical devices such as artificial bone implants in individuals with severely diseased thumb basilar OA joints for which there is still no satisfactory replacement for advanced OA [28] and for surgical planning based on a particular patient’s wrist type (row vs. column) or bone morphology to better reconstruct their normal biomechanics post-surgery [5].

Prior work on carpal bone segmentation has focused extensively on wrist images acquired from CT [1, 4, 8, 37]. Anas et al. [1] and Chen et al. [4] describe methods to segment the carpal bones based on a registration procedure to estimate the pose of the wrist by determining the orientation of the hand relative to the forearm. Anas et al. reported an average Jaccard index of 86% [1] while Chen et al. reported an average Jaccard index of 87% for the eight carpal bones [4]. This is very similar to the mean Jaccard index of 87% found in our paper. However, despite automation, other techniques had long computational times and steps which would not directly translate to MRI carpal bone segmentation, such as use of a segmentation initiation via thresholding. From an image segmentation standpoint, CT has several obvious advantages that simplify the delineation task, including standardized Hounsfield units for bones and tissues, a high spatial resolution, and a high speed of image acquisition (helpful in reducing motion artifacts) [23, 40, 34]. MRI on the other hand has superior contrast resolution for evaluation of wrist injuries and other conditions, therefore is the most commonly used imaging modality for that purpose, and does not involve ionizing radiation. However it suffers from motion (due to longer acquisition times), bias field, non-standardized image values, and partial voluming [44]. A recent method by Włodarczyk et al. [46], an expansion on their earlier work [45], first found seed locations using the multi-Otsu thresholding algorithm on a user defined region of interest of the carpal bone area. These marker locations were then applied to a watershed algorithm for the final segmentation with a Dice overlap co-efficient of 89 ± 12% for the carpal bones. Parameter selection sensitivity however was not justified or evaluated across MRIs of different resolutions or different noise characteristics. Kock et al. [20] proposed an approach in which bounding boxes were automatically found around each carpal bone followed by thresholding each box using a Gaussian mixture algorithm with a mean point-to-mesh error of 0.48 mm. There has also been work on using statistical shape models [36] and meshes [10], but the initialization accuracy remained a challenge and negatively affected the final segmentation and computational time.

The use of WRIST to quantify wrist pathologies may enhance epidemiological studies of wrist diseases, thus contributing to improved diagnostics and accelerated identification of optimal treatment plans. For a computational tool which achieves this goal to be broadly relevant and useful, it needs to be computationally efficient while also having a high mean Dice overlap coefficient as compared with expert manual segmentations. One of our goals was to accelerate the delineation of the segmentation process. Our method took 20.8 seconds per bone in serial mode and 5.1 seconds per bone in parallel mode. Expert observers reported spending 4 hours per MRI scan to manually segment the eight carpal bones. In comparison, other reported computational times for the MRI based carpal bone segmentation methods include 6.17 minutes [20], <9 minutes [46], and others simply reported as <30 minutes [10, 29, 45]. The methods from CT had computational times also quite long with <20 minutes [1] and <40 minutes [8].

The computational time was an important aspect while designing the proposed method which led to choosing a semiautomated approach for identifying the bones in the image over a fully automated one. Unfortunately, the high computational cost and low accuracy of the recognition step of the bone segmentation within the volumetric CT or MRI exam is currently a limiting factor for automated methods in the clinical environment. It takes a high performance workstation 20+ minutes to attempt to identify the 8 carpal bones [1, 10, 45, 29] while a human observer could do the same task in several seconds with a single click on each bone. Conversely, finding the exact boundaries (the delineation step) is very time consuming for a human observer, but a computer can do this much faster. We took the best approach of both steps to have the human observer click once per bone and then have the computer find the exact boundaries of the bones (using our level set-based approach), growing from the user click within each bone. For many clinical tasks, the tradeoff between semi-automated and much faster computational speed could be justified over a slower but automated tool. The proposed method can also easily be extended by finding the seeds locations in an automated way, such as by using an anatomical atlas, if this can be done in a computationally efficient manner. The marginal variance in computational times of our method is likely due to the iterative nature of the proposed method convergence. If the initial iteration number is sufficient, only one cycle needs to be done otherwise the method would have to segment several times resulting in a longer computational time.

Our proposed tool could be used to help construct a statistical shape model of the carpus. While providing initial seed locations for carpal bones is a fairly quick process for users familiar with WRIST evaluating limited numbers of MR images, we acknowledge that this process can become time consuming for greater image quantities, e.g. 100 scans. We aim to address the initial seed location selection by assessing the utility of atlases for providing the initial seed.

There were several limitations of the study which should be noted. First, two of the MR images of the participants with OA had motion artifacts, especially affecting the trapezium and trapezoid. The segmentation accuracy was lower in these images compared to the other images. Motion artifacts continue to be a challenge for carpal bone segmentation. Secondly, the shape detection level set is fairly robust to small missing boundaries, but leakage into the background did occur when there were large missing boundaries or substantial partial voluming at the interface of tendon and bone. The anatomical prior information on carpal bone dimensions did help with the leakage by automatically adjusting the level set iteration number, but additional prior knowledge on mean shape and variation could increase the robustness of the method. Lastly, other open source methods such as Seg3D are available, and we will do a segmentation comparison in future work [38].

5. Conclusion

In this work we created an open source computational toolkit, WRIST, for the segmentation of the carpal bones from wrist MR images and integrated it into the 3D Slicer platform. The tool achieved good agreement with two expert observers and generated the segmentations in significantly less time than other methods in the literature. Our proposed method was demonstrated to be quite robust to both the parameter selection and the initial seed location such that the user could use this tool to obtain fairly accurate segmentations. WRIST may assist musculoskeletal researchers for in vivo analysis of wrist morphology, kinematics, and biomechanics.

Highlights (for review).

• A computational toolkit for fast carpal bone segmentation from MRI was created

• Method incorporated anatomical knowledge and shape-detection level sets

• Achieved shorter computational time and higher agreement with 2 expert observers