Fluctuation Analysis of Peak Expiratory Flow and Its Association with Treatment Failure in Asthma

Abstract

Rationale: Temporal fluctuations have been demonstrated in lung function and asthma control, but the effect of controller therapy on these fluctuations is unknown.

Objectives: To determine if fluctuations in peak expiratory flow (PEF) are predictive of subsequent treatment failure and may be modified by controller therapy.

Methods: We applied detrended fluctuation analysis to once-daily PEF data from 493 participants in the LOCCS (Leukotriene Modifier Corticosteroid or Corticosteroid-Salmeterol) trial of the American Lung Association Airways Clinical Research Centers. We evaluated the coefficient of variation of PEF (CVpef) and the scaling exponent α, reflecting self-similarity of PEF, in relation to treatment failure from the run-in period of open-label inhaled fluticasone, and the treatment periods for subjects randomized to (1) continued twice daily fluticasone (F), (2) once daily fluticasone plus salmeterol (F + S), or (3) once daily oral montelukast (M).

Measurements and Main Results: The CVpef was higher in those with treatment failure in the F and F + S groups in the run-in phase, and all three groups in the treatment phase. α was similar between those with and without treatment failure in all three groups during the run-in phase but was higher among those with treatment failure in the F and F + S groups during the treatment phase. Participants in all three groups showed variable patterns of change in α leading up to treatment failure.

Conclusions: We conclude that increased temporal self-similarity (α) of more variable lung function (CVpef) is associated with treatment failure, but the pattern of change in self-similarity leading up to treatment failure is variable across individuals.

At a Glance Summary

Scientific Knowledge on the Subject

Analysis of the variability and self-similarity of peak expiratory flow data in asthma may reflect asthma severity and control in patients, but the effects of controller therapy on temporal variability in lung function have not been investigated.

What This Study Adds to the Field

We have applied an analysis of the variability and temporal self-similarity of peak expiratory flow data to a large study of patients who underwent randomization to different controller therapy. Our results demonstrate treatment failure is associated with a higher temporal self-similarity of more variable peak flow, but the degree of self-similarity leading up to treatment failure is highly variable among subjects.

Asthma is now recognized to be a complex disease perhaps best characterized by a fluctuating phenotype. As with all complex systems, it is possible that important prognostic information may be contained in the way that lung function changes over time (1–3). Indeed, variations in peak expiratory flow (PEF) (4–8), oscillatory resistance (9–11), respiratory system impedance (2, 12, 13), and the complexity of the breathing pattern (3) have all been shown to relate to asthma severity or control. Furthermore, the qualitative manner in which each of these quantities varies with time seems to be independent of the time-scale over which they are examined (14–16). This property, known as self-similarity, implies the existence of long-range memory in lung function and suggests that it ought to be possible to predict future lung function based on time-series analysis of past lung function measurements.

Detrended fluctuation analysis (DFA) is a numerical method for determining a scaling coefficient, α, that reflects the strength of long-range memory in self-similar time series (15). In particular, α = 0.5 when the data in the series are completely uncorrelated (i.e., white noise), whereas α greater than 0.5 indicates increasingly strong correlations (16). Previous studies have shown that a higher value of α predicts less severe asthma and better control, suggesting that the relative stability that comes with increased lung function memory translates into greater stability of the disease itself (4–6). By the same token, however, increased long-term memory could make it difficult to escape from a detrimental perturbation, and indeed a higher α value has been linked to an increase in asthma exacerbations when mean lung function is poor (8). Thus, analysis of the temporal variations in lung function parameters can provide important clinical insights beyond those apparent in the mean values alone, indicating that the better signal may be the noise.

Based on these notions, we hypothesized that the value of α provided by DFA of lung function time series would be associated with treatment failure and affected by changes in asthma controller therapy. We tested this hypothesis in PEF time series data from a large randomized clinical trial of asthma control therapy conducted by the American Lung Association’s Airways Clinical Research Centers network. Some of the results of these studies have been previously reported in the form of an abstract (17).

Methods

Study Design

The LOCCS (Leukotriene Modifier, Corticosteroid or Corticosteroid-Salmeterol) trial was a multicenter, randomized, controlled clinical trial comparing three different 16-week treatment regimens within a group of 493 patients with mild-to-moderate asthma that were stabilized on 100 μg fluticasone inhaled twice daily over a 4- to 6-week run-in period (18). The subjects were divided into three treatment groups: (1) continued fluticasone, 100 μg inhaled twice daily (F); (2) fluticasone, 100 μg plus salmeterol, 50 μg inhaled once daily (F + S); and (3) montelukast, 10 mg orally once daily (M). All participants recorded daily PEF using a home PEF meter. The primary outcome was time to treatment failure, defined by a drop in PEF greater than 35% from baseline for 2 or more days, a drop in prebronchodilator FEV₁ greater than 20%, an increase in use of short-acting β-agonists (SABA) by 10 inhalations per day for 2 or more days, the need for oral corticosteroids, an unscheduled health care visit for asthma, or refusal of the participant or their physician to continue in the trial. Further details of the clinical trial can be found in the published manuscript (18). We chose to analyze the data from this study because it provided the unique opportunity to examine whether baseline data from the run-in period would be associated with treatment failure during the subsequent treatment phase, and whether α was affected differently by different controller therapies. Previous work with DFA in asthma has only been conducted in the setting of SABA and long-acting β-agonist (LABA) therapy.

Data Analysis

We followed the method of DFA as first described by Peng and coworkers (19) (see online supplement). We determined α for each subject during the run-in phase and the treatment phase. We also calculated the coefficients of variation of PEF corresponding to these same time periods. Finally, in those subjects who experienced treatment failure, we compared the change in α during the period preceding the day of treatment failure with the change in α during the period following the day of treatment failure by calculating the slope of change of α during each time period.

Statistical Analysis

Data from the current study were expressed as median (interquartile range), with comparisons made within groups using the Wilcoxon signed rank test and between groups using the Wilcoxon rank sum test. All analyses were performed with Matlab R2012A (MathWorks, Inc., Natick, MA), Visual Basic 6.0 (Microsoft, Inc., Redmond, WA), and JMP Pro 10.0 (SAS Institute Inc., Cary, NC), and two-sided P values less than 0.5 were considered statistically significant.

Results

The baseline features of the subjects at enrollment are listed in Table 1. The subjects were mostly young patients with asthma who, by definition, had suboptimal control of asthma (asthma control questionnaire >1.5), but who had normal baseline lung function with airway hyperresponsiveness in the mild-to-moderate range. Despite excellent adherence to therapy (>90% in all groups), more patients in the M group had treatment failure as compared with those in fluticasone F or F + S groups, with the hazard ratio for treatment failure for M group versus F group and M group versus F + S group being statistically significant (P = 0.03) (18).

Table 1.

Demographics, Baseline Features, and Treatment Failure Rates by Treatment Group

Characteristic	Fluticasone (n = 167)	Fluticasone + Salmeterol (n = 161)	Montelukast (n = 165)
Age, yr	29 ± 15	31 ± 15	32 ± 15
Male, %	39	38	43
FEV1, % predicted	86 ± 13	86 ± 16	86 ± 13
PEF, % predicted	91 ± 18	90 ± 19	93 ± 18
PC20, mg/dl	3.0 ± 2.6	1.8 ± 2.7	2.6 ± 2.1
ACQ (1–6)	1.6 ± 0.8	1.8 ± 0.8	1.6 ± 0.9
Treatment failure, %	20.2	20.4	30.3*

Definition of abbreviations: ACQ = asthma control questionnaire; PC₂₀ = provocative concentration causing a 20% fall in FEV₁; PEF = peak expiratory flow.

^*Hazard ratio, 1.6 (P = 0.03) for treatment failure in montelukast group versus fluticasone or fluticasone + almeterol group.

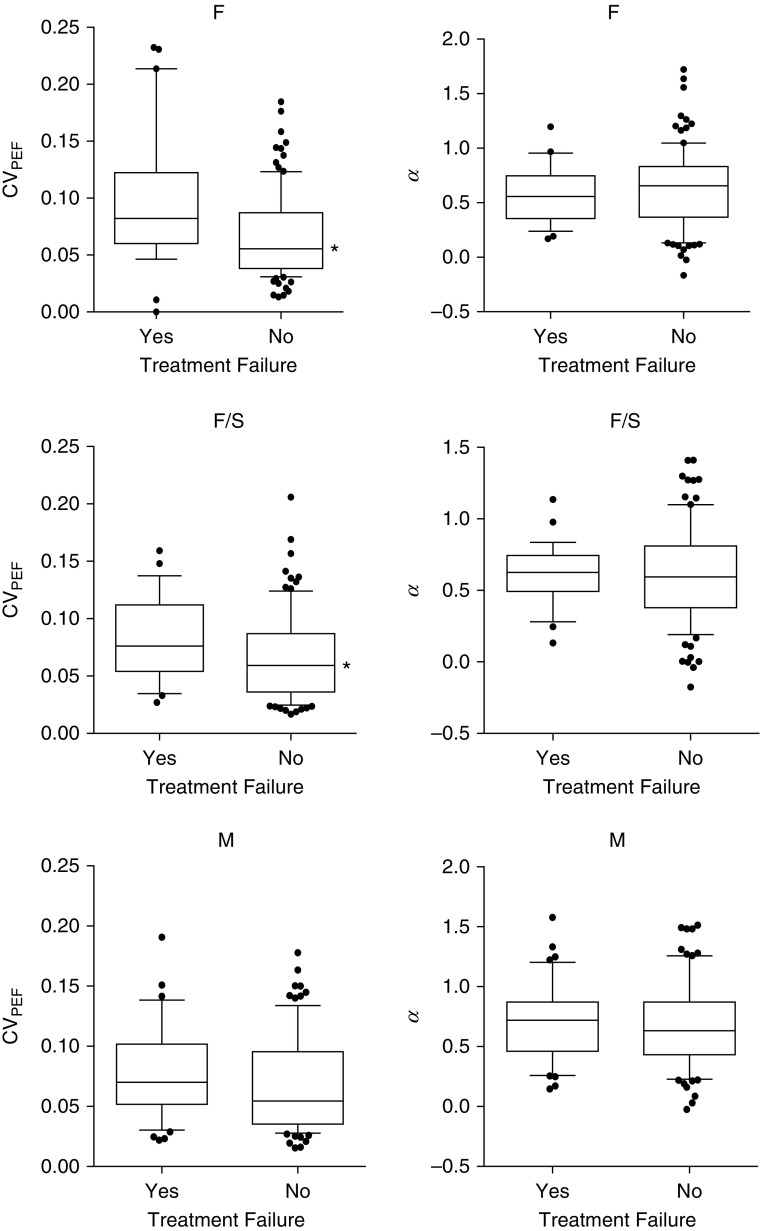
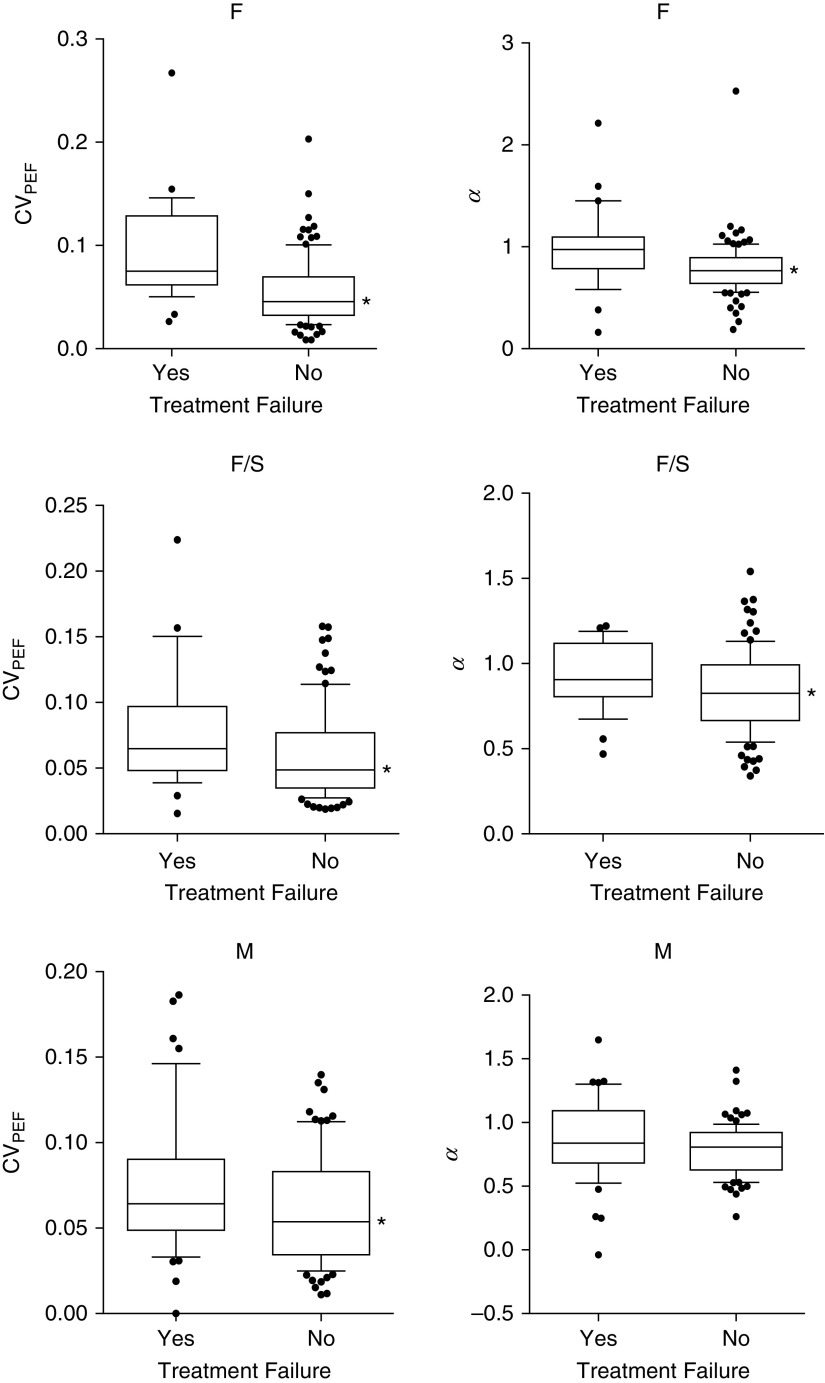
The differences in coefficient of variation of PEF (CVpef) and α between the run-in phase and the treatment phase for each group are shown in Figure 1. In the F and F + S groups, CVpef declined and α increased going from the run-in phase to the treatment phase. In the M group, only α changed significantly, with an increase during the treatment. The differences in CVpef and α during the run-in phase between those with and without treatment failure for each group are shown in Table 3. During the run-in phase, those participants in the F and F + S groups who had subsequent treatment failure had a higher CVpef compared with those without treatment failure, but there was no difference in α between those with and without treatment failure. No differences in CVpef or α, were seen between those with and without treatment failure among participants in the M group. During the treatment phase, treatment failure among those in the F and F + S groups was associated with a higher CVpef and α (Figure 2), but this was true only for a higher CVpef among those in the M group, because α did not differ between those with and without treatment failure.

Figure 1.

Differences in coefficient of variation of peak expiratory flow (CVpef) and α based on treatment failure during the run-in phase. Data shown are for the fluticasone group (F), fluticasone/salmeterol group (F/S), and montelukast group (M). Box-and-whisker plots represent median (central horizontal line), 25–75th percentiles (box), and 10–90th percentiles (whiskers). Significant differences were seen in the CVpef in the F and F/S groups as shown by the asterisk (P < 0.05). The difference in CVpef in the M group was nearly significant (P = 0.06). There were no differences in α between treatment failure or no treatment failure in any of the three groups.

Figure 2.

Differences in coefficient of variation of peak expiratory flow (CVpef) and α based on treatment failure during the treatment phase. Data shown are for the fluticasone group (F), fluticasone/salmeterol group (F/S), and montelukast group (M). Box-and-whisker plots represent median (central horizontal line), 25–75th percentiles (box), and 10–90th percentiles (whiskers). Significant differences were seen in the CVpef in all three groups as shown by the asterisk (P < 0.05). Differences in α were only seen in the F and F/S groups.

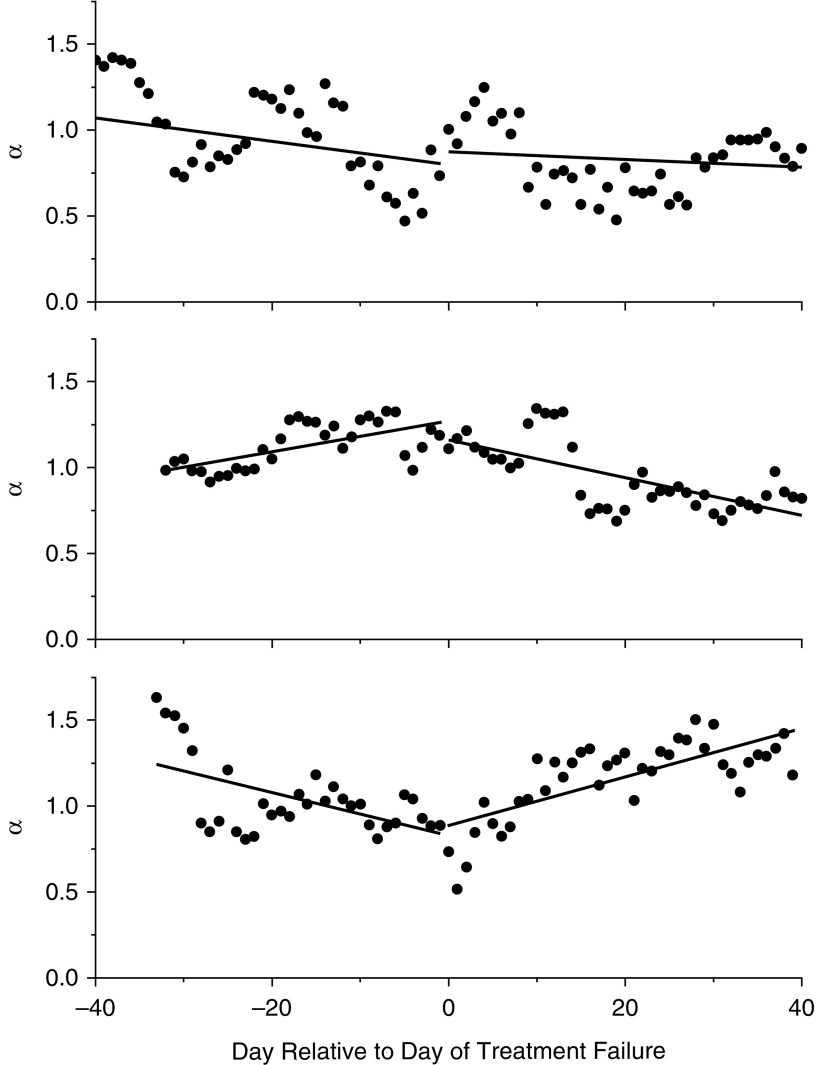
When analyzed among those with treatment failure who had sufficient data (n = 26), we noticed three patterns of change in α over time when examining α during 40-day windows of time before the day of treatment failure compared with the period of time following the day of treatment failure. The slope increased, decreased, or stayed the same in different individuals (Figure 3), and although the sample size was small, the general patterns of change did not differ between therapeutic groups (P = 0.78). Similarly, the median slope of α versus time did not differ statistically between the periods before and after the treatment failure day across individuals (slope before = 0.0046 vs. slope after = 0.0028; P = 0.71).

Figure 3.

Representative plots of α versus day relative to day of exacerbation from three different participants with treatment failure. α was calculated from 40-day window lengths that slid forward and backward from the day of exacerbation by one day at a time. Slopes of α were calculated based on linear regression of the data before and after the day of treatment failure. Three general patterns were observed: (1) no significant change in slope (top); (2) α increasing, then decreasing (middle); and (3) α decreasing, then increasing (bottom).

Discussion

A key finding of our study is that treatment failure in asthma is associated with persistently increased variability of lung function, the increased variability being reflected in an increased CVpef and its persistence in an increased α. This is consistent with previous work (4–6), and presumably reflects that persistence of excessively labile lung function is more likely to lead to loss of disease control. Of note, it was a difference in CVpef and not α during the run-in phase that was associated with treatment failure among participants in the F and F + S groups, whereas there was no difference in CVpef or α during the run-in phase among those with treatment failure in the M group. However, differences in both the CVpef and α were associated with treatment failure during the treatment phase among those in the F and F + S groups, but only differences in CVpef were seen in the M group. Thus, different controller therapies had different influences on CVpef and α. Finally, there were variable patterns of change in α leading up to treatment failure in all groups, with some participants having an increase, some a decrease, and some no change in self-similarity of lung function at the point of treatment failure.

We believe these results support the concept of treatment failure being associated with a higher self-similarity (α) of more variable lung function (CVpef). Our data suggest that both factors played a role in patients on F and F + S, but the variability in lung function (CVpef) was the more important factor in those on M. Overall, these findings concur with the notion that the way in which lung function varies over time may be predictive of a future catastrophic event (15). This idea was first articulated by Que and colleagues (12), who described the temporal self-similarity of lung function and suggested that increased variability in lung function could increase the probability of otherwise rare, potentially fatal, loss of lung function. The genesis of this self-similarly remains unclear, but some have suggested that it stems from the fractal geometry of the airway tree itself (5, 12, 20).

Our results support the growing appreciation that analysis of temporal fluctuations in lung function can provide important clinical insights. This complements several prior studies, most of which (2, 10–13), although not all (21), show associations between variability of lung function and measures of asthma severity or control. Several approaches to assessing temporal variability have been used by various investigators, such as approximate entropy (3) and the conventional variance and SD. We chose to assess the strength of long-range correlations in our data using DFA because this method has become widely accepted for analyzing fluctuations in biologic time series, such as those associated with heart rate variability and neuronal oscillations (22). In particular, DFA is suitable for application to time series having power spectra that conform to power-law functions of frequency, where the exponent of the power law is related to the DFA scaling coefficient α. DFA is thus closely related to other measures of temporal structure, such as the autocorrelation function and the Hurst coefficient (23). As such, DFA does not provide new information above that offered by these other measures. However, DFA is thought to be better suited to cope with physiologic data in which statistical properties, such as mean and variance, can change constantly over time (19). The coefficient α provided by DFA has been extensively investigated in various biomedical contexts and thus provides a well-characterized and accepted metric for quantifying memory in dynamic biologic processes.

The method of DFA was first applied to asthma by Frey and colleagues (14), who analyzed PEF time series from subjects with asthma and showed that treatment with SABA reduced α compared with placebo, whereas treatment with LABA increased α compared with placebo. These data were then applied to a model of conditional probability of risk of airway obstruction, and the resulting risk was shown to be increased by use of SABA and decreased by use of LABA, demonstrating how SABA and LABA have effects on lung function that differ in their implications for future adverse events. Importantly, this difference is apparent from an analysis of lung function variability but not of absolute value. Studying the same data set, Thamrin and colleagues (6) showed that a higher baseline α value was associated with better clinical responses with LABA, but not SABA. Both studies (6, 14) also suggested that there may be an optimum range for α either side of which is deleterious to asthma status. This echoes the idea proposed by Macklem (24, 25) that respiratory health is best served by an appropriate balance between randomness and order. This may be seen in the use of heart rate variability as an index of cardiac health (26). It is also consistent with the proposition that a lower α may reflect higher airway lability or instability, but a higher α could translate to persistence of low lung function, or rigidity or inability to adapt to perturbation.

Previous findings support this concept of balance between low versus high α. Thamrin and colleagues (4) studied the relationship between α and asthma control and exacerbations in two distinct populations: subjects with mild-to-moderate and severe uncontrolled asthma. In both populations, higher α and PEF were associated with better asthma control, up to a point. However, in the subjects with mild-to-moderate asthma, α was significantly higher in patients who had an exacerbation versus those who had not (4), similar to our findings. Furthermore, in the population with severe asthma, only PEF distinguished those with and without an exacerbation (4). Thamrin and colleagues (4, 6) suggested that the presence of low PEF dictates the patient’s asthma severity, regardless of α, whereas a high α coupled with low PEF indicates persistence of low lung function and relates to asthma control. These findings imply different but complementary roles for PEF and α as biomarkers of future asthma control (4, 7, 16). Thus one can envision scenarios of good control associated with high PEF and high α (persistence of good lung function), and poor control associated with low PEF and high α (persistence of poor lung function), with high or low PEF in the setting of low α having variable control. As discussed subsequently, the data associated with the higher treatment failure in the M group (Figure 2) suggest the novel finding that M might have led to wider swings in lung function and more clinical instability, as reflected by the failure of α to increase in patients with treatment failure who had a high CVpef.

Thamrin and colleagues (8) have further demonstrated that the individual conditional probability for poor control can be calculated from an algorithm incorporating information from both PEF and α. Because our data only involved the analysis of one treatment failure event per patient, and did not incorporate data from past events, such an approach would not be possible on an individual level.

The current study design was unique in that it allowed us to examine whether there were any differences in these parameters between continuation of run-in therapy (F) and changes in controller therapy (F + S and M). In the F group a higher CVpef during the run-in and treatment phases was significantly associated with treatment failure, but α was significantly associated with treatment failure only during the treatment phase. The same was true of the F + S group. No differences in any of these parameters from the run-in phase were associated with treatment failure in the M group, but a higher CVpef from the treatment phase was associated with treatment failure. How do these findings then relate to the primary outcome of the LOCCS trial, which demonstrated that the F and F + S groups maintained similar and lower rates of treatment failure than the M group?

The data demonstrate similar changes in parameters in the F and F + S groups, which differed from the changes in parameters in the M group. We speculate that the different changes in CVpef and α in the F and F + S groups versus the M group might be related to the different primary outcomes in these groups. Our findings suggest that even though a higher CVpef and higher α were associated with treatment failure (as in the F and F + S group), it may be worse to have only a higher CVpef without a higher α (as in the M group), because the overall treatment failure rate was higher in the M group. Looking again at the run-in versus treatment phase data (Table 2), we note that treatment with F and F + S resulted in a decrease in CVpef and increase in α, but participants who subsequently had treatment failure had a higher CVpef and higher α. Treatment with M resulted in an increase in α and no change in CVpef, but participants who subsequently had treatment failure had a higher CVpef only (Figure 2). Perhaps the overall higher rate of treatment failure in the M versus F or F + S groups is related to the lack of further increase in α in the M group, suggesting that this increase is somehow beneficial. We speculate that treatment failure may be associated with not only increased self-similarity (higher α) of more variable lung function (higher CVpef), as was seen for F and F + S, but also increased variability in lung function without increased self-similarity, as was seen in the M group, which could lead to wider swings in PEF with greater instability.

Table 2.

Changes in CVpef and α by Treatment Group from the Run-In Phase to the Treatment Phase

Treatment Group	Run-in Phase	Treatment Phase	P Value*
Fluticasone	n = 132	n = 132
CVpef	0.06 (0.04–0.09)	0.05 (0.04–0.07)	<0.01
α	0.62 (0.37–0.83)	0.81 (0.66–0.94)	<0.01
Fluticasone + salmeterol	n = 124	n = 124
CVpef	0.06 (0.04–0.09)	0.05 (0.04–0.08)	0.05
α	0.60 (0.39–0.77)	0.84 (0.70–1.01)	<0.01
Montelukast	n = 132	n = 132
CVpef	0.06 (0.04–0.09)	0.06 (0.04–0.09)	0.72
α	0.63 (0.44–0.85)	0.83 (0.66–0.94)	<0.01

Definition of abbreviation: CVpef = coefficient of variation of peak expiratory flow.

Data are given as median (interquartile range).

^*P value based on Wilcoxon signed rank test.

Our study also allowed us to examine how α changed over time leading up to treatment failure. We found that patients with treatment failure had variable patterns of change, with an increase, decrease, or no change in α before treatment failure compared with α after treatment failure, indicating that the relative influences of variability and self-similarity of lung function have different strengths in different individuals. As previously speculated (6, 14), there may be an optimum value of α near 1, and perhaps patients about to have treatment failure tend to stray away from α = 1 (either rising or falling) before their exacerbation. Our findings suggest that the more consistent change in CVpef associated with treatment failure (Figure 2) may make this a more useful indicator than α. However, we believe α is still important because it seems to be the key factor that differentiated the worse clinical response to M than to F or F + S. Given the higher variability of α during the shorter run-in phase, we suggest that that the CVpef may be more reliably obtained during short periods of time and have clinical significance related to prediction of treatment failure, such has been shown in response to withdrawal of inhaled corticosteroid therapy (7).

These conclusions and speculations must be viewed in the context of the limitations of the present study. This was an observational, retrospective cohort study only, and as with all such studies, our findings apply to the particular group of subjects with asthma we studied and were not informed by the application of interventions designed to test a specific hypothesis. However, the sample size was large, involved multiple clinical centers and diverse patients, and involved commonly used controller medications. Another potential limitation is that the robustness of DFA is directly related to the length and completeness of the time series being analyzed, and our once-daily PEF data sets were modest in length with a range of 24–60 data points during the run-in phase, and 24–153 data points during the treatment phase, compared with 300 points in previous studies (4–6). Thamrin and colleagues (6) conducted a sensitivity analysis to examine the effects of reducing the data length and percentage of missing data and found that decreasing the number of data points from 300 to 100 reduced the significance of the relationship between α and symptoms but increased the significance between % predicted PEF and symptoms.

These findings may explain why we were only able to detect a significant relationship between CVpef, but not α, and treatment failure (in the F and F + S groups) during the run- in phase of limited data length, but such a relationship was detected during the treatment phase of greater data length. We also conducted a sensitivity analysis to missing data, and found that the data were robust to missing up to two consecutive data points (see online supplement), which was the rule we used to select data sets. Another issue is that the definition of treatment failure included changes in the same quantity that generated our time-series, namely PEF. This runs the risk of biasing the association between treatment failure and the variability indices α and CVpef. Mitigating against this is the fact that only 11% of the subjects with treatment failure in our study had a drop in PEF (18), but a definition of failure based on an independent measurement might have been preferable.

In conclusion, we have shown that long-term memory and variability in PEF data from the LOCCS trial are associated with treatment failure, although the changes seen varied with type of controller therapy. With F and F + S, treatment failure was associated with a higher CVpef and α, whereas with M it was associated with a higher CVpef only. Thus, different controller therapies may have different effects on the variability and stability of lung function changes over time. The pattern of change in α before treatment failure was highly variable and did not differ between treatment groups, which may reflect the onset of the chaotic oscillations in lung function that would be expected to accompany loss of control and treatment failure. These findings add to the growing body of evidence that variability in lung function is important in understanding treatment failure. In addition, understanding disease mechanisms on the basis of lung function fluctuation analysis may allow for the earlier detection of therapeutic benefit in therapeutic trials, shortening the length and reducing the cost of bringing new treatments to practice (27). The tools for assessing lung function variability are readily accessible and straightforward to use, so we anticipate they will play an increasing role in the diagnosis, prognosis, and treatment of asthma.