The Aggregation Free Energy Landscapes of Polyglutamine Repeats

Abstract

Aggregates of proteins containing polyglutamine (polyQ) repeats are strongly associated with several neurodegenerative diseases. The length of the repeats correlates with the severity of the disease. Previous studies have shown that pure polyQ peptides aggregate by nucleated growth polymerization and that the size of the critical nucleus (n*) decreases from tetrameric to dimeric and monomeric as length increases from Q₁₈ to Q₂₆. Why the critical nucleus size changes with repeat-length has been unclear. Using the associative memory, water-mediated, structure and energy model, we construct the aggregation free energy landscapes for polyQ peptides of different repeat-lengths. These studies show that the monomer of the shorter repeat-length (Q₂₀) prefers an extended conformation and that its aggregation indeed has a trimeric nucleus (n* ∼ 3), while a longer repeat-length monomer (Q₃₀) prefers a β-hairpin conformation which then aggregates in a downhill fashion at 0.1 mM. For an intermediate length peptide (Q₂₆), there is an equal preference for hairpin and extended forms in the monomer which leads to a mixed inhomogeneous nucleation mechanism for fibrils. The predicted changes of monomeric structure and nucleation mechanism are confirmed by studying the aggregation free energy profile for a polyglutamine repeat with site-specific PG mutations that favor the hairpin form, giving results in harmony with experiments on this system.

Graphical abstract

1. INTRODUCTION

The origin of at least eight neurodegenerative diseases can be genetically traced to the presence of proteins having long repeats of polyglutamine (polyQ).¹ The severity of these diseases typically depends on the polyQ repeat-length. One of these afflictions, Huntington’s disease (HD) arises only in patients having proteins with 36 repeats or more; and individuals with genes coding for longer repeats acquire symptoms earlier.² It has been established that the rate of aggregation increases with the repeat-length both in vivo and in vitro.³

While glutamine is amphiphilic, the aggregates of polyQ appear to be amyloids having the β-strand as their basic unit.^4–8 Why such amphiphilic sequences that do not conform to the usual hydrophobic patterns of most amyloidogenic fragments should aggregate has been mysterious.⁹ Primary nucleation has been considered to be the rate-limiting step in polyQ aggregation.^10,11 Experiments on pure polyQ repeat peptides show that the critical nucleus size decreases from n* = 4 to 1 as the repeat-length grows from Q₁₈ to Q₂₆.³ Simulations of protein aggregation remain challenging even with coarse-grained models,¹² as most of the coarse-grained models suffer from the question of realism to fold globular proteins even when they are adequate to capture many interesting polymer physics aspects of aggregation. To address the origin of this biophysically striking length dependence of aggregation, in this paper, we explore the free energy landscapes for aggregation of oligomers of polyQ sequences having different repeat-lengths using the coarse-grained associative memory, water-mediated, structure and energy model (AWSEM) force field. The AWSEM force field, while being efficient to simulate, also has been shown to predict the structures of protein monomers^13,14 as well as details of their assembly.^15–17 We have previously used the force field to study the free energy landscape of a mechanical prion, also rich in glutamine, that is involved in memory.¹⁷ We find that while the simple polyQ peptides longer than 30 residues prefer a hairpin structure in the monomer, for shorter lengths an extended structure is favored. The critical nucleus size inferred from the simulated aggregation free energy landscapes for the different length peptides agrees well with the laboratory results. At the laboratory concentration of peptide, the free energy profile for Q₂₀ shows a nucleation barrier near the trimer, while the Q₃₀ peptide aggregates in a downhill fashion at the same concentration. For a polyQ peptide of intermediate length (Q₂₆), inhomogeneous nuclei for aggregation are observed. These nuclei lead to branched structures rather than simple one-dimensional (1D) fibers. The simulations suggest that the mixed, inhomogeneous character of the nucleation species for the intermediate length peptide is the cause of this “branching” behavior. These results suggest a way in which fiber growth may be controlled with point mutations in peptide sequence.

2. METHODS

2.1. The Abbreviated AWSEM Force Field

A detailed description of the AWSEM force field has already been given in Davtyan et al.¹³ Briefly, AWSEM is a predictive coarse-grained protein folding force field that employs three sites per amino acid whose parameters are learned from structural data using an algorithm based on energy landscape theory.¹⁸ The AWSEM Hamiltonian summarized in eq 3 consists of a backbone term V_backbone, a many body burial term V_burial, a contact term V_contact, and a hydrogen-bonding term V_HB.

The amino acid residues in the AWSEM force field are all encoded to adopt the L-configuration through the chirality term, V_χ, inside the backbone term. The chirality term, given in the following equation, ensures the orientation of the C_β atom relative to the plane formed by the C′, C_α, and N atoms. The value χ₀ = −0.83 ų corresponds to the L-type amino acid.¹³

$$V_{\chi }={\lambda }_{\chi }{\displaystyle \sum _{i=2}^{N-1}{\left({\chi }_i-{\chi }_0\right)}^2}$$ (1)

$${\chi }_i=\left(r_{C_i^{\text{'}}{C}_{\alpha i}}\times r_{C_{\alpha i}{N}_i}\right)\cdot r_{C_{\alpha i}{C}_{\beta i}}$$ (2)

The hydrogen-bonding term, V_HB, is associated with the secondary structural weight in AWSEM which encodes a bias for the α-helix conformation and another bias for β-strand hydrogen-bond formation. While the strength for these terms for normal globular proteins is based on secondary structural prediction, for intrinsically disordered proteins like polyQ, secondary structure prediction may not be adequate. We have tuned the strength in our previous paper on the CPEB protein to study the aggregation of Q-rich proteins.¹⁷ In that analysis, we determined the stability of secondary structures with different secondary structural bias weights and compared the stability from the AWSEM simulations with the statistics from separate all-atom simulations. A set of secondary structural bias weights was then chosen so that the relative stability of different structures is similar for both the all-atom simulations and the AWSEM simulations. Details may be found in the SI of ref¹⁷. We use the same weights here.¹⁷

Additional local-in-sequence interactions governed by the fragment associative memory term, V_FM, are ordinarily determined by bioinformatic sequence matching.¹³ These interactions are normally useful for structural prediction. These are not included in the force field used in the present study, because very few local sequences of polyQ have been structurally characterized in the Protein Data Bank.¹⁴ Such sequences are usually classified as being “intrinsically disordered”. We therefore call the present version of the force field, abbreviated AWSEM.

$$V_{\text{total}}=V_{\text{backbone}}+V_{\text{contact}}+V_{\text{burial}}+V_{\text{HB}}$$ (3)

The full AWSEM force field has already been used with much success in predicting globular protein structures for both monomers and dimers. It has also been used to study the initial stages of misfolding and aggregation.^15,16 We have previously used the abbreviated AWSEM force field to explore the aggregation of another Q-rich peptide CPEB, which has been postulated to be a mechanical prion involved in memory.¹⁷

2.2. Order Parameters for Umbrella Sampling and Free Energy Calculations

To survey the energy landscape in a quantitative way, it is useful to employ a variety of collective order parameters to classify structural ensembles. The structural similarity of two different protein configurations is generally characterized by a local order parameter, Q^αβ, which is given by the equation:

$$Q^{\alpha \beta }=\frac{2}{\left(N-2\right)\left(N-3\right)}{\displaystyle \sum _{j>i+2}\exp [-{\left(r_{ij}^{\alpha }-r_{ij}^{\beta }\right)}^2/2{\delta }_{ij}^2)]}$$ (4)

where N is the total number of residues. When a folded structure is known (or postulated), it is useful to choose one of the structures in the comparison to be the (assumed) native structure. We then call Q^αβ simply Q.

We have used umbrella sampling to enhance the sampling of conformations for free energy calculations. A harmonic potential in Q with respect to a final fibril structure found in our simulated annealing runs is used to restrain constant temperature molecular dynamics simulations to give configurations within a range of reference values:

$$V_{Q-\text{bias}}=\frac{1}{2}{k}_{Q-\text{bias}}{\left(Q-Q_0\right)}^2$$ (5)

with k_Q−bias = 200 kcal/mol. The reference values for Q₀ are chosen to be equally spaced from 0 to 0.98 with a step size 0.02. Data from different windows are stitched together using the weighted histogram analysis method (WHAM) to construct full free energy landscapes.

2.3. Simulation Details

All simulations were performed using the software of the large-scale atomic/molecular massively parallel simulator (LAMMPS). The AWSEM force field is now available in this open source format.¹³ All the umbrella sampling simulations for multiple peptide chains are performed in a cubic box (500 A × 500 A × 500 A) with periodic boundary condition for 20 million steps at 370 K. The initial configurations of the umbrella sampling for oligomer simulations are six monomers randomly distributed over the cubic box to give a nominal concentration of 0.1 mM. The peptides are started in extended conformations. In fact monomer configurations equilibrate rapidly. Because of this, the details of these initial conformations are erased by thermal motions long before aggregation begins. Free energy profiles are calculated and extrapolated to the physiological temperature (300 K) using the weighted histogram analysis method (WHAM). We run the umbrella sampling at a higher temperature where oligomers readily form and disassociate. Simulation at 370 K enhances considerably the sampling efficiency. The extrapolation to physiological temperature is indeed rather short and should not affect the results very much.

2.4. Correction for the Concentration of Free Monomers

During simulations, as aggregates form, the concentration of free monomers changes because of the small size of the simulation box. This change must be accounted for in order to relate simulations to macroscopic experiments that are carried out at essentially fixed laboratory concentrations and chemical potentials. We describe in this section how to carry out the corrections for this effect. Additional details on the strategy may be found in our earlier paper on amyloid-β aggregation.¹⁹

Suppose that a system has a total of N monomers in a volume V at temperature T and that some of these n monomers aggregate to form oligomers. If only one oligomer of size n is formed, then there are the N − n free monomers remaining in solution once the single oligomer has formed. The probability that there is at least one n-oligomer in the system according to Reiss and Bowles’s approach²⁰ is given by

$$P_n=\frac{Q_n\left(N,V,T\right)}{Q\left(N,V,T\right)}=\frac{Q\left(N-n,V,T\right)q_n\left(V,T\right)}{Q\left(N,V,T\right)}=q_n\left(V,T\right){\mathrm{e}}^{n\mu /k_{\mathrm{B}}T}$$ (6)

where Q_n(N, V, T) denotes the partition function of the system constrained to contain at least one n-oligomer and that Q(N, V, T) represents the total unconstrained partition function; q_n(V, T) is the partition function of the oligomer in which the interaction with the remaining N − n monomers is included; Q(N − n, V, T) is the partition function for the decoupled remaining N − n monomers; and μ is the chemical potential of a monomer. In the derivation leading to eq 6, the following equation is used:

$$Q_n\left(N,V,T\right)=Q\left(N-n,V,T\right)q_n\left(V,T\right)$$ (7)

which provides an analytical scheme so as to decouple the configuration integral for the n-oligomer (q_n(V, T)) from the remaining N − n monomers, denoted by Q(N − n, V, T). The potential energy includes three components: (1) the interactions within the n-oligomer; (2) the interactions between the n-oligomer and the remaining N − n monomers; and (3) the interactions within the remaining N − n monomers. Note that the internal structural details are irrelevant to the theoretical development of the correction factors. This theoretical approach is basically the same as that employed in the physical cluster approach to the nucleation of liquids from gases.²¹

Now, given the fact that in our simulations a large n-oligomer is rare in the small simulation box, P_n is roughly same as the probability that there is exactly one n-oligomer in the system. It follows that

$$F_n=-k_{\mathrm{B}}T\ln P_n=-k_{\mathrm{B}}T\ln q_n-n_{\mu }$$ (8)

This result is used to compute the thermodynamic potential for the grand canonical ensemble F_n − nμ. The gradients of this potential determine the growth or dissociation of clusters of size n in a system of fixed chemical potential μ.

When we get the free energy for the grand canonical ensemble F_n − nμ at concentration C₀, we can extrapolate the free energy to a different concentration C₁ by using eq 9:

$$F_n\left(C_1\right)=F_n-n{\mu }_1=F_n\left(C_0\right)-n\left({\mu }_1-{\mu }_0\right)=F_n\left(C_0\right)-\mathit{nkT}\ln \frac{C_1}{C_0}$$ (9)

where μ₁ and μ₀ are the chemical potentials of the free monomers at concentration C₁ and C₀, respectively.

3. RESULTS

3.1. The Structural Preference of Monomeric PolyQ for Being an Extended β-Strand versus Being a β-Hairpin Depends on Length

In solution monomeric polyQ peptides have been investigated both experimentally and computationally by many groups leading to their being classified as “intrinsically disordered”.^22–25 Circular dichroism (CD) suggests that polyQ peptides are largely disordered and gives little hint of there being any difference between the short polyQ sequences and longer ones.^23,26–28 The CD analysis suggests that Q₄₀ has about 10% α-helix content and only a trace amount of β-sheet and β-turn.²⁹ The solved crystal structure of the Huntingtin exon1 Htt17Q-EX1 fused with maltose binding protein, the exon itself consisting of an amino-terminal α-helix, poly17Q, and a polyproline 3−10 helix, suggests that the polyQ region itself adopts multiple conformations, including α-helix, random coil, and extended loop.²⁴

Finding the structure of the aggregated form long has been a challenge. Perutz first proposed the repeats could form a β-helix, whose helical repeat would offer an explanation for how length could affect the age-of-onset.³⁰ More recent X-ray analyses, ss-NMR data, and mutational studies, however, argue against this structural picture and instead favor a standard β-strand model for the aggregate.^4–8 The stabilities of different structures of polyQ have also been addressed computationally using all-atom simulations. These suggest the β-hairpin model is the most stable form for Q₄₀.³¹

We study primarily in this paper the pure polyglutamine repeat peptides, Q₂₀, Q₂₄, Q₂₆, Q₃₀, and Q₄₀, using the abbreviated AWSEM force field. For each monomer, we compute 1D free energy profiles using umbrella sampling with respect to an order parameter that measures generic hairpin formation: the number of contacts formed by each residue. The hairpin structure (having an average number of contacts per unit length around 0.45) dominates thermodynamically over the extended structure (with an average number of contacts per unit length around 0) for monomeric Q₃₀ and Q₄₀. But in Q₂₀, the extended structure is favored(Figure 1). For Q₂₄ and Q₂₆, the two classes of conformations are equally favorable. For the longest peptide that we studied, polyQ (Q₅₀), the most favorable state turns out to be a three-strand β hairpin structure (see Figure S1). Hairpin states form much more easily in longer repeats. Consistent with the proposed idea that the hairpin is the building block for the fiber form, we see the trend of monomer structure alone suggests an explanation for the length dependence of polyQ aggregation. We wish to remind the reader that for all lengths of peptide, the thermal ensemble is rather broad, as evidenced by the modest free energy barriers seen in Figure 1. Nevertheless the aggregation mechanism can be understood using the structural preferences described by these two configurational classes.

Figure 1.

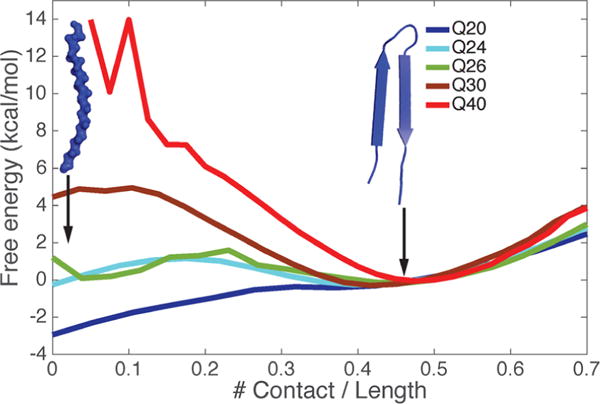
Free energy profiles for monomers of different lengths reveal their different structural preferences between extended β-strand and β-hairpin. Results for polyQ peptides of different lengths are color-coded.

3.2. The Calculated Critical Nucleus Size (n*) for Q₂₀ is 3–4

The rate of aggregation depends on concentration. The grand canonical potential for following the aggregation process is F_n − nμ, where μ is the chemical potential set by the monomer concentration. At very low concentration, F_n − nμ monotonically increases with n favoring the monomer, but when the solution is supersaturated, F_n − nμ eventually decreases with n favoring a large aggregate. In between, there may be a nucleation barrier at a finite number of monomers aggregated into a unit. If n, the aggregate size, is a sufficiently good reaction coordinate, then the peak in F_n − nμ indicates the size of the critical nucleus, which in turn determines the concentration dependence of the aggregation rate near that chemical potential. If the critical nucleus size is n*, the nucleation rate will vary as C^n*, where C is the concentration.

Experiments show that the critical nucleus size (n*) of polyQ is length dependent. To compute the free energy profile at a fixed laboratory concentration and a physiological temperature, we first compute the aggregation free energy for the entire simulation box as a function of the total number of inter-residue contacts in a system containing six Q₂₀ monomers (nominal concentration ∼0.1 mM) at 300 K. As shown in the 1D free energy plot at this nominal concentration, the free energy of formation of an oligomer is uphill until four units are assembled, while it is downhill afterward. We visualized structures in each of the contact number basins. As shown in Figure 2A, each basin corresponds with a different size oligomer. This free energy profile versus contact number suggests that the critical nucleus size is around 4 at the nominal simulation concentration (Figure 2A). The formation of larger oligomers of Q₂₀ is not favored in the simulation with fixed box size and total monomer count. The aggregation process is energetically favored (Figure 2B), since the potential energy decreases monotonically as the oligomer grows, but the entropy cost of adding monomers to the large cluster is too large once the monomers in the simulation box are depleted.

Figure 2.

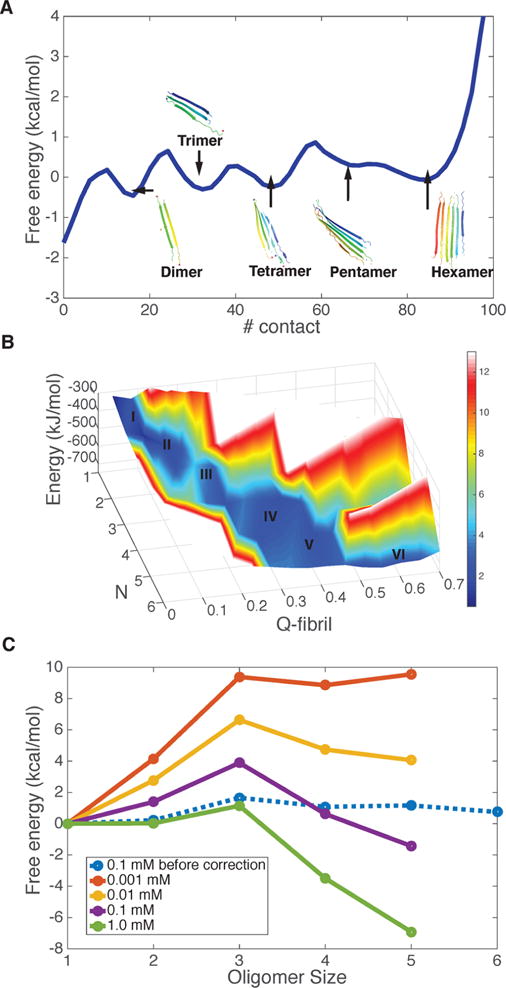
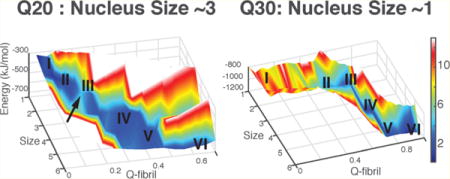
Aggregation free energy landscape for Q₂₀ at 300 K. (A) The free energy profile as a function of the number of total residue–residue contacts in the simulation system with six Q₂₀ peptide chains. Representative structures of different oligomers are shown in each free energy basin of the progress in different oligomeric states. (B) The energy and free energy surfaces for aggregation of Q₂₀ are plotted as a function of the oligomer size (N), along with its structure similarity compared to the final fiber form (Q_fibril). The z-axis is the energy of the system, which decreases monotonically as the oligomer size increases. The color indicates the free energy. The local basins for different oligomer states are labeled by size. A free energy barrier occurs around N = 3. (C) The grand canonical free energy for different oligomer states as corrected for concentration changes shows the saturation value of the concentration of free monomers.

To exactly compute the critical nucleus size at a fixed laboratory concentration and the physiological temperature, we must calculate the free energy as a function of the size of the oligomer (color red in Figure 2C) but keep the concentration for free monomers fixed. In the simulations with a finite box, however, the monomers are depleted as the large cluster grows, an effect that is negligible in the laboratory. Fortunately a correction for this effect can be carried out using the Reiss physical cluster approach as described in the Methods section. After the correction for the change in concentration of free monomers, the grand canonical free energy profile, F_n − nμ, shows a peak at size 3 for the laboratory concentration of 0.1 mM, suggesting that the critical nucleus size measured under these conditions should be 3 (Figure 2C). Experiments for Q₂₀ at the same concentration give a somewhat larger nucleus n ∼4. When we extrapolate the concentration to 1 μM, the aggregation free energy profile is uphill; while the profile becomes downhill asymptotically at a strong supersaturation (1 mM). The critical saturation concentration (c*) is therefore predicted to be between 10–100 μM. This prediction compares well with experiments that show that a polyglutamine repeat of a similar length of 23 does not aggregate at 52 μM, but that aggregation proceeds slowly at the concentration of 103 μM³ at the physiological temperature.

The structures of the pentamers and hexamers found in our simulation resemble the models proposed by Schneider et al.⁵ These structures suggest the fiber form will be composed simply of layers of extended β-strands when the repeat-length is short.

3.3. The Calculated Critical Nucleus Size (n*) for Q₃₀ Is 1

The simulations suggest the extended structure is the preferred form of the monomer for Q₂₀, and the critical nucleus size for aggregation is ∼3–4. We now examine the aggregation for Q₃₀ whose monomers show a preference for the hairpin structure. Again we perform simulations with six peptide chains in a box (the nominal concentration is ∼0.1 mM) and compute the free energy profile for forming aggregates of Q₃₀ at the physiological temperature. Now the free energy profile as directly simulated (even with monomer depletion) is almost downhill when we use the total number of contacts in the simulation cell as the reaction coordinate. The profile exhibits only a single peak which occurs when the hairpin in the monomers is formed from an extended state. The small free energy (∼2k_BT) barrier that occurs during the restructuring of the monomeric hairpin suggests the critical nucleus size as measured by concentration dependence would appear to be 1 for Q₃₀ (Figure 3A). The free energy barrier during hairpin formation is indeed the rate-limiting step in aggregation of longer polyglutamine repeats. As we increase the repeat length, the barrier starts to vanish (Figure 1), which leads to the higher aggregation rates observed in experiments.³²

Figure 3.

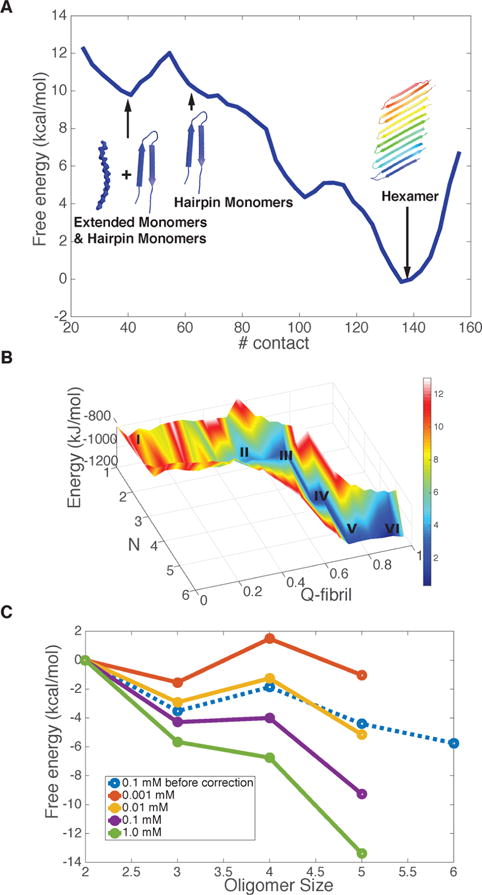
Aggregation free energy landscape for Q₃₀ at 300 K. (A) The free energy profile as a function of the number of total residue–residue contacts in the finite size simulation system with six Q₃₀ peptide chains. Representative structures in each basin illustrate the progression through the different oligomeric states. (B) The energy and free energy surfaces for aggregation of Q₃₀ are plotted as a function of the oligomer size (N), and its structure similarity compared to the final fiber form (Q_fibril). The z-axis is the energy of the system, and it decreases monotonically as the oligomer size increases. The color indicates the free energy, which includes the entropy cost of addition at concentration 0.1 mM. The local basins for different oligomer states are labeled by size. (C) The grand canonical free energy for different oligomer states as corrected for the finite size effect is shown for different concentrations of free monomers.

The free energy profile after making the correction for the changing concentration of free monomers in the simulation exhibits an even more downhill behavior (Figure 3C), in harmony with the relatively high aggregation rate of Q₃₀ in vitro. This sort of behavior is referred to by Ferrone as a “monomeric” aggregation nucleus.³³ When we extrapolate the concentration to 1 μM, there is a barrier in the aggregation process; while it becomes much more downhill under supersaturation (1 mM). The predicted critical concentration (c*) is between 1 and 10 μM, and this value compares well with experiments showing that solubility limit for Q₃₀K₂ is around 5 μM at 303 K.³⁴ The most favorable oligomeric structures from the free energy basin are antiparallel β-hairpin sheets. This structural prediction agrees well with what has been inferred from experimental ssNMR on aggregates and point mutation studies.⁸ We did not observe in our simulations either the parallel β-hairpin structures or the β-arch structures which had been postulated by others.^5,35 We also notice that other forms of β-structures like β-arch have been observed computationally,³⁶ employing much more crudely coarse-grained simulations, in comparison with the AWSEM model. In contrast, the AWSEM prediction of the fibril structure compares very well with the 2D-FTIR results from Zanni’s group.⁷

3.4. “Mixed or Inhomogeneous” Nucleation for Q₂₆ Leads to Branched Filaments

As the polyQ length increases from 20 to 30 units, the hairpin structure begins to dominate over the extended form in the monomer, and the critical nucleus size for aggregation decreases from 4 to 1. For an intermediate length peptide, Q₂₆, the simulation results suggest that both the extended form and hairpin form of the monomer are equally favorable. In this case, how does aggregation occur? We again compute the 1D free energy profile at the physiological temperature (Figure S2A) using the total number of contacts in the simulation box as the reaction coordinate. This profile shows a peak in the formation of hairpin structures from extended form, and the critical nucleus size is 1 at 300 K. But the most favorable final fiber form structure turns out to be a mixture of hairpins and extended chains (Figure S2A), instead of the simple pure antiparallel hairpins formed for Q₃₀. As shown in the 1D free energy plot as a function of the size of oligomer, the free energy of forming an oligomer is downhill before forming a desired antiparallel β-hairpin hexamer, while forming a desired antiparallel β-hairpin hexamer is uphill (Figure S2B). The free energy profile after making the correction for changing the concentration of free monomers in the simulation exhibits a downhill behavior (Figure S2B). The predicted critical concentration (c*) is between 1 and 10 μM at the physiological temperature (refer to the SI for details).

We observed several different intermediate structures during nucleation simulations (Figure 4A). These turned out to be a mixture of β-hairpins and extended β-strands. The calculations suggest the mechanism for aggregation will have a mixed or inhomogeneous set of nuclei (Figure 4B). The variety of distinct nuclei comes from there being two equally favorable conformations for Q₂₆. As the chain grows, the extended monomers can attach onto the hairpins and vice versa. This attachment widens the fiber in a direction perpendicular to the main fiber axis. We call this mechanism “branching”. Walters et al. have shown in their experiments that while polyQ sequences of a shorter length and those of a longer length form fibers with clear bundles, the fiber morphology of the intermediate length peptides Q₂₆ shows a lateral alignment.²⁵ We see that this lateral alignment phenomenon is explained by the present simulations.

Figure 4.

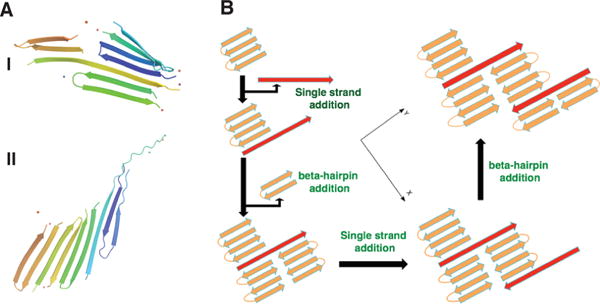
Proposed mechanism for the formation of mixed nuclei in the aggregation of Q₂₆. (A) Selected representative structures for Q₂₆ with different topologies. (B) A schematic diagram showing the of formation of “branched” oligomers from mixed nuclei. The different monomer components are color-coded, with brown representing the hairpin structure and red indicating the peptide takes on an extended structure.

3.5. Q₁₂PGQ₁₂ Nucleation

The possible involvement of the hairpin in the nucleation mechanism had already suggested studying the aggregation of peptides that encourage the formation of hairpins.^8,25,37. Wetzel and co-workers have constructed peptides in which Q’s in the middle of the sequence are mutated to proline and glycine (PG mutation). Such a mutation stabilizes a hairpin at the location of the PG kink. They have shown that Q₉PGQ₉ now already shows downhill aggregation behavior.^8,25 Further more, the PG mutation eliminates the lateral alignment behavior in fiber morphology.²⁵

We examined these same peptides using our simulation approach. We computed the free energy profiles for Q₁₂PGQ₁₂ monomers. We see that there is a very much enhanced β-hairpin propensity (Figure 5A). Now already at length 26, the free energy difference favors the hairpin by about 6 kcal/mol. The aggregation free energy profile at the physiological temperature without the depletion correction for Q₁₂PGQ₁₂ shows the nucleation process is downhill, with the antiparallel hairpin fiber becoming the most stable final state (Figure 5B). After making a depletion correction, the free energy profile is downhill (Figure 5C). The predicted critical concentration is between 1 and 10 μM at 300 K, agreeing perfectly with what is found for the polyglutamine peptide PG mutations using L-amino acids(Q₁₀ PGQ₁₁)⁸. The L-PG mutation does not enhance the aggregation rate significantly, but the mutation facilitates β-hairpin formation in the aggregates leading to a “monomeric nucleus” with n* ∼ 1.⁸ Kar et al. have also studied the PG mutations to D-form amino acids. This mutation not only leads to n* ~ 1 but also enhances the aggregation with a critical concentration of 0.4 μM.⁸ We did not carry out any simulations of this system with its backbone of unnatural chirality, which requires modification of the abbreviated AWSEM software.

Figure 5.

Changing the structural preference for 26 length repeats by making point mutations alters the nucleation behavior at 300 K. (A) An inserted L-PG mutation makes the hairpin conformation more favorable. (B) The free energy profile as a function of the number of total residue–residue contacts in a simulation system with six Q₁₂PGQ₁₂ peptide chains. Representative structures in each basin illustrate the progression through the different oligomeric states. (C) The grand canonical free energy for different oligomer states as corrected for the finite size effect for different concentration of free monomers.

4. DISCUSSION

4.1. The Persistence Length of PolyQ Peptides Explains Their Structural Preferences

Our simulations suggest that the monomer’s structural preferences do greatly influence fiber nucleation and growth. Polymer physics provides an explanation for the structure change with length. Increasing the chain length increases the probability for collapse. The persistence length of polyQ in solution corresponds to ∼3–4 residues in sequence.²³ Two parts of a peptide chain can only make contacts when they are separated by at least 4 persistence lengths.³⁸ In Q₂₀ (4–5 persistent lengths), the probability to make contacts and collapse is still small, but the collapse probability is much larger for Q₄₀.

4.2. Why Does the Nucleus Possess a Similar Structure to the Proposed Fiber Form?

In our recent work on the aggregation of Aβ40, we found the oligomers of small size must reconfigure by rearranging before they can form the most stable fiber (i.e., they “backtrack”). The Aβ40 first assembles into prefibrilar forms which are thought by some to be the key to the pathology, and then these prefibrilar oligomers rearrange into parallel β-hairpin structures. In contrast, for polyglutamine repeats, the nucleus already resembles the final β-strand structure of the fiber form. Unlike what happened for Aβ40, the monotonous nature of the sequence leads to a relatively simple aggregation mechanism that underlies the simple length dependence of fiber nucleation and assembly.

The situation is more complicated for the in vivo aggregation of the species involved in HD, peptides based on Huntingtin exon1. Recent studies on the full-length Huntingtin exon1 do find evidence of oligomers of heterogeneous structures. These small oligomers have been proposed to be the pathogenic culprits in this case too.^39–41 We are currently studying the aggregation of Huntingtin exon1 peptide and plan to report on our results for these much larger systems later.

4.3. The Branching Nucleation Behavior Suggests a Way To Control Fiber Morphology

In our simulations, when the polyglutamine repeat length is either rather short or rather long, additional β-strands would attach to the existing aggregate primarily by following the direction of the fiber axis. At intermediate length, attaching the two equally favorable conformations of the monomer to the aggregate gives rise to a “branching” mechanism which leads to lateral alignment. The aggregation free energy landscape suggests that the introduction of the PG mutations would eliminate the lateral alignment, and indeed this is seen. These results together give us confidence that simulations can guide the control of fiber morphology in vitro. Fiber growth control has long been a problem in macromolecular engineering and tissue engineering. The morphology of DNA fibers has been carefully controlled using “DNA bricks”, and the size of such fibers can reach beyond the nanometer level.⁴² By mutating polyglutamine sequences, it should be possible to tune the preference for different monomer conformations, thus influencing fiber morphology. A protein gel made up of different polymeric β-strands may allow the modification of the gel’s mechanical properties, which may be of practical use.