A longitudinal network analysis of social dynamics in rooks corvus frugilegus: repeated group modifications do not affect social network in captive rooks

Abstract

Numerous studies have investigated the remarkable variation of social features and the resulting structures across species. Indeed, relationships are dynamic and vary in time according to various factors such as environmental conditions or individuals attributes. However, few studies have investigated the processes that stabilize the structures within a given species, and the behavioral mechanisms that ensure their coherence and continuity across time. Here, we used a dynamic actor-based model, RSiena, to investigate the consistency of the temporal dynamic of relationships of a group of captive rooks facing recurrent modifications in group composition (i.e., the loss and introduction of individuals). We found that changes in relationships (i.e., formation and removal) followed consistent patterns regardless of group composition and sex-ratio. Rooks preferentially interacted with paired congeners (i.e., unpopular attachment) and were more likely to form relationships with individuals bonded to a current social partner (i.e., “friends of friends”, or triadic closure). The sex of individuals had no effect on the dynamic of relationships. This robust behavioral mechanisms formed the basis of inter-connected networks, composed of sub-structures of individuals emerging from the enmeshment of dyadic and triadic motifs. Overall, the present study reveals crucial aspects of the behavioral mechanisms shaping rooks social structure, suggesting that rooks live in a well-integrated society, going far beyond the unique monogamous pair-bond.

Numerous species live in groups, which vary widely in forms and complexity, from simple aggregations to more complex form of sociality as found in social mammals or some birds’ species like corvids (Sumpter 2006). In social species, the social structure is characterized by the nature, the quality and also the patterning of relationships (Hinde 1976). While the structure tend to be stable in a given species, the relationships that underlie the structure are not static, and they can vary in strength and stability over time (Silk et al. 2006a, 2006b). Numerous factors are expected to modulate the way individual interact, and thus ultimately the form taken by sociality, such as environmental conditions (e.g., habitat, resource distribution, predation risk; Banks et al. 2007; Kluever et al. 2008; Henzi et al. 2009), individual attributes (e.g., age, sex; Sosa 2016), personality (Pike et al. 2008; Aplin et al. 2013), or group constraints (e.g., size or demography; Dazey et al. 1977). However, if numerous studies have investigated the variability of the social features according to internal and external pressures, very few examined the processes that stabilize the structures. To fully understand the diversity of forms taken by sociality, we must not only consider the processes that challenge social structures, but also those that ensure their coherence and continuity across time, group composition, generations, and environments (Thierry 2007; Jacobs and Petit 2011; Sosa 2014).

In numerous species, the coherence and continuity of grouping patterns can be ensured by general rules of attraction and repulsion among group members, which generally relates to the number of individuals aggregating and to the distance and alignment with closest neighbors (e.g., birds’ flocks in flight or fish schools; Couzin et al. 2002; Krause and Ruxton 2002; Sumpter 2006). However, if those rules provide a valuable background for the understanding of grouping patterns, more and more studies also showed that individuals are not identical and interchangeable, and inter-individual differences can significantly influence collective patterns (e.g., physiology, social status; Nagy et al. 2010; Petit and Bon 2010; Jolles et al. 2013a). This may become even more complicated in highly social species, where group structures result from more intricate patterns of interactions among group members. Macaques for instance show great variations of their social structures from one species to another, but within each species, a remarkable consistency and stability of their social features and interaction patterns is also observed (also referred to as social style, Thierry 2007; Duboscq et al. 2013). Those social styles are characterized by the co-variation of several social traits (e.g., development of social tolerance, dominance asymmetry, maternal permissiveness), unduly conserved and consistent across groups, generations, and environments (Thierry 2007, 2013). In highly social species, the structure can thus be partially independent of its components (i.e., individuals), as it persists over time while individuals vary (i.e., temporal variations of individuals attributes, group composition, or sex-ratio) and eventually disappear (e.g., death or migration).

One way to investigate the consistency and the robustness of social patterns is to follow and analyze the temporal dynamics of relationships over time (i.e., the formation and removal of relationships). However, such investigation must be performed at the structure level, in the sense that all changes occurring in the network (i.e., define by the enmeshment of all relationships) must be considered simultaneously. Indeed, in a cohesive structure, changes occurring in one relationship can potentially affect the others (Hinde 1976). Such challenging investigations are now made possible and improved by the use of dynamic actor-based approaches like RSiena (Snijders 2001; Snijders et al. 2010; Pinter-Wollman et al. 2014; Ripley et al. 2015). RSiena was first created to study the dynamic of human social relationships (Steglich et al. 2006; Mercken et al. 2010; Schaefer et al. 2011), but has also recently been successfully applied to explore the dynamic of social interactions in animal species (Ilany et al. 2015; Borgeaud et al. 2016; Pasquaretta et al. 2016). In more details, among the patterns that can be explored, two are susceptible to favor network cohesion: (1) first the growth-preferential attachment (PA), which states that individuals preferentially form relationships with highly connected group members (i.e., generally more central or popular individuals; PA; Barabási and Albert 1999); (2) and secondly, the triadic closure (TC), which states that individual preferably form relationships with common partners, a process also known as “my friends’ friends have now become friends of mine” (TC; Banks and Carley 1996). When found in a network, the PA and the TC highlight that nodes (i.e., individuals) do not randomly form new connections, and therefore display heterogeneous levels of connectivity. This heterogeneity probably has two main consequences: firstly, all individuals will contribute differently to the network cohesion, and secondly, it should ensure the assimilation of new individuals within the network without damaging its global cohesion (Barabási and Albert 1999; Lusseau 2003). In addition, such structures are also expected to be highly resilient to the random removal of group members (Lusseau 2003; Manno 2008; Sosa 2014). PA and TC could thus be particularly interesting to investigate in highly social species facing constant perturbations or modifications of the group composition.

Among birds, in which sociality is far less often studied compared with mammals, rooks Corvus frugilegus appear to meet all conditions for the emergence of intricate social structures, and robust social patterns. They are indeed well known for their social abilities, notably their ability to collect and use social information (Clayton and Emery 2007; Emery et al. 2007; Scheid et al. 2008). Rooks breed in colonies of tens or hundreds of birds, but also live in groups throughout the year, joining massive winter roosts out of the breeding season, that can sometimes reach thousands of individuals. They form long-term and sophisticated monogamous pair bonds, but can also bond out of the pair with several partners (i.e., in juveniles, Emery et al. 2007; Scheid et al. 2008; but also in adults, Boucherie et al. 2016). In line with this, it was also found that triads make up a significant proportion of rooks flocks in the wild (on average, 14%; Jolles et al. 2013a) and were also reported in captive groups (Richards 1976). Furthermore, their colonial dynamic is thought to express high level of fission–fusion dynamics (Emery 2004; Clayton and Emery 2007; Mikolasch et al. 2013), which relates to “the extent of variation in spatial cohesion and individuals membership over time” (Aureli et al. 2008). Indeed, in the wild, rooks alternatively merge and split from the main colony, foraging in smaller subgroups during the day and roosting all together at night (Goodwin 1955; Swingland 1977; Roell and Bossema 1982). Thus, their social structure faces recurrent modifications of the group composition and membership over time. Altogether, it makes rooks an ideal model to investigate in a non-primate species, if and how consistent and robust patterns can shape the dynamic of relationships, and possibly ensure the permanency of the structure.

In this study, we investigated the consistency of the relationships pattern in a group of captive rooks facing recurrent modifications of group composition (i.e., losses and additions of new individuals). To do so, we used a dynamic actor-based model, RSiena, to examine the temporal dynamic of relationships over three different four-month periods (i.e., in 2012, 2014, and 2015). We first tested whether the temporal dynamic of relationships followed growth-PA (i.e., relationships are preferentially formed with popular individuals), TC (i.e., my friends’ friends have now become friends of mine), and whether it was influenced by the sex of individuals for each year. Then, we investigated whether the social status (i.e., socially paired or solitary), the sex (i.e., male or female), and the group origin of the individual (i.e., original or newly added member), but also the breeding period (i.e., before or during the breeding period), had an effect on the quantity of relationship in which individuals were involved (i.e., individuals’ degree). We also tested whether the social status and the breeding period had an effect on the directionality of interactions (i.e., identity of preferential partners and responsibility in relationship formation). Finally, we evaluated the resilience of the social structure facing recurrent group modifications, using the network entropy, an indicator of social network disorder.

Materials and Methods

Subject and study site

We studied all the spatial associations and social interactions among a group of captive birds over three non-consecutive years. Captivity reduces the possibility of noise linked to external pressures such as environmental changes, thus providing an ideal opportunity to collect substantial amount of data for a complex modeling approach, and allowing us to focus specifically on group modifications, that is, losses and introduction of new individuals. All birds were easily identified by colored leg rings. Birds were housed in a large outdoor aviary (18 m ×6 m  × 3.5 m) on the Cronenbourg campus in Strasbourg, France. In 2012, the flock was composed of 11 adults birds (9 males and 2 females), collected as nestlings from a wild local colony between 2006 and 2007. This group composition remained stable from 2010 until April 2013. Several major disruptions of the group composition and sex-ratio then occurred between 2013 and 2015: i) six new birds rescued from hunting trap in south Alsace were added into the group (one male and five females), ii) and five individuals escaped or died (for more information about the modifications of the group composition, see Table 1). The aviary contained wooded perches, platforms, suspended baskets, ropes, vegetation cover, and branches, as well as two small water pools for enrichment and bathing. Birds were fed daily with a mixture of pellets and fresh products (eggs, yoghurt, and fruit) and had ad libitum access to water.

Table 1.

Modifications of the group composition and the sex-ratio over time

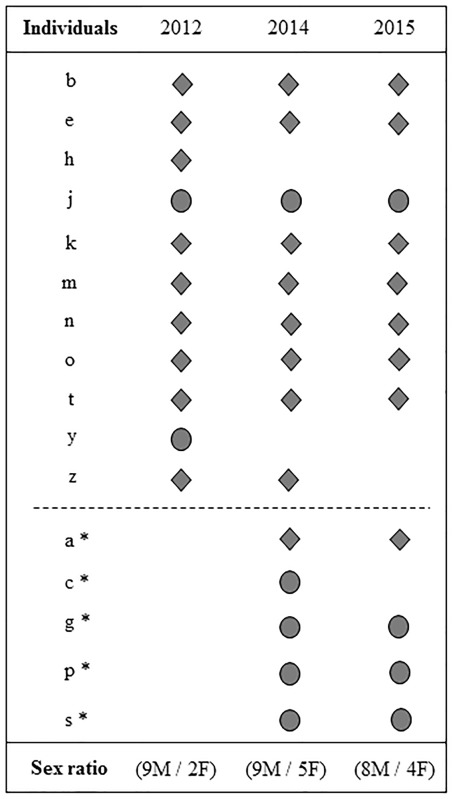Notes: Diamonds represent males, and circles females. Asterisks indicate new individuals added into the group. In 2012, the group composition had been stable since 2010. In April and June 2013, two individuals escaped after rodents damaged the aviary (h, male; y female); in October 2013, six new individuals were added to the group (a, juvenile male; c, g, p, s, w, females), one of which escaped a few days afterwards and thus do not appear in the table (w, female). Finally, two other birds died of natural causes in May and August 2014 (z, male; c, female).

Data collection

Data were collected through four-month periods (from January to the end of April) in three non-consecutive years: (1) in 2012, when group composition had been stable since 2010; (2) in 2014 and 2015, following modifications of the group composition (Table 1). Note that all modifications of group composition occurred between collection periods. Half of the data collection period covered a non-breeding period (from January to the end of February), and the other half part of the breeding season (from March to the end of April). For this group, the beginning and the end of the breeding period were, respectively, defined as the day at which the individuals started building nests, and as the day at which they started dismantling them (usually in the end of May). Spatial proximities (perch proximity, ground proximity) and affiliative interactions (allofeeding, allopreening, and contact-sit) were recorded with 10-min individual focal sampling (Altmann 1974). Ad libitum sampling was used to record the rarest behaviour (allofeeding). Perch or ground proximity events were recorded if two birds were 10–50 cm apart when perching or 0 to 1 m apart on the ground, respectively. Contact-sit was recorded when two birds were less than 10 cm apart when perching. Allofeeding was recorded when one bird actively put a food item into the beak of another (Scheid et al. 2008), and allopreening was considered to have occurred when one bird ran its beak through the feathers of another. All observations were conducted between 08:00 and 18:00 hours by a single observer (PB). For each observation session, all individuals were observed in a random order (i.e., same amount of time for all), for a total of 08:40, 07:10, and 06:00 hours per individual and per respective year (2012, 2014, and 2015). The direction of spatial approaches and affiliative interactions was only recorded in 2014 and 2015 and was later used to investigate individual preferences and responsibilities.

Data analysis

Dynamic analysis, RSiena modeling

We ran a dynamic agent-based model with R (version 3.1.3; R Core Team 2015) and the RSiena package (version 1.1-232; Ripley et al. 2015). Siena (Simulation Investigation for Empirical Network Analysis) is a dynamic model based on Markov processes that permits longitudinal network analyses. The RSiena model operates on a series of consecutive matrices. Therefore, we constructed 12, 13, and 12 consecutive matrices for 2012, 2014, and 2015, respectively, summing the data per week (the number of observation sessions per week ranged from two to five). Two consecutive matrices were separated by at least 2 days without observations. We worked with symmetrical binary matrices, where the value of 1 indicated non-random relationships. We used an individual sociality index based on spatial associations and affiliative interactions to distinguish non-random relationships from others (see Appendix 1 for the calculation of the sociality index). Non-random relationships included social pairs (i.e., relationships representing more than 50% of the summed sociality indices of each partner) and extra-pair affiliations. In addition, individuals were defined as “solitary”, if they were not involved in a social pair. Note that individuals could not be involved in more than one social pair at a given time. However, both paired and solitary individuals could be involved in several extra-pair affiliations.

As a prerequisite for RSiena, we first computed a Jaccard index for each year (2012, 2014, and 2015) to control that there was sufficient diversity between two consecutive matrices but also sufficient similarity to indicate the successive states of the same network. When the Jaccard index equals 0, the degree of similarity between two matrices is null. When it equals 1, the matrices are considered to be exactly the same. The Jaccard index has to be higher than 0.2 to allow for the use of RSiena modeling (Ripley et al. 2015).

To explain network changes over time, we ran a dynamic agent-based model for each year and considered four potential structural effects: 1) the growth-PA; 2) the TC process; 3) the homophily and heterophily of relationships according to the sex of individuals, that is, whether individuals preferentially interact with individuals of their sex, or in the contrary with this opposite sex; 4) and the individuals responsibility on the changes rate in relationships according to their sex. Calculation details of both PA and TC values are described in Table 2 (see also the RSiena manual, Ripley et al. 2015). The effect of density was also included in the model, as required by the creators of RSiena (Ripley et al. 2015). 1000 permutations were performed, and the Wald-type test was used to estimate the explanatory power of each effect. Each model was validated by running a goodness of fit test, which compared the observed values with simulated values for each of the three years.

Table 2.

Calculation details for the growth PA and the TC effects

Model	Formula	Description
Preferential attachment (PA)	$PA\left(i\right)={\displaystyle \sum }_j{x}_{ij}{\displaystyle \sum }_h{x}_{hj}$	Analyses the popularity of each individual. This effect reflects individual preference for links with popular individuals (i.e., individuals with the highest degrees receive more incoming links). PA(i) is defined, for individual i, as the number of relations received by individual j, to whom i is linked. Here xij in {0, 1} denotes a link between i and j.
Triadic closure (TC)	$TC\left(i\right)={\displaystyle \sum }_{j,h}{x}_{ij}{x}_{ih}{x}_{jh}$	Analyses the transitivity of the connection pattern for each individual. This describes the « friends of my friends are my friends » phenomenon. TC(i) is the number of transitive patterns including individual i in the network, that is, i is linked to j and h, which are also linked together. Here xij in {0, 1} denotes a link between i and j.

Effect of social status on the quantity and directionality of interactions

First, we ran a generalized linear mixed model (GLMM; function “glmer” in R package lme4 v.1.1-9; Bates et al. 2014) using a Poisson distribution and a log link function to test the effect of the individual social status (i.e., socially paired or solitary), the breeding period (i.e., before or during the breeding period), the sex of the individual (i.e., male or female), and the individual group status (i.e., original or newly added member), on the average degree of connectivity of each individual (i.e., the response variable: the total number of social partners an individual is connected to). Individual identity and week nested in year were used as random factors.

The direction of spatial approaches and affiliations (hereafter called directed interactions; only available for 2014 and 2015) was then used to answer two questions. Firstly, do solitary individuals favor individuals with a particular social status (i.e., paired or solitary) for interaction? This was achieved using a GLMM that was adapted for proportions with a binomial distribution and logit link function (GLMM; using the “cbind” command in function “glmer” in R package lme4 v.1.1-9; Bates et al. 2014), to compare the proportion of interactions emitted by solitary toward paired or other solitary individuals. Given that the number of solitary and socially paired individuals varied from one matrix to another, we divided the proportions of directed interactions by the proportion of each type of relationships in the networks (i.e., solitary–solitary or solitary–paired relationships). Secondly, which of the paired and solitary individuals were the most active when interacting together? Similarly, we used a GLMM adapted for proportions with a binomial distribution and logit link function to compare the proportion of interactions emitted by paired individuals toward solitary individuals and by the latter toward the former. In the two models, we also added the breeding period (i.e., before or during the breeding period) as fixed factor, and the week number nested in year as random factor.

Entropy

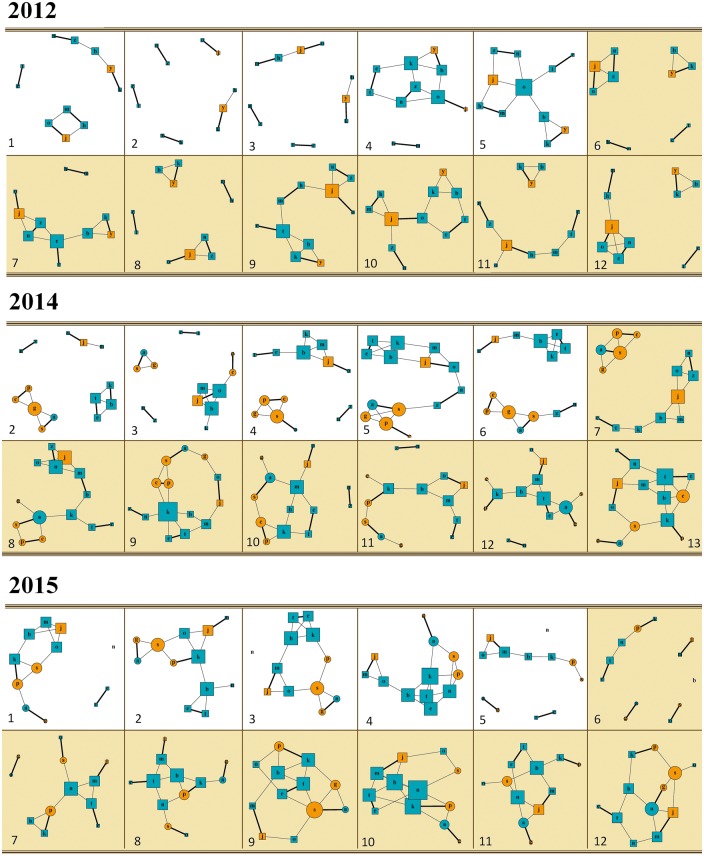
We then investigated whether the modification of the group composition impacted the entropy of the network, used here as a measure of network disorder. Originally established to measure the inconsistency of a source of information, entropy measures the heterogeneity of the individual’s degrees in a graph (i.e., total number of social partner an individual is connected to). For an undirected network, the entropy is maximal (i.e., equals to 1) if all individuals have the same degree. The entropy was computed for each matrix in each year, using Matlab software (Matlab version R2015a 8.5.0). We then used a linear model (LM; function “lm” in R package stats v.3.1.3; R Core Team 2015) to investigate how the year (2012, 2014, and 2015), the week number, and the interaction between year and week number affected the network entropy (i.e., response variable). All statistics were performed in R version 3.1.3 (R Core Team 2015), with the significance threshold set at α = 0.05. All results are discussed using the estimated parameter values provided by the models. All networks were visualized using R package igraph (i.e., in total 2012: 12, 2014: 13, 2015: 12 networks; package igraph v.0.701; Csardi and Nepusz 2006; Figure 2).

Figure 2.

Temporal modifications of the social networks of social pairs and extra-pair affiliations, computed per week between January and the end of April, in 2012, 2014, and 2015. The thicker lines represent the social pairs, and the thinner the extra-pair affiliations. Females are represented in orange and males in blue. Squares represent original group members, and circles newly added members (i.e., present in the group in 2014 and 2015). The size of the nodes (i.e., individuals) is proportional to the degree of the individual in the network (i.e., total number of social partners an individual is connected to). Finally, networks with colored background occur during the breeding season (i.e., March to the end of April). Note that to homogenize the visualization, the first network in 2014 is not reported here, as 13 networks were used in 2014 instead of 12 in 2012 and 2015.

Ethical note

Research was purely observational, adhered to the guidelines of the Association for the Study of Animal Behavior, and respected European and French legislation. The study was approved by the regional ethical committee on animal experimentation under the license no. A67-382.

Results

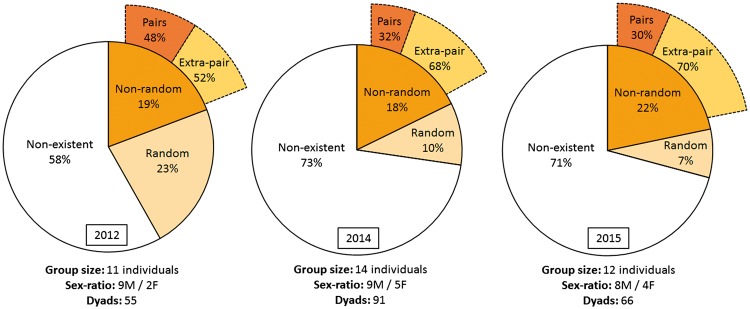
Over the three years, on average in each network, random and non-random relationships (i.e., social pairs and extra-pair relationships) represented less than half of all potential relationships in the group (Figure 1). In addition, on average in each network, more than half of the non-random relationships were extra-pair relationships (Figure 1).

Figure 1.

Average proportions of non-existent relationships, random relationships, and non-random relationships (i.e., social pairs and extra-pair relationships) over all potential relationships in the group, per networks, and per year. The group size, the sex-ratio, and the maximum number of relationships that can be formed in the group according to group size are indicated below (i.e., Dyads).

Over all the different networks, we identified 7 (2012), 10 (2014), and 6 (2015) different social pairs (i.e., identified in at least one network), indicating that some social pairs varied from one network to another, especially in 2012 and 2014 (Figure 2). Three social pairs over 7 (2012, m–h, e–t, n–z), 5 over 10 (2014, c–p, b–m, b–k, e–t, n–z), and 1 over 6 (2015, e–t) were same–sex pairs, and all but one in 2014 and all but two in 2015 were composed of individuals with the same group status (original, or newly added group member; Figure 2). Note that among all social pairs, 3 over 7 (2012, j–o, k–y, n–z), 3 over 10 (2014, j–o, k–p, n–z), and 3 over 6 (2015, a–g, j–m, k–p) built nests and attempted to breed.

However, none of those nesting pairs successfully produced surviving offspring during the study. Besides, over all the different networks, we identified a total of 26 (2012), 44 (2014), and 41 (2015) different extra-pair relationships, of which 73% (2012), 59% (2014), and 54% (2015) were same-sex relationships (Figure 2). In addition, 68% (2014), and 63% (2015) of those extra-pair relationships were composed of individuals with the same group status (original, or newly added group member; Figure 2).

Triads occurred, and we identified a total of 22 (2012), 54 (2014), and 37 (2015) occurrences per year over all the different networks. 91% (2012), 57% (2014), and 49% (2015) of those triads were composed of a social pair with another paired individual or a solitary. Among the triads that did not comprise a social pair, 4.5% (2012), 30% (2014), and 32% (2015) were composed of a majority of solitary individuals, and 4.5% (2012), 13% (2014), and 19% (2015) were composed of a majority of paired individuals (Figure 2; see e.g., triad b-t-k in the ninth week of 2012).

Dynamic analysis, RSiena modeling

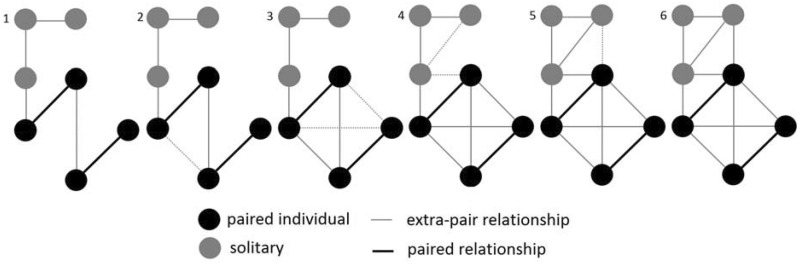
The Jaccard indices were above 0.2 in 2012, 2014, and 2015, ensuring sufficient changes in consecutives networks to permit the use of RSiena modeling. The density of connection significantly increased in 2012 and 2014, but remained stable in 2015 (Table 3). Note that the following results concern the dynamic of relationships over time in the networks over the three years, and relates indifferently to both social pairs and extra-pairs relationships. The RSiena results show that over time, rooks were more likely to form a relationship with less-connected individuals, that is, individuals with a lower degree (i.e., a reverse effect of PA, see Table 3). Over time, rooks were also more likely to form relationships with individuals that were already connected to their current social partners (i.e. TC; see Table 3 for statistical results and Appendix 2 for theoretical illustration). However, for each year, we found no significant effect of the homophily/heterophily, indicating that over time, rooks did not show any preferences for same/opposite sex partners when forming relationships (Table 3). In addition, the sex of the individuals had no impact on the rate of changes in relationships over time in the network, except in 2015, where males were more responsible than females for changes in relationships (Table 3). See Figure 2 for networks visualization.

Table 3.

Dynamic actor-based model according to the year (2012, 2014 and 2015) showing results for the three structural effects: density, TC, and PA

Model	Estimate	Standard error	t-ratio	P
2012
Density	4.60	1.85	−0.01	<0.05*
Triadic closure	1.71	0.52	0.02	<0.001***
Preferential attachment	−1.82	0.63	0.01	<0.01**
Homophily/heterophily	−1.37	0.66	−0.00	0.06
Sex on rate change: male	3.53	7.32	−0.02	0.57
Overall maximum convergence ratio: 0.080 Goodness of fit: 0.106
2014
Density	1.75	0.67	0.04	<0.01**
Triadic closure	1.33	0.26	0.01	<0.001***
Preferential attachment	−1.07	0.26	0.04	<0.001***
Homophily/heterophily	−0.11	0.23	0.0	0.61
Sex on rate change: male	0.03	0.34	−0.06	0.91
Overall maximum convergence ratio: 0.070 Goodness of fit: 0.068
2015
Density	0.37	0.50	0.01	0.44
Triadic closure	0.72	0.23	−0.01	<0.001***
Preferential attachment	−0.49	0.19	0.01	<0.01**
Homophily/heterophily	0.18	0.21	0.01	0.41
Sex on rate change: male	1.12	0.58	−0.01	0.04
Overall maximum convergence ratio: 0.036 Goodness of fit: 0.664

Notes: The overall maximum convergence ratio of the model is below 0.25 in all years, indicating a satisfactory convergence of the algorithm. In addition, the goodness of fit is above 0.05 in all years, indicating that the average values are close to the values observed in the data (Ripley et al. 2015).

^*** < 0.001,

^** < 0.01,

^* ≤ 0.05.

Effect of social status on the quantity and directionality of interactions

For all three years studied, solitary individuals were involved in significantly more relationships than socially paired individuals (i.e., they showed a higher degree than paired individuals; GLMM: solitary vs. paired, estimates = 0.25, standard error = 0.08, Z = 3.25, P < 0.01). However, neither the group status (GLMM: original vs. newly added member, estimates = −0.01, standard error = 0.13, Z = −0.12, P = 0.91), the sex of the individual (GLMM: male vs. female, estimates = −0.05, standard error = 0.11, Z = −0.46, P = 0.65) nor the breeding period (GLMM: before vs. during the breeding period, estimates = −0.07, standard error = 0.07, Z = −0.96, P = 0.34), had a significant effect on the individual degree (Figure 2).

Considering the direction of interactions for 2014 and 2015 (i.e., associations and affiliations), we found that solitary individuals preferentially interacted with paired individuals than other solitary individuals (GMM: solitary toward paired vs. solitary, estimates = 2.65, standard error = 1.10, Z = 2.51, P < 0.05), with an increased preference during the breeding period (GMM: before vs. during the breeding period: estimates = −3.06, standard error = 1.45, Z = −2.12, P < 0.05). Finally, we found that interactions between solitary and paired individuals were initiated significantly more often by the solitary individuals (GLMM: solitary vs. paired, estimates = 1.23, standard error = 0.39, Z = 3.17, P < 0.01), and this both before and during the breeding season (GLMM: before vs. during the breeding period, estimates = −0.03, standard error = 0.36, Z = −0.08, P = 0.94).

Entropy

The entropy of the network was similar for all three years and in all weeks (average value of 0.66 in 2012, 0.64 in 2014 and 0.71 in 2015; LM; Year: F = 1.71, P > 0.05; Week: F = 2.67, P > 0.05; Year × Week: F = 0.82, P > 0.05).

Discussion

This study investigated the temporal dynamics of social relationships (i.e., social pairs and extra-pair affiliations), in a social network of captive rooks facing repeated modifications in group composition. Using RSiena, an innovative tool for the study of sociality, we found that the dynamic of rooks relationships was not random, but followed two consistent patterns, namely TC and “unpopular attachment” (hereafter referred to as UA; i.e., the reverse effect of PA). These two patterns intervened in the same way on the dynamics of relationships both before and after the modifications in group composition (i.e., losses and introduction of individuals), which did not affect the level of network entropy. Despite the addition of new females in the group to compensate an initially strongly unbalanced sex-ratio, neither the dynamic of relationships nor the individual degree, were affected by the sex of individuals. In addition, neither the group origin of the individual, nor the breeding period, had an effect on individuals’ degree.

More specifically, the temporal dynamics of relationships did not follow PA in any of the three years considered, but rather a reverse mechanism that could be termed “UA” (for PA see also Barabási and Albert 1999). This indicates that rooks were more likely to form new relationships with individuals who had fewer connections in the network. As it happens, the less connected individuals were found to be, predominantly, the paired individuals. This makes sense as, by definition, socially paired individuals primarily interact with one social partner (i.e., at least 50% of their interactions), which necessarily limits the number of social partners they can interact with. Combined, the UA and the low degree of paired individuals suggest a general attractor effect of pairs on social interactions. Consistently, we found that solitary individuals also interacted significantly more often with paired individuals, and that they were generally responsible for the establishment of these relationships. This was even more true during the breeding period, which may be due to the fact that solitary individuals cannot attempt to reproduce and may try to have access to females or juveniles. Alternatively, they may just try to interfere in the reproduction of mixed pairs (Goodwin 1955).

TC—“my friends’ friends have now become friends of mine”—significantly increased over time for each year (see also Banks and Carley 1996; Borgeaud et al. 2016). Rooks thus preferentially formed relationships with individuals that were already connected to one of their current social partners, resulting in the formation of triads within the network. Consistently with the attractor effect of the pair, most triads formed in the networks were centred on social pairs. More precisely, most triads resulted from the completion of a pair with either another paired or a solitary individual, or were composed of a majority of paired individuals interacting together, and more rarely of a majority of solitary individuals. Overall, the attractor effect of the pair and the TC gives the social structure its shape. This shape, an arrangement and overlap of dyadic and triadic motifs, forms the basis of an inter-connected network composed of more complex sub-structures of individuals (groups of four individuals, or more).

Major modifications occurred in this group: addition of wild individuals, modification of sex ratio (strongly unbalanced at the beginning of the study). Thus, we could have expected these modifications to damage the social structure and to induce social instability (as shown by Ilany et al. 2013), disturbing the general pattern of interactions of the group. However, all results on relationships dynamics remained consistent over the three years (i.e., UA, TC, individuals’ degree, directionality of interactions). In addition, neither the group status, the sex of the individuals, nor the breeding period, affected individuals’ degree of connectivity in the network. And, despite important changes in sex-ratio, the sex of the individual had no effect on the dynamic of relationships expected in 2015, where males were slightly more responsible than females for the changes occurring in the network. Finally, group modifications did not altered the level of network disorder (i.e., entropy). Overall, this highlights that the dynamics of relationships are not random in rooks, and follow robust and consistent behavioral patterns. This provides the structure a certain degree of resilience to perturbations, ensuring some continuity and coherence over time. Those results reinforce the hypothesis that rooks social structure is more complex than just an aggregate of isolated pairs (Boucherie et al. 2016). They further suggest that rooks live in a well-integrated society, in which the diversity of relationships (i.e., in terms of stability and quality), may results in numerous feedbacks on individuals patterns of interactions, stabilizing the structure (Sumpter 2006; Thierry 2007).

More broadly, the formation and the continuity of a cohesive network of affiliative relationships beyond pairs, might increase some of the advantages associated with group living, while allowing to better deal with its competitive aspect (Dunbar 1989; Krause and Ruxton 2002). For instance, in rooks, affiliates are more likely to tolerate each other’s, especially in the context of food competition (Emery et al. 2007; Seed et al. 2008; Jolles et al. 2013b). Bonding with familiar congeners or closely nesting neighbors possibly facilitate the emergence of cooperative behaviors (e.g., collective nest vigilance, limitation of nests pilfering; Ogilvie 1951). Bonding with neighbors may also ensure a safer breeding environment, by reducing local stress, due to neighbor agitations and conflicts (Lewis et al. 2007; Jovani and Grimm 2008). This could explain why rook breeding parameters are not negatively affected by the very close proximity of other nests in rookeries (i.e., clutch size, number of hatchlings; Kasprzykowski 2008). Note that structural processes such as TC are also expected to promote reciprocity and cooperative behaviors in networks (Banks and Carley 1996; Walker et al. 1997; Buskens 2002; Lou et al. 2013; Righi and Takács 2014). Furthermore, individuals may become solitary after their partner’s death in the wild (Goodwin 1955; Jennings 1955). By bonding with paired individuals, they may guarantee their continued inclusion within the colony (Goodwin 1955). This inclusion may also help them reform a new pair more quickly.

It is important to bear in mind that the subjects in this study were captive rooks. It could be argued that spatial associations were influenced by captivity, as there is a higher probability that group members encounter each other than in the wild. If true, almost all group members should have been linked by non-random relationships—that is, social pairs or extra-pair affiliations. However, this was not the case. Non-random and random relationships made up less than half of all potential relationships in the network. Another limitation could be the strongly unbalanced sex ratio at the beginning of the study. Same-sex relationships occurred, both in pairs and extra-pairs relationships, as it is often the case when partners of the opposite sex are lacking (Kotrschal et al. 2006). However, same-sex relationships are also expected in highly social species (Mitani et al. 2000; Sterck et al. 1997). In addition, in this group, individuals showed no tendency to bond preferentially with same sex individuals (i.e., homophily), or on the contrary to avoid same-sex individuals (i.e., heterophily). It shows that social bonding can go beyond the reproductive function in rooks (Emery et al. 2007; Boucherie et al. 2016), and that the dynamic of relationships cannot be solely explained by individuals mating strategies, and the necessity to start or maintain (mated) pair bonds.

This study uses a stochastic agent-based model RSiena to investigate the temporal dynamics of relationships in captive adult rooks. We found that changes in rooks’ relationships followed robust and consistent patterns, regardless of the group composition or the sex-ratio, and to a certain extent without being affected by the breeding period. Rooks social structure was flexible enough to allow temporal variations without being dismantled. This makes sense considering that wild populations of rooks exhibit high level of fission–fusion dynamics, requiring individuals to deal with constant modifications of individuals’ membership in the different colony parties (Emery 2004; Clayton and Emery 2007; Mikolasch et al. 2013). Further investigations are now needed (1) to confirm the robustness of social patterns in other groups (in particular in wild populations) and across ecological contexts, and (2) to test for the existence of other structural mechanisms in rook. To the best of our knowledge, this is the first study to identify and explore the robustness of the social patterns in social birds. Our findings provide a reliable starting point for a closer examination of social dynamics in corvids, but also for the comparison of the robustness of social processes with other bird species.

Author contributions

Palmyre Boucherie conceived and designed the study, collected field data, conceived and performed the data analyses, and wrote the manuscript; Sebastian Sosa conceived and performed the data analyses; Cristian Pasquaretta performed the data analysis and contributed to the writing of the manuscript; Valérie Dufour conceived and designed the study, and contributed to the writing of the manuscript. All authors have given their final approval for publication.

Funding

Palmyre Boucherie was supported by a PhD Grant from the French Government.

APPENDIX 1

Construction of binary matrices

In order to discriminate the non-random relationships (i.e., social pairs and extra-pairs affiliations) from others in each matrix, we used spatial proximities (ground proximity: GP, perch proximity: PP) and affiliations (allofeeding: Fe, allopreening: Pr, and contact-sit: Cs) to compute a sociality index inspired by Silk et al. (2006b), for all potential relationships as follows:

$$\text{S}i{j}^{\text{1}}=\frac{(\left(\text{GP}i{j}^{\text{1}}/{\text{GP}}^{\text{1}}\right)\pm \left(\text{PP}i{j}^{\text{1}}/{\text{PP}}^{\text{1}}\right)\pm \left(\text{Fe}i{j}^{\text{1}}/{\text{Fe}}^{\text{1}}\right)\pm \left(\text{Pr}i{j}^{\text{1}}/{\text{Pr}}^{\text{1}}\right)\pm \left(\text{CS}i{j}^{\text{1}}/{\text{CS}}^{\text{1}}\right))}{5}\text{ x 1}00,$$

where GPij¹ equals the frequency of ground proximity for the dyad ij, divided by GP¹, which equals the overall mean of ground proximity for all dyads for matrix 1. We followed the same procedure for all other variables: PP, Fe, Pr, and Cs. The numerator refers to the number of variables.

Higher (lower) values of the index indicate stronger (weaker) relationships. We then computed the sociality indices of each individual, summing all the sociality indices for the relationships in which each individual was involved. Based on previous data, we considered that individuals were involved in a social pair when the sociality index of the relationship represented more than 50% of each individual’s sociality indices, and in an extra-pair affiliation when the sociality index of the relationship represented 5–50% of each individual sociality index, or more than 50% for only one of the two partners. Thus, individuals could only be socially paired with one partner at the same time, but they could be involved in several extra-pair affiliations.

APPENDIX 2

Theoretical illustration showing the progressive structural effect of TC (i.e., “my friends’ friends are now friends of mine”), from step 1 to step 6, in a network composed of paired and solitary individuals.