Is cascade reinforcement likely when sympatric and allopatric populations exchange migrants?

Abstract

When partially reproductively isolated species come back into secondary contact, these taxa may diverge in mating preferences and sexual cues to avoid maladaptive hybridization, a process known as reinforcement. This phenomenon often leads to reproductive character displacement (RCD) between sympatric and allopatric populations of reinforcing species that differ in their exposure to hybridization. Recent discussions have reinvigorated the idea that RCD may give rise to additional speciation between conspecific sympatric and allopatric populations, dubbing the concept “cascade reinforcement.” Despite some empirical studies supporting cascade reinforcement, we still know very little about the conditions for its evolution. In the present article, we address this question by developing an individual-based population genetic model that explicitly simulates cascade reinforcement when one of the hybridizing species is split into sympatric and allopatric populations. Our results show that when sympatric and allopatric populations reside in the same environment and only differ in their exposure to maladaptive hybridization, migration between them generally inhibits the evolution of cascade by spreading the reinforcement alleles from sympatry into allopatry and erasing RCD. Under these conditions, cascade reinforcement only evolved when migration rate between sympatric and allopatric populations was very low. This indicates that stabilizing sexual selection in allopatry is generally ineffective in preventing the spread of reinforcement alleles. Only when sympatric and allopatric populations experienced divergent ecological selection did cascade reinforcement evolve in the presence of substantial migration. These predictions clarify the conditions for cascade reinforcement and facilitate our understanding of existing cases in nature.

The theory of reinforcement states that natural selection directly favors the evolution of prezygotic isolation to avoid costly hybridization during secondary contact and is seen today as an important mechanism of speciation (Dobzhansky 1940; see Servedio and Noor 2003; Coyne and Orr 2004 for reviews). While older theoretical models suggested that reinforcement was unlikely (e.g., Moore 1957; Bigelow 1965; Cain et al. 1999; Spencer et al. 1986; Sanderson 1989), more recent models have generally favored the process (e.g., Liou and Price 1994; Kelly and Noor 1996; Servedio and Kirkpatrick 1997; Servedio 2000, 2001, 2004; Sadedin and Littlejohn 2003; Yukilevich and True 2006). As a result, some have begun to think about further consequences of reinforcement for sexual selection and mating trait evolution within species (Howard 1993; Ryan and Rand 1993; Higgie and Blows 2007; Ortiz-Barrientos et al. 2009; Pfennig and Pfennig 2009; Hoskin and Higgie 2010; Abbott et al. 2013).

The pattern of reproductive character displacement (RCD) in sympatric populations has long been recognized as an important signature for detecting reinforcement (e.g., Coyne and Orr 2004). However, Howard (1993) and more recently Ortiz-Barrientos et al. (2009), Pfennig and Pfennig (2009), and Hoskin and Higgie (2010), have suggested that RCD in sympatry may also cause sexual isolation between sympatric and allopatric populations of the reinforced species. This has been dubbed “cascade reinforcement” (Ortiz-Barrientoz et al. 2009) since reinforcement between 2 species can have cascading effects on mate choice within species if sympatric populations substantially diverge from their allopatric counterparts in mating traits.

This idea has recently received support from several empirical studies that seem to show that reinforcement drives sexual divergence between sympatric and allopatric populations of the same species. This has been suggested for spadefoot toads Spea multiplicata and S. bombifrons (e.g., Pfennig and Simovich 2002; Pfennig and Ryan 2006; Pfennig and Rice 2014), and for green-eyed tree frogs of Litoria (Hoskin et al. 2005), both of which differ in female mating preferences for male calls between sympatric and allopatric populations. Indeed, these studies have demonstrated that divergence between sympatric and allopatric populations has occurred to such an extent that these populations are now both strongly sexually isolated from each other. A similar pattern has also been described between sea rock-pool beetles Ochthebius quadricollis and O. urbanelliae (Porretta and Urbanelli 2012). Other examples of cascade reinforcement show more asymmetrical patterns of sexual isolation. A case between Drosophila serrata and D. birchii involves D. serrata allopatric females discriminating against sympatric males (Higgie and Blows 2007, 2008), while reinforcement between D. recens and D. subquinaria (Jaenike et al. 2006; Dyer et al. 2014; Bewick and Dyer 2014) and between killifish Lucania goodei and L. parva (Kozak et al. 2015) involves sympatric females discriminating against allopatric males.

Ortiz-Barrientos et al. (2009) and Hoskin and Higgie (2010) have outlined several predictions for the evolution of cascade reinforcement. They suggest that cascade reinforcement should evolve when: 1) there is asymmetrical gene flow primarily from allopatry into sympatry, and 2) when sympatric reinforcement alleles are highly deleterious in allopatry either because migrant sympatric females experience higher search costs compared to local allopatric females or choose males in allopatry with sexually or ecologically inferior traits (Ortiz-Barrientos et al. 2009).

The latter hypothesis has led them to argue that cascade reinforcement can evolve even when sympatric and allopatric populations only differ in their exposure to the hybridizing species with little or no ecological divergence. For instance, Hoskin and Higgie (2010, p. 410) state that: “This kind of selection will generate a pattern of divergence in mating signals, and potentially speciation among populations, with little divergence in other ecological traits.” Similarly, Ortiz-Barrientos et al. (2009) argue that cascade reinforcement can occur between “ecologically similar pairs of populations.” (p. 169) This argument stems from the notion that species recognition traits are expected to be under strong stabilizing sexual selection from females, which is theorized to prevent reinforcement alleles that evolve in sympatry from spreading and establishing in allopatric populations (Moore 1957; Patterson 1978; Barton and Hewitt 1985; Spencer et al. 1986; Sanderson 1989; Coyne and Orr 2004, p. 371). However, it is still unclear if cascade reinforcement and RCD can evolve only in the presence of differential exposure to maladaptive hybridization without ecological differences between allopatric and sympatric populations.

Of course, there are also alternative outcomes to cascade reinforcement. The first alternative is the prevention of reinforcement altogether due to genetic swamping from allopatry (“the swamping effect”; Moore 1957; Bigelow 1965; Sanderson 1989). This has long been a major challenge for reinforcement in general, but little work has been done to study how much migration from allopatry to sympatry would prevent reinforcement (but see Liou and Price 1994, for some exploration of this question). It is also possible that reinforcement alleles from sympatry may be able to spread to allopatric populations rather than get stuck in sympatry and thus erase any evidence of RCD (e.g., Ortiz-Barrientos et al. 2009). This in turn would cause “species-wide reinforcement” (i.e., both sympatric and allopatric populations would evolve stronger sexual isolation from the foreign species: Coyne and Orr 2004). While it is expected that this should occur when migration is rampant between sympatric and allopatric populations (Ortiz-Barrientos et al. 2009), it is still unclear how much migration is necessary to overcome the stabilizing sexual selection in allopatry (sensu Patterson 1978; Spencer et al. 1986; Sanderson 1989).

Given the accumulating evidence for cascade reinforcement, it is unfortunate that very little is known about the conditions that lead to its evolution versus alternative evolutionary outcomes such as species-wide reinforcement. While older theoretical studies speculated on how migration and gene flow between sympatric and allopatric populations might affect reinforcement, these studies were concerned with how it would prevent reinforcement altogether (Moore 1957; Sanderson 1989; Cain et al. 1999; Liou and Price 1994). Recent models of reinforcement have generally avoided the question of RCD by focusing on 2-island models of speciation (e.g., Servedio and Kirkpatrick 1997; Servedio 2000, 2004; Yukilevich and True 2006) or dealing with other aspects of reinforcement in a spatially explicit context (Sadedin and Littlejohn 2003). Models of McPeek and Gavrilets (2006) and Pfennig and Ryan (2006) studied within-species divergence as a result of RCD from other species, but only when sympatric and allopatric populations were completely geographically isolated (i.e., no migration/gene flow).

Here, we begin to explore the theoretical conditions for cascade reinforcement with gene flow by using Monte-Carlo individual-based computer simulations. We focus on the intriguing possibility that cascade can evolve in a purely sexual selection context with nothing else differentiating sympatric and allopatric populations except the cost of hybridization with another nascent species (sensu Ortiz-Barrientos et al. 2009; Hoskin and Higgie 2010). We then explore a scenario which incorporates one type of ecological divergent selection between sympatric and allopatric populations. We study both the overall probability of reinforcement and the relative outcomes of cascade versus species-wide reinforcement under different migration scenarios. This generates testable predictions about the conditions by which different outcomes of reinforcement can evolve in nature when sympatric and allopatric populations exchange migrants.

Materials and Methods: the Model

The present model is based on Yukilevich (2012) and broadly follows other population genetic models of reinforcement and sexual selection, including Felsenstein (1981), Kirkpatrick (1982), Kelly and Noor (1996), Servedio and Kirkpatrick (1997), Servedio (2000, 2004), and Servedio and Burger (2014). Our model assumes diploid, sexually-reproducing females and males with discrete nonoverlapping generations, residing in three island populations. The model is coded in program C and contains 4 recombining loci situated on the same chromosome, including 2 fitness-related loci A and B, male sexual cue locus C, and female mating preference locus D (see below for details). The assumption of few genes of large effect governing both fitness and behavior traits is mostly made for simplicity and transparency (as in previous models of reinforcement; see above). However, simple genetic models may not necessarily be unrealistic because the number of fitness and mating behavior genes that diverge to cause speciation between nascent species may actually be very small compared to their overall genetic architecture (see Doi et al. 2001; Tauber et al. 2003; Greenberg et al. 2003; Ortiz-Barrientos and Noor 2005; Chung et al. 2014, for genes of major effect contributing to speciation). Below, we discuss how more complex genetic architectures may affect our results (see section “Discussion”).

The historical scheme of the model

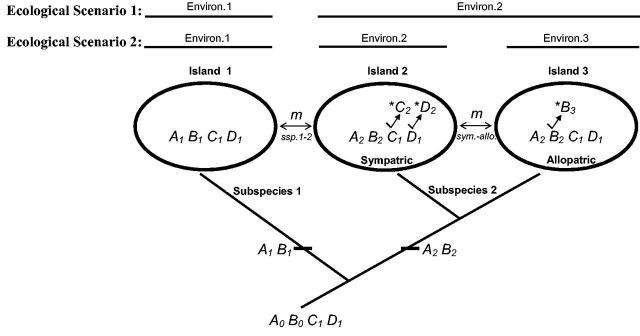
We assume that an ancestral population allopatrically splits into 2 “subspecies” (see Figure 1). The 2 subspecies diverge at fitness-related loci resulting in partial postzygotic isolation (i.e., partial zygote inviability), but otherwise maintain the same mating preferences and sexual cues and hence would mate randomly upon contact. We also assume that subspecies 2 has split into 2 geographical populations, one that is geographically closer to subspecies 1 than the other (Figure 1). The 2 subspecies then comeback into secondary contact and can exchange migrants at a given migration rate (m_ssp1-2), ranging from 0 to 0.5, which can only directly occur between subspecies 1 and the geographically closer population of subspecies 2 (henceforth “sympatric population”). The more geographically distant population of subspecies 2 cannot directly exchange migrants with subspecies 1 (henceforth “allopatric population”). The sympatric and allopatric populations of subspecies 2 can also exchange migrants at an independent migration rate (m_sym-allo) ranging from 0 to 0.5. Migration rates m_ssp1-2 and m_sym.-allo. can be symmetrical or asymmetrical between each pair of connected populations.

Figure 1.

Theoretical scheme of reinforcement speciation. Shown are 3 “island” populations and an ancestral scenario of divergence. The model assumes an ancestral population allopatrically splitting into 2 “subspecies” (subspecies 1 in island 1 and subspecies 2 in islands 2 and 3) that diverged in fitness-related loci. The second subspecies is split into 2 distinct island populations, a population that directly exchanges migrants with subspecies 1 (“sympatric population” in island 2) and a population that is not directly connected to subspecies 1 (“allopatric population” in island 3). Migration rate between subspecies 1 and 2 (m_ssp1-2) and between sympatric and allopatric populations of subspecies 2 (m_sym.-allo.) are independent and can be symmetrical or asymmetrical between each pair of interacting populations (see text). Shown are ancestral genotype and subsequent substitutions at A-D loci as well as introduced mutations at these loci upon simulation (indicated by astericks). Two different ecological scenarios are explored depending on whether sympatric and allopatric populations of subspecies 2 occupy the same (“Ecological Scenario 1”) or different (“Ecological Scenario 2”) environments (see section “Model”).

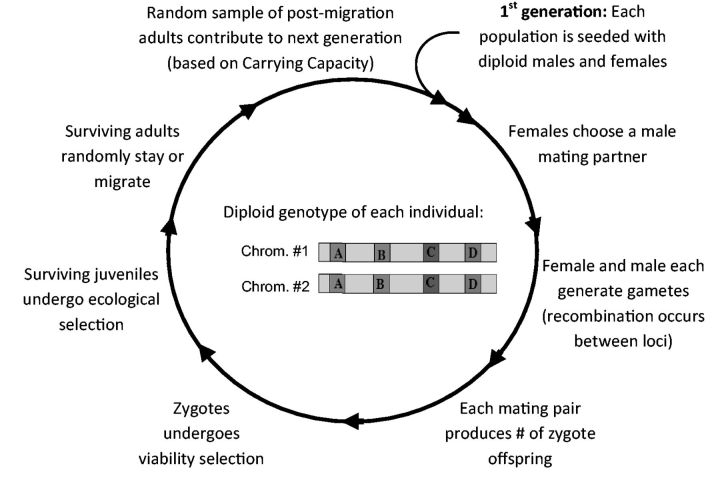
Life cycle of each population

At the onset of simulations, we initially seed each population with equal number of diploid males and females based on given allelic frequencies at all 4 loci in the model (see Figure 2). Each female chooses a male mating partner based on her mating preference locus and his sexual cue trait locus (see below; males are polygynous). Female and male gametes can undergo recombination between alleles at four loci (recombination rate ranges from 0 to 0.5). Each mating pair then produces a number of zygote progeny determined by a fecundity parameter and these offspring then experience zygote viability selection based on 2 epistatically interacting fitness loci (see below). Surviving juveniles are then exposed to divergent ecological selection against migrant homozygotes and hybrids at an ecological fitness locus (see below). Finally, the surviving adults are randomly assigned to remain in the local population or to migrate to the other population based on the migration rate parameters. Post-migration adults are then sampled at random to contribute to the next generation until they reach a carrying capacity of the population. This group makes up the pool of families for the next generation (Figure 2).

Figure 2.

Life cycle per generation for each of the 3 simulated populations. Simulations loop in the direction shown (clockwise). Also shown is a graphical illustration of each individual’s diploid genotype consisting of 4 independent loci, A, B, C, and D (see Table 1 for description of loci and their alleles). Additional details of each stage of the life cycle are described in text.

Zygote viability

The first two loci, A and B, determine viability of zygotes in the model (Table 1). We assume that the ancestral population was fixed for A₀ and B₀ alleles. During allopatric divergence, the two subspecies are assumed to have fixed different substitutions at these loci, with subspecies 1 fixing A₁ and B₁ alleles and subspecies 2 independently fixing A₂ and B₂ alleles. Since A₁ has never been in the same genetic background with B₂, and A₂ never with B₁, this creates postzygotic Dobzhansky–Muller incompatibility (DMI) in hybrids that have either: A₁ and B₂ or A₂ and B₁ in the same genotype (e.g., A₁₂B₁₂). All hybrid progeny with mismatched A and B alleles experience DMI’s. This assumption is made so as to increase the likelihood of reinforcement so we can focus on comparing the evolution of cascade versus alternative outcomes. The DMI hybrid incompatibility is expressed as zygote inviability (i.e., zygote to juvenile survival step in the life cycle of each population: see Figure 2). For simplicity, all simulations assumed selection against hybrids (s) of 0.55 (i.e., w = 0.45) relative to AB double homozygotes (i.e., A₁₁B₁₁ and A₂₂B₂₂) in all 3 populations.

Table 1.

Description of each locus in the model with initial allelic frequencies in all 3 populations

Locus	Trait expression	Max. number of alleles	Initial conditions
A	(D-M)epistatic incompatibility with B locus	2	A1 fixed in ssp.1, A2 fixed in ssp.2 (both sympatric and allopatric populations)
B	(D-M)epistatic incompatibility with A locus & Divergent Ecological Fitness	3	Ecological scenario 1: B1 fixed in ssp.1, B2 fixed in ssp.2 (both sympatric and allopatric populations) Ecological scenario 2: B1 fixed in ssp.1, B2 fixed in sympatric ssp.2 and 0.95 in allopatric ssp.2 B3 is 0.05 in allopatric ssp.2
C	Male sexual cue trait for D locus	2	C1 fixed in ssp.1 and in allopatric ssp.2, C2 is 0.05 in sympatric ssp.2
D	Female mating preference for C locus	2	D1 fixed in ssp.1 and in allopatric ssp.2, D2 is 0.05 in sympatric ssp.2

Divergent ecological fitness

Locus B also functions as an ecological fitness locus which determines relative fitness in different ecological environments of each population (Table 1). We make this assumption for simplicity and it is unlikely to alter our conclusions if this was a distinct locus in the model. Ecological selection occurs at the juvenile to adult survival step in the life cycle of each population (see Figure 2). We explore 2 ecological scenarios: Ecological scenario 1 assumes that subspecies 1 resides in environment 1 and sympatric and allopatric populations of subspecies 2 both occupy the same environment 2 (see Figure 1). Genotype B₁₁ is assumed to be most fit in environment 1 while B₂₂ is most fit in environment 2. For simplicity, foreign homozygote migrants and B₁₂ hybrids experience selection (s) of 0.55 (w = 0.45) in all simulations (i.e., hybrids on average fall in between ecological niches: Schluter 2000). Ecological scenario 2 assumes that each population resides in its own environment; subspecies 1 in environment 1, and subspecies 2 sympatric and allopatric populations now occupy different environments, 2 and 3, respectively (see Figure 1). We again assume that genotype B₁₁ is most fit in environment 1 and B₂₂ is most fit in environment 2, but now a third allele B₃ is introduced, making B₃₃ genotype most fit in environment 3. B₃ mutation is introduced at 5% allelic frequency in allopatric population of subspecies 2 (Figure 1). Results remain the same if B₃ is also initially 5% in sympatric population (data not shown). For simplicity, we explore two selection regimes: Regime 1: All foreign homozygote migrants and all hybrids (i.e., B₁₂, B₁₃, B₂₃) have selection (s) of 0.55 (w = 0.45) and Regime 2: where these genotypes experience selection (s) of 0.90 (w = 0.10).

Female mating preference and male sexual cue trait

Here we explore a “two-allele” model of reinforcement (sensu Felsenstein 1981; Servedio 2000). Locus C is only expressed in males and determines the male sexual cue trait with 2 alleles C₁ and C₂. The C locus is the target of female mating preferences (sexual selection) during the mate-selection step in the life cycle of each population (see Figure 2; Table 1). In turn, female mate preference is determined by locus D, with its corresponding two preference alleles D₁ and D₂. Table 2 describes female mating preference functions used in simulations: D₁₁ females prefer to mate with C₁₁ males over C₁₂ or C₂₂ males, while D₂₂ females prefer C₂₂ males over C₁₂ or C₁₁ males (Table 2). This causes female sexual selection on the male sexual cue locus, while female preference is selectively neutral without reinforcement selection (i.e., Fisherian sexual selection: Kirkpatrick 1982). Strong female mating preferences are assumed so as to increase the speed of speciation (i.e., homozygote D locus females have 20 times higher likelihood of mating with preferred homozygote than heterozygote males at C locus; e.g., Higashi et al. 1999; Servedio and Burger 2014). F1 hybrid females D₁₂ either mate randomly with male genotypes at C locus (i.e., random mating hybrid model) or prefer to mate with C₂₂ males over C₁₂ or C₁₁ males to the same extent as D₂₂ females (i.e., dominant novel preference model; see Table 2).

Table 2.

Female mating preference functions based on D locus genotypes, which is the probability that a female of a given genotype at D locus will mate with a male of a given genotype at C locus upon encounter

	Male genotypes
Female genotypes	C11	C12	C22
Random mating hybrid model (hybrid females mate randomly)
D11	1	0.05	0
D12	0.5	0.5	0.5
D22	0	0.05	1
Dominant novel mating preference model (hybrid females prefer novel male cue)
D11	1	0.05	0
D12	0	0.05	1
D22	0	0.05	1

We assume that ancestrally all populations are initially fixed or nearly fixed for D₁ female mating preference allele and its corresponding C₁ male cue trait allele. This generates sexual selection against the novel C₂ male cue allele. We start our simulations by introducing the novel D₂ preference and C₂ male cue trait alleles at 5% initial frequency in sympatric population of subspecies 2 (Figure 1). Results do not differ if these alleles are introduced in both sympatric and allopatric populations of subspecies 2 (data not shown). Introducing these alleles at lower than 5% initial frequency increases the chance of their loss due to genetic drift and sexual selection (data not shown).

Search costs to novel female mating preference (D₂₂)

We also explored a scenario where the novel female mating preference genotype (D₂₂) may initially suffer a direct fitness cost relative to more established female mating preference genotype (D₁₁). In this case, females that strongly prefer rarer male genotypes suffer search cost of finding them compared to females that prefer more common male genotypes. The search cost is expressed in terms of fecundity reduction of females compared to maximum fecundity in the population (i.e., the more males a female samples before she accepts a mate, the fewer offspring she can sire during the breeding season). Therefore, females that search for rarer males (in this case, D₂₂ females initially searching for rare C₂₂ males), should suffer greater fecundity reduction compared to common established female and male genotypes (initially D₁₁ and C_11, respectively). For simplicity, we assume this is a linear fitness reduction and thus model the process using a linear slope equation: y = m(slope)*x + b, where b is the maximum fecundity parameter per family in the population, x is the number of males a female has to sample before she accepts (determined by female preference strength and frequency of male genotype), m(slope) is a negative slope parameter representing the severity of search cost, and y is the realized fecundity per family taking search cost into consideration (ranging from 0 to b).

Ecological fitness cost to males with a novel sexual cue trait (C₂₂)

We also explore a scenario where the male sexual cue trait experiences stabilizing natural selection in all 3 populations, such that the established male cue trait C₁₁ has optimal ecological fitness relative to the novel C₂₂ male cue trait genotype (e.g., Hoskin et al. 2005). We model this scenario by imposing additional selection (a distinct parameter in the model) against C₂₂ males during the juvenile to adult survival stage in the life cycle of each population.

Definitions and criteria for speciation

We define reinforcement when the sympatric population of subspecies 2 becomes sexually isolated from subspecies 1 as a result of secondary contact. We distinguish 2 possible outcomes: The first is cascade reinforcement, defined when the sympatric population of subspecies 2 evolves to be sexually isolated from both subspecies 1 and from the allopatric population of subspecies 2 as a result of secondary contact between subspecies 1 and 2. This generates RCD. The second is species-wide reinforcement, defined when both sympatric and allopatric populations of subspecies 2 evolve to be sexually isolated from subspecies 1 as a result of secondary contact between subspecies 1 and 2. This would not generate RCD pattern. Finally, simulations may result in the: 1) Loss of novel male sexual cue allele (C₂) and/or loss of novel female mating preference (D₂) allele from all populations, and 2) Loss of fitness loci genetic variation among populations (i.e., genetic extinction; Spencer et al. 1986).

For each general ecological scenario, we explored a total of 121combinations of migration parameters between the 2 subspecies and between sympatric and allopatric populations of subspecies 2. For each combination of migration parameters, we simulated the process with 10 replicates, with each replicate being run for 500 generations after which 1 of the 4 possible outcomes was determined (described above; to ensure that the outcome represents an equilibrium state, we ran representative simulations for 2,000 generations; see section “Results”). The probability of each of the 4 outcomes was based on 10 replicates per combination of explored parameters. Migration rates across simulated populations varied from 0 to 0.5. Other assumptions of the model included: carrying capacity (K) and population size (N_{adults (both sexes)} = 50,000 (50:50 sex ratio) = N_families = 25,000; maximum fecundity_{(per family)} = 10; s_{(DMI selection against A-B loci hybrids)} = 0.55; s_{(Ecological selection at B locus against hybrids)} = 0.55 or 0.90; s_{(Ecological selection at B locus against foreign homoz.)} = 0.55 or 0.90; recomb. rate_{(between all loci)} = 0.25 (which was varied from 0.05 to 0.5 in several simulations), and female mating preference probability matrix in Table 2.

Results

Ecological scenario 1 (sympatric and allopatric populations occupy the same environment)

The first reinforcement scenario we explored was when there were no ecological differences between sympatric and allopatric populations of subspecies 2 (“ecological scenario 1” in Figure 1).

Neutral female mating preference and sexual selection on male cue trait

Before we explored secondary contact, we first studied a scenario without migration between subspecies. We introduced the novel female mating preference D₂ and male sexual cue C₂ alleles at low frequency (e.g., at 5%) in the sympatric population of subspecies 2. We found that these alleles randomly fluctuated in frequency and were lost from the population approximately 95% of the time (data not shown; corresponding to m_ssp1-2 = 0 in Figure 3). This is because without selection against hybridization, female mating preference allele D₂ is selectively neutral and is thus only affected by genetic drift, which in turn determines the evolution of its preferred novel male sexual cue trait C₂. These neutral dynamics serve as a control for our models of secondary contact below.

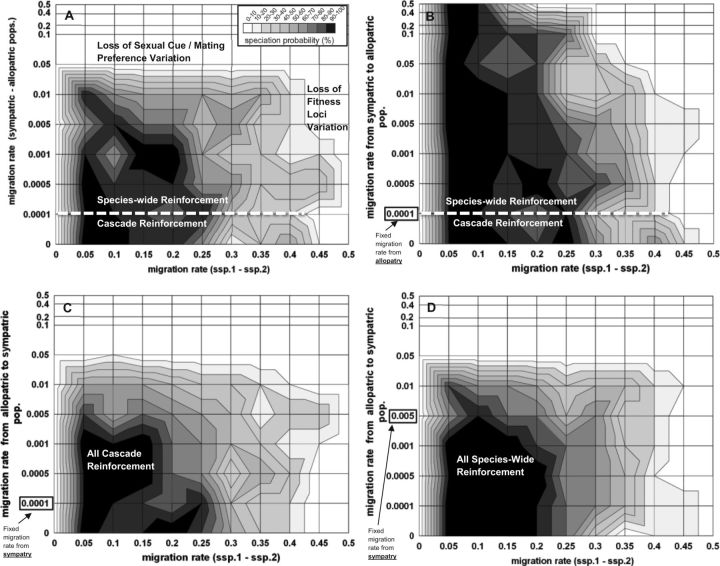
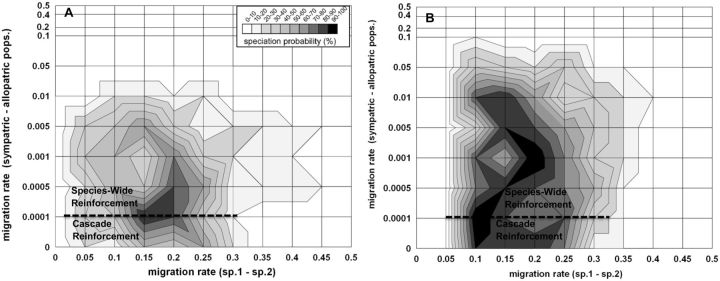
Figure 3.

The probability of reinforcement speciation between subspecies 1 and 2 (z-axis; see insert for shading designation) when subspecies 2 sympatric and allopatric populations occupy the same ecological environment (see “Ecological Scenario 1” in Figure 1). The two outcomes of reinforcement speciation can either be cascade reinforcement or species-wide reinforcement (see text for definitions), for which the parameter space of each is noted in the plot (e.g., designated by a white-dashed line). Also shown are 2 alternative outcomes to speciation: 1) Loss of variation at A-B fitness loci or 2) Loss of variation at C-D loci (applies to all panels). The probability of speciation is determined for each intersection of symmetrical migration rate between subspecies 1 and subspecies 2 (m_ssp1-2; linear x-axis), and migration rates between sympatric and allopatric populations of subspecies 2 (m_sym.-allo.; log y-axis). The rest of the graph is interpolation of these points (i.e., shape of the probability space). Different migration rate scenarios between sympatry and allopatry include: (A) Symmetrical migration rates; (B) Fixed migration rate from allopatry to sympatry at 0.0001 and variable rate from sympatry to allopatry; (C) Fixed migration rate from sympatry to allopatry at 0.0001 and variable rate from allopatry to sympatry; (D) Fixed migration rate from sympatry to allopatry at 0.005 and variable rate from allopatry to sympatry. Additional parameters are: N_{adults (both sexes)} = 50,000; N_families = 25,000; fecundity _{(per family)} = 10; s_{(DMI selection against A-B loci hybrids)} = 0.55; s_{(Ecological selection at B locus against hybrids)} = 0.55; s_{(Ecological selection at B locus against foreign homoz.)} = 0.55; Recomb. rate_{(between all loci)} = 0.25; See Table 2: random mating hybrid model for female mating preference probability matrix.

Probability of reinforcement

Secondary contact between subspecies 1 and 2 causes maladaptive hybridization and ecological divergent selection. We found the highest probability of reinforcement for intermediate migration rates between subspecies 1 and 2 (i.e., x-axis of all panels of Figure 3; m_ssp1-2 between 0.05 to 0.25). Lower migration rates produced weak selective pressures for novel mating preference D₂, resulting in the loss of C₂ or D₂ alleles from the population, while higher migration rates caused the loss of genetic variation at the A and B fitness loci (i.e., genetic extinction; Spencer et al. 1986; data not shown). Reinforcement between subspecies 1 and 2 occurred because C₂ and D₂ behavioral alleles became genetically associated with A₂ and B₂ fitness alleles. Since the ancestral C₁ and D₁ behavioral alleles are initially found in both A₁₁B₁₁ (ssp. 1) and A₂₂B₂₂ (ssp. 2) genetic backgrounds, D₁₁ females with A₂₂B₂₂ genotypes (from ssp.2) migrate and mate with males that carry A₁₁B₁₁ genotype (from ssp.1), which produce maladaptive A₁₂B₁₂ hybrids. In contrast, D₂₂ females with A₂₂B₂₂ genotype (from ssp.2) preferentially mate with C₂₂ males that also carry the A₂₂B₂₂ genotype, thus avoiding the cost of hybridization.

We further found that migration between sympatric and allopatric populations of subspecies 2 was also equally important for the overall likelihood of reinforcement (y-axis of Figure 3). Focusing on the scenario where migration rate between sympatry and allopatry is symmetrical (Figure 3A), reinforcement only occurred when their migration rate was 0.05 or less per generation, with the highest probability of reinforcement occurring for lowest migration rates (i.e., m_sym.-allo. = 0 to 0.005). Higher than 0.05 migration rate resulted in the loss of novel C₂ male cue and D₂ female mating preference alleles from sympatric population (i.e., “swamping effect” from allopatry).

Cascade versus species-wide reinforcement

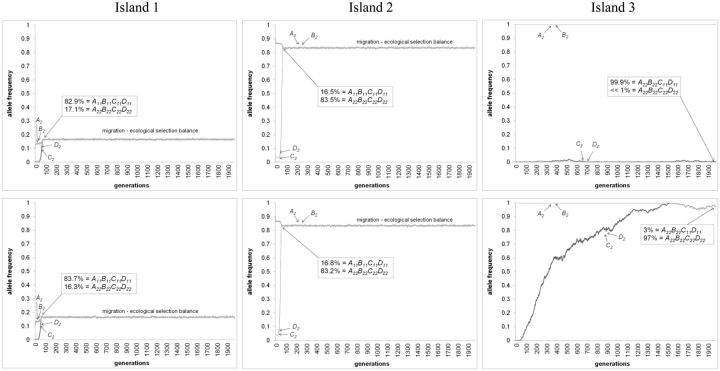
Moreover, we were able to distinguish between two outcomes of reinforcement: Cascade versus species-wide reinforcement (see section “Model” for definitions). First, cascade reinforcement was only observed when migration rates between sympatry and allopatry were very low (in our model less than 0.0001 per generation, which based on our population sizes, roughly equals Nm ≤ 1; Figure 3A). In this scenario, C₂ and D₂ alleles rose to fixation in the sympatric population of subspecies 2 due to reinforcement selection (resulting in A₂₂B₂₂C₂₂D₂₂ genotype), while C₁ and D₁ alleles remained fixed in subspecies 1 and in allopatric population of subspecies 2. Figure 4 upper panels shows the evolutionary dynamics of this process leading to RCD between sympatry and allopatry. After speciation, islands 1 and 2 are each composed of multiple reproductively isolated species that no longer exchange gene flow because they no longer produce F1 hybrids (i.e., C₁₂ and D₁₂ genotypes are absent; e.g., in island 1, A₁₁B₁₁C₁₁D₁₁ is 82.9% and A₂₂B₂₂C₂₂D₂₂ is 17.1%). These species remain indefinitely in migration-selection balance. In island 3 (i.e., in allopatry), A₂₂B₂₂C₂₂D₂₂ migrants exist at very low frequency and are also reproductively isolated from the ancestral population A₂₂B₂₂C₁₁D₁₁. Changing recombination rate from 0 to 0.5 between C and D loci did not affect these results (data not shown).

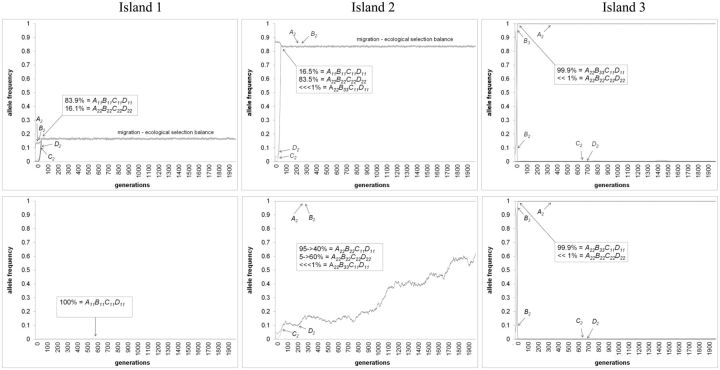
Figure 4.

Examples of simulation runs of Ecological Scenario 1 resulting in: (Upper panels) Cascade reinforcement and (Lower panels) Species-wide reinforcement. Unique parameters for panels: Upper) m_sym.-allo = 0.00001; Lower) m_sym.-allo = 0.001. Shared parameters are: m_ssp1-2 = 0.10; N_{adults (both sexes)} = 50,000; N_families = 25,000; fecundity_{(per family)} = 10; s_{(DMI selection against A-B loci hybrids)} = 0.55; s_{(Ecological selection at B locus against hybrids)} = 0.55; s_{(Ecological selection at B locus against foreign homoz.)} = 0.55; Recomb. rate_{(between all loci)} = 0.25; See Table 2: random mating hybrid model for female mating preference probability matrix. See section “Model” for initial allelic frequencies.

Higher migration rates than 0.0001 between sympatry and allopatry resulted in species-wide reinforcement after 500 simulated generations (Figure 3A). Here, C₂ and D₂ alleles rose to fixation in sympatric population of subspecies 2 and simultaneously spread and fixed within the allopatric population (see Figure 4 lower panels for dynamics). This did not generate RCD between sympatric and allopatric populations, but instead resulted in A₂₂B₂₂C₂₂D₂₂ genotype increasing to even higher frequency in allopatry than in sympatry because the allopatric population was not exposed to migrants of subspecies 1 (see Figure 4 lower panels). This shows that reinforcement alleles from sympatry spread and fix in allopatric populations even if the novel male sexual cue allele is sexually selected against in allopatry (see section “Discussion” for explanation). Once again, altering recombination rate did not change these results (data not shown).

Asymmetrical migration rates between sympatry and allopatry

We then asked whether the limiting factor for cascade reinforcement was due to migration from allopatry or from sympatry (see Figures 3B–D). Increasing the sympatric migration rate while keeping a low allopatric migration rate at or below 0.0001 did not alter the parameter space for cascade reinforcement (Figure 3B). In contrast, a low sympatric migration rate (0.0001 or less) favored cascade reinforcement even when allopatric migration rate was as high as 0.01-0.05 (Figure 3C). This indicates that the limiting factor in the evolution of cascade reinforcement is high sympatric migration rate into allopatry (i.e., the spread of reinforcement alleles into allopatry). To test whether this is due to the relative or absolute migration rates between sympatric and allopatric populations, we increased the sympatric migration rate to 0.005 while varying the allopatric rate from 0 to 0.5 (Figure 3D). All outcomes resulted in species-wide reinforcement, even when the relative allopatric migration rate into sympatry was much higher than the sympatric migration rate into allopatry (Figure 3D). These results indicate that cascade reinforcement could not occur in our model when absolute sympatric migration rate was too high, irrespective of the relative allopatric migration rate. This occurs because a sufficiently high migration rate from sympatry causes reinforcement alleles to spread and fix in allopatry.

Fitness costs to novel reinforcement alleles

We then asked if our results are robust to the introduction of explicit fitness costs to novel female mating preference (search cost to D₂) and to novel male sexual cue (ecological cost to C₂; see section “Model” for details). We found that even minor costs to either novel female mating preferences (Figure 5A) or male sexual cues (Figure 5B) reduced the overall probability of reinforcement. For instance, reinforcement decreased substantially even with a search cost to novel female mating preference of m(slope) = -0.0005, where a female loses only 1 offspring for every 2,000 males she samples (Figure 5A; but see below for reinforcement occurring with more severe search costs when novel mating preference is dominant). However, introducing such costs did not alter the relative parameter space of cascade versus species-wide reinforcement (see Figure 5).

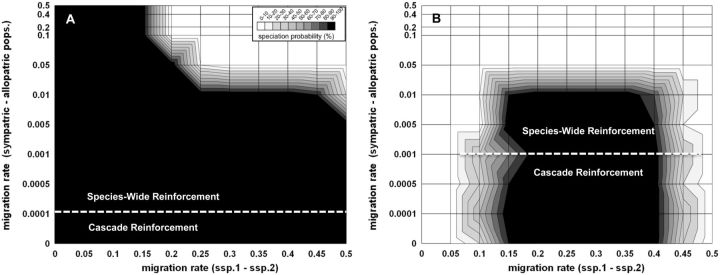
Figure 5.

The effects of: (A) Search cost to novel female mating preference (D₂₂), and (B) Ecological fitness cost to novel male cue trait (C₂₂) on the probability of cascade reinforcement versus species-wide reinforcement (z-axis) for Ecological Scenario 1 in Figure 1. All other parameters and starting conditions are identical to Figure 3A. See section “Model” for details on how fitness costs to females and males was modeled.

Dynamics of dominant novel female mating preference allele

All simulations above assumed that the novel female mating preference allele D₂ required 2 copies to be expressed (i.e., the heterozygote females D₁₂ showed no mating preference). However, we also briefly explored the effect of a dominant novel female mating preference, in which case heterozygote females carrying a single D₂ allele showed the same mating preferences as homozygote D₂₂ females (see Table 2: dominant novel preference model). As expected, with no search costs, the overall probability of reinforcement increased dramatically across the explored parameter space because novel female mating preference and male sexual cue were able to increase in frequency fast enough to overcome the “swamping effect” from allopatry (Figure 6A). However the relative importance of cascade versus species-wide reinforcement remained the same.

Figure 6.

The effect of a genetically dominant novel female mating preference allele over the ancestral female preference on speciation. See Table 2: dominant novel preference model for details. (A) No female search costs, (B) Female search costs at m(slope) = −0.02, where a female loses 1 offspring for every 50 males she samples. All other parameters are identical to Figure 3A.

When search costs were added to the dominant preference model, we found that reinforcement could occur under a wider range of migration rate parameters compared to a model with random mating hybrid females (compare Figures 5A and 6B). We also found a particular search cost for which reinforcement selection could fix the dominant D₂ allele and its corresponding male sexual cue C₂ in sympatry, but was not able to spread the novel reinforcement alleles into allopatry (i.e., resulting in RCD/cascade reinforcement; see Figure 6B). However, even in this particular case, cascade only occurred if the migration rate from sympatry to allopatry was 0.001 or less per generation (Figure 6B). Less severe search costs resulted in species-wide reinforcement (e.g., no search cost of Figure 6A), while more severe search costs prevented the evolution of reinforcement altogether (data not shown).

In conclusion, when there were no ecological differences between sympatric and allopatric populations of subspecies 2, cascade reinforcement only occurred with very little migration rate from sympatry to allopatry (at most 0.0001 per generation) and at most 0.01–0.05 migration rate from allopatry to sympatry. These limitations remained when novel preference and cue experienced explicit costs and only slightly relaxed when the novel female mating preference was dominant over the ancestral allele.

Ecological scenario 2 (sympatric and allopatric populations occupy different environments)

We then explored an ecological scenario where each island population resides in a different environment such that now there is ecological divergent selection also between sympatric and allopatric populations of subspecies 2 (“ecological scenario 2” in Figure 1). Note that ecological divergent selection and sexual selection are based on different loci in this model. The B locus experiences ecological divergence between sympatry and allopatry, while the C locus is the target of sexual selection (see section “Model”). Figure 7 shows the probability of reinforcement when ecological divergent selection at locus B is either 0.55 (Figure 7A) or 0.90 (Figure 7B).

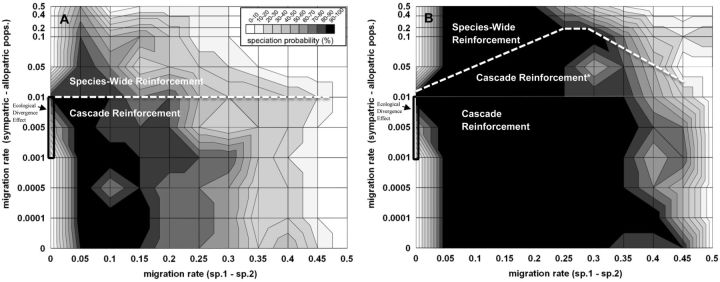
Figure 7.

The probability of reinforcement speciation between subspecies 1 and 2 (z-axis; see insert for shading designation) when subspecies 2 sympatric and allopatric populations occupy different environments (“Ecological Scenario 2” in Figure 1). The two outcomes of reinforcement speciation can either be cascade reinforcement or species-wide reinforcement (see text for definitions), for which the parameter space of each is designated by a white-dashed line. Migration rates are symmetrical between subspecies 1 and subspecies 2 (x-axis) and between sympatric and allopatric populations of subspecies 2 (as in Figure 3A). All 3 populations experience divergent ecological selection at the B locus (see section “Model” for details). Plot A shows results when s (ecological selection) = 0.55 against foreign homozygotes and heterozygotes at B locus. Plot B shows results when s = 0.90. *Cascade reinforcement in plot B is separated into 2 sections (see text for distinction). All other parameters and starting conditions are identical to Figure 3A.

Not surprisingly, the presence of ecological divergent selection between sympatric and allopatric populations allowed reinforcement to occur even with very high migration rates (m_ssp1-2 and m_sym.-allo. as high as 0.45) and increased its probability across the whole parameter space (compare with Figure 3A). Particularly interesting is the effect of ecological divergent selection on cascade versus species-wide reinforcement. Figure 7 shows that cascade reinforcement can evolve with pre-selection migration rates of 0.01 per generation between sympatric and allopatric populations of subspecies 2 (see Figure 8 upper panels, for example of dynamics). In this scenario, island 2 (sympatric population) evolves to be predominantly composed of A₂₂B₂₂C₂₂D₂₂ genotype, while island 3 (allopatric population) rapidly evolves the B₃ allele which leads to A₂₂B₃₃C₁₁D₁₁ as the predominant genotype (see Figure 8A). These remain reproductive isolated from each other.

Figure 8.

Examples of simulation runs of Ecological Scenario 2 that result in the evolution of novel female mating preference D₂₂ and male sexual cue C₂₂ in sympatric population of subspecies 2 (i.e., RCD) for 2 scenarios: (Upper panels) Ecological divergent selection and reinforcement selection and (Lower panels) Ecological divergent selection only. Unique parameters are: Upper panels) m_ssp1-2 = 0.10; Lower panels) m_ssp1-2 = 0. Shared parameters are: m_sym.-allo = 0.001; N_{adults (both sexes)} = 50,000; N_families = 25,000; fecundity_{(per family)} = 10; s_{(DMI selection against A-B loci hybrids)} = 0.55; s_{(Ecological selection at B locus against hybrids)} = 0.55; s_{(Ecological selection at B locus against foreign homoz.)} = 0.55; Recomb. rate_{(between all loci)} = 0.25; See Table 2: random mating hybrid model for female mating preference probability matrix. See section “Model” for initial allelic frequencies.

When ecological divergent selection between sympatry and allopatry was increased to 0.90, we observed the pattern of RCD even with 0.05–0.10 preselection migration rates per generation (see Figure 7B). However, with such high migration rates, the sympatric population had a proportionately high frequency of A₂₂B₃₃C₁₁D₁₁ migrants from island 3 that in turn mated with A₁₁B₁₁C₁₁D₁₁ migrants from island 1 and produced maladapted F1 A₁₂B₁₃C₁₁D₁₁ hybrids (see asterisk in Figure 7B; data not shown). Despite this observation, the pattern of RCD between sympatric and allopatric populations of subspecies 2, once established, persisted indefinitely even with very high migration rates. This expands the overall parameter space of cascade reinforcement and in turn restricts species-wide reinforcement to only very high migration rates (Figure 7).

The relative contribution of reinforcement selection versus ecological divergent selection for cascade reinforcement

While ecological divergent selection between sympatric and allopatric populations clearly facilitates cascade reinforcement, it is important to determine the relative contribution of ecological versus reinforcement selection for the evolution of RCD and sexual isolation between sympatric and allopatric populations. We thus compared the evolution of RCD with only ecological divergent selection (m_ssp1-2 = 0: Figure 9) versus when both selection pressures were acting simultaneously (m_ssp1-2 = 0.10: Figure 9).

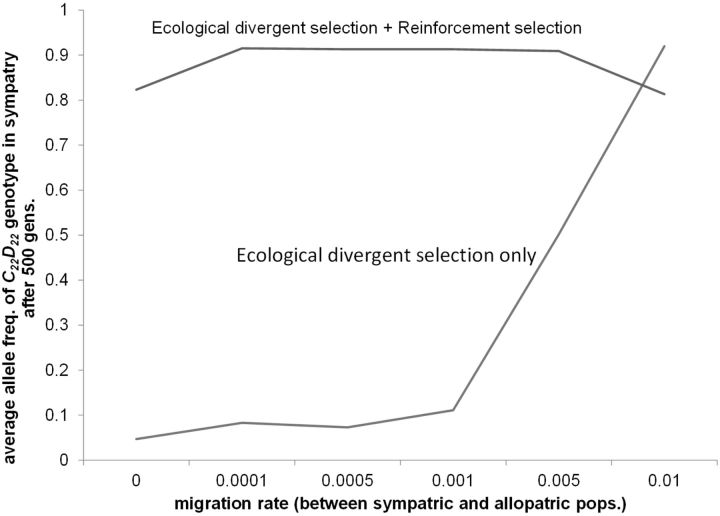
Figure 9.

The relative contribution of ecological divergent selection versus reinforcement selection to the evolution of RCD in sympatric population of subspecies 2. The average final frequency of C₂₂D₂₂ genotype in the sympatric population of subspecies 2 is shown after 500 generations for scenarios with: (A) Ecological divergent selection and reinforcement selection versus (B) Ecological divergent selection only. Scenario A was simulated with m_ssp1-2 = 0.10 (i.e., secondary contact). Scenario B was simulated with m_ssp1-2 = 0 (i.e., no secondary contact). Other parameters are identical to Figure 7A. The average frequency of genotype is based on 10 simulation runs per migration rate between sympatric and allopatric populations (m_sym.-allo; x-axis). Results are only shown for migration rates that resulted in cascade reinforcement (see Figure 7A).

Our results showed that ecological divergent selection between sympatric and allopatric populations alone drove the evolution of RCD when migration rates between sympatry and allopatry were 0.001 or higher (see Figure 8 lower panels for dynamics and Figure 9). This occurred in our model because hybrids fall-in-between 2 ecological niches, resulting in average underdominance across these environments. In contrast, RCD with lower migration rates than 0.001 between sympatry and allopatry could not evolve unless there was reinforcement selection (Figure 9). These results imply that while the evolution of RCD is still largely attributed to reinforcement selection with zero or very low migration rates between sympatric and allopatric populations (i.e., when m_sym.-allo. = 0 to 0.001), this assignment becomes much more difficult when these populations exchange more migrants (m_sym.-allo. > 0.001). Below we discuss what this result implies for the evolution of cascade reinforcement.

Discussion

In the present article, we explored the theoretical conditions for cascade reinforcement relative to alternative outcomes of secondary contact when sympatric and allopatric populations experienced gene flow. All of our scenarios assumed secondary contact between previously allopatric subspecies that produce partial zygote inviability and also experience divergent ecological selection between their environments. Following previous work on the topic, we define cascade reinforcement as when sympatric populations evolve to be sexually isolated from their allopatric counterparts because of RCD from another subspecies (e.g., Ortiz-Barrientos et al. 2009; Hoskin and Higgie 2010). Our focus was primarily to determine whether cascade reinforcement can evolve when sympatric and allopatric populations differ only in the cost of hybridizing with another nascent species (sensu Ortiz-Barrientos et al. 2009; Hoskin and Higgie 2010). To contrast this, we also explored the effect of one type of ecological divergent selection between sympatric and allopatric populations on the evolution of RCD and cascade reinforcement. Before we discuss our major findings it is important to consider the limitations and assumptions of our model.

Definitions of cascade reinforcement

First, our study focused on a “two-allele” mating preference model (sensu Felsenstein 1981), where a novel female mating preference in sympatry diverges from an ancestral mating preference for a different male sexual cue. This causes sympatric and allopatric populations to become sexually isolated in both directions. We refer to this as “symmetrical cascade reinforcement,” which has been described between green-eyed tree-frogs of Litoria (Hoskin et al. 2005), spadefoot toads S. multiplicata and S. bombifrons (e.g., Pfennig and Simovich 2002; Pfennig and Ryan 2006; Pfennig and Rice 2014), and between sea rock-pool beetles of Ochthebius (Porretta and Urbanelli 2012). However, other cases appear to show “asymmetrical cascade reinforcement,” for instance, where sympatric females strongly discriminate against allopatric males, but allopatric females mate randomly (e.g., Jaenike et al. 2006; Dyer et al. 2014; Bewick and Dyer 2014; Kozak et al. 2015). We briefly describe the outcome of this scenario below.

Limitations of the current model

Given our focus on studying gene flow between simulated populations, we were forced to keep other parameters more or less constant such as strength of selection, mating preference matrix, and to some extent recombination rates. Our preliminary results suggest that varying these parameters had a relatively minor effect on the evolutionary outcome of cascade reinforcement compared to the effect of gene flow and divergent ecological selection between sympatric and allopatric populations that we did explore in some detail (see below).

Second, as is typical of most models of reinforcement (e.g., Felsenstein 1981; Kirkpatrick 1982; Kelly and Noor 1996; Servedio and Kirkpatrick 1997; Servedio 2000, 2004), our model assumed that the genetic and phenotypic architecture of DMIs and mating phenotypes were based on traits and loci of large effect. Simple genetic models of speciation should not necessarily be seen as unrealistic because the number of fitness and mating behavior genes that diverge to cause speciation between nascent species may actually be very small compared to the overall genetic architecture of these traits (e.g., Doi et al. 2001; Tauber et al. 2003; Greenberg et al. 2003; Ortiz-Barrientos and Noor 2005; Chung et al. 2014). Barton and Hewitt (1981) and others (e.g., Servedio and Noor 2003) have pointed out that the likelihood of reinforcement should be reduced when the genetic architecture of fitness and mating traits becomes more complex and when mating preferences are weaker and based on multiple sexual traits. Future work should expand our results to more complex genetic architectures governing cascade reinforcement.

We also assumed that populations reside in discrete habitats or “islands” (following most reinforcement models; see above). While using islands simplifies the model and computation, and may be applicable to natural systems residing in discrete habitats, it forces all individuals within each island to experience the same level of migration and gene flow, and avoids the physical limitations of rare individuals finding suitable mates. Such limitations may be important in more geographically continuous populations and if studied explicitly in the future, may enhance the likelihood of cascade reinforcement.

Cascade reinforcement with no ecological differences between sympatry and allopatry

First, we found that high allopatric migration rate (in our simulations 0.05 per generation) into sympatry prevented the evolution of reinforcement, ultimately swamping out the novel female mating preference and male sexual cue in sympatry. The only time reinforcement occurred with such high migration rates from allopatry was when the novel female mating preference allele was assumed to be genetically dominant over the ancestral preference and did not experience search costs. These findings are consistent with historical criticisms of reinforcement (e.g., Bigelow 1965; Barton and Hewitt 1985; Sanderson 1989) and suggest that when sympatric and allopatric populations do not experience ecological divergence, reinforcement between subspecies may only occur when there is limited migration from allopatry into sympatry.

Sexual selection against reinforcement male cues in allopatry does not prevent the spread of reinforcement alleles outside the zone of contact

When the only difference between sympatric and allopatric populations is exposure to maladaptive hybridization with the foreign subspecies (ecological scenario 1), our results revealed that cascade reinforcement was highly unlikely. Specifically, cascade reinforcement in this context could only evolve with very little migration rate from sympatry to allopatry (less than 0.0001 per generation; effectively Nm ≤ 1). These limitations remained when the novel female preference experienced explicit search cost and when the novel male sexual cue experienced an ecological fitness cost. In this model, higher migration rates from sympatry to allopatry always allowed the novel reinforcement alleles to spread and ultimately fix in the allopatric population, which resulted in “species-wide reinforcement.” These results held for cases where the ancestral females across all populations were initially assumed to be randomly mating rather than having a sexual preference for an ancestral male trait (data not shown). In such cases, we found that a random mating allele was rapidly eliminated from all three island populations because the preference alleles were favored by reinforcement selection and aided by Fisherian sexual selection (data not shown).

By exploring different asymmetrical migration rate scenarios, we also discovered that the limiting migration rate was absolute rather than relative from sympatry. Meaning that higher than 0.0001 migration rate from sympatry to allopatry resulted in reinforcement alleles spreading and eventually fixing in allopatry, even if migration rate was much higher from allopatry into sympatry. Thus contrary to suggestions (Ortiz-Barrientos et al. 2009), our results show that it is not asymmetrical migration rate between sympatry and allopatry that matters, but rather the absolute migration rate from sympatry that dictates whether cascade can evolve.

In general, these results challenge the assumption that cascade reinforcement can evolve between ecologically similar populations that only differ in their exposure to reinforcement selection (sensu Ortiz-Barrientos et al 2009; Hoskin and Higgie 2010). However, we did find that the signature of RCD and cascade can still “linger” for many hundreds of generations until allopatric populations reach equilibrium (Ortiz-Barrientos et al. 2009).

Why species-wide reinforcement wins out over cascade reinforcement in the presence of gene flow between sympatry and allopatry

Our findings challenge previous arguments that stabilizing sexual selection in allopatry should restrict sympatric reinforcement alleles from spreading into allopatry (Moore 1957; Patterson 1978; Barton and Hewitt 1985; Spencer et al. 1986; Sanderson 1989; Coyne and Orr 2004, p. 371; but see Liou and Price 1994, p. 1457). This does not happen in our model for the following reason: While it is true that the novel sympatric male sexual cue is strongly sexually selected against by allopatric females, this matters very little because sympatric females also migrate into allopatry and prefer this novel male sexual cue proportional to their frequencies. At the same time, the novel sympatric female mating preference is on average selectively advantageous over the ancestral female mating preference in sympatry (due to reinforcement selection). Migration from sympatry to allopatry thus inevitably increases the frequency of the sympatric female mating preference allele in allopatry every generation since there is nothing else preventing its rise outside the zone of contact.

Interestingly, we found that imposing a search cost to the novel female mating preference allele did not generally alter the above results. Instead, the search cost determined if the new reinforcement mate preference allele would evolve in the first place in sympatry and if it did, then it would typically spread into allopatry and fix. The only time we observed high search costs prevent the spread of a novel sympatric mating preference allele into allopatry was when we assumed the novel preference allele to be genetically dominant. We were then able to identify a specific level of search cost that perfectly counter-balanced the dominant mutation’s advantage. However, it does not appear that such a case would be general, and even in this case, migration rate from sympatry still had to be lower than 0.001 per generation to get cascade reinforcement. These findings do not support the suggestion that high search costs of novel reinforcement mating preferences will prevent their spread into allopatry (e.g., Ortiz-Barientos et al. 2009).

Does male-biased dispersal aid the evolution of cascade reinforcement?

Our results lead to the prediction that if sympatric males with the novel sexual cue trait were instead the primary migrants into allopatry (and females were generally sedentary), it is conceivable that cascade reinforcement could occur under a wider range of sympatric migration rates than is found in the present model. This is because under male-biased dispersal, it is likely that males with the novel sexual cue trait would not be able to mate successfully in allopatry and this would in turn prevent both the male trait and the novel female mating preference from spreading into allopatry. Future work is necessary to test this hypothesis. With this possible exception our results generally suggest that when sympatric and allopatric populations only differ in their exposure to reinforcement selection, cascade reinforcement appears unlikely to occur in the presence of gene flow.

The role of divergent ecological selection between sympatry and allopatry for the evolution of cascade reinforcement

Migration rates between sympatric and allopatric populations may often exceed 0.0001 per generation in many biological systems including in some of the described empirical cases of cascade reinforcement (e.g., Rice and Pfennig 2010; Bewick and Dyer 2014). Thus, we explored whether ecological divergent selection between sympatric and allopatric populations could possibly facilitate cascade reinforcement under a wider range of migration rates (ecological scenario 2). Divergent ecological selection in our model was based on a fitness locus that was distinct from the sexual cue locus such that these could recombine. Foreign homozygote and heterozygote individuals at the ecological fitness locus experienced divergent ecological selection when they migrated between sympatric and allopatric populations, such that hybrids on average had lower fitness than homozygote individuals (i.e., hybrids were maladaptive between ecological niches).

We found that the overall probability of reinforcement and the parameter space of cascade reinforcement relative to species-wide reinforcement increased substantially and evolved when migration rates between sympatry and allopatry were much higher than 0.0001 per generation. This was because the female mating preference and male sexual cue alleles in sympatry and allopatry became genetically associated with the ecological fitness allele in each population and this prevented the novel sympatric reinforcement alleles from spreading and fixing in allopatry. We expect that decreasing recombination rate between ecological and sexual traits would increase the likelihood of this scenario even further.

However, despite this encouraging observation, we found that divergent ecological selection between sympatry and allopatry all by itself could cause the evolution of sexual isolation between these populations when migration rates were higher than 0.001 per generation. This poses a potential problem for empirical studies of cascade reinforcement since for those cases with such migration rates it becomes difficult to tease apart whether reinforcement selection or ecological selection or both caused sexual isolation between sympatric and allopatric populations. This issue appears to require further attention in our understanding of how and why patterns of cascade reinforcement are generated in nature and whether ecological divergence between sympatric and allopatric populations should be a part of this definition.

In conclusion, our results provide a general theoretical framework for understanding when RCD will lead to speciation between sympatric and allopatric populations (i.e., cascade reinforcement) versus when it will lead to reinforcement alleles spreading into allopatric populations (i.e., erasing RCD and leading to species-wide reinforcement). In general, our model revealed that cascade reinforcement was unlikely to evolve between sympatric and allopatric populations exchanging migrants if the only difference between them is divergent sexual selection due to reinforcement selection. This potentially implies that natural populations that do show patterns consistent with cascade reinforcement have likely either diverged with very little gene flow or were partially or completely driven by ecological divergent selection rather than pure reinforcement selection.