Speciation along a shared evolutionary trajectory

Abstract

Groups of organisms—whether multiple species or populations of a single species—can differ in several non-exclusive ways. For example, groups may have diverged phenotypically, genetically, or in the evolutionary responses available to them. We tested for the latter of these—response divergence—between 2 species of woodrats: Neotoma fuscipes and Neotoma macrotis. Based on random skewers analyses we found that, despite being well differentiated both phenotypically and genetically, N. fuscipes and N. macrotis appear to be diverging along a shared evolutionary trajectory (r° = 0.895, P = 0.114). Because these species are currently in secondary contact, their phenotypic evolution being along a shared evolutionary axis has important implications. In particular, that their response to selection arising from interspecific interactions will be constrained along the same evolutionary trajectory may reduce the potential for reinforcing selection to maintain species boundaries.

A major goal in evolutionary biology is to identify the patterns and processes associated with divergence among groups of organisms. Describing and quantifying patterns of divergence is necessarily multi-faceted because groups of organisms can diverge from one another in several ways. For example, groups may exhibit phenotypic divergence, wherein they differ from one another in mean trait values of phenotypic characters ranging from morphology to behavior. Groups may also exhibit genotypic divergence wherein genetic differentiation has occurred. Additionally, groups may diverge in their potential evolutionary responses to selection, placing them on distinct evolutionary trajectories. This third type of divergence, which we will refer to as response divergence, has been suggested but has rarely been explicitly tested and compared with phenotypic and genotypic divergence of natural populations (Cheverud and Marroig 2007).

Response divergence, as defined here, is largely an outcome of differences among groups in the patterns of how traits vary and covary. Trait variances and covariances are of central importance in evolutionary biology (Steppan et al. 2002) because these relationships among traits, both phenotypically and genetically, determine how populations may respond to selection (Lande and Arnold 1983). Currently many methods are available for comparing how populations differ in trait variances and covariances (reviewed by Roff et al. 2012, Aguirre et al. 2014). One criticism of most methods, however, is that they are often detached from the general body of evolutionary theory and so inferences can be difficult to tie to evolutionary outcomes regarding population divergence and selection responses (Aguirre et al. 2014).

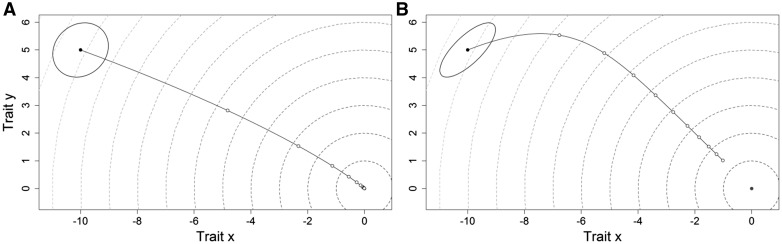
Group differences in (co)variances connect to differences in selection responses because how traits covary within groups and relative differences in trait variability among groups change the evolutionary trajectories available, that is, response divergence. For example, if 2 groups are evolving toward the same optimum and from the same starting point, how traits are correlated and how much variation is present within traits will affect how the populations move along a fitness landscape and how many generations are required to reach an optimal phenotype. While these populations will eventually reach the same optima (if stationary), the amount of time required to do so can differ greatly as will mean genotypes and phenotypes along the way (Figure 1). At any single time point along these paths, the populations will appear to have evolutionary diverged because of the effects of covariances on responses even if ultimately they are evolving toward the same phenotypic optima. Further, with moving optima, the two populations maybe prevented from reaching the same location within an adaptive landscape.

Figure 1.

Example responses of 2 populations (A and B) to selection on 2 traits (x and y). In both populations, the optimum is located at x = 0, y = 0, both populations start with the same trait means (−11, 5), selection occurs over 1,000 generations, and the strength of selection is the same for both populations. Plotted in both A and B are the bivariate distributions (solid ellipse), the change in populations means in response to selection (solid line), and the fitness landscape (dashed gray lines). Population means in 100 generation steps are plotted as small open circles along the response trajectory. In population A, the 2 traits are positively but weakly correlated (r = 0.15). In population B, the two traits are positively and more strongly correlated (r = 0.75).

Response divergence can best be understood in the context of the multivariate response to selection. The evolutionary change in trait means as a response to linear selection (denoted as the vector Δz) can be estimated as (Lande 1979; Lande and Arnold 1983):

$$\Delta \mathbf{z}=\mathbf{G}\mathbf{\beta }$$ (1)

where G is a matrix with additive genetic variances of traits along its diagonal and additive genetic covariances off the diagonal and β is the selection gradient (i.e., selection differentials standardized by trait (co)variances). In contrast to phenotypic divergence and genotypic divergence, which are current attributes of populations, response divergence corresponds to differences in Δz, the expected change of trait means in response to selection. The set of values in Δz corresponds to a location in multivariate space and, for the same β, groups may end up with different genotypic and phenotypic trait means even after just one generation of selection due to differences in G. Such a difference represents a divergence in evolutionary trajectories, placing groups on different evolutionary paths.

Whether groups exhibit response divergence in this sense will largely be based on how the (co)variation summarized by G is oriented in multivariate space. For example, for any G there will be a direction in multivariate space in which the greatest additive genetic variance is oriented (i.e., “g_max”, Schluter 1996). g_max influences selection responses because selection will not initially be simply in the direction of greatest fitness increase but instead will also be influenced by the direction of greatest variation (Figure 1B; this curving effect continues until g_max is orthogonal to the optima). The influence of g_max on evolutionary processes can be quite profound, with differences in g_max explaining a substantial amount of variation in patterns of morphological divergence (e.g., Schluter 1996). Differences in g_max can, therefore, be indicative of response divergence. However, differences in g_max may not sufficiently demonstrate response divergence as other directions in multivariate space may contain substantive amounts of variation and likewise impose effects on evolutionary responses. Thus, an overall demonstration of response divergence at the level of G becomes necessary.

Cheverud and Marriog (2007) and Calsbeek and Goodnight (2009) have, however, argued that the statistical demonstration of statistical differences in phenotypes and in G do not necessarily correspond to divergence in available evolutionary trajectories. As a result, determining how phenotypic and genotypic divergence relate to response divergence can be difficult to determine (Cheverud and Marroig 2007). Indeed, the correspondence between phenotypic, genotypic, and response divergence has rarely been assessed (but see de Oliveira et al. 2009, Porto et al. 2009).

While not typically explicitly articulated, the concept of response divergence is consistent with many existing approaches to evaluating differences among population G’s. For example, one approach of comparing matrices is to challenge G matrices from two or more groups with random β’s (i.e., multiplying the G matrices by β vectors, equation 1) and compare the response vectors (Δz’s). This approach—known as a “random skewers” analysis (Cheverud and Marriog 2007)—then estimates the correlation between responses allowing a pairwise estimation of response divergence. An analogous approach, “selection skewers”, incorporates phenotypic information (Calsbeek and Goodnight 2009). Similarly, the angle between g_max vectors for each pair of groups will estimate the degree of response divergence imposed by one direction of available variation. Comparisons of G matrix eigenvalues achieves a similar function (Krzanowski 1979; Roff et al. 2012; Aguirre et al. 2014), while more complicated analyses can reveal additional details of how matrices might differ (e.g., “tensor analysis”: (Hine et al. 2009, Aguirre et al. 2014); “hierarchical analysis” (Arnold and Phillips 1999; Roff et al. 2012)). Of this variety of approaches, random and selection skewers approaches along with a calculation of the angle between g_max vectors best test for the presence of response divergence while alternative analyses can identify specific differences among populations in how traits vary and covary.

To address correspondence among the phenotypic, genotypic, and response divergence and to understand the potential evolutionary dynamics between recently diverged species in secondary contact, we sought to determine whether previously identified phenotypic and genotypic differences between 2 species of woodrats (Neotoma fuscipes and Neotoma macrotis) were associated with response divergence. We tested for response divergence in skull morphology between the 2 species using1) random skewers analysis, which tests for congruence between groups in response to random selection gradients; and 2) a test of whether most morphological variation was oriented differently in multivariate space for the 2 species. We also 3) used hierarchical (Flury) analyses, and 4) modified tensor analyses to determine relevant matrix differences that might contribute to response divergence.

Materials and Methods

To test for interspecific phenotypic, genotypic, and response divergence we used data previously collected from N. fuscipes and N. macrotis (Matocq and Murphy 2007). These two species are sister lineages that diverged from a common ancestor approximately 2 million years ago (Matocq 2002b) and share 2 major contact zones: one in the Salinas Valley of California (Matocq 2002a) and the other in the foothills of the central Sierra Nevada of California (Matocq and Murphy 2007).

Matocq and Murphy (2007) measured 11 craniodental traits for 82 individuals captured across the contact zone in the Sierra Nevada of California (Figure 2). We adjusted measurements for differences due to allometry (Matocq and Murphy 2007) and estimated covariances among these craniodental traits. Phenotypic covariances often correspond to genetic covariances (Cheverud 1988; Roff 1996; Dochtermann 2011), a common and often appropriate assumption for morphological traits like skull morphology (Cheverud 1996; de Oliveira et al. 2009; Porto et al. 2009) but see (Willis et al. 1991), and thus we used phenotypic variances and covariances in lieu of genetic variances and covariances to test for evolutionary divergence. Unfortunately, because these were wild caught individuals and we used phenotypic measure, these data could conflate differences between the populations in gene by environment interactions with genetic differences in morphology. Because of our final results we do not consider such conflation to significantly affect our inferences.

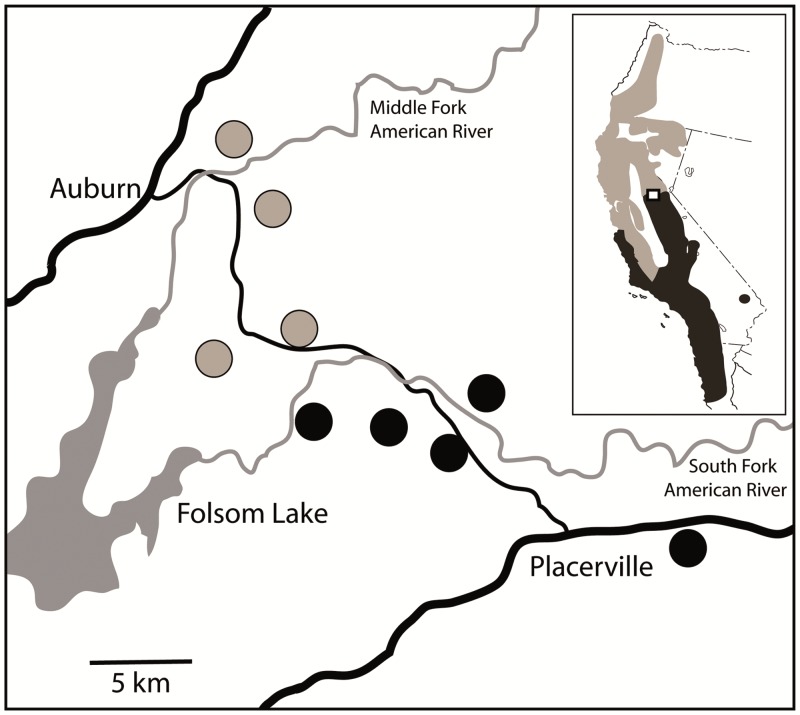
Figure 2.

Sampling locations for N. fuscipes (gray fill) and N. macrotis (black fill). Inset shows the location of sampling locations in California, USA, in an area of secondary contact. Gray shading shows range of N. fuscipes and black shading shows the range of N. macrotis.

To determine whether the 2 species exhibited response divergence, we conducted a “random skewers” analysis (Cheverud and Marroig 2007). Using phenotypic covariance matrices we determined whether the 2 Neotoma species have diverged to the point of now being on different evolutionary trajectories. The random skewers approach tests for differences among groups in response to selection (i.e., Δz; equation 1) when exposed to the same selection gradient (i.e., β; equation 1). This difference is tested by applying a set of randomly generated selection gradients (here N = 1,000) to the covariance matrices estimated for each group. We then evaluated the vector correlation (r°, i.e., $\frac{\mathit{A}·\mathit{B}}{\Vert \mathit{A}\Vert \Vert \mathit{B}\Vert }$) between groups among the set of responses to determine whether the response trajectories for the 2 species were shared. Following Calsbeek and Goodnight (2009) we were primarily interested in whether this correlation differed from 1, which was tested via randomization using the RAND.SKEWER function of Roff et al. (2012) in the R programming language.

To determine whether variation in skull morphology is similarly oriented for the 2 species, we conducted a test of whether “the multivariate direction of greatest (variation)” differed between the 2 species (Schluter 1996). This “direction of greatest variation” is typically estimated from estimates of genetic parameters as “g_max” but here was estimated from phenotypic data, i.e., as “p_max”. To test whether p_max differed between the species we first calculated r° between the estimates for each species. Next, using randomization (N = 1,000), we estimated the null distribution of r° values to calculate the P value for the observed r° versus a null expectation of 1.

To further explore potential differences between the 2 species in trait variances and covariances, we also conducted a hierarchical analysis following Arnold and Phillips (1999) and a partial tensor analysis following Hine et al. (2009). Hierarchical analyses assess a range of possible ways in which matrices might differ (see Figure 2 in Roff 2000) and which can be indicative of whether selection and drift have influenced population divergence. In a hierarchical analysis whether or not 2 populations exhibit common principal components versus unrelated structures (e.g., orthogonal greatest eigenvectors) is first tested. Next, a hypothesis of proportional (co)variance is tested versus unrelated structure, followed by a test between matrix equality versus unrelated structure (i.e., a jump-up approach; Arnold and Phillips 1999). Hierarchical testing was conducted via randomization testing (N = 500) using the MATRIX.TESTS function of Roff et al. (2012). Tensor analyses (Hine et al. 2009) likewise compares matrix structure but reveals which particular traits are primarily contributing to matrix differences. Here we estimated a fourth order covariance tensor which we then summarized in matrix form and extracted the resulting 66 element diagonal. We used randomization testing (N = 1,000) to test which traits showed differences between the two populations in variances or covariances. Because this approach required testing for differences in 66 parameters so to control for family-wise error we a priori set our critical P value to 0.001.

Finally, because random skewers analysis and the high vector correlation between p_max ‘s for the 2 species demonstrated a lack of response divergence (see below), we compared the placement of the 2 species along a shared p_max. To do so we first conducted a principal components reduction of the phenotypic scores of the entire dataset, pooling N. macrotis and N. fuscipes. The first component, corresponding to their shared p_max, explained 57% of the observed variation (the second pc, p₂, only explained 9.7%). We then used an unequal variance t-test to compare pc scores between the 2 species. This tested for whether the 2 species differed in their location along p_max and p₂, and thus whether they have diverged along this shared evolutionary trajectory as is generally predicted (Schluter 1996).

Results

Despite previous demonstration of phenotypic and genetic divergence (Matocq and Murphy 2007), N. fuscipes and N. macrotis did not differ according to a random skewers analysis. The average response vector correlation (r°) was 0.895, which did not differ from 1 (P = 0.114). Likewise, the majority of variation (p_max) was oriented in the same direction for the 2 species (r° = 0.977, P = 0.509). Consistent with these results, hierarchical analysis indicated that the covariance matrices for the 2 species were equal (P = 0.312, Table 1). Tensor analysis likewise did not detect differences between N. macrotis and N. fuscipes (Table S1).

Table 1.

Hierarchical analysis results

Hierarchical level	P
Equality	0.312
Proportionality	0.634
CPC	0.716

P values are from randomization and indicate whether the hierarchical level being evaluated cannot be rejected on the basis of comparing its fit versus that of unrelated structure. Here N. fuscipes and N. macrotis exhibited equivalent covariance matrices.

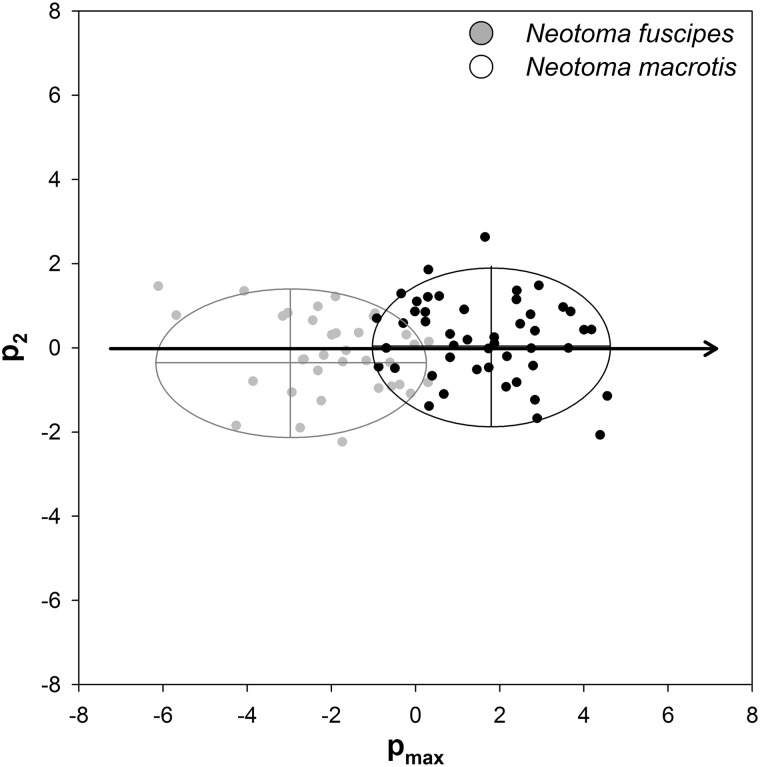
Finally, despite the lack of response divergence found via random skewers analysis and the comparison of p_max vectors and, consistent with the findings of Matocq and Murphy (2007), the 2 species have phenotypically diverged along this shared evolutionary trajectory (t_72.25=10.66, P ≪ 0.001; Figure 3). The 2 species did not differ in their second principal component (p₂, t_74.33=1.60, P = 0.11; Figure 3).

Figure 3.

Relative orientations of variation in skull morphology. Ellipses represent the 95% range of variation for the 2 main directions of variation (p_max and p₂) for each of the 2 species while points correspond to the scores for members of each species. p_max scores were estimated using principal components analysis and are the phenotypic equivalent of g_max while p₂ is the multivariate direction with the second greatest variation (the second principal component). The arrow represents the location of p_max relative to p₂ for the 2 species jointly. The 2 species have diverged in their location along the joint p_max (t₃₄=7.97, P ≪ 0.001; Figure 3) but not in their second principal component (p₂, t₃₄=1.22, P = 0.23; Figure 3).

Discussion

Combined, these results suggest that N. fuscipes and N. macrotis do not exhibit response divergence. While the hierarchical analyses and examination of the fourth-order covariance tensor are consistent with the general conclusion, that the 2 species do not demonstrate response divergence is primarily based on results from the random skewers analysis and comparison of the phenotypic equivalent of g_max (i.e., p_max). The first of these analyses demonstrated that the correlation in response vectors for the 2 species was 0.895 and did not significantly differ from 1. The p_max for each species were similarly highly correlated (r° = 0.977). However, as our sample sizes were quite small for estimating covariance matrices for 11 traits, it is possible that we were simply unable to detect a biologically significant effect with statistical significance.

Three main pieces of information suggest otherwise. First, the actual observed values from the random skewers test and the comparison of p_max vectors suggest strong similarity between the 2 populations. Second, we used bootstrapping to estimate a 95% confidence interval (CI) around the r° for the 2 species’ p_max. The lower bound for r° was 0.72 which, while representing a much greater angle between the vectors still indicates that variation was largely oriented in the same direction (Supplementary Text 2). Finally, as for p_max, we again used bootstrapping to estimate the 95% CI around both the average response vector correlation (r° 95% CI: 0.70: 0.86), again indicating relatively high correspondence. Combined, this suggests that our failure to detect statistically significant differences is due to an absence of biologically significant differences. That is, despite significant divergence in other genetically and for mean morphology, the two species are morphologically differentiating along a shared evolutionary axis.

As proposed by Cheverud and Marriog (2007) and Calsbeek and Goodnight (2009), our findings suggest that statistically significant phenotypic and genotypic differences are not necessarily representative of response divergence. This conclusion is important to keep in mind when comparing population, species, or other levels of grouping. In particular, researchers often—and reasonably—infer that mean differences indicate divergence. However, as was the case here with wood rats, such a demonstration is not necessarily indicative of how populations may evolve in the future.

Matocq and Murphy (2007) suggested that the morphological differences between N. fuscipes and N. macrotis in the areas surrounding the region of secondary contact of the two species may be due to character displacement arising from competition for resources and shifts in resource use. In particular, variation in the traits discussed here correspond to potential dietary differences between the species (Matocq and Murphy 2007), mirroring fine-scale diet divergences observed at contact zones between other closely related species of woodrats (Shurtliff et al. 2014). Our analyses are consistent with this explanation but suggest that divergence between the 2 species has been constrained or facilitated along the same evolutionary trajectory. This finding is generally consistent with earlier analyses which have likewise found divergence to primarily occur in the phenotypic directions with the greatest variation (Schluter 1996).

The highly concordant selection responses and evolutionary trajectories maintained across this species boundary have potentially important implications for the potential pace and direction of phenotypic evolution in response to interspecific interactions between these lineages when they come into contact. Possible implications in secondary contact include: first, selection along “lines of least genetic resistance” (i.e., g_max; Schluter 1996) will be more rapid than selection in other directions. As a result, character displacement resulting from competition resulting in selection along this line could be accelerated under secondary contact. Such an outcome would thereby facilitate coexistence of the 2 species. Simultaneously, however, this character displacement would be constrained by the shared evolutionary trajectories. How this might affect the efficacy of reinforcing selection in secondary contact is currently unclear.

Besides just differences via selection, the finding that the 2 species do not exhibit response divergence and the maintenance of evolutionary trajectories could also lead to an erosion of species differences and species boundaries due to drift. Just as selection responses are more rapid in directions with greatest variation, so too is drift greater in those directions. Under relaxed selection, our 2 species would primarily exhibit drift along the same phenotypic axes. Thus, possible divergence due to drift will be limited in phenotypic space relative to if there were no correlations among craniodental traits. Indeed, the 2 populations exhibit phenotypic divergence along p_max but not in the direction with the second most variation (p₂, Figure 3). Indeed, following the rationale of Roff (2000), our hierarchical analysis results are consistent with a hypothesis of drift (though selection cannot be rejected without additional data).

Whether and which of any of these inferences are appropriate is currently unclear. How an absence of divergence in evolutionary trajectories facilitates or constrains ecological and reproductive character evolution in response to species interactions in zones of secondary contact also requires further empirical and theoretical investigation. The limitations and opportunities of response along a shared evolutionary axis may play a fundamental role in phenotypic evolution, particularly in areas of sympatry between closely related species.