Navigating the currents of seascape genomics: how spatial analyses can augment population genomic studies

Abstract

Population genomic approaches are making rapid inroads in the study of non-model organisms, including marine taxa. To date, these marine studies have predominantly focused on rudimentary metrics describing the spatial and environmental context of their study region (e.g., geographical distance, average sea surface temperature, average salinity). We contend that a more nuanced and considered approach to quantifying seascape dynamics and patterns can strengthen population genomic investigations and help identify spatial, temporal, and environmental factors associated with differing selective regimes or demographic histories. Nevertheless, approaches for quantifying marine landscapes are complicated. Characteristic features of the marine environment, including pelagic living in flowing water (experienced by most marine taxa at some point in their life cycle), require a well-designed spatial-temporal sampling strategy and analysis. Many genetic summary statistics used to describe populations may be inappropriate for marine species with large population sizes, large species ranges, stochastic recruitment, and asymmetrical gene flow. Finally, statistical approaches for testing associations between seascapes and population genomic patterns are still maturing with no single approach able to capture all relevant considerations. None of these issues are completely unique to marine systems and therefore similar issues and solutions will be shared for many organisms regardless of habitat. Here, we outline goals and spatial approaches for landscape genomics with an emphasis on marine systems and review the growing empirical literature on seascape genomics. We review established tools and approaches and highlight promising new strategies to overcome select issues including a strategy to spatially optimize sampling. Despite the many challenges, we argue that marine systems may be especially well suited for identifying candidate genomic regions under environmentally mediated selection and that seascape genomic approaches are especially useful for identifying robust locus-by-environment associations.

Landscape Genomics in the Sea

Previously formidable questions regarding evolutionary and ecological processes in natural populations are quickly becoming tractable thanks to genotyping enabled by massively parallel sequencing technologies (MPS, i.e., next-generation sequencing) (Davey and Blaxter 2011). In particular, signatures of selection can now be evaluated in populations across entire genomes, allowing investigators to ask questions about how environmental factors influence selective and neutral genomic diversity within and among natural populations. By borrowing from the fields of landscape ecology, remote sensing, and oceanography, many abiotic factors can also be quantified across relevant spatial scales to describe land or seascape attributes and used to predict intraspecific genomic diversity. These spatially explicit population genomic investigations are the natural extensions of landscape (Manel et al. 2003; Balkenhol and Cushman 2015) and seascape genetics (Selkoe et al. 2008; Riginos and Liggins 2013; Selkoe et al. 2015, 2016). Here, we define landscape genomics as studies that use landscape composition and configuration as statistical predictors of population genomic patterns (as in Balkenhol and Cushman 2015), such that landscape genomics might be considered a specialized subdiscipline of population genomics (Dyer 2015). We consider landscape genomics to refer to any habitat, not exclusively terrestrial, whereas seascape genomics is the subcategory of landscape genomics in the marine setting. For marine taxa, clearly ocean currents are important aspects of the seascape (Selkoe et al. 2008; Liggins et al. 2013; Selkoe et al. 2015) along with other spatial factors such as habitat configuration (Riginos and Liggins 2013) and strong environmental gradients (Schmidt et al. 2008; Selkoe et al. 2016).

Quantifying compositions and configurations of landscapes enables the discovery of spatial, temporal, and environmental factors associated with local adaptation and differing demographic histories (Manel et al. 2010). It is well appreciated that correlations between geographic features and allele frequencies of specific loci can reveal candidate adaptive loci (a “bottoms up” approach: Barrett and Hoekstra 2011). But such correlations can also uncover ecological features that are candidates for causing locus-specific selection (Rellstab et al. 2015). Furthermore, spatial correlations between landscape variables and genome-wide variation can identify which landscape variables influence overall structuring of genetic variation (sensuMeirmans 2015), which are likely to delineate evolutionarily distinct groups. In addition to exploratory investigations, explicit and quantifiable geographic predictors can be used to test a priori hypotheses. For example, functional assays or quantitative trait locus mapping might predict environmentally mediated selection on a given locus so that demonstrating a locus-by-environment association would provide an independent test of that prediction. Spatially explicit landscape variables can similarly be used to reframe traditional questions from population genetics and phylogeography in terms of testable hypotheses, such as evaluating the permeability of barriers to gene flow (Treml et al. 2015).

Many population genomic studies include the goal of examining loci under spatially variable selection, and the marine context offers several distinct advantages for empirical investigations of how selection operates in natural populations. A striking aspect of coastlines in particular is the abundance of strong environmental features such as intertidal zonation, embayments, estuaries, and freshwater outflows (Schmidt et al. 2008; Selkoe et al. 2016). These are landscapes that lend themselves to sampling paired and environmentally contrasting locations at a fine scale, greatly enhancing the statistical power to detect loci structured across environmental gradients. In addition, because of their large effective population sizes, marine species may be especially capable of responding to environmental changes via natural selection. The efficacy of selection scales with N_e and therefore strong selection could be characteristic of many marine species (Allendorf et al. 2010; Gagnaire et al. 2015; Bierne 2016). Large effective population sizes potentially combined with high capacity for gene flow create a situation in which repeated adaptations from standing variation appears likely (as in Colosimo et al. 2005) although adaptation via recurrent mutations and/or differing polygenic combinations are also probable (Gagnaire and Gaggiotti 2016). The spatial context of adaptive polymorphisms can yield insights regarding the sources of selection so that careful spatial sampling design should be an integral component of geographic adaptation studies.

Although landscape genetic and genomics research is well underway in terrestrial settings (see case studies and reviews in Balkenhol et al. 2015) the uptake of spatially explicit seascape information has generally been slow for marine genetic studies (Riginos and Liggins 2013; Selkoe et al. 2015). The considerations for undertaking seascape genomic investigations are considerable as the interdisciplinary nature of the enterprise relies on tools from spatial ecology and oceanography along with genomics. In this review, we first identify attributes that make seascape genomics distinct from much of terrestrial landscape genomics. Of course these issues will be shared with some taxa from other habitats (e.g., asymmetric flows in rivers and wind pollinated plants) but are routinely encountered among marine organisms. We describe commonly used tools and approaches for accommodating these “challenges”, which are delineated by (1) spatial predictors, (2) genetic response variables, and (3) statistical approaches assessing the response variables in light of the predictors; this tripartite structure aligns with the three core attributes of seascape genomic studies under our operational definition (matching in Balkenhol and Cushman 2015). We then highlight the few examples of published seascape genomic studies to date and describe how these studies have approached the three core aspects of seascape genomic inference. We also discuss how the emerging results across studies inform our understanding of which spatial factors are important predictors of genetic structuring and evaluate the evidence for adaptation from standing genetic variation. Finally, we propose specific experimental design strategies for efficiently sampling (using a case study of Atlantic Europe), and we suggest some promising new directions for the field.

Three Notable Challenges for Seascape Genomics

Quantifying the “sea”scape

Spatial genomic approaches seek to quantify the influence of several landscape properties on genomic patterns, such as i) habitat suitability and composition (i.e., environmental and ecological attributes of a population’s location), ii) habitat configuration (i.e., relative placement of given habitat relative to other suitable habitat patches), iii) “matrix” characteristics (i.e., the traversability or cost of dispersing or migrating between habitat patches), and iv) the spatial (and temporal) scale of these attributes (i.e., to what distance are environmental parameters influencing populations or individuals and what geographic and temporal extent is appropriate for the question).

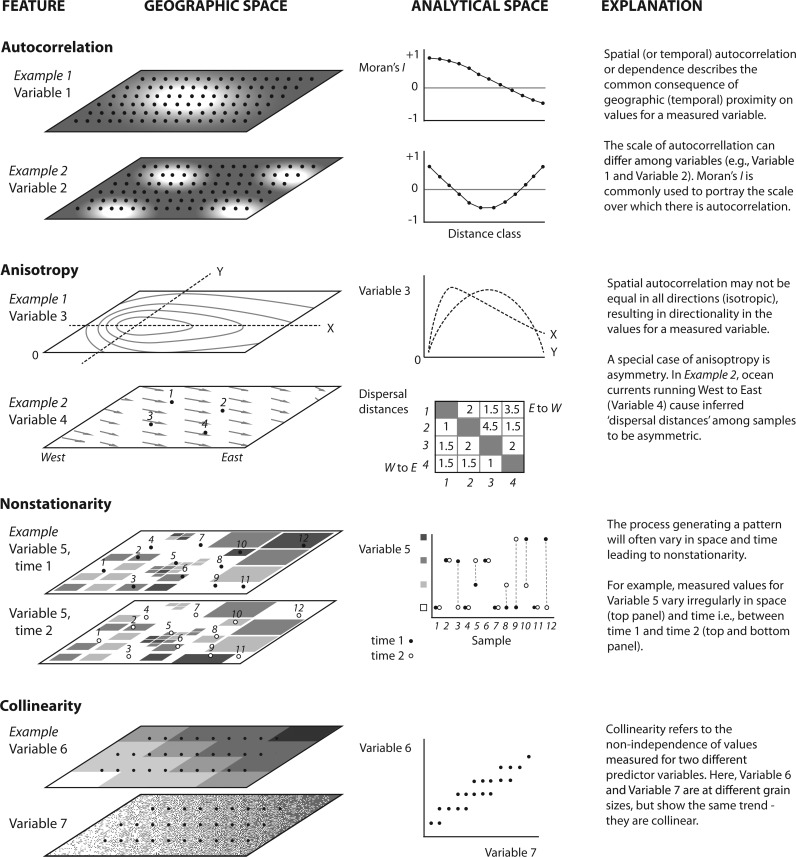
To progress in this multidisciplinary arena, clear and precise spatial terminology is important to avoid misinterpretation and misuse. Although others have provided spatial ecological glossaries related to landscape genetics (Storfer et al. 2007), several key concepts are revisited here and illustrated in Figure 1: scale, autocorrelation, isotropy, stationarity, and collinearity. The spatial and temporal scale of the data (or sampling) consists of two aspects, the size of the study area or extent and the resolution of sampling or grain. In practice, these spatial aspects of a study should be articulated. For example, in a recent study, Saenz-Agudelo et al. (2015) set their extent based on the entire geographic range size of the focal anemonefish, the seascape consisting of the Red Sea and Arabian Sea, and used an implicit grain size of 4 km (9-year mean) based on the available satellite data for their environmental variables of interest. Ideally, a genomic sampling strategy should be well aligned with the grain size (e.g., determining the location and proximity of populations or individuals) and extent (e.g., determining appropriate study area) of the environmental data. Unfortunately, there is inconsistency in how the remote sensing, geography, and ecological communities use the terms “large” and “small”, therefore we adopt the scale modifiers fine and broad to specify whether scale is in reference to a small area with greater detail or a large area with lower resolution, respectively (Turner and Gardner 2015). Spatial (and temporal) autocorrelation or dependence describes the common consequence of geographic (temporal) proximity on environmental and ecological phenomena: “near things are more related than distant things” (Tobler 1970). This often results in a lack of independence of data at nearby locations (Dale and Fortin 2014), obviously violating the independence assumptions in parametric statistics. The common pattern of isolation by distance is a manifestation of spatial autocorrelation commonly observed in population genetic data. Furthermore, this autocorrelation or non-independence may not be equal in all directions (isotropic), resulting in directionality in the patterns, or anisotropic spatial patterns. For example, asymmetric winds and ocean currents may result in more individuals dispersing downstream (e.g., east to west along equatorial currents) than across-stream, resulting in an elongated, or anisotropic, dispersal kernel. In fact, most environmental data, such as temperature, salinity, and productivity, show anisotropic patterns and may strongly influence the spatial genomic patterns we observe across many marine and terrestrial organisms. The concept of stationarity is also of particular interest and refers to the property whereby the underlying process generating a pattern does not change in space or time (i.e., the modeled relationship or response remains constant). Unfortunately, dynamic environmental and ecological processes (such as, seasonal currents and temperature, recruitment patterns) are rarely stationary. Stationarity is largely scale-dependent, a property required to extrapolate from sampled locations to unsampled sites, and an important assumption for many spatial statistics. Finally, collinearity refers to the non-independence of predictor variables and is a common characteristic of spatial ecological and environmental data. In marine systems, common examples of collinearity among data layers include latitude with mean annual temperature, and depth with distance from coastline. Collinearity may lead to problems in parameter estimation in regression-based analyses, making interpretation difficult (Dormann et al. 2013; Prunier et al. 2015). Text Box 1 along with Figures 2 and 3 and Table 1 describe spatial environmental characteristics for Atlantic European coastlines as an example to illustrate these phenomena.

Figure 1.

Key concepts relevant to the properties of spatial and environmental variables used in seascape genomic analyses. These properties should be considered during the project design as they will influence which variables and what representative values of variables may be used. Moreover, these properties will help determine what methods are appropriate for analysis. The figure displays examples of the concepts in geographic space and their manifestations in analytical space. Points in the geographic space depict the location of sampling, and dashed lines represent a transect (Anisotropy, Example 1 only).

Text Box 1. Quantifying the seascape in the Northeast Atlantic

To illustrate the challenges of quantifying the spatial attributes of seascapes, we focus on the Northeast Atlantic, including the North and Baltic Seas of northern Europe. This region has been the recent focus of considerable seascape genomic research investigating the environmental drivers of allele frequencies (Table 3). Here, we combine a number of commonly used seascape factors (e.g., sea surface temperature, salinity, depth, and net primary productivity) with other potential drivers of genetic diversity, including a thermal stress metric and a novel proxy for Pleistocene habitat stability (all listed in Table 1; detailed spatial methods are included in the appendix). The mean thermal stress frequency (TSF) was derived from a temperature anomaly database (Selig et al. 2010) and represents the long-term mean frequency at which weekly temperatures exceed the climatological mean by more than 1 degree C in the previous 52 weeks. The Pleistocene habitat suitability layer (PLEIS) simplistically represents the proportion (0 to 1) of the surrounding seascape that remained submerged for the majority of the time during the Pleistocene (2.6 million to 11,700 years ago), based on the sea level models of Voris (2000). For many benthic-associated taxa (e.g., cod, turbot, sole, hake, and many benthic invertebrates) this habitat suitability layer may identify regions of the seascape that functioned as stable refugia during this time of sea level changes. High values (close to 1) in this layer are places where the vast majority of the surrounding benthic environment (100 km radius) is at a depth of 50 to 250 meters.

 These eight environmental layers along with their first and second principal components are mapped and presented in Figure 2. Collinearity among multiple environmental variables can be accommodated by reducing them down to two (or more) principal components (i.e., PCA analysis). Summarising the data using a biplot (Figure 3) highlights uncorrelated environmental variables as perpendicular vectors (as with SSS and PLEIS). For variables that are highly collinear for a given landscape, it may be difficult to establish statistical genetic associations with either variable in isolation; for example, a locus that is statistically associated with sdSST will also have a statistical association with sdNPP. This collinearity in environmental data may be minimised with a strategic sampling design (Text Box 2). Spatial autocorrelation across many of the layers is visually apparent in that proximate locations tend to have similar values resulting in a ‘smooth’ appearance. The degree of this spatial autocorrelation was quantified using the Moran’s I measure (Table 1), whereby a maximal value close to + 1 for a given distance class indicates that all values within this range are very similar. The majority of environmental layers are highly autocorrelated (I > 0.70) at distances less than 25 km, with this correlation dropping at increased distances (Table 1). Generally, this would support a spatial sampling strategy across the seascape where sample sites are located at more than 50 km apart to minimise spatial autocorrelation within layers. See Text Box 2 for sampling strategies to minimise confounding spatial factors and maximise the likelihood for quantifying genetic environment associations within complex seascapes.

Figure 2.

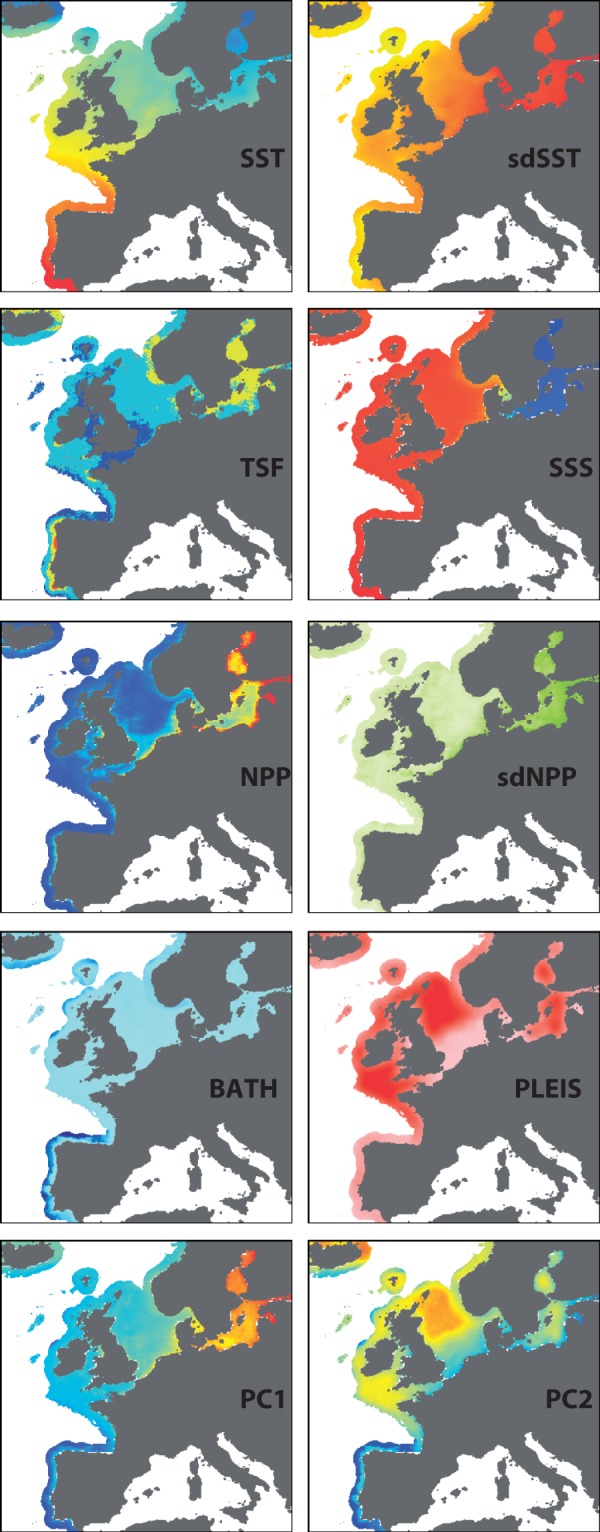
Spatial patterns in environmental variables of Atlantic European coastal waters. Eight select coastal seascape variables are shown including mean sea surface temperature (SST), standard deviation of sea surface temperature (sdSST), mean thermal stress frequency (TSF), mean sea surface salinity (SSS), mean net primary productivity (NPP), standard deviation of net primary productivity (sdNPP), bathymetry (BATH), and Pleistocene habitat suitability (PLEIS). In addition, the values for principal components 1 and 2 describing the eight coastal variables are also shown. PC1 and PC2 account for 47.1% and 17.9% of the variance among variables, respectively.

Figure 3.

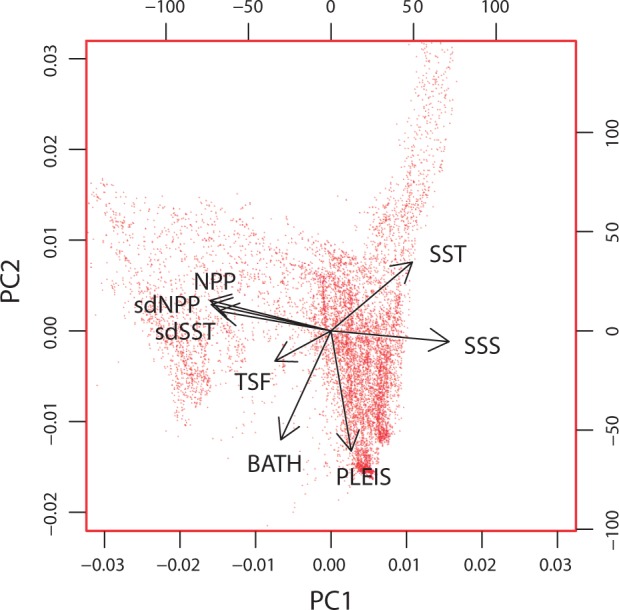
Biplot indicating PCA-based loadings of European seascape variables. PCA results showing environmental variables (vectors) plotted onto PC1 and PC2 from 10,000 randomly selected points in the seascape.

Table 1.

Descriptive statistics for eight select seascape variables for the northeast Atlantic region

							Moran’s I by distance (km)a
Layer	Abbrev	Min	Max	Mean	Standard deviation	Units	25	50	100	200	500	Data source
Mean sea surface temperature	SST	2.197	19.859	10.600	2.916	°C	0.66	0.60	0.50	0.39	0.26	NOAA
Standard deviation of sea surface temperature	sdSST	1.201	8.211	3.587	1.595	°C	0.74	0.69	0.63	0.58	0.47	NOAA
Mean thermal stress frequency	TSF	0.00	22.00	1.10	0.84	freqencyb	0.45	0.39	0.30	0.23	0.15	CoRTAD
Mean sea surface salinity	SSS	2.108	36.524	29.928	10.607	unitlessc	0.72	0.64	0.57	0.51	0.37	World Ocean Atlas 2013 v2
Mean net primary productivity	NPP	478	12,788	2,063	1697	C m−2 day−1	0.73	0.62	0.52	0.44	0.35	Ocean Productivity web
Standard deviation of net primary productivity	sdNPP	276	15,945	3,521	3,080	C m−2 day−2	0.76	0.67	0.59	0.52	0.39	Ocean Productivity web
Bathymetry	BATH	−5,029	839	−266	654	Metres	0.86	0.71	0.45	0.30	0.17	ETOPO1
Habitat exposure during Pleistocene low sea level stands	PLEIS	0.000	1.000	0.398	0.297	unitlessc	1.00	0.99	0.98	0.87	0.35	Derived from ETOPO1

^aMoran’s I is a measure of spatial autocorrelation and can range from −1 (complete negative spatial autocorrelation) to +1 (complete positive spatial autocorrelation). Values were estimated from 10,000 random points and values above 0.70 (high spatial autocorrelation) are in bold.

^bMean frequency of thermal stress anomalies ≥ 1 °C over the previous 52 weeks.

^cSSS: g/kg seawater; PLEIS: proportion.

We focus here on five key issues for describing spatial attributes of seascape environments that accompany the aforementioned general concerns for analyzing any spatial data. First, the strong asymmetric physical flows and dynamics that dominate this fluid environment (like riverine systems) exacerbate all the spatial challenges highlighted previously. Although physical flows in terrestrial systems (including, winds, elevation gradients) can influence genomic patterns, the extent, strength, and ubiquity of asymmetry in marine systems are striking. The spatial-temporal patterns and scale of autocorrelation (or variability) and anisotropy, in particular, are largely tied to the dynamics of the physical environment (Figure 1). Second, these asymmetric dynamics resulting in anisotropic patterns lead to inherent non-stationarity (Dale and Fortin 2014), particularly as the study extent increases or grain becomes finer. Third, the vast and continuous extent of the marine environment, in itself, presents challenges for study design (study extent and sampling design) and for justifying a priori population structure or barriers to migration and gene flow. Environmental and genetic sampling in the marine environment, the fourth key issue, is more physically and technically difficult, more costly, and more susceptible to errors compared with most terrestrial and freshwater systems. As a result, the majority of genetic and genomic studies in the marine environment are confined to the nearshore and near-surface periphery of the oceans. Indeed, with our strong dependency on data derived from remote sensing products (Table 2), oceanographic models, in situ instrumentation, and shipboard measurements, our understanding and quantification of the oceans are equally focused on this periphery. Finally, the fifth key issue of seascape genomic work relates to the common two-phase life histories of marine organisms and the two important, yet often quite different, spatial scales of influence. Although the importance of fine-scale habitat characteristics and demographics are well recognized in the literature, the influence of the broad-scale intervening and heterogeneous environment (i.e., the “matrix”) is often ignored or oversimplified (for instance, distance-based measures used as a proxy for dispersal through the matrix). The dispersing larvae of many marine taxa are underdeveloped (small, limited sensory systems, limited mobility) and spend some time adrift or traversing this dynamic and heterogeneous matrix where their condition, location, and downstream influence on genomic patterns are strongly influenced by the broad-scale (yet fine grained) environmental setting—characterizing the path of these dispersing larvae is a key goal of “connectivity” modeling (Kool et al. 2013).

Table 2.

Seascape properties and sample data sources useful for marine population genomic investigations

Parameters	Source	URL
Latitude & Longitude	World Geodetic System 1984 (used for the Global Positioning System, GPS, satellite navigation systems)	http://earth-info.nga.mil/GandG/publications/ tr8350.2/tr8350_2.html
Latitude & Longitude	ESRI ArcGIS Basemaps	https://www.arcgis.com/home/item.html?id=f11 bcdc5d484400fa926dcce68de3df7
Shoreline representation	GSHHG—A Global Self-consistent, Hierarchical, High-resolution Geography Database	http://www.ngdc.noaa.gov/mgg/shorelines/gshhs.html
Bathymetry and topography	ETOPO1 integrated topography and bathymetry product	http://www.ngdc.noaa.gov/mgg/global/global.html
Seafloor topography	Scripps Institute, UC San Diego	http://topex.ucsd.edu/WWW_html/mar_topo.html
Global distribution of coral reefs	UNEP WCMC	http://data.unep-wcmc.org/datasets/1
Ocean currents	HYCOM	http://hycom.org/dataserver/
Ocean temperature	The Group for High Resolution Sea Surface Temperature (GHRSST)	https://www.ghrsst.org/
Ocean temperature and derivatives	NASA Earth Observations (NEO)	http://neo.sci.gsfc.nasa.gov/view.php?datasetId= AVHRR_SST_M
Ocean temperature	World Ocean Atlas 2013 version 2	https://www.nodc.noaa.gov/OC5/woa13/
Ocean temperature and derivatives	The Coral Reef Temperature Anomaly Database (CoRTAD)	http://www.nodc.noaa.gov/sog/cortad/
Sea surface salinity	NASA Earth Observations (NEO)	http://neo.sci.gsfc.nasa.gov/view.php?datasetId= AQUARIUS_SSS_M
Sea surface salinity	World Ocean Atlas 2013 version 2	https://www.nodc.noaa.gov/OC5/woa13/
Surface photosynthetically active radiation (PAR)	NASA MODIS satellite	http://modis.gsfc.nasa.gov/data/dataprod/par.php
Chlorophyll a	NASA Earth Observations (NEO)	http://neo.sci.gsfc.nasa.gov/view.php?datasetId= MY1DMM_CHLORA
Future climate scenarios	NCAR’s GIS Program Climate Change Scenarios GIS data portal	https://gisclimatechange.ucar.edu/
Human population density	NASA Socioecomonic Data and Applications Center (SEDAC)	http://sedac.ciesin.columbia.edu/data/set/gpw-v3- population-density/

Note: Depending on a study’s objectives, appropriate measures might include means, minimums, maximums, or variance of some parameters.

To address these aforementioned issues, biophysical modeling (i.e., simulation models that combine oceanographic data with biological attributes) can provide predictions about dispersal that are specific to the location and species (Treml et al. 2012, 2015; Kool et al. 2013; Liggins et al. 2013). It is important to keep in mind, however, that such models are essentially detailed hypotheses about movement and should be evaluated against other predictors of dispersal (such as overwater distance (OWD), least cost paths (LCPs), etc.). Furthermore, biophysical models (and other predictors of dispersal) will typically only model the dispersal trajectory of an organism and will not include environmental variables that influence subsequent survival and reproduction. In marine systems, larval settlement and recruitment is a period of particularly high mortality that undoubtedly influences genetic patterns across the seascape (see Treml et al. 2015 for an extended discussion). Thus, predictors of dispersal need to be evaluated alongside other relevant hypotheses.

As a common goal of many population genomic studies is to identify or corroborate genetic–environment associations, it is also important to recognize that the environmental differences between locations are multifarious and thus once candidate loci are uncovered other methodologies will be required to fully demonstrate a functional relationship between a specific selective agent and locus-specific selection. At broad scales there is vastly different structure in gradients and patterns between environmental variables (e.g., compare sea surface temperature (SST) to TSF, Figure 2). As a result, any associations between environmental predictors and genomic structure quantified in one region may not be transferable to other regions of the seascape. However, the relatively modest level of collinearity among marine environmental data (at least for Europe: Figure 3 and also correlation matrices in Table A2) suggests that identifying individual environmental predictors in locus-by-environment associations should often be possible.

Describing marine metapopulation structure using genomic data

Direct observations of pelagic animals are fleeting and essentially impossible for planktonic larvae. Thus, population genetic methodologies have long been employed with the goal of inferring metapopulation dynamics in marine species. However, most pelagically dispersing marine species have large ranges, large census sizes, high levels of dispersal among subpopulations, and life-history strategies to cope with the stochasticity of the marine environment. This combination of metapopulation characteristics gives rise to four theoretical problems for the inference of marine population structure, particularly when relying on methods based on conventional population genetic models (see also extended discussions in Whitlock and McCauley 1999; Waples and Gaggiotti 2006; Faurby and Barber 2012; Palumbi and Pinsky 2013; Gagnaire et al. 2015; Gagnaire and Gaggiotti 2016). First, high levels of gene flow among subpopulations lead naturally to low differentiation that often cannot be statistically distinguished from zero (Waples 1998). Second, these metapopulation characteristics also translate into large global effective population sizes (i.e., weak genetic drift) that contribute to high global genetic diversities, which in turn can greatly decrease the maximum differentiation value for markers with more than two alleles (e.g., microsatellites; reviewed in Meirmans and Hedrick 2011). Third, weak genetic drift with migration slows the approach to equilibrium such that historical and contemporary gene flows are difficult to distinguish (Slatkin 1985; Marko and Hart 2011). Non-equilibrium processes of special concern include asymmetric or source-sink dynamics and range expansions, often mediated by the strong physical flows. Finally, at fine scales, geographically inconsistent (or chaotic) patterns of genetic structure have often been attributed to patchy temporal variation in the source of larval recruitment and variance in reproductive success (Johnson and Black 1984; Hedgecock 1994; Eldon et al. 2016). As a consequence, the seemingly basic problem of delimiting subpopulations and characterizing metapopulation structure has remained largely unsolved in the marine realm (Waples and Gaggiotti 2006; Gagnaire et al. 2015).

Although landscape genetic studies have focused predominantly on genome averaged F_ST or genetic distance estimates between pairs of populations (or individuals), other summary statistics can be used. They include measures of site-specific population diversity (Liggins et al. 2013; Wagner and Fortin 2015), group membership from clustering or assignment methods (François and Waits 2015), measures of nestedness in terms of genetic composition (Ulrich et al. 2009; Liggins et al. 2015), or even allele frequencies and individual genotypes. Some genetic distance estimates can accommodate the inherent non-independence of pairwise measures. For example, conditional genetic distance (Dyer et al. 2010) measures the co-variance among all population pairs that is independent of the co-variance they have with all other sampled populations. Nonetheless, this frequent reliance on genetic distance measures to implicitly draw conclusions about gene flow is problematic as F_ST and genetic distances are affected by many factors other than gene flow (Whitlock and McCauley 1999; Marko and Hart 2011). In principal, gene flow can be inferred to yield directional estimates of population relationships by assignment tests or coalescent models, however, in practice estimates of gene flow are rarely included in seascape genetic or genomic studies (Riginos and Liggins 2013 and Table 3). Although advances in genotyping technology promise to resolve subtle genetic structure, methods to measure genetic structure and gene flow that are coupled with flexible underlying metapopulation models will also be crucial.

Table 3.

Methodological approaches from empirical seascape genomic studies: elements of experimental design including spatial parameters, analyses, and genetic loci

Organism	Location	Spatial parametersa	Spatial predictor(s)	Genetic response variable(s)	Analytical approachb	Type and numb of locic	Unit genotyped	Number of Pops.	Number of Individuals	Outlier testsd	Number of outlier locie	Reference
Continuous seascape variables with genomic data
cod	North Atlantic—mostly Europe	LAT, LONG, temperature at spawning time, salinity at spawning time	Location-specific values of each of the spatial parameters in turn	Allele frequencies at individual outlier loci	SAM	tSNPs, SNPs (86,12)	Ind	18	708	BayeScan	7	Nielsen et al. (2009a)
cod	Greenland & Iceland	LAT, LONG, distance to nearest coastline, annual maximum, mean and range for annual bottom spring temperature (maximum, mean, and range), surface spring temperature (maximum, mean, and range), and annual mean bottom salinity; initially 24 variables were examined and then reduced to this subset to reduce correlations among variables	Each of the spatial parameters in turn	Allele frequencies of all loci with covariance conditioned on neutral loci	BayEnv	tSNPs (935)	Ind	20	847	BayeScan; Hierarchical	47	Therkildsen et al. (2013)
cod	Greenland	SST (mean, maximum and minimum), sea bottom temperature (mean, maximum and minimum), barotropic stream function	Least cost paths based on ocean climate suitability (created using species distribution modeling based on spatial parameters) between sampled population and spawning grounds	Posterior membership to Icelandic group	Linear model	tSNPs (81)	Ind	6	872	None	NA	Bonanomi et al. (2015)
cod	Baltic and North Sea	SST, temperature at spawning depth, SSS, salinity at spawning depth, dissolved oxygen (both at surface and spawning depth)	Location-specific values of each of the spatial parameters in turn	Population allele frequencies	BayEnv	SNPs (8809)	Ind	7	194	BayeScan; Fdist	326	Berg et al. (2015)
anemonefishes	Red Sea + Oman	Three barriers (arising from circulation or upwelling), OWD, environmental variables: day time SST, SSS, chlorophyll, color dissolved organic matter, particulate organic carbon	Combinations of various putative barriers, overwater distance, first PC of combined environmental variables	Distance matrix based on population pairwise FST values	Linear models with model support assessed by AIC	ddRAD (4559)	Ind	11	144	LFMM	98	Saenz-Agudelo et al. (2015)
			The first PC of the combined environmental variables	Individual genotypes	Latent factor mixed effects model
hake	Europe—mostly Mediterranean	SST, SSS, OWD	Location-specific values of each of the spatial parameters in turn	Allele frequencies at outlier loci with covariance conditioned on neutral loci	BayEnv	tSNPs (381)	Ind	19	850	BayeScan; Hierarchical	17	Milano et al. (2014)
herring	European North Atlantic	SST, mean spawning period surface temperature, SSS, mean spawning period surface salinity, OWD, LAT, LONG	Location-specific values of each of the spatial parameters in turn (excluding OWD), with a covariance matrix estimated from non-outlier loci	Population allele frequencies	BayEnv	tSNPs (281)	Ind	18	607	BayEnv; BayeScan; Hierarchical	10	Limborg et al. (2012)
			Distance matrices based on (1) SST, and (2) SSE with OWD as the additional distance matrix	Distance matrix based on population pairwise FST for each outlier locus	Partial Mantel
sole	European North Atlantic	SST, sea bottom temperature, SSS, mixed layer depth, maximum density gradient, chlorophyll concentration, surface productive layer, OWD, LAT, LONG	Environmental parameters conditioned on LAT and LONG and MEMs based on PcoA of distance matrix of shortest OWDs	Genotypes with analyses performed separately for neutral and outliers	partial RDA	tSNPs (476)	Ind	16	650	Fdist; Bayescan	13	Diopere chap 5, 2014
stickleback	Baltic and North Sea	SST, SSS	Location specific values of each of the spatial parameters in turn	Allele frequencies at outlier loci with covariance conditioned on neutral loci	BayEnv	RADseq (9404)	Pools	10	360	BayeScan; Fst quantile	94	(Guo et al. 2015)
Continuous seascape variables with targeted microsatellites
herring	Baltic and North Sea	Temperature at spawning and in April, salinity at spawning and in April, BPD, OWD, distance to the mouth of the Baltic, fishing pressure, LAT, LONG	Location-specific values of each temperature and salinity parameters in turn using both BPD and OWD as the additional distance matrices	Distance matrix based on population pairwise FST , partitioned for all loci, non-outliers, and the single outlier locus	Mantel and partial Mantel	gl Msats (51,17)	Ind	15	694	BayeScan; Fdist	1	Teacher et al. (2013)
			Location-specific values of each temperature and salinity parameters along with distance to the mouth of the Baltic, LAT, LONG	By locus allele frequencies (all loci)	MatSAM
			Combinations of location specific values of each temperature and salinity parameters along with distance to the mouth of the Baltic, fishing pressure	Population heterozygosity and allelic richness partitioned for all loci, non-outliers, and the single outlier locus	GLMs
sticklebacks	Baltic and North Sea	SST, SSS, BPD, OWD, LAT, LONG	SST and SSS in turn	Population allele frequencies for outlier loci	SAM	gl Msats (20, 20)	Ind	38	973	BayeScan; Fdist	9	DeFaveri et al. (2013)
			SST and SSS in turn with OWD as the additional distance matrix	Distance matrices based on population pairwise FST for outlier loci (individually and as a group)	Partial Mantel tests
			Combinations of SST, SSS, LAT, LONG	Population allele frequencies separately for genic and non genic loci	GESTE with Bayesian model selection
turbot	Europe (not Med)	Habitat variables: SST, sea bottom temperature, SSS, sea bottom salinity, oxygen concentration, primary production; Hydrodynamic variables: bottom shear stress, depth of pycnocline, density-based stratification index; LAT, LONG	All habitat and hydrodynamic variables, a matrix representing sampling year, and distance-based MEMs using a truncated distance matrix (PCNM approach)	Genotypes, with analyses performed separately for neutral and outliers and for different geographical partitions	RDA and partial RDA with dbMEM/PCNM to describe geographic distance and spatial correlations	gl Msats (12, 6)	Ind	290	999 (466 for some analyses)	BayeScan; Fdist	3	Vandamme et al. (2014)
Nominal seascape variable(s), with genomic data
anchovy	Europe (Atlantic, Mediterranean)	Open water versus coastal; nested sampling design with 2 habitats in 2 locations	Habitat	Joint allele frequency spectrum between pairs of populations	Custom model	RADseq (5628)	Ind	4	128	δαδι	431	{LeMoan: 2016be}
litorinid snail	Europe (Sweden, UK, Spain)	habitat: wave versus crab; nested sampling design with 2 habitat sites in 3 locations	Habitat	Proportion of shared outlier loci	Identifying sets of loci that are outliers in multiple habitat comparisons	RNAseq (6790)	pools	6	∼480	Fst quantile	NA	Westram et al. (2014)
			Habitat	Allele frequencies of SNPs from outlier contigs	Determining whether allele frequency changes between habitats are consistent across locations
litorinid snail	Sweden—3 island locations <10 km distant	habitat: wave versus crab; nested sampling design with 2 habitat sites in 3 locations	Habitat	Proportion of shared outlier loci	Identifying sets of loci that are outliers in multiple habitat comparisons	RADseq (4187)	Ind	6	130	Fdist	4-636 (depending on comparison)	Ravinet et al. (2016)
			Habitat	Individual genotype (presence/absence of alleles)	Binomial GLM
seagrass	Wadden Sea, North Sea (50 kms)	tidal position: tidal flat (exposed to air twice per day) or tidal creek (permanently submerged)	OWD	Distance matrix based on population pairwise FST	Mantel	gl Msats (14, 11)	Ind	6	485	DetSel; Fdist	3	Oetjen and Reusch (2007)
			OWD and habitat category	Distance matrix based on population pairwise FST	Partial Mantel
			Marker type and habitat	Distance matrix based on population pairwise FST	2-way ANOVA

^aLAT =  latitude; LONG  =  longitude, SST =  mean annual surface temperature; SSS  = mean annual surface salinity, OWD = overwater distance, BPD = biophysical distance. Many studies simply report “temperature” or “salinity” in which case we assume that SST and SSS, respectively, are implied.

^bBayEnv (Günther and Coop 2013); GESTE (Foll and Gaggiotti 2006); GLM is a general linear model; SAM/ matSAM (Joost et al. 2008).

^ctSNPs: Transcriptome-derived SNPs; gl Msats: gene linked microsatellites. In parentheses is the number of loci included in analyses (post filtering); if study includes both gene linked loci and non-gene linked loci then 2 numbers are reported, respectively.

^dBayEnv is the method of Coop et al. (2010); BayeScan is the method of Foll and Gaggiotti (2008); DetSel is from the method of Vitalis et al. (2003); Fdist is the method of Beaumont and Nicols (1996) regardless of which program was used for the analysis; LFMM is based on the method of Frichot et al. (2013) ; δαδι is the method of Gutenkunst et al. (2009).

^eAs defined by authors.

Other practical issues involve the bioinformatic methods required to pre-process MPS data. For marine species, high levels of polymorphism are common (another manifestation of large effective population sizes). When no reference genome is available, this variability can pose difficulties for clustering orthologous loci and subsequent identification of Single Nucleotide Polymorphism (SNP) variation. For example, bioinformatic pipelines that do not explicitly handle indels with an alignment algorithm can erroneously split reads from the same locus into multiple clusters (Puritz et al. 2014; Mastretta Yanes et al. 2015). Conversely, alignment-based clustering approaches (e.g., Eaton 2014) when used with a higher clustering threshold to account for higher variation and indels are inherently more prone to falsely joining paralogs as orthologs. In restriction-enzyme-based approaches (Andrews et al. 2016) null alleles can be common for marine species due to polymorphisms in restriction sites (as in Ravinet et al. 2016). Furthermore, marine species are less likely to have additional genetic resources, such as linkage maps so that physical relationships among contigs are generally unknown. See Willette et al. (2014) for a more complete discussion of the use of a variety of MPS methods in marine systems.

In summary, complications for both acquiring robust genomic data and using such data to describe underlying metapopulation dynamics persist. Moreover, as inferred metapopulation dynamics are often used to inform the null expectation for neutral loci from which locus-specific evidence for natural selection is extrapolated, these complications will also impinge on investigators' ability to detect loci under selection and locus-by-environment relationships.

Statistical links between seascapes and genomes

A key goal for spatial genomic studies is to simultaneously evaluate the effects of multiple landscape attributes including environmental gradients, habitat configurations, and matrix characteristics on genetic patterns (see Riginos and Liggins 2013 for a full discussion of relevant marine spatial variables and Table 3 here for examples from recent studies). Although clustering methods (including assignment tests) and ordinations based on genotypes alone (such as principal components analysis, PCA) are useful for describing relationships among individuals and often for discovering emergent spatial patterns, we focus here on methods that support hypothesis testing: whether hypotheses are couched in terms of landscape attributes predicting genetic patterns for a) select loci (i.e., outliers that are putatively under environmentally mediated selection); b) sets of loci in the case of polygenic adaptation; or c) average patterns across all or most loci. If each genotyped locus is considered as an observation of evolutionary processes then genomic investigations can potentially have thousands (or more) response variables. Landscape variables can also be numerous (Table 2), thus spatial genomic analyses routinely encompass multiple predictive and response variables. Sets of variables are likely to be collinear and non-stationary, for example, population densities (and by association, N_e) differing across a species’ range either spatially or temporally (see Eldon et al. 2016) would be examples of non-stationarity (and discussed for spatial variables in “Quantifying the ‘sea’scape”). Historical relationships also lead to spatial non-independence among genetic loci (Stone et al. 2011). Therefore, ascribing one-to-one (landscape attribute-to-locus) relationships may be impossible in many circumstances. Taking all these issues into consideration, it is hardly surprising that the question of how to robustly demonstrate statistical associations between spatial and genetic variables is a topic of lively debate and discussion. Here, we briefly discuss some of the commonly utilized empirical approaches, especially in light of the aforementioned issues, and refer to topic-specific reviews for further reading. Overall there are no universally superior methods and investigators need to consider whether the strengths and limitations of a given approach are appropriate given their aims and study system.

Because population genomic studies typically seek to uncover and describe the action of natural selection, most studies will try to identify loci that are candidates for carrying a strong imprint of selection. The goal then may be to examine these putatively selected loci further and/or to remove such loci from analyses whose aim is to infer historical relationships and gene flow (see Table 3 for examples of such approaches in seascape genomic studies). In particular, outlier methods identify loci with anomalous allele frequency changes among populations and subsequently such outlier loci are considered as candidates for selection (see recent reviews by Lotterhos and Whitlock 2014; de Villemereuil et al. 2014; Lotterhos and Whitlock 2015; Gagnaire and Gaggiotti 2016). Some methods specifically look for outliers in reference to spatial variables such as environmental gradients in line with the expectation that such gradients may promote local adaptation at selected loci (reviewed by Rellstab et al. 2015). Most of these environmental association approaches are presently limited to the evaluation of a single spatial variable at a time (i.e., BayEnv: Günther and Coop 2013; LEA: Frichot et al. 2013; BayeScEnv: de Villemereuil and Gaggiotti 2015). This limitation will lead to spurious correlations when there is collinearity among spatial variables. One solution for using outlier detection methods with multiple spatial variables is to summarize the common features of the spatial variables as orthogonal principal components (PCs) (illustrated with case study in Text Box 1) and undertake outlier analyses using PCs as single spatial predictor variables (de Villemereuil and Gaggiotti 2015). Specific methods differ in their sensitivities to spatial correlation structures such as isolation by distance, range expansions, and hierarchical population structure (Lotterhos and Whitlock 2014; de Villemereuil et al. 2014; Whitlock and Lotterhos 2015; Frichot et al. 2015; Gagnaire and Gaggiotti 2016). To our knowledge there has been no formal examination of how asymmetric gene flow could bias outlier detection methods, although range expansions are also directional and therefore it seems likely that asymmetric gene flow could be an important source of bias. Thus, pragmatically an investigator should consider the most likely scenario of population structure and choose outlier detection methods appropriate for that scenario, with joint consideration of multiple methods advisable (de Villemereuil et al. 2014).

Outlier methods are not well suited to identifying genotypes with small effects on fitness and since phenotypes are often affected by many loci (i.e., polygenic), outlier detection methods may overlook many selected loci. We refer readers to Gagnaire and Gaggiotti (2016) in this same issue for a detailed discussion of polygenic selection in marine populations and de Villemereuil et al. (2014) for comparisons of specific outlier detection methods under various scenarios of population structure. Of particular interest in the context of landscape genomics are methods to detect polygenic selection using multivariate statistics, which can describe relationships among multiple predictive variables and multiple response variables, such as multiple spatial variables and sets of loci. For example, Bourret et al. (2014) used canonical discriminant analysis and general linear models to partition differentiation among salmon based on river sampling location, life stage, and cohort year. Thus, multiple predictors were tested for associations with multiple loci; this approach could be modified to include multiple spatial variables.

Once outlier or other potentially selected loci are identified, a common strategy for analysis is to focus on putatively neutral loci or distinct sets of neutral and outlier loci (examples in Table 3). Often summary statistics of multiple genetic loci, such as average F_ST, are used to reduce the dimensionality of the response data. Such genome-wide averages are then used to describe relationships between populations and individuals (see Guillot et al. 2009 and Wagner and Fortin 2015 for extensive discussions, and Liggins et al. 2013 for a marine perspective). This strategy is aligned with population genetic analyses using less numerous loci (e.g., microsatellites, allozymes, DNA sequences). Most often, sampled locations and populations (or individuals) are implicitly considered as independent observations and multiple regression types of methods are invoked for hypothesis testing using pairwise F_ST estimates (or genetic distances) as the dependent variable. The problems arising from non-independence are most evident in describing relationships between locations using such pairwise population metrics in that allele frequencies from each location contribute to multiple observations. Historically, Mantel or partial Mantel tests (Smouse et al. 1986) have been used most frequently to test significance between the predictive variable(s) and genetic summary statistics, using permutation to overcome the assumed non-independence among observations (i.e., population pairs). However, Mantel tests are prone to false positives and are not appropriate when there is high spatial autocorrelation among many samples (discussed by Guillot and Rousset 2013; Legendre et al. 2015). Other multiple regression type methods have been suggested for assessing multiple spatial variables, including standard multiple regression (Spear et al. 2005), multiple regression on distance matrices (Legendre et al. 1994), linear mixed models (Pavlacky et al. 2009; Dudaniec et al. 2013), and multivariate analyses with constrained ordinations (discussed further below). Generalized dissimilarity modeling and decision trees could be useful alternatives to regression type methods (Thomassen et al. 2010). In general, procedures accommodating correlated error structures and model selection often differ across studies and further development in this topic is needed (Guillot and Rousset 2013).

Of the regression type statistics used in landscape genetics, multivariate methods are increasingly popular (see Borcard et al. 1992; Jombart et al. 2009; Manel et al. 2010; Wagner and Fortin 2015 for detailed discussions of multivariate statistics in landscape genetics). Multivariate statistics are commonly employed in spatial ecology and have many useful properties in the context of landscape genetics including flexibility in the types of input data, management of collinearity through ordination, and modifications to measure and address autocorrelation. Multivariate methods typically use constrained ordination to reduce the number of variables, with PCA as a familiar ordination technique. For example, redundancy analysis (RDA) describes suites of associations between predictive and response variables with ordination as a key step for reducing dimensionality and describing collinearity. Allele frequencies of sampled populations can serve as the observed variables themselves (allowing many response variables) or principal coordinates analysis can be used to decompose genetic distance matrices into orthogonal eigenvectors (distance-based RDA: Legendre and Anderson 1999) so that dbRDA can be used to describe genome wide genetic structure. Additionally tests of, and corrections for, spatial correlation structures can be accommodated within a multivariate framework such as using Moran’s eigenvector maps (MEMs) (Borcard and Legendre 2002; Dray et al. 2006). Thus, because the theory for ecological spatial analyses is well-developed, such multivariate methods can be easily modified for landscape genomics. In the case of seascape genomic studies, there is starting to be some uptake of multivariate methods (Vandamme et al. 2014), yet Mantel tests are still commonly encountered (Table 3).

Standard multiple regression and multivariate methods (reviewed above) assume isotropy and stationarity, which are poorly aligned with the presumed asymmetric larval dispersal and gene flow driven by the ocean currents. Asymmetric eigenvector maps modeling (Blanchet et al. 2008) is a technique for extending multivariate analysis for directional processes but has not yet been used in a genetic context. An alternative to conventional statistical analyses is to construct specific population genetic scenarios and use simulations to yield predictions that can be compared against empirical genetic data. Such models can be fully customized, using information from oceanography, habitat configuration, and species’ early life histories and can include directional vectors of migration and differing population sizes (as in Crandall et al. 2012; Foster et al. 2012; Blanco-Bercial and Bucklin 2016). Although such integrated model comparisons are well established in population genetics (Knowles 2009), they are largely absent from the landscape genetic literature. Such an approach could be especially useful in situations where anisotropy or non-stationarity are likely, including asymmetrical gene flow and varying population sizes. In addition, expanding simulation approaches to uncover outlier loci would have great utility for landscape genomics. In summary, statistical and customized model-based approaches that can both capture spatial properties and genetic variation across thousands (or more) loci are sorely needed in landscape genomics, with anisotropy an issue of key relevancy for advancing genomic inferences in marine systems.

Findings from Empirical Seascape Genomic Studies

To date, only a few studies strictly fall within the purview of seascape genomics. We surveyed the literature for studies that used multiple spatially explicit variables and genotyped populations or individuals for a large number of loci (see the Appendix for detailed search methods). For inclusion in this review, the spatial analysis had to be more sophisticated than a simple isolation by distance analysis or qualitative examination of clustering (including assignment tests). We did, however, retain studies that contrasted one habitat against another in spatially paired comparisons. Studies employing amplified fragment length polymorphism (AFLPs) or microsatellite loci were not considered except if some of the loci were specifically selected with an a priori expectation of being more likely to encompass targets of selection, such as studies that contrasted transcriptome derived microsatellites versus anonymous microsatellites. Despite using extremely permissive definitions of both seascapes and genomics, we found a surprisingly low number of published studies with only 16 studies that fit our criteria (Table 3). In this section, we describe common elements of published seascape genomic studies and illustrate how spatial analyses can identify the seascape attributes associated with selective and neutral genetic variation.

Favored seascapes, loci, and analyses

Most studies targeted northern Europe, especially the transition between the North Sea and Baltic Sea. By and large, spatial explanatory variables have been relatively simple with OWDs, mean SST, and mean sea surface salinity (SSS) predominating. OWD measures, which are basic LCP metrics, implicitly assume that all intervening parts of a marine landscape are equally traversable, isotropic, and are weighted by geographic distance alone. Biophysical models (Cowen and Sponaugle 2009; Treml et al. 2012) attempt to quantify dispersal probabilities and thus could be more biologically realistic (Crandall et al. 2012) and such biophysical distances were included among explanatory variables in a few studies (Table 3). For nektonic species that can move against currents as adults, the intervening seascape could also be explicitly quantified in other manners (using habitat configurations, environmental attributes, etc.) to develop resistance surfaces that may be more relevant to adult movement than geographic distance alone. The only marine study to implement such a habitat-based resistance approach used habitat suitability modeling to yield an along-coast LCP distance between adult cod populations and spawning grounds; the study showed that the suitability-based distances were better than OWD in terms of predicting individual genotypes (Bonanomi et al. 2015) suggesting that the predicted resistance captured attributes of the ocean environment that were more relevant to cod migration than distance alone. Thus, there are substantial opportunities to consider more biologically relevant spatial explanatory variables and to quantify the habitat and environmental matrix surrounding sampled locations.

Because a central goal of landscape genomics is to identify loci showing strong associations with environmental features, one might expect to find sampling designs include replicated environmental features (Lotterhos and Whitlock 2015; Rellstab et al. 2015). Furthermore, where multiple environmental factors are investigated, sampling design should seek to minimize the collinearity among those factors. Aside from studies using paired habitat contrasts (Table 3: Nominal seascape variables) few studies reported purposefully planning their sampling to capture replicated environmental contrasts or examined correlations among spatial variables (with Limborg et al. 2012 and Therkildsen et al. 2013 as exceptions). Thus there is scope to increase power to detect genetic–environmental associations by considering the sampling design more carefully. Another notable aspect of sampling was that population-level sampling predominated in these evaluated studies in contrast to terrestrial landscape genetics where individual-level approaches are common (Dyer 2015).

The most commonly used genetic markers were targeted SNPs typically designed from transcriptomic data and thus mostly in gene coding regions. Several studies similarly employed targeted microsatellites linked to gene coding regions. Only a few published studies used MPS to obtain contig sequences and SNPs (such as ddRAD and RADseq). Although some lag time is expected in the uptake of new technologies, the penetrance of MPS methods for terrestrial taxa suggests some possible additional impediment for marine studies. These early seascape genomic studies have focused predominantly on commercially fished species (cod, herring, hake, sole) that have been the focus of substantial previous genetic research, especially transcriptome sequencing, and for some, the focal loci were integrated with linkage maps (e.g., cod, sole, sticklebacks). This slow progress of using genomic approaches for non-model marine organisms may well reflect their phylogenetic distance from the closest reference genome as well as the technical difficulties associated with highly polymorphic marine species (as discussed previously).

In seeking to uncover statistical links between seascape features and specific loci, outlier locus identification methods have been used extensively, including methods that can include spatial variables (Table 3). Most studies identify several such outlier loci (1–23% of loci), matching percentages reported from terrestrial genomic studies. Given that many marine populations are likely to be hierarchically structured and out of migration-genetic drift equilibria, false positives are a concern and perhaps prevalent (de Villemereuil et al. 2014; Lotterhos and Whitlock 2014). Some studies preliminarily used non-spatial outlier tests, with the identified outlier loci then tested for associations with environmental variables (Table 3); nearly all such studies report statistical associations between the outlier loci and environmental variables. Although this two-step analysis should not necessarily be problematic, the high potential for covariance among multiple spatial factors (including geographic distance) has been largely overlooked, weakening the correlative inference and the problem of false positives remains.

A few seascape genomic studies have implemented analyses where multiple predictive variables are jointly evaluated. For example, constrained ordination methods (RDA and partial RDA) were used to estimate the influence of environmental variables on individual genotypes of turbot (Vandamme et al. 2014) and sole (Diopere 2014). Environmental variables were considered in combination with (or for partial RDAs, conditioned upon) longitude, latitude, and MEMs (an approach using ordination to describe autocorrelated spatial structure: Dray et al. 2006). The total proportion of variation explained was small and, hence, consistent with high gene flow in these pelagic fishes, but significant. Thus, these analyses demonstrated significant associations between genotypes of individual fishes and their location of capture, with additional significant variation for combinations of environmental variables. In a different approach, Saenz-Agudelo et al. (2015) used a modified linear modeling method to evaluate the strength of putative barriers on population pairwise F_ST values, with OWD and environment (PC1 of combined environmental variables) as spatial variables, to show that both barriers and environmental distance contribute to population differentiation. These few examples highlight the importance of multiple spatial factors in describing observed genetic structure.

The geography of variation for outlier and non-outlier loci

The expectation that locally adapted alleles will co-segregate with specific environmental attributes suggests that spatial patterns for outlier loci will differ from spatial patterns of unlinked neutral loci. In a hypothetical situation where only selected and unlinked neutral loci are examined, one would, therefore, expect to find contrasting spatial patterns between outlier and non-outlier loci with genetic differentiation at selected loci correlating with environmental features and neutral differentiation correlated with landscape attributes that diminish gene flow. In reality, genetic hitchhiking via physical linkage on a chromosome will yield environmental associations for loci that are physically linked to selected loci (reviewed by Gagnaire et al. 2015). Both selected loci and linked neutral loci can get “trapped” by geographical locations of low gene flow (Barton 1979; Gagnaire et al. 2015) and if there is some reproductive isolation between semi-differentiated taxa, alleles associated with reproductive isolation can become “coupled” with locally adapted alleles (Bierne et al. 2011). Causing further complications, there is no simple way (using only spatial data and genotypes) to demonstrate that an outlier locus is the direct target of selection and therefore outliers themselves have the potential to be linked to unknown selected loci.

With these important considerations in mind, what are the emerging empirical patterns among seascape genomic studies? Are spatial patterns of outliers different from those of non-outlier loci? Are environmental factors more closely associated with outliers and suppressors of dispersal associated with non-outlier loci? For the limited data to date, there are examples of both concordance and contrasting spatial patterns for outlier and non-outliers. For instance, spatial clustering groups for outlier loci matched that of non-outlier loci for both herring (Limborg et al. 2012) and sole (Diopere 2014) but with more pronounced spatial structure for the outliers; similarly, DeFaveri et al. (2013) showed much greater spatial structure in stickleback microsatellites linked to functional genes than non-gene-linked loci. Dissecting gradients of differentiation, however, multivariate analyses demonstrated that environmental variables explained a significant amount of variability in sole among outlier loci but not among non-outlier loci when analyses were conditioned upon spatial variables (Diopere 2014). In turbot, SST, SSS, and bottom shear stress explained significant genotypic variation for both outlier and non-outlier loci but additional environmental factors were also significant for outlier genotypes (Vandamme et al. 2014). With a limited number of studies for comparison, it appears that spatial correlations between outlier and non-outlier loci are common. Whether or not specific environmental factors can enhance spatial predictions for outlier loci remains to be determined. For studies to have the greatest sensitivity for detecting associations with environmental factors, we recommend that spatial covariance in relevant environmental factors be examined as part of the project design to best guide sampling efforts and subsequent comparative analyses (see Text Box 2). In particular a priori predictions of where dispersal might be low (Treml et al. 2015) could be used to test the prediction that many alleles will not traverse such low dispersal locations (Barton 1979; Bierne et al. 2011; Gagnaire et al. 2015) and these low dispersal locations could be contrasted against strong environmental gradients where gene flow should not be impeded.

Text Box 2. Developing sampling strategies in complex seascapes

When designing sampling for seascape genomic studies, adopting some a priori yet simple spatial approaches may increase the likelihood of identifying clear genetic-environmental associations. Demonstrating such associations is likely to be impaired with ad hoc, opportunistic, or other non-spatial sampling strategies. Targeting paired sample sites at distances beyond high autocorrelation thresholds within an environmental data layer can be the first step in this direction (Text Box 1). However, developing spatially-explicit sampling strategies may be more powerful, such as implementing a stratified-random design across multiple environmental gradients and a range of distance classes when possible. We illustrate this approach using two contrasting sampling goals: 1) an exploratory study to identify broad genetic environment associations, and 2) sampling to test a priori hypotheses regarding the influence specific environmental factors have on the spatial structure of candidate loci. Mapping environmental gradients within the seascape is central to both goals, allowing ‘hotspots’ of environmental change to be visualised and targeted.

 To explore broad genetic-environment associations (first goal), one could map PC scores from a principal components analysis (Figure 2) and use a moving window analysis to identify regions of strong environmental gradients or ‘hotspots’ (Figure 4: with a 75 km-window implemented representing a grain that exceeds the strongest signals of spatial autocorrelation). These hotspots derived from the mapped PC scores would be strong candidate regions (e.g., coastal Portugal, southern North Sea) to sample and explore genetic-environmental associations while considering the distance of the species’ dispersal potential. This targeted strategy may maximise the likelihood of finding these associations while allowing one to sample at appropriate distances to minimise strong autocorrelation among sites and accommodate the dispersal scales of interest.

 An analogous approach would also be helpful for testing a priori hypotheses regarding the influence of specific environmental factors (second goal). For illustration, consider if one was interested in quantifying the influence of SSS and NPP. These layers are highly (negatively) collinear in Europe (correlation = - 0.77, Appendix Table 2) and both are strongly autocorrelated at distances to 25 km. Again, one could overcome these challenges by mapping the strong environmental gradients (as above) in both layers (Figure 4) and consider sampling where hotspots exist in one layer and strong gradients are absent in the other. Although the strong environmental gradients found near the North Sea – Baltic Sea transition area are present in both layers, other hotspots in the NPP data that overlay non-hotspot regions in the SSS layer may represent opportunities for targeted sampling. These regions (e.g., coastal Portugal, inner Baltic Sea) may allow the differential influence of NPP spatial genetic patterns to be quantified. As there are no obvious regions where hotspots exist in the SSS layer and not in the NPP layer, the direct effect of SSS on the genetic structure may be difficult to distinguish in this seascape.

A related issue regarding the spatial properties of adaptive variation centers on the importance of parallel adaptive evolution, or to what extent the same alleles are reused in multiple locations with similar environmental characteristics. Addressing this issue suggests an experimental design whereby a series of population pairs from contrasting habitats are sampled (Rellstab et al. 2015; Meirmans 2015; Lotterhos and Whitlock 2015) and examined for overlapping outlier loci across habitat contrasts (Table 3: Nominal seascape variables). Because many gradients in marine habitats are replicated at local scales including tidal height of intertidal zones, exposed headlands to sheltered embayments along coastlines, and open coastlines to estuaries, seascapes offer natural spatial replications for such investigations (Schmidt et al. 2008). If habitat-specific alleles can be identified and shown to have different origins, then this is evidence for independent adaptive evolution (convergence) whether by new mutations or via selection on pre-existing variants (Le Moan et al. 2016). Habitat-specific alleles that are identical or related indicate that there is a shared historical origin to the adaptation and because gene flow should be more extensive for marine taxa, reuse of the same alleles from standing genetic variation may be more prevalent in marine taxa when compared with terrestrial or freshwater taxa. Whereas the spatial distributions of alleles can shed some light on the spread of related alleles, the observation of replicated genetic environment associations for some loci is not sufficient for distinguishing between primary differentiation by habitat from shared ancestral polymorphism and secondary contact between differentiated taxa (Bierne et al. 2013). As noted previously, a typical scenario involves genotyping many loci across a genome without knowing definitively whether outliers are direct targets of selection or linked to selected loci and therefore inference regarding independent or shared ancestry of specific alleles is weak.

Nonetheless, several studies have employed a replicated habitat design to look for parallel adaptive evolution. For example, paired sampling designs have been used by both Ravinet et al. (2016) and Westram et al. (2014) for adjacent ecomorphs in the littorine snail Littorina saxatilis (so-called wave and crab habitat types) and for open water and coastal anchovies (Le Moan et al. 2016). Littorine snails and anchovies differ substantially in their dispersal potential, as littorine snails are direct developers (no pelagic larval phase), whereas anchovy are large mobile fish with planktonic larvae. In all cases, only a few shared outlier loci were found among multiple habitat contrasts (but more than expected by chance alone). This suggests that at least some shared variation is used in parallel in multiple habitats. For anchovy, this inference was strengthened by modeling that supported a scenario of isolation between the open water and coastal ecotypes followed by secondary contact and gene flow, implying that adaptive alleles predate recent connections between the ecotypes (Le Moan et al. 2016). It is impossible to directly compare proportions of shared outliers across studies, as experimental designs were substantially different including type of loci and filtering thresholds. The finding that some markers have consistent associations with habitat across population pairs, however, points to standing genetic variation as being a source for adaptation for marine species even for species with greatly contrasting natural histories.

Comments on seascape genomic studies to date

The prevailing emphasis of seascape genomics studies on single spatial predictors (per analysis) indicates that greater scrutiny for collinearity among seascape variables is warranted. It is still common practice for seascape genomic studies to evaluate a series of models each with a single predictive spatial variable (including serial implementations across several spatial variables, with analysis such as BayEnv, SAM, as well as Mantel tests based on population pairwise distances) or partial Mantel tests for two spatial variables. Only two marine population genomic studies that we encountered estimated asymmetric directionality of gene flow (Blanco-Bercial and Bucklin 2016; Saenz-Agudelo et al. 2015). Although we have argued that the often replicated environmental gradients in marine systems provide an excellent backdrop for testing theories regarding the geography of genetic variation, how to discern the relative influence of selection on loci and how their genetic architecture (including recombination with linked loci and interactions among loci) remain a substantial challenge in population genomics especially for non-model organisms (Gagnaire and Gaggiotti 2016). As the field of seascape genomics moves forward, it will be important to capitalize upon developments in population genomics and also to develop and utilize analyses suited to the inherently complex and spatio-temporally variable attributes of seascapes. In the following section we highlight potentially useful solutions to select issues.

Project Design Considerations and New Directions of Inference

Strategic sampling for genetic–seascape associations

Although concerns for sampling an adequate number of loci for non-model organisms are now diminished with breakthroughs in genomic technologies, as always, field sampling remains an important aspect of a study’s design. The spatial configuration of sampling can greatly affect an investigator’s ability to statistically distinguish among potentially correlated spatial factors. For example, a seascape genomic approach could be used in an exploratory manner to generate hypotheses about a number of distinct spatial factors and their associations with genetic patterns. In which case, optimizing collecting locations to minimize correlations among these spatial factors would be sensible, for example targeting sites that maximize the distance in environmental PC-space while minimizing geographic distance (see case study in Text Box 2 and Figure 4). Alternatively, an investigator might have an a priori hypothesis regarding a specific spatial (usually environmental) factor and could leverage the greatest statistical power by including proximate sampling locations that differ by the factor of interest, for example sampling across environmental gradients (Text Box 2 and Rellstab et al. 2015; Lotterhos and Whitlock 2015).

Figure 4.

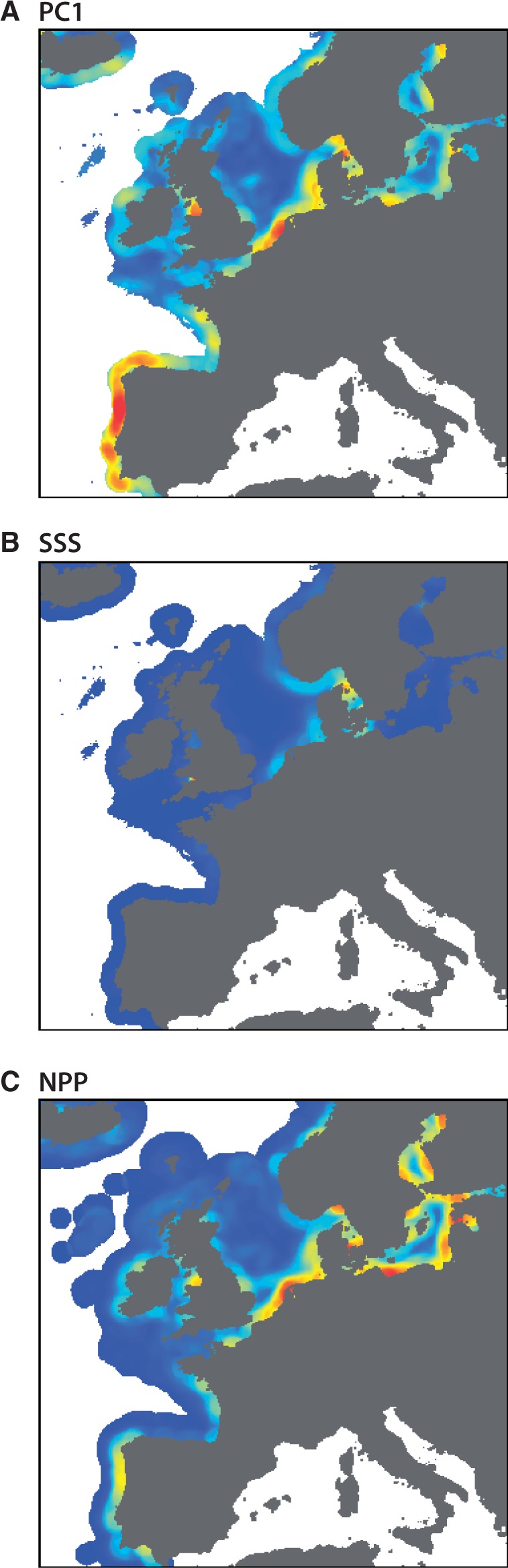
Hotspots of spatial gradients in seascape variables. Regions of strong environmental gradients or “hotspots” were identified using a moving window analysis to quantify the level of variation in the surrounding seascape. The hotspot regions could be targeted for genetic sampling to increase the likelihood of quantifying genetic environmental associations. (A) Hotspots for PC1 would be useful for exploratory analyses of many spatial variables simultaneously; gradients for (B) SSS and (C) NPP could be targeted to confirm predicted relationships between environmental variables and select loci.

Importantly, the ability of different sampling designs to discriminate among hypotheses can be statistically evaluated based on seascape data alone, ahead of any genomic inquiries. After the broad seascape setting and ecological elements have been aligned with the study objectives, specific spatial properties should be considered. Ideally in formulating a sampling strategy, spatial and temporal autocorrelation (Getis and Ord 1992) should be quantified within the (ecologically meaningful) environmental data layers at multiple scales. An appropriate spatial sampling interval to maximize statistical power to distinguish among competing seascape variables should strive to span and exceed the distance of spatial autocorrelation among the variables, while considering the “known” spatial extent of the species’ dispersal potential. Similarly, the spatial (and temporal) patterns in stationarity may be evaluated by mapping the mean and variance of environmental data (Figure 2, e.g.). If there is strong spatial structure representing non-stationarity, then compartmentalizing the analysis for different regions (e.g., geographically weighted regressions across Ecoregions: Spalding et al. 2007) may be advantageous. In planning for multivariate analyses, the covariance and correlation structure between predictors must be considered. If predictors are highly correlated (collinear), decisions will need to be made to reduce (i.e., remove the less meaningful correlated predictor) or accommodate (e.g., eigenanalysis, PCA) this collinearity (Wagner and Fortin 2015). Thus, in some seascapes it will be impossible to treat pertinent landscape features as independent predictors, a limitation probably best realized at the project design phase. After identifying the spatial structure in autocorrelation, stationarity and collinearity within and among the predictors, a sampling strategy can then be developed with these constraints in mind (see case study in Text Box 2).

Coincident with evaluating potential sampling locations is the issue of total sample number (and associated costs). Individual-based sampling schemes can be more effective for increasing spatial coverage than population sampling schemes as the number of locations (and therefore landscape heterogeneity) can be better sampled for the same genotyping expenses, and simulations suggest that as few as 3–6 individuals per site might be sufficient to detect genetic differentiation (Prunier et al. 2013) and even to accurately discern outlier loci for biallelic markers such as most SNPs (Lotterhos and Whitlock 2015). Genetic differences between pairs of individuals can be used in spatial analyses like conventional population statistics (Rousset 2000) or multilocus genotypes (especially with bi-allelic SNP loci) can be described with ordination (Jombart et al. 2009). Outlier detection based on genotyped individuals is possible using the methods LFMM (Frichot et al. 2013) and PCAdapt (Duforet-Frebourg et al. 2014), although outlier detection based on individual genotypes is prone to false positives (de Villemereuil et al. 2014). For multiallelic loci such as DNA sequences, however, larger population sample sizes are advisable (Gaggiotti OE, personal communication).

Another approach that can be cost-effective (reducing molecular costs) for increasing locations is to use a pooled sequencing approach (Schlötterer et al. 2014) where libraries are constructed for a mix of individuals. Methods for estimating population statistics tailored to sampling issues arising with pooling procedures are well developed (Kofler et al. 2011) and once population parameters are estimated, spatial analyses can proceed as with a typical population study. The major disadvantage of the pooling approach is that covariance among loci (including linkage disequilibria) within the population cannot be estimated and thus analyses based on individual genotypes such as admixture or parentage detection cannot be conducted, a problem if cryptic taxa are present.

Selecting appropriate genomic loci

Although genomic methods for non-model organisms are now tractable, there is a growing array of choices regarding the exact nature of the markers and the subsequent analyses that they would support (see Davey and Blaxter 2011; Andrews et al. 2016). These methods can be largely divided into targeted and non-targeted approaches, and vary in recovering hundreds of loci to genetic variation across the entire genome. Targeted approaches include arrays and sequence capture for predetermined SNPs (e.g., SNP arrays: Seeb et al. 2011), exons (e.g., exon bait capture: Bi et al. 2012), transcripts (e.g., targeted RNA-seq: Mercer et al. 2012), or informative sequence loci flanking ultra-conserved elements (Faircloth et al. 2012). The advantages of these approaches are that they allow for much greater control of the number of loci (therefore also ensuring optimal coverage), usually work with varying degrees of DNA quality and quantity, and are less likely to return contaminant loci (a pervasive problem for symbiotic marine invertebrates such as corals). The disadvantage of these approaches is that they require initial development (and often optimization), which is usually costly and time-consuming (and therefore less attractive for one-off projects). Non-targeted approaches range from whole-genome shotgun (WGS) resequencing, transcriptome sequencing (RNA-seq: De Wit and Palumbi 2012), to reduced representation methods (reviewed by Andrews et al. 2016) targeting sequence regions adjacent to restriction sites (e.g., RAD-seq, GBS and CROPS) or other repetitive sequences (e.g., nextRAD). These methods do not require any prior development, and they provide a panel of loci “randomly” distributed across the genome (or transcriptome). Whereas the number of loci can be reasonably well determined in reduced representation methods, problems with obtaining sufficient locus coverage are frequent, there is no protection against sequence contamination, and DNA input requirements can be relatively high.

A related issue to consider is whether individual SNPs or DNA haplotypes are better suited to the study goals and analyses. Although many analytical methods are designed for unlinked SNPs, DNA sequences provide a historical context that can greatly expand inferences regarding selection. For example, DNA sequencing of long haplotypes can reveal whether divergence between alleles is ancient or recent and provide insights regarding the nature of selection (as in Bierne 2010). Moreover, coalescent analyses and other emerging methods can retrieve more genealogical information from haplotypic data than from unlinked SNPs (see below).

Including metrics and analyses that incorporate asymmetric movement

To date, seascape genomic studies have primarily based their spatial inferences on classical allele-frequency measures of population diversity and population structure and assessed these genetic estimates against single or multiple landscape attributes, implicitly assuming symmetric exchange among equally sized populations. The rise of genomic sequencing methods provides access to new types of information that, together with new theoretical methods, have the potential to relax these assumptions and provide greater insight into underlying metapopulation processes, including asymmetric (anisotropic) gene flow. Thus, these methods could be especially useful for landscape genomics in systems likely to experience asymmetric gene flow such as marine taxa.

Such new population genomic methods that infer complex dynamics including asymmetric gene flow can be categorized by the type of information they access. Coalescent samplers reconstruct the genealogical relationship among alleles, calculating the likelihood of the data given defined metapopulation models via simulations that vary population genetic parameters of interest (Beerli and Palczewski 2010; Baele et al. 2012; Robinson et al. 2014). The models can include population divergence, asymmetric gene flow, and population size changes, and thus can be quite powerful in a model selection framework (Carstens et al. 2009). These methods also produce Bayesian posterior distributions for each model parameter that integrate the (often considerable) uncertainty in the parameter estimate; the Bayesian posteriors can be subsequently used as response variables in a regression framework (Crandall et al. 2012). With the increase in sampled loci leading to a linear increase in computation time, approximate Bayesian computational methods, wherein posterior distributions are constructed via a rejection algorithm based on summary statistics rather than intensive likelihood computations are becoming attractive for coalescent models and other methods (Hickerson et al. 2005; Beaumont 2010; Roux et al. 2013).

Still more theoretical approaches are emerging as genomic sampling becomes denser. Allele frequency spectra contain the empirical distribution of thousands or millions of SNPs; the likelihood of frequency spectra for joint population analyses can be quickly calculated under a variety of demographic models that include range expansions, demographic growth and asymmetric migration and through coalescent modeling or a diffusion approximation (Gutenkunst et al. 2009; Peter and Slatkin 2013; Xue and Hickerson 2015; Le Moan et al. 2016). A related method uses SNP frequency data to build a maximum likelihood tree of populations (Pickrell and Pritchard 2012). Directional migration events are then inferred between populations with a higher than expected covariance, and added to the tree to create a population graph. Another class of methods considers the length of haplotypes that are identical by descent, with haplotypes from older migration events expected to be shorter due to recombination (Pool and Nielsen 2009; Palamara and Pe'er 2013). Clinal analyses using large haplotype blocks, especially when there is introgression from a genetically distinct source, could be used to estimate how connectivity differs by spatial location (Gagnaire et al. 2015). In summary, it is likely that spatial hypothesis testing will continue to rely on both (i) multiple regression type tests with genomic-derived population estimators, and (ii) custom models informed by landscape attributes and based on coalescent and population genetic principles for evaluating empirical data against specific processes. In all, the many theoretical and analytical advances in population genomics hold promise for relaxing the assumptions of symmetrical gene flow and gene flow-drift equilibrium and will be especially useful to marine researchers.

Conclusions and New Directions for Seascape Genomic Studies

The major challenge of seascape genetics is to deduce the key spatial processes that affect spatio-temporal genetic structure in an environment that is highly variable in both space and time, and where simple spatial or oceanographic metrics are unlikely to capture the inherent biological complexity of dispersal and population sizes (previous sections of this paper and Liggins et al. 2013; Riginos and Liggins 2013; Selkoe et al. 2015). Indeed the relevant seascape attributes are likely to differ by spatial scale and species biology: grain size, extent, and temporal durations of organizing spatial processes can vary by orders of magnitude (Figure 1 in Riginos and Liggins 2013). The high temporal variance of marine systems is matched by the observation of seemingly chaotic genetic patterns within species (Johnson and Black 1984; Hedgecock 1994; Eldon et al. 2016). However, for temporally variable spatial factors that can be quantified (such as ocean currents using data from remote sensing and observation buoys) seascape genomics could provide a framework for testing these predictors against genetic observations using appropriately matched spatial-genetic time series.

Multispecies comparisons can uncover spatial factors that have broad scale effects across ecological communities, in that shared patterns across species (whose age at reproductive maturity is likely to differ) could filter out short-term chaotic variability. Indeed, idiosyncratic species genetic patterns are common (Ayre et al. 2009; Dawson et al. 2014) but consistencies are also observed particularly over large geographic scales (Pelc et al. 2009; Toonen et al. 2011; Altman et al. 2013; Gaither and Rocha 2013; Liggins et al. 2016). Thus, whether or not spatial patterns of outlier loci will also be species-specific or reveal commonalities either in terms of spatial concordance or gene function remains to be seen. Regardless, deducing which landscape attributes shape genomes is an important and tractable goal (Thomassen et al. 2010; Meirmans 2015). Such generalities can be inferred only from comparative studies, even if uncovering the ultimate sources of selection and their relationships to genome architectures remains a substantial challenge (Bierne et al. 2011; Gagnaire and Gaggiotti 2016: with compounded difficulty when considering multiple species). Approaches from seascape genomics are well suited to identifying the overarching spatial factors that affect microevolutionary dynamics across suites of species. Moreover, repeat sampling across multiple species could be especially useful for gaining insights to these processes. For example, transition zone locations where genetic discontinuities are observed among many taxa often are subject to fluxes in oceanographic and environmental conditions. These fluxes create conditions for natural experiments where the genomic responses of different species (differing in sensitivity to such changes) could be monitored and used to test specific hypotheses. For instance, in turbot, changes in allele frequencies at the hydrographically active Baltic/North Sea transition showed significant correlation with environmental shifts (Vandamme et al. 2014).

If marine species do have greater sensitivity to selection, they may be especially well suited for detecting relatively fast responses to altered selective regimes, including those arising from human impacts (Allendorf et al. 2010). At present, climate change induced range shifts are underway for many marine species with greater velocities than those that typify terrestrial taxa (Poloczanska et al. 2013). These rapid changes to the range structures of marine species could yield important insights to the evolutionary dynamics of range expansions (and contractions), especially the role of adaptation in facilitating range expansions. Moreover, for some harvested species, there may be historical fisheries data (including tissue samples) to contrast spatial dynamics at different time points (Nielsen et al. 2009a, 2009b; Bonanomi et al. 2015). Because natural selection and range changes are inherently spatial processes, the inclusion of tools and approaches from seascape genomics can enhance such investigations.

As a field, we are riding a wave of genomic enthusiasm with many new studies underway that seek to capitalize upon our newfound powers to reveal and learn from genomic diversity. However, similarly revolutionary technological innovations are reshaping oceanography and remote sensing. While daunting to consider both fields, a deeper understanding of the fundamental questions surrounding dispersal, gene flow, and selection will be achieved by recognizing and embracing the spatial and temporal complexity of structuring processes in the marine environment.

Major Points

• Seascape genomic studies test for associations between landscape configuration or composition of marine systems and allelic variation across many loci.

• Marine landscapes are spatially complex and variable over time.

• Large population sizes and high dispersal are prevalent among marine taxa obscuring the interpretation of common population genetic metrics and causing practical difficulties for applying genomic genotyping methods.

• There has been much recent development of methods to statistically evaluate landscape and genetic associations; investigators need to carefully consider the importance of underlying assumptions among methods, some of which are certain to be violated in any analysis.

• Empirical seascape genomic studies have identified correlations between environmental factors and spatial genetic structures particularly for outlier loci, however, the small number of studies to date precludes inferring general trends.

• Seascape genomic studies can greatly increase their power to detect genetic-environment associations by implementing spatial analyses as part of the sample design planning.

• Methods that estimate asymmetric gene flow, especially those based on coalescent and allele frequency spectra, could be especially valuable for seascape genomic studies.

• Basic principles and analyses from spatial ecology can be readily incorporated in population genomic studies to increase inferential strength and yield new insights regarding evolutionary processes.

Appendix

Specific methods: Environmental data analysis methods

We downloaded environmental data layers (sources listed in Text Box 1, Table 1) in their native format, projected them all to a global Molleweide projection and resampled to a 5 km by 5 km grid cell size. Sea surface temperature (GHRSST, 0.25deg, 7-day running mean, NOAA’s NCDC, L4 Blended product using AVHRR and AMSR) and net primary production data were downloaded for 2010 only. For all other environmental data layers, the full suite of available dates was used (see individual data providers, Table 1). Data were then extracted for the coastal zone to exclude those regions outside our area of interest (marine habitat within 100 km of the coastline or less than 250 m deep). Layer statistics were calculated on these extracted data, mapped, and used for all spatial analyses. Spatial autocorrelation statistics (Moran’s I) were calculated for each environmental data layer and across a range of distance classes (reported in Textbox 1, Table 1). All resampled environmental data were rescaled before completing the PCA in ArcGIS (ESRI 2015. Environmental Systems Resource Institute, ArcMap Release 10.2. Redlands, CA).

Recent publications in seascape genomics

Initially we queried the Web of Science (WOS, Thomson-Reuters: search conducted 26 August 2015) for relevant papers. Pilot searches revealed that there were few papers in this topic area and also that there were no consistent sets of keywords being used by authors to identify their work to this topic area. For example, searches for “seascape genomics” or “marine landscape genomics” [Boolean terms: TS = (seascape genomic* OR marine landscape genomic*)] yielded zero papers. Replacing the genomic root word with “genetics” yielded 126 papers in total. Because we knew that some suitable papers existed and were not being found with these specific terms, we expanded our keywords to capture spatially explicit marine landscapes [TS = (seascape OR marine landscape)) and population genomic data (TS = (population genomic* OR next generation sequencing OR RAD OR genotyping by sequencing OR SNP*)]. This combination of search terms yielded 37 papers, of which 18 were completely spurious, 6 were review or theoretical papers with only 2 of those touching on marine specific issues, and 11 were empirical with 5 fitting into the purview of seascape genomics. Of these 5 papers, 2 employed SNP markers (≥98 loci: Nielsen et al. 2009b; Limborg et al. 2012) and three used microsatellites with some of those microsatellites targeting gene coding regions (≥17: DeFaveri et al. 2013; Teacher et al. 2013; Vandamme et al. 2014). Given that standard keyword searching was failing to locate suitable papers, we took a more informal approach and searched WOS based on authors known to us to be undertaking genomic research programs, emailed many researchers directly (asking them to forward our requests, and solicited advanced copies of in press publications). We excluded studies of anadromous species such as salmon and eels because these life histories with adult migration are substantially distinct from the life histories of most marine taxa, and the spatial variables examined in these studies tended to focus on the freshwater environment. Studies including brackish populations (notably the Baltic Sea), however, were retained.

Table A1.

Covariance matrix for 8 select seascape variables for the Northeast Atlantic region

Layer	SST	sdSST	TSF	SSS	NPP	sdNPP	BATH	PLEIS
SST	0.307	−0.098	−0.074	0.113	−0.098	−0.094	−0.104	−0.010
sdSST	−0.098	0.188	0.044	−0.139	0.136	0.133	0.052	−0.036
TSF	−0.074	0.044	0.191	−0.058	0.050	0.050	0.025	0.000
SSS	0.113	−0.139	−0.058	0.175	−0.137	−0.139	−0.035	0.012
NPP	−0.098	0.136	0.050	−0.137	0.182	0.170	0.047	−0.044
sdNPP	−0.094	0.133	0.050	−0.139	0.170	0.182	0.044	−0.031
BATH	−0.104	0.052	0.025	−0.035	0.047	0.044	0.203	0.044
PLEIS	−0.010	−0.036	0.000	0.012	−0.044	−0.031	0.044	0.203

Table A2.

Correlation matrix for 8 select seascape variables for the Northeast Atlantic region

Layer	SST	sdSST	TSF	SSS	NPP	sdNPP	BATH	PLEIS
SST	1	−0.41	−0.31	0.49	−0.41	−0.40	−0.42	−0.04
sdSST	−0.41	1	0.23	−0.76	0.73	0.72	0.27	−0.18
TSF	−0.31	0.23	1	−0.32	0.27	0.27	0.13	0.00
SSS	0.49	−0.76	−0.32	1	−0.77	−0.78	−0.18	0.07
NPP	−0.41	0.73	0.27	−0.77	1	0.93	0.24	−0.23
sdNPP	−0.40	0.72	0.27	−0.78	0.93	1	0.23	−0.16
BATH	−0.42	0.27	0.13	−0.18	0.24	0.23	1	0.22
PLEIS	−0.04	−0.18	0.00	0.07	−0.23	−0.16	0.22	1

Funding

LL was supported by an Allan Wilson Centre for Molecular Ecology and Evolution Postdoctoral Fellowship and the Rutherford Foundation New Zealand Postdoctoral Fellowship.