Phylogenetic framework for coevolutionary studies: a compass for exploring jungles of tangled trees

Abstract

Phylogenetics is used to detect past evolutionary events, from how species originated to how their ecological interactions with other species arose, which can mirror cophylogenetic patterns. Cophylogenetic reconstructions uncover past ecological relationships between taxa through inferred coevolutionary events on trees, for example, codivergence, duplication, host-switching, and loss. These events can be detected by cophylogenetic analyses based on nodes and the length and branching pattern of the phylogenetic trees of symbiotic associations, for example, host–parasite. In the past 2 decades, algorithms have been developed for cophylogetenic analyses and implemented in different software, for example, statistical congruence index and event-based methods. Based on the combination of these approaches, it is possible to integrate temporal information into cophylogenetical inference, such as estimates of lineage divergence times between 2 taxa, for example, hosts and parasites. Additionally, the advances in phylogenetic biogeography applying methods based on parametric process models and combined Bayesian approaches, can be useful for interpreting coevolutionary histories in a scenario of biogeographical area connectivity through time. This article briefly reviews the basics of parasitology and provides an overview of software packages in cophylogenetic methods. Thus, the objective here is to present a phylogenetic framework for coevolutionary studies, with special emphasis on groups of parasitic organisms. Researchers wishing to undertake phylogeny-based coevolutionary studies can use this review as a “compass” when “walking” through jungles of tangled phylogenetic trees.

Introduction

The cornerstone of evolutionary processes organizing the web of life and responsible for many of the major events in the history of life is coevolution (Thompson 2010, 2012; Thompson and Medel 2010). In fact, Charleston and Libeskind-Hadas (2014) recently mentioned that this process occurs at all biological levels, from “small-scale” such as genes that function inside biological entities (e.g., viruses) and change function in response to the changes that other individuals’ genes undergo (e.g., host cells), to “major-scale” such as phenotypic changes between two ecologically closely related populations such as diversification patterns of parasites in response to those of their host species (e.g., codiversification). The classic definition of coevolution is reciprocal evolution between interacting species, driven by natural selection (Thompson 2005). Based on this strict concept, several authors mentioned that measuring and testing coevolutionary hypotheses focusing using only phylogenetic approaches can lead to erroneous matching of coevolutionary events. For example, in a vicariant scenario, cospeciation can show patterns of phylogenetic concordance caused by common biogeographic processes rather than by reciprocal natural selection (Weber and Agraval 2012; Brockhurst and Koskella 2013; Althoff et al. 2014; Poisot 2015). However, limiting coevolution to reciprocal selection is outdated because coevolution can also take place when a third party is acting as the selective agent. Thus, the use of molecular clock to estimate the divergence date between species in phylogenetic reconstructions can resolve the “misconception” caused by vicariant events and cospeciation processes (Kumar 2005; Drummond et al. 2006; Ho 2014). For example, based on the node dates of 2 phylogenetic trees (one of hosts and the other of parasites), it is possible to detect cophylogentic events, given a similar timeframes and geographic spaces, thus inferring coevolutionary processes (Rønsted et al. 2005; Reed et al. 2007; Ramsden et al. 2009; Ricklefs and Outlaw 2010). Therefore, incorporating time-calibrated phylogenies into studies of coevolution provides an important and powerful test of coevolutionary hypotheses (Segraves 2010; Venditti et al. 2010; Doyon et al. 2011).

Cophylogeny is a phylogenetic systematic approach to detect coevolutionary processes between two, or more, taxa. Cophylogeny is the reconstruction of past relationships among ecologically linked groups of organisms from their phylogenetic information (Charleston and Little 2009; subsequently used by Baudet et al. 2014). The aim of cophylogenetic analysis is to explain the relationships between mutually evolving pairs of 3 types of historical associations: 1) genes/species, 2) host/parasite, and 3) endemism/areas (Page and Charleston 1998; Ronquist 1998). In this context, cophylogeny is considered an integrative approach. During the past two decades, based on empirical data and phylogenetic methodologies, this approach was strongly supported by the international scientific community using different ecological interactions, for example, Batesian mimicry, virus–host, plant–insect mutualism, development, and cultural roots (Ceccarelli and Crozier 2007; Therani et al. 2010; Gottschling et al. 2011; Cruaud et al. 2012; Legendre et al. 2013). In these cophylogenetic approaches, different concepts of evolutionary events conceived in subdisciplines comparable to evolutionary biology (e.g., molecular systematics, historical biogeography, and cophylogenetical methods), can be analogous and interpreted as the same principle (overview in Page 2003). For example, the main evolutionary events in molecular systematics and phylogenomics (speciation, duplication, loss, and horizontal gene transfer), which reconcile gene trees and species trees, correspond to cospeciation, duplication, lineage sorting, and host-switching, respectively, in cophylogenetical studies (Doyon et al. 2011; Stolzer et al. 2012; Szöllősi et al. 2013). On the other hand, phylogenetic methods in biogeography estimate ancestral ranges along the branches and at the nodes reflecting evolutionary events such vicariance, sympatric speciation, dispersal, and extinction, analogous to cophylogenetic events (Ronquis 1998; Martínez-Aquino et al. 2014). Based on the theoretical and methodological advances of each discipline, coevolutionary inference can be integrated using similar approaches. However, each discipline holds its explicit assumptions and particular difficulties, and real-life coevolutionary processes rarely are simple, therefore, exploring coevolutionary hypotheses in any biological system can be complex. Furthermore, the cophylogenetic methods implemented in various software packages and programs (with unique tools and features) have increased in the past few years (Balbuena et al. 2013; Baudet et al. 2014; Drinkwater and Charleston 2014; Libeskind-Hadas et al. 2014). In this context, the problem is not only the theoretical aspects, but also computational (Libeskind-Hadas and Charleston 2009; Ovadia et al. 2011).

Several reviews on the topic of coevolution mention the advantages and disadvantages of cophylogenetic methods (Paterson and Banks 2001; Charleston 2002, 2003; Stevens 2004; Doyon et al. 2011; Keller-Schmidt et al. 2011; de Vienne et al. 2013; Charleston and Libeskind-Hadas 2014). On the other hand, analytical advances in inferring coevolutionary processes using molecular data, phylogenetic and genealogical analysis, molecular clock dating, and parametric biogeography, can be implemented in cophylogenetic methods (Ronquist and Sanmartín 2011; Froeschke and von der Heyden 2014; De Baets et al. 2015). Therefore, it is necessary to develop a study program to explore coevolutionary questions and venture into a “jungle” of phylogenetical trees of the biotic interactions (“jungle,” in the original context mentioned by Charleston 1998). In this context, the aim of this article is to provide an overview of a phylogenetic framework as an introduction for advanced students and researchers trained in coevolutionary studies. I briefly mention the foundations of phylogenetic, biogeographical, and cophylogenetical methods, with a focus on host–parasite systems. Furthermore, I provide a guide for exploring coevolutionary systems with insights into current methodologies and directing future walks into the “jungles of tangled trees.” Finally, I describe some of the computer programs with improved versions for phylogenetic methods, as an introduction to coevolutionary analyses.

Parasitology in Coevolutionary Studies

Coevolutionary studies largely have their origins in the discipline of parasitology because one of the aims of parasitology is to describe the “cause and effect” of ecological interactions in host–parasite systems. During the development of parasitology, the concept of cospeciation was suggested as a means of inferring coevolution. The idea of cospeciation originated in parasitological studies of wildlife at the beginning of the 20th century (Fahrenholz 1913; Kellog 1913; also see de Vienne et al. 2013). These studies used the phylogenetic relationships of the hosts, and looked for phylogenetic congruence between hosts and their parasites using 2 principles: 1) Fahrenholz rule, parasite phylogeny mirrors that of its hosts; and 2) Szidat rule, primitive hosts harbour primitive parasites (Fahrenholz 1913; Szidat 1940). In this context, the first studies in parasitology expected to discover concurrent and interdependent bifurcations of host and parasite lineages, for example, cospeciation (de Vienne et al. 2013). However, cospeciation is not always interesting in the context of host–parasite coevolution (Ronquist 1995), and is found in few real-life biological models (e.g., Hafner and Nadler 1988; Hughes et al. 2007; Desai et al. 2010; Cuthil and Charleston 2013). Currently, to distinguish coevolution from cospeciation, the cospeciation is defined such the process whereby a symbiont speciates at the same time as another species (this may result from vicarious events or from narrow host specificity) (de Vienne et al. 2013). On the other hand, other authors suggested that the coevolution without macroevolutionary changes (e.g., without cospeciation), but a high degree of cospeciation is usually a sign of coevolution (Ronquist 1998; Page 2003; Charleston and Perkins 2006).

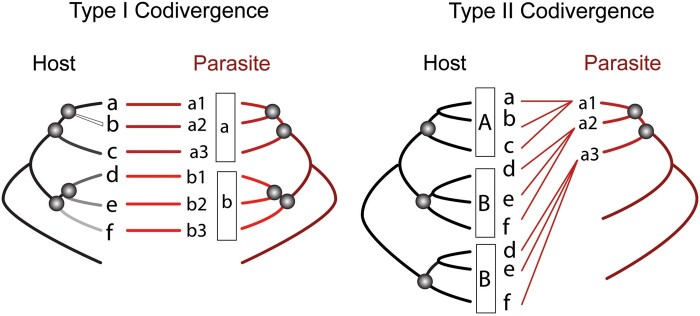
Coevolution in host–parasite systems is considered an asymmetric relationship between groups of ecologically linked taxa, because 1 organism is evolving much more slowly than the other (Charleston and Libeskin-Hadas 2014). These patterns of asymmetric coevolution are commonly found in real biological models (Badets et al. 2011; Demastes et al. 2012; Martínez-Aquino et al. 2014), and may be differentiated from strict coevolution and cospeciation, using the term codivergence as parallel divergence of ecologically associated lineages within two distinct phylogenies (Page 2003). In this sense, coevolutionary processes can be detected from codivergence events between phylogenetic trees of a symbiotic association, using the nodes and their divergence dates plus other biological information (e.g., specificity, morphological adaptation), at distinct taxonomic levels, to detect patterns of diversification from strains/population to biological radiations (Zietara and Lumme 2002; Göker et al. 2011; Cuthill and Charleston 2013). For example, Martínez-Aquino et al. (2014), using empirical data of a host–parasite system, discovered 2 types of codivergence: 1) Type I Codivergence, in which the divergence of an intraspecific parasite lineage occurs in response to the speciation event of its host; and 2) Type II Codivergence, the divergence of the parasite lineage is a result of the diversification process of its host, and subsequent colonisation (host-switching events) by parasite lineages of new hosts strictly belonging to the same taxonomic group with monophyletic affinities, for example, genus, tribe, subfamily, and family (Figure 1). In fact, the codivergence occurred at distinct phylogenetic–genealogical levels and involved a complex of coevolutionary events that occurred at different spatiotemporal scales. Therefore, it is valid to say that codivergence is a special type of coevolution (Mallet 1999; Wright 2011; Cuthill and Charleston 2012; Nadeau et al. 2014), and can promote the processes and patterns of diversification (e.g., cospeciation, host-switching, and vertical transference parasites) between organisms with symbiotic associations. On the other hand, it is also possible to use the codivergence concept to explain the event where a parasite lineage (e.g., an evolutionarily independent lineage, from strains/populations to higher taxonomic levels), infecting a host lineage diverges into two new lineages at the same moment as its host (modified from Charleston 2011).

Figure 1.

Two empirical patterns in the evolution of host–parasite associations.

Each pattern is given as a tanglegram. Different intensities of shading represent different lineages for host and parasite phylogenies. The codivergence event is indicated using matching circles. The lower-case letters represent a “species,” and the numbers next to lower-case letters an “intraspecific lineage”; upper-case letter represent a “supra-specific group,” for example, genus, tribe, subfamily, and family. Type I Codivergence—The divergence of 6 intraspecific lineages of 2 parasitic species (lower-case letters “a” and “b” within square) occurs in response to the speciation events of its hosts. Type II Codivergence—The divergence of 3 intraspecific lineages of parasitic species “a” occurs in response to the speciation events of its hosts (at level supra-specific, capital letters A, B, and C within square), and subsequent colonisation (via host-switch) of parasite lineages to new hosts with monophyletic affinities, for example, the taxon hosts included in A (a, b, and c), is associated with the parasite lineage “a1” (different cophylogenetical hypothetical pattern can be revised from Page 1994b; Ronquist 2003; de Vienne et al. 2013).

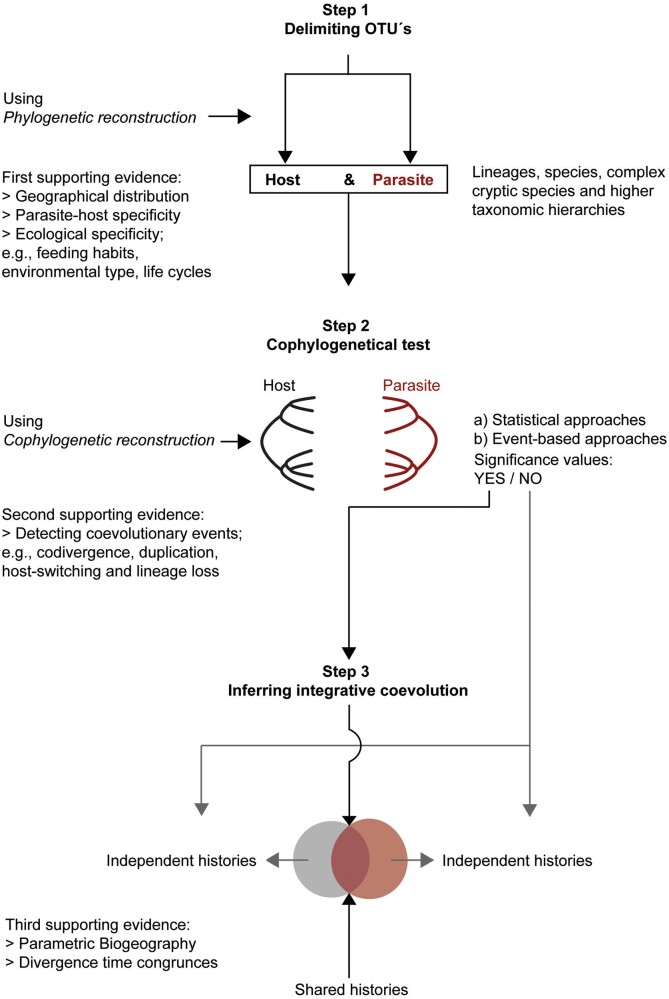
At the moment, numerous theoretical, methodological, and conceptual advances implemented in software are available for analyzing empirical data of biological models in host–parasite systems (or analogous systems). In this context, it is possible to propose a study program based on a phylogenetic framework for discovering coevolutionary processes. It involves working in 3 steps. 1) Finding the boundaries of Operational Taxonomic Units (OTUs), from the histories of populations and paralogous gene families to individual genomes and their ancestral reconstructions (Yang and Rannala 2012). A problem in cophylogenetic studies is the support for the terminal tips, in the host and parasite trees. Phylogenetic analyses based on coalescence can delimit OTUs and eliminate possible failures in both topologies (Ceccarelli et al. 2012; Fujita et al. 2012; Cartens et al. 2013; Zhang et al. 2014). Furthermore, the detection of OTUs specifically in symbiotic organisms can be achieved through integrative taxonomic approaches, following a specialized protocol for coevolutionary studies (Padial et al. 2010; Pérez-Ponce de León and Nadler 2010; Yates et al. 2011). 2) Contrast biological symbiotic models with an ecological interaction (e.g., host-specificity, mimetic associations, and evolutionary behavior), to test coevolutionary hypotheses. Approaches to cophylogenetical reconstruction are powerful tool for inferring coevolutionary processes between two OTUs (see next section). 3) Order each OTU into geographical areas (e.g., endemics, province, sub-regions, and regions; Ebach et al. 2008), to detect geographical congruence patterns and infer integrative coevolution. These 3 steps represent a guide for coevolutionary studies in a phylogenetic framework (Figure 2). The general idea is to compare the observed biological and phylogenetic patterns between two taxonomically unrelated groups of OTUs displaying a close ecological association (e.g., parasitism), suggest a possible evolutionary correlation, and test this coevolutionary hypothesis, while taking into account the biogeographical histories of the taxa involved.

Figure 2.

Flow chart to coevolutionary studies using phylogenetic approaches.

Flow chart showing a step-by-step hypothetical phylogenetic framework. Step 1 is designed to delimit OTUs at any taxonomic level. Step 2 is designed to test cophylogenetic hypotheses with statistical and event-based approaches. Step 3 is the final description of the coevolution process inferred under a phylogenetic framework, supplemented with parametric biogeographic tests and divergence time congruence between 2 independent groups.

Cophylogenetic Methods in Coevolutionary Studies

Cophylogenetic methods are classified into three approaches: 1) pattern-based methods, 2) event-based methods, and 3) statistical methods (Page 2003; Ronquist 2003; Charleston and Libeskind-Hadas 2014). One of the pattern-based methods, namely Brookś Parsimony Analysis (BPA), was the first method developed for cophylogenetical analysis (Brooks 1981). The BPA method uses a “posterior interpretation” and, to date, there are no publicly distributed software packages implementing said method (Page 1990, 1994a; Ronquist and Nylin 1990; Page and Charleston 2002). Nevertheless, readers interested in a more detailed review of BPA approaches are directed elsewhere (Mejía-Madrid 2013 and citations therein). In this section, the focus is restricted entirely to state-of-the-art cophylogenetical methods for which software/websites are available, with updated versions, since programs to identify the algorithms that best explain the observed data, and their pitfalls, are constantly evolving with computational and theoretical advances (Table 1) (Charleston 2011; Keller-Schmidt et al. 2011; Libeskind-Hadas et al. 2014).

Table 1.

Available software/site web for cophylogenetic analyses

Statistical test of congruence methods
Name. CONGRUENCE INDEX [Icong] (de Vienne et al. 2007).
Optimization version. Not applied.
Characteristics. Available on line.
Test. Maximum Agreement Subtrees (MAST).
Data feature. Trees (without branch lengths).
Web address. http://max2.ese.u-psud.fr/icong/index.help.html
Name. PARAFIT (Legendre 2002).
Optimization version. AxPARAFIT (Stamatakis et al. 2007).
Characteristics. AxParfit use a software tool CopyCat, simplifies the usage of Parafit, including the preparation of input data, the use of taxonomic data, the analysis even of sizeable lists of hosts and associates, and the display of the results (Meier-Kolthoff et al. 2007). Furthermore, MRCA link algorithm is possible use like complement to take phylogenetic non-independence into account (Schardl et al. 2008).
Test. Global fit method.
Data feature. Trees or alignments of sequence of DNA (converted into distance matrices) and ultrametric Tree (only in MRCA link extensions).
Web address. http://sco.h-its.org/exelixis/web/software/AxParafit/index.html

Event-Based methods
Name. TreeFitter (Ronquist and Nylin 1990).
Optimization version. TreeFitter 1.3b1 (Ronquist 2002)
Characteristics. TreeFitter has a command-line interface without graphical interface.
Test. Generalized-parsimony based on specific likelihood events.
Data feature. Matrix of event-costs user-specified.
Web address. http://sourceforge.net/projects/treefitter/
Name. CoRe-Pa (Merkle et al. 2010).
Optimization version. CoRe-Pa 0.5.1 is based on a predecessor called Tarzan (Merkle and Middendorf 2005).
Characteristics. CoRe-Pa 0.5.1 offer graphical user interfaces and tools for editing pairs of trees and their tip assignments and viewing the reconstructions. Inferring cophylogenetical histories without assigned costs to the coevolutionary events using randomized tests.
Test. Parameter-adaptive and randomization test.
Data feature. Dated and undated trees.
Web address. http://pacosy.informatik.uni-leipzig.de/49-0-CoRe-PA.html
Name. Jane (Conow et al. 2010).
Optimization version. Jane 4, with a complement tool available in the Xscape software to tree reconciliation (Libeskind-Hadas et al. 2014).
Characteristics. Jane 4 offer graphical user interfaces and tools for editing pairs of trees and their tip assignments and viewing the reconstructions. Inferring cophylogenetical histories with assigned costs to the coevolutionary events use a Pareto-optimal reconciliations.
Test. Node mapping techniques through of dynamic programming algorithm with gradient descendent meta-heuristic and genetic algorithm approaches.
Data feature. Date tree and without date.
Web address. http://www.cs.hmc.edu/∼hadas/jane/
Name. TreeMap (Page 1994b).
Optimization version. TreeMap 3.0b (Charleston 2012), with a node mapping algorithm to reduce the time and space complexity in the cophylogeny reconstruction problem where the host tree’s node ordering is fixed (Drinkwater and Charleston 2014).
Characteristics. TreeMap 3.0b offer graphical user interfaces and tools for editing pairs of trees and their tip assignments and viewing the reconstructions. Inferring cophylogenetical events with searching all solutions that are optimal to choice of event costs, with the option to limit the
number of host-switch events, use a Pareto-optimal solutions.
Test. Node mapping techniques through of dynamic programming algorithm with meta-heuristic framework.
Data feature. Date tree and without date.
Web address. http://sydney.edu.au/engineering/it/∼mcharles/

The statistical approaches

Congruence index

The congruence index is a measure of similarity between two trees (host and parasite) to determine the largest subtree common to both trees. This method determines the minimum number of leaves (tips in trees) and then collapses the internal nodes with only one child (descendent node), that have to be removed in each phylogeny to render the trees identical. In this context, the size of the maximal agreement subtree (MAST) is a simple, yet robust measure of topological congruence (de Vienne et al. 2007). It is important to clarify that this test is useful for getting a ‘‘first and rapid (computationally cheap) insight into the topological congruence between two trees’’ (de Vienne et al. 2009; Kupczok and von Haeseler 2009), before proceeding onto more detailed analyses (such as those reviewed below).

Parafit

Using this method, one can perform a statistical test for a particular global hypothesis of coevolution while testing the significance of each Host–Parasite (H–P) link of the association, thus identifying the species involved in cospeciation and the incongruences in the list of H–P links, producing a joint scenario of the cospeciation and incongruent events with the null model of independence of the H–P associations (Legendre 2002). This method reconstructs coevolutionary scenarios, assessing the global congruence between two trees, based on null hypotheses generated via randomization (Nieberding et al. 2010). However, these statistical analyses of congruence neither point out where the 2 trees differ, nor do they provide explanations for those differences (Charleston and Libeskind-Hadas 2014). On the other hand, in Parafit it is possible to implement a method of MRCAlink (most-recent-common-ancestor link), to apply to ultrametric host and parasite trees and identify all corresponding nodes for pairwise comparisons of the MRCAs’ (most recent common ancestor) ages (Schardl et al. 2008).

The event-based approaches

In event-based approaches, the cophylogenetic reconstruction uses three variables (H, P, and ϕ): a host tree H, a parasite tree P, and a function ϕ that associates each parasite tip with a host tip. The triple interaction (H, P, ϕ) is represented graphically as a tanglegram. The objective is to map P onto H to associate ancestral nodes of P with locations in H. Host and parasite tips are associated as specified by ϕ and each ancestral association places a node p in P on a node or an edge of H, implying a set of evolutionary events that link the two trees, for example, cospeciation, duplication, lineage sorting, and host-switching (Merkle and Middendorf 2005; Merkle et al. 2010; Charleston and Libeskind-Hadas 2014). In this context, the aim is to find a reconstruction of P and H that is consistent with the tip mapping ϕ and that minimizes the total cost of the events in the mapping.

Ronquist and Nylin (1990) first proposed a reconstruction method (TreeFitter) that explicitly measured the fit between the data and a particular reconstruction in terms of the number of postulated specific evolutionary events. TreeFitter addressed for the first time the relevance of choosing between alternative reconstructions by specifying a cost (or weight) for each type of event, and then calculating a summary statistic determining the likelihood of the reconstruction (Ronquist 1995). The cost assigned to each type of event is inversely related to the likelihood of its occurrence. The basic idea is to construct a cost matrix of each event, analogous to a transition matrix for nucleotide substitution probabilities in molecular models, for example, transition/transversion. In this context, Ronquist and Nylin (1995) termed the technique “transformation weighting” (generalized parsimony) in combination with statistical tests (Farris 1973; Sankoff 1975; Felsenstein 1981). In fact, it is not sufficient to include only a parsimony score when reconstructing the coevolutionary events that took place in the historical associations of species, which is why several cophylogenetical methodologies based on parsimony also implement random permutation tests to detect congruence between two trees, for example, Jane, CoRe-Pa, and TreeMap. In these tests, the parasite tree P or the association between host and parasite tips is randomized for a certain number of iterations and the score is recomputed for each randomization. If x% or less of random trials do not get as good a score as the original P, then P is significantly congruent at the x% level. That is, x (or more accurately x/100) serves as an empirical p-value (Charleston 2011; Libeskind-Hadas et al. 2014). In the next section, I give an overview of selected software implementing event-based approaches.

TreeFitter

This method relies on parsimony-based tree fitting (Ronquist 2002; Sanmartín and Ronquis 2004). TreeFitter includes criteria to evaluate the coevolutionary reconstruction with the minimum cost such as most-parsimonious reconstruction detected by heuristic searches, randomization tests (e.g., terminal permutation tests), polynomial algorithms (fast enough to be applicable to real-life-sized problems), and implement event-based options to treat the problem of widespread taxa (e.g., dispersal/switching events) (for more details see Sanmartín et al. 2001; Ronquist 2002; Sanmartín and Ronquis 2004).

CoRe-Pa

This event-based reconciliation method uses a parameter-adaptive approach. This event-based method does not require any cost settings for the cophylogenetic events of interest in advance (such as TreeFitter), but seeks the cheapest reconstruction in which the costs are inversely related to the relative frequency of the corresponding event (Merkle et al. 2010). Note the difference between event-based maximum parsimony reconcilations (such as TreeFitter), in which the model defines event costs a priori, and CoRe-Pa where the event costs are assigned during analysis (also see Wieseke et al. 2013).

CoRe-Pa is a follow-up to an earlier program, Tarzan (Merkle and Middendorf 2005) and is based on dynamic programming, can handle associations of parasites with multiple hosts, and includes the handling of divergence timing information. In addition, the costs are obtained by a statistical optimization criterion (Merkle et al. 2010). In this sense, the optimization finds event costs that are inversely proportional to the frequency of events in the maximum parsimony reconstructions that they induce (Ronquist 2003; Merkle et al. 2010). This approach ignores the ordering of the host nodes so as to allow the best host-switch to be recovered in polynomial time; however, the mathematical optimization technique of CoRe-Pa does not clarify whether the inferred costs are biologically realistic or give rise to the most plausible reconstructions (e.g., ancestral speciation inferred to have occurred after speciation of descendant nodes) (Conow et al. 2010; Cruaud et al. 2012; Charleston and Libeskind-Hadas 2014).

Jane

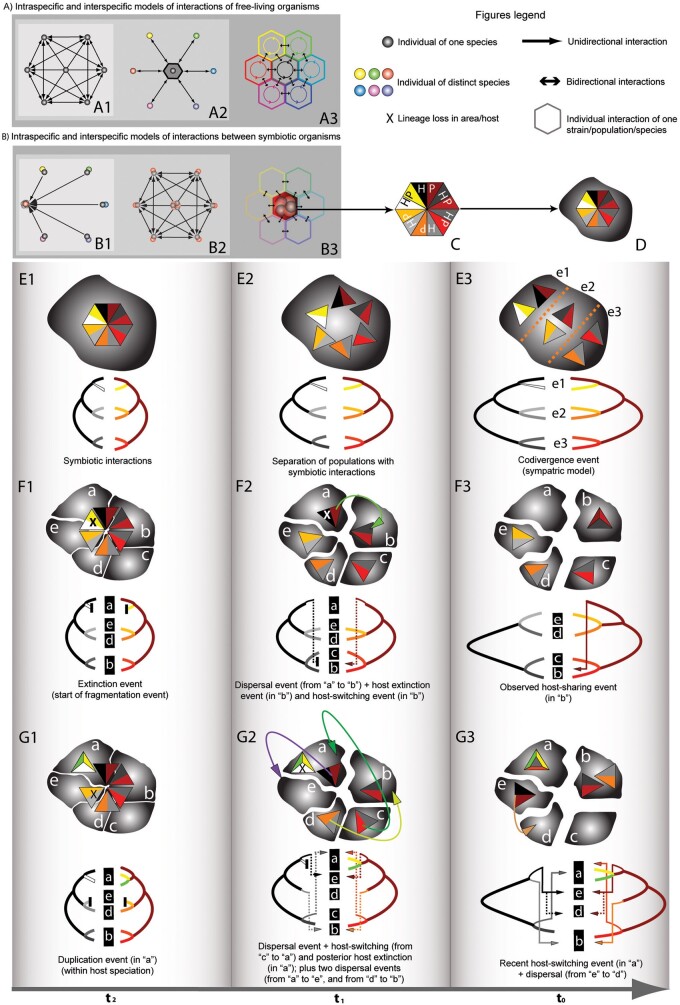
This method use a meta-heuristic framework, testing a genetic algorithm with an internal fitness function that is evaluated through a dynamic programing algorithm (Conow et al. 2010). To find a reconciliation of minimal total cost, Jane is able to provide solutions that are always correct and often optimal (a major revision on computational characteristics and problems of this method is mentioned from Libeskind-Hadas and Charleston 2009; Yodpinyanee et al. 2011; Drinkwater and Charleston 2014). A characteristic of Jane is that it can discover preferential host-switching, based on a specification of the maximum permitted host-switching distance, depending on the distance from the original host to the new host (it is possible to select different host-switch costs for different regions of the host tree and set ranges of times in both the host and parasite trees). In this context, theoretical multi-host process (e.g., widespread) are also detected for parasites under the event of “failure to diverge,” using the “most recent common ancestor solution” (Conow et al. 2010; Charleston and Libeskind-Hadas 2014). This feature can be useful in a biogeographical context to tested hypotheses of dispersal in distinct areas and time, for example, Bayesian Island Model (Sanmartín et al. 2008) (Figure 3).

Figure 3.

Scheme of biological levels of ecological interactions.

The intersection of (A) and (B) shows hierarchical units for each level of biological interaction. (A) A classic model of interactions between individuals of free-living of different strains/populations/species. A1 = Interactions between individuals of the same strain/population/species (black bidirectional arrowheads). A2 = Interactions of only one individual of A1 with 6 individual of different strains/populations/species (black bidirectional arrowheads). A3 = Interactions between and among strains/populations/species (colour/shaded and black bidirectional arrowheads). (B) A model of coevolutionary interactions between two individuals of different strains/populations/species. B1 = Specific interactions represented by black unidirectional arrowheads between individuals of the same strain/population/species (gray circles), versus only one individual of a strain/population/species (red/light gray circle). B2 = Coevolutionary interactions between individuals of two strains/populations/species (gray and red/light gray circles). B3 = Interactions between and among strains/populations/species with other strains/populations/species. Although there are interactions with other species, the coevolutionary interaction represented by superimposed black and red/light gray circles in the central hexagon are close. On the geographic mosaic theory (in which the populations differ in their characteristic and specialisations with respect to the species with which they interact; Thompson 2005). (C) A hexagon that represents 6 potential interactions of a coevolutionary association between 2 strains/populations/species (HP = Host–Parasite association). (D) The same hexagon on a geographic area (gray amorphous polygon). (E–G) Three models of evolution of the cophylogenetic interactions represent by curvigrams in gradual space-time (t_o, t₁, and t₂). E1 = First proximity of strain/population/species is represented by hexagons superimposed on the same space. E2 = Separation in sympatry represented by triangles. E3 = Actual separation of triangles by ecological factors (e1, e2, and e3, represented by a dashed line). F1 = Beginning of the fragmentation of the ancestral area (in the time t₂), by vicariant events, and posterior reticulation of the hexagon (“mosaic fragmentation”). F2 = The fragmentation of ancestral area continues in another time (t₁). F3 = Current distribution with a vestigial geographic mosaic. The figures in (G) show a reticulate model of geographic mosaic. G1 = Beginning of the fragmentation of the ancestral area. G2 = The fragmentation of the ancestral area continues in another time (t₁). G3 = Current distribution with a vestigial geographic mosaic. The black to white curvigram represents host/area associated to the colour curvigram (parasite/symbiont). Lowercase letters in (E–G) represent the reticulate fragmentation of the ancestral area and its associated terminal taxa of the cophylogenetical curvigrams.

TreeMap

Based on empirical evidence, the evolution of this software shows the advances in cophylogenetics through developing algorithms and principles for cophylogenetical reconstruction. For example, the first version of TreeMap 1 used a heuristic algorithm and an exact algorithm to find a single maximal reconstruction named “maximise cospeciation” (Page 1994b). Posteriorly, Charleston (1998) designed the “Jungles” algorithm, which was implemented in TreeMap 2.0b (Charleston and Page 2002); subsequently, several theoretical concepts and mathematical techniques were developed until reaching TreeMap 3, for example, Pareto optimal, p-values and node mapping algorithm (Charleston and Perkins 2006; Libeskind-Hadas and Charleston 2009; Charleston 2012; Drinkwater and Charleston 2014). In contrast to TreeFitter, CoRe-Pa, and Jane, TreeMap does not use explicit event costs but rather seeks to find all solutions that are optimal for some choice of event costs. At the moment, TreeMap 3 works with an exact algorithm to detect optimal reconstructions through multiple Pareto-optimal solutions that are optimal for different event costs. An option to limit the number of host-switching events is implemented in TreeMap 3 to reduce running time because exact algorithms grow exponentially with the number of tips in the trees. TreeMap 3 finds solutions that are guaranteed to be valid and of optimal cost (assuming the number of host-switches is not constrained) (Charleston and Libeskind-Hadas 2014). Although it is still not publicly available, the main principle of this approach is mentioned in their web service, with the plans to include this approach in the next version, for example, likelihood test and Bayesian parameter estimations (http://sydney.edu.au/engineering/it/∼mcharles/).

Phylogenetics in Historical Coevolutionary Biogeographic Studies

The advances of phylogenetics in historical biogeography, through event-based approaches, can also be applied to find cophylogenetic events using its probabilistic algorithms (Ronquist and Sanmartín 2011). For example, models designed to explore cophylogenetic events (e.g., TreeFitter) or similarly, models designed to explore biogeographical events such as Dispersal–Extinction–Cladogenesis (DEC) (Ree and Smith 2008), have been applied to discover coevolutionary history through space and time in complex ecological interactions and diversification patterns (Sanmartín and Ronquist 2004; Martínez-Aquino et al. 2014). In fact, these methods can be complementary to an integrative evolutionary reconstruction of biodiversity (Weckstein 2004; Cruaud et al. 2012; Wilson et al. 2012; Murray et al. 2013). To implement this idea, it is important to use parametric biogeographic models on reticulate scenarios, for example, island model of areas, analogous to “host” by simulating particular events of host-switching (Sanmartín et al. 2008) (Figure 3). In this sense, is possible to compare results obtained by cophylogenetic methods with those obtained through parametric biogeographical methods and support, or reject, the coevolutionary hypotheses.

In the context of phylogeographic approaches, the premise of identifying ecological traits using phylogenetic/genealogical tools for inferring coevolution has been mentioned (Rannala and Michalakis 2003; Nieberding et al. 2010; du Toit et al. 2013). However, it is important to elucidate the conceptual distinction between “comparative phylogeography” and “co-phylogeography,” in the sense of detecting coevolutionary process (e.g., codivergence in co-phylogeography) versus phylogeographic process (e.g., vicariant events in comparative phylogeography). It is common to find studies of comparative phylogeography that use the word “idiosyncrasy” to explain genetic discordances or genealogical incongruences, because frequently 2 taxa with geographical codistribution—but without ecological interaction—are compared (Avise 2009; Gutiérrez-García and Vázquez-Domínguez 2011; Smith et al. 2011). In the sense of co-phylogeographic studies, it is possible to find coevolutionary patterns because the hypothesis in this case is not “only” exploring congruence in geographical space, but within ecologically closely related taxa (Whiteman et al. 2007; Štefka et al. 2011; Mizukoshi et al. 2012). These studies involved finding cophylogenetical patterns at different taxonomic levels, but can show the same pattern as the geographic mosaic theory, reticulate populations differ in their characteristics and specialisations with respect to the species with which they interact (Thompson 2005), from strains to higher taxonomic levels (Figure 3). Future studies on these issues can resolve the differences mentioned in this review.

Concluding Remarks

The cophylogenetic problem is fascinating and the theoretical and methodological development, applying technologies that link phylogenetics and historical biogeography, is rapidly advancing. For example, during the time of writing this review, new methods with their respective software have appeared, for example, Procrustes Approach to Cophylogeny (PACo), which includes statistical approaches with procrustes techniques (Balbuena et al. 2013) and Coevolution Assessment by a Likelihood-free Approach (COALA), including event-based approaches based on Bayesian ABC techniques (Baudet et al. 2015) (in addition to the great advances offered by the contributions of the bioinformatics community in the libraries of the R platform in a coevolutionary context [R 3.2.0 http://www.r-project.org/]). In fact, at this moment the international scientific community working on cophylogenetic studies is developing new scripts, or computational packages using computational simulations. However, it is imperative to obtain more empirical data to test the functionality of these computational techniques with the support of phylogenetic trees, their areas of distribution and possible coevolutive processes. Obviously, with the development of new phylogenetic trees, plus multi-disciplinary studies that include ecological and experimental evidence to support the construction of study programs as suggested in this article, the field of coevolution will continue to advance (e.g., Nyman 2010; Mramba et al. 2012; Hadfield et al. 2014).

Funding

A.M-A was supported by a postdoctoral fellowships (No. 238789) provided by Consejo Nacional de Ciencia y Tecnología (CONACyT, México), and his research is supported by the grant No. 201441 entitled “Plataformas de observación oceanográfica, línea base, modelos de simulación y escenarios de la capacidad natural de respuesta ante derrames de gran escala en el Golfo de México”, financed by the Sectorial Hidrocarbon Fund CONACyT-SENER to the CIGoM Consortium.