Recent applications of light scattering measurement in the biological and biopharmaceutical sciences

1. Introduction

Measurement of the average intensity of excess scattering, termed static light scattering (SLS), has become one of the most widely used techniques for the determination of molar mass, and in some cases, the size of macromolecules in solution. Similarly, development of the theory of fluctuations in light scattering intensity and commercially available instrumentation for experimental measurement of these fluctuations on a microsecond time scale, termed dynamic light scattering (DLS) or quasi-elastic light scattering, has led to widespread use of this technique to measure the short-time diffusion coefficient and apparent size of macromolecules in solution. For a comprehensive review of the theory and practice of SLS, see [1], for DLS, see [2].

The present introduction to light scattering methodology and review of recent literature – 2013 to present – was undertaken for several reasons: (1) to bring the techniques of SLS and DLS to the attention of a broad audience of researchers in the biological and biopharmaceutical sciences; (2) to illustrate the various purposes to which these techniques have recently been put; and (3) to suggest ways in which future studies of various phenomena can be made more informative.

We begin with a summary of the principles underlying each of the types of measurements to be discussed here and common relations utilized in analysis of experimental data. Details will be found in the cited references. Next, various research objectives will be introduced, and citations to the literature will be grouped according to these objectives. Most of the papers cited report studies of proteins in solution, but we shall also cite studies of synthetic peptides and nanoparticles, which have recently become of interest to the biopharmaceutical industry as potentially targetable drug carriers. Finally, we address several topics of concern to the reviewer.

The number of light scattering-related publications in the biological and biopharmaceutical science fields from 2013 onward is very large, and appears in an extraordinarily broad range of journals. It is likely that some possibly important contributions have been inadvertently missed, and apologies are offered in advance to the authors of the missing citations.

2. Methods

2.1 Static light scattering of macromolecules in dilute solution

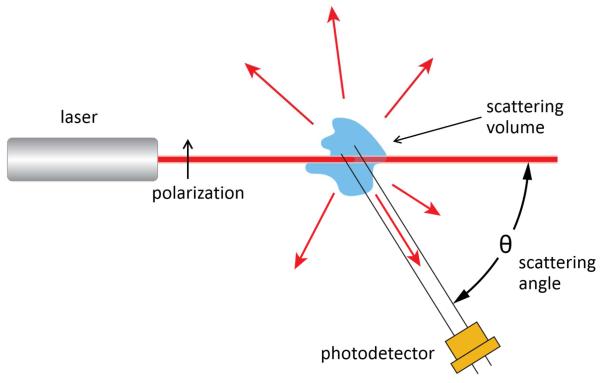
A laser-based light scattering photometer instrument, schematically indicated in Figure 1, measures the average intensity of light I (w,θ) scattered by sample in the scattering volume at w/v concentration w and scattering angle θ, and reports the excess Rayleigh ratio R, calculated according to

$$R\left(w,\theta \right)=k_{\mathit{inst}}\left[I\left(w,\theta \right)-I\left(0,\theta \right)\right]$$ [1]

where k_inst is an instrumental constant determined by calibration with a scattering standard, and i(0,θ) is the intensity of light scattered by pure solvent. Data collected from a solution of a single species of macromolecule are conventionally analyzed in the context of the Zimm-Debye formulation of static light scattering. In the dilute limit, the dependence of R upon w and θ is given by

$$R\left(w,\theta \right)=k_{\mathit{opt}}{\left(\frac{d\tilde{n}}{\mathit{dw}}\right)}^2\mathit{MwP}\left(\theta \right)\left[1-2A_{2}P\left(\theta \right)w+O\left(w^2\right)\right]$$ [2]

Here K_opt is an optical constant calculated according to

$$K_{\mathit{opt}}=\frac{4{\pi }^2{\tilde{n}}_0^2}{{\lambda }_0^4{N}_A}$$ [3]

where ${\tilde{n}}_0$ denotes the refractive index of solvent, λ₀ the wavelength of incident light in vacuum, and N_A Avogadro’s number. $\left(d\tilde{n}∕\mathit{dw}\right)$ denotes the specific refractive increment of solute, M the molar mass of solute, A₂ a measure of the effective interaction between scattering molecules, and P(θ) a structure factor calculated according to

$$P\left(\theta \right)=1-\frac{16{\pi }^2{\tilde{n}}_0^2}{3{\lambda }_0^2}\langle r_g^2\rangle {\sin }^2\left(\theta ∕2\right)+O\left[{\sin }^4\left(\theta ∕2\right)\right]$$ [4]

where the quantity $\langle r_g^2\rangle$ denotes the mean square radius of the scattering solute, discussed below. If the largest dimension of the scattering particle is much less than the wavelength of the incident light (< ~ 35 nm) as in the case of most proteins and small protein complexes, P(θ) ≈ 1, e.g., angular dependence of excess scattering is negligible. Given independently determined values of K_opt and $\left(d\tilde{n}∕\mathit{dw}\right)$, the values of M and A₂ (and $\langle r_g^2\rangle$ in the case of a sufficiently large scattering solute) are obtained by extrapolation of data obtained at various solute concentrations and scattering angles to infinite dilution and zero scattering angle.

1.

Schematic of an apparatus for measurement of static light scattering. Collection of angle-dependent data may be implemented either by varying the angular position of a single detector or by positioning detectors at multiple angles, as in modern MALS instruments.

The quantity A₂ is conventionally identified as the second virial coefficient in the expansion of the osmotic pressure in powers of solute concentration. Different laboratories may express concentration using different units, most commonly g/l or moles/l, and less commonly the number density ρ (molecules/cm³), or φ (unitless volume fraction). Thus the initial concentration dependence of light scattering may be specified as values of other parameters, the most common of which is B₂₂ = A₂/M . It should be kept in mind that all of these parameters are proportional to A₂ and are readily interconvertible by appropriate scaling of concentration units.

Although a more rigorous interpretation of A₂ has been presented [3, 4], it is not obvious whether or when the distinction between the more rigorous interpretation and the conventional one is qualitatively or quantitatively significant in aqueous solutions of macromolecules. We shall therefore adopt the conventional interpretation of A₂ for the present review. Statistical thermodynamics provides an exact relation between A₂ and an orientationally averaged potential of mean force U(r) acting between two molecules of the scattering species separated by center-to-center distance r in a dilute solution [5].

$$A_2=\frac{2\pi N_A}{M}\underset{0}{\overset{\infty }{\int }}\left\{1-\exp \left[-U\left(r\right)∕\mathit{kT}\right]\right\}{r}^2\mathit{dr}$$ [5]

where k denotes the Boltzmann constant and T the absolute temperature. Hence the experimentally measured value of A₂ is frequently utilized as a qualitative or semi-quantitative measure of the nature (net attractive or net repulsive) and strength of interaction between molecules of the scattering solute in a solution, and its dependence upon experimental conditions. This will be discussed further below.

The mean square radius $\langle r_g^2\rangle$ of a scattering species is defined as

$$\langle r_g^2\rangle \equiv \sum _{i=1}^n{\left(r_i-\stackrel{‒}{r}\right)}^2/n$$ [5]

where r_i denotes the location of the ith scattering element, and $\stackrel{‒}{r}$ the center of mass of the solute particle. The definition of a “scattering element” is somewhat subjective and depends upon the detail with which the structure of the scattering particle is described (e.g., at the level of individual atoms, amino acid residues, or monomers within an oligomer). When the size of the particle, expressed as r_g , becomes greater than about 0.05 λ₀ , the value of P(θ) will decrease sensibly with increasing scattering angle, as indicated in equation [4], and the value of $\langle r_g^2\rangle$ may be calculated from the initial slope of the dependence of the scattering intensity, extrapolated to infinite dilution, upon sin² (θ/2). When only one scattering species is present, analysis of the relation between molar mass and r_g can provide information about the structure of the scatterer [6, 7].

Acquisition of data on the angular dependence of scattering intensity by simultaneous collection of data at multiple angles, a technique known as multi-angle light scattering (MALS), is particularly useful when measuring scattering as a function of elapsed time on a time scale of seconds. The addition of a MALS detector to instrumentation for size exclusion chromatography makes possible real-time determination of the absolute mass, and in some cases the size and/or composition, of material eluting from the size exclusion column [1].

2.2 Dynamic (or quasi-elastic) light scattering in dilute solution

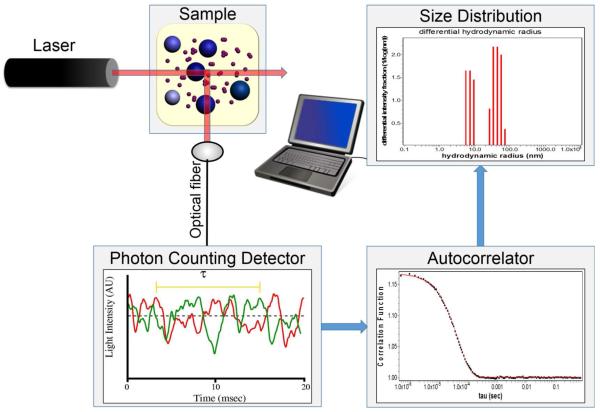
Fluctuations in light scattering intensity on the microsecond time scale are collected by the instrument, and the correlation between the intensity measured at any given time t and the intensity at an arbitrary elapsed time t + τ is expressed as an autocorrelation function calculated according to

$$g^{\left(2\right)}\left(\tau \right)=\frac{\langle I\left(t)\right)I\left(t+\tau \right)\rangle }{\langle I{\left(t\right)}^2\rangle }$$ [6]

where the brackets indicate an average over all t. This process is illustrated schematically in Figure 2. The autocorrelation function for a single dilute scattering species is given by

$$g^{\left(2\right)}\left(\tau \right)=1+\beta \exp \left(-2{\mathit{Dq}}^2\tau \right)$$ [7]

where β denotes the measured value in the short time limit (typically a function of the instrument), θ the independently determinable scattering vector

$$q=\frac{4\pi {\tilde{n}}_0}{{\lambda }_0}\sin \left(\theta ∕2\right)$$ [8]

and D the apparent coefficient of self-diffusion, which may be expanded in powers of the w/v solute concentration w:

$$D\left(w\right)=D_0\left[1+k_{D}w+O\left(w^2\right)\right]$$ [9]

Here D₀ denotes the diffusion coefficient of an isolated scattering solute molecule in solvent, and k_D a measure of the concentration dependence of D, the physical meaning of which will be discussed subsequently. The diffusion of an isolated sphere of radius r in a continuum solvent of viscosity η is given by the Stokes-Einstein relation

$$D_0=\frac{\mathit{kT}}{6\pi \eta r}$$ [10]

It should be kept in mind that this is an ideal model that may be applied fairly accurately to dilute suspensions of large spherical particles (e.g., polystyrene or silica spheres), but holds only approximately at best for biological molecules that may deviate significantly from sphericity and may interact with the solvent and cosolutes in ways that are not taken into account in the derivation of the Stokes-Einstein relation. Nevertheless, most commercially available DLS instruments report their results not directly, in terms of the diffusion coefficient, but indirectly, in terms of an apparent hydrodynamic radius r_h,apparent obtained from the following inexact transformation of equation [9]

$$r_{h,\mathit{apparent}}=\frac{\mathit{kT}}{6\pi \eta D}$$ [11]

without requiring extrapolation of D to the dilute limit D₀.

2.

Schematic of a system for measurement and analysis of dynamic light scattering. (A) Rapid fluctuations of scattered light intensity are recorded at a resolution of ~ 1 μs. (B) The raw data are processed in firmware to yield the autocorrelation function given in text equation [7]. (C) The detailed shape of the autocorrelation function may be processed using various algorithms to yield an estimate of the intensity-weighted distribution of the size of equivalent spherical particles representing scattering species.

Provided that the range of sizes of scattering species in a mixture is not too great, the experimentally measured autocorrelation function g⁽²⁾ (τ) may be analyzed according to a variant of equation [7] to yield an apparent D, which is actually an intensity-weighted or so-called z-average of the diffusion coefficients of all species:

$$D_{\mathit{apparent}}=D_z=\frac{\sum _i{w}_i{M}_i{D}_i}{\sum _i{w}_i{M}_i}$$ [12]

where w_i and M_i respectively denote the w/v concentration and molar mass of the ith scattering species. Thus the value of r_h,apparent calculated by substituting D_apparent for D in equation [11] is

$$r_{h,\mathrm{apparent}}=\frac{\mathit{kT}}{6\pi \eta }\frac{\sum _i{w}_i{M}_i}{\sum _i{w}_i{M}_i{D}_i}=\frac{\sum _i{w}_i{M}_i}{\sum _i{w}_i{M}_i∕r_{h,i}}$$ [13]

2.3 Composition gradient static and dynamic light scattering of dilute solutions

Composition gradient static light scattering (CG-SLS) was devised initially as a means for detecting and quantitatively characterizing reversible macromolecular self-association and hetero-association [8, 9]. For a comprehensive review of the theory and practice of CG-SLS, see [10]. Consider a solution containing two potential reactant species, A and B. Any reversible association taking place in the solution may be characterized by a reaction scheme of the following type:

$$\mathit{aA}+\mathit{bB}\rightleftarrows A_a{B}_b$$ [14]

where the lower case letters denote the stoichiometric amounts of the reactant indicated by the corresponding upper case letter. Note that self-association is a special case of reaction scheme [14] when a > 1 and b = 0, or a = 0 and b > 1. In a solution sufficiently dilute such that all reactants behave thermodynamically ideally, the equilibrium association constant for formation of any complex A_aB_b (denoted by {ab} for brevity) is given by

$$K_{\mathit{ab}}\equiv \frac{c_{\mathit{ab}}}{c_{10}^a{c}_{01}^b}=\frac{M_A^a{M}_B^b}{{\mathit{aM}}_A+{\mathit{bM}}_B}\times \frac{w_{\mathit{ab}}}{w_{10}^a{w}_{01}^b}$$ [15]

where c_ab and w_ab respectively denote the molar concentration and w/v concentrations of {ab} at equilibrium. There may be many complexes {ab} of one or both reactants in equilibrium with monomeric reactants {10} and {01}. By invoking mass conservation constraints, the concentration of each species present in the equilibrium mixture may be calculated as a function of the total concentrations of each reactant and the equilibrium constant associated with the formation of each complex. Assuming that the complexes are small relative to the wavelength of incident light, equation [2] may then be generalized to

$$R\left(w_{A,\mathit{tot}},w_{B,\mathit{tot}}\right)=K_{\mathit{opt}}\sum _{a,b}{\left(\frac{d\tilde{n}}{{\mathit{dw}}_{\mathit{ab}}}\right)}^2\left({\mathit{aM}}_A+{\mathit{bM}}_B\right)w_{\mathit{ab}}$$ [16]

where the sum is taken over all species in the postulated reaction scheme. The value of the refractive increment of each species {ab} may be precisely calculated as the weight average of the refractive increments of pure A and B. The composition dependence of the Rayleigh ratio may then be calculated as a function of the total concentrations of A and B and the equilibrium constants for formation of each complex [10].

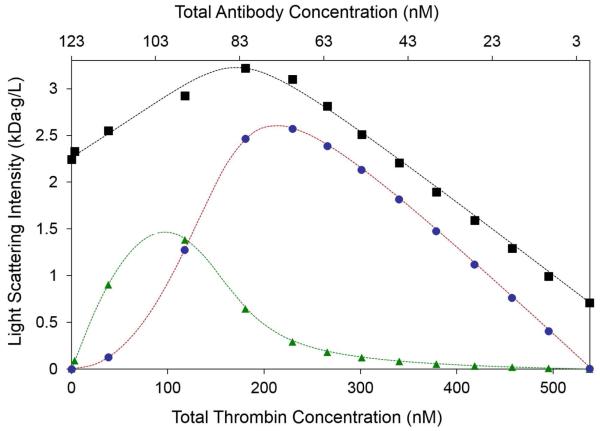
Application of the analysis above has been facilitated by the development of automated instrumentation for the delivery to the light scattering photometer of sequential aliquots of solution containing gradients of solute composition [9, 10]. The molar mass and self-association equilibria of a protein can be characterized quickly through automated measurement and modeling of the dependence of scattering intensity upon the concentration of a protein in 10 to 20 increments of concentration [8]. The molar masses of each reactant in a protein mixture and their self- and hetero-association equilibria can be characterized quickly through automated measurement and modeling of the dependence of scattering upon the composition of a sequence of solutions in which the concentration of A decreases as the concentration of B increases, varying the mole fraction of B from 0 to 1. [9-11]. The shape of the profile of scattering intensity across this “cross-gradient” may be analyzed in the context of several candidate association models to determine the simplest scheme that accounts for the observed data [9, 10]. Results of a typical CG-MALS cross-gradient experiment are shown in Figure 3a.

3a.

R/K_opt plotted as a function of composition measured in a cross-gradient of increasing concentration of thrombin and decreasing concentration of antithrombin antibody. Black squares: measured data, black dashed curve: best-fit of model in which antibody can reversibly bind thrombin to either of two sites with equal affinity, blue points and curve: calculated contribution of 1:1 complex to total scattering, red points and curve: calculated contribution of 2:1 complex to total scattering. Figure reproduced from [10] by permission.

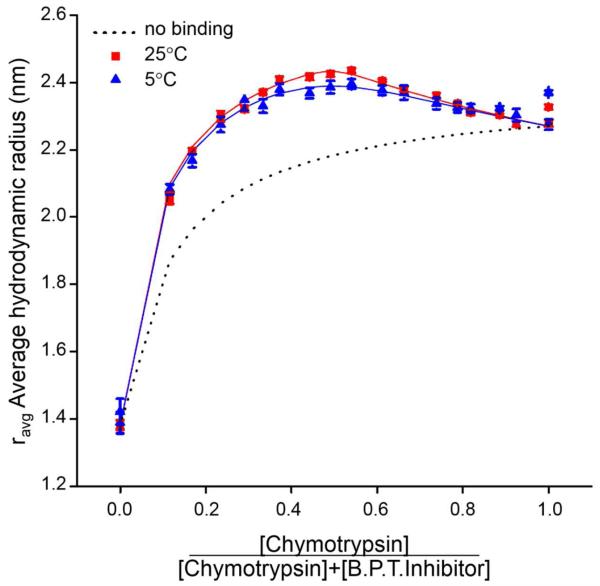
A similar strategy may be employed to analyze the composition dependence of the z-average value of D (equation [12]), or, alternatively, the apparent or average value of hydrodynamic radius (equation [13]) reported by measurements of DLS. However, in order to model the dependence of D_z or the average r_ht on solution composition, it is necessary to make some assumption regarding the relationship between D_i and M_i . If it is assumed that protein complexes are compact and roughly spherical, then according to eqn [9], $D_i\propto M_i^{-1∕3}$. Analysis of data in the literature indicated that this relation is approximately correct for globular proteins, but does not hold for highly anisotropic (e.g., rodlike) molecules, complexes, and particles [12]. For a self-associating protein, if we assume that the diffusion coefficients of small protein oligomers obey the above relation, the diffusion coefficient of i-mer may then be expressed as D_i ≈ D₁i^−1/3. Analogous relations have been presented for hetero-associating systems [13]. Composition gradient DLS has been implemented through the use of automated gradient delivery to a DLS flow cell [12] and through creation of solute gradients in a series of wells in a microplate followed by simultaneous measurement of DLS in each of the series of wells in a microplate reader [13, 14]. The results of pilot studies of reversible homo- and hetero-association carried out via CG-DLS were validated by comparison with the results of CG-SLS applied to the same systems [12, 13]. The results of a CG-DLS cross-gradient experiment are presented in Figure 3b.

3b.

r_h,apparent plotted as a function of the mole fraction of α-chymotrypsin in cross-gradient mixtures of α-chymotrypsin and bovine trypsin inhibitor at two temperatures. Symbols: measured data at two temperatures, solid curves: best-fits of a model in which the two reactants can reversibly form a 1:1 complex with a temperature-dependent affinity, dashed curve: hypothetical dependence of r_h,apparent upon composition in the absence of heteroassociation. Figure reproduced from [13] by permission.

2.4 Electrophoretic light scattering

In the presence of an electric field, charged molecules migrate with a velocity v that is equal to the product of electrophoretic mobility μ_E and the magnitude of the field E. When the electric field is oriented perpendicular to incident light, the Doppler effect will cause the frequency of light scattered at an angle facing toward the direction of collective particle motion to be greater than that scattered at the same angle facing away:

$$\frac{\Delta f}{f}\propto \frac{{\tilde{n}}_0\nu }{c}$$ [17]

where c denotes the speed of light. This shift is extremely small, but may be detected by monitoring an interference pattern created by juxtaposition of attenuated incident and scattered light, permitting accurate measurement of the electrophoretic mobility [15, 16]. The effect of electrophoretic migration on the frequency of scattered light and the production of an interference pattern enabling analysis of the very small frequency shift are illustrated schematically in Figure 4. When the hydrodynamic radius can be simultaneously measured via DLS, an effective charge termed the Debye-Hückel-Henry charge may be calculated from the solvent viscosity, the hydrodynamic radius, the electrophoretic mobility , the Debye-Hückel inverse screening length and the Henry function [16]. If the scatterers are large relative to the thickness of the ionic layer, another effective charge termed the zeta potential may be calculated from colloid theory, but the physical meaning of this quantity applied to proteins, which are much smaller than colloidal particles, is unclear [16]. However, both effective charges, whether realistic measures of the true net charge of the molecule or not, are proportional to the electrophoretic mobility and hence the true net charge. Thus measured changes in either effective charge (or a directly measured electrophoretic mobility) with changing experimental conditions provide a valid qualitative measure of corresponding changes in the electrostatic component of protein-protein interactions.

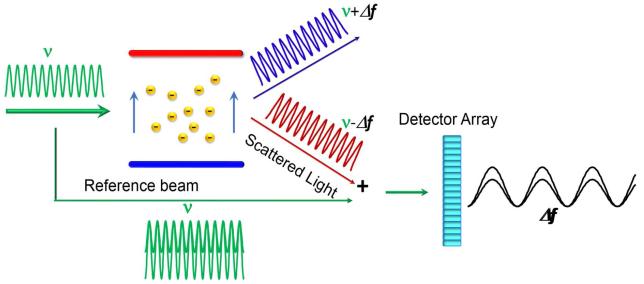
4.

Schematic of an apparatus for measurement of electrophoretic light scattering. At a particular instant of time, a solution of negatively charged macromolecules is exposed to an electric field perpendicular to an incident laser light beam of frequency ν. Due to the Doppler effect, the frequency of light scattered at an angle in the general direction of the positive electrode toward which the molecules are migrating, is upshifted by an increment of Δf, and the frequency of light scattering at the opposite angle, away from the direction of electrophoretic migration, is downshifted by the same amount. When the scattered light is juxtaposed with an equal intensity of incident light, an interference pattern is formed having a measurable period of Δf, which is proportional to the electrophoretic mobility as indicated in text equation [17].

3. Applications

3.1 Characterization of mass and size of individual macromolecular solutes

By far the most common use of light scattering in the biological and biopharmaceutical sciences has been, and continues to be, the determination of the mass and/or state of aggregation of individual species of macromolecules in peaks eluting from size-exclusion chromatographic columns (SEC-MALS) [1] or field-flow fractionation cassettes (FFF-MALS) [17]. The configuration of a system for implementation of SEC-MALS analysis is illustrated in Figure 5. The combination of MALS and refractive index detectors enable the real-time determination of the mass of substances of known refractive increment. Addition of the optional UV detector permits facile composition analysis of conjugate substances containing significant mass fractions of UV absorbing and non-UV absorbing material such as heavily glycosylated proteins or membrane proteins solubilized in micelles of surfactants or phospholipids [18].

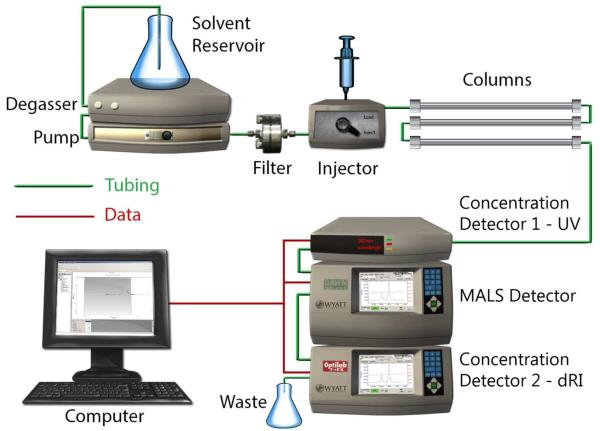
5.

Schematic of a system for the MALS analysis of eluent from a size exclusion column (SEC-MALS). The eluent is passed successively through a UV flow detector (optional), a MALS flow detector, and a differential refractive index flow detector.

Analysis of chromatographic data is customarily performed by software provided by the manufacturer of the light scattering detector, utilizing relations described above. It is usually assumed that the eluting solutes are sufficiently dilute that the A₂ term on the right hand side of equation [2] is negligible, although this may not always be true, particularly in the case of highly charged solutes in solutions of low ionic strength. The validity of the assumption may be checked by injecting multiple samples of different total concentration.

Conventional analysis of SEC data relies on calibration of a particular column with a set of size exclusion “standards” (typically denatured proteins) and application of an empirical correlation between elution volume and molar mass. This procedure is subject to often considerable error if and when a protein or protein complex is extremely aspherical or interacts with the gel matrix material. In contrast, it is emphasized that the mass of the material in an eluting peak calculated via SEC-MALS analysis follows from first principles and is free from potential error arising from failure of the assumptions inherent in the conventional analysis.

Between 2013 and the present, hundreds of publications have appeared in which the standard procedures described above were employed as a routine tool for quality control during the process of purification or production of a biological macromolecule, i.e., to ensure the homogeneity and lack of aggregation of the source material. These publications are not reviewed here, but an extensive online bibliography may be found at http://www.wyatt.com/bibliography.

A list of recent publications in which SEC-MALS was employed to detect and characterize functionally significant homo- and hetero-oligomerization of native and mutated proteins is presented in Table 1. It should be noted that the publications listed in this and subsequent tables were selected on the basis of features of interest to the reviewer.

Table 1.

Determination of the of mass, size and composition of isolated macromolecules and macromolecular complexes in dilute solution

The molar mass of the chaperone protein trigger factor was determined by SEC-MALS in the absence and presence of a fragment of unfolded alkaline phosphatase. [58]. It was found that isolated trigger factor is dimeric in solution, but dissociates to monomer in order to bind unfolded protein.

SEC-MALS was used to establish that Ctf4, which acts as a linker protein in the eukaryotic replisome, is a trimer in solution, in agreement with the X-ray crystal structure. [59]

The molar mass of a solubilized membrane protein, nhTMEM16,encapsulated within a micelle of surfactant, was determined by size exclusion chromatography in conjunction with MALS, UV, and RI detectors. [60] Global analysis of signals from the three detectors indicated that the solubilized protein was present as a dimer, in agreement with the X-ray crystal structure.

SEC-MALS was used to measure the molar masses of a ubiquitin trimer (21.4 kDa), a caspase activation domain (23.2 kDa) and the tight complex formed by mixing the two (112.5 kDa) [61]. The results are in quantitative agreement with a model complex consisting of a tetramer of caspase activation domains binding a single ubiquitin trimer.

The molar mass of a complex of a myosin fragment (Myo4p) and an adaptor molecule (She3p) was measured via SEC-MALS and found to be equal to that of the hetero- trimer Myo4p + 2 She3p. [62] Additional SEC-MALS experiments on mixtures of Myo4, She3p, a second adaptor protein (She2p) and/or ribonucleotide signaling sequences referred to as zipcodes revealed the presence of higher-order complexes. However, the molar masses of the complexes so detected were strongly dependent upon solute concentration, indicative of reversible association, rendering the interpretation of these SEC-MALS chromatograms ambiguous, and qualitative at best. Observations such as these should be followed up by CG-MALS studies (Sections 2.3 and 3.4) in order to obtain unambiguous information about the strength and stoichiometry of equilibrium associations.

SEC-MALS was used to determine the molar masses of complexes of the Cμ4 domain of immunoglobulin IgM [63]. When a particular cysteine residue is deleted, this domain forms a noncovalent dimer in dilute solution. In the native domain covalently linked dimers are found that exist in slow equilibrium with hexamers of dimers. Analogous complexes of Cμ4 domains are found within the intact immunoglobulin, indicating that the overall quaternary structure of IgG derives from oligomerization of this domain.

3.2 Characterization of protein conformational and colloidal stability

Measurements of both SLS and DLS have been used extensively to monitor unfolding and aggregation of proteins in solution under a variety of conditions. Many recent publications in this category are listed in Table 2.

Table 2.

Determination of the stability of proteins and peptides, and formation of irreversible aggregates

Measurements of DLS were used to monitor the stability of BSA and a fusion protein, SP1, with respect to urea-induced unfolding [20]. As urea concentration increased, the average hydrodynamic radius of BSA increased in three steps, which were attributed to the two-step unfolding of individual domains within the BSA molecule, and it is stated that the results are in general accord with results of previously published CD and fluorescence measurements. SP1 consisted of a mixture of monomer and small aggregates that could be separated by SEC. The average hydrodynamic radius of monomer under reducing conditions increased by about 30% with increasing urea, which was attributed to unfolding of the monomer. The average hydrodynamic radius of the soluble aggregates decreased from that of the aggregate to that of the unfolded monomer, corresponding to unfolding-coupled dissociation.

Concurrent measurement of DLS and Raman spectra as a function of temperature was used to characterize thermal unfolding and aggregation of lysozyme at pH 4 [19]. Upon heating from 20 to 80°C and recooling of solutions with concentrations below ~ 40 mg/ml, spectral features present prior to onset of thermal stress regained their original appearance, indicating near-complete reversibility, but at higher concentrations irreversibility was observed. Similarly, following recooling, DLS autocorrelation functions from more dilute solutions indicated almost complete reversion of protein to native monomer, while at higher concentrations, substantial populations of large aggregates were formed irreversibly. Although these results are reasonable, no comparison with previous published studies of lysozyme stability was presented, preventing a clear-cut validation of the quantitative aspect of the measurement.

Concurrent measurement of DLS and Raman spectra as a function of temperature, and as a function of time following thermal stress, were used to characterize thermal unfolding and aggregation of BSA and gamma globulin at pH 7 at various concentrations below 40 mg/ml [50] . The time and temperature dependence of average rh were compared with that of the peak wavelength of the amide 1 band. Since both signals seem to respond approximately synchronously to changes in conditions, it is not obvious that measurement of the Raman spectral shift provides information about the mechanism of either unfolding or aggregation above and beyond that provided by analysis of the time-dependent average rh .

The irreversible aggregation of a glycosylated and a non-glycosylated monoclonal antibody (IgG1) was studied via measurement of time-dependent SEC-MALS and DLS [64]. Early events in the aggregation process were detected by SEC-MALS experiments conducted at a series of elapsed time following initiation of aggregation via exposure to denaturing conditions, enabling quantification of the relative abundances of monomer and small oligomers as a function of elapsed time. Kinetic models were fit to these data. Additional DLS measurements provided an estimate of an average hydrodynamic radius, from which the authors estimated the so-called fractal dimension of aggregates. It is questionable whether their calculations took into account either the polydispersity of the aggregate or, if so, how polydispersity affects the averaging process.

DLS and SLS were used to characterize self-association and aggregation in solutions of crystallins [65]. Results indicate that under the conditions of the experiments, α-A and α-B crystallins exist as mixtures of monomers with rh on the order of 3 nm and small oligomers with rh ~ 10 nm, whereas γ-S crystallin exists as a mixture of monomers with rh ~ 3 nm and large aggregates with rh ~ 100 nm. Addition of either α-A or α-B to γ-S appears to suppress formation of the large oligomer of γ-S.

SEC-MALS and DLS were used to investigate the mechanism of aggregation of one IgG2 and two IgG1 monoclonal antibodies at low pH [66]. Proteins were chromatographed at various time intervals following initiation of aggregation by lowering of pH to 4.5, 4, and 3. MALS analysis of eluate indicated progressive formation of dimer, and trimer at pH 4.5 and 4, and subsequent aggregation to higher oligomers at pH 3. At longer times DLS detected large increases in average hydrodynamic radius indicating formation of large irreversible aggregates.

SLS and DLS were used together with fluorescence and circular dichroism measurements to characterize the process of unfolding and subsequent aggregation of a monoclonal antibody [67]. The antibody was incubated in a series of increasingly concentrated guanidine hydrochloride (GuHCl) solutions. Changes in fluorescence and CD spectra were observed after 1 day of incubation in GuHCl concentrations exceeding 1.2 M. Parallel measurements of chromatography, sedimentation velocity, and DLS indicated the appearance of significant amounts of “high molecular weight species” following six days of incubation in GuHCl concentrations exceeding 1.2 M. The terms “aggregate” and “high molecular weight species” are not defined, but the presence of such species are inferred qualitatively from observations of accelerated elution from a SEC column, accelerated sedimentation velocity, and an increase in average hydrodynamic radius. Measurements of the concentration dependence of SLS revealed no significant effect of GuHCl on the second osmotic virial coefficient at concentrations of up to 2 M, although the duration of incubation preceding the reported results was not specified.

The effects of GuHCl, Urea, and temperature upon the stability and state of association of a large invertebrate hemoglobin (HbGp, MW 3.6 × 106) were studied via DLS and CD spectroscopy [68]. Prior studies showed that native HbGp consists of 144 globin chains of molar mass 16 – 19K and 36 chains of molar mass 25-32K. At low concentrations of denaturant, the native protein dissociates into progressively smaller subunits, but at higher concentrations of denaturant, protein starts to unfold and subsequently to aggregate. Thermal stability is reduced in the presence of denaturant. No quantitative analysis is presented.

DLS was used to characterize the effect of various anions on the rate of aggregation of two thermally stressed antibodies and upon the interaction parameter kD measured in dilute solutions of the native antibodies [69]. A correlation was observed between decreasing values of kD and an increasing rate of aggregation.

DLS and CD spectroscopy were used to investigate the effect of various sugars upon the concentration dependence of diffusion and stability of a monoclonal antibody with respect to thermally-induced aggregation [70]. The authors report a roughly linear correlation between the magnitude of kD measured in the presence of various sugars at a concentration of 0.5 M, and the initial rate of increase of the average rH following rapid heating to 45°C, taken as an measure of thermal stability. A similar correlation was reported between the magnitude of kD and an estimate of melting temperature obtained from the temperature dependence of far-UV ellipticity. Comments: The time dependence of MW derived from measurements of SLS would be a more easily interpreted measure of the rate of aggregation than the time dependence of the average rh. If this study were to be carried out at different temperatures, an Arrhenius plot could be used to extrapolate the aggregation rate to near-room temperatures.

A strong correlation was reported between decreasing kD measured by DLS in dilute solution and increasing opalescence (90° light scattering at 633 nm) for two mAbs over a wide range of pH and buffer compositions [71]. While the data do support a qualitative correlation between kD and the magnitude of protein-protein interaction, the measurements of scattering were reported in nephelometric units, so no calculation of A2 from the presented data is possible.

CG-MALS was used to measure the value of B22 in solutions of a mAb containing varying concentrations of lithium sulfate and ammonium sulfate at pH 7, 8, and 9 [72]. The solubility of antibody in solutions containing different buffers was determined by incubation for two weeks followed by filtration. A general condition-independent correlation between increasing negative values of B22 and decreasing solubility was observed that was in qualitative agreement with either of two previously proposed semi- empirical models.

ELS was used to measure the effective charge on glycosylated Fc1 antibody domains, and concentration-dependence of SLS was used to measure nonspecific interactions between Fc1 molecules [23]. Under the conditions of the reported experiments, the net charge was estimated to be slightly positive at pH 4 but close to zero at pH 5 and 6. The nonspecific interactions between Fc molecules were reported to be slightly more repulsive than expected for purely steric repulsion at pH 4 but indistinguishable from purely steric repulsion at pH 5 and 6. Electrostatic interactions were reported to be much smaller than those observed in intact IgG molecules under similar experimental conditions.

SLS was used in conjunction with measurements of circular dichroism, Raman scattering, and viscosity to characterize the formation of irreversible aggregates of α- chymotrypsinogen at acid pH, elevated temperature and moderate concentration (2015). Loss of native structure as a function of time was monitored by CD and Raman scattering. Loss of native monomer correlated strongly with weight average size of monomer as predicted by a previously proposed model for irreversible aggregation. Solution viscosity was found to scale with aggregate size and concentration. [21]

SLS and ELS were used to characterize PPI in solution of a mAb in acetate and citrate buffers, and additional measurements of SANS and SAXS were used to characterize morphology of aggregates formed in the two buffers [73]. PPI and the deduced mechanism of protein aggregation in the two buffers were significantly different under conditions such that the proteins bore a net positive charge in low ionic strength solutions. The difference was attributed to preferential interaction of citrate anions with the protein relative to acetate anions.

SLS and DLS were used, in conjunction with measurements of turbidity, fluorescence, CD, and proton NMR, to characterize the effects of various small molecule solutes (arginine, lysine, GuHCl) and pH upon the aggregation of insulin [74]. Arginine was found to stimulate aggregation at concentrations up to 100 mM but to inhibit it at higher concentrations. The pH dependence of the rate of aggregation was opposite in the absence and presence of arginine. No quantitative analysis is provided.

A novel instrument capable of simultaneously measuring DLS and thioflavin-T fluorescence within a single sample cell was utilized to probe aggregation kinetics of poly-glutamine peptides of different length known to form amyloid fibers in vitro [75]. Fluorescence was taken as a measure of amyloid fiber formation as a function of time, while DLS reported average size of aggregates. Lag times reported by DLS were significantly greater than those reported by fluorescence, suggesting that overall aggregation may involve bundling of individual fibers that is not reported by fluorescence.

A novel system was constructed to simultaneously measure the stopped flow kinetics of fibrin formation via MALS and SAXS [22]. Fibrin formation was initiated by enzymatic cleavage of fibrinopeptides A followed by immediate and simultaneous introduction of the aggregating solution into the MALS and SAXS flow cells. The reaction was followed until gelation occurred, and data collected via the three techniques was processed to obtain estimates of the time evolution of MW, $\langle R_g^2\rangle$, and $\langle R_c^2\rangle$, where RC denotes the radius of a fiber cross-section. The time evolution of $\langle R_c^2\rangle$ could not satisfactorily be accounted for by the conventional dual-strand fiber model. A new model for the initial stages of fibrin aggregation called “Y-ladder” was proposed, and it was shown that this model could simultaneously account for the time evolution of all three measured quantities.

The irreversible aggregation of a mAb following thermal stress was characterized via a conventional measurement of DLS to characterize the evolution of average aggregate size, and a parallel measurement of the DLS of tracer particles in protein solution to monitor the time evolution of viscosity [76]. A fractal dimension of aggregate was calculated by comparing the apparent radius of aggregate to that of the monomeric mAb. The viscosity at any given time point depends upon both the average aggregate size and the amount of aggregate. The authors propose an approximate method for estimating the “average” amount of aggregate, and a function of both average amount and average size quantities that correlates with viscosity, but the physical basis of these approximations is unclear.

DLS was used together with other methods to characterize the irreversible aggregation of insulin following heating to 65°C at pH 2 [77]. Analysis of autocorrelation functions measured at various time points following initiation of aggregation indicated no appreciable change in protein size under a half hour. At 45 minutes large particles appeared with values of rh exceeding those of monomer by a factor of 10 – 30. Between 60 and 100 minutes a broader distribution of larger particles including a significant amount of aggregate with hydrodynamic radii 100+ - fold greater than that of monomer appeared. No quantitative model was suggested.

An instrument designed to measure SLS at 90° from multiple solutions in parallel was utilized to follow slow aggregation of two mAbs under various conditions [78]. The authors claim to be able to measure MW and second and higher virial coefficients from data obtained at a single scattering angle. This would only be possible in the absence of significant self-association leading to angular dependence of scattering, so plots of increasing MW at long time are probably only of qualitative value in comparing the relative tendencies of antibodies to aggregate under different conditions.

Time-dependent measurement of DLS was used to characterize the aggregation of a charged amphiphilic peptide at pH 2, under varying conditions of ionic strength, buffer composition, and amount of organic cosolvent [79]. The dependence of the z-average diffusion coefficient of peptide upon time was analyzed in the context of a Smoluchowski-type model for irreversible aggregation. It was concluded that the aggregation is not diffusion limited and that the activation barrier is due largely to repulsive electrostatic interaction between peptides. They argue that the enhancement of aggregation by increasing the concentration of salt and the amount of organic cosolute is due to reduction of the activation barrier. However, it is difficult to understand how the addition of organic cosolvent, which reduces the dielectric constant of solvent, would diminish repulsive electrostatic fiber-fiber interactions.

SLS and DLS were used in combination with mass spectroscopy and SAXS measurements to probe the mechanism by means of which a small organic molecule (a tannin) induces the aggregation of an intrinsically disordered protein, IB5 [80]. The dependence of scattering intensity upon the mole ratio of tannin to protein was analyzed to yield the average amount of tannin bound per molecule of protein, and estimates of aggregate size from DLS measurement together with estimates of aggregate mass from SLS and MS yielded estimates the average number of protein molecules per aggregate. Dissociation of aggregates at long time was attributed to redistribution of tannins between protein molecules.

The results of DLS measurements are qualitatively described as indicating that increasing concentrations result in increasingly larger and more polydisperse distributions of the size of Rubisco activase [81]. No quantitative data are presented.

SEC-MALS was utilized together with measurements of fluorescence and NMR to characterize initial events in the formation of amyloid by transthyretin [82]. Following initiation of aggregation at pH 2 by addition of NaCl, solutions of transthyretin were chromatographed, and the resulting elution profiles were analyzed to yield estimates of the relative amount of monomer, oligomers and higher aggregates as a function of elapsed time. A simple two step kinetic model for aggregation assuming instantaneous unfolding upon addition of salt was proposed.

In principle, the response of a protein to stress can be monitored in two ways. The first is to gradually increase and decrease the perturbation – either a change in temperature or the concentration of a denaturing cosolute – in small increments, and to measure what ideally would be a change in the equilibrium state of the system. This is a reasonable approach when the protein is highly dilute and the rate of irreversible second- and higher order reactions would be expected to be slow relative to the relaxation time for unimolecular unfolding and refolding. One example of what appears to be reversible folding and unfolding of lysozyme at pH 4, monitored by changes in r_h,apparent and in Raman spectral peaks, was presented by Lewis & coworkers [19]. Unfortunately the highly processed results are presented in just a single figure, and analysis of the raw data is only superficially described, preventing a critical assessment of the work.

It appears that most investigators lack the patience to pursue the quasi-equilibrium approach, and instead opt to apply a temperature jump and follow time-dependent changes of SLS or DLS. At low protein concentrations one might hope to be able to temporally discriminate between reversible unfolding and subsequent irreversible aggregation, but this reviewer has found no clear-cut demonstration of such discrimination. It appears that under the conditions in which the published temperature-jump experiments have been carried out, aggregation proceeds immediately upon unfolding and reversibility is unattainable.

It has been reported [69.70] that the rapidity with which a variety of proteins aggregate, as quantified by the initial slope of either the scattering intensity or the apparent hydrodynamic radius with time following the temperature jump, is highly correlated with either B₂₂ or k_D measured via SLS or DLS respectively in dilute solution under conditions such that the protein is native. Since a negative value of either of these parameters is generally regarded as an indicator of net attractive interactions between protein molecules, which would be expected to enhance any tendency to aggregate, the correlation is not unexpected, but a quantitative mechanistic relationship between the two observations remains to be elucidated.

Isothermal denaturation by urea, guanidinium hydrochloride, and related cosolutes does not ordinarily lead to aggregation and hence does not affect SLS, which is sensitive only to changes in mass. However, unfolding does lead to changes in DLS, which is sensitive to changes in scatterer size. We are aware of only one publication reporting the use of DLS to monitor chemical denaturation, and the work presented is only preliminary [20]. The technique is promising and deserves further development.

The use of MALS and/or DLS, sometimes in conjunction with other methods of macromolecular characterization (e.g., CD, fluorescence or Raman spectroscopy, SAXS, SANS), to monitor the progress of irreversible aggregation following an initiating event provides information about the time evolution of aggregate size, which has been used to develop models for the mechanism of aggregate formation (see for example [21, 22]). Measurement of effective charge via ELS has also been found to correlate with the rate of irreversible aggregation of glycosylated and non-glycosylated Fc-1 antibody fragments [23]; the tendency to aggregate diminishes with increasing effective charge.

3.3 Characterization of nonspecific protein-protein interactions in slightly concentrated solution

A substantial number of publications has appeared during the last three years in which A₂ (or B₂₂) and/or k_D, and other measured properties of solutions of well-studied model proteins or selected monoclonal antibodies have been measured as functions of pH, ionic strength, and buffer salts. Correlations between the dependence of these solution properties upon the independent variable(s) have been presented, and in some cases theoretical explanations have been offered. Many of these publications are listed in Table 3.

Table 3.

Quantitative characterization of nonspecific intermolecular interactions between macromolecules in dilute solution

CG-SLS was used to quantify interactions between each of four proteins (BSA, ovalbumin, ovomucoid, and soybean trypsin inhibitor) and sucrose, and self- interaction between molecules of each protein and sucrose in phosphate-buffered saline (150 mM NaCl) at pH 7.4 [32]. Sucrose was found to be moderately self- attractive, and each of the proteins except STI more self-repulsive than predicted on the basis of steric repulsion alone. The interaction between sucrose and all four proteins is net repulsive. However, the magnitude of the interaction between sucrose and BSA, ovalbumin and ovomucoid can be accounted for by steric repulsion alone, whereas that between sucrose and STI indicates the presence of a partially compensating attractive interaction in addition to steric repulsion.

A linear correlation was found between kD measured by concentration-dependent DLS and B2 measured by concentration-dependent sedimentation equilibrium for three monoclonal antibodies [26].

CG-MALS was used to determine B2 of BSA as a function of pH and salt [56]. Results obtained were compared with measurements made on BSA solutions under similar conditions via SLS and complementary methods.

CG-MALS was used to measure the dependence of scattering intensity upon composition in mixtures of a monoclonal antibody and two PEGs of different size [31]. The data were analyzed using formalism appropriate to mixtures of two scattering species to obtain estimates of B22, B33, and B23 (the two-body coefficients in the power series expansion of osmotic pressure), where species 2 is antibody and species 3 is PEG. The reported Bij were essentially independent of pH between 5 and 9. B33 was significantly positive and independent of pH, indicating self-repulsion of PEGs. B22 and B23 were immeasurably small and independent of pH to within the uncertainty of measurement. These vanishingly small values and their apparent pH independence are unexpected and unexplained. Unfortunately, neither the raw data nor details of the analysis were presented.

CG-MALS and CG-DLS were used to measure concentration-dependence of SLS and DLS in solutions of a mAb containing various concentrations of sodium sulfate, chloride, and thiocyanate at pH values between 6 and 8.3 [48]. SLS measurements were made at antibody concentrations up to 100 g/l, and indicated that all three salts suppressed self-association of the antibody to varying extents. Particular attention was paid to the behavior at limiting low concentration in order to determine B22 and kD. The results are not satisfactorily accounted for by current models of colloid and protein electrostatics, indicating the presence of ion-specific effects.

CG-MALS was used to measure the apparent B22 of lysozyme in solutions containing various concentrations of PEG 2000, 6000, and 12000 and various concentrations of sodium chloride or sulfate [30]. The dependence of B22 of protein upon polymer concentration at higher salt concentrations is reported to be non-monotonic, decreasing at low polymer concentration and subsequently increasing for concentrations exceeding around 20 g/l. The authors account for this behavior with a model in which the conformation of polymer is assumed to contract with increasing concentration at low concentrations but then expands and progressively unfolds with increasing concentration at higher concentrations. Comment: it would be more appropriate to analyze the data in the context of a model containing a mixture of two scattering species, protein and polymer (see for example [31, 33]). The nonspecific interaction between protein and polymer could then be correctly evaluated in terms of a cross-virial coefficient which may or may not be dependent upon salt concentration.

Measurements of SLS were used to quantify PPI between molecules of either of two mAbs in solutions containing buffer only and containing 100 mg/ml trehalose or ethylene glycol [28]. The authors assert that the addition of either polyol converts a negative or negligible value of A2, depending upon the mAb, to a substantially positive values at pH 5, 7, and 9. It is argued that this is the origin of the stabilizing effect of polyols against protein aggregation. Comment: The data should be analyzed in the context of a model treating both protein and cosolute as scattering species. Such a model takes into explicit account self-interaction of protein, self-interaction of cosolute, and hetero-interaction of protein and cosolute, as shown in [32].

Batch measurements of SLS over a range of protein concentration was used to measure apparent mass and B22 of three mAbs in solutions containing varying concentrations of sodium chloride and ammonium sulfate and as a function of pH between 4 and 10 in phosphate buffer [47]. At pH 6.5 two of the three antibodies underwent self-association with increasing concentration of NaCl, but the value of A2 for all three was small and almost independent of NaCl concentration. Association of the same two antibodies was enhanced in the presence of ammonium sulfate, and the value of A2, initially ~ 0, became increasingly negative with increasing concentrations of ammonium sulfate. In dilute phosphate buffer, the apparent molar mass of all three antibodies was approximately independent of pH. That of two of the three antibodies in the limit of infinite dilution was approximately equal to that of a monomer, whereas that of the third indicated the presence of some irreversibly formed oligomer. The authors attribute the differences between the effects of NaCl and (NH4)2SO4 to specific ion effects rather than global electrostatics.

DLS and ELS were used to measure kD and zeta potential (proportional to electrophoretic mobility) of a monoclonal antibody as a function of pH between 5 and 7 and salt concentration [83]. kD was found to be most negative near the isoionic point (pH at which electrophoretic mobility ~ 0) and low salt concentration. At pH 6.1, turbidity was observed to be maximal at a concentration of ~65 g/l and at low ionic strength. When a solution of this composition was cooled to 4°C, phase separation was observed after 12 h. Comment: The authors incorrectly attribute enhanced turbidity to incipient liquid-liquid phase separation. The increasing turbidity as the pH approaches the isoionic point is due to the attenuation of net repulsive electrostatic interactions between antibody molecules as net charge diminishes. When, in addition, the temperature is lowered below a critical value, the enthalpic contribution to total interaction between antibody molecules becomes sufficiently attractive to overcome the entropic barrier to phase separation.

CG-SLS, CG-DLS and ELS were used to measure B22, kD, and zeta potential of a mAb as a function of pH and ionic strength in two different buffers ([25]. Results were fit using model interaction potentials incorporating a Debye-Huckel approximation for long range repulsive electrostatic interaction and a semi-empirical Baxter adhesive potential for short-range attractive interaction. A strong linear correlation between B22 (proportional to A2) and kD was found over the range of pH and ionic strength studied, the slope of which was predicted approximately using the model potential with contributions only from excluded volume and short range adhesion.

CG-SLS and/or CG-DLS, and/or ELS were used to measure B22, kD and zeta potential of a mAb as a function of pH between 5 and 9 and ionic strength between 10 and 350 mM in solutions containing a wide variety of salts, salt mixtures, and buffers [46]. Analysis of the results permits distinction between ion-specific effects (e.g. ion binding and protein-water competition for specific ions) and nonspecific electrostatic effects (e.g. ion screening). Electrostatic effects on protein-protein interaction seem to saturate at ionic strengths on the order of 300 mM.

SLS was used to measure B22 of wild-type human γ-crystallin (HGS) and two deamidated mutants [84]. Comparison of CD spectra and stability with respect to GuHCl denaturation indicate that deamidation did not significantly affect the conformation or conformational stability. However, the SLS results indicated that deamidation did significantly diminish repulsive protein-protein interaction under the conditions employed, hence increasing the potential for aggregation.

SLS was used to measure B2 of bovine lactoferrin as a function of ionic strength over the range 5 – 500 mM at pH 7 [85]. The results indicated that the dependence of B2 upon ionic strength was non-monotonic, initially decreasing to a significantly negative value with ionic strength until 25 mM, and then increasing and becoming slightly positive at around 100 mM, with only a slight further increase at higher ionic strength. The experimentally observed non-monotonic dependence of B2 upon ionic strength qualitatively resembled that predicted by a Monte Carlo simulation of the interaction between two lactoferrin molecules using a simplified interaction potential combining anisotropic electrostatic interaction and an isotropic short-ranged Lennard Jones potential.

Measurements of SLS and DLS were employed to characterize protein-protein interactions and aggregation of alpha-chymotrypsinogen in acidic solution [24]. Analysis of the dependence of scattering intensity on protein in solutions containing varying concentrations of NaCl at pH 3.5 indicated that PPI became less repulsive with increasing salt concentration. At 100 mM NaCl, attractive interaction appeared to almost entirely compensate for both electrostatic and excluded volume repulsion. A cursory inspection of kD values obtained from DLS measurements suggested net attractive interactions at the highest salt concentrations, but a more detailed comparison of kD with corresponding values of B22 values obtained from SLS indicated that although there is a linear correlation between kD and B22, a positive offset exists, indicating that under certain circumstances, a positive kD of small magnitude may not necessarily reflect net attractive PPI.

Measurements of SLS and DLS were employed to characterize interactions between monoclonal antibodies as a function of the concentration of added cyclodextrin [29]. The authors assert on the basis of a simplistic analysis of SLS and DLS results that for both proteins, PPI became more repulsive upon addition of cyclodextrin. Comment: the incorrectness of the model used to analyze the SLS data is clearly shown in Fig SI-1, since the Debye plots appear to indicate that the molecular weight of protein decreases substantially with increasing cyclodextrin concentrations. This non-physical result is due to the neglect of cyclodextrin as an explicit scattering species. A complete analysis of cyclodextrin-protein interaction requires global modeling of the intensity of scattering on the concentrations of both cyclodextrin and antibody in mixtures of two scattering species, with explicit allowance for the contributions to scattering of antibody-antibody, cyclodextrin-cyclodextrin and cyclodextrin-antibody interactions, as demonstrated in [32].

SLS and DLS were employed to characterize the state of association of BSA in the presence of varying concentrations of yttrium chloride, the salt being of particular interest due to the presence of the trivalent cation [86]. For a fixed concentration of protein, the scattering intensity was observed to increase as ${\left(1-c_{\mathit{salt}}∕c^{\ast }\right)}^{-1}$ where c* indicates the salt concentration corresponding to divergence of scattering. DLS autocorrelation functions were interpreted in the context of a two species model. It was assumed that the larger of the species corresponded to a cluster of BSA molecules, the size of which increases with increasing salt concentration, approaching 100 nm at csalt approaches c*. The diffusion coefficient of the smaller species also decreases significantly as csalt approaches c*, and this observation is not accounted for.

Measurements of ELS and DLS were used to measure the electrophoretic mobility and kD of three mAbs in dilute solution, and the apparent hydrodynamic radius and viscosity of concentrated solutions of each mAb at pH values of 4, 5, 6, 7, 8, and 9 [27]. The apparent isoionic point of each antibody was taken to be the pH at which the electrophoretic mobility changed sign. For each of the antibodies, the value of kd reached a (negative) minimum, the apparent hydrodynamic radius reached a maximum, and the viscosity reached a maximum at a pH very close to the pI for that antibody. It is concluded that attractive interactions detected by measurement of kD at low concentration or by measurement of apparent hydrodynamic radius at high concentration are highly correlated with increased viscosity at high concentration.

CG-SLS was employed to quantify self- and hetero-PPI in solutions of ovalbumin, ovomucoid, and RNaseA, and three binary mixtures of the three proteins, at total w/v concentrations of up to 40 mg/ml in .05 M phosphate buffer at pH 6, 7, 8 and 8.8, and pH and .05 M phosphate + 0.15 M NaCl buffer at pH 7 [33]. Comparison of the best-fit interaction coefficients Bij with those predicted for pure steric interaction yielded a quantitative measure of the sign and magnitude of long-range interactions between molecules of species i and j under the conditions of measurement. Variation of the interaction parameters with pH demonstrated the effect of net charge upon PPI, and pH- dependent changes in sign were confirmed by measurement of electrophoretic mobility of each protein at different pH values.

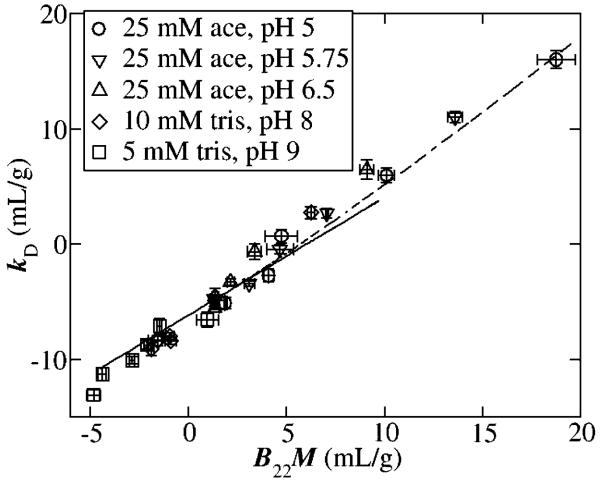
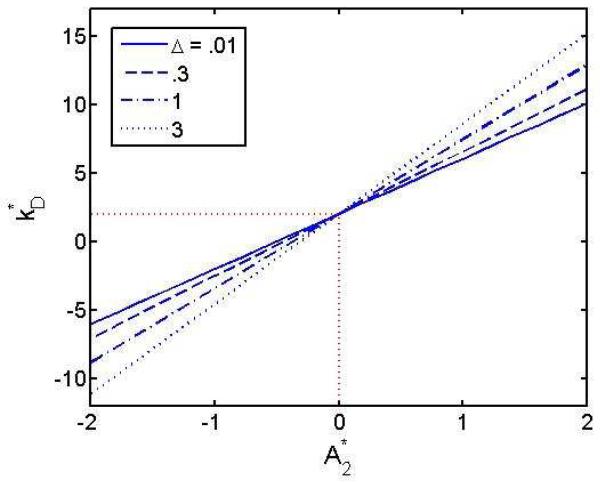
Several publications report observation of a linear or near-linear correlation between the values of k_D and B₂₂ (or A₂) observed under varying experimental conditions [24-26], as illustrated in Figure 6. The linear correlation may be accounted for by theory, as explained in Section 4.3 below.

6.

Plot of k_D against A₂ (B₂₂M) measured in solutions of a monoclonal antibody at different pH values in different buffers. Figure reproduced from [25] with permission.

A strong correlation has been reported between decreasing values of k_D or increasing values of r_h,apparent measured using DLS at low antibody concentration and increased viscosity at high concentration [27].

Several publications report measurement and analysis of the composition dependence of SLS in solutions containing mixtures of scattering solutes in the context of models incorporating intermolecular interactions [28-33]. In order to correctly analyze the results of such measurements it is necessary to explicitly take into account the presence of each solute and their self- and hetero-interactions, which was not always done (see comments in the relevant entries in Table 1).

3.4 Characterization of reversible specific associations in dilute solution

Recent publications describing characterization of specific associations by measurement of light scattering are listed in Table 4.

Table 4.

Characterization of specific associations in dilute solution

DLS was used to detect heteroassociation of a trypsin/chymotrypsin inhibitor, BTCI, and the 20S proteasome [87]. Unfortunately, no measurements of the dependence of DLS upon the composition of BTCI – proteasome mixtures was performed, so a composition gradient analysis is not possible.

CG-MALS was used to characterize the equilibrium association between streptavidin and an anti-streptavidin antibody [88] Due to the multivalent nature of both streptavidin and antibody, a variety of large streptavidin-antibody complexes may be formed. The dependence of weight-average molar mass upon the concentrations of streptavidin and antibody may be accounted for quantitatively with an analytically soluble model containing three association constants and the molar masses of the two macromolecular reactants.

A review of various methods, including CG-SLS and DLS, used to characterize the self-association of the bacterial division protein FtsZ under various conditions was published [89]. This review provides an excellent example of how light scattering can be used in conjunction with complementary techniques to provide a comprehensive, multidimensional picture of a thoroughly studied self-associating protein.

SEC-MALS was used to verify the formation of physical complexes of proteins involved in base excision DNA repair and to determine their stoichiometries [90]. DLS was used to estimate the sizes of the complexes.

CG-MALS was used to characterize the reversible monomer-dimer equilibrium of the N-terminal domain of the bicarbonate transporter protein NBCel-A [91]. A disease- related mutant of this domain was found to aggregate irreversibly under Zoidentical conditions.

CG-DLS and CG-MALS were used to measure the effect of variation in temperature, pH, buffer type, and Hofmeister anions upon the reversible self-association of a monoclonal antibody [92]. The self association scheme best describing the data (monomer – trimer – (trimer)2 – (trimer)3 - …) was found to be unaffected by changes in conditions, and the same as characterized previously [35], but equilibrium constants and corresponding relative stabilities of these states were affected. For example, increasing temperature was found to inhibit self-association and increasing salt concentration promoted self-association.

CG-MALS was used to characterize associations between a peptide derived from the calcium-activated potassium channel (SKp) and calmodulin (CaM) in the absence and presence of saturating Ca and at low and high protein concentrations [93]. Systematic variation of solution composition revealed that In the presence of 2 mM Ca, SKp and CaM were found to reversibly form complexes with SKp/CaM stoichiometries of 1:1, 2:1, and 1:2. In the absence of Ca the 1:2 complex was not observed.

DLS was employed together with differential scanning calorimetry to examine the relationship between temperature, self-association, thermal stability, and ligand binding of folate binding protein (FBP) [94]. The authors inferred changes in the state of association of FBP from changes in the apparent hydrodynamic radius and the distribution of hydrodynamic radii reported by the DLS instrumentation. Estimates of molar mass and states of association were presented without explanation of how the values were derived from DLS data.

SEC-MALS and CG-MALS were used to determine the states of association of signal transduction proteins Vie-A-His6, Vie-B, and VieS-C, and to detect and quantify reversible hetero-association between various mixtures of these proteins [95]. Each pair of proteins except VieA-His6/VieB was reported to combine to form complexes of distinct stoichiometry.

CG-DLS was used to quantitatively characterize the effects of N-trimethylamine oxide (TMAO) and guanidine hydrochloride (GuHCl) on the reversible dissociation of the α2β2 tetramer of cyanmethemoglobin into αβ dimers [14]. The dependence of the z- average diffusion coefficient upon the concentrations of TMAO and/or GuHCl could be quantitatively accounted for by a model in which the free energy of dissociation decreased linearly with increasing concentration of GuHCl and increased linearly with increasing concentration of TMAO. The compensating effects of the two cosolutes in mixtures were independent of each other.

CG-SLS and DLS were used in conjunction with measurements of sedimentation velocity and fluorescence correlation spectroscopy to characterize the effect of potassium upon the self-assembly of FtsZ [96]. Whereas it was previously shown that KCl inhibits the self-association of FtsZ when bound to guanine diphosphate (FtsZ- GDP), it was found that KCl non only facilitates the self-association of FtsZ when bound to guanine triphosphate (FtsZ-GTP) but also increases the size of the large oligomeric species of FtsZ formed at sufficiently high protein concentration. In contrast, addition of KCl decreases the size of the large oligomeric species of FtsZ formed at sufficiently high concentrations of FtsZ binding a slowly hydrolyzing analog of GTP.

CG-MALS was used to determine the stoichiometry and equilibrium association constants for formation of hetero-complexes formed by the proteins αSNAP and either SNARE or V7-SNARE [97]. Under the conditions of measurement, SNARE could bind up to 4 molecules of αSNAP, and V7-SNARE could bind up to 2 molecules of αSNAP.

Specific associations of native proteins may be either reversible or irreversible on the time scale of a particular experiment, depending upon the magnitudes of rate-limiting association and dissociation rate constants. Those complexes characterized by tight non-covalent binding, resulting in immeasurably slow rates of dissociation, may be separated as individual species by various techniques of fractionation, most prominently size-exclusion chromatography, and their masses and compositions determined in real time by SEC-MALS. A tutorial in the analysis of complexes using SEC-MALS has recently been published [34].

The detection and analysis of complexes that are in rapid equilibrium with reactant species presents a greater challenge to the experimenter, as the presence and quantity of such complexes can only be detected in a solution containing both the reactants and the complexes. Reversible associations may result in detectable changes in spectroscopic or hydrodynamic properties, but quantitative analysis of the composition dependence of such properties in systems containing multiple association states can be problematic. However, when the refractive increments of reactant species have been independently determined, equation [16] informs us that the measured dependence of SLS upon the total concentrations of each reactant may be unambiguously interpreted as a function of molar mass and association equilibrium constants leading to the formation of all significant species [10]. Many recent studies of reversible association by CG-SLS, including some in systems comprising multiple states of self- and hetero-association, have been facilitated by the use of a commercial system for highly automated and integrated sample delivery to SLS and concentration flow detectors, data collection and analysis (Calypso, Wyatt Technology). Figure 3a shows data obtained using gradients created by this system together with the results of analysis by Calypso software.

Reversible associations may also be detected and quantified through composition-dependent changes in the z-average diffusion coefficient, or alternatively, the average or apparent hydrodynamic radius [12, 13]. The resolution and range of this method of analysis are not as great as those afforded by CG-SLS, but may be entirely satisfactory for characterization of simple associations, such as a monomer-dimer equilibrium within a limited range of interaction strength, as illustrated in Figure 7 [14]) . In addition, the very low quantity of sample required to measure DLS and the rapidity of data acquisition make this an attractive option for detection of interactions over a broad range of experimental conditions or within a panel of candidate binding partners, to be followed by more detailed study of the system under selected conditions or binding partners via CG-SLS [35].

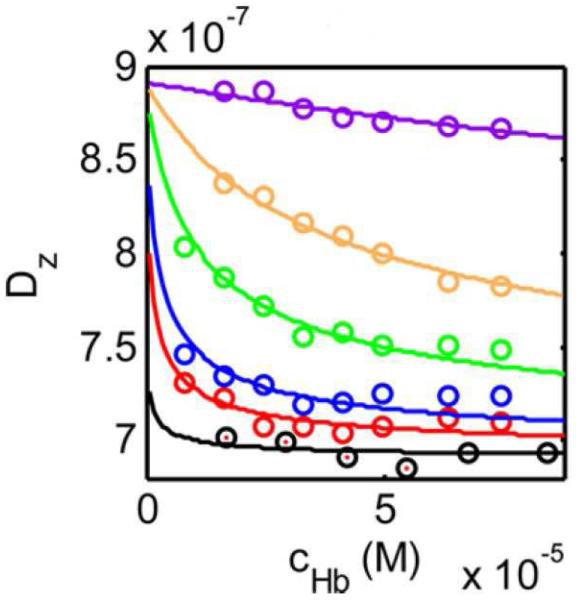
7.

D_z plotted as a function of the total concentration of cyanmethemoglobin in the presence of the following concentrations of guanidium hydrochloride (GuHCl): 0 (black), 0.1 M (red), 0.2 M (blue), 0.4 M (green), 0.6 M (yellow), 1.0 M (purple). Symbols: data, plotted curves, best-fits of a model in which an α₂β₂ tetramer with D = 6.9 × 10⁻⁷ cm²/s can reversibly dissociate to form two αβ dimers with D = 8.9 × 10⁻⁷ cm²/s, and the equilibrium dissociation constant increases with increasing GuHCl concentration. Figure reproduced from [14] with permission.

3.5 Characterization of macromolecular interactions in concentrated protein solution

DLS was used to characterize the state of association of proteins in solutions at concentrations exceeding 100 g/l [36]. The article reviews a number of studies from the corresponding author’s laboratory, the results of which have been interpreted as revealing the presence of very small amounts of large (~ 100 nm) liquid-like clusters of highly concentrated protein (~ 500 g/l) that are in metastable equilibrium with monomeric protein. It is proposed that such highly concentrated clusters provide a favorable environment for the nucleation of crystals.

CG-MALS was utilized together with measurements of SAXS and viscosity to investigate the relationship between reversible self-association of a mAb and viscosity of concentrated (175 mg/ml) antibody solutions [37]. The dependence of light-scattering intensity upon antibody concentration (0 – 175 mg/ml) was measured in 20 mM His buffer, pH 6 and various concentrations of sodium sulfate, which enhanced antibody self-association. The concentration dependence of scattering intensity was fit by a model combining repulsive excluded volume interactions and multiple states of association (clustering) in equilibrium. The best-fit stoichiometry of the largest cluster calculated to be the predominant species at 175 mg/ml for each sulfate concentration, was found to correlate linearly with the measured solution viscosity for all sulfate concentrations, as indicated in Figure 8.

8.

Viscosity of a self-associating monoclonal antibody (mAb1) in the presence of varying concentrations of Na₂SO₄ and a non-associating mAb (mAbE) at a concentration of 175 mg/ml plotted against the maximum cluster size obtained by fitting an interacting hard sphere model to the experimentally measured concentration dependence of SLS over the range 0 – 175 mg/ml under each set of conditions. Figure reproduced from [37] with permission.

3.6 Characterization of supermolecular assemblies

Changes in the size of casein micelles upon encapsulation of various amounts of a drug were quantitated by measurement of DLS. The results are reported to be in good agreement with other estimates of size obtained from SAXS and cryo-TEM measurements. [38].

Changes in the apparent hydrodynamic radii of DMPC and DMPG micelles upon encapsulation of various amounts of a cationic peptide were measured by DLS. As expected, micelles expanded with increasing amount of incorporated peptide. No quantitative analysis was provided [39].

DLS was used to measure the size of detergent micelles and of complexes of membrane proteins and detergents of varying alkyl chain lengths [40]. In the absence of detergent, bacteriorhodopsin formed large aggregates (r_h ~ 500 – 1000 nm) . Following incubation with Triton-X, the predominant species in solution exhibited an average r_h ~ 6 nm, slightly larger than micelles of pure Triton-X (r_h ~ 5 nm). Measurements on other protein-detergent complexes indicated a lack of correlation between protein molecular weight and the size of the protein-detergent complex, suggesting that the treatment of the complexes as equivalent spheres may be an oversimplification.

The interaction between lysozyme and silver nanoparticles (NP) was studied by DLS and electron microscopy [41]. The hydrodynamic radii of isolated lysozyme and NP were independent of temperature up to 55°C. Upon heating a mixture of lysozyme and NP to 55°C the average hydrodynamic radius increased from 14 to 16.5 nm. Hysteresis was observed upon cooling but the average hydrodynamic radius eventually returned to the pre-heating value. Analysis of distribution of sizes indicated that heating of the mixture was associated with a significant broadening of the size distribution.

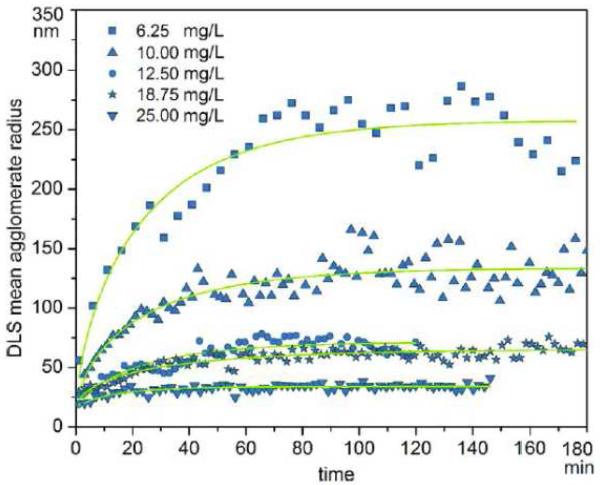
Measurements of DLS were used to characterize the effect of hemoglobin upon the kinetics and equilibria of clustering of gold NP [42]. In the absence of protein, NP aggregate indefinitely at pH 4, but in the presence of Hb or BSA, NP form stable finite clusters that may dissociate upon dilution of NP. The higher the concentration of added Hb, the smaller the size of the stable clusters, but the relaxation time for their formation is not markedly affected, as indicated in Figure 9. The authors propose a model according to which binding of the Hb to the NP surface modulates NP aggregation by reducing the attractive interaction between between NP.

9.

r_h,apparent of gold nanoparticle clusters plotted as a function of elapsed time following sample preparation in the presence of various concentrations of hemoglobin (6.2, 10, 12.5, 18.75, 25 mg/ml). The limiting size of clusters diminishes with increasing Hb concentration. Figure reproduced from [42] with permission.

In a validation study, a comparison of various methods of viral particle detection indicated that field-flow fractionation in combination with MALS detection and analysis can provide reliable identification and quantitation of influenza virus particles in various media [43].

3.7 Miscellaneous applications of interest

The ability of DLS to quantitate the amounts of small and large scattering species in binary mixtures was explored over a wide range of relative scattering particle sizes and compositions [44]. This is an important study that reveals the strengths and limitations of the method and the particular instrument employed. Validation studies such as this should be routinely conducted whenever a new DLS or other sizing instrument is introduced into the laboratory.

The electrophoretic mobility of lysozyme at pH 7.15, measured by ELS, was found to vary widely in different buffers at a uniform ionic strength of 10 mM [45]. This finding mandates the inclusion of buffer-specific effects in calculations of properties such as net charge, heretofore based upon electrostatic theories that neglect such effects. Ion-specific effects were also reported in several other studies [46-48].

It was demonstrated that the same MALS and UV flow detectors and analytical procedures employed in conventional SEC-MALS can be used in conjunction with a Size Exclusion - Ultra High Pressure Liquid Chromatography (SE-UHPLC) column to obtain reliable values of M_w and r_h,apprarent for each peak eluting from the column. The advantages of using a SE-UHPLC column in place of a conventional SEC column include faster elution times, increased resolution, and smaller samples [49].

4. Topics of concern

4.1 Meaning of r_h,apparent in mixtures

A number of published DLS studies refer to a “mean” or “z-average” hydrodynamic radius. The value of the apparent r_h reported by several commercial DLS instruments is the peculiar average given in equation [13], which is related to a z-average of the inverse of r_h. We prefer to call this quantity r_h,apparent to emphasize that it is not a number-, weight- or intensity weighted (z-) average of r_h. If one attempts to analyze the concentration or time dependence of r_h,apparent by modeling it as a z-average of the hydrodynamic radii of individual species present in a mixture, one may obtain seriously inaccurate results, depending upon the distribution of species. When modeling the experimentally measured dependence of r_h,apparent upon time or any other experimental variable in the context of a hypothetical reaction scheme, it is essential to employ equation [13].

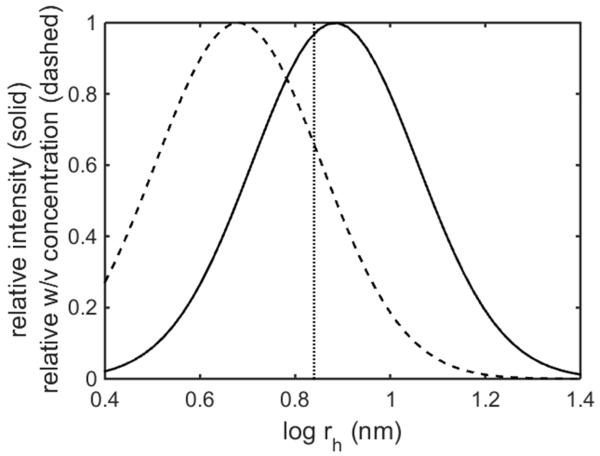
4.2 Caution is required when interpreting scattering intensity distributions

A significant number of publications reviewed here involving measurements of DLS presented the results of these measurements in the form of plots of relative scattering intensity against the logarithm of r_h or d_h = 2r_h. Ordinarily these plots are generated by manufacturer-provided software using algorithms, such as inverse Laplace transforms, that are unfamiliar to the great majority of users of these instruments. In what follows we provide two illustrations of how naive interpretations of such plots may lead to qualitatively incorrect conclusions.

Let us first consider the recently published intensity distribution of the diameter of hydration of purified human serum albumin (HSA) at 20°C [50]. This distribution, scaled to a maximum value of unity, is reproduced as a solid curve in Figure 10A. At this temperature, the protein is presumed to be native and homogeneous. The diffusion coefficient of a scattering particle with a given hydrodynamic radius is given by the Stokes-Einstein relation, equation [10]. It has been found that the diffusion coefficient of many compact globular proteins may be calculated to within experimental precision as a function of molar mass M using the following empirical relation [12]

$$D\left({\mathit{cm}}^2∕s\right)\approx 2.91\times {10}^5∕M^{0.343}$$ [18]

Combination of equations [10] and [18] leads to the following relation that is approximately valid for η = 1 cP (the viscosity of dilute aqueous solutions) and T = 20°C:

$$\log d_h\left(\mathit{nm}\right)\approx -0.82+0.343\log M$$ [19]

and its inverse

$$M\approx {10}^{2.39+2.92\log d_h\left(\mathit{nm}\right)}$$ [20]

Equation [19] was used to calculate the value of log d_h for HSA (MW 70,000), and this is indicated in Figure 10A as a dotted vertical line, in good agreement with the maximum of the published distribution. If the purified protein is homogeneous, the distribution of log d_h should be represented as a sharp spike at the position of the dotted line. Even an investigator who is unfamiliar with the analysis should recognize that the reported distribution, with a width at half height corresponding to a factor of three in d_h (or a factor of ~ 30 in hydrodynamic volume) could not possibly correspond to that of a native and presumably homogeneous protein.

10.

A. Relative distribution of scattering intensity plotted against log d_h for HSA at 20°C, replotted from [50], solid curve. Relative distribution of w/v concentration calculated as described in text, dashed curve. Dotted line indicates approximate value of log d_h expected for a homogeneous protein of M = 70,000.

B. Relative distribution of scattering intensity plotted against log d_h for HSA at 70°C, replotted from [50], black curve. Relative distribution of w/v concentration calculated as described in text, red curve.

There are then two possible explanations for the appearance of this broad distribution: either the HSA studied was in fact quite heterogeneous, or the reported distribution is an artifact. We can rule out the first option rather simply as follows. Recalling that the scattering intensity is proportional to the product of the molar mass and the w/v concentration (equation [2]), the size distribution of the weight/volume concentration of scatterers may be estimated as a function of hydrodynamic diameter according to

$$w\left(\log d_h\right)\propto I\left(\log d_h\right)∕M\left(\log d_h\right)$$ [21]

The dashed curve in Figure 10a indicates the scaled distribution of w/v concentration calculated from the distribution of scattering intensity using equations [20] and [21]. According to the calculated distribution, half of the protein should exist as fragments with molecular weight < 27000, which is obviously unrealistic.

Given a protein as well studied as albumin, the results should have been examined to see whether they make sense and are consistent with well-known properties of this molecule being studied. If not, why not? In this particular case, the answer is that in the presence of experimental noise, the mathematical deconvolution of the autocorrelation function performed by the instrument is subject to some uncertainty and reports an artificially broad distribution. Given prior knowledge (i.e. the homogeneity of the protein studied), the autocorrelation function could have - and should have - been modeled by a the function appropriate to a single species, namely equation [7]. One may ask whether artificial broadening of the reported distribution really is a problem, since the maximum of the distribution of log d_h in this example corresponds to approximately the correct molecular weight. The answer is that artificial broadening introduced by automated data processing within the instrument, details of which are hidden from the user, will in a similar fashion be added to real distributions of molar mass and hydrodynamic diameter in solutions containing mixtures of scattering species, rendering analysis of the reported distributions misleading at best and qualitatively incorrect at worst.

As described in Section 3.2 and Table 1, numerous investigators have utilized DLS as a method of characterizing colloidal stability and for monitoring the kinetics of irreversible aggregation. It is not uncommon to see results comparable to those plotted as a black curve in Figure 10b, in which the distribution of scattering appears as multimodal and spread over a large range of log d_h. In this instance, there appear to be three scattering modes with “average” values of log d_h (nm) equal to 1.0, 1.8, and 2.6 respectively. Inspection of the plotted intensity distribution would leave the naive user with the impression that the bulk of the protein has undergone a great deal of aggregation, forming species thousands of times larger than the monomer. However, when one calculates the distribution of w/v concentration as described above, plotted as a red curve in Figure 10b, an entirely different qualitative picture appears. The largest scatterers comprise an infinitesimal fraction of total protein, and 99% of the protein appears to exist as relatively small oligomeric species. It is the educated guess of this reviewer that the autocorrelation function from which the published intensity distribution was derived could be modeled quantitatively as deriving from a small set of discrete oligomers – probably not more than three or four - comprising almost all of the protein, together with one or two significantly larger species in vanishingly small amounts.

The purpose of the above comments is not to engender distrust in the results of DLS measurements, but rather to engender a healthy skepticism regarding the results of automated calculations, the details of which are not understood by the investigator. Cautious interpretation of the “real” results, which are the autocorrelation functions derived from analysis of fluctuations in scattering intensity, may yield valuable insight into the underlying thermodynamic and transport properties of macromolecules in the solutions being studied.

4.3 Specific vs nonspecific interactions

The astute reader may have already noticed that there are two possible ways to interpret the concentration dependence of the Rayleigh ratio R, measured via SLS at low concentration, as indicated by equations [2] and [16] respectively. According to the fluctuation theory of static light scattering [52], in the absence of specific associations, a negative value of A₂ (R/w increasing with concentration) indicates a net attractive interaction between two solute molecules, and a positive value (R/w decreasing with concentration) indicates a net repulsive interaction. But an increase in R/w with increasing concentration may also be attributed to the formation of specific equilibrium complexes at low concentration, as the abundance of complexes would increase with concentration, leading to a gradual increase in the weight-average molar mass (cf. equation [16]).

Similarly, there are two possible ways to interpret the concentration dependence of the apparent diffusion coefficient D measured via DLS at low concentration, as indicated in equations [9] and [12] respectively. We recall that DLS results from fluctuating interference between light waves scattered from molecules in the immediate vicinity of each other, due to fluctuations in their positions relative to each other. These fluctuations reflect both direct and hydrodynamic interactions between the scatterers. In the absence of specific associations, net attractive interactions between near neighbors will tend to slow fluctuations due to a positive correlation between their positions, leading to a negative k_D, while net repulsive interactions (including steric repulsion) will tend to accelerate fluctuations due to a negative correlation between their positions, leading to a positive k_D. In the presence of specific association equilibria leading to complexes with lifetimes significantly longer than the fluctuation sampling time, the abundance of equilibrium complexes will increase with increasing solute concentration, and the average rate of diffusion will decrease due to the increased mass (or size) of the complexes relative to that of monomer, leading also to a negative value of k_D.

How can one determine whether a negative value of A₂ or k_D is due to a weak nonspecific attractive interaction or to specific associations occurring at low concentration? The answer is that one cannot distinguish the two, given only information about the limiting concentration dependence at low concentration. This holds true for measurements of both static and dynamic light scattering. Measurements must be made at increasingly higher concentrations until it becomes clear whether or not the concentration dependence of R and/or D over a range of concentrations spanning at least two orders of magnitude and preferably greater may be modeled to within experimental precision by a unique and finite set of specific association equilibria. Quantitative modeling of the concentration dependence over a sufficiently broad range of concentration may require explicit consideration of the concentration dependence of both specific associations and nonspecific interaction [52].

4.4 The linear correlation between k_D and A₂ is no mystery

Several theoretical interpretations of k_D have been presented, the most recent of which are found in [24] and [25]. Here we examine the consequences of an earlier treatment due to Muschol & Rosenberger [53]. Consider two scattering particles that interact directly via a spherically symmetric potential of mean force W(x), where x is the distance between the surfaces of the particles. In this treatment k_D is taken to be the sum of effects arising from thermodynamic interaction, quantified as k_S, and hydrodynamic interaction, the magnitude of which is quantified as k_H. The results of the analysis presented in [53] are summarized below.

$$k_S=8+24\underset{0}{\overset{\infty }{\int }}{(1+x)}^2\left\{1-\exp \left[-W\left(x\right)\mathit{kT}\right]\right\}\mathit{dx}$$ [18]

$$k_H=6+12\underset{0}{\overset{\infty }{\int }}\left(1+x\right)\left\{1-\exp \left[-W\left(x\right)\mathit{kT}\right]\right\}\mathit{dx}$$ [19]

The dependence of D upon concentration is then given by

$$D=D_0\left[1+\left(k_S-k_H\right)\varphi +O\left({\varphi }^2\right)\right]$$ [20]

where the dimensionless volume fraction of scattering particles φ is equal to the product of the w/v concentration and the specific volume $\stackrel{‒}{\nu }$, in units of reciprocal concentration. Thus $A_2=k_S\stackrel{‒}{\nu }$ and $k_D=\left(k_S-k_H\right)\stackrel{‒}{\nu }$ . To illustrate the relation between A₂ and k_D we utilize the square well (SW) potential of mean force, which is the simplest potential that can incorporate “soft” attractive or repulsive interactions in addition to steric repulsion.

$$w\left(x\right)=\{\begin{array}{cc}\infty \hfill & x<0\hfill \\ \epsilon \hfill & 0\le x<\Delta \hfill \\ 0\hfill & \Delta \le x\hfill \end{array}\phantom{\}}$$ [21]

Δ is a measure of the range of the soft interaction and ε a measure of the strength of the soft interaction in units of kT, the thermal energy. A negative value of ε indicates an attractive soft interaction and a positive value a repulsive interaction. A useful measure of the magnitude of soft interactions alone is

$$A_2^{\ast }\equiv \frac{A_2}{A_2^{\mathit{HS}}}-1=\frac{k_S}{k_S^{\mathit{HS}}}-1$$ [22]

where $A_2^{\mathit{HS}}$ and $k_S^{\mathit{HS}}$ denote the respective magnitudes of A₂ and k_S expected for hard spheres, i.e., when W(x) = 0 for all x > 0. A positive value of $A_2^{\ast }$ is indicative of net repulsive soft interactions, and a negative value indicative of net attractive soft interactions. Using the relations given above, we can readily calculate the value of $k_D^{\ast }=k_D∕\stackrel{‒}{\nu }=k_S-k_H$ as a function of $A_2^{\ast }$ for various values of Δ, as shown in Fig 11. We observe a nearly linear relationship between the values of $A_2^{\ast }$ and $k_D^{\ast }$ that may be approximately described by $k_D^{\ast }\approx 2+s{A}_2^{\ast }$, where the slope s varies with the range (or more generally, the shape) of the potential function W(x). This result agrees well with the results of several reported measurements of both A₂ and k_D via parallel measurement of the concentration dependence of SLS and DLS [24-26]. It should be noted that $k_D^{\ast }$ will be positive in the absence of soft interactions due to the omnipresent steric repulsion, and this offset must be taken into account when interpreting the significance of a measured value of k_D.

11.

Plot of $k_D^{\ast }$ against $A_2^{\ast }$, calculated as described in text for various values of Δ, the range of the square well potential relative to the diameter of the spherical hard particle. The depth of the square well is determined by the values of $A_2^{\ast }$ and Δ.

4.5 Validation and confirmation are important

While searching the literature in preparation for this review, the reviewer found a substantial number of published measurements of the SLS and/or DLS of solutions of well-studied and commercially available model proteins, such as lysozyme or bovine serum albumin, under conditions of varying pH, ionic strength, temperature, and/or buffer composition. In most of these publications there did not seem to be any effort made to replicate the precise conditions or verify results previously reported by other laboratories. The reviewer strongly believes that if prior measurements of SLS, DLS, ELS or a related property of solutions of any commonly available protein have been reported, it is incumbent upon researchers studying the same protein using the same or complementary techniques to compare their results with the previously published results in order to validate their methodology. If the results of any two measurements of the same property made on nominally identical solutions differ significantly, the origin of the discrepancy must be elucidated if the results of either measurement are to be taken seriously.

One cannot replicate measurements from other laboratories if the property being measured is that of one or more proprietary monoclonal antibodies that have not been previously studied outside of the authors’ laboratory. In this event, publication in the open literature should require a commitment by the authors to provide upon request an amount of the studied antibodies sufficient to validate the results.

Four recent examples of the type of comparison studies recommended here deserve special mention:

1. The electrophoretic mobility of BSA in 10 mM Tris + 10 mM NaCl at pH 8.1 was measured using ELS in two different instruments, capillary electrophoresis, and membrane confined electrophoresis [54]. Results obtained by the various methods were in general but not precise agreement, and values of the Debye-Hückel-Henry effective charge calculated from these mobilities were likewise in general but not precise agreement with results calculated from hydrogen ion titration and analysis of amino acid sequence and protein structure.

2. CG-MALS and sedimentation equilibrium were used to characterize the equilibrium self-association of the chaperone protein ClpB [55]. The dependence of weight-average molar mass upon protein concentration was independently measured by the two techniques, and results of both sets of measurements were accounted for quantitatively by a single model according to which ClpB self-associates to reversibly form hexamer and dodecamer.

3. CG-DLS, CG-MALS and sedimentation equilibrium measurements were used to quantitatively characterize reversible self-association of a monoclonal antibody [35]. The data obtained from all three types of measurements were quantitatively accounted for by a model in which the antibody could reversibly self-associate to form a trimer, and the trimers so formed could weakly self-associate at higher concentration to form oligomers of indefinite size according to an isodesmic scheme. The authors recommend the use of CG-DLS to rapidly screen large numbers of samples for self-association, followed by CG-MALS for detailed quantitation of self-association detected in the CG-DLS screen.

3. SLS was utilized to measure the dependence of B₂₂ upon pH in solutions of BSA containing various concentrations of NaCl, including 150 mM NaCl [56]. In an earlier publication, published data on the concentration dependence of turbidity, sedimentation equilibrium, and osmotic pressure of BSA at various pH values in 150 mM NaCl were analyzed in the context of an effective hard spherical particle model [57]. According to this model, the osmotic pressure may be expanded in powers of the effective volume fraction φ_eff of non-diffusible solute:

$$\Pi ∕\mathit{RTc}=1+4{\varphi }_{\mathit{eff}}+O\left({\varphi }_{\mathit{eff}}^2\right)$$

Here φ_eff = v_effw, where w is the w/v concentration of solute and v_eff is the effective volume of the hard particle representation of solute, in units of reciprocal concentration. Thus the second virial coefficient of the osmotic pressure is 4v_eff, enabling a straightforward calculation of v_eff corresponding to each reported value of B₂₂. The values of v_eff calculated from the measurements of Ma et al [56] are plotted as a function of pH together with the previously published values of v_eff calculated from other measurements of colligative properties in Figure 12, and it may be seen that the dependence of v_eff upon pH derived from all of the measurements are in reasonably good agreement, establishing semi-quantitative consistency between results obtained in several laboratories using different but complementary techniques.

12.

v_eff, the specific volume of an equivalent hard particle representation of BSA, calculated from the concentration dependence of different colligative properties as described in the text, plotted against pH in buffers containing 150 mM NaCl. Circles indicate values derived from SLS data of [56]. Triangles, squares, and diamond are values respectively derived from turbidity, osmotic pressure and sedimentation equilibrium data as described in [57].

In all four of the preceding examples, the general agreement between results obtained by complementary methods provides credence to the results of each measurement and their respective interpretations.

Conclusions

When utilized properly, light scattering technology can provide absolute and accurate determination of the molar mass and state of association of a variety of biological macromolecules. Moreover, recent developments in instrumentation and software have extended the utility of light scattering measurement, enabling it to provide much new information about protein-protein interactions, stability, and the equilibria and kinetics of biochemical reactions in dilute solution, and more recently, in concentrated solutions as well.

However, there seems to be a tendency on the part of many casual users of DLS instrumentation to over-interpret the results of measurements. This is due in large part to a lack of knowledge by the user of how raw data are acquired and processed to yield the end results displayed by manufacturer’s software. This reviewer strongly recommends that each publication of processed DLS data be accompanied by on-line supplementary files containing tables of the original autocorrelation functions. Access to these files will enable unbiased observers to determine whether the conclusions of the authors based upon these data are justified.