Adding levels of complexity enhances robustness and evolvability in a multilevel genotype–phenotype map

Abstract

Robustness and evolvability are the main properties that account for the stability and accessibility of phenotypes. They have been studied in a number of computational genotype–phenotype maps. In this paper, we study a metabolic genotype–phenotype map defined in toyLIFE, a multilevel computational model that represents a simplified cellular biology. toyLIFE includes several levels of phenotypic expression, from proteins to regulatory networks to metabolism. Our results show that toyLIFE shares many similarities with other seemingly unrelated computational genotype–phenotype maps. Thus, toyLIFE shows a high degeneracy in the mapping from genotypes to phenotypes, as well as a highly skewed distribution of phenotypic abundances. The neutral networks associated with abundant phenotypes are highly navigable, and common phenotypes are close to each other in genotype space. All of these properties are remarkable, as toyLIFE is built on a version of the HP protein-folding model that is neither robust nor evolvable: phenotypes cannot be mutually accessed through point mutations. In addition, both robustness and evolvability increase with the number of genes in a genotype. Therefore, our results suggest that adding levels of complexity to the mapping of genotypes to phenotypes and increasing genome size enhances both these properties.

1. Introduction

Classical evolutionary models do not account for the robustness and evolvability of phenotypes [1]. They thus fail to explain some evolutionary phenomena, such as punctuated equilibria [2,3], constrained evolution [4] or the origins of novelty [5,6]. In recent years, several research groups have tried to understand this important question by studying computational mappings of molecular genotypes to phenotypes. Some of these maps try to remain faithful to biological phenomena, such as RNA secondary structure [7–14], protein secondary structure [15–20], gene regulatory networks [21–24] and metabolic networks [25–28]. More abstract models have also been developed, such as the polyomino [29–31] and toyLIFE [32], as well as the Fibonacci map [33] and simple combinatorial maps [34,35]. The robustness and evolvability of phenotypes have also been recently studied for the artificial life AVIDA system [36].

Even though all these models focus on different aspects of molecular biology, all of them share some common properties. First, the mapping from genotype to phenotype is highly degenerate: many genotypes encode the same phenotype. Additionally, phenotype abundance (the number of genotypes encoding it) is not evenly distributed: most phenotypes are rare, while a few of them are extremely abundant. The probability density function associated with phenotype abundance is a log-normal distribution for a wide variety of models [14,34], although in some cases it has been found to be a power law [33,34]. This implies that rare phenotypes will not play a central role in evolution: they are hard to find in a genotype space that is filled with abundant phenotypes [12,14,37]. This degeneracy is usually accompanied by the formation of neutral networks, networks of genotypes encoding the same phenotype, in which two genotypes are connected if they differ in one point mutation—i.e. if the strings representing each genotype differ in one letter [7,16,21,25,38]. The degree of a node in such a neutral network—the number of neutral neighbours it has—is called genotypic robustness. It is usually normalized by the total number of neighbours in genotype space, and thus represents the fraction of neighbours with the same phenotype [5]. Inside a particular neutral network, the degree distribution is highly heterogeneous, but usually unimodal [13,39]. Additionally, in RNA, the average degree of a neutral network grows linearly with the logarithm of its abundance [13]—this positive correlation is also observed in the polyomino model [30], the HP model [31] and simple genotype–phenotype maps [34], and is suggested by empirical data [40]. Neutral networks of abundant phenotypes percolate genotype space: they contain genotypes that share almost no letters [5,7,21]. Conversely, most abundant phenotypes are easily accessed from each other: traversing a neutral network, many phenotypes can be found at its boundary [5,21,25]. Moreover, abundant phenotypes are typically found just a few mutations away from a random genotype [5,9,30]—i.e. they are highly evolvable. This means that these phenotypes are easily accessible from any other phenotype, so that the search for new phenotypes among abundant ones is a fast evolutionary process.

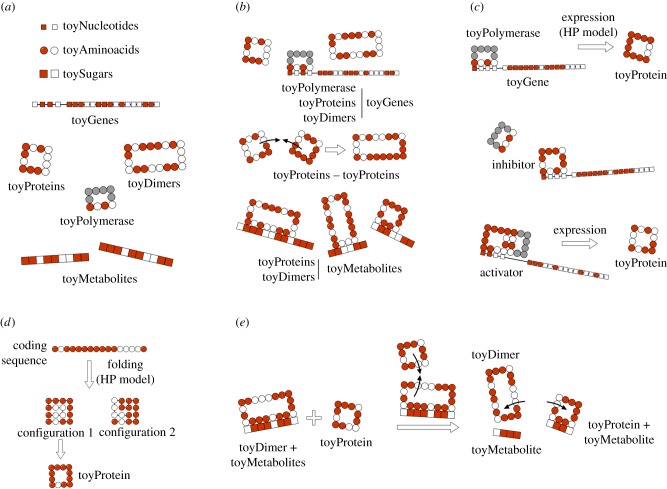
In [32], we presented toyLIFE, a multilevel model of a genotype–phenotype map (see figure 1; electronic supplementary material, §S1 for a summary of toyLIFE's definition). toyLIFE includes genes, proteins, regulatory networks and a simple metabolism. Genes are binary strings of fixed length, divided in two regions—a promoter and a coding region (figure 1a). The coding region is translated into a sequence of 16 amino-acids that folds on a 4 × 4 lattice, following the rules of the HP protein-folding model [15–17] (figure 1a,d). Once folded, we only distinguish proteins by their perimeter and folding energy—note that this definition of folded protein is different from other versions of the HP model. In toyLIFE, there are 2710 different proteins (electronic supplementary material, figure S3), most of them obtained from more than one sequence. However, there are no neutral mutations: every change in a coding region will result (most of the time) in a non-folding protein or (more rarely) in a different functional protein. This is very different from what has been observed in other versions of the HP model [17–20]. Proteins in toyLIFE interact with each other to form dimers, and both proteins and dimers regulate gene expression (figure 1c) and interact with metabolites (figure 1b). The phenotype in toyLIFE can be defined in multiple ways. Here, we will focus on a metabolic definition of phenotype (figure 1e), similar to the one presented in [25,41]: the set of metabolites that a genotype can metabolize (electronic supplementary material, §S2). toyLIFE is, to our knowledge, the only multilevel genotype–phenotype map incorporating genetic dynamics, protein folding, regulatory networks and metabolism.

Figure 1.

Brief overview of toyLIFE. (a) The three basic building blocks of toyLIFE are toyNucleotides, toyAminoacids and toySugars. They can be hydrophobic (H, white) or polar (P, red), and their random polymers constitute toyGenes, toyProteins and toyMetabolites. The toyPolymerase is a special polymer that will have specific regulatory functions. These polymers will interact between each other following an extension of the HP model, for which we have chosen the interaction energies E_HH = − 2, E_HP = − 0.3 and E_PP = 0 [17]. (b) Possible interactions between pairs of toyLIFE elements. toyGenes interact through their promoter region with toyProteins (including the toyPolymerase and toyDimers); toyProteins can bind to form toyDimers, and interact with the toyPolymerase when bound to a promoter; both toyProteins and toyDimers can bind a toyMetabolite at arbitrary regions along its sequence. (c) A toyGene is expressed (translated) when the toyPolymerase binds to its promoter region. The sequence of Ps and Hs of the toyProtein will be exactly the same as that of the toyGene coding region. If a toyProtein binds to the promoter region of a toyGene with a lower energy than the toyPolymerase does, it will displace the latter, and the toyGene will not be expressed. This toyProtein acts as an inhibitor. The toyPolymerase does not bind to every promoter region. Thus, not all toyGenes are expressed constitutively. However, some toyProteins will be able to bind to these promoter regions. If, once bound to the promoter, they bind to the toyPolymerase with their rightmost side, the toyGene will be expressed, and these toyProteins act as activators. (d) toyProteins fold on a 4 × 4 lattice, following a self-avoiding walk (SAW). For each binary sequence of length 16, we fold it into every SAW and compute its folding energy, following the HP model. Then we choose the SAW that yields the minimum folding energy. (e) Metabolism in toyLIFE. A toyDimer is bound to a toyMetabolite when a new toyProtein comes in. If the new toyProtein binds to one of the two units of the toyDimer, forming a new toyDimer energetically more stable than the old one, the two toyProteins will unbind and break the toyMetabolite up into two pieces. We say that the toyMetabolite has been catabolized. (Online version in colour.)

In this paper, we investigate the characteristics of the metabolic genotype–phenotype map of toyLIFE. First, we want to assess if toyLIFE shares the properties of most computational genotype–phenotype maps studied before. We will see that, in spite of toyLIFE's complexity, its properties are very similar to many of these maps. Second, we wish to explore the robustness and evolvability of this map. The regulatory and metabolic functions of toyLIFE are built on a non-robust, non-evolvable version of the HP model, in which proteins can hardly evolve without going through non-folding intermediate steps. We show in this article that both robustness and evolvability are enhanced by the superposition of additional levels of organization. Third, we will explore how robustness and evolvability change when genome size is increased. We show that they increase significantly, and that we can explain this tendency in the light of toyLIFE's details.

2. Degeneracy of the genotype–phenotype map

The size of genotype space in toyLIFE grows very quickly with the number of genes in a genotype. Since a gene in toyLIFE is a binary string of length 20, there are 2²⁰ different genes. A genotype is formed by choosing g genes from this set with replacement (the order of genes is irrelevant). Hence, the number of genotypes with g genes is 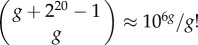(electronic supplementary material, §S1). For g = 2, this number is 5.5 × 10¹¹, for g = 3, it is 1.9 × 10¹⁷, and for larger values of g it keeps growing almost exponentially. A complete exploration of these genotype spaces is well beyond our computational possibilities in general. However, using computational tricks, we have exhaustively analysed the g = 2 and g = 3 cases—i.e. we have limited our study to two-gene and three-gene genotypes.

We have restricted ourselves to studying those genotypes that are able to catabolize at least one metabolite—these will be called viable genotypes. The remaining (non-viable) genotypes are unable to catabolize any metabolite. For g = 2, there are 1.1 × 10⁹ viable genotypes, representing little more than 0.2% of all genotypes. For g = 3, this number is 1.0 × 10¹⁵—approximately 0.5% of all genotypes. In both cases, the great majority of genotypes are unable to catabolize any metabolite. But note that the space of viable genotypes is still enormous.

Among these viable genotypes, many of them catabolize exactly the same metabolites—they encode the same metabolic phenotype. For g = 2, there are only 775 different phenotypes, corresponding to an average of 1.4 × 10⁶ genotypes per phenotype. For g = 3, there are 26 492 phenotypes, corresponding to an average of 3.8 × 10¹⁰ genotypes per phenotype. In other words, for both g = 2 and g = 3, the degeneracy of the genotype–phenotype map is huge. From now on, we will refer to the set of phenotypes found for g = 2 and g = 3 as 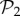and 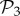, respectively.

The distribution of phenotype abundances is highly skewed (figure 2a), similarly to what has been observed for other genotype–phenotype maps. In both cases, the distribution can be empirically fitted to a log-normal distribution. We obtained the parameters empirically from the log-transformed data, using maximum-likelihood. For both g = 2 and g = 3, the rank distributions (electronic supplementary material, figure S9) show a long tail, confirming that, indeed, while few phenotypes are very abundant, most of them are rare. For g = 3, this is especially striking, since 300 phenotypes in 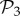represent nearly 99% of all genotypes—which means that the remaining 1% is distributed among approximately 26 000 phenotypes.

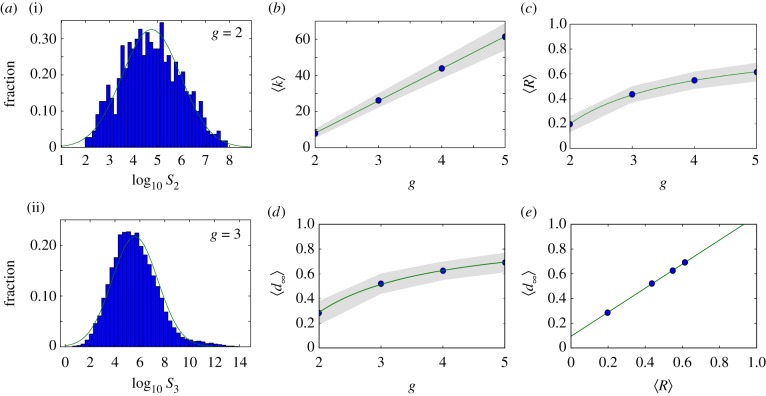
Figure 2.

Neutral networks in toyLIFE. (a) The distribution of the number of genotypes per phenotype—phenotype abundance, S—for g = 2 (S₂, a(i)) follows a log-normal distribution, with probability density function 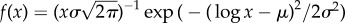, where μ is the mean and σ is the standard deviation of the normally distributed logarithm of the variable. Here μ = 4.742 and σ = 1.224, obtained using maximum-likelihood. For g = 3, the distribution of phenotype abundances (S₃, a(ii)) is again very close to a log-normal distribution with μ = 5.604 and σ = 1.838. The log-normal fit is worse than in (a) because there is a small bump in the right part of the distribution, where more abundant phenotypes are—due to the over representation of two-gene phenotypes (see text). (b) Average degree of nodes (circles) in neutral networks (see electronic supplementary material, figure S12 for the degree distribution) versus gene number g. The average degree 〈k〉 of a node grows linearly with gene number g, as 〈k〉 = − 27.6 + 17.8 g (line). (c) Average robustness (circles) versus gene number g. Robustness grows with gene number, and we can find a nonlinear relationship between both variables: 〈R〉 = 0.895 − 1.392/g (line). (d) There is a nonlinear relationship between g and 〈d_∞〉, the final distance that is reached in a random walk in which genotypes are forced to get away from the starting genotype every step: 〈d_∞〉 = 0.965 − 1.354/g (line). The circles represent 〈d_∞〉. (e) There is a linear relationship between 〈d_∞〉 and the average robustness of the genotypes as obtained in c, given by: 〈d_∞〉 = 0.094 + 0.972〈R〉 (line), very close to the 〈d_∞〉 = 〈R〉 fit. In all cases, the grey area encompasses two standard deviations, and the fits in (b–e) were obtained using the least-squares method. (Online version in colour.)

All phenotypes in 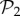are also found in 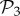: we can always add a gene whose product does not fold into any protein to a viable two-gene genotype. A pertinent question, therefore, is how abundant the phenotypes belonging to 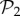are in three-gene genotype space. We find that phenotypes in 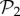take up 99.6% of genotypes in g = 3 (electronic supplementary material, §S4). This means that the 775 phenotypes in 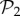dominate the space of phenotypes for g = 3. Only special combinations of three proteins and three promoters will yield most of the phenotypic diversity observed for g = 3. The majority of genotypes will be extensions of two-gene genotypes with a third gene that does not interfere with their function.

We can re-compute the histogram in figure 2a(ii) taking the 775 phenotypes from 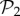as a separate set from the remaining 25 717 phenotypes in 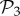that are not in 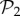(electronic supplementary material, §S4). This reveals that the small bump observed in the right part of the distribution of phenotypes in 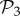(figure 2a) is due to the phenotypes in 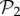. When we eliminate these phenotypes, the resulting distribution is much closer to a log-normal. In a sense, it is as if both sets were somehow independent: one is formed by two-gene genotypes with a third, non-interfering gene, and the other is formed by all combinations of three genes that encode new phenotypes. This influence of 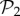phenotypes decays linearly when genotype size increases (electronic supplementary material, §S5), although they keep representing more than 80% of genotype space for g ≤ 13.

3. Neutral networks in toyLIFE

Robustness can be defined as 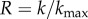, where k is the degree of a node in a neutral network, and 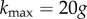is the maximum number of point-mutation neighbours. In other words, R is the normalized degree of a node. We can sample genotypes for different genotype sizes, represented by g (gene number), and plot the histogram of values of R (electronic supplementary material, figure S12). All the resulting distributions are unimodal, as has been observed in other genotype–phenotype maps [5,13]. toyLIFE genotypes become more robust as g increases. In fact, there is a linear relationship between g and 〈k〉, the average degree of a node in a neutral network (figure 2b): 〈k〉 = − 27.6 + 17.8g. But 〈R〉 = 〈k〉/20g, so we obtain 〈R〉∼0.891 − 1.378/g, which is very close to the least-squares fit 〈R〉 = 0.895 − 1.392/g, shown in figure 2c. The linear relationship between 〈k〉 and g with slope 17.8 indicates that, on average, for every gene we add to a genotype, nearly 18 out of 20 new mutations will be neutral. This implies that 〈R〉 saturates at a value close to 0.9 when g increases. This result is consistent with the results of §2, which showed that newly added genes rarely interfere with an existing phenotype. These new genes can be viewed as ‘junk’ in the sense that they do not have any effect on metabolic function and that mutations in their sequence tend to be neutral. We will see later on that junk genes are however important, in that they enhance evolvability in toyLIFE genotypes.

Also, taking into account that 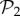phenotypes dominate in 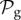for g ≤ 13 (electronic supplementary material, §S5), we can estimate that S_g∼17.8^gS₂, so logS_g∼q + glog17.8, where q is a constant. Combining this result with the linear relationship between g and 〈k〉, we obtain for toyLIFE the linear relationship between 〈k〉 and logS, that has been observed previously for other models [13,30,31,34] (but see figure 3 for a direct verification of this relationship).

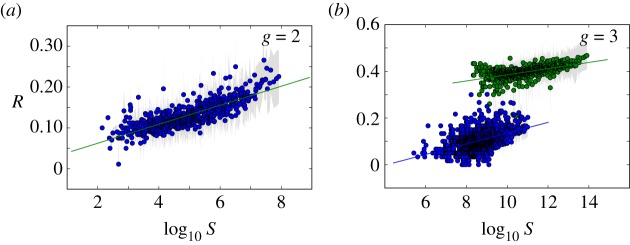
Figure 3.

Phenotypic robustness is linearly related to the logarithm of phenotype abundance. For g = 2 and g = 3, we sampled 10⁷ genotypes and computed their robustness. Then we assigned each of them to their corresponding phenotypes, and estimated phenotypic robustness, the average robustness for all genotypes encoding a given phenotype (see text). (a) Phenotypic robustness in g = 2 versus the logarithm of phenotype abundance. The line represents the power-law relationship R_p = 1.037 S^0.023₂. (b) For g = 3, we separated those phenotypes belonging to 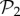(green circles, above) from the rest (blue circles, below). Both sets show a power law relationship between phenotypic robustness and phenotypic abundance: R_p = 1.790 S^0.013₃ for phenotypes in 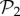(green line) and R_p = 0.805 S^0.023₃ for the remaining 25 717 phenotypes (straight lines). Grey area encompasses two standard deviations, and the fits were obtained using the least-squares method. (Online version in colour.)

In other genotype–phenotype maps, neutral networks tend to have one giant component [18], although this is not always the case: too short RNA sequences form neutral networks that are highly disconnected [13]. Although network analysis is almost impossible for g≥3, as networks are enormous, for g = 2 we can perform network analyses on all 775 phenotypes exhaustively, and compute their connected components (electronic supplementary material, §S7). We observe that most phenotypes are distributed in highly fragmented neutral networks: the genotypes encoding a given phenotype form many disjoint connected components, which are typically small. Abundant phenotypes tend to have a larger number of connected components, and we can find a relatively good power-law fit between the abundance of the phenotype S₂ and the number of components C: C = 0.25S^0.7₂ (electronic supplementary material, §S7). We also observe a huge variation in the size of connected components in g = 2: although more than 98% of connected components are smaller than 1000 nodes, some of them reach up to approximately 10⁷ nodes. The high fragmentation of neutral networks is due to the HP model that underlies protein folding in toyLIFE: there are no neutral mutations within proteins (electronic supplementary material, §S1 and figure S3). Most mutations in a protein sequence yield proteins that do not fold, and few mutations yield one functional protein from another. Remember that each phenotype is defined by a list of metabolites that a genotype is able to catabolize. A given phenotype can be encoded by more than one protein combination, which will be characterized by different interactions and regulatory functions, but will catabolize the same metabolites. When a phenotype is generated by several protein combinations, it will be difficult to mutate from one combination to another, and as a consequence these combinations will usually be found in disjointed connected components. In fact, the number of connected components associated with a phenotype is positively correlated with the number of protein combinations that generate it (electronic supplementary material, §S7).

For g≥2, we can estimate the distribution of neutral networks in genotype space using neutral random walks: starting at a randomly chosen genotype, we perform a mutation on it. If the resulting mutant genotype belongs to the same neutral network—if it encodes the same phenotype—the mutation is accepted. The random walk continues when we mutate the new genotype again. If the mutant genotype does not belong to the neutral network, the mutation is rejected, and we try to find a new neutral neighbour for the original genotype (this process will not work if the starting genotype does not have neutral neighbours, a rare case). We performed 1000 neutral random walks of length 10 000 for genotype sizes g = 2 to g = 5 (electronic supplementary material, figure S15). At each time step t, we computed d_H(g₀, g_t), the Hamming distance (normalized number of different positions) between the original genotype g₀ and the genotype visited at time t, g_t. d_H(g₀, g_t) is a random variable for each t, and so we can compute its average and standard deviation (electronic supplementary material, figure S15). If there were no restrictions to the nodes that can be visited in a random walk, we would expect 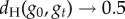when 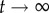. In other words, if there are no restrictions, the correlation between g₀ and g_t is lost when t grows, and the distance between them tends to the value it would have, on average, if we randomly picked two genotypes from the network. Thus, the evolution of d_H(g₀, g_t) is a good measure of the size and extension of neutral networks in genotype space. For g = 2, 〈d_H(g₀, g_t)〉 ∼ 0.25 when 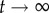, implying that networks do not extend very far. Considering that the total genotype space has diameter 40, this means that the average distance between the initial genotype and the final one is close to 10. This is not a very high value, and it is consistent with our previous analysis showing that neutral networks in g = 2 tend to be fragmented and small. For g > 2, 〈d_H(g₀, g_t)〉 ∼ 0.4 when 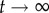, which implies that the fragmented networks of g = 2 space are becoming more connected as g grows, facilitating the navigability of genotype space. This suggests that neutral networks for g > 2 span large fractions of genotype space, a result consistent with other genotype–phenotype maps.

A different way to estimate the diameter of a neutral network is to perform neutral random walks in which we force d_H(g_t, g_t+1) > d_H(g_t−1, g_t). That is, in addition to imposing that a mutation is neutral in order to accept it, we also require it to increase the distance to the original genotype. More specifically, the process is computed as follows. We randomly choose a genotype, and perform mutations on it, increasing the distance every time step, until this distance can increase no longer—if, after a large number of trials, we cannot find a neutral mutant that is farther apart from the original genotype, we stop the process. We will denote the final distance obtained in such random walks by d_∞. For g = 2 and g = 3 we randomly sampled 10 000 genotypes, whereas for g = 4 and g = 5 we sampled 1000 genotypes (figure 2d; electronic supplementary material, figure S16). Consistent with previous results, random walks did not get very far for g = 2, reaching an average final distance 〈d_∞〉 ∼ 0.28. For g > 2, the final distance d_∞ increases. This result confirms the previous observation that navigability in these genotype spaces is enhanced. For g = 3, 〈d_∞〉 is a little over 0.5, while for g = 4 and g = 5 it reaches 0.6 and 0.7, respectively. In fact, the growth of 〈d_∞〉 with g is very similar to the growth of 〈R〉 obtained in figure 2c. In that case, we had 〈R〉 = 0.895 − 1.392/g. Here, it is 〈d_∞〉 = 0.965 − 1.354/g (figure 2d). Unsurprisingly, the similarity of the fits implies a linear relationship between 〈d_∞〉 and 〈R〉: 〈d_∞〉 = 0.094 + 0.972〈R〉 (figure 2e), very close to the identity function. This result has several implications. First, as g grows, neutral networks are more and more connected, and they span larger fractions of genotype space. It is easier to get from one extreme of the genotype network to the other without changing the phenotype. Secondly, this increased connectivity is due to the increase in robustness: the robustness of a genotype is a good predictor for the size of the connected component it belongs to. This can be easily explained in light of our previous discussion on robustness. Adding a new gene to a genotype will endow the latter with an average of 18 new neutral mutations with which to explore genotype space (figure 2b). Because the new gene will not interfere with the phenotype with a high probability, it follows that we can mutate most of its nucleotides, one by one, getting farther away from the original genotype. In other words, new genes in toyLIFE allow for increased navigability of genotype space, because they are mostly junk genes. As we will see later on, this property will have important consequences for evolvability.

The fact that robustness is a good predictor for the size of a genotype's connected component can be combined with the positive correlation between the logarithmic abundance of a phenotype and the size of its largest connected component (electronic supplementary material, §S7) to deduce the linear relationship between the logarithm of phenotype abundance and phenotypic robustness, giving yet another heuristic argument for this relationship. We now turn to compute it explicitly.

Phenotypic robustness is defined as the average of genotypic robustness for all genotypes encoding a phenotype 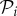, that is

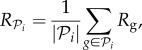where 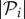is the number of genotypes encoding 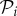. For g = 2 and g = 3 we sampled 10⁷ genotypes and computed their robustness. We then assigned each genotype to its corresponding phenotype and averaged the values of robustness for all genotypes encoding each phenotype. Note that this procedure samples abundant phenotypes more often. For g = 2, we find a good fit to a linear relationship between the logarithm of phenotype abundance and estimated phenotypic robustness (figure 3a). For g = 3, we identified those phenotypes belonging to 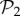(being the most abundant, they were sampled the most) in green, and the rest in blue (figure 3b). The figure shows separate relationships between the logarithm of phenotype abundance and phenotypic robustness. The two sets of phenotypes cluster in two different groups, confirming once more the idea that these two sets are qualitatively different. Phenotypes belonging to 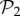are much more robust, as a result of them having one spare junk gene.

4. Robustness and position in genotype

Instead of considering the degree of a node in a neutral network, we can focus on the neutrality of a given position of the genotype. A genotype formed by g genes can be thought of as a binary string of length 20g—remember that genes in toyLIFE have 20 nucleotides, the first four forming the promoter region and the remaining 16 constituting the coding region. For a given sequence, the position i = 1, …, 20g can either be neutral or not—that is, when we mutate that position, we can get a new genotype with the same phenotype or not. We can thus define the random variable

Because r_i is a random variable, we can sample it and estimate its mean. Differences between positions may yield insights into the details of the genotype–phenotype correspondence in toyLIFE—i.e. some positions may always be neutral, or always constrained. This is what we have done in figure 4, for genotype sizes g = 2 to g = 5. We sampled 10⁷ genotypes for g = 2 and g = 3, and 10³ genotypes for g = 4 and g = 5, and computed r_i for every i = 1, …, 20g and every genotype. The order of genes does not matter in toyLIFE by construction—implying 〈r_i〉 = 〈r_i+20h〉, for any h = 0, 1, …, g − 1—so we are interested in the values of robustness for each gene. This is why in figure 4 we only show the average values 〈r_i〉 for 0 ≤ i < 20. Note that promoter regions tend to be more robust than coding regions. This is partly due to the lack of robustness in the version of the HP model that underlies protein folding in toyLIFE (electronic supplementary material, §S1 and figure S3). However, note that the superposition of regulatory and metabolic levels of the phenotype makes the average robustness of coding regions grow, in spite of the non-robust protein folding model. For g = 4 and g = 5, the average robustness in these regions reaches values as high as 0.5 (remember that these genotypes tend to have junk genes that increase overall robustness as g grows).

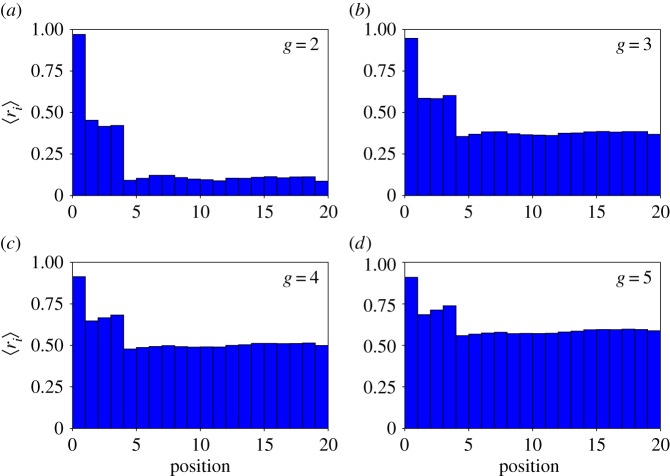
Figure 4.

Different positions in the genome have different neutralities. We sampled 10⁷ genotypes for g = 2 (a) and g = 3 (b) and 10³ genotypes for g = 4 (c) and g = 5 (d), and measured r_i for i = 1, …, 20. For each i we then computed 〈r_i〉 and plotted them versus genomic position. Note the high robustness of the first position in the promoter region, and the low robustness in the coding regions. (Online version in colour.)

Inside the promoter region, which only affects gene regulation, the first position is particularly robust. This means that the regulatory changes it induces have no phenotypic effect at the metabolic level. This may be due to two reasons: either changes in the first position of the promoter region do not affect the regulatory function—the temporal pattern of gene expression determined by the interactions among proteins—or changes in the regulatory function rarely alter the metabolic phenotype. We performed the following simple test of these hypotheses. For each position in the promoter region, we sampled 10⁴ genotypes of size g = 3. We then mutated that position and computed the new regulatory function and the new metabolic phenotype. From all 10⁴ mutations in the first position, 40% were neutral in both the regulatory and the metabolic sense, 54% affected the regulatory function but did not affect the metabolic phenotype, and the remaining 6% changed both—this means that the robustness for the first position in this sample was 94%. For the rest of the positions, 27% of the mutations did not alter either the regulatory function or the metabolic phenotype, 32% changed regulation but not metabolism and 41% changed both. This corresponds to a robustness of 59%, consistent with what we observed in figure 4. In other words, for the first position only 9% of the mutations that affected regulation had any effect on the metabolic phenotype. In addition, 40% of mutations did not affect the regulatory function at all. For the rest of the positions, however, the number of mutations that altered regulation, 73%, was higher. Among these, roughly 55% had an effect on phenotype as well. So both reasons posited above are at work: not only is the number of mutations affecting regulatory function lower in the first position of the promoter region, but also when these mutations do alter the regulatory function, they rarely change the phenotype.

The lower robustness of coding regions, compared to promoter regions, is correlated with a higher evolvability, as will be discussed in the next Section.

5. Accessibility and evolvability

So far, we have limited our discussion of the properties of the genotype–phenotype map in toyLIFE to the abundance of phenotypes and the organization of their neutral networks, without paying any attention to the connections between different phenotypes. In this section, we will focus on the latter question, which amounts to studying evolvability, or how accessible phenotypes are.

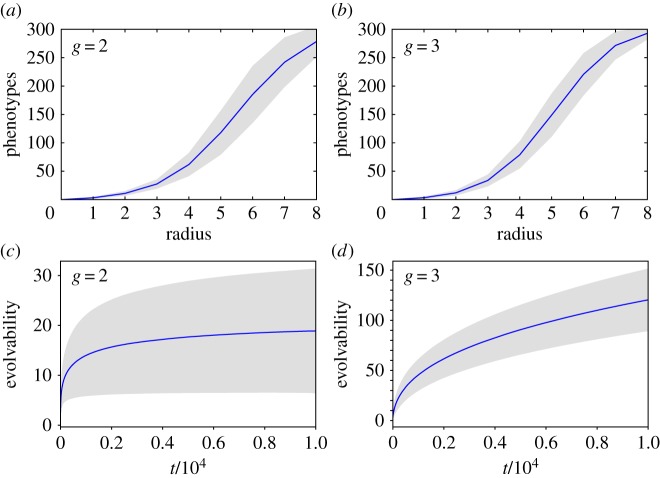
The neutral networks of different phenotypes tend to be highly interwoven in most computational genotype–phenotype maps, so that connections between them are very common. The Vienna RNA group described a property of RNA neutral networks called shape space covering [7,9]. It implies that one can find most common phenotypes a few mutations away from any given genotype. We checked for the existence of this property in toyLIFE. We sampled 100 genotypes for g = 2 and g = 3 and computed the phenotypes of all neighbours at distances 1 to 8. We observed how many of the 300 most common phenotypes appeared in this set of neighbours. The results are shown in figure 5a,b. For both g = 2 and g = 3 and most sampled genotypes, the number of phenotypes discovered after eight mutations was close to 300. This implies that toyLIFE also shares the shape space covering property: most phenotypes are just a few mutations away from any given phenotype. Observe, however, that for g = 2 this means a higher relative distance compared with g = 3—remember that the diameter of this network is 40—and that the number of phenotypes discovered at that distance is lower by comparison.

Figure 5.

Evolvability in toyLIFE. A genotype–phenotype map has the shape space covering property if, given a phenotype, we only need to explore a small radius around a sequence encoding that phenotype in order to find the most common phenotypes. We tested this property in toyLIFE by sampling 100 genotypes for g = 2 (a) and g = 3 (b), and counting how many of the 300 most common phenotypes appeared in a radius of distance 8 around a given genotype. The results are consistent with shape space covering. For g = 2 (c) and g = 3 (d), we also measured the cumulative number of phenotypes in the neighbourhood of a neutral random walk—evolvability—for 10 000 genotypes. Evolvability is much higher for g = 3. Lines show average values, while grey areas encompass two standard deviations. (Online version in colour.)

Shape space covering means that phenotypes are easily accessible from each other through a few number of mutations. A relevant detail in the metabolic genotype–phenotype map in toyLIFE is that this accessibility is due only to mutations in proteins. If we mutate only the promoters, the number of visited phenotypes is never larger than 2, regardless of the distance. For g = 2, we can give a clear explanation to this peculiarity: of the 135 318 pairs of proteins that yield a metabolic function, only 16 yield two different metabolic phenotypes when combined with different promoters. The rest are able to generate only one phenotype. Changing only the promoters will not affect the metabolic function, and will not help in finding new phenotypes. This is consistent with the high robustness of the promoter region.

Another way to study evolvability is to compute the connections between different phenotypes directly. We say that two phenotypes are connected if at least two genotypes from each phenotype are one point mutation away from each other. We can then create a network of phenotypes, whose nodes will be the phenotypes themselves, and the edges the connections between them. This network of phenotypes is undirected and weighted—the weight of an edge between two phenotypes is the sum of all point mutations connecting two genotypes encoding each phenotype. This network admits self-loops, whose weight is twice the number of edges connecting genotypes encoding a single phenotype—in other words, it is the sum of the degrees of all the nodes encoding that phenotype, which is proportional to the phenotype's robustness. For g = 2, where we can compute the whole network of genotypes with their corresponding phenotypes, we can build this phenotype network exhaustively. The network is formed by a giant component that includes 767 phenotypes. We also find six additional tiny components, five of them with just one phenotype and the remaining one with three phenotypes (electronic supplementary material, §S9). Thus, for g = 2, some phenotypes will be unreachable by point mutations from other phenotypes. For g = 3, we cannot build the phenotype network exhaustively, but resorting to a numerical approximation using random walks (electronic supplementary material, §S9), we can estimate the network of connections between the 775 phenotypes in 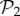—in order to study how the addition of one gene alters the connections between these phenotypes. The results show that all phenotypes in 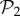now belong to one giant component (electronic supplementary material, §S9). The number of connections between phenotypes has greatly increased as well. This is again due to the additional junk genes. They do not only increase robustness, but also allow for increased connections between phenotypes.

This increased connectivity can also be measured in an alternative way. In previous work [5], evolvability has been estimated as the number of new phenotypes discovered in a neutral random walk along a neutral network. In figure 5c,d, we have performed such an analysis for 10 000 genotypes for g = 2 and g = 3. The results show that evolvability is much higher for g = 3. While the number of discovered phenotypes almost stops growing for g = 2, it grows quickly in g = 3, and to a much higher value than for g = 2. Again, this is due to the higher average number of connections between phenotypes for g = 3 (electronic supplementary material, §S9).

6. Discussion and conclusion

Throughout this article, we have explored the properties of the metabolic genotype–phenotype map in toyLIFE. This map is highly degenerate, with many more genotypes than phenotypes, and large neutral networks traversing genotype space. The distribution of phenotype abundances is very heterogeneous, and more abundant phenotypes tend to be more robust. Common phenotypes are easily accessed from each other, and large neutral networks allow for a fast exploration of phenotype space.

All of these properties have been described in other genotype–phenotype maps [7–31,33,34]. This is somewhat striking, given that the genotype–phenotype map in toyLIFE is more complex than the rest of these models. It is the only model that incorporates intermediate levels of phenotypic expression: genes are first translated into proteins, which fold and interact with each other, generating complex regulatory networks that will determine the metabolic capacities of a genotype. And yet the main properties shared by the rest of genotype–phenotype maps appear here as well.

Two particular results stand out. The first is the log-normal distribution of phenotype abundances, which has also been observed in RNA [14] and predicted for simple combinatorial genotype–phenotype maps [34]. The second is the positive correlation between phenotypic robustness and the logarithm of phenotype abundance, which has also been described before [13,30,31,34]. The fact that these two relationships (as well as other phenomena, such as shape space covering) are so widespread points to a general property of these maps, which must be related to combinatorics and network theory. Previous work [34] has shown that, when the abundance of a phenotype can be inferred from the genotype sequence in simple genotype–phenotype maps, we can use combinatorial arguments to explain the appearance of a log-normal distribution and the linear relationship between phenotypic robustness and the logarithm of phenotype abundance. These arguments would explain the presence of these properties in the case of RNA, but do not seem to be easily translatable to toyLIFE. We need to devote more efforts into understanding this seemingly general property of genotype–phenotype maps.

The high robustness and evolvability of the metabolic phenotype in toyLIFE, particularly when genome size increases, is remarkable because our model is built on a particularly non-robust, non-evolvable version of the HP protein-folding model. Proteins in toyLIFE are sequences of 16 amino-acids that fold on a 4 × 4 lattice. One protein is defined by its perimeter and its folding energy: this is a very different definition of protein than the one used in most versions of the HP model [15–20], which define a protein by its folded structure. As we have already mentioned, there are no neutral networks in the protein space in toyLIFE, and evolvability is very limited. However, when these proteins are paired to interact with each other, generating regulatory networks and performing metabolic functions, the resulting genotypes are robust and evolvable. So it would seem that adding levels of expression to a phenotype enhances both robustness and evolvability. This hypothesis could be tested, for instance, by adding another level of complexity to the phenotype in toyLIFE and checking how both of these properties are changed. If there is indeed a relationship between complexity and both robustness and evolvability, this result would suggest that more complex genotype–phenotype maps could have an evolutionary advantage.

Alternatively, we could change the folding process in toyLIFE and allow for promiscuous proteins—proteins that can fold in different shapes with the same energy [42]. This would increase connectivity in protein space and would affect the levels of robustness and evolvability at the metabolic level. Determining the extent of this change would give us some insight into the relationship between different levels of phenotypic expression.

On a related note, our results show that adding genes to toyLIFE genotypes increases both robustness and evolvability. Neutral networks of two-gene genotypes are not very navigable, reaching only a small portion of genotype space, and connecting with a small number of adjacent phenotypes. However, adding a new gene to the genotype changes everything: now phenotypes are easily accessed from each other and neutral networks span genotype space. Robustness, as we haven seen, keeps growing with genome size. The explanation behind this fact is that most of the new genes will not alter the metabolic phenotype, and will act as junk genes. However, they can mutate without restriction, enhancing the navigability of a neutral network. Increased navigability allows for increased connectivity between phenotypes, thus enhancing evolvability [43]. In other words, junk genes have creative potential, in the sense that they allow populations to explore a given neutral network, and then encounter new, unexplored phenotypes. This is interesting because it extends the usefulness of redundancy in complex genomes [44,45] to include seemingly inert elements, whose only function is to increase robustness and evolvability. It is also reminiscent of the abundance of introns and non-coding DNA in eukaryotic genomes [46]: if this non-functional DNA also enhances robustness and evolvability in living cells, this would suggest new arguments for the maintenance of junk DNA.

Finally, the appearance of junk genes is possibly a result of the fact that interactions in toyLIFE are limited to be pairwise. There are neither trimers nor tetramers in toyLIFE, only dimeric proteins. Only one protein or dimer can interact with a metabolite at a given moment, and so on. As a consequence, when a new gene is added to a two-gene genotype that performs a metabolic function, it will have little potential to create new functions. In fact, one would expect the opposite: that adding a new gene would disrupt the existing interactions, thus yielding a non-viable metabolic phenotype. However, this is not what we observe. When adding new genes to two-gene genotypes, most genotypes keep their original function. We will need to perform a more detailed exploration of this phenomenon in order to clarify the reasons behind it.

As a final comment, note that we have not defined fitness for toyLIFE. Previous work [47] suggests that the fitness landscape appearing from complex genotype–phenotype maps is highly rugged and constrains evolutionary paths. Further work with toyLIFE should explore possible definitions of fitness and their corresponding fitness landscapes.

Data accessibility

There are no data associated with this paper.

Authors' contributions

P.C., S.M. and J.A.C. conceived the study. P.C. performed research and data analysis. P.C., A.W., S.M. and J.A.C. discussed the results, wrote the paper and approved the final version of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

P.C., S.M. and J.A.C. acknowledge support by the Spanish Ministerio de Economía y Competitividad and FEDER funds of the EU through grants VARIANCE (FIS2015-64349-P) (P.C. and J.A.C.) and ViralESS (FIS2014-57686-P) (S.M.). A.W. acknowledges support by ERC Advanced Grant 739874, by Swiss National Science Foundation grant 31003A_146137, by an EpiphysX RTD grant from SystemsX.ch, as well as by the University Priority Research Program in Evolutionary Biology at the University of Zurich. P.C. acknowledges additional support from EMBO grant ASTF 652-2014.