Towards personalized computational oncology: from spatial models of tumour spheroids, to organoids, to tissues

Abstract

A main goal of mathematical and computational oncology is to develop quantitative tools to determine the most effective therapies for each individual patient. This involves predicting the right drug to be administered at the right time and at the right dose. Such an approach is known as precision medicine. Mathematical modelling can play an invaluable role in the development of such therapeutic strategies, since it allows for relatively fast, efficient and inexpensive simulations of a large number of treatment schedules in order to find the most effective. This review is a survey of mathematical models that explicitly take into account the spatial architecture of three-dimensional tumours and address tumour development, progression and response to treatments. In particular, we discuss models of epithelial acini, multicellular spheroids, normal and tumour spheroids and organoids, and multi-component tissues. Our intent is to showcase how these in silico models can be applied to patient-specific data to assess which therapeutic strategies will be the most efficient. We also present the concept of virtual clinical trials that integrate standard-of-care patient data, medical imaging, organ-on-chip experiments and computational models to determine personalized medical treatment strategies.

1. Introduction

In the last decade, an increased understanding has developed around the notion that cancer is not a single disease. While all cancers manifest themselves as an uncontrolled growth of abnormal cells, they are actually distinct neoplastic disorders that possess different genetic and epigenetic alterations, underlying molecular mechanisms, histopathologies and clinical outcomes [1,2]. Such a heterogeneous family of diseases should be treated with therapies that are tailored to the features of particular tumours. With this goal in mind, the term ‘precision medicine’ was created to describe a healthcare model that focuses on developing effective treatments based on patients' genetic, molecular and environmental factors [3]. This does not imply developing unique medical treatments for each individual person, but stratifying patients based on the predicted response to or risk of a given therapy. With respect to cancer treatment, the goal is to match each patient with the most accurate and effective treatment, without the need to create pharmaceuticals for each individual tumour. Recently, several research groups have discussed this concept in the context of melanoma, lung, breast and gastrointestinal tumours [4,5], as well as biomarker development, analyses of histomorphology and epigenomics [6,7].

Tumours undergo dynamic spatio-temporal changes, both during their progression and in response to therapies. Tumour clonal composition may change, if the drug-sensitive cells are killed; cellular phenotypes and features can evolve, contributing to high heterogeneity; and the tumour microenvironment can be altered, resulting in the emergence of specific tumour niches. Because of this inevitable tumour plasticity, therapeutic strategies should be adaptable enough to address the emerging targets rather than using a one-size-fits-all approach. Adjusting treatment schedules to the responding tumour is the foundation of the adaptive therapy concept [8,9]. The idea behind such therapies is to use mathematical modelling and computer simulations to examine which administration schedules predict the most promising therapeutic responses.

In recent years, there has been enormous progress in the development of novel experimental cultures that can mimic the structure and function of living tissues and so can more faithfully represent tumour behaviour under treatment. In addition to typical two-dimensional (2D) cultures, in which cells are grown in monolayers covered by a medium with dissolved nutrients and drugs, more realistic three-dimensional (3D) cultures of multicellular spheroids have been developed [10,11]. In these models, the cells are grown embedded within hydrogels that mimic the extracellular matrix (ECM) and provide structural support and microenvironmental context. This enables intracellular signalling and cell differentiation similar to that observed in vivo. As a result, the non-transformed epithelial cells can undergo epithelial polarization, creating hollow spherical acini with a shell of epithelial cells enclosing the inner lumen. These cultures serve as an experimental model of normal organ development. Various non-tumorigenic cell lines have been grown as hollow acini, including those originating from the breast [12], kidney [13], lung [14], pancreas [15] or prostate [16]. Such 3D cultures have also been used to examine changes in both the growth and morphology of non-tumorigenic cells in altered microenvironments [17,18], to delineate the oncogenetic mechanisms of mutated cells [19,20] and to test the response of tumour cells to various treatments [21,22].

Self-organizing epithelial acini were among the first 3D in vitro cultures where individual cells were able to develop the structure and function (to some extent) of the organ from which they were derived. Other organoid cultures include branching morphogenesis of mammary [23] or salivary [24] glands, and the development of multi-layered multi-lineage cysts [25], cortical polarized tissues [26] and interstitial crypts [27]. Additionally, several 3D co-culture systems have been developed that allow for investigation of how the different types of cells interact with one another. These include co-cultures of tumour cells with cancer-associated fibroblasts, which show that cells' mechanical collaboration results in tumour cells' migration, led by fibroblasts [28]. These 3D co-cultures of tumour cells, endothelial cells and fibroblasts allow for mimicking of the tumour microenvironment and testing its response to chemo- and radiotherapy as a whole complex system [21]. In addition to 3D cell cultures with immortalized cell lines, patient-derived tumour organoid cultures have recently been established as personalized models for precision medicine [29,30].

In this review, we first discuss a variety of mathematical models that are in silico analogues of 3D experimental cultures, such as normal epithelia, tumour spheroids and organoids. They mimic the progression of tumour development from normal tissues to invasive tumours. We also present models that go beyond the in vitro cultures and recreate conditions characteristic of tumour tissues. These models form an excellent base for applications to precision medicine and personalized oncology. This is a very active area of research, and thus it would be impossible to discuss all modelling achievements. Therefore, our main focus is on recent papers, published in the last 10 years. We also restricted our review to models (discrete, continuous and hybrid) that trace both the spatial and temporal dynamics of tumour cells, though we did not limit our review to any certain tumour type. Models that act on the cell population level or simplify tumour morphology and reduce dimensionality of the modelling problem often neglect intratumoral and intercellular heterogeneity and will not be discussed in this review. Our overarching goal is to present quantitative frameworks that complement experimental approaches and can be incorporated into the precision medicine pipeline. The review is organized as follows. The first five sections show the current state of adequate mathematical modelling, and the next two suggest which research areas would enhance applications of in silico models to precision medicine. In §2, we discuss the mathematical modelling of acinar structures and their mutants. In §3, we present computational models of tumour multicellular spheroids. Section 4 is devoted to in silico simulations of epithelial tissues and pre-invasive tumours. Section 5 focuses on mathematical models of vascularized tumours and angiogenesis. In §6, we present models of tumour response to anti-cancer therapies. In §7, we recommend areas of active biomedical research that should be incorporated into mathematical models of tumours. Section 8 offers a discussion of organ-on-chip approaches, which are emerging experimental tools for precision medicine research. We conclude in §9 with a discussion on integrating all mathematical, computational and experimental approaches when using the virtual clinical trials concept in order to predict the most effective treatments for patients' tumours with specific characteristics. In the future, such methods can play a supportive role in personalized medical care.

2. Mathematical models of epithelial acini

Epithelial acini, the stable 3D spherical structures composed of a shell of tightly packed epithelial cells enclosing a hollow lumen, are in vitro experimental models of epithelial ducts and cysts. Experimentally, they are used to investigate how individual cells can self-arrange into complex 3D morphologies and to identify specific mechanisms that would prevent tumour origination. The important area of current research is the examination of whether anti-cancer treatments induce changes in the normal acinar structure and function, with the goal of designing therapies that will not harm normal tissues.

Various mathematical models have been used to test the rules for cell self-arrangement into epithelial acini. Grant et al. [31] used a 2D hexagonal cellular automaton (CA) model to represent a central cross-section through a growing epithelial acinus. The authors specified a minimal set of axioms that govern the behaviour of each individual cell based on the host cell state and the contents of the neighbouring automaton cells. This accounted for cell–cell interactions, if the neighbouring automaton cell was occupied by another cell, or cell–microenvironment interactions, if the neighbouring automaton cell was empty. The computational procedure reproduced several experimentally relevant cellular systems, including normal hollow cysts, inverted cysts and pre-cancerous lesions. This model has been subsequently extended to simulate alveolar morphogenesis and quantitatively compare the simulated results with in vitro studies on alveolar AT II cell cultures [32]. This model was also used to investigate dynamic changes in cell phenotypes, including cell polarization, depolarization and anoikis, in computational analogues of the experimental Madin–Darby canine kidney (MDCK) cysts [32,33]. Such an integrated system yielded a way to formulate and test plausible hypotheses of in vitro cellular and phenotype dynamics based on computational axioms and axiom-to-phenotype mapping. The authors further extended this approach to explicitly include cell shape by using the cellular Potts model, in which each cell is composed of several grid points [34] (figure 1a). Computational analysis of the orientation of cell division showed that acinar structures were sensitive to alterations in the axis of cell division that, in certain cases, resulted in aberrant morphologies.

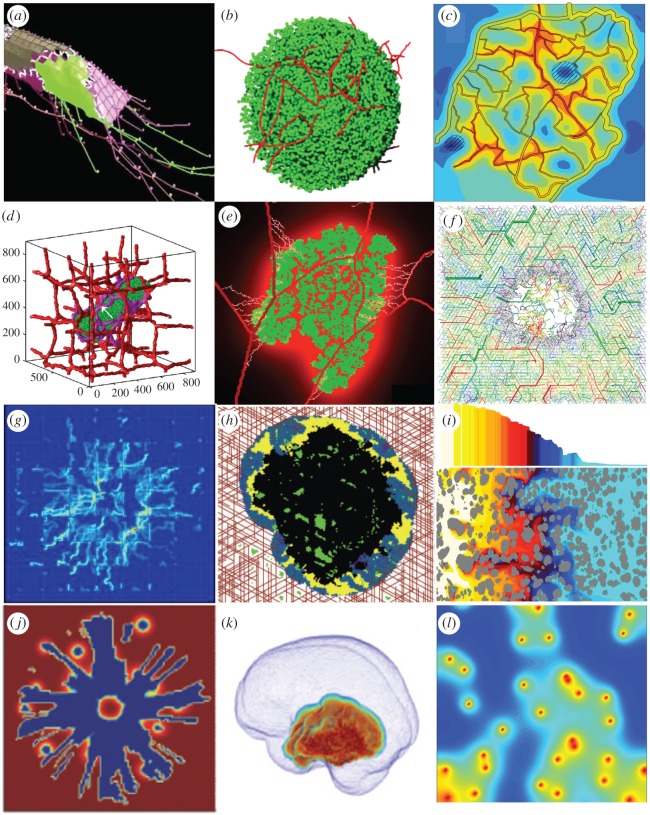
Figure 1.

Snapshots from simulations of normal organoids, multicellular spheroids and early tumour development. (a) A multi-lumen MDCK cyst analogue simulated using the Potts model, from [34]. (b) A 2D cross-sectional view of the MCF10A in silico acinus modelled using the hexagonal CA model, from [35]. (c) An MCF10A acinus simulated by the IBCell model, from [36]. (d) An analogue of the NSCLC spheroid with a necrotic core simulated with Voronoi tessellation-based CA, from [37]. (e) An invasive (fingered) spheroid modelled with the 3D Potts model, from [38]. (f) A stem cell-generated spheroid simulated with the CA model, from [39]. (g) An off-lattice agent-based model reproducing metabolite distribution inside the spheroid, from [40]. (h) Off-lattice agent-based model of spheroids exposed to the cell-cycle inhibitors, from [41]. (i) An agent-based hybrid model of a spheroid exposed to radiation, from [42]. (j) Micropapillary pattern of DCIS simulated with the IBCell model, from [43]. (k) DCIS with calcification simulated with an off-lattice agent-based model, from [44]. (l) Organization of stem cells in the intestinal crypt modelled using an off-lattice agent-based approach, from [45]. All images reprinted with permission.

Tang et al. [35] proposed a full 3D hexagonal CA model of acini development and validated it with experimental data from breast acini derived from the MCF10A non-tumorigenic cell line (figure 1b). The authors constructed phenotypic transition maps between normal and aberrant morphologies and identified the morphological stability conditions for preserving acinus-like topology. The model was subsequently employed to simulate the growth of MCF10A cells that overexpressed the AKT-1 gene. These simulations showed that controlling the rates of proliferating and apoptotic cells was not sufficient to reproduce the sizes and morphologies of experimental MCF10A-AKT-1 spheroids and that additional communication between the mutated cells and the ECM had to be included in the model to reproduce the development of mutated structures.

Rejniak [46] achieved a microscopic view on cell–cell and cell–ECM interactions during acini formation with a mathematical model of deformable cells equipped with a set of membrane pseudo-receptors. In this model, the extrinsic cues, either from other cells or from the ECM, alter the expression of cell membrane receptors. The receptor signature (defined as a proportion of receptors engaged in cell–cell adhesion, growth, death, cell–ECM adhesion or apical markers) determines whether the host cell will remain quiescent or initiate a process of proliferation, epithelial polarization or apoptosis. The individual cells were able to generate various morphologies corresponding with different receptor signature proportions, and the inspection of the whole threshold parameter space, known as Morphocharts [47,48], allowed for identification of the necessary and sufficient conditions for cell self-arrangement into stable hollow epithelial acini [49,50]. This model, named IBCell (after ‘immersed boundary model of the cell’), was calibrated to the experimental MCF10A cell cultures and then used to delineate the molecular differences between this non-tumorigenic cell line and the MCF10A-HER2 mutant cells [36] (figure 1c). In addition to the known differences in cell proliferation and apoptosis between mutant and non-tumorigenic cells, computer simulations indicated that HER2 cells might lose negative feedback from auto-secreted ECM proteins, which were responsible for the stabilization of acinar morphologies in the MCF10A cells. That was confirmed experimentally by the differential expression of laminin proteins around the perimeters of both kinds of structures [51].

3. Mathematical models of tumour multicellular spheroids

In silico models of 3D tumour masses, usually called multicellular tumour spheroid (MCS) models, represent the initial phases of avascular tumour development or the formation of (micro)-metastases. When compared with 2D monolayer models, MCS models more accurately recapitulate the dynamics of tumour growth, complex cell–cell and cell–ECM interactions, tumour heterogeneity and intratumoral drug penetration. Therefore, they are able to more accurately predict how tumour masses respond to treatments than the 2D monolayer models. Radszuweit et al. [52] performed a comparative analysis between the growth kinetics of 2D monolayers and that of 3D spheroids via a CA single-cell, coarse-grained model together with an analytical model that only considered cell division and migration (i.e. it neglected other processes, such as mutations or apoptosis). The mapping between 2D and 3D results supported observations that the more accurate spatial predictions of population growth are achieved when using 3D modelling approaches. The simulated results were compared with in vitro and in vivo experiments with murine embryonic fibroblasts (NIH3T3).

The development of spatially diverse regions—a necrotic core, a ring of quiescent cells and a viable rim of rapidly proliferating cells—that is characteristic of large MCSs has been simulated using various modelling approaches, such as continuous models [53,54], CAs [55] or the immersed boundary IBCell model [56]. In particular, Piotrowska & Angus [57] modelled the impact of metabolites on necrotic core formation using a many-cell CA model, in which each automaton site can harbour several tumour cells. The authors calibrated their model to the mammary carcinoma EMT6/Ro cell line and discussed nutrient-dependent inefficiency in the production of necrosis caused by hydrogen ion metabolites. Jagiella et al. [37] used 3D agents defined by an unstructured lattice to model cells surrounded by local concentrations of nutrients and ECM. The authors presented the impact of metabolites excreted by dying cells (growth inhibitor) on the development of a necrotic core and compared the in silico results with non-small-cell lung cancer (NSCLC) 3D cell cultures (figure 1d). The emergent MCS structure was investigated as a function of cell metabolism under nutrient-rich and nutrient-poor growth conditions and lactate-dependent cell death.

Meyer-Hermann [58] modelled cell invasive movement within and migration out of the MCS via the agent-based Delaunay–Voronoi hybrid model (the Delaunay Object Dynamics) with cells represented by weighted dynamic vertices. Exploitation of model parameters defining cell elastic properties showed that cell shapes are directly linked to the overall pattern of tumour cell invasion. In this model, the adaptable internal cellular structures affected the MCS features and the collective behaviour of individual cells in tumours or lymphoid tissue. The formation of finger-like invasive tumour cohorts arising from MCS was modelled by Anderson et al. [59] using three distinct mathematical models (a hybrid CA, an evolutionary CA and the immersed boundary framework) to examine the impact of nutrient availability as a driving force for tumour cell invasion. The three models independently concluded that tumour invasion might be due to tumour cells' interactions with their microenvironment and results from cancer cells adapting to selective microenvironmental pressures.

The necessity of incorporating tumour heterogeneity and subclonal populations has been approached through discretization of cellular components, which in turn allows for cell–cell and cell–ECM interactions. Poplawski et al. [38] compared the development of smooth (non-invasive) and fingered (invasive, figure 1e) boundaries of avascular tumours using a 3D cellular Potts model. Two morphology-related parameters were incorporated, diffusion limitation and tumour tissue–ECM surface tension, and the authors showed that the sensitivity of 3D tumour fingered morphology to tumour–ECM surface tension increases with the size of the diffusion-limitation parameter. These results are in agreement with experimental observations, where tumour spheroids embedded in a 3D collagen matrix in hypoxic conditions developed a branched tubular structure yet remained unbranched in normoxic conditions. Lorenzo et al. [60] used the phase-field method to account for the transformation of healthy cells to cancer cells and diffusion–reaction equations incorporating nutrient consumption and prostate-specific antigen (PSA) production to reproduce the growth patterns of prostate tumours. The authors used isogeometric analysis with B-spline or T-spline functions to reproduce the fingered growth of shape-unstable prostate spheroids in two and three dimensions. These computations indicated that tumour fingering minimizes the distance from inner cells to external nutrients, contributing to cancer survival and further development.

Enderling [61] used the CA model to investigate the link between tumour morphology and the fractions of cancer stem cells to non-stem cells. These two cancer cell subpopulations differ in four traits: cell proliferative capacity, probability of symmetric versus asymmetric divisions, migration potential and spontaneous cell death. By varying these traits, the model was able to generate various tumour morphologies, from large spherical clusters to a collection of smaller tumour nodules (self-metastases). The identification of the fraction of cancer stem cells has an important consequence for effective tumour treatment. If tumour survival were dependent on a small subpopulation of cancer stem cells, then therapies targeting this cell population would provide an effective therapeutic treatment. The same modelling approach was used in [39] to investigate tumour cellular heterogeneity and the heterogeneity of the cancer stem cell population (figure 1f), as judged from cells harvested in simulated core needle biopsies. The authors concluded that less than 10% of the phenotypic heterogeneity of the total tumour population could be observed in the biopsies, including cases when cancer stem cells with low tumorigenic potential may be isolated within aggressive tumours. These simulations showed that single biopsy data may suggest treatment approaches that are not effective in eliminating the tumour as a whole.

For the sake of minimizing the computational cost of agent-based models, the inclusion of tumour microenvironment (nutrients, drugs, ECM density) often relied on continuous representation for exogenous factors (that is, the models were hybrid [62]). More recent development of advanced 3D off-lattice individual-based hybrid models includes a highly efficient model by Cytowski & Szymanska [63], wherein the authors simulated large systems (10⁹ cells) by taking advantage of efficient algorithms and high-performance computing. Kim et al. [64] combined continuum descriptions for tumour regions of stable density (such as the necrotic core) and discrete agent-based descriptions for tumour regions with highly proliferating cells. With this model, the authors very efficiently addressed the impact of the environment on tumour cell population growth and adaptation to the multi-layered structure and on the role of the nutrient supply (glucose and oxygen) in the development of the necrotic core. Milotti & Chignola [40] developed an off-lattice agent-based model with Delaunay triangulation to represent cell shapes and used it to simulate pre-vascular solid tumour growth below the diagnostic detection limit (figure 1g). The model quantified the main metabolic pathways, growth, proliferation and death dynamics of tumour cells and reproduced biochemical and mechanical cell–cell and cell–environment interactions. These simulations showed complex internal flows of nutrients and movements of cells that cannot be observed experimentally. These predictions provide novel clues as to tumour development and potential therapies.

In silico MCS frameworks have been used to model various anti-cancer treatments and combination therapies. Kim et al. [41] used an off-lattice agent-based model to investigate combined therapies with cell-cycle checkpoint inhibitors. The authors considered cyclin-dependent kinases (CDKs), which are crucial in the regulation of cell-cycle progression and so represent attractive targets in anti-cancer therapy. The simulated results showed that, since CDK inhibitors may halt cell-cycle progression at different checkpoints, the emerging MCS structure (tight versus dispersed colonies) had a strong impact on drugs' efficacy (figure 1h). Kempf et al. [42,65] addressed the important aspects of radiotherapy-induced local oxygen fluctuations within the MCS with an agent-based Delaunay–Voronoi hybrid model (figure 1i). The authors proposed a method by which an image-guided tool could improve treatment schedules and oxygenation monitoring. Angus & Piotrowska [66] simulated multi-dose radiotherapy protocols with a 2D many-cell CA model calibrated to 18 treatment protocols from the experimental literature. This model reproduced irradiation responses to multiple stimulations and predicted that inter-fraction timing variations within one fractional dose might significantly and cost-effectively enhance clinical treatment efficacy. An alternative study by Gao et al. [67] used the cellular Potts model to simulate the irradiation of glioblastomas and radioresistance of both cancer stem cells and cancer cells. These simulations revealed that, in order to match experimental observations, the fractionated radiation treatment must induce a shift from asymmetric to symmetric divisions of glioma stem cells. Karolak et al. [68] addressed immunotherapeutic interactions in the MCS co-culture of melanoma cells and T cells with a 3D off-lattice agent-based model. This study predicted the necessary ratio of T cells to tumour cells to eradicate the tumour cell spheroid.

4. Mathematical models of epithelial tissues and early tumour development

The hallmarks of early tumour development are upregulated proliferation and cell non-responsiveness to signals that control normal tissue homeostasis. This results in the uncontrolled growth of tumour cells. However, initial tumour development is confined to and often restricted by the host tissue morphology. For example, tumours that arise from epithelial tissues initially repopulate the ductal and lobular lumens, leading to ductal carcinoma in situ (DCIS) in breast ducts, prostatic intraepithelial neoplasia in prostate glands or polyps in colonic crypts.

Several mathematical models addressed the initiation and early progression of ductal carcinomas. Rejniak & Dillon [43] investigated properties of tumour cells that enable the emergence of various forms of DCIS, including solid, cribriform, tufts or micropapillary patterns observed in breast and prostate pre-invasive ducts (figure 1j). Using two deformable cell models based on the immersed boundary method [46,69], they predicted the tumours' aggressiveness and invasive potential by classifying them with respect to their proliferative index and distortion of the axis of cell division. The authors compared both features with the properties of epithelial homeostatic maintenance in normal epithelial cells. Similar DCIS patterns were modelled by Norton et al. [70] via an agent-based model to represent both the epithelial and myoepithelial cells that form the normal breast duct. The authors took into consideration the mechanical effects of intra-ductal pressure and myoepithelial contraction, as well as cellular proliferation, apoptosis, adhesion and polarization, to delineate mechanisms of DCIS progression. Boghaert et al. [71] used the principles of the cellular Potts model to examine the relative rates of cell proliferation and apoptosis that governed which of the four morphologies (micropapillary, cribriform, solid and comedo) would emerge. All of these models reproduced DCIS histologies observed in cross-sections of the epithelial ducts. Macklin and co-workers. [44,72] considered a longitudinal section through the breast duct to investigate the emergence of the necrotic core microstructure and intraductal calcification (figure 1k). This agent-based model represented cells as particles with phenotypes determined by genomic-/proteomic- and microenvironment-dependent stochastic processes. Cell motion and interactions between individual cells and interactions between cells and the basement membrane were modelled using the balance of biomechanical forces. This model predicted that necrotic cell lysis can act as biomechanical stress relief, leading to linear DCIS growth. The authors also provided a method for patient-specific calibration of the model based on clinical histopathology data to validate model predictions. Butner et al. [73] used a similar longitudinal morphology of the breast duct to simulate growth and elongation of the duct terminal end buds (TEBs) with a hybrid hexagonal CA model. The authors studied the role of cellular differentiation pathways, such as endocrine and paracrine signalling, in the development of mammary glands, and they showed that the distribution of cellular phenotypes within the TEBs was highly heterogeneous, allowing for significant plasticity in phenotypic distributions while maintaining biologically relevant growth behaviour.

The colon crypt is another epithelial tissue that has been extensively modelled; van Leeuwen et al. [74,75] developed a multi-scale model combining ordinary differential equations (ODEs) describing the intracellular signalling pathways with an off-lattice agent-based model with Voronoi tessellation to represent individual epithelial cells and their shapes. The authors used this model to investigate the role of the Wnt-β-catenin pathway in maintaining the structure of the epithelial crypts, as well as tissue morphology alterations that resulted from mutations most commonly observed in human colorectal cancer. The 3D version of this model was used to compare two hypotheses of monoclonal conversion in the colon crypts: the asymmetric division of stem cells or microenvironmental signalling cues [76]. This model was used to simulate Delta-Notch distribution in the cells forming the villi of small intestines [77], and to investigate active and passive migration of cells in the crypts [78]. A similar 3D model was also used to simulate spatio-temporal organization of stem cells within the interstitial crypt and address stem cell competition within this tissue [45,79] (figure 1l). The model predicted that the epithelial tissue could fully recover even after elimination of a subpopulation of functional stem cells, which challenged the current view of colorectal crypt stem-cell-dependent organization. Bravo & Axelrod [80] proposed another model of a virtual colon crypt based on the CA concept to simulate cell dynamics and cell type plasticity in normal crypts and in tumours under different therapy protocols. The model was calibrated with measurements of human biopsy specimens and verified by its ability to reproduce the experimentally observed monoclonal conversion by neutral drift and formation of adenomas as well as by the robust ability of crypts to recover from perturbation by cytotoxic agents.

5. Mathematical models of vascularized tumours and angiogenesis

A major step in the transition from an avascular benign tumour to an invasive and metastatic one is the recruitment of vessels from the surrounding tissues (a process of angiogenesis) and the development of a vascular network. This de novo vascularization enables more sufficient transport of nutrients to the tumour, which leads to rapid outgrowth of tumour tissue, tumour cell extravasation to the bloodstream and metastatic spread to distant organs.

Several mathematical models have been proposed to address the process of angiogenesis and the complexity of the vascular network formation. Bentley and co-workers [81,82] modelled the early stages of new vessel growth (the formation of vessel sprouts, figure 2a) using the cellular Potts model integrated with laboratory experiments. The authors simulated endothelial cell rearrangement on the tips of the growing vascular sprouts and identified that differential adhesion dynamics between endothelial cells regulated by Notch/vascular endothelial growth factor receptor (VEGFR) signalling led to competition for the tip-cell position. This model also demonstrated that the rate of tip-cell selection determined the length of sprout extension and regulated the topology of the vascular network. Bauer et al. [93] also used the cellular Potts framework to model vascular branching in response to both tumour-secreted pro-angiogenic factors and endothelial cell interactions with the surrounding ECM. The authors showed that differences in the matrix binding affinity of vascular endothelial growth factor (VEGF) isoforms resulted in vastly different capillary morphologies. Merks and co-workers [94,95] addressed the formation of more complex vascular networks by coupling the cellular Potts model with chemo-mechanical interactions between endothelial cells and the ECM. Systematic exploration of cell migratory responses to the gradients of an autocrine secreted diffusible chemoattractant allowed for predicting the complexity of the generated vascular network topologies. These studies also included the role of ECM remodelling and mechanical properties in vascular sprouting. Perfahl et al. [83] used an off-lattice agent-based model to represent individual endothelial cells and the mechanical forces between them. This study showed that the degree of branching and the network density depend on whether the parent vessel was stretched or compressed; new sprouts were formed when the parent vessel was highly compressed. The computationally generated vascular networks showed a good qualitative comparison with experimental results (figure 2b).

Figure 2.

Snapshots from simulations of angiogenesis, vascularized tumour growth and tumour treatments. (a) Cellular Potts model of the vessel sprout formation, from [82]. (b) Off-lattice agent-based model of the vascular network formation and branching, from [83]. (c) Structural adaptation of tumour vasculature in response to external factors modelled as a network composed of straight vascular segments, from [84]. (d) Three-dimensional cellular Potts model studying vascular remodelling during the tumour growth, from [85]. (e) A hybrid CA model of tumour-induced angiogenesis and growth within a digitized vasculature, from [86]. (f) Heterogeneous CA vascular network, from [87]. (g) Distribution of a blood-borne drug simulated with the hybrid model of discrete vasculature, continuous tumour mass and drug kinetics, from [88]. (h) The Krogh cylinder model of the vasculature and the CA model of the tumour simulating treatment with an angiogenesis inhibitor, from [89]. (i) Tumour response to HAP treatment simulated with the regularized Stokeslets method, from [90]. (j) ECM degradation by chemotactic glioma simulated by a continuous model, from [64]. (k) Glioma spread within the 3D brain architecture modelled using the continuous model, from [91]. (l) Tumour oxygenation predicted by the 2D hybrid CA model, from [92]. All images reprinted with permission.

The complex topology of tumour vasculature leads to irregular distribution of nutrients within the tumour tissue and non-uniform penetration of the tumour tissue by drug molecules. Secomb et al. [84,96] used the Green's function method to model time-dependent solute transport through the microvascular network with realistic geometries and solute transvascular exchange, diffusion and wash-out within the tumour tissue. The authors investigated the structural adaptation of tumour vasculature and its pruning in response to haemodynamic and metabolic stimuli as well as spatial patterns and frequency distributions of both oxygen and VEGF concentrations around vascular networks of distinct topologies (figure 2c). Welter and co-workers [87,97] modelled the complex hierarchical tree-like vascular structures via a hybrid model combining a discrete triangular grid-based vascular network and a continuous description of a homogeneous medium representing host or tumour cells. The authors investigated the relation between the morphology of tumour vasculature and the intra- and extravascular transport characteristics of blood flow, oxygen distribution, interstitial fluid pressure and drug delivery efficiency.

A transition from avascular to vascularized tumours that included angiogenesis and vessel remodelling was modelled by Wcislo et al. [98] with an off-lattice agent-based model with semi-harmonic central forces simulating mechanical resistance, coupled with reaction–diffusion equations to describe changes in the levels of both oxygen and tumour angiogenic factor. This study explained the mechanisms of inward cell motion in avascular tumours, stabilization of tumour growth by external pressure and trapping of healthy cells by the invading cohorts of tumour cells. Shirinifard et al. [85] used a 3D multi-scale cellular Potts model to computationally investigate patterns of vascular remodelling due to tumour outgrowth (figure 2d). The authors observed that avascular tumours grew along the nearest blood vessel before initiating the processes of angiogenesis and anastomosis (formation of closed loops by growing capillaries). The interplay between healthy and tumour cells during the angiogenesis process was addressed by Perfahl et al. [99] with a CA model coupled with a system of ODEs describing the concentrations of various intracellular proteins. This model was also used for simulations initiated with the experimentally derived vascular network to predict the patterns of possible vascular remodelling. Stéphanou and co-workers [86,100] relied on realistic murine vascular topologies for calibration of a hybrid CA model of tumour-induced angiogenesis (figure 2e). The authors observed that tumour dormancy was a potential consequence of the intense vascular changes in the host tissue. The vascular changes in the larger vessels affected the efficiency of oxygen delivery in the vascular network and, in consequence, kept tumour cells mostly in a non-proliferative hypoxic state. Caiazzo & Ramis-Conde [101] investigated the effects of hypoxia on the changes in glioblastoma cellular architecture and the development of pseudo-palisade patterns with a hybrid off-lattice agent-based model. This study showed that heterogeneity in cellular response to hypoxia was a crucial factor in pseudo-palisade formation, and that the selective processes based on the metabolic switch were responsible for tumour outgrowth and invasion.

6. Mathematical models of anti-cancer therapies

Since cancer is a complex systemic disease that evolves in response to treatment and can adapt to changing environmental conditions, it is difficult to predict which anti-cancer treatments or treatment combinations will be the most effective for a given patient's tumour. Mathematical modelling provides tools to test different therapeutic strategies to determine the most efficient protocols that will administer the right treatment at the right time and in the right dose. All major types of anti-cancer treatments—chemo-, radiation- and immunotherapies, as well as their combinations—have been modelled using spatially explicit mathematical frameworks.

One major impediment to successful chemotherapy is an inefficient penetration of drug molecules through the tumour tissue. If drug molecules do not reach the tumour cells in sufficient quantities, the drugs will fail to eradicate these cells. Several barriers to drug penetration were investigated by mathematical models. Rejniak et al. [102] modelled the role of tumour tissue architecture on drug diffusive and advective interstitial transport with the regularized Stokeslets method. The authors showed that, if both modes of transport contribute to drug movement equally (that is, the Péclet number has a moderate value), the depth of tissue penetration by the drug molecules strongly depends on tissue architecture. Therefore, histology samples, routinely collected in the clinic during diagnostic biopsies, may help to predict how well a given drug will penetrate a tumour. Boujelben et al. [103] used magnetic resonance imaging (MRI) from a rodent brain to define a 3D vascular network as a source of the drug in a continuous diffusion–reaction mathematical model. The authors investigated how physiological parameters of blood flow rates, vessel permeability and tissue diffusion interact nonlinearly in drug delivery to gliomas. Targeted therapeutics have been developed to reduce systemic drug toxicity. The novelty of targeted drugs or imaging agents is that their molecules bind to the specific cell membrane receptors expressed on tumour cells but not on normal cells. Karolak and co-workers [51,104] used an off-lattice agent-based model defined by a digitized tumour tissue histology to explore the optimal design of targeted agents that will ensure maximal efficacy for a given patient's tumour. The authors observed that agents that have moderate affinity but are quickly released from the vasculature bound to the cell-surface receptors with similar efficacy to high-affinity molecules released at a slower rate. These predictions may help in designing chemical compounds of preferable properties to ensure the maximal effect in tumours with given receptor expression levels. Another class of therapeutic agents that allow for controlled release of drug cocktails is nanoparticles. Curtis and co-workers [88,105] investigated nanoparticle efficiency by employing a hybrid model with a discrete vasculature, continuous description of tumour mass and drug kinetics governed by diffusion–reaction equations. The authors showed that, although nanoparticles of larger diameter could deliver higher drug concentrations within the tumour tissue, these were outperformed by small nanoparticles that were more uniformly distributed within the tumour tissue and thus were more efficient, despite their low drug loading (figure 2g).

Since vascularized tumours are a prerequisite to tumour invasion and metastasis, drugs that target tumour vasculature are promising anti-cancer treatments. Gevertz [89,106] modelled angiogenesis inhibitors and vascular disrupting agents in brain tumours with a CA model to represent the cells, a Krogh cylinder model to represent the vasculature and a continuous description of growth factors and both drugs' concentrations (figure 2h). This model showed that the treatment combination can exert less antitumour activity than a stand-alone angiogenesis inhibitor treatment. Using a simulated annealing algorithm, the model identified that a pulsed treatment strategy minimized the number of active tumour cells remaining after two cycles of angiogenesis inhibitor treatment. Furthermore, three or four rounds of optimal therapy administration yielded permanent growth inhibition of the simulated tumours. The effects of combining antiangiogenic agents and cytotoxic nanoparticles on normalization of leaky tumour vessels and efficacy in control of tumour size were modelled by Yonucu et al. [107] using the continuous partial differential equation model that took into account tumour growth, angiogenesis and interstitial fluid pressure. The authors observed differences in drug extravasation that depended on the scheduling of combined therapy with increased overall effects when the therapy was administered concurrently.

A different class of treatments has been developed to target cells in the areas of low oxygen levels (hypoxia) that emerge in large, poorly vascularized tumours. To eradicate tumour cells in these areas, hypoxia-activated pro-drugs (HAPs) were designed such that the cytotoxic compounds can only be released when the oxygen level is very low. Mathematical models explored how to effectively use HAPs. Foehrenbacher et al. [108] used a Green's function approach to calculate tumour response to this treatment and the 3D spatial and longitudinal gradients of oxygen and drug concentrations. The authors showed that, to increase HAPs' antitumour activity, the rates of effector stability and pro-drug activation should be optimized. Wojtkowiak et al. [90] presented an integrated in vitro–in vivo–in silico study that used metabolic profiling to improve HAP activity by combining it with short-term hypoxia sensitizers (figure 2i). The authors showed that acute increases in tumour hypoxia can be beneficial for improving the clinical efficacy of HAPs, but the timing and order of administration of each of the therapeutics must be tightly coordinated due to the short half-life of HAPs.

Clinically, the development of drug resistance is a significant impediment in cancer treatment. Investigating how resistance arises and how to overcome it is crucial for cancer biology and mathematical oncology modelling. The emergence of drug-induced resistance in tumour cells in response to drug and oxygen gradients that can dynamically change over the course of treatment was modelled using an off-lattice hybrid agent-based model [109,110]. The authors identified the resistance-prone regions in the tumour tissue, such as hypoxic niches and tissue sanctuaries, in which tumour cells can survive either by repairing the damage or by increasing their tolerance to drug-induced damage. The authors also showed that heterogeneous microenvironmental factors, rather than cells' clonal heritage, may drive drug-induced resistance. Lindsay et al. [111] developed a stochastic model to explore a spectrum of treatment regimens combining a HAP and cytotoxic drugs. The authors found that the combined therapies delayed tumour resistance longer than any monotherapy schedule and that sequentially alternating single doses of each drug led to minimal tumour burden and maximal reduction in the probability of developing resistance.

Most anti-cancer drugs are administered by intravenous injection; however, other alternative routes may be more effective. Kanigel Winner et al. [112] compared intravenous injections and intraperitoneal infusions for ovarian cancers using a cellular Potts framework. This model revealed that intraperitoneal infusion is the superior route for smaller, avascular tumours. Larger tumours will benefit from both delivery routes combined. Kim et al. [64] investigated how a direct post-surgery injection of the chemoattractant into the tumour resection site can reduce the spread of glioblastoma cells. The authors used a hybrid model combining the off-lattice agent-based framework with the continuous description of the tumour microenvironment, and ODEs for intracellular signalling. The model predicted that cell migration towards the chemoattractant depends on the balance between random and chemotactic motility in addition to oxygen and glucose availability (figure 2j).

Radiation therapy is another standard anti-cancer treatment for numerous kinds of tumours. A 3D mathematical model that combined the full 3D brain architecture and continuous diffusion–reaction equations has been used to simulate radiation treatment in glioblastomas [92,113] (figure 2k). The authors quantified the effects of regional resistance to radiation as an effect of heterogeneous intratumoral hypoxia, and they showed how tumour-specific models can aid in the construction of effective treatment protocols. Scott et al. [93] modelled the variations in oxygen tension that regulate tumour response to radiation therapy with a 2D hybrid CA model (figure 2l). The authors showed that, for relatively low vessel density, radiation efficacy is decreased when vessels are more homogeneously distributed, and the opposite is true when vessel organization is normalized. Powathil et al. [114,115] modelled a combination of radiation and chemotherapy by coupling the ODEs for the cell cycle, the diffusion–reaction equations for oxygen and drug kinetics, and the agent-based models to represent cells and vessels. This multi-scale model predicted optimal patient-specific multi-modality treatment protocols.

In addition to classical chemo- and radiotherapy, there is growing interest in the development and optimization of immunotherapy protocols. Owen et al. [116] developed a mathematical model of engineered macrophages that target tumour cells in hypoxic regions, combining a many-cell CA framework with diffusion–reaction equations for oxygen, growth factors and therapeutics. Model simulations predicted a synergistic effect of combining conventional and macrophage-based therapies; however, the efficacy of this combined treatment was the greatest when the macrophage-based therapy was administered shortly before or concurrently with chemotherapy. Leonard et al. [117] proposed a mathematical model simulating how macrophages can deliver a nanodrug to metastatic lesions in the liver, combining the level-set method to represent the evolving tumour, discrete representation of the tumour vasculature and diffusion–reactions equations for drug and metabolites dynamics, integrating it with laboratory experiments. The model predicted the macrophage and the encapsulated nanodrug concentrations needed inside the lesion to achieve growth inhibition. The use of preventative vaccinations to stimulate cytotoxic T lymphocytes (CTLs) to improve their immunotherapeutic capabilities was modelled by Kim & Lee [118] using a combination of agent-based modelling and delay differential equations. The authors showed that a pool of 3% of anti-cancer memory CTLs could eliminate a developing tumour before it reaches an average size of 1000 cells, and a pool of only 1% of CTLs could eradicate a growing tumour of diameter of 0.35 mm.

7. Areas for inclusion in mathematical modelling of precision medicine

This review covers a variety of mathematical models of cancer that vary as far as which details of the tumour cells are included, the number of cells the model can handle, the complexity of the tumour microenvironment, and the computational costs of each model. We included examples of lattice-based CA models, lattice-free particle models, multi-grid cellular Potts models and deformable viscoelastic cells, as well as continuous population dynamic models. The fact that so many different models are currently used to address cancer-related problems means that each of them has some advantages (thus being used in some cases) and disadvantages (thus other models being used in other cases). The interested reader is referred to other publications [119–122] for more details on different mathematical frameworks and the differences between them. However, these models' applicability to precision medicine would benefit from the inclusion of some of the intracellular-, cellular- and intercellular-scale phenomena that we identified in this section. Although these biological processes take place on different spatial and time scales, they overlap functionally. Likewise, the scalability transformations between multiple resolution scales of the mathematical models offer prospects for improvements, though this process is more challenging in practice. Therefore, building up multi-scale links requires collaborations between multiple interdisciplinary groups in order to effectively collect the data for integration and design experiments to validate predictions.

7.1. Structural biology

Advancements in structural biology deliver a high-resolution view of various biomolecules, such as protein systems (from enzymes to receptors to transcription factors), nucleic acid polymers (RNA or DNA), lipid membranes or small molecules. An atomistic representation of these structures provides a unique opportunity to investigate personalized local interactions and conformational dynamics, which drive the early stages of the majority of biological processes. This approach allows for translation of the effects of clinically identified point mutations or sequence variations in oncogenic transformations and signalling. The identified cross-correlations between biological scales can reveal how protein folding, protein–ligand binding, protein–DNA recognition, DNA sequence variations, epigenetic modifications or DNA damage drive early signalling events in cancer development. Furthermore, multi-scale computational approaches could be a valuable tool in estimating the emergence of cellular heterogeneity and phenotypic diversity [123]. The conformational dynamics of biological systems on the atomistic level has the potential to inform the next steps in the mathematical modelling scheme, but this topic remains unexplored. This is due to several limitations, primarily the large size of the systems, computational costs and short time scales involved. Various approaches can overcome the limitations related to the nano- to millisecond time scales of early events in many biological processes, such as enhanced sampling methods with free energy calculations [124], the support of massively parallel supercomputers [125] or coarse-graining models [126,127]. This allows for the investigation of larger systems and global conformational phenomena [126,127], which could be further translated to cellular networks.

7.2. Cancer genomics

Targeting of a single DNA base or amino acid resolution is the highest level of detail concerning the human genome, and is extremely suitable for personalized studies. The subsequent potential conformational studies of the genetic material provide the opportunity to speculate about systems' behaviour, response to treatment and drug effectiveness in relation to an individual patient. The correctness of this approach has been demonstrated with next-generation sequencing (NGS) methods, which successfully support tumour molecular profiling and clinical decisions in personalized treatment through multi-variate analyses [128]. These detailed interpretative tools allow for the identification of abnormalities in gene expression, epigenetic control, signalling pathways, biomarkers and cancer progression [129]. The NGS of a tumour before and after treatment provides different mutation profiles, which may further benefit clinical decisions. For example, the extracted quantitative data on point mutations may support atomistic computer simulations, but the various expression levels can investigate inter- and intracellular interactions, signalling pathways and networks. Details about the protein levels or germline and somatic mutations used in personalized cancer care [130] and data interpretation [131] provide input for the modelling of cancer cellular phenotypes and subclonal diversity. This, in turn, renders the single cell a bridging unit between intrinsic and extrinsic signals from gene expression to interactions including cells and stroma. It is therefore necessary to incorporate genomic information into all resolution levels of mathematical modelling of organoids and tumour tissues, although this requires effort, in order to address the heterogeneity and dynamics of personalized tumour evolution and treatment.

7.3. Cell mechanobiology

While cancer may be manifested by genetic changes, the mechanical interactions between individual cells and between the cells and their microenvironment are the factual demonstrations of cancer becoming malignant, invasive and metastatic. The malignant cells exert forces on other cells to compete for space, physically detach from the tumour mass and migrate through the ECM. All of these activities require the coordination of biological and mechanical processes. Normal cells develop specialized connections with other cells (cadherins) and with the external microenvironment (integrins) that provide mechanical attachment and transmit forces. These mechanical signals sensed by the cell result in the activation of intracellular biochemical signalling pathways (a process called mechanotransduction) that, in turn, regulate cellular behaviour [132]. All cellular life processes in non-malignant cells (death, proliferation, differentiation) must be tightly controlled and coordinated to enable tissue turnover and preserve tissue homeostasis [133]. However, the disruption of normal tissue architecture is one of the initial steps in cancer progression. The early pre-invasive forms of breast cancer are characterized by filled ductal lumens and ductal disorganization (DCIS) [134]. It has also been shown that changes in the ECM structure and its stiffness and mechanics can promote or suppress the formation of malignant multicellular spheroids in 3D cell cultures [135]. Thus, microscopic changes in cell or ECM mechanics can deregulate molecular mechanisms of mechanotransduction. The physical basis for early epithelial cancers can be a product of either an altered force balance on the cellular or tissue levels or a perturbed cellular response to mechanical stimuli [136]. However, the mechanism by which such physical forces and mechanical stimuli contribute to cellular decision-making is still not fully understood. Mathematical models that incorporate various mechanical aspects can play a fundamental role in delineating the role of mechanobiology in cancer initiation and progression [137,138].

7.4. Medical imaging

Imaging approaches in oncology have long supported early cancer detection (mammography), diagnosis (pathology) and monitoring of treatment response (tomography or magnetic resonance). The need for more accurate and faster analyses of these images led to the development of the fields of digital pathology and radiomics, which aim for high-throughput automatic evaluation of clinical imaging, such as histopathology, microscopy, MRI, computed tomography (CT) or positron emission tomography (PET). Current advances include protocols to reconstruct the spatial 3D architectures of DCIS from 2D histology images stained with haematoxylin and eosin (H&E) [139] and multi-tiered content-based image algorithms for classification of tumour grades [140]. Histology samples and digital microscopy analyses were also used to evaluate the differences between distinct regions of interest within the same tumour [141]. Such approaches allow for the assessment of tumour phenotypic features and tumour microenvironment landscapes at different levels of resolution [142]. Certain automated tools (BioSig3D [143] or AMIDA [144]) were developed for high-throughput screening of fluorescent images of MCSs. While histology and microscopy images provide invaluable information about individual cells, both rely on tissue or cell fixing and staining and do not allow for monitoring of the same cells or tissue regions over time. In contrast, radiological images do not require invasive surgical procedures and enable longitudinal observation of the changes in tumour progression or the response to treatment during the therapy. Additionally, these radiological images are not merely pictures: they represent a rich source of often underutilized data [145,146]. Current advances in the analysis of these clinical images include high-throughput quantification methods (radiomics) of a large number of imaging features from MRI, CT and PET/CT images to develop prognostic signatures that predict tumour phenotype, correlate with treatment outcomes [147] and distinguish between different predictive tumour genotypes [148]. These methods can identify tumour subregions, called habitats, with differential imaging characteristics (tissue perfusion and vascular permeability) that correlate with tumour aggressiveness [149]. Other methods include the use of diffusion magnetic resonance imaging (dMRI) to analyse brain fibre orientation and dispersion with parametric spherical deconvolution methods [150,151]. This enhances our knowledge of potential routes of glioma cell spread along the ECM fibres. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) of breast cancer patients was also used for pharmacokinetic studies predicting tumour response to neoadjuvant chemotherapy [152,153]. DCE-MRI was used to identify quantitative pharmacokinetic parameters that correlate with patients' outcomes.

While the above efforts highlight recent improvements and novel techniques for linking medical imaging data to microenvironmental, phenotypic or genomic features, the images show only a one-time snapshot of the tumour state. Mathematical models provide the means to visualize and analyse tumour dynamic changes, thereby adding dynamics to the static imaging data. Several models described in this review used medical images for computational simulations (histology, MRI or PET images). However, a broader use of such data would improve the accuracy, validation and predictions of mathematical models. For example, the association of pre-treatment MRI images with a reaction–diffusion model defined on an anatomically accurate human brain phantom allowed for predictions of the untreated survival of a cohort of glioblastoma patients and their stratification based on the predicted tumour aggressiveness [154]. Patient-specific MRI data taken before and after the first cycle of neoadjuvant therapy in patients with breast cancer were coupled with a biomechanistic mathematical model to predict whether a patient would achieve a complete pathological response [155]. PET/CT imaging data from patients with head and neck carcinoma were used to inform a dynamic voxel-based model that predicted radiation therapy response under uniform and non-uniform tumour tissue oxygenation patterns [156]. PET/CT scans from patients with pancreatic tumours were used to predict tumour growth dynamics with a model using an elastic-growth decomposition technique to represent possible deformations of the pancreas [157]. Dynamic, spatio-temporal mathematical oncology models should therefore combine different types of imaging techniques at various resolution and time scales, and incorporate data from landscape pathology, genomics, fibre analysis and radiomics habitats at various stages of tumour development and treatment. With achievement of these prospects, the clinical use of mathematical modelling would become more effective for personalized surgery by guiding and defining tumour margins, for designing personalized schedules of treatment combinations, for predicting treatment efficacy and for developing methods to overcome resistance.

8. Organ-on-chip platform as an experimental model for testing personalized responses to therapy

All of the mathematical models described in the previous sections are computational analogues of either in vitro or in vivo experimental models. These experimental systems have been developed progressively to delineate various aspects of tumorigenesis and tumour response to therapies. They range in complexity from examinations of single cells, to 3D cell model systems, to organotypic cultures, to explant models, to in vivo animal models [158–160]. The in vitro experiments are well controlled, but they represent only one organ as opposed to the systemic response to the treatment. In contrast, for animal experimentation, the difficulty lies in controlling the complexity of the systemic response, so large numbers of animals must be used to gain statistical significance. The organ-on-chip microfluidic devices may be able to combine the best of both approaches. Current advances and successes in microfluidic systems have led to their widespread use in biological applications. The use of microfluidics in cell and tissue cultures offers significant advantages over traditional Petri dish approaches, as this maintains the cell-to-fluid ratio close to physiological levels, reducing dilution of metabolites, hormones, and autocrine and paracrine signals [161]. Additionally, microfluidics can provide a wide range of physical and chemical stimuli through precise control of the shear stresses and flow switching [162,163]. Unlike animal model systems, most microfluidic devices are fabricated from optically transparent materials that permit visualization of various cellular processes (sometimes in real time) through bright field and fluorescent imaging [164,165]. The choice of softer fabrication materials offers further control of such mechanical stresses as tension or compression.

At the forefront of tissue engineering, disease modelling and human organ construct development is a new class of microfabricated microfluidic tissue bioreactors, termed organ-on-chip bioreactors. These microphysiological systems are capable of maintaining live cultures for weeks and even months and can replicate complex organ environments, including 3D multicellular organ structures, nutrient supply and waste removal, oxygenation states, interstitial flows and a variety of microenvironmental gradients [163,165]. These systems are composed of individually addressable micro-compartments to permit precise regulation of a specific organ layer or tissue area and individualized tissue perfusion [166,167]. As such, they hold promise as attractive platforms for future drug development. Tumour biology, for example, can be explored within a more realistic organ environment containing human primary or derived cells and tissues that are held under relevant chemical and physical conditions, thus providing realistic scenarios of drug delivery and penetration into tissue [160,168]. To date, there are multiple organs-on-chips in different states of development, including cardiovascular, liver, blood–brain barrier, mammary, intestine and skin bioreactors [167,169]. The future goal is to link together these miniaturized organ systems to monitor ‘whole body’ responses to tumour spread or antitumour therapeutics, to address questions of drug metabolism and off-target effects, or to optimize and individually tailor treatment regimens for cancer patients. The first steps in this direction have already been taken [170,171]. Individual or interconnected organs-on-chips will also serve as a quick test platform for parametrization of functional processes that bridges the gap between the initial computer model development and its subsequent fine-tuning.

9. Discussion and outlook

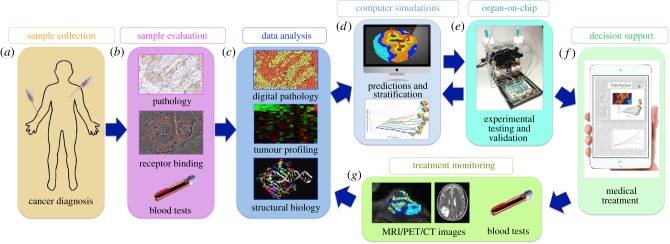
Mathematical modelling and computational systems biology have already proven to be useful tools for integrating vast amounts of diverse data into a coherent, multi-scale description of cancer, for dissecting complex interactions between different cancer components, and for revealing the intricate mechanisms behind tumour initiation, progression and metastatic spread [172,173]. Mathematical methods, by their nature, can simultaneously handle multiple variables that describe different elements of the whole cancer system. These can be applied to represent various tumour features, intercellular interactions and a wide range of treatment combinations and schedules in order to optimize anti-cancer therapy [174,175]. When calibrated with patients' data and tested with validated experimental models, these relatively fast and inexpensive mathematical oncology methods could be used to design effective therapeutic strategies for each individual patient in the form of patient-specific virtual clinical trials (figure 3). We envision that this protocol will include the collection of various data during the tumour diagnosis (figure 3a) and evaluation of these data by pathologists, radiologists and hospital laboratories (figure 3b). These data will also be quantitatively analysed using biostatistics, bioinformatics and various ‘-omics’ (proteomics, genomics, metabolomics, pathomics, etc.) approaches (figure 3c). Subsequently, the specific mathematical models will be calibrated and used to perform an extensive set of simulations to probe the pharmacokinetics and pharmacodynamics relationships of the available anti-cancer agents in order to find their synergistic combinations, and to design the most efficient administration protocols (figure 3d). The most promising treatment schedules will be tested using the organ-on-chip bioreactors (figure 3e). The hope is that, in the future, this approach will serve as a supportive tool for decision-making in the clinic (figure 3f). When additional data are collected (figure 3g) and analysed (figure 3c) to monitor the effectiveness of the therapy, these data can be incorporated into the computational model (figure 3d) and tested in the organ-on-chip bioreactor (figure 3e) to adjust the treatment in the clinic (figure 3f). This process can be repeated and the therapy can be adapted according to tumour response. Currently, there are a handful of mathematical models that propose to use similar concepts [176–180] and show potential for designing the most efficient combination therapies, the most effective therapy schedules and an optimal toxicity–efficacy balance. They also promise to be useful in selecting those patients who are most likely to benefit from a given therapy. Therefore, when virtual clinical trials are incorporated into routine patient care they will give clinicians additional tools for making decisions to improve a patient's quality of life and control the tumour's spread. Since computational simulations can be individualized to the properties of a particular tumour, such approaches are a step towards precision medicine and personalized care.

Figure 3.

Schematics of Virtual Clinical Trials. (a) Collection of standard-of-care data in the clinic. (b) Data evaluation for diagnostic purposes. (c) Quantitative data profiling, screening and analysis. (d) Design, calibration and simulations of mathematical models. (e) Experimental testing and treatment validation with an organ-on-chip platform. (f) Supportive tool for clinical decision-making based on mathematical and organ-on-chip predictions. (g) Collection of longitudinal data for treatment monitoring. (c–g) Treatment adaptation by repeating the analysis, mathematical and experimental predictions, and treatment monitoring processes.

Data accessibility

All data discussed in this review paper were previously published and are available from publications listed in the References section.

Authors' contributions

This review manuscript was written jointly by A.K., D.A.M., L.J.M. and K.A.R.

Competing interests

The authors declare no competing interests.

Funding

This work was supported by the National Institutes of Health/National Cancer Institute grant U01 CA202229-01 (to L.J.M., K.A.R. and D.A.M.). This work was supported in part by the Shared Resources at the H. Lee Moffitt Cancer Center & Research Institute, an NCI Designated Comprehensive Cancer Center, through the National Institutes of Health grant P30-CA076292. This publication was made possible by NIH/NCATS 5UH3TR000491-04 and the U.S. EPA grant no. 83573601 (to L.J.M. and D.A.M.). Its contents are solely the responsibility of the grantee and do not necessarily represent the official views of the U.S. EPA. Further, the U.S. EPA does not endorse the purchase of any commercial products or services mentioned in the publication.