Optimizing targeted vaccination across cyber–physical networks: an empirically based mathematical simulation study

Abstract

Targeted vaccination, whether to minimize the forward transmission of infectious diseases or their clinical impact, is one of the ‘holy grails’ of modern infectious disease outbreak response, yet it is difficult to achieve in practice due to the challenge of identifying optimal targets in real time. If interruption of disease transmission is the goal, targeting requires knowledge of underlying person-to-person contact networks. Digital communication networks may reflect not only virtual but also physical interactions that could result in disease transmission, but the precise overlap between these cyber and physical networks has never been empirically explored in real-life settings. Here, we study the digital communication activity of more than 500 individuals along with their person-to-person contacts at a 5-min temporal resolution. We then simulate different disease transmission scenarios on the person-to-person physical contact network to determine whether cyber communication networks can be harnessed to advance the goal of targeted vaccination for a disease spreading on the network of physical proximity. We show that individuals selected on the basis of their closeness centrality within cyber networks (what we call ‘cyber-directed vaccination’) can enhance vaccination campaigns against diseases with short-range (but not full-range) modes of transmission.

1. Introduction

Strategies for countering infectious diseases have been actively developed in recent years [1], the two most prominent methods being monitoring and vaccination [2–8]. In the case of monitoring, the goal is to forecast an outbreak by observing only a small, high-risk subpopulation that is expected to become infected at an early stage of an outbreak. The goal of vaccination is to reduce the effective size of the susceptible population below a threshold in order achieve ‘herd immunity’ [9]. From a network perspective, we approach herd immunity by decreasing the number of links between susceptible individuals in a population, across which the disease may be transmitted [8]. While full knowledge of the outbreak state (in the case of monitoring) or full population protection (in the case of vaccination) are preferable, neither is practically feasible [10,11]. For this reason, targeted strategies that involve interventions focused on a small, carefully selected subpopulation are of major interest [7,10,12–17]. It has been shown that densely connected populations, such as schools [18,19], universities [10] or hospitals [20], play a significant role in large outbreaks [21], offering numerous paths for diseases to propagate. Such cohesive communities may also serve as ‘living laboratories’ for studying the structure of interpersonal networks, making them especially interesting in the advancement of epidemiological control efforts. For diseases with person-to-person transmission, direct identification of optimal target groups requires knowledge of the structure of the physical contact network, collection of which is usually a time-consuming and complex task [10,18,22,23], limiting the feasibility of this approach. Communication networks, such as online social networks or call detail records (CDRs) may provide an accessible proxy of the structure of contacts among individuals, and immunization strategies that take advantage of the structure of these networks have been suggested [8]. However, due to the known topological differences between communication networks and networks of person-to-person proximity contacts [18,23–25], the role of digital communication networks in locating epidemiologically relevant target individuals remains largely unknown [25]. This study addresses this digital–physical divide: we ask whether it is possible to extract information solely from individuals' cyber networks (in this case, Facebook and phone call networks) in order to alter patterns of disease spread across the corresponding network of physical interactions between those same individuals.

Our study focuses on a densely connected population of 532 university students whose physical and cyber data make up the Copenhagen Network (CN) Study, which includes records of Facebook friendships, Facebook activity/feeds, CDRs and Bluetooth scans to measure person-to-person contacts, collected with high temporal resolution over 2 years (details of the measurement are provided in Material and methods). By simulating outbreaks of diseases with different transmission characteristics over the physical component of this empirical network, we are able to gauge the effectiveness of mining digital communication network data to guide targeted outbreak vaccination strategies. We compare our targeted results to both random immunization (RI) (which we predict would yield poor outcomes) and a theoretically near-optimal colocation strategy (CS) [5], whereby individuals in closest actual physical proximity to infected individuals are somehow identified and targeted for vaccine administration. We will henceforth refer to CS as optimal, based on previous results by Smieszek & Salathé [5], indicating that this strategy displays equivalent performance to that of an optimal target group found by brute-force optimization. Unfortunately, CS is logistically infeasible in a realistic setting, since public health officials do not have access to the type of physical proximity data collected here. This study therefore explores, for the first time, whether a group of individuals' digital records can be used to robustly approximate characteristics of their physical proximity networks. In particular, we study whether targeted interventions based on these digital networks, allow us to approximate an optimal vaccination strategy, which can only be derived from the physical proximity network.

2. Material and methods

2.1. Data collection

The CN Study collected physical proximity (by recording Bluetooth scans), CDRs, Facebook friendship and Facebook feed data between 2012 and 2014 for 532 students at the Danish Technical University who volunteered to participate in the study [23]. Data collection was performed using Nexus smartphones with a pre-installed data collector application, which were handed out to students, with subsequent data collection on multiple channels: location, Wi-Fi scans, Facebook feed, CDRs and Bluetooth scans with a temporal resolution of 5 min. The original study was based on data from 1000 smartphones, but here we consider data from the 532 participants with a data quality of at least 60% in the period of interest (based on availability of proximity data; see electronic supplementary material, §S1 for details on data quality). Results reported in this paper correspond to the period of February 2014, which is located in the beginning of the students' second semester and is representative of typical contact patterns (no exams, vacations, etc.). See electronic supplementary material, §S1 for the details of data collection and data filtering.

2.2. Contact and communication networks

We constructed three networks from the data collected during the CN Study: physical proximity networks, cellphone calls and Facebook interactions. Bluetooth scans were used to construct the temporal proximity networks in two ways: the scan list data provided all interactions in a full-range (up to 10–15 m) that are the basis for the simulations on full-range disease spread (we refer to this network as the full-range proximity network). By restricting contacts to signal strengths of RSSI >−75 dBm, the short-range network (range up to 1 m) was obtained (short-range proximity network) [26]. The full-range and short-range networks provide rough approximations for airborne (e.g. measles) and droplet (e.g. influenza) modes of pathogen transmission, respectively [27–29]. It should be noted that the threshold of −75 dBm is highly conservative in order to reduce the likelihood of observing false positives, therefore the typical distance between pairs of individuals in the short-range network is below 1 m. Each link represents at least one observation of a contact between two individuals within a 5 min time bin. In other words, if there is a link in any 5 min bin throughout the period of interest, we add a 5 min link to the simulation extending an (possibly shorter) interaction to 5 min. The temporal resolution of 5 min has been shown to capture the key dynamics of person-to-person networks [18,30]. We stress that while sensor-based proximity networks are a highly useful model to assess the impact of immunizations strategies, they suffer from important limitations [31–33]; see Discussion for details. Digital communication networks were constructed separately for CDR and records of Facebook activity. These networks describe the communication between the participants via phone calls or interactions on Facebook, respectively, and were aggregated over the period of interest, resulting in undirected static graphs (i.e. not recording who called whom). Properties of all networks are illustrated in figure 1.

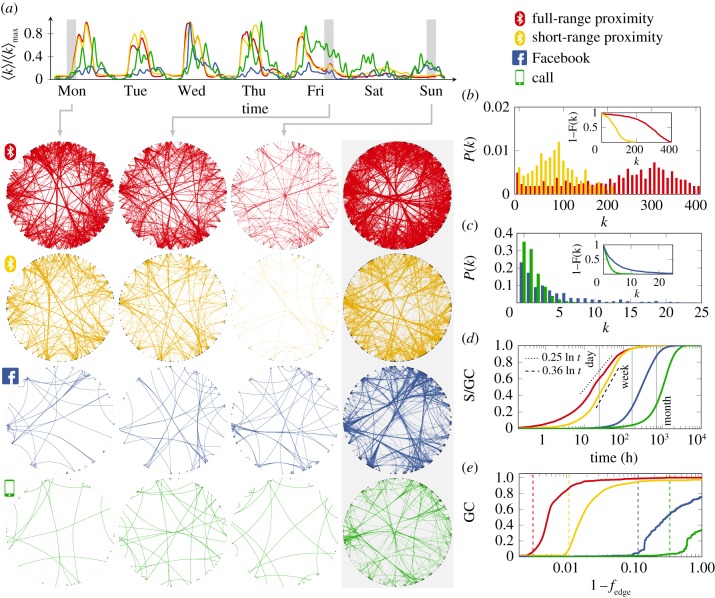
Figure 1.

Characteristics of the person-to-person and communication networks. (a) Average degree (〈k〉) of the networks, normalized by the maximum of each trend. Curves show weekly trends averaged over four months. Snapshots correspond to 4 h aggregated networks; last column shows the entire networks. Individuals belonging to the same communities are grouped together. (b) Degree distribution of the person-to-person networks; inset shows the cumulative distribution. (c) Degree distribution of the communication networks; inset shows the cumulative distribution. (d) Fraction of the giant component (S) reached in an invasive percolation process. Black dashed lines are guidance for the slopes. (e) Size of the giant component (GC) after the removal of f_edge fraction of the strongest links. Dashed lines indicate the percolation threshold of the configuration model with the same average number of first and second neighbours.

2.3. Epidemiological model

After assessing a variety of network metrics, we chose to use closeness centrality (i.e. the average distance of a node to all other nodes following contacts in the network) as the criterion for targeting vaccination (see Network Measures for definitions and electronic supplementary material, §S1.3 and §S4.1 for more details on the various selection methods). As we are interested in the dynamics of a single unfolding epidemic event, we focus on epidemics without an endemic state. Index cases are chosen randomly with uniform distribution over the initially susceptible population (those not vaccinated). All data are the result of the statistics calculated over an ensemble of at least 1000 simulations with varying initial conditions, that is, a randomly chosen index case population. To evaluate the efficacy of vaccination focusing on specific target groups, we measure the relative outbreak size during susceptible–infectious–recovered (SIR) epidemics simulated on both the short- and full-range proximity networks. The relative outbreak size is the number of infected individuals divided by the size of the initial susceptible population, and therefore accounts only for the network effect (see electronic supplementary material for details). In our model, vaccination is assumed to provide full immunity with no side effects and we study the extent to which vaccination reduces the final outbreak size. Epidemic parameters were chosen to be consistent with expected infectious periods (3–4 days) and basic reproduction numbers (2 < R₀ < 3) of real-world infectious diseases such as influenza [34]. We simulated the dynamics of the short- and full-range diseases using a classic form of the SIR model with infection probability β, and average infectious period T. This model is intentionally simplistic, intended to illustrate the structural effects of vaccination in terms of a full-range versus a short-range transmission, rather than emulate a specific disease. The probability of infection per contact event and expected infectious period at each time step are β^full = 0.002, T^full = 3 days and β^short = 0.01, T^short = 4 days for the full- and short-range proximity networks, respectively. The infection probabilities above correspond to physical rates of infection of β^full_phys = 0.717 day⁻¹ and β^short_phys = 0.591 day⁻¹, and the basic reproduction numbers of R^full₀ = 2.151 and R^short₀ = 2.364, which is within the range of R₀ for influenza [7]. More details on the parameter adjustment, analysis and the behaviour of SIR dynamics on the proximity networks are presented in electronic supplementary material, §S2.

2.4. Network measures

We use three basic network properties to summarize the structure of the different networks: the average number of contacts (average degree), average fraction of connected neighbours (average clustering coefficient) and the average number of steps between all pairs of nodes (average path length). Target groups of size n are obtained from the digital communication networks by ranking individuals in the aggregated graphs by their closeness centrality, defined by

2.1

where N is the number of nodes in the graph and d_ij denotes the distance between nodes i and j, i.e. the lowest number of steps to reach node j from node i. If the graph is not connected, we set d_ij = N for nodes that are separated. After ranking individuals according to C_C, we select the ones with the highest centrality to obtain a group of desired size. In the case of colocation-based target groups, individuals are ranked based on their total time spent in the proximity of others, that is

2.2

where γ_ijt = 1 if participants i and j have been in close proximity at time t, and zero otherwise. Ranking all members by their weight, we select the ones with the largest value to include in the target groups, following the strategy of Smieszek & Salathé [5]. Strategies based on other centrality measures as well as the details of the selection are discussed in more details in electronic supplementary material, §S1.3 and §S4.

Vaccination efficiency based on communication network target groups is compared to immunization strategies based on RI and a near-optimal CS set of targets. During random selection, a number of individuals are chosen randomly from the population, providing a lower bound for intervention performance; conversely, colocation target groups include individuals with the highest fraction of time spent in proximity of others. Colocation-based target groups establish an approximate upper bound for intervention performance [5]. They rely on full knowledge of the person-to-person proximity network topology, but are not strictly optimal, as they do not consider temporal dynamics.

3. Results

Basic structural characteristics of the static aggregated networks are shown in table 1 and figure 1. The figure shows the average of 16 weeks of data, whereas each circular network (figure 1b) corresponds to an aggregate of 4 h sampled from the first week. Statistics (figure 1c–f) are based on four months of data. While activity in all four networks (full- and short-range proximity, Facebook and call networks) follows distinct daily schedules and rhythms, digital channels show strong bursts of activity outside of work periods: lunch breaks, evenings and weekends (figure 1a). Individuals that are highly connected are drawn next to each other in the layout (dense group of nodes in the plot). Note that some of the links between these densely connected parts of the population are represented by all channels, whereas some communication is only present in the cyber (telephone and online) communication networks. Both short-and full-range networks of physical proximity feature more than 10-fold higher edge density compared to these cyber networks (figure 1b,c, and reflected in the reciprocal relationship between average degree k and average path length l of these networks listed in table 1); this means, colloquially, that the study subjects had more contact via physical interactions and they spent more time with their friends in real life than they did electronically. The degree distributions of the person-to-person networks are consistent with an approximate normal distribution, whereas those of the communication networks follow a power-law distribution, supported by both the Akaike information criterion and Kolmogorov–Smirnov goodness-of-fit-based model selection (confirming earlier published findings on proximity networks) [18,23].

Table 1.

Static properties of the person-to-person and digital communication networks. Basic network characteristics are reported for the static aggregated networks: number of diads (E), average degree (〈k〉), average clustering (C) and average path length (ℓ). For definitions, see Material and methods.

network	E	〈k〉	C	ℓ
full-range proximity	69 055	259.6	0.644	1.53
short-range proximity	20 690	77.78	0.356	1.91
Facebook	1 261	4.741	0.150	3.87
call	354	1.331	0.102	7.03

The proximity networks contain a large number of links (of the order of 10⁵–10⁶ across the observation period), revealing a highly dynamic set of real-world physical contacts, in contrast with the relatively sparser corresponding cyber networks. Figure 1d shows how these differences are reflected in the time respecting network connectivity, that is, when the temporality of the links is taken into consideration. The majority of nodes in the physical networks can be reached in a relatively short time—over 40% in a day and over 95% in under a week—in contrast with the digital networks which require more than a month to be fully explored, as quantified by an invasion percolation process with transmission probability 1, i.e. a process that propagates from node to node across every edge of the network without fail. Curves show the average of 1000 realizations over random initial conditions. When compared with the full-range network, the short-range network includes only the most frequent contacts, as suggested by the slope of the invasion curve: after a transient delay in the invasion level (approx. 10 h), a majority of the giant components in the short-range network can be explored in a shorter time, meaning that most of the links describe frequent contacts in that network (black dashed lines are included to highlight the slopes of the short- and full-range contact networks). The robustness of the aggregated networks is illustrated by the change in the size of their giant component (i.e. the largest connected component in a graph) after the removal of a random set of links, as shown in figure 1e. The giant component is the largest connected set of nodes in the network. An invasion curve represents the number of nodes that are infected during an invasion process, divided by the size of the giant component. An invasion process is a susceptible–infected model with an infection rate of 1.

Figure 2a depicts the median infection time restricted to the target vaccination groups (i.e. individuals selected on the basis of their closeness centrality within the digital communication networks, hereafter referred to as the ‘cyber-directed vaccination’ group) compared to randomly selected (RI) and colocation-based strategy (CS) vaccination groups. All curves are the median of 10 000 simulations. As a measure of performance, we use corrected time of infection [5]. The corrected time of infection is defined as τ_i = t_i/p_i, where t_i is the average time of infection and p_i is the probability of infection for user i. The correction by the probability of infection ensures that individuals of high vulnerability (those who are more exposed to the disease) are weighted higher in the monitoring scenario where the goal is to detect the outbreak at the earliest possible time with high probability. On average, individuals selected based solely on the basis of their digital records become infected significantly earlier (24% and 18% earlier than the population average, corresponding to 3 and 2 days) for both short- and full-range networks, results that are only 14% and 19% worse on average than the hypothetically optimal CS, respectively. As shown in electronic supplementary material, §S3, these hypothetical gold-standard colocation-based groups also become infected significantly earlier [5,10]. Also note that—in contrast with the full-range network—for the short-range interactions, the corrected time among the cyber-directed target individuals does not differ significantly from the optimal time.

Figure 2.

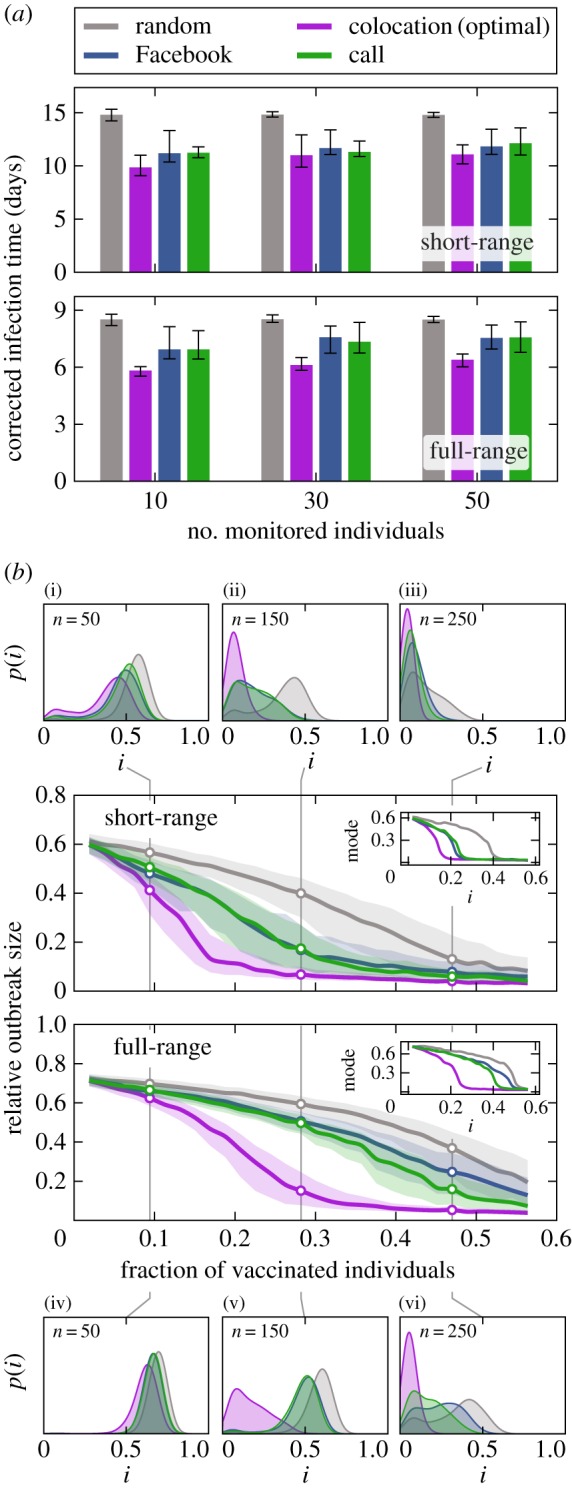
Vaccination effectiveness and outbreak dynamics. (a) Median corrected time of infection among members of the social target groups compared to random (grey) and optimal (purple) groups. Error bands denote lower and upper quartiles. (b) Relative outbreak size under different immunization strategies for diseases with short-range (top) and full-range (bottom) transmission. Error bands mark the lower and upper quartiles. Insets show the mode of the distributions over all realizations. Outbreak size distributions p(i) are shown for target groups of 50, 150 and 250 individuals; in the case of short range in subfigures (i)–(iii) and for full range in subfigures (iv)–(vi). The size of the target groups is indicated for each distribution.

To assess the efficacy of cyber-directed vaccination, we measured the relative outbreak size in the presence of the immunized target group; that is, the total number of infections (I_∞) divided by the initial number of susceptible individuals (S₀): i_rel = I_∞/S₀, excluding the vaccinated subpopulation from the calculation, and thus measuring only the network effect. In figure 2b, the median relative outbreak sizes are plotted against the fraction of the population immunized. Results are calculated over 1000 simulations with minimum outbreak sizes of 5% among the initial susceptible population. The hypothetical optimal colocation vaccination strategy (CS) reduces outbreak size by more than 80% after the immunization of 20% and 30% of the network in short- and full-range transmission, respectively (relative to the unvaccinated population). Using digital networks to identify targets for the proposed cyber-directed vaccination strategy, achieving a similar 80% outbreak size reduction would require vaccinating 32% and 50% of the network in short- and full-range transmission, respectively. For diseases spreading via short-range interactions, cyber-based strategies are effective and outperform RI even for small target groups, approaching the performance of the CS once more than 20% of the population has been vaccinated. If the disease transmission occurs on the full-range person-to-person network, however, cyber-directed vaccination strategies do not significantly outperform the RI strategy. This effect is more pronounced in the small target group size regime (less than 20% of the population). Figure 2b reveals an inherent difference between the fraction of immunized individuals needed to reach the same reduction of outbreak size in the short- and full-range networks, respectively. The effect of vaccination is generally weaker in the highly connected full-range network. Insets show the mode of the distributions over all realizations, indicating a clear separation of the strategies, and a higher efficacy of cyber-directed vaccination in the case of short-range interactions. At low levels of immunization f_v < 0.1 (where f_v denotes the vaccinated fraction of the population) (subplots (i) and (iv) in figure 2b), the effect of vaccination is low, due to the high density of edges in both person-to-person proximity networks. At high levels of immunization (figure 2b subplots (iii) and (vi)), with more than half of the population vaccinated, the digital communication network target groups contain the majority of socially active individuals, resulting in the cyber-directed vaccination strategy approximating the optimal CS also for full-range transmission. In the intermediate range 0.1 < f_v < 0.5 (subplots (ii) and (v) in figure 2b), cyber-directed vaccination is significantly more effective than random vaccination and approaches the efficiency of the optimal strategy in the case of short-range transmission. The intuitive reason behind this difference between the short- and full-range networks is that the structure of the full-range proximity network is strongly influenced by many random encounters, not captured by the corresponding (but presumably intentional) digital networks (see electronic supplementary material, §S4.1 for an elaborated analysis of vaccination in the proximity networks). The observations above are further supported by a Mann–Whitney test calculated over the distribution of relative outbreak sizes for different strategies. The tests show a significantly higher similarity between cyber-directed and optimal strategies in the case of short-range interactions (see electronic supplementary material for details).

The performance of cyber-directed vaccination is robust with respect to different centralities used for selection of the target groups (degree, k-coreness, betweenness) and variation in how communication channels are constructed (using calls and text messages). In electronic supplementary material, §S4.1, we investigate the robustness of the results in detail with respect to different strategies.

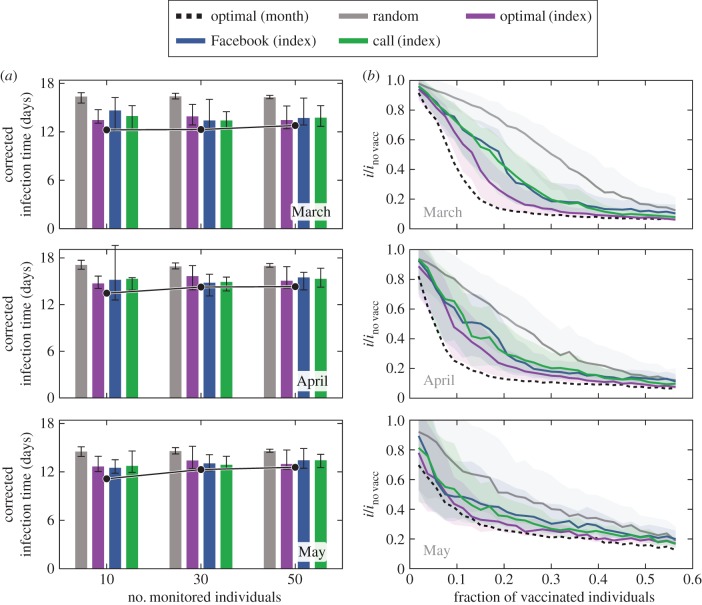
Regardless of the target selection strategy, implementing targeted vaccination assumes network stability (i.e. that targets identified before an outbreak takes place remain critical to disease propagation during the vaccination phase). To analyse the trade-off between performance of targeted intervention and the time gap between identification and intervention, we fixed the period that forms the basis of our target individual selection (February, index month) and calculated monitoring and immunization performance for outbreaks in subsequent months (March, April and May, outbreak months), as shown in figure 3. We compared the performance of cyber-directed strategies based on the index month to RI and two types of CS: colocation based on proximity data in the index month and on proximity data in the outbreak month. Cyber-based target groups show significantly lower infection time relative to random monitoring in these subsequent months, although target groups based on the index month do not perform as well as the optimal groups calculated in the outbreak months (figure 3a) due to the small changes in the social structure of the population. Immunizing members of the index month, target groups outperform random vaccination in all three outbreak months, as seen in figure 3b. We start by estimating CS target groups based on February data. Now, we consider the fraction of vaccinated individuals needed to achieve an 80% decrease in the number of infected, relative to the outbreak size in the unvaccinated scenarios in subsequent months. We find that for both March and April, we require 17% immunization, versus 56% in May. Analogously, strategies based on the cyber networks, which use information only from the index month of February, require immunization levels of 30%, 35% and 56% for March, April and May, respectively, to achieve the same 80% decrease. The high overlap between the error bands (lower and upper quartiles) between optimal and cyber-directed vaccination, indicate the statistical similarity of the two strategies in March. As the index month's contact patterns become more and more outdated and less informative of the actual month of the simulation (April and May), cyber-directed vaccination curves separate less from the random vaccination, underscoring the decreasing predictive power of data from February.

Figure 3.

Robustness of digitally identified target group effectiveness. (a) Median infection time as a measure for monitoring effectiveness in consecutive months: social (green and blue for call and Facebook-based communication groups), CS based on February (optimal index, purple), RI (grey) and CS based on the same month data (optimal month, black). Error bars correspond to lower and upper quartiles. (b) Performance of cyber-directed vaccination based on the index month applied in consecutive months. Shown are the relative outbreak size for each vaccination strategy (i), divided by the outbreak size in the same months in the absence of vaccination (i_no vacc). Communication network-based vaccination is compared against RI (grey), CS in index month (purple) and CS in the corresponding month (dashed black). Curves represent median values over 1000 simulations; error bands denote the lower and upper quartiles.

4. Discussion

If the goal of an optimized targeted vaccination strategy is to disrupt forward transmission of disease, then immunizing individuals with the greatest likelihood of infecting the largest number of their network neighbours is critical. Specifically, a good candidate for immunization (when focusing on a single age group) should be highly exposed to the disease and simultaneously exhibit high potential to transmit the infection. Using data from multiple layers of social interactions captured in the CN Study, we show that the digital communication (cyber) networks can be used to predict which individuals are central to epidemic spread based on close person-to-person proximity, yielding prime candidates for outbreak-limiting immunization. The performance of targeted vaccination based on cyber network structure, however, is strongly affected by the nature of pathogen transmission, displaying high efficacy in the case of short-range transmission, but less utility when an infection spreads via full-range contacts. Practically, this means that diseases that require very close encounters (similar to droplet spreading) can be effectively contained by network-directed targeted vaccination, whereas in the case of full-range transmissions (closer to airborne diseases), targeting individuals using communication networks will perform more poorly in containing an outbreak.

This result arises from the inherent structure of short-range physical contacts: close contacts in the person-to-person network frequently correspond to social ties and therefore communication networks contain more relevant information about the structure of the short-range network. Assuming that the online/offline behaviour observed in this student population is representative of the full population, our findings suggest that, when considering real-world diseases, online social networks and CDR data can serve as a valuable resource for epidemic intervention. Regarding one of the most basic differences between the above transmission types (their physical range of infection), public health officials trying to implement innovative immunization strategies may benefit from cyber network data in the case of droplet diseases, but not during airborne infections, as we expect real-world airborne transmission networks to have even more connections between socially unconnected individuals than the full-range network examined here due to the characteristics of airborne diseases (the ability to suspend in rooms, transmission via contact with inanimate surfaces, etc.).

The communication and social networks analysed in this study have varying degrees of resilience in the face of disruption (a detailed analysis of the network characteristics affecting monitoring and vaccination can be found in electronic supplementary material, §S3.2 and S4.2). When removing the f_edge fraction of the links randomly from the network, we found that physical proximity networks break down at a density close to that of the random networks, whereas digital communications become disconnected when a smaller fraction of links are removed. These findings are consistent with previous work: proximity networks are structurally homogeneous with a well-defined average degree, while communication networks are characterized by heterogeneous degree distributions [10,12,18,24,35]. Thus it is critical to reiterate that physical proximity networks which approximate the actual paths supporting the spreading of infectious diseases and communication networks are fundamentally different both in a structural and dynamical sense, e.g. how infectious diseases spread through these networks. Fortunately, it does not follow that strategies gleaned from examining communication networks are incapable of informing real-world practice; on the contrary, we find that control strategies based on cyber networks are robust with respect to temporal changes—that is, that target groups can be identified months before an outbreak and still provide a significant improvement over interventions based on randomly selected groups, provided that a disease spreads via short-range transmission (see electronic supplementary material, §S5 for more detail).

4.1. Limitations

It is important to acknowledge that our model of epidemic processes on person-to-person proximity networks is a major simplification of the underlying biological processes, and yet it serves our aim in this paper. The detailed transmission of droplet and airborne diseases is not fully captured by reciprocal Bluetooth measurements, e.g. transmission of biological pathogens is not merely characterized by distance but is also affected by many other environmental characteristics and individual behaviour. Droplet transmission requires individuals to face each other in close proximity [27,36], while airborne pathogens can stay suspended in the air or settle on surfaces, significantly increasing the opportunity for infection [36]. However, these characteristics amplify the differences between person-to-person networks by effectively removing superfluous links from the short-range network and adding additional noise to the full-range network. Thus, the efficacy of using digital communication channels in targeted monitoring and vaccination can be expected to be even higher for a true droplet network and closer to random for airborne transmission.

Our study is carried out in a student population. These individuals may have different contact patterns than the general population, including older adults or children [18]. In particular, the student population is likely to be the one for which the communication networks most reflect the characteristics of real face-to-face networks, potentially in terms of connected individuals and in terms of time lag between the digital connection and real face-to-face contacts [37]. In this sense, we acknowledge that the participants in the study are not necessarily representative of ‘the public’; they represent a single specific population, a fact known to result in an underestimation of epidemic risk [38]. Nevertheless, it should be noted that our results rely solely on the comparisons within this same population, and the structural differences are restricted to that of connectivity. Although it is well known that vital dynamics and ageing (that are not included in our model) have a strong impact on the spreading process [39], in the cohort that forms the basis of the current study, individuals are members of the same age class and therefore we can neglect these effects. Finally, Bluetooth signals are able to pass through walls, which introduces non-physical contacts and unrealistic spreading events in the dataset; however, the fraction of links that can be potentially associated with these cases is, we believe, negligible.

4.2. Conclusion

In this paper, we have taken a first step towards investigating how knowledge of the cyber network structure of a population (in this case consisting of telecommunication and social interaction platforms) can be used to identify target groups for efficient targeted vaccination. Our most notable finding is that, in our modelling framework, relatively subtle differences in the structure of disease transmission mechanisms, formulated here as a dichotomous choice between droplet-like and airborne routes, may have a profound impact on final epidemic size when using cyber networks as a basis for targeted vaccination. The corollary of this is that for diseases with short-range transmission modes, we find that using cyber-based targeting strategies can dramatically decrease final outbreak size even when vaccine coverage in the targeted population is realistically low (around 20%). As digital communication data of the types modelled here may allow for early detection and containment of infectious outbreaks in densely connected populations (i.e., in schools, universities, workplaces and neighbourhoods), our work also supports increased collaboration between practitioners in public health and operators of social networks and telecommunication companies.

Ethics

Prior to the study, all participating students were informed of the data collection method and the research goals. Data collection, anonymization and storage were approved by the Danish Data Protection Agency, and comply with both local and EU regulations. Data are from Copenhagen Networks study (http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0095978). The entire Copenhagen Networks Study, including the current study, has been approved by the Danish Data Protection Agency (DDPA) Journal no. 2012-41-0664. The DDPA is the relevant legal entity in Denmark.

Data accessibility

The full dataset contains personally identifiable telecommunication networks, Facebook networks. According to the Act on Processing of Personal Data, such data cannot be made available in the public domain. We confirm that the data are available upon request to all interested researchers under conditions stipulated by the DDPA. Data inquiries should be addressed to the Social Fabric steering committee (http://sodas.ku.dk), to be reached at sljo@dtu.dk or ddl@econ.ku.dk.

Authors' contributions

E.M. and A.S. carried out the statistical analyses, and participated in the design of the study and drafted the manuscript. S.L., A.S.P. and N.H. conceived of, designed and coordinated the study, and helped draft the manuscript. All the authors gave their final approval for publication.

Competing interests

The authors declare that they have no competing financial interests.

Funding

This work was supported by the Villum Foundation (Young Investigator Programme ‘High Resolution Networks’ grant (to S.L.)), The Danish Council for Independent Research (Sapere Aude Programme ‘Micro dynamics of influence in social systems’) and the University of Copenhagen (UCPH Excellence Programme for Interdisciplinary Research Social Fabric grant). N.H. was supported by the Cornell Institute for Disease and Disaster Preparedness and New York-Presbyterian Hospital. Funders had no role in the design of the study and collection, analysis and interpretation of data, nor did they have a role in writing the manuscript.