Approximate Bayesian Computation for Spatial SEIR(S) Epidemic Models

Abstract

Approximate Bayesian Computation (ABC) provides an attractive approach to estimation in complex Bayesian inferential problems for which evaluation of the kernel of the posterior distribution is impossible or computationally expensive. These highly parallelizable techniques have been successfully applied to many fields, particularly in cases where more traditional approaches such as Markov chain Monte Carlo (MCMC) are impractical. In this work, we demonstrate the application of approximate Bayesian inference to spatially heterogeneous Susceptible-Exposed-Infectious-Removed (SEIR) stochastic epidemic models. These models have a tractable posterior distribution, however MCMC techniques nevertheless become computationally infeasible for moderately sized problems. We discuss the practical implementation of these techniques via the open source ABSEIR package for R. The performance of ABC relative to traditional MCMC methods in a small problem is explored under simulation, as well as in the spatially heterogeneous context of the 2014 epidemic of Chikungunya in the Americas.

1. Introduction

The study of epidemics is complicated by the fact that real human populations exhibit complex structure and interact in subtle ways over both space and time. Nevertheless, in an increasingly globalized world, the ability to model pathogen outbreaks, predict ongoing spread, and evaluate interventions represents crucial abilities of public health practitioners. In this work we present a class of algorithms and statistical framework ideally suited to meet this need, in addition to a discussion of our open source software, AB-SEIR, which implements them.

1.1. Approximate Bayesian Computation

Approximate Bayesian Computing is generally attributed to the work of Rubin (1980), which concerns interpretation and implementation of practical modeling techniques for applied Bayesian statisticians. Among other contributions, this work introduced one of the most commonly used algorithmic approaches to ABC: the rejection algorithm. This procedure provides an intuitive introduction to approximate Bayesian computing techniques. We therefore begin our approach to the subject by introducing the requisite notation, and describing the basic ABC rejection algorithm.

Define a p × 1 parameter vector θ with p dimensional parameter space Θ and prior distribution π_Θ(θ). Further define an N × 1 vector of observed data, y, with a likelihood or data generating distribution denoted by f_Y(y|θ). Finally, define a distance function (such as the Euclidean distance) between appropriately sized vectors x and y: ρ(y, x). As a Bayesian sampling technique, the goal of ABC is to make inference about the posterior distribution, f_Θ(θ|Y) ∝ f_Y(y|θ)π_Θ(θ).

The general pattern of rejection sampling ABC is quite simple. We first generate repeated samples θ_i from the prior distribution for θ. Each of these samples, indexed by i, is in turn used to generate a replicate data set x_i from the likelihood. Parameters which generate replicate data sets which are sufficiently ‘close’ to the observed data y, according to the distance function ρ and a tolerance ε, are retained, while the rest are discarded. Details of this procedure are given in Algorithm 1.

Note that this approach does not require the user to evaluate the potentially expensive or unavailable likelihood function, but does require the ability to draw samples from it (Rubin, 1980; Beaumont, 2010). In its original formulation, the tolerance, ε, was taken to be zero (Rubin, 1980). The key insight of the rejection approach is clear in this context: accepting only parameters which produce replicate data identical to the observed response is equivalent to conditioning on that observed data. The distribution of parameter values conditional on the observed data is the posterior distribution: our inferential target. The most commonly applied version of the algorithm, however, generally includes the aforementioned nonzero tolerance, and employs a distance measure which depends only on a set of summary statistics of x and y, thus rendering the inference ‘approximate’.

Algorithm 1.

ABC Rejection Algorithm

Require: Define a tolerance ε > 0, and let ‘←’ denote assignment
1:	for i ← 1 to n do
2:	d ← ∞
3:	while d > ε do
4:	draw θi ~ π(Θ)
5:	draw xi ~ fY(y|θ)i
6:	d ← ρ(y, xi)

1.2. Sequential Algorithms

Numerous improvements and extensions have been proposed to this basic algorithm, generally focusing on obtaining increased sampling efficiency. In particular, many authors note that sampling performance can be extremely poor in situations where prior distributions on the parameter vector θ are diffuse with respect to the posterior distribution, especially for high dimensional problems (Beaumont et al., 2009; Beaumont, 2010; Blum and François, 2010; Del Moral et al., 2012; Neal and Huang, 2015; Sisson et al., 2007). Sun et al. (2015) apply several such improvements in the context of non-spatial deterministic and stochastic compartmental epidemic models. Here we emphasize a single algorithm, though the software described in later sections is the focus of ongoing research in this area. We implement a slightly modified version of the sequential Monte Carlo algorithm proposed by Beaumont et al. (2009), which we find both intuitive and effective. As with the rejection algorithm, Beaumont et al. (2009) begin by drawing proposed parameters from their prior distribution. Instead of repeating this step, however, subsequent sets of parameters are re-sampled and then perturbed from previously accepted values according to a set of weights. Data is then simulated as before, and parameters are accepted according to a decreasing sequence of ε values. Weights are updated using an importance sampling step to preserve the target posterior distribution. This approach can provide dramatic efficiency gains over the rejection algorithm.

Our adaptation of this algorithm introduces four primary modifications. First, we employ a batch size, N ≥ n, over which simulations and distance evaluations may be conducted in parallel with no need for communication between nodes. This is important, because even with the sequential parameter updates, acceptances can become quite rare as ε decreases. Second, we permit the first iteration to employ a larger batch size than subsequent sequential step. This ensures that the algorithm starts at a practical ε, rather than spending too much time at unnecessarily permissive tolerances. Third, we implement a specific ε schedule: ε_t+1 = cε_t, where 0 < c ≤ 1. This obviates the need for investigators to manually specify a sequence of ε values, a process which depends on the scale of observed values as well as the chosen set of prior distributions. Finally, we generalize the perturbation kernel to permit a multivariate Gaussian distribution. For problems which exhibit correlation among the parameters, we have found the multivariate approach can be more efficient.

These modifications imply two potential modes of convergence, beyond specifying a required terminating ε value. First, the investigator may specify a desired number of sampling epochs. Second, users may choose to specify a maximum number of batches of size N which will execute for a particular value of ε before the sampler will simply return the current sample of n parameter values. This latter mode enables the algorithm to adapt the termination of the sequence of ε values to the difficulty of sampling by specifying a termination acceptance rate. This acceptance rate is generally chosen based on the computational resources available. Background on the development of sequential Monte Carlo ABC is available in Beaumont (2010).

1.3. Model Selection in SMC-ABC

Beyond the ability to fit models which would be otherwise computationally infeasible, ABC techniques provide a natural way to compare the relative evidence for different models. Informally, sets of parameters and models which produce better simulated data are more probable than others. This can be used to compare a set of candidate models, and in fact the ratio of acceptance rates between two models is an estimate of the Bayes Factor comparing the two (Beaumont, 2010).

In the SMC-ABC context, however, such comparisons are a bit more problematic. Care must be taken to employ comparable instantiations of the algorithm. For example, comparison between non-converged and converged algorithm runs is obviously not reasonable, because the acceptance rates are not comparable.

With this in mind, we assume that the two models to be compared, ${ℳ}_1$ and ${ℳ}_2$ with prior probabilities π₁ and π₂, were either run to the same terminating minimum acceptance rate (i.e., arbitrarily large T, identical n, N), or were forced to run until the same ε threshold was reached. In this way, we ensure that the algorithm has the opportunity to overcome diffuse priors, while allowing users to avoid the potentially infeasible task of running a poor model to the same ε value as a reasonable one. Assuming that each of the the sequences of distributions has converged, we may employ the ratio of acceptance rates at the next iteration to estimate the Bayes Factor comparing the two models. Other model comparison criteria, such as the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002), are often used in a Bayesian context. Models fit with ABC, however, do not generally rely on the form of the likelihood, and are therefore more naturally compared using Bayes Factors.

1.4. Spatial SEIR(S) Models

Compartmental epidemic models take many forms, and can be implemented using deterministic systems of ordinary and partial differential equations or stochastic difference equations. The approximate computational approach described here is applicable to general discrete time stochastic compartmental models, specifically in a Bayesian context. We focus on the important subset of compartmental epidemic models known as stochastic spatial SEIR models. A brief introduction to these techniques is provided here, and a more complete discussion of the spatial SEIR model class is available in Brown et al. (2015). Additional information on more general compartmental processes is available in the extensive compartmental modeling literature (Cook et al., 2007; Deardon et al., 2010; Hooten et al., 2011; Jewell et al., 2009; Kermack and McKendrick, 1927). More recently, King et al. (2016) have considered a much more general class of Partially Observed Markov Processes (POMP), which can considered to encompass spatial SEIR models. Their associated software implements a number of algorithmic approaches to inference in this setting, including ABC-SMC techniques. In contrast, our software is specific to spatial SEIR and SEIRS models, and is therefore optimized for the specification and fitting of these models in particular.

Stochastic spatial SEIR models track individuals in structured populations through four disease states: susceptible, exposed, infectious, and removed. Susceptible individuals are capable of contracting a particular pathogen. Those who have done so are considered to have transitioned to the exposed category. Exposed individuals transition to the infectious compartment when they become capable of transmitting the infection, and subsequently to the removed compartment once the infection has run its course. Finally, for certain pathogens, it makes sense to assume that individuals may return to the susceptible population after immunity wanes. Of course, numerous variations of this framework exist in the literature, including models which separate the removed population by mortality/immunity; these choices must ultimately reflect the nature of a particular pathogen of interest.

These compartments and associated transitions are defined over discrete time, t_i : i = 1, …, T, and discrete space: s_j : j = 1, …, n. Epidemic state information is therefore conveniently arranged into a set of T by n matrices: S, E, I, R, S^∗, E^∗, I^∗, and R^∗. In this notation, the first four matrices capture compartment membership counts, and the second four (with asterisks) capture transitions into each compartment. For example, [S]_ij denotes the number of susceptible individuals in location s_j at time t_i, and [E^∗]_ij is the number of such individuals in the process of transitioning to the exposed compartment at the same time/location. This approach gives rise to the intuitive set of difference equations and chain binomial structure given in (1).

$$\begin{array}{ll}{\mathbf{S}}_{i+1}={\mathbf{S}}_i-{\mathbf{E}}_i^{\ast }+{\mathbf{S}}_i^{\ast }\hfill & {\mathbf{S}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{R}}_{ij},{\pi }_{ij}^{\left(RS\right)}\right)\hfill \\ {\mathbf{E}}_{i+1}={\mathbf{E}}_i-{\mathbf{I}}_i^{\ast }+{\mathbf{E}}_i^{\ast }\hfill & {\mathbf{E}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{S}}_{ij},{\pi }_{ij}^{\left(SE\right)}\right)\hfill \\ {\mathbf{I}}_{i+1}={\mathbf{I}}_i-{\mathbf{R}}_i^{\ast }+{\mathbf{I}}_i^{\ast }\hfill & {\mathbf{I}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{E}}_{ij},{\pi }_j^{\left(EI\right)}\right)\hfill \\ {\mathbf{R}}_{i+1}={\mathbf{R}}_i-{\mathbf{S}}_i^{\ast }-{\mathbf{R}}_i^{\ast }\hfill & {\mathbf{R}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{I}}_{ij},{\pi }_j^{\left(IR\right)}\right)\hfill \end{array}$$ (1)

The transition probabilities are labeled for the two compartments they link. For example, ${\pi }_{ij}^{\left(SE\right)}$ gives the probability a susceptible individual in location s_j at time t_i will transition to the exposed population. This binomial approach is far from the only option for motivating the transition matrices, but does allow a natural and flexible hierarchical specification of the distribution of such quantities.

We consider the E to I transition, which captures the latent period of a pathogen, and the I to R transition, which captures the infectious duration, to be primarily properties of the pathogen, and therefore unlikely to vary substantially over space. We currently provide two models for these quantities, the exponential compartment membership model of Lekone and Finkenstädt (2006), and the path specific SEIR (PS-SEIR) structure of Porter and Oleson (2013, 2015).

The exponential model, presented in Equation 2, allows for irregularly spaced time points via the inclusion of a temporal offset (h_i), but is otherwise rather inflexible. This specification corresponds to an exponentially or geometrically distributed compartment membership time, on the continuous and discrete timescale respectively (Brown et al., 2015). These probability distributions are certainly mathematically convenient, but the implication that remaining compartment membership periods do not depend on the amount of time already spent in a disease state is almost never true in practice. Nevertheless the use of constant transition probabilities often provides a reasonable fit, and provides computational benefits.

$${\pi }_i^{\left(EI\right)}=1-\text{exp}\left(-h_i{\gamma }_{\left(EI\right)}\right)$$

$${\pi }_i^{\left(IR\right)}=1-\text{exp}\left(-h_i{\gamma }_{\left(IR\right)}\right)$$ (2)

The PS SEIR structure (Porter and Oleson, 2013, 2015) allows for non-exponential latent and infectious times to be incorporated into a SEIR model with population level mixing. This more general transition model is easily adapted to the spatial SEIR framework described here by modifications to the latent and infectious period specifications. Consider defining E as a T by n by m₁ array, where m₁ is the maximum time an individual may remain in a latent state, and consider defining I as a T by n by m₂ array, where m₂ is the maximum time an individual may remain in an infectious state. We subscript our additional dimension by l, where l = 1, … , m₁ for E and l = 1, …, m₂ for I. Next, in (1), we replace

$${\mathbf{E}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{S}}_{ij},{\pi }_{ij}^{\left(SE\right)}\right)$$

$${\mathbf{I}}_{ij}^{\ast }\sim \text{binom}\left({\mathbf{E}}_{ij},{\pi }_j^{\left(EI\right)}\right)$$

with

$${\mathbf{E}}_{ij}^{\ast }\sim {\displaystyle \sum _{l=1}^{m_1}\text{binom}\left({\mathbf{E}}_{\mathit{ijl}},P\left(Z_1\le l+h_i|Z_1>l\right)\right)}$$

$${\mathbf{I}}_{ij}^{\ast }\sim {\displaystyle \sum _{l=1}^{m_2}\text{binom}\left({\mathbf{E}}_{\mathit{ijl}},P\left(Z_2\le l+h_i|Z_2>l\right)\right)},$$ (3)

where ${\mathbf{E}}_{ij}^{\ast }$ represents the (i, j) element of the transition matrix obtained by summing the exposure array over l = 1, …, m₁ and ${\mathbf{I}}_{ij}^{\ast }$ is defined similarly for the infectious array.

Those individuals who do not transition from one compartment to the next are handled via the diagonalization process (described in Porter and Oleson, 2013), by which we define

$$X_{\mathit{ijl}}\equiv \text{binom}\left({\mathbf{E}}_{\mathit{ijl}},P\left(Z_1\le l+h_i|Z_1>l\right)\right){\mathbf{E}}_{i+1,j,l+1}={\mathbf{E}}_{\mathit{ijl}}-X_{\mathit{ijl}}$$

$$Y_{\mathit{ijl}}\equiv \text{binom}\left({\mathbf{I}}_{\mathit{ijl}},P\left(Z_2\le l+h_i|Z_2>l\right)\right){\mathbf{I}}_{i+1,j,l+1}={\mathbf{I}}_{\mathit{ijl}}-Y_{\mathit{ijl}}.$$

The success of this technique depends on the judicious selection of Z₁ and Z₂. Wearing et al. (2005) suggests that a gamma distribution may be appropriate for many infectious diseases, while Porter and Oleson (2013) provides evidence that a Weibull distribution may be appropriate for some infectious diseases. ABSEIR allows users to specify arbitrary distributions for latent and infectious periods, allowing users to employ the best available experimental and surveillance based data on these transition processes. In addition to conditioning on these user specified distributions, we also allow users to employ fully parameterized Weibull membership times, with gamma hyperpriors. The software is also readily extensible to other parameterized distributions.

The remaining two transitions present additional important choices for the modeler, for the exposure and reinfection processes may be expected to vary over space and time. To capture the exposure process, we assume that each location has an epidemic intensity which varies throughout the epidemic. To structure this term, each location is associated with a T by p design matrix X_j such that the intensity time series for the location can be calculated as X_j β^SE for the shared parameter vector β^SE. Computationally, we find it convenient to concatenate each of these location specific design matrices row-wise into a single matrix X^SE, and in one step compute the T by n intensity matrix η from the Tn by 1 column vector X^SEβ^SE. The p parameters may be used to incorporate intercepts, demographic effects, intervention summaries, and innumerable other spatiotemporal variables. This provides a rich basis for model fitting and selection.

Before one may compute the final form of the exposure probability, it is necessary to specify the spatial structure of the population under study. As in Brown et al. (2015), we propose to specify such structure using a number of n×n ‘distance’ matrices, {D_z} and associated autocorrelation parameters {ρ_z}. The resulting parametric form is given in Equation 4, and additional discussion and motivation is available in the aforementioned manuscript.

$${\pi }_{ij}^{\left(SE\right)}=1-\text{exp}\left({\left\{-{\eta }_{i.}-{\displaystyle \sum _{z=1}^Z{\rho }_z\left({\mathbf{D}}_z{\eta }_{i.}\right)}\right\}}_j^{h_i}\right)$$ (4)

The ABSEIR software also permits users to specify contact structures which vary over time, and which have a delayed contact effect. This functionality was primarily intended to capture the effects of environmental reservoirs and external influences on contact rates.

The propensity of some pathogens to confer only temporary immunity can be incorporated into the probability of transitioning from the R compartment to the S compartment, a reinfection process. While numerous potential parameterizations of this process exist, we currently consider only the case in which a temporally varying vector of probabilities is shared among all spatial units. We denote this n × l matrix X^(RS), and associate it with l parameters: {β^(RS)}. The vector of reinfection probabilities is then given by ${\pi }_i^{\left(RS\right)}=1-\text{exp}\left(-{\left[{\mathbf{X}}^{\left(\mathbf{R}\mathbf{S}\right)}{\beta }^{\left(\mathbf{R}\mathbf{S}\right)}\right]}_{\mathbf{i}}\right)$

These models generally require the inclusion of informative prior information concerning the duration of compartment membership time. Fortunately, for most infectious diseases there exists high quality information on the duration of these disease states; study of the duration of latent and infectious periods is commonplace. Other parameters are less straightforward to inform based on prior studies. These include spatial autocorrelation terms and linear predictor coefficients which drive the epidemic. While not generally the subject of truly informative priors, we can often place reasonable prior bounds on these terms; extremely large linear predictor coefficient values are improbable, for example, because they have unreasonable implications for epidemic behavior (e.g., the entire population becomes infected very quickly, or the epidemic dies out immediately). This will be explored via example.

1.5. ABC for Spatial SEIR Models

Stochastic spatial SEIR models are ideally suited to approximate Bayesian computation, for while the numerous unobserved compartment values cause the parameter space to grow rapidly in the number of location/time points, relatively few parameters are required to simulate such data. For this reason, ABC can be thought of as a dimension reduction strategy for such models. More formally, we partition the unknown parameters into two components: θ = [β^(SE), β^(RS), γ_(EI), γ_(IR), ρ], and ζ = [S, E, I, R, S^∗, E^∗, I^∗, R^∗]. No matter which compartment, transition matrix, or combination thereof the observed data y relates to, we may simulate it from the conditional distribution P (ζ|θ). The application of ABC to models in this class is thus quite straightforward; the observed data, Y, may be compared to any appropriate compartment, A, using a Euclidean distance metric as described in Equation 5. Missing values at a particular time/location, (t_i, s_j), are dealt with using the indicator function I_obs(i, j), which is equal to one if A_ij is observed.

While the point-wise euclidean distance is far from the only option for comparing simulated epidemics to observed data, it has a number of attractive properties. First, as evident from the included indicator function, such a metric naturally incorporates missing data. Second, this form applies to both cumulative and non-cumulative surveillance counts without modification. Finally, unlike simpler problems where observations are exchangeable, in simulations of spatial SEIR models, there exists a unique simulated value for each location-time. This direct correspondance naturally invites a point-wise norm comparison, of which the Euclidean distance is an example.

$$\sqrt{{\displaystyle \sum _{i=1}^T{\displaystyle \sum _{j=1}^n{I}_{\mathit{obs}}\left(i,j\right){\left(A_{ij}-Y_{ij}\right)}^2}}}$$ (5)

2. Software

The ABSEIR R package provides a user friendly interface for specifying models in the spatial SEIR(S) class. The software implements the aforementioned SMC-ABC algorithm with a variety of tunable parameters, and facilitates numerical and graphical summary of model results. Parallelism between simulations is achieved via the threading capabilities of modern C++. Implementing parallel simulations at the C++ level, as opposed to using process-level parallelism such as that provided by the ‘parallel’ R-pacage (R Core Team, 2013), enables ABSEIR to distribute work between multiple cores with minimal overhead. This is important for SMC-ABC models, because while the work of simulating epidemics dwarfs the rest of the algorithmic computational cost, numerous iterations may still be required. Low level parallelism is particularly beneficial for the ability of software to control how memory is accessed and copied.

Models are specified by constructing a set of model components:

• DataModel: describes the relationship of the observed data to the epidemic quantity of interest

• ExposureModel: captures the exposure covariate structure X^SE and specifies prior parameters for β^SE

• ReinfectionModel: determines whether a model includes a reinfection process, and if so defines X^RS and prior parameters for β^RS

• DistanceModel: defines, for models incorporating more than one spatial location, the set of distance matrices {D_z} and prior distributions for the autocorrelation parameters {ρ_z}

• TransitionPriors: specifies a model for the E to I and I to R transitions using prior transition probabilities and associated effective sample sizes. The software also provides utility functions to assist in the creation of of exponential transition models, arbitrary distribution path-specific models, and fully parameterized Weibull path-specific transition models.

• InitialValues: provides S₀, E₀, I₀, and R₀, vectors of compartment membership counts at the beginning of the study period

• SamplingControl: indicates which algorithm is to be used in fitting the model, as well as values of the requisite tuning parameters

Additional detail, and complete examples, about all of these objects is available via the ABSEIR package documentation and vignettes. Upon creation of the required model components, samples from the posterior are drawn using the SpatialSEIRModel function, which is also documented on-line.

The creation of so many model components may seem cumbersome, but we find that this approach is more natural for this class of complex hierarchical models than calling functions with huge numbers of parameters. Moreover, this compartmentalization greatly facilitates the comparison of competing models, as shared components may simply be reused. An important example of such reuse arises when comparing several candidate models. For example, when evaluating the evidence for an intervention effort, a user may simply create two different ExposureModel objects, with and without the intervention effect. Evidence in favor of the intervention model may subsequently be obtained using an approximate Bayes Factor computed by the compareModels function.

3. Methods

3.1. Simulation Studies

The spatial SEIR(S) model class described here is based on, and is a superset of, that employed in Brown et al. (2015), so the MCMC based libSpatialSEIR library used in that work provides the most natural point of comparison in terms of both in assessing the reasonableness of the approximations employed by ABSEIR as well as the gains in computational efficiency. We therefore begin by comparing the parameter estimates and required runtime for SEIR data simulated over a single spatial unit, based on the analysis of the 1995 outbreak of Ebola in the Democratic Republic of the Congo performed in the aforementioned manuscript as well as in Lekone and Finkenstädt (2006). Simulations run for 150 time points from an initial state with 5,363,499 susceptible population members and 1 infectious member.

Three sets of parameters are each used to generate replicate epidemics to be analyzed, and specific parameter values are given in Table 1. Average epidemic size is modified by varying the exposure process intercept term, ${\beta }_0^{\left(SE\right)}$, which modifies overall epidemic intensity. An intervention term, ${\beta }_1^{\left(SE\right)}$ is associated with a piecewise linear covariate, which is equal to zero up to time point 66, at which point it becomes linear in time. This model assumes that the contribution of the intervention term increases over time, analogous to the specification of Lekone and Finkenstädt (2006). Fifty epidemics are simulated for each of these parameter values, and each is analyzed using both the MCMC based libSpatialSEIR and ABC based ABSEIR libraries.

Table 1.

Single Location SEIR - MCMC Parameter Estimation Performance

	${\beta }_0^{\left(SE\right)}$	${\beta }_1^{\left(SE\right)}$	γ(EI)	γ(IR)
θ1	−1.4	−0.055	5	7
θ2	−1.2	−0.055	5	7
θ3	−1.0	−0.055	5	7

Of course, the exact posterior distribution is generally unavailable for spatial SEIRS models, so we must compare our approximate methods to converged MCMC chains. We examine marginal posterior coverage, interval width, and ‘bias’ when compared to parameter values used to simulate the data for epidemics of several sizes. Importantly,

3.2. Chikungunya

Upon establishing the performance and accuracy of our method and software, we next consider a considerably more complex problem as a demonstrative example: the spread of Chikungunya in the Americas during 2014. Chikungunya is a virus transmitted by mosquitoes and has origins in Africa and Southeast Asia. In recent years, the pathogen has been seen in the Caribbean, the Americas, and southern Europe (Khan et al., 2014; Leparc-Goffart et al., 2014; Dumont and Tchuenche, 2012). The most common symptoms include fever and joint pain, and which can sometimes last for weeks or years (World Health Organization, 2015). The virus is spread by Ades aegypti and Ades albopictus mosquitos, and since 2013 has colonized much of the Caribbean (Leparc-Goffart et al., 2014; World Health Organization, 2015). Local spread has been observed in Florida, and given the geographic range of the insect vectors, many experts continue to worry about increased spread throughout the southern United States (Mowatt and Jackson, 2014).

From a control perspective, Dumont and Tchuenche (2012) pursue mathematical models of the efficacy of sterile insect technique, expansion on the previous work of Dumont and Chiroleu (2010) which studied an outbreak on Réunion Island. Cauchemez et al. (2014) explore an invasion time model to similar data, choosing to model the probability that the virus would colonize particular areas of the Caribbean over time.

The data of interest is provided by the Pan American Health Organization and WHO in the form of weekly epidemiological reports of cumulative suspected and confirmed cases of Chikungunya in 55 PAHO administrative regions throughout 2014 and the beginning of 2015 (PAHO and WHO, 2014). Data is available irregularly both spatially and temporally, and is contained in separate PDF tables by week. A Python script was employed to construct a readily analyzable case count data set, although irregular reporting remains a concern.

According to the CDC, the typical incubation/latent period for Chikungunya is between 3 and 7 days, up to 12. This indicates a very high probability that an infected individual will become infectious by the beginning of the week after being exposed; a fact which is important given the weekly granularity of the available data. To encode this prior information, we chose to use an exponential transition process with an exposed-to-infectious rate term γ^(EI) with a mean of 2.5 and effective prior sample size of 100. This implies approximately a 92% chance that an exposed individual will transition to infectious within the first week. The model is still free to modify γ^(EI), but it would need to overcome the prior information. Less is known about the duration of the infectious period, so a much less informative prior was chosen. The prior distribution for γ^(IR) was chosen to have mean 0.5 and effective prior sample size of only 10. This implies a median transition time of one week, but permits much longer possible infectious durations should the model overcome the weak prior information to select a smaller γ^(IR).

The exposure process parameters, β^(SE) were assigned independent N(0, 1) prior distributions, because these distributions provide enough flexibility for the simulated epidemics to encompass the entire range of plausible epidemic, while avoiding placing substantial prior probability on extremes of epidemic behavior. Spatial autocorrelation terms were given Beta(1, 40) priors, which constrains the contribution arising from contact between nations to reflect less than 10% of the contact intensity occurring within nations, a conservative constraint.

With these prior specifications, we consider four candidate models, intended to illustrate some of the varying complexity which can be employed by this model class. In all cases, two distance matrices, denoted D_z in Equation 4, are employed. The first provides an overall contact process between all all administrative regions in the study. This matrix is a 55 × 55 square matrix with $\frac{1}{55}$ on the off diagonals and 0 along the diagonal. The second measure of distance between spatial locations is a gravity model, weighted based on squared distance between administrative region centroids and relative population sizes. Specifically, the geodesic distance δ_ij is computed between region centroids for location i and location j. The distance metric is then computed as $\sqrt{\frac{n_i{n}_j}{{\delta }_{ij}^2}}$, where n_i, n_j denote the population sizes in each region. The resulting matrix is then rescaled by its maximum value to ensure that no element is greater than 1, matching the scale of the prior distribution of the autocorrelation parameters.

Temporal variability is captured using natural splines with varying degrees of freedom, and it is this process that is used to differentiate the candidate models. Three of the models employ a categorical variable based on population size rather than on overall intercept. These models also include an interaction between the population factor and the spline basis, permitting separate temporal intensities by population size. The overall intercept model assumes that epidemic intensity is homogeneous between spatial locations, even though contact between locations may not be. The population factor model allows intensity to vary spatiotemporally, in addition to permitting the same spatial contact process. Clearly, these models are relatvely artificial, and a more comprehensive study could include information on demographics, environmental influences, and human behavior such as travel rates and economic dependence. Nevertheless, the inclusion of temporal bases of varying complexity allows investigators without access to such information to determine the relative complexity of the underlying population dynamics (Brown et al., 2015). Even these relatively generic models permit researchers to quantify reproductive behavior in each location. The model indices are described in Table 5.

Table 5.

Chikungunya Analyses - Model Indices

Model Index	Description
1	Population-factor, 3 DF Temporal Basis
2	Population-factor, 4 DF Temporal Basis
3	Population-factor, 6 DF Temporal Basis
4	Single Intercept, 3 DF Temporal Basis

We begin the evaluation of the adequacy of the four included models by examining the approximate Bayes Factors in favor of each, assuming that each had equal prior probability. We additionally consider the posterior predictive distributions of the final selected model and the least preferred model, and visualize two example locations for empirically adjusted reproductive number trends (Brown et al., 2015). Finally, we illustrate the average reproductive number trend across all locations.

This complex epidemic and the aforementioned irregular data availability provide an ideal test bed for the construction of new models of the spread of Chikungunya. In particular, this example highlights the ability of such techniques in general, and our software in particular, to deal with both cumulative and non-cumulative data, missing data, and to compare models of competing complexity in order to evaluate the dominant factors driving epidemic spread. Due to the large number of spatial locations, no comparison to MCMC techniques was feasiblez.

4. Results

4.1. Simulation Studies

In Tables 2 and 3, we compare posterior coverage and bias between MCMC and ABC techniques, respectively. Both coverage and bias are within reasonable limits, especially in light of the dramatic difference in required computation time, presented in Table 4. Interestingly, larger epidemics are associated with improved performace for the ABC algorithm, however this observation is based on a single shared terminating acceptance rate. Other compromises between computation time and accepted bias/coverage performance are possible through the choice of different algorithm tuning parameters. Moreover, even for these small epidemics, examination of the posterior and posterior predictive distributions of compartment values compared to the true data indicates that meaningful epidemic patterns are being learned (Figure 1).

Table 2.

Single Location SEIR - MCMC Parameter Estimation Performance

		95% Cr.I.		Estimate
Intercept	Parameter	Coverage	Width	Bias	Bias%
−1	Intercept	0.98	0.195	−0.047	−4.733
	Intervention	1	0.014	0.001	2.278
	E to I Transition	1	0.044	0.003	1.259
	I to R Transition	1	0.021	0.001	0.918
−1.2	Intercept	0.92	0.288	−0.056	−4.628
	Intervention	0.98	0.019	0.001	2.571
	E to I Transition	1	0.029	0.000	0.184
	I to R Transition	1	0.018	0.000	0.118
−1.4	Intercept	1	0.470	−0.034	−2.416
	Intervention	0.98	0.036	−0.002	−3.019
	E to I Transition	1	0.025	0.000	−0.165
	I to R Transition	1	0.018	0.000	−0.127

Table 3.

Single Location SEIR - ABC Parameter Estimation Performance

		95% Cr.I.		Estimate
Intercept	Parameter	Coverage	Width	Bias	Bias%
−1	Intercept	1	0.249	−0.013	−1.309
	Intervention	1	0.014	<0.001	−0.370
	E to I Transition	1	0.032	<0.001	−0.198
	I to R Transition	1	0.023	<0.001	−0.107
−1.2	Intercept	0.9	0.326	0.019	1.547
	Intervention	0.98	0.040	−0.007	−13.017
	E to I Transition	1	0.034	−0.001	−0.260
	I to R Transition	1	0.023	<0.001	0.054
−1.4	Intercept	0.96	0.511	0.085	6.065
	Intervention	0.88	0.106	−0.027	−48.166
	E to I Transition	1	0.034	<0.001	−0.471
	I to R Transition	1	0.024	−0.007	−0.007

Table 4.

Single Location SEIR - Required ABC and MCMC based Runtimes (minutes)

		Quantiles
Intercept	Outcome	0%	25%	50%	75%	100%
1	MCMC	6.8	14.68	24.02	45.11	72.07
	ABC	1.86	3.41	4.44	5.11	6.07
1.2	MCMC	6	7.64	15.17	23.06	72.3
	ABC	0.95	1.79	2.36	2.89	3.47
1.4	MCMC	6.05	6.98	13.24	14.77	45.02
	ABC	0.66	1.15	1.38	1.57	2.11

Figure 1.

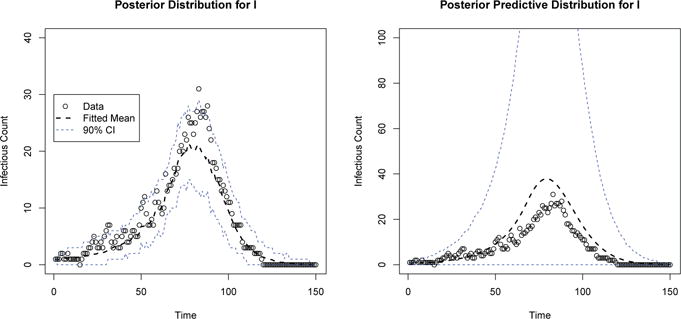
Posterior and Posterior Predictive Distributions for Infectious Count

4.2. Chikungunya

The raw case counts, as reported by PAHO and processed by our team, are illustrated in Figure 2. In this graphic, rows of the image correspond to individual administrative regions, sorted by cumulative cases over the course of the study. Columns correspond to PAHO epidemiological weeks spanning 2014 and early 2015. As this figure clearly illustrates, updates to estimated cases are quite sparse, even in heavily affected regions. The ability to seamlessly and appropriately deal with missing data is thus seen to be quite useful in practice.

Figure 2.

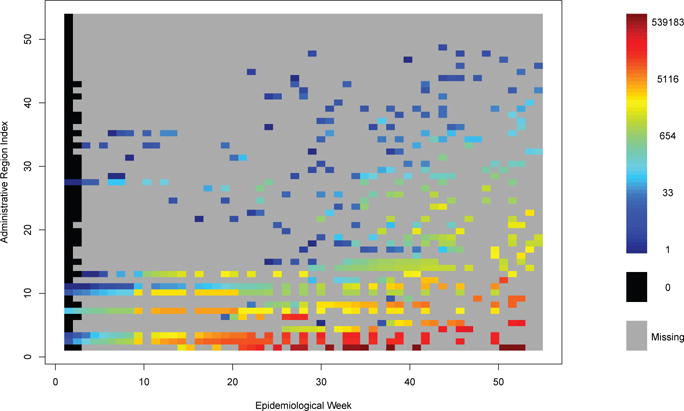
Reported Cumulative Chikungunya Cases by Administrative Region and Epidemiological Week

All four models were fit to a stringent terminating acceptance rate of 250 accepted particles per 4M epidemic simulations. The resulting approximate Bayes factors are presented in Table 6. Only model 3, which incorporates a six degree of freedom temporal basis and the simpler of the two spatial components, had factors uniformly greater than one, and strongly so. The reason for this strong preference becomes apparent when examining the posterior predictive distributions.

Table 6.

Chikungunya Analyses - Approximate Bayes Factors (row vs. column index)

	1	2	3	4
1	1.0	Inf	0.07	Inf
2	1.2	1.0	0.7	3.4
3	15.21	Inf	1.0	Inf
4	0.0	0.3	0.2	1.0

Figure 3 presents posterior predictive distributions cases determined by Model 4 (underspecified) in two of the regions with the largest incidence: The Dominican Republic and Colombia. In this example, the posterior predictive distribution demonstrates a very poor fit in the dominican republic, and an acceptable one in Colombia. In contrast, the final accepted model illustrated by Figure 4 illustrates a much more reasonable distribution for both. This predictive distribution is, in fact, the epidemic proposal distribution. Clearly, the latter model produces epidemics which match the observed data far more frequently.

Figure 3.

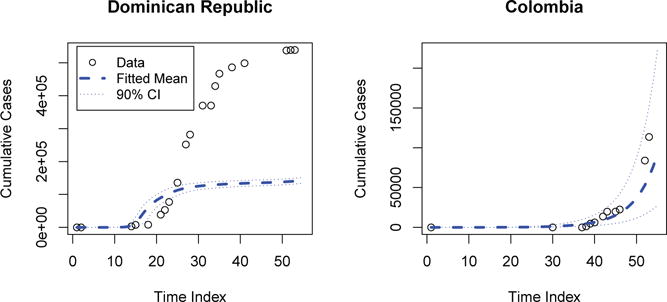
Underspecified Posterior Predictive Distribution: Cases for The Dominican Republic and Colombia

Figure 4.

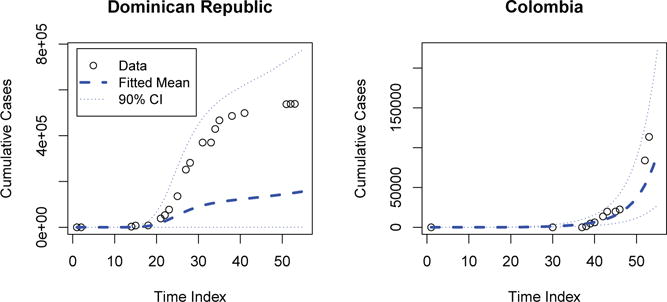
Final Posterior Predictive Distribution: Cases for The Dominican Republic and Colombia

Even so, the fit is far from perfect. This indicates that our set of candidate models is probably not sufficiently flexible to capture diverse epidemic behavior throughout this heterogeneous region. In particular, while nations which are similar in size may have epidemic features in common, this is likely to be geographically heterogeneous. This issue could be avoided with better temporal and location specific covariates, such as drivers of mosquito population growth. Additionally, improved drivers of spatial contact of human populations such as airline and nautical traffic may be of interest, as the weighted gravity model appears to have little support. Even so, these simple models are a reasonable way to characterize pathogen reproductive behavior.

Empirically adjusted reproductive number curves (Brown et al., 2015) are presented for these two locations in Figure 5, and mean EA-RN trends for all locations in 6. The observed heterogeneity highlight the substantial difference in baseline epidemic intensity which is observed throughout the region.

Figure 5.

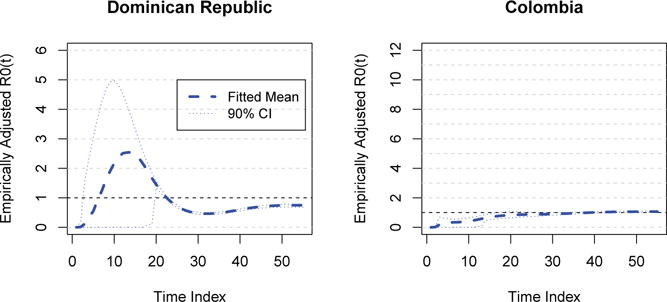
Reproductive Numbers: The Dominican Republic and Colombia

5. Discussion

We have demonstrated that approximate Bayesian computing techniques have strong application in the world of compartmental epidemic models, both to expand the scope of problems to which existing techniques may be applied, and to push the methodological boundaries of compartmental model specification. The ease with which competing models may be compared further illustrates the range of potential uses of these techniques.

The ability to fit and compare numerous models of complex epidemic processes dramatically improves on our previous work in this domain. In particular, we feel that the comparison of candidate spatial and single location models for the Chikungunya epidemic highlights the need for improved environmental, demographic, and behavioral explanatory information about the problem. We hope that the general tools and techniques highlighted by this work encourage others with access to such data to continue to expand investigations of nuanced epidemic models, and will continue to study this important public health issue in the future.

Despite the obvious utility of these methods and software, there are a number of avenues for further improvement. First, given the highly parallel nature of these problems, we hope in the future to extend this software to heterogeneous computing architectures. In particular, modern graphics processing units (GPUs) present a cost effective tool for massively parallel problems (Scarpino, 2012). Moreover, recent and ongoing improvements in heterogeneous computing frameworks provide a rich landscape which would benefit from better integration with the R statistical computing environment (Lutz, 2014; The Khronos Group, 2015).

Second, the SEIR(S) compartment structure, while flexible, does not accommodate all pathogens and disease processes. Indeed, many infectious disease problems represent a complex interplay of multiple host and vector species, and may involve important disease states not captured by traditional techniques. With this need in mind, we hope to apply the techniques developed here to generic compartmental modeling software in the future, while retaining the high level nature of model specification in ABSEIR.

Finally, numerous extensions and improvements to our example analysis of Chikungunya data are possible. In particular, better information about the human dynamics of travel in the region would be useful in informing mitigation strategies. Nevertheless, we feel that the set of tools provided by ABSEIR will encourage and enable such investigation by Biostatisticians and Epidemiologists studying the problem.

Figure 6.

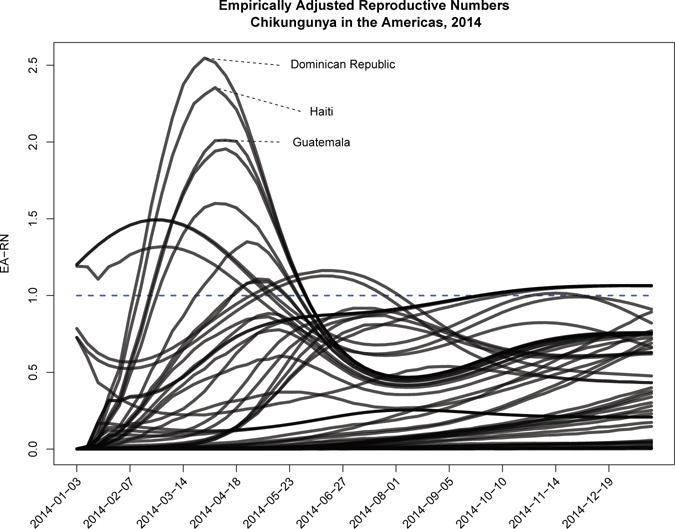
Reproductive Numbers: Mean National Reproductive Number Trends