Relative dosimetry with an MR‐linac: Response of ion chambers, diamond, and diode detectors for off‐axis, depth dose, and output factor measurements

Abstract

Purpose

The purpose of this study was to acquire beam data for an MR‐linac, with and without a 1.5 T magnetic field, by using a variety of commercially available detectors to assess their relative response in the magnetic field. The impact of the magnetic field on the measured dose distribution was also assessed.

Methods

An MR‐safe 3D scanning water phantom was used to measure output factors, depth dose curves, and off‐axis profiles for various depths and for field sizes between 2 × 2 cm² and 22 × 22 cm² for an Elekta MR‐linac beam with the orthogonal 1.5 T magnetic field on or off. An on‐board MV portal imaging system was used to ensure that the reproducibility of the detector position, both with and without the magnetic field, was within 0.1 mm. The detectors used included ionization chambers with large, medium, and small sensitive volumes; a diamond detector; a shielded diode; and an unshielded diode.

Results

The offset of the effective point of measurement of the ionization chambers was found to be reduced by at least half for each chamber in the direction parallel with the beam. A lateral shift of similar magnitude was also introduced to the chambers’ effective point of measurement toward the average direction of the Lorentz force. A similar lateral shift (but in the opposite direction) was also observed for the diamond and diode detectors. The measured lateral shift in the dose distribution was independent of depth and field size for each detector for fields between 2 × 2 cm² and 10 × 10 cm². The shielded diode significantly misrepresented the dose distribution in the lateral direction perpendicular to the magnetic field, making it seem more symmetric. The percentage depth dose was generally found to be lower with the magnetic field than without, but this difference was reduced as field size increased. The depth of maximum dose showed little dependence on field size in the presence of the magnetic field, with values from 1.2 cm to 1.3 cm between the 2 × 2 cm² and 22 × 22 cm² fields. Output factors measured in the magnetic field at the center of the beam profile produced a larger spread of values between detectors for fields smaller than 10 × 10 cm² (with a spread of 2% at 3 × 3 cm²). The spread of values was more consistent when the output factors were measured at the point of peak intensity of the lateral dose distribution instead (except for the shielded diode which differed by up to 2% depending on field size).

Conclusions

The magnetic field of the MR‐linac alters the effective point of measurement of ionization chambers, shifting it both downstream and laterally. Shielded diodes produce incorrect and misleading dose profiles. The output factor measured at the point of peak intensity in the lateral dose distribution is more robust than the conventional output factor (measured at central axis). Diodes are not recommended for output factor measurements in the magnetic field.

1. Introduction

Many cancer treatment centers^{1, 2, 3, 4, 5} are currently implementing a new radiation treatment technology that combines diagnostic‐level magnetic resonance imaging (MRI) with a linear accelerator, referred to as an MR‐linac. Such systems enable the real‐time visualization and tracking of the target during treatment with high soft‐tissue contrast, with the potential to reduce treatment margins. However, this combination results in the radiotherapy photon beam being used in the presence of a strong magnetic field (current ranges are between 0.35 T and 1.5 T). This magnetic field disrupts the deposition of dose (in a patient or a phantom) by deflecting the paths of the secondary electrons via the Lorentz force.^{6, 7, 8, 9, 10, 11} In addition, the dose–response of the detectors used to characterize and calibrate the beam is also affected.^{11, 12, 13, 14, 15, 16, 17, 18, 19}

Most of the work done so far to characterize the behavior of detectors in a magnetic field has focused on the effect of the magnetic field on the absolute dose–response of the detector as a function of magnetic field strength and detector orientation under certain conditions. Significant changes to the dose–response of both ionization chambers^{11, 12, 13, 14, 15, 16} and solid‐state detectors^{17, 18, 19} have been observed. However, the effect of the magnetic field on relative dosimetry measurements is unclear. Safely commissioning treatment planning systems for use with the MR‐linac requires the collection of accurate beam data, which requires knowledge of how the detectors that are typically used to measure these data respond in the magnetic field.

Because relative dosimetry measurements are expressed in terms of the ratio of the dose at a point to the dose at some reference point, the magnetic field effects might be expected to be cancelled out. However, this is contingent on the effects of the magnetic field being constant with depth, off‐axis position and field size. In conventional beams, the choice of detector used for certain types of measurements (e.g., small field output factors, depth dose curves) is important, but whether this choice must be reconsidered when the detector is to be used under the influence of a magnetic field is not clear. An important consideration in relative dosimetry is the effect of the magnetic field on the position of the effective point of measurement (EPOM) of the detectors being used. Our preliminary Monte Carlo study²⁰ indicated that the offset of the EPOM of a Farmer chamber may be reduced by half in a 1.5 T magnetic field and that a lateral shift in the EPOM of similar magnitude is also introduced. That study applied the technique of Kawrakow²¹ to both vertical and lateral dose calculations and the data are provided here as Data S1. Diodes may also exhibit a similar effect, as a Monte Carlo study by Gargett et al.²² calculated that the dose distribution detected by a silicon diode array in a magnetic field was shifted with respect to the dose to water. Additionally, Monte Carlo simulations performed by Reynolds et al.¹⁷ showed that the dose–response of a diamond and diode detector varied significantly (up to 14% depending on the detector and position) at the field edges when a transverse 0.5 T magnetic field was present compared to the case of no magnetic field. Looe et al.²³ also showed using simplified Monte Carlo detector models that the measured lateral shift in the dose distribution varies with the detectors density; with the shift being largest for low density and smallest for high density.

Here, we present a series of water tank measurements obtained in the beam of an MR‐linac both with a 1.5 T magnetic field and with no magnetic field. Our aim was to study the effects of the magnetic field on several commercially available detectors used for relative dosimetry measurements, including large‐ and small‐volume ionization chambers, shielded and unshielded diodes, and a diamond detector. The response of each detector was assessed with respect to each other as a function of depth, off‐axis distance, and field size, with two aims: one to determine whether any of these detectors exhibit unusual or unique behavior in the presence of a magnetic field and the other to determine which type of detector is most appropriate to use for each type of measurement with an MR‐linac and which type, if any, should be avoided. The effects of the magnetic field on the dose distribution are also examined and discussed.

2. Methods

2.A. Equipment setup

Measurements were performed at The University of Texas MD Anderson Cancer Center with an MR‐linac system which was developed by Elekta AB (Stockholm, Sweden) in cooperation with UMC (Utrecht, The Netherlands) and Philips Healthcare (Best, The Netherlands). This system consists of a linear accelerator capable of producing a ~7 MV flattening‐filter‐free photon beam mounted to a cylindrical wide‐bore MRI system with a 1.5 T magnetic field parallel to the axis of the bore. It also has an on‐board MV imaging system. The Elekta MR‐linac system is similar to the experimental system described by Raaymakers et al.⁴ Phantoms and detectors had to be setup without the aid of a light‐field or in‐room laser system as the MR‐linac is not equipped with these features; instead setup was facilitated by the use of an on‐board MV imaging system. Most measurements for the current study were obtained both with and without the magnetic field.

The water phantom used was a noncommercial MR‐compatible motorized water tank constructed by PTW (Freiburg, Germany) (Fig. 1). The design of this water phantom is similar to the one described by Smit et al.²⁴; it is 24 cm high, 63 cm wide (perpendicular to the axis of the MRI bore), and 43 cm long (parallel to the axis) and allows software‐controlled movement of detectors in three dimensions with 0.1 mm accuracy. Measurements were obtained with the gantry at 0° and the isocenter at a depth of 10 cm, resulting in a source‐to‐surface distance (SSD) of 133.5 cm and about 10 cm of water beyond the isocenter for backscatter. The restricted height of the phantom limited the scanning depths to between the isocenter and just above the surface of the water. For the larger volume ionization chambers, the maximum depth achieved was up to 4 mm upstream of the isocenter owing to the size of the detector and the holders available combined with the location of the detector's EPOM.

Figure 1.

MR‐compatible motorized 3D scanning water phantom with a PTW 30013 Farmer chamber. [Color figure can be viewed at wileyonlinelibrary.com]

The angular alignment between the scanning axes of the water phantom and the collimator axes of the beam was measured by placing ball bearings in grooves at the bottom of the tank that aligned in a cross pattern parallel with the phantom's horizontal scanning axes, and then recording an image with the on‐board MV imaging system. The alignment of the ball bearings as they appeared in the image was compared with the edges of the field to obtain agreement within 0.1°. The alignment of the horizontal plane relative to the surface of the water was checked visually by scanning the detector across the water surface while the tank was in place inside the bore and checking for divergence between the water and the detector as it moved across the tank. Plastic shims were used to tilt the tank to compensate for any observed inclination.

Scans were obtained with the following detectors: PTW 31022 PinPoint 3D Ion Chamber (S/N 151730, nominal sensitive volume 0.016 cm³), PTW 31021 Semiflex 3D Ion Chamber (S/N 141490, nominal sensitive volume 0.07 cm³), PTW 30013 Farmer chamber (S/N 007115, nominal sensitive volume 0.6 cm³), PTW 60019 microDiamond (S/N 122683), PTW 60016 Diode P (S/N 000617), and PTW 60018 Diode SRS (S/N 000201). This group of detectors covers ionization chambers with sensitive volumes ranging from small (the PinPoint 3D) to large (the Farmer chamber), both shielded (the Diode P) and unshielded (the Diode SRS) diodes, and a diamond detector (the microDiamond). Ionization chamber measurements were obtained with the long axis of the chamber oriented perpendicular to the beam and parallel with the magnetic field. Diode and microDiamond measurements were obtained with the long axis oriented parallel with the beam and, therefore, perpendicular to the magnetic field. In each case, the length of cable that was placed inside the water phantom was minimized to reduce the influence of any spurious signals caused by irradiation of the cable. Scans were step‐based (as opposed to continuous), and the charge readings at each measurement point were measured with a PTW TANDEM T10016 electrometer (S/N 060403) and recorded with the PTW MEPHYSTO mc² tbaScan software (v 3.2.51), which also controlled the positioning of the detector. The control unit for the water tank was located beyond the 5 Gauss line of the magnetic field and the electrometer was located in the control room outside of the bunker. A bias voltage of +300 V was used for the ionization chamber measurements; no bias was applied for the diamond or diode detector measurements. A noncommercial large‐volume ionization chamber (Sun Nuclear Corporation, Melbourne, FL, USA) was mounted to the gantry at the back of the linac, where it could collect back‐scattered radiation, and was used as a reference detector to normalize the influence of fluctuations in the beam dose rate even at small field sizes. The integration time used for each measurement varied from 0.25 to 0.4 s depending on the detector used and was set, so that a satisfactory level of noise was achieved without compromising the measurement time too much. The step resolution varied with depth and field size.

The position of the isocenter was determined by placing a ball bearing in a slot on the detector holder and imaging it with the on‐board MV imaging system from four different gantry angles 90° apart (45°, 135°, 225°, and 315°). These angles were used because the horizontal (longitudinally oriented) bar that supports the detector holder obscures the images at 90° and 270° by overlapping with the ball bearing. Hence, we used 45°, 135°, 225°, 315° to keep the bar far away from the ball bearing in the projected images. The apparent shift in the position of the ball bearing in each image was used to determine the displacement of the ball from the isocenter in the three orthogonal directions: vertical; parallel with the axis of the bore (inline); and perpendicular to the axis of the bore (crossline). The position of the ball bearing was then corrected using this information and the process was repeated until the displacement of the ball bearing from the isocenter was within 0.1 mm in each direction. Water was then added to the tank up to the mid‐point of the ball bearing and then a further 10 cm of water was added based on a measurement from a ruler secured to the inside wall of the tank.

2.B. Detector alignment correlation

Measurements were divided across three stages: during the first and third stage, the magnet was active, and in the second stage the magnet was inactive. During the first stage, the horizontal position of the detector was set by using the known displacement between the position of the ball bearing (positioned at the isocenter as described previously) and the assumed position of the sensitive volume of the detector. This produced an uncertainty in the position of the detectors relative to the central axis of the beam of up to 0.7 mm in the direction perpendicular to the magnetic field (based on measurements obtained in the third stage, see below). Only a subset of the data collected while the magnet was active was taken during this stage. During the second stage, when the magnetic field was off, the horizontal position of the detectors was based on the mid‐point of the measured 1 × 1 cm² field profiles to ensure that the sensitive volume of the detectors was positioned at the point of peak intensity at all field sizes (i.e., the beam central axis). This technique could not be used for the measurements obtained with the magnetic field on because of the distortion of the beam profiles caused by the Lorentz force and also because of the possible effects of the magnetic field on the response of the detectors themselves. During the second stage, once each detector was positioned at isocenter, MV images were recorded (Fig. 2). For the third stage, when the magnetic field was brought back up, these images were used as a reference to reposition the detectors at the same point. This repositioning was done with in‐house software that compared detector features in images recorded when the magnet was off to the same features in new images recorded with the magnet on. The software then used the position of these features in each image to calculate the relative displacement between the detector positions. In the case of the diode or diamond‐based detectors, the fact that the length of the detector was parallel with the beam (combined with the high density of some of the components) provided features with high contrast for the comparison [Fig. 2(b)]. In the case of the ionization chambers, the sensitive volumes themselves provided contrast owing to their low density. After the position of the detectors was corrected, the displacement between the features tracked in the images was always within 0.1 mm. For all measurements, the orientation of the chambers was always kept consistent by means of fiducial marks on the outer casing of each detector. The reproducibility of the detector position with this method was tested by repeating the same setup on four occasions (three on the same day, one on a different day). In each case, the centers of the measured profiles were within 0.1 mm of each other. Once the detectors were in place, profiles were re‐measured at the 10 × 10 cm² field size and compared with those measured during the first stage. The relative shift in the horizontal axes was calculated and used to correct all of the first stage data to remove the uncertainty introduced by positioning the detector relative to the ball bearing, so that it could be more accurately compared to the data acquired when the magnetic field was off.

Figure 2.

Examples of the MV portal images used to position (a) the PTW 30013 Farmer and (b) the PTW 60016 Diode P detectors, positioned with its central axis parallel with the beam axis. Window and level settings have been applied to enhance contrast.

The geometric accuracy of the MV images was calibrated using the water tank itself by moving a detector at isocenter by known lateral distances and measuring the displacement of the image of the detector on the MV images. The calibration of the pixel width was 0.2 mm. Sub‐pixel precision was achieved by interpolating linearly between pixel values. Noise in the images was reduced by averaging 21 or more pixels that were laterally adjacent. Ultimately, the geometric accuracy was confirmed by attempts to position detectors based on the information from the MV images, i.e., when moving detectors laterally the image of the detectors consistently moved by the same amount to within 0.1 mm.

For ionization chambers, the alignment of the detector at the water surface was established by placing the center of the chamber (not the EPOM) at the surface of the water. The error associated with this technique was quantified by measuring the position of d _max measured with the Semiflex 3D on five different days (three with the magnetic field on, two with the magnetic field off) and the maximum difference observed was 0.21 mm. Since the same technique was used for each detector, the error was assumed to be the same in each case. In some of the earliest measurements, the conventional vertical shift was applied to account for the EPOM of the detector; however, this was retroactively removed during data analysis. For the diodes and diamond detector, the alignment of the detector at the water surface was established by measuring a depth dose curve up through the surface of the water with sub‐millimeter steps. The build‐up material on top of the detector maintains a fixed depth once the detector leaves the water, and when this happens the dose curve becomes constant. The point at which this occurs was assumed to be the point at which the tip of the detector is at the surface of the water. Then, the distance from the tip of the detector to the sensitive volume (given by the manufacturer) was used to establish the alignment of the detector at the water surface.

The strength of the magnetic field at the MV imaging panel is below 10 mT and therefore it should not have affected the images produced. To verify this, the difference between the position of the center of the field on the MV images with and without the magnetic field was quantified by measuring it on 31 images (21 with magnetic field, 10 without) and comparing the values. The mean and standard deviation of the difference between the beam center with and without the magnetic field was found to be 0.030 ± 0.043 mm along the horizontal axis of the images (perpendicular to the magnetic field) and 0.003 ± 0.048 mm along the vertical axis of the images (parallel to the magnetic field). Therefore, the effect of the magnetic field on the portal images is negligible.

2.C. Measurements

Inline and crossline profiles, depth dose curves and output factors were measured for the following field sizes: 22 × 22 cm², 10 × 10 cm², 5 × 5 cm², 3 × 3 cm², and 2 × 2 cm². Output factors were measured at a depth of 10 cm (or at the closest depth possible), whereas profiles were measured at depths of 1.3 cm, 5 cm, and 10 cm (or at the closest depth possible). Output factors were also measured for a 1 × 1 cm² field, with corresponding profiles also measured at this field size for a depth of 10 cm only. Measurements with the Farmer chamber were limited to the 10 × 10 cm² field size only and did not include profile measurements in the inline direction. The diode detectors were not used to measure profiles and depth dose curves at the 22 × 22 cm² field size.

To correct for misalignments between the sensitive volume of the detectors and the central axis of the beam, the central axis deviation (defined as the position of the mid‐point between the 50% values at the beam penumbra in the profile measurements) was measured for each detector for the 10 × 10 cm² field at a depth of 10 cm without a magnetic field in both the inline and the crossline directions. This value was then used to correct all of the profile data (including those measured with the magnetic field on) by shifting the data by this amount. An exception to this is the Farmer chamber profile data, for which data correlated with MV images without the magnetic field were not available. In this case, the central axis deviations of the measured profiles were corrected based on the position of the sensitive volume relative to the center of the beam as visible on the MV images with the magnetic field active. To test the consistency of this technique to that used for the other detectors, it was also applied to the data for the PinPoint 3D chamber and the result obtained was within 0.1 mm of that obtained with the original technique.

The experimental errors involved in the measurements are summarized as follows: (a) error on vertical detector position setup with solid‐state detectors: 0.3 mm (based on observed variance between detectors); (b) error on vertical detector position setup with ionization chambers: 0.21 mm (based on observed variance from day‐to‐day); (c) error on lateral detector position setup with MV images: 0.1 mm (within precision of water tank, based on observed variance from day‐to‐day); (d) error on lateral detector position setup with ball bearing: up to 0.7 mm (based on retroactive comparison to MV positioning technique); (e) effect of magnetic field on position of beam in portal images: <0.05 mm (no statistically significant difference, based on comparison of images with and without magnetic field); (f) error on output factor measurements: 1% for 1 × 1 cm², 0.5% for 2 × 2 cm², 0.3% for other fields (based on comparison of output factor measurements from day‐to‐day).

3. Results

3.A. Depth dose curves

3.A.1. Ionization chamber effective point of measurement (EPOM)

The effect of the magnetic field on the position of the EPOM of the ionization chambers used in this study was examined by comparing the position of $d_{\mathit{max}}$ reported by each detector for a 10 × 10 cm² field. The standard deviation of the position of $d_{\mathit{max}}$ measured with the solid‐state detectors (microDiamond, Diode P, Diode SRS) was within 0.3 mm both with and without the magnetic field. For the purpose of this analysis, the average value measured with these three detectors was taken as a reference value and assumed to be correct for each case. These average values also agreed within 0.3 mm with the values from Monte Carlo data provided by Elekta both with and without the magnetic field. The position of $d_{\mathit{max}}$ recorded by each of the ionization chambers (measured relative to the center of the chamber) was then compared to this value and used to estimate the shift required to correct for the EPOM of the chamber. The results are shown in Fig. 4. The offset of the EPOM from the center of each ionization chamber was reduced by at least 49% in each case when used in the 1.5 T magnetic field.

Figure 4.

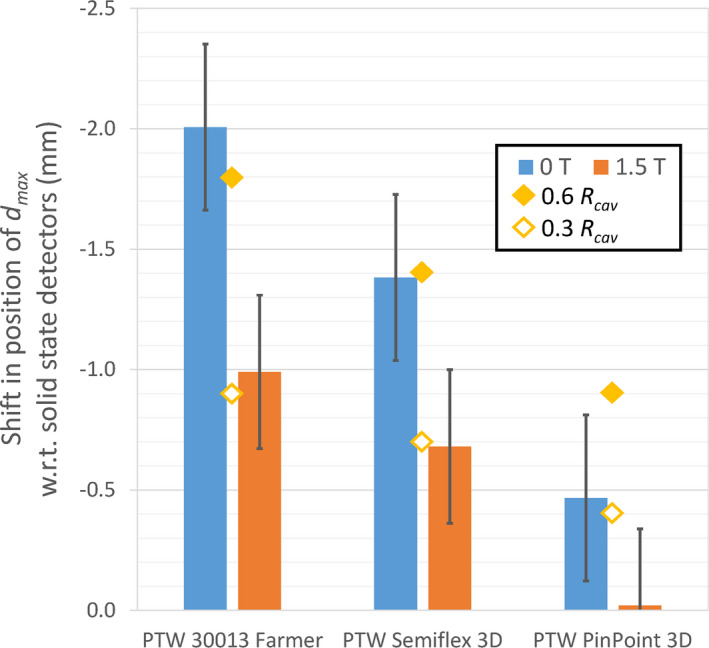
Relative shifts required to align the position of $d_{\mathit{max}}$ in the depth dose curves measured by each ionization chamber with the average position reported by the solid‐state detectors. Results are shown both with and without a 1.5 T magnetic field. The uncertainties shown are the combined uncertainties on the position of the ionization chambers and the solid‐state detectors. The values of 0.6 and 0.3 times the cavity radius are also shown for comparison. [Color figure can be viewed at wileyonlinelibrary.com]

3.A.2. Detector response for percentage depth doses

The percentage depth doses (PDDs) measured with each detector are shown in Fig. 3 for a 10 × 10 cm² and a 2 × 2 cm² field, both with and without the 1.5 T magnetic field. The EPOM determined from Fig. 4 is accounted for in these plots. When the magnetic field is present, the PDDs measured by each detector differ from each other with depth at the smaller field size. Specifically, the ionization chambers (PinPoint 3D and Semiflex 3D) differ from the solid‐state detectors (microDiamond, Diode SRS and Diode P), with the difference being greater for the Semiflex 3D (1.3% of maximum) than for the PinPoint3D (0.9% of maximum) relative to the average of the PDD measured at a depth of 10 cm by the solid‐state detectors (which had a standard deviation of 0.2% of maximum).

Figure 3.

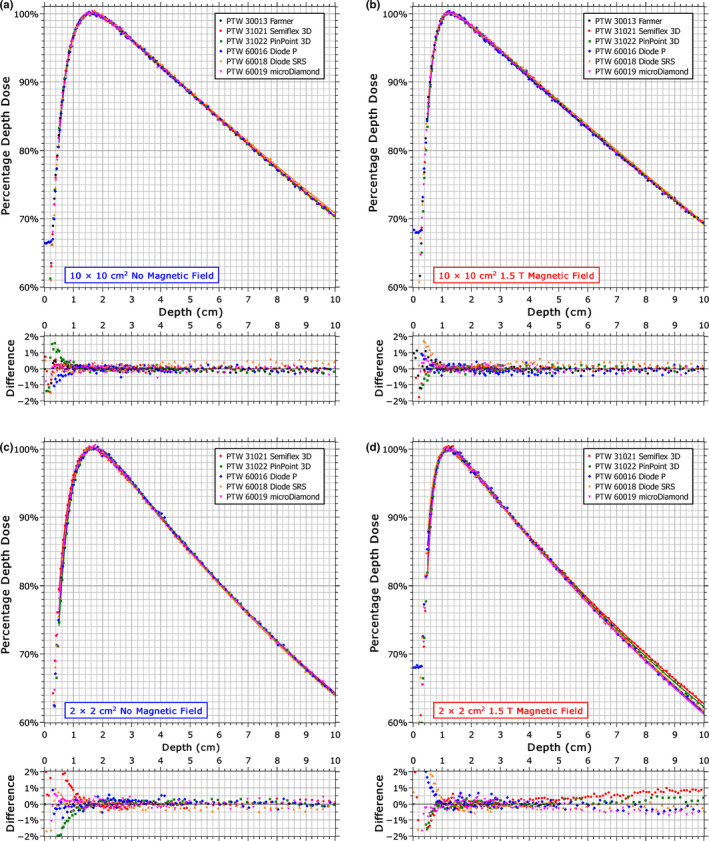
Percentage depth dose curves measured by each detector with and without a 1.5 T magnetic field for a 10 × 10 cm² field (a, b) and for a 2 × 2 cm² field (c, d). The data were normalized to the maximum of a best‐fit curve; represented by the solid lines (RMS error ~0.2%). The differences shown are with respect to the mean value at each point and are relative to the maximum dose. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Profile measurements

3.B.1. Lateral shifts

The magnetic field induces a lateral shift in the dose distribution toward the direction perpendicular to the magnetic field.⁶ Profiles measured in this direction (the crossline direction) by each detector were shifted off‐center, as measured by the relative position of the mid‐point between the 50% dose points on either side of the profile with and without the magnetic field. However, the magnitude of the shift in the crossline direction varied from detector to detector with the values ranging from 0.55 mm to 2.36 mm for a 10 × 10 cm² field (Table 1 and Fig. 5). In contrast, no significant shift was observed in the inline direction. Part of the discrepancy resulted from the asymmetry in the profile shape induced by the magnetic field. Volume averaging across the penumbral region produces an apparent shift due to the asymmetry of the penumbra. This was quantified by taking the profiles measured by the SRS diode (which has the smallest active area of 1 mm², excluding the Diode P) and integrating it across a range of lengths around each measurement point to represent the different active thicknesses of each detector and then re‐calculating the change in the profile central axis (CAX) deviation. This was then used to correct the CAX deviations recorded from each detector for the effects of volume averaging, and these results are also shown in Table 1. The remaining discrepancies resulted from the effects of the magnetic field on the detector response. This does not apply to the inline direction as the profiles there are symmetric.

Table 1.

Deviations from the beam central axis (CAX) of the center of the dose profiles measured by various detectors in a 1.5 T magnetic field in both the inline direction (parallel with the magnetic field) and the crossline direction (perpendicular to the magnetic field). CAX deviations in the crossline direction are shown based on the value measured from the raw data and the value when corrected for the effects of volume averaging. Uncertainty is ±0.1 mm. Positive values indicate a shift toward the average direction of the Lorentz force (patient left when head‐first supline)

Detectors	CAX deviations (mm)
	Inline	Crossline (raw value)	Crossline (corrected)
PTW 30013 Farmer	N/A	2.36	2.16
PTW Semiflex 3D	−0.07	2.05	1.92
PTW PinPoint 3D	0.04	1.07	1.01
PTW microDiamond	0.09	0.83	0.79
PTW Diode SRS	0.01	0.83	0.82
PTW Diode P	0.01	0.55	0.54

Figure 5.

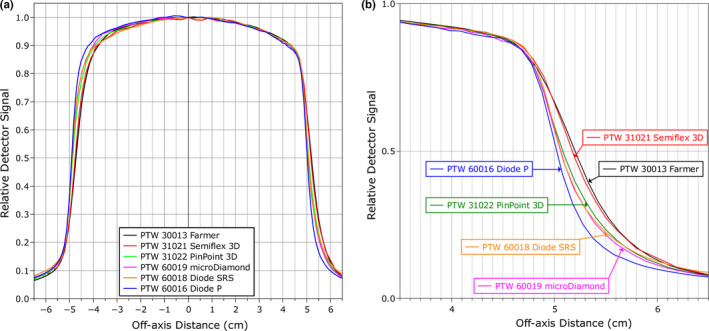
(a) Profiles for a 10 × 10 cm² measured in the crossline direction (perpendicular to the magnetic field) with each detector in a 1.5 T magnetic field. The signal from each detector is normalized to the central axis. (b) A close‐up plot of the right‐hand side penumbra. [Color figure can be viewed at wileyonlinelibrary.com]

The variation in the measured lateral shift with depth was less than 0.1 mm for the Diode P and microDiamond detectors, and within 0.2 mm for the Semiflex 3D, PinPoint 3D, and Diode SRS for both the 10 × 10 cm² and 2 × 2 cm² fields. Measurements with the Farmer chamber were obtained only for the 10 × 10 cm² field; however, no variation in the lateral shift with depth was observed with that detector at that field size. The variation in the lateral shift with field size was less than 0.1 mm between the 10 × 10 cm² and 2 × 2 cm² fields for the Semiflex 3D, PinPoint 3D, and microDiamond detectors. For the diode detectors, the field size variation was 0.4 mm for the Diode P detector and 0.2 mm for the Diode SRS detector. Due to the limited space in the water phantom, the profile data for the 22 × 22 cm² field were insufficient to characterize the lateral shift at that field size.

3.B.2. Detector response off‐axis

The effect of the magnetic field on the detector response was also examined independently from the influence on the apparent shift of the dose distribution by comparing the profiles from each detector with the shift removed. Figure 6 shows the crossline profiles for the 10 × 10 cm² and 2 × 2 cm² fields. The qualitative profile shape agreement was generally good between the detectors except for the shielded diode (PTW Diode P), which is much more symmetric in both cases. Measuring the symmetry as the ratio of the areas between the center and the 20% dose point on either side of the profile gives a value with the shielded diode of 100.3% versus an average of 101.4% for the other detectors for the 10 × 10 cm² field and 103.9% versus 108.4% for the 2 × 2 cm² field. Other differences observed between the detectors include a broader penumbra measured by the Semiflex 3D for the 2 × 2 cm² field, which is most likely due to volume averaging, and an over‐response out‐of‐field by the Diode SRS for the 10 × 10 cm² field, which is typical of unshielded diodes in large fields because of the over‐response of the silicon to low‐energy photons.²⁵

Figure 6.

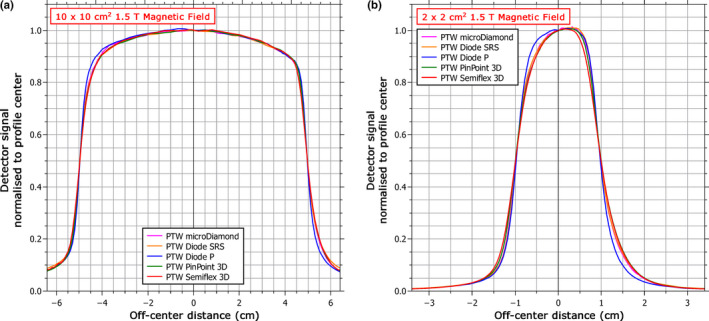
Measured profiles for each detector in the crossline direction (perpendicular to the magnetic field) for both (a) a 10 × 10 cm² field and (b) a 2 × 2 cm² field. Each profile has been shifted to remove the offset produced by the magnetic field and then normalized to the center point. [Color figure can be viewed at wileyonlinelibrary.com]

Because the asymmetry of the profile is induced by the magnetic field, it is worth comparing the shape of the profile measured with the shielded diode in the magnetic field to that measured without the magnetic field. This is shown in Fig. 7 with the lateral shift induced by the magnetic field removed (see Section 3.B.1). For the 10 × 10 cm² field, the profile measured with the magnetic field is in good agreement with the profile measured without the magnetic field, with a γ pass rate²⁶ of 96.6% using the criteria of 2% (global) and 0.2 mm. However, when the magnetic field was on, there was a relative over‐response out‐of‐field of ~10% (relative to the local dose). This was also observed in the inline direction. This increase in the out‐of‐field dose in the presence of the magnetic field was not observed with any other detector. For the 2 × 2 cm² field, no increase was observed in the out‐of‐field dose, but the profiles with the magnetic field no longer agree with those without the magnetic field as closely, as the former became noticeably more asymmetric. The γ pass rate in this case was 89.2%.

Figure 7.

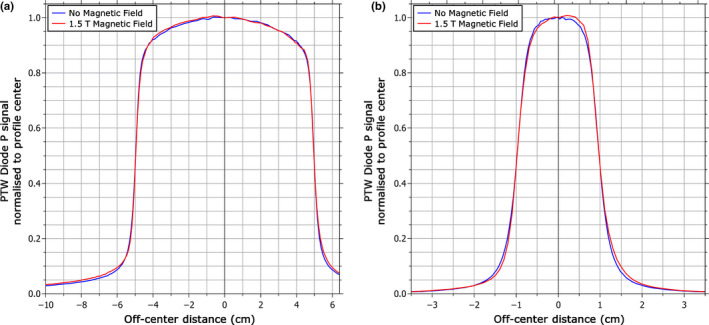
Crossline profiles measured by the PTW Diode P shielded diode detector with and without the 1.5 T magnetic field for (a) a 10 × 10 cm² field and (b) a 2 × 2 cm² field. The lateral shift induced by the magnetic field has been removed for this comparison. [Color figure can be viewed at wileyonlinelibrary.com]

3.C. Output factors

The fact that the apparent lateral shift in the dose distribution measured by each detector was different means that output measurements made with different detectors at the same position would actually measure the output at different points along the dose gradient relative to each other. To remove the influence of the lateral shift of the measured profiles from the measurement of the output factors, the profiles were normalized based on the output factor measurements and then shifted to remove the lateral shift. The output factors were then resampled from the center point of each profile [Figs. 8(a) and 8(b)]. This ensured that the output was sampled at the same point along the lateral dose distribution, so that differences between detectors were due solely to differences in detector response rather than from effectively sampling different points. In order to reduce the influence of noise in the profile measurements from propagating to the resampled output factor measurement, each profile was smoothed using a moving window average before the output factors were applied and resampled. The averaging window width was 2.1 mm in each case except for the 1 × 1 cm² field where a width of 1.1 mm was used. Due to the asymmetry of the beam profile induced by the magnetic field, the output at the profile center did not always coincide with the maximum intensity. Therefore, the output factors were also resampled at the point of maximum intensity for each field [Figs. 8(d) and 8(e)]. Full profile information was not available for the 22 × 22 cm² field due to the limited space in the water phantom, so no corrections for the lateral shift were applied to the output factors at this field size. However, the profile information that is available shows that a shift of 1–3 mm should not affect the measured output. Therefore, the data for the 22 × 22 cm² shown in Figs. 8(d)–8(f) are the same data shown in Figs. 8(a)–8(c). The ratio of the output factors measured with the magnetic field to those measured without it is shown for each detector in Figs. 8(c) and 8(f).

Figure 8.

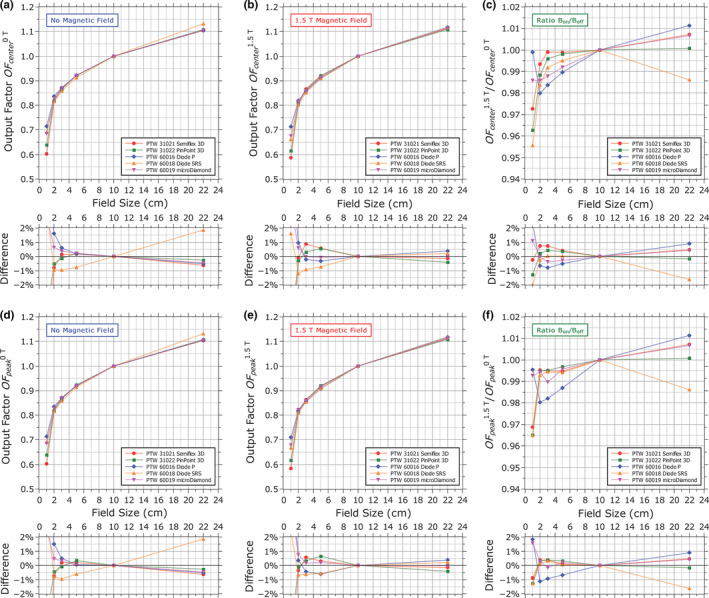
Output factors measured (a, d) without the magnetic field and (b, e) with the magnetic field either at the center of each dose profile after removing the lateral shift induced by the magnetic field (a, b), or measured at the maximum intensity of the profile at each field size (d, e). The ratios with/without magnetic field are shown in (c, f). The percentage difference relative to the mean is shown for each case. Output factors are relative to a 10 × 10 cm² field and all measurements were performed at a depth of 10 cm. Uncertainties in output factor measurements are 1% for the 1 × 1 cm² field, 0.5% for the 2 × 2 cm², and 0.3% for all other fields. [Color figure can be viewed at wileyonlinelibrary.com]

Looking first at the output factors that were sampled at the profile center, $O{F}_{\mathit{center}}$, the magnetic field appears to reduce the output at small field sizes. This was expected as the profiles become more asymmetric and the peak of the distribution shifts off‐center. However, most detectors experienced this reduction at a different rate, with a spread of 1.5% for the 3 × 3 cm² field. There was also a spread in the measured values of $O{F}_{\mathit{center}}$ when the magnetic field was present, with a spread of 1.3% for the 5 × 5 cm² field which increased as the field size was reduced. With no magnetic field, the values of $O{F}_{\mathit{center}}$ measured by each detector agreed to within 0.7% from the 22 × 22 cm² field down to the 3 × 3 cm² field with the exception of the unshielded diode (Diode SRS) which differed by 1–2% depending on field size.

Looking at the output factors that were sampled at the point of maximum intensity, $O{F}_{\mathit{peak}}$, the spread of the values with the magnetic field present was similar in this case to $O{F}_{\mathit{center}}$. However, the values of $O{F}_{\mathit{peak}}$ were split into groups: with the microDiamond, Semiflex 3D, and PinPoint 3D agreeing with each other to within 0.5% for all fields down to the 3 × 3 cm² field while the two diode detectors both differed from them by about 1% [Fig. 8(e)]. The magnetic field still appears to reduce $O{F}_{\mathit{peak}}$ at small field sizes [Fig. 8(f)]. However, in this case, the drop in $O{F}_{\mathit{peak}}$ measured by each detector was 1% or less for fields down to 2 × 2 cm², with the exception of the shielded diode (Diode P) which showed drops in $O{F}_{\mathit{peak}}$ of up to 2% for these fields. For the 1 × 1 cm² field, the Semiflex 3D, PinPoint 3D and Diode SRS each shown a drop in $O{F}_{\mathit{peak}}$ of 3.2–3.5% in the magnetic field compared to their respective measurements without the magnetic field [Fig. 8(f)]. However, the values of $O{F}_{\mathit{peak}}$ measured by the Diode P and microDiamond show the relative drop to be only 0.5–0.7%, respectively.

Most detectors reported a higher output at the 22 × 22 cm² field size when the magnetic field was present, although this value ranged from less than 0.1% with the PinPoint 3D chamber to 1.1% for the shielded diode. Curiously, the anomalous output factor measured without the magnetic field with the unshielded diode at the 22 × 22 cm² field (difference of ~2%), which was indicative of an over‐response to low‐energy photons, was not observed when the magnetic field was present.

3.D. Beam characteristics

Aside from assessing detector responses, the measurement data were also used to contrast other properties of the dose distribution when the magnetic field was present to when it was not. The profile asymmetry and shifts induced by the magnetic field, as well as the differences in $O{F}_{\mathit{center}}$, are described above. The variation in the position of $d_{\mathit{max}}$ as a function of field size is shown in Fig. 9 for both cases. These values are an average of the position of $d_{\mathit{max}}$ measured with each detector (except for the Farmer chamber). The EPOM determined from Fig. 4 is accounted for in these plots. When the magnetic field is present, the variation in $d_{\mathit{max}}$ with field size is much smaller than when the magnetic field is not present, remaining relatively constant at 1.2–1.3 cm between the 2 × 2 cm² and 22 × 22 cm² fields. The PDD is shown in Fig. 10 for 2 × 2 cm², 10 × 10 cm², and 22 × 22 cm² fields (as measured with the microDiamond detector); the PDD tended to be lower in the presence of the magnetic field (although the rate of reduction of the PDD after d _max is unchanged), but as the field size increased this difference becomes smaller, and for the 22 × 22 cm² field the PDDs at depths beyond the build‐up region with and without the magnetic field were in good agreement with each other.

Figure 9.

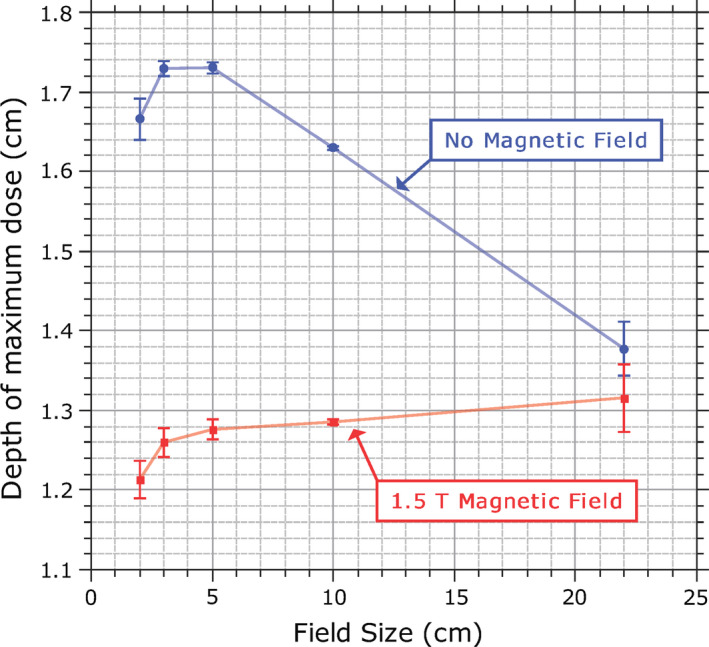
Variation in the depth of maximum dose with field size both with and without the 1.5 T magnetic field. Values are averaged across each detector (excluding the Farmer chamber). Error bars represent the standard deviation. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 10.

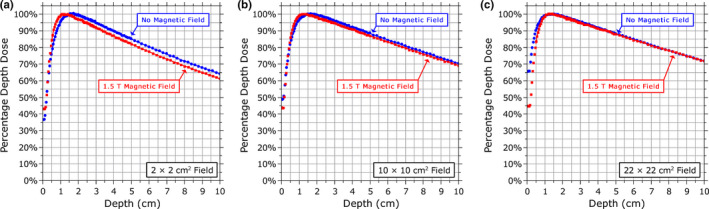
Comparison of the percentage depth dose curves measured with the PTW microDiamond detector with and without a 1.5 T magnetic field for (a) a 2 × 2 cm² field, (b) a 10 × 10 cm² field, and (c) a 22 × 22 cm² field. [Color figure can be viewed at wileyonlinelibrary.com]

4. Discussion

4.A. Effective point of measurement

The most significant effect of the magnetic field on the measurement of depth dose curves is the change of the EPOM of ionization chambers. For both the Farmer and Semiflex 3D chambers, the offset of the EPOM from the center of the chamber was reduced by 49% by the 1.5 T magnetic field (and by 96% for the PinPoint 3D chamber). This may be explained by the fact that the Lorentz force results in the secondary electrons having a preferential direction of lateral motion. Consequently, on average they do not arrive at the chamber from directly above but instead they arrive at an angle. This effect was observed in our previous Monte Carlo study²⁷ which showed that the modal angle at which the secondary electrons approach the ionization chamber in a 1.5 T magnetic field is 39.64° ± 0.15°. This also explains why the off‐axis profiles measured by the ionization chambers are also shifted. This behavior could be understood by considering that if the beam was coming from that direction, as a consequence the EPOM would be directed that way instead of directly above. If the standard approximation of 0.6 × R _cav is used to determine the EPOM offset, then this would predict a vertical shift of 0.46 × R _cav and a horizontal shift in the crossline direction of 0.38 × R _cav for a 1.5 T magnetic field. However, this model is not complete, because the electrons do not arrive from this angle symmetrically; as can be seen from Fig. 4, a better approximation for the vertical EPOM in a 1.5 T magnetic field is 0.3 × R _cav , at least for the larger volume chambers.

To put the numbers in Table 1 into context, Monte Carlo data provided by Elekta using a full‐head model of the MR‐linac with a lateral voxel thickness of 0.5 mm showed a lateral shift in the water profiles from a 10 × 10 cm² beam of 1.55 mm. This implies that not only are the larger volume ionization chambers overestimating the shift induced by the magnetic field but also that the PinPoint 3D and solid‐state detectors (diodes and diamond detector) are underestimating it. The range in measured shifts was from 0.6 mm toward Patient's Left (Farmer chamber) to 1.0 mm toward Patient's Right (Diode P) relative to the Monte Carlo value (assuming head‐first supline). This Monte Carlo value needs to be verified independently; however, a shift in the dose distribution measured with diodes was predicted by Gargett et al.²² The shift of the EPOM is likely to be a function of the magnetic field strength and thus the effect should be lower for low‐field strength MRIgRT systems such as the ViewRay system (0.35 T). These effects were not observed by Wang et al.²⁸ from profile and PDD measurements performed in a nonmotorized water phantom on a ⁶⁰Co ViewRay system. However, the shift in the EPOM would have been difficult to detect with manually positioned detectors (due to the short build‐up region of ⁶⁰Co beams) and the profiles were measured with EBT2 radiochromic film which is unlikely to misrepresent the position of the dose distribution due to its near water equivalency.

The issue of understanding the lateral shift in the profiles measured by the solid‐state detectors must be handled differently, because ordinarily the EPOM of these detectors lies within the semiconductor material acting as the sensitive volume. Gargett et al.²² attributed the shift in the dose distribution in silicon relative to water to an imbalance of low‐energy electrons on either side of the beam profile resulting in an over‐response on one side and an under‐response on the other in proportion to the relative mass collisional stopping power ratios. However, this alone would not explain the differences between the two types of diode or the shift observed with the microDiamond detector or PinPoint 3D ionization chamber. In this case, the lateral shift seems to result in part from a shielding effect, where the high‐Z/high‐density materials inside these detectors are dampening the tendency of the secondary electrons to spiral because of the higher scattering cross‐section. This is evidenced by the fact that the apparent profile shifts are underestimated rather than overestimated and also by the fact that the effect is strongest for the shielded diode, which contains the most high‐Z/high‐density material of all of the detectors. The profiles measured with the shielded diode in the magnetic field also more closely (although not completely) resemble the dose distribution in the absence of the magnetic field. This strongly suggests that the shielding in the diode is inhibiting the effects of the Lorentz force. This may also explain the behavior of the PinPoint 3D chamber, because the air volume in that chamber is so small that its effect may be negligible relative to the shielding effect of the material surrounding the air volume.

4.B. Detector responses

Because of their inhibiting effects on the Lorentz force (as described in Section 4.A), shielded diodes should be avoided for the acquisition of beam commissioning data in a magnetic field. The profiles measured by the unshielded diode (Diode SRS) and the microDiamond detector, however, do not significantly differ from those measured with the PinPoint 3D and Semiflex 3D ionization chambers in‐field, although the unshielded diode over‐responds when out‐of‐field, presumably because of the over‐response of silicon to low‐energy photons as a result of the higher mass attenuation coefficient. The magnetic field did not particularly affect the response of any of the detectors as a function of depth for large fields, including the shielded diode. However, for the 2 × 2 cm² field, the depth dose curves measured by the ionization chambers diverged from those measured by the solid‐state detectors. Although the Semiflex 3D detector is susceptible to volume‐averaging effects at this field size (and the depth dose curve was measured in a high‐gradient region of the dose profile owing to the shifted and asymmetric dose distribution), the smaller volume PinPoint 3D should not be as affected, so this explanation seems unlikely. The dose–response of ionization chambers in small fields may vary with depth in a magnetic field. Since the EPOM of the Semiflex 3D is shifted laterally, some of this discrepancy may be due to the PDD being measured slightly off‐axis.

Measuring output factors at the center of the beam profile ($O{F}_{\mathit{center}}$) produced a spread of values from each detector [Fig. 8(b)]. Gradient effects, such as volume averaging, that exist at the central axis due to the asymmetry induced by the magnetic field may be causing the disparity. However, the output factors were more consistent when they were resampled at the point of maximum intensity instead ($O{F}_{\mathit{peak}}$). This also resulted in good agreement (<0.5%) between the ratio of output factors with and without magnetic field for all but the shielded diode for fields between 2 × 2 cm² and 10 × 10 cm² [Fig. 8(f)]; implying that there is no significant magnetic field effect on the dose–response of these detectors at the point of peak intensity of these fields. Therefore, it is recommended to perform output measurements at the point of maximum dose along the beam profile for each field size below 10 × 10 cm². In the case of the reference 10 × 10 cm² field and larger fields, the output can still be measured at the central axis and therefore still be directly linked to the reference dose measurement because the dose at the central axis coincides with the point of peak intensity at these field sizes [Fig. 5(a)]. Output factors can also be measured at the central axis if the output values are later adjusted to match the maximum dose value using off‐axis ratios derived from profile measurements. However, if this is done, it is important that the same detector be used to measure the profiles as was used to measure the output factor, or differences in the lateral shift combined with gradient effects could lead to errors. There was good agreement (within 0.5%) between the output factors measured in the magnetic field by the Semiflex 3D and PinPoint 3D ionization chambers and the microDiamond detector [Fig. 8(e)]. Both diodes agreed with each other but differed from the other detectors by about 1%. Considering the anomalous behavior observed in profile measurements for the Diode P, it is most likely that these results are less reliable than those measured by the other detectors. Therefore, we recommend avoiding diode detectors for output factor measurements in a magnetic field.

For fields smaller than 2 × 2 cm², it is unclear which detector should be used as the microDiamond and Diode P both agree that the output at the 1 × 1 cm² field size is less than 1% lower with the magnetic field than without it while the other detectors measured the output to be over 3% lower. Without knowledge of the actual dose distribution in water, it is difficult to determine which detector is most suitable for this type of measurement. Other detectors that are often used as reference dosimeters for small field output factor measurements such as plastic scintillators and radiochromic film could be used to investigate this; however, there is evidence that both of these types of detector are also susceptible to magnetic field effects.^{19, 29} A future Monte Carlo study may be able to address this by modeling the dose–response of each detector as a function of field size.

4.C. Beam characteristics

In addition to studying the relative response of the detectors, the beam data also allowed us to make observations about the characteristics of the beam itself. As observed in previous studies, the dose distribution became asymmetric and offset in the direction perpendicular to the magnetic field. When the magnetic field was present, the output factors were generally measured to be lower for small fields relative to the 10 × 10 cm² field and higher for larger fields than in the case without the magnetic field. The shortened range of the electrons in the magnetic field compresses the build‐up region and enhances the dose at $d_{\mathit{max}}$.¹¹ This results in generally lower PDDs beyond the build‐up region when the magnetic field is present [Figs. 10(a) and 10(b)]. However, as the field size increases, the increase in electron contamination encountered in the absence of the magnetic field also enhances the dose at $d_{\mathit{max}}$ and tends to cancel this effect, resulting in smaller differences between the PDDs with and without the magnetic field at depth for larger field sizes [Fig. 10(c)]. For fields larger than 22 × 22 cm², this trend would likely continue and ultimately result in the PDD at depth being greater with the magnetic field than without it.

The variation in the position of $d_{\mathit{max}}$ with field size both with and without the 1.5 T magnetic field is shown in Fig. 9. The data plotted are the mean position of $d_{\mathit{max}}$ measured by each detector with the standard deviations shown as error bars. Without the magnetic field, the depth of maximum dose reached a maximum at about a 3 × 3 cm² field size and ranged from 1.4 cm to 1.7 cm. This is consistent with conventional beams where at large fields $d_{\mathit{max}}$ shifts toward the phantom surface owing to the effect of collimator scatter and electron contamination, whereas at small fields a similar shift occurs because of the effect of the reduced phantom scatter. When the magnetic field is present, the position of $d_{\mathit{max}}$ shows a much smaller dependence on field size, with a range from 1.2 cm to 1.3 cm. These values are consistently closer to the phantom surface than their counterparts without the magnetic field. The reduced value of $d_{\mathit{max}}$ in a magnetic field has been observed before^{10, 11} and is a result of the reduced range of the secondary electrons in the magnetic field, resulting in the depth dose curve shifting closer to the depth kerma curve. The reduction of $d_{\mathit{max}}$ with field size, as observed without the magnetic field, was not observed with the magnetic field, likely because of the lack of electron contamination. Instead, the position of $d_{\mathit{max}}$ increased with field size across the range of fields measured, although it seemed to plateau at larger field sizes, probably as changes in phantom scatter become negligible. For fields larger than 22 × 22 cm², this trend would likely continue for even larger fields until ultimately the position of $d_{\mathit{max}}$ is actually deeper in the phantom with the magnetic field than without.

4.D. Practical implications

The shift in the EPOM of ionization chambers, both laterally and vertically, has implications for calibrating MRIgRT devices and for acquiring beam data to commission treatment planning systems. The change in the vertical shift may affect the determination of beam quality and tissue‐maximum ratios because of errors in the determination of the depth of maximum dose if not accounted for. Meanwhile, the lateral shift of the EPOM has implications for the nonuniformity correction of Farmer chamber output measurements in flattening‐filter‐free beams, as the output would be averaged over an offset and asymmetric region of the dose gradient rather at the center. The lateral shift of the dose profiles observed with both ionization chambers and solid‐state detectors also has implications for the use of ion chamber or diode arrays in QA devices designed for routine or patient‐specific QA, as the measured dose distribution may be shifted relative to the true dose distribution. This should be investigated before such a system is used clinically. The use of a shielded diode to acquire beam data for commissioning a treatment planning system should be avoided, because this type of detector significantly misrepresents the lateral dose distribution.

The variation in output factors between detectors when measured along the central axis means that special attention must be paid toward how these output factors are measured and ultimately applied toward monitor unit calculations. Output factors can be measured along the central axis as usual if the beam profile data are also measured with the same detector. In this case, the point at which the output is being measured along the beam profile is consistent between the output measurement and the profile measurement. Corrections for any lateral shift in the beam profile must be applied after the output factors are applied and, if necessary, corrected output factors can be resampled at the central axis from the corrected normalized beam profile data. This procedure may increase the uncertainty of the output factors; depending on the level of noise in the profile data. Alternatively, if different detectors are required for output factor and profile measurements, the output factors can be measured at the point of peak intensity at each field size and then applied to the point of peak intensity of the profile data. In this case, the detector must be scanned around the area where the peak is suspected to be until the peak is found before measuring the output. Central axis output factors can then be resampled at the central axis as before from the corrected and normalized beam profile data. This technique is more time‐consuming and is subject to the same low noise requirements as the previous technique. Therefore, we recommended that output factors and profile measurements be acquired with the same detector.

5. Conclusion

The magnetic field of the MR‐linac alters the EPOM of ionization chambers, shifting it both downstream and laterally. Diodes and diamond detectors underestimate the lateral shift in the dose distribution induced by the Lorentz force. Shielded diodes in particular seem to significantly counteract the effects of the Lorentz force, resulting in incorrect and misleading dose profiles. The variation of the depth of maximum dose with field size is significantly reduced in the presence of a 1.5 T magnetic field. The measured lateral shift in the dose distribution was depth and field size independent for each detector for fields between 2 × 2 cm² and 10 × 10 cm². The dose–response of ionization chambers seems to be depth‐dependent at small field sizes. Output factors should be measured at the point of peak intensity in the dose distribution and diodes are not recommended for output factor measurements in the magnetic field.

Conflict of interest

This project was partially funded by Elekta Inc. James Dolan, Stefan Pencea and Nicholas Schupp are Elekta employees.

Supporting information

Data S1. Monte Carlo Calculation of a Farmer Chamber's Effective Point of Measurement in a Magnetic Field.