Stereological analysis of individual lung lobes during normal and aberrant mouse lung alveolarisation

Abstract

The quantitative assessment of the lung architecture forms the foundation of many studies on lung development and lung diseases, where parameters such as alveoli number, alveolar size, and septal thickness are quantitatively influenced by developmental or pathological processes. Given the pressing need for robust data that describe the lung structure, there is currently much enthusiasm for the development and refinement of methodological approaches for the unbiased assessment of lung structure with improved precision. The advent of stereological methods highlights one such approach. However, design‐based stereology is both expensive and time‐demanding. The objective of this study was to examine whether ‘limited’ stereological analysis, such as the stereological analysis of a single mouse lung lobe, may serve as a surrogate for studies on whole, intact mouse lungs; both in healthy lungs and in diseased lungs, using an experimental animal model of bronchopulmonary dysplasia (BPD). This served the dual‐function of exploring BPD pathobiology, asking whether there are regional (lobar) differences in the responses of developing mouse lungs to oxygen injury, by examining each mouse lung lobe separately in the BPD model. Hyperoxia exposure resulted in decreased alveolar density, alveoli number, and gas‐exchange surface area in all five mouse lung lobes, and increased the arithmetic mean septal thickness in all mouse lung lobes except the lobus cardialis. The data presented here suggest that – in healthy developing mice – a single mouse lung lobe might serve as a surrogate for studies on whole, intact mouse lungs. This is not the case for oxygen‐injured developing mouse lungs, where a single lobe would not be suitable as a surrogate for the whole, intact lung. Furthermore, as the total number of alveoli can only be determined by an analysis of the entire lung, and given regional differences in lung structure, particularly under pathological conditions, the stereological assessment of the whole, intact lung remains desirable.

Introduction

Robust quantitative data about the lung structure constitute the basis of studies on lung anatomy and studies that address structural perturbations to the lung that occur under pathological conditions (Weibel et al. 2007; Weibel, 2017). The past decade has seen substantial advances in methodological approaches to quantify elements of lung structure. These advances include the implementation of stereological methods for the assessment of parameters that describe or reveal changes in the lung structure which are either causes of lung disease or accompany the development of lung disease, both in experimental animals (Mühlfeld & Ochs, 2013; Ochs & Mühlfeld, 2013; Mühlfeld et al. 2015) and in humans (Hyde et al. 2004; Ochs et al. 2004). Key parameters of interest include the accurate determination of the total lung volume, which is based on the original mathematical relationships described by Archimedes of Syracuse (undated) and Cavalieri (1653), and which were later applied to the determination of lung volume (Scherle, 1970; Michel & Cruz‐Orive, 1988; Tschanz et al. 2011). In addition to lung volume measurements, quantification of the total number of alveoli, the alveolar density, the arithmetic mean septal thickness, and the total gas‐exchange surface area of the lung remain meaningful measurements to study lung (patho)physiology (Mühlfeld et al. 2013).

Disorders of lung development such as bronchopulmonary dysplasia (BPD) (Northway et al. 1967) are accompanied by alveolar simplification in the lungs of newborns, where alveolar simplification is evident by reduced alveolar density and a reduction in the total number of alveoli in the lung, which underlies a decreased gas‐exchange surface area (Surate Solaligue et al. 2017). These disturbances to lung structure are also a characteristic of emphysema in adults (Yildirim et al. 2010; Limjunyawong et al. 2015). All of these pathological changes to lung structure constitute hallmarks of disease. Furthermore, alterations to elements of the lung structure are the primary readouts in studies that employ animal models, either to validate the causality of candidate pathogenic pathways (for example, using gene‐ablation and pathway inhibitor studies; Nardiello & Morty, 2016) or in pre‐clinical drug development studies, to evaluate the efficacy of a candidate pharmacological or other medical interventions. Thus, the ability reliably to detect changes in lung structure with a high degree of precision is a priority in lung research today. The introduction of design‐based stereology to quantify elements of the lung structure has introduced a much‐needed unbiased approach, with increased precision, compared to the more classical morphometric approaches for the assessment of mean linear intercept (MLI), radial alveolar count (RAC), and septal thickness. These morphometric approaches remain useful and important, with the caveats of being more restricted, possibly biased, and less precise. With these concerns in mind, stereological analyses are now among the formal recommendations by learned societies for the study of lung structure (Hsia et al. 2010).

A key barrier to the broader implementation of stereological analyses in investigative laboratories is the added time and work burden, where the line‐ and point‐counting, which generates the core primary data of a stereology study, cannot be automated. Currently, analyses are performed on randomly selected regions of entire lungs obtained from experimental animals. To explore whether the time and work burden of a mouse lung stereology study can be reduced, we set out to assess whether the stereological analysis of a single lung lobe could serve as a surrogate for the stereological analysis of an entire lung. In parallel, this study served as the first side‐by‐side comparison of the alveolar structure, assessed by design‐based stereology, of individual mouse lung lobes. To explore the single‐lobe approach in diseased lungs, an animal model of BPD was then employed to investigate whether oxygen injury to the developing lung generated regional (lobar) variation in lung structure. This served the dual function of permitting a side‐by‐side comparison of lung alveolar structures at the level of the individual lung lobes, in healthy and diseased lungs.

Materials and methods

Approvals for studies with experimental animals

All animal procedures were approved by the local authorities, the Regierungspräsidium Darmstadt (approval number B2/277).

Mouse model of bronchopulmonary dysplasia

The hyperoxia‐based model of BPD in mice was used as described previously (Nardiello et al. 2017b). Newborn C57BL/6J mice were randomised within 2 h of birth to equal‐sized litters, and litters were maintained in chambers either with a normoxic (21% O₂) or a hyperoxic (85% O₂) gas‐mixture atmosphere. Nursing dams were rotated every 24 h, and received food ad libitum. Pups were euthanised on post‐natal day (P)14, with an overdose of sodium pentobarbital (500 mg kg⁻¹, intraperitoneal; Euthoadorm^®, CP‐Pharma, Burgdorf, Germany; 1207DT).

Design‐based stereology

All methods employed for the analysis of lung structure were based on American Thoracic Society/European Respiratory Society recommendations for quantitative assessment of lung structure (Hsia et al. 2010). The protocol employed for the design‐based stereological analysis of neonatal mouse lungs has been described in detail previously (Nardiello et al. 2017b; Pozarska et al. 2017; Rath et al. 2017). Mouse lungs were fixed through intratracheal installation of a mixture of 1.5% (w/v) paraformaldehyde (Sigma, Darmstadt, Germany; P6148) and 1.5% (w/v) glutaraldehyde (Serva, Heidelberg, Germany, 23116.02) in 150 mm HEPES (Sigma; H0887) dissolved in phosphate‐buffered saline (PBS; Sigma; D8537), pH 7.4. Lungs were fixed at a hydrostatic pressure of 20 cm H₂O for 24 h at 4 °C. In selected instances, post‐fixation, the five mouse lung lobes were separated, and whole, intact lungs or individual lung lobes were embedded in 3% (w/v) agar (Sigma; 05039), and sectioned at 1.5 mm in a custom‐made sectioning device with a Feather Trimming Blade [No. 130, Type (S), pfm Medical AG, Cologne, Germany].

The total volume of the whole, intact lung or of individual lung lobes, was measured using Cavalieri's principle (Michel & Cruz‐Orive, 1988). Agarose‐embedded whole, intact lungs or individual lung lobes were treated with 1% (w/v) osmium tetroxide (Roth, Karlsruhe, Germany; 8371.3) in 0.1 m sodium cacodylate (Serva, Heidelberg, Germany; 15540.03), and 2.5% (w/v) uranyl acetate (Serva, Darmstadt, Germany; 77870.01) in ddH₂O; embedded in glycol methacrylate (Technovit 7100; Heareus Kulzer, Hanau, Germany; 64709003), and collected by systematic uniform random sampling for stereological analysis (Schneider & Ochs, 2014). Tissue blocks were sectioned at 2 μm, and every first and third section of a consecutive series of sections throughout the block was stained with Richardson's stain (Richardson et al. 1960) for the determination of total number of alveoli and alveolar density. For the analysis of all other stereological parameters, every 10th section of a consecutive series passing through the same Technovit block was stained with Richardson's stain and assessed. Images of tissue sections were captured by scanning with a NanoZoomer‐XR C12000 Digital slide scanner (Hamamatsu Photomics Deutschland, Herrsching am Ammersee, Germany).

Determinations were made using the NewCast PLUS™ computer‐assisted stereology system (Visiopharm, Hoersholm, Denmark), where event‐counting was performed on 3% of each section for the whole, intact lung studies. For individual lung lobe studies, the per cent coverage of the tissue sections for each lobe was: lobus (l.) cranialis, 15%; l. medius, 20%; l. caudalis, 10%; l. cardialis, 25%; l. sinister, 7%. Coverage was set such that at least 200 events could be counted on every section. Parameters assessed included the arithmetic mean septal thickness [τ (sep)], gas‐exchange surface area (S), as well as total alveoli number (N) and alveolar density (N _v), as described previously (Pozarska et al. 2017; Rath et al. 2017). Specific to the present study, the arithmetic mean septal thickness, τ (sep), was assessed by two different approaches using the individual lung lobes. A cumulative average arithmetic mean septal thickness,$\overline{\mathrm{\tau }}(\text{sep})$ was determined by the mathematical relationship:

$$\overline{\mathrm{\tau }}\left(\text{sep}\right)=\frac{\sum \mathrm{\tau }\left(\text{sep, lobe}\right)}{N\left(\text{lobe, lung}\right)}$$

where $\sum \mathrm{\tau }\left(\text{sep, lobe}\right)$ represents the sum of the arithmetic mean septal thickness obtained for each of the five lung lobes, and $N\left(\text{lobe, lung}\right)$ represents the number of lobes that make up the intact lung (in this case, the integer 5). Alternatively, a proportional contribution of the individual lung lobes to the overall arithmetic mean septal thickness, ${\mathrm{\tau }}^{\propto }\left(\text{sep}\right)$, was also determined from the mathematical relationship:

$${\mathrm{\tau }}^{\propto }\left(\text{sep}\right)=\frac{2\times \sum V\left(\text{sep, lobe}\right)}{\sum S\left(\text{alv epi, lobe}\right)}$$

where $\sum V\left(\text{sep, lobe}\right)$ represents the sum of the septal volume obtained for each of the five lung lobes, and $\sum S\left(\text{alv epi, lobe}\right)$ represents the sum of the gas‐exchange surface area obtained for each of the five lung lobes. Similarly, a cumulative average mean alveolar density, ${\overline{N}}_v\left(\text{alv/lung}\right)$, was determined by the mathematical relationship:

$${\overline{N}}_v\left(\text{alv/lung}\right)=\frac{\sum N_v\left(\text{alv/par, lobe}\right)}{N\left(\text{lobe, lung}\right)}$$

where $\sum N_v\left(\text{alv/par, lobe}\right)$ represents the sum of the alveolar density obtained for each of the five lung lobes, and $N\left(\text{lobe, lung}\right)$ represents the number of lobes that make up the intact lung (in this case, the integer 5). Alternatively, a proportional contribution of the individual lung lobes to the overall mean alveolar density, $N_v^{\propto }\left(\text{alv/lung}\right)$, was determined by the mathematical relationship

$$N_v^{\propto }\left(\text{alv/lung}\right)=\frac{\sum N\left(\text{alv, lobe}\right)}{\sum V\left(\text{par, lobe}\right)},$$

where $\sum N\left(\text{alv, lobe}\right)$ represents the sum of the number of alveoli obtained for each of the five lung lobes, and $\sum V\left(\text{par, lobe}\right)$ represents the sum of the parenchymal volume obtained for each of the five lung lobes. The coefficient of error (CE), the coefficient of variation (CV), as well as the squared ratio between both (CE ²/CV ²) were measured for each stereological parameter (Tables 1 and 2), and the quotient threshold was set at 0.5. A CE ²/CV ² < 0.5 indicated that sufficient counting had been undertaken, where the CE ²/CV ² value relates to the optimal statistical efficiency in stereology (Gundersen & Østerby, 1981; Hyde et al. 2007).

Table 1.

Stereological parameters for the assessment of lung architecture in individual lung lobes, and in whole, intact lungs, in mice at post‐natal day 14 with normal lung development

Parameter				Lobus Cranialis			Lobus Medius			Lobus Caudalis			Lobus Cardialis			Lobus Sinister			Intact Lung
				Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)
V (lobe) [cm3]		V (lung) [cm3]		0.0414 (0.0056)			0.0272 (0.0030)			0.0582 (0.0092)			0.0276 (0.0074)			0.0846 (0.0149)			0.2410 (0.0299)
CE	CV		CE²/CV²	0.055	0.136	0.167	0.045	0.110	0.167	0.065	0.159	0.167	0.109	0.266	0.167	0.072	0.176	0.167	0.056	0.124	0.200
V V (par/lobe) [%]		V V (par/lung) [%]		0.9255 (0.0229)			0.9055 (0.0227)			0.8968 (0.0237)			0.8897 (0.0244)			0.9073 (0.0194)			0.8920 (0.0561)
CE	CV		CE²/CV²	0.010	0.025	0.167	0.010	0.025	0.167	0.011	0.026	0.167	0.011	0.027	0.167	0.009	0.021	0.167	0.028	0.063	0.200
N (alv, lobe) 106		N (alv, lung) 106		0.9053 (0.1689)			0.5170 (0.0706)			1.1590 (0.3913)			0.4594 (0.1707)			1.4550 (0.3408)			4.0040 (0.4198)
CE	CV		CE²/CV²	0.076	0.187	0.167	0.056	0.137	0.167	0.138	0.338	0.167	0.152	0.372	0.167	0.096	0.234	0.167	0.0469	0.1048	0.200
N V (alv/par, lobe) 107 [cm−3]		N V (alv/par, lung) 107 [cm−3]		2.3710 (0.3465)			2.1040 (0.1736)			2.0190 (0.3311)			1.8560 (0.4651)			1.8940 (0.2745)			1.8770 (0.2041)
CE	CV		CE²/CV²	0.060	0.146	0.167	0.041	0.091	0.167	0.068	0.152	0.167	0.087	0.194	0.167	0.058	0.130	0.167	0.049	0.109	0.200
S V [cm−1]		S V (lung) [cm−1]		849.40 (66.43)			793.10 (83.29)			748.80 (53.06)			769.80 (71.10)			757.00 (78.28)			802.20 (32.98)
CE	CV		CE²/CV²	0.032	0.078	0.167	0.043	0.105	0.167	0.029	0.071	0.167	0.038	0.092	0.167	0.042	0.103	0.167	0.018	0.041	0.200
S (alv epi, lung) [cm2]		S (alv epi, lung) [cm2]		32.82 (7.37)			19.39 (1.91)			39.06 (6.68)			18.61 (3.98)			58.24 (12.89)			171.70 (17.63)
CE	CV		CE²/CV²	0.092	0.224	0.167	0.040	0.099	0.167	0.070	0.171	0.167	0.087	0.214	0.167	0.090	0.221	0.167	0.046	0.103	0.200
τ (sep, lobe) [μm]		τ (sep, lung) [μm]		8.9150 (0.9215)			9.2410 (1.1210)			10.5700 (1.3310)			11.5200 (1.8650)			10.5100 (1.5960)			10.8200 (0.9956)
CE	CV		CE²/CV²	0.042	0.103	0.167	0.050	0.121	0.167	0.051	0.126	0.167	0.066	0.162	0.167	0.062	0.152	0.167	0.041	0.092	0.200
MLI (lobe) [μm]		MLI (lung) [μm]		27.7400 (3.0150)			30.3500 (5.6540)			30.5500 (5.0120)			27.5800 (3.9580)			30.7200 (4.8340)			28.3000 (0.9860)
CE	CV		CE²/CV²	0.044	0.109	0.167	0.076	0.186	0.167	0.067	0.164	0.167	0.059	0.144	0.167	0.064	0.157	0.167	0.016	0.035	0.200

alv, alveoli; alv air, alveolar airspaces; alv epi, alveolar epithelium; CE, coefficient of error; CV, coefficient of variation; l., lobus; MLI, mean linear intercept; N, number, N_V, numerical density; P, post‐natal day; par, parenchyma; S, gas‐exchange surface area; S_V, surface density; τ (sep), arithmetic mean septal thickness; V, volume; V_V, volume density. Values are presented as mean (SD), n = 5–6 lungs or lobes per group.

Table 2.

Stereological parameters for the assessment of lung architecture in individual lung lobes, and in whole, intact lungs, in mice with aberrant lung development after exposure to 85% O₂ for the first 14 days of post‐natal life

Parameter				Lobus Cranialis			Lobus Medius			Lobus Caudalis			Lobus Cardialis			Lobus Sinister			Intact Lung
				Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)			Mean (SD)
V (lobe) [cm3]		V (lung) [cm3]		0.0334 (0.0055)			0.0262 (0.0047)			0.0566 (0.0136)			0.0212 (0.0041)			0.0693 (0.0086)			0.1891 (0.0136)
CE	CV		CE²/CV²	0.062	0.165	0.143	0.068	0.181	0.143	0.091	0.240	0.143	0.073	0.194	0.143	0.063	0.140	0.143	0.032	0.072	0.200
V V (par/lobe) [%]		V V (par/lung) [%]		0.9190 (0.0322)			0.9140 (0.052)			0.8995 (0.0155)			0.9155 (0.0310)			0.8722 (0.0259)			0.8840 (0.0238)
CE	CV		CE²/CV²	0.013	0.035	0.143	0.022	0.057	0.143	0.007	0.017	0.143	0.013	0.034	0.143	0.011	0.030	0.143	0.012	0.027	0.200
N (alv, lobe) 106		N (alv, lung) 106		0.3310 (0.0656)			0.2572 (0.0416)			0.3509 (0.0818)			0.1360 (0.0330)			0.4428 (0.0964)			1.1270 (0.1816)
CE	CV		CE²/CV²	0.075	0.198	0.143	0.061	0.162	0.143	0.088	0.233	0.143	0.092	0.242	0.143	0.082	0.218	0.143	0.072	0.161	0.200
N V (alv/par, lobe) 107 [cm−3]		N V (alv/par, lung) 107 [cm−3]		1.0980 (0.2520)			1.0880 (0.1707)			0.6913 (0.0626)			0.7001 (0.0837)			0.7001 (0.0702)			0.6743 (0.0946)
CE	CV		CE²/CV²	0.087	0.230	0.143	0.087	0.230	0.143	0.059	0.157	0.143	0.045	0.120	0.143	0.034	0.091	0.143	0.063	0.140	0.200
S V (lobe) [cm−1]		S V (lung) [cm−1]		520.8000 (53.2900)			544.2000 (82.4600)			451.2000 (23.9100)			489.5000 (104.1000)			454.2000 (31.4600)			475.6000 (10.8100)
CE	CV		CE²/CV²	0.039	0.102	0.143	0.057	0.152	0.143	0.020	0.053	0.143	0.080	0.213	0.143	0.026	0.070	0.143	0.010	0.023	0.200
S (alv epi, lobe) [cm2]		S (alv epi, lung) [cm2]		16.0500 (3.5600)			13.0100 (3.1630)			22.9600 (5.4500)			9.2740 (1.2550)			27.3100 (2.4540)			79.5900 (7.7700)
CE	CV		CE²/CV²	0.084	0.222	0.143	0.092	0.243	0.143	0.090	0.237	0.143	0.051	0.135	0.143	0.034	0.090	0.143	0.044	0.098	0.200
τ (sep, lobe) [μm]		τ (sep, lung) [μm]		11.8800 (3.0580)			11.7100 (1.8080)			13.9700 (1.4080)			14.2000 (3.4390)			14.1800 (1.9520)			15.4400 (0.6954)
CE	CV		CE²/CV²	0.097	0.257	0.143	0.058	0.154	0.143	0.038	0.101	0.143	0.092	0.242	0.143	0.052	0.138	0.143	0.020	0.045	0.200
MLI (lobe) [μm]		MLI (lung) [μm]		53.7500 (5.5440)			51.4800 (8.7090)			60.9200 (6.0140)			55.8900 (10.3200)			60.1100 (4.9330)			53.2600 (2.4920)
CE	CV		CE²/CV²	0.039	0.103	0.143	0.064	0.169	0.143	0.037	0.099	0.143	0.070	0.185	0.143	0.031	0.082	0.143	0.021	0.047	0.200

alv, alveoli; alv air, alveolar airspaces; alv epi, alveolar epithelium; CE, coefficient of error; CV, coefficient of variation; MLI, mean linear intercept; N, number, N_V, numerical density; P, post‐natal day; par, parenchyma; S, gas‐exchange surface area; S_V, surface density; τ (sep), arithmetic mean septal thickness; V, volume; V_V, volume density. Values are presented as mean (SD), n = 5–7 lungs or lobes per group.

Sex genotyping of mice

The sex of each experimental animal was determined by simultaneously screening for the male‐specific Sry locus and the sex‐independent Il3 genes, as described previously (Lambert et al. 2000). The sex of each experimental animal is indicated in all graphs.

Statistical analysis

Data are presented in scatter plots as mean ± SD. Differences between experimental groups were evaluated using a one‐way anova with Tukey's post hoc modification for multiple comparisons. Two‐group comparisons were made by unpaired Student's t‐test. All statistical analyses were performed with GraphPad prism 6.0. Statistical outliers were screened for, using Grubbs’ test, and none was found.

Results

Oxygen injury blunts mouse lung alveolarisation

The exposure of newborn C57BL/6J mice to 85% O₂ from the day of birth up to and including P14 caused perturbations to the structure of the lungs, comparing normoxia (21% O₂)‐exposed (Fig. 1A) with the hyperoxia (85% O₂)‐exposed (Fig. 1B) mouse pups. Visual inspection of Richardson‐stained lung sections revealed fewer and larger alveoli and reduced alveolar density in the 85% O₂‐exposed lungs (Fig. 1A,B; quantified in Fig. 1E,H). Higher‐magnification images also demonstrated that 85% O₂ exposure generated increased thickness of the alveolar septa (Fig. 1C,D, quantified in Fig. 1F). These data validated the utility of hyperoxia in the present study as a viable injurious stimulus to limit proper lung alveolarisation in this experimental animal model of BPD (Nardiello et al. 2017a,b).

Figure 1.

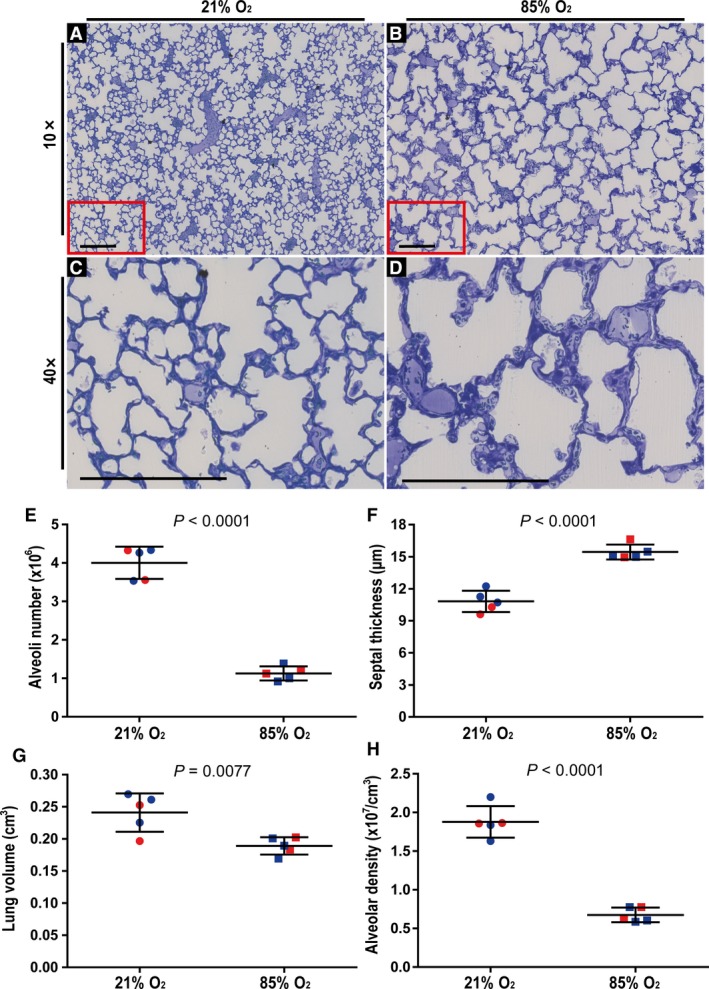
Validation of the impact of hyperoxia exposure on post‐natal lung alveolarisation in an experimental mouse model of bronchopulmonary dysplasia. Visual inspection of histology sections from mice exposed to (A) 21% O₂ revealed normal lung architecture, whereas (B) a reduction in the number and an increase in the size of the alveoli was clearly evident in lungs from mice exposed to 85% O₂ for the first 14 days of post‐natal life. Similarly, under higher magnification (C,D), an increase in the arithmetic mean septal thickness comparing lung sections from (C) 21% O₂‐exposed mouse pups and (D) 85% O₂‐exposed mouse pups, was clearly evident. Sections represent the same trends observed in another four mice in each experimental group. (C,D) Higher‐magnification images of the regions demarcated by the red box in (A) and (B), respectively. Scale bar: 200 μm. The (E) total number of alveoli in the lung, (F) arithmetic mean septal thickness, (G) lung volume, and (H) alveolar density were quantified by stereology analyses and lung volume determination using Cavalieri's principle. Male animals are indicated by blue symbols, and female animals by red symbols. Data reflect mean ± SD (n = 5 animals per experimental group). Comparisons were made by unpaired Student's t‐test.

Oxygen injury impacts lung volume

The five lobes that make up the mouse lung could be effectively separated from each other post‐fixation for subsequent individual analysis (Fig. 2A). During normal lung development in 21% O₂‐exposed mouse pups, at P14 the l. sinister exhibited the largest lung volume (Fig. 2B, Table 1), followed by the l. caudalis, and then the l. cranialis, with the l. medius and l. cardialis being the smallest lung lobes in terms of volume, and exhibiting approximately similar volumes (Fig. 2B, Table 1). These trends were preserved in newborn C57BL/6J mice exposed to 85% O₂ from the day of birth up to and including P14 (Fig. 2B, Table 2), where oxygen injury did not alter lung lobe volumes of the l. medius, l. caudalis, or l. cardialis, compared with 21% O₂‐exposed pups (Fig. 2B). However, oxygen injury did generate a smaller lung volume for the l. cranialis and the l. sinister compared with 21% O₂‐exposed mouse pups with normal lung development (Fig. 2B). Oxygen injury also generated a smaller volume of whole, intact lungs in mice exposed to 85% O₂ (Fig. 1G; Tables 1 and 2). Oxygen injury did not appreciably impact the proportional contribution of individual lung lobes to total lung volume (Fig. 2C), with the exception of a minor effect on the two smallest lung lobes. In mice exposed to 21% O₂, the l. medius was the smallest lobe, and in mice exposed to 85% O₂, the l. cardialis was the smallest lobe (Fig. 2C).

Figure 2.

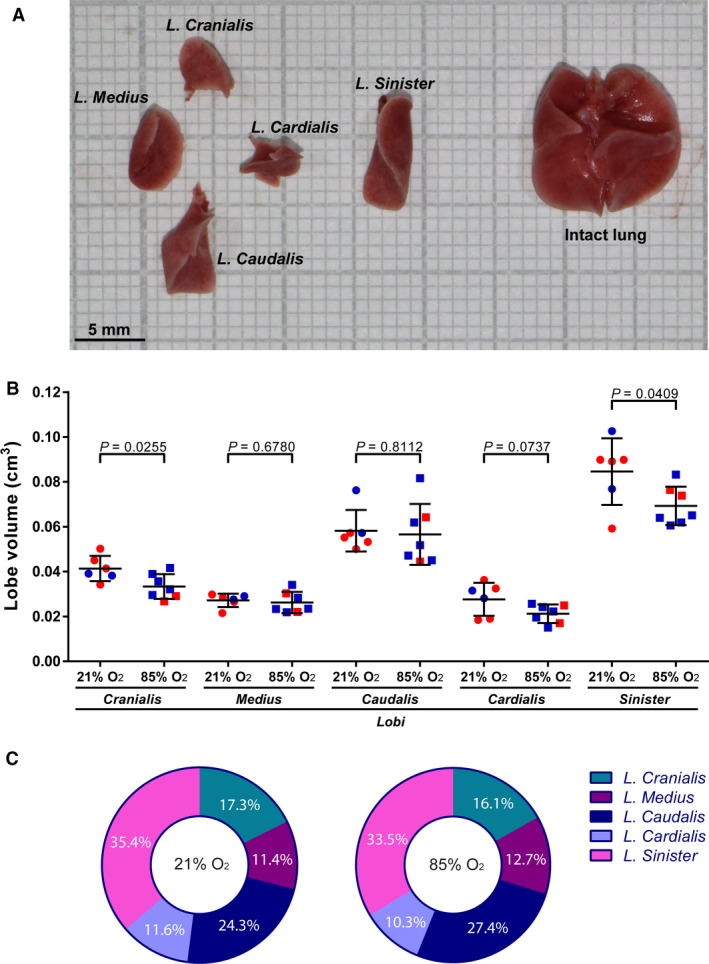
Determination of lung lobe volumes during normal and aberrant late lung development. On the 14th day of post‐natal life, lungs were extracted from mouse pups and separated into constituent lobes. (A) Illustration of the separated lung lobes (left) and intact lungs (right) from a 21% O₂‐exposed mouse pup. (B) Comparison of the volume of the lung lobes from mice with normal (21% O₂‐exposed) and aberrant (85% O₂‐exposed) late lung development. Male animals are indicated by blue symbols and female animals by red symbols. Data reflect mean ± SD (n = 6–7 animals per experimental group). Comparisons were made by unpaired Student's t‐test. (C) Pie charts comparing the contribution to total lung volume (as a sum of the volume of five lobes from the same animal) of individual lung lobes, in mice with normal (21% O₂‐exposed) and aberrant (85% O₂‐exposed) late lung development. The percentages indicated describe the average values obtained from six to seven animals per experimental group.

Oxygen injury stunts post‐natal lung alveolarisation in all lung lobes

The alveolar density in the five lung lobes of mouse pups with normal lung development (21% O₂‐exposed) appeared largely similar by visual inspection (Fig. 3A, upper panel of the 21% O₂ group). However, quantitative analysis revealed that the alveolar density exhibited variability across the lung lobes, with the l. cranialis, the l. medius and the l. caudalis exhibiting the highest alveolar density (Fig. 4A). The remaining two lobes exhibited a reduced alveolar density compared with that of the l. cranialis (Fig. 4A). In terms of representativeness of alveolar density of individual lung lobes to the alveolar density of whole, intact lungs, all five lobes exhibited alveolar density that was comparable to that of intact lungs (assessed by one‐way anova with Tukey's post hoc modification of the data in Table 1).

Figure 3.

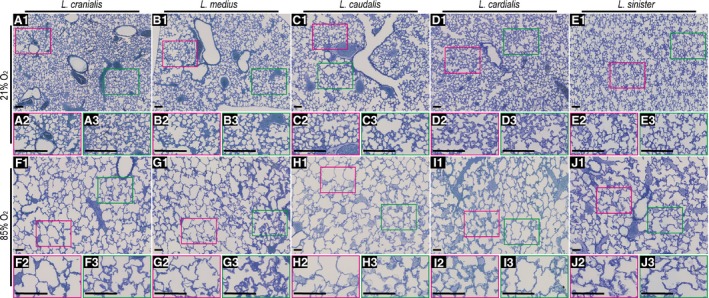
Gross morphology of lung lobes from mice during normal and aberrant late lung development. For mice undergoing normal (21% O₂‐exposed) and aberrant (85% O₂‐exposed) late lung development, a low‐magnification view is presented in the upper panel of each oxygen‐exposure group, and two higher‐magnification views are presented for each lobe below the low‐magnification panel (extracted from the areas demarcated by red and green boxes), to highlight structural variability within the same lobe. Sections represent the same trends observed in another six to seven mice in each experimental group. Scale bar: 100 μm.

Figure 4.

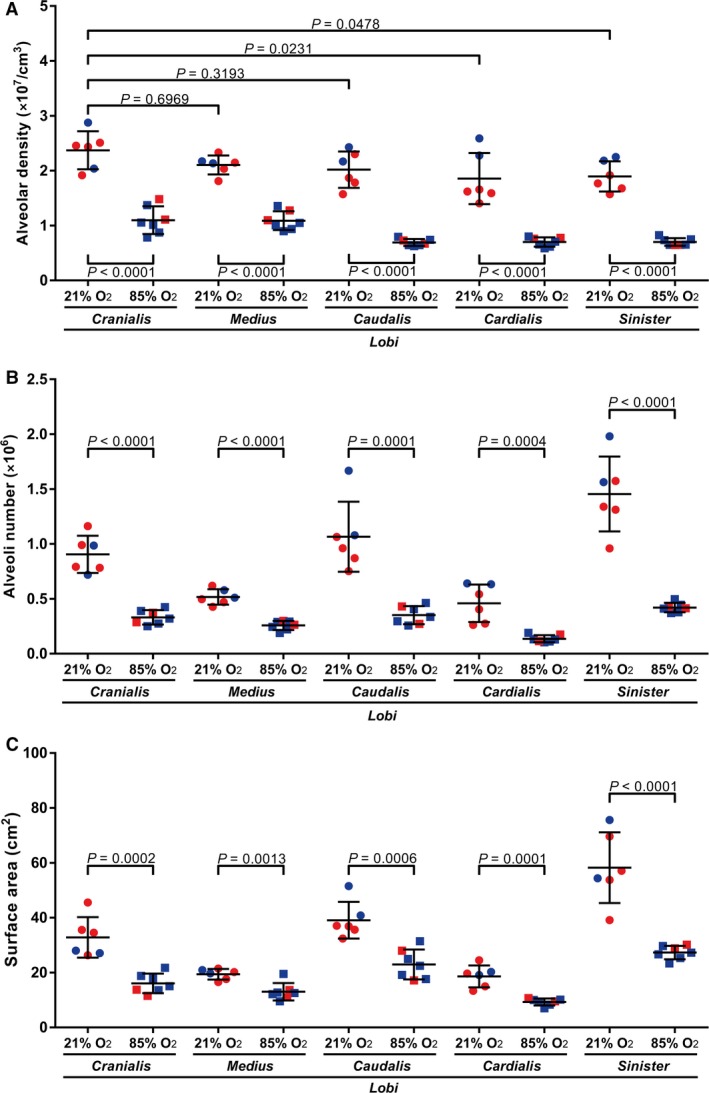
Stereological analysis of alveolar density, alveoli number, and gas‐exchange surface area, in individual lobes of lungs from mice during normal and aberrant late lung development. The (A) alveolar density, (B) total number of alveoli in the lung, and (C) gas‐exchange surface area were determined in the lungs of mice with normal (21% O₂‐exposed) and aberrant (85% O₂‐exposed) late lung development. Male animals are indicated by blue symbols and female animals by red symbols. Data reflect mean ± SD (n = 6–7 animals per experimental group). (A) Statistical comparisons were made by one‐way anova with Tukey's post hoc modification. (B,C) Statistical comparisons are only illustrated for pairwise comparisons between the 21% O₂‐ and 85% O₂‐exposed groups, using an unpaired Student's t‐test. Additional stereology parameters are provided in Tables 1 and 2.

As the largest mouse lung lobe, the l. sinister contained the largest number of alveoli in normally developing mice (Fig. 4B, Table 1). Consistent with being the second‐ and third‐largest lobes, the l. caudalis and the l. cranialis, respectively, each contained more alveoli than did the l. medius or the l. cardialis (Fig. 4B), which are the smallest two lobes of the mouse lung, by volume (Fig. 2C, Table 1). As the gas‐exchange surface area is directly related to the number of alveoli and the alveolar density, the trends in gas‐exchange surface area (Fig. 4C) directly paralleled trends in alveolar density (Fig. 4A) and total alveoli number (Fig. 4B).

Exposure of newborn C57BL/6J mice to 85% O₂ for the first 14 days of post‐natal life had a pronounced impact on the alveolarisation of all five mouse lung lobes (Fig. 3). Quantitative analysis revealed a reduction in alveolar density (Fig. 4A), total alveoli number (Fig. 4B), and gas‐exchange surface area (Fig. 4C) in all five lobes, comparing 21% O₂‐exposed with 85% O₂‐exposed mouse lungs. Changes to the architecture of the developing mouse lung lobes were not uniform within the lobes, where regional differences in lung structure are highlighted (in Fig. 3) by comparing different regions within the same lung section that are demarcated by red and green boxes, and presented as a magnified image below the image panel. For example, regional changes in apparent alveoli number and diameter (assessed by visual inspection) are documented for the l. cranialis (compare Fig. 3F2,F3), the l. caudalis (compare Fig. 3H2,H3) and the l. sinister (compare Fig. 3J2,J3). Similarly, regional changes in apparent septal thickness (also assessed by visual inspection) are documented for the l. medius (compare Fig. 3G2,G3) and the l. cardialis (compare Fig. 3I2,I3).

Oxygen injury differentially impacts arithmetic mean septal thickness in lung lobes

The arithmetic mean septal thickness in the five lung lobes of mouse pups with normal lung development (21% O₂‐exposed) appeared largely similar by visual inspection (Fig. 3, upper panel of the 21% O₂ group). Indeed, no quantitative changes in arithmetic mean septal thickness within the 21% O₂‐exposed group were noted, comparing all five lung lobes with each other, and with whole, intact lungs (P > 0.05 for all arithmetic mean septal thickness data presented in Table 1, when assessed by one‐way anova with Tukey's post hoc modification).

The arithmetic mean septal thickness measured in whole, intact mouse lungs from oxygen‐injured (85% O₂‐exposed) mouse pups was increased (Fig. 1F). The numerical value of the arithmetic mean septal thickness was higher in all five lobes from lungs from oxygen‐injured mouse pups, compared with the corresponding lung lobes from 21% O₂‐exposed littermates. The arithmetic mean septal thickness was increased in the l. cranialis, the l. medius, the l. caudalis and the l. sinister from lungs from oxygen‐injured mouse pups compared with the same lobes from 21% O₂‐exposed littermates (Fig. 5), while the arithmetic mean septal thickness of the l. cardialis was similar in lungs from mouse pups exposed to 21% O₂ and 85% O₂.

Figure 5.

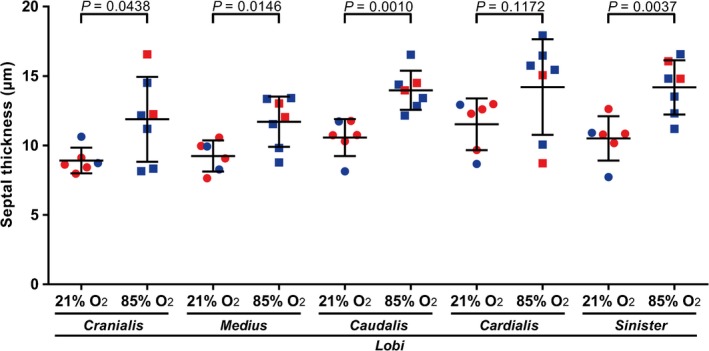
Stereological analysis of arithmetic mean septal thickness in individual lobes of lungs from mice during normal and aberrant late lung development. The arithmetic mean septal thickness was determined in the lungs of mice with normal (21% O₂‐exposed) and aberrant (85% O₂‐exposed) late lung development. Male animals are indicated by blue symbols and female animals by red symbols. Data reflect mean ± SD (n = 6–7 animals per experimental group). Statistical comparisons are only illustrated for pairwise comparisons between the 21% O₂‐ and 85% O₂‐exposed groups, using an unpaired Student's t‐test.

No quantitative changes in arithmetic mean septal thickness within the 85% O₂‐exposed group were noted, comparing all five lung lobes with each other, and with whole, intact lungs (P > 0.05 for all arithmetic mean septal thickness data presented in Table 2, when assessed by one‐way anova with Tukey's post hoc modification).

The intact lung structure is largely reflected by the summa loborum in normally developing, but not aberrantly developing lungs

During normal lung development (21% O₂‐exposed mouse pups), the lung volume estimated by Cavalieri's principle for a whole, intact lung was comparable to the lung volume obtained mathematically from the sum of the volumes of the five constituent lung lobes, where the lobe volumes had been determined separately for each lobe (summa loborum; Fig. 6A). Similarly, for the determination of total number of alveoli (Fig. 6C) and gas‐exchange surface area (Fig. 6E) during normal lung development, values obtained for the whole, intact lungs were comparable to values obtained for the summa loborum. However, during aberrant lung development, the value for total alveoli number assessed by the summa loborum approach was 28% higher than that obtained by direct analysis of whole, intact lungs (Fig. 6D). Furthermore, while the values for lung volume (Fig. 6B) and gas‐exchange surface area (Fig. 6F) assessed by the summa loborum approach were comparable to those obtained by direct analysis of the whole, intact lung (P > 0.05), the numerical value of the means for both parameters was higher in the summa loborum approach. In fact, the higher magnitude of the mean lung volume in the summa loborum approach may have led to the (now significantly) increased (by 28%) total alveoli number assessed in the summa loborum approach.

Figure 6.

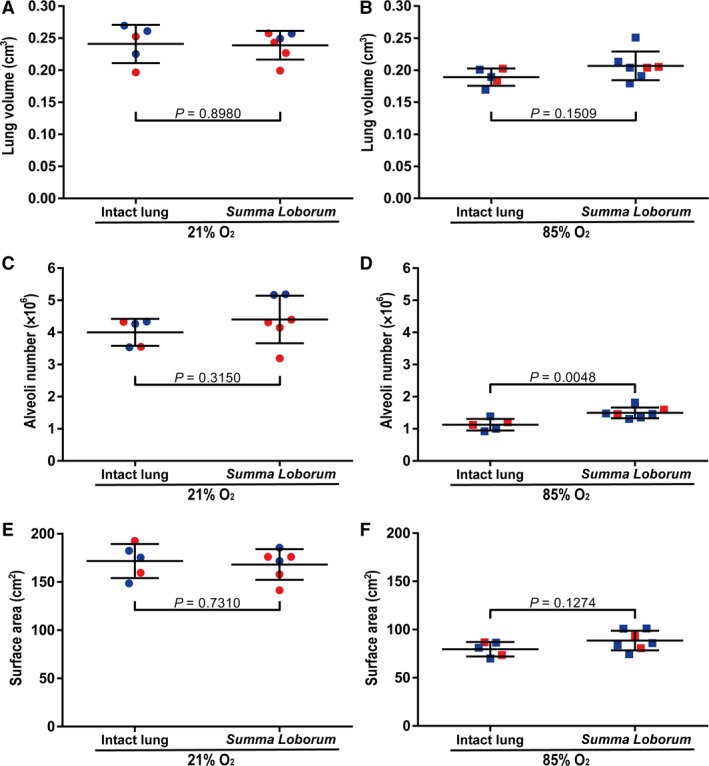
Comparison of lung volume, alveoli number, and gas‐exchange surface area obtained using intact lungs vs. individual lung lobes. (A,B) Lung volume, (C,D) total alveoli number, and (E,F) gas‐exchange surface area were determined either directly, using whole, intact lungs, or mathematically, by the sum of the volumes of the five constituent lobes that had been determined separately for each lobe (summa loborum). Determinations were made for lungs of mice undergoing (A,C,E) normal (21% O₂‐exposed) or (B,D,F) aberrant (85% O₂‐exposed) late lung development. Male animals are indicated by blue symbols and female animals by red symbols. Data reflect mean ± SD (n = 6–7 animals per experimental group). Comparisons were made by unpaired Student's t‐test.

For alveolar density (Fig. 7A) and arithmetic mean septal thickness (Fig. 7C) – two parameters that cannot be summed from individual lobes – the values obtained in whole, intact, normally developing lungs were comparable to the average values obtained when the data for the five individual lung lobes were considered together as a whole. Two different approaches were adopted when the five lung lobes were considered together as a whole (stratified samples): either an average value of the five lung lobes (‘cumulative average’) was calculated or a proportional contribution by the five lung lobes, based on lobe volume (‘proportional contribution’) was calculated. These calculations are described in detail in the Methods section. When comparing values for alveolar density in normally developing lungs, the values obtained with whole, intact lungs were in complete agreement with the values obtained with stratified samples (Fig. 7A). Similarly, for the arithmetic mean septal thickness in normally‐developing lungs, the values obtained with whole, intact lungs were in complete agreement with the values obtained with stratified samples (Fig. 7C). However, this was not the case in aberrantly developing lungs, where the two approaches utilising data from individual lung lobes (stratified samples) from oxygen‐injured lungs were in agreement with one another, but the data obtained from both stratified sample approaches led to the estimation of a higher alveolar density (Fig. 7B) and a lower arithmetic mean septal thickness (Fig. 7D), when compared with the values from whole, intact oxygen‐injured lungs.

Figure 7.

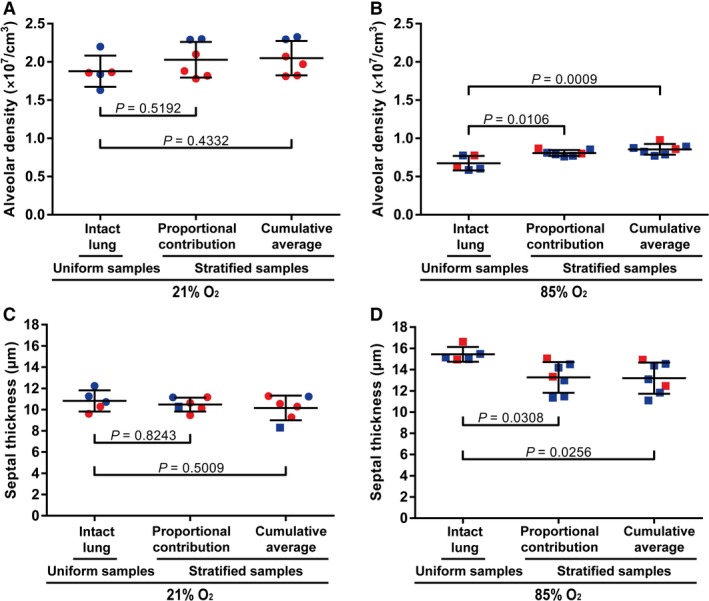
Comparison of alveolar density and arithmetic mean septal thickness obtained using uniform vs. stratified samples. The alveolar density obtained by stereological analysis of intact lung samples vs. stratified (separated lobe) samples was compared for the lungs of mice with (A) normal (21% O₂‐exposed) and (B) aberrant (85% O₂‐exposed) late lung development. Similarly, the arithmetic mean septal thickness obtained by stereological analysis of intact lung samples vs. stratified (separated lobe) samples was compared for the lungs of mice with (C) normal (21% O₂‐exposed) and (D) aberrant (85% O₂‐exposed) late lung development. Male animals are indicated by blue symbols and female animals are by red symbols. Data reflect mean ± SD (n = 6–7 animals per experimental group). Comparisons were made by one‐way anova with Tukey's post hoc modification.

Discussion

Advances in the quantitative assessment of lung structure have the capacity to impact significantly our understanding of lung physiology and disease. Notable among these advances, the development of stereological approaches to study the lung architecture has introduced a method of obtaining high‐precision, robust, and minimally biased data. Using stereology, pathological or developmental changes in the total number of alveoli, the arithmetic mean septal thickness, and gas‐exchange surface area, among other parameters, may be detected with high precision. One of the practical drawbacks of the stereological approach is the increased time and financial burden placed on investigators, in comparison with alternative approaches. This has limited the enthusiasm for widespread implementation of stereological approaches for the study of lung architecture in investigative laboratories. To explore potential solutions to this problem, we embarked on a study to assess whether ‘limited stereology’, that is to say, the stereological analysis of representative parts (in this case, lobes) of the lung, may serve as a surrogate for ‘intact lung’ or ‘whole lung’ studies, in investigations on mouse lung structure.

In lungs from mice at P14, the five lobes that make up the mouse lung could be successfully separated from each other. The l. sinister was the largest lung lobe, by volume, followed by the l. caudalis, and the l. cranialis, with the l. medius and l. cardialis being the smallest lung lobes in terms of volume and exhibiting approximately similar volumes. This observation contrasts with reports in 6‐week‐old male Ivanova SIVZ rats, where the l. medius is reported to be larger than the l. cranialis (Zeltner et al. 1990). During normal mouse lung development, all mouse lung lobes exhibited alveolar density that was comparable to the alveolar density assessed in intact lungs (Fig. 4A, Table 1, and associated statistical analyses presented in the Results section). Furthermore, the arithmetic mean septal thickness of all mouse lung lobes was comparable to the arithmetic mean septal thickness assessed in intact lungs (Fig. 5, Table 1, and associated statistical analyses presented in the Results section). As such, in normally developing healthy mice, all lung lobes are appropriate surrogates for the studies on whole, intact lungs, for the measurement of alveolar density and arithmetic mean septal thickness. This idea is supported by the observations that both the proportional contribution values and the cumulative average values for alveolar density and arithmetic mean septal thickness approximate the values obtained for both parameters made in whole, intact lung (Fig. 7A,C). It is important to note that both parameters are also ‘volume independent’, that is to say, the values are independent of the measurement of lobe or lung volume using Cavalieri's principle.

For other parameters, including the total alveoli number and gas‐exchange surface area, the magnitude of both parameters was proportional to the unit (either lobe or lung) volume. As such, it is critical that the lung volume is correctly measured. Lung volume determination was undertaken using Cavalieri's principle, as this has been documented to be more accurate in lungs from neonate and young (as opposed to adult) mice (Pozarska et al. 2017). There is no way to confirm that each individual lung lobe was fully or uniformly inflated in our study. The alveolar structure of each lobe noted by visual inspection (Fig. 3) suggested that all five lobes were fully and uniformly inflated. Furthermore, the sum of the volumes of the lung lobes (summa loborum) was perfectly in line with the lung volume determined in whole, intact lungs (Fig. 6A), suggesting that the degree of inflation of the lobes was uniform and comparable in the separated lung lobe study and in the whole, intact lung study. Furthermore, the mean linear intercept (roughly, the average distance between two adjacent septa) would decrease if lung tissue was compressed due to underinflation. However, the MLI values for individual lung lobes as well as the MLI values for whole, intact lungs were all comparable to one another in the lungs of normally developing mouse pups (Table 1; P > 0.05 for every comparison made by one‐way anova with Tukey's post hoc modification, for the MLI data in Table 1). As additional support for lung lobes being uniformly inflated, we note that the arithmetic mean septal thickness would increase if lung tissue was collapsed due to underinflation. The consistently comparable MLI and arithmetic mean septal thickness across all five lung lobes and the intact lungs of normally developing mouse pups lends strong support to the notion that the lungs and lobes were ‘properly’ inflated.

Turning to measurement of lung structure in a pathological context, we have employed a mouse model of BPD, where exposure of newborn mice to normobaric hyperoxia, stunts lung development, leading to fewer, larger alveoli, and increased septal thickness (Buczynski et al. 2013; Silva et al. 2015). In the lung structure analyses, several perturbations to lung alveolarisation were noted throughout the developing lung, where approximately 4 million alveoli were noted in normally developing lungs, while only 1 million alveoli were noted in aberrantly developing lungs. In terms of alveoli number, alveolar density, and gas‐exchange surface area, all mouse lung lobes were equally impacted, with regional variability in disturbances to lung structure being noted within the affected lobes. This was not true for arithmetic mean septal thickness, which was consistently increased in all lung lobes after exposure to hyperoxia, except for the l. cardialis, where no increase was noted. It is important to stress at this junction that ‘regional’ effects were considered at the level of individual lobes. There are other ways to describe ‘regions’ of the lung. For example, pathological perturbations to the lung structure may preferentially impact the pleural regions or the regions adjacent to the hilus. The data reported here would not reveal these regional effects, which were considered at the level of the individual lobes. In lung pathology where lung structure is not uniformly impacted, using a selected lung lobe as a surrogate for the entire lung would not be useful. Similarly, a study on an entire lung may also not be useful. This concept of regional differences is also relevant to developing lung, where lung development does not proceed uniformly throughout the lung, but rather starts in the proximal regions and then extends into the peripheral regions (Schittny, 2017); and the cranial part of the lung is thought to develop faster than the caudal part (Warburton et al. 2010). Stereological approaches that could selectively address the pleural or hilus regions of the lung (or any other lung region that cannot be physically isolated for individual analysis) may also be applied, although there is some risk of bias, depending on how reliably and reproducibly these subregions of the lung are delineated as the reference volumes.

In oxygen‐injured lungs, the proportional contribution and cumulative average values for alveolar density and arithmetic mean septal thickness of lung lobes did not approximate the values obtained for both parameters in whole, intact lungs (Fig. 7B,D). Also, the summa loborum for total alveoli number (1.52 million) was higher than the total alveoli number obtained from whole, intact lungs (1.13 million; Fig. 6D). The reasons for these discordant data, as marginal as the differences are in oxygen‐injured developing lungs, are not yet apparent. One concern may be that the systematic uniform random sampling of individual lobes, when combined, does not necessarily represent systematic uniform random sampling of the entire, intact lung. Another possibility is that the increased tissue coverage of the individual lobe study yielded more precise data, as, cumulatively, the individual lobe approach examined 13% of the entire lung, whereas for the intact, whole‐lung studies, 3% of the entire lung was examined.

Although the sex of each animal studied is indicated in all data plots, this study was not powered to evaluate sex as a modifier of alveolarisation in specific lung lobes. This is an important issue, given reports that sex may influence the responses of developing mouse lungs to hyperoxia exposure (Lingappan et al. 2016), although sex does not appear to be a modifier of normal lung alveolarisation up to P14 (Pozarska et al. 2017). Although the data here do not obviously suggest sex as a modifier of lobe alveolarisation at P14, it is important to note that sex may indeed be a modifier of lobe alveolarisation at later ages.

In sum, these data represent the first side‐by‐side comparison of stereology‐based analyses of the mouse lung architecture at the level of individual lobes, during normal and aberrant post‐natal lung development. These data indicate that in healthy mouse lungs, stereology‐based analyses of individual lung lobes may serve as surrogates for all parameters investigated in the present study. Furthermore, in terms of the pathobiology of BPD, the individual lung lobe studies indicate that – with the exception of arithmetic mean septal thickness – no specific lung lobe is more or less impacted by oxygen injury, where the exposure of newborn mice to a hyperoxic environment appears to uniformly stunt lung alveolarisation throughout the entire developing lung. However, given that the total number of alveoli in the lung can only be determined by an analysis of the entire lung, and given the regional differences in lung structure, particularly under pathological conditions, the stereological assessment of the whole, intact lung remains desirable. Thus, in studies addressing the impact of oxygen toxicity on lung alveolarisation, the assessment of the entire, intact lung remains the recommendation of these investigators.

Author contributions

T.V.H. and C.N. performed stereology analyses; C.N. and D.E.S.S. performed hyperoxia studies on mice; T.V.H., C.N., D.E.S.S., J.A.R.C., and P.R. processed stereology data; T.V.H. performed PCR analyses; T.V.H., C.N., P.R., K.M., I.V., S.H., K.A., W.S., and R.E.M. conceptualised experimental studies; K.M., S.H., K.A., W.S., and R.E.M. provided facilities; T.V.H., C.N., D.E.S.S., J.A.R.C., P.R., K.M., I.V., S.H., K.A., W.S., and R.E.M. analysed data; T.V.H., C.N., P.R., and R.E.M. wrote the manuscript.