Utilizing networks for differential analysis of chromatin interactions

Abstract

Chromatin conformation capture with high-throughput sequencing (Hi-C) is a powerful technique to detect genome-wide chromatin interactions. In this paper, we introduce two novel approaches to detect differentially interacting genomic regions between two Hi-C experiments using a network model. To make input data from multiple experiments comparable, we propose a normalization strategy guided by network topological properties. We then devise two measurements, using local and global connectivity information from the chromatin interaction networks, respectively, to assess the interaction differences between two experiments. When multiple replicates are present in experiments, our approaches provide the flexibility for users to either pool all replicates together to therefore increase the network coverage, or to use the replicates in parallel to increase the signal to noise ratio. We show that while the local method works better in detecting changes from simulated networks, the global method performs better on real Hi-C data. The local and global methods, regardless of pooling, are always superior to two existing methods. Furthermore, our methods work well on both unweighted and weighted networks and our normalization strategy significantly improves the performance compared with raw networks without normalization. Therefore, we believe our methods will be useful for identifying differentially interacting genomic regions.

1. Introduction

Chromatin organization plays an important role in many molecular level cell activities, such as gene expression regulation, DNA replication and repair.^1,2 Many experimental approaches have been devised to detect chromatin interactions between genomic loci that are close in three-dimensional space but may be far separated in a linear genome.^3–7 One of the approaches, chromatin conformation capture with high-throughput sequencing (Hi-C),⁶ captures genome-wide chromatin interactions. Existing research shows that there are many changes in chromatin interactions between experiments of different conditions.^8,9 Changes in chromatin interactions impact chromatin organization and function. Therefore, finding Hi-C data differences between experiments is important to new biological discoveries and the differences may help to reveal the underlying mechanisms related to biological conditions being studied.

A few computational tools have been developed to compare chromatin interactions and they have a common limitation. They either pool replicates or treat replicates separately, but do not allow users to decide according to their replicate quality, availability and research goals. Existing approaches fall into two categories; one tries to identify differential interactions, and the other reports genomic regions with significantly different interaction patterns. DiffHiC is a Bioconductor package to detect differential interactions.¹⁰ It uses a generalized linear model and quasi-likelihood methods to estimate biological variability of separated replicates. Owing to limited number of replicates and large number of interactions in real data, it often fails to detect any statistically significant patterns after correction for the multiple comparisons problem. HiBrowse is a user-friendly web-tool to detect differential interactions of separated replicates.¹¹ The web-tool is consisting of a range of hypothesis-based and descriptive statistics. Similar to diffHiC, it also suffers from low statistical power due to multiple comparisons. Also, because of its web-only feature, HiBrowse cannot be applied to analyze large-scale data sets. MDM proposes two models for pooled ChIA-PET count data to identify differential chromatin interactions mediated by a protein of interest.^7,12 Both models incorporate the data dependency and the extent to which a fragment pair is related to a pair of DNA loci of interest. But it cannot process Hi-C chromatin interaction data because it is intended for chromaitn interactions mediated by a protein of interest.

To the best of our knowledge, HOMER is the only available program that is designed to identify genomic regions whose interaction patterns are significantly different under different conditions.¹³ It pools replicates at first and correlates genomic regions’ interactions of one experiment with the ones of the other experiment. Therefore, it does not consider biological variability. Moreover, it ignores the inter-chromosomal interactions. In our opinion, a novel method is needed to allow users to decide when to pool replicates and when to treat them separately.

Chromatin interaction data can be represented as networks, which are widely used in differential analysis of biological data. A paper conducts a differential analysis of networks constructed from microarray data under two experimental settings.¹⁴ Another paper proposes a network-based method to assess the degree of topological difference between two DNA methylation experiments.¹⁵ But there is no research applying networks to compare chromatin interaction data.

In this study, we propose two novel approaches to identify differentially interacting genomic regions between experiments by constructing networks from chromatin interaction data while accommodating the option for users to pool replicates or treat them separately. Our paper has four major contributions. First, our methods provide the flexibility of pooling replicates or treating them separately. Second, we are the first using networks to carry out differential analysis of chromatin interaction data. Third, we propose a novel normalization strategy guided by network topological properties to make data comparable from different experiments. Fourth, we devise two measurements to assess interaction differences with local and global information from interaction networks. We show that while the local method works better in detecting changes from simulated networks, the global method performs better on real Hi-C data. The local and global methods, regardless of pooling, are always superior to two existing methods. Furthermore, our methods work well on both unweighted and weighted networks and our normalization strategy significantly improves the performance compared with raw networks without normalization.

The rest of this paper is organized as follows. Section 2 describes our methods in detail, which includes network construction, network normalization and two measurements of differential genomic regions. Section 3 evaluates our methods with simulated networks, real data sets and different configurations. We conclude in Sec. 4.

2. Methods

We propose two network-based methods to identify differentially interacting genomic regions. They can process pooled data and treat replicates separately. When replicates are treated separately, our methods consider biological variability. The workflow of our methods is shown in Fig. 1. Rather than starting from raw reads, our methods take processed chromatin interactions as input since a lot of studies have been done.^16–22 Our methods are comprised of three parts, network construction, network normalization and differential measurements. The output of our methods are two ranked genomic region lists according to two differential measurements.

Fig. 1.

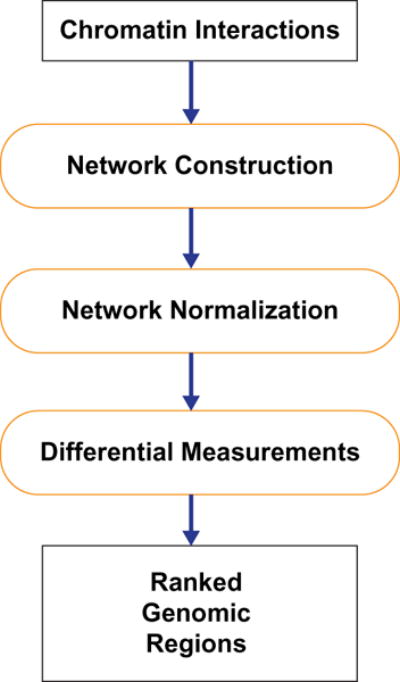
A typical workflow of analyzing chromatin interaction data.

2.1. Network construction

Each chromosome is divided into equal sized bins, whose size is customized by users. Later, we will show that the performance of different bin sizes is robust. Bins from all chromosomes are arranged in tandem and numbered in an ascending order. To construct a Hi-C network, we create a node for each bin and connect two nodes by an edge if there are chromatin interactions between the corresponding bins in the input. The edge is weighted by the number of chromatin interactions between these two bins. When replicates are treated separately, the above procedure is applied to each replicate, respectively.

2.2. Network normalization

Chromatin interaction data of different experiments may have different sizes because of different sequencing depths or amounts of DNA used in experiments, which makes the networks quite different in number of edges. To make the networks comparable, we need to normalize them. A commonly used approach to normalize data is utilizing a cutoff to remove low frequency data. Since real networks are quite different from randomly generated ones on network topological properties, we assume when a right cutoff is selected, network topological properties will reach their optima compared to randomly generated networks. During the revision stage of this paper, Yan et al.²³ published a network modularity-based algorithm, MrTADFinder, to identify topologically associating domains from HiC data, which confirms our idea that network topological properties can be utilized to guide the construction of HiC networks. Besides, biological functional networks are generally sparse.^24,25 Therefore, our normalization strategy is to create sparse networks with optimal network topological properties when compared with randomly generated networks. We try different cutoffs and select the cutoff according to Clustering Coefficient (CC),²⁶ which is a measure of the degree to which nodes in a network tend to cluster together. In undirected networks, the CC_n of a node n is defined by Eq. (1), where K_n is the number of neighbors of n and E_n is the number of connected pairs between all neighbors of n. The network clustering coefficient (NCC) is the average of the CCs for all nodes in the network as defined by Eq. (2):

$${\text{CC}}_n=\frac{2\ast E_n}{K_n\ast (K_n-1)},$$ (1)

$$\text{NCC}=\frac{{\displaystyle {\sum }_{i=1}^M{\text{CC}}_i}}{M}.$$ (2)

A series of cutoffs are used to generate unweighted networks with a targeted edge density (e.g. 1%). The NCC is calculated for each unweighted network, respectively. Network randomization is carried out 100 times on each unweighted network by changing nodes’ edges but maintaining their degrees unchanged, and NCCs are also calculated for these 100 randomized networks. Zscores are estimated by comparing the real network’s NCC over the average and standard deviation of the randomized networks’ NCCs, as defined in Eq. (3). The zscores are plotted as a function of the cutoffs, and when the zscores reach the peak, the corresponding cutoff is selected as the optimal cutoff for constructing the sparse chromatin interaction networks. When applying the cutoff and turning raw networks into matrices with 0 and 1, we get unweighted networks; when applying the cutoff and keeping the high frequency edges’ weights, we get weighted networks. In Sec. 3.3.2, we will show that the results on these two types of normalized networks are similar:

$$\text{z score}=\frac{{\text{NCC}}_{\text{real}}-\text{mean}({\text{NCC}}_{\text{random}})}{\text{std}({\text{NCC}}_{\text{random}})}.$$ (3)

2.3. Differential measurements

To identify differentially interacting nodes between two (or two groups of) networks, we propose two measurements to identify nodes whose connections changed significantly. For a node, both its degree and neighbors are important to its connections. Meanwhile, its neighbors’ connections are also important to its connectivity, for example, connecting to a hub node and connecting to a non-hub node are different. Therefore, we propose two measurements, Hi-C Differences with local information (HD^L) and Hi-C Differences with global information (HD^G). HD^L only uses local information from chromatin interaction networks, while HD^G uses both local and global information.

2.3.1. HD^L

HD^L combines a node’s degree and neighbors to find the node’s connection differences between experiments. Assume there are h networks from experiment A, and there are k networks from experiment B. For experiment A, networks are represented in matrices as $P_{ij}^1$, $P_{ij}^2$, … $P_{ij}^h$; for experiment B, networks are represented in matrices as $Q_{ij}^1$, $Q_{ij}^2$, …, $Q_{ij}^k$. $q_{ij}^r$ represents the number of edges between node i and node j in the rth network of experiment A and $p_{ij}^s$ represents the number of edges between node i and node j in the sth network of experiment B. Assume there are n nodes in a Hi-C interaction network. The measurement is shown in Eqs. (4) and (5). Equation (4) is used to find a node’s difference between two networks by calculating the Euclidean distance based on the node’s connection vectors. Euclidean distance captures any difference in node degree and neighbors. Equation (5) is used to calculate the average of differences between experiments. When interaction patterns of the node are significantly different, HD^L generates a high score; when the node’s interaction patterns are similar, HD^L produces a low score:

$$D_i^{rs}=\sqrt{{\displaystyle \sum _{j=1}^n(p_{ij}^r-q_{ij}^s)}},$$ (4)

$${\text{HD}}_i^L=\frac{{\displaystyle {\sum }_{r=1,s=1}^{r=h,s=k}{D}_i^{rs}}}{h\ast k}.$$ (5)

2.3.2. HD^G

HD^G utilizes global information by applying Random Walk with Restart (RWR) to each network, respectively.²⁷ RWR is a well-known machine learning algorithm used to measure the relevance scores between nodes by imagining that starting from each node there is a random walker, which at each step, either moves to a randomly chosen neighbor, or jumps back to the starting node. We formulate the procedure in Eq. (6). I is an identity matrix and denotes the matrix of initial relevance scores; p (fixed at 0.5 in this study) represents the probability for a random walker to jump back to the starting node and restart the walk; M is the Hi-C network transition probability matrix; S_n is a probability matrix, where S_n (i, j) represents the probability for a random walker started at node i to reach node j after n steps. When the random walk procedure reaches an equilibrium, as the walkers randomly choose their routes so they would cover all paths between nodes, the RWR probability matrix represents relevance between nodes which implicitly includes global topology information. Equations (4) and (5) are used on RWR probability matrices of different experiments:

$$S_n=(1-p)\ast M\ast S_{n-1}+p\ast I.$$ (6)

3. Results and Discussion

We first use simulated networks to validate the two differential measurements. Then, to compare with other approaches, we apply our methods on real Hi-C data sets,²⁸ and investigate the functional relevance measured by the correlations between each method’s result and genomic features that are known to be important for regulating chromatin conformation, including CCCTC-binding factor (CTCF) binding sites and several histone modification markers. We also show that our methods work well on both unweighted and weighted networks and our normalization strategy significantly improves the performance compared to raw networks without normalization. Furthermore, the performance of different bin sizes is robust.

3.1. Performance on simulated networks

To validate differential measurements, we test them on simulated networks. First, an unweighted network of 1000 nodes is generated with a parameter, c, which represents the number of clusters in the network and is initialized to 1. For the simulated network, intra-cluster nodes have a higher uniform probability to connect than inter-cluster nodes and probabilities are chosen such that intra-cluster connectivity per node is roughly 40 and inter-cluster connectivity is roughly 10. Then the network is copied and 100 nodes are selected randomly. We completely rewire these 100 nodes’ edges in a random way. Therefore, these two networks are significantly different in the 100 randomly selected nodes, which serve as the ground truth. Thereafter, we use the two networks as network templates. For each network template, three replicates are generated, respectively, by rewiring template edges with a parameter, p, which specifies the percentage of edges in the template network to be rewired. When rewiring the edges, these nodes’ neighbors are modified, but these nodes’ degrees maintain unchanged. HD^L and HD^G are then applied to these six network replicates to identify top-100 differentially interacting nodes. The numbers of true positives among the 100 predicted nodes are counted. The above procedure is repeated 10 times and the mean and standard deviation of true positives are calculated. The whole experiment is repeated by setting the parameter, c, to 2, 4, and 8, respectively.

Overall, as shown in Table 1, HD^L performs very well on simulated networks. When p ≤ 0.2, HD^L finds all true positives. As p increases, HD^L still delivers a strong performance. Until p ≥ 0.6, the performance decreases tremendously. Therefore, HD^L can recover all significantly changed nodes when variability between multiple replicates of the same experiment is small. When more edges are randomly rewired, the replicates start losing similarity from each other until all six networks essentially become unrelated. Note that even at p = 0.7, a true positive rate of 50% is still significant, as the expectation from randomly guessing would only be 10%.

Table 1.

HD^L mean and standard deviation of true positives.

	p = 0.2	p = 0.3	p = 0.4	p = 0.5	p = 0.6	p = 0.7	p = 0.8
c = 1	100 ± 0	99.2 ± 0.6	96.8 ± 1.2	90.4 ± 1.9	74.1 ± 3.7	53.8 ± 4.3	33.7 ± 3.0
c = 2	100 ± 0	99.7 ± 0.5	96.5 ± 1.3	89.7 ± 2.2	75.1 ± 3.6	57.1 ± 2.7	31.6 ± 5.5
c = 4	100 ± 0	99.4 ± 0.7	98.3 ± 1.1	91 ± 1.6	76.9 ± 4.2	56.6 ± 3.6	36.9 ± 2.9
c = 8	100 ± 0	99.9 ± 0.3	98.3 ± 0.9	92.7 ± 1.5	81.3 ± 2.8	60.6 ± 4.2	36.7 ± 4.8

HD^G also performs well on simulated networks as shown in Table 2. Like HD^L, it demonstrates the same pattern as p increases despite it is slightly worse than HD^L. However, for HD^G increasing the number of clusters in the networks constantly improves the performance especially when p ≥ 0.5. This improvement can be explained by the fact that HD^G harnesses the clustering structure to mitigate the effect of biological variability of the same experiment. The benefit of using network topology information turns out to be significant on real data, which is expected to be highly modular. The clusters of simulated networks are just simple reflections of the modularity of real networks. Unlike the simulated network where the interactions within each cluster is random, a real network has modular structure at different hierarchies and therefore can benefit more from the global method.

Table 2.

HD^G mean and standard deviation of true positives.

	p = 0.2	p = 0.3	p = 0.4	p = 0.5	p = 0.6	p = 0.7	p = 0.8
c = 1	100 ± 0	98.6 ± 0.8	95.2 ± 2.4	87.7 ± 2.5	70.4 ± 3.7	51.1 ± 4.7	32.4 ± 2.6
c = 2	100 ± 0	99.1 ± 0.7	95.6 ± 1.8	87.2 ± 2.9	72.2 ± 4.2	52.9 ± 2.3	29.7 ± 5.4
c = 4	99.9 ± 0.3	99 ± 0.8	97.1 ± 1.4	88.5 ± 1.8	73.6 ± 3.6	53.5 ± 3.6	34.9 ± 1.8
c = 8	100 ± 0	99.5 ± 0.7	97.8 ± 1.0	92.1 ± 1.4	79 ± 3.7	59.6 ± 5.1	35.5 ± 5.1

3.2. Network normalization analysis

The real Hi-C data are obtained from two cell lines, human embryonic stem cells (hESC) and lung myofibroblasts (IMR90).²⁸ Each cell line has two replicates. The data are given as interaction matrices, where the genomic sequence is split into bins of 100 kilobases (kb), and the numbers of interactions (Hi-C reads) between the genomic loci in bin pairs are recorded. As the four matrices have very different numbers of total reads, and the numbers of reads have a wide distribution, the initial networks are highly dense and are suspected to have many spurious connections.

To facilitate meaningful comparison between experiments, we propose an automated procedure to convert each interaction matrix into a sparse network by finding an appropriate cutoff on the number of interactions (see Sec. 2). For the four data sets, as shown in the left of Fig. 2, the x-axis shows the average connectivity of the resulting network after applying some cutoff and the y-axis is the zscore of CC. The data points in Fig. 2, from left to right, correspond to keeping top 0.01%, 0.025%, 0.075%, 0.1%, 0.25%, 0.5%, 0.75%, and 1% of all edges to generate sparse networks. These zscores display a similar pattern, which increases first and then decreases and reaches its optimum at around 0.075% (roughly 25 connections per node). When replicates are pooled together, as shown in the right of Fig. 2, these patterns are somewhat different, with the peak slightly shifting toward the right. To test how dramatic the results can be affected by the network normalization step, we deliberately selected a cutoff to have a relatively denser network for the pooled data set, with a density cutoff set at 0.25% resulting in the average connectivity per node roughly at 75.

Fig. 2.

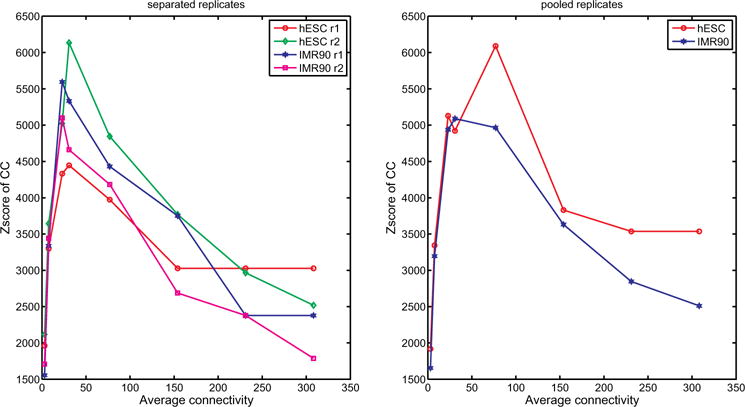
CC zscores versus average connectivity.

Table 3 shows some key statistics of the network properties after normalization. As can be seen, while using different cutoffs for the separated and pooled data sets, all networks are highly modular (CC > 0:55) despite being rather sparse. However, for the separated data sets (first four columns), there are notable differences between the four networks, including CC, and average shortest distance, and size of the largest component, both between the two replicates of the same cell line and between cell lines. In comparison, in the pooled data set (last two columns), the networks from the two cell lines are highly similar.

Table 3.

Separated and pooled replicates network statistics.

Network property	IMR90 r1	IMR90 r2	hESC r1	hESC r2	IMR90	hESC
Number of edges	343,653	347,515	299,653	351,264	1,077,046	1,093,670
CC	0.722	0.694	0.636	0.735	0.573	0.586
Number of components	2872	2865	2625	2647	2674	2406
Size of the largest component	25,421	23,500	28,129	24,998	28,140	28,404
Average shortest distance	7.81	18.72	16.10	36.35	5.83	6.66
Average degree	24.7	24.7	21.3	25.4	76.5	77.0

3.3. Performance on real Hi-C data sets

To compare with other methods, we test our methods on real Hi-C data sets. We also test our methods under different configurations, which include unweighted and weighted networks, normalized and raw networks and different bin sizes.

3.3.1. Comparison with other approaches

As there is no ground truth for the chromatin interaction changes in real data, to evaluate the performance of our methods and compare with other approaches, we investigate the functional relevance by calculating the correlations between the predicted differential measurement scores and the changes of genomic features that are known important for regulating chromatin structure. CTCF is a very important protein that regulates chromatin three-dimensional structure. CTCF binding sites are usually enriched at highly interacting regions and can be viewed as separators between functional domains in chromosomes.²⁰ Meanwhile, histones which are proteins used to build chromosomes are important indicators for chromatin structure, and many histone modification markers are enriched at Hi-C enriched or depleted regions.²⁸

First, we download CTCF binding sites data and available histone modification data for each cell line.^29,30 After the genomic sequence is divided into 100 kb-sized bins, the CTCF binding sites falling into the bins are counted. These counts are normalized to the same range by scaling them according to the total counts of CTCF binding sites of two cell lines. The absolute differences of these normalized counts between the two cell lines are calculated. Finally, Spearman correlation coefficients are calculated between these absolute differences and each method’s measurement scores, respectively. The above procedure is also applied to histone modification data for correlations.

Since these genomic features are enriched at either highly interacting regions or rarely interacting regions, if two cell lines are significantly different in chromatin structure at certain genomic regions, then the patterns of these genomic features are also expected to be significantly different between the two cell lines. Therefore, the chromatin interaction difference scores and the genomic features’ difference scores (ignoring signs of changes in both) should be positively correlated.

As shown in Table 4, both HD^L and HD^G perform significantly better than diffHiC and HOMER, demonstrated by the much higher correlations with the genomic features. In fact, HD^G has the highest positive correlations for all the features tested and keeping the replicates separated provides slightly better results than pooling them for most features except in H3K4me1 and H4K20me1. HD^L results in reasonably well positive correlations for almost all features, except CTCF. The failing of HD^L at CTCF is probably due to the fact that CTCF is usually an indicator of long-range interactions between distal and proximal regulatory regions, and therefore cannot be captured by the HD^L scores, whose calculation are usually dominated by the much more frequent short-range interactions present in most HiC data. In comparison, by the random walk procedure, the HD^G calculation is able to take into consideration both short-range and long-range interactions, resulting in much better agreement with CTCF binding sites. Pooling samples do not change the performance of HD^L significantly. In comparison, neither diffHiC nor HOMER can capture all genomic features. DiffHiC has significant correlations (> 0:1) with 4 out of the 8 total features, while HOMER has only 1.

Table 4.

Functional relevance measured by the correlations between differential interaction scores and genomic feature scores. In our methods, P represents pooling replicates; S represents treating replicates separately.

Method	CTCF	H3K4me1	H3K4me2	H3K4me3	H3K9ac	H3K27me3	H3K36me3	H4K20me1
diffHiC	−0.106	0.195	0.129	−0.036	0.110	−0.054	0.088	0.151
HOMER	0.053	0.091	0.112	0.015	−0.027	0.018	−0.103	−0.137
HDL (P)	−0.048	0.202	0.148	0.093	0.161	0.040	0.183	0.188
HDG (P)	0.283	0.299	0.301	0.256	0.268	0.274	0.246	0.224
HDL (S)	−0.012	0.197	0.155	0.104	0.163	0.063	0.174	0.174
HDG (S)	0.342	0.288	0.303	0.307	0.283	0.299	0.269	0.205

We further compare the results from different methods in a pairwise manner. As can be seen in Table 5, HD^L (P) and HD^L (S) are highly similar (Pearson correlation coefficient = 0.78), followed by HD^G (P) and HD^G (S) (Pearson correlation coefficient = 0.42). HD^L (S) and HD^G (S) also give a somewhat similar result (Pearson correlation coefficient = 0.31), but HD^L (P) and HD^G (P) have a very low correlation. On the other hand, diffHic is correlated with HD^L to some extent. HOMER result is correlated with HD^L (P) but not HD^L (S), probably because HOMER itself uses pooled replicates. When the top-1000 bins predicted from each method are compared as shown in Table 6, the conclusion is similar to that drawn from the correlation analysis in which diffHic and HOMER are significantly different from each other and from HD. Somewhat surprisingly, although the pooled and separated data sets have very different network density, HD^G (P) and HD^G (S) share almost half of the top-1000 bins, much higher than numbers of bins shared by other methods (including HD^L-P and HD^L-S). This indicates that the random walk procedure is able to overcome the low data coverage problem by essentially predicting additional interactions from known interactions, as shown in other applications.³¹

Table 5.

Correlations between the results from different methods. In our methods, P represents pooling replicates; S represents treating replicates separately.

Method	diffHiC	HOMER	HDL (P)	HDG (P)	HDL (S)	HDG (S)
diffHiC	1	−0.0237	0.2746	−0.0065	0.1781	−0.124
HOMER	−0.0237	1	0.1417	0.0445	0.0746	0.0226
HDL (P)	0.2746	0.1417	1	0.0456	0.7831	0.1972
HDG (P)	−0.0065	0.0445	0.0456	1	0.0248	0.4235
HDL (S)	0.1781	0.0746	0.7831	0.0248	1	0.3147
HDG (S)	−0.124	0.0226	0.1972	0.4235	0.3147	1

Table 6.

Intersection between top-1000 differentially interacting bins from each method. In our methods, P represents pooling replicates; S represents treating replicates separately.

Method	diffHiC	HOMER	HDL (P)	HDG (P)	HDL (S)	HDG (S)
diffHiC	1000	80	128	12	80	9
HOMER	80	1000	49	28	31	28
HDL (P)	128	49	1000	47	144	35
HDG (P)	12	28	47	1000	39	466
HDL (S)	80	31	144	39	1000	42
HDG (S)	9	28	35	466	42	10

3.3.2. Comparison of unweighted and weighted networks

There are two types of normalized networks, unweighted and weighted ones. In the previous section, the functional relevance is calculated on the unweighted networks. Compared to unweighted networks, weighted ones keep the weight information for high frequency edges. To evaluate our methods’ performance on weighted networks, we scale the normalized weights of two experiments to the same range and calculate the functional relevance by measuring correlation coefficients between the differential interaction scores based on weighted networks and difference scores of genomic features. We compare the results with the ones of unweighted networks. As shown in Fig. 3, for each genomic feature, the performance on weighted networks is better than or close to the performance on unweighted networks. It can be explained by that keeping weights can maintain some subtle interaction difference information which may be ignored by unweighted networks. For weighted networks, the global method is also better than the local method except H3K4me1 and H4K20me1.

Fig. 3.

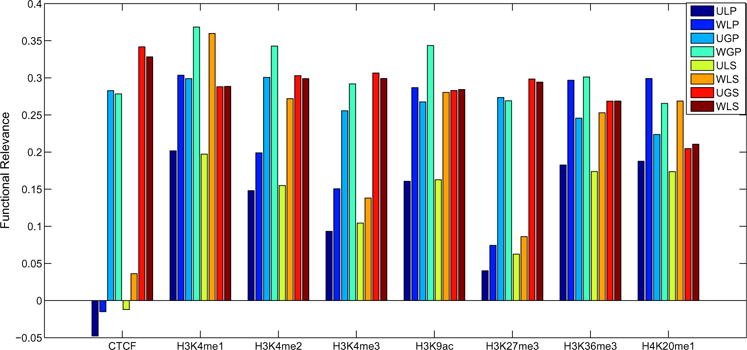
Comparison of unweighted networks and weighted networks on functional relevance measured by the correlations between differential interaction scores and genomic feature scores. We run our methods under different configurations represented by three capital letters. The first letter indicates unweighted networks (U) or weighted networks (W). The second letter indicates local method (L) or global method (G). The third letter indicates pooling replicates (P) or treating replicates (S) separately.

3.3.3. Comparison of normalized and raw networks

In this section, we compare the performance between normalized weighted networks and raw networks without normalization. First raw networks’ weights are scaled to the same range, then for each genomic feature, the correlation coefficient is calculated by using our methods under different configurations. As shown in Fig. 4, for each genomic feature, apparently, the results on normalized weighted networks are much better than raw networks. Therefore, our normalization strategy can help us improve the performance significantly. A possible reason is our normalization can recover the real differences information from the noisy data by resorting to network topology information.

Fig. 4.

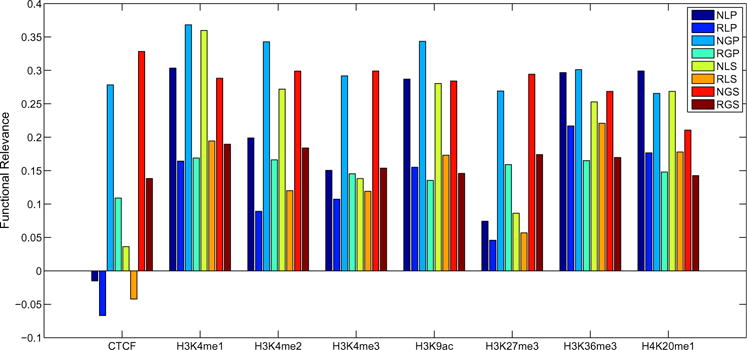
Comparison of normalized networks and raw networks without normalization on functional relevance measured by the correlations between differential interaction scores and genomic feature scores. We run our methods under different configurations represented by three capital letters. The first letter indicates weighted normalized networks (N) or raw networks without normalization (R). The second letter indicates local method (L) or global method (G). The third letter indicates pooling replicates (P) or treating replicates (S) separately.

3.3.4. Comparison of different bin sizes

In previous sections, our results are based on the bin size of 100 kb. In this section, we divide the genomic sequence into 200 kb bins and 50 kb bins, apply our methods and calculate functional relevance by measuring correlations with genomic features, respectively. We compare the results with the ones of bin size of 100 kb. As shown in Fig. 5, the left compares results between 100 and 200 kb, and the right compares results between 100 and 50 kb. In the left figure, the points are scattered close around the 45° line equally, which means the performance of 100 and 200 kb is very robust. In the right figure, there are more points below the 45° line. One possible explanation for this is few interactions in a relatively shorter genomic region has low capability to distinguish one from the other. But they are still close to the line. So, the performance between 50 and 100 kb is more or less consistent.

Fig. 5.

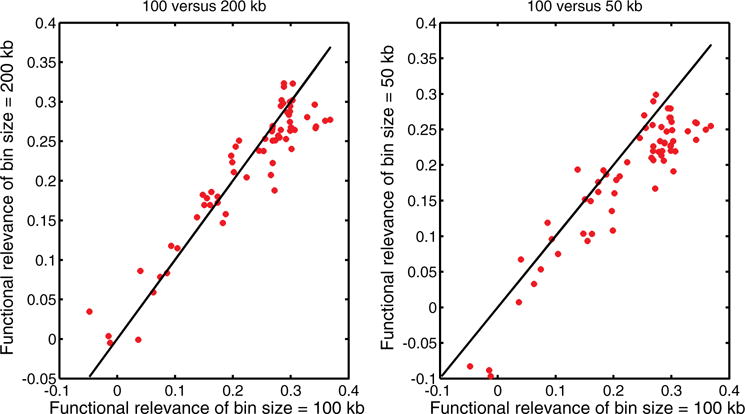
Comparison of different bin sizes on functional relevance defined in Table 4.

4. Conclusions

In this study, we propose two approaches to find differentially interacting genomic regions between experiments by using a network model. Our paper has four major contributions. First, we allow users to decide whether to pool replicates or to treat them separately. Second, to the best of our knowledge, we are the first to apply a network model to detect differentially interacting regions with chromatin interaction data. Third, we propose a novel strategy guided by network topological properties to automatically normalize network data from different experiments. Finally, we devise two measurements to calculate HiC differential patterns from two perspectives, one using local information and the other using the combination of local and global information. We show that the local method is slightly better than the global method on simulated networks. On real HiC data, evaluated by functional relevance with known genomic features, the global method is significantly better than the local method, and both methods are superior to the two existing methods. Meanwhile, our methods work well on both unweighted and weighted networks and our normalization strategy significantly improves the performance compared with raw networks without normalization. Furthermore, the results of different bin sizes are robust. Therefore, we believe our methods will be useful for identifying differentially interacting genomic regions.

Biographies

Lu Liu is an Assistant Professor of College of Information Technology and Engineering at Marshall University. He holds a Ph.D. in Computer Science from the University of Texas at San Antonio (2017), an M.S. and B.S. in Computer Science from Beijing University of Posts and Telecommunications (2011 and 2008). His research interests are bioinformatics, computational biology, machine learning, and data science.

Jianhua Ruan is an Associate Professor of Computer Science at The University of Texas at San Antonio. He received his M.S. and Ph.D. in Computer Science from California State University (2002) and Washington University in St. Louis (2007), respectively, and B.S. in Biology from the University of Science and Technology of China (1998). His research interests lie in broad areas of bioinformatics, network biology, and data mining.