Granger Causality Analysis of Interictal iEEG Predicts Seizure Focus and Ultimate Resection

Abstract

BACKGROUND

A critical conceptual step in epilepsy surgery is to locate the causal region of seizures. In practice, the causal region may be inferred from the set of electrodes showing early ictal activity. There would be advantages in deriving information about causal regions from interictal data as well. We applied Granger's statistical approach to baseline interictal data to calculate causal interactions. We hypothesized that maps of the Granger causality network (or GC maps) from interictal data might inform about the seizure network, and set out to see if “causality” in the Granger sense correlated with surgical targets.

OBJECTIVE

To determine whether interictal baseline data could produce GC maps, and whether the regions of high GC would statistically resemble the topography of the ictally active electrode (IAE) set and resection.

METHODS

Twenty-minute interictal baselines obtained from 25 consecutive patients were analyzed. The “GC maps” were quantitatively compared to conventionally constructed surgical plans, by using rank order and Cartesian distance statistics.

RESULTS

In 16 of 25 cases, the interictal GC rankings of the electrodes in the IAE set were lower than predicted by chance (P < .05). The aggregate probability of such a match by chance alone is very small (P < 10⁻²⁰) suggesting that interictal GC maps correlated with ictal networks. The distance of the highest GC electrode to the IAE set and to the resection averaged 4 and 6 mm (Wilcoxon P < .001).

CONCLUSION

GC analysis has the potential to help localize ictal networks from interictal data.

ABBREVIATIONS

GC

Granger causality

iEEG

intracranial electroencephalography

IAE

ictally active electrode(s)

ECoG

electrocorticography

MEG

magnetoencephalography

fMRI

functional magnetic resonance imaging

LTM

Long-Term Monitoring

RZ

resection zone

HFO

high-frequency oscillation

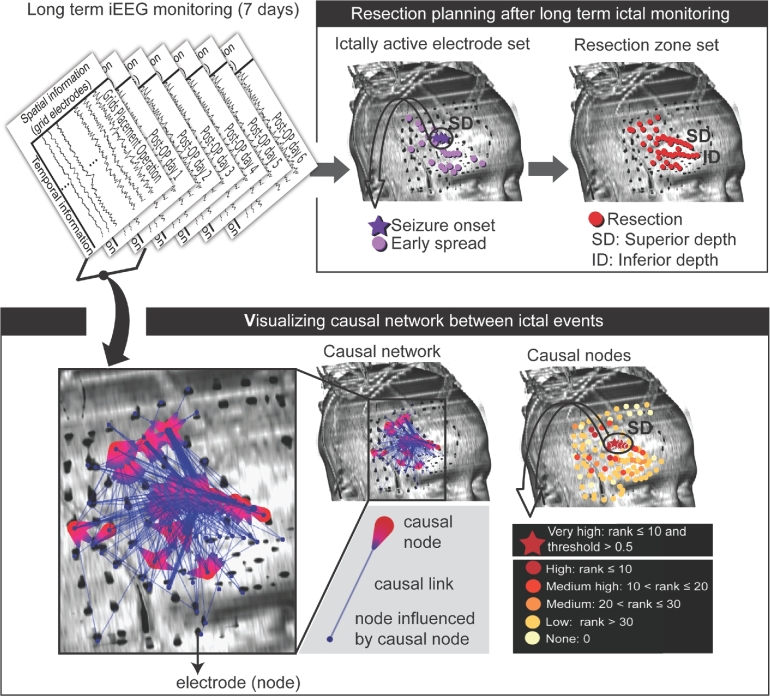
Though surgical resection offers patients the possibility of becoming seizure-free, it is significantly underused in epilepsy therapy.^1-3 One major challenge of resective surgery is to locate the anatomic site of seizure origin and remove the causal region. Often, ictal intracranial electroencephalography (iEEG) is used to specify the seizure origin, which is assumed to be the causal part of the seizure network. In practice, the anatomic site of seizure origin is indicated by the set of ictally active electrodes (IAE). The IAE set is typically determined by epileptologists from ictal iEEG and communicated to the surgeon when planning resection strategy. In order to obtain ictal data, it is necessary to wait for 1 or more seizure during the invasive monitoring period, typically requiring a week in our institution (Figure 1). If interictal data could be mined to reveal aspects of the seizure network, which currently drives the practice of waiting for seizures, it is possible that some invasive monitoring cases could be managed in one stage.

FIGURE 1.

IAE set, determined conventionally, and the causal nodes obtained from the technique of GC for patient 1 are shown. During a week of invasive monitoring (upper left panel), the IAE (including “seizure onset” indicated by dark purple stars and “early spread” indicated by light purple dots) was identified for 12 seizures and the area around the IAE including superior depth (SD) and inferior depth (ID) electrodes was then removed (upper right panel). The causal connectivity map (spatial information) was determined from interictal iEEG data (temporal information) obtained on the night of surgery, more than 9 h before the first seizure recordings (bottom left panel). Each causal link (blue line) connects the causal node (red teardrop shaped symbol) and a node influenced by the causal node (blue solid circle). Each node was evaluated based on the causal strength, rank-ordered, and color-coded from the most influential to the least influential node based on the ranks (bottom right panel). The red stars denote very high-ranked causal nodes, which are within the top 10 ranks with higher than the causal strength threshold value of 0.5. The causal nodes map simplifies and makes the complex causal network interpretable. In patient 1, the most influential causal nodes were identified along the SD electrodes consistent with the IAE (compare the circle and arrow from the upper right panel and those from the bottom right panel).

British economist Sir Clive Granger developed a computational approach to identify what he called “causal” influences among several variables sampled over time. This approach defined causality as a tendency for the past values of one variable to improve the accuracy of a prediction for the future value of another variable. In his Nobel address on the work,⁴ he emphasized that such statistical inferences could point to meaningful interactions in a network, even when knowledge about the hidden mechanisms responsible is lacking. We sought to apply this approach to interictal electrocorticography (ECoG) data, where it seemed possible that there could be subtle clues to the seizure focus not immediately visible to the eye.

Other investigators have looked at algorithms aimed at finding directional influences of one region on another, rather than simple correlation to reveal networks. Epstein et al⁵ demonstrated that a related method using Granger algorithms on data resolved into frequency spectra can reveal network alterations in the immediate pre-ictal period. With a different frequency-based algorithm, Wilke et al⁶ showed that the causal network characteristics in the gamma band (30-50 Hz) observed during interictal periods are qualitatively similar to those observed during ictal events. But, neither of these studies focused on testing whether interictal baseline can be used to predict which nodes are statistically correlated with the location of the seizure focus.

In this study, we asked a utilitarian question: Can interictal baseline iEEG predict the seizure network (practically represented by the IAE set of electrodes) and ultimate resection? The interictal data segments of 25 epilepsy patients were randomly selected from the iEEG recordings early in the invasive monitoring process. Conditional Granger causality (GC) formulated in the time domain^7-9 was used to reveal causal connectivity from multichannel iEEG data (Figure 1). Our choice to use the time domain method had the advantage of simplifying data processing steps and reducing calculation time at the potential cost of revealing less about specific frequency bands compared with other methods such as directed transfer function and spectral GC, and high-frequency oscillations (HFOs).^5,6,10,11 For this study, we sought a method that could be implemented as simply and practically as possible. The time domain-based GC method could achieve this by revealing causal connectivity with fewer processing steps while making minimal assumptions about the data.^9,12 It can be applied directly to a variety of types of data such as EEG, MEG (magnetoencephalography), fMRI (functional MRI), iEEG used for two stage resections, or ECoG used for one stage resections.^9,12

After performing GC calculations, which graphically display high-causality regions of the brain (in the Granger sense), we were struck with the similarity of the GC maps and the set of electrodes tagged by neurologists in ictal data as active at or near the very beginning of a seizure. We denote this group of electrodes as the IAE, and compared GC maps with this set in 2 different ways. First, do the IAE electrodes rank higher in causality than would be expected from at random? Second, do the highest causality electrodes turn out to be closer to the IAE set (or the surgical resection, for that matter), than predicted by chance?

Any new approach to analyzing interictal iEEG data might be used to supplement the status quo procedures, such as localization of spikes or other interictal signatures. If the GC data exactly duplicated spike data (which would be the case, for example, if the algorithm functioned as an automated spike detector), it might add less supplementary value than if it contributed nonoverlapping information, so we analyzed this as well. A potential advantage of the GC algorithm would be that it could be employed irrespective of whether spikes appeared to be present or not.

Our findings may one day enable a practical approach for extracting data from intraoperative or extraoperative corticography, aiding in the identification and visualization of causal networks.

METHODS

Patients

We retrospectively examined interictal iEEG recordings from 25 consecutive patients with medically refractory epilepsy who underwent long-term invasive monitoring for planning surgical resection. Before surgical implantation of electrodes and subsequent resective surgery, patients’ informed consent for surgical treatment was always obtained. Our retrospective review of intracranial EEG signals, clinical information of each patient, and surgical outcomes was approved by our Institutional Review Board as a post hoc review not requiring consent.

Invasive monitoring was recommended for each of these patients by consensus of the multidisciplinary Epilepsy Surgery Conference, on the basis of perceived need for iEEG data to permit optimal planning of a surgical resection. Typically, better definition of seizure onset zone or functional anatomic regions, or both was determined after consideration of all data less invasively obtained. Resections were performed in 24 out of 25 patients at the time of grid removal. The demographic information and 1-yr Engel class¹³ follow-up outcomes are summarized in Table 1. The patient series was consecutive and not selected by outcome or other clinical factors.

TABLE 1.

Demographic and Clinical Information Including Etiology, Pathology, Resection Procedure, and 1-yr Follow-up Outcome for 25 Patients

Pt. No.	Age(yr)/gender	Etiology	Pathology	Resection procedure	Engel classa
1	8/F	Cortical dysplasia of the right inferior frontal gyrus	Gliosis and dysplastic neurons	Right frontal lesionectomy	Ia
2	2.25/M	Left frontal lesion	FCD Type IIB, Low grade glial neoplasm	Resection of tumor and small additional resection of cortex adjacent to the cavity	Ia
3	18/F	Unknown	Gliosis	Left mesial temporal nonlesional resection	Ia
4	18/M	Unknown	Gliosis	Left anterior and mesial temporal resection	Ia
5	18/F	Extensive bilateral heterotopia	FCD Type IA, Hippocampal gliosis	Right temporal resection	Ia
6	19/F	Lesion in left superior temporal gyrus	WHO Grade I-II Ganglioglioma	Resection of tumor in the superior temporal sulcus	Ia
7	11/M	Unknown	FCD Type IIIA, Gliosis	Left anterior temporal resection and additional resection of lateral and basal seizure focus	III
8	10/F	Right mesial frontal DNET	Recurrent/residual low-grade glioma	Resection of parasagittal brain tumor	Ia
9	10/M	Focal cortical dysplasia; Prior year left frontal resection	FCD Type IIA, Gliosis	Extension of prior resection, four years earlier, of a left frontal cortical dysplasia	Ia
10	16/M	Unknown	MTS, Gliosis	Left anterior mesiotemporal resection	Ia
11	2/F	Unknown	Microglia activation, Gliosis, Neuronal injury	Left parietal and frontal cortex resection	Ia
12	6/M	Left frontal focal cortical dysplasia	FCD Type IIA	Functional disconnection of left frontal lobe anterior to motor strip	Ia
13	20/F	Right parietal oligodendroglioma	Cerebral gray and white matter with extensive reactive changes (oligodendroglioma 11 years earlier, then gliosis 4 years earlier)	No resection was done due to concern over motor deficit	N/A
14	10/M	Unknown (focal seizures, epileptic encephalopathy)	Cortex and white matter with reactive changes	Right frontal resection	Ia
15	16/F	Left temporo-occiptal subcortical heterotopia	FCD Type IIA, Vascular malformation	Resection of seizure focus on the left side	Ia
16	17/M	Left mesial temporal lesion	FCD Type IIA, HS	Left temporal lobe and medial structures resection	Ib
17	12/M	Left mesial temporal sclerosis, Left temporal dysplasia	FCD Type IIA, HS, Gliosis	Left mesial temporal lobe resection	Ia
18	13/F	Unclear: MRI scans suggest some possible cortical dysplasia in the anterior-superior temporal gyrus	FCD Type IIA, Gliosis	Partial left temporal lobectomy	Ib
19	18/M	Presumed cortical dysplasia of left para-hippocampal gyrus (MTLE)	MTS, Gliosis	Left temporal tip and mesial temporal resection	Ia
20	10/M	Right MCA in utero stroke affecting inferior frontal temporal and parietal areas with intraparenchmyal cyst and encephalomalacia	FCD Type IA, Gliosis	Extension of resection of right frontal cortical dysplasia (prior surgery 5 years earlier)	Ia
21	10/F	Right Frontal lobe lesion (medial superior)	FCD Type IIB	Resection of right mesial frontal lesion in the vicinity of the motor strip	Ia
22	18/M	Nonlesional, left frontal	Irregularities of cortical development	Left mesial frontal resection	Ia
23	8.5/F	Suspected right parasagittal cortical dysplasia	Irregularities of cortical development, Gliosis	Resection of large cortical dysplasia, duraplasty	Ia
24	2/M	TSC due to a de novo TSC2 mutation	Severe dysplasia and abnormal glioneuronal cells	Right frontal resection for multiple subcortical tubers	Ia
25	18/F	Presumed left frontal cortical dysplasia	FCD Type IIB	Left frontal cortical resection	II

DNET: Dysembryoplastic neuroepithelial tumors, FCD: Focal cortical dysplasia, HS: Hippocampal Sclerosis, MCA: Middle cerebral artery, MTLE: Mesial temporal lobe epilepsy, MTS: Mesial Temporal Sclerosis, TSC: Tuberous sclerosis complex, WHO: World Health Organization.

^aClass I: Free of disabling seizures, Class II: Rare disabling seizures, Class III: Worthwhile improvement, Class IV: No worthwhile improvement.¹¹

Data Collection and Preprocessing

The iEEG data were recorded with subdural and/or depth electrodes (Ad-Tech, Racine, Wisconsin) to accurately identify IAE. The total number of electrodes for each patient ranged from 64 to 154 (103 ± 26, mean ± standard deviation). We analyzed the first 20 min interictal baseline segment without technical disruptions or clinical events noted on EEG annotations. The segments were considered baseline recordings for each patient, and no effort was made to include or exclude other electrical features such as spikes. For most of the cases (21 out of 25), the segment analyzed preceded any clinical or electrographic seizure. The details of the data collection and preprocessing are described in the Supplemental Digital Content.

GC Analysis

Causality analysis among the data streams from pairs of electrodes was calculated by applying Granger's statistical approach to baseline interictal data. The Granger method concludes that one time series causes (or “Granger-causes”) another time series if the past values of the first data improve the prediction of the future movement of the other. The GC algorithm is based on linear regression modeling, with additional details (called model order estimation and model validation) determined from the data. This was accomplished using the Granger causal connectivity analysis (GCCA) toolbox,⁹ which allows determination of causal inference among each possible pair of electrode-specific iEEG data streams. Graphical visualization of the causal relations among the components of the epileptogenic network was projected on imaging-based diagrams. The details have been discussed in the Supplemental Digital Content.

Statistical Analysis

Statistical Validation Using Rank Order Sum

We compared the results of the GC calculation described above to 2 relevant regional subsets of the electrodes, culled from the Long-Term Monitoring (LTM) report for each patient. Each of these reports was generated by one of 10 individual Board-certified neurologists (listed in the Acknowledgements). For purposes of this paper, the “ictally active electrode” set, was defined as the collection of electrodes identified in the LTM report as either “seizure onset zone” or “early spread.” The subset of electrodes defining the brain volume actually resected (based on the operative note) defined the “Resection Zone”, or RZ. The subset of electrodes for interictal spiking (spikes set) was also identified from LTM report where neurologists summarized their EEG readings over the entire week of monitoring. Calculation of causality values and clinical interpretation of iEEG were performed blinded to each other.

To quantify similarity between the IAE set and the set of high-causality electrodes, we rank-ordered the magnitude of causal influence of each electrode and summed up the rank order value of the IAE set (Figure 2). This rank order sum was used as a statistic to test the null hypothesis that the estimated rank order sum for each patient is not different from what is expected by chance. A Monte Carlo simulation technique was used to create the sample distribution of the rank order sum as follows.^14,15 The expected random distribution of the sum of possible rank orders from N_IAE electrodes (the number of the IAE taken from a total set of N_t electrodes) was determined by randomly selecting N_IAE integers from the set {1,2…,N_t}, summing them, and repeating this process a large number of times (10⁵ replications were used in this study to ensure the convergence of the distribution).¹⁶ If the GC results yielded a sum of rank orders well out on the tail of this Monte Carlo determined distribution, the probability of such an event happening by chance could be determined directly from the percentage area under the distribution curve to the left of the observed GC value. By this means, individual P values could be computed for each case. To determine whether the results of the 25 individual cases combined are significant under the same null hypothesis, Fisher's method was applied to compute overall P value.^17-19 The exact P value was computed using the method of Kaever and his colleagues.²⁰

FIGURE 2.

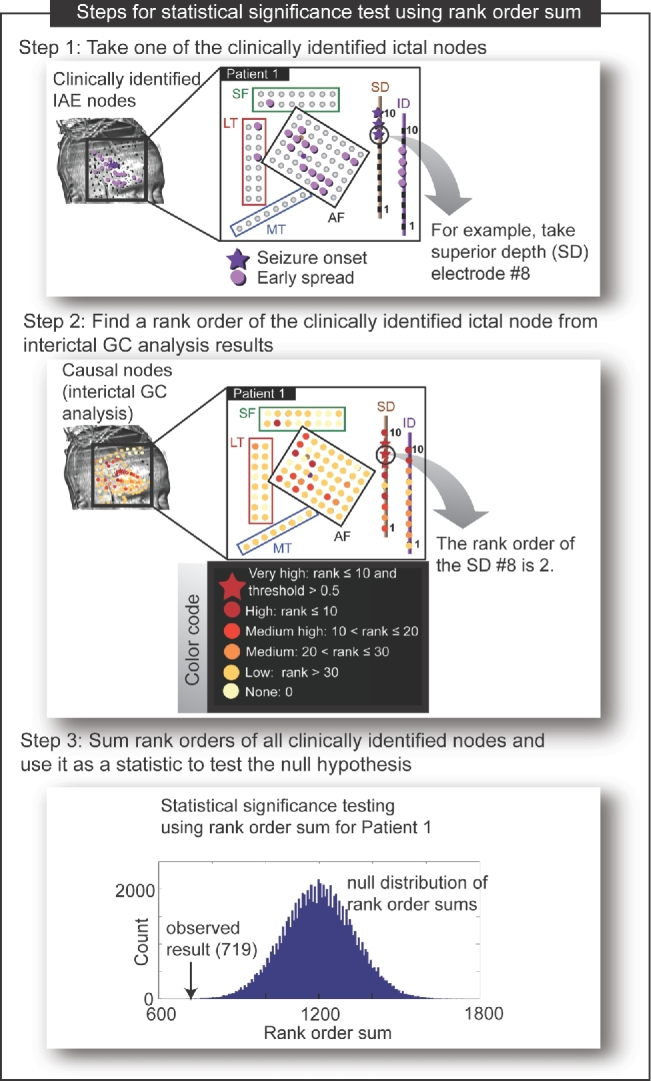
Visual depiction of steps for the rank order approach used for the statistical comparison between the IAE set and the causal nodes. For clear presentation, the IAE nodes (shown in step 1) and the causal nodes (shown in step 2) are marked on the schematic diagram of grids used for patient 1. The grid electrodes are placed on the brain in 4 different locations (anterior frontal [AF], subfrontal [SF], lateral temporal [LT], and mesial temporal [MT]) and depth electrodes are placed in the brain in 2 locations (SD 10 contacts and ID 10 contacts). The null distribution was simulated to test significance of the rank order sum indicated by the arrow shown in step 3 (P value = .00006).

Statistical Comparison With Spikes Set

To probe whether interictal spikes per se are either necessary or sufficient to yield strong GC ratings of individual electrodes, we compared the set of electrodes determined to have spiking in the final LTM report to the set with the same number of electrodes with the highest GC calculated from our data. If GC analysis acted in effect as a spike detector, these sets would be expected to agree in most cases.

Statistical Validation Using Average Minimum Pairwise Distance

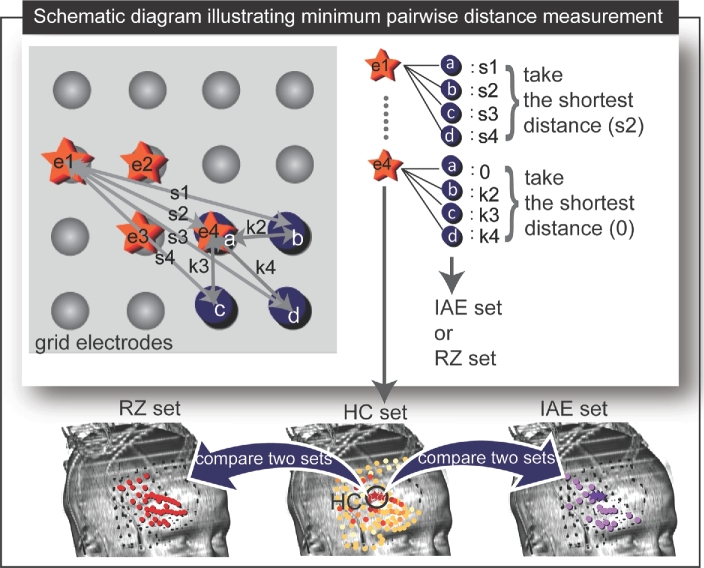
As an alternative statistical test, and based on coordinates obtained from the CT scan, we calculated the distance from the highest ranked electrode, and the averaged distance from the top 5 electrodes in each patient to the actual IAE set and the RZ. We selected these 2 arbitrary examples of highest causality regions to the RZ to allow the calculation to be made agnostic to the actual size or number of electrodes in contact with the RZ, which would not necessarily be known at the time of calculation of the GC maps in future applications of this technique. It should be also noted that the distance is calculated from one set of electrodes to another set of electrodes. The Wilcoxon paired signed-rank test was applied to compare the GC-determined distances and the distances expected by chance. This approach yields a more physically meaningful result (giving a measure in millimeters), and has been used by others.^6,21-24 Because the P value for proximity might depend on the number of electrodes included as “highest causality” nodes, we repeated the calculation for all multiples of 5 from 10 to 60. A schematic view of the distance calculation is shown in Figure 3.

FIGURE 3.

Comparison between the RZ set of electrodes and the highest causality (HC) set of electrodes and between the HC set and the IAE set using average minimum pairwise distance calculation (patient 1). In the upper panel, a schematic diagram shows HC set (stars labeled as “e1” to “e4”) and IAE set or RZ set (solid circles labeled as “a” to “d”). The distances between each element of HC set and each element of IAE set (or RZ set) are denoted by “s” and “k.” For example, the shortest distance between “e1” (one of the elements from HC set) and each element of IAE (or RZ) set is indicated as “s2.” Similarly, the shortest distance between “e4” and each element of IAE (or RZ) set is 0 since “e4” and “a” (one of the elements of IAE (or RZ) set) coincide each other. The distances were used to compare HC set with IAE set and RZ set as illustrated in the lower panel.

RESULTS

Visual analysis of the network graphs of the causal interactions identified by the GC method appeared to show a concentration of “causal nodes” in and around the IAE and the RZ (see Figures 1-3 for the results of patient 1). The desire to quantify this similarity led us to simplify the network maps by depicting diagrams of high- and low-causality regions. Using the simpler depiction, we were then able to assess whether the clinically identified zones had particularly high presence of causality. The graphical images continued to show a striking similarity to the IAE and the RZ, prompting us to determine the probability for each case that the concentration of high GC in the clinically identified zones could be achieved by chance alone. The Monte Carlo methods described above allowed calculation of actual probabilities.

Some cases, exemplified in Figure 4, showed extremely high similarity to the IAE and the RZ. In the cases of patient 3 and patient 6, both yielded statistically significant results in the rank order approach (P = .009 for patient 3 and P = .003 for patient 6) and also showed their close proximity to the IAE and to the RZ (0 mm from the highest electrode for both cases; <10 and <5 mm from top 5 electrodes for patient 3 and patient 6, respectively). This is what prompted us to look at distance from the highest causality nodes (top 1 and top 5 electrodes) to the ultimate IAE and RZ, in addition to rank-order similarities in the first place. The complete set of P values is shown in Table 2. Given that some cases appeared to support the concept that GC maps from interictal iEEG predict the IAE, it is reasonable to ask whether the results from all 25 cases could represent a result based on chance alone. The answer to this question can be calculated using Fisher's method of combining multiple independent tests of the same hypothesis, which gives a P value of less than 10^–20.

FIGURE 4.

Some cases showed remarkable similarity between the high-causality electrodes and the IAE set. Two of those patients (patient 3 and patient 6) who showed excellent concordance between high causal nodes and the IAE (P = .009 and P = .003 by rank order, respectively) are shown. The volume-rendered CT images and the causal connectivity maps of the patients are shown. The rank-ordered and color-coded causal nodes obtained from GC analysis can be visually as well as statistically compared (by calculating rank order sum and Cartesian distance) with the IAE set and with the RZ.

TABLE 2.

Statistical Comparison (by Rank Order and Distance) of Electrodes Highlighted by the GC Map (Based on Interictal Baseline Data) Compared With the Ictally Active Electrode (IAE) Set Identified From Ictal Data and Ultimate Resection. Individual Patients are Shown in Order of Rank Order Correspondence, with Best Correspondence (Lowest P value) at the Top of the List

Comparison of the causality ranking of the IAE set with the causality rankings of a set of the same number of electrodes selected by chance (by sum of the rank orders)					Comparison of the distances of the 1 or 5 highest causality electrodes to the IAE set or RZ set compared with the corresponding expected distance of electrodes selected at random.
Patient number	Rank order sum	Rank order sum by chance	Probability of obtaining observed value by chance		Distance from highest causality electrode to IAE set (mm)	Mean distance from top five electrodes to IAE set (mm)	Expected distance of random set of electrodes to IAE set (mm)	Distance from highest causality electrode to RZ set (mm)	Mean distance from top five electrodes to RZ set (mm)	Expected distance of random set of electrodes to RZ set (mm)
22	2566	3595	<.001		0	12	13	0	35	42
14	646	1013	<.001		0	4	15	0	5	27
1	719	1199	<.001		5	1	12	0	0	11
12	1447	1936	.002		0	8	12	0	2	28
13	1317	1807	.002		0	53	37	N/Aa	N/A	N/A
6	829	1210	.003		0	4	15	0	4	24
21	389	676	.005		8	30	39	0	31	39
23	912	1212	.007		0	2	18	0	1	18
2	558	769	.008		0	14	21	11	19	25
3	817	1067	.009		0	8	17	0	9	27
25	345	620	.01		6	20	27	0	21	27
24	1050	1356	.02		0	9	16	0	22	25
5	901	1177	.02		11	10	15	0	2	12
10	479	647	.02		18	8	14	44	9	20
15	1063	1284	.05		18	23	20	18	28	23
8	2696	3099	.05		0	7	11	0	20	28
4	437	548	.06		10	14	12	0	2	13
11	203	260	.13		0	14	17	0	12	16
20	713	838	.16		21	21	30	0	10	21
18	593	657	.20		15	14	11	0	7	10
19	286	325	.24		10	15	18	0	10	14
17	914	977	.28		0	14	20	0	5	17
16	456	475	.39		16	19	18	10	6	16
9	611	595	.57		10	25	19	0	34	21
7	1810	1732	.70		10	8	17	0	2	33
Combined P value: < 10−20				Mean	6	14	19	4	12	22
				Median	5	14	17	0	9	22
				Pairedb	P < .0001	P = .003		P < .001	P < .001

^aNot applicable: no resection was done.

^bWilcoxon signed rank test.

The particular cases of poor similarity between the GC maps and the IAE are instructive to study. Two cases (patient 4 and patient 7) are shown in Figure 5. Neither attained statistical significance in the rank order calculation (P = .06 and P = .7, respectively), but in both cases and some other P > .05 cases, high-causality electrodes seem close to the actual resections. In almost all cases, visual inspection shows that the causal electrodes cluster within or near the IAE and RZ, and the statistics bear out the clear statistical correlation of the interictal GC analysis with ictal analysis. Thus, in 12 of 25 cases the top GC electrode was later identified as one of the IAE, and the mean distance from the nearest IAE electrode averaged 6 mm (median, 5 mm) over all cases. In 20 of 24 cases, the top GC electrode was actually in the RZ, with a mean distance from that zone of 4 mm considering all cases. These distances are small, considering that spatial resolution is limited to about 10 mm, the distance between electrodes. Looking at the 5 electrodes, for example, the Wilcoxon signed-rank test is also highly significant as shown in Table 2, but the same calculation yields statistical significance at the P < .05 level for any sample set size computed, up to 60. At present, our computational methods do not yield an estimate of the size of the IAE set or RZ set. Such comparisons require arbitrary cutoffs.

FIGURE 5.

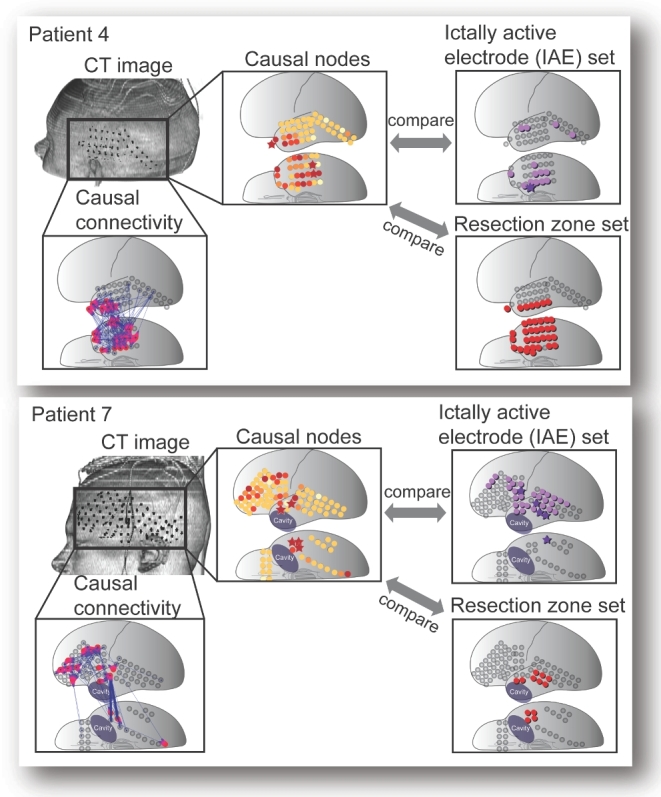
Several cases showed poor similarity to the IAE set. Two of such cases (patient 4 and patient 7) with weaker statistical correlation between high causal nodes and the IAE (P = .06 and P = .70, respectively) are shown, arranged as in Figure 4. The volume-rendered CT images and the causal connectivity maps of the patients are shown. The rank-ordered and color-coded causal nodes obtained from GC analysis can be visually as well as statistically compared (by calculating rank order sum and Cartesian distance) with the IAE and with the RZ. In patient 4, the most causal nodes clearly suggest the temporal lobe, though with less emphasis on the small focus of onset observed in the ictal iEEG. The high-causality nodes virtually all resided within the resection. In patient 7, where monitoring was done around a previous resection cavity, the causality map pointed to a broader region, including much of the lateral frontal lobe. The resection in this particular case included only temporal tissue.

Are interictal spikes necessary or sufficient to result in high-causality ranking? Comparing the set of electrodes recorded as showing spikes with a set of the same number of elements with the highest GC ratings, there was only 33 ± 4% (mean ± standard error) overlap. This suggests that spikes are neither necessary nor sufficient to yield high GC. One particular example (patient 6) illustrated the dissociation between GC and interictal spiking. Invasive monitoring focused on distinguishing 2 radiographic targets: a small left hippocampus vs a 10 mm left superior temporal gyrus lesion. Grids were placed over both areas to distinguish true onset of seizure and to allow functional mapping. We were able to identify and analyze episodes where interictal spikes were seen in the mesial temporal strip but not over the lateral temporal grids. In these same epochs, strong causal influence concentrated on the nonspiking superior temporal gyrus lesion. The superior temporal gyrus lesion proved to be the ictal origin and its removal resulted in seizure freedom. These observations suggest that GC is not a simple spike detector, meaning that GC may supplement rather than duplicate conventional iEEG interpretation.

DISCUSSION

The motivation of this study was to search for signatures of putative ictal networks in interictal recordings, which could one day improve the efficiency of analysis of intracranial data in epilepsy surgery. By viewing interictal iEEG data through the computational lens of GC, we generated statistical connectivity maps, and found that these diagrams often bore resemblance to the expert readings of the ictal iEEG information which had not been recorded when the interictal data were sampled. In this paper, we compared the regions of high GC against the IAE set and RZ set found clinically, and found that GC could predict, far better than expected by chance, these regions specified by our current practice. For practical utility, we were interested in whether GC analysis in the time domain could give clues to the anatomic location and extent of the epileptogenic cortex without the need for observing a seizure. Time domain analysis was chosen, because it avoids several time-consuming computational steps: it does not need frequency decomposition and integration over all frequency ranges to obtain GC results. GC maps based on interictal iEEG proved to correlate statistically with the ultimate ictal EEG interpretations, and the maps were “predictive” in the sense that the ictal data require typically days of waiting for seizures. It should be noted that the IAE set, a practical judgment of the electroencephalography team, may or may not represent the more abstract concept of “epileptogenic zone” or “ictogenic zone.”^25,26 However, since the outcomes of these operations, using this approach to reading and categorizing the ictal EEG, yielded good results (92% Engel I at 1 year), readings of the neurologists usually yielded excellent advice regarding the resection target.

Future Directions to Achieve Further Development of Causal Network Analysis for Use in Surgical Planning

This statistical correlation is only the first step in the quest to develop a clinically useful method. Several additional necessary or highly desirable steps are evident, and suggest further research directions. The first of these might be a more intuitive understanding of what high GC results mean in terms of traditional EEG interpretation. This could be gleaned from comparison of other methods of analysis of interictal data with the computational analysis by GC method. Most obviously, the reading of individual samples of iEEG by human experts could be systematically compared with the GC analysis of the same samples. Such comparison was not yet included in our study design, but could inform us about the relationship between the GC map and various interictal features of iEEG. Similarly, interictal features which may be detected by other digital techniques, such as HFOs^27-29 could also be correlated with the time-domain GC map. It should be noted that the method implemented in this study actually filters-out HFOs before making its calculations. Since HFOs are not visible to this algorithm, additional data from HFOs, or a modified GC method including higher frequency data, might significantly improve the method outlined here. Similarly, an algorithm to identify and include conventional features such as spikes, which may also occur independently of the GC calculation, might enhance the utility of an automated method for interictal data display.

A second need is technical: optimal computational speed. The present studies were done retrospectively, but incorporation into active surgical decision making will be progressively more feasible as the computational speed increases. The actual calculations for this paper were not optimized for speed, but recently, using parallel computing, we have been able to reduce hours to a few minutes for the analysis of 20 s of 100 channels.

With progress on the steps stated above, the investigation of GC analysis performed intraoperatively may begin. Initial applications might focus on one stage resections with planned ECoG. We foresee progressing by supplementing conventional interpretation by neurologists with automated visualization of networks. If this approach yields information useful to surgeons, appropriately validated at some point, it might be included in making intraoperative decisions about whether a long-term invasive monitoring is necessary to see a seizure or whether GC with other modalities (such as a spike localization and an HFO detection) could in some cases obviate the need for a long-term invasive monitoring with a second craniotomy.

Limitations

This early investigation has limitations. One is that the study population may be not typical for all epilepsy surgery practices. In this study, the series of patients happened to include a large number of lesional cases and also turned out to have generally good surgical outcomes. This perhaps helped illustrate how the graphical models correspond with the conventional advice given by epileptologists, but testing in more varied populations will be useful. A broader mix of outcome results might help determine whether resections including the most causal electrode zones improve outcome. Another limitation is that there is still the need to determine how large the resection set should be. This will be one of several computational improvements that we might imagine in the future. We can, however, now conclude that useful information can be mined from interictal corticography.

CONCLUSION

Our findings from the application of time domain GC analysis to interictal iEEG suggest that the value of interictal data as a surgical planning tool can be enhanced computationally. The technique described in this paper can produce graphical depictions of interesting networks without actually recording seizures. Evaluation in the operating room will be needed to assess the potential impact of GC analysis on surgical decision making.

Disclosure

The authors have no personal, financial, or institutional interest in any of the drugs, materials, or devices described in this article.

Supplementary Material

nyx195_supp

Supplemental digital content is available for this article at www.neurosurgery-online.com.

Supplemental digital content is available for this article at www.neurosurgery-online.com.

COMMENTS

The authors have used sophsiticated analyses to demonstrate that Granger Casuality can be used to identify seizure onset regions, using interictal data, in a selected population. This is a nice addition to the ongoing efforts to use timeseries information to identify seizure onset zones from interictal data. The idea that the interictal state can replicate the spread pattern of seizures is attractive. It will be very important to determine whether this method works in non-lesional cases for several reasons. First, in lesional cases (which characterizes the majority of the cases in this report) there is much less doubt as to the seizure onset zone and, in some centers, long-term invasive monitoring is avoided completely. This is perhaps increasingly the case as imaging methods improve. Second, it is the non-lesional cases that are most in need of avoiding extensive invasive monitoring. Thirdly, non-lesional cases are at higher risk of being multi-focal and it is not clear if this method will hold in this situation. If invasive monitoring is ‘close’ but not exact to the onset, will Granger Causality give an answer anyway? This will be a false positive, but only if it would lead to an incorrect resection. This line of work will be of great interest especially as increasingly sophisticated analyses (Granger Causality as well as other directional analyses are applied, such as Direct Transfer Function, Phase Slope Index, Phase Amplitude Coupling, etc), higher frequency sampling, and machine learning algorithms that can analyze all data (electrophysiology, imaging, etc) are applied to the localization problem.

Jeffrey G. Ojemann

Seattle, Washington

This article describes a novel and sophisticated method for the prediction of epileptogenic zones using interictal iEEG data. Traditionally, seizure onset zones are the primary source of information for surgical decision making. The authors time domain Granger Causality analysis provides an alternative data point that does not require the patient to have a seizure and has the long-term potential to decrease the duration of iEEG monitoring. Algorithms that visualize and quantify network activity in the brain, as described in this article, are valuable and may provide new insights on the dynamics of seizures and interictal activity.

Sara Hanrahan

Adam O. Hebb

Englewood, Colorado