Neural reactivations during sleep determine network credit assignment

Abstract

A fundamental goal of motor learning is to establish neural patterns that produce a desired behavioral outcome. It remains unclear how and when the nervous system solves this “credit–assignment” problem. Using neuroprosthetic learning where we could control the causal relationship between neurons and behavior, here we show that sleep–dependent processing is required for credit-assignment and the establishment of task-related functional connectivity reflecting the casual neuron-behavior relationship. Importantly, we found a strong link between the microstructure of sleep reactivations and credit assignment, with downscaling of non–causal activity. Strikingly, decoupling of spiking to slow–oscillations using optogenetic methods eliminated rescaling. Thus, our results suggest that coordinated firing during sleep plays an essential role in establishing sparse activation patterns that reflect the causal neuron–behavior relationship.

Introduction

Hallmarks of learning a new skill include a significant reduction of movement variability and a concomitant reduction in both the extent and variability of neural firing^1–7. This process is associated with increasingly sparse task–related neural activation patterns^5–8. A theoretical framework for the underlying computation is frequently labeled the “credit assignment problem”, i.e. determination of how a single neuron in a highly interconnected biological network causes a behavior^9,10. Past work has suggested that a key goal of credit assignment is to select neural activity that truly reflects the causal neuron–behavior relationship^8,11. However, it remains unknown how a complex and interconnected biological neural network can solve this computation.

We hypothesized that sleep–dependent reactivations may play an important role in network credit assignment. A large body of work indicates that sleep plays an important role in memory consolidation^12–14. More specifically, reactivation of neural activity during sleep has been implicated in memory consolidation^12,14–17. However, there has been great debate regarding the specific computational role of such reactivations^12–14. Two commonly cited possibilities are that sleep–dependent reactivations lead to: (i) a general strengthening of functional connectivity, or (ii) a process of renormalization with both strengthening and weakening of functional connectivity^12,14,18. In the case of renormalization, a theoretical prediction is that after a period of sleep, there may be rescaling of task-related activity (e.g. neural activations not causally linked to performance are selectively downscaled)¹⁸. Interestingly, such a process of rescaling of task–activations could be used for network credit assignment.

Here we used a neuroprosthetic–learning task, where the “decoder” and the causality of the neuron–behavior relationship are set by the experimenter^8,11,19–24, to evaluate whether NREM sleep plays a role in credit assignment. Unlike natural motor behaviors, neuroprosthetic control offers a unique paradigm to study plasticity; a small set of neurons is chosen to causally control actuator movements (i.e. ‘direct’ neurons)^8,19. In contrast, ‘indirect’ neurons show task–related activity even though they do not cause actuator movements^8,11,25. Importantly, while past work has shown that learning proficient control through putative error–correction processes leads to increased activity of direct neurons and diminished activity of indirect neurons^{8,11,20,25,26}, it remains unclear how and when this fundamental credit–assignment process is solved. Here we show that neural spiking triggered by slow–oscillations during sleep plays an essential role in credit assignment.

Results

Rescaling of Task Activity

In five rats implanted with microwire arrays in primary motor cortex (M1), we monitored sets of direct (TR_D) and indirect (TR_I) neurons during the initial learning (hereafter BMI₁), during a period of sleep and subsequent task–performance upon awakening (hereafter BMI₂). A linear decoder with randomized weights converted the firing rates of two randomly chosen TR_D neurons into the angular velocity of the actuator. The decoder weights were held constant during the session to exclusively rely on neural learning. Notably, there are studies demonstrating that decoder adaptation can still induce long-term plasticity²⁷. However, this was done in non-human primate models performing more complex tasks. In our experiments, animals trained to control the angular velocity of a feeding tube via modulation of neural activity. At the start of each trial, the angular position of the tube was set to 0° (Fig. 1a–b, P₁). If the angular position of the tube was held for >300 ms at position P₂ (90°), a defined amount of water was delivered (i.e. a successful trial); a trial was stopped if this was not achieved within 15 s. Over a typical 2–hour session, animals were able to learn the task. Consistent with past results²³, after a period of NREM sleep, task performance improved at the start of BMI₂ (also called BMI_2Early; Fig. 1c, P < 0.05 for each of the 10 individual comparisons of BMI_1Late and BMI_2Early; overall paired t test, t₉ = 7.62, *P < 10⁻⁴).

Figure 1. Rescaling of task activations after sleep.

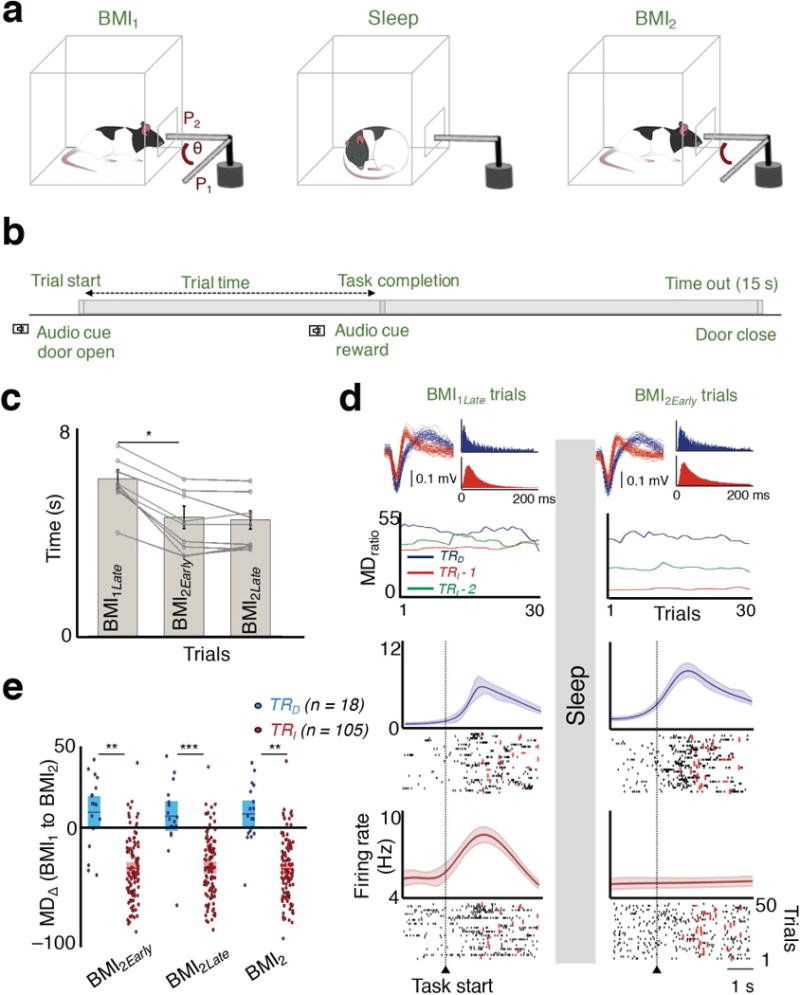
a, The practice sessions were separated by a block of sleep. Rats learned direct neural control of a feeding tube (θ = angular position). Successful trials required movement from P₁ to P₂ within 15 s. b, A typical trial structure is depicted. c, Comparison of trial times. A significant reduction in completion time was found between BMI_1Late to BMI_2Early (n = 10 sessions; paired t test, t₉ = 7.62, *P < 10⁻⁴). d, At the top are the waveforms and inter-spike interval histograms of the neurons analyzed below (color-coded). Plot below shows the trend in the modulation depth ratio (MD_ratio) during BMI performance for three neurons before and after sleep. Another neuron whose waveform is not shown is depicted in green. Below are the peri–event histograms from BMI_1Late and BMI_2Early trials, respectively for the TR_D and TR_I neurons (in same color convention). Thick line represents mean; shaded area is the jackknife error. Below the PETHs are representative spike rasters from multiple trials. Red dot indicates task completion time for each trial. e, Average modulation depth change (MD_∆) between BMI₁ and BMI₂ (mean in solid line ± s.e.m. in box; unpaired t tests; BMI₁ and BMI_2Early t₁₂₁ = 6.79, **P < 10⁻⁹; BMI₁ and BMI_2Late t₁₂₁ = 6.31, ***P < 10⁻⁸; BMI₁ and BMI₂ t₁₂₁ = 6.96, **P < 10⁻⁹).

We next compared the activity of TR_D and TR_I neurons during task–performance immediately prior to and after sleep (i.e., intervening sleep or Sleep_post, duration: 36.94 ± 1.06 min, mean ± s.e.m., n = 10 sessions; paired t test of Sleep_pre and Sleep_post durations: t₉ = 0.056, P = 0.95). We specifically measured the change in the peak-firing rate during task performance relative to the baseline rate prior to the ‘GO’ cue (i.e. ‘modulation depth’ or MD). The majority of TR_D cells increased their modulations (~67%), whereas a majority of TR_I cells reduced their modulation (~90%). Strikingly, while TR_D neurons experienced a slight but significant increase in modulation depth (7.39 ± 5.89 %, Wilcoxon signed-rank test, Z = −1.81, P = 0.03), there was a substantial net decrease in the MD of TR_I neurons (–31.76 ­± 2.18 %, paired t test, t₁₀₄ = 14.58, P < 10⁻²⁶) (Fig. 1, d–e). In addition, we found that the time spent in sleep predicted the extent of TR_I downscaling (Spearman correlation, r = –0.71, P < 0.05).

Changes in Functional Coupling During Sleep

We next compared the changes in functional connectivity in the recorded M1 neural ensembles during NREM sleep epochs prior to and after training. We specifically calculated the magnitude of spike–spike coherence (SSC) for TR_D – TR_D, and TR_D – TR_I, pairs both during the sleep that followed training (Sleep_post) and the sleep that preceded (Sleep_pre). The SSC is a pair-wise measure of how phased locked two neurons are across of frequencies²⁸. For TR_D – TR_I, pairs, the TR_D neuron with stronger task-related modulation was chosen for SSC calculation relative to the other TR_I neurons. We observed that the Sleep_post SSC curves for TR_D – TR_D unit pairs showed a significant increase in the 0.3 – 4 Hz band (Fig. 2a); this frequency band reflects slow-oscillatory activity during NREM sleep^13,14. At the population level, these increases were greater for TR_D – TR_D pairs than TR_D – TR_I pairs (129.78 ± 10.29% increase for TR_D − TR_D pairs and 56.30 ± 4.73% increase for TR_D – TR_I pairs; unpaired t-test, t₁₂₁ = 6.95, P < 10⁻⁷). We didn’t observe any significant differences near the spindle band (8–20 Hz) or ripple (100–300 Hz) frequency bands (data not shown). This indicates that the decoder coupled direct units (i.e. TR_D – TR_D) were significantly more likely to fire synchronously during slow-oscillations in relation to their coupling with indirect units (i.e. TR_D – TR_I) during Sleep_post. We also found that the firing rate of the neurons did not significantly change between the two epochs (mean firing rate for the two epochs: 6.54 ± 0.66 Hz to 6.62 ± 0.64 Hz, paired t tests, TR_D neurons: t₁₇ = −1.65, P = 0.11; TR_I neurons: t₁₀₄ = 0.049, P = 0.96). This may be consistent with a recent study regarding the firing changes in NREM²⁹, where firing rate changes were evident during certain phases of sleep and with monitoring of the entire sleep period.

Figure 2. Changes in functional connectivity of direct neuronal pairs and reactivation microstructure.

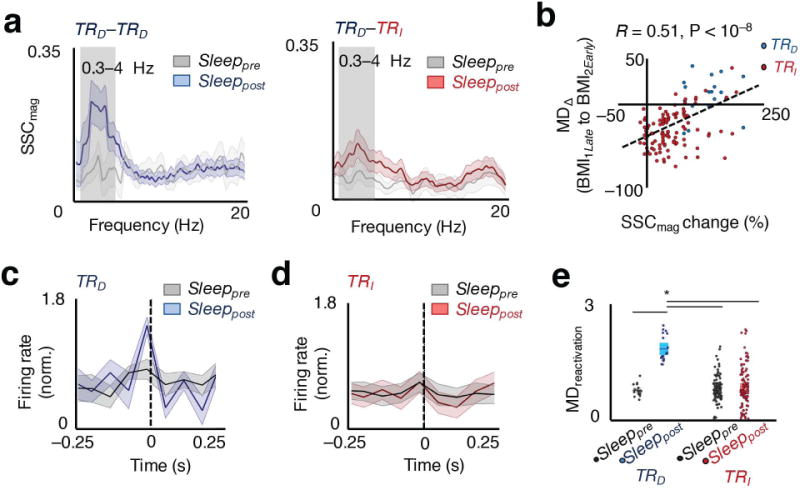
a, Example plot of SSC as a function of frequency during sleep prior to (Sleep_pre) and after (Sleep_post for TR_D – TR_D; red for TR_D – TR_I pairs) skill acquisition. The lighter band is the jackknife error. The box highlights the 0.3 – 4 Hz band. b, Relationship between SSC change before and after learning, and change in task-related modulation after sleep, MD_Δ (BMI_1Late to BMI_2Early), spearman correlation, r(123) = 0.51, P < 10⁻⁸. c, Average modulation depth during reactivations (MD_reactivation, i.e. ratio of peak to tails) of TR_D neurons from Sleep_pre to Sleep_post. d, MD_reactivation of TR_I neurons from Sleep_pre to Sleep_post. e, Average modulation depth during Sleep_pre to Sleep_post reactivations for TR_D and TR_I neurons (mean in solid line ± s.e.m. in box, one-way ANOVA, F_3,242 = 34.28, P < 10⁻¹⁷; significant post hoc t tests, *P < 0.05).

We next wondered whether individual pairwise changes in the post–learning functional connectivity could predict rescaling. As also indicated above, for each neuron we calculated a single SSC value by using a single TR_D neuron as a “reference”. We thus examined if the specific changes in SSC could predict the MD changes for TR_D and TR_I units from BMI₁ to BMI₂ (Fig. 2b). Interestingly, we found that SSC changes were a strong predictor for rescaling (Pearson correlation, r = 0.51, P < 0.05), indicating that functional connectivity changes during sleep could account for our observed changes in task activations after sleep.

We also examined whether the precisely temporal pattern of spiking (i.e. “microstructure”) of sleep reactivations^23,30,31 could also predict rescaling. In contrast to the general functional connectivity analysis, this approach is based on detection of temporally precise “reactivation events” that reflect the firing patterns that emerge with learning^23,30,31. Importantly, our past work has shown that such reactivation events are also tightly related to slow oscillations²³. We specifically used principal components analysis to create a template to reflect the ensemble activity that emerged with learning^23,30,31. Subsequently, we evaluated the instantaneous reactivation strength during the two sleep epochs. We further measured the “microstructure” by binning the neural activity identified using reactivation analysis (i.e. using coarser time bins of 50 ms) with smaller time bins of 5 ms. In principle it is possible that the average microstructure of reactivations could resemble: (i) activity during BMI₁, (ii) activity during BMI₂, or (iii) evolve over time during sleep. Detailed analysis of the identified reactivation events indicated that there was no evolution of patterns in sleep (data not shown).

We next examined whether the microstructure of reactivation events more closely resembled task-activity during BMI₁ or during BMI₂. We thus examined the specific modulation of TR_D and TR_I neurons during the high percentile reactivation events (see Methods). We found that, at the population level, modulation of TR_D neurons was significantly greater around the reactivation events than for TR_I, thus resembling the task activations evident during BMI₂. In other words, the identified reactivation events did not resemble BMI₁ where there was similar modulation of TR_D and TR_I. Modulation of TR_D neurons was also greater than in Sleep_pre, while they remained unchanged for the TR_I population from Sleep_pre to Sleep_post (Fig. 2c–e; one way ANOVA, F_3,242 = 34.28, P < 10⁻¹⁷). Such increased modulation was not apparent in randomly selected parts of Sleep_post (Supplementary Fig. 1; unpaired t test, t₁₂₁ = −0.69, P = 0.49). Together, these results suggest that after learning, sleep reactivations demonstrated firing patterns that resembled, on average, the rescaled pattern. Interestingly, at the level of single neurons, the depth of modulation during reactivations (i.e. Fig. 2c–e) predicted how a neuron changed its task–related firing rate during BMI₂ (i.e. significant relationship between lack of firing during reactivations and downscaling of task activity, linear regression, R² = 0.17, P < 10⁻⁵, Supplementary Fig 2). Thus, we found that direct task related units fired more coherently during sleep, as indicated by the elevated SSC, as well as more robustly around reactivations, and their relative modulation depth were significantly greater than for indirect units during task performance in BMI₂.

The Role of Reward

What determines the microstructure of reactivations? We first compared the differences between TR_D and TR_I firing during BMI₁; it was difficult to distinguish the two populations based on the evolution of firing patterns locked to trial onset (Fig. 3). However, as recent studies suggest that neural activity linked to reward can be preferentially reactivated^32–34, we also compared activity patterns locked to reward delivery. Notably, we found that it was substantially easier to distinguish the two populations in this “frame of reference”; TR_D neurons showed a more robust and consistent modulation around reward (Fig. 3a). We quantified this by comparing the activity of pairs of neurons around task start and prior to reward. The peak modulation depth ratio for TR_D neurons around task–start versus task–end was significantly different (respectively 16.20 ± 0.96 versus 26.25 ± 1.24, paired t-test, t₁₇ = −6.81 P < 10⁻⁵). On the other hand, the modulation depth of TR_I neurons did not significantly vary between the two frames of reference (13.84 ± 0.45 versus 12.86 ± 0.26 respectively, paired t-test, t₁₀₄ = 1.95 P = 0.053).

Figure 3. Consistency of reward and frames of reference.

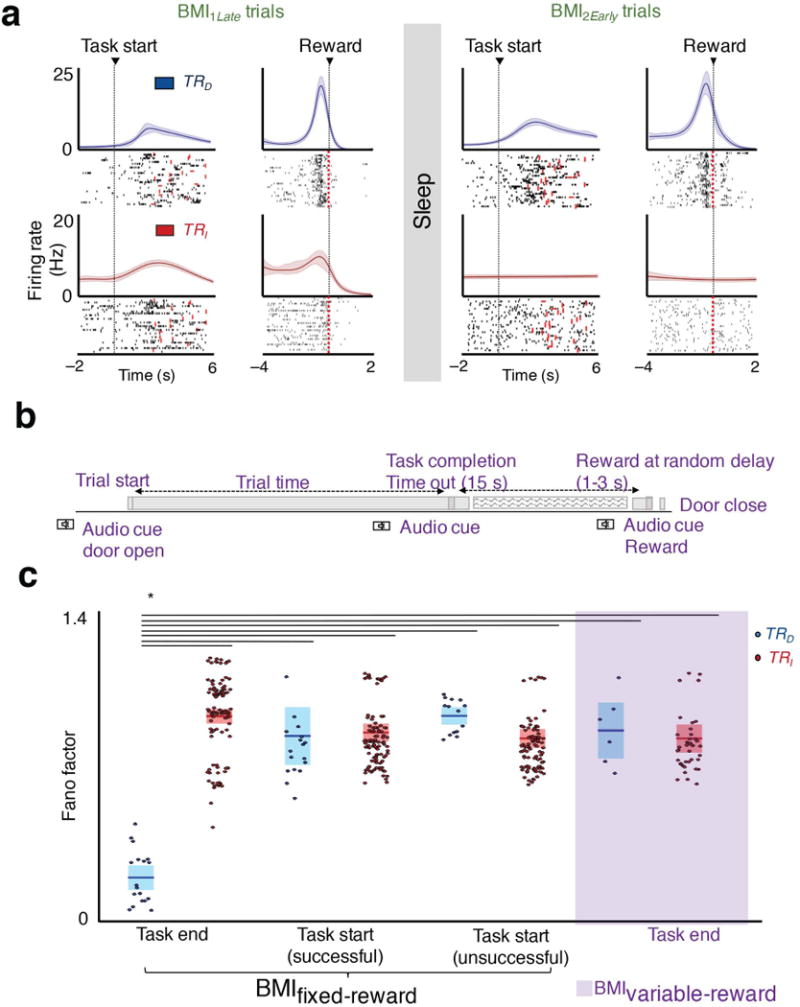
a, Neural firing centered to task start and task end/reward for the same session for regular BMI training (i.e. BMI_fixed-reward). The lighter band is the jackknife error. b, Schematic of “variable-reward” BMI training. b, Schematic of variable-reward BMI trials. c, Average Fano factor of TR_D and TR_I neurons for the four sets of conditions, namely task-start (successful and unsuccessful trials are separately parsed) and task-end/reward frame in BMI_fixed-reward, and task end in BMI_{variable-reward} (mean in solid line ± s.e.m. in box, task start and task end in BMI_fixed-reward one-way ANOVA, F_5,350 = 41.20, P < 10⁻³²; task end in BMI_fixed-reward and BMI_{variable-reward} one-way ANOVA, F_3,166 = 83.86, P < 10⁻³², significant post hoc t tests, *P < 0.05).

In general, we also noted that there was an apparent reduction in the variability of firing patterns for TR_D neurons as opposed to TR_I neurons associated with task completion. We quantified changes using the Fano factor method^35,36 (FF), which is a statistical measure of the trial-to-trial variability of neural firing. We found that TR_D neurons had the lowest FF at task end, which coincided with reward (Fig 3c). These values were lesser than for task start of successful trials, and even lower than for task start of unsuccessful trials. Importantly, when we matched for firing rates between the two frames using a subset of the neurons, we still observed the same decline in FF for the TR_D neurons in the task completion frame (TR_D neurons’ FF : 0.37 ± 0.007 and 0.68 ± 0.016 for the task end and task start frame, TR_I neurons’ FF : 0.71 ± 0.002 and 0.62 ± 0.002 for task end and task start respectively; one-way ANOVA, F_5,350 = 41.20, P < 10⁻³²). This suggested that the consistency of neural firing relative to reward may be an important determinant of rescaling.

To specifically dissociate task completion from reward, we performed ‘variable reward’ experiments (i.e. BMI_{variable-reward}) where we uncoupled task completion from reward (Fig. 3b). This is contrasted from experiments we have outlined above in which the reward was delivered at a fixed interval after task completion (i.e. BMI_fixed-reward). More specifically, the water was delivered after a variable delay of 1–3 seconds after trial completion. While the animals could learn the task (30.62 ± 6.47% improvement from BMI_1Early to BMI_1Late; paired t-test, t₃ = 4.46, P < 0.05), we did not observe significant performance gains from BMI_1Late to BMI_2Early as typically seen in BMI_fixed-reward trials (Fig 1c). Interestingly, we also did not observe the rescaling effect; the change in modulation depth from BMI_1Late to BMI_2Early was 14.03 ± 7.89% and 3.35 ± 2.31% respectively for TR_D and TR populations (paired t-test, t₅ =−1.95, P = 0.10 for TR_D, t₄₀ = −1.46, P = 0.15 for TR_I).

We then used these experiments to assess if our observed changes were truly related to reward or simply task completion. Interestingly, for BMI_{variable-reward} experiments, we no longer observed the reduction in FF for TR_D neurons at task completion (one–way ANOVA, F_3,166 = 83.86, P < 10⁻³², post-hoc t–test, P < 0.05; Fig. 3c). Moreover, they were indistinguishable from indirect neurons. Together, this data suggests that the lack of a temporally precise link between task completion and reward altered the differential modulation of the two populations previously seen. We then examined how the firing patterns of individual neurons changed for each of these two frames. We thus calculated the pairwise correlation between the sets of neurons during either trial start trial end. Consistent with our hypothesis, the correlated firing between pairs of TR_D – TR_D and TR_D – TR_I was significantly different for the reward–based frame for BMI_fixed-reward relative to the BMI_{variable-reward} condition (i.e. ‘Pairwise Correlation’, Fig. 4a, one–way ANOVA, F_7,304 = 8.36, P < 10⁻⁸, post-hoc t–test, P < 0.05).

Figure 4. Pairwise correlation of neural firing during task performance and reactivations during sleep.

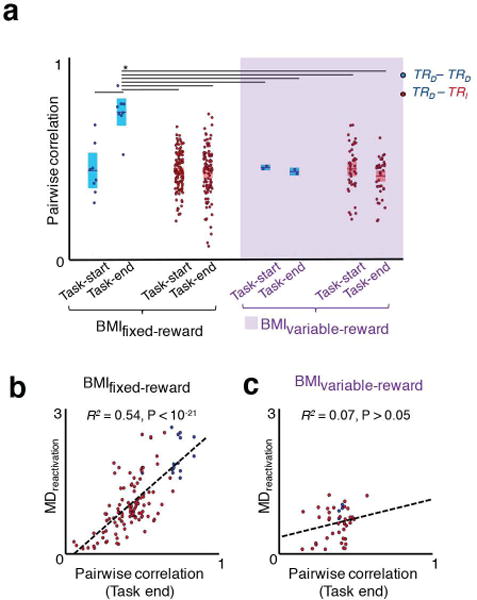
a, Pairwise correlation of neural firing for TR_D – TR_D and TR_D – TR_I pairs around task start and task end in BMI_fixed-reward and BMI_{variable-reward} paradigms (mean in solid line ± s.e.m. in box; one-way ANOVA, F_7,304 = 8.36, P < 10⁻⁸; significant post hoc t tests, *P < 0.05). b, Relationship of individual neural pairwise (i.e. at task end) and reactivation during sleep in BMI_fixed-reward sessions (linear regression R² = 0.54, P < 10⁻²¹; neural pairs are in same convention as Fig 4a). c, Relationship of individual neural pairwise correlations at task end and reactivation during sleep in BMI_{variable-reward} sessions (linear regression R² = 0.07, P > 0.05; neural pairs are in same convention as Fig 4a).

What is the effect of reward on reactivations? Interestingly, we found that neural co-firing in the reward frame could strongly predict the microstructure of reactivations for the BMI_fixed-reward experiments (Fig. 4b; R² = 0.54, P < 10⁻²¹); this relationship was not significant relative to task start (spearman correlation, r = 0.12, P = 0.19), or for the BMI_{variable-reward} experiments (Fig 4c, R² = 0.07, P > 0.05). Together, our results indicate that firing patterns found within reactivation events are most closely related to the consistency of neural firing relative to the time of reward.

Closed-Loop Inhibition of Spiking Activity During Slow Oscillations

We next used closed-loop optogenetic methods to evaluate the casual role of the changes in sleep³⁷ functional connectivity in triggering both the offline performance gains and rescaling. We injected five rats with Jaws, a red–shifted halorhodopsin that is a potent silencer of neural activity³⁸. After a period of several weeks, we performed a second surgery to implant microwire arrays attached to a cannula for fiber optic stimulation. The animals showed robust expression and ~60% neurons responded to optical stimulation by reducing firing (~43% average reduction, Fig. 5a–c). Using each animal as its own control, we compared the effects of either allowing normal sleep (n = 8 sessions; ‘OPTO_OFF’) or conducting closed–loop perturbations (n = 11 sessions ; ‘OPTO_UP’) to decouple spiking activity during UP states (i.e. activated states hallmarked by neural firing during NREM sleep; Fig. 5b)^14,39. We considered each session from a given animal as an independent observation. Optogenetic inhibition during OPTO_UP experiments was specifically triggered during slow-oscillations either by simple thresholding of filtered LFP during UP states (n = 8) or thresholding of power in the slow–wave band (n = 3; see Methods). For the OPTO_DOWN experiment, we exclusively used the filtered LFP to trigger the LED (Fig 5d). These experiments were randomly interleaved among the animals. For the optogenetic experiments, we selected TR_D cells that responded to optical stimulation with reduced firing. Figure 5b and c show examples of a TR_D neuron with normal firing during Sleep_pre and suppressed firing during optogenetic stimulation linked to UP states (Sleep_post; population averages in Fig 5c). The stimulation pulses during OPTO_UP and OPTO_DOWN experiments had similar incidences (Supplementary Fig 3a) and proportion compared to total time spent in sleep (Supplementary Fig 3b). All rats tolerated this manipulation without affecting total duration of sleep when compared with the OPTO_OFF group (Supplementary Fig 4). Furthermore, there were no quantitative changes in sleep power across the three conditions (Fig. 5e, f; Fig 5f is a quantification of the 0.3–4 Hz band).

Figure 5. Optogenetic inhibition of neural activity during sleep.

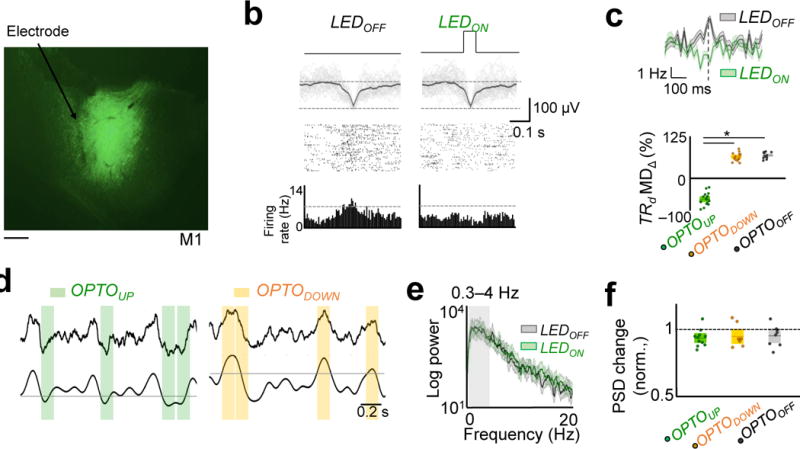
a, Fluorescence image of a coronal brain section showing neurons expressing Jaws (green) in M1. Scale bar is 500 μm. b, UP state triggered LED inhibition of a TR_D cell in Sleep_post as compared to the activity of same cell in Sleep_pre without stimulation. Rasters are shown along with raw traces of the local-field potential (LFPs) based on threshold crossing of the LFP. Dark line is the mean LFP. Bottom-most row shows histogram of firing activity. c, Top: Average modulation depth (MD) of a TR_D cell in a representative OPTO_UP experiment. Bottom: Average modulation depth (MD) of TR_D cells around slow-oscillations in OPTO_UP, OPTO_DOWN, and OPTO_OFF experiments (mean in solid line ± s.e.m. in box, one-way ANOVA, F_2,41 = 425.75, P < 10⁻²⁷; significant post hoc t tests, *P < 0.05). d, Examples of the raw and filtered (0.3–4 Hz) traces and the stimulation period for respective OPTO_UP and OPTO_DOWN experiments. e, Power spectrum of LFP from Sleep_pre and Sleep_post in an OPTO_UP experiments. The lighter band is the jackknife error. f, Power spectral changes (in 0.3 – 4 Hz) for OPTO_UP, OPTO_DOWN, and OPTO_OFF experiments (one-way ANOVA, F_2,27 = 0.13, P = 0.87).

Interestingly, we observed significant worsening of performance only in the OPTO_UP experiments (Fig. 6a–b). Figure 6a shows two examples of learning following pre- and post-sleep from two sessions in the same animal. Typically we observed a worsening of performance relative to the end of the previous session in OPTO_UP experiments, but the performance level was still better than the earliest trials. This was not the case with respective OPTO_DOWN and OPTO_OFF experiments. Together, these experiments suggest that decoupling of spiking during the UP states of slow-oscillations is sufficient to prevent offline gains. This also strongly suggested that such a process is activity-dependent and appeared to at least require the local firing of action potentials during sleep. Additionally, we also found that the performance worsening in BMI₂ in the OPTO_UP experiments was associated with increased firing variability of TR_D neurons in both task-start and task-end frames of reference and was comparable to that of TR_I neurons (TR_D neurons Fano factor: 1.04 ± 0.04 and 1.11 ± 0.08 at task end and task start; TR_I neurons Fano factor: 1.07 ± 0.017 and 1.09 ± 0.02 at task end and task start; one- way ANOVA, F_3,220 = 0.44, P = 0.72; P > 0.05 for all post hoc multiple comparisons). This was not the case after robust learning sessions where TR_D neurons were associated with a significant reduction in FF at task end (Fig 3c).

Figure 6. Optogenetic inhibition during UP states prevents consolidation.

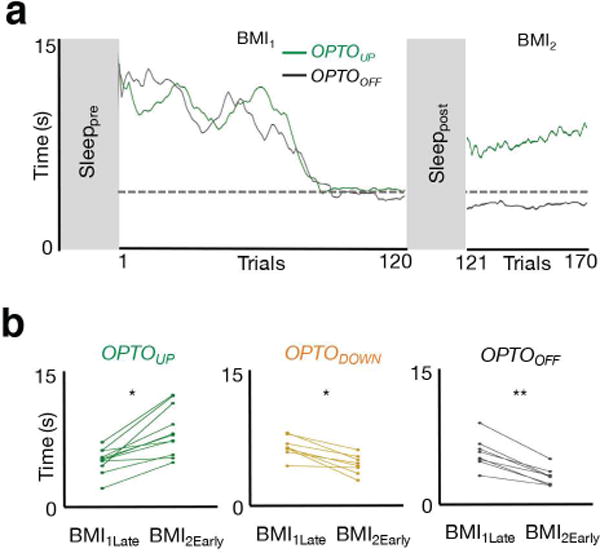
a, Learning curves from two BMI sessions in the same rat with and without optogenetic inhibition during sleep (i.e. OPTO_UP and OPTO_OFF sessions, respectively). b, Performance changes from BMI_1Late to BMI_2Early in each of the three respective conditions (OPTO_UP sessions paired t test t₁₀ = -5.52, *P < 10⁻³; OPTO_DOWN sessions paired t test t₇ = 5.12, *P < 10⁻³; OPTO_OFF sessions paired t test t₇ = 7.73, **P < 10⁻⁴).

Optogenetic Inhibition and Rescaling

We next examined the extent of rescaling for the three experimental groups. Sessions with OPTO_UP stimulation did not demonstrate rescaling of task activity in BMI₂, whereas the OPTO_DOWN and OPTO_OFF conditions resulted in the expected rescaling of TR_I neurons as previously observed (Fig. 7a). Furthermore, we evaluated neural dynamics using spike-field coherence (SFC, see methods regarding equalizing the number of spikes); SFC was significantly reduced for TR_I neurons from Sleep_pre to Sleep_post in the OPTO_UP group (Fig. 7b–c). Finally, we also assessed whether the extent of average SFC change (ΔSFC_mag from Sleep_pre to Sleep_post) of TR_D neurons could predict the extent of rescaling of TR_I neurons from BMI₁ to BMI₂ (MD_Δ). Notably, we found a significant relationship between these changes in the SSC and the rescaling phenomenon (Fig. 7d; R² = 0.66, P < 10⁻⁶). Together, these results suggest that our measured changes in sleep functional connectivity after learning may be required for the performance gains, the reduced variability of direct neurons and the rescaling of task related activity.

Figure 7. Optogenetic inhibition during UP states prevents rescaling of task activations.

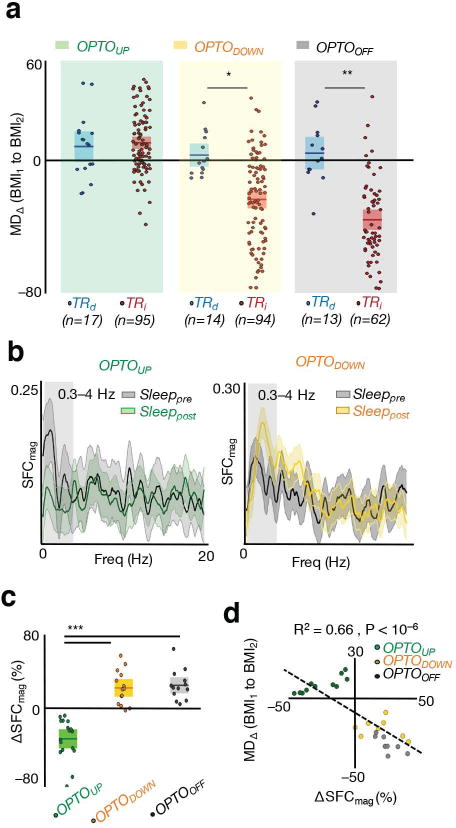
a, Rescaling of TR_D and TR_I neurons measured through modulation depth change (MD_∆) from BMI₁ and BMI₂ in OPTO_UP, OPTO_DOWN, and OPTO_OFF experiments (mean in solid line ± s.e.m. in box; OPTO_UP sessions unpaired t test t₁₁₀ = −0.47, P = 0.64; OPTO_DOWN sessions unpaired t test t₁₀₆ = 3.67, *P < 10⁻³; OPTO_OFF sessions paired t test t₇₃ = 5.52, **P < 10⁻⁶). b, Example plot of SFC as a function of frequency in Sleep_pre and Sleep_post in OPTO_UP and OPTO_DOWN experiment for two TR_D neurons. The lighter band is the jackknife error. c, Averaged SFC changes from Sleep_pre to Sleep_post for TR_D neurons in OPTO_UP, OPTO_DOWN, and OPTO_OFF groups (mean in solid line ± s.e.m. in box, one-way ANOVA, F_2,41 = 44.83, P < 10⁻¹⁰; significant post hoc t tests, ***P < 0.05). d, Averaged SFC changes for TR_D cells versus averaged rescaling of TR_I cells from BMI₁ to BMI₂ in OPTO_UP, OPTO_DOWN, and OPTO_OFF groups (linear regression R² = 0.66, P < 10⁻⁶).

Discussion

In summary, we found striking evidence for rescaling of task–related neural activity after a period of NREM sleep. We specifically found that there was selective downscaling of TR_I neural populations (i.e. non–causal) in comparison to TR_D neurons (i.e. causal) during task performance after NREM sleep. Our results further revealed how individual TR_D and TR_I neurons might be chosen for downscaling; we found that patterns of activity during sleep were predictive of task–related rescaling. During task practice, activity patterns that were most consistently related to rewarded outcomes matched the “microstructure” of reactivations. A more gross measure of neural firing linked to slow-oscillatory activity (i.e. SSC in 0.3–4 Hz band) could also predict rescaling. Finally, we found that closed-loop optogenetic suppression of neural spiking during UP states prevented both performance gains and rescaling. Together, our results suggest that NREM sleep plays an essential role in determining task-related functional connectivity that reflects the causal neuron behavior relationship. A net result of this process is to assign network credit assignment and to create sparser patterns of task-related activity.

Rescaling and Sleep-Dependent Memory Processing

Two commonly cited possibilities for the role of sleep in memory consolidation are: (i) a general strengthening of synaptic connectivity, or (ii) a process of renormalization with net weakening of synaptic connectivity^12,14,18. In the former, sleep is noted to have an active role in strengthening memories through enhanced local and distant connectivity, thus resulting in systems consolidation. In contrast, in the latter, renormalization of synaptic strengths is believed to restore synaptic homeostasis and thereby benefit memory functions. It is worth noting that both processes could occur but may operate over distinct timescales during long periods of sleep¹⁴. For example, recent evidence suggests that sleep is important both for pruning and growth of new spines^40–42. Functionally, this could account for both the increases and decreases in neural firing after sleep²⁹. Interestingly, a theoretical prediction is that synaptic renormalization may lead to rescaling of activity¹⁸; to our knowledge there is no direct evidence. For natural learning, assessment of task-dependent renormalization is likely to be difficult given that the causality of neural activity to behavior is largely still unknown.

Neuroprosthetic learning allows us to readily distinguish neural activity that is causal for actuator movements (i.e. TR_D) versus activity that is non-causal. Using this task, we found evidence of rescaling of task activity; specifically, that the task-related modulation of causal neurons were slightly but significantly enhanced, while non-causal neurons showed selective downscaling of task-related modulation. While our specific experiments do not allow us to make conclusions regarding changes in synaptic strength, they do reveal that sleep-dependent processing can rescale task-dependent activations. At the very least, our results suggest that sleep-dependent processing does not exclusively strengthen functional connectivity as assessed by task-related neural firing. Moreover, given that we also found a small but significant improvement in task performance as well as increased modulation of direct task-neurons we cannot not exclude that a strengthening process may also simultaneously occur. Interestingly, our experiments using optogenetic suppression of spiking during the UP states suggests that our observed rescaling is driven by an activity-dependent process. Thus, our results also suggest that reactivations during sleep may be involved in a process of rescaling of task activity; this notion is also broadly in line with predictions that renormalization may rely upon the synchronous activity evident during slow oscillations ¹⁸.

Neuroprosthetic Memory Consolidation and Slow Oscillations

Our closed-loop optogenetic manipulation was triggered by phases of slow-oscillations during sleep. We found that while suppressing neural spiking during UP state (Fig 5b–d) perturbed sleep-dependent effects, similar perturbations in the DOWN state did not have detectable effects. This suggests that the spontaneous reactivation of both task and non-task related neurons during UP states are required for sleep-dependent gains. Importantly, our intervention did not appear to grossly affect sleep duration or the power-spectrum of sleep. However, it is still possible that other known processes that are linked to slow-oscillations might play a role. For example, it is known that spindles are associated with activity during UP states^13,14. While we did not detect gross changes in power, it is still possible that disruption of spiking during slow-oscillations could affect spindles. Moreover, there is also a known link between cortical slow-oscillations and hippocampal ripples^13,14. Future work can elucidate how other processes might contribute to consolidation after learning.

Our results further suggest that both performance gains and rescaling are regulated by spiking activity linked to slow-oscillations. More specifically, NREM sleep appears to have a three-fold effect on neural activity and performance. Firstly, there was a significant effect of enhanced performance. Secondly, there was a slight but significant increase in the modulation depth of TR_D units. Finally, there was downscaling of TR_I activity. The latter two appear to be related to a rescaling effect in which the two populations are differentially modified. Our OPTO_UP intervention affected both performance gains and the rescaling effect. Interestingly, while it might seem that the modulation depth of TR_D units was still increased, we observed a significant increase in task-related variability for TR_D. Such enhanced variability may reflect poor consolidation of task activity patterns and underlie the degradation of performance after the OPTO_UP intervention. It can be likened to ‘erosion’ of memory where rats forgot the neural activity pattern in BMI₁ and had to relearn the task again. Together, this suggests that rescaling of the two neural populations may occur simultaneously during UP states.

Interestingly, the SSC analysis in Figure 2 suggests that the precise relationship between rescaling and SSC may be complex. There are at least three possibilities for why we measured a general increase in SSC in the setting of a largely selective enhancement of direct neurons. Firstly, it is possible that there is an elevated threshold for plasticity. In other words, the intercept of our linear regression line suggests that the zero crossing (i.e. threshold for enhancement) is for values greater than a zero change in SSC. Alternatively, it is possible that the general increase in SSC represents active processing of both populations during slow-oscillations. In this view, the system might actively sample both weak and strong functional connectivity in order to ultimately determine credit assignment. Such active sampling would appear to result in a general increase in SSC. It is also worth noting that for hippocampal replay, there may be dissociation between the external experience and internal processing⁴³. Thus, it is also possible that the elevated SSC represents a schema for internal representation that is not strictly related to the actual awake experience.

Our results might also suggest that both performance gains and rescaling are optimized by the same mechanisms. However, it is still possible, that there is differential regulation of these two aspects of task performance. In both rodent and non-human primate models of neuroprosthetic learning, there is a dissociation between performance gains and rescaling^8,23. For example, at the end of a typical practice session there were performance gains in the absence of rescaling (i.e. firing of non-causal activity). Similarly, past work in non-human primates has indicated that rescaling can take days to occur even in the presence of performance gains; the task used was substantially more complex than for rodents. This suggests that performance gains do not absolutely require rescaling. In our experiments, however, we found that sleep-dependent performance gains and rescaling were evident after a period of sleep. Moreover, disruption of spiking linked to slow-oscillations resulted in both degradation of performance and rescaling. This suggests that sleep-dependent processing co-regulates both processes. However, given that sleep is a collection of heterogeneous and non-stationary phenomena^12,14, it is still quite possible that these two aspects can be dissociated. For example, our optogenetic intervention did not specifically examine the role of spindle activity that is coincident with slow-oscillations (i.e. as opposed to all spiking linked to it). Future work can help determine if performance gains and rescaling are always co-regulated during sleep.

Role of Reactivation in Credit Assignment

Our analysis specifically identified that timing of task activity relative to reward may determine credit assignment. Especially during “early learning”, co-firing of direct and indirect neurons occured over multiple seconds. It is likely that the animals were exploring patterns of neural activity that could successfully complete the task. Notably, traditional task-related PETHs for neuroprosthetic performance are calculated based on trial start; this is also typical for natural learning^31,35. However, based on the extensive history on the role of reward in learning^32–34, we also examined PETHs that were associated with task end and reward delivery. Interestingly, the frame relative to reward was the most predictive of rescaling and sleep-related reactivations. We also found that by perturbing the link between reward and task completion (i.e. the “variable reward” experiments in Fig 3,4) we no longer observed these phenomena. Together, these results are consistent with the growing notion that the patterns and extent of reward shapes learning and offline processing^10,44.

What might be a computational role for our observed rescaling of cortical activity and its association with reward? In general, reward–related reactivation may be a broad mechanism to learn and remember experiences that lead to successful outcomes^32–34,45. More specifically, the observed optimization of functional connectivity during sleep may provide important insight into the biological implementation of reinforcement learning (RL), a widely studied theoretical and experimental model for reward-based learning^10,44. In RL, there is a noted tradeoff between “exploration” (i.e. gather new knowledge) versus “exploitation” (i.e. optimize decisions based on current knowledge)⁴⁶; it remains unclear how this is precisely achieved in biological systems. Our data suggests that sleep–dependent processing can allow for more targeted exploration based on knowledge accumulated regarding reward–related neural firing during awake behaviors. Sleep may thus allow further exploration of the statistics of the causal relation of neural activity to successful outcomes. The net result is the establishment of neural activity patterns that appear to reflect the causal neuron-behavior relationship.

Methods

Animals/Surgery

Experiments were approved by the Institutional Animal Care and Use Committee at the San Francisco VA Medical Center. We used a total of ten adult Long–Evans male rats (n = 5 were used for optogenetic experiments). No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^23,31. Animals were kept under controlled temperature and a 12–hour light: 12–hour dark cycle with lights on at 06:00 AM. Probes were implanted during a recovery surgery performed under isofluorane (1–3%) anesthesia. Atropine sulfate was also administered prior to anesthesia (0.02 mg/kg b.w.) The post–operative recovery regimen included administration of buprenorphine at 0.02 mg/kg b.w and meloxicam at 0.2 mg/kg b.w. Dexamethasone at 0.5 mg/kg b.w. and Trimethoprim sulfadiazine at 15 mg/kg b.w. were also administered post–operatively for five days. We used 32–channel microwire arrays; arrays were lowered down to 1400–1800 µm in the primary motor cortex (M1) in the upper limb area (1–3 mm anterior to bregma and 2–4 mm lateral from midline). The reference wire was wrapped around a screw inserted in the midline over the cerebellum. Final localization of depth was based on quality of recordings across the array at the time of implantation. All animals were allowed to recover for 1–week prior to start of experiments. Data collection and analysis were not performed blind to the conditions of the experiments.

Viral injections

We used a red-shifted halorhodopsin, Jaws (AAV8-hSyn-Jaws-KGC-GFP-ER2, UNC Viral Core) for neural silencing in 5 rats for optogenetic experiments³⁸. Viral injections were done at least 2.5 weeks prior to chronic microelectrode array implant surgeries. Rats were anesthetized, as stated before and body temperature was maintained at 37°C with a heating pad. Burr hole craniotomies were performed over injection sites, and the virus was injected using a Hamilton Syringe with 34G needle. 500nl injections (100 nl per min) were made into deep cortical layers (1.4 mm from surface of brain) at two sites in M1 (coordinates relative to bregma: posterior, 0.5 mm and lateral, 3.5 mm; and anterior, 1.5 mm and lateral, 3.5 mm). After the injections, the skin was sutured and the animals were allowed to recover with same regimen as stated above. Viral expression was confirmed with fluorescence imaging. Optogenetic inhibition significantly reduced firing in M1 neurons, with a reduction in 50–70% of recorded cells.

Electrophysiology

We recorded extracellular neural activity using tungsten microwire electrode arrays (MEAs, Tucker–Davis Technologies or TDT, FL). We recorded spike and LFP activity using a 128–channel TDT–RZ2 system (Tucker–Davies Technologies). Spike data was sampled at 24414 Hz and LFP data at 1018 Hz. ZIF–clip based analog headstages with a unity gain and high impedance (~1 GΩ) was used. Optogenetic experiments, including controls, were done with digital headstages primarily because of the ability to pass the optical fiber through the commutator. Only clearly identifiable units with good waveforms and high signal–to–noise were used. The remaining neural data was recorded for offline analysis. Behavior related timestamps (i.e. trial onset, trial completion) were sent to the RZ2 analog input channel using a digital board and synchronized to neural data. We initially used an online sorting program (SpikePac, TDT) for neuroprosthetic control. We then conducted offline sorting²³.

Behavior

After recovery, animals were typically handled for several days prior to the start of experimental sessions. Animals acclimated to a custom plexiglass behavioral box (Fig. 1a) during this period. The box was equipped with a door at one end. Initially, water delivery from the actuator was not introduced and they were just acclimatized to the box. Towards the end of the acclimation period, the rats typically fell asleep while in the box. Animals were then water scheduled such that water (from the feeding tube illustrated in Fig. 1a) was available in a randomized fashion while in the behavioral box. We monitored body weights on a daily basis to ensure that the weight did not drop below 95% of the initial weight. Behavioral sessions were conducted in the morning, with second sessions conducted in the afternoon. We recorded neural data from the rats for 2 hours prior to start of BMI training (that comprised Sleep_pre). The rats were then allowed to perform the task over a ~2–hour session (BMI₁). Recorded neural data was entered in real–time from the TDT workstation to custom routines in Matlab. These then served as control signals for the angular velocity of the feeding tube. The rats typically performed ~180–200 trials per session. These sessions typically lasted from 90 to 120 minutes based on the rate of trial completion. Following this, we recorded neural data from animals for a 2–hour period (including Sleep_post). The animals then continued with another 90 to 120 minute training session (BMI₂). Sorted units at the beginning of the recording were checked for maintenance throughout the second training session.

Neural control of the feeding tube

During the BMI training sessions, we typically randomly selected two well–isolated units as ‘direct’ and allowed their neural activity to control the angular velocity of the feeding tube. In two of the 10 sessions (i.e. from the 5 non-viral injected rats), there was only one neuron selected as the direct unit. The remaining neurons in all the experiments (i.e. indirect) were there recorded but not causally linked to actuator movements. We did not find any systematic differences in waveform shape (i.e. narrow vs. broad) or baseline firing rate for these two populations. These units maintained their stability throughout the recording as evidenced by stability of waveform shape and interspike–interval histograms. We binned the spiking activity into 100 ms bins. We then established a mean firing rate for each neuron over a 3–5 minute baseline period. During this period the animals were typically transitioning between walking, exploring and periods of rest.

The mean firing rate was then subtracted from its current firing rate at all times. The specific transform that we used was:

$${\theta }_v=C\ast ( G_1\ast r_1(i)+ G_2\ast r_2(i))$$

where θ_v was the angular velocity of the feeding tube, r₁(i) and r₂(i) were firing rates of the direct units. G₁ and G₂ were randomized coefficients that ranged from +1 to –1 and were held constant after initialization. C was a fixed constant that scaled the firing rates to arrive at a value for angular velocity. The animals were then allowed to control the feeding tube via modulation of neural activity. The tube started at the same position at the start of each trial (P₁ in Fig. 1a,b). The calculated angular velocity was added to the previous angular position at each time step (100 ms). During each trial, the angular position could range from –45 to +180 degrees. If the tube stayed in the ‘target zone’ (P₂ in Fig. 1a; spanned 10° area) for a period of 300 ms, a water reward was delivered. In the BMI_{variable-reward} experiments (n = 4 sessions in two rats), the rats correctly positioned the tube, but reward delivery (i.e. the water from the tube) was randomly delayed by a period ranging from 1–3 seconds. In contrast, the BMI_fixed-reward (i.e. typical BMI session), the reward was delivered with a fixed delay of ~200 ms relative to task completion. In the beginning of a session, most rats were unsuccessful at bringing the feeding tube to position P₂. Most rats steadily improved control and reduced the time to completion of the task during the first session. We obtained multiple learning sessions from each animal. These sessions were typically several days to 1 week apart to ensure that new units were recorded. Consistent with past studies, we also found that incorporation of new units into the control scheme required new learning^8,23.

Closed-loop sleep experiments using optogenetics

Three types of experiments were conducted using the 5 JAWS injected animals, namely: (i) OPTO_UP (n = 11); (ii) OPTO_DOWN (n = 8); and (iii) OPTO_OFF (n = 8). These experiments were largely randomly interspersed among the animals. However, while the OPTO_DOWN were only conducted in 3 animals, these animals also contributed to the OPTO_UP and OPTO_OFF experiments. In general, we identified the phases of the LFP associated with ‘UP’ and ‘DOWN’ states based on the relationship of the neural spiking to the LFP. For example, as shown in Figure 5, the negativity in our LFP signals was associated with neural spiking and thus consistent with an UP state, which are natural states of increased activity during slow oscillations.

The closed-loop interventions were conducted by triggering the LED light based on real-time detection of cortical states. We used a custom script in the RPvdsEx Prgram (TDT) to identify slow oscillations in real-time during sleep blocks. In the OPTO_UP experiments, we conducted two types of triggering (n = 3 power based; n = 8 filtering based). In both cases, the LED light was delivered during cortical ‘UP’ states by placing a manual threshold on filtered LFP trace; the manual threshold was selected visually to coincide with the respective phase on the slow oscillations as noted below. For the “power based” triggering, we used the following approach. The algorithm/workstation calculated the LFP power in the 0.1 – 4 Hz range and compared it to the threshold. Once the threshold was exceeded for >100 ms, LED illumination (625nm Fiber-Coupled LED (ThorLabs), with 200/400 μm diameter optic fibers (Doric Lenses) was triggered for 100 ms. For the ‘filtering based’ approach, we used a real-time implementation of a Butterworth filter to filter the raw LFP in a 0.1–4 Hz band (Figure 5d). The UP state was determined by setting a ‘negative’ threshold on the LFP (i.e. as displayed in the convention in Figure 5d). The LED was again triggered when it was respectively above/below this threshold. Notably, this type of stimulation was exclusive to the UP state. Because we did not observe any differences we combined both sets as the OPTO_UP condition.

During OPTO_DOWN sessions, we directly placed a ‘positive’ threshold on the filtered LFP; thus the stimulation was triggered during threshold crossings of ‘DOWN’ (i.e. DOWN states with natural periods of quiescence during slow oscillations). These stimulations were also typically brief (i.e. 100 ms). A typical example is shown in Fig 5. Supplementary Fig 3 shows that total incidents of 100 ms stimulations were similar in both OPTO_UP and OPTO_DOWN experiments, and the light was on for a similar proportion of time. Finally, a group of control experiments called OPTO_OFF (i.e. where no stimulation was triggered) was also conducted in the JAWS injected rats. Durations of total pre and post sleep were similar in all 3 session types (Supplementary Fig 4). We also calculated LFP power and SFC changes for individual neurons in all 3 groups.

Data Analysis

Sessions and changes in performance

Analysis was performed in Matlab (Mathworks, Natick, MA) with custom–written routines. A total of 10 BMI_fixed-reward training sessions recorded from 5 rats were used for our initial analysis. All of these sessions demonstrated ‘robust learning’ (i.e. > 3 SD drop in time to completion in the last 1/3 of trials or ‘late’ trials in comparison to the first 1/3 of trials or ‘early’ trials). These sessions were followed by a second training session (i.e. BMI₂). In Fig. 1c we compared changes in task performance across sessions. Specifically, we compared the performance change between BMI_1Late, BMI_2Early and BMI_2Late by calculating the mean and standard error of the time to completion during the last third trials in BMI₁ and the first and last third trials BMI₂ (Fig. 1c). We used a paired t–test to assess statistical significance.

Task–related activity

The distinction between TR_D and TR_I neurons was based on whether units were used for the direct neural control of the feeding tube. The change in modulation depth (MD_∆) was calculated by comparing the peak activity around the task (in the 5 second window after the task start/4 sec prior to task-end/reward) over baseline firing activity (averaged activity of 4 seconds prior to task start) on the peri-event time histograms (PETH, bin length 50 ms). In other words, the MD_∆ is a measure of the modulation of firing rate relative to the pre-task start baseline rate. Modulation of baseline firing activity after the ‘Go cue’ (task start) or prior to receipt of ‘reward’ (task end) was calculated and this was compared for TR_D and TR_I neurons from BMI₁ to BMI₂ (MD_∆ change from BMI₁ to BMI₂). This was calculated across the last third of trials from BMI₁ and first and last third of trials from BMI₂ (BMI_2Early and BMI_2Late respectively). In a BMI session with approximately 200 trials, these values were averaged across ~65 trials. To ensure that any online training effects were not contributing to the observed reduction in MD_∆ of TR_I units, in a subset of these sessions we also averaged MD_∆ for just 30 trials before and after; no significant differences were evident.

For Figures 1 and 3, PETH were smoothed using a Bayesian adaptive-regression spline algorithm, implemented within MATLAB using toolboxes downloaded at (http://www.cnbc.cmu.edu/~rkelly/code.html)^31,47. The algorithm automatically optimized for the number and location of “knots” (i.e., regions in which a new local regression model improves the overall fit of the curve) was determined automatically using a Markov chain Monte Carlo implemented to optimize the Bayes Information Criteria and thereby, offered a better visualization of dynamic changes in the rate of change of spike trains. These curves were not used for other sets of analysis.

Identification of NREM oscillations

Identification of pre and post–NREM epochs was performed by combined visual assessment of presence of low–frequency, high amplitude slow–wave oscillations as well as a 3 SD threshold of the filtered data (0.3 – 4 Hz). If there was a sustained reduction > 1.5 seconds in the amplitude of the slow-wave activity below threshold during a continuous epoch we excluded these segments^23,31.

Coherency measure

We used the Chronux toolbox to calculate the SSC (http://chronux.org/) ⁴⁸. Its magnitude is a function of frequency and takes values between 0 and 1. For it’s calculation, the pre- and post-sleep were segmented into 20-s segments and then the coherency measured was averaged across segments. For the multitaper analysis, we used a time-bandwidth (TW) product of 10 with 19 tapers. To compare coherences across groups, a z score was calculated using the programs available in the Chronux Toolkit. Coherence between activity in two regions, C_xy was calculated and defined as

$$C_{xy}=\frac{\left|R_{xy}\right|}{\sqrt{R_{xx}}\sqrt{R_{yy}}}$$

where R_xx and R_yy are the power spectra and R_xy is the cross-spectrum. More specifically, it is a pairwise measure of synchronized co-firing of neurons in a frequency dependent manner. For example, during NREM sleep, it can quantify synchronous co-firing relative to low frequency oscillation’s in the 0.3–4 Hz range. Our previous work has also shown that SSC values are related to the spike cross-correlogram measured during UP states²³.

Spectral analysis were calculated in segmented NREM epochs and averaged across these epochs across animals. Mean coherence was calculated between 0.3 – 4 Hz. Significance testing on coherence estimates was performed on mean estimates between TR_D – TR_D and TR_D – TR_I pairs using unpaired t-tests. The task-related direct unit with the greatest depth modulation was used to calculate SSC for every other unit. Similarly, for SFC analysis in optogenetic experiments, mean power changes in the 0.3–4 Hz band were compared for OPTO_UP; OPTO_DOWN and OPTO_OFF experiments. We also equaled the number of spikes in pre- and post- sleep^23,28 to account for the changes in firing rates; this was especially pertinent for the optogenetic intervention studies.

Ensemble activation analyses

To characterize ensemble reactivations following sleep, we performed an analysis that compared neural activity patterns during Sleep₁ and Sleep₂ with a template that was created during task execution in BMI₁ ^23,30,31. We first computed a pairwise unit activity correlation matrix during BMI₁ by concatenating binned spike trains (t_bin = 50 ms) for each neuron across trials (0.5s prior to the onset of trial up to 5s after the onset of BMI task for each trial). This concatenated spike train was z-transformed, and then organized into a 2-D matrix organized by neurons (x) and time (B for number of time bins). From this spike count matrix, we calculated the correlation matrix (C_task), and then calculated the eigenvector for the largest eigenvalue from this correlation matrix to study. This eigenvector was used as the ensemble template of activity, which was then projected back on to the neural activity trains from the same population of neurons during Sleep₁ and Sleep₂. This projection was a linear combination of Z-scored binned neural activity from the two blocks above, weighted by the PC ensemble (i.e., the eigenvector) calculated from the BMI₁ matrix. This linear combination has been described as the “activation strength” of that particular ensemble. In this analysis we focused on the first eigenvector, as the first PC explained most task-related variance (see Supplementary Figure 5 for two examples).

Reactivation triggered peri-event time histogram (“microstructure” of reactivation)

We also constructed time histograms of single unit activity around reactivation events. We binned spike counts from 250 ms before and after ensemble reactivation events using a 5 ms bin size and calculated the mean/standard error of the binned neural firing. The reactivation events that were chosen for PETHs were those with a reactivation strength that was significantly greater than for the pre- sleep block. Usually top 10–20 percentile reactivation strengths from the post-sleep fulfilled this criterion. Once the PETHs were constructed, the modulation depth around reactivations (MD_reactivation) was calculated by comparing the peak of firing during reactivation to the mean baseline firing (i.e. at the tails). t-test was performed to compare MD_reactivation between TR_D and TR_I units, and also their levels in pre-sleep. We also checked for MD_reactivation of TR_D and TR_I units at random low-percentile reactivation events and their MD_reactivation was indistinguishable (Supplementary Fig 1).

Analyses of neural firing variability and neuronal pair correlations

The modulation characteristics of each neuron in the BMI task in the two frames of reference (namely, ‘task-start’ and ‘task-end’) were examined using the following: (1) Fano factor, which is a statistical measure of the dynamics of the firing rate of a cell^35,36; and (2) Cross-correlation calculated between the rates of cell pairs. Fano factor, F is defined as follows:

$$F= \frac{{\sigma }^2}{\mathrm{\mu }}$$

where σ² is the variance and μ is the mean of a spike count process (here in a 50 ms time window). μ was the average firing rate and was calculated as follows:

$$\mu = \frac{1}{\mathrm{B}}{\displaystyle \sum }_{\mathrm{n}=1:\mathrm{B}}\mathrm{C}(\mathrm{n})$$

where C(n) is the spike counts in 50 ms time window and B is the total window sample number. Since, fano factor can be influenced by firing rate, we also compared fano factor in task start and task end frames of reference where the firing rates were similar and we still found similar trends. Cross-correlation, on the other hand, measured the similarity of two firing rate series (50 ms bins) as a function of the displacement of one relative to the other. This pairwise correlation of the neural activity was calculated for TR_D – TR_D and TR_D – TR_I neuronal pairs using Matlab’s xcorr function (Fig. 4). Time series of concatenated binned spike counts were created either around task start (first 1 sec) or around task end (from trial end to 1 sec prior). Statistical comparisons were performed using a repeated-measures ANOVA, followed by post-hoc t tests to identify specific time points that were significantly different.

Statistics

There were a total of 10 robust BMI learning sessions that we used (BMI_fixed-reward) for analyzing the trends from BMI₁ to BMI₂. There were a total of 18 TR_D and 105 TR_I units in these experiments. There were also 4 BMI_{variable-reward} sessions where we had 6 TR_D and 41 TR_I neurons. Optogenetics experiments (in JAWS injected rats) had 11 sessions with OPTO_UP stimulation (with 17 TR_D and 95 TR_I units), 8 sessions with OPTO_DOWN stimulation (with 14 TR_D and 94 TR_I units), and 8 sessions with OPTO_OFF stimulation (with 13 TR_D and 62 TR_I units). We also recorded sleep prior to (Sleep_pre) and after (Sleep_post) after BMI₁. In all these experiments, we performed paired t-test to compare performance changes from BMI₁ to BMI₂; MD_∆ change for TR_D or TR_I units from BMI₁ to BMI₂; MD_reactivation change and firing rate changes for TR_D and TR_I units from Sleep_pre to Sleep_post; SSC_mag changes for TR_D – TR_D and TR_D – TR_I neuronal pairs from Sleep_pre to Sleep_post (Fig. 1c, 6b). Data distribution was tested for normality and non-parametric test was substituted if needed (Wilcoxon signed rank test). Unpaired t–tests were also used for comparisons such as MD_reactivation in TR_D versus TR_I units pools; MD_∆ change for TR_D versus TR_I units from BMI₁ and BMI₂; and features of stimulation in OPTO_UP and OPTO_DOWN experiments (Fig. 1e, 7a; Supplementary Fig. 1, 3). We also performed one–way ANOVA with multiple comparisons (test of homogeneity of variances was done) wherever significance assessment was required (Fig. 2e, 3c, 4a, 5c,f, and 7c; Supplementary Fig. 4). We also used linear regression or correlation to evaluate trends between MD_reactivation versus MD_∆ change from BMI₁ and BMI₂, or correlated firing around task start or task end; pairwise firing correlation of TR_D – TR_D and TR_D – TR_I neuronal pairs versus MD_reactivation; between time spent in NREM sleep and MD_∆ change from BMI₁ and BMI₂ for different units; and SSC_mag changes for TR_D – TR_D and TR_D – TR_I neuronal pairs versus MD_∆ change for TR_D or TR_I units from BMI₁ to BMI₂; and SFC changes in optogenetics experiments, versus MD_∆ change (Fig. 2b, 4b,c 7d; Supplementary Fig. 2).