Abstract
We tested the ability of a single Compton camera (CC) to produce 3-dimensional (3D) images of prompt gammas (PGs) emitted during the irradiation of a tissue-equivalent plastic phantom with proton pencil beams for clinical doses delivered at clinical dose rates. PG measurements were made with a small prototype CC placed at three different locations along the proton beam path. We evaluated the ability of the CC to produce images at each location for two clinical scenarios: 1) the delivery of a single 2 -Gy pencil beam from a hypo-fractionated treatment [~9 × 108 protons], and 2) a single pencil beam from a standard treatment [~1 × 108 protons]. Additionally, the data measured at each location were combined to simulate measurements with a larger scale, clinical CC and its ability to image shifts in the Bragg Peak (BP) range for both clinical scenarios. With our prototype CC, the location of the distal end of the BP could be seen with the CC placed up to 4 cm proximal or distal to the BP distal falloff. Using the data from the simulated full scale clinical CC, 3D images of the PG emission were produced with the delivery of as few as 1 × 108 protons, and shifts in the proton beam range as small as 2 mm could be detected for delivery of a 2 Gy spot. From these results we conclude that 3D PG imaging for proton range verification under clinical beam delivery conditions is possible with a single CC.
1. Introduction
Since the Compton camera (CC) was first proposed for medical imaging (Todd et al., 1974), many researchers have studied its use for a wide range of medical applications, including 2D and 3D imaging of prompt gamma (PG) emission from a patient during proton radiotherapy as a means of providing in vivo verification of the delivered proton beam range (Frandes et al., 2010; Gillam et al., 2011; Golnik et al., 2016; Hueso-Gonzalez et al., 2016; Kim et al., 2013; Kormoll et al., 2011; Krimmer et al., 2015; Llosa et al., 2012; Lojacono et al., 2013; McCleskey et al., 2015; Munoz et al., 2017; Peterson et al., 2010; Polf et al., 2015; Richard et al., 2011; Robertson et al., 2011; Roellinghoff et al., 2014; Rohling et al., 2017; Seo et al., 2010; Solevi et al., 2016; Thirolf et al., 2016; Thirolf et al., 2014). In standard Compton imaging, information pertaining to the energy deposited by and spatial coordinates of gammas that interact at least twice in the stages of a CC is used to create the images. For a gamma that interacts twice in the CC (i.e., a double scatter event), using the a priori assumption that the gamma is fully absorbed in the second scatter the best estimate of the initial energy is
| (1) |
where E1 is the energy deposited in the first interaction and E2 is the energy deposited in the second interaction in the CC. For a gamma that interacts at least three times in the CC (i.e. a triple scatter event) the initial energy can be determined without the need to assume full absorption using
| (2) |
where mec2 is the rest mass of the electron and θ2 is the second scattering angle, defined as the angle between vector v1, which connects the first interaction point (x1, y1, z1) and the second interaction point (x2, y2, z2) in the CC, and vector v2, which connects the second interaction point and the third interaction point (x3, y3, z3). Next, the initial scattering angle (θ1) can be calculated using
| (3) |
The point of gamma emission is constrained to lie on the surface of a cone (or cone segment if the Compton scattered electron is tracked (Kim et al., 2012; Kurosawa et al., 2012; Thirolf et al., 2016)), called the cone-of-origin, with an opening angle equal to θ1, whose vertex corresponds to the first interaction location and whose axis is defined by v1. The cone-of-origin is used to produce an image of the measured gamma emission using either back projection or statistical image reconstruction methods.
For “standard Compton imaging” (i.e. Compton imaging using (1) or (2) to determine Eo) the image spatial resolution and signal-to-noise ratio are limited by physical characteristics of the detector such as pixel size, energy resolution, and Doppler broadening (Kormoll et al., 2011; Mackin et al., 2013; Wilderman et al., 1997a). Compton imaging also suffers from false double and triple scatters from non-Compton scatter events, such as coincident detection of separate gammas and the interaction of neutrons and other secondary particles in separate detection stages of the CC within the coincidence window during beam delivery. In addition pair production events, and gammas that Compton scatter twice, but do not deposit their total energy (Hueso-Gonzalez et al., 2017; Ortega et al., 2015; Rohling et al., 2017) also effect the imaging capabilities of the CC. These events greatly increase image noise and reduce the achievable spatial resolution of PG imaging (Ortega et al., 2015; Solevi et al., 2016). One technique researchers have studied to remove and reduce the effects of these “bad scatter events” is by limiting the initial PG energy range to > 2 MeV (Polf et al., 2009b; Rohling et al., 2017) or to an energy window around a specific PG emission lines (Hilaire et al., 2016; Hueso-Gonzalez et al., 2017). Although energy-selection methods like these have shown some promise, their implementation still requires a double scattered PG to deposit its full energy to correctly identify its Eo. This does remove many bad scatter events, but it can also remove true double scatter events in which a PG does not deposit its full energy. This results in a large reduction in the number of measured scatter events (both bad and true events) that can be used for reconstruction, making PG imaging during the delivery of clinical doses difficult. As such, the purpose of this study was to determine:
whether 3D PG imaging is possible for beams delivered at clinical doses/dose rates, and
whether shifts in the proton Bragg peak (BP) range of ≤ 5 mm can be detected with PG images produced with a single CC.
For this study, we used a small-scale prototype CC to measure PG emission from a tissue-equivalent plastic phantom irradiated with clinical proton pencil beams. Measurements were made for the delivery of clinical doses of 31 cGy and 200 cGy with a clinical treatment plan containing a single pencil beam of either 120 MeV or 180 MeV. Images of measured PG emission were reconstructed for the delivery of full range 180 MeV and 120 MeV pencil beams and for the 120 MeV beam range shifted by 3 mm and 5 mm.
2. Materials and Methods
2.1. Polaris J Compton Imager
For this study, we used the prototype Polaris J detection system (H3D Inc., Ann Arbor, MI, USA) shown in figure 1. The Polaris J consists of four separate detector stages, each containing a Polaris detection platform (Zhang et al., 2007), electronically linked to form the full CC. Each detector contains a 2 × 2 array of CdZnTe (CZT) crystals; each crystal is pixelated 11 × 11 in the x- and z-directions on the planar cathode. The crystals in stages 1 and 2 are 2 cm long × 2 cm wide × 1.5 cm thick, and stage 3 and 4 crystals are 2 cm long × 2 cm wide × 1 cm thick.
Figure 1.
(a) The prototype Polaris-J CC consisting of 4 detection stages labeled 1–4 and the Sychronization-coincidence timing module (SCT), with black squares showing the positioning of the CZT crystals in the stages. (b) The experimental setup for the measurements with the Polaris J on the treatment couch next to the HDPE phantom. (c) Schematic (not to scale) of the experimental setup showing the proton beam (black arrow) incident on the phantom from the negative z-direction. The dashed rectangle shows the position of the water equivalent plastic slabs used to shift the beam range. For the 180 MeV pencil beam, measurements were made with the CC positioned so that the center of the CZT array in stage 1 was located at z = 4 cm (P1), z = 0 cm (P2), and z = −4 cm (P3). For the 120 MeV pencil beam, measurements were made at P2, P3, and P4 (Z = − 8 cm).
For this study, the Polaris J was configured to measure gamma events in multistage/double coincidence mode, which requires that at least two events be measured in separate stages within the 1.5 μs coincidence window for the event to be recorded. The detection system records the energy deposited (E) in each interaction; the x, y, and z coordinates of each interaction; and the stage in which the event occurred. For each measurement, the recorded PG interactions were saved in a list-mode-format data file. More details on the Polaris J detector system are provided in McCleskey et al. (2015).
2.2. Measurements
All irradiations were performed at the Maryland Proton Treatment Center (MPTC) using the Varian ProBeam treatment delivery system (Varian Medical Systems, Palo Alto CA, USA) in a treatment room with an isocentric rotating gantry and a pencil beam scanning treatment nozzle. Single proton pencil beams of either 180 MeV or 120 MeV were delivered to a high density polyethylene (HDPE, [C2H4, ρ = 0.96 g/cm3]) phantom, 33 cm lateral width × 27 cm anterior-posterior height × 10 cm superior-inferior thickness, with rounded edges to mimic the outer contour of a patient body as shown in Figure 1. The HDPE phantom was placed on the patient treatment couch with the central axis of the pencil beam incident at the mid-point of its height and thickness. For irradiation with the 180 MeV pencil beam, the phantom was aligned so that treatment isocenter (0, 0, 0) was located at a depth of 21 cm in the phantom, which located the distal 90% falloff of the Bragg peak (BP) at z = 1.0 cm. For the 120 MeV pencil beam irradiations, the phantom was aligned with treatment isocenter located at a depth of 10.6 cm in the phantom, locating the distal 90% falloff of the BP being located also at z = 0.3 cm.
For the irradiation of the phantom, two treatment plans were created using the Eclipse treatment planning system (version 13.7, Varian Medical Systems, Palo Alto, CA) to deliver 2 Gy with a single pencil beam to a primary reference point located at the depth of the BP maximum and positioned at the center of a cylindrical (3 mm radius × 3mm height) clinical target volume. The first plan contained a single 120 MeV pencil beam and the second plan contained a single 180 MeV pencil beam. Both beams traveled along the z-axis. Each 2 Gy treatment plan was delivered in clinical treatment delivery mode and the beam current, delivery time, and Monitor Units (MU) delivered for each irradiation were obtained from the treatment delivery log files. From these values, we determined the number of protons extracted from the treatment nozzle for the delivery of 2 Gy of dose at the depth of the BP maximum to be 9.03 × 108 for the 180 MeV beam and 6.29 × 108 for the 120 MeV beam. The MUs for 120 MeV beam were then scaled to deliver the approximate number of protons delivered for a single highly-weighted pencil beam of a treatment field (~1 × 108 protons), which depends on factors such as the beam size and spacing used for treatment delivery, as well as many others. The treatment plans for the each scenario were then delivered to the HDPE phantom for these studies. Treatment delivery parameters for each beam energy and each number of protons delivered are shown in Table 1.
Table 1.
Beam delivery parameters for each pencil beam energy
| Beam Energy (MeV) | Beam current1 (nA) | Irradiation time (ms) | Number of protons delivered | Dose Delivered (cGy) | Monitor Units delivered |
|---|---|---|---|---|---|
| 180 | 0.52 | 276 | 9.03 × 108 | 200 | 316.6 |
| 120 | 0.33 | 305 | 6.29 × 108 | 200 | 263.7 |
| 49 | 1.00 × 108 | 31.8 | 41.3 |
Beam current at exit of the treatment nozzle
PG measurements were conducted with the CC stages arranged as shown in figure 1. The CZT array of CC stage 1 was located at y = −15.3 cm from the beam central axis for the 120 MeV beam and y = −47.6 cm for the 180 MeV beam. The stages 2 and 3 arrays were located 12.8 cm behind stage 1 in the negative y-direction, with stage 2 located +5.1 cm in the z-direction and stage 3 located −5.1 cm in the z-direction. The CZT array of stage 4 was centered at isocenter along the z-direction (identical to stage 1) and located 12.8 cm behind stages 2 and 3 in the negative y-direction. For the 180 MeV beam, measurements were made at three different camera locations (figure 1): (P1) the CC shifted 4 cm beyond isocenter (Z = 4 cm), (P2) the CC centered at the isocenter (z = 0 cm), and (P3) the CC shifted 4 cm proximal to isocenter (z = −4 cm). For the 120 MeV beam, measurements were made with the CC centered at P2, P3, and P4 (z = −8 cm). The data collected were combined to simulate PG emission measurements obtained with a CC containing a 4 × 12 cm2 first stage CZT array.
This setup was not an exact approximation of a larger camera because double scatter events in which a PG initially scatters in a first stage at a given measurement position are not able to scatter in the second, third, or fourth stages located at different CC positions when several separate measurements are made. However, it was the best approximation of a larger scale CC achievable with our current prototype.
Measurements were made for the 120 MeV pencil beam at P2, P3, and P4 for both the 2 Gy pencil beam and the single distal layer pencil beam. These measurements were conducted for the delivery of a full range pencil beam and with the range of the beam shifted by 3 mm and 5 mm by placing slabs of water equivalent plastic in front of the water phantom. For the 180 MeV pencil beam, only a measurement for the delivery of a full range, 2 Gy pencil beam at each position was conducted. Due to beam time restrictions, this set of measurements was conducted only once for each beam energy.
2.3. Data Processing
To improve the final images, we identified and removed “bad scatter” events not caused by a true double or triple scattered PG from the data prior to reconstruction using three different methods: 1) a Broad-Energy range, 2) an Energy-Window around a specific PG emission line, and 3) the distance-of-closest-approach/Compton-line-filter (D2C) filtering technique (Draeger et al., 2017). For the Broad-Energy filter, only PGs with initial energies between 2 MeV – 6.5 MeV (determined using eqns (2) or (3)) were kept as in previous studies (Polf et al., 2015; Rohling et al., 2017). For the Energy-Window filter, since an HDPE phantom was used, we windowed around the 4.44 MeV emission, shown to be the most intense PG emission from 12C* (Clegg et al., 1961) and well correlated with the proton depth dose profile (Polf et al., 2009a; Polf et al., 2013; Smeets et al., 2012; Verburg et al., 2013; Verburg et al., 2012).
The D2C method uses a-priori information about the pencil beam along with information about expected PG emission energies to remove bad scatter events from the measured data prior to reconstruction. The advantage of the D2C technique is that its determination of the most likely Eo does not require the double-scattered PG to be fully absorbed. For D2C filtering, two steps were used. In step 1, a distance-of-closest-approach (DCA) filter (Mackin et al., 2013; Wilderman et al., 1997b) was used to remove measured PG scatter events whose cones-of-origin do not come within a specified distance of the beam central axis and thus could not have been caused by a gamma originating along the proton beam path. First a cone-of-origin for each PG was created using the measured E1 value and the assumed Eo = 4.44 MeV. Then the DCA, defined as the shortest distance from the surface of the event cone-of-origin to the beam spot central axis is calculated. If the DCA is less than our DCA filter limit (5 mm for this study) the event is kept for reconstruction. In this study we used a DCA filter distance of 5 mm, roughly corresponding to the 1-sigma size of the pencil beams. In step 2, the value of E2 in the data file is corrected to be the assumed Eo (4.44 MeV) minus E1 for all double scatter events that pass the DCA filter. This is to ensure that the Eo value calculated by the reconstruction software (using eq. 1) is equal to our DCA assumed Eo.
2.4. Reconstruction
The images were reconstructed using an iterative method described by Mackin et al. (2012) and similar to the method described by Andreyev et al. (2011). A key idea behind this method is that for image reconstruction each cone-of-origin is represented by a single point on the cone’s surface. The iterations are used to choose the “representative” points. For the first iteration, a representative point, ri, is randomly chosen for each cone, i. Each ri must lie on the surface of cone i and be in the volume to be reconstructed. The gamma emission probability density is estimated using a 3D histogram of the representative points. For the second and subsequent iterations, another random point, βi, is selected for each cone i, again on the surface of cone i and in the volume to be reconstructed. The estimated emission probability densities of the new point, ρ(βi), and the representative point, ρ(ri), are compared using the inequality
| (7) |
where U is a uniformly distributed random number drawn from the interval [0,1). U is re-drawn for each comparison. If (7) is true, then the position of the representative point for cone i is moved to βi, and the gamma emission probability density estimate is updated to incorporate the change. The step of selecting random points, comparing them to representative points, and updating the emission probability density estimate are repeated for a fixed number of iterations or until an approximately steady state is achieved.
Because several of the final measured datasets, especially after filtering had a limited number of PG events, it was necessary to choose more than one random point on a PG cone-of-origin and iteratively move it around the cone surface independently of other points. This effectively increased the number of random points used for the iterative reconstruction, which helped to improve the smoothness of the final image. Therefore, the number of random points per PG cone-of-origin used for reconstruction was increased based on the number of events so as to limit statistical noise in the image as much as possible.
This reconstruction process was carried out for the Broad-energy filtered, Energy-window filtered, and D2C filtered datasets. In all cases, 500 iterations of the reconstruction algorithm were used. A reconstruction volume of 60 cm in the x, y, and z dimensions, with 5 mm bins in x and z and 2 mm bins in y, was used to iteratively determine the final estimated emission distribution of the measured PGs. To produce the final reconstructed image for each dataset, the list of final gamma coordinates determined during the iterative process was binned into 3D histograms with 2 mm3 voxels.
2.5. Data Analysis
The reconstructed PG emission measurements were then compared to dose profile measurements of the 180 MeV pencil beam by placing Gafchromic EBT2 film (International Specialty Products, Wayne, NJ, USA) between the two slabs of the HDPE phantom aligned in the XZ-plane. Lateral dose profiles were extracted at the depth of the BP for comparison with the PG profiles.
The final 3D histograms of the PG emission from the 120 MeV pencil beam were processed into a series of 150 slices (in the same manner as a CT dataset) with dimensions of 50 cm × 50 cm × 0.2 cm with a 0.4 cm × 0.4 cm × 0.2 cm voxel size. The reconstructed 3D PG images and the delivered pencil beam treatment plans, as well as the planning CT dataset (exported from the TPS) of the HDPE phantom were then loaded into the in-house RAVIN V© (RAnge Verification IN Vivo) range verification and analysis software. Using RAVIN V, the PG image was registered and overlaid onto a CT scan of the HDPE phantom for a 2D, slice-by-slice visual comparison to the planned dose distribution. Additionally, 1D profiles were extracted from the PG and TPS dose slice images within the RAVIN V software to determine if shifts in the PG range could be detected from the PG images.
3. Results and Discussion
3.1. Detection efficiency
Single stage detection rates for the experiments ranged from ~15 000 counts per second (cps) up to ~18 000 cps for the 180 MeV and 120 MeV beams, respectively. Based on the beam delivery times, this correlates to a maximum estimated instantaneous count rates of ~54 000 (18 000 cps/0.276 second irradiation) and ~59 000 for the 180 MeV and 120 MeV beams, respectively, resulting in maximum measurement dead times of ~15% per CC stage. These instantaneous count rates are well within achievable count rate limits for CZT (Perez and He, 2001) and well below flux rates known to induce charge polarization effects within the crystals (Rodrigues, 2012). Table 2 shows, for each beam energy the number of measured double/triple scattered PG events used for reconstruction for the raw, unfiltered data and the data filtered with each filtering technique for the delivery of the 2 Gy pencil beam at each CC position and for the combined data. For the raw, unfiltered data we see a maximum double/triple coincidence detection rate of 5.76 × 10−6/proton and 8.61 × 10−6/proton for the CC located at the depth of the BP for the 180 MeV and 120 MeV pencil beam, respectively. Detection rates increased to 1.52 × 10−5/proton and 2.34 × 10−5/proton for the large array (all positions combined) camera for the 180 MeV and 120 MeV pencil beams, respectively. For the filtered data from a single CC measurement position the double/triple coincidence detection rates ranged from 1.92 × 10−6/proton and 1.54 × 10−6/proton for the broad energy and D2C filters, respectively, down to 9.63 × 10−8/proton for the energy-window filter for the 180 MeV beam. Detection rates for the 120 MeV pencil beam were 7.01 × 10−6, 3.31 × 10−6, and 2.5 × 10−7 for the broad-energy, D2C, and energy-window filters, respectively for the combined CC. This detection rate for the energy-windowed data agrees with the “order of magnitude” estimation of coincidence detection rates of ~10−7 for 4.44 MeV PGs for a CC reported by Hueso-Gonzalez et al. (2017).
Table 2.
PGs measured at each detector position for 2 Gy delivered with a single pencil beam1.
| Beam energy (MeV) | Camera position | Unfiltered | Broad energy | Energy window | D2C |
|---|---|---|---|---|---|
| 180 | P1 | 3584 | 1151 | 42 | 594 |
| P2 | 5198 | 1735 | 87 | 1392 | |
| P3 | 4943 | 1272 | 60 | 814 | |
| Combined | 13 725 | 4158 | 189 | 2800 | |
| 120 | P2 | 5413 | 1624 | 62 | 786 |
| P3 | 5157 | 1547 | 50 | 712 | |
| P4 | 4130 | 1239 | 46 | 581 | |
| Combined | 14 700 | 4410 | 158 | 2079 |
coresponding to 9.03 × 108 protons for 180 MeV and 6.29 × 108 protons for 120 MeV.
3.2. 3D images
3D image reconstructions were performed with the measured PG data using a single PC workstation containing an 8 core, 2.6 MHz CPU and 24 GB of memory. Multi-threaded image reconstructions (using 8-cores) took from 40 to 150 seconds depending on the number of PG events and the number of independent points on the surface of each cone-of-origin used for the reconstruction.
Figure 2 shows the energy spectra of the data processed with standard Compton imaging methods with broad-energy and a narrow energy-window filtering, and D2C filtering for use in the 3D reconstructions of PG emission from the 180 MeV pencil beam irradiations. With the D2C method only events identified as 4.44 MeV were used for reconstruction in contrast to the other techniques which used a wider initial energy range.
Figure 2.
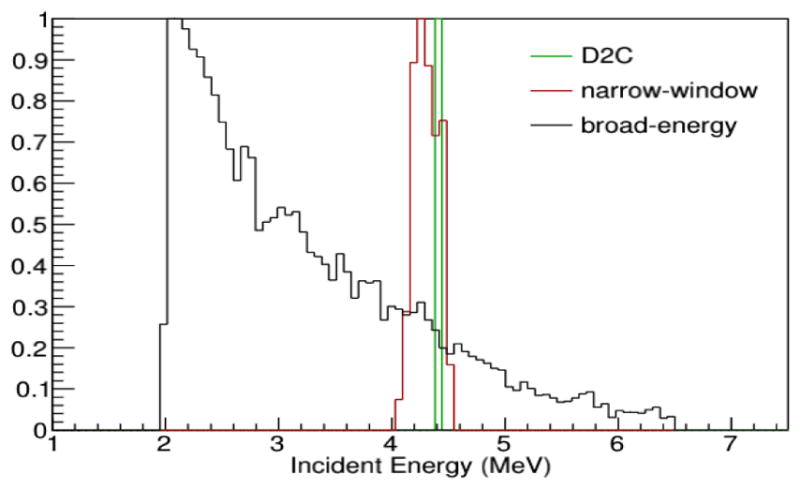
Energy spectra of the PGs for the three data filtering methods used for reconstruction.
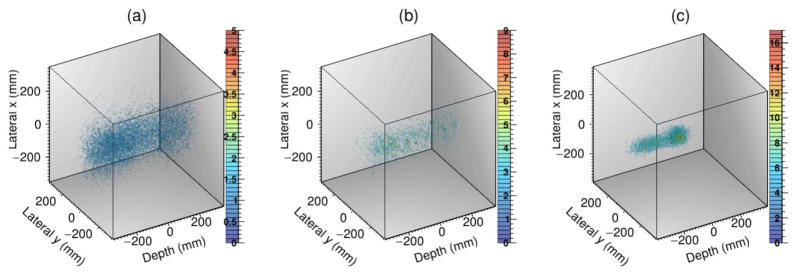
Figure 3 shows the 3D images reconstructed with the 180 MeV pencil beam PG data filtered with the three techniques. Since only 13 725 PG events were contained in the broad-energy filter data file, 5 independent points on the cone-of-origin for each event were chosen for the iterative reconstructions. Additionally, with only 189 PG events in the combined narrow energy-window filtered data, 360 independent points were chosen on each cone-of-origin. For the D2C data, only 2800 events were in the data file, so 25 independent points were chosen on the surface of the cone-of-origin for each event for iterative reconstruction. Even when more events per cone were included, and the final 3D images created with the broad energy and narrow energy-window filters did not converge into an image of the pencil beam, but instead were dispersed nearly uniformly in all three directions such that the beam range and lateral size could not be determined. However, the D2C filtering technique, revealed the image of the beam path could be seen, from the entrance of the phantom (z = −21 cm) to the end of the beam range at z = 1 cm. Because the 3D image of the pencil beam was only resolvable with the D2C filtered data, further analysis of PG imaging under clinical delivery conditions was conducted using only D2C filtered data.
Figure 3.
3D images for the (a) broad energy range filtered data, (b) for the 4.0 – 4.5 MeV energy-window filtered data, and (c) for D2C filtered data for PG measured during 180 MeV pencil beam irradiation of the HDPE phantom.
3.3. Individual and combined CC position images
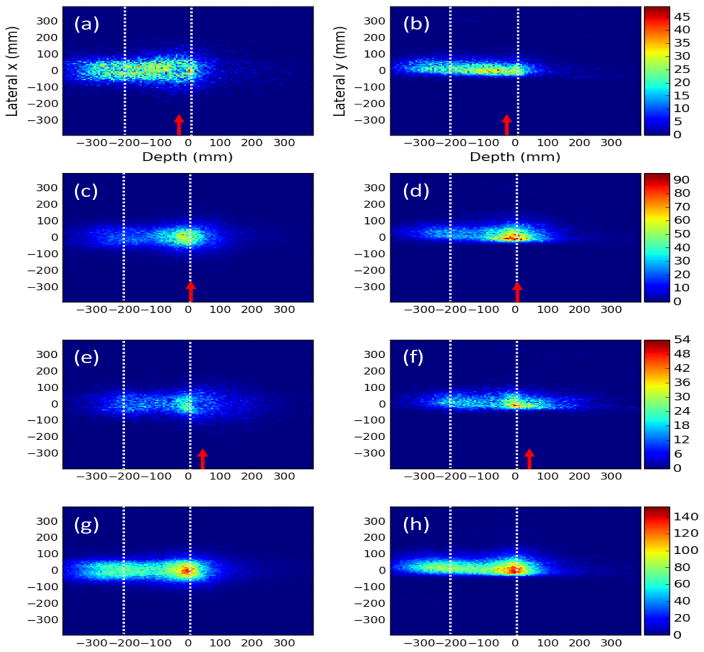
Figure 4 shows 2D projection images in the XZ and YZ planes created from the 3D PG images of the D2C filtered data for 180 MeV pencil beam measurements made at each CC position. An image of the beam can be seen in the single CC images at P1, P2, and P3. Even with the CC placed up to ±4 cm from the distal edge of the BP, the beams distal edge could still be correctly located in the images. However, large variations in the images can be seen which we attribute to variations in the sensitivity of the CC and achievable resolution of the images along the full range of the beam in the phantom. Figure 5 shows the 1D profiles extracted along the x- and y-axes at the depth of the BP maximum, and along the z-axis from the 2D projection of the simulated full-scale CC. In the PG depth profile, the location of the proximal increase of the profile matched the location of the HDPE phantom entrance for the images with the combined CC and with the CC placed at P1. The distal falloff of the reconstructed PG emission profile was located 2 to 4 mm proximal to the distal fall off of the BP at each CC location and for the combined CC data. The distal falloff of the PG images occurred at the same depth in the images regardless of the location of the CC, indicating that the distal falloff in the PG images is indeed due to the falloff of PG emission at the end of the proton beam range and not simply due to the position of the edge of the CC detector.
Figure 4.
XZ projection images for the CC placed at (a) P3, (c) P2, and (e) P1 as indicated by red arrows and for the (g) data measured at each position combined for D2C filtered data measured during delivery of 2 Gy with a 180 MeV pencil beam. YZ projection images are shown for (b) P3, (d) P2, and (f) P1 as indicated by red arrows and the (h) data measured at each position combined. Dashed gray lines represents the entrance of the phantom (−210 mm) and the depth of the distal 90% range (3 mm) of the proton pencil beam.
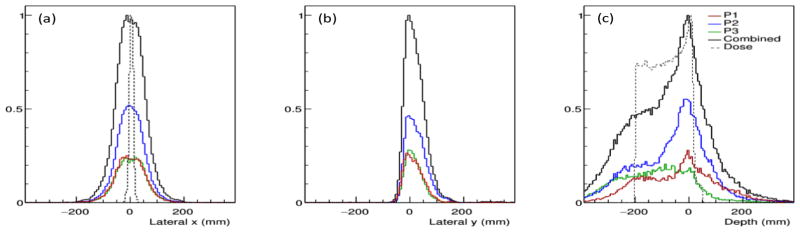
Figure 5.
Lateral profiles in the (a) x-direction and (b) y-direction, and (c) the depth dose profile for the 2 Gy (9.03 × 108 protons) 180 MeV pencil beam, along with the lateral x-direction dose and depth dose profiles from the EBT Gafchromic film measurement of the dose.
In the profiles shown in Figure 5 we see the lateral profiles of the PG images centered about x = 0 mm for each measurement position and the full-scale CC. However the images are less symmetric in the y-direction, with a much sharper falloff in intensity on the negative side of the profile and with a peak value at approximately y = −3 mm for the measurement at each position and for the full-scale CC. The lateral profiles of the PG emission also do not conform well to the measured lateral width of the beam. We believe this is because of the large CC distance from isocenter required to ensure that the coincidence count rate did not overwhelm the camera during the 180 MeV beam delivery. At larger distances any small variations in the cone-of-origin shape and orientation caused by uncertainty in the recorded energy deposition or by the finite CZT pixel size will have a magnified effect on the position of the backprojected cone in the reconstruction volume, thus producing blurring in the images. From our previous experience (Draeger et al., 2017) and from 120 MeV pencil beam images shown in Section 3.4, we observed that images obtained closer to the isocenter not did suffer from these artifacts and showed better agreement between the lateral PG and dose profiles.
3.4 PG image based beam range analysis
Images of the reconstructed PG emission (data from the three measurement positions combined) for the delivery of 6.29 × 108 (2 Gy) and 1 × 108 protons along with dose are shown in Figure 6 overlaid onto the CT images of the HDPE phantom. The distal range and lateral width of the PG emission are similar to those of the dose profile. The image for the delivery of 1 × 108 protons is much noisier than the image for the delivery of 6.29 × 108 protons because the number of PG events is reduced to only 532 for the delivery of the full range beam. Owing to this extremely low number of usable D2C-filtered PG events measured during the delivery of 1 × 108 protons, 500 independent points were chosen on the surface of each PG cone-of-origin for the reconstruction. By contrast, only 30 independent points were chosen on the surface of each of the 2079 cones-of-origin used for reconstruction of the PG emission from the delivery of 6.29 × 108 protons.
Figure 6.
2D slices in the XZ plane from y = −4 mm to y = +4 mm of the dose and reconstructed PG images overlaid on the CT image of the HDPE phantom. (a) PG image for delivery of 6.29 × 108 protons (2Gy). (b) Dose exported from the TPS. (c) PG image for the delivery of 1 × 108 protons. The red line represents the y-axis.
The PG images also had roughly the same profile in the x-direction as the dose profile. However, in the negative y-direction, the PG profile does not falloff as rapidly as the dose profile on the slices at y = −2 mm and y = −4 mm in images from the delivery of 6.29 × 108 protons or 1 × 108 protons. In the positive y-direction the falloff of the PG and dose profiles are much more similar. This asymmetry is an artifact of the image reconstruction algorithm in which the chosen points on the cones-of-origin can be drawn toward the surface of the camera (negative y-direction, see Fig. 1c) during the iterative reconstruction process, especially for cases in which the size of the camera is smaller than or similar to the size of the PG source (the beam range, in our application). As these artifacts arise from the image reconstruction algorithm, they act to elongate the PG image reconstruction profile in the negative y-direction, as opposed to artifacts caused by uncertainties in the measured energy deposition and CC distance from isocenter that caused a truncation of the PG image in the negative y-direction.
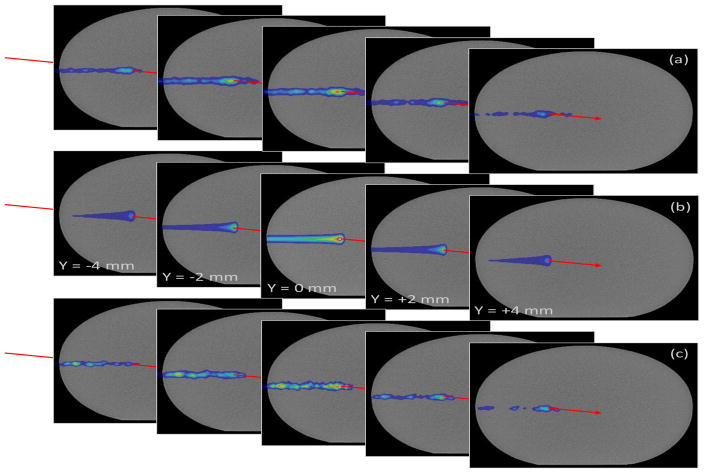
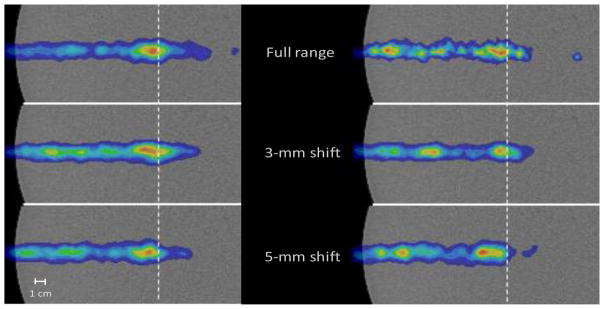
Central-slice images of the PG emission from the full range and the 3 mm and 5 mm range-shifted 120 MeV pencil beam compared to the dose profile for the full range pencil beam are shown in Figure 7. From these images, we see that the distal end of the PG emission profile shifts to shallower depths as the beam range is shifted. This qualitatively shows that a shift in the beam range can be visualized on a single slice of the 3D PG image. These images demonstrate that it is possible to detect a range shift of as little as 3 mm for the delivery of as few as 1 × 108 protons with the 4 cm × 12 cm CC simulated with our prototype.
Figure 7.
Close up of the central slice PG images (XZ-plane, y = 0 mm) for the delivery of 6.29 × 108 protons (left column) and 1 ×108 protons (right column) for the full range 120 MeV pencil beam, 3 mm range shifted, and 5 mm range shifted pencil beams, each normalized to its respective maximum value. The gray dashed lines represent the depth of the distal 90% of the full range pencil beam.
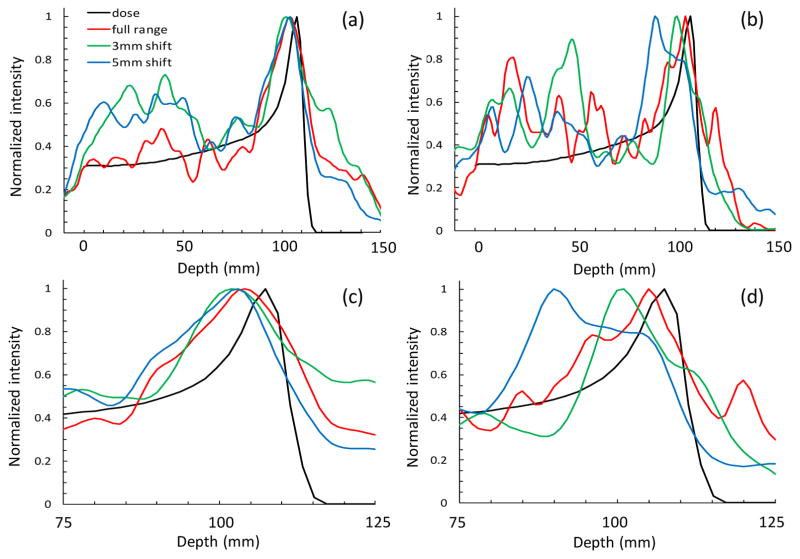
Figure 8 shows 1D central axis profiles of the PG emission extracted from images of the delivery of 6.29 × 108 and 1 × 108 protons. The shape of the PG emission profile roughly resembles that of the dose profile from the delivery of 6.29 × 108 protons. For the delivery of the 1 × 108 protons the 1D PG emission profiles are much noisier, similar to the 2D slices of the PG emission images. A clear shift in the distal falloff of the PG emission is visible as the range of the proton beam shifted by 3 mm and 5 mm. Analysis of the 1D profiles shows that, for the delivery of 6.29 × 108, the distal falloff of the PG emission for the full range beam intersects the distal falloff of the dose profile at 80% of maximum level, at a depth of 110 mm in the phantom. As the beam range is shifted by 3 mm and 5 mm, the depth of the distal 80% of the PG emission profile shifts to 108 mm and 106 mm, thus predicting shifts of 2 mm and 4 mm respectively. For the delivery of 1 × 108 protons, the distal PG falloff intersected the distal dose falloff at a value of 70% of the maximum at a depth of 111 mm in the phantom for the full range beam. The distal 70% values of the 3 mm and 5 mm range shifted PG images occurred at depths of 107 mm and 106 mm, predicting shifts of 4 mm and 5 mm respectively.
Figure 8.
Central axis 1D profiles extracted from the reconstructed PG images for (a) 6.29 × 108 protons and (b) 1 × 108 protons for the full range and for range sifts of 3 mm and 5 mm compared to the central axis depth dose profile for the full range 120 MeV pencil beam. (c) and (d) show a close up of the final 5 cm of the beam range to highlight the shift in the PG profile as the beam range was shifted.
From these data, for the delivery of a 2 Gy dose with a single pencil beam, we estimate that the smallest visible shift is ~2 mm, since a discernable difference can be seen in the distal falloff of the 3 mm shifted and 5 mm shifted measurements. Due to restriction on available beam time only a single set of measurements was performed for each beam range, and we were not able to gather statistics on the reproducibility of the positioning of the distal 70% and distal 80% falloffs for determining the beam range and range shifts. However, these initial tests show the potential of CC based 3D imaging of PGs as a means of measuring and evaluating the in vivo dose delivery and beam range.
3.5 Clinical application of Compton imaging in proton therapy
For clinical use, at a minimum a two-stage CC with a detector array as large as the one simulated in our study (4 cm × 12 cm) would be needed. This would require six CZT modules like the ones used in our current prototype camera, at a cost of ~€ 35,000 each for a total cost of ~€ 210,000 including all needed electronics and software. This is at least a full order of magnitude cheaper than previously published estimates (Rohling et al., 2017). This estimate represents the cost of a “developmental prototype” CC in which many of the internal data acquisition/readout electronics were custom fabricated. In a commercial system, component fabrication would be standardized, thus reducing the manufacture cost and likely resulting in a decrease in the final CC price. In addition, as demonstrated in this study, a CC needs no large collimators and can operate independently of the beam delivery system, needing no beam-on trigger pulses for accurate time-of-flight discrimination or signal timing analysis. Also, it does not require additional systems for monitoring and analyzing the duty cycle and micro-bunch time structure of the beam extracted from the accelerator, making it potentially easy to deploy and use across multiple treatment delivery systems.
CC imaging, unlike other PG imaging methods, offers the ability to perform a full 3D evaluation of the in vivo profile of the delivered proton pencil beam. This capability would be important for evaluating dose delivery in cases where the beam range uncertainty may be minimal, but dose delivery to critical structures lateral to the tumor is still of high concern. As one example, consider treatments such as peri-orbital tumors of the eye. In this case the range of the beam may only be a few centimeters resulting in a range uncertainty of less than 2 mm (Paganetti, 2012). The true uncertainty would arise from anatomy and tumor position changes or lateral shifts of a few millimeters, potentially moving structures such as the lens of the eye or the optic nerve into the treatment volume for any given treatment fraction. Since the region is mostly homogeneous, such a shift would most likely not result in a detectable shift in the beam range. Therefore, simply measuring 1D PG profiles may not adequately detect this type of dose delivery error. In cases like this, a full 3D image of the in vivo beam delivery that can be registered and overlaid onto a daily CT image and evaluated against the daily anatomical alignment would be needed to fully detect and appreciate the implications of each daily treatment delivery. Such 3D dose evaluation methods will become even more important in the future as many proton treatment centers move toward hypo-fractionated/dose-escalated treatment regimens.
Despite the advantages of CCs for PG based beam range verification, much work still needs to be done to allow their full deployment into the clinic. The beam current for the delivery system used in the study was ~0.5 nA, which is on the lower end of the 0.1 nA to 4 nA range of beam currents (at the exit of the treatment nozzle) used clinically at the MPTC. Additionally, other researchers have reported beam currents at the nozzle exit from other beam delivery systems of up to 2 nA (Pausch et al., 2016). This means the count rate needed for a clinical CC would be at least 4 times higher than that achievable with our current prototype and potentially up to an order of magnitude higher (Hueso-Gonzalez et al., 2017). While it is possible for CZT detectors to handle such count rates (Perez and He, 2001), a redesign of the data buffering and readout electronics is currently underway to allow full and accurate readout at these high data throughput levels.
4. Conclusions
From the results of this study, we conclude that it is possible to produce 3D images of PG emission for clinical doses delivered at clinical dose rates using a single, full-scale clinical prototype CC. We found that using “standard Compton imaging” techniques were not adequate, possibly due to image artifacts and degraded image resolution caused by inadequate energy resolution in our CC and large CC to source distances used in the study. We were only able to produce full 3D images using more involved energy determination and event selection methods such as D2C. With clinical prototype CC, we were able to detect shifts in the beam range as small as 2 mm for the delivery of 2 Gy (6.29 × 108 protons) and shifts as small as 3 mm for the delivery of a single distal energy layer pencil beam (1 × 108 protons).
Acknowledgments
The research reported in this publication was supported by the National Institutes of Health National Cancer Institute under award number R01CA187416. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. An international patent application (Polf et al 2016) on the D2C imaging technique is pending.
References
- Andreyev A, Sitek A, Celler A. Fast image reconstruction for Compton camera using stochastic origin ensemble approach. Med Phys. 2011;38:429–35. doi: 10.1118/1.3528170. [DOI] [PubMed] [Google Scholar]
- Clegg AB, Foley KJ, Salmon GL, Segel RE. Gamma radiation from the medium energy proton bombardment of lithium, beryllium, boron, carbon, and nitrogen. Proc Phys Soc. 1961;78:681–94. [Google Scholar]
- Draeger E, Peterson S, Mackin D, Chen H, Beddar S, Polf JC. Feasibility Studies of a New Event Selection Method to Improve Spatial Resolution of Compton Imaging for Medical Applications. IEEE T Rad Plasma Med Sci. 2017;1:358–67. doi: 10.1109/TRPMS.2017.2703095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frandes M, Zoglauer A, Maxim V, Prost R. A tracking Compton-scattering imaging system for hadrom therapy monitoring. IEEE Trans Nucl Sci. 2010;57:144–50. [Google Scholar]
- Gillam JE, Torres-Espallardo I, Lacasta C, Llosa G, Barrio J, Stankova V, Solaz C, Rafecas M. Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2011. IEEE; 2011. vol. Series. [Google Scholar]
- Golnik C, Bemmerer D, Enghardt W, Fiedler F, Hueso-Gonzalez F, Pausch G, Romer KE, Rohling H, Schone S, Wagner A, Kormoll T. Tests of a Compton imaging prototype in a monoenergetic 4.44 MeV photon field — a benchmark setup for prompt gamma-ray imaging devices. J Inst. 2016;11:P06009. [Google Scholar]
- Hilaire E, Sarrut D, Peyrin F, Maxim V. Proton therapy monitoring by Compton imaging: influence of the large energy spectrum of the prompt-gamma radiation. Phys Med Biol. 2016;61:3127–46. doi: 10.1088/0031-9155/61/8/3127. [DOI] [PubMed] [Google Scholar]
- Hueso-Gonzalez F, Fiedler F, Golnik C, Kormoll T, Pausch G, Petzoldt J, Romer KE, Enghardt W. Compton Camera and Prompt Gamma Ray Timing: Two Methods for In Vivo Range Assessment in Proton Therapy. Front Oncol. 2016;6:80. doi: 10.3389/fonc.2016.00080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hueso-Gonzalez F, Pausch G, Petzoldt J, Romer KE, Enghardt W. Prompt Gamma Rays Detected With a BGO Block Compton Camera Reveal Range Deviations of Therapeutic Proton Beams. IEEE TRPMS. 2017;1:76–86. [Google Scholar]
- Kim CH, Park JH, Seo H, Lee HR. Gamma electron vertex imaging and application to beam range verification in proton therapy. Med Phys. 2012;39:1001–5. doi: 10.1118/1.3662890. [DOI] [PubMed] [Google Scholar]
- Kim SM, Seo H, Park JH, Kim CH, Lee CS, Lee SJ, Lee DS, Lee JS. Resolution recovery reconstruction for a Compton camera. Phys Med Biol. 2013;58:2823–40. doi: 10.1088/0031-9155/58/9/2823. [DOI] [PubMed] [Google Scholar]
- Kormoll T, Fiedler F, Schone S, Wustemann J, Zuber K, Enghardt W. Compton imager for in vivo dosimetry fo proton beams-a design study. Nucl Intstrum Methods Phys Res A. 2011;626–627:114–9. [Google Scholar]
- Krimmer J, Ley JL, Abellan C, Cachemiche JP, Caponetto L, Chen X, Dahoumane M, Dauyergne D, Freud N, Joly B, Lambert D, Lestand L, Letang JM, Magne M, Mathez H, Maxim V, Montarou G, Morel C, Pinto M, Ray C, Reithinger V, Testa E, Zoccarato Y. Development of a Compton camera for medical applications based on silicon strip and scintillation detectors. Nucl Instrum Meth A. 2015;787:98–101. [Google Scholar]
- Kurosawa K, Kubo H, Ueno K, Kabuki K, Iwaki S, Takahashi M, Taniue K, Higashi N, Miuchi N, Tanimori T, Kim D, Kim J. Prompt gamma detection for range verification in proton therapy. Current Applied Physics. 2012;12:364–8. [Google Scholar]
- Llosa G, Barrio J, Cabello J, Crespo A, Lacasta C, Rafecas M, Callier S, de la Taille C, Raux L. Detector characterization and first coincidence tests of a Compton telescope based on LaBr3 crystals and SiPMs. Nucl Instrum Meth A. 2012;695:105–8. [Google Scholar]
- Lojacono X, Richard MH, Ley JL, Testa E, Ray C, Freud N, Letang JM, Dauvergne D, Maxim V, Prost R. Low Statistics Reconstruction of the Compton Camera Point Spread Function in 3D Prompt-gamma Imaging of Ion Beam Therapy. Ieee Transactions on Nuclear Science. 2013;60:3355–63. [Google Scholar]
- Mackin D, Peterson S, Beddar S, Polf J. Evaluation of a stochastic reconstruction algorithm for use in Compton camera imaging and beam range verification from secondary gamma emission during proton therapy. Phys Med Biol. 2012;57:3537–53. doi: 10.1088/0031-9155/57/11/3537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackin D, Polf J, Peterson S, Beddar S. The effects of Doppler broadening and detector resolution on the performance of three-stage Compton cameras. Med Phys. 2013;40:012402. doi: 10.1118/1.4767756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCleskey M, Kaye W, Mackin D, Beddar S, He Z, Polf JC. Evaluation of a multistage CdZnTe Compton camera for prompt γ imaging for proton therapy. Nucl Intstr Met Phys Res A. 2015;785:163–9. [Google Scholar]
- Munoz E, Barrio J, Etxebeste A, Ortega PG, Lacasta C, Oliver JF, Solaz C, Llosa G. Performance evaluation of MACACO: a multilayer Compton camera. Phys Med Biol. 2017;62:7321–41. doi: 10.1088/1361-6560/aa8070. [DOI] [PubMed] [Google Scholar]
- Ortega PG, Torres-Espallardo I, Cerutti F, Ferrari A, Gillam JE, Lacasta C, Llosa G, Oliver JF, Sala PR, Solevi P, Rafecas M. Noise evaluation of Compton camera imaging for proton therapy. Phys Med Biol. 2015;60:1845–63. doi: 10.1088/0031-9155/60/5/1845. [DOI] [PubMed] [Google Scholar]
- Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol. 2012;57:R99–117. doi: 10.1088/0031-9155/57/11/R99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pausch G, Petzoldt J, Berthel M, Enghardt W, Fiedler F, Golnik C, Hueso-Gonzalez F, Lentering R, Romer K, Ruhnau K, Stein J, Wolf A, Kormoll T. Scintillator-Based High-Throughput Fast Timing Spectroscopy for Real-Time Range Verification in Particle Therapy. Ieee Transactions on Nuclear Science. 2016;63:664–72. [Google Scholar]
- Perez JM, He Z. Stability and characteristics of large CZT coplanar electorde detectors. IEEE Trans Nucl Sci. 2001;48:272–7. [Google Scholar]
- Peterson SW, Roberts D, Polf JC. Optimizing a 3-stage Compton camera for measuring prompt gamma rays emitted during proton radiotherapy. Phys Med Biol. 2010;55:6841–56. doi: 10.1088/0031-9155/55/22/015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polf J, Avery S, Mackin D, Beddar S. Imaging of prompt gamma rays emitted during delivery of clinical proton beams with a Compton camera: feasibility studies for range verification. Phys Med Biol. 2015;16:7085–99. doi: 10.1088/0031-9155/60/18/7085. [DOI] [PubMed] [Google Scholar]
- Polf J, Peterson S, Ciangaru G, Gillin M, Beddar S. Prompt gamma-ray emission from biological tissues during proton irradiation: a preliminary study. Phys Med Biol. 2009a;54:731–43. doi: 10.1088/0031-9155/54/3/017. [DOI] [PubMed] [Google Scholar]
- Polf JC, Panthi R, Mackin DS, McCleskey M, Saastamoinen A, Roeder BT, Beddar S. Measurement of characteristic prompt gamma rays emitted from oxygen and carbon in tissue-equivalent samples during proton beam irradiation. Phys Med Biol. 2013;58:5821–31. doi: 10.1088/0031-9155/58/17/5821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polf JC, Peterson S, McCleskey M, Roeder BT, Spiridon A, Beddar S, Trache L. Measurement and calculation of characterisitic prompt gamma ray spectra emitted during proton irradiation. Phys Med Biol. 2009b;54:N519–N27. doi: 10.1088/0031-9155/54/22/N02. [DOI] [PubMed] [Google Scholar]
- Richard MH, Chevallier M, Dauvergne D, Freud N, Henriquet P, Le Foulher F, Letang JM, Montarou G, Ray C, Roellinghoff E, Testa E, Testa M, Walenta AH. Design Guidelines for a Double Scattering Compton Camera for Prompt Imaging During Ion Beam Therapy: A Monte Carlo Simulation Study. IEEE Trans Nucl Sci. 2011;58:87–94. [Google Scholar]
- Robertson D, Polf JC, Peterson S, Gillin M, Beddar S. Material efficiency studies for a Compton camera designed to measure characteristic prompt gamma rays emitted during proton beam radiotherapy. Phys Med Biol. 2011;56:3047–59. doi: 10.1088/0031-9155/56/10/010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigues ML. PhD Thesis High flux experiments and simulations of pulse-mode position sensitive CdZnTe pixelated detectors. Departmet of Nuclear Engineering, University of Michigan; 2012. ( https://cztlab.engin.umich.edu/wp-content/uploads/sites/187/2015/03/Miesher-Rodrigues.pdf) [Google Scholar]
- Roellinghoff F, Benilov A, Dauvergne D, Dedes G, Freud N, Janssens G, Krimmer J, Letang JM, Pinto M, Prieels D, Ray C, Smeets J, Stichelbaut F, Testa E. Real-time proton beam range monitoring by means of prompt-gamma detection with a collimated camera. Physics in medicine and biology. 2014;59:1327–38. doi: 10.1088/0031-9155/59/5/1327. [DOI] [PubMed] [Google Scholar]
- Rohling H, Priegnitz M, Schoene S, Schumann A, Enghardt W, Hueso-Gonzalez F, Pausch G, Fiedler F. Requirements for a Compton camera for in vivo range verification of proton therapy. Physics in medicine and biology. 2017;62:2795–811. doi: 10.1088/1361-6560/aa6068. [DOI] [PubMed] [Google Scholar]
- Seo H, Kim CH, Park JH, Kim JK, Lee JH, Lee CS, Lee JS. Development of double-scattering-type Compton camera with double-sided silicon strip detectors and NaI(Tl) scintillation detector. Nucl Instrum Meth A. 2010;615:333–9. [Google Scholar]
- Smeets J, Roellinghoff F, Prieels D, Stichelbaut F, Benilov A, Busca P, Fiorini C, Peloso R, Basilavecchia M, Frizzi T, Dehaes JC, Dubus A. Prompt gamma imaging with a slit camera for real-time range control in proton therapy. Phys Med Biol. 2012;57:3371–405. doi: 10.1088/0031-9155/57/11/3371. [DOI] [PubMed] [Google Scholar]
- Solevi P, Munoz E, Solaz C, Trovato M, Dendooven P, Gillam JE, Lacasta C, Oliver JF, Rafecas M, Torres-Espallardo I, Llosa G. Performance of MACACO Compton telescope for ion-beam therapy monitoring: first test with proton beams. Physics in medicine and biology. 2016;61:5149–65. doi: 10.1088/0031-9155/61/14/5149. [DOI] [PubMed] [Google Scholar]
- Thirolf PG, Aldawood S, Bohmer M, Bortfeldt J, Castelhano I, Dedes G, Fiedler F, Gernhauser R, Golnik C, Helmbrecht S, Hueso-Gonzalez F, Kolff HVD, Kormoll T, Lang C, Liprandi S, Lutter R, Marinsek T, Maier L, Pausch G, Petzoldt J, Romer K, Schaart D, Parodi K. A Compton camera prototype for prompt gamma medical imaging. Epj Web Conf. 2016:117. [Google Scholar]
- Thirolf PG, Lang C, Aldawood S, vd Kolff HG, Maier L, Schaart DR, Parodi K. Development of a Compton Camera for Online Range Monitoring of Laser-Accelerated Proton Beams via Prompt-Gamma Detection. EPJ Web of Conferences. 2014;66:11036. [Google Scholar]
- Todd R, Nightengale J, Everett D. A proposed gamma camera. Nature. 1974;251:132–4. [Google Scholar]
- Verburg JM, Riley K, Bortfeld T, Seco J. Energy- and time-resolved detection of prompt gamma-rays for proton range verification. Phys Med Biol. 2013;58:L37–49. doi: 10.1088/0031-9155/58/20/L37. [DOI] [PubMed] [Google Scholar]
- Verburg JM, Shih HA, Seco J. Simulation of prompt gamma-ray emission during proton radiotherapy. Phys Med Biol. 2012;57:5459–72. doi: 10.1088/0031-9155/57/17/5459. [DOI] [PubMed] [Google Scholar]
- Wilderman SJ, Rogers WL, Knoll GF, Engdahl JC. Monte Carlo calculation of point-spread functions of Compton scatter cameras. Ieee Transactions on Nuclear Science. 1997a;44:250–4. [Google Scholar]
- Wilderman SJ, Rogers WL, Knoll GF, Engdahl JC. MonteCarlo calculation of point-spread functions of Compton scatter cameras. IEEE T Nucl Sci. 1997b;44:250–4. [Google Scholar]
- Zhang F, He Z, Seiffert CE. A prototype 3D position sensitive CdZnTe detector array. IEEE Trans Nucl Sci. 2007;54:843–8. [Google Scholar]