Microstructurally Anchored Cardiac Kinematics by Combining In Vivo DENSE MRI and cDTI

Abstract

Metrics of regional myocardial function can detect the onset of cardiovascular disease, evaluate the response to therapy, and provide mechanistic insight into cardiac dysfunction. Knowledge of local myocardial microstructure is necessary to distinguish between isotropic and anisotropic contributions of local deformation and to quantify myofiber kinematics, a microstructurally anchored measure of cardiac function. Using a computational model we combine in vivo cardiac displacement and diffusion tensor data to evaluate pointwise the deformation gradient tensor and isotropic and anisotropic deformation invariants. In discussing the imaging methods and the model construction, we identify potential improvements to increase measurement accuracy. We conclude by demonstrating the applicability of our method to compute myofiber strain in five healthy volunteers.

1 Introduction

Heart disease, including myocardial infarction (MI) and hypertrophic cardiomyopathy (HCM), heterogeneously impacts left ventricular (LV) structure and function. Global metrics of myocardial function, such as ejection fraction (EF), however, may be preserved despite the presence of disease, and this masks regional functional deficits that portend a poor clinical outcome.

Displacement ENcoding with Stimulated Echoes (DENSE) magnetic resonance imaging (MRI) encodes time-resolved Eulerian cardiac displacements directly into the MRI signal phase [1, 20]. The displacement field derived from DENSE MRI can be used to calculate several regional measures of cardiac function, including radial (E_rr) and circumferential (E_cc) strain. Deformation-based biomarkers show clinical promise and regional sensitivity for the diagnosis of, for example, ischemic cardiac pathologies (e.g., MI) and inherited cardiac pathologies (e.g., HCM and Duchenne muscular dystrophy).

Aletras et al. [2] employed DENSE to identify depressed systolic E_cc in regions of Late Gadolinium Enhanced (LGE) defined focal and diffuse fibrosis in HCM, as well as in hypertrophic regions for which LGE MRI findings were negative. The authors speculate that functional deficits absent positive findings of fibrosis may be explained by microstructural remodeling of myofiber geometry. In fact, considerable attention has been given to the link between MRI based strain measures and local microstructure, e.g., the work of Tseng et al. [15] or the recent work of Wang et al. [17] where in vivo displacement data and ex vivo cardiac Diffusion Tensor Imaging (cDTI) data were combined to study myofiber strains and reorientation.

Recent advances in cDTI [3, 14] enable in vivo measurements of local myofiber orientation and microstructural rearrangement during the cardiac cycle [9]. Combining cDTI with DENSE displacement data permits computing microstructurally anchored myofiber deformation to characterize myocyte performance in vivo. Here, in agreement with the current literature, we use the term myofiber orientation and deformation. However, we emphasize that we compute the averaged myofiber deformation since the acquired in vivo cDTI data provide averaged (or preferential) myofiber orientation within a voxel, not single cardiomyocyte orientation.

Building on these recent advances in cDTI and DENSE imaging techniques, our objectives were to: 1) Construct a computational framework to evaluate in vivo myofiber (anisotropic) and extracellular matrix (isotropic) deformation metrics based on single-slice DENSE and cDTI data; 2) Evaluate sources of error in our modeling framework using an analytic computational deforming phantom (CDP) of cardiac motion that provides ground truth kinematics; 3) Demonstrate the applicability of our framework in healthy volunteers (N = 5) and compute in vivo myofiber and matrix deformation.

2 Methods

A long term goal is to apply our framework in a clinical setting under the constraint of limited acquisition time. Therefore, we base our computational framework on single-slice DENSE and cDTI data. Validation of our computational framework and evaluation of the error involved with our assumptions requires the knowledge of a ground truth, which is provided here by a cardiac CDP (Section 2.3).

2.1 Single-Slice Model Construction with cDTI and DENSE

The epicardial and endocardial borders of the LV myocardium at each cardiac phase were defined using cubic spline interpolation and a motion guided segmentation algorithm [13](Fig. 1A). The region between the borders defining the first cardiac phase recorded in the DENSE sequence after the QRS trigger was meshed with linear triangular finite elements (FE) (Fig. 1E).

Fig. 1.

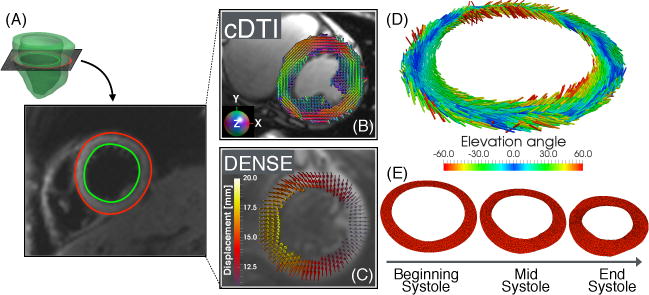
(A) LV short-axis single-slice (B) including myofiber preferential orientations (principal eigenvectors) from cDTI and (C) Lagrangian displacement vectors from beginning to end systole. (D) Interpolated myofiber preferential orientations at FE quadrature points after cDTI-DENSE registration and (E) FE-based mesh deformation through systole driven by the DENSE measured displacement field.

Using an open-source post-processing tool [12], myocardial (3D) Lagrangian displacements u_i (Fig. 1C) at each cardiac phase were computed by unwrapping the displacement encoded phase data. Subsequently, the myocardial displacements u_i computed at the center of each image voxel were linearly interpolated to the nodes of the FE mesh (Fig. 1E). Here and in the following i = 1, 2, and 3 represents, respectively, the component along the X₁, X₂, and X₃ coordinate and we assume, without loss of generality, that the single-slice is initially in the X₁ — X₂ plane and the LV long-axis is coaxial with X₃.

All cDTI images were registered to DENSE using a rigid translation and rotation in the X₁ − X₂ plane, followed by a non-rigid transformation step. Rotation and rigid translation were determined by matching the two RV insertion points in the cDTI and DENSE images. Subsequently the cDTI magnitude images were segmented using cubic splines as was previously done for the DENSE magnitude images. The cubic spline DENSE and cDTI segmentations were then transformed into binary masks and registered using the b-spline based registration algorithm outlined in [11]. The computed non-rigid registration did not include a rotation component, as the proper rotation was already taken into account by matching the RV insertion points. The same rigid translation and rotation, and non-rigid registration based on the magnitude images were applied to all cDTI images encoding different diffusion directions (Fig. 1B).

cDTI acquired diffusion tensors were interpolated using linear invariant interpolation [6] to the location of the FE quadrature points where the deformation invariants were computed (Fig. 1D). At these locations, the myofiber preferential orientation was computed as the principal eigenvector f of the interpolated diffusion tensors. Finally, f was rotated around X₃ using the previously computed rigid rotation to account for the change in LV orientation between cDTI and DENSE images.

2.2 Calculation of the Deformation Gradient and Invariants

The deformation gradient tensor F was computed using FE interpolation functions and the displacements u_i calculated from DENSE at each FE node with initial position X_i. In the reference configuration corresponding to the first DENSE image, we assume that all nodes have the same X₃. For displacements acquired only within a single short-axis slice, we cannot directly compute the third column of the deformation gradient ∂φ_i/∂X₃, where φ_i = X_i + u_i. In order to evaluate F using only single-slice data, we make the following two assumptions: 1) the myocardium is incompressible, i.e., det F = 1; and 2) intra-slice torsion is very small, therefore u₁ and u₂ are not a function of X₃. Consequently, we evaluate F as:

$$\mathbf{F}=\left[\begin{array}{ccc}\partial {\phi }_1/\partial X_1& \partial {\phi }_1/\partial X_2& 0\\ \partial {\phi }_2/\partial X_1& \partial {\phi }_2/\partial X_2& 0\\ \partial {\phi }_3/\partial X_1& \partial {\phi }_3/\partial X_2& 1/(F_{11}{F}_{22}-F_{21}{F}_{12})\end{array}\right]$$

Subsequently, we compute the right Cauchy-Green deformation tensor C = F^⊤F and a selection of its isotropic (I₁, R₁, R₂, R₃) and anisotropic invariants (I₄, I₅) to characterize, respectively, extracellular matrix and myofiber kinematics. In particular: I₁ = tr(C), $R_1=\sqrt{\mathbf{C}:\mathbf{C}}$, $R_2=\sqrt{3/2}\sqrt{\overline{\mathbf{C}}:\overline{\mathbf{C}}}/R_1$ where $\overline{\mathbf{C}}=\mathbf{C}-1/3$ tr(C) I, $R_3=3\sqrt{6}\text{det}\left(\overline{\mathbf{C}}/\sqrt{\overline{\mathbf{C}}:\overline{\mathbf{C}}}\right)$, $I_4=tr\left(\mathbf{C}\left(\mathbf{f}\otimes \mathbf{f}\right)\right)$, and $I_5=tr\left({\mathbf{C}}^2\left(\mathbf{f}\otimes \mathbf{f}\right)\right)$. Further details on the construction of these sets of invariants are discussed in [4, 7]. One of the simplest choices to characterize myocardial deformation consists of adopting I_l (isotropic) and I₄ (anisotropic) invariants, which measure, respectively, the sum of the squares of the principal stretches and the the square of the myofiber stretch. Additionally, I₄ is related to the Green-Lagrange myofiber strain E_ff through $E_{ff}=0.5\cdot \left(I_4-1\right)$ while the more common circumferential strain E_cc is computed by projecting E in the circumferential direction c, i.e., $E_{cc}=0.5\cdot \left(tr\left(\mathbf{C}\left(\mathbf{c}\otimes \mathbf{c}\right)\right)-1\right)$.

2.3 Computational Deforming Phantom

In order to evaluate the model’s accuracy for computing myocardial deformation, we constructed a 3D Computational Deforming Phantom (CDP) in which ground truth strain values were known by construction. The motion of the CDP and the corresponding exact deformation gradient tensor are determined analytically by the functions described in Appendix B of [8]. Importantly, the analytic mapping presented in [8] allows decoupling the slice displacements into in-plane deformation and intra-slice torsion. Using the 3D CDP, we evaluated the effect of computing the invariants of C from a single short-axis slice of data and our model (see Sec. 2.2) using the following tests:

• Test 1Effect of using a single slice model in absence of intra-slice torsion. We evaluate the effect of analyzing 3D CDP motion using only single slice data.
• Test 2Effect of FE interpolation and including intra-slice torsion. Based on the analytical functions in [8] and including intra-slice torsion, we assigned the exact displacements to the nodes of a regular grid as it would be sampled by the DENSE experiment. Subsequently, we interpolated the displacements to the nodes of our FE mesh.
• Test 3Effect of pipeline processing. We computed the Eulerian displacements at a fixed short-axis slice location in the CDP. Based on the Eulerian displacement components and a chosen encoding strength k_e, we assigned a phase value to the center of each image voxel (uniform 2×2mm grid). These constructed DENSE phase images corresponding to the motion of the CDP were subsequently processed identically to in vivo images. The computed displacements were interpolated to the nodes of the FE mesh. This test reproduced the entire pipeline from DENSE image processing to the calculation of deformation invariants, including image segmentation and displacement interpolation from Eulerian to Lagrangian in the DENSE processing toolbox.

We report the mean (μ) and standard deviation (σ) for the analytically (μ_an, σ_an) and numerically (μ_num, σ_num) computed invariants, together with the percent error of the means $\left(\frac{\left({\mu }_{\mathrm{an}}-{\mu }_{\mathrm{num}}\right)\cdot 100}{{\mu }_{\mathrm{an}}}\right)$ and the pointwise percent error $\left(\frac{(I_i^{\mathrm{an}}-I_i^{\mathrm{num}})\cdot 100}{I_i^{\mathrm{an}}}\right)$, where I_i (or R_i) represents one of the computed invariants. We included myofiber preferential orientation data in the CDP in order to compare computed and analytic myofiber stretch. The modeled myofiber helix angle varies linearly from 39.5° (endocardial) to −53.5° (epicardial) as measured in [5].

2.4 In Vivo Image Acquisition

Using an IRB approved protocol, a single mid-ventricular short-axis slice was acquired in healthy volunteers (N = 5) using DENSE and cDTI at 3T (Prisma, Siemens) after obtaining informed consent. All imaging used navigator triggered free breathing. DENSE: balanced 4-point encoding, 2.5×2.5×8mm, TE/TR=1.04/15ms, k_e=0.06cycles/mm, N_avg=3, spiral interleaves=10, T_scan=5 min. CODE [3] cDTI: 2×2×5mm, TE/TR= 74/4000ms, b-value=0,350s/mm², N_avg=10, N_dir=12, T_scan=4 min.

3 Results

We first evaluated our modeling framework using the tests listed in Section 2.3 and subsequently demonstrated its application in healthy volunteers.

3.1 Model Evaluation: From 3D Motion to a 2D Short-Axis Slice

Table 1 compares the deformation invariants computed analytically and numerically when intra-slice torsion is set to zero in the CDP and exact displacements are applied to the nodes of the FE mesh without interpolating from a regular grid (Test 1). The mean percent error between analytically and numerically computed invariants is small (< 1%).

Table 1.

Exact (analytical) and computed (numerical) deformation invariants at peak systole neglecting intra-slice torsion (Test 1).

	I1	R1	R2	R3	I4	I5
μan ± σan	3.46 ± 0.05	2.27 ± 0.06	0.58 ± 0.02	0.84 ± 0.11	0.79 ± 0.05	1.31 ± 0.12
μnum ± σnum	3.46 ± 0.05	2.27 ± 0.05	0.58 ± 0.02	0.84 ± 0.12	0.79 ± 0.05	1.31 ± 0.12
% error	2.10−3	0.01	0.03	0.13	−0.01	−0.02

Subsequently, we compared the analytical and numerical deformation invariants including: 1) intra-slice torsion; and 2) interpolation of the displacement field from a uniform grid to the FE nodes (Test 2). The mean percent errors between analytically and numerically computed invariants remain small (Table 2), but the pointwise comparison (Fig. 2) highlights regions of larger discrepancies.

Table 2.

Exact (analytical) and computed (numerical) deformation invariants at peak systole including intra-slice torsion and displacement interpolation to FE nodes (Test 2).

	I1	R1	R2	R3	I4	I5
μan ± σan	3.46 ± 0.04	2.28 ± 0.05	0.58 ± 0.02	0.83 ± 0.13	0.80 ± 0.08	1.33 ± 0.19
μnum ± σnum	3.46 ± 0.05	2.28 ± 0.06	0.58 ± 0.02	0.84 ± 0.12	0.79 ± 0.05	1.31 ± 0.14
% error	0.04	0.02	−0.03	−1.50	1.10	1.36

Fig. 2.

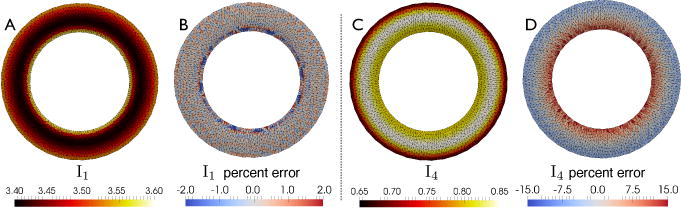
Isotropic (I₁) and anisotropic (I₄) deformation invariants: analytic invariants (A and C) and pointwise % error between analytical and numerical values (B, D) computed in Test 2.

3.2 Model Validation: Effect of Pipeline Processing

Table 3 summarizes the error introduced by the entire post-processing pipeline in the calculation of the deformation invariants (Test 3). Figure 3 shows the pointwise comparison for I₁ (isotropic) and I₄ (anisotropic) deformation invariants. Percent error of mean values are smaller for I₁ and I₄ among the isotropic and anisotropic invariants, respectively.

Table 3.

From simulated imaging data to deformation invariants in the single slice model (Test 3).

	I1	R1	R2	R3	I4	I5
μan ± σan	3.46 ± 0.05	2.28 ± 0.06	0.58 ± 0.02	0.82 ± 0.12	0.80 ± 0.05	1.33 ± 0.14
μnum ± σnum	3.34 ± 0.11	2.13 ± 0.13	0.51 ± 0.09	0.73 ± 0.35	0.82 ± 0.06	1.26 ± 0.10
% error	3.61	6.5	13.16	11.01	−2.51	5.20

Fig. 3.

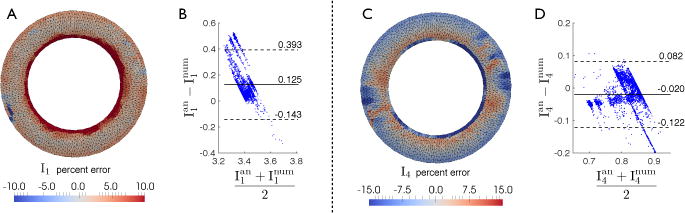
Pointwise comparison and Bland-Altman plot for I₁ (A, B) and I₄ (C, D) computed analytically and using the single slice model with DENSE simulated data (Test 3). The biases in the Bland-Altman plots are 0.125 for I₁ (B) and −0.020 for I₄ (D).

3.3 In Vivo Results

We demonstrated the applicability of our framework in vivo by combining DENSE and cDTI data from a single-slice. The modeling framework was used to compute I₁ from DENSE displacements alone and myofiber deformation I₄ from co-registered in vivo DENSE and cDTI (Fig. 4). We also computed the time evolution of averaged I₁ and I₄ deformation invariants in each healthy volunteer (Fig. 5). Intersubject average I₄ at peak systole is equal to 0.74 ± 0.03, which corresponds to average myofiber strain equal to −12.8% ± 1.6%.

Fig. 4.

(A) Displacement vectors from beginning to end systole in a healthy volunteer. (B) cDTI myofiber vectors f acquired at mid-systole. (C, D) Peak systolic deformation invariants I₁ and I₄.

Fig. 5.

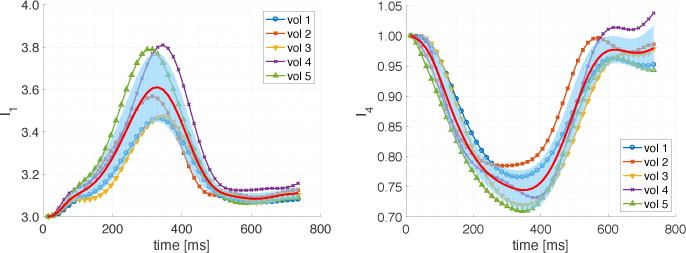
Time evolution of averaged I₁ (isotropic) and I₄ (anisotropic) deformation invariants in healthy volunteers (N = 5) together with intersubject mean (red line) and standard deviation (blue shaded region).

4 Discussion

We have implemented a computational modeling framework to calculate microstructurally anchored deformation invariants from DENSE and cDTI imaging data. The comparison of exact (analytic) and numerically computed deformation invariants permits evaluating sources of error in the modeling framework and possible remedies.

We observed that the 2D model approximation (Test 1) led to deformation invariants close to the exact analytical values (error < 1%) if intra-slice torsion is neglected (Table 1).

The agreement, however, between exact and numerical deformation invariants worsens when intra-slice torsion is included in the CDP to provide more realistic cardiac motion (Table 2, Test 2). Lower agreement is expected since correctly representing torsion requires data from parallel short-axis slice locations and our acquired data was purposefully restricted to a single short-axis slice. Indeed, one of our assumptions in Sec. 2.2 was the presence of a negligible intra-slice torsion. This assumption, of course, can be relaxed by acquiring data at two adjacent short-axis slices.

Lastly, we compared the analytic deformation invariants to the ones computed after the entire processing pipeline, starting from simulated DENSE images (Table 3, Test 3). Other studies have evaluated the accuracy of strain measures computed from DENSE displacements. Wehner et al. [18] report that measured DENSE strains show good agreement with those computed from Tagged MRI in human volunteers. Young et al. [19] echo these results, and also demonstrate that measured DENSE strains in a rotating deforming gel phantom show good agreement with those computed analytically for the phantom. Our results complement these studies by comparing computed deformation invariants with analytic values available through the CDP. This comparison with exact analytic values enables determining which deformation invariants are less affected by the assumptions and discretization steps included in our modeling pipeline.

To understand the spatial distribution of the differences between analytical and numerical deformation invariants, we compared I₁ and I₄ pointwise (Figs. 2 and 3). Although their average difference is small, local differences can be much larger, especially in the epicardial and endocardial regions where the effect of intra-slice torsion appears to be larger and the correction outlined above may be most useful. We notice that the results in Fig. 3(B,D) are not uniformly scattered but partially clustered along distinct “bands”. This may be due to the inhomogeneous error in I₁ and I₄ across the myocardial wall as illustrated in Fig. 3(A,C).

After evaluating several sources of error in our model, we showed its applicability to in vivo acquired data (Figs. 4, 5). Leveraging the measured patient-specific cDTI myofiber orientations permits estimating a measure of myofiber function (I₄), which is inherently microstructurally anchored. The averaged I₄(≈ 0.75) values across all volunteers (Fig. 5) is consistent with values of myofiber strain reported in the literature [16]. In vivo averaged I₁ (≈ 3.6) is consistent with the analytic values computed from the CDP ( $I_1^{\mathit{an}}\approx 3.5$ – Table 3). In this study, we focused on comparing I₁ and I₄ because these deformation invariants are commonly used to formulate material energy laws describing passive cardiac mechanics, e.g., [7,10].

In this work, we have evaluated the model assumptions for interpolating displacements from a single short-axis slice of cine DENSE data to compute the deformation invariants. These approximations can have a significant impact on the computed values since the displacement field is differentiated to calculate F, and this operation can amplify experimental noise. Accurate calculation of F is central to computing myofiber strain and deformation invariant biomarkers. Future validation of our computational model will include evaluating the effect of non-rigid registration of DENSE and cDTI data and the effect of experimental noise on both DENSE and cDTI data. We foresee that a higher order FE scheme or a meshless method, together with a more sophisticated displacement interpolation method, may be necessary to decrease the effect of experimental noise.

An additional step in validating our single slice framework consists in repeating the tests presented herein using a different CDP to reproduce different cardiac motion, especially if specific cardiac phases are of particular interest. For example, to determine an optimal strategy to analyze passive cardiac kinematics, we want to test our framework using a CDP that closely reproduces the motion during diastole, since different numerical assumptions may lead to a different amount of error in different cardiac phases.

Finally, we emphasize that the proposed framework may be easily extended to the full 3D case, in which several short-axis DENSE and cDTI slices are combined to construct a 3D finite element model. In the 3D case, no assumption about intraslice torsion is necessary, thereby avoiding one major source of error in the current framework.

In conclusion, a computational framework was developed to evaluate extracellular matrix and myofiber kinematics based on single-slice DENSE and cDTI data. Our preliminary results suggest that I₁ (isotropic) and I₄ (anisotropic) invariants have the lowest average error among the invariants considered and consequently may form a robust basis for describing systolic cardiac kinematics and formulating strain energy laws for the heart.