Effects of Tuning Conditions on Near Field of MRI Transmit Birdcage Coil at 64 MHz

Abstract

This study investigates how the tuning conditions of a 64 MHz/1.5 T radio frequency (RF) birdcage coil modeled with an RF circuit and 3D electromagnetic co-simulation affect the electric and magnetic near-field distribution. Four models were implemented with different tuning conditions and difference between numerical results and measurements was evaluated. The results show that the simulated near-field depends significantly on coil tuning conditions, especially in volumes close to the ASTM phantom walls. Further extensive evaluations should be conducted to cover proper match between measurement and numerical results.

I. Introduction

Magnetic resonance imaging (MRI) is widely used for medical diagnosis and follow-up examination. MRI systems use a high power radio frequency (RF) transmitter to generate a magnetic field that elicits the MRI signal. The deposition of this RF power in the patient results in tissue heating, which may be particularly significant in patients with implanted passive or active metallic medical device, due to the antenna effect of the implants [1].

Clinical 1.5 Tesla MRI systems are the most distributed worldwide. The most common RF transmitter for these systems is a birdcage coil, typically excited by two RF sources in quadrature. The near-field generated by the RF transmitter depends on the geometry of the transmitter radiative elements (i.e., coil length and diameter), as well as on the feed sub-circuit and radiative element decoupling [2]. Birdcage coils installed in clinical MRI systems have fixed tuning conditions – optimized for coil loaded with a patient – that are based on proprietary techniques implemented to improve field polarization and homogeneity.

RF-induced heating cannot be easily assessed in-vivo, thus computational models, validated against experimental measurements, have been widely used for safety assessment of patients undergoing MRI. A phantom filled with conductive medium is often used to evaluate discrepancy between near field generated by a physical MRI coil and the one obtained from numerical simulations. The goals of this study were: 1) to perform electromagnetic simulations of a 64 MHz RF birdcage body coil with variable tuning conditions; 2) to evaluate difference between numerical results and measurement done at commercially available RF birdcage body coil.

II. Methods

A. Theoretical background

The RF feed sub-circuits provide impedance matching functionality to ensure maximum power transfer to the coil from the amplifier. The RF feed sub-circuits can be represented by a single variable reactance element, for example trim capacitor, or a more sophisticated multi-element sub-circuit.

The birdcage coil tuning ─ as optimization of any other multi-channel RF transmitter ─ is guided by the minimization of an error function (EF), which is a measure of the difference between the actual and desired array conditions (“optimization criteria”). Commonly used criteria for multi-channel RF transmitters, at the desired frequency, are: a) the element reflection coefficient S_xx must be set and equal to a required value (i.e., S_{xx_t}) for each array element; b) the element coupling S_xy must be equal to a required value (i.e, S_{xy_t}) for each decoupled element pair. Hence:

$$EF=\sum _{\mathit{Elem}}{w}_x{\mid S_{xx}-S_{xx\_t}\mid }^2+\sum _{\mathit{all}\_\mathit{dec}}{w}_{xy}{\mid S_{xy}-S_{xy\_t}\mid }^2$$ (1)

where: Elem is number of elements (inputs) of the transmitter, all_dec is number of decoupled element pairs, w_x and w_xy are weighting factors. The weighting factors may have different values from one criterion to another, and they are used to emphasize one vs. the other optimization criteria. For the case herein evaluated, namely a birdcage coil excited by two RF sources, Elem = 2 and all_dec = 1.

Because a birdcage coil has several resonance modes resulting in similar scattering parameter values at the different resonance frequencies, the circuit level optimization based on EF defined in (1) can result in improper rung currents that should be for generation of circularly polarized magnetic field [3]:

$$I_n=I_0·e^{i2\pi n/16}$$ (2)

Therefore our EF included criteria for both S parameter values and I_n, i.e. included the third term:

$$\sum _{\text{all}\_\text{rung}}{\mathrm{w}}_{\mathrm{r}}{\mid {\mathrm{I}}_{\mathrm{n}}-{\mathrm{I}}_0·e^{-2\mathrm{\pi }\mathrm{n}/16}\mid }^2$$ (3)

When a coil is loaded by a human model or a phantom more than one local minimum of EF occur, and their location (i.e. values of variable components) substantially depends on ratios between waiting factors w_x, w_xy and w_r.

A 16 rung birdcage coil becomes a 16 element array if the coil is connected to 16 power sources with independently defined RF amplitudes and phases. As known from MRI transmit array theory, an increased number of RF sources allow generating a current distribution with smaller variations from required pattern. It was also shown in [5] that single optimization minimum is obtained for EF = |P_refl|², where P_refl is the total power reflected by the entire multi-channel RF transmitter array. The birdcage tuning procedure using the P_refl for a given load could be proposed as a good approach to model a commercial birdcage coil, for which the field optimization techniques are typically confidential information.

B. Numerical simulations

The numerical simulations were performed using RF circuit and 3D EM co-simulation [4]. The RF circuit simulations were performed with ADS 2015 (Agilent, Santa Clara, CA, USA), and the 3D EM simulations with HFSS 2014 (ANSYS, Canonsburg, PA, USA).

The MRI coil simulated was a 64 MHz 16-rung high pass birdcage body coil, with an inner diameter of 740 mm, and 16 rectangular copper rungs (570 mm long, 25 mm wide and 4 mm thick). The rings were made of copper strips (40 mm wide and 4 mm thick). Along the rings a 5-mm gap centered between each two adjacent rungs hosted a capacitor as defined by the high pass birdcage functionality. The coil was shielded by a copper enclosure (Fig. 1). The dimensions of the coil were based upon the dimensions of the Medical Implant Test System (MITS1.5) for 1.5 Tesla RF Safety Evaluation (Zurich Med Tech, Zurich, Switzerland) that was used for the measurements. However, there was no exact match between the physical and modeled coil geometries or operational frequencies. Similar to commercially available coil, the MITS system has fixed tuning conditions. In the numerical part of this study, the coil was loaded with ASTM phantom [6] and then tuned. To replicate the setup of the measurements, the unloaded coil model was simulated with tuning conditions previously obtained for loaded conditions.

Figure 1.

64 MHz high pass 16 rung birdcage coil.

The Q factor of all capacitors was defined at the beginning of the optimization process. Two options were investigated: a) Q = 365 (similar to the losses of capacitors used in MITS1.5), and b) Q = 10000 (corresponding to a practically loss free condition). Overall, four different tuning cases were studied. In case #1 the RF feed sub-circuit was a single trim capacitor and capacitor Q factor was equal to 365. In case #2 the RF feed sub-circuit was the multi-element sub-circuit shown in Fig. 2 and the capacitor Q factor was equal to 365. In case #3 the RF feed sub-circuit was the same as in case #2 but with a capacitor Q factor equal to 10000. In case #4 the capacitor Q factor was equal to 365 and the EF was as defined in (3).

Figure 2.

RF feed sub-circuit used for case#2 and case#3 with capacitor Q factor value of 365 and 10000 respectively.

For the birdcage investigated, the following components were optimized: a) complex impedance of each element of RF feed sub-circuit, b) complex impedance of capacitors placed in each ring gap. S_{xx_t} was equal to -20 dB and S_{xy_t} was equal to −16 dB. The amplitude and phase of the RF sources used to excite the coil were fixed, namely same amplitudes with the phase shift between RF sources 90°, as in quadrature excitation.

C. Experimental measurements

Electromagnetic field measurements were collected using the DASY5NEO robotic measurement system (SPEAG, Zurich, Switzerland) with the ER3DV6 electric field probes (SPEAG) and the H3DV7 magnetic field probe (SPEAG). Measurements were performed in unloaded condition for two axial and 5 coronal planes. For each measurement point the probes returned three RMS values – one for each field component x, y, and z; the total magnitude was then computed based on the quadratic norm.

The comparison between measured and simulated field was performed for each measured plane, with all results normalized to the norm of the magnetic field vector at the center of the RF-coil (||H_iso||).

III. Results and Discussion

In case #1, as it shown in Fig. 3, the ADS optimization was not able to find a solution that fulfilled S parameter criteria (Fig. 3a). The range of current amplitudes was from 0.6 to 1.1 A at the resonant frequency for transmit power of each RF source equal to 1W (Fig. 3b). For the case of coil unloaded, S₁₁ increased, S₂₁ decreased (Fig. 3c), and the range of current amplitudes was also smaller (i.e., from 0.9 to 1.2 A) (Fig. 3d).

Figure 3.

a) and b) ASTM phantom as a load. a) Cases #1, #2, and #3: S parameters; Case #4: Power reflected. b) Rung currents (values in A) for all cases. The transmit power of each RF source was 1W. c) and d) Unloaded coil with tuning condition obtained for ASTM phantom. c) Cases #1, #2, and #3: S parameters; Case #4: P_refl. d) Rung currents (Values in A) for all cases. The transmit power of each RF source was 1W.

In case #2 the ADS optimization was able to find a solution that fulfilled the S parameter criteria (i.e, S_{xx_t} = −20dB). The multi-element sub-circuit substantially improved S₂₁ of the birdcage coil (Fig. 3a) whereas the rung currents (Fig. 3b) did not meet the criteria defined by (1) and (3). In the case of unloaded coil, when comparing to case #1 the S₁₁ was smaller, S₂₁ was comparable (Fig. 3c), and the range of current amplitudes was decreased (Fig. 3d).

In case #3, when compared to case #2, the capacitor losses decreased, resulting in an increase of current amplitudes (i.e., up to 1.8 A), but also in degraded S parameters (Fig. 3a) and in a significantly broad range of currents in rungs (i.e., 0.6 to 1.5 A) (Fig. 3b). For unloaded coil, S₁₁ was = − 4 dB (value characteristic of a non-tuned coil) and P_refl was 27% of transmit power, while the current amplitudes were still larger compared to the cases #1 and #2.

In case #4, the optimization P_refl resulted in a value of P_refl equal to zero (Fig. 3a) and rung currents (Fig. 3b) close to the values defined by (2). Conversely, in the case of coil unloaded the variation of current amplitudes was the largest (i.e., from 0.6 to 1.2 A at the resonant frequency) when compared to the other cases (i.e., 0.6 to 1.2 A).

The ASTM phantom is used to evaluate the evaluate RF induced heating due to the presence of an implant. The heating is directly related to the electric field incident along the implant. The different tuning conditions affect the incident electric field. Moreover, as shown in Figure 4, the electric field distribution inside the ASTM phantom substantially depends on the plane selected within the phantom and its distance from the iso-center. Specifically, the distribution of electric field in planes at 3 cm from the iso-center was visibly different than the electric field at the iso-center. It is worth noticing that there are implants (e.g., orthopedic implants) for which the cross section is bigger than 3cm, thus such difference may become significant when evaluating RF-induced heating for large implants.

Figure 4.

Magnitude of electric (a, b, c) and magnetic (d) field for all cases. All results were normalized to the magnitude of the magnetic field at the isocenter of the RF-coil (i.e., ||Hiso||). a) and d) results for the central coronal plane (xz = 0); b) Results for the coronal plane xz = − 30mm from the iso-center. c) results for the coronal plane xz = + 30mm from iso-center.

Because the magnetic field at the central coronal (xz = 0) plane (Fig. 4d) (i.e, ||H_iso||) depends on the tuning conditions, normalizing the results of E-field to ||H_iso|| may not allow a direct quantitative comparison between different tuning conditions. The results for one of the measured axial planes inside the coil (z = −140 mm) are presented in Fig. 5. All the cases resulted in a rather uniform distribution of magnetic field as expected.

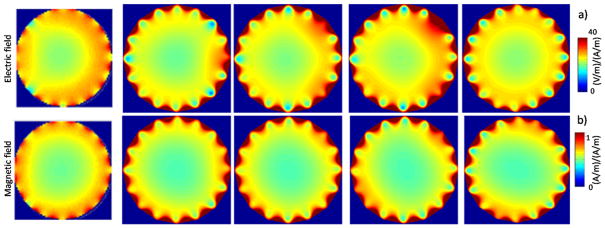
Figure 5.

Magnitude of electric (a) and magnetic (b) field in the physical coil and all numerical cases studied. Images are for the axial plane xy = 140 mm from the iso-center. All results were normalized to the magnitude of the magnetic field at the iso-center of the RF-coil (||Hiso||).

Additionally, when conducting the validation process it is also important to take into consideration the reverse engineering steps that include: a) coil component tolerances, b) variation of trimming elements with unknown precise values, and c) dependence of RF sources amplitudes and phases on the near field optimization procedure. The focus of this study was on the effect of tuning conditions on the electromagnetic field induced in a phantom at 64 MHz, as this may affect the evaluation of RF-induced heating for implanted devices. While the effect of coil geometry at 64 MHz has been extensively studied in literature, the reflected power caused by mismatch or detuning occurring for cases when the actual coil load differs from the one for which the coil was designed to be perfectly matched/tuned. Additional work may be of interest to evaluate how changing loading conditions (i.e., asymmetric loads) may affect such mismatch, both at 64MHz and also at higher frequencies (i.e., 128 MHz).