Multiscale mechanics of the cervical facet capsular ligament, with particular emphasis on anomalous fiber realignment prior to tissue failure

Abstract

The facet capsular ligaments encapsulate the bilateral spinal facet joints and are common sources of painful injury due to afferent innervation. These ligaments exhibit architectural complexity, which is suspected to contribute to the experimentally observed lack of co-localization between macroscopic strain and microstructural tissue damage. The heterogeneous and multiscale nature of this ligament, combined with challenges in experimentally measuring its microscale mechanics, hinders the ability to understand sensory mechanisms under normal or injurious loading. Therefore, image-based, subject-specific, multiscale finite-element models were constructed to predict the mechanical responses of the human cervical facet capsular ligament under uniaxial tensile stretch. The models precisely simulated the force-displacement responses for all samples (R²=0.99±0.01) and showed promise in predicting the magnitude and location of peak regional strains at two different displacements. Yet, there was a loss of agreement between the model and experiment in terms of fiber organization at large tissue stretch, possibly due to a lack of accounting for tissue failure. The mean fiber stretch ratio predicted by the models was found to be significantly higher in regions that exhibited anomalous fiber realignment experimentally than in regions with normal realignment (p<0.002). The development of microstructural abnormalities was associated with the predicted fiber-level stretch (p<0.009), but not with the elemental maximum principal stress or maximum principal strain by logistic regression. The multiscale models elucidate a potential mechanical basis for predicting injury-prone tissue domains and for defining the relationships between macroscopic ligament stretch and microscale pathophysiology in the subfailure regime.

1 Introduction

Supraphysiologic soft tissue loading can alter the mechanical and sensory functions of that tissue even in the absence of overt, macrostructural failure (Provenzano et al. 2002; Lee et al. 2008; Quinn and Winkelstein 2008; Quinn and Winkelstein 2009). The cervical facet capsular ligament, a common anatomical source of pain, particularly from neck trauma, is a prime example of a tissue in which subfailure biomechanical responses underlie its pathophysiologic changes, leading to pain and dysfunction (Lord et al. 1996; Panjabi et al. 1998; Lee et al. 2004; Cavanaugh et al. 2006; Dong et al. 2012; Crosby et al. 2014). The facet capsular ligament encloses the bilateral facet joints of the spine that form the multi-axis articulation and mechanically couple motions between adjacent spinal levels (Jaumard et al. 2011). The facet capsular ligament is a fibrous soft tissue primarily comprised of elastin fibers and dense collagen fiber bundles, and is innervated by afferents (Lu et al. 2005; Quinn et al. 2007; Jaumard et al. 2011; Kallakuri et al. 2012; Crosby et al. 2014). Tensile strains that exceed the physiologic range, but are still below the failure threshold for the facet capsular ligament, induce persistent pain in vivo (Lee et al. 2008; Dong et al. 2012; Ita et al. 2017). However, it is not yet well understood how the microstructural mechanics are altered during ligament loading and may translate the tissue-level deformations into local loading that may influence the afferents embedded in the tissue.

The fibrous structure in the cervical facet capsular ligament is anisotropic, with the collagen fibers being strongly aligned in some sub-regions and unaligned in others (Kallakuri et al. 2012; Ban et al. 2017). Varied matrix organization can lead not only to heterogeneous stress and strain in the ligament (Quinn and Winkelstein 2008; Quinn and Winkelstein 2009; Quinn and Winkelstein 2010), but also to non-uniform distribution of loads and local matrix deformation. In the case of loading during tissue trauma, such heterogeneity can present various injury levels for different afferents depending on their location in the ligament. The complex tissue structure and the lack of visible rupture during injury (Quinn and Winkelstein 2008; Quinn and Winkelstein 2009) complicate the identification of injury-prone regions of the cervical facet capsular ligament.

Macroscopic strain is commonly used as a metric characterizing the mechanical tolerance of soft tissues (Siegmund et al. 2001; Robinson and Tranquillo 2009; Voycheck et al. 2014), but it lacks the resolution to localize microscopic alterations in the subfailure regime (Quinn and Winkelstein 2008; Quinn and Winkelstein 2009). As such, more sensitive, image-based techniques that detect microstructural changes have been developed (Tower et al. 2002; Park and de Boer 2008; Quinn and Winkelstein 2009; Voycheck et al. 2014). For example, quantitative polarized light imaging (QPLI) has been used to assess collagen kinematics in real-time during loading of the cervical facet capsular ligament ex vivo and demonstrates that anomalous fiber realignment occurs prior to visible rupture and in areas of eventual tissue rupture (Quinn and Winkelstein 2008; Quinn and Winkelstein 2009). Anomalous realignment (AR) of fibers, detected by statistical analyses of the polarized light images, has been defined as excessive reorganization of the local collagen matrix that is substantially more than expected in the majority of the tissue (Quinn and Winkelstein 2009). The onset of anomalous fiber realignment typically accompanies signs of compromised tissue integrity, like decreased tissue stiffness, and occurs at strains that induce pain in vivo (Quinn and Winkelstein 2008; Quinn and Winkelstein 2009; Dong and Winkelstein 2010). Although excess fiber rotation indicates microscopic tissue damage and relates to changes in the tissue’s macromechanics, the cause of anomalous fiber realignment and its effects on local mechanics are less well-known, partially due to the difficultly in experimentally measuring tissue micromechanics. Further, predicting when and where microscale injury may develop in the cervical facet capsular ligament during loading is confounded by the high inter-subject variability in the fibrous tissue structure (Ban et al. 2017).

Multiscale computational models are useful tools to probe the structure-function relationships in heterogeneous tissues (Breuls et al. 2002; Weinberg et al. 2010; Erdemir et al. 2015; Thunes et al. 2016). Although fully macroscale modeling approaches are able to simulate macroscopic tissue behaviors and the average fiber rotation, those models cannot accurately predict rotations of individual fibers and over-estimate the fiber stretch (Chandran and Barocas 2006). To capture fine details of the complex tissue architecture and predict microstructural mechanics, we and others have developed a finite element (FE)-based multiscale model that incorporate microstructural details that can be obtained using imaging techniques into the macroscopic tissue framework (Chandran and Barocas 2007; Sander et al. 2009b; Zarei et al. 2017). That multiscale model has been employed to describe the heterogeneity of fiber forces and orientation in the collagen matrix during stretch (Sander et al. 2009a), to assess the effects of fiber alignment on macroscale mechanics of collagen tissue analogs (Hadi and Barocas 2013) and to predict tissue-level failure based on fiber damage (Hadi et al. 2012; Vanderheiden et al. 2015). Furthermore, sample-specific multiscale models constructed using collagen organization data from optical coherence tomography have shown promise in capturing the structural and mechanical complexities of the lumbar facet capsular ligaments (Zarei et al. 2017). Therefore, image-based multiscale modeling is hypothesized as a feasible approach to predict the macro- and micro-scale tissue behaviors relevant to damage detection in the cervical facet capsular ligament.

The goals of this study were to develop subject-specific multiscale models of the cervical facet capsular ligament based on QPLI data and to use those models to evaluate various micro- and macro-scale mechanical parameters that may be used to predict microscopic tissue damage. Separate models were constructed to simulate the geometry, fibrous structure, and force-displacement responses of individual human facet capsular ligaments. To test the model performance, the predicted tissue strains and fiber orientation were compared to the experimental counterparts. Several mechanical metrics, including high-resolution macroscale stress and strains and fiber-level stretch, were assessed in simulations, and their co-localization with the experimentally detected anomalous fiber alignment was evaluated.

2 Materials and methods

2.1 Mechanical loading and imaging of cervical facet capsular ligaments

Tissue-level mechanics and collagen fiber orientation data were derived previously from experiment using an integrated mechanical testing and polarized light imaging system (Quinn and Winkelstein 2009). Briefly, the C4/C5 human facet joints were dissected with the ligament-bone attachment preserved. The width and thickness of unloaded specimens were measured using a digital caliper, and was used to estimate the cross sectional area. The bone-ligament-bone specimens were cast in aluminum cups that were fixed to the testing machine and underwent uniaxial tensile loading at 0.5mm/s applied by a testing machine (Instron 5385; Instron Corporation, Norwood, MA), with tissue forces and displacements acquired at 1kHz. Prior to testing, a grid of 15–24 fiducial markers was drawn using a felt-tipped pen on the ligament mid-substance surface and tracked during loading to calculate regional strains in each four-node element (Figure 1). All samples were mechanically pre-conditioned between 0 and 0.5mm for 30 cycles and pre-stressed to 5kPa to ensure consistent reference position (Quinn and Winkelstein 2009). Polarized light imaging with 12.5pixel/mm resolution was performed at the pre-stressed resting configuration and continuously during loading until tissue failure. Polarized light images were used to characterize tissue anisotropy in terms of pixel-wise collagen fiber orientation and alignment strength, by fitting the light intensity measures to a harmonic equation, as described previously (Tower et al. 2002; Quinn and Winkelstein 2008). The fiber orientation angles indicated by polarized images were average measures through the sample thickness and were used to generate two-dimensional incremental orientation maps every 0.04s over 20 images; vector correlation performed on the orientation maps detected anomalous fiber realignment (Quinn and Winkelstein 2009). In the current study, only specimens with sufficient light transmission and well-defined anomalous fiber realignment in the mid-substance prior to tissue rupture were analyzed (n=7 out of the 16 originally tested (Quinn and Winkelstein 2009); age 63±15 years; 2 females). The specimens that were excluded had either (1) low signal-to-noise ratio during polarized light imaging, leading to no detection of anomalous fiber realignment, or (2) the onset of collagen disorganization occurring only along the boundaries, which may not be accurately captured by the model due to boundary artifacts.

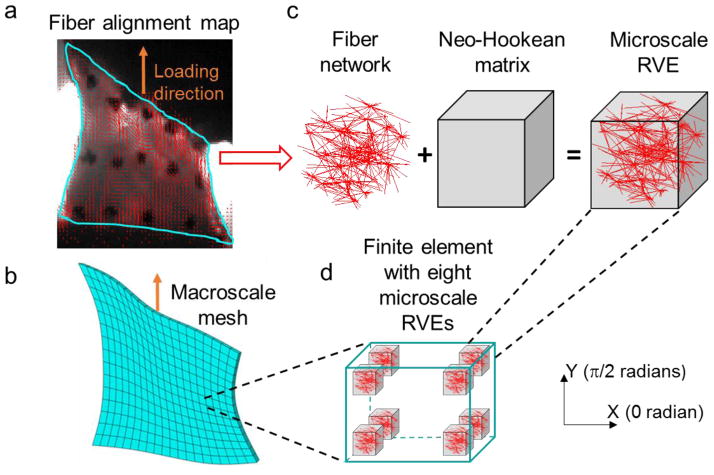
Figure 1.

Schematic showing the construction of the multiscale model. (a) Polarized light images of the cervical facet capsular ligament were used to create (b) the macroscale tissue mesh and to derive (c) the local fiber orientation for the representative volume elements (RVEs). Microscale RVEs are (d) located at the eight Gauss integration points in each finite element and comprised of a fiber network in a neo-Hookean matrix. The network and the matrix deform independently during uniaxial tension simulating the experimental loading condition.

2.2 Image-based multiscale model

An image-based multiscale FE method, as described in previous studies (Sander et al. 2009a; Zarei et al. 2017), was used to construct computational models of each cervical facet capsular ligament based on the inferred tissue structure from QPLI. Briefly, in this method, each finite element contains eight representative volume elements (RVEs) located at each of the eight Gauss integration points (Figure 1). These RVEs are composed of a network of fibers embedded in a Neo-Hookean matrix (Figure 1). The fiber network is constructed using the derived local collagen fibers orientation. The fiber network and the Neo-Hookean matrix are not coupled, allowing the network to deform non-affinely, but they are constrained to have the same macroscopic-scale deformation (Alford and Taber 2008; Ateshian et al. 2013). Upon deformation of each element, the underlying RVEs deform and generate stress, which is averaged and passed up to the macroscale. This process iterates until the equilibrium is achieved.

Individual fibers in the fiber networks of the RVEs are governed by the following phenomenological constitutive equation (Billiar and Sacks 2000):

$$F=A[\mathit{exp}(BE)-1],$$

where F and E are force and Green strain for each fiber, and A and B are two constitutive constants. The Neo-Hookean matrix inside the RVEs was assumed to have low compressibility (Poisson’s ratio ν=0.48). Therefore, there were three fitting parameters, namely the two constitutive constants A and B for fibers, and the shear modulus of the Neo-Hookean matrix G_mat.

QPLI data and sample geometry in the undeformed state were used to construct separate models for each individual cervical facet capsular ligament. First, based on the polarized light images taken in the pre-stressed reference position, a geometry representing the shape of the tissue was created and meshed with eight node linear hexahedral elements in Abaqus CAE (version 6.11-1, Dassault Systems Americas Corp., Waltham, MA) (Figure 1). Each tissue continuum was meshed into approximately 300 finite elements based on convergence studies. Next, fiber alignment maps derived from the QPLI data were registered to the created tissue geometries. A previously developed tensor-based averaging method (Zarei et al, 2017) was then used to coarsen the high-resolution QPLI orientation map and acquire the mean fiber orientation and alignment strength for each finite element. To generate fiber networks in each RVE based on the elemental fiber orientation and alignment strength, isotropic Delaunay networks composed of interconnected fibers were first created using random seed points in the three-dimensional space. The fibers were linked to each other at their contact points by rigid, freely rotating crosslinks. Each network was stretched geometrically according to the local alignment strength and rotated such that the primary network orientation was aligned with the element’s calculated fiber orientation. The transformed network was then cropped to a cubic subsection (1×1×1) to be used in the RVEs. The number of fibers in the final cubic network was controlled to be in the range between 350 and 450, and the eight RVEs in the same finite element all contained the same initial fiber network. Those fiber networks were constructed in MATLAB (R2014a). The dimension of a single RVE is on the order of 10–30 microns, which is much smaller than the length scale for structural variation (300–400 microns) observed in the same set of human cervical facet capsular ligaments (Ban et al. 2017). Therefore, the structural variation in actual ligaments is sufficiently slow so that a smooth interpolation between RVEs is acceptable.

The geometric data obtained from Abaqus CAE and MATLAB were input into an in-house C-based multiscale computational framework. The multiscale code was executed on an IBM BladeCenter Linux Cluster at the Minnesota Supercomputing Institute. To simulate the experimental loading condition, the upper boundary in the constructed model was pulled uniaxially along the vertical direction (Figure 1); the bottom boundary was fixed, and the lateral boundaries were unconstrained, but no lateral contraction was allowed along the upper and bottom boundaries to mimic ligament-bone attachment. Boundary forces were computed as a function of the applied displacement during each simulation. The force-displacement results from the model were matched to those from the experiments by tuning the three fitting parameters, A, B, and G_mat using trial and error. Specifically, one parameter at a time was adjusted and the match between the resulting force-displacement responses were visually assessed from the model and that from experiment. When a good match was observed, the coefficient of determination (R²) was calculated to ensure high agreement between model and experiment. Although the trial-and-error method cannot guarantee the uniqueness of the fit, high accuracy of the estimated parameters were ensured by calculating the ellipsoidal confidence region around the center of these final choices (Draper and Smith, 2014). The width of the 95% confidence interval of the sample with the lowest R² is as low as about 1% of the estimated values for all three fitting parameters. The average RVE Cauchy stress (sum of the fiber network and the Neo-Hookean matrix contributions) and the Green strain generated were also acquired at different displacements, based on which the maximum principal stress and maximum principal strain fields were produced for each sample. Nodal displacements of the FE mesh and fiber networks were recorded during simulations to track the macroscale model deformation and the microscale fiber stretch and orientation.

2.3 Comparison between experiments and models

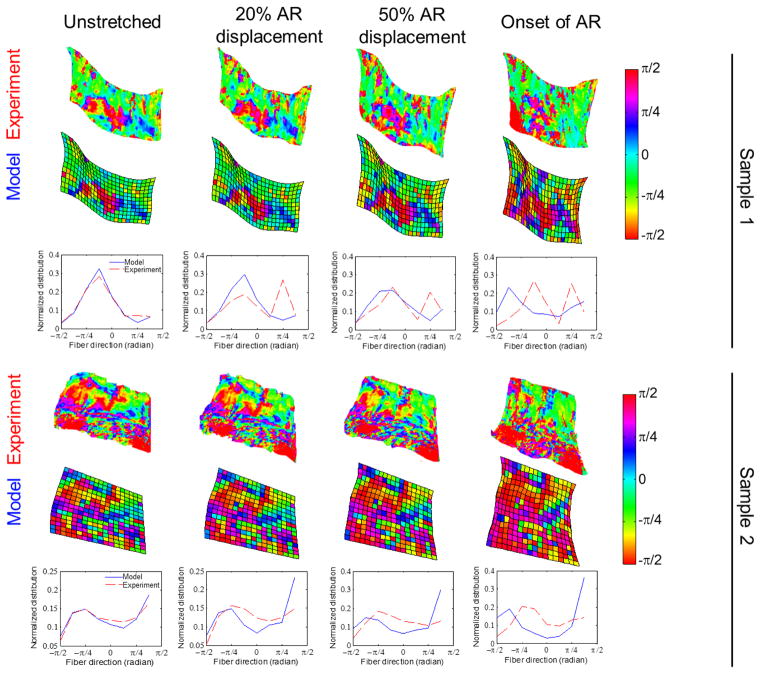
The force-displacement responses between the experiment and model were compared by measuring the coefficient of determination (R²) and the root mean squared error (RMSE). Model nodes that were closest to the locations of the experimental fiducial markers were tracked during the simulation to compute the regional strain at 50% displacement towards the onset of AR and at the onset of anomalous fiber realignment. For example, if AR initially occurred at 3mm of displacement, points were analyzed at 1.5mm displacement and at 3mm displacement. Maximum principal strains in each of the four-node sub-regions were calculated using LS-DYNA (Livermore Software Technology Corp., Livermore, CA) (Quinn et al. 2007). We visualized the spatial distribution of the maximum principal strains and compared the locations of the measured and predicted peak strains. To test whether the model generated strain magnitudes that were within a similar range as those from the experiment, paired t-tests compared the experimental and predicted peak maximum principal strain in each sample. Strain direction was measured as the angle from the horizontal direction. Circular variance, which captures the variation in a set of dihedral angles, was calculated as a measure of the heterogeneity in strain directions acquired from different sub-regions within the same sample. A lower circular variance indicates higher similarity in regional strain directions within the given sample. Circular variances were computed for each specimen and its corresponding model and were compared between the experiment and model using paired t-tests. Since a total of four strain-related comparisons were compared between the model and experiment, Bonferroni correction was performed to counteract errors that may arise from multiple comparisons by adjusting the significance level from 0.05 to 0.05/4=0.0125. Pixel-wise and elemental-wise color maps showing the local fiber orientation were generated for the experiment and the model, respectively. The fiber orientation maps measured from the experiment and those predicted by the model were visually compared to examine whether the experimental fiber organization displays a different spatial profile from model prediction. The angle distribution functions normalized by total counts were generated at displacements equal to 20%, 50%, and 100% of the displacement at the onset of anomalous fiber reorganization for both of the experiment and the model.

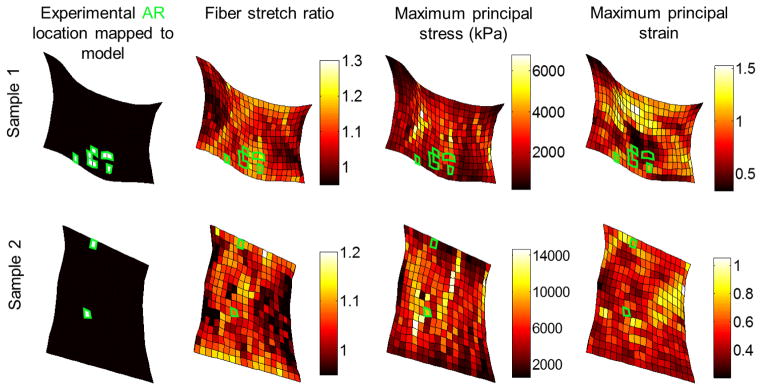
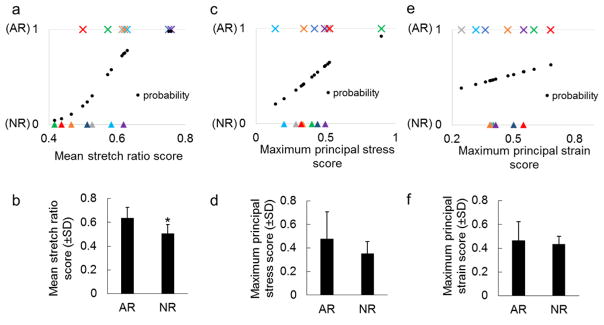
Next, several additional metrics characterizing tissue mechanics from the model were compared with the development of anomalous fiber realignment measured experimentally. To do this, the macroscopic-scale maximum principal stress, macroscopic-scale maximum principal strain, and microscopic-scale fiber stretch were derived, normalized and correlated to the initiation of anomalous fiber realignment, using the same approach for each comparison. First, the AR locations identified in the experiment were mapped to the model by overlying the model mesh on the polarized light images at the onset of AR. Finite elements that co-localized with tissue domains sustaining anomalous fiber realignment were assigned an AR score of 1 (AR elements) and 0 otherwise (normal realignment; NR elements). The metric of interest was calculated across the eight RVEs for each finite element. Using these measurements, an injury score was computed for each finite element to indicate the degree of change in mechanics and chance of injury at different spatial locations across the entire tissue domain. Each metric was mapped to the range of 0–1 using min-max scaling $x_{\mathit{normalized}}=\frac{x-\mathit{min}(x)}{\mathit{max}(x)-\mathit{min}(x)}$, and the data were smoothed by a 3×3 average filter. A score closer to 1 indicates the condition more prone to injury (e.g., higher maximum principal strain). Paired t-tests compared the average scores of AR elements and NR elements from all samples. Logistic regression of the AR score against each of the mean stress, strain and fiber stretch ratio scores determined the relationships between different mechanical metrics and the development of anomalous collagen realignment. Bonferroni correction was performed to adjust the significance level from 0.05 to 0.0167 for the three paired t-tests.

3 Results

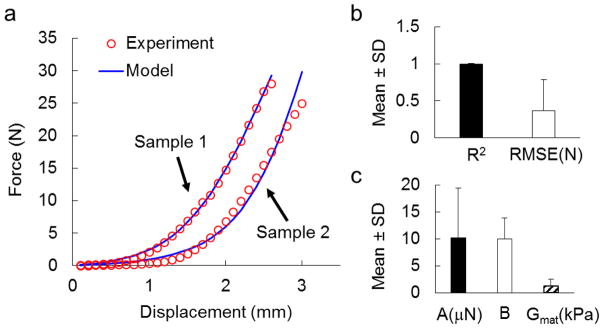
The force-displacement responses in the subfailure regime were well predicted for all specimens (Figure 2). The experimentally acquired and computationally predicted force-displacement curves demonstrated high similarity, even for the sample with the lowest coefficient of determination (Figure 2a). The agreement in force between experiment and model was further confirmed quantitatively by high R² values and low RMSEs. The average R² value was 0.99±0.01 (mean±standard deviation), indicating nearly perfect goodness-of-fit; the RMSE was 0.37±0.42N (mean±standard deviation), which was less than 3% of the mean maximum force from the seven samples (Figure 2b). The fitting parameters used to tune the forces varied from sample to sample. The average best-fit values for parameters A, B, and G_mat across all samples were 10.2±9.2μN, 10.0±3.9 and 1.2±1.3kPa (mean±standard deviation), respectively (Figure 2c). The large variation observed in the fitting parameters – for the fiber stiffness and matrix shear modulus parameters in particular – demonstrated the inter-subject variability in mechanical properties of the cervical facet capsular ligaments.

Figure 2.

Simulated force-displacement responses from the model. (a) Two representative samples demonstrate the agreement in force-displacement responses between the experiment and model. Samples 1 and 2 have the highest and lowest coefficient of determination (R²) among the 7 samples, respectively. (b) High R² values (close to 1) and low root mean squared errors (RMSE) verify the accuracy in force prediction. (c) Best-fit parameters for the multiscale model show large variations among different samples. Error bars represent standard deviations.

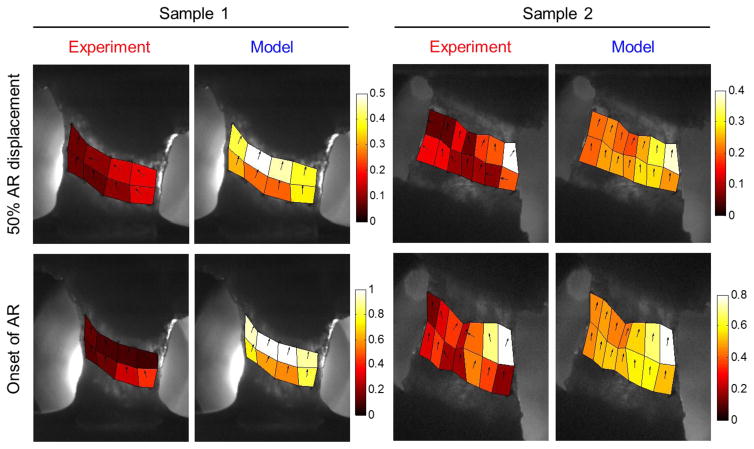
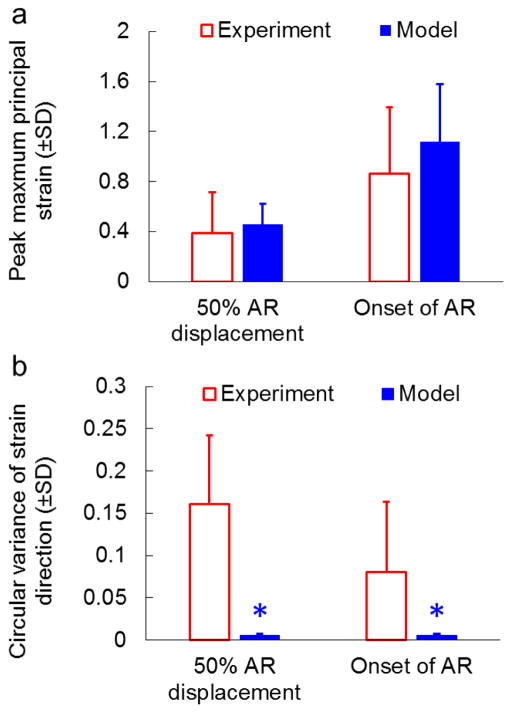
Accuracy of the multiscale model in predicting regional strains also differed from sample to sample. Locations of the peak maximum principal strain were correctly predicted in two samples; another three samples had experimental peak strains located in regions that corresponded to areas of high, but not peak maximum principal strain in the model; the predicted and experimentally measured strain fields in the other two samples were dissimilar. For example, although Sample 1 exhibited high agreement in the force-displacement responses (Figure 2a), the predicted maximum principal strain was substantially different from the measured strain in terms of the location, magnitude and direction of the peak maximum principal strain (Figure 3). In contrast, the model of Sample 2 accurately predicted the location of the peak strain, and the simulated peak maximum principal strain exhibited similar magnitude and direction to that observed experimentally (Figure 3). Comparing the experimental and simulation results of all seven samples, no significant difference (p>0.37) was found in the magnitude of the peak maximum principal strain at either 50% AR displacement or the onset of AR (Figure 4a). Overall, the predicted maximum principal strain was slightly larger than the experimentally measured strains. Differences in strain direction also existed: the directions of the maximum principal strain in the model were mostly aligned along the loading direction, while the strain directions in the experiment were highly non-uniform (Figure 3). The circular variance of strain directions was significantly higher in the experiment than in the model at 50% AR displacement (p=0.001); although no significant difference was detected at the onset of AR (p=0.028; greater than the Bonferroni corrected p value of 0.0125), the circular variance of strain directions predicted by the model is consistently lower than that from the corresponding experimental sample (Figure 4b).

Figure 3.

Comparison of regional maximum principal strain profiles between experiment and model for the samples shown in Figure 2. The vectors indicate the direction of maximum principal strains. Strain maps of these two representative samples show heterogeneous strain directions in the experiment and uniform strain direction in the model. The location and the magnitude of the peak strain are well predicted in Sample 2, but not in Sample 1, at both 50% AR displacement and the onset of anomalous realignment (AR).

Figure 4.

Quantification of regional maximum principal strain profiles for all samples. (a) Comparison of peak maximum principal strains between the experiment and model. The peak strains from all 7 samples are not different between the experiment and the model at either 50% AR displacement (p=0.629) or the onset of AR (p=0.380). (b) Comparison of circular variances of strain directions between the experiment and model. At both 50% AR displacement and the onset of AR, the circular variance is significantly lower in the model (*p<0.028), indicating more consistent regional strain directions in the model than in the experiment. Error bars indicate the standard deviations.

In addition to discrepancies observed in the macroscale strain direction, the experiment and model also showed differences in the orientation of the microscopic networks during loading. The alignment maps derived from QPLI and the simulated fiber orientation maps had similar distributions at the pre-stressed reference position for all seven samples, verifying the accuracy of the tensor averaging method (Figure 5). The predicted fiber alignment maps remained similar to those of the experiment measurements at small displacements, but the differences became more evident with increasing applied deformation (Figure 5). In the simulations, fibers reoriented towards the vertical loading direction; surprisingly, the inferred reorganization of the collagenous structure from QPLI was non-uniform within each sample and between different specimens (Figure 5).

Figure 5.

Comparison of fiber orientation between the experiment and the model. Alignment maps and angle distributions are shown for the samples shown in Figure 2 at various displacements up to the onset of anomalous fiber realignment (AR). Differences between the simulated and experimentally measured fiber orientation are minimal initially in the pre-stressed resting configuration. The discrepancy between the two is amplified with increased tissue deformation.

The development of anomalous fiber realignment in the facet capsular ligament associated with the microscopic fiber stretch, but not with the macroscale maximum principal stress or maximum principal strain calculated by the multiscale model (Figures 6 & 7). The fiber stretch ratio map, maximum principal stress field, and maximum principal strain field obtained from the same sample model exhibit different patterns (Figure 6). The predicted fiber stretch and tissue stresses and strains were highly heterogeneous within each sample and between different samples (Figure 6). Most of the finite elements whose regions sustained AR in the experiment co-localized with regions of high fiber stretch ratio in the model (Figure 6). Significant association between AR occurrence and fiber stretch was detected by logistic regression (p<0.009) (Figure 7a). For all seven samples, the average fiber stretch score was higher in the elements that sustained AR than in those that did not (Figure 7a), leading to a significant difference in fiber stretch scores between AR (anomalously realigned) and NR (normally realigned) elements as tested by the paired t-test (p<0.002) (Figure 7b). Some, but not all, AR elements had high stresses; the logistic regression showed no significant correlation between the development of AR and the stress magnitude (p=0.171) (Figures 6 & 7c). Although the mean stress score was higher in AR elements than in NR elements, the difference was not significant (p=0.081) (Figure 7d). Similar to stress, the predicted maximum principal strain did not associate with the emergence of AR and neither did the mean strain magnitude differ between the AR and NR elements (p>0.3) (Figures 6 & 7).

Figure 6.

Spatial distribution of anomalous fiber realignment and predicted fiber stretch ratio, maximum principal stress and maximum principal strain for two representative samples. The simulated mechanical outcomes display heterogeneous spatial patterns. Anomalous fiber realignment (AR) mapped to the model (shown by the white elements in plots in the first column) tends to locate in regions with high fiber stretch ratio (as displayed in maps in the second column). Green boxes outline the locations of the experimental AR mapped to the model in all distribution maps.

Figure 7.

Comparison of different injury scores in regions with and without microstructural damage. The stretch ratio score (a) shows significant correlation with the occurrence of AR by logistic regression (p<0.009) and (b) significantly higher values in anomalous realignment (AR) elements than in normal realignment (NR) elements (*p<0.002). No significant association is detected by logistic regression between the development of AR and (c) the maximum principal stress score or (e) the maximum principal strain score. Neither (d) the maximum principal stress score nor (f) the maximum principal strain score differs between AR and NR regions. Symbols with the same color in (a), (c) and (e) represent the AR (×) and NR(▲) elements from the same specimen. Predicted probability (●) from logistic regression models are shown in (a) (c) and (e). Error bars show the standard deviations.

4 Discussion

In this study, image-based multiscale models were used to simulate the mechanical behavior of the cervical facet capsular ligament during ex vivo uniaxial tension, a common injury modality to this ligament (Panjabi et al. 1998; Winkelstein et al. 2000; Siegmund et al. 2001). The models demonstrated varied capabilities in predicting different kinematic and kinetic outcomes across multiple length scales (Figures 2–5), potentially due to limitations in either or both of the computational and imaging methods. Those multiscale models were employed to evaluate the relationships between different mechanical metrics and the development of microstructural tissue injury. Among these metrics, fiber-level stretch was found to have the highest correlation with the occurrence of anomalous fiber realignment (Figures 6 & 7). Previous experimental studies investigating the structure-function relationships of soft tissues have examined the (dis)connections between collagen fiber alignment and macroscopic deformation and their contributions to tissue failure (Quinn and Winkelstein 2009; Alavi et al. 2013; Voycheck et al. 2014). Complementing prior experiments, this study provides a hierarchical platform to further reveal the complex relationships between various micro-, meso- and macro-scale mechanical responses in heterogeneous tissues, especially adding to the understanding of potential mechanical conditions necessary to produce microstructural damage prior to visible rupture of the cervical facet capsule.

By incorporating sample-specific fiber architecture to account for the large structural variation in the cervical facet capsular ligaments (Quinn and Winkelstein 2008; Kallakuri et al. 2012; Ban et al. 2017), our models captured the non-uniform multiscale mechanics of this ligament. The 7 specimens that are included in the current study are considered representative of the typical facet capsular ligament since they have varied force-displacement relationships (Figure 2), distinct fibrous structures (Ban et al. 2017) and anomalous fiber realignment that develops at different sub-regions and displacements (Quinn and Winkelstein 2009). Macroscopically, the subfailure force-displacement responses during ex vivo ligament stretch were predicted with high accuracy in the simulations (Figure 2). By estimating the peak strain magnitudes and identifying regions that may undergo large strains during loading (Figures 3 & 4), our model also showed promise in capturing the heterogeneity in the local strain distribution within and across samples. However, not all experimental tissue-level strain fields were predicted accurately (Figure 3). The inaccurate strain estimation may have arisen from simplifications due to insufficient experimental characterization, such as that which comes from assuming any structural variability through the ligament thickness can be ignored, and homogenization of collagen fiber density across the finite element mesh (Jaumard et al. 2011; Iorio et al. 2016). The prediction accuracy of regional strains may be enhanced by performing a localized fit of the model parameters, A, B, &G_mat and using the macroscopic displacement data, which may lead to overall improvement of the model performance Microscopically, the tensor averaging method enabled consistency between the initial fiber orientations in the model and those acquired experimentally at the pre-stressed resting configuration. Yet, our model did not accurately simulate the network reorganization process during ligament loading, especially at larger strains (Figure 5). These discrepancies between the model and the experiment have raised additional questions regarding the model and the imaging technique. First, it is unclear whether certain material behaviors that are missing in our model, such as viscoelasticity and microstructural failure, could play important roles in modulating tissue-level strains and network reorganization during loading of the cervical facet capsular ligaments. Second, the question of whether polarized-light imaging provides sufficient structural detail to construct a comprehensive multiscale model is still unclear.

Theoretically and experimentally, collagen fibers in many soft tissues and engineered tissue analogs have been observed to realign towards the loading direction during uniaxial tension (Figure 5) (Tower et al. 2002; Vader et al. 2009; Voycheck et al. 2014; Zhang et al. 2016). However, the alignment maps derived from QPLI in this study suggest that collagen fibers in the cervical facet capsular ligament rotate in different directions during stretch, with some fibers even reorienting away from the primary loading axis (Figure 5) (Quinn and Winkelstein 2008; Ban et al. 2017). The differences in fiber orientation distribution between the model and the experiment become more apparent as the applied tissue deformation increases (Figure 5). One possible reason for this discrepancy is the emergence of microstructural tissue damage prior to visible rupture of the actual tissue that was not simulated in the model. The source of microstructural injury may be failure of individual fibers or fiber bundles, and/or impairment of non-fibrillar matrix.

Measuring fiber failure and/or matrix failure in real-time during tissue loading are challenging, but their occurrence may be indicated by the altered collagen kinematics (e.g. anomalous collagen realignment). Anomalous collagen realignment could result from stress redistribution among undamaged fibers upon failure of load-bearing fibers, and/or from fiber rotation away from the non-fibrillar matrix when the interactions between the two are compromised. In the current study, neither fiber failure nor matrix failure was incorporated in our models. Nonetheless, the predicted maximum fiber stretch at the onset of anomalous fiber realignment (1.23–1.66) in all samples exceeds the breaking threshold (6–22%) of collagen fibers estimated from other ligament and tendons (Morgan and Mitton 1960; Liao and Belkoff 1999; Yamamoto et al. 1999). This difference suggests that microscopic collagen failure likely occurs prior to the detection of abnormal fiber reorientation. It could also indicate that fibers in the facet capsular ligament initially have significant crimping, which would lead to a greater apparent fiber stretch in the model than actually occurs in the tissue, despite that the early compliant tissue responses in the tissue was simulated by fiber realignment in our model. The ability of the current model to accurately predict fiber strain and failure is further limited by simplified fiber-fiber interactions. The crosslinks were constructed with arbitrary density and distribution and enabled only fiber rotation but not fiber bending or sliding. Although the predict macroscopic force-displacement responses match those observed in experiments (Figure 2), more work is needed to elucidate the details of these fiber-fiber interactions both experimentally and computationally. Nevertheless, the co-localization of anomalous fiber realignment and high fiber stretch ratio (Figure 6) implies that fiber-level impairment is involved in the development of microscopic tissue injury leading to eventual gross failure. In addition to microstructural damage, the presence of elastic fibers and ground substances with varying quantities in the facet capsule (Yahia and Garzon 1993; Yamashita et al. 1996) may also affect the motion and deformation of the local fibrous networks. Although other fibrillary components could be introduced to individual RVEs by modulating the assigned fiber properties (Witzenburg et al. 2017), their distribution and orientation cannot be directly acquired experimentally using QPLI due to the lack of birefringence. Additional studies using immunohistochemistry and confocal microscopy may provide more structural information on different fibrillar and non-fibrillar components in the facet capsular ligament to improve the current model.

Polarized light imaging has been widely used to evaluate matrix reorganization and its relationships to macroscale mechanical responses in simple collagen-based tissue analogs (Sander et al. 2009a; Raghupathy et al. 2011; Zhang et al. 2016). Although this imaging tool has also been employed to study the structure-function relationships in real tissues (Tower et al. 2002; Quinn and Winkelstein 2008; Quinn et al. 2010), limitations of QPLI become obvious and confound the structural findings when applied to complex tissue systems. One pitfall of this technique that affects the construction of the multiscale model is its limited resolution. Despite the resolution being adjustable, QPLI produces pixel-wise alignment, which corresponds to the average angle from a fiber group containing an unknown number of fibers that may only be partially captured within a given pixel. Such measurements cannot provide enough information about fiber density or length to be translated directly into detailed RVE networks on the scale of 10–20μm (Hadi et al. 2012). Therefore, other imaging methods, such as second harmonic generation microscopy (Chen et al. 2012) and scanning electron microscopy (Provenzano and Vanderby 2006; Zarei et al. 2017), may prove necessary to assess the collagen fibrillary structure in normal unloaded cervical facet capsular ligament tissue in order to construct more precise and detailed models. In the current model, we assumed identical fiber networks through the sample thickness, because the orientation derived from QPLI is the thickness-averaged alignment (Tower et al. 2002; Quinn and Winkelstein 2008). Although the model thickness was determined based on the average thickness of individual specimens measured experimentally and so varies from sample to sample, a uniform thickness was assumed within each model. Varied tissue thickness, as well as non-uniform fiber density in the actual ligament specimens, can affect the degree of light transmission and depolarization, leading to inconsistent estimation of fiber alignment. Depth-dependent collagenous structure may be better captured by other imaging modalities, such as polarization-sensitive optical coherence tomography (Park and de Boer 2008; Claeson et al. 2015, Zarei et al. 2017).

Despite those methodological issues, our model complements the experimental assessment of the cervical facet capsular ligament and further elucidates the multiscale nature of the ligament’s response to loading. Compared to tissue-level force responses, regional strains are more dependent on the underlying fibrous structure information. Differences in fiber realignment between model and experiment did not affect the model’s ability to predicting the force-displacement responses (Figure 2). In contrast, different fiber realignment patterns during loading (non-uniform in experiment and uniformly towards the loading direction in model) seem to affect the primary direction of regional strains, leading to non-uniformly oriented maximum principal strain vectors in the experiment and vertically aligned strain vectors in the model (Figures 3 & 5). The association between collagen fiber alignment and tissue strains has also been implicated by previous studies, which used fiber orientation to establish full field strains in the cervical facet capsule (Quinn and Winkelstein 2010) and correlated primary fiber alignment and regional strain to predict failure of the glenohumeral capsule (Voycheck et al. 2014).

Macroscopic strain measurements are common mechanical metrics that define the injury thresholds of soft tissues (Siegmund et al. 2001; Robinson and Tranquillo 2009; Voycheck et al. 2014). Despite possible associations between collagen fiber alignment and macroscale strains, disconnection between the location of microstructural tissue damage indicated by anomalous fiber realignment and the region of maximum principal strains has been identified previously in the cervical facet capsular ligament (Quinn and Winkelstein 2009). The lack of correlation between macroscopic strain and/or stresses and microscale tissue injury may occur in anisotropic tissues because large tissue deformations and stresses in the fiber alignment direction can be borne by the elongation and strength of the fiber bundles and strains perpendicular to the aligned fibers have less impact on the microstructure during loading (Korenczuk et al. accepted). Using multiscale models, we were able to increase the resolution of the measured macroscopic strains from regional to elemental (Figures 3 & 6). Similar to regional strains computed by tracking fiducial markers in the experiment, our predicted elemental strains did not effectively indicate where microstructural tissue damage initiated (Figures 6 & 7). Elemental maximum principal stresses, on the other hand, exhibited different spatial distribution from the element strains and had high values in regions of anomalous realignment in some cases, but they still lacked sensitivity in accurately predicting the location of collagen disorganization (Figures 6 & 7).

Among the three mechanical variables examined, fiber stretch ratio is the best metric in terms of detecting injury-prone domains, because regions sustaining anomalous fiber realignment show higher fiber-level stretch in all of the samples evaluated (Figures 6 & 7). Previous work using a FE-based discrete fiber network model to simulate collagen tissue analogs (Zhang et al. 2016) reported that at a maximum fiber axial strain of around 15% (strain > 4% in most fiber along the loading direction), neurons embedded in the collagen matrix are activated by uniaxial tension and express signaling molecules that play a role in different pain models (Ji et al. 1999; Dina et al. 2005). High fiber stretch ratios in the current model exceed the previously defined threshold for neuronal activation in all samples. Large deformation of collagen fibers may be transferred to neuronal deformation via cell-collagen adhesions (Tomaselli et al. 1993; Khalsa et al. 2000). Failure of load-bearing fibers can occur under excessive stretch, and can lead to stress redistribution among intact fibers and subsequent fiber reorientation to accommodate macroscopic deformation. Fiber reorganization may exert local forces on the included cells and form stress concentrations at cell-collagen adhesions, initiating neuronal signaling cascades to process noxious stimuli (Cullen et al. 2007; Sander et al. 2009a). The association between fiber-level changes and neuronal responses is supported by the observation that abnormal fiber realignment occurs at capsule strains that induces facet pain in vivo (Quinn and Winkelstein 2009; Dong et al. 2012). Collectively, these findings suggest that coupled fiber-level responses in the subfailure regime, such as anomalous realignment and excessive stretch or breakage, likely underlie pathophysiologic changes of the cervical facet capsular ligament in the context of pain.

In summary, this study demonstrates the ability of our imaging-based model to predict heterogeneous, multi-scale mechanical responses of the cervical facet capsular ligament, a common source of neck pain from neck injury. Variations in model performance when predicting different mechanical outcomes likely associate with limitations related to the imaging technique and the model itself. Nevertheless, by incorporating sample-specific fibrous structures, the model shows promise in identifying tissue domains that are prone to injury during loading prior to visual rupture. Fiber-level measurements are more sensitive than macroscopic stresses or strains in detecting microstructural tissue damage and may have direct impact on the sensory afferents that innervate the facet capsule.