Biophysical properties of microvascular endothelium: Requirements for initiating and conducting electrical signals

Abstract

Objective

Electrical signaling along the endothelium underlies spreading vasodilation and blood flow control. We use mathematical modeling to determine the electrical properties of the endothelium and gain insight into the biophysical determinants of electrical conduction.

Methods

Electrical conduction data along endothelial cell (EC) tubes (40 μm wide, 2.5 mm long) isolated from mouse skeletal muscle resistance arteries were analyzed using cable equations and a multicellular computational model.

Results

Responses to intracellular current injection attenuate with an axial length constant (λ) of 1.2–1.4 mm. Data were fitted to estimate the axial (r_a; 10.7 MΩ/mm) and membrane (r_m; 14.5 MΩ·mm) resistivities, EC membrane resistance (R_m; 12 GΩ), EC-EC coupling resistance (R_gj; 4.5 MΩ) and predict that stimulation of ≥30 neighboring ECs is required to elicit 1 mV of hyperpolarization at distance = 2.5 mm. Opening Ca²⁺-activated K⁺ channels (K_Ca) along the endothelium reduced λ by up to 55%.

Conclusions

High R_m makes the endothelium sensitive to electrical stimuli and able to conduct these signals effectively. Whereas the activation of a group of ECs is required to initiate physiologically relevant hyperpolarization, this requirement is increased by myoendothelial coupling and K_Ca activation along the endothelium inhibits conduction by dissipating electrical signals.

Introduction

The resistance vasculature consists of branching arteriolar networks and the feed arteries from which they are supplied. As respective vessels are arranged in series and parallel, matching blood flow to local tissue requirements requires coordinated dilatation of distal and proximal branches.¹ In this manner, coordinated vasodilation along and among parallel branches of resistance networks depends primarily upon the interplay between electrical and Ca²⁺ signaling events.^2,3 In particular, endothelial cell (EC) hyperpolarization that evokes vasodilation arises from Ca²⁺ activation of small- and intermediate-conductance calcium-activated K⁺ channels (SK_Ca and IK_Ca). This electrical signal is transmitted from cell-to-cell along the wall of arterioles to ascend into proximal feed arteries to attain peak levels of functional hyperaemia.^4–6 Electrical conduction along the endothelium is attributed to the axial arrangement of ECs and their strong electrical coupling through gap junctions.^7,8

The interplay between gap junction patency underlying axial resistance and the activity of ion channels that govern membrane resistance (e.g., K⁺ channels) determines whether an electrical signal of a given magnitude and duration is localized or is conducted along the vessel wall.⁹ For example, with constant axial resistance, electrical conduction along the endothelium of resistance arteries becomes impaired by excessive opening of SK_Ca and IK_Ca as demonstrated directly with the pharmacological channel opener NS309 and indirectly with the G_q-coupled muscarinic receptor agonist acetylcholine (ACh).¹⁰ By the same effect of lowering cellular membrane resistance, opening large-conductance Ca²⁺-activated K_Ca channels in smooth muscle cells (SMCs) can also attenuate electrical conduction along intact vessels.¹¹

Conducted vasodilation has been mostly investigated by examining the spread of the vasomotor response in situ and in vivo, but further insight into the underlying electrical signaling is needed. Given the central role of signal transmission through the endothelial layer in this phenomenon,⁸ the electrical properties of the endothelium in representative vascular beds requires characterization. Estimates for the endothelial coupling resistance have only been provided in cultured monolayers¹² or have been deducted from electrical propagation along intact arterioles of the guinea-pig mesentery.¹³ There is also a paucity of data for the membrane resistivity of ECs in intact microvascular endothelium.

Recent experimental advances have enabled investigation of the nature and properties of electrical conduction along the endothelium of resistance microvessels without the influence of the smooth muscle layer or the confounding effect of culturing conditions that alter cell phenotype.^10,14 Experiments with endothelial tubes freshly isolated from feed arteries of mouse skeletal muscle have confirmed that the endothelium can conduct membrane potential (V_m) changes, with a length constant (λ) λ 1.4 mm, a value similar to the λ of electrical decay and of spreading dilatations in intact microvessels which previous studies have shown to be 1.1–1.6 mm in guinea pig arterioles¹⁵ and 1.1–1.9 mm in hamster skeletal muscle feed arteries.¹⁶

In the present study, we used mathematical modeling to determine the electrical properties of native intact microvascular endothelium and to thereby gain insight into the biophysical determinants of electrical conduction. We analyzed electrophysiological data¹⁰ using one- and two-dimensional cable equations, and a discrete-cell model of microvascular endothelial tubes that integrates Ca²⁺ and V_m dynamics in ECs.¹⁷ We validated the applicability of cable equations to characterize conduction in EC tubes and extracted electrical parameters for native microvascular endothelial cells. Further, the multicellular computational model of the endothelial layer was utilized to link electrical properties of ECs to the conduction of electrical signals. Applying defined electrophysiological properties using the discrete model can thereby: (a) account for the current-voltage relationships of ion channels and serve as a benchmark for cable equations;¹⁸ and (b) evaluate the effect of experimental interventions that influence ion channels to affect the resistance of cell membranes.¹⁰ Our analysis examines the determinants of endothelial sensitivity to agonist stimulation and predicts minimal requirements for effective ascending vasodilation along feed arteries of skeletal muscle.

Methods

In silico analyses of experiments in endothelial tubes

We analyzed data from an experimental study of electrical conduction along endothelial tubes freshly isolated from superior epigastric arteries of C57BL/6 mice.¹⁰ V_m responses to injecting current into a single EC were measured at defined distances to characterize electrical conduction along the endothelium. Thus, in response to hyperpolarizing or depolarizing current pulses (0.1–3 nA, 2s), V_m was recorded at 0.05, 0.5, 1, 1.5 and 2 mm remote from the local site of current injection. A typical endothelial tube used in these experiments had length L = 2.5 mm, diameter D = 40 μm and contained ~2000 ECs.^10,19

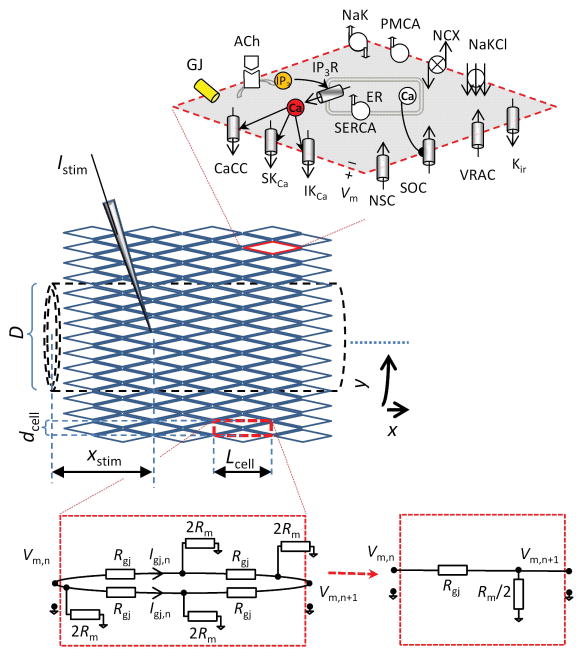
Different theoretical approaches were used to extract parameters associated with electrical conduction. These parameters included the length constant of signal attenuation (λ), axial (r_a) and membrane (r_m) resistivities, EC membrane resistance (R_m), the resistance of EC-EC coupling through gap junctions (R_gj), and the effect of SK_Ca/IK_Ca activation on λ. We start with a simple estimation of R_m based upon the cable input resistance and λ, then present a differential equation for current spread in a continuum cable model with its one- and two-dimensional solutions then follow with our implementation of detailed multicellular discrete models of the endothelial tube (Fig. 1).

Figure 1.

Discrete multicellular model of endothelial tube. Idealized diamond-shaped ECs, each with length = 35 μm (L_cell), width = 8.6 μm (d_cell), and thickness d, are arranged into a cylinder (dashed lines) with N_circum (= 14) cells encompassing the circumferential direction (y) and 71 cells encompassing the axial direction (x). Under control conditions, each EC is coupled to its four immediate neighbors through gap junctions. The total number of ECs in the discrete model of an endothelial tube of length L = 2.5 mm and diameter D = 38 μm is 1988. Each EC is modeled as described in Silva et al.¹⁷ and contains: store-operated Ca²⁺channels (SOC); nonselective cation channels (NSC); volume regulated anion channels (VRAC); Ca²⁺-activated Cl⁻ channels (CaCC); small- and intermediate-conductance Ca²⁺-activated K⁺ channels (SK_Ca and IK_Ca); Na⁺-K⁺-ATPase (NaK); plasma membrane Ca²⁺-ATPase (PMCA); Na⁺/Ca²⁺ exchanger (NCX); Na⁺/K⁺/Cl⁻ cotransporter (NaKCl); sarcoplasmic endoplasmic reticulum Ca²⁺-ATPase (SERCA); and IP₃ receptors (IP₃R). The electrical equivalent diagram of a rectangular region (dashed red line), which incorporates four halves of ECs and four gap junctions is shown (bottom right). Each EC has a total membrane resistance R_m, each EC-EC coupling has resistance R_gj, and there are N_circum such rectangular regions in the circumferential direction. The effective membrane and axial resistivities of the endothelial tube can be derived from N_circum parallel units having membrane resistance of R_m/2 and axial resistance of R_gj over distance L_cell.

Estimation of R_m from the cable input resistance

In an isolated cell, the change in membrane potential (ΔV_m) upon application of a stimulus current (I_stim) is described by Eq. 1:

$$\mathrm{\Delta }{V}_m=R_m{I}_{\mathit{stim}}$$ (1)

where R_m is the membrane resistance of an individual cell. In a population of cells (i.e., endothelial tube), a current I_stim will spread from the stimulated cell through gap junctions to other ECs, and the V_m change in a nearby cell will be:

$$\mathrm{\Delta }{V}_{m,n}=R_{m,n}{I}_{\mathit{stim},n}$$ (2)

where I_stim,n = Σ_GJsI_gj,n is the net stimulus current at nth EC, and it is equal to the sum of all gap junction currents entering/leaving the nth EC (Fig. 1). I_stim,n is equivalent to current loss at nth EC. Summation of Eq. 2 over the total number of ECs (N_cells) over which the I_stim is distributed, gives:

$${\mathrm{\sum }}_{n=1}^{N_{\mathit{cells}}}\mathrm{\Delta }{V}_{m,n}={\mathrm{\sum }}_{n=1}^{N_{\mathit{cells}}}{R}_{m,n}{I}_{\mathit{stim},n}$$ (3)

Assuming linear and identical membrane resistances R_m,n = R_m for all N_cells:

$$N_{\mathit{cells}}{\mathrm{\sum }}_{n=1}^{N_{\mathit{cells}}}\frac{\mathrm{\Delta }{V}_{m,n}}{N_{\mathit{cells}}}=R_m{\mathrm{\sum }}_{n=1}^{N_{\mathit{cells}}}{I}_{\mathit{stim},n}$$ (4)

Thus, in general:

$$N_{\mathit{cells}}\mathrm{\Delta }{\overline{V}}_m=R_m{I}_{\mathit{stim}},\text{and}{R}_m=N_{\mathit{cells}}\frac{\mathrm{\Delta }{\overline{V}}_m}{I_{\mathit{stim}}}$$ (5)

where ΔV̄_m is the mean ΔV_m over N_cells.

Assuming that I_stim is applied at one end of an endothelial tube and V_m decays exponentially along the tube length:¹⁰

$$\mathrm{\Delta }{V}_m=\mathrm{\Delta }{V}_{m,x0}\times e^{\frac{-x}{\lambda }},\mathit{for}0\le x\le L.$$ (6)

where ΔV_m,x0 is the ΔV_m at the local site of current injection (x − x_stim = 0) and λ is the electrical length constant of the endothelial “cable” as determined from the recorded ΔV_m profile. The mean V_m response can be approximated by:

$$\mathrm{\Delta }{\overline{V}}_m=\frac{\mathrm{\Delta }{V}_{m,x0}}{L}{\int }_{x=0}^L{e}^{\frac{-x}{\lambda }}dx=\frac{\mathrm{\Delta }{V}_{m,x0}}{L}\lambda \left(1-e^{\frac{-L}{\lambda }}\right).$$ (7)

Combining Eqs. 5 and 7, yields a first estimation of R_m based on the cable input resistance (R_in = ΔV_m,x0/I_stim) and the length constant of signal’s attenuation (λ):

$$R_m=N_{\mathit{cells}}\frac{\mathrm{\Delta }{V}_{m,x0}}{I_{\mathit{stim}}}\frac{\lambda \left(1-e^{\frac{-L}{\lambda }}\right)}{L}$$ (8)

Continuum cable model

An endothelial tube can be approximated as a continuum two-dimensional sheet of finite width and length with sealed edges.^20,21 The steady-state response (V = ΔV_m(x,y)) to a current stimulus at the point (x_stim, L_circum/2) is given by the Helmholtz equation on a rectangular domain 0 ≤ x ≤ L, 0 ≤ y ≤ L_circum with sealed boundary conditions:

$$\frac{d}{{\rho }_{xx}}\frac{{\partial }^{2}V}{\partial x^2}+\frac{d}{{\rho }_{yy}}\frac{{\partial }^2{V}^2}{\partial y^2}-\frac{1}{{\rho }_m}V(x,y)=-I_{\mathit{stim}}\delta \left(x-x_{\mathit{stim}},y-\frac{L_{\mathit{circum}}}{2}\right),$$ (9)

where δ is the Dirac’s delta function at (x_stim, L_circum/2); L_circum is the tube’s circumference; d is the thickness of the endothelium (Fig. 1); ρ_xx and ρ_yy are the resistivities of the endothelium in the axial and circumferential directions per unit cross sectional area, respectively; and ρ_m is the membrane (leakage) resistivity of the endothelium per unit surface area.

One-dimensional cable solution

In small arterioles (diameter < 50 μm), current spread in the circumferential direction can be neglected assuming cells encircling the vessel are isopotential, and one-dimensional solution of the Helmholtz equation (Eq. 9) yields the short cable equation:²²

$$\mathrm{\Delta }{V}_m(x)=\frac{I_{\mathit{stim}}\lambda r_a}{2}\left(\mathit{exp}(-\mid x_{\mathit{stim}}-x\mid /\lambda )+\mathit{exp}(-(x_{\mathit{stim}}+x)/\lambda )+\frac{\mathit{exp}(-L/\lambda )\left(\mathit{cosh}((x_{\mathit{stim}}+x)/\lambda )+\mathit{cosh}((x_{\mathit{stim}}-x)/\lambda )\right)}{\mathit{sinh}(L/\lambda )}\right),$$ (10)

where ΔV_m(x) is change in membrane potential along endothelial tube of length L, induced by stimulus current I_stim injected at distance x_stim from the tube’s end, and r_a is the resistivity of an endothelial tube in the axial direction.

If L ≫ λ and x_stim λ 0, Eq. 10 simplifies to the exponential solution for a semi-infinite cable:

$$\mathrm{\Delta }{V}_m(x)=I_{\mathit{stim}}\lambda r_a\mathit{exp}(-x/\lambda ),\text{for}x\ge x_{\text{stim}}.$$ (11)

Since the endothelial tubes used in the experiments were of relatively short length compared to the electrical length constant (i.e., L = 2.5 mm vs. λ = 1.38 mm), Eq. 10 was used to determine λ and r_a by fitting ΔV_m data from.¹⁰ Given r_a and λ, the membrane resistivity to charge loss along an endothelial tube (r_m) can then be determined from the relationship:

$$r_m=r_a{\lambda }^2$$ (12)

Figure 1 depicts the idealized arrangement of ECs and gap junctions used to relate the resistivities r_m and r_a to R_m and R_gj, respectively. For this application, R_gj represents the combined resistance of gap junctions and the cytoplasm. The rectangular region on Figure 1 (dashed red lines) incorporates four halves of neighboring ECs with four membrane appositions coupled through gap junctions. Its electrical equivalent diagram (Fig. 1) yields:

$$r_m=\frac{(R_m/2)L_{\mathit{cell}}}{N_{\mathit{circm}}},R_m=2r_m{N}_{\mathit{circum}}/L_{\mathit{cell}},$$ (13)

$$r_a=\frac{R_{gj}}{N_{\mathit{circum}}{L}_{\mathit{cell}}},R_{gj}=r_a{N}_{\mathit{circum}}{L}_{\mathit{cell}},$$ (14)

where L_cell (λ35 μm) is the length of an EC in the axial direction, N_circum = L_circum/d_cell is the number of ECs encompassing the circumference of the endothelial tube (n = 14), and d_cell (λ8.6 μm) is the width of an EC in the circumferential direction (Fig. 1).

Two-dimensional cable solution

The two-dimensional ΔV_m profile in the endothelial tube is the Green’s function of the Helmholtz equation (Eq. 9), which can be written as the double infinite series sum:²³

$$\begin{gathered} G(x,y,{\xi }_{\mathit{stim}},{\eta }_{\mathit{stim}})=\frac{1}{ab}{\mathrm{\sum }}_{n=0}^{\infty }{\mathrm{\sum }}_{m=0}^{\infty }\frac{{\epsilon }_n{\epsilon }_{m}cos(p_{n}x)cos(q_{m}y)cos(p_n{\xi }_{\mathit{stim}})cos(q_m{\eta }_{\mathit{stim}})}{p_n^2+q_m^2+\frac{1}{{\lambda }^2}} \\ {p}_n=\frac{\pi n}{a},q_m=\frac{\pi m}{b},{\epsilon }_n=\{\begin{array}{ll}1\mathit{for}\hfill & n=0,\hfill \\ 2\mathit{for}\hfill & n\ne 0.\hfill \end{array} \end{gathered}$$ (15)

When applied to endothelial tubes, a = L, b = L_circum, ξ_stim = x_stim, d = thickness of the endothelium and η_stim = L_circum/2 (the stimulus position has to be symmetrical in the circumferential direction). Combining Eqs. 9 and 15 gives:

$$\mathrm{\Delta }{V}_x(x,y)=I_{\mathit{stim}}\frac{{\rho }_{xx}}{d}G\left(x,y,x_{\mathit{stim}},\frac{L_{\mathit{circum}}}{2}\right).$$ (16)

Eq. 16 was used to determine ρ_xx/d and λ by fitting conduction data. Given ρ_xx/d and λ, the membrane resistivity per unit surface area, ρ_m, can be determined from the relationship:

$$\frac{{\rho }_m}{\raisebox{1ex}{${\rho }_{xx}$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}=\frac{r_m}{r_a}={\lambda }^2.$$ (17)

based on the assumed shape of EC as a rhombus (Fig. 1), we can determine the membrane resistivities per unit vessel length (r_m) and per cell (R_m):

$$R_m=\frac{2{\rho }_m}{d_{\mathit{cell}}{L}_{\mathit{cell}}},r_m=\frac{{\rho }_m}{d_{\mathit{cell}}{N}_{\mathit{circum}}}$$ (18)

And combining Eqs. 14, 17 and 18 we can determine the axial resistivities per unit vessel length (r_a) and per cell (R_gj):

$$R_{gj}=\frac{{\rho }_{xx}}{d}\frac{L_{\mathit{cell}}}{d_{\mathit{cell}}},r_a=\frac{{\rho }_{xx}}{d}\frac{1}{N_{\mathit{circum}}{d}_{\mathit{cell}}}$$ (19)

Discrete model of the endothelial tube

A multicellular model of an endothelial tube was developed by coupling discrete ECs. To define the number and coupling of ECs in the model, we assume the idealized geometry of endothelial tubes as depicted in Figure 1. ECs are arranged into a cylinder with 14 cells encompassing the circumferential direction (N_circum = 14), and 71 cells encompassing the axial direction with an average cell length of 35 μm (L_EC). This gives a total number of 1988 ECs (N_cells) for an endothelial tube 2.5 mm long. Under control conditions, each EC is coupled electrochemically to its four immediate neighbors making lateral connections (i.e., not through the end-to-end points). The coupling represents nonselective gap junctions and allows intercellular fluxes of K⁺, Na⁺, Cl⁻, Ca²⁺, and inositol (1,4,5)-trisphosphate (IP₃). Respective fluxes are estimated based on the intercellular electrochemical gradients.²⁴ Intercellular fluxes at the ends of the tube are set to zero, i.e., the model has sealed ends similarly to the short cable equations. Each EC is modeled as described in Silva et al..¹⁷ Thus, each EC is isopotential and well-mixed (zero dimensional), i.e., V_m and cytosolic contents are assumed to be uniform withing each EC. A set of 11 ordinary differential equations describe cell membrane electrophysiology along with changes in V_m and intracellular concentrations of Ca²⁺, Na⁺, K⁺, Cl⁻ and IP₃. Stimulation with ACh is simulated by increasing the production rate of IP₃ (Q_IP3) with Q_IP3 increasing by 55 nM/s per arbitrary unit (a.u.) of ACh. A schematic diagram of the single EC with the implemented intracellular and plasma membrane components is shown in Fig. 1. We set the R_m and R_gj as the free parameters to be determined by fitting model output to the experimental data. [Note: R_m was adjusted by scaling all channel conductances in the EC model¹⁷ by the same factor, including the maximum K_Ca conductance G_KCa,max].

Conduction in intact vessels vs. in isolated endothelium

An electrical analogue of the intact vessel^24,25 allows formulation of a simplified analytical formula for extrapolating EC tube data and predicting λ in the intact vessel. The circuitry in a coupled two cell-layer system incorporates the endothelial (r_m,EC) and SMC (r_m,SMC) membrane resistivities, connected through the myoendothelial (ME) resistivity (r_ME, i.e., resistance between endothelial and SMC layers over a unit length and proportional to ME R_gj).

The current that is injected (or generated through channel opening) in an EC will spread (i.e., conduct) primarily along the endothelium. As current spreads it leaks through two parallel pathways; through the EC membrane as determined by r_m,EC or by passing through the myoendothelial gap junctions and then through the SMC membrane. The net resistance for the second pathway is simply the sum r_ME and r_m,SMC (i.e., these resistances are in series). Thus, the combined leak resistivity in the intact vessel (r_m,EC-SMC) can be calculated from the parallel connection of r_m,EC with r_ME and r_m,SMC combined in series:

$$r_{\mathrm{m},\text{EC}-\text{SMC}}=(r_{\mathrm{m},\text{SMC}}+r_{\text{ME}})\times r_{\mathrm{m},\text{EC}}/(r_{\mathrm{m},\text{SMC}}+r_{\text{ME}}+r_{\mathrm{m},\text{EC}}).$$ (20)

Assuming that the whole-vessel axial resistivity is not significantly affected by the presence of SMCs (i.e., r_a,SMC ≫ r_a,EC and r_a,EC-SMC λ r_a,EC), equations 12 and 20 yield:

$${\lambda }_{EC-\mathit{SMC}}/{\lambda }_{EC}=\sqrt{r_{\mathrm{m},\text{EC}-\text{SMC}}/r_{\mathrm{m},\text{EC}}}=\sqrt{(r_{\mathrm{m},\text{SMC}}+r_{\text{ME}})/(r_{\mathrm{m},\text{SMC}}+r_{\text{ME}}+r_{\mathrm{m},\text{EC}})},$$ (21)

where λ_EC-SMC is the length constant in the presence of the SMC layer (i.e., the intact vessel) and λ_EC is the length constant of the isolated endothelium.

Statistics

The parameters estimated from the cable equations are given as best fit values ± 95% confidence interval. Parameters obtained from different experiments and fittings were compared with Student’s t-test. Differences were accepted as statistically significant with P < 0.05.

Results

Data analysis using cable equations

To provide a first estimate of R_m we use Eq. 8, and the reported responses for a typical current injection in an endothelial tube 2.5 mm long (i.e., ΔV_m,x0 λ −11.6 mV, I_stim = −1 nA, λ = 1.38 mm, and L = 2.5 mm).¹⁰ The value of λ has been obtained from the distance over which ΔV_m was attenuated to 1/e = 37% of the signal at its origin, thus assuming the exponential decay in an infinite cable (Table 1).¹⁰ According to Eq. 8, an R_m of 10.6 GΩ is predicted for N_cells = 2000 (Table 1). An R_m of 9 GΩ is predicted if we assume a smaller number of cells (N_cells = 1700) to account for possible overestimation of the number of ECs in the isolated tubes or a scenario in which some ECs lack strong gap junction coupling and do not participate in current dissipation. This predicted value of R_m is four-fold higher than previous estimates based upon cultured human umbilical vein ECs.²⁶

Table 1.

Endothelial tube parameters estimated under different experimental and theoretical schema (best fit ± 95% confidence interval).

Data source	Fitting	λ (mm)	ra (MΩ/mm)	rm (MΩ·mm)	Rm (GΩ)	Rgj (MΩ)
Control experiment	1-dim. inf. cable[1] x−xstim≥50μm	1.38±0.08			10.6
	1-dim. short cable[2] x−xstim≥50μm	1.16±0.12*	10.7±1.9	14.5±1.0†	11.6±0.8‡	5.2±0.9§
	1-dim. short cable[2] x−xstim≥500μm	1.14±0.33	11.3±7.6	14.6±2.5	11.7±2.0	5.5±3.7
	2-dim. short cable x−xstim≥50μm				11.2±1.1	4.5±0.9
	Discrete model[3]				11.9	4.5
Discrete model (Rm = 11.9 GΩ, Rgj = 4.5 MΩ)	1-dim. short cable[4] x−xstim≥50μm	1.17	10.6	14.5	11.6	5.2
	1-dim. short cable[4] x−xstim≥500μm	1.23	9.5	14.2	11.4	4.6
	2-dim. short cable x−xstim≥50μm				11.3	4.4
NS309 experiment	1-dim. inf. cable x−xstim≥50μm	0.85±0.06			4.0[5]
	1-dim. short cable x−xstim≥50μm	0.78±0.05*	8.8±1	5.3±0.3†	4.2±0.2‡	4.3±0.5§
	1-dim. short cable x−xstim≥500μm	0.78±0.12	8.6±3.5	5.3±0.8	4.2±0.6	4.2±1.7
	2-dim. short cable x−xstim≥50μm				4.0±0.3	3.5±0.6
ACh experiment	1-dim. inf. cable x−xstim=500μm	0.61 (55% drop)			2.1[6] (80% drop)

^[1]– Eqs. 6 and 8.

^[2]– Eqs. 10, 12–14.

^[3]– R_m and R_gj in discrete model (Fig. 1).

^[4]– Eqs. 10, 12–14 fitting discrete model.

^[5]– R_m′ = (λ ′/λ)² × R_m = (0.85mm/1.38mm)² × 10.6 GΩ

^[6]– R_m′ = (λ ′/λ)² × R_m = (0.61mm/1.38mm)² × 10.6 GΩ

^*– significantly different (P < 0.003)

^{†, ‡}– significantly different (P < 10⁻⁶)

^§– significantly different (P < 0.038)

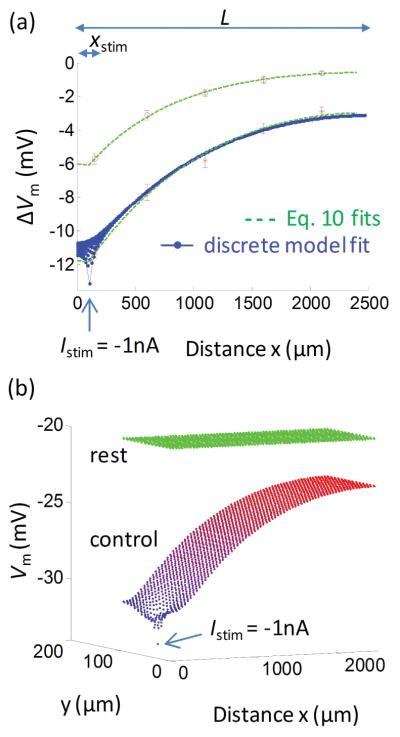
In Figure 2a we fit representative ΔV_m data before (red stars) and following (red circles) NS309-induced opening of SK_Ca/IK_Ca channels using the short cable equation (Eq. 10; dashed green lines). Results are summarized in Table 1. The short cable equation yields λ = 1.16±0.12 mm, r_a = 10.7±1.9 MΩ/mm, and r_m = 14.5±5.5 MΩ·mm for the control data. To convert the r_m and r_a (resistivities) to R_m and R_gj (resistances), we assume the number, arrangement and coupling of ECs are the same as indicated in the discrete model (Fig. 1). According to Eqs. 12–14, R_m = 11.6±0.8 GΩ and R_gj = 5.2±0.9 MΩ.

Figure 2.

(a) Fittings of the cable and discrete models to experimental data. Data were taken from experiments ¹⁰ under control conditions (red stars) and following NS309 induced opening of SK_Ca/IK_Ca (red circles), corresponding to I_stim = −1 nA of current injection. Fitting short cable equation (Eq. 10) to the control and NS309 data yields λ = 1.16±0.12 mm and 0.78±0.05 mm, respectively (dashed green lines). Fitting of the discrete endothelial tube model gives a family of ΔV_m profiles (blue dotted lines). The most negative profile corresponds to the ECs located at the circumferential position that incorporates the stimulus point. Only this profile from the discrete model was used to fit the data. The remaining profiles predict V_m responses at different positions in the circumferential direction; all merge to the same profile within ~400 μm distance from the stimulus. (b) V_m profiles in axial and circumferential directions predicted in the discrete model fitting the control data in (a). Under resting conditions, all 1988 cells have V_m = −20 mV (green dots). Each dot represents V_m in individual EC. Injection of I_stim = −1 nA into a single EC (at site indicated by arrow) creates strong V_m hyperpolarization and gradients in both circumferential (y) and axial (x) dimensions from the local site of intracellular current injection. In these simulations, values for EC membrane resistance and coupling resistance were R_m = 11.9 GΩ and R_gj = 4.5 MΩ. At distances x − x_stim> 400 μm, V_m profile is effectively isopotential in the circumferential direction, and the stimulus current spreads only in the axial direction.

The short cable fitting was repeated using data points at distances greater than or equal to 500 μm away from the injection site (i.e., the first data point at x−x_stim = 50 μm was excluded to avoid the effect of two-dimensional current spread at the site of current injection). Because of the reduced number of data points, the fitted parameters λ and r_a had greater variance; however the resulting values were not significantly different than before exclusion of the 50 μm site (Table 1).

The two-dimensional cable equation (Eq. 16) yields slightly lower (but not statistically different) estimates of R_m = 11.2±1.1 GΩ and R_gj = 4.5±0.9 MΩ, as compared to the results from the one-dimensional short cable equation (Table 1).

Data analysis with discrete-cell model

In Figure 2a, control data were also fitted by the discrete model (blue dotted lines). Each dot represents ΔV_m from the initial resting level of V_m,rest = −20.1 mV, following a −1 nA current injection. Similar results can be obtained with different values for resting EC V_m, which typically range from −20 mV to −40 mV. ΔV_m drops most rapidly close to the injection site where the current spreads with a gradient in two dimensions; i.e., circumferentially and axially (x−x_stim < 100 μm) (see also Fig. 2b). For these simulations, values for the EC membrane and coupling resistances were optimized to fit the experimental control data (Fig. 2a, stars). The resulting values were 11.9 GΩ for R_m and 4.5 MΩ for R_gj. For these simulations, EC R_m was adjusted by scaling all currents and volumes in the EC model with a common factor, so that the relative magnitudes of the currents and intracellular Ca²⁺ concentration ([Ca²⁺]_i) responses remained the same as in the original EC model.¹⁷

In Figure 2b we depict the V_m values in all 1988 cells of the multicellular discrete model as a function of circumferential and axial distance from the site of current injection, from which the ΔV_m profiles in Figure 2a were obtained. The predicted V_m profile shows steep V_m gradients in axial dimension close to the injection site, where the injected current also dissipates in the circumferential direction. The V_m gradient becomes isopotential circumferentially within a few cell lengths (i.e., within 100 μm) and after that point signal attenuation in the axial direction is only due to current loss through the EC membrane. The two-dimensional V_m profile close to the injected cell deviates from the circumferentially isopotential behavior²⁰ described by one-dimensional cable equations (both infinite and short cable equations) and explains the local dispersion shown in Figure 2a near the site of current injection.

Evaluation of cable equations for parameter estimation

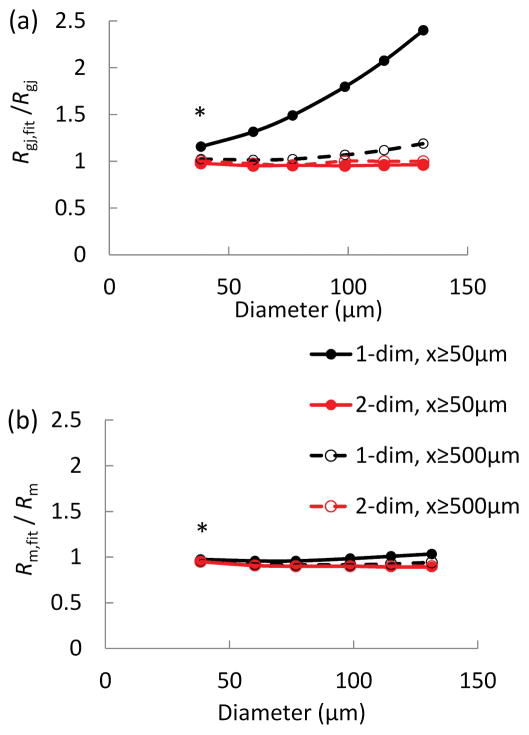
To evaluate the performance of the various fitting scenarios in the extraction of EC R_m and EC-EC R_gj, we used the discrete model with defined R_m (= 11.9 GΩ) and R_gj (= 4.5 MΩ) to simulate conduction data without the confounding effects of experimental errors. Predicted ΔV_m values were taken at distances away from the injection site similar to how the experiments were actually performed (i.e., x−x_stim = 50, 500, 1000, 1500, 2000 μm). We then evaluated the accuracy of the one- and two-dimensional short cable equations in extracting the R_m and R_gj values from these computational data. The one-dimensional short cable equation (Eq. 10) applied for distant points (i.e., x−x_stim ≥ 500 μm, where V_m is circumferentially isopotential) and the two-dimensional cable equation applied for all points (i.e., x−x_stim ≥ 50 μm) yielded estimates of R_m and R_gj with 5% and 2% error, as compared with values used in the discrete model (Table 1). When the one-dimensional short cable equation fitted all points (including the point closest to injection site where V_m is not circumferentially isopotential), R_gj was overestimated by 15% compared to the actual value, i.e., 5.2 MΩ vs. 4.5 MΩ (Table 1).

To investigate the overestimation of R_gj and its dependence on the diameter of an endothelial tube, additional simulations were performed with the discrete model. As tube diameter increases, more current can spread in the circumferential direction. Figure 3 shows the estimation errors of R_gj (a) and R_m (b) as a function of endothelial tube diameter (D) using different fitting approaches. Figure 3a shows that fitting axial ΔV_m data that include the 50 μm point (i.e., x−x_stim ≥ 50 μm) with the one-dimensional equation (Eq. 10) overestimates significantly R_gj for vessels with diameter D > 50 μm (diamond symbols). This is because the two-dimensional current spread around the injection site in larger tubes increases the apparent signal attenuation in the axial direction and overestimates axial resistivity. At the same time, the error for R_m remains relatively small for all fitting scenarios and diameters (Fig. 2b). This is because membrane resistivity depends mostly on input resistance and the total number of cells (compare Eq. 5) and is less sensitive to the curvature of the fitted profile or the arrangement of ECs in the circumferential/longitudinal direction.

Figure 3.

(a–b) Estimations of the error for coupling resistance (a) and membrane resistance (b) as a function of endothelial tube circumference for different fitting schema. The discrete model with known R_m (= 11.9 GΩ) and R_gj (= 4.5 MΩ) (Fig. 1a) and control diameter D_control = 38 μm was expanded in the circumferential direction to simulate hypothetical endothelial tubes with increasing diameters (D). Model predictions of ΔV_m in response to current injection at x_stim were used to simulate V_m measurements along an endothelial tube. The simulated ΔV_m were fitted with one- and two-dimensional cable equations (Eqs. 10 and 16) to estimate R_gj,fit (a) and R_m,fit (b). The fittings were performed with ΔV_m at x−x_stim= 50, 500, 1000, 1500, and 2000 μm (in the axial direction) (diamond and square symbols), and ΔV_m only at x−x_stim≥ 500 μm (triangles and crosses). Fitting the two-dimensional equation recovers correctly R_gj and R_m (R_gj,fit/R_gj λ 1 and R_m,fit/R_m λ 1) for all diameters and data points (a, b squares and crosses). On the other hand, the one-dimensional equation overestimates R_gj (R_gj,fit/R_gj≫ 1) when applied to data with the 50 μm point from vessels > 50 μm in diameter (a, diamond symbols).

Effect of nonuniform EC-EC coupling

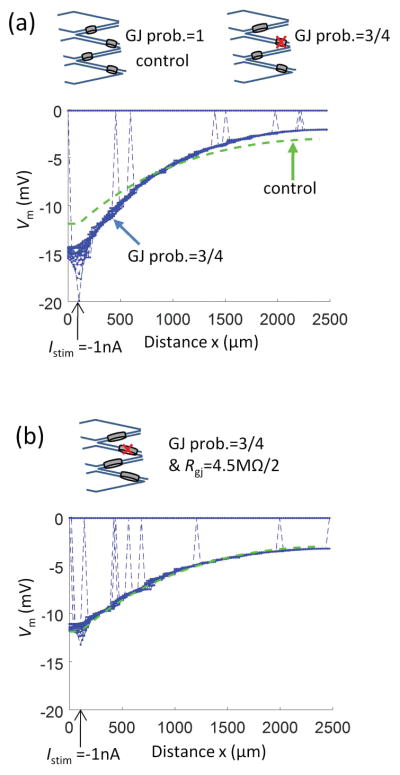
In the control endothelial tube model, each EC connects to each of its four neighboring ECs with the same gap junctional resistance. In vivo, the number of connections and the gap junction density may vary between individual cells or their effective number may be modulated by physiological stimuli (e.g., by phosphorylation or nitrosylation). We tested a hypothetical scenario of nonuniform EC-EC coupling, where the probability of gap junction occurrence (or functional coupling) between two neighboring ECs is reduced below 100% (Fig. 4a, b). Figure 4a shows the consequence of reducing the number of functional couplings between neighboring ECs by 25% (i.e., an EC is coupled, on average, to three of its four neighbors). Each EC-EC coupling has R_gj (= 4.5 MΩ) as in the control model. Using the same hyperpolarizing current I_stim = −1 nA injected to a single EC located at x_stim = 0.1 mm, the reduced gap junctional coupling (crossed ovals) not only decreases the intercellular electrical coupling, it also increases the input resistance (R_in = ΔV_m,x0/I_stim) from the control 13.1 MΩ to 19.4 MΩ (Table 2). This effect results in greater V_m change (hyperpolarization) at the site of stimulation (relative to control; green dotted line) with steeper decay of the signal along the endothelial tube’s length. Figure 4b shows that a two-fold reduction in R_gj is required in order to compensate for the 25% smaller probability of EC-EC contacts. Because of the random determination of EC-EC couplings, a small number of ECs happens to be electrically isolated (as indicated by the broken lines connecting the profiles to the resting ΔV_m at 0 mV). While this is unlikely to occur in normal endothelial tubes, it may happen in disease states, e.g., sepsis.¹²

Figure 4.

Impact of reduced gap junctional coupling on electrical conduction along resistance artery endothelium. (a) Representative simulation where the probability of gap junction connection between the two neighbor ECs is reduced from 100% (the control model) to 75%. (b) The resistance of individual EC-EC connections is reduced by half from the control R_gj of 4.5 MΩ in (a). In both panels the same hyperpolarizing current I_stim = −1 nA was injected into a single EC at x_stim = 100 μm. The one-dimensional short cable (Eq. 10) fit of the control profile from Figure 2a is also shown for reference to control conditions (dashed green line).

Table 2.

Effect of reducing gap junctional coupling on cable parameters of endothelial tubes.

Discrete model		Fitted cable parameters (mean ± SD, n = 3)
Probability of GJ coupling	Rgj (MΩ)	λ (mm)	rm (MΩ·mm)	ra (MΩ/mm)	Rm (GΩ)	Rgj (MΩ)	Rin (MΩ)
1.0 (control)	4.5 (control)	1.23	14.2	9.5	11.4	4.6	13.1
0.90	4.5	1.09 ± 0.01	14.4 ± 0.04	12.1 ± 0.3	11.5 ± 0.03	5.9 ± 0.2	14.7 ± 0.3
0.75	4.5	0.85 ± 0.01	14.7 ± 0.4	20.2 ± 0.9	11.8 ± 0.4	9.9 ± 0.4	19.4 ± 0.6
0.75	4.5/2	1.2 ± 0.05	14.5 ± 0.3	10.1 ± 1	11.6 ± 0.2	4.9 ± 0.5	13.1 ± 0.2

The effect of reducing the probability of EC-EC coupling on the cable properties is presented in Table 2. Reducing the probability to 90% and 75% shortened λ by 11% and 31%, respectively, with respect to the control model. The apparent axial resistivity (r_a) increased by 27% and 112%, respectively, while the effect on the apparent membrane resistivity (r_m) was only 1% and 3%, respectively. [The apparent R_m of an EC and the EC-EC R_gj determined from Eqs. 13 and 14 change proportionally to r_m and r_a, respectively]. The reduction of EC-EC contacts by 25% effectively doubles the apparent r_a. To fully compensate the loss of 25% of connections and reproduce the experimentally observed r_a, EC-EC R_gj has to be approximately half of our estimated value (Table 2). Reducing the number of EC-EC contacts to 50% created small isolated clusters of ECs and inhibited electrical conduction (not shown). If the total gap junction number is preserved but distributed to only 75% of EC-EC contacts, r_a increases by 50% (compare to 112% when 25% of EC-EC contacts were deleted) and λ drops by 20% (compare to 31%), while if the 75% of the control gap junctions are distributed uniformly to all EC-EC contacts r_a increase by 33% and λ drops by 13%.

Effect of ion channel activation in endothelial tubes

In our functional experiments¹⁰, opening SK_Ca/IK_Ca channels directly with NS309 (1 μM) reduced the V_m response recorded at 500 μm (i.e., at a distance corresponding to ~14 ECs placed end-to-end) from the site of current injection by ~40% as compared to control conditions (Fig. 2a, red circles vs. red stars). Fitting the NS309 data with the short cable equation at x−x_stim > 50 μm (Eq. 10) predicts a ~30% reduction in the λ from 1.16±0.12 to 0.78±0.05 mm (or from 1.38±0.08 mm to 0.85±0.06 mm if exponential fit is used), and a ~60% drop in R_m from 11.6±0.8 GΩ under control conditions to 4.2±0.2 GΩ (Table 1). A ~17% drop in R_gj from 5.2±0.9 MΩ to 4.3±0.5 MΩ (P < 0.038) is also predicted (Table 1), although NS309 has not been reported previously to activate gap junctions. The change in R_gj is likely to be an artefact arising from fitting the one-dimensional cable equation too close to the stimulation (Figure 3a). No significant change in R_gj is predicted with the one- and two-dimensional cable equations when fitted at x−x_stim >500 μm and >50 μm, respectively (Table 1).

In complementary experiments, stimulation with a maximal concentration of ACh (3 μM) that evoked hyperpolarization via indirect opening of SK_Ca/IK_Ca channels reduced V_m response at the 500 μm distance by ~70%.¹⁰ Fitting Equation 11 yields a λ of 0.61 mm under global stimulation of all ECs with ACh, i.e., 55% drop compared to the control value of λ (=1.38 mm). The fitting used the control value of r_a since V_m response was measured only at one remote site. This decrement in λ corresponds to 80% reduction in R_m from 10.6 GΩ to ~2.1 GΩ during maximal SK_Ca/IK_Ca channel activation with ACh (Eq. 12–13) (Table 1).

Effect of ion channel activation in EC model

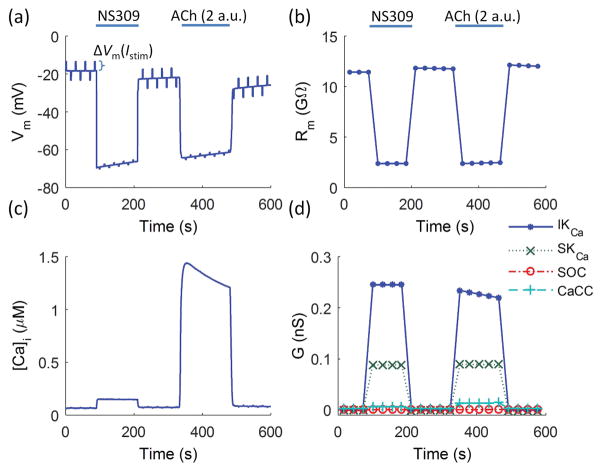
We tested whether the single EC model¹⁷ could predict responses in line to the experimentally observed effect of opening ion channels in the plasma membrane. Figure 5 shows predicted changes in V_m and R_m in response to stimulation with NS309 and ACh. Stimulation with NS309 was simulated by directly setting the whole-cell conductances of SK_Ca and IK_Ca to their maximum values in the model equations [i.e., G_SKCa([Ca²⁺]_i) = G_SKCa,max (= 0.09 nS) and G_IKCa([Ca²⁺]_i) = G_IKCa,max (= 0.25 nS)] (NS309). Stimulation with a maximal concentration of ACh (3 μM) was simulated by 2 a.u. of ACh, which corresponds in the EC model to near maximal Ca²⁺-mediated opening of SK_Ca, IK_Ca, and Ca²⁺-activated chloride (CaCC) channels (Fig. 5a–d). To determine R_m at a given time point, current pulses were applied periodically (2 s/pulse every 30 s) (Fig. 5a) and the resulting change in V_m was normalized by the injected current to give R_m as the ratio of ΔV_m/I_stim (Fig. 5b). Figure 5a shows ΔV_m excursions in response to a current of ±0.4 pA (similar values of R_m were obtained when stronger stimulations were applied). As expected, the model predicts a drop in R_m following channel opening. (Note in Figure 5a the diminished amplitude of ΔV_m excursions in response to constant-amplitude I_stim during hyperpolarization after channel opening.) NS309 and ACh (2 a.u.) reduced R_m by ~80% (from R_m = 11.5 GΩ to R_m = 2.4 GΩ) (Fig. 5b), which would correspond to a theoretical drop in λ by 55% (from 1.38 mm to 0.62 mm) (Eqs. 12 and 13).

Figure 5.

Impact of SK_Ca/IK_Ca activation on endothelial membrane potential and membrane resistance predicted by the isolated EC model.¹⁷ (a) Predicted V_m during direct maximum (100%) opening of SK_Ca/IK_Ca (NS309) followed by application of ACh (2 a.u.). To determine R_m at individual time points, current pulses were applied periodically (±0.4 pA for 2 s every 30 s), whereby the ratio of the resulting ΔV_m to the injected current corresponded to R_m. (b) Predicted changes in R_m (defined as ΔV_m/I_stim) show ~80% drop during direct SK_Ca/IK_Ca opening with NS309 and during indirect SK_Ca/IK_Ca opening with ACh (from R_m = 11.5 GΩ to R_m = 2.4 GΩ). [Ca²⁺] transient and corresponding changes in channel conductance (G) during the stimulations are shown in (c) and (d).

Computational modeling shows that stimulation with NS309 and ACh (2 a.u.) can reduce EC R_m to the maximal levels observed in the experiments (Fig. 5b vs. Table 1, ACh (3 μM)). In contrast to the direct opening of SK_Ca/IK_Ca channels using NS309, the R_m response to ACh stimulus is mediated indirectly by a [Ca²⁺]_i transient (Fig. 5c). Unlike SK_Ca and CaCC channels which remain fully open under these conditions (due to their higher affinity for Ca²⁺ [i.e., K_SKCa = 237 nM²⁷ and K_CaCC = 287 nM²⁸], IK_Ca channels progressively close as the [Ca²⁺]_i decreases (Fig. 5c,d) due to their lower affinity for Ca²⁺ (K_IKCa = 740 nM²⁹). Consequently, R_m increases following the Ca²⁺ transient decay during stimulation with ACh (Fig. 5b). Figure 5d illustrates the whole-cell conductances of designated plasma membrane channels. [The conductances were calculated as the ratio of ΔI_S/ΔV_m, where ΔI_S is the change in the whole-cell current through channels S]. CaCCs and SOCs do not significantly affect the total R_m because of their relatively low whole-cell conductance compared to the conductance of IK_Ca and SK_Ca channels in the model.

Transmembrane current required for EC hyperpolarization

The high EC membrane resistivity (R_m = 12 GΩ) suggests that a relatively small transmembrane current can significantly alter V_m in an isolated EC. Assuming single channel conductance (g_KCa) of 6.8pS and open probability (P_o) of 0.8 for SK_Ca and 17.1pS and 0.7 for IK_Ca,^30,31 and a maximum electrochemical gradient (V_m,rest − E_K) of ~60 mV, an estimate for the effect of single K_Ca channel on V_m can be attained based on the equation:

$$\mid \mathrm{\Delta }{\mathrm{V}}_{\mathrm{m}}\mid =P_o{g}_{\mathit{KCa}}(V_{m,\mathit{rest}}-E_K)R_m$$ (22)

where E_K is the Nernst potential for K⁺.

Eq. 22 predicts up to 4 or 8 mV of hyperpolarization per single SK_Ca or IK_Ca channel activation, respectively. The effect of subsequent K_Ca channel activation will be reduced as result of a decrease in the electrochemical gradient and in R_m. The effect of N_KCa channels can be approximated by

$$\mid \mathrm{\Delta }{\mathrm{V}}_{\mathrm{m}}\mid =\frac{N_{\mathit{KCa}}{P}_o{g}_{\mathit{KCa}}}{\frac{1}{R_m}+N_{\mathit{KCa}}{P}_o{g}_{\mathit{KCa}}}(V_{m,\mathit{rest}}-E_K)$$ (23)

[Note: Eq. 23 is derived from ΔV_m = (V_m − V_m,rest) = −I_NKCa R_m = −N_KCaP_og_KCa (V_m − E_K)R_m ↔ (1 + N_KCaP_og_KCa) (V_m − V_m,rest) = −N_KCaP_og_KCa (V_m,rest − E_K)R_m]

For 5 activated SK_Ca or 5 IK_Ca channels, Eq. 23 predicts approximately 15 and 30 mV of hyperpolarization, respectively.

Transmembrane current required for conducted hyperpolarization

The high sensitivity of V_m to K_Ca channel opening in the isolated EC is not observed during local stimulation of the endothelial layer. This is a result of current loss through gap junctions to neighboring unstimulated ECs and is reflected by the input resistance in the isolated finite endothelial layer of the experiments, R_in= 13 MΩ, which is significantly less than R_m (12 GΩ). R_in suggests that nanoAmperes of transmembrane current is required to evoke mVolts of hyperpolarization at the local site. Such hyperpolarizing currents could be attained through stimulation of several ECs.

In Figure 6 we used the discrete endothelial tube model to examine how many ECs should be stimulated at the local site to invoke local and distal hyperpolarizations similar to those observed in the experiments in response to current injection at one end. The V_m in one row of overlapping ECs (Fig. 1) is depicted as circles prior and as stars following stimulation with Ach. We stimulate a number of ECs columns at one end of the tube with saturating [ACh] (3 a.u.) for 1 minute and the corresponding V_m profiles (stars) are obtained. Identical profiles are assumed along the tube circumference due to symmetry. In experiments, 13 mV of local hyperpolarization was obtained with −1 nA current injection (Fig. 2). Model predicts that in order to produce a similar level of hyperpolarization approximately 56 ECs (2.8% of total ECs) need to be exposed to saturating [ACh]. Furthermore, millivolt-level hyperpolarization is achieved at 2.5mm away from the local site with stimulation of 14 ECs (i.e. one EC column).

Figure 6.

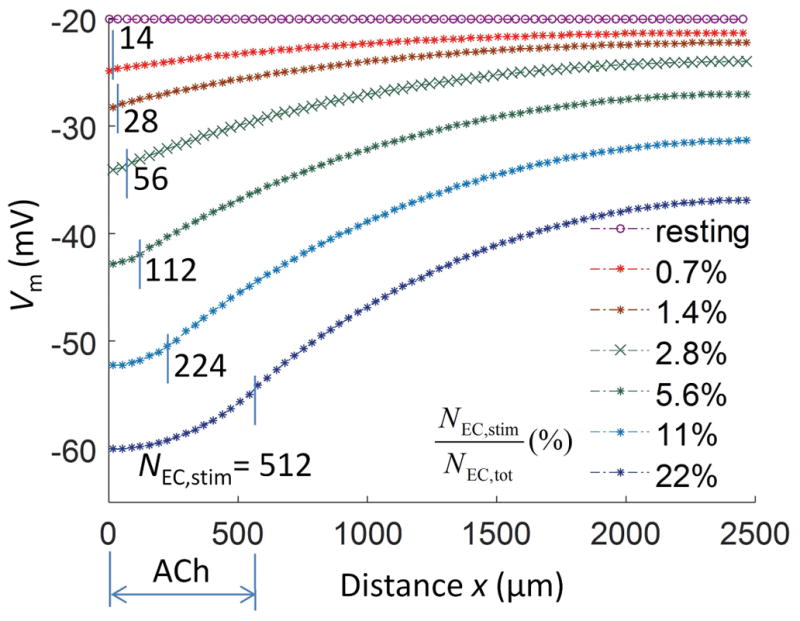
Initiation and conduction of hyperpolarization reflects how many endothelial cells are stimulated. In the discrete multicellular model, profiles of spreading hyperpolarization (V_m) in the axial direction (x) are shown for different number of ECs stimulated (N_EC,stim) with ACh. The total number of ECs N_EC,tot = 1988. In each profile (stars), ECs at the site of stimulation were exposed to saturating [ACh] (3 a.u.). The resting V_m profile is shown for reference (circles). Approximately 56 ECs require stimulation to evoke a conducted response (green crosses) similar to injecting I_stim = −1 nA (compare with Fig. 2a) and millivolt-level hyperpolarization is achieved at 2.5mm away from the local site with stimulation of 14 ECs (i.e. one column). The magnitude of hyperpolarization is a saturating function (Michaelis-Menten type) of N_EC,stim (Eq. 24).

In vivo, the EC layer is significantly larger than the isolated segments of the experiments, is connected to SMCs through myoendothelial gap junctions and current can spread bidirectionally. Thus, the required number of ECs that need to be exposed to Ach locally, in order to generate a physiologically relevant electrical conduction would be higher. The magnitude of local hyperpolarization (ΔV_m,x0) and the total hyperpolarizing current (I_stim,total) depend on the number of stimulated ECs at the local site (N_EC,stim) according to the following equation.

$$\mid \mathrm{\Delta }{V}_{m,x0}\mid \approx (V_{m,\mathit{rest}}-E_K)\frac{N_{EC,\mathit{stim}}{G}_{\mathit{KCa}}{R}_{in}}{1+N_{EC,\mathit{stim}}{G}_{\mathit{KCa}}{R}_{in}},$$ (24)

[Note: Eq. 24 is derived from Delta;V_m,x0 = (V_m,x0 − V_m,rest) = −I_stim,totalR_in = − N_EC,stimG_KCa(V_m,x0 − E_K)R_in ↔ (1 + N_EC,stimG_KCa)(V_m,x0 − V_m,rest) = − N_EC,stimG_KCa(V_m,rest − E_K)R_in]

For an EC layer of infinite length, R_in (R_in = r_m/2λ = 6 MΩ) will be reduced relatively to the isolated EC tube. Furthermore, the total membrane resistivity of the coupled EC-SMC system (r_m,EC-SMC) may be reduced relatively to the isolated endothelium as current may leak through both cell membranes (see Eq. 20). Equations 6 and 24 predict that for λ = 1.2 mm and R_in = 6 MΩ, opening of approximately 4700 SK_Ca (or 2100 IK_Ca channels) is required to generate 1 mV of hyperpolarization at a distal site, 2.5 mm away. This corresponds to K_Ca channels in 32–74 ECs (for maximum whole-cell K_Ca conductance (G_KCa,max = 0.35-0.8 nS)) significantly more than the requirement in the unidirectional spread in finite length of the experiments (Fig. 6).

Conduction in intact vessels vs. in isolated endothelium

The above predictions for conduction through the EC layer may underestimate the hyperpolarizing current requirement for conduction in vivo by not considering current spread to the smooth muscle layer. The effect will depend on the level of myoendothelial coupling and the resistivity of the smooth muscle membrane. Assuming similar current leakiness through the EC and SMC membranes (i.e., r_m,SMC + r_ME = r_m,EC) equations 20 and 21 predict that λ_EC-SMC is reduced to 70% of λ_EC and r_m,EC-SMC to half the r_m,EC. Then R_in,EC-SMC = r_m,EC-SMC/(2λ_EC-SMC) will be approximately 4.3MΩ or 28% less than that in the endothelial layer (and almost 1/3 of the R_in in the 2.5 mm isolated EC tube). The reduction in λ and in R_in,EC-SMC combined, increases the local stimulatory requirement (to achieve 1 mV of hyperpolarization at 2.5 mm away) by three-fold (15000 SKCa or 7000 IK_Ca) corresponding to the recruitment of 100–230 ECs (G_KCa,max = 0.35-0.8 nS).

Discussion

Recent experimental advances have provided the first data defining electrical conduction along the endothelium without the influence of the smooth muscle layer or the confounding effect of cell culture on EC morphology and phenotype.¹⁰ In this theoretical study, we have analyzed experimental data to determine the electrical properties of native intact microvascular endothelium (Table 1). One- and two-dimensional cable equations (Eqs. 10, 11 and 16) were fitted to the experimental data points enabling rigorous estimates of λ, r_a, r_m, R_m, R_gj (Table 1). We show that the estimated values differ depending on the equation used to fit the data and the selection of measurement points used to define the behavior of electrical signals over designated distances. Measurements near the site of stimulation (e.g., using intracellular current injection) should be analyzed with caution to account for the two dimensionality of current spread away from the stimulus site, particularly as vessel diameter increases (Fig. 3a). Independent predictions illustrate that global opening of SK_Ca/IK_Ca along the endothelium, either directly (e.g., with NS309) or indirectly through Ca²⁺ elevation secondary to stimulation with ACh, inhibited electrical conduction in the model of an endothelial tube.

Endothelial R_gj

Our analyses of data from endothelial tubes¹⁰ (Fig. 2a) with a discrete multicellular model (Fig. 2b) suggests an average resistance of EC-EC coupling through gap junctions (R_gj) to be 4.5 MΩ. This value of R_gj is based on the model with four cell boundaries participating in gap junctional coupling per EC. In vivo, the number of connections and their resistance may vary between individual cells and can be reduced in disease states, e.g., sepsis.¹² In particular, if the probability of gap junction connectivity of an EC with each of its four neighbors is reduced to 75%, then the actual resistance of intercellular coupling must be ~half of the original estimate for maintaining electrical signal transmission (Fig. 4b). This situation is different from 75% of gap junction channels being open in each of the four EC-EC contacts. Thus, a 2.25 MΩ (= 4.5/2 MΩ) R_gj is predicted assuming that 75% of cell-to-cell contacts have open gap junctions (Table 2). These estimated values of R_gj (= 2.2 to 4.5 MΩ) agree with a 3.3 MΩ R_gj measured in cultured monolayers of microvascular ECs derived from rat skeletal muscle.¹²

Although r_a is derived from the experimental V_m profiles, our estimation of EC-to-EC coupling resistance depends on the assumed geometry of ECs and the spatial arrangement of individual gap junction channels around cell borders and with neighboring cells. The EC-EC coupling resistance, R_gj, accounts for the combined resistance for current to traverse both the gap junctions and the cytoplasm. The model does not account explicitly for the cytoplasmic resistance because ECs are simplified as zero-dimensional and isopotential. Given the geometry of ECs and a typical cytoplasmic resistivity of ~1.5 Ω·m, the bulk cytoplasmic resistance could be ~1 MΩ, i.e., 20–40% of R_gj. [Theoretical estimations in cardiac myocytes attributed 48% of the total resistivity to cytoplasmic resistance and the remaining 52% to gap junctional resistance.³²] The significant contribution of the gap junction pore to EC-to-EC coupling suggests that axial resistivity will increase as EC length decreases and more membranes have to be traversed per unit vessel length.

Endothelial R_m

Our calculated values for resting R_m are significantly higher (P < 0.01) in freshly isolated endothelial tubes (11.6 ± 0.8 GΩ in 1-dimensional cable fit, Table 1) than previously reported in cultured human umbilical vein endothelial cells (HUVEC) (2.3 ± 1.3 GΩ, N = 26)²⁶ or in nonconfluent macrovascular ECs (1–5 GΩ).³³ This discrepancy can be attributed to differences in EC size and volume (single EC dimensions of ~35 μm × 8.6 μm × 0.5 μm and volume of ~0.1 pL in endothelial tubes approximated here). EC length can span up to 140 μm, depending on species and vessels.^7,25,34–36 For example, ECs were 104±2.5μm and 55±1.7μm long in situ in arterioles of the hamster cheek pouch and feed arteries of its retractor skeletal muscle, respectively. ³⁶ The volume of single ECs can range from 0.4 pL in arterioles⁷ to 3 pL in cultured HUVEC.³⁷ Since the total number of ion channels is likely to be lower in ECs having smaller volume and membrane surface area, the difference in EC dimensions between those in the resistance microvasculature relative to cultured HUVECs may contribute to the 5-fold greater R_m for ECs in microvascular endothelial tubes. In addition, culture can introduce alterations in cell morphology (e.g., “cobblestone” appearance), the ion channel expression profile [e.g. emergence of large-conductance K_Ca channels³⁸] and thereby increase transmembrane ion fluxes while reducing R_m. Similarly, the K_Ca conductance predicted from our experimental data is smaller than previous reports.³⁹

Optimal fitting of conduction data and extraction of parameters

The one-dimensional cable equations assume one-dimensional current transport, an assumption that fails when the current is injected through a single EC and it spreads in both axial and circumferential directions close to the injection site (Fig. 2b). Thus, we tested if incorporation of data close to the site of current injection can significantly skew our estimation of λ, r_a, r_m and derived R_m and R_gj. We found that the short cable equation overestimated R_gj relative to a model that accounts for transport in both circumferential and axial dimensions (Fig. 3a). This estimation error will increase significantly in vessels with larger diameters because of more current spread in the circumferential direction. In our examples, incorporation of a data point at 50 μm away from the site of intracellular current injection introduces significant error for tubes having diameters > 50 μm (Fig. 3a). Thus conduction parameters can be described most accurately with the two-dimensional cable equation, independent of tube diameter or selection of the 50 μm point. However, the two-dimensional function (Eq. 16) predicts incorrectly an infinite V_m response to a finite I_stim at x = x_stim, i.e., ΔV_m(x=x_stim,y =0) → −∞ for I_stim = −1 nA. Since actual ΔV_m at x = x_stim is finite (e.g., ΔV_m,x0 λ −13 mV for I_stim = −1 nA), ΔV_m,x0 (if measured) should never be included for fitting with the two-dimensional equation. A more physiological ΔV_m at the stimulation site can be predicted by replacing the point injection (represented by the δ function in Eq. 9) with current injected over a finite area.²¹ In the case of endothelial tubes when current is injected into a single isopotential EC, the size of the stimulation site should correspond to the area of one EC surface, i.e., L_cell×d_cell/2.

Electrical conduction along arterioles and microvascular endothelium has typically been analyzed with one-dimensional short-cable (Eq. 10) or exponential (Eq. 11) equations.^15,18,20,22 An exponential decay in passive electrical spread is expected in an infinite cable (Eq. 11). However, given the finite length and sealed ends of isolated vessel¹⁶ and endothelial tube segments¹⁰ and the respective λ, an infinite cable approximation may give inaccurate λ, r_a, or r_m. The short cable equation (Eq. 10) accounts for the finite tube length, yielding an estimate of λ that is reduced by ~15% compared to the estimate based upon an exponential fit (Eq. 11) for the data set from Figure 2 (Table 1). For a given r_a, r_m, and I_stim, the ΔV_m response at the end of a short vessel segment (x = 2.5 mm) with sealed ends (short cable equation) is ~4-fold higher compared to the prediction assuming infinite length.

Overall, our analyses suggest that the one- and two-dimensional cable equations can adequately model electrical conduction in endothelial tubes having diameters < 150 μm only at x − x_stim ≥ 500 μm and x − x_stim ≥ 50 μm, respectively. However, there may be a statistical advantage in incorporating all available values when analyzing experiments with a limited number of data points and comparing preparations from different experimental groups such as old vs. young.

Conduction in intact vessels

Approximating equations enable extrapolation of the parameters derived from EC tube data (λ, R_gj, R_m) to estimate the electrical properties of intact vessels and to thereby estimate the physiological relevance of the EC tube data. Our results agree with the general notion that axial transmission of vasodilation is mediate by electrical signaling conducted predominantly through the endothelial layer. Assuming physiological values for myoendothelial coupling and smooth muscle membrane resistivity shows, however, that in these microvessels the presence of the smooth muscle layer could significantly affect ascending vasodilation (i.e. λ reduced by 30%, local stimulatory requirement increases by three-fold for same ΔV_m at 2.5mm). The accuracy of these predictions can increase with tissue-specific measurements of myoendothelial coupling resistance and smooth muscle cell membrane resistivity, and by accounting for the dynamic regulation of membrane resistances and the ability of changes in one cell layer to modulate resistivity and charge loss in the other (i.e. opening of K_Ca channels in ECs to hyperpolarize and close voltage-operated Ca²⁺ channels in SMCs).

The predicted λ for the intact vessel (~1 mm) is less than the values reported for intact vessels in other vascular beds (>1 mm).^15,16 Possible explanations for such discrepancy include: (a) impaired conduction in experiments with isolated endothelial tubes; (b) the presence of a facilitation mechanism in intact vessels that has not been accounted for in the model, e.g., through inward rectifier K_ir channels; (c) overestimation of the current leak through SMCs; and (d) greater EC length in the intact vessel versus in the endothelial tube (as the predicted λ is proportional to the assumed EC length of 35 μm in isolated tubes).¹⁹

Conduction inhibition in endothelial tubes by open K_Ca

The EC model predicts that SK_Ca/IK_Ca channel opening reduces R_m significantly (by up to 80% (Fig. 5b)). Remarkably, this change was accomplished assuming a total maximum K_Ca conductance of 0.35nS which is below what has been previously measured in ECs (0.8 nS³⁹). The multicellular model relates changes in EC R_m to changes in λ and predicts a decrease in λ following global stimulation with ACh or direct opening of SK_Ca/IK_Ca.

The levels of inhibition predicted here corroborate experimental data that show reduction of λ following SK_Ca/IK_Ca channel opening (reduced to 0.8 mm with NS309 and to 0.6 mm during global stimulation with ACh).¹⁰ Note that the actual conduction experiments¹⁰ reflect the use of 1 μM NS309 as a submaximal concentration for opening SK_Ca/IK_Ca; i.e., with less than 100% of these channels open. Thus, both theory and experiments confirm the significant role of endothelial SK_Ca/IK_Ca as modulators of conduction.

Transmembrane current requirement for hyperpolarization and conduction

The high membrane resistivity (R_m = 12 GΩ) estimated from the experimental data suggests that small transmembrane currents can significantly alter V_m. Thus, in an isolated EC, up to 4 and 8 mV of hyperpolarization is predicted per single SK_Ca or IK_Ca channel activation, respectively. The prediction that a few activated K_Ca channels per EC can lead to significant hyperpolarization suggests that the EC layer is sensitive to globally-applied agonists that elevate [Ca²⁺]_i. On the contrary, the small input resistance of the EC layer (R_in = 13 MΩ in the 2.5 mm isolated EC tube; R_in = 6 MΩ in the isolated EC layer of infinite length) suggests that significant current needs to be generated at a site for local hyperpolarization and conduction. We predict that recruitment of several thousand K_Ca channels is required for achieving physiologically relevant hyperpolarization millimeters away for intact vessels of similar size and electrical properties. Given the estimated K_Ca channel density from the analysis of the isolated tube data (G_KCa,max = 0.35 nS) or from reported values in porcine coronary endothelium (G_KCa,max = 0.8 nS), 100–230 ECs in intact vessel (vs. 30–75 ECs in the isolated infinite endothelial layer) need to be activated locally (directly through agonist binding to cell surface receptors or indirectly through intercellular Ca²⁺ spread) for achieving 1 mV of hyperpolarization at a distance of 2.5 mm. Future studies are needed to evaluate whether such a requirement is fulfilled in vivo or if mechanisms exist to enhance ascending vasodilation and minimize local stimulatory requirements.

Conclusions

We analyzed the properties of electrical conduction along native intact microvascular endothelium based upon recent experimental data and detailed computational modeling. This approach allows quantitation of the biophysical factors that govern electrical conduction along resistance microvessels. Since electrical conduction underlies spreading vasomotor/diameter responses in resistance networks, our computational results can facilitate the understanding of blood flow control in the microcirculation and provide mechanistic insight into aberrations in diseased states that can be tested experimentally.

Fitting of the experimental data yielded axial (r_a) and membrane (r_m) resistivities of 10.7 MΩ/mm and 14.5 MΩ·mm, respectively. We predict a membrane resistance (R_m) for the isolated EC of 11.9 (10–14) GΩ, an EC-EC coupling resistance (R_gj) of 4.5 (2.7–5.2) MΩ, an input resistance (R_in) for the isolated 2.5mm EC tube of 13 MΩ, and an ACh-recruited K_Ca conductance of 0.35 nS per EC (corresponding to 15 SK_Ca and 20 IK_Ca). The high R_m makes the microvascular EC membrane sensitive to stimulation (up to 4 or 8 mV of hyperpolarization predicted per single SK_Ca or IK_Ca opening per EC) and allows for efficient conduction. We estimate that local activation of 4700 SK_Ca or 2100 IK_Ca (i.e. recruitment of 30–75 ECs) is required for eliciting 1 mV of hyperpolarization at a distance of 2.5mm through passive electrical conduction along the endothelium. In vivo, local sensitivity to agonists and conduction efficiency may be reduced relative to the isolated EC segment as a result of coupling to SMCs.

The electrical properties characterized here suggest that a significant number of K_Ca channels and thus of ECs need to be recruited locally in order to achieve physiological significant levels of hyperpolarization. The stimulatory requirement may be increased by myoendothelial coupling and relaxed by the presence of mechanisms that facilitate electrical conduction. Contrary to the need for local K_Ca recruitment, open K_Ca channels throughout the vessels inhibit conduction by reducing λ by as much as 55%.

Perspective

Electrical conduction along resistance networks underlies spreading vasodilation but there is much to be learned with respect to the role of membrane ion channels in modulating electrical signal transmission from cell to cell along the vessel wall. To fill this gap, we used recent experimental data, theoretical analysis, and a detailed computational model to link the electrical properties of the endothelium, channel opening, and agonist stimulation to the properties of electrical conduction. The methodology developed here can be applied towards understanding alterations in Ca²⁺ homeostasis, ion channel activity and electrical conduction associated with endothelial dysfunction such as that observed during advanced age and cardiovascular disease.

Although our focus was on electrical conduction along the endothelium of a resistance artery, studies have also presented evidence for signal propagation at the capillary level as well.⁴⁰ Capillaries may sense neural activity in the brain⁴¹ or contraction in skeletal muscle⁴² and transmit signals to upstream feeding arteries to modulate local blood flow. Our theoretical analysis and derived parameters will facilitate future modeling studies that will examine conduction in the integrated vascular network. However, the assumption that passive, bidirectional electrotonic spread underlies signal propagation along the endothelium needs to be evaluated in other vessels, particularly in light of evidence for regenerative signal transmission⁴¹ and preferential upstream propagation of electrical signals.⁴²

Abbreviations

ACh

acetylcholine

a.u.

arbitrary unit

CaCC

Ca²⁺-activated Cl⁻ channels

[Ca²⁺]_i

intracellular Ca²⁺ concentration

d

thickness of the endothelium

D

diameter of an endothelial tube

d_cell

width of an EC in the circumferential direction

dim.

dimensional

EC

endothelial cell

E_K

Nernst potential for K⁺

G

whole-cell conductance

IK_Ca

intermediate-conductance Ca²⁺-activated K⁺ channels

IP₃

inositol (1,4,5)-trisphosphate

IP₃R

IP₃ receptors

I_stim

stimulus current

L_cell

length of an EC in the axial direction

L_circum

circumference of an endothelial tube

ME

myoendothelial

N_circum

number of ECs encompassing the circumference of the endothelial tube

r_a

resistivity of an endothelial tube in the axial direction per unit length

R_gj

resistance of cell-to-cell coupling through gap junctions

R_in

input resistance

r_m

membrane (leakage) resistivity of an endothelial tube per unit length

R_m

cell membrane resistance

SK_Ca

small-conductance Ca²⁺-activated K⁺ channels

SMC

smooth muscle cell

V_m

membrane potential

x

axial distance

x_stim

axial position of stimulus

ΔV_m

change in V_m

ΔV_m,x0

ΔV_m at the stimulus site (i.e., signal origin)

λ

electrical length constant

ρ_xx

effective resistivity of the endothelium in the axial direction per unit cross sectional area

ρ_yy

effective resistivity of the endothelium in the circumferential direction per unit cross sectional area;

ρ_m

effective membrane resistivity (leakage) of the endothelium per unit surface area.