An Integrated Inverse Model-Experimental Approach to Determine Soft Tissue Three-Dimensional Constitutive Properties: Application to Post-Infarcted Myocardium

Abstract

Knowledge of the complete three-dimensional (3D) mechanical behavior of soft tissues is essential in understanding their pathophysiology and in developing novel therapies. Despite significant progress made in experimentation and modeling, a complete approach for the full characterization of the 3D soft tissue behavior remains elusive. A major challenge is the complex architecture of soft tissues, such as myocardium, which endows them with strongly anisotropic and heterogeneous mechanical properties. Available experimental approaches for quantifying the 3D mechanical behavior of myocardium are limited to pre-selected planar biaxial and 3D cuboidal shear tests. These approaches fall short in pursuing a model-driven approach that operates over the full kinematic space. To address these limitations, we took the following approach. First, based on a kinematical analysis and using a given strain energy density function (SEDF), we developed an optimal paths based on the full 3D deformation gradient tensor. We then applied this optimal set to obtain novel experimental data from a 1-cm cube of post-infarcted left ventricular myocardium. Next, we developed an inverse finite element (FE) simulation of the experimental configuration embedded in a parameter optimization scheme for estimation of the SEDF parameters. Notable features of this approach include: (i) enhanced determinability and predictive capability of the estimated parameters following an optimal design of experiments, (ii) accurate simulation of the experimental setup and transmural variation of local fiber directions in the FE environment, and (iii) application of all displacement paths to a single specimen to minimize testing time so that tissue viability could be maintained. Our results indicated that, in contrast to the common approach of conducting pre-selected tests and choosing an SEDF a posteriori, the optimal design of experiments integrated with a chosen SEDF and full 3D kinematics, leads to a more robust characterization and predictive capabilities of the mechanical behavior of myocardium. The methodology proposed and demonstrated herein will ultimately provide a means to reliably predict tissue-level behaviors, thus facilitating organ-level simulations for efficient diagnosis and evaluation of potential treatments. While applied to myocardium, such developments are also applicable to characterization of other types of soft tissues.

1. Introduction

Knowledge of the complete three-dimensional (3D) mechanical behavior of soft tissues is essential in understanding their physiology and in developing novel therapies. The strong local anisotropy and transmural variations in the architecture of soft tissues, such as the myocardium, necessitate a 3D modeling approach to accurately characterize and predict their behavior. Existing in-vitro experimental observations of the mechanical behavior of myocardium (Dokos et al. 2002; Sommer et al. 2015) have demonstrated the intrinsic 3D nature of the mechanical response of myocardium. Developing appropriate 3D constitutive forms that are consistent with the local fibrous architecture of cardiac tissues is a first step in modeling their behavior. However, a remaining challenge is to reliably characterize the constitutive behavior of myocardium in full 3D, which requires the development of fully integrated computational-experimental inverse models that can properly estimate the material parameters of a chosen constitutive model, with minimal dependence on the applied boundary conditions and experimental noise, and evaluate their predictive capability.

In past decades, several constitutive models have been developed for the mechanical behavior of myocardium. Most models consider the myocardium to be anisotropic, which is consistent with its fibrous architecture (Robinson et al. 1983). Phenomenological approaches (Humphrey et al. 1990a; Sacks and Chuong 1993) have assumed that the myocardium to be a transversely isotropic solid consisting of parallel myofibers embedded in an isotropic matrix. More recent constitutive models (Costa et al. 2001; Holzapfel and Ogden 2009; Schmid et al. 2006) are based on a structurally motivated description using a “fiber-sheet-sheet normal” local coordinate system as introduced by LeGrice et al. (1995). This description, supported by histological studies of the microstructure of myocardial tissues (Young et al. 1998), represents myocardium as a composite of layers, or sheets, where each sheet is predominantly occupied with locally parallel myofibers and is interconnected with adjacent sheets via a spatial network of collagen fibers. According to this fiber organization, the myocardium is assumed to be locally orthotropic in the scale of 250–500 μm. Moreover, although myocardium has been considered to be nearly homogeneous across the wall thickness at certain regions of the heart (Dokos et al. 2002; Sommer et al. 2015), for general samples of myocardium, this assumption is too simplistic.

The common approach of most prior studies in constitutive model development for myocardium has been to use existing experimental data and develop a new or identify an existing constitutive form that matches those data in an optimal sense (Holzapfel and Ogden 2009; Humphrey and Yin 1987; Humphrey et al. 1990a; Schmid et al. 2006, among others; Yin et al. 1987). Despite the significant insights provided by these studies, the resulting models may not be able to fully predict the behavior of myocardium under general 3D in-vivo loading conditions. This is a direct result of the models being quantified/designed based only on existing experimental tests that (i) do not necessarily reflect the complete 3D responses of the myocardium, and (ii) are not originally devised to optimally quantify a given model. Indeed, for each specific constitutive model, there exists a need to identify displacement paths from a full kinematic space that are “optimal” for estimating the unknown material parameters, i.e. they minimize the dependence of the estimates to the applied loading paths and to the experimental noise for the given model. Additionally, considering the need to maintain tissue viability, optimal experiments should minimize both the number of cuts made to the tissue to avoid damage, as in 2D biaxial studies (Humphrey et al. 1990a; Sacks and Chuong 1993), and the total number of necessary loading protocols and associated total testing time.

With this perspective in mind, an alternative approach is first to choose an appropriate 3D constitutive model for the soft tissue in question and utilize it to identify what strain paths are “optimal” for estimating the material parameters. While intuitive, this approach has largely been overlooked in the biomechanics literature. Yet, it is critical for characterizing highly anisotropic 3D soft tissues, where the parameter estimation is expected to be quite sensitive to variations in loading conditions and noise in the data. Furthermore, a remaining integral component of the characterization of cardiac and other soft tissues that has not been widely employed is a robust computational-experimental inverse methodology that can accurately estimate mechanical properties by eliminating the errors that occur in linking the experiments to modeling, such as inaccurate reproduction of boundary conditions, ignoring the architecture and heterogeneity of the sample, etc.

The only study known to the authors that investigates the optimal design of experiments in the context of mechanical characterization of soft tissues is the work of Lanir et al. (1996b). Also, motivated by the work of Rivlin and Saunders (1951), other approaches used theoretically derived experiments to determine the constitutive form and parameters. Related approaches by Humphrey et al. (1990a) identified an explicit form of an invariant-based transversely isotropic constitutive relation based on novel 2D biaxial experiments, and demonstrated the predictive capability of the model through capturing 2D equibiaxial data that were not used in the parameter estimation (Humphrey et al. 1990b). However, these studies were limited to planar (2D) analyses, whereas, as mentioned earlier, more recent studies on the microstructure and mechanical response of myocardium (Dokos et al. 2002) have demonstrated that myocardium is locally orthotropic, and thus biaxial tests and transversely isotropic models alone are not sufficient to fully characterize the myocardium behavior (Holzapfel and Ogden 2008). Moreover, transmural variations in myocardial structures preclude tractable applications of constant invariant test needed to determine optimal SEDF forms.

Given the thick walled nature of the heart, it is surprising that only a few experimental works have dealt with 3D mechanical characterization of the myocardium, due to various technical difficulties. Perhaps most notable are the works of Dokos et al. (2002) and Sommer et al. (2015), in which simple shear tests were conducted on cuboidal specimens of myocardium in three different orientations. Several studies have used the experimental data of Dokos et al. to develop new orthotropic constitutive models for the myocardium (Holzapfel and Ogden 2009; Schmid et al. 2006) or estimate the material constants based on the existing models via inverse analytical/computational models (Göktepe et al. 2011; Schmid et al. 2008). In a more recent study, Sommer et al. (2015) conducted similar shear tests on passive human left ventricle myocardium, although they complemented the shear tests with 2D biaxial test of planar cuts of myocardium specimens. In both experimental studies, the three specimens (required to perform all possible shear tests) were cut from adjacent regions of the lateral left ventricular (LV) midwall closer to the base where a significant variation in the fiber orientation is not expected. From an experimental point of view, these studies provided useful insights into the anisotropic nature of myocardium, however, as described earlier, the modeling efforts based on these studies will be still hampered by the limitation in identifying the optimal loading paths for a chosen energy function, the variability in the specimens and the question of the significance of fiber structure in parameter estimation.

Overall, in order to fully characterize the 3D behavior of myocardium and other soft tissues for a given strain energy density function (SEDF), there remains a need for an integrated approach that enables: (i) identification of the optimal loading paths from a general set of full 3D deformation modes including tension, compression, and shear, (ii) acquisition of a 3D dataset derived from the optimal experimental design from a single cuboidal specimen (such geometry provides the convenience and capability to apply an arbitrary deformation and minimize the number of cuts and total testing time to maintain the viability of the tissue), and (iii) comprehensive inverse finite element (FE) simulations to determine the best parameter estimates. Identifying optimal deformation modes is particularly important because myocardial tissues undergo complex combinations of deformation modes, and it is expected that loading paths consisting of both simple shear and other 3D loading conditions are better choices for characterizing the myocardium response, i.e. they lead to estimates with higher predictive capabilities for the behavior of the myocardium under general loading conditions. However, the lack of appropriate instrumentation that can implement these paths has limited the exploration of optimal design of experiments to date. Finally, it is important to note that such integrated approaches lay the groundwork for identifying, evaluating, and improving optimal forms of SEDFs. For example, there remains a need to minimize the covariance between various terms to increase the predictive capability of SEDFs under loading paths that were not used in parameter estimation.

Motivated by such needs, we have developed the following novel integrated simulation-experimental approach to address: (i) the design and execution of an optimal set of experimental loading paths from a wide range of possible 3D deformation modes, (ii) acquisition of internal fiber structure, and (iii) inverse modeling performed on the optimal dataset to obtain best estimation of the parameters of the SEDF selected a priori. To the best of our knowledge, the present paper is the first work that carries out a full 3D study including optimal design, experimental tests, and inverse computational modeling to characterize the mechanical properties of soft tissues.

2. Methods

2.1 General considerations

Two important theoretical topics that arise in determining multi-axial properties of cardiac tissues are the appropriate form of constitutive model and optimal choice of experimental tests to estimate the model parameters. Following such considerations, two essential remaining components of the problem are the development of appropriate experimental methods capable of subjecting a full range of 3D deformation to a single tissue specimen, as well as a computational pipeline for parameter estimation. Thus, a new methodology is required that combines: (i) the choice of constitutive form, (ii) an associated optimal design of experiments approach with optimal choices of kinematic paths, (iii) the collection of experimental data following the determined loading paths, and lastly, (iv) the implementation of a fully integrated numerical inverse modeling approach to provide reliable estimates for the constitutive model parameters (Figure 1). In the following, we delineate the basics of this methodology and introduce the novel instrumentation as an integral part to execute the methodology, with one full trial on infarcted myocardium specimen.

Figure 1.

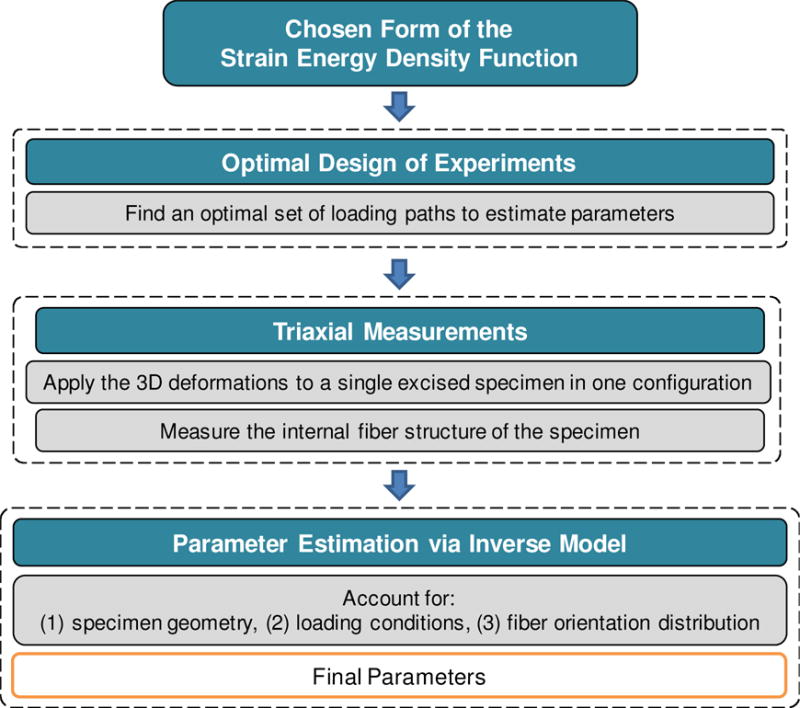
Overview of the integrated computational-experimental inverse model. The model is based on a chosen SEDF and kinematic space that drives the optimal design of experiments, and integrates corresponding experimental data and FE simulations to characterize the constitutive behavior of soft tissues.

We first chose a candidate form of the SEDF based on the locally orthotropic behavior of the myocardium. Although our proposed methodology can be exteneded to address the optimal choice of SEDF, we confined our attention to a single choice of SEDF since our present focus is optimal parameter estimation. We then conducted an optimal design of experiments to find an optimal set of displacement paths, given the chosen SEDF and transmural distribution of fiber orientation within the test specimen. We then developed a triaxial mechanical testing device for applying deformation modes in full 3D on a single cuboidal specimen. We validated the device using cubic samples of synthetic elastomers. Next, we carried out the tests resulting from the optimal experimental design by applying controlled displacements on cuboidal samples of long-term (4 weeks) post-infarcted ovine myocardium. This case study allowed us to focus on passive (non-contracting) mechanical properties without additional considerations of maintaining viable tissue, since infarcted tissues are non-viable, largely collagenous, and non-contractile. Finally, to estimate the material parameters using the acquired experimental data, we developed an inverse algorithm that integrates the experimental measurements and the corresponding results from a sequence of FE simulations into a non-linear regression method.

2.2 3D kinematics

Consider a cubic specimen undergoing deformations as described by the tensor F=Grand x Using the polar decomposition theorem, F can be decomposed into F = RU, where R is a proper orthogonal tensor representing the rotation, and U is the right-stretch tensor. Note that the right Cauchy-Green tensor is defined as C = F^TF and the Green-Lagrange strain tensor by E = (C − I) / 2, where I is the identity tensor. Here, as we are concerned with characterizing the 3D anisotropic elastic properties of soft tissues, we start with the fully populated deformation gradient

$$\mathbf{F}=\left(\begin{array}{ccc}{\mathrm{\lambda }}_1& {\mathrm{\kappa }}_{12}& {\mathrm{\kappa }}_{13}\\ {\mathrm{\kappa }}_{21}& {\mathrm{\lambda }}_2& {\mathrm{\kappa }}_{23}\\ {\mathrm{\kappa }}_{31}& {\mathrm{\kappa }}_{32}& {\mathrm{\lambda }}_3\end{array}\right),$$ (1)

where the Cartesian coordinate system {e₁,e₂,e₃} is used as the fixed laboratory coordinate system. The above deformation state corresponds to a superposition of a stretching state consisting of three stretches λ₁, λ₂ and λ₃ along orthogonal axes e₁,e₂, and e₃, respectively, together with six shearing terms, κ₁₂, κ₂₁, κ₁₃, κ₃₁, κ₂₃, and κ₃₂.

Recent studies on the context of characterizing non-linear elastic materials (Freed and Srinivasa 2015; Srinivasa 2012) have indicated that the decomposition of the deformation gradient F into an orthogonal matrix and an upper triangular matrix (known as the QR decomposition) as an alternative to the traditional polar (RU) decomposition. A counterpart to this decomposition is the decomposition of the deformation gradient F into an orthogonal matrix and lower triangular matrix (denoted by QL decomposition) takes the form of $\mathbf{F}={\mathbf{R}}_{\text{QL}}\stackrel{\sim }{\mathbf{F}}$ where R_QL is a proper orthogonal matrix and $\stackrel{\sim }{\mathbf{F}}$ is given by

$$\stackrel{\sim }{\mathbf{F}}=\left(\begin{array}{ccc}{\stackrel{\sim }{\mathrm{\lambda }}}_1& 0& 0\\ {\stackrel{\sim }{\mathrm{\kappa }}}_{21}& {\stackrel{\sim }{\mathrm{\lambda }}}_2& 0\\ {\stackrel{\sim }{\mathrm{\kappa }}}_{31}& {\stackrel{\sim }{\mathrm{\kappa }}}_{32}& {\stackrel{\sim }{\mathrm{\lambda }}}_3\end{array}\right).$$ (2)

Noting the objectivity of the material behavior from change of the observer (Ogden 1997), it follows that it suffices to consider F of the form (2). In other words, a QL decomposition allows us to work with six kinematical variables instead of nine without loss of generality. In addition, two important advantages of such decomposition over the traditional RU decomposition are: (i) suitability in conducting experiments based on the kinematical variables in Eq. (2) since the off-diagonal components of $\stackrel{\sim }{\mathbf{F}}$ correspond to simple shear modes while those of U correspond to more complex shear deformations, and (ii) the possibility of developing associated constitutive models with minimal covariance. Details of such advantages are presented in Srinivasa (2012) and Freed and Srinivasa (2015). In this work, for ease of notation, we therefore re-label the deformation gradient in Eq. (2) as F (we drop all tilde signs in (2)).

2.3 Constitutive model

Upon ignoring time-dependency effects, myocardium, like many other soft fibrous tissues, can be modeled as a pseudoelastic material (Fung 1993), implying that its mechanical behavior in loading can be described by a stored elastic energy function W(F) =W(E). Assuming the incompressibility, the second Piola-Kirchhoff (PK) stress tensor S can then be described in terms of the strain energy function W for an incompressible hyperelastic material through

$$\mathbf{S}=\frac{1}{2}\left(\frac{\partial \mathrm{W}}{\partial \mathbf{E}}+\frac{\partial \mathrm{W}}{\partial {\mathbf{E}}^{\mathrm{T}}}\right)-\mathrm{p}{\mathbf{C}}^{-1},$$ (3)

where p is an unknown hydrostatic pressure enforcing the incompressibility constraint J = det(F) = 1.

Various mathematical forms of the stored energy function have been proposed for mechanical behavior of normal or diseased myocardium based on structural information and specific test conditions to which they were fitted (see Table 1 in Chabiniok (2016) for a list of the proposed forms). Herein we choose a specific functional form of the strain energy density function W(E) to characterize the local behavior of the myocardium, which is incompressible and orthotropic. A common form to describe such behavior is a Fung-type model (Fung 1993), given by

$$\mathrm{W}(\mathbf{E})=\frac{1}{2}{\mathrm{c}}_0[{\mathrm{e}}^{\text{Q(}\mathbf{E}\text{)}}-1],$$ (4)

where c₀ is a positive constant. Also, Q is a quadratic form in E_ij given by

$$\mathrm{Q}={\mathrm{B}}_{i\text{jkl}}{\mathrm{E}}_{i\mathrm{j}}{\mathrm{E}}_{\text{kl}},$$ (5)

where B is a fully symmetric fourth-order tensor¹ whose components characterize the stiffness of the material in all directions. It is important to note that the above constitutive model characterizes the tissue at the ensemble level, where the local material symmetry can be assumed to be uniform. For the class of orthotropic materials, the principal (preferred) directions of material symmetry are characterized by an orthonormal basis $\left\{{\mathbf{e}}_{\mathrm{i}}^{\ast }\right\}$,(i = 1,2,3), which we refer to as the tissue basis, and in general is not aligned with the laboratory basis {e_i}. The components of tensor B in the coordinate {e_i} are related to those in the coordinate $\left\{{\mathbf{e}}_{\mathrm{i}}^{\ast }\right\}$ through

$${\mathrm{B}}_{i\text{jkl}}={\mathrm{Q}}_{\text{im}}{\mathrm{Q}}_{\text{jn}}{\mathrm{Q}}_{\text{kp}}{\mathrm{Q}}_{\text{lq}}{\mathrm{B}}_{\text{mnpq}}^{\ast },$$ (6)

where the second-order tensor Q (not to be confused with the quadratic form Q) is a proper orthogonal matrix, and ${\mathrm{B}}_{\text{mnpq}}^{\ast }$ denotes the components of the tensor B in ._. For the special case when the basis $\left\{{\mathbf{e}}_{\mathrm{i}}^{\ast }\right\}$ coincides with the basis {e_i} (i.e. when Q = I), the quadratic form Q is expressed as

$$\mathrm{Q}={\mathrm{c}}_1{\mathrm{E}}_{11}^2+{\mathrm{c}}_2{\mathrm{E}}_{22}^2+{\mathrm{c}}_3{\mathrm{E}}_{33}^2+4{\mathrm{c}}_4{\mathrm{E}}_{12}^2+4{\mathrm{c}}_5{\mathrm{E}}_{13}^2+4{\mathrm{c}}_6{\mathrm{E}}_{23}^2+2{\mathrm{c}}_7{\mathrm{E}}_{11}{\mathrm{E}}_{22}+2{\mathrm{c}}_8{\mathrm{E}}_{11}{\mathrm{E}}_{33}+2{\mathrm{c}}_9{\mathrm{E}}_{22}{\mathrm{E}}_{33}$$ (7)

where the components of E are given relative to the basis {e_i} and the dimensionless constants c₁, c₂,… c₉ C₁, C₂,…, C₉, are related to the components ${\mathrm{B}}_{\text{ijkl}}^{\ast }$ as ${\mathrm{c}}_1={\mathrm{B}}_{1111}^{\ast }$, ${\mathrm{c}}_2={\mathrm{B}}_{2222}^{\ast }$, ${\mathrm{c}}_3={\mathrm{B}}_{3333}^{\ast }$, ${\mathrm{c}}_4={\mathrm{B}}_{1212}^{\ast }$, ${\mathrm{c}}_5={\mathrm{B}}_{1313}^{\ast }$, ${\mathrm{c}}_6={\mathrm{B}}_{2323}^{\ast }$, ${\mathrm{c}}_7={\mathrm{B}}_{1122}^{\ast }$, ${\mathrm{c}}_8={\mathrm{B}}_{1133}^{\ast }$, and ${\mathrm{c}}_9={\mathrm{B}}_{2233}^{\ast }$. Also, it is interesting to note that, based on the above-defined quadratic form, the energy function W takes the functional form

$$\text{W(}\mathbf{E}\text{)}=\mathrm{\Psi }{\text{(E}}_{11}^2{\text{,E}}_{22}^2{\text{,E}}_{33}^2{\text{,E}}_{12}^2{\text{,E}}_{13}^2{\text{,E}}_{23}^2\text{),}$$ (8)

which is a special case for the general form Ψ (E₁₁, E₂₂, E₃₃, ${\mathrm{E}}_{12}^2$, ${\mathrm{E}}_{13}^2$, ${\mathrm{E}}_{23}^2$, E₁₂, E₁₃, E₂₃,) given by Adkin and Green (Green and Adkins 1960) for orthotropic materials.

The stress tensor S is obtained from the SEDF in Eq. (4) with Eq. (3) and is expressed as

$$\mathbf{S}={\mathrm{c}}_0(\mathbf{B}E){\mathrm{e}}^{\mathrm{Q}(\mathbf{E})}-\mathrm{p}{\mathbf{C}}^{-1}.$$ (9)

For later use, it is useful to introduce the traction vector on the face of the specimen

$$\mathbf{p}=\mathbf{P}n,$$ (10)

where P = FS is the first PK stress tensor, and n denotes the normal vector in the undeformed configuration. Finally, it is useful to mention that, for convenience in tensorial operations, we make use of the matrix and vector representations and for the symmetric fourth-order and second-order tensors, respectively, introduced by Mehrabadi and Cowin (Mehrabadi and Cowin 1990).

A specialized form of the quadratic form (7) (where the constants c₇,c₈, and c₉ are zero) was introduced by Costa et al. (2001) to model the 3D behavior of myocardium:

$$\mathrm{W}(\mathbf{E})=\frac{1}{2}{\mathrm{c}}_0[{\mathrm{e}}^{{\mathrm{c}}_1{\mathrm{E}}_{11}^2+{\mathrm{c}}_2{\mathrm{E}}_{22}^2+{\mathrm{c}}_3{\mathrm{E}}_{33}^2+4{\mathrm{c}}_7{\mathrm{E}}_{12}^2+4{\mathrm{c}}_8{\mathrm{E}}_{13}^2+4{\mathrm{c}}_9{\mathrm{E}}_{23}^2}-1].$$ (11)

Later on, Schmid et al. (2006) and Schmid et al. (2008) conducted comparative studies between several 3D models for myocardium and examined the goodness of fit, determinability, as well as the stability of the models in parameter estimation under fixed simple shear loading conditions. They found that, overall, the Costa model is most suitable for inverse material parameter estimation for myocardium under simple shear loading. Therefore, we consider the reduced Costa form (11) to be an appropriate choice for this first study. Finally, we note that the incompressibility constraint is a common assumption when modeling the mechanical behavior of myocardium. This is because myocardium, like many soft tissues, contains a high volume of water, so without perfusion it exhibits an approximately incompressible behavior when subjected to mechanical loading (Guccione et al. 1991; Vossoughi et al. 1980). Due to tissue incompressibility, we have restricted our experimental procedure to isochoric deformations only and the incompressibility constraint was locally satisfied in the FE simulations as well.

2.4 Objective function and parameter estimation

Given the constitutive relation (11) for the local behavior of the tissue, our goal is to determine a suitable set of loading paths, perform the experiments, and estimate optimal parameters via a rigorous parameter estimation algorithm. To this end, we measure forces on all faces from both experiments and corresponding computational simulations, and then transfered them into a nonlinear least squares regression procedure to estimate the parameters. The objective function Φ for this procedure can be expressed as

$$\mathrm{\Phi }(\mathbf{\alpha })={\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{P}(\text{Paths})}{\displaystyle \sum _{\mathrm{n}=1}^{\mathrm{F}(\text{Faces})}{\mathbf{W}}_{\text{m,n}}}}{\displaystyle \sum _{\mathrm{q}=1}^{\mathrm{D}(\text{Data})}{\Vert \widehat{\mathbf{p}}-\mathbf{p}(\mathbf{\alpha })\Vert }_{\text{m,n,q}}^2}$$ (12)

where α = {c₀,c₁,c₂,…,c₆ } denotes the set of unknown parameters, ║ ║ denotes the L₂-norm of a vector, and $\widehat{\mathbf{p}}$ and p denote the stress vectors (defined in Eq. (10)) associated with the experiments and computational/analytical modeling, respectively. Also, P is the number of loading paths, F is the number of relevant faces for each loading path, and D is the number of data points collected from each faces. The constants w_m,n are positive weights that may reflect variations in precision among measurements, and also can be used, for example, to normalize all the measured tractions to the same scale or compensate for the variation in the number of data points among the loading paths. The optimal set of parameters α* then can be obtained via the minimization of the objective function (12)

$${\mathbf{\alpha }}^{\ast }:=\arg \underset{\mathbf{\alpha }}{min}\mathrm{\Phi }(\mathbf{\alpha }).$$ (13)

The appropriate selection of these points influences the accuracy of the response surface and, ultimately, the rate of convergence with respect to measured data.

2.5 Optimal Design of Experiments

In the context of 3D tests there is a large range of potential loading paths that can be applied. Thus it is important to obtain an optimal combination of these paths which results in the best determinability of the unknown constitutive parameters. Indeed, by making use of this optimal set of loading conditions, the parameters can be estimated using only the necessary number of modes/protocols, and such estimates are least sensitive to variations in the loading paths and small errors in the experimental data. Following this goal, in this work, we assume that the chosen constitutive model (11) in combination with Eq. (7) is an appropriate representation of the tissue behavior, and we seek to design an optimal set of experiments to estimate the involved parameters (α). For practical purposes, we conduct the optimization over chosen sets of simple displacement paths (Figure 2) although our analysis can be extended to optimize over more general and complex kinematical sets. We chose ten sets of six displacement paths as the kinematic admissible space (Table 1), denoted by d. Set 1 consists of all six simple shear modes (referred to as is all-simple-shear), and the remaining nine sets are basic subsets of the lower-triangular form (2) (Table 1). For convenience in notation, in this table and elsewhere, we use the notations X, Y, and Z to denote the directions aligned with the laboratory coordinate system e₁, e₂, and e₃, respectively.

Figure 2.

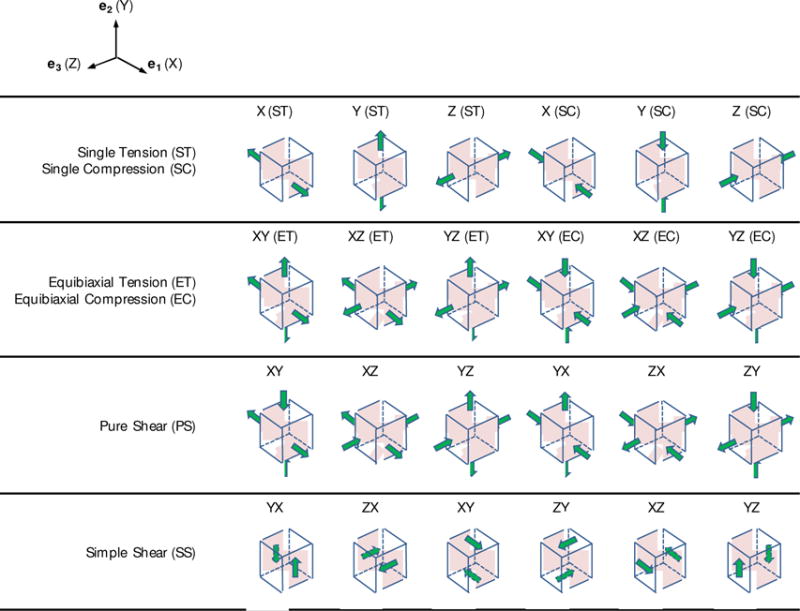
Schematic illustration of basic 3D displacement paths considered.

Table 1.

The chosen sets of displacement paths (Figure 2) considered in the optimal design of experiments. ST (single tension), ET (equibiaxial tension), SC (single compression), EC (equibiaxial compression), SS (simple shear), PS (pure shear).

Set 1	SS: XY, XZ, YZ, YX, ZX, ZY	Set 6	PS: XY, XZ, ST: Y, SS: YX, ZX, ZY
Set 2	ST: X, Y, Z, SS: YX, ZX, ZY	Set 7	ST: X, Y, SC: Z, SS: YX, ZX, ZY
Set 3	ET: XY, XZ, YZ, SS: YX, ZX, ZY	Set 8	ET: XY, XZ, EC: YZ, SS: YX, ZX, ZY
Set 4	SC: X, Y, Z, SS: YX, ZX, ZY	Set 9	ET: XY, XZ, YZ, SC: X, Y, Z
Set 5	PS: XY, XZ, YZ, SS: YX, ZX, ZY	Set 10	PS: XY, XZ, YZ, YX, ZX, ZY

2.5.1 Optimal Design Criteria

A general criterion to determine the optimal design of experiments for a given model is to minimize the covariance between the unknown parameters involved in the model. The information regarding this covariance is included in determination of the confidence region, which is a multi-dimensional neighborhood around the optimum set of parameters, α* (Beck and Arnold 1977). We base our optimal design on information-based criteria, which aim to minimize the certain measures of the confidence region. We assume that the measurement errors (i) are additive, i.e.

$$\mathbf{\epsilon }=\widehat{\mathbf{p}}-\mathbf{p}(\mathbf{\alpha })$$ (14)

(ii) have zero mean, and (iii) are uncorrelated, normally distribution, and have constant variance. Thus,

$$\mathbf{\epsilon }\sim \mathcal{N}(\mu ,{\sigma }^2),{[\mathrm{cov}(\mathbf{\epsilon })]}_{\text{ij}}=0,\text{for}\mathrm{i}\ne \text{j,}$$ (15)

where $\mathcal{N}(\mu ,{\sigma }^2)$ is a normal distribution with the mean μ=0 and variance σ², and cov(·) denotes the variance-covariance matrix of a vector. For ordinary least square problems (i.e. w_m,n = 1) and upon these assumptions, the variance-covariance matrix (Beck and Arnold 1977) is approximately given by

$$\mathrm{cov}({\mathbf{\alpha }}^{\ast })\approx {\mathbf{M}}^{-1}{\mathrm{s}}^2,$$ (16)

where M = J^TJ is usually referred to as the information matrix. It should be noted that the above approximation is exact for the case of linear least-square problems. Here, J is the sensitivity matrix defined as the derivative of the model (here, p(α)) with respect to the parameters, calculated at α = α* (Beck and Arnold 1977). For the case of the objective function Φ (Eq. (12)), the components of the matrix M can be calculated as

$${\mathrm{M}}_{\text{ij}}={{\displaystyle \sum _{\mathrm{m}=1}^{\mathrm{P}}{\displaystyle \sum _{\mathrm{n}=1}^{\mathrm{F}}\left\{\left[\frac{\partial {\mathbf{T}}_{\mathrm{k}}}{\partial {\alpha }_{\mathrm{i}}}({\mathbf{\alpha }}^{\ast })\right]\left[\frac{\partial {\mathbf{T}}_{\mathrm{k}}}{\partial {\alpha }_{\mathrm{j}}}({\mathbf{\alpha }}^{\ast })\right]\right\}}}}_{\text{m,n}},$$ (17)

where the vector T is defined by

$$\mathbf{T}=\left[{({\mathrm{p}}_1)}_1,{({\mathrm{p}}_2)}_1,{({\mathrm{p}}_3)}_1,{({\mathrm{p}}_1)}_2,{({\mathrm{p}}_2)}_2,{({\mathrm{p}}_3)}_2,\dots ,{({\mathrm{p}}_1)}_{\mathrm{D}},{({\mathrm{p}}_2)}_{\mathrm{D}},{({\mathrm{p}}_3)}_{\mathrm{D}}\right].$$ (18)

Also, in relation (16), the parameter S² ≈ ε^Tε / (P×F×D − ρ) is the estimated variance of the observed error where ρ is the number of unknown parameters.

Several optimality criteria have been proposed to minimize the confidence region, which are usually given in terms of maximizing certain measures of the information matrix M. The three most popular criteria are A-, D-, and E-optimality (Pukelsheim 2006), which we use in our study, and they are defined below:

A-optimality

The aim of A-optimality is to minimize the trace of the inverse of M, which equivalently can be written as

$$\underset{\mathbf{d}}{max}{\mathrm{\Delta }}_{\mathrm{A}}=\underset{\mathbf{d}}{max}{\left[\text{trace}({\mathbf{M}}^{-1})\right]}^{-1}.$$ (19)

D-optimality

This optimality is the most popular criterion, which aims to maximize the determinant of the information matrix

$$\underset{\mathbf{d}}{max}{\mathrm{\Delta }}_{\mathrm{D}}=\underset{\mathbf{d}}{max}\det (\mathbf{M}).$$ (20)

The above criterion is equivalent to the D-optimality criterion developed by Nathanson and Saidel (1985) based on the notion of “indifference region” and in terms of the Hessian matrix.

E-optimality

Finally, the aim of E-optimality is to maximize the minimum of the eigenvalues of the information matrix

$$\underset{\mathbf{d}}{max}{\mathrm{\Delta }}_{\mathrm{E}}=\underset{\mathbf{d}}{max}min[\text{eig}(\mathbf{M})].$$ (21)

Another less commonly used, but conceptually similar optimality criterion, is to minimize the correlation between the model parameters. The (approximate) correlation coefficient K_ij, defining the correlation between the parameters α_i and α_j is obtained by scaling the components variance-covariance matrix as follows (Beck and Arnold 1977)

$${\mathrm{K}}_{\text{ij}}\approx \frac{{\left({\mathbf{M}}^{-1}\right)}_{\text{ij}}}{\sqrt{{\left({\mathbf{M}}^{-1}\right)}_{\text{ij}}\sqrt{{\left({\mathbf{M}}^{-1}\right)}_{\text{ij}}}}}(\text{no}\text{summation}\text{over}\mathrm{i}\text{and}\mathrm{j}).$$ (22)

The diagonal components of the matrix K are equal to 1, and the off-diagonal components takes the values between −1 to 1, with 0 denoting no correlation between the associated parameters. The optimality criterion, referred to as M-Optimality in some previous works (Lanir et al. 1996a; Schmid et al. 2006), aims to maximize det(K) toward the value of one (Nathanson and Saidel 1985) and can be defined as

$$\underset{\mathbf{d}}{max}{\mathrm{\Delta }}_{\mathrm{M}}=\underset{\mathbf{d}}{max}\det (\mathbf{K}).$$ (23)

2.5.2 Optimal design case study: post-infarcted myocardium

The optimality framework developed in the previous subsection, as well as the inverse model, which will be discussed later, can be used to characterize the mechanical behavior of soft tissues as long as the assumptions of orthotropic symmetry and incompressibility are considered to be reasonable. However, in this study, we specialize our approach to model the 3D behavior of non-viable, post-infarct myocardium. Note that while post-infarct myocardium is structurally different from normal myocardium, its internal fibrous structure is sufficiently similar to normal myocardium to be used in the present study, as detailed in the following.

Recent histological studies on the microstructure of myocardial tissues indicate that myocardium is composed of layers (or sheets) of tissue separated by “cleavage planes.” Each sheet is predominantly occupied with locally parallel myofibers that run through the plane of the sheet, and are interconnected with a spatial network of connective tissue (Figure 3a). This network, comprised of endomysial, perimysial, and epimysial categories of collagen fibers, supports the myofibers and capillaries to maintain the arrangement and distributes the load across the tissue. Endomysial collagen wraps around the individual myofibers within the lamina, either as a fine weave running around peripheral surface of myofibers or as the transverse links connecting adjacent myofibers (Intrigila et al. 2007; Robinson et al. 1986). Perimysial collagen forms fibers connecting the adjacent laminae as well as runs peripheral around a group of myofibers bundling them together. Epimysial collagen is a sheath of connective tissue that surrounds the entire muscle (Robinson et al. 1983).

Figure 3.

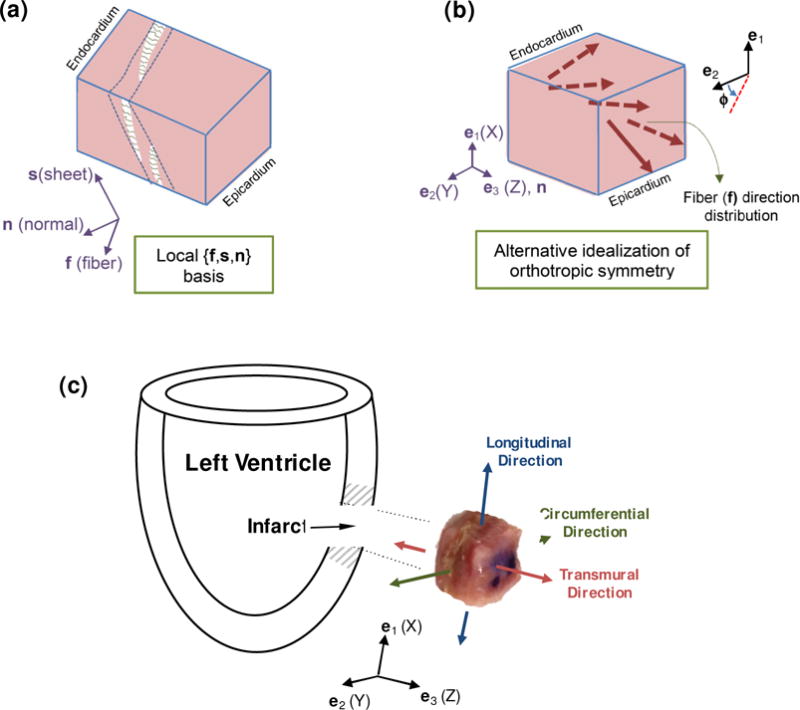
(a) Schematic illustration of fiber variation based on the microstructural basis {f,s,n}. (b) Alternative characterization of the mean fiber orientation from endocardium to epicardium. (c) Schematic of the acquisition location and anatomical orientation of the specimen. The edges of the specimens were aligned with the circumferential, longitudinal, and transmural directions of the left ventricle. Representative infarcted myocardium specimen after sectioning (10×10×10 mm) with anatomical orientations superimposed. Coordinate system shown indicates the coordinate system of the TRIAX.

Based on this description, the microstructure of myocardium can be characterized by an orthonormal set of base vectors in the undeformed configuration consisting of: the unit vector f aligned with the average fiber direction (or fiber axis), the unit vector s, which is in the plane of sheet and orthogonal to the fiber axis, and the unit vector n, which is normal to the plane of sheet (Figure 3a). We have used an alternative, but similar, representation of the local orthotropic symmetry of myocardium that we assume is preserved in long-term post-infarcted tissue. More specifically, we assume the local orthotropic symmetry is uniform at a given wall depth and is characterized by the orthogonal axes: mean fiber direction at the given depth f, normal to the epicardial/endocardial plane (n in the e₃ direction), and normal to the two formers which lies in the epicardial plane. The fiber axis f changes transmurally while the normal direction n is fixed throughout the thickness (Figure 3b). The orthogonal matrix characterizing the orientation of the local orthonormal axes relative to the fixed anatomical basis {e_i} is defined as

$$\mathbf{Q}=\sin [\mathrm{\varphi }(\mathrm{Z})]({\mathbf{e}}_1\otimes {\mathbf{e}}_1+{\mathbf{e}}_2\otimes {\mathbf{e}}_2)+\cos [\mathrm{\varphi }(\mathrm{Z})]({\mathbf{e}}_1\otimes {\mathbf{e}}_2-{\mathbf{e}}_2\otimes {\mathbf{e}}_1),$$ (23)

where the function ϕ(Z) characterizes the variation of the mean fiber direction along the direction Z, and it measures positive anti-clockwise relative to e₂ (Figure 3b). For simplicity, we further assume that the mean fiber orientation f varies linearly throughout the transmural direction from the endocardium to the epicardium as

$$\mathrm{\varphi }(\mathrm{Z})={\mathrm{\varphi }}_{\text{endo}}+\frac{1}{2\mathrm{H}}(2\mathrm{Z}+\mathrm{H})({\mathrm{\varphi }}_{\text{epi}}-{\mathrm{\varphi }}_{\text{endo}}),$$ (24)

where the subscripts “endo” and “epi” refer to the angle measured at the sub-epicardium and sub-endocardium surfaces, respectively. Here, we assume that ϕ_endo = 70° and ϕ_epi =−50° which are consistent with histological data reported in (Young et al. 1998).

Next, the preliminary estimates for the material properties α were taken from the work of Schmid et al. (2006) (Table 2a). Schmidt et al. used the reduced form (11) and developed an analytical model for a cubic sample subjected to shear deformations. Their study was based on the assumption of the homogeneous deformation and uniformity of the preferred directions throughout the sample. They estimated the material parameters c₀,c₁, …,c₆ using experimental data of Dokos et al. (2002), in which cubic specimens (∼3×3×3 mm) were cut from the lateral left ventricular midwall, approximately aligned with the preferred directions (f, n, and s) and subjected to cycles of six simple shear deformations aligned with the preferred directions.

Table 2.

(a) Preliminary estimates for the material parameters in the Fung model for passive myocardium (Schmid et al. 2006). (b) Estimated values of the Fung parameters for postinfarction myocardium sample based on optimal set of displacement paths.

Parameter		c0 (kPa)	c1	c2	c3	c4	c5	c6
(a)	Preliminary estimates for passive myocardium	0.22	42.50	7.80	18.60	5.45	5.50	4.47
(b)	Estimated values for post-infarct myocardium	0.43	3.87	2.01	7.05	2.22	1.33	4.84

2.5.3 Affine-deformation analytical solution

Determination of the optimal set of displacement paths requires solving the boundary value problem and comparing the results based on the proposed optimality criteria (19)–(21). To obtain a tractable analytical solution to determine the best set of displacement paths, we assume that the deformation in the cuboidal specimen is uniform. The solutions based on this assumption are expected to be an upper bound for the exact solution, and thus are expected to qualitatively capture the behavior of the specimen for the range of deformation of interest. In essence, we find this assumption to be sufficient for our purpose in determining the best set of displacement paths. Implementing this assumption, the stress S generated in the cube under the applied strain E is given by

$$\mathbf{S}=\frac{1}{2\mathrm{H}}\left(\frac{\partial }{\partial \mathbf{E}}+\frac{\partial }{\partial {\mathbf{E}}^{\mathrm{T}}}\right)\left({\displaystyle \underset{-\mathrm{H}/2}{\overset{\mathrm{H}/2}{\int }}\mathrm{W}(\mathbf{E},\mathrm{Z})\text{dZ}}\right)-\mathrm{p}{\mathbf{C}}^{-1},$$ (25)

where Z is the direction along which the preferred directions of the material vary, and H is the length of the specimen in this direction. We further note that, in the above expression, W(E,Z) depends on Z through the orthogonal matrix Q.

The higher and lower limits for the principal stretches (the principal values of the stretch tensor E) were set to be λ _max = 1.3 and λ _min = 1/13, respectively, as bounds in the kinematic space d. These values were chosen to cover the range of physiologically realistic strains induced in the myocardium. For instance, according to these limits, the highest tensile stretch in the single and equibiaxial tensile tests were set at 1.3 and $\sqrt{1.3}$, respectively. Also, the limiting values for the tensile and compressive stretches in the pure shear mode were 1.3 and 1/ 1.3, respectively. Furthermore, following the simple shear kinematics (Ogden 1997), the highest shear deformation was set to be κ = 1.3−1/ 1.3 ≈ 0.53. In the calculation of the matrix M = J^T J, the derivatives in relation (17) were performed using central finite differences. We used the trapezoidal technique to carry out the integration in relation (25).

2.5.4 Evaluation of optimal design of experiments

So far, we developed a methodology to find the optimal set of displacement paths that leads to “better” estimation of the parameters, given an appropriately chosen constitutive model with a set of parameters. Next, in order to assess the importance of utilizing an optimal set of displacement paths versus a non-optimal set, we used synthetic data generated with a constitutive model of known parameters. A critical test to evaluate the overall goodness of the estimation procedure was to check how the estimates can predict the behavior of the material cube under loading paths different from those used to estimate the parameters. After conducting the comparisons between the values of optimality criteria (19)–(21), and (23) for all deformation sets given in Table 1, Set 5 (comprising of three pure shear and three simple shear modes) was chosen as the optimal set (see Subsection 3.1). We examined the predictive capability of the parameters obtained from the optimal set by using synthetic test data. More specifically, we compared the predictive capability of parameters estimated using the optimal Set 5 with parameters obtained from using the all-simple-shear Set 1, which will be referred to as the “sub-optimal” Set. In order to further assess our choice, we examined the identifiability of the parameters estimated form the optimal set by introducing noise to the synthetic data and evaluating the variations in the parameters. Similarly, we made comparisons with the case of the sub-optimal set. The procedure of these examinations is described as follows.

Relation (25) with material model (4) and the complete quadratic form (7) was used to generate synthetic data. The values of the constants α = {c₀, c₁,…, c₆} were kept the same as those given in Table 2(a). The additional constants were set to be c₇ = −12, c₈ = −9, c₉ = −6. A linear distribution of fiber orientation (based on Eq. (24)) with ϕ_endo = 70° and ϕ_epi = −50° was assumed. The synthetic data was generated for all the displacement paths in optimal and suboptimal sets (i.e., Sets 5 and 1) (see Table 1 for the paths.) Next, relation (25) with the reduced Fung model (Eq. (11)) (referred to as “affine” myocardium model) was used to fit the synthetic data from each set. To examine the predictive capability of both optimal and sub-optimal sets, the affine myocardium model with the estimated parameters from each set was used to generate stress-stretch data for new displacement paths (not included in optimal and suboptimal sets) and compare against the corresponding synthetic data. Moreover, to examine the identifiability of the parameters when estimated using optimal and sub-optimal sets, random noises with Gaussian distribution $\mathcal{N}(0,{\sigma }^2)$ was added to synthetic data, and the parameters in the affine model were re-estimated. Two levels of noise (σ = 0.05 and σ =0.1) were used, and 100 trials were conducted for each level.

2.6 Triaxial Mechanical Testing Device

2.6.1 Development and Specifications

We developed a novel triaxial mechanical testing device (herein referred to as TRIAX), featuring a novel tissue attachment system that can apply individual or combined deformation modes according to the full 3D formation gradient tensor and measure the resulting 3D forces. The device consists of six attachment systems controlled by linear motion actuators, which impose shear and/or tensile/compressive deformations (Figure 4a). The resulting forces, both parallel and perpendicular to the axes of the device, are detected using IP65/IP68 force-torque load cells, one for each of the three pairs of arms, corresponding to each axis of the specimen.

Figure 4.

Overview of the TRIAX device. (a) A view of the TRIAX device showing the six arms with novel pad attachment systems. (b) Novel pad attachment where the pull-resistant threads (shown slack) are used for flexibility in engaging and disengaging of the cuboidal specimen from the arm. (c) Each pad consists of nine pins glued to the specimen. (d) A view of the full TRIAX system featuring the attachment systems, and fluid bath.

We initially devised an attachment method using a flat, square surface (Figure 5b), which restricted the motion of the entire face and could not be disengaged from the sample between different deformation protocols. We then designed a novel pad attachment system to fulfill the need for applying multiple deformation protocols on different planes of the same specimen. This technique introduces a minimally restricted pad attachment (Figure 4b) that replaces the previously used (full) flat plate attachment. Each pad consists of a 9-pin array glued to the sample using cyanoacrylate-based gel adhesive (Loctite). The pull-resistant threads are used for flexibility in engaging and disengaging different faces of the sample, allowing for selective restriction of the deformation of the specimen face of interest (Figure 4c shows a close-up view of the attachment on a myocardium specimen, where the attachments are engaged on the one axis and disengaged on the other). The size of a specimen was typically 1×1×1 cm and mechanical testing was performed under immersion in a fluid bath at 37° C to reproduce an in-vivo testing environment (Figure 4d). The TRIAX was controlled by a Windows PC running in-house software written using the LabVIEW (National Instruments) programming language.

Figure 5.

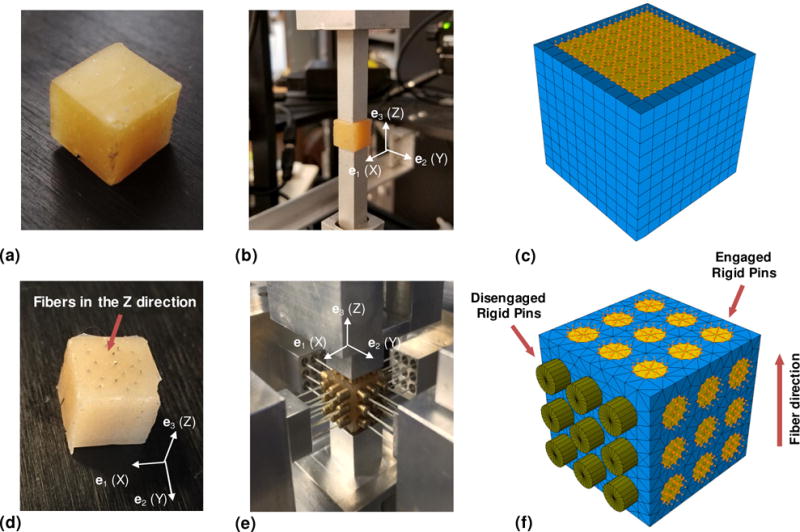
(a) Isotropic elastomer cube. (b) Isotropic sample mounted for testing with flat-plate attachment of initial TRIAX design. The flat-plate restricts motion of the entire adhered surface. (c) Simulated sample (blue) with adhered surface boundary conditions (yellow). (d) Anisotropic elastomer cube, fabricated by reinforcing one material direction (Z) of the isotropic elastomer with thin steel needles. (e) Anisotropic elastomer mounted in TRIAX for 3D deformation testing, using minimally-restricted pad attachment, with lateral axes disengaged and retracted. (f) Simulated sample (blue) with adhered surface boundary conditions (yellow). Disengaged attachments are modeled as rigid disks affixed to the cube that can move freely.

2.6.2 Validation of the simulation-experimental pipeline

The entire analysis pipeline was validated using both isotropic and anisotropic synthetic urethane gel samples of known properties, as follows. The corresponding results are given in Appendix A.

Isotropic elastomer

We first characterized the properties of cubic samples of an isotropic rubber elastomer (Figure 5a). Samples were fabricated from isotropic urethane rubber (VytaFlex® 10, Smooth-On, Inc.) by casting its mixed components into custom 1×1×1-cm cubic molds. All samples were cured for 24 hours at room temperature before testing. We attached the samples on one axis to flat plate attachment systems using cyanoacrylate adhesive (Figure 5b). The samples were subjected to a set of cyclic one-axis tensile and shear deformations that were achieved by fixing the one attachment system in place while translating the other both parallel and perpendicular to the axis of attachment, while continuously measuring the displacement of the linear stages and the force response of the sample using the load cell.

For validation purposes, we assumed that the mechanical behavior of the elastomer can be characterized using an incompressible neo-Hookean model with only one unknown shear modulus parameter, i.e.W(E) = μ₀ tr(E). Using FE inverse modeling, we estimated the shear modulus μ ₀ from a tensile test and used the estimated parameter to compare the fitted model against the experimental data collected in the simple shear test of the same cubic specimen.

Anisotropic elastomer

Anisotropic synthetic rubber samples were fabricated beginning with the same manner as described above. After the rubber cured, 18–20 thin steel needles were carefully inserted into one face of the cubic sample, parallel with the cube edges, in order to reinforce the rubber in one direction and create a transversely isotopic material (Figure 5d). Using cyanoacrylate adhesive, we attached each specimen to the array of pins in the attachment system, which allowed us to selectively engage only the faces on which deformation was directly applied, while only performing the gluing once (Figure 5e). Within the TRIAX, each sample was subjected to an optimized set of testing protocols consisting of cyclic one- and two-axis tensile, compressive, and shear deformations.

The mechanical behavior of the fiber-reinforced elastomer (with fibers being aligned with the e₃ direction) was characterized by an incompressible transversely isotropic Fung-type energy function of the form W(E) = b₀[e^Q(E)−1]/2 with the following reduced expression for Q

$$\mathrm{Q}(\mathbf{E})={\mathrm{b}}_1({\mathrm{E}}_{11}^2+{\mathrm{E}}_{22}^2+2{\mathrm{E}}_{12}^2)+{\mathrm{b}}_2{\mathrm{E}}_{11}{\mathrm{E}}_{22}+{\mathrm{b}}_3({\mathrm{E}}_{11}+{\mathrm{E}}_{22}){\mathrm{E}}_{33}+{\mathrm{b}}_4{\mathrm{E}}_{33}^2+{\mathrm{b}}_5({\mathrm{E}}_{13}^2+{\mathrm{E}}_{23}^2).$$ (26)

From the complete testing dataset, we selected two single tension deformations (in the transverse and axial directions) and two simple shear deformations (transverse and longitudinal) subsets in order to estimate the parameters b₀,b₁,…,b₅ of the transversely isotropic Fung-type model (26). The fitted model was then compared against perpendicular shear and compressive tests, as well as an equibiaxial stretch test, to evaluate the predictive capability of the model and the TRIAX methodology. Pilot simulations suggested that it was sufficient to include only b₁,…,b₅ for parameter estimation and choose b₁ a priori. We performed the simulations for b₁=1.

2.7 Post-infarcted myocardium case study

2.7.1 Mechanical testing

We selected infarcted left ventricle (LV) myocardium tissue as the prototype example of soft tissue to characterize with the TRIAX methodology, in light of the fact that maintaining tissue viability and arresting active contraction would not be a primary concern. We induced ischemic infarction located at the posterior of the LV via ligations along the obtuse marginal artery within a cohort of 3 adult Dorset sheep with weights ranging 40–50 kg. Four weeks after the initial infarction, the animals were euthanized with rapid injection of chilled potassium chloride. The hearts were then exsanguinated and explanted, and the infarct region was determined to be roughly 20% of the total LV surface area. The entire infarct region was cut out (Figure 3c) and immediately placed in chilled cardioplegic solution with ~20 mM 2,3-butanedione monoxime (BDM) to prevent hypercontraction of the tissue due to cutting. From the infarct region, we then used microtome blades to cut out a 10×10×6 mm section that spanned the entire transmural thickness of the heart wall (Figure 3c), and allowed the tissue to relax into an unloaded state before testing in the TRIAX.

Each infarct sample was mounted in the TRIAX to 9-pin attachment systems with cyanoacrylate adhesive, such that the transmural direction of the tissue was aligned with the e₃ direction. We collected a full 3D deformation set for each sample using the optimal set of experiments consisted of three one-axis simple shear and three two-axis pure shear modes (Set 5 in Table 1). All protocols were applied for 5 consecutive cycles, in which the last 3 cycles were recorded after an initial preconditioning stage of 2 cycles. All mechanical testing was performed while the specimen was immersed in the fluid bath containing cardioplegic solution with BDM circulated and heated to 37° C.

2.7.2. Histological measurements

In addition to the mechanical testing dataset, we measured the transmural variation in fiber structure of the infarct tissue in order to obtain the sample’s local material directions for the model and estimation of material parameters. Measurements were performed by cutting thin sections of the sample along the transmural direction and analyzing their collagen structure using small angle light scattering (SALS) (Sacks et al. 1997). Briefly, following removal from the TRIAX, the infarct tissue was fixed in 10% neutral buffered formalin for 24 hours in order to prevent further degradation of the sample between testing and sectioning. The samples were then embedded in optimal cutting temperature (OCT) compound and snap-frozen in liquid nitrogen. 34 sections of 25-μm thickness throughout the endocardial to epicardial surface were placed on glass slides and scanned for SALS. A low-energy laser (633 nm HeNe, 10 mW) was raster scanned in 250-μm increments across each section, and the diffracted laser pattern was analyzed on a charge-coupled device camera in order to develop a local orientation distribution function (ODF) representing the fiber orientation at each node of the scan. From each ODF, quantities such as mean fiber direction and orientation index (a normalized measure of the strength of alignment) were computed. Using custom image registration and 3D reconstruction analysis routines, we aligned the images of each section with each other, and a planar preferred direction was determined from the aligned mean directions of all the locations associated with the tissue.

2.8 Inverse modeling

Noting the complex boundary conditions involved in our experimental characterization of tissues and also the need for incorporating the non-homogeneous structural properties of tissue into the parameter estimation procedure, we developed an inverse computational model by recourse to a FE solver. Specifically, our inverse model consists of a series of forward FE simulations that account for (histologically measured) structural properties of the tissues and generate a multiprotocol stress-strain dataset to be compared to the experimental data. The least square minimization technique was used to estimate the optimal values for the material constants α^∗ = {c₀,c₁,c₂,…,c₆} which minimizes the objective function (12), i.e. the squared norm of differences between the stress vectors measured by the experiments and those calculated via forward FE solutions. In this work, the weights w_m,n in (12) were set equal to one for all the analysis because (i) the data used herein (whether synthetically generated or experimental) included the same number of points for all the involved loading paths, and (b) the level of deformation was adjusted for each loading type to keep the stress values in the same range.

The optimal design of experiments (Subsection 2.5) was based on the choice of the Costa model, the initial material parameters for ovine myocardium (given in Table 2a), and an approximate transmural distribution of fiber orientation. In order to verify the results of this design, we repeated the optimal design with the estimates for infarcted ovine myocardium obtained from inverse modeling together with the corresponding fiber orientation data obtain from the histology.

3. Results

3.1 Optimal set of loading paths

The results of the numerical comparisons between different sets of loading paths (shown in Table 1) are presented in Table 3. Recalling that D-optimality is the most important criterion, the numerical results of Table 3 indicate that Set 5 (highlighted in green) is the most optimal among the ten sets considered here. We also notice from Table 3 that the results from A-optimality and E-optimality criteria are consistent with this conclusion. Set 5 consists of a combination of simple shear modes with and pure shear modes (Table 1). Although the results in Table 3 indicate that the M-optimality criterion was higher for Set 2 (consisting of three single tension and three shear modes), the difference from that of Set 5 was not significant enough to override the D-optimality of Set 5. In this connection, one may use the formula for the efficiency of the optimal criteria (Atwood 1969; Nathanson and Saidel 1985) to weigh the improvement of one criterion over the decline of the other. Based on these considerations, Set 5 was the preferred choice for conducting the experiments. On the other hand, the deformation Sets 9 and 10, which include no simple shear modes (see Table 1), lead to a singular information matrix M, which signals an identifiability problem (Appendix B) for these two specific sets. These two sets are highlighted in red in Table 3.

Table 3.

The calculated values of four design criteria for the ten different sets of displacement paths shown in Figure 2 using the preliminary material constants in Table 2a.

	ΔA (100)	ΔD (1017)	ΔE (100)	ΔM (10−5)
Set 1	0.38	8.6E-6	0.48	0.13
Set 2	2.22	5.4E-2	3.34	3.17
Set 3	0.49	1.6E-6	0.80	0.15
Set 4	0.50	1.1E-6	0.90	0.11
Set 5	2.48	2.69	3.34	0.40
Set 6	2.38	1.49	3.34	0.24
Set 7	1.43	2.3E-3	3.31	0.43
Set 8	0.93	2.3E-3	1.73	0.45
Set 9	0.0	0.0	0.0	Undefined
Set 10	0.0	0.0	0.0	Undefined

The outcome of the optimal design for the myocardium case study was examined using synthetic data from a fictitious material cube (as described in Subsection 2.5.4). The affine myocardium model (25) fit the synthetic data for Sets 1 and 5 (referred to as optimal and suboptimal sets) equally well (r² ≈ 1 for both sets). The estimated parameters from each set were then used to predict the behavior of the fictitious cube under two biaxial tension loading paths, namely (F₁₁ −1) / (F₂₂ −1) = 2 (Figure 6a) and (F₁₁ −1) / (F₂₂ −1) = 0.5 (Figure 6a). These paths were chosen as they may represent typical loading conditions on myocardium in passive inflation during diastole. For these examples, the parameters estimated using the optimal set offered a significantly better predictive capability (Figure 6b,d). This was also mainly the case for other loading paths that produce larger deformation along the fibers. The parameters estimated using the optimal set exhibited markedly less sensitivity to the presence of noise in the synthetic data compared to those estimated using the suboptimal set (Figure 7).

Figure 6.

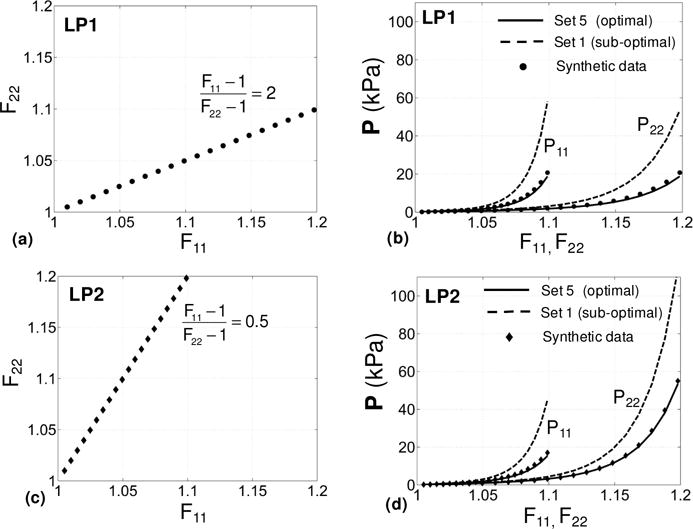
Comparisons between the predictive capability of the parameters estimated using the optimal Set 5 and that of those estimated using Set 1 (all-simple-shear) for two different loading paths. (a,c) Two biaxial extension loading paths (LP1 and LP2) used to evaluate the predictive capability. (b) Results for LP1. (d) Results for LP2. Results for the stress components P₁₁ and P₂₂ are given as functions of F₁₁ and F₂₂, respectively.

Figure 7.

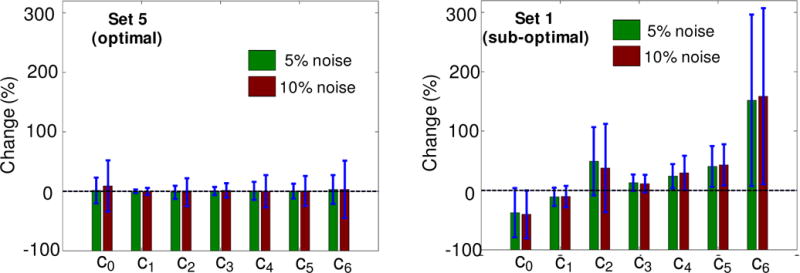
Comparisons between the effect of noise on parameter estimation for optimal and sub-optimal loading sets. (a) Optimal Set 5. (b) Sub-optimal loading Set 1 (all-simple-shear). The dashed line correspond to original estimates without any noise for each set. Results show that the optimal set is significantly less sensitive to noise than the sub-optimal set.

3.2 Post-infarcted myocardium

3.2.1 Mechanical response and optimal parameters

We were able to perform the mechanical loading and unloading of the post-infracted myocardium specimens up to very large ranges of deformation. The specimens consistently exhibited non-linear behavior with typical hysteresis of soft tissues under both simple shear and pure shear loading paths (Figure 8). Then, for parameter estimation, we confined our attention to loading paths and a physiologically relevant range of deformation.

Figure 8.

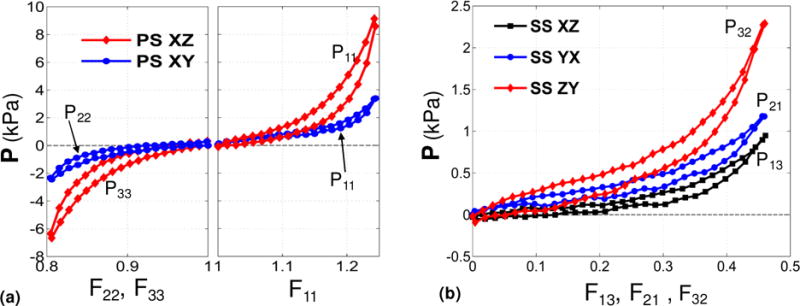
Representative stress-stretch measurements from mechanical testing of post-infarcted specimen. (a) Pure shear loading paths XZ and XY. (b) Simple shear loading paths XZ, YX, and ZY.

Five displacement paths consisting of three pure shear deformation modes and two simple shear modes were sufficient to estimate the unknown parameters {c₀, c₁,…, c₆} in the Fung model (Table 2b). A good fit was observed for all protocols with r² ≈ 0.93 (Figure 9). To our best of our knowledge, these experimental data are the first 3D mechanical testing data that characterizes shear, tension, and compression properties of a soft tissue. All displacement paths involved large deformations under which the tissue exhibited non-linear behavior. For simple shear modes (Figure 9-d,e), the stress-stretch curves exhibited a “J-shape” characteristic which corresponds to exponential stiffening of the soft tissue and is typical under simple shear modes (Dokos et al. 2002). However, for pure shear modes (Figure 9a,b,c), the stress-stretch curves showed a “S-shape” characteristic corresponding to a “stiffening-softening-stiffening” behavior of the soft tissue under these modes.

Figure 9.

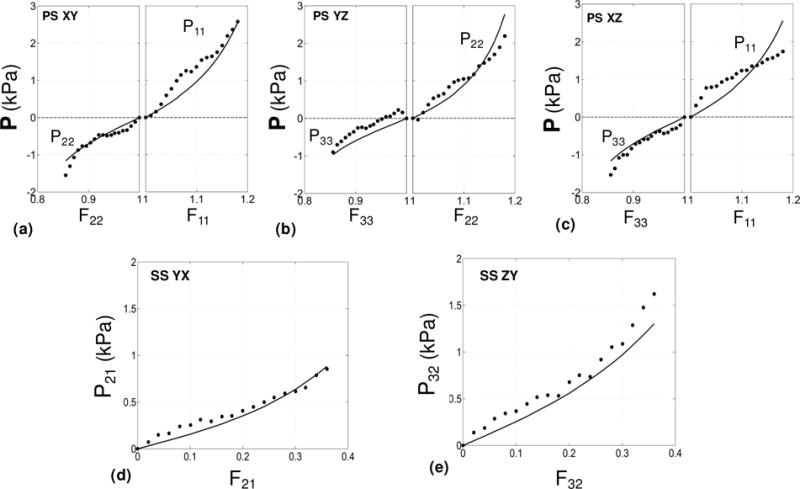
The fit of the Fung constitutive model to the measured mechanical response of the infarcted myocardial cube. Results are given for the relevant components of the P stress as functions of the associated deformation. (a) Pure shear (XY). (b) Pure shear (YZ). (c) Pure shear (XZ). (d) Simple shear (YX). (e) Simple shear (ZY).

3.2.2 Histological measurements

The mean fiber orientation (ϕ) exhibited significant variation from the endocardial to epicardial surfaces of the infarcted specimen (Figure 10), obtained from the histological measurements of unstained cryosections. This observation was consistent with the changes in fiber orientation established in previous work (Scollan et al. 1998; Young et al. 1998) and myocardial scar tissue (Costa et al. 2001; Young et al. 1998). Using SALS, we determined the mean fiber orientation angle, i.e. the angle with respect to the circumferential direction of the ventricle (Figure 3), to change from +63° to −29° from the endocardial to epicardial sides of the sample (Figure 10b), which is comparable to the change in mean fiber angle observed in literature. The substantial change in fiber orientation within the tissue sample confirmed the need to experimentally quantify and include varying material directions within the FE simulations.

Figure 10.

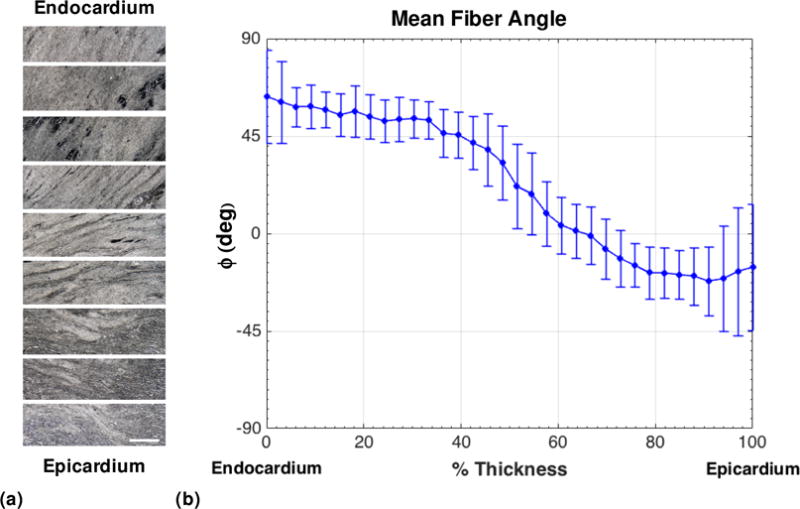
(a) Representative light microscopy views of unstained sections from endocardial to epicardial surfaces of the infarct specimen. Scale bar=100 μm. The horizontal direction corresponds to the circumferential direction. (b) Mean orientation angle of collagen fibers in each section of the infarcted specimen from endocardial to epicardial surfaces, analyzed using small angle light scattering. ϕ =0° corresponds to the circumferential direction.

3.2.3 Verification of optimal design results

We repeated the optimal design (described in Subsection 2.4) using the new estimates for parameters {c₀, c₁,…, c₆} from the infarcted ovine heart along with corresponding histological measurements (Figure 10). The results of the numerical comparisons between different sets of loading conditions (shown in Table 1) are presented in Table 4. The numerical values of A- and D-optimality criteria indicate that deformation Set 5 (highlighted in green) is still the most optimal among the eight sets considered here (Table 4). The values for E- and M-optimality are also very close to the highest values for these criteria, which make Set 5 the overall optimal choice for the displacement paths.

Table 4.

The calculated values of four design criteria for the first eight sets of displacement paths shown in Figure 2 using the estimated material constants of the infarct myocardium in Table 2b and the fiber orientation distribution shown in Figure 11.

	ΔA (10−3)	ΔD (10−4)	ΔE (10−3)	ΔM (10−5)
Set 1	3.1	0.21	5.1	14.1
Set 2	3.3	0.56	5.0	10.4
Set 3	1.4	9.3E-3	2.2	15.0
Set 4	2.2	4.2E-2	3.1	12.2
Set 5	3.9	2.07	6.7	6.3
Set 6	3.2	0.73	5.2	5.0
Set 7	1.3	2.6E-2	1.8	1.8
Set 8	3.7	0.65	7.7	4.7

3.3 Finite element simulations

Representative results of FE simulations for the selected components of the Cauchy stress tensor σ are illustrated in Figure 11. (σ is related to the first PK stress tensor through σ = FP^T.) The resulting asymmetry in the stress distribution is consistent with the actual fiber distribution (Figure 10) incorporated into the FE model. Although the stress concentration around the pins is evident, the stress distributions are fairly uniform in the central region of the cube. This may suggest that the results of the theoretical optimal design (which is based on the assumption of homogenous deformations) would still be guiding valid for the case of the 9-pin attachment. It is further interesting to observe that the lateral face in the pure shear deformation is fairly undeformed, at least in the central region (Figure 11), complying with the material incompressibility.

Figure 11.

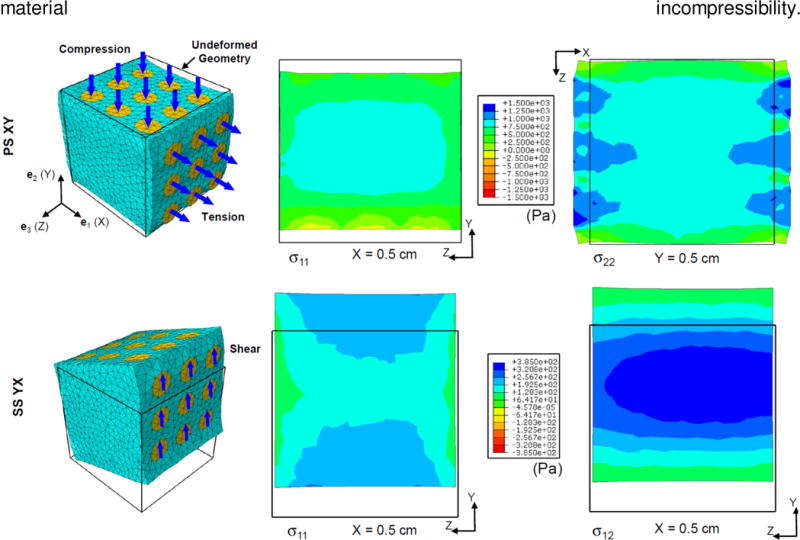
Representative FE simulation results. (a) Pure shear (XY). Normal components of the Cauchy stress s are shown at two midplane cross sections. (b) Simple shear (YX). Normal and shear components of s are shown at the midplane X=0.5 cm.

4. Discussion

The goal of the present study was to develop a novel integrated computational-experimental approach to drive optimal design of experiments for quantifying the full 3D mechanical behavior of cardiac tissues. The key results of our study demonstrated that the efficient and definitive characterization of this behavior demands conducting optimal design of experiments and using an integrated inverse model. Discussion of specific results is given in the following.

4.1 Optimal design of experiments

An important finding from our optimal design analysis was that the optimal set of 3D displacement paths consists of both simple shear modes and pure shear modes that involve tensile and compressive stretches. Our analysis suggested that this optimal set reflects a considerably better “determinability” for estimating 3D properties than the all-simple-shear deformation set. That is, material parameters estimated through the optimal set would be less sensitive to the type of boundary conditions used for their estimation and to small errors in the experimental data. In contrast, the deformation sets which included no simple shear modes (see Table 1) were found to lead to an identifiability problem (Table 3).

It is further interesting to point out that the influence of pure shear modes in optimality of Set 5 can be seen to be consistent with the results of Lanir et al. (Lanir et al. 1996b) for optimal design of two-dimensional tests. In that work, using a similar D-optimality criterion based on the determinant of the Hessian matrix, the authors concluded that the optimal biaxial test corresponded to stretching the sample in one direction and constraining it in the other (orthogonal) in-plane direction. These boundary conditions correspond to the pure shear deformation in the context of incompressible materials.

Finally, it is worth mentioning the contrast between our optimal set of loading paths and combined 2D–3D experiments consisting of 3D simple shear tests on a full-thickness cubic specimen and 2D standard biaxial tests on a 2D cut of the specimen (Sommer et al. 2015). Although the combined tests are more informative than 3D simple shear tests alone, such tests do not necessarily represent an optimal choice of experiments drawn from searching the full kinematic space, and the models quantified based on these experiments may not be able to sufficiently predict the behavior of myocardium under other loading path, particularly biaxial modes of deformation on a 3D cube. In contrast, choosing an appropriate constitutive model first, and conducting the optimal experiments determined from probing the full kinematic space will enhance the predictive capability of the model. Overall, although such comparison needs further investigation, the approach of applying all loading paths in a 3D setting on a single cubic specimen seems to be a more convenient choice.

4.2 TRIAX device and analysis pipeline validation

To the best of our knowledge of the biomechanics literature, this is the first time a full 3D mechanical testing device was developed to apply arbitrary 3D deformations involving both shear and tension/compression to all six faces of a cuboidal specimen. Related devices to date have been limited in their applicability. For instance, a triaxial device developed to test lung parenchyma (Hoppin et al. 1975) was limited to apply only tensile forces, and the triaxial device of Dokos et al. (2000) was limited to apply shear (and possibly tension/compression) at two faces of a cube at a time.

We also used soft isotropic and anisotropic synthetic materials to demonstrate the reliability and reproducibility of the TRIAX device in measuring the mechanical behavior of anisotropic soft tissues, as well as the effectiveness of our inverse modeling approach to characterize the mechanical properties of such materials. The mechanical testing of soft synthetic materials was successfully conducted for a moderate range of deformations within which the measured stress-stretch curves exhibited nearly linear behavior (Figures 12 and 13 in Appendix A). This was sufficient for our purpose to evaluate the ability of the TRIAX device to provide consistent measurements among different mechanical tests of anisotropic materials. It is important to note that the neo-Hookean model and the material model (26) may not be the best descriptors to completely and accurately characterize the behavior of the synthetic materials under arbitrary deformation, as our purpose here was not to accurately characterize the mechanical behavior of these materials, but to examine the effectiveness of the TRIAX device to produce consistent results for tissue-like materials under different displacement paths. From our results, it was clear that the device was able to accurately measure the shear characteristics of small tissue-like samples within the physiological ranges of strain.

4.3 Insights from the overall fit

As expected, the stress-stretch behavior of myocardium was non-linear under all displacement paths, however, it exhibited different characteristics for simple shear and pure shear modes. The typical “exponential” stiffening was observed for simple shear, while a softening-stiffening characteristic was observed for pure shear modes. Noting the Fung model(4) used in our inverse model is best suitable to capture mainly exponential stiffening characteristics in soft tissue, the presence of both characteristics posed a major difficulty in accurately capturing the mechanical behavior of the infarcted specimen for all modes. This comprehensive set of experiments demands new forms of constitutive models for soft tissues that are able to produce different characteristics of soft tissues and not only pure stiffening. This matter concerns both finding a complete and suitable set of kinematical variables that are minimally covariant and positing versatile forms of constitutive models in terms of these variables.

As mentioned above, our FE model was equipped with actual fiber orientation distribution measured from histology of the same specimen. In our pilot calculation, we investigated the effect of this distribution on the overall fit and found that the estimated parameters are generally sensitive to the prescribed distribution of the fiber orientation. Also, the idealizing assumption of planar orientation of fibers in this work was sufficient to capture the collective behavior of the specimen for all modes, however, in reality, the fibers may have slight to moderate “out-of-plane” orientation. In particular, the experiments (b), (c) and (e) (see Figure 9), that involve out-of-plane measurement of forces, led to comparably poorer fit in general. This is likely due to the fact that the out-of-plane orientation of fibers was neglected in our inverse model.

4.4 Properties of infarcted myocardium

To our best knowledge, this is the first time the 3D mechanical properties of long-term infarcted ovine myocardium have been reported. The few studies which have reported 2D biaxial mechanical properties of infarcted ovine myocardium (Gupta et al. 1994; Morita et al. 2011). Here, we made comparisons with the 2D biaxial properties of infarcted ovine myocardium from the work of Gupta et al. (1994) with the corresponding properties from our estimated Fung model. To obtain stress estimates for 2D tensile biaxial deformations from our model in (4), we calculated stress under plane-stress condition with all shear strain to be equal to zero. For an equibiaxial deformation with the stretches stretch λ = 1.1, the in-plane longitudinal and circumferential components of the Cauchy stress read as σ_L = 0.64 kPa and σ_C = 0.59 kPa, which are comparable to the values σ_L = 1.18 kPa and σ_C = 0.39 kPa reported in Gupta et al. (1994) for a 6-week infarcted ovine sample (see Fig. 6 in Gupta et al. (1994)). Their results indicated a stronger anisotropy than that reflected in our measurements, however, this discrepancy could be largely due to the choice of longitudinal and circumferential axes. In contrast, Morita et al. (2011) reported a nearly isotropic biaxial properties for 8-week infracted ovine myocardium (see Fig. 5A in Morita et al. (2011)), which is more consistent with our predictions for biaxial properties.

4.4 Importance of conducting optimal design of experiments

The optimal choice of displacement paths aims at minimizing the covariance between the estimated parameters and makes such estimates as less sensitive to the chosen loading conditions and experimental noise as possible. We observed from the prediction results (Figure 6) that the parameters estimated using the optimal set can offer a better predictive capability for common modes of deformation in in-vivo myocardium versus the estimates from all-simple-shear set. In addition, the estimation using the optimal set indicated a stronger determinability of the parameters (Figure 7). Such observations highlight the importance of using an optimal set of strain paths for tissue characterization. In fact, although a complete non-optimal set of strain paths will be sufficient to quantify a 3D form of SEDF for myocardium and to provide an excellent fit of the form to those paths, it may fall short in adequately describing the behavior of myocardium under general boundary conditions during a cardiac cycle. For this reason, the optimal design of experiments was included in our proposed approach to enhance the predictive capability and determinability of a given SEDF, and proved indispensable for a reliable descriptor of myocardium mechanical behavior under in-vivo loading conditions.

4.5 Limitations

The histological measurements on the fiber orientations incorporated into the inverse model did not account for out-of-plane fiber orientation and in-plane variations in the orientations. The significance of accounting for the full 3D fiber structure remains unexplored and will be the subject of future studies. As emphasized throughput the paper, the optimal set of loading paths generally depends on the choice of the constitutive model as well as the preliminary information on the fibrous structure of the tissue. This can be perceived as a limitation, but is also intrinsic to the nature of modeling nonlinear materials, as different models may need different mechanical tests for the estimation of their parameters in order to reach their highest predictive capability and determinability. Such topic requires a thorough investigation, and one needs to explore different forms of constitutive models (for instance invariant-based models) to determine how strong the dependence of the optimal set on the chosen energy function is. Such investigation was beyond the scope of the current study. The length-scale of the constitutive modeling was limited to a rather macroscopic scale representing the behavior of a tissue element of the size of ~1mm with a mean fiber orientation. Such modeling was sufficient for our purpose here to estimate the effective mechanical response of the tissue at this length scale, but more advanced structural models that approach the myocardium at a smaller length scale (Avazmohammadi et al. 2016) can be used to gain insights into contribution of each fiber type (myofibers and collagen fibers) and the mechanical interactions among them. Finally, the case study considered in this work was limited to estimating passive behavior of myocardium, and the inverse model and the optimal design of experiments laid out in this work can be used to optimally estimate and predict the behavior of the coupled passive-active behavior of myocardium.

5. Concluding remarks and future directions

In this work, we presented a novel integrated computational-experimental inverse model for estimation of the three-dimensional mechanical properties of cardiac tissues, and applied and verified the model for the case of passive post-infarction left ventricular myocardium. The approach consisted of the following three main steps for a given SEDF: (i) conduct an optimal design of experiment to determine the optimal set of loading paths based on the chosen SEDF, (ii) conducting the experimental tests derived from the optimal design, and (iii) integrating the acquired experimental mechanical and histological data into an inverse finite element pipeline to determine the unknown material parameters. We found that the inclusion of optimal design of experiments was critical in our inverse model to minimize the dependence of the estimated values of the SEDF constants on the applied boundary conditions, and therefore to improve the predictive capability of the SEDF to capture the behavior of the myocardium under general in-vivo loading conditions. Ultimately, our approach will enable complete representation of 3D behavior of any soft tissue wherein a macroscopic cuboidal specimen (5–10 mm) can be obtained.

Appendix A: Validation of the analysis pipeline

In this appendix we provide the results for the validation of the simulation-experimental pipeline using isotropic and anisotropic synthetic samples as described in Subsection 2.6.2.

Isotropic gel

Single tension and simple shear tests with flat plate attachment on the same specimen (see Figure 5b) led to matched properties. The FE model (see Figure 5c) equipped with (single-parameter) neo-Hookean material description provided reliable fit to the stress-strain data of single tension test (see Figure A1-a) with r² = 0.99. The estimated value of unknown shear modulus was 35.77 kPa. This value was used in FE simulations to compare against the simple shear test date, and an overall good agreement was found with r² = 0.96 (Figure A1–b). The agreement was particularly good for smaller deformations (up to 0.04 shear).

Transversely isotropic rubber

The FE model (see Figure 5f) equipped with transversely isotropic Fung material model (Eq. (26)) was used to fit the stress-strain data from the first set of tests comprising of two single tension tests and two simple shear tests in the transverse and longitudinal directions. The overall fit was very good (Figure A2-a,b) with r² = 0.97. The FE model with the estimated values (Table 5) were used to compare against the data from the second set of tests comprising of equibiaxial test in longitudinal and transverse directions, the perpendicular simple shear, and the single compression in the transverse direction (Figure 13c,d,e). The overall fit was satisfactory to validate the robustness of the device for mechanical testing of anisotropic materials. This result also underscores how optimal design of experiments can be used to derived model parameters with good predictive capabilities.

Figure A1.

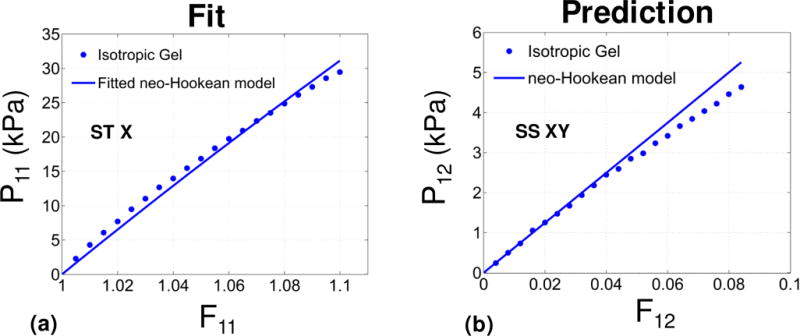
Validation for the case of isotropic gel. Results are given for the relevant components of the P stress as functions of the associated deformation. (a) Single tension (ST) (b) simple shear (SS). Markers and solid lines denote the experimental data and a fitted neo-Hookean model, respectively. The model was fitted only using the ST test, and was used to recover the data for the SS test.

Figure A2.

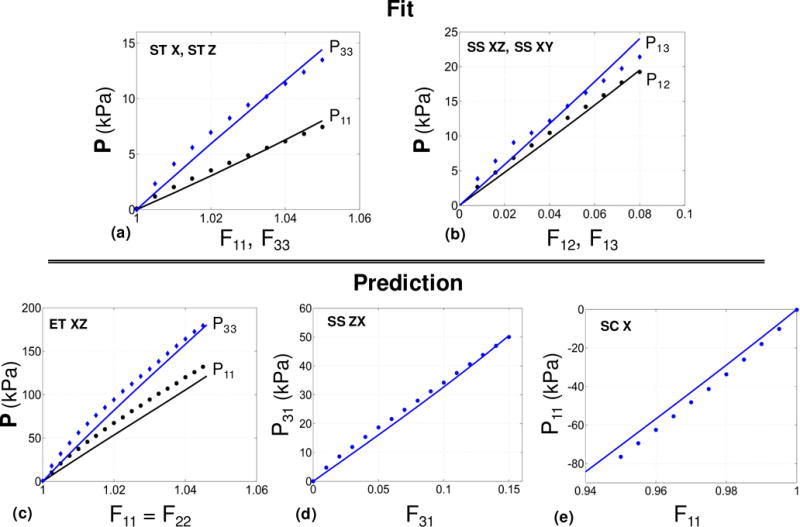
Validation for the case of anisotropic gel. Results are given for the relevant components of the P stress as functions of the associated deformation. (a) Single tension along and transverse to the needles (ST). (b) Simple shear in transverse and longitudinal directions (SS). (c) Equibiaxial tension along and transverse to the needles (ET XZ). (d) Simple shear in the plane of fibers (SS ZX). (e) Single compression in the transverse direction (SC X). Markers and solid lines denote the experimental data and a fitted transversely isotropic Fung model, respectively. The model was fitted only using the UT and SS tests, and was used to recover the data for the BT, SS2 and UC tests.

Table 5.

Estimated values of the Fung parameters for synthetic fiber-reinforced rubber.

b0 (kPa)	b2	b3	b4	b5
3.85	1.91	6.74	2.53	1.31

Appendix B

In this appendix, we discuss a simple example of optimal design of mechanical testing to characterize the mechanical behavior of a transversely isotropic solid based on a three-parameter constitutive model. Our attention is restricted to D-optimality criterion and we show how this criterion can guide the experiments to accurately estimate the material constants. We assume that the solid material with preferred direction along e₃ is characterized by following energy function

$$\mathrm{W}(\mathbf{E})=\frac{1}{2}{\mathrm{c}}_0\left\{\exp \left[{\mathrm{c}}_1({\mathrm{E}}_{11}^2+{\mathrm{E}}_{22}^2)+{\mathrm{c}}_3{\mathrm{E}}_{33}^2\right]-1\right\},$$ (27)

where c₁ and c₃ characterize the in-plane and out-of-plane stiffness of the material, respectively. In a similar manner as discussed in Subsection 2.4, we use the objective function Φ to estimate the parameters. To be able to visualize the objective function in three-dimensional space, we assign a value to c₀ and use mechanical tests to estimate c₁ and c₃. We compare the values of the D-optimality criterion Δ_D, defined in (20), for three sets each of which is composed of two deformation protocols as follows:

• Set 1: Simple shear XY and simple shear ZX (see Figure 2)

• Set 2: Single tension X and simple shear ZX

• Set 3: Single tension X and single tension Z

We calculated the objective function for numerical values c₀ = 3kPa, c₁ = 2 and c₃ = 5 (Figure A3). A zero value for Δ_D indicates that c₁ and c₃ are not uniquely identifiable (Figure A3-a) through the first Set, and the increasing value of Δ_D for Sets 2 and 3 reflects the modifying stability of the optimization process (Figure A3-b,c).

Figure A3.

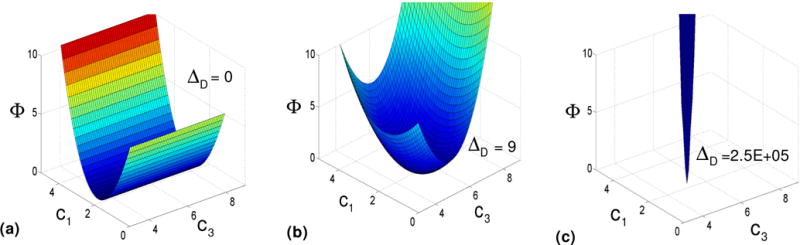
3D surfaces of the objective function F (defined in (12)) for the energy function (28). Results for (a) Set 1, (b) Set 2, and (c) Set 3, as defined in Appendix A.