Abstract
Real-time quantification of head impacts using wearable sensors is an appealing approach to assess concussion risk. Traditionally, sensors were evaluated for accurately measuring peak resultant (R1-38) skull accelerations and velocities. With growing interest in utilizing model-estimated tissue responses for injury prediction, it is important to evaluate sensor accuracy in estimating tissue response as well. Here, we quantify how sensor kinematic measurement errors can propagate into tissue response errors. Using previous instrumented mouthguard validation datasets, we found that skull kinematic measurement errors in both magnitude and direction lead to errors in tissue response magnitude and distribution. For molar design instrumented mouthguards susceptible to mandible disturbances, 150%–400% error in skull kinematic measurements resulted in 100% error in regional peak tissue response. With an improved incisor design mitigating mandible disturbances, errors in skull kinematics were reduced to <50%, and several tissue response errors were reduced to <10%. Applying 30° rotations to reference kinematic signals to emulate sensor transformation errors yielded below 10% error in regional peak tissue response; however, up to 20% error was observed in peak tissue response for individual finite elements. These findings demonstrate that kinematic resultant (R1-38) errors result in regional peak tissue response errors, while kinematic directionality errors result in tissue response distribution errors. This highlights the need to account for both kinematic magnitude and direction errors, and accurately determine transformations between sensors and the skull.
Keywords: Brain Tissue Response, Finite Element, Wearable Head Impact Sensors, Mild Traumatic Brain Injury
1 Introduction
The Center for Disease Control estimates 1.6 to 3.8 million sports-related concussions to occur annually in the United States alone (Langlois et al, 2006). A large fraction of concussions are unreported (Kroshus et al, 2014a; Elliott et al, 2015), in part, because the associated signs and symptoms are subjectively evaluated and are difficult to detect (Kroshus et al, 2014b). Thus, there is a pressing need for more objective and quantitative concussion diagnostics. (R1-4)
Concussions are an injury to the brain usually resulting from trauma to the head (Mittenberg and Strauman, 2000). However, it is currently technologically infeasible to observe the brain directly for injury in real time for immediate removal from play to prevent further injury (R1-5). Instead, some biomechanics (R1-6) researchers have relied on wearable head impact sensor technologies that measure skull kinematics following impact to develop injury risk metrics and, in the future, identify concussions when they occur (Rowson et al, 2011; Camarillo et al, 2013; Campbell et al, 2016; Wu et al, 2016b).
The three most basic wearable sensor form factors in use today are sensors mounted on headgear (Rowson et al, 2011; Campbell et al, 2016; Wu et al, 2016b), on skin (Wu et al, 2016b), or in instrumented mouthguards (R1-7) (Camarillo et al, 2013). Most available sensors are designed to measure skull kinematics using a combination of linear accelerometers and/or angular gyroscopes (R1-8), and most have undergone validation testing (R1-9) on anthropomorphic test dummies (ATDs) (Jadischke et al, 2013; Bartsch et al, 2014; Campbell et al, 2016; Siegmund et al, 2016), with a few being evaluated further in cadavers (Kuo et al, 2016) and in human subjects (Wu et al, 2016b).
These wearable sensors, particularly the Head Impact Telemetry System (HITS), have allowed researchers to collect skull kinematic measurements from tens of thousands of impacts and hundreds of concussions over the last decade (Brolinson et al, 2006; Broglio et al, 2011; Beckwith et al, 2012). From these measurements, several researchers have developed skull kinematics-based injury metrics to assess the potential risk of concussion (R1-10) (Takhounts et al, 2010; Rowson et al, 2012).
However, the relation between skull kinematics and the resulting tissue responses that lead to injury in the brain is not intuitive. This is because the brain is a deformable body with an intricate geometry and nonlinear material properties, as well as complex brain-skull boundary conditions (Nicolle et al, 2005; Hrapko et al, 2008; Prevost et al, 2011; Forte et al, 2017; Budday et al, 2017). As a result, many skull kinematics-based injury metrics are limited in their ability to predict tissue-level injuries. A recent study identified a high correlation between brain strains and skull kinematics-based injury metrics based on angular velocity components, but correlations with many traditional injury risk metrics derived from linear accelerations were relatively low (Gabler et al, 2016). This supports previous research suggesting that angular measures are responsible for tissue deformations that are thought to result in injury (Kleiven, 2006, 2007). (R1-11)
Because of the limitations of skull kinematics-based injury metrics, researchers have begun exploring how the brain responds to measured skull kinematics using finite element (FE) simulations (Kleiven and Hardy, 2002; Takhounts et al, 2008; Ji et al, 2015). These studies have allowed researchers to predict how the brain deforms, and is possibly damaged, by mechanical insults to the head (Giordano and Kleiven, 2014; Ji et al, 2014b). This has prompted the development of injury metrics based on tissue response, which, unlike their skull kinematic counterparts, provide insight into how brain injury occurs at the tissue level (Wright and Ramesh, 2012; Giordano and Kleiven, 2014; Ji et al, 2014b).
Because injury metrics based on tissue response are becoming commonplace, are wearable head impact sensors, typically evaluated for skull kinematics measurement accuracy, capable of estimating tissue responses accurately as well? (R1-12) While most sensors are evaluated on their ability to measure peak skull kinematics resultants (R1-38), this may be (R1-13) insufficient for estimating their ability to predict tissue responses due to the complexity of tissue responses.
In this study, we evaluate how skull kinematic measurement errors in American football, resulting from external disturbances on sensors, or errors in sensor transformations to the head center of gravity, propagate as errors in tissue responses. We also suggest new skull kinematic error metrics that may be better at predicting tissue response errors. Sensor developers and biomechanics researchers evaluating sensor accuracy can use these new skull kinematic error metrics to make inferences on the expected error in predicting tissue response. This reduces the reliance on computationally demanding FE simulations and allows for rapid evaluation of sensors for predicting tissue response. (R1-16)
2 Methods
In this study (R1-17), we used impact data collected from laboratory experiments with two instrumented mouthguards in an anthropomorphic test dummy (ATD) to generate three datasets for analysis. All computations were performed using Matlab (Mathworks, Waltham MA). (R1-33)
2.1 Skull Kinematic Errors from External Disturbances
We used previously published experimental results on two mouthguard systems with varying susceptibility to mandible disturbances to explore how skull kinematic measurement errors resulting from external disturbances on sensors manifest as tissue response errors (Kuo et al, 2016). The accuracy of one instrumented mouthguard (molar design) was shown to be susceptible to mandible disturbances, wherein an unconstrained mandible would interact with the sensors, placed near the molars, during impact. After subsequent redesign, a second instrumented mouthguard (incisor design) was shown to mitigate disturbances from the mandible by placing sensors at the incisors and removing material from the bite plane, effectively isolating them from mandible effects (Figure 1). Impact data were collected using the molar design and incisor design mouthguards to obtain datasets with substantial and minimal skull kinematic errors respectively.
Fig. 1. Comparison of Instrumented Mouthguard Designs.
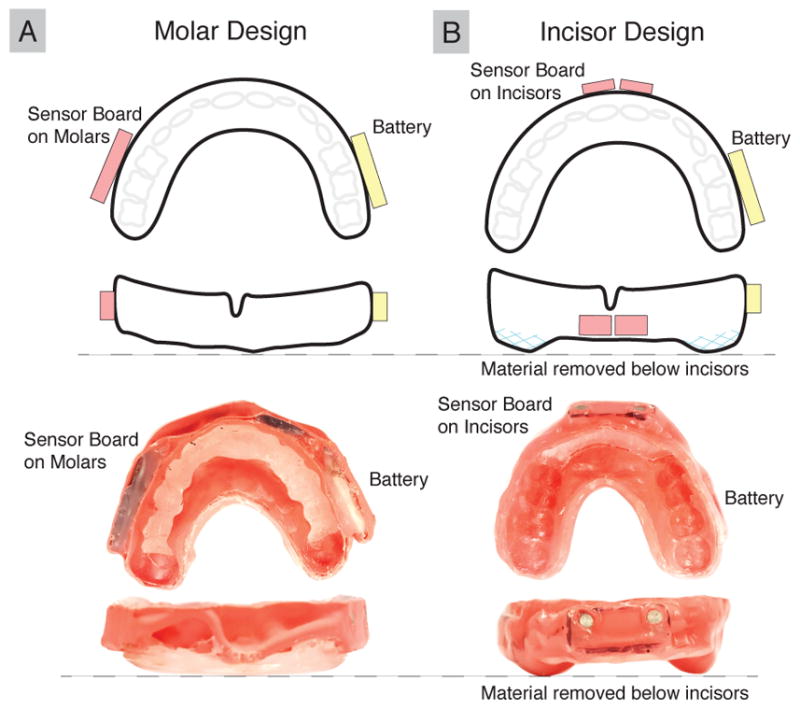
(A) The molar design mouthguard is susceptible to mandible disturbances, whereas (B) the incisor design isolates the sensors from the mandible by placing them at the incisors and removing material from the bite plane to prevent direct mandible interaction near the sensors.
Both instrumented mouthguard designs were formed to the dentition of a custom 50th percentile anthropomorphic test dummy (ATD) (Kuo et al, 2016). Both included a tri-axial linear accelerometer sampling at 1000Hz with a CFC180, fourth-order 300Hz Butter-worth low-pass filter (SAE, 1995). Additionally, both included a tri-axial gyroscope, with the molar design using a sampling rate of 1000Hz and a fourth-order 184Hz Butterworth low-pass filter (manufacturer specified (Kuo et al, 2016))(R1-18), and the incisor design using a sampling rate of 8000Hz and a CFC180, fourth-order 300Hz Butterworth low-pass filter. The gyroscope bandwidth was increased in the incisor design following a study that showed current gyroscope bandwidths were insufficient to fully capture impact dynamics in American football (Wu et al, 2016a). We used a five-point stencil (R1-19) to differentiate angular velocity signals to obtain angular acceleration. All kinematics were then transformed to the ATD center of gravity and aligned with anatomical anterior-posterior (A/P) axis, left-right (L/R) axis, and superior-inferior (S/I) axis (R1-23) (Kuo et al, 2016).
The ATD was equipped with a tri-axial linear accelerometer and a tri-axial gyroscope at the center of gravity (measured with the mandible (Camarillo et al, 2013)) (R1-20) and aligned with anatomical axes. Linear accelerometer signals were collected at 100kHz with a CFC1000, fourth-order 1650Hz Butterworth low-pass filter. Angular gyroscope signals were collected at 100kHz with a CFC180, fourth-order 300Hz Butterworth low-pass filter. As with the mouthguards, we differentiated the angular velocity signals using a fourth-order stencil to obtain angular acceleration. The mandible was left unconstrained to exercise the worst-case scenario for the instrumented mouthguards (Kuo et al, 2016).
To collect impact data, we equipped the mouthguard onto the ATD, which was fitted into a medium size Riddell Speed helmet and dropped from several heights and orientations. We selected three drop heights: 10cm, 60cm, and 100cm, which resulted in impacts ranging from 15g – 150g, and six impact locations: vertex, frontal, frontal oblique right (oblique), parietal, occipital, and facemask (Figure 2), to reproduce impact scenarios commonly seen in American football (Crisco et al, 2010). We performed three trials for each combination of mouthguard drop height, and impact location, resulting in 54 total drop trials per mouthguard design. Data from all systems were collected using a 10g linear acceleration trigger with 10ms pre-trigger and 90ms post-trigger.
Fig. 2. Impact Locations Observed in American Football.
Impacts were conducted using a free drop setup over a range of impact locations and heights. Impact locations (A) vertex, (B) frontal, (C) oblique, (D) parietal, (E) occipital, and (F) facemask were chosen to represent impacts commonly observed in American football. Briefly, the headform was hoisted to a specified height and orientation using a net, and released to impact an aluminum plate (Kuo et al, 2016). (R1-22).
2.2 Skull Kinematic Errors due to Coordinate System Transformation
Wearable sensors cannot be physically placed at the head center of gravity. Thus, transforming sensor kinematics to the head center of gravity is necessary, and relies on a rigid body assumption (Camarillo et al, 2013; Siegmund et al, 2014; Campbell et al, 2016; Wu et al, 2016b). The transformation defines (R1-21) the relative orientation of the sensor axes with respect to the anatomical axes, and the projection vector from the sensor to the head center of gravity. Error in each estimate will result in skull kinematic errors, even if the sensor has perfect accuracy at its location. Because only the relative orientation affects both linear and angular skull kinematics, and tissue responses are known to be more sensitive to angular kinematics (Gabler et al, 2016), we focused on how sensor skull kinematic errors resulting from imperfect orientations might manifest as tissue response errors.
To emulate skull kinematic errors resulting from imperfect orientations, we rotated the coordinate system for the ATD reference skull kinematics obtained during drop impacts for the incisor design. For each of the six impact locations, we took a 100cm impact trial as a representative most severe case. We then applied a coordinate rotation about one of the anatomical axes (A/P, L/R, S/I (R1-23)) at six angles: −30°, −20°, −10°, 10°, 20°, 30°. This resulted in 108 rotated trials.
2.3 Skull Kinematic Error Metrics
We computed 18 skull kinematic error metrics, which included both commonly reported and newly developed metrics. The most commonly reported skull kinematic error metrics for sensor accuracy evaluation are computed from linear acceleration, angular velocity, and angular acceleration resultants (R1-38). We included three metrics representing absolute value of the relative difference (R1-28) in peak resultant (R1-38) skull kinematics (Equation 1) between reference measures (reference angular velocity, angular acceleration, or linear acceleration resultant (R1-38) ) and mouthguard or rotated trial measures (mouthguard or rotated trial angular velocity, angular acceleration, or linear acceleration resultant (R1-38) ). We also included three metrics representing normalized root mean squared error of resultant (R1-38) skull kinematics (Equation 2) (Camarillo et al, 2013; Bartsch et al, 2014; Siegmund et al, 2014; Kuo et al, 2016), with n representing the number of samples in an impact (downsampled to the lowest sampled signal) (R1-25).
Because previous literature has suggested tissue responses are directionally dependent (Kleiven, 2006; Zhao et al, 2016), we introduced new skull kinematic error metrics based on tri-axial linear acceleration, angular velocity, and angular acceleration components aligned with anatomical axes. These included nine metrics representing absolute value of the relative difference (R1-28) in peak absolute value of component skull kinematics (Equation 3) between reference measures (reference angular velocity, angular acceleration, or linear acceleration components ), and mouthguard or rotated trial measures (mouthguard or rotated trial angular velocity, angular acceleration, or linear acceleration components ). In addition, we included three new metrics representing the instantaneous axis error (Equation 4). The instantaneous axis error describes the angle between the angular velocity, angular acceleration, or linear acceleration vector in the reference, and the angular velocity, angular acceleration, or linear acceleration vector in the mouthguard or rotated trial. The kinematics vector of the reference and mouthguard or rotated trial were taken at the time when the resultant kinematics were at their respective maximums. (R1-26) In all equations, refers to the reference measure, and refers to the mouthguard or rotated trial measure. For skull kinematic components, we normalized by the peak resultant (R1-38) value because in some cases, the components are near 0.
| (1) |
| (2) |
| (3) |
| (4) |
2.4 Tissue Response Error Metrics
For tissue response analysis, we used the Worcester Head Injury Model (WHIM; Figure 3 (Ji et al, 2015; Zhao et al, 2016, 2017a) to simulate impact skull kinematics from the reference, instrumented mouthguards, and rotated trials. Principal strain, principal strain rate, and fiber strains were obtained from each simulation. To determine fiber strains, strain tensors were projected onto 64,272 white matter voxels using fiber orientation information obtained from diffusion tensor imaging (DTI) (Ji et al, 2015) (R1-27). WHIM was validated against relative brain-skull displacement and pressure data in cadaveric impacts as well as in vivo brain strains from tagged brain MRI data. It has been recently used to assess tissue responses of injury-level impacts (Ji et al, 2014b), to simulate American National Football League (NFL) impacts to predict injury (Zhao et al, 2017a), and to evaluate the performance of a pre-computation technique for real-time response estimates (Zhao et al, 2017b). WHIM contains 115,228 elements partitioned into several major brain regions. We focused our analysis on the cerebrum, corpus callosum, and brain stem as these regions have been previously implicated in injury studies (Giordano and Kleiven, 2014; Patton et al, 2015; Zhao et al, 2017a).
Fig. 3. WHIM Used to Predict Tissue Response.
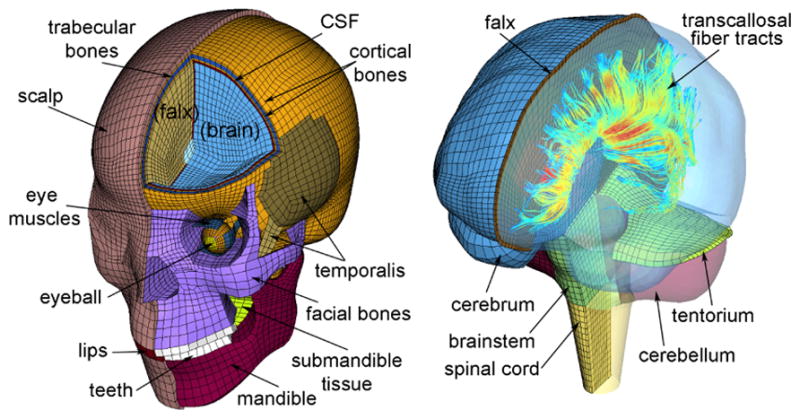
The Worcester Head Injury Model (WHIM) consists of 115,228 elements and has been previously validated against cadaveric and in vivo impact tests. WHIM can also generate fiber strains by projecting strain tensors onto 64,272 white matter voxels.
We first computed five tissue response error metrics to characterize differences in tissue response magnitude in the three brain regions of interest (cerebrum, corpus callosum, and brain stem; 5×3=15). Tissue response error metrics included the absolute value of the relative difference (R1-28) in peak principal strain, peak principal strain rate, cumulative strain damage measure 10% (CSDM 10%), and 50% population principal strain and strain rate (pop50) between reference and mouthguard or rotated trials. CSDM 10% describes the number of elements that exceed 10% over an entire simulation (Takhounts et al, 2003). The pop50 measure describes the principal strain or strain rate that was exceeded by 50% of elements (Sullivan et al, 2015). The peak strain or strain rate value was computed for each element over an entire impact, and pop50 represented the peak strain or strain rate value exceeded by 50% of elements. (R1-29)
Next, we introduced two tissue response error metrics to assess the differences in response distribution in the three brain regions of interest (2×3=6). They included the absolute value of the relative differences (R1-28) in average element-wise peak principal strain and peak principal strain rate between reference and instrumented mouthguard or rotated trials. We computed peak strain and strain rate absolute value of the relative differences (R1-28) for single finite elements between reference and mouthguard or rotated trial, and average them over elements in each brain region to calculate (R1-30) these error metrics.
Finally, we defined two tissue response error metrics computed from fiber strains for the whole brain. For the first, we computed the absolute value of the relative difference (R1-28) in peak fiber strain between the reference and mouthguard or rotated trial. For the second, we found the absolute value of the relative difference (R1-28) of peak fiber strain for individual white matter voxels between reference and mouthguard or rotated trial, and computed the average voxel-wise error over the whole brain. In total, 23 tissue response error metrics were evaluated.
2.5 Correlation and Multivariate Analysis
Skull kinematic error metrics and tissue response error metrics were computed from all data collected using the reference ATD kinematics, and the instrumented mouthguards or rotated trials. To assess how errors in sensor skull kinematics measurements propagate into predicted tissue responses, we performed a correlation analysis between individual skull kinematic error metrics and individual tissue response error metrics, and further, a multivariate regression to fit the 23 tissue response error metrics against the 18 skull kinematic error metrics. For the multivariate regression, we performed the minimization presented in Equation 5. We minimized the sum over all impacts of the error between the observed tissue response error metric errtissue for a single impact and the linear combination of skull kinematic error metrics for a single impact to obtain a set of linear coefficients a⃗. We performed this regression 23 times, once for each tissue response error metric, to obtain independent linear coefficients a⃗ relating the skull kinematic error metrics to each tissue response error metric. (R1-31) For the multivariate regression, we also standardized the skull kinematics based error metrics and tissue response error metrics over all impacts by subtracting out an error metric’s mean and normalizing by an error metric’s standard deviation. (R1-32) The resulting standardized (R1-32) coefficients a⃗ described the relative importance of each skull kinematic error metric in predicting tissue response error metrics. The coefficients were constrained to be positive to be physically meaningful.
| (5) |
3 Results
Validation datasets from both a molar design and an incisor design mouthguard were evaluated. In addition, ATD reference signals from the incisor design trials were rotated to emulate errors in sensor transformation to the head center of gravity. For the molar design mouthguard, we recorded 53 of 54 trials, with one 10cm facemask impact being missed. For the incisor design, we recorded all 54 impacts. For the rotated trials, we assessed 108 trials.
3.1 Effect of Skull Kinematic Errors on Brain Tissue Response Errors
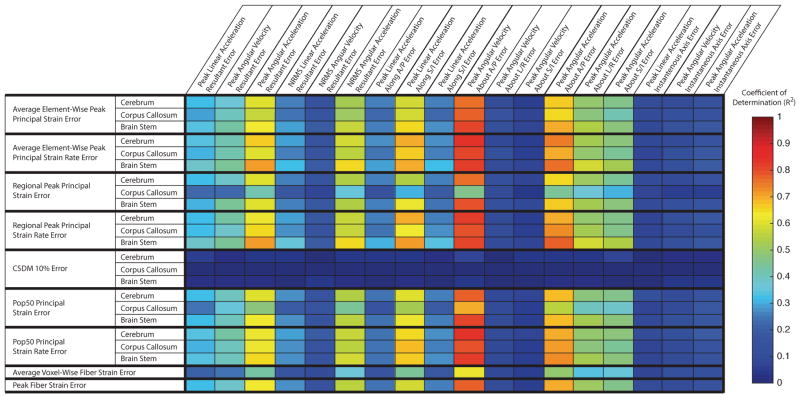
Results from the correlation analysis show that several skull kinematic error metrics correlated well with most tissue response error metrics (Figure 4). Particularly, the error in peak absolute angular velocity about A/P (R1-23) had the highest correlation with most tissue response error metrics (R2 > 0.7), with the exception of the errors in CSDM 10%, regardless of the brain region (R2 < 0.5).
Fig. 4. Correlations between skull kinematics error metrics and tissue response error metrics.
Here, we show correlations between skull kinemtic error metrics and tissue response error metrics collected over all molar design mouthguard, incisor design mouthguard, and rotated trials. (R1-36) Error in peak absolute angular velocity about A/P (R1-23) correlates best with most tissue response error metrics. Error metrics based on angular acceleration and error in peak linear acceleration along the L/R axis also have R2 > 0.5 correlation with the majority of tissue response error metrics. (R1-23) CSDM 10% error in all brain regressions do not correlate well with any skull kinematics error metrics.
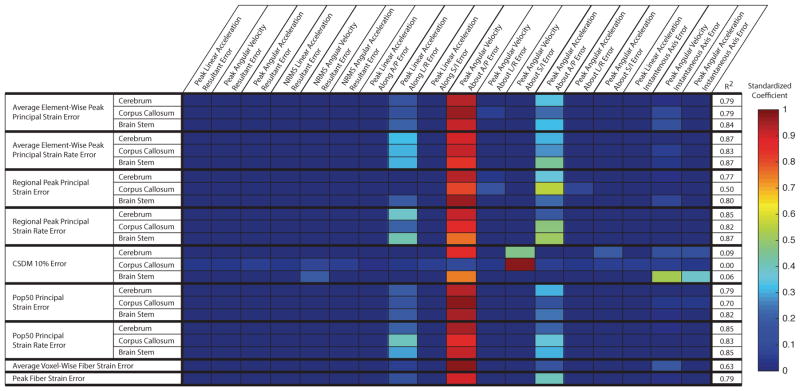
Results from the multivariate analysis described the relative importance of the skull kinematic error metrics in contribution to tissue response error metrics (Figure 5). Again, the error in peak absolute angular velocity about A/P (R1-23) had the largest coefficient relating it to all but one tissue response error metric (regional CSDM 10% error in the corpus callosum) (R1-32). For the regional CSDM 10% error in the corpus callosum, the multivariate analysis yielded a poor fit (R2 = 0.0) (R2-5), suggesting that it was not well estimated (R1-35) by any linear combination of our skull kinematic error metrics.
Fig. 5. Multivariate regression shows angular velocity component best predicts tissue response error metrics.
Standardized (R1-32) coeffcients from the multivariate regression analysis represent the contribution of a skull kinematic error metric to the prediction of the tissue response error metric. Here, we observe that error in absolute peak angular velocity about A/P (R1-23) has the largest contribution to most tissue response error metrics. For the corpus callosum CSDM10% error metric, where error in absolute peak angular velocity about A/P (R1-23) is not the largest contributor, the multivariate fit is poor with R2 = 0.0.
Error in the peak angular acceleration about the A/P axis also contributed to the prediction of several tissue response error metrics. (R1-32, R1-44). None of the error metrics computed from resultant (R1-38) skull kinematics contributed to the prediction of tissue response error metrics. In addition, linear acceleration error metrics had the least contribution overall.
3.2 Example Cases
Next, we show examples where the average element-wise peak principal strain error with respect to reference was within the top 10% from each of our datasets (molar design, incisor design, and rotated trials). In each case, we show a regression of the peak principal strain in each finite element between the reference and mouthguards or rotated trials. We repeat this for the peak principal strain rate in each finite element, and for the peak fiber strain in each white matter voxel. Since the tissue response error metrics are computed from these tissue responses, the regressions represent the expected tissue response errors.
In addition, we show the components and resultant (R1-38) of linear acceleration, angular velocity, and angular acceleration from the reference and mouthguards or rotated trials. Because skull kinematics error metrics are derived from the skull kinematics resultant (R1-38) and components, these traces represent the expected skull kinematic error metrics for the selected case.
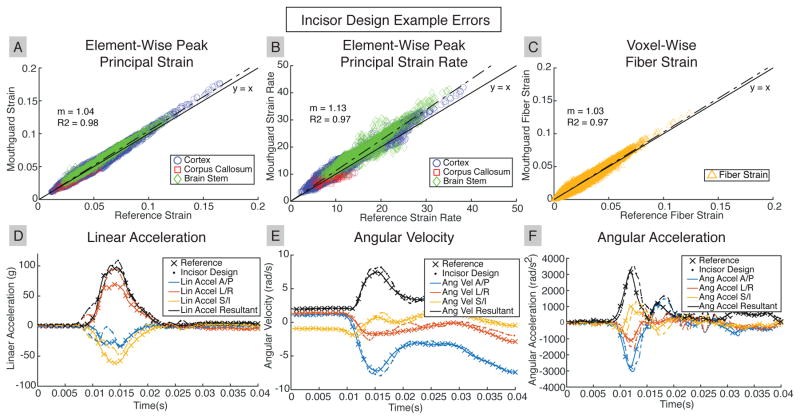
Figure 6 presents data from the third trial of the 100cm oblique drop for the incisor design. In general, the incisor design had good accuracy, as demonstrated by the close match between the predicted strains with the reference responses. The incisor design peak resultant (R1-38) kinematics were within 10% of the reference angular velocity, and within 20% of the reference linear and angular acceleration.
Fig. 6. Accurate Skull Kinematics from Incisor Design result in Accurate Brain Tissue Response.
A representative case for the incisor design shows near one-to-one prediction of (A) peak principal strain, (B) peak principal strain rate, and (C) fiber strain. (D), (E), (F) Reference skull kinematics are predicted well by incisor design measurements.
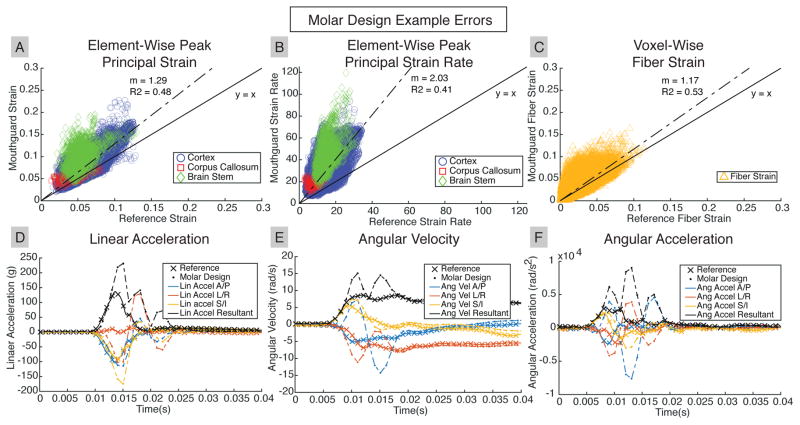
Figure 7 presents data from the second trial of the 100cm frontal drop for the molar design. The molar design substantially over-predicted tissue responses compared with the reference. This design had large high frequency oscillations in angular velocity, which amplified over-predictions in angular acceleration after differentiation. In turn, this affected linear acceleration measurements following projection to the head center of gravity.
Fig. 7. Skull Kinematic Overestimation in Molar Design Results in Overestimation in Brain Tissue Responses.
A representative case for the molar design shows substantial overestimation of (A) peak principal strain, (B) peak principal strain rate, and (C) fiber strain. In addition, the element or WM voxel that achieved peak values differed between the molar design and the reference. Large oscillations and overestimates in (D), (E), (F) molar design skull kinematics are responsible for tissue response overestimates.
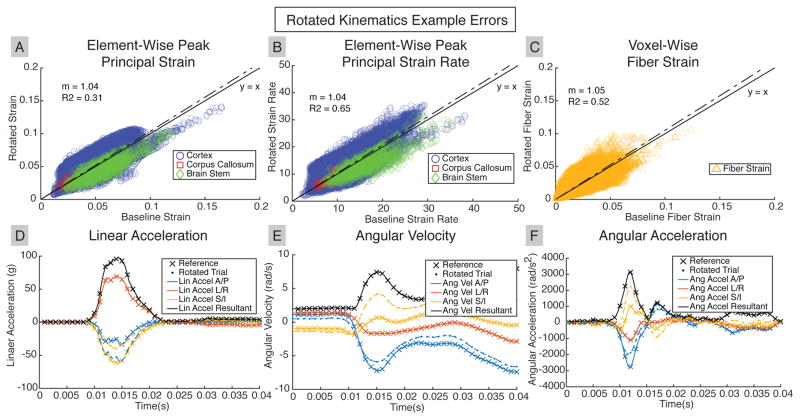
Figure 8 presents data from a rotated trial representing a 30° rotation of the skull kinematics coordinate system about L/R (R1-23) for the third oblique 100cm drop (with identical reference as that used for the incisor design case in Figure 6). While little change was observed in general tissue response magnitude (fitted slope close to 1.0), element-wise strain and strain rate distributions had high variance (R2 from linear regression of 0.31, 0.65 and 0.52 for peak principal strain, peak principal strain rate, and fiber strain, respectively).
Fig. 8. Rotated Skull Kinematics Result in Distribution Errors in Brain Tissue Response.
A representative case for the rotated trials shows little error trends of (A) peak principal strain, (B) peak principal strain rate, and (C) fiber strain. However, there were large tissue response errors in individual elements or WM voxels. (D), (E), (F) Rotated skull kinematics have the same resultants (R1-38) as reference, but errors in kinematic components result in a change of strain distribution within the brain.
In all three cases, there were larger errors in both regional and element-wise peak principal strain rate than in regional and element-wise peak principal strain.
3.3 Error Trends
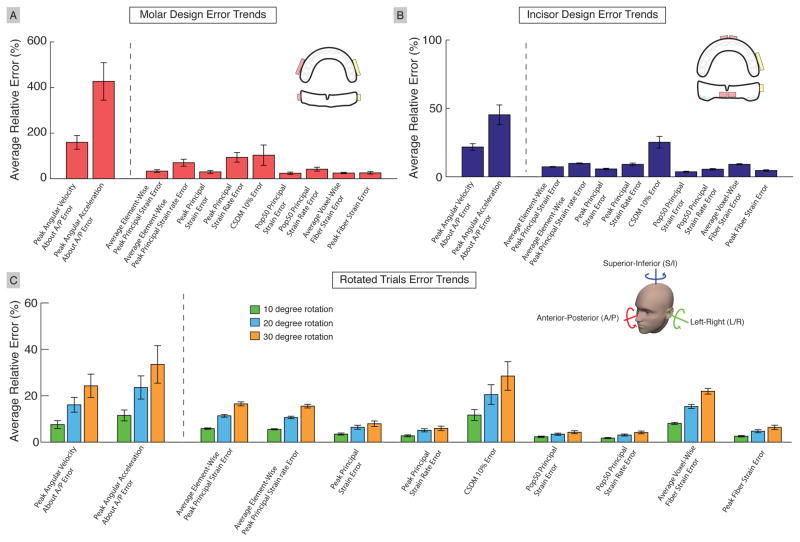
In the multi-regression analysis, we determined that the error in peak absolute angular velocity about A/P (R1-23) had the most contribution of tissue response errors, with additional contribution from error in peak absolute angular accelration about A/P (R1-44). Thus, we aggregated errors in peak absolute angular velocity about A/P (R1-23), errors in peak absolute angular acceleration about A/P (R1-44), and errors in tissue responses over the entire brain for all data collected in Figure 9. The molar design shows over 150% error in peak absolute angular velocity about A/P (R1-23) and over 400% error in peak absolute angular acceleration about A/P (R1-44), which corresponded with tissue response errors ranging from 30%–100%. Overall, the skull kinematic errors were larger than the tissue response errors, indicating that tissue responses, while correlated with the skull kinematic errors, do not have a one-to-one relation with them.
Fig. 9. Aggregated Errors from Instrumented Mouthguard Designs and Rotated Trials.
(A) Average relative errors for the molar design showing large errors in peak angular velocity about A/P (R1-23), and large errors in peak angular acceleration about A/P (R1-44). We observe that the skull kinematic errors are larger than the tissue response errors. (B) Average relative errors for the incisor design showing small skull kinematic and tissue response errors. (C) Average relative errors for the rotated trials show errors increasing as rotation angle increases. Negative and positive rotations of the same angle (10°, 20°, and 30°) are combined. (R1-40) Unlike both mouthguard trials, the average element-wise errors and average voxel-wise errors are larger than peak errors, indicating that individual elements and WM voxels have significant errors. Error bars represent the standard error over trials in each dataset (R1-39)
The incisor design shows an overall error of less than 50% in both skull kinematics and tissue responses. Again, tissue response errors were less than the skull kinematic errors, with some tissue responses having less than 10% error. Finally, for the rotated trials, both the skull kinematic and tissue response errors increased with the increase in the rotational angle applied to the reference skull kinematics, as expected. However, we also observed that the average element- or voxel-wise errors were greater than the peak response errors. This indicated significant change in tissue response distribution occurred even with the absence of change in magnitude.
4 Discussion
Translating skull kinematic errors into tissue response errors may provide better insight into the uncertainty in estimating brain model response using noisy wearable sensor data (R1-41). In this work, we presented an analysis of how sensor measured skull kinematic errors, resulting from external disturbances or coordinate system transformations, can propagate into tissue response errors. We evaluated the effect of kinematic errors resulting from external disturbances by assessing the ability of two mouthguards, a previously published mouthguard that is susceptible to mandible disturbances (molar design), and an improved version designed to mitigate these disturbances (incisor design), to predict reference tissue responses. We also evaluated the effect of kinematic errors resulting from imperfect transformations by rotating the coordinate system of ATD reference kinematics and observing how tissue responses altered.
As expected, both sources of skull kinematic error could propagate into tissue response errors. Our correlation analysis identified that error in peak absolute angular velocity about A/P (R1-23) had the strongest correlation with most tissue response error metrics. The multivariate regression analysis also found this same kinematic error metric had the largest contribution in predicting most tissue response error metrics. This observation agreed well with previous studies that suggest tissue responses are sensitive to rotations (Hernandez et al, 2015; Patton et al, 2015; Zhao et al, 2016) about A/P (R1-23), potentially as a result of the presence of the falx, a stiff membrane that runs down the great longitudinal fissure (Smith and Meaney, 2000).
However, while the multivariate analysis showed few other contributors to the prediction of tissue response error metrics, the correlation analysis showed several additional skull kinematic error metrics correlating well with most tissue response error metrics. Further analysis showed that the skull kinematic error metrics based on angular acceleration, and the error in peak absolute linear acceleration along the L/R axis (R1-23), were well correlated (R2 > 0.6) with error in peak absolute angular velocity about A/P (R1-23). This high correlation among kinematic error metrics between themselves could be responsible for their correlation with tissue response error metrics. In particular, it is known that linear acceleration does not play a large role in brain strain development (Takhounts et al, 2010; Gabler et al, 2016; Ji et al, 2014b). In addition, this correlation among kinematic error metrics suggests possible multi-collinearity in the multivariate regression. This multi-collinearity suggests that one of the other highly correlated skull kinematic error metrics (angular acceleration error metrics in particular) could also have higher contribution in the multivariate regression. But this would need to be investigated with additional data in which skull kinematic error metrics are not as well correlated. (R1-43).
Errors in CSDM 10% did not correlate well with most skull kinematic error metrics (Figure 4), and had poor fits (R2 < 0.5) in the multivariate regression as well (Figure 5). This was likely because of the relatively low impact magnitude for most ATD drop tests in this study that, in turn, resulted in relatively low brain strain magnitudes. Since CSDM relies on a pre-determined strain threshold (10%), many low severity impacts resulted in zero or near-zero CSDM values.
Error in average voxel-wise white matter fiber strains, characterizing the error in response distribution, also had a poor multivariate regression fit (R2 < 0.5, Figure 5). In contrast, the element-wise maximum principal strain error, which also characterizes error in response distribution, had a relatively good multivariate regression fit (R2 > 0.6, Figure 5). This discrepancy highlights the added uncertainty to the former due to the inherently strong directional dependency of white matter fiber strains on skull kinematic inputs.
From our examples in each of the three datasets (molar design, incisor design, and rotated trials), we observed how tissue responses were affected by skull kinematic errors. With the molar design, large overestimates in all skull kinematics led to overestimates in tissue responses. With the incisor design, however, we saw up to 25% error in skull kinematic resultants (R1-38) but relatively small error in element-wise tissue responses (<10%). These observations imply that tissue response estimates can tolerate some error in skull kinematics, and the error in skull kinematics represent an upper bound for expected error in tissue response. This was further supported by the lack of substantial global over- or under-estimation of average (R1-45) tissue responses in the rotated trials dataset, as skull kinematic resultants (R1-38) remained unchanged following rotation. Taken together, these findings suggest that a poor estimate of skull kinematic resultant (R1-38) may result in a poor estimate of the tissue response severity.
For the rotated trials, while there was no clear trend of global over- or under-estimation, large errors in tissue response were observed in individual elements. This was because of the change in angular rotation directionality that led to large errors in tissue response distribution. With more research implicating tissue deformations in specific brain regions as being responsible for injury (Hernandez et al, 2015; Zhao et al, 2017a), it is important that sensors are able to properly predict tissue response distribution and locate possible tissue damage. Following a 30° rotation of ground truth ATD data representing an error in transforming sensor measurements from the local sensor frame to the anatomically aligned skull frame, we found individual finite elements had an average of 20% error in strain and strain rate (maximum 26% for strain and 22% for strain rate) (R1-46). This finding then suggests that a poor estimate of kinematic directionality may result in a poor estimate of tissue response distribution.
4.1 Limitations
There are a few important limitations to note. First, we used an ATD as our testing platform. No ATD can precisely recreate human head dynamics; however, previous literature published with this ATD has shown that is capable of producing mandible disturbances, which we believe are a primary source of external errors for instrumented mouthguards (Kuo et al, 2016). (R1-47) Future validation studies using cadavers (Kuo et al, 2016; Hardy et al, 2007) or other surrogate models (Forte et al, 2016) may be more representative of in vivo conditions. (R2-2)
Second, we limited our study to American football because it is currently the most heavily studied sport in concussion biomechanics (Brolinson et al, 2006; Crisco et al, 2010; Beckwith et al, 2012; Rowson et al, 2012; Ji et al, 2014b; Zhao et al, 2017a). Our drop test protocol was designed to produce impacts that spanned the range of those observed in American football and have been used in previous literature (Kuo et al, 2016). (R2-4) We acknowledge that there may be slight variations between impacts for a single condition in the drop test, but these variabilities do not affect the relative difference between measurements of the ATD reference sensors and the instrumented mouthguard sensors in a single impact. (R2-3) Other contact sports such as soccer and hockey also observe high concussion rates; however, it is known that other sports (particularly, unhelmeted sports), have different impact frequency-domain characteristics that may not be adequately captured by our current wearable devices for a tissue-response evaluation (Wu et al, 2016a). Despite this, the trends that errors in kinematic magnitude result in errors in tissue response magnitude, and errors in kinematic directionality result in changes in tissue response distribution, are generalizable to any measurable impact scenario. (R1-14)
Third, we used the instrumented mouthguard as our sensor system for evaluation. The instrumented mouthguard form factor has been evaluated by several research groups (Bartsch et al, 2014; Siegmund et al, 2016; Kuo et al, 2016), though each has investigated different implementation of the instrumented mouthguard form factor. (R1-48) We expect that similar trends will appear for other wearable sensor systems in which larger kinematic measurement errors will result in larger tissue response errors (Jadischke et al, 2013; Campbell et al, 2016; Wu et al, 2016b), as this trend does not depend on the how the disturbance originated, simply that the disturbance results in an error in kinematic magnitudes. (R1-15) In addition, the rotated dataset was generated solely from ATD reference data, and represents how changes in tissue response distribution manifest as a result of improper rotation of sensor kinematics data to the anatomical-aligned axes. (R1-49)
Similarly, the WHIM was chosen to evaluate tissue response because it has been used extensively to investigate concussive biomechanics (Ji et al, 2014a; Zhao et al, 2016, 2017a). Other finite element models (Kleiven, 2006; Takhounts et al, 2008) may yield differnce results in response magnitude (Ji et al, 2014a); however, as the response trends appear to remain across models, we anticipate similar findings to follow using other models as well.
In conclusion, we have demonstrated the importance of accurate evaluation of sensor measured skull kinematics in terms of model-estimated tissue responses. Based on our results, we recommend future wearable sensor validations to assess the accuracy in both component magnitude and direction. Similarly, tissue response metrics should be evaluated for both magnitude and distribution of tissue responses, as both could occur as a result of errors in the input skull kinematics. A greater emphasis should also be placed on obtaining an accurate transform from the sensor to the head center of gravity, as the errors can lead to mismatch in tissue response distribution.
Acknowledgments
This study was supported by the National Institutes of Health (NIH) National Institute of Biomedical Imaging and Bioengineering (NIBIB) 3R21EB01761101S1, the Stanford Child Health Research Institute Transdisciplinary Initiatives Program, and the Stanford Bio-X Graduate Research Fellowship Program. Additional funding was provided by the NIH Grants R01 NS092853 and R21 NS088781.
Contributor Information
Calvin Kuo, Stanford Departments of Mechanical Engineering and Bioengineering, 443 Via Ortega, Shriram Center Room 202, Stanford CA 94305.
Lyndia Wu, Stanford Departments of Mechanical Engineering and Bioengineering, 443 Via Ortega, Shriram Center Room 202, Stanford CA 94305.
Wei Zhao, Worcester Polytechnic Institute Department of Biomedical Engineering, 60 Prescott St, Gateway Park 4004, Worcester MA 01605.
Michael Fanton, Stanford Departments of Mechanical Engineering and Bioengineering, 443 Via Ortega, Shriram Center Room 202, Stanford CA 94305.
Songbai Ji, Worcester Polytechnic Institute Department of Biomedical Engineering, 60 Prescott St, Gateway Park 4004, Worcester MA 01605.
David B. Camarillo, Stanford Departments of Mechanical Engineering and Bioengineering, 443 Via Ortega, Shriram Center Room 202, Stanford CA 94305
References
- Bartsch A, Samorezov S, Benzel E, Miele V, Brett D. Validation of an “Intelligent Mouthguard” Single Event Head Impact Dosimeter. Stapp Car Crash Journal. 2014;58:1–27. doi: 10.4271/2014-22-0001. [DOI] [PubMed] [Google Scholar]
- Beckwith JG, Greenwald RM, Chu JJ. Measuring head kinematics in football: correlation between the head impact telemetry system and Hybrid III headform. Annals of biomedical engineering. 2012;40(1):237–48. doi: 10.1007/s10439-011-0422-2. URL http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3248620&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broglio SP, Eckner JT, Martini D, Sosnoff JJ, Kutcher JS, Randolph C. Cumulative head impact burden in high school football. J Neurotrauma. 2011;28(10):2069–2078. doi: 10.1089/neu.2011.1825. URL http://www.ncbi.nlm.nih.gov/pmc/articles/PMC4346237/pdf/neu.2011.1825.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brolinson PG, Manoogian S, McNeely D, Goforth M, Greenwald R, Duma S. Analysis of linear head accelerations from collegiate football impacts. Current sports medicine reports. 2006;5(1):23–8. doi: 10.1097/01.csmr.0000306515.87053.fa. URL http://www.ncbi.nlm.nih.gov/pubmed/16483513. [DOI] [PubMed] [Google Scholar]
- Budday S, Sommer G, Birkl C, Langkammer C, Haybaeck J, Kohnert J, Bauer M, Paulsen F, Steinmann P, Kuhl E, et al. Mechanical characterization of human brain tissue. Acta biomaterialia. 2017;48:319–340. doi: 10.1016/j.actbio.2016.10.036. [DOI] [PubMed] [Google Scholar]
- Camarillo DB, Shull PB, Mattson J, Shultz R, Garza D. An instrumented mouthguard for measuring linear and angular head impact kinematics in American football. Annals of biomedical engineering. 2013;41(9):1939–49. doi: 10.1007/s10439-013-0801-y. URL http://www.ncbi.nlm.nih.gov/pubmed/23604848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell KR, Warnica MJ, Levine IC, Brooks JS, Laing AC, Burkhart TA, Dickey JP. Laboratory Evaluation of the gForce Tracker, a Head Impact Kinematic Measuring Device for Use in Football Helmets. Annals of Biomedical Engineering. 2016;44(4):1246–1256. doi: 10.1007/s10439-015-1391-7. [DOI] [PubMed] [Google Scholar]
- Crisco JJ, Fiore R, Beckwith JG, Chu JJ, Brolinson PG, Duma S, McAllister TW, Duhaime AC, Greenwald RM. Frequency and location of head impact exposures in individual collegiate football players. Journal of athletic training. 2010;45(6):549–59. doi: 10.4085/1062-6050-45.6.549. URL http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2978006&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott MR, Margulies SS, Maltese MR, Arbogast KB. Accounting for sampling variability, injury under-reporting, and sensor error in concussion injury risk curves. Journal of Biomechanics. 2015;48(12):3059–3065. doi: 10.1016/j.jbiomech.2015.07.026. URL http://linkinghub.elsevier.com/retrieve/pii/S0021929015004194. [DOI] [PubMed] [Google Scholar]
- Forte AE, Galvan S, Manieri F, y Baena FR, Dini D. A composite hydrogel for brain tissue phantoms. Materials & Design. 2016;112:227–238. [Google Scholar]
- Forte AE, Gentleman SM, Dini D. On the characterization of the heterogeneous mechanical response of human brain tissue. Biomechanics and modeling in mechanobiology. 2017;16(3):907–920. doi: 10.1007/s10237-016-0860-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabler LF, Crandall JR, Panzer MB. Assessment of Kinematic Brain Injury Metrics for Predicting Strain Responses in Diverse Automotive Impact Conditions. Annals of Biomedical Engineering. 2016;44(12):3705–3718. doi: 10.1007/s10439-016-1697-0. [DOI] [PubMed] [Google Scholar]
- Giordano C, Kleiven S. Evaluation of Axonal Strain as a Predictor for Mild Traumatic Brain Injuries Using Finite Element Modeling. Stapp car crash journal. 2014;58(14) doi: 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- Hardy WN, Mason MJ, Foster CD, Shah CS, Kopacz JM, Yang KH, King AI, Bishop J, Bey M, Anderst W, et al. A study of the response of the human cadaver head to impact. Stapp car crash journal. 2007;51:17. doi: 10.4271/2007-22-0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez F, Wu LC, Yip MC, Laksari K, Hoffman AR, Lopez JR, Grant GA, Kleiven S, Camarillo DB. Six Degree-of-Freedom Measurements of Human Mild Traumatic Brain Injury. Annals of Biomedical Engineering. 2015;43(8):1918–1934. doi: 10.1007/s10439-014-1212-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrapko M, Van Dommelen JAW, Peters GWM, Wismans JSHM. Characterisation of the mechanical behaviour of brain tissue in compression and shear. Biorheology. 2008;45(6):663–676. doi: 10.3233/BIR-2008-0512. [DOI] [PubMed] [Google Scholar]
- Jadischke R, Viano DC, Dau N, King AI, Mc-Carthy J. On the accuracy of the Head Impact Telemetry (HIT) System used in football helmets. Journal of biomechanics. 2013;46(13):2310–5. doi: 10.1016/j.jbiomech.2013.05.030. URL http://www.ncbi.nlm.nih.gov/pubmed/23891566. [DOI] [PubMed] [Google Scholar]
- Ji S, Ghadyani H, Bolander RP, Beckwith JG, Ford JC, McAllister TW, Flashman La, Paulsen KD, Ernstrom K, Jain S, Raman R, Zhang L, Greenwald RM. Parametric comparisons of intracranial mechanical responses from three validated finite element models of the human head. Annals of biomedical engineering. 2014a;42(1):11–24. doi: 10.1007/s10439-013-0907-2. URL http://www.ncbi.nlm.nih.gov/pubmed/24077860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Zhao W, Li Z, McAllister TW. Head impact accelerations for brain strain-related responses in contact sports: a model-based investigation. Biomechanics and Modeling in Mechanobiology. 2014b;13(5):1121–1136. doi: 10.1007/s10237-014-0562-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji S, Zhao W, Ford JC, Beckwith JG, Bolander RP, Greenwald RM, Flashman La, Paulsen KD, Mcallister TW. Group-Wise Evaluation and Comparison of White Matter Fiber Strain and Maximum Principal Strain. Journal of Neurotrauma. 2015;14:1–14. doi: 10.1089/neu.2013.3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiven S. Evaluation of head injury criteria using a finite element model validated against experiments on localized brain motion, intracerebral acceleration, and intracranial pressure. Int J Crashworthines. 2006;11(1):65–79. doi: 10.1533/ijcr.2005.0384. URL http://www.tandfonline.com/doi/abs/10.1533/ijcr.2005.0384. [DOI] [Google Scholar]
- Kleiven S. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp car crash journal. 2007;51:81. doi: 10.4271/2007-22-0003. [DOI] [PubMed] [Google Scholar]
- Kleiven S, Hardy WN. Correlation of an FE Model of the Human Head with Local Brain Motion–Consequences for Injury Prediction. Stapp car crash journal. 2002;46(November):123–44. doi: 10.4271/2002-22-0007. URL http://www.ncbi.nlm.nih.gov/pubmed/17096222. [DOI] [PubMed] [Google Scholar]
- Kroshus E, Baugh CM, Daneshvar DH, Viswanath K. Understanding Concussion Reporting Using a Model Based on the Theory of Planned Behavior. Journal of Adolescent Health. 2014a;54(3):269–274e2. doi: 10.1016/j.jadohealth.2013.11.011. URL http://linkinghub.elsevier.com/retrieve/pii/S1054139X13007696. [DOI] [PubMed] [Google Scholar]
- Kroshus E, Kubzansky LD, Goldman RE, Austin SB. Norms, Athletic Identity, and Concussion Symptom Under-Reporting Among Male Collegiate Ice Hockey Players: A Prospective Cohort Study. Annals of Behavioral Medicine. 2014b;49(1):95–103. doi: 10.1007/s12160-014-9636-5. URL http://link.springer.com/10.1007/s12160-014-9636-5. [DOI] [PubMed] [Google Scholar]
- Kuo C, Wu LC, Hammoor BT, Luck JF, Cutcliffe HC, Lynall RC, Kait JR, Campbell KR, Mihalik JP, Bass CR, Camarillo DB. Effect of the mandible on mouthguard measurements of head kinematics. J Biomech. 2016;49:1845–1853. doi: 10.1016/j.jbiomech.2016.04.017. URL http://dx.doi.org/10.1016/j.jbiomech.2016.04.017. [DOI] [PubMed] [Google Scholar]
- Langlois Ja, Rutland-Brown W, Wald MM. The epidemiology and impact of traumatic brain injury: a brief overview. The Journal of head trauma rehabilitation. 2006;21(5):375–8. doi: 10.1097/00001199-200609000-00001. URL http://www.ncbi.nlm.nih.gov/pubmed/16983222. [DOI] [PubMed] [Google Scholar]
- Mittenberg W, Strauman S. Diagnosis of mild head injury and the postconcussion syndrome. J Head Trauma Rehabil. 2000;15(2):783–791. doi: 10.1097/00001199-200004000-00003. URL http://www.ncbi.nlm.nih.gov/pubmed/10739967. [DOI] [PubMed] [Google Scholar]
- Nicolle S, Lounis M, Willinger R, Palierne JF. Shear linear behavior of brain tissue over a large frequency range. Biorheology. 2005;42(3):209–23. URL http://www.ncbi.nlm.nih.gov/pubmed/15894820. [PubMed] [Google Scholar]
- Patton DA, Mcintosh AS, Kleiven S. The Biomechanical Determinants of Concussion: Finite Element Simulations to Investigate Tissue-Level Predictors of Injury During Sporting Impacts to the Unprotected Head. 2015:264–268. doi: 10.1123/jab.2014-0223. [DOI] [PubMed] [Google Scholar]
- Prevost TP, Balakrishnan A, Suresh S, Socrate S. Biomechanics of brain tissue. Acta Biomaterialia. 2011;7(1):83–95. doi: 10.1016/j.actbio.2010.06.035. URL http://dx.doi.org/10.1016/j.actbio.2010.06.035. [DOI] [PubMed] [Google Scholar]
- Rowson S, Beckwith JG, Chu JJ, Leonard DS, Greenwald RM, Duma SM. A six degree of freedom head acceleration measurement device for use in football. Journal of Applied Biomechanics. 2011;27(1):8–14. doi: 10.1123/jab.27.1.8. [DOI] [PubMed] [Google Scholar]
- Rowson S, Duma SM, Beckwith JG, Chu JJ, Greenwald RM, Crisco JJ, Brolinson PG, Duhaime AC, McAllister TW, Maerlender AC. Rotational head kinematics in football impacts: an injury risk function for concussion. Annals of biomedical engineering. 2012;40(1):1–13. doi: 10.1007/s10439-011-0392-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAE. SAE J211-1 (1995): Instrumentation for Impact Test, Part 1, Electronic Instrumentation. 1995;552:25. doi: 10.1520/G0154-12A. [DOI] [Google Scholar]
- Siegmund GP, Guskiewicz KM, Marshall SW, DeMarco AL, Bonin SJ. A headform for testing helmet and mouthguard sensors that measure head impact severity in football players. Annals of biomedical engineering. 2014;42(9):1834–45. doi: 10.1007/s10439-014-1052-2. URL http://www.ncbi.nlm.nih.gov/pubmed/24920257. [DOI] [PubMed] [Google Scholar]
- Siegmund GP, Guskiewicz KM, Marshall SW, DeMarco AL, Bonin SJ. Laboratory Validation of Two Wearable Sensor Systems for Measuring Head Impact Severity in Football Players. Annals of Biomedical Engineering. 2016;44(4):1257–1274. doi: 10.1007/s10439-015-1420-6. [DOI] [PubMed] [Google Scholar]
- Smith DH, Meaney DF. Axonal damage in traumatic brain injury. Porg Clin Neurosci. 2000;6(6):483–492. [Google Scholar]
- Sullivan S, Eucker Sa, Gabrieli D, Bradfield C, Coats B, Maltese MR, Lee J, Smith C, Margulies SS. White matter tract-oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities. Biomechanics and Modeling in Mechanobiology. 2015;14(4):877–896. doi: 10.1007/s10237-014-0643-z. URL http://link.springer.com/10.1007/s10237-014-0643-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takhounts EG, Eppinger RH, Campbell JQ, Tannous RE. On the development of the SIMon finite element head model. Stapp Car Crash Journal. 2003;47:107. doi: 10.4271/2003-22-0007. [pii] [DOI] [PubMed] [Google Scholar]
- Takhounts EG, Ridella SA, Hasija V, Tannous RE, Campbell JQ, Malone D, Danelson K, Stitzel J, Rowson S, Duma S. Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model. Stapp Car Crash Journal. 2008;52(November):1. doi: 10.4271/2008-22-0001. [pii] [DOI] [PubMed] [Google Scholar]
- Takhounts EG, Ridella SA, Rowson S, Duma SM. Kinematic Rotational Brain Injury Criterion (BRIC) Enhanced Safety of Vehicles. 2010:1–10. [Google Scholar]
- Wright RM, Ramesh KT. An axonal strain injury criterion for traumatic brain injury. Biomechanics and modeling in mechanobiology. 2012;11(1–2):245–60. doi: 10.1007/s10237-011-0307-1. URL http://www.ncbi.nlm.nih.gov/pubmed/21476072. [DOI] [PubMed] [Google Scholar]
- Wu LC, Laksari K, Kuo C, Luck JF, Kleiven S, Dale’ Bass CR, Camarillo DB. Bandwidth and sample rate requirements for wearable head impact sensors. Journal of Biomechanics. 2016a;39(0):2918–2924. doi: 10.1016/j.jbiomech.2016.07.004. URL http://linkinghub.elsevier.com/retrieve/pii/S0021929016307448. [DOI] [PubMed] [Google Scholar]
- Wu LC, Nangia V, Bui K, Hammoor B, Kurt M, Hernandez F, Kuo C, Camarillo DB. In Vivo Evaluation of Wearable Head Impact Sensors. Annals of Biomedical Engineering. 2016b;44(4):1234–1245. doi: 10.1007/s10439-015-1423-3,1503.03948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Ford JC, Flashman LA, McAllister TW, Ji S. White matter injury susceptibility via fiber strain evaluation using whole-brain tractography. Journal of Neurotrauma. 2016;33(20):1834–1847. doi: 10.1089/neu.2015.4239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Cai Y, Li Z, Ji S. Injury prediction and vulnerability assessment using strain and susceptibility measures of the deep white matter. Biomechanics and Modeling in Mechanobiology. 2017a:1–19. doi: 10.1007/s10237-017-0915-5. http://dx.doi.org/10.1007/s10237-017-0915-5. [DOI] [PMC free article] [PubMed]
- Zhao W, Kuo C, Wu L, Camarillo DB, Ji S. Performance evaluation of a pre-computed brain response atlas in dummy head impacts. Annals of biomedical engineering. 2017b:1–14. doi: 10.1007/s10439-017-1888-3. [DOI] [PMC free article] [PubMed]