Application of the 4D XCAT Phantoms in Biomedical Imaging and Beyond

Abstract

The four dimensional (4D) eXtended CArdiac-Torso (XCAT) series of phantoms was developed to provide accurate computerized models of the human anatomy and physiology. The XCAT series encompasses a vast population of phantoms of varying ages from newborn to adult, each including parameterized models for the cardiac and respiratory motions. With great flexibility in the XCAT’s design, any number of body sizes, different anatomies, cardiac or respiratory motions or patterns, patient positions and orientations, and spatial resolutions can be simulated. As such, the XCAT phantoms are gaining a wide use in biomedical imaging research. There they can provide a virtual patient base from which to quantitatively evaluate and improve imaging instrumentation, data acquisition, techniques and image reconstruction and processing methods which can lead to improved image quality and more accurate clinical diagnoses. The phantoms have also found great use in radiation dosimetry, radiation therapy, medical device design, and even the security and defense industry. This review paper highlights some specific areas in which the XCAT phantoms have found use within biomedical imaging and other fields. From these examples, we illustrate the increasingly important role that computerized phantoms and computer simulation are playing in the research community.

I. Introduction

In many modern areas of science and engineering, computer simulation is an essential tool for evaluating and optimizing new technologies. Through simulation, researchers are able to perform experiments entirely on the computer. Computer-based human body models or phantoms serve as virtual subjects while accurate physics-based computer algorithms are used to operate on or interact with the phantoms to perform particular experiments. The subject’s anatomy as well as experimental parameters are completely under the researcher’s control giving them the ability to perform any study they wish. With this advantage, simulation has become an indispensable complement to theoretical derivations, experimental methods, and studies in biomedical imaging and other areas of research and development.

Computerized phantoms play an important role in simulation. As such, many different kinds of models have been developed over the years. Over four-hundred phantoms by different universities and companies have been developed to investigate medical imaging applications and dosimetry as shown in Tables 1–3 and Fig. 25 in the article by George Xu¹. Many other phantoms have also been developed for use within bioengineering, medical device design, and other fields^2–7. These references only capture a small amount of what is currently available. Many different phantoms can be seen throughout this special issue.

Table 1.

Application of the NCAT/XCAT phantoms by other researchers according to peer-reviewed publications listed in PubMed.

Application (with selected references)	Total number of papers
CT imaging methods (image quality, image processing, and quantitation)17–21	11
CT image reconstruction22–26	12
SPECT/PET imaging methods (image quality, image processing, and quantitation)27–31	31
SPECT/PET image reconstruction32–36	24
PET/SPECT attenuation, scatter correction37–40	17
SPECT collimator/detector optimization41–45	6
MRI imaging methods (evaluation and image processing)46–50	5
Radiation Dosimetry51–55	12
Radiotherapy56–60	11
Motion (effect, estimation, and compensation)61–65	23

Within our work, we developed the 4D XCAT phantom⁸ to provide a computational model of the human anatomy and physiology primarily for use in biomedical imaging research. Figure 1 shows how the XCAT has evolved over the years. The XCAT phantom started off as a model of the male torso. This first generation XCAT was called the 4D NURBS-based cardiac-torso (NCAT) phantom^9–11. It was developed to investigate the effects of motion on nuclear medicine imaging, specifically single-photon emission computed tomography (SPECT) and positron emission tomography (PET). The organs and structures in the NCAT were defined by manually segmenting the Visible Human Male x-ray computed tomography (CT) dataset from the National Library of Medicine (NLM) using the SURFdriver program, www.surfdriver.com. 3D polygon models were then fit to each segmented structure within SURFdriver and imported into the Rhinoceros modeling software, www.rhino3d.com. The polygon models were each composed of thousands of triangles. For a more compact definition, cubic non-uniform rational b-spline (NURBS) surfaces were fit to each polygon model using Rhinoceros.

Fig. 1.

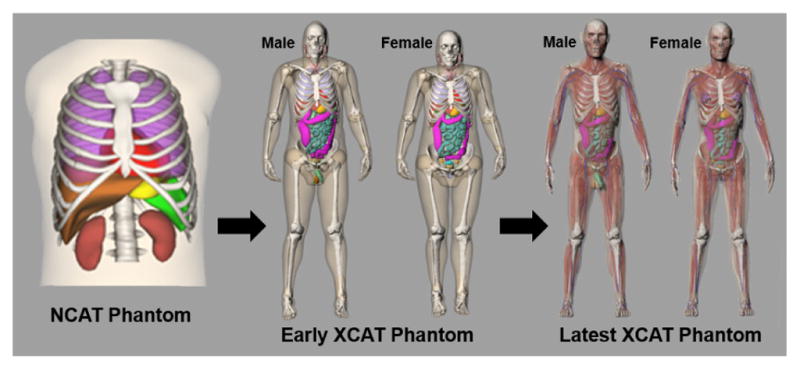
The predecessor of the XCAT phantom was the NCAT, a model of the male human torso; females were modeled by adding breast surfaces to the torso. The NCAT was extended by adding more detailed structures and creating separate male and female anatomies, giving rise to the latest XCAT phantom models.

The NCAT phantom pioneered the development of a new type of computational model, hybrid phantoms¹. These phantoms are initially defined as sets of segmented patient imaging data. Surface representations such as NURBS are then used to define the structures. The surface definition gives the structures the added flexibility to be deformed by simply applying transformations to the points that define their shape to simulate patient motions or variations in anatomy. The NCAT phantom was setup to include models for the beating heart and respiratory motions based upon deformations derived from 4D cardiac and respiratory CT data⁹.

The NCAT was initially extended into a whole-body male and female models by additional segmentation of the Visible Human Male and Female full body CT datasets creating the first version of the XCAT phantom. To provide an even higher level of anatomical detail, the XCAT phantom was then revamped based upon the Visible Human anatomical datasets from the NLM⁸. The anatomical data consisted of much higher resolution color pictures taken of the individual body slices (0.33 mm pixel size as compared to 0.898 mm’s for the CT). The anatomical images were segmented on a tablet computer using ImageSegment, a graphical application written in our laboratory. ImageSegment allowed for more efficient segmentation than SURFdriver as it allowed a user to skip slices in contouring an object; cubic spline interpolation was used to interpolate between slices. The segmented structures were converted into polygon models using ImageSegment, and then fit with NURBS surfaces using Rhinoceros. Thousands of surfaces were created to model the male and female anatomies. Individual surfaces were created for each bone, muscle, and blood vessel.

The Visible Human male and female subjects were both larger individuals in terms of body habitus. Using the flexibility of the NURBS, the XCAT male and female models were tailored to match 50^th percentile characteristics in terms of body size and organ masses according to the PeopleSize anthropometric software, www.openerg.com/psz/index.html, and the International Commission on Radiological Protection (ICRP) Publication 89¹².

Both male and female XCAT phantoms are highly detailed anatomically and include parameterized models for the anatomy and the cardiac and respiratory motions, Fig. 2. Table 2 in Segars et al⁸ list the various anatomical and motion parameters that can be modified in the XCAT.

Fig. 2.

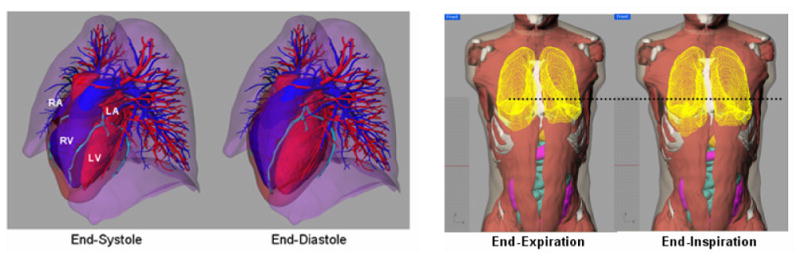
Cardiac and respiratory models of the XCAT phantom. Each includes a set of parameters to simulate different normal and abnormal motions.

Using methods from computational anatomy, the XCAT male and female models have been expanded into a population of models representing the human body of varying ages, heights, and weights from newborn to adult^13–15 as shown in Fig. 3. In this process, a template XCAT anatomy (male or female) is transformed (by applying a high-level transformation to the surface points) to match the anatomical framework provided by segmented patient CT data. This method allows for the efficient generation of new, highly detailed phantoms as not every structure needs to be segmented from the CT data. The transformed template can fill in objects that are not easily segmented (individual muscles, blood vessels, etc.). Each new model contains the same amount of anatomical definition as the original template as well as its cardiac and respiratory models.

Fig. 3.

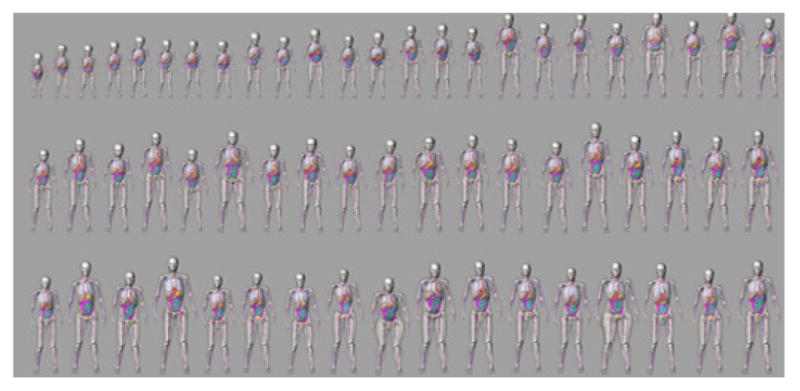
Population of new XCAT models. Selected models at various ages, heights, and weights are shown.

The XCAT series of phantoms comprise the first four dimensional library of computational models incorporating both spatial and temporal information. They realistically model the human anatomy, cardiac and respiratory motions and provide representative samples of the variation in a population. They also have great flexibility due to their surface definition. Unlike 3D shape models¹⁶ used for atlas-based segmentation and comparisons of shapes or physiological parameters within a population, the phantoms do not currently define the anatomy in a statistical way. However, each phantom can serve as a jumping point from which to create new models through user-defined deformations. Any number of different anatomies, motions or patterns, subject positioning and orientation can be created.

With its high level of realism and great flexibility, the 4D XCAT is gaining wide use in scientific research. Hundreds of imaging-focused academic groups around the globe as well as several research labs within commercial imaging companies (e.g. GE, Philips, Siemens, Samsung, and Microsoft) have obtained access to the phantoms. Also, communities in radiation dosimetry, radiation oncology, and the defense industry have acquired the phantoms for their applications. According to PubMed, over a hundred and fifty peer-reviewed journal articles (outside of the authors of this paper) have used the NCAT/XCAT phantoms. Table 1 lists the different applications found for these papers. The total number of papers found for each application are given as well as five selected references for each.

In this review paper, we highlight specific areas in which the XCAT phantoms (in its various versions) have been applied. These areas include some of the topics listed above as well as other bioengineering applications. Through the presented examples, we illustrate how computerized phantoms and computer simulation can provide vital tools in research.

II. Evaluation of Medical Imaging techniques

The original target application for the XCAT phantoms was to serve as virtual patients for biomedical imaging research to evaluate and improve imaging devices and techniques. Such evaluation would ideally be achieved through clinical trials. However, it is exceedingly impractical and costly to attempt a clinical trial for the many new nuances of an increasing number of technological offerings. Each imaging technique involves several selectable parameters for image acquisition, reconstruction, processing and analysis. It would be ethically and practically impossible to test every combination of parameters and every task on every type of patient under clinical conditions.

Physical phantoms⁶⁶ can be used as a surrogate for patients in clinical evaluations. They can be simple test objects or have realistic anatomical form. They can even be 3D printed from computerized models⁶⁷. The disadvantage to physical phantoms, though, is that it would be prohibitively expensive to fabricate a series of models representing a realistic range of patient sizes and variations especially when motion is considered.

Computer simulation offers a more practical approach to optimization and evaluation. In imaging simulation, a computerized phantom (e.g. the XCAT) serves as the virtual patient. It is then imaged using an accurate computerized model of the imaging system and its performance characteristics and physics of the imaging process. With recent advances, accurate models of various imaging systems have been achieved using analytical and Monte Carlo (MC) methods. Through the combination of computerized phantoms and models for the imaging process, patient-quality imaging data from different modalities can be generated, Fig. 4.

Fig. 4.

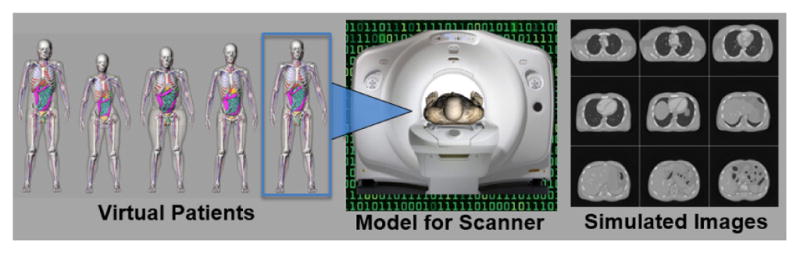
Computed tomography (CT) simulation using an XCAT phantom chosen from the population.

These simulation tools enable clinical experiments to be conducted virtually with complete user control of the subject’s anatomy, imaging device, and protocol. The exact anatomy of the phantom is known, thus providing a “gold standard” or “truth” from which to quantitatively evaluate the effects of the imaging system, technique, acquisition protocol and the image reconstruction and processing methods on the final image quality. The image quality can be degraded through the effects of the imaging system and the imaging process. By altering the system design parameters and selecting the techniques and associated parameters, one can witness their effects on the resulting images as compared to the known phantom. The optimum system design and imaging technique parameters can be determined by those that give the highest image quality for a given task. The radiation dose to the organs and anatomical structures from different protocols can also be calculated to assess patient risk from radiation exposure. None of these things are possible using live subjects.

With the advantages offered by simulation, the 4D XCAT has found great use in biomedical imaging research to investigate the effects of anatomical, physiological, physical, and instrumentational factors on the imaging process and to study image acquisition strategies, processing and reconstruction methods, and visualization techniques, all with the goal of improving image quality for more accurate diagnoses. Below we highlight different applications of the XCAT in these areas. Please note that in the references for some studies, the NCAT phantom is indicated. As mentioned earlier, the NCAT is the first generation XCAT phantom.

A. Comparison of Reconstruction Methods: Gated Myocardial Perfusion SPECT

In a series of studies by Lee et al^68–71, the XCAT phantom and its model for the cardiac motion was used to evaluate different reconstruction methods in myocardial (MP) SPECT. The XCAT was used to simulate a male adult (50^th percentile in height and weight) with a normal cardiac motion as well abnormal motions including perfusion and wall motion abnormalities. An analytical projector model was used to simulate the SPECT imaging process. Projection data with 8 and 16 gates/cardiac cycle were generated including the effects of attenuation, collimator-detector response, and scatter (ADS). These physical and instrumentational effects can degrade the resulting images. The projection data were reconstructed with different methods including: 3D filtered back projection (FBP) without ADS corrections, 3D ordered subset expectation maximization (OS-EM) with ADS corrections, and a proposed 4D rescaled block iterative maximum a posteriori (RBI-MAP) algorithm that includes ADS corrections as well as a correction for cardiac motion.

Figure 5 shows the results from the different methods for 8 gates reconstructed over the cardiac cycle. Correcting for the physical effects of attenuation, detector response, and scatter can be seen to improve the reconstructed images. Further correction of motion using the 4D RBI-MAP method provides the best results as validated using image quality indices (normalized mean squared error and averaged normalized standard deviation) and human observer studies⁷¹.

Fig. 5.

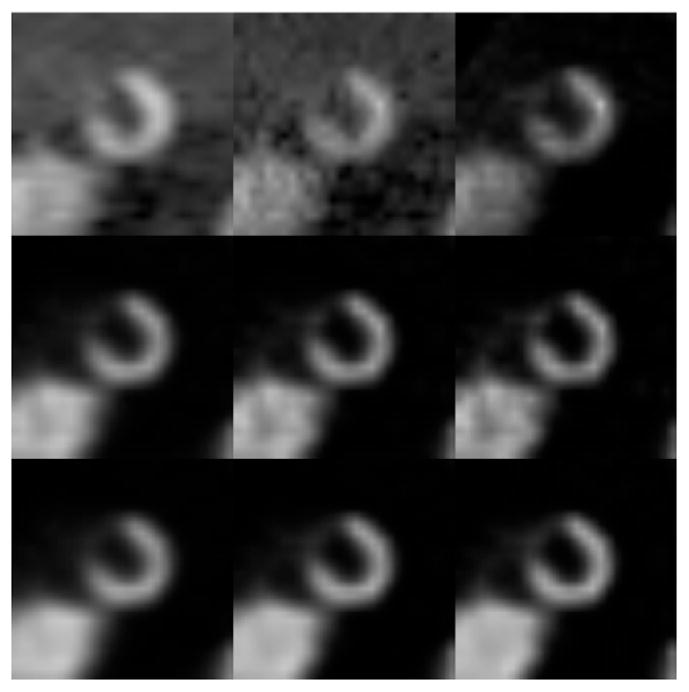
The first frame of the short axis reconstructed images of the XCAT heart in an 8 frame cardiac gating scheme (Top left to right: FBP (ramp, cutoff=0.25), FBP (ramp, cutoff=0.5), and OS-EM without any correction (16 updates); Middle: OS-EM with ADS corrections (16, 32, 48 updates); Bottom: 4D RBI-MAP with ADS corrections (16, 32, 48 updates).

With the development of new image acquisition strategies and reconstruction methods, computer phantoms and simulation tools provide an efficient means with which to test and optimize these techniques. The XCAT has been used to investigate many reconstruction techniques in PET, SPECT and CT as shown in Table 1.

B. Effect of Anatomy: Evaluation of Quantitative Imaging Methods for Organ Activity and Residence Time Estimation

With the flexibility to model different body types, the XCAT phantom can be used to investigate the effects of anatomy on medical imaging techniques. He et al⁷³ developed an initial population of 49 phantoms with realistic variations in patient anatomy, biodistribution, and biokinetics and used them to evaluate quantitative imaging methods in radioimmunotherapy.

111In ibritumomab tiuxetan SPECT and planar data were simulated from the phantom population using Monte Carlo simulation tools. The projections from the phantoms were used to evaluate the accuracy and variation in accuracy of residence time estimation methods that used a time series of SPECT and planar scans.

The results indicated that the processing methods differed both in terms of their average accuracy and the variation of the accuracy over the population of phantoms. The variations in accuracy due to the phantom variations were larger than those due to the noise (< 2% as measured in a previous study). This demonstrates the importance of using phantom populations to capture the effects of different anatomies in quantitatively evaluating imaging methods.

C. Effect of Respiratory Motion: CT-based Attenuation Correction in SPECT

Motions such as the cardiac, respiratory, and patient voluntary motions can cause artifacts in medical images which can lead to the misdiagnosis of patients. The XCAT phantom can be used to simulate different types of motions to study these effects and to develop compensation methods for them.

One representative study⁷² used the phantom to investigate the extent of respiratory artifacts using different CT scanners ranging from single-slice to state-of-the-art multi-slice units and examine the effects on reconstructed SPECT images using CT-based attenuation correction (CTAC). The XCAT phantom was used to realistically model different patient respiratory patterns while In-111 ProstaScint and Tc-99m Sestamibi SPECT emission projection data were generated from them. CT images were simulated as well using different scanners with varying rotation speeds and converted into attenuation maps for CTAC in reconstructing the SPECT data. The CT images as well as the reconstructed SPECT images were analyzed for the effects of respiratory motion.

Figure 6 shows example acquired and simulated respiratory artifacts in a slower acquisition CT scanner. These artifacts were found to increase with slower rotation speeds and to affect SPECT reconstructions using CTAC. Despite being less susceptible to motion, the fastest CT scanner was still found to result in artifacts in the SPECT reconstructed images due to the mismatch between the CT (breathhold) and SPECT (average motion) data.

Fig. 6.

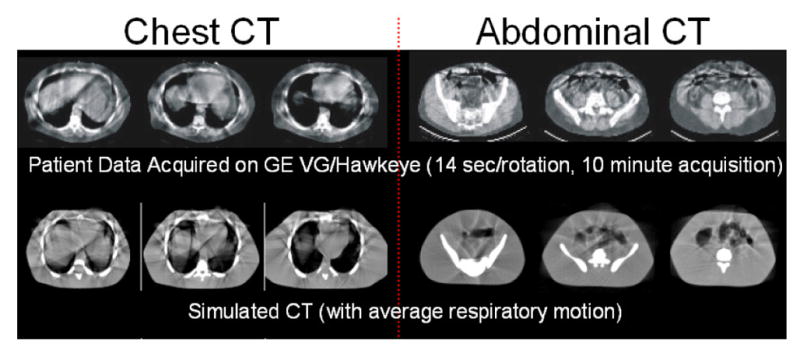
(Top) Type of respiratory motion artifacts that can occur in CT images acquired with a slower acquisition scanner (14 seconds per rotation)⁷². Artifacts appear as streaks and discontinuities. (Bottom) Simulated images generated from the 4D XCAT show similar artifacts.

D. Effect of Cardiac Motion on CT and MRI

The XCAT phantom has provided a valuable simulation tool to study the effects of cardiac motion as well. As an example of this work, in Fung et al⁷⁴, the XCAT cardiac model was used to investigate the effect of different stent diameters and heart rates on CT angiography images.

The 4D XCAT was used to simulate patients with no cardiac motion and with motion at different heart rates (50–110 beats/minute). Various stents of known size and location were placed within the coronary arteries. CT data was generated for each case based upon the Definition Flash dual-source CT scanner (Siemens Healthcare). The motion-free images were analyzed to assess the effect of stent diameter on the intra-lumen attenuation while the images with motion were used to assess the effect of heart rate on motion artifacts.

The results showed that attenuation differences from normal increase as the stent diameter decreases most likely due to the spatial resolution of the system. Motion artifacts, Fig. 7, were seen to increase with the heart rate and were worse for vessels such as the left circumflex (LCX) and the right coronary artery (RCA) which move the most and less for the left coronary artery (LAD) which moves the least. Significant artifacts were seen in the RCA even at a low heart rate. The pilot study illustrated the importance of optimizing the time resolution with regard to heart rate and vessel location for improved CT images at a reduced patient dose.

Fig. 7.

Coronary CT angiography simulation using the 4D XCAT phantom with coronary stents and the heart beating at (left to right) 50bpm, 70bpm, 90 bpm and 110bpm⁷⁴. Artifacts from the cardiac motion can be seen as streaks around the coronary vessels (zoom-ins shown for 90 bpm).

E. Compensation Methods for Voluntary Motion: PET Brain Imaging

Voluntary patient motions can also pose problems in medical imaging especially for applications that require long acquisitions. Since they are defined with NURBS surfaces, the XCAT phantoms can be easily modified to simulate voluntary motions such as shifting, repositioning, head motions, etc.

In Rahmim et al⁷⁵, the XCAT was used to simulate patient head motion to investigate a reconstruction-based compensation method for PET brain imaging. The XCAT was setup to simulate various head motions while Monte Carlo a methods were used to simulate the PET imaging acquisition. Different reconstruction methods were used to reconstruct the data including the method developed in the article, Fig. 8. The proposed method can be seen to greatly reduce the motion artifacts qualitatively and quantitatively.

Fig. 8.

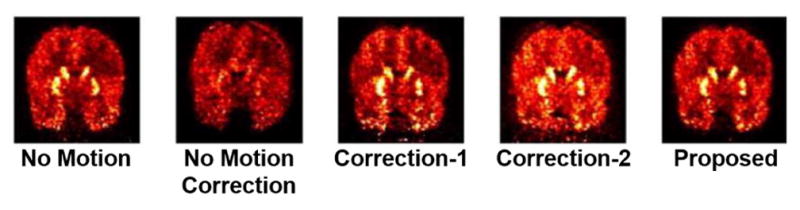
PET simulations performed using an adult male XCAT phantom⁷⁵. Reconstructed images after 3 iterations (32 subsets); (column 1) no motion, (column 2) no motion correction, (column 3) Motion Correction Method 1, (column 4) Motion Correction Method 2, (column 5) a proposed Motion Correction reconstruction method. Coronal slices are shown.

The previous studies show that patient involuntary and voluntary motions are important considerations in biomedical imaging. Careful work must be done to design protocols or methods to reduce artifacts. Many studies, as can be seen in Table 1, have been performed to investigate the effects of motion and to develop compensation methods for them. Phantoms, with the ability to simulate motion, can be instrumental in this research.

III. RADIATION DOSIMETRY

In addition to optimizing system design, imaging technique, data acquisition strategy and image reconstruction and processing methods, computerized phantoms provide a powerful tool to study radiation dosimetry. There is an increasing awareness and concern in medical imaging about possible population risk from exposure to ionizing radiation, particularly for nuclear medicine and x-ray CT⁷⁶. An important area for future biomedical research and clinical application is personalized medical procedures, i.e., optimizing techniques to fit the attributes of individual patients (sex, age, body type) so as to obtain diagnostic quality images at the lowest possible radiation dose.

Computerized models, such as the XCAT, provide a practical means with which to optimize and compare imaging applications in terms of image quality and radiation dose. Imaging of computational phantoms can be simulated repeatedly under many different scanning conditions and parameters without any fear of radiation exposure. As mentioned earlier, in addition to being able to simulate medical images from computational phantoms, it is also possible to calculate the radiation dose to the organs and structures. This is typically done using Monte Carlo methods, which realistically simulate photon transport for different imaging procedures within a patient or object as defined by a computational phantom. With these methods, the radiation exposure of the different organs can be calculated and compared to assess the effects of various scanning devices and parameters and to derive relationships with which to estimate the dose for patients.

The XCAT phantom has found great use in radiation dosimetry, Table 1. For our work, we developed and validated a Monte Carlo method to accurately assess radiation dose from x-ray-based examinations⁷⁷. When combined with the XCAT models, the MC program can provide accurate dose estimates for specific patients⁷⁸. The MC program can be used to simulate different imaging devices and protocols for comparison^79–81.

Using our MC method and our library of XCAT models, we have performed several studies investigating patient and population specific dosimetry. The following highlights the results from some of the representative studies.

A. Uncertainties in CT Dosimetry: XCAT as Compared to Other Computational Phantoms

One study investigated the uncertainties in CT dose and risk estimation associated with different types of computational phantoms (in comparison with the XCAT models) for a representative group of CT protocols⁸². The main purpose of this study was to provide insight into the effects that different types of reference phantoms have on CT dosimetry and thus lead to a better understand of radiation dose received by patients undergoing CT examinations.

Organ doses were estimated for 13 typical body and neurological CT protocols. The MC program⁷⁷ was setup to simulate a LightSpeed VCT clinical system from GE Healthcare. For each protocol, four methods were used, each using a different set of reference phantoms: (1) the standard adult male and female XCAT phantoms with organ masses matched to ICRP 89 values⁸³, (2) the reference male and female phantoms described in ICRP publication 110⁸⁴ which also had organ masses matched to those from ICRP 89, (3) a commercial dosimetry spreadsheet (ImPACT group, London, England) with its own hermaphrodite stylized phantom⁸⁵, and (4) another widely used dosimetry spreadsheet (CT-Expo, Medizinische Hochschule, Hannover, Germany) with its associated male and female stylized phantoms⁸⁶.

In the analysis, it was found that, despite closely matched organ masses, total body weight, and height, large differences in organ dose existed between the phantoms due to variation in organ location, spatial distribution, and the dose approximation method (used to estimate dose to organs not explicitly defined as none of the phantoms had all radiosensitive organs). Similar to the results of Section II.B, the findings illustrate the importance of compiling a large number of accurate, but anatomically diverse phantoms to capture the internal and external variations in patients.

B. Dose in CT and Other X-ray Based Modalities

Several comprehensive studies have been performed to investigate patient-specific radiation dose and cancer risk for pediatric and adult CT^87–90. Typical body and neurological CT protocols and their associated scan parameters were once again modeled using the Monte Carlo program⁷⁷. The MC program was then used to estimate organ dose from different sub-populations of the XCAT phantoms (pediatric and adult). From the data, the different factors affecting dose were evaluated including patient size, patient age, and scanning parameters.

For the body protocols, the dose to the individual organs fully or partially inside the scan coverage was found to decrease with an increase in the average chest diameter of the phantom patient. The dose for the organs outside the scan coverage showed a weaker correlation with patient size but a strong correlation with the distance between the center of the organ and the center of the scan region. This was due to that fact that the dose distributed to these organs was primarily from scattered radiation whereas the absorption is exponentially related to the distance from the center of the scan region to the organ center outside the scan.

The dose results obtained from neurological protocols for the organs fully or partially inside the scan coverage showed a relatively weak correlation with patient size and dose to individual organs. However, the correlation was generally stronger for large organs, such as the brain, that were located entirely inside the corresponding scan coverage and for the distributed organs (bone, marrow, and skin). For the organs outside the scan coverage, as with the body protocols, the organ dose strongly correlated with the distance between the center of the scan region and the center of the organ.

The effective dose was found to decrease exponentially with an increase in patient size. The exponential correlation for body protocols was strong (r > 0.87), but weaker for neurological protocols (r < 0.41)⁹⁰. For neurological protocols, effective dose was more strongly correlated with the measured trunk height of the patient than with the patient diameter.

When normalized by the dose–length product (DLP), the organ and effective doses were found to be independent of collimation, pitch, and tube potential (<15% variation⁹⁰) meaning the results are largely scanner-independent. They can be further applied to other CT systems with reasonable accuracy. These numbers are averaged across the entire population of phantoms or patients, however. For a given patient, this discrepancy can be as large as 25%^{89, 90}. These results indicate that as a first order approximation, we can generalize across scanners. However, true patient specific organ dose calculations need to take the exact scanner into account.

Based upon the relationships found in the studies, a dose estimation smart phone application⁹⁰ was designed and developed to be used as a tool to estimate dose to patients, Fig. 9. The dose calculator can be used by radiologists to conveniently estimate and report the dose values for a patient across a multiplicity of CT scan protocols. Using similar techniques to those above, the application is currently being extended to include radiography and tomosynthesis exams.

Fig. 9.

iPhone dose calculator developed based upon dose estimations from a series of XCAT adult phantoms⁹⁰.

From our work we concluded that correlations of dose with patient size and age or other factors (organ center distance from scan center, trunk length, etc.) can be used to estimate patient-specific dose for patients. Such relationships can provide guidance in the design and optimization of imaging protocols, tailoring them to the individual patient’s characteristics. Computational phantoms like the XCAT provide the means with which to derive these relationships and to identify their limitations.

C. Tube Current Modulation in CT

Many dose estimation models, such as those above, are based on fixed tube current simulation while the majority of CT scans are currently done with tube current modulation (TCM) techniques. A study was completed using our simulation tools to evaluate how different implementations of TCM affect the organ dose in chest and abdomen-pelvis CT⁷⁹.

Using a female adult XCAT phantom as the patient, various implementations of TCM were modeled in terms of modulation control strength, α. Organ dose was normalized by the volume-weighted CT dose index (CTDI_vol) to obtain dose conversion factors that are relatively independent of system specifics and scan parameters. The organ dose conversion factors were found to be a strong function of α, suggesting the need for TCM-specific organ dose conversion factors. However, for any α value (i.e., across modulation schemes), organ dose could be approximated using a scheme based on conversion factors established for fixed-mA scans. This was possible by multiplying fixed-mA conversion factors by an organ CTDI_vol derived from the tube currents at the location of an organ and the variation in organ volume along the longitudinal direction.

The results indicate that it is possible to estimate organ doses for TCM scans with good accuracy (~20%) with the knowledge of the mA modulation profiles using organ conversion factors derived from fixed-mA scans. As such, it is possible to develop a generic approach to assess organ dose across modulation schemes for patients using simulated results from phantoms.

D. Effects of Contrast on CT Dosimetry

Contrast enhancement is employed in over 60% of CT imaging studies. Contrast not only markedly impacts CT image quality but can also affect the radiation dose by as much as 70%⁹¹. A physiologically based pharmacokinetic (PBPK) model of the human cardiovascular system was recently developed and incorporated it into the XCAT phantom framework to simulate contrast dynamics⁹².

With the enhanced XCAT models, an initial study was performed to investigate the impact of contrast medium on radiation dose in a typical CT abdominal scan⁹³. The dose estimation was performed on 58 XCAT adult phantoms using the PBPK model to simulate patient-specific iodine concentration-time results for a commonly used uni-phasic intravenous injection protocol. MC methods were used to estimate the dose as a function of time for a common abdomen CT examination protocol used at our institution. The time varying organ and effective dose increment values were compared to those calculated for an un-enhanced CT examination. The simulation results using contrast indicated up to a 53% increase in the normalized organ doses. The calculated effective dose normalized by DLP showed up to a 28% increase with respect to the un-enhanced CT exam.

The results demonstrate the impact that contrast enhancement can have on patient dose. The biological effects of this were investigated in a separate study for iodine contrast⁹⁴. The relationship between radiation dose and injected contrast medium as a function of time studied in this work can be used as a guide to optimize contrast administration for individuals to reduce dose as well as any biological effects.

E. Comparison of Modalities

Dosimetry data from computerized phantoms can also be used to compare different imaging modalities. In the study by Zhang el al⁹⁵, a clinical radiography system used for chest radiography and tomosynthesis (Definium 8000, VolumeRAD, GE Healthcare) was compared to a clinical CT system (LightSpeed VCT, GE Healthcare).

The organ doses and effective doses were estimated from 59 adult male and female XCAT phantoms for each modality using typical protocols. From the simulated results, chest CT was found to have the highest dose, followed by tomosynthesis (12% that of chest CT) and radiography (1.3% that of chest CT), Fig. 10. Patient body size was found to have a much greater impact on the radiation dose of chest CT examinations as compared to radiography and tomosynthesis. This would indicate a greater benefit for larger patients in choosing chest tomosynthesis over CT.

Fig. 10.

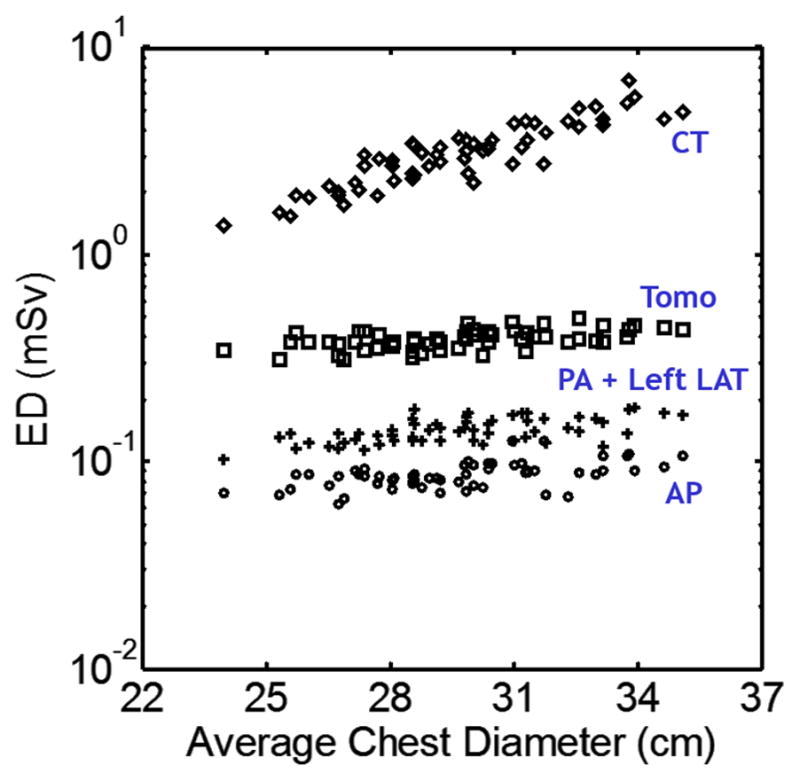
Distribution of effective dose with respect to patient size for CT, Tomosynthesis (Tomo), posteroanterior + left lateral radiography (PA + Left LAT), and anteroposterior radiography (AP)⁹⁵. With increasing patient average chest diameter, the effective dose for CT increased considerably in an exponential fashion, while effective dose for radiographic modalities only increased slightly.

F. Prospective Dosimetry

In addition to providing a patient base from which to retrospectively study radiation dose, the XCAT phantoms can provide a radiation dose library from which to prospectively predict the radiation dose for a given patient before the exam takes place. In the following study⁸⁰, a selected clinical patient, represented by a particular XCAT phantom, was optimally matched (based upon trunk height) with another XCAT phantom in the library to obtain a representation of the patient’s anatomy. The organ dose from a clinical abdominopelvic CT protocol was calculated for the two phantoms and compared. This was done for each of 58 adult XCAT models. In all phantom cases, the predicted organ dose (from the matching phantom) showed good agreements with organ dose from the patient XCAT model across all organs, and modulation profiles. Figure 11 shows the results from one matched pair of XCAT models.

Fig. 11.

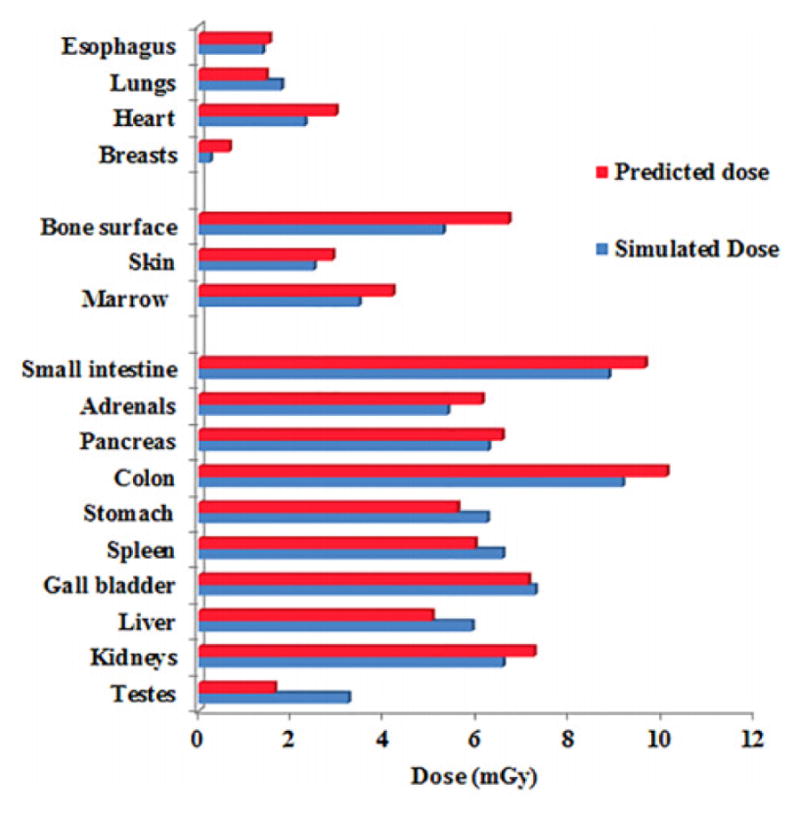
Predicted and simulated organ dose for a patient undergoing a clinical abdominopelvic CT imaging protocol⁸⁰.

With an atlas of computational phantoms that cover a broad range of human anatomy, a new clinical patient, prior to their exam, can be matched to a corresponding model that closely resembles the patient in terms of the locations of major organs. Dose measurements for the particular exam under various scanning parameters will have been pre-computed using MC techniques. These measures can be used to predict the dose that the patient will receive. Such prediction models when tied to image quality metrics can allow one to optimize the CT protocol by adjusting the scanning parameters to achieve a target diagnostic performance with the knowledge of organ dose in advance of a CT exam.

IV. RADIATION THERAPY

Patient respiratory motion offers a major challenge for radiation therapy (RT). The motion not only varies from individual to individual, but also within the same patient for different breaths. New techniques in RT require extensive validation, but in order to perform a thorough assessment to validate the robustness of a given technique, a large amount of patient data is required. Such data may not be feasible to collect due to radiation concerns or manufacturer imposed constraints on clinical systems.

Computational phantoms and simulation techniques offer an alternative method for studies in radiation therapy. With their ability to simulate different patient motions and anatomies, the XCAT series of phantoms have provided a valuable tool for research in radiation therapy, Table 1. The following section presents some applications in this line of research.

A. 4D Radiotherapy Research Framework

An integrated program in Matlab was developed in order to facilitate the characterization and implementation of the XCAT models in 4D radiation therapy research⁹⁶. From it, one can: (1) generate 4D XCAT images with customized parameter files, (2) review 4D XCAT images, (3) generate composite images from 4D XCAT images, (4) track motion of selected regions-of-interest (ROI), (5) convert XCAT raw binary images into a DICOM format, and (6) analyze clinically acquired 4D CT images and real-time position management (RPM) respiratory signals.

Using the program, the respiratory pattern of the XCAT phantom can be individually customized to simulate even complex and irregular respiratory motion. In addition, the anatomy of 4D XCAT phantom can be customized to best approximate a real patient’s anatomy. The high flexibility of 4D XCAT phantom makes it a potential patient-specific 4D quality assurance tool.

The computer program developed in this work can be used to generate, review, analyze, process, and export the 4D XCAT images for 4D RT research. Figure 12 shows the beam arrangement and dose distribution of the lung stereotactic body radiation therapy (SBRT) plan created on one particular XCAT phantom. These results are comparable to clinical plans of real patients. The program offers a robust workflow to implement the 4D XCAT phantom for 4D RT research. We are currently using it to investigate optimal 4D CT imaging techniques for RT.

Fig. 12.

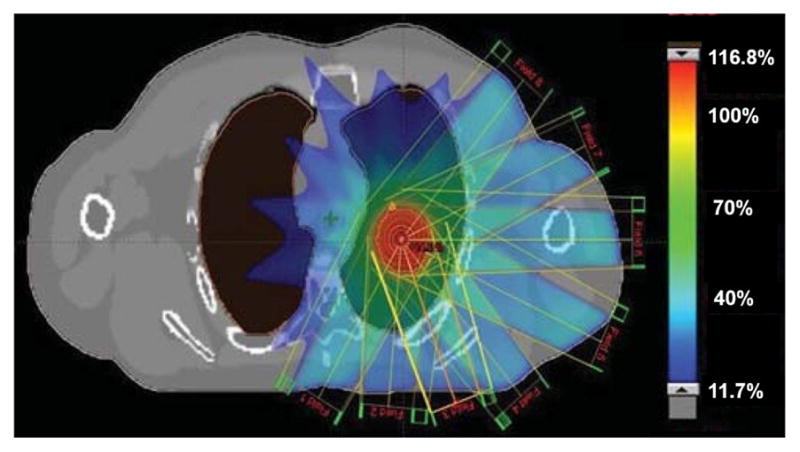
Beam arrangement and dose distribution of a lung SBRT plan created on the XCAT phantom⁹⁶. Colorbar shows Planning target volume dose (%).

B. Feasibility of 4D MRI

As an alternative to CT, the XCAT phantom has also been used to test the clinical feasibility of a 4D MRI technique for radiation therapy⁹⁷. 4D MRI yields no radiation dose to patients and can provide improved soft-tissue contrast without significantly adding imaging time and cost.

The proposed 4D-MRI technique involves continuously acquiring axial images throughout the breathing cycle using fast 2D cine-MR imaging and then retrospectively sorting the images by respiratory phase. The body area of the axial MR images was used as an internal respiratory surrogate to extract the breathing signal. To test the method, a male adult XCAT phantom was setup to include the following parameters: maximum diaphragm motion of 3.0 cm, maximum chest surface motion of 1.0 cm, and a breathing period of 5s. A spherical tumor of 3 cm in diameter was simulated in the liver. 4D MRI images were then simulated from the phantom, breathing normally, mimicking the imaging process of the proposed technique. Motion trajectories of the tumor were determined from the simulated 4D MRI and compared to the known motions as output from the 4D-XCAT.

The simulated images, Fig. 13, and the tumor motion trajectory showed good consistency with the known truth as provided by the 4D-XCAT phantom. The results demonstrated the feasibility of a novel retrospective 4D-MRI technique that uses body area as a respiratory surrogate. The XCAT phantom has been further applied to investigate other strategies for 4D MRI to improve temporal/spatial resolution^{98, 99}.

Fig. 13.

Sagittal (a) and coronal (c) XCAT images compared to the sagittal (b) and coronal (d) images of simulated 4D-MRI⁹⁷.

C. 4D-Cone beam CT (CBCT) Development and Evaluation

The XCAT phantom is also being applied to investigate methods for 3D/4D cone-beam CT (CBCT). 3D CBCT is the current technique for target localization prior to radiation delivery, while 4D CBCT is an emerging on-board imaging technique for target localization.

4D CBCT images are generated differently from 4D CT. Instead of combining reconstructed axial slices per respiratory phase, 2D projections are acquired over multiple respiratory cycles and then sorted according to phase prior to reconstruction. In order to generate 4D CBCT datasets, the acquired slice/projection must be correlated with respiratory phase, typically using external markers to serve as surrogates for the measurement of respiratory phase. However, the relationship of these markers with respiratory motion is uncertain and can lead to mismatching of projections.

A novel technique based on Fourier Transform theory was developed to directly extract respiratory information from projections without the use of an external surrogate¹⁰⁰. To comprehensively evaluate the markerless technique, a simulation study was performed using the XCAT phantoms¹⁰¹. The phantoms were used to model different patient anatomies as well as variations in the respiratory motion (including changes in respiratory cycle duration, inspiration to expiration ratio, diaphragm motion amplitude, AP chest wall motion amplitude, and tumor and organ derived trajectories). The results of the study demonstrated the robustness of the markerless technique for a variety of respiratory and anatomical scenarios.

V. OTHER APPLICATIONS

In addition to the above fields and beyond Table 1, the XCAT models have found applications in other areas of research for the defense industry and for electromagnetic (EM) radiation simulation, computational fluid dynamics (CFD), and for medical device analysis and design. In these areas, the XCAT phantom is often converted into a finite-element (FE) model for analysis.

In a study performed by the Advanced Physics Laboratory (APL) at Johns Hopkins University¹⁰², the chest anatomy of a 50^th percentile male (height and weight) XCAT phantom was manually converted into a FE model. The FE model was used to study the blast effects on the human torso and to aid in the design of personal protective equipment. Figure 14 shows one computer simulation illustrating the progression of the blast pressure wave as it acts upon the outer surface of the XCAT.

Fig. 14.

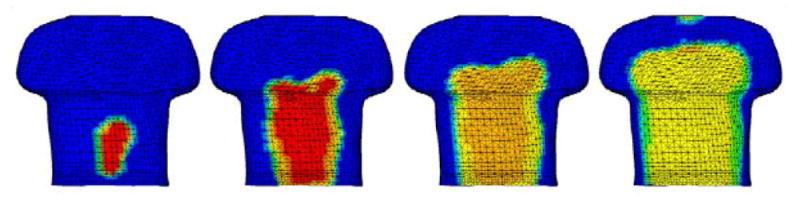
Torso of an XCAT phantom showing the blast loading time progression, from left to right, for 0.10 ms, 0.12 ms, 0.140ms, and 0.18ms¹⁰².

In the above work, the XCAT model was manually converted into a FE model which is a laborious process. Working with Kerim Genc from Simpleware and Marc Horner from ANSYS, a pipeline using the ScanIP software was developed to efficiently convert the surface-based XCAT phantoms into FE models¹⁰⁴ to perform analysis for different applications.

In a study done by Randles et al¹⁰³, the vasculature of a male adult XCAT phantom (50^th percentile) was converted by ScanIP into a FE model and then used to investigate fast computational methods to simulate flow in arterial networks, Fig. 15. The idea is that medical imaging can be used to obtain the specific geometry of a patient’s circulatory system. Simulations using such models have been previously restricted due to their computational cost. A faster method, such as that developed here, will enable patient-specific blood flow simulations for improved diagnosis/treatment of patients with a range of vascular diseases.

Fig. 15.

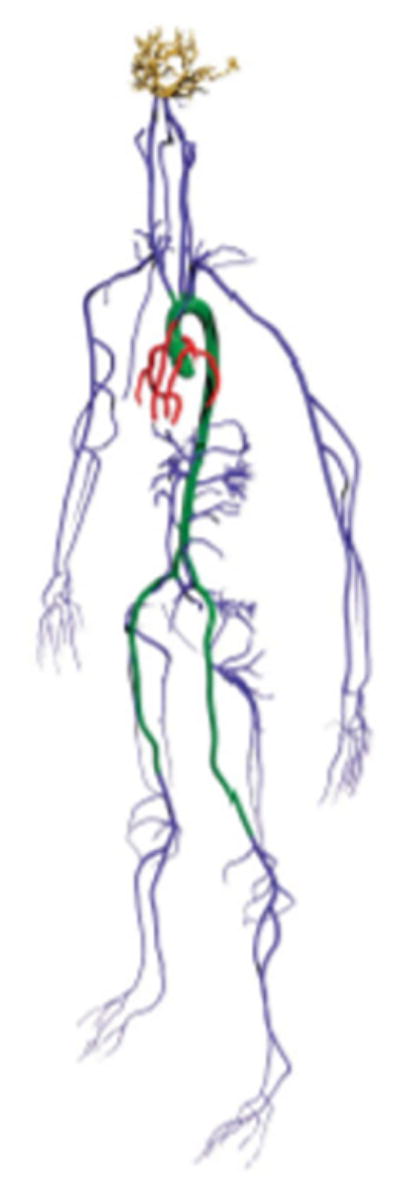
FE model of the XCAT arterial network¹⁰³.

In another study, Seckler et al¹⁰⁵ utilized a FE XCAT cardiac model to investigate the effect of various patient-, device-, and lead-depending parameters on the risk of electromagnetic interferences (EMIs) in patients with bipolar cardiovascular implantable electronic devices (CIEDs). EMIs have the potential to cause CIEDs, such as pacemakers and implantable cardioverter-defibrillators, to malfunction posing a serious risk to patients. The objective of the simulations using the XCAT was to ascertain the risk of EMI for different CIED lead placements, heart positions in the thorax and tissue conductivities of the organs by numerically calculating the voltage induced in bipolar leads. Figure 16 shows example results for the current induced in the body due to electric and magnetic fields. The voltage induced in the distal end of bipolar leads depends on the current. Through these simulations and comparison to human data, the study demonstrated that the lead-tip’s position and orientation are decisive parameters regarding the susceptibility of bipolar CIEDs.

Fig. 16.

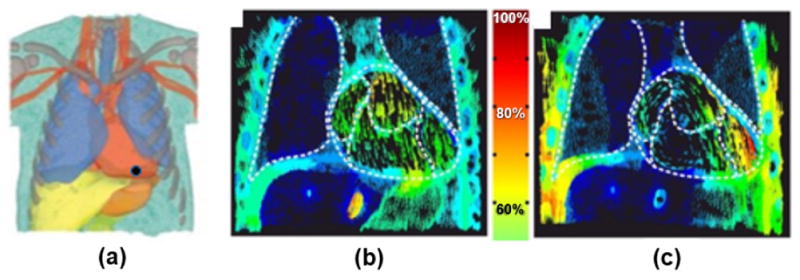
FE cardiac simulations using the XCAT¹⁰⁵. (a) The XCAT-male FE model, position of the tip electrode is indicated with a black dot. Current density distribution in the XCAT model for (b) the electric field and (c) the magnetic field. The color scale in the middle indicates the portion of the current density.

VI. CONCLUSIONS

With their ability to realistically model the human anatomy and physiology at different ages and body sizes, the 4D XCAT phantoms, originally developed for biomedical imaging research, have found a wide use in a variety of different fields. This review paper highlighted some of those uses. For reference, Table 2 summarizes the various tools of the XCAT and common programs that have been used with it for research. Many other tools are also available as can be found in the literature and on the internet.

Table 2.

Summary of tools developed for the XCAT and common programs used with it. Different phantom representations (voxelized, FE mesh, polygon mesh, or NURBS surfaces) are required for different programs. XCAT tools indicated by an asterisk can be obtained by contacting paul.segars@duke.edu.

*XCAT phantom software and models
XCAT program: generates phantoms (typically within minutes) as voxelized images, NURBS or polygon mesh surfaces given user-defined parameters
XCAT library of phantoms: work with the XCAT program or can be saved in a variety of 3D formats (stl, iges, obj, step, sat, dxf, etc.)
Tools to view XCAT phantoms as voxelized images
ImageJ,	imagej.nih.gov/ij
AMIDE,	amide.sourceforge.net
ANALYZE,	analyzedirect.com
MATLAB,	www.mathworks.com/products/matlab.html
Any program that can read raw binary images (32 bit float, little endian)
Tools to view XCAT phantoms as surfaces
Rhinoceros,	www.rhino3d.com
*Rhinoscripts to input/output the phantoms
Tools to deform or reposition the XCAT phantoms
Anatomical and motion parameters within the XCAT software8 *Rhinoscripts to manipulate XCAT surfaces within Rhinoceros software
Tool to convert XCAT phantoms into FE models to input into FE analysis software
ScanIP,	www.simpleware.com/software/scanip/
Monte Carlo methods for simulating SPECT, PET, and X-ray projection data and calculating radiation dose from XCAT phantoms (operate mostly on voxelized representations of the phantoms, some may include the ability to use NURBS or polygon meshes)
MCNP,	mcnp.lanl.gov
SIMIND,	www.msf.lu.se/forskning/the-simind-monte-carlo-program
SimSET,	depts.washington.edu/simset/html/simset_main.html
EGSnrc,	www.nrc-cnrc.gc.ca/eng/solutions/advisory/egsnrc_index.html
GATE,	www.opengatecollaboration.org/
GEANT-4,	geant4.cern.ch/
PENELOPE,	www.oecd-nea.org/tools/abstract/detail/nea-1525
Li et al.77
*Analytical method for simulating X-ray projection data from XCAT phantoms (calculates projections directly from the NURBS surface definition of the phantoms without voxelization)
XCAT X-ray projector106
Reconstruction algorithms for reconstructing SPECT, PET, or X-ray projection data into medical images
Users typically use their own software Reconstruction packages such as the Michigan Image Reconstruction Toolbox (MIRT), web.eecs.umich.edu/~fessler/code, are also publically available
MRI simulators for generating MRI images from XCAT phantoms
MRISIM107,	github.com/BIC-MNI/mrisim
OD1N,	http://od1n.sourceforge.net/

The different applications presented here illustrate the increasing importance of simulation methods and tools in research. Simulation gives researchers the ability to perform experiments virtually that would be otherwise impossible with live subjects. As such, they are providing a valuable precursor or ultimately an alternative to clinical trials.

In clinical studies, the knowledge of the true disease state is often difficult or impossible to obtain. Second, even if truth is available, it is difficult, expensive, time consuming, and often very impractical or impossible to obtain a sufficient number of clinical studies. Due to radiation concerns, some studies may not even be ethically permissible.

Physical phantoms offer an alternative to live patients, but it would be prohibitively expensive to fabricate a series of them modeling the various anatomical variations seen in a population. In addition, motions such as the cardiac and respiratory motions are not easily incorporated into physical test objects.

Through user-defined computational phantoms and physics-based operators, simulation provides a known truth from which to quantitatively evaluate, optimize, and compare different methods or techniques. There are no limits in a virtual world, any number of different anatomies or parameters can be generated and tested. It is possible to conduct experiments quickly and cost effectively via simulation, giving researchers the ability to answer fundamental questions that can only be practically answered given the precise controls afforded in the virtual domain. With a sufficient level of realism, virtual methodologies may even be used to replace actual clinical trials.

Current research in the development of computerized phantoms strives for increased realism. Despite its progress and utility, the XCAT phantom, as other computational models, still has much room to grow. This is exemplified by the applications of the XCAT in medical imaging. Other than dosimetry, the phantom has been primarily used for lower resolution modalities such as nuclear medicine. Like current computational phantoms, the organs and structures within the XCAT phantoms are modeled as homogeneous and include only simplified, geometrical models for pathologies. As a result, the phantoms, while adequate for dosimetry studies, are limited in their ability to assess image quality in higher resolution modalities such as CT and MRI. The images simulated with them are far too unrealistic as can be seen in Fig. 6. To overcome this limitation, we are currently investigating adding finer anatomical detail for additional structure definition¹⁰⁸ and the use of volumetric textures¹⁰⁹ to model the interior heterogeneity of the structures in the XCAT phantoms.

As the XCAT phantoms and other computational models get more and more realistic, they will find even greater use in biomedical and bioengineering research. Newer methods and applications including textured organs and dynamic perfusion are also underway that are expected to expand the use and utility of the XCAT phantoms in virtual simulations.