Abstract
The main goal of this paper is to introduce the concept of iso-perceptual manifold for perception of body configuration and related variables (kinesthetic perception) and to discuss its relation to the equilibrium-point hypothesis and the concepts of reference coordinate and uncontrolled manifold. Hierarchical control of action is postulated with abundant transformations between sets of spatial reference coordinates for salient effectors at different levels. Iso-perceptual manifold is defined in the combined space of afferent and efferent variables as the subspace corresponding to a stable percept. Examples of motion along an iso-perceptual manifold (perceptually equivalent motion) are considered during various natural actions. Some combinations of afferent and efferent signals, in particular those implying a violation of body’s integrity, give rise to variable percepts by artificial projection onto iso-perceptual manifolds. This framework is used to interpret unusual features of vibration-induced kinesthetic illusions and to predict new illusions not yet reported in the literature.
Keywords: Reference coordinate, uncontrolled manifold, iso-perceptual manifold, perceptual equivalence, kinesthetic illusion
Introduction
The main goal of this paper is to introduce a theoretical framework for perception of body configuration and related variables (e.g., velocities, joint moments of force, contact forces, etc.) collectively addressed as kinesthetic perception. The discussion is limited to conscious perception as reported by a person or produced in a matching task, which is viewed as a result of measurement performed within a frame of reference with the help of a measuring device. We understand the frame of reference to be an abstract coordinate system and a set of reference points that locate and orient the coordinate system; these will be addressed as reference coordinates (RCs). Defining such a frame of reference is associated with efferent processes, i.e. those involving signals from the brain to the spinal cord and to the muscles for motor action production. Playing the role of measuring device are afferent signals, i.e., those from peripheral sensory receptors to the spinal cord, brain stem and to the brain, reflecting deviations of the system from the RCs. Interactions between efferent and afferent signals are presumed to happen at different hierarchical levels and can lead to perception of salient variables at the levels of individual muscles, joints, limbs, and the whole body.
This paper first introduces a number of concepts and theoretical views developed primarily in the field of motor control (reviewed in Latash 2010, 2016; Feldman 2015). These include: (1) the equilibrium-point hypothesis and its recent generalization to the control of multi-effector movements with changes in the body referent configuration; (2) relations between actual objective physical body states (and possibly dynamical states) with the current RC and afferent information; and (3) the uncontrolled manifold (UCM) concept (Scholz and Schöner 1999) and its relation to the classical problem of motor redundancy (Bernstein 1967). Then, the novel concept of iso-perceptual manifold (IPM) is introduced. This concept refers to the invariance of percepts at different levels of analysis despite variable efferent and afferent signals. The IPM concept refers to sub-manifolds in the state spaces of afferent and efferent variables that produce the same (stable) percept, which may not necessarily match physical reality. The IPM concept is illustrated with particular emphasis on biased and illusory percepts. These include several well-known illusions and some new illusions that are predicted to exist but have not been described in the literature.
The general scheme accepted in the paper is that action in the environment may be coupled to perceptual information without updating the picture of the world (cf. ecological psychology, Kugler and Turvey 1987; Richardson et al. 2008). Signals at some point within this loop can be used to update the picture of the world and, for example, lead to verbal reports on percepts or to thoughts not reflected in overt actions as exemplified by the two-system hypothesis of visual perception (cf. Goodale 1993; Milner and Goodale 2008).
Since this is the first paper to introduce the IPM concept, its goals are limited by both reasonable paper size and competence of the author. As such, numerous aspects of the overall scheme remain to be refined, developed, and illustrated. These include, in particular, philosophical aspects of perception and its relation to objective physical variables, psychology of kinesthetic perception and perception-action coupling, neurophysiology of such central concepts as efferent copy and referent configuration, potential role of different feedback loops and other sensory modalities such as the visual and vestibular systems, the mathematical apparatus associated with the described approach, and explanatory power of this approach in comparison with other approaches. Addressing all these aspects adequately in a single paper is impossible; besides, the author admits that some of those issues are beyond his expertise. Reflecting the current, early stage of development of the IPM concept, the paper uses purposefully simplified illustrations and omits certain potentially important topics. Such simplifications and omissions, which are in need of further development, are mentioned explicitly in further text.
The introduced conceptual scheme raises more questions than it answers. There is, however, already an illustration that the suggested approach is productive: Since the first version of this paper was written, one experimental study motivated by this approach has been performed and published (Reschechtko et al. 2017).
Reference coordinates: Their role in perception and action
The traditional view on kinesthetic perception considers it a consequence of an interaction between two neural processes, afferent and efferent. One of the most influential concepts linking afferent and efferent processes has been that of the efferent copy (von Holst and Mittelstaedt 1950), also known as corollary discharge (Sperry 1950). Within this scheme, two types of changes in afferent signals are considered: exafference due to changes in external forces and reafference due to self-initiated action. Exafference always contributes to perception while reafference does not, unless it deviates from its expected level based on the efferent copy. In addition, the efferent copy plays an important role in modification of commands to muscles in response to changes in sensory information.
A simplified version of this scheme, associating efferent copy with the output signals from alpha-motoneurons, has been criticized recently (Feldman 2009, 2015, 2016). Further, a recent study has concluded that some muscle activations, in particular those during the Kohnstamm phenomenon, are not accompanied by an efferent copy (De Havas et al. 2015), in contradiction to its original definition. Despite these criticisms, the basic principle that the central nervous system actively processes signals related to its internal state for both motor and perceptual processes – the reafference principle – remains valid and is accepted in this paper.
A particular scheme of interactions between afferent and efferent processes has been suggested within the framework of the equilibrium-point (EP) hypothesis (Feldman 1966, 1986) and its recent development as the control of movements with changing spatial RCs for the involved effectors (reviewed in Latash 2010, 2016; Feldman et al. 2013; Feldman 2015). Within this approach, the neural control of an action can be adequately described as setting time changes of RCs for salient variables at any level of analysis: from the whole body, to the endpoint of a limb, to individual joints, and to individual muscles. Figure 1 illustrates this concept for an arbitrary vector variable X and associated force vector FX. The physiological meaning of RC is subthreshold depolarization of a corresponding neuronal pool; in particular, at a single-muscle level, RC is equivalent to the threshold (λ) of the stretch reflex or, equivalently, to subthreshold depolarization of the alpha-motoneuronal pool.
Figure 1.
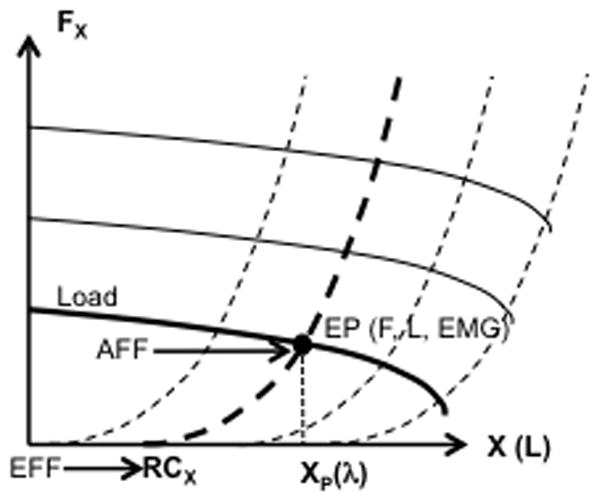
The plot shows a family of dependences of a force vector FX on a spatial vector variable X (the dashed line). The efferent process (EFF) defines a referent coordinate (RCX), while the afferent signals (AFF) inform on deviation of X from RCX. At a single-muscle level, RCX is equivalent to the stretch reflex threshold (λ), while FX is muscle force (F) and X is muscle length (L). For a given external load (the solid curves show a family of load characteristics), the system comes to an equilibrium point (EP) with a combination of F, L, and muscle activation (EMG), which is the point of intersection of two characteristics (shown as thick lines) defined by the actual external load and values of λ.
Within this scheme, the neural control of a single muscle can be described as setting a value of λ, while performance variables, such as muscle length, force, and activation level emerge depending on the external load. Changing λ leads to a nearly parallel translation of the dependence of muscle force on muscle length (see the family of dashed curves in Fig. 1). External load may also be represented on the force-length plane as a line; the family of solid lines in Fig. 1 illustrates arbitrary load characteristics of different magnitude. For a given load characteristic and given λ (shown as thick lines in Fig. 1), the point of intersection defines an equilibrium state (equilibrium point, EP, the filled circle in Fig. 1) with a combination of muscle activation level, force, and length. Note that, if the external load were zero (this is an unlikely situation given the presence of antagonist muscles and gravity), the muscle would shorten and come to rest at a length value equal to λ and zero activation. For this reason, λ can be called reference length or RC of the muscle.
Within this scheme, voluntary movements are produced by a change in λ with or without a change in the external load. Note that effects of a change in λ on muscle activation and mechanical consequences depend on the external load characteristic. For example, the same change in λ leads to a movement in isotonic conditions and to a change in force in isometric conditions. Involuntary movements occur if the external load changes while λ is kept unchanged.
This approach associates the efferent process (EFF in Fig. 1) with setting a frame of reference defined by the corresponding RC, within which afferent signals (AFF in Fig. 1) are measured and interpreted. This basic idea has been developed recently by the group of Feldman (Feldman 2009; Feldman et al. 2013) who have suggested that position sense is an additive function of a centrally set RC and deviations from the RC signaled by afferents. These authors schematized this idea with an equation Q = RC + P where Q stands for perceived position, and P for the position-sensitive afferent signals.
Stability of the perceived world and one’s own body is at least as functionally important as stability of action in that world: Without a stable picture of the world, one has no chance of generating purposeful movements in it. Within this paper, we address only one aspect of stability – namely dynamical stability of states and trajectories – issues of structural stability are not considered. Given the many sensory modalities and numerous sources of sensory information within each of the modalities, the overall sensory space is very high dimensional. Since sensory signals are interpreted within reference frames defined by the ongoing efferent processes, the dimensionality of the relevant space becomes even larger. The principle of abundance (Gelfand and Latash 1998; Latash 2012) considers the apparently redundant design of the human body (with respect to both motor and perceptual functions) as a beneficial feature that allows ensuring stability of salient variables in a task-specific way across the range of behaviors and helps to avoid negative interference when two or more variables are produced simultaneously. In this paper, we develop this approach for perception and introduce a number of novel concepts, such as IPM and perceptual equivalence, which allow addressing stability of salient percepts. Later, we illustrate this approach using several examples including vibration-induced kinesthetic illusions.
Systems of coordinates
Experimental studies of action and perception involve measuring variables that are indirectly related to the involved neural processes. In most studies, these are performance variables directly linked to task success. Other variables, which may be recorded, reflect outputs of elements that contribute to the task-related performance (e.g., joint rotations, digit forces and moments, muscle activations, etc.) and are addressed here as elemental variables. Some variables may not be directly measured but computed based on measured or assumed parameters of the system; these include, for example, joint torques, muscle forces, motion of the center of mass of the body or its segment, etc.
While these variables provide a wealth of valuable information, they reflect the combined effect of both the neural process and environmental factors such as the external force field. There have been several attempts to make a step toward identifying systems of coordinates reflecting neural processes based on measured performance variables. One of the dominant ideas, originating from the classical studies by Bernstein (1947, 1967), has been that elements are united by the central nervous system into relatively stable groups to reduce the number of parameters manipulated at task-related neural levels. In particular, analysis of correlations within large sets of performance variables and other methods have been used to reduce typically high-dimensional sets of elemental variables within an action to lower-dimensional sets of variables addressed as synergies or modes (d’Avella et al. 2003; Krishnamoorthy et al. 2003; Ivanenko et al. 2004; Ting and Macpherson 2005; Santello et al. 2016). To avoid ambiguity, we will use here the term mode for groups of recorded variables to be able to use synergies for neural organizations providing for stability of salient variables (reviewed in Latash 2008; Latash and Zatsiorsky 2016).
The word synergy has been used in at least two other meanings. In the clinical literature, this word has a strong negative connotation; it implies stereotypical patterns of motion or muscle activation interfering with intentional movements (e.g., flexion synergy and extension synergy) frequently seen after stroke (DeWald et al. 1995). As already mentioned, synergy has also been used to mean coordinated action of elements (muscles, digits, joints, limbs, and persons) with the purpose of ensuring stability of patterns of salient, task-specific performance variables such as resultant force, coordinate of the limb endpoint, etc. (reviewed in Latash et al. 2007; Latash 2008). This definition implies a crucial role of the central nervous system, although synergic patterns observed in experimental studies may depend on other factors such as the external force field and non-neural processes within the organism. Synergies, in this meaning, involve two important components. The first one is uniting potentially numerous elemental variables into a smaller number of groups (modes); further, the neural controller may use only one control variable to modify all the elemental variables within each mode. For a comprehensive discussion on modes see a recent review by Santello and colleagues (2016) with the accompanying comments and the authors’ response. The second step is using a set of modes as a coordinate system and ensuring stability of task-specific salient performance variables within that system. Experimental studies within this framework have been mostly performed in spaces of elemental variables representing kinetic, kinematic, or electromyographic outputs of the elements. Only recently, a step has been made towards defining synergies stabilizing behavior in spaces of hypothetical neural control variables associated with reference coordinates for the elements and the whole effector (Ambike et al. 2016; Reschechtko and Latash 2017).
Another coordinate system has been suggested recently that allows ensuring stability of performance using local control organized about each coordinate independently of possible changes in other coordinates (Akulin et al. 2015). A term control coordinates has been suggested for this system. Unlike modes, control coordinates are sensitive to task changes, particularly to changes in conditions that affect stability of performance. When a person encounters a novel task, he/she may search for an adequate set of control coordinates that would allow implementing local control rules. A specific example of control coordinates may be the eigenmovements (Alexandrov et al. 2001): kinematic coordinates representing linear combinations of joint rotation organized in such a way that motion along each coordinate depends only on torque vector along that particular coordinate.
Transformation across sets of coordinates has been a non-trivial issue. This can be done relatively easily only for sets of coordinates linked by linear transformations. In such cases, matrices of partial derivatives (Jacobian matrices, J) can be used. Using J matrices allows resolving the problem of different units used in different coordinate sets. Such matrices have been defined using different methods, for example explicit models of the system (if available, e.g., in studies of multi-digit action and multi-joint motion) as well as linear regressions between sets of coordinates. The two methods have been shown to lead to similar results (Freitas et al. 2010). The idea of J matrices has been used primarily for efferent (motor) variables.
Transformations among systems of coordinates are inherent to the problem of perception. Indeed, individual sensors generate neural signals reflecting specific mechanical variables (sometimes modulated by a neural input, such as the system of γ-motoneurons). This step already involves transformation from mechanical variables (e.g., newtons and meters) into neural variables (e.g., millivolts). RCs can also be expressed in either mechanical or neural variables. For example, λ may be expressed in muscle length units (meters, as in Fig. 1) or in units of depolarization of the alpha-motoneuronal membrane (millivolts, see Feldman 2015). As such, the mechanism of the stretch reflex plays the role of a translator between the languages of mechanics and neural processes. Further, these elemental variables are expected to produce meaningful percepts, e.g., those of joint configuration, contact forces with the environment, and/or body position in space. This step involves another transformation of coordinate systems. Some of these transformations will be considered later in more detail.
Redundancy, abundance, and the uncontrolled manifold
Any functional behavior is accompanied by variations in both intrinsic states of the body and the environment. Changes in the environment are commonly unpredictable; they include changes in both external forces and sensory signals, for example when stepping on a pebble during walking. These factors make dynamic stability a crucial feature of functions and behaviors.
One of the universal features of the system for movement production is the typical excess of elemental variables at any level of analysis as compared to constraints associated with typical tasks (cf. the problem of motor redundancy, Bernstein 1967). As a result, any task can be performed using an infinite number of patterns of elemental variables. Traditionally, motor redundancy has been viewed as a computational problem for the central nervous system, assuming that it had to “eliminate the redundant degrees of freedom” (Bernstein 1947). Optimization approaches have been commonly used to address such problems (reviewed in Prilutsky and Zatsiorsky 2002). An alternative view, the principle of abundance (Gelfand and Latash 1998; Latash 2012), considers the apparently redundant design of the human body as a beneficial feature that allows ensuring stability of salient performance variables across behaviors. The term synergy has been used to address such hypothetical organizations (reviewed in Latash 2008; Latash and Zatsiorsky 2016).
This approach assumes a hierarchical control scheme with a sequence of few-to-many mappings (Fig. 2). A low-dimensional input associated with a set of RCs for task-related salient variables (RCTASK) is transformed within this scheme into a high-dimensional set of control signals that define RCs for elements participating in the behavior (e.g., λ for the involved muscles). A number of mechanisms have been suggested to ensure relatively low variability of salient performance variables as compared to variability of elemental variables, ranging from optimal feedback control schemes to neural back-coupling schemes (Todorov and Jordan 2002; Latash et al. 2005; Martin et al. 2009). Control signals at different levels of the described hierarchy have been associated with spatial RCs for the level-specific effectors. For example, during a reaching movement, control at the task-specific level may be described as a reference hand trajectory (for simplicity, we do not consider here changes in apparent stiffness properties of the effector; cf. control of impedance, Hogan 1985). Further, it is transformed into a set of reference trajectories at the joint level associated with the reciprocal and co-activation commands (r- and c-commands, Feldman 1980). At the next stage, the {r;c} pairs are transformed into reference trajectories for individual muscles, which are equivalent to time-dependent changes in the thresholds of the stretch reflex (λ). Note that the mapping illustrated in Fig. 2 is not prescriptive and may be affected by signals not illustrated in the figure, including afferent information. Of course, the process in Fig. 2 does not by itself define physical states of the body, which are at all times also affected by the current afferent signals and induced reflex effects (such feedback loops are not shown in the figure).
Figure 2.
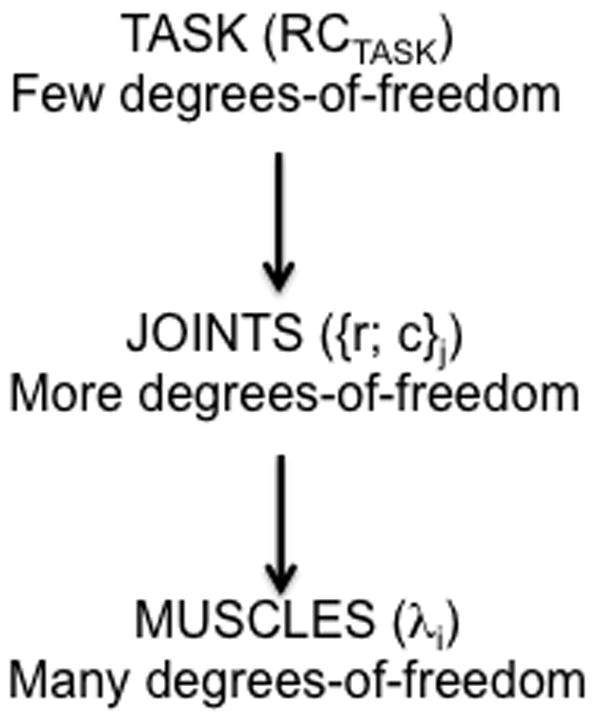
An illustration of a hierarchical control scheme with a sequence of few-to-many mappings. A task-related low-dimensional input (RCTASK) is transformed within this scheme into a high-dimensional set of control signals to elements such as the r- and c-commands for the joints and λs for the muscles. Feedback loops between levels are not shown.
The few-to-many mappings in Fig. 2 do not imply computational processes, such as, for example, a pseudo-inverse, or another optimization-based mapping. This topic is too broad to be considered here in detail; it has been addressed in several publications (Martin et al. 2009; Park et al. 2010). Such mappings may be based, for example, on local back-coupling loops similar to schemes described in the literature (Latash et al. 2005; Martin et al. 2009).
The UCM concept (Scholz and Schöner 1999; reviewed in Latash et al. 2007) originates from the idea of task-specific stability of sub-spaces within a high-dimensional space of elemental variables (Schöner 1995). UCM, by definition, is a collection of sub-manifolds forming a partition of the space of elemental variables (by definition a foliation) within which a particular salient performance variable remains unchanged. If a group of elemental variables is organized to ensure stability of a performance variable, two outcomes can be expected. First, if a task is performed several times, variance of elemental variables estimated at a comparable phase across trials is expected to be low in directions leading to changes in the salient performance variable, i.e., in directions orthogonal to the UCM, as compared to directions within the UCM. Second, if a quick action is performed, relatively large deviations are expected within the UCM (the, so-called, motor equivalent motion, Mattos et al. 2011) even if the purpose of the action has been to change the salient variable, i.e., to move orthogonal to the UCM (non-motor equivalent motion). Metrics of the variance and motor equivalence analysis have been studied across motor systems, tasks and populations (reviewed in Latash and Zatsiorsky 2016).
Figure 3 illustrates the UCM concept for the task of producing a constant value of a performance variable, which is the sum of the outputs of two effectors (e.g., pressing with two fingers to generate a magnitude of total force). The UCM for this task is a line with negative slope corresponding to the equation E1 + E2 = C, where E stands for the output of an effector and C is a constant. If a person performs this task many times, the cloud of data points is expected to represent an ellipse elongated along the UCM such that inter-trial variance within the UCM is larger than variance orthogonal to the UCM (VUCM > VORT) reflecting lower stability within the UCM as compared to stability orthogonal to the UCM. If a person is asked to produce a quick change in the performance variable and then return to the previous value, the new state will show deviations both along the UCM (motor equivalent, ME) and orthogonal to the UCM (non-motor equivalent, nME); ME > nME is expected. Note that Fig. 3 does not assume any kind of control of probabilities within the central nervous system, for example as proposed in schemes based on Bayesian decision-making (Körding and Wolpert 2003; Franklin and Wolpert 2011). In contrast, the unequal variances and unequal magnitudes of deviation in different directions reflect different stability properties along those directions. We do not know what physical/physiological processes lead to selective stabilization of salient performance variables reflected in the observed distributions of inter-trial variance and motor equivalence. The issue of saliency is definitely beyond the scope of this paper. We assume, however, that such physical/physiological processes exist (e.g., similar to those described in Latash et al., 2005; Martin et al. 2009) and do not consider in this paper computational schemes, for example optimal feedback control schemes (Todorov and Jordan 2002; Diedrichsen et al. 2010), which can lead to a similar structure of variance.
Figure 3.
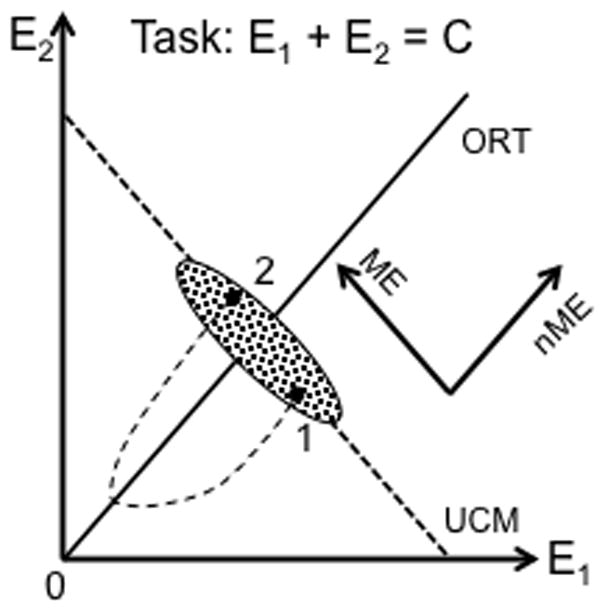
An illustration of the UCM concept for the task of producing a constant value of the sum of the outputs of two effectors: E1 + E2 = C. The UCM is shown with the thick dashed line with negative slope, while the orthogonal direction (ORT) is shown as a thick, solid line. If a person performs this task many times, the cloud of data points is expected to represent an ellipse elongated along the UCM. If a person is asked to produce a quick change in the performance variable and then return to the previous value, the new state will show deviations both along the UCM (motor equivalent, ME) and orthogonal to the UCM (on-motor equivalent, nME); ME > nME is expected.
Efferent processes for perception
Effects of action on perception have been known for a long time. These effects range from those limited to perception of a single joint position to perception of limb configuration and whole-body position in space. Arguably, one of the oldest examples is the illusion of motion of the environment when one displaces the eyeball by pressing on it with a finger. This illusion is absent when a similar eyeball motion is produced naturally. One interpretation is that eye motion leads to motion of the projection of the environment across the retina, which leads to different percepts depending on the efferent process associated with this motion. An alternative interpretation is that the apparent transient motion perceived during pressing on the eye is a consequence of a corollary discharge induced by the effort to keep fixation (Stark and Bridgeman 1983).
Another well-know example is the illusion of rotation of a symmetrical circular object induced by alternating presentation of two motionless circular objects with radial connectors turned with respect to each other (see Fig. 4; also see Zwickel et al. 2007). In this illusion the two objects are perceived as one, rotating either clockwise or counterclockwise, with about equal probabilities. If the viewer imagines that the object is a steering wheel and then tries to rotate this imagined wheel with his hands, the direction of the illusory motion stabilizes to become congruent with the ongoing rotation of the imagined steering wheel.
Figure 4.
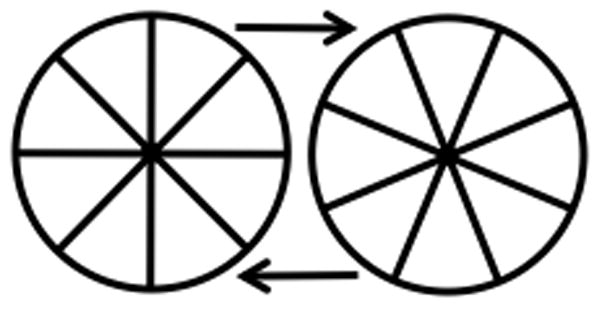
An illusion of rotation of a symmetrical circular object may be induced by alternating presentation of two motionless circular objects with radial connectors turned with respect to each other. The two objects are perceived as one, rotating either clockwise or counterclockwise, with about equal probabilities. If the viewer imagines that the object is a steering wheel and then tries to rotate this imagined wheel with their hands, the direction of the illusory motion stabilizes to become congruent with the ongoing rotation of the imagined steering wheel.
The aforementioned scheme of interactions between afferent and efferent processes for a single muscle within the equilibrium-point hypothesis of motor control is illustrated in Figure 5. Setting a value of λ sets a force-length muscle dependence, F(L), and thus contributes to solving the problem of perceiving muscle length and force. Indeed, for a given λ, only points on the F(L) dashed line are possible as equilibrium states of the system “muscle + reflexes + load”. Consider now changes in different proprioceptive signals along the F(L) curve. All of them are expected to increase with an increase in the distance of points on this curve from λ. Indeed, as one moves along the F(L) curve from λ to the right, muscle length increases, which is expected to lead to an increase in the activity level of muscle spindle endings. At the same time, muscle force increases leading to an increase in the activity of Golgi tendon organs. Muscle activation level also increases along the F(L) curve. As a result, any of the aforementioned signals can be used to identify a point on the F(L) curve and disambiguate the problem of perceiving these two variables. In other words, spindle endings contribute to perception of force, Golgi tendon organs contribute to perception of length, and even activity from the α-motoneuronal pools can also be used to perceive F and L. Of course, this requires an assumption that the controller uses λ to define a reference frame and other signals to define a point within that reference frame.
Figure 5.
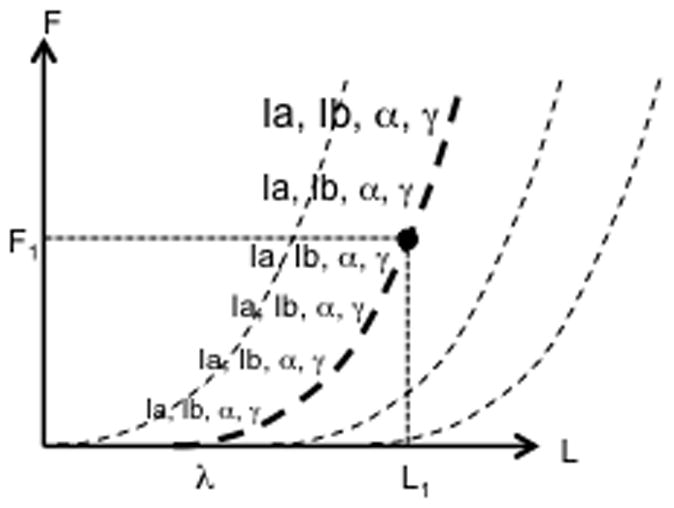
Setting a value of λ defines a dependence of muscle force on muscle length, F(L) shown as a thick dashed line, from a family of possible F(L) characteristics shown as thin dashed lines. As one moves along a specific F(L) curve from λ to the right, all the relevant afferent (e.g., Ia and Ib) and efferent (e.g., α and γ) signals increase.
The abundance of sensory signals contributing to kinesthetic perception does not lead to ambiguity in interpreting each signal individually. In contrast, it makes the perception of a point on the F(L) curve robust to possible problems with any one of the signals, for example due to a pathology or surgery. This view is supported by observations of nearly unchanged joint position sense following total joint replacement surgery (Cross and McCloskey 1973; Karanjia and Fergusson 1983; Wada et al. 2002). So, the central nervous system is able to recalibrate itself and use only a subset of available reliable sources of sensory information to perceive joint position and torque. Observations of vibration-induced kinesthetic illusions (VIKI, see later) suggest, however, that the central nervous system can be misled by artificial changes in signals along some of the relevant sources of sensory information.
Hierarchical organization of action and perception: The concept of iso-perceptual manifold
Within the described scheme of control with RCs, a relatively low-dimensional set of task-specific RCs defined at the top level of a hierarchy leads to higher-dimensional sets of RCs at lower levels (e.g., those corresponding to actions by individual limbs, digits, joints, etc.) down to RCs (equivalent to λs) for the numerous muscles involved in typical actions (Fig. 2). The apparently redundant, actually abundant, transformations RCTASK => RCEFFECTORS stabilize trajectories of salient, task-specific performance variables defined by RCTASK, likely with an important role played by feedback loops, both within the central nervous system and involving sensory signals that reflect changes in the salient performance variables (as in Latash et al. 2005; Martin et al. 2009). This general scheme has been indirectly supported by studies showing the importance of sensory variables for stabilization of motor performance. In particular, the importance of visual information has been demonstrated in several recent studies (Ranganathan and Newell 2008, 2009; Parsa et al. 2016, 2017). Another study documented impaired ability of healthy persons to organize stabilization of salient variables when somatosensory signals from involved muscles were distorted by high-frequency muscle vibration (Arpinar-Avsar et al. 2013).
Here, we suggest a scheme that unites stabilization of salient performance variables and stabilization of salient percepts (Figure 6). Within this scheme, sensory information is postulated reflecting not local variables measured by individual sensors (such as muscle spindle endings, Golgi tendon organs, etc.) but variables salient at the effector-specific and body-specific level (such as limb endpoint position/velocity in space, force vector produced by the limb endpoint, total force and moment produced by a set of digits, etc.). Presence of such signals within the body has been supported by results of several studies. In particular, Bosco and Poppele (2002) have shown that the modulation of activation levels of neurons in the spinocerebellar tract during locomotion is related to changes in general characteristics of the hindlimb, such as its total length and orientation, rather than to muscle- and joint-specific variables. A recent study has provided evidence for links of complex variables salient to grasping with activation in the medial parietal cortex (Fattori et al. 2017).
Figure 6.

Two processes contributing to perception at different levels: The descending process, {RC}n => {r; c}i => λj, n < i < j, and the ascending process, {Ia; Ib; II}p => {α;f}q => {S}m, p > q > m. The subscripts stand for dimensionalities of the corresponding spaces. At each level, length and force sense emerges at the level of interaction between {λ} and {Ia; Ib; II}, between {r; c} and {α;f}; and between {RC} and {S}. Perception of relevant state variables (a vector P) can be expressed as: P = RC + S. The “+” sign in this equation should be viewed as symbolic. For simplicity, the figure is not showing interactions between the ascending and descending processes and feedback loops among levels.
The scheme in Fig. 6 illustrates two symmetrical processes that link multi-dimensional sets of variables on the periphery to lower-dimensional sets at higher levels of the hierarchy. This scheme is purposefully simplified with no interactions between the two hypothetical processes, descending and ascending. Such interactions may play an important role, but we leave this aspect of the scheme to be developed in future. The descending process, {RC}n => {r; c}i => λj, has been described earlier (Latash 2010, 2017). Here, the subscripts n, i, and j stand for dimensionality at each level, n < i < j. The parallel ascending process, which is intimately intertwined with the descending one, has not been analyzed. We express it as {Ia; Ib; II}p => {α;f}q => {S}m, where p > q > m are dimensionalities of the involved sensory variables. Within this notation, only one intermediate level is postulated for simplicity, {α;f}q, corresponding to combinations of perceived coordinate (e.g., joint angles α) and force (f) vectors relevant for that level. In Figure 6, perceptual state estimates are generated at each level but not all may be consciously perceived. For example, in a reaching task, perceptual state estimates are assumed to exist at the levels of muscles and joints while the person may have troubles reporting on those variables at levels below the task-relevant level. The scheme in Fig. 6 is a simplified reflection of a physical/physiological system where processes proceed without any particular purpose beyond the step of formulating a task (this aspect remains outside the scope of this paper). In contrast to typical control-theoretical schemes, where purposes play a major role, no teleological aspects are presumed in the scheme in Fig. 6.
Based on everyday experience, we know that our perception of the body state is stable despite possible changes in both afferent and efferent processes as long as they are changed in a balanced way. For example, co-contracting muscles acting about a joint without moving it is associated with veridical perception of the joint being motionless. Position of an effector is also adequately perceived during pressing against an external stop with varying forces (Feldman and Latash 1982b). Note that in both mentioned examples, efferent signals (from both α and γ motoneurons) and afferent signals (e.g., from muscle spindle endings and Golgi tendon organs) are all changed. Hence, a manifold may be expected to exist in the high-dimensional space of afferent and efferent variables corresponding to stable perception of unchanged joint position. This manifold will be further addressed as iso-perceptual manifold (IPM).
More formally, we assume that, at a given level of analysis (e.g., one of the levels illustrated in Fig. 6), relevant afferent and efferent signals form a N-dimensional space, SN. This space may be viewed as the product of two factors (foliations in the original space), efferent and afferent, which we will associate here for simplicity with two sub-manifolds with the dimensionalities NE and NA. This step skips a few important issues. In particular, variables in the efferent and afferent spaces may not be independent. For example, this may be due to the well-known phenomenon of alpha-gamma co-activation, which is expected to produce changes in afferent signals from muscle spindle endings with changes in the efferent command to the muscle. Another potentially important issue, which is not discussed here, is the interaction of different sensory modalities, which may benefit from Bayesian estimation (Weiss et al. 2002; Körding and Wolpert 2006).
Perception of a set of j salient kinesthetic variables, Kj, is associated with measuring a vector P in a j-dimensional subspace in SN. This step assumes the existence of an origin of coordinates that allows the definition of P. Assuming that the percept is stable, i.e., Ṗ = 0, afferent and efferent signals can vary within a M-dimensional sub-space. The relation between the dimensionalities M, N, and j may be non-trivial because efferent and afferent signals represent joint variables, which are described together by a joint distribution. For the purposes of illustrating the concept of IPM, we assume that M = N – j. This M-dimensional sub-space is the IPM at the selected level of analysis.
As a result, a family of IPMs is presumed to exist within the afferent-efferent space parametrized by perceptions. This family may be constrained by a priori knowledge of the body. As described later, some IPMs may not exist because they violate constraints of body integrity. The IPM structure may be even considered as an alternative definition of perception affecting not only reported perception (which is the only type discussed in the paper) but also unconscious inference, i.e. an involuntary, pre-rational mechanism that may be responsible for a variety of phenomena including optical illusions (Wilson and Brekke 1994; Clifford et al. 2015).
In the next few examples, counting dimensionalities of spaces and sub-spaces should be taken as a simplified exercise. For example, within the suggested scheme, muscle length and force sense (j = 2) emerges at the level of interaction between {λ} and {Ia; Ib; II}. According to the EP-hypothesis (Feldman 1986), the efferent space for a single muscle is one-dimensional (NE = 1). In fact, one can introduce λs for individual motor units so that the muscle-relevant λ becomes embedded in a very high-dimensional space of individual mini-λs specific to individual alpha-motoneurons; λ corresponds to the lowest mini-λ within the pool. This aspect is not considered here to keep the lowest level of analysis at the level of individual muscles. It is hard to estimate dimensionality of the afferent space. If each of the main types of afferent signals is viewed as a single dimension, then NA ≥ 3; once again, this value refers to proprioceptive modalities, not to the number of receptors. In addition, the system of γ-motoneurons, dynamic and static, may be viewed as adding two more dimensions to the afferent system. So, the IPM is at least two-dimensional. While we do not know what the lowest reasonable level of analysis is, intuitively, considering individual neurons and subcellular structures (such as sensory endings) as degrees-of-freedom seems an overestimation.
The joint/digit/limb position sense emerges as a result of interaction between {r; c} and {α;f}. At this level, percepts may be relatively high-dimensional, corresponding, for example, to perception of position and orientation of the effector as well as to perception of the force and moment vector produced by the effector on the environment. For a single joint with one kinematic degree-of-freedom, j = 2 (joint angle and moment of force, although one may want to add one more dimension for the sense of joint capsule tension caused by muscle co-contraction), while for a limb j ≥ 6. The efferent process may be associated with defining reference coordinate (and, possibly, reference orientation) for the effector and its ellipsoid of apparent stiffness (cf. Flash and Mussa-Ivaldi 1990; Tsuji et al. 1995); then NE ≥ 9. It is hard to estimate the dimensionality of the afferent system, NA. Conservatively, it is about twice the number of muscles – corresponding to assumed higher-order afferent signals reflecting their length and force – plus the number of joints (reflecting the presence of articular receptors). This makes the IPM at least three-dimensional for a single joint and potentially higher-dimensional for a limb.
At the task level, perception is based on estimating {S} signals within the referent frame provided by {RC}. For example, one may try to estimate the weight and location/orientation of an object lifted by the two arms, or one’s body orientation with respect to the vertical, etc. The dimensionality of relevant efferent and afferent spaces, NA and NE, would be different in each of those examples. However, it seems safe to assume that the inequality j < (NA + NE) holds for all natural situations.
Note that at each level illustrated in Fig. 6, the efferent process defines a reference point, while sensory signals inform on deviations from that reference point. As a result, perception of relevant state variables (a vector P) can be expressed as: P = RC + S. In this equation, the "+" sign should be viewed as symbolic rather than reflecting addition of numbers or vectors. This equation is similar to, and may be viewed as a generalization of, the one proposed by the group of Feldman (Feldman 2009; Feldman et al. 2013) in the form Q = R + P for perception of muscle length and effort (see in more detail later).
Uncontrolled manifold and iso-perceptual manifold
The term uncontrolled manifold implies that the system of effector-level (elemental) variables does not need to be controlled as long as it resides within the UCM for salient performance variables (Scholz and Schöner 1999). While it is tempting to use the same term for stabilization of percepts, this would be misleading. Indeed, within the UCM hypothesis, the structure of inter-trial covariance among elemental variables (e.g., Fig. 3) is assumed to reflect an unobservable neural process related to stabilization of low-dimensional salient performance variables.
Within the framework developed in this paper, afferent and efferent elemental variables lead to low-dimensional percepts that may or may not correspond to actual physical body states. The elemental variables are often impossible to measure and they may be incommensurate; in addition, mappings of individual afferent and efferent elemental variables on perception of salient mechanical variables such as forces and coordinates are all but unknown, and there is no clear way of linearizing these mapping with a J matrix. For these reasons, descriptions within this paper must remain rather general.
UCM and IPM are defined in different spaces and may be viewed as sub-manifolds (or foliations) within those spaces that may be related to each other. It is also important that the UCM approach is about the neural control process over sets of elemental variables, while here we discuss extraction of information, veridical or not, from different sets of elemental variables.
An IPM is viewed as a reflection of a non-observable neural process leading to stable perception of salient variables in the presence of substantial variability at the level of elemental variables. Within each IPM, elemental variables are of two origins, those related to efferent processes (defining RC) and those related to afferent processes (defining the sensory contribution of perception, S). Stabilization of RC at a task-specific level may be viewed as based on a higher-dimensional set of elemental variables {r; c}i or λj. Further, we will address them as EV (efferent variables). Stabilization of S is viewed as based on a set of afferent variables {α;f}q or {Ia; Ib; II}p, addressed further as AV (afferent variables). As the described example of adequate perception of joint position under different co-contraction levels suggests, there may be co-variation between RC and S stabilizing P.
Figure 7 illustrates the idea of interaction among efferent and afferent signals leading to IPM. In this figure, for simplicity, we assume that the UCM and IPM are defined within spaces that share efferent variables (which may not be generally true) and that they are linear manifolds (which is commonly not true). Consider a toy example with only two elements at a lower level of the hierarchy (E1 and E2) and only two sources of relevant afferent information (A1 and A2). We also assume that the elemental variables sum up to produce relevant RC and S:
| (1a) |
| (1b) |
Figure 7.
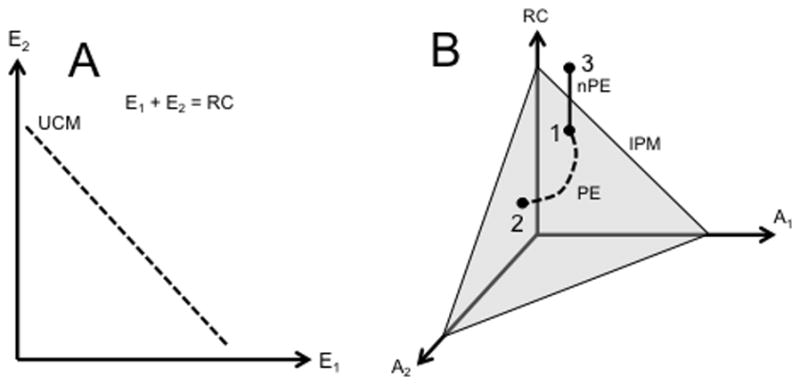
An illustration of the idea of interaction among efferent and afferent signals leading to iso-perceptual manifold, IPM. A: The UCM in the space of two efferent variables, {E1; E2}, corresponding to stabilization of their sum: E1 + E2 = RC. B: A subspace in the space of afferent variables, {A1; A2}, corresponding to their constant sum A1 + A2 = S (the thick solid line). Stability of a percept (P) is defined by the sum (RC + S) illustrated as a plane (IPM) in the three-dimensional space spanned by RC, A1, and A2. Motion along the IPM is perceptually equivalent (PE) motion (the dashed trajectory from point 1 to point 2). A change in the efferent process without a change in afferent signals (point 3) is an example of non-perceptually equivalent (nPE) motion to a new IPM. The figure is simplified in two aspects. First, it shows linear manifolds. Second, it assumes sharing of elemental variables between the UCM and IPM.
Panel A of Fig. 7 shows the linear UCM in the space {E1; E2} corresponding to stabilization of their sum, see Eq. (1a); the UCM represents a line with negative slope on the {E1; E2} plane. Panel B shows a subspace similar to the UCM corresponding to a constant sum of A1 and A2 (the thick solid line, Eq. (1b)). However, stability of a percept (P) is defined by the sum (RC + S). Stability of this variable corresponds to a plane in the three-dimensional space spanned by RC, A1, and A2. This plane is the IPM. It is impossible to illustrate it in the full four-dimensional space relevant to this example because of the limitations imposed by the two-dimensional medium (page).
One of the central features of the UCM concept is that UCM is always specific to a particular performance variable. This feature allowed using quantitative analysis of inter-trial variance within the UCM framework as a method of testing hypotheses on different variables that can potentially be stabilized by the central nervous system (Scholz and Schöner 1999; Scholz et al. 2000). In contrast, IPM is situation and preconception specific. For example, a percept of a six-legged dog on the street is probably going to be unstable: The viewer will rub the eyes and try to substitute this illegal percept with another one of a four-legged dog running at a high speed. In a sci-fi movie, however, such a percept may be perfectly legal and will not lead to substitution. We will return to the role of preconceptions later.
Perceptual Equivalence
Within the UCM hypothesis, motion within a high-dimensional space of elemental variables can be viewed as superposition of two components. One of them, motor equivalent (ME), leads to no change in a salient performance variable, i.e., it proceeds within the UCM for that variable. The other component leads to a change in that salient performance variable – non-motor equivalent (nME, see Fig. 3). Similarly, changes in a high-dimensional space of sensory-motor signals may be viewed as leading to no change in perception of an important variable (along the IPM, perceptually equivalent, PE) and to a change in perception of that variable (orthogonal to the IPM, non-perceptually equivalent, nPE).
There are many examples of perceptual equivalence. For example, when a person presses against a stop, there is no illusion of a change in the joint position (Feldman and Latash 1982a) despite the fact that all major groups of proprioceptors change their level of activity. Golgi tendon organs respond to the increased tendon force, articular receptors react to changes in the joint capsule tension, spindle endings react to changes in muscle fiber length (which changes despite the fact that the muscle-tendon unit length remains constant) and to changes in activity of γ–motoneurons due to the α–γ co-activation, and motor commands to muscles crossing the joint (λ) are changed as well. A somewhat simplified interpretation of this effect was offered as counter-directional shifts in the two components of muscle length (joint position) sense: In the reference coordinate defined by λ and in the activity level of length-sensitive receptors (Feldman 2009). While this scheme represented a step forward in understanding of joint position sense, it reduced the multi-dimensional space of neural processes that contribute to joint position sense to only two processes, afferent and efferent, similar to the earlier equation: P = RC + S, without considering the fact that both RC and S are embedded into high-dimensional spaces. A more complete interpretation would be a shift along the corresponding IPM, i.e. a PE motion illustrated as the dashed trajectory over the IPM from point 1 to point 2 in Fig 7B.
A classical study by Hulliger et al. (1982) provided evidence for no change in the activity level from length sensitive spindle endings following movement leading to a change in the corresponding muscle length. This is an example of nPE motion to a new IPM (corresponding to the adequately perceived new joint position) along the axis representing activity of length-sensitive endings (illustrated as the straight trajectory from point 1 to point 3 in Fig. 7B).
Vibration-induced sensory-motor effects
When a high-frequency, low-amplitude vibrator is placed over the belly of a muscle or over its tendon, kinesthetic illusions are frequently, but not always, reported (Goodwin et al. 1972; Lackner and Levine 1979; Roll and Vedel 1982; Roll et al. 1989). These illusions have been interpreted as resulting from the vibration-induced unusually high levels of activity of the primary endings of muscle spindles, which are sensitive to muscle length and velocity (Matthews and Stein 1969). This interpretation sounds feasible and is able to account for some features of the vibration-induced kinesthetic illusions (VIKI), such as illusions compatible with an increase in the length of the muscle subjected to vibration; such illusions are typically observed in the absence of vision (Goodwin et al. 1972; Lackner and Taublieb 1984; Roll and Vedel 1982).
Note also that muscle vibration also induces motor effects. These range from the tonic vibration reflex in the muscle group subjected to vibration, to reflex activation of other muscles of the limb, to complex motor reactions. In particular, vibration-induced muscle reflexes can be seen in different muscle groups depending on the initial body posture and some other factors (Latash and Gurfinkel 1976; Gurfinkel and Latash 1979). These patterns have been hypothesized to reflect involvement of spinal circuits responsible for locomotion; this hypothesis has been supported in studies of locomotor-like actions seen in some healthy person during muscle vibration (Gurfinkel et al. 1998; Selionov et al. 2009; Solopova et al. 2016). Standing persons show postural deviations from the vertical under vibration applied to muscles of the legs (Eklund and Hagbarth 1967; Hayashi et al. 1981) and, to a lesser degree, to other parts of the body (Lund 1980; Roll et al. 1989); these vibration-induced fallings have been interpreted as secondary effects of VIKI.
As mentioned earlier, kinesthetic perception and motor action have been linked in several theories (von Holst and Mittelstaedt 1950; Feldman and Latash 1982a; Feldman 2009); therefore, motor effects of vibration could also contribute to the variety of kinesthetic illusions. Possible effects of vibration on the efferent component of kinesthetic perception have been discussed over 30 years (Feldman and Latash 1982a,b; Roll et al. 1989; Feldman 2009; Feldman et al. 2013) and supported by recent studies of the effects of vibration on unintenional force drifts seen in the absence of visual feedback (Reschechtko et al. 2017) as well as by demonstrations of changes in corticospinal excitability during VIKI (Mancheva et al. 2017). In addition, Feldman and colleagues (2013) have discussed certain features of VIKI based on ideas closely related to the IPM concept.
A number of features of VIKI have remained largely unexplained. These include, in particular, the fact that subjects vary broadly in their sensitivity to muscle vibration: Some of them report strong VIKI (sometimes even leading to reports of anatomically impossible limb configurations, Craske 1977), while others feel only mild illusions, and still others report no consistent illusions at all. Another unexplained feature is that the direction of VIKI may reverse when sensory signals of other modalities are manipulated (Feldman and Latash 1982c). There is also a mismatch in the perceived joint position and velocity: Subjects report joint displacements that are much smaller as compared to those expected from the product of the reported joint velocity and time of observation (Sittig et al. 1985).
Let us consider within the proposed scheme possible effects of high-frequency vibration applied to a muscle group. While vibration spreads across body segments (Eklund 1971), for simplicity let us assume that only the muscle directly subjected to vibration responds with a very high level of activity of length- and velocity-sensitive spindle endings (Brown et al. 1967). One of the common arguments is that the unusually high activity along those sensory channels creates an illusion of the muscle being stretched leading to reports of corresponding joint rotations and other effects (Goodwin et al. 1972; Lackner and Taublieb 1984; Roll and Vedel 1982). So, according to this interpretation, PL = (AL), where PL stands for perception of muscle length and AL stands for afferent signals from length-sensitive spindle endings.
This argument and interpretation do not look convincing. Indeed, multiple muscles cross any joint, including bi-articular and poly-articular muscles. Sensory receptors in muscle groups, aside from those in the muscle directly subjected to vibration, are expected to provide veridical information about the actual joint position. So, for example, if a flexor muscle group is subjected to vibration, AL from the flexors may suggest that the flexor muscles are being stretched at a high velocity while AL from the extensors suggests that their length does not change. In this situation, the person is expected to report violation of the limb integrity corresponding to muscles detaching from their natural insertion points and/or bone deformation. This does not happen, however. A number of conclusions can be drawn from typical reports of joint position illusions corresponding to stretch of the muscle subjected to vibration (and shortening of the antagonist!).
In particular, the central nervous system avoids percepts of disjointed body even if afferent information suggests this. Interestingly, anatomically impossible rotations do not seem to be precluded (Craske 1977). Besides, there is also the so-called Pinocchio illusion (Burrack and Brugger 2005): If a person is asked to touch the tip of his/her nose with a fingertip of an arm and then vibration is applied to the elbow flexors, some subjects report perceiving their nose being slowly elongated. This last illusion is reported by only a handful of naïve persons. It can be interpreted as a consequence of three factors: (a) the head is correctly perceived as motionless, (b) there is contact between the fingertip and nose at all times, and (c) there is an illusion of elbow extension induced by the vibration. When the brain is forced to reconcile these three percepts, one solution is indeed creating a percept of nose elongation.
Three more effects make the traditional interpretation of VIKI questionable. First, the direction of illusory motion can be reversed by applying seemingly irrelevant stimuli of different modality (visual or auditory) and even by performing a cognitive task (Feldman and Latash 1982c). Second, healthy subjects show large variability in these effects, and it takes some time to “learn” how to experience VIKI (personal experience). Third, when vibration is applied simultaneously to agonist and antagonist muscle groups, no consistent illusion is reported while inter-trial variability of position sense is increased (Fuentes et al. 2012). These observations suggest that, unlike everyday perceptual experiences, VIKI are unstable. This conclusion suggests direct links of VIKI to the concept of IPM.
Recently, the group of Feldman (Feldman et al. 2013) have interpreted VIKI within an approach to position sense and sense of effort that is similar in many aspects to the scheme proposed in this paper. In that study, the authors suggested a simple equation linking actual position of body segments (Q) to a centrally defined referent coordinate (R) and afferent signals (P) reporting on deviations of the body from R: Q = R + P. This framework was used to interpret a range of perceptual phenomena including VIKI and a “no-motion illusions” when muscle vibration produces reflex muscle activation changes that lead to motion without the subject being aware of the motion. The equation Q = R + P may be seen as a reflection of interactions at any of the hierarchical levels, e.g. those illustrated in Figure 6. Here we accept the basic idea of Feldman and colleagues and try to develop it for various aspects of VIKI focusing on the issue of stability of percepts.
Figure 8 illustrates a situation when two afferent signals (e.g., from spindle endings in the flexor and extensor muscles) are used for kinesthetic perception of joint position. Note that this is a two-dimensional projection of a system involving more afferent signals as well as efferent signals; there is an IPM in that higher-dimensional system corresponding to veridical perception of the state of the joint. The initial state of the system is point P1 corresponding to a particular joint angle value, αP1, where the subscript P refers to a perceived value. Assume now that joint motion is associated with coordinated changes in the length of the two muscles: when one muscle stretches, the other shortens. For example, this may be associated with the following relation between the two afferent signals: A1A2 = C, where C is a constant. For every αP, there is an IPM in the hidden higher-dimensional space. For all possible αP values, there is a family of IPMs; each IPM within this family intercepts the plane in Fig. 8 in a point on the line A1A2 = C corresponding to coordinated changes in the two elemental afferent variables. The dashed line in Fig. 8 is a particular example of a projection on the {A1A2} space of allowed combinations of afferent and efferent signals (e.g., those corresponding to coordinated changes in the length of the opposing muscles during natural joint motion) that belong to IPMs; we will address this line as AIPM.
Figure 8.
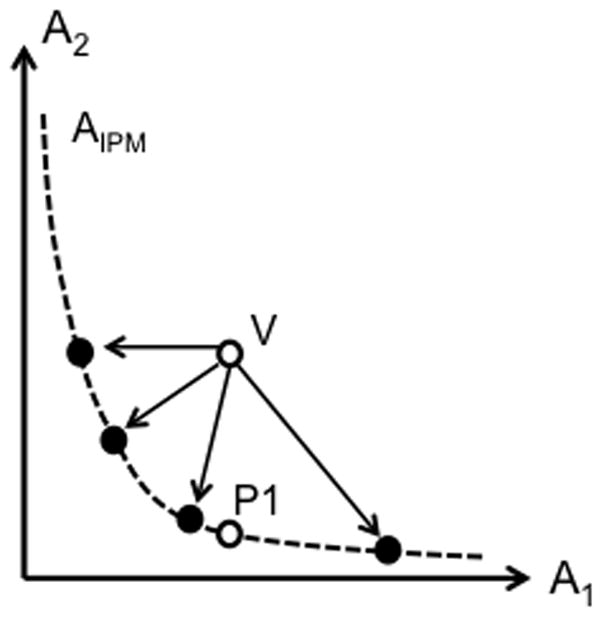
Two afferent signals (A1 and A2, e.g., from spindle endings in the flexor and extensor muscles) are used for kinesthetic perception. During natural joint motion, A1 and A2 change together along a line (the dashed line, AIPM). The initial state of the system in point P1 corresponds to a particular joint angle value, αP1. Vibration leads to an increase in A2 without a change in A1 to a disallowed point (V) off the AIPM. To avoid perceiving violation of the anatomical integrity, the new point is projected onto the AIPM line. This projection can be realized in an infinite number of ways (e.g., the black points on the AIPM curve), and the ultimate percept will depend on where on the AIPM line the new point will emerge.
Imagine now that one of the afferent signals is increased as a result of muscle vibration without changes in the other signal (point V). The new combination of signals is off the AIPM line. Point V corresponds to a disallowed muscle length combinations corresponding to violation of the anatomical integrity of the joint. To create an allowed percept of joint position, point V has to be projected onto the AIPM line such that it may be associated with an IPM, even though this projection will not be compatible with the actual combination of afferent (and efferent) signals. It seems safe to assume that projection can be realized in an infinite number of ways, and the ultimate percept will depend on where on the AIPM line the new point will emerge (see the black points on the AIPM curve in Fig. 8). The process of projecting the new actual point V to AIPM may lead to unstable solutions, i.e., those showing spontaneous motion along the AIPM, depending on other factors including those mentioned earlier (such as experience with vibration stimuli, sensory stimuli of other modalities, cognitive task, vibration of the antagonist, etc.)
In more general terms, the process of creating a percept may be viewed as search for a meaningful (allowed) IPM “closest” to the actual set of afferent and efferent signals. Metric of closeness is unknown to us and, based on the mentioned observations, this metric may change with other afferent and efferent processes. Sometimes, there may be more than one IPM satisfying this criterion. In such cases, loss of stability may be revealed in effects of other sensory modalities, cognitive processes (e.g., counting backwards), and other factors. While the mentioned features of VIKI can be interpreted using the IPM concept, we have to admit that these observations fall short of providing direct support for this scheme.
An example: Single-joint position and torque perception
Consider the problem of perceiving joint angle and torque. This problem is associated with defining a point on the angle-torque plane, {Pα; PT}. Assuming a simple joint crossed by only two muscles, flexor and extensor, the efferent process may be associated with setting two values of λ, {λFL; λEXT} or an equivalent pair of variables, r-command and c-command, {r; c} (Fig. 9, panel A). These commands define the intercept of the torque-length line with the length axis and the slope of that line, respectively. Assume also that projection of the multi-dimensional afferent space (including all the afferent systems from both muscles) on the torque-length line may be expressed as a change in a higher-order variable A (a weighted sum of afferent signals from various sources that increases with distance from r), which has the value of A1. Then:
| (2a) |
| (2b) |
Figure 9.
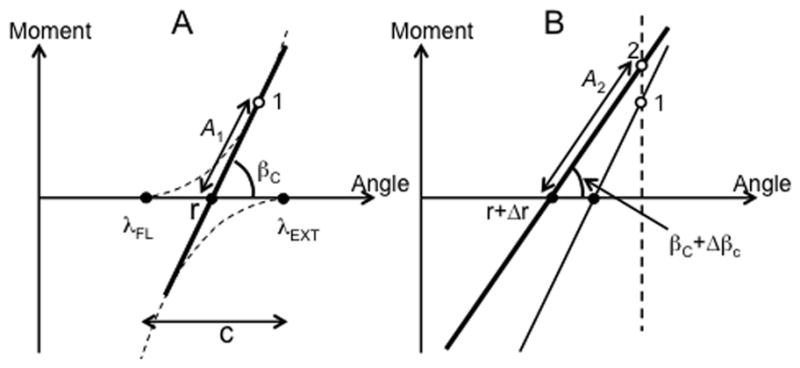
A: The control of a joint crossed by only two muscles, flexor and extensor, can be described with setting two values of λ, {λFL; λEXT} or an equivalent pair of variables, r-command and c-command. The r-command sets the intercept of the torque-length line with the length axis and the c-command defines the slope of that line. Projection of the multi-dimensional afferent space on the torque-length line may be expressed as a value A1 of a higher-order variable A. B: When a person presses against a stop r-command shifts by Δr and βc shifts by Δβc. The value of A changes to A2.
Imagine that a person presses against a stop (panel B in Fig. 9). This is associated with a shift in r by Δr and possibly in c by Δc leading to a change in the angle βc by Δβc. Veridical perception of the increased joint torque and unchanged joint position means that
| (3a) |
| (3b) |
where A2 is the new value of A. Equation 2a gives a specific form for the IPM for Pα in the reduced efferent-afferent space:
| (4) |
Consider now what can be expected if a vibrator is placed on one of the muscles crossing the joint. First, the increased spindle activity from the muscle with the vibrator will not be accompanied by decreased activity from the antagonist. Since this means violation of joint integrity, the new point of the joint torque-length characteristic will reflect a process similar to the one illustrated in Fig. 9 leading to a new value of A, AV. Equations (2) suggest that this will be accompanied by a change in both Pα and PT. i.e. illusions in both joint position and torque.
Figure 10 illustrates possible effects of vibration on perception of coordinate of an effector and force along that coordinate. Imagine that in an initial state illustrated by point 1 (black circle), vibration leads to an increase in activity of length sensitive receptors only (point 2). If this signal is interpreted in an unchanged system of coordinates (RC1), the dot has to be projected on the original force-length line. While such projections can be performed in different ways (e.g., to points 2a or 2b), they are likely to correspond to perception of higher force. To perceive a change in coordinate (classical VIKI) without a change in force, the system of coordinates would have to shift (to RC2 in Fig. 10). While effects of vibration on RC shifts have been postulated (Feldman and Latash 1982a) and confirmed in a recent study (Reschechtko et al. 2017), the lack of force illusions is only possible if the RC shift and sensory signal change are perfectly balanced. This is not impossible but does not seem likely given the different origins of the sensory shift and hypothetical effects of vibration on RC. Indeed, force illusions under vibration have been reported in two studies (Cafarelli and Kostka 1981; Reschechtko et al. 2017). In particular, in the latter study, vibration of the antagonist muscle (finger extensors during a finger pressing task) led to consistent overestimation of force magnitude, which is expected within the described scheme.
Figure 10.
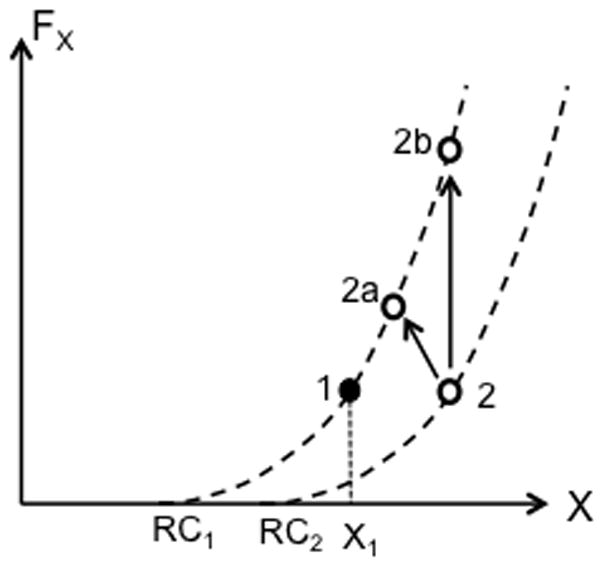
Possible effects of vibration on perception of coordinate of an effector (X) and force along that coordinate (FX). The initial state is shown with the black circle (point 1). Vibration leads to an increase in activity of length sensitive receptors only (point 2). If this signal is interpreted in an unchanged system of coordinates (RC1), the dot is projected on the original force-length line. Such projections can be performed in different ways (e.g., to points 2a or 2b), and are likely to correspond to perception of higher force. To perceive a change in coordinate (classical VIKI) without a change in force, the system of coordinates would have to shift to RC2.
Note that the classical assumption that muscle length perception is based on signal from muscle spindle endings (and gamma-system) and muscle force (joint torque) perception is based on signals from Golgi tendon organs leads to a different prediction. Length and torque perception become decoupled. Since vibration is an effective stimulus for the primary spindle endings but not for Golgi tendon organs, length illusions are expected not accompanied by torque illusions.
Other illusions and predictions of new illusions
The mentioned example of disallowed muscle length combinations corresponding to loss of anatomical body integrity is arguably an extreme example of a more general phenomenon mentioned briefly earlier: The role of preconceptions in interpreting sensory signals. Consider the following well-known illusion. If you cross the index and middle fingers of a hand and close your eyes, and then another person touches both fingers simultaneously with an object (e.g., a finger), you will feel as if you were touched with two objects. This happens because, in everyday life, the radial surface of one of the fingers and the ulnar surface of the other finger cannot be touched with a single small object simultaneously. So, even though you know that the fingers are crossed, the preconception leads to an illusion.
Another example of the role of preconceptions is the classical size-weight illusion (e.g., Ernst, 2009; Buckingham, 2014): If you are presented with two similar objects of the same weight but different size (e.g., two cubes), the smaller object is perceived as heavier. Here the cause for the illusion is violation of a natural expectation that the smaller object would be proportionally lighter. In these examples, the veridical sensory signals are misinterpreted because they are projected on an allowed sub-space (shown as AIPM in Fig. 8) based on preconceptions.
It is possible that implicit constraints play a role in movements driven by sensory stimuli, including those generated by the spinal cord. For example, a series of experiments on the spinal frog wiping reflex performed in the 1980s in Moscow (reviewed in Latash 1993, 2008; also see Berkinblit et al. 1986) demonstrated the amazing ability of the spinal frog to reach the irritating stimulus on its back with the toes of the ipsilateral hindlimb even in conditions of artificial loading of the hindlimb or fixation of one of its joints. The frog, however, was unable to reach the stimulus and wiped consistently below its actual location if a “glove” was placed on the forcefully flexed toes of the hindlimb. Within the current framework, the frog’s spinal cord was unable to incorporate the veridical sensory information on the actual toe configuration (which was impossible in everyday frog’s life) into an image of the body configuration (cf. Fukson et al. 1980) and performed the action as if the toes were naturally extended.
The current framework allows predicting illusions and other phenomena that, to our knowledge, have never been reported. In particular, Figures 9 and 10 suggest that perception of muscle length (joint angle) and muscle force (joint torque) are intimately linked: They are based on a weighted combination of neural signals from the same sources. This implies, in particular, that VIKI are likely to be accompanied by illusions of force, not only of position/velocity. Such illusions have been observed recently in a study motivated by the described scheme (Reschechtko et al. 2017). This study also has confirmed that vibration leads not only to changes in the afferent signals but also in the RC involved in the perception process (cf. Feldman and Latash 1982a; Feldman et al. 2013).
Another illusion following the scheme in Figure 1 has only been reported informally (Latash 2008; Latash and Zatsiorsky, 2016), although a full-scale experiment was performed in the 1980s. In that study, index finger motion was produced by electrical tetanic stimulation of the extrinsic hand muscles, and the subjects used a psychophysical scale to report finger position in a new steady state. In this situation, one can expect the sensory signals to be interpreted in a wrong system of coordinates because the natural link between activation of spinal motoneurons and muscle activation was distorted. Indeed, the finger displacement was consistently overestimated corresponding to perception of shorter length of the muscle subjected to the stimulation.
The concept of IPM implies the existence of a particular structure of variance reflecting stability of perception of a task-specific variable ensured by co-varied adjustments in perception of lower-level (elemental) variables. This prediction is somewhat similar to the phenomenon of structured inter-trial variance as explored within the framework of the UCM hypothesis (reviewed in Latash et al. 2007; Latash 2008). For example, a person may be expected to show small errors in perception of fingertip position in space during pointing as compared to perception of individual joint angles of the arm. Along similar lines, one may be expected to show accurate perception of the total force and/or moment of force produced by a set of digits on a hand-held object while perception of individual fingers forces is expected to be less accurate.
Experimental exploration of the mentioned phenomena may be non-trivial. While action by elements may be quantified with a degree of objectivity and accuracy at both task-specific and element levels, perceptions are much harder to quantify objectively. Using verbal reports and psychophysical scales leads to poor resolution and reproducibility. Using reproduction of a percept by action involves many potentially confounding factors such as the necessity to produce another action, memory, and/or action by another effector. All these methods have an element of subjectivity, which seems to be unavoidable. One problem is that persons may match their percepts paying attention to sensory information (as one would hope) or try to match their “commands” (efferent processes, RCs). Several studies have suggested that humans do indeed sometimes match efferent processes, i.e., “doing the same” rather than “moving to the same magnitude of a positional or force variable”. This can lead to significant errors in mechanical variables that are to be reproduced (Rymer and D’Almeida 1980; van Doren 1998).
Concluding comments
To summarize the main message of the paper, at each level of the assumed hierarchy, afferent (sensory) signals from multiple sources are estimated within a frame of reference provided by the multiple ongoing efferent processes adequately described as time-varying spatial reference coordinates. Percepts emerge within the high-dimensional afferent-efferent system of variables (elemental variables). Typically they are stable under variations of any of the individual elemental variables; this stability can be formalized using the notion of the iso-perceptual manifold (IPM). Many everyday actions are associated with coordinated changes in both afferent and efferent elemental variables that preserve stability of salient percepts; this is an example of perceptual equivalence – motion along the IPM. Stability can be violated under strong distortions of elemental variables leading to illusions, e.g., under high-frequency muscle vibration. Both veridical and illusory perceptions are constrained by sets of preconceptions that do not allow certain kinds of percepts, e.g., ones violating body integrity. In such cases, points in the original space of elemental variables are projected to an allowed IPM leading to actually reported illusions. This scheme allows interpreting a number of well-known illusions and predicting illusions that have not yet been reported in the literature. Testing some of these predictions is in the immediate plans of our group.
Numerous issues have remained outside or only been alluded to in the current paper. These obvious “holes” in the discourse are due partly to the limited expertise of the author and partly to reasonable size of a journal paper. The following incomplete list mentions some of the obvious issues in need of further clarification, definition, and discussion. First, there is a philosophical issue of defining perception and of its relation to the IPM concept. Second, the mathematical definitions and computational apparatus of the UCM and IPM concepts remain to be developed rigorously. Third, the paper contains numerous obvious simplifications such as non-interacting afferent and efferent hierarchical processes, shared variables in the spaces where UCM and IPM are defined, linear manifolds, etc. It would be highly desirable to eliminate at least some of these simplifications to move the IPM concept closer to real-life situations. Fourth, it would be very interesting to link the geometrical, physical, and physiological concepts presented in the paper with the framework of Bayesian estimation and decision-making, for example as it has been recently suggested based on minimization of variational free energy (Friston et al. 2017a,b).
Highlights.
Stability of perception is considered within the efferent-afferent space;
The concept of iso-perceptual manifold is introduced corresponding to stable percepts;
The concept is used to analyze kinesthetic illusions produced by muscle vibration;
New illusions are predicted not yet reported in the literature.
Acknowledgments
The author is grateful to Dr. Sasha Reschechtko for his comments on an earlier version of the manuscript. The preparation of this manuscript was in part supported by NIH grants R01 NS035032 and R21 NS095873.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akulin VM, Carlier F, Solnik S, Latash ML. Neural control of redundant (abundant) systems as algorithms stabilizing subspaces. 2015 Preprint: arXiv:1506.06920. [Google Scholar]
- Alexandrov AV, Frolov AA, Massion J. Biomechanical analysis of movement strategies in human forward trunk bending. I. Modeling. Biol Cybern. 2001;84:425–434. doi: 10.1007/PL00007986. [DOI] [PubMed] [Google Scholar]
- Ambike S, Mattos D, Zatsiorsky VM, Latash ML. Synergies in the space of control variables within the equilibrium-point hypothesis. Neurosci. 2016;315:150–161. doi: 10.1016/j.neuroscience.2015.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arpinar-Avsar P, Park J, Zatsiorsky VM, Latash ML. Effects of muscle vibration on finger interaction and coordination. Exp Brain Res. 2013;229:103–111. doi: 10.1007/s00221-013-3597-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkinblit MB, Feldman AG, Fukson OI. Adaptability of innate motor patterns and motor control mechanisms. Behav Brain Sci. 1986;9:585–638. [Google Scholar]
- Bernstein NA. On the Construction of Movements. Medgiz; Moscow (in Russian): 1947. [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Bosco G, Poppele RE. Encoding of hindlimb kinematics by spinocerebellar circuitry. Arch Ital Biol. 2002;140:185–192. [PubMed] [Google Scholar]
- Brown MC, Engberg I, Matthews PB. The relative sensitivity to vibration of muscle receptors of the cat. J Physiol. 1967;192:773–800. doi: 10.1113/jphysiol.1967.sp008330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckingham G. Getting a grip on heaviness perception: a review of weight illusions and their probable causes. Exp Brain Res. 2014;232:1623–1629. doi: 10.1007/s00221-014-3926-9. [DOI] [PubMed] [Google Scholar]
- Burrack A, Brugger P. Individual differences in susceptibility to experimentally induced phantom sensations. Body Image. 2005;2:307–313. doi: 10.1016/j.bodyim.2005.04.002. [DOI] [PubMed] [Google Scholar]
- Cafarelli E, Kostka CE. Effect of vibration on static force sensation in man. Exp Neurol. 1981;74:331–340. doi: 10.1016/0014-4886(81)90173-4. [DOI] [PubMed] [Google Scholar]
- Clifford CW, Mareschal I, Otsuka Y, Watson TL. A Bayesian approach to person perception. Conscious Cogn. 2015;36:406–413. doi: 10.1016/j.concog.2015.03.015. [DOI] [PubMed] [Google Scholar]
- Craske B. Perception of impossible limb positions induced by tendon vibration. Science. 1977;196:71–73. doi: 10.1126/science.841342. [DOI] [PubMed] [Google Scholar]
- Cross MJ, McCloskey DI. Position sense following surgical removal of joints in man. Brain Res. 1973;55:443–445. doi: 10.1016/0006-8993(73)90310-7. [DOI] [PubMed] [Google Scholar]
- d’Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- De Havas J, Ghosh A, Gomi H, Haggard P. Sensorimotor organization of a sustained involuntary movement. Front Behav Neurosci. 2015;9:185. doi: 10.3389/fnbeh.2015.00185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWald JP, Pope PS, Given JD, Buchanan TS, Rymer WZ. Abnormal muscle coactivation patterns during isometric torque generation at the elbow and shoulder in hemiparetic subjects. Brain. 1995;118:495–510. doi: 10.1093/brain/118.2.495. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Shadmehr R, Ivry RB. The coordination of movement: optimal feedback control and beyond. Trends Cogn Sci. 2010;14:31–39. doi: 10.1016/j.tics.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eklund G. Some physical properties of muscle vibrators used to elicit tonic proprioceptive reflexes in man. Acta Soc Med Upsal. 1971;76:271–280. [PubMed] [Google Scholar]
- Eklund G, Hagbarth KE. Vibratory induced motor effects in normal man and in patients with spastic paralysis. Electroencephalog Clin Neurophysiol. 1967;23:393. [PubMed] [Google Scholar]
- Ernst MO. Perceptual learning: inverting the size-weight illusion. Curr Biol. 2009;19:R23–R25. doi: 10.1016/j.cub.2008.10.039. [DOI] [PubMed] [Google Scholar]
- Fattori P, Breveglieri R, Bosco A, Gamberini M, Galletti C. Vision for prehension in the medial parietal cortex. Cereb Cortex. 2017;27:1149–1163. doi: 10.1093/cercor/bhv302. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Superposition of motor programs. I. Rhythmic forearm movements in man. Neurosci. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. J Mot Behav. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG. New insights into action-perception coupling. Exp Brain Res. 2009;194:39–58. doi: 10.1007/s00221-008-1667-3. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Referent control of action and perception: Challenging conventional theories in behavioral science. Springer; NY: 2015. [Google Scholar]
- Feldman AG. Active sensing without efference copy: referent control of perception. J Neurophysiol. 2016;116:960–976. doi: 10.1152/jn.00016.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG, Ilmane N, Sangani S, Raptis H, Esmailzadeh N. Action-perception coupling in kinesthesia: a new approach. Neuropsychologia. 2013;51:2590–2599. doi: 10.1016/j.neuropsychologia.2013.09.013. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Interaction of afferent and efferent signals underlying joint position sense: Empirical and theoretical approaches. J Mot Behav. 1982a;14:174–193. doi: 10.1080/00222895.1982.10735272. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Afferent and efferent components of joint position sense: Interpretation of kinaesthetic illusions. Biol Cybern. 1982b;42:205–214. doi: 10.1007/BF00340077. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Inversions of vibration-induced senso-motor events caused by supraspinal influences in man. Neurosci Lett. 1982c;31:147–151. doi: 10.1016/0304-3940(82)90107-0. [DOI] [PubMed] [Google Scholar]
- Flash T, Mussa-Ivaldi F. Human arm stiffness characteristics during the maintenance of posture. Exp Brain Res. 1990;82:315–326. doi: 10.1007/BF00231251. [DOI] [PubMed] [Google Scholar]
- Freitas SMSF, Scholz JP, Latash ML. Analyses of joint variance related to voluntary whole-body movements performed in standing. J Neurosci Meth. 2010;188:89–96. doi: 10.1016/j.jneumeth.2010.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, FitzGerald T, Rigoli F, Schwartenbeck P, Pezzulo G. Active inference: A process theory. Neural Comput. 2017a;29:1–49. doi: 10.1162/NECO_a_00912. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Lin M, Frith CD, Pezzulo G, Hobson JA, Ondobaka S. Active inference, curiosity and insight. Neural Comput. 2017b;29:2633–2683. doi: 10.1162/neco_a_00999. [DOI] [PubMed] [Google Scholar]
- Fuentes CT, Gomi H, Haggard P. Temporal features of human tendon vibration illusions. Eur J Neurosci. 2012;36:3709–3717. doi: 10.1111/ejn.12004. [DOI] [PubMed] [Google Scholar]
- Fukson OI, Berkinblit MB, Feldman AG. The spinal frog takes into account the scheme of its body during the wiping reflex. Science. 1980;209:1261–1263. doi: 10.1126/science.7403886. [DOI] [PubMed] [Google Scholar]
- Gelfand IM, Latash ML. On the problem of adequate language in movement science. Motor Control. 1998;2:306–313. doi: 10.1123/mcj.2.4.306. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. The Ecological Approach to Visual Perception. Boston, MA: Houghton Mifflin; 1979. [Google Scholar]
- Goodale MA. Visual pathways supporting perception and action in the primate cerebral cortex. Curr Opin Neurobiol. 1993;3:578–585. doi: 10.1016/0959-4388(93)90059-8. [DOI] [PubMed] [Google Scholar]
- Goodwin GM, McCloskey DI, Matthews PB. The contribution of muscle afferents to kinaesthesia shown by vibration induced illusions of movement and by the effects of paralysing joint afferents. Brain. 1972;95:705–748. doi: 10.1093/brain/95.4.705. [DOI] [PubMed] [Google Scholar]
- Gurfinkel VS, Latash ML. Segmental postural mechanisms and reversal of muscle reflexes. Agressologie. 1979;20B:145–146. [Google Scholar]
- Gurfinkel VS, Levik YS, Kazennikov OV, Selionov VA. Locomotor-like movements evoked by leg muscle vibration in humans. Eur J Neurosci. 1998;10:1608–1612. doi: 10.1046/j.1460-9568.1998.00179.x. [DOI] [PubMed] [Google Scholar]
- Hayashi R, Miyake A, Jijiwa H, Watanabe S. Postural readjustment to body sway induced by vibration in man. Exp Brain Res. 1981;43:217–225. doi: 10.1007/BF00237767. [DOI] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. Biol Cybern. 1985;52:315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Hulliger M, Nordh E, Vallbo AB. The absence of position response in spindle afferent units from human finger muscles during accurate position holding. J Physiol. 1982;322:167–179. doi: 10.1113/jphysiol.1982.sp014030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556:267–82. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karanjia PN, Ferguson JH. Passive joint position sense after total hip replacement surgery. Ann Neurol. 1983;13:654–657. doi: 10.1002/ana.410130612. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian decision theory in sensorimotor control. Trends Cogn Sci. 2006;10:319–326. doi: 10.1016/j.tics.2006.05.003. [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy V, Goodman SR, Latash ML, Zatsiorsky VM. Muscle synergies during shifts of the center of pressure by standing persons: Identification of muscle modes. Biol Cybern. 2003;89:152–161. doi: 10.1007/s00422-003-0419-5. [DOI] [PubMed] [Google Scholar]
- Kugler PN, Turvey MT. Information, natural law, and the self-assembly of rhythmic movement. Hillsdale, NJ: Erlbaum; 1987. [Google Scholar]
- Lackner JR, Levine MS. Changes in apparent body orientation and sensory localization, induced by vibration of postural muscles; vibratory myesthetic illusions. Aviat Space Environ Med. 1979;50:346–354. [PubMed] [Google Scholar]
- Lackner JR, Taublieb AB. Influence of vision on vibration-induced illusions of limb movement. Exp Neurol. 1984;85:97–106. doi: 10.1016/0014-4886(84)90164-x. [DOI] [PubMed] [Google Scholar]
- Latash ML. Control of Human Movement. Human Kinetics; Urbana, IL: 1993. [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy) Exp Brain Rese. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Towards physics of neural processes and behavior. Neurosci Biobehav Rev. 2016;69:136–146. doi: 10.1016/j.neubiorev.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Biological movement and laws of physics. Motor Control. 2017;21:327–344. doi: 10.1123/mc.2016-0016. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky VM. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Gurfinkel VS. Tonic vibration reflex and position of the body. Physiologiya Cheloveka (Hum Physiol) 1976;2:593–598. [Google Scholar]
- Latash ML, Zatsiorsky VM. Biomechanics and Motor Control: Defining Central Concepts. Academic Press; New York, NY: 2016. [Google Scholar]
- Lund S. Postural effects of neck muscle vibration in man. Experientia. 1980;36:1398. doi: 10.1007/BF01960120. [DOI] [PubMed] [Google Scholar]
- Mancheva K, Rollnik JD, Wolf W, Dengler E, Kossev A. Vibration-induced kinesthetic illusions and conticospinal excitability changes. J Mot Behav. 2017;49:299–305. doi: 10.1080/00222895.2016.1204263. [DOI] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Computa. 2009;21:1371–1414. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Latash ML, Park E, Kuhl J, Scholz JP. Unpredictable elbow joint perturbation during reaching results in multijoint motor equivalence. J Neurophysiol. 2011;106:1424–1436. doi: 10.1152/jn.00163.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner AD, Goodale MA. Two visual systems re-viewed. Neuropsychologia. 2008;46:774–785. doi: 10.1016/j.neuropsychologia.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Park J, Zatsiorsky VM, Latash ML. Optimality vs. variability: An example of multi-finger redundant tasks. Exp Brain Res. 2010;207:119–132. doi: 10.1007/s00221-010-2440-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, O’Shea DJ, Zatsiorsky VM, Latash ML. On the nature of unintentional action: A study of force/moment drifts during multi-finger tasks. J Neurophysiol. 2016;116:698–708. doi: 10.1152/jn.00180.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parsa B, Terekhov A, Zatsiorsky VM, Latash ML. Optimality and stability of intentional and unintentional actions: I. Origins of drifts in performance. Exp Brain Res. 2017;235:481–496. doi: 10.1007/s00221-016-4809-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exer Sport Sci Rev. 2002;30:32–38. doi: 10.1097/00003677-200201000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganathan R, Newell KM. Motor synergies: feedback and error compensation within and between trials. Exp Brain Res. 2008;186:561–570. doi: 10.1007/s00221-007-1259-7. [DOI] [PubMed] [Google Scholar]
- Ranganathan R, Newell KM. Influence of augmented feedback on coordination strategies. J Mot Behav. 2009;41:317–330. doi: 10.3200/JMBR.41.4.317-330. [DOI] [PubMed] [Google Scholar]
- Reschechtko S, Cuadra C, Latash ML. Force illusions and drifts observed during muscle vibration. J Neurophysiol. 2017 doi: 10.1152/jn.00563.2017. in press e-pub. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Latash ML. Stability of hand force production: I. Hand level control variables and multi-finger synergies. J Neurophysiol. 2017;118:3152–3164. doi: 10.1152/jn.00485.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson MJ, Shockley K, Fajen BR, Riley MA, Turvey MT. Ecological psychology: Six principles for an embodied-embedded approach to behavior. In: Calvo P, Gomila T, editors. Handbook of cognitive science: An embodied approach. New York, NY: Elsevier; 2008. pp. 161–187. [Google Scholar]
- Roll JP, Vedel JP. Kinaesthetic role of muscle afferents in man, studied by tendon vibration and microneurography. Exp Brain Res. 1982;47:177–190. doi: 10.1007/BF00239377. [DOI] [PubMed] [Google Scholar]
- Roll JP, Vedel JP, Roll R. Eye, head and skeletal muscle spindle feedback in the elaboration of body references. Prog Brain Res. 1989;80:113–123. doi: 10.1016/s0079-6123(08)62204-9. [DOI] [PubMed] [Google Scholar]
- Rymer WZ, D’Almeida A. Joint position sense. The effects of muscle contraction. Brain. 1980;103:1–22. doi: 10.1093/brain/103.1.1. [DOI] [PubMed] [Google Scholar]
- Santello M, Bianchi M, Gabiccini M, Ricciardi E, Salvietti G, Prattichizzo D, Ernst M, Moscatelli A, Jorntell H, Kappers AM, Kyriakopoulos K, Schaeffer AA, Castellini C, Bicchi A. Hand synergies: Integration of robotics and neuroscience for understanding the control of biological and artificial hands. Phys Life Rev. 2016;17:1–23. doi: 10.1016/j.plrev.2016.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schieber MH. Voluntary descending control. In: Zigmond MJ, Bloom FE, Landis SC, Roberts JL, Squire LR, editors. Fundamental Neuroscience. Academic Press; San Diego etc: 1999. pp. 931–949. [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G, Latash ML. Identifying the control structure of multijoint coordination during pistol shooting. Exp Brain Res. 2000;135:382–404. doi: 10.1007/s002210000540. [DOI] [PubMed] [Google Scholar]
- Schöner G. Recent developments and problems in human movement science and their conceptual implications. Ecol Psychol. 1995;8:291–314. [Google Scholar]
- Selionov VA, Ivanenko YP, Solopova IA, Gurfinkel VS. Tonic central and sensory stimuli facilitate involuntary air-stepping in humans. J Neurophysiol. 2009;101:2847–2858. doi: 10.1152/jn.90895.2008. [DOI] [PubMed] [Google Scholar]
- Sittig AC, Denier van der Gon JJ, Gielen CC. Separate control of arm position and velocity demonstrated by vibration of muscle tendon in man. Exp Brain Res. 1985;60:445–453. doi: 10.1007/BF00236930. [DOI] [PubMed] [Google Scholar]
- Solopova IA, Selionov VA, Zhvansky DS, Gurfinkel VS, Ivanenko Y. Human cervical spinal cord circuitry activated by tonic input can generate rhythmic arm movements. J Neurophysiol. 2016;115:1018–1030. doi: 10.1152/jn.00897.2015. [DOI] [PubMed] [Google Scholar]
- Sperry RW. Neural basis of the spontaneous optokinetic response produced by visual inversion. J Comp Physiol Psychol. 1950;43:482–489. doi: 10.1037/h0055479. [DOI] [PubMed] [Google Scholar]
- Stark L, Bridgeman B. Role of corollary discharge in space constancy. Percept Psychophys. 1983;34:371–380. doi: 10.3758/bf03203050. [DOI] [PubMed] [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93:609–613. doi: 10.1152/jn.00681.2004. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Tsuji T, Morasso PG, Goto K, Ito K. Human hand impedance characteristics during maintained posture. Biol Cybern. 1995;72:475–485. doi: 10.1007/BF00199890. [DOI] [PubMed] [Google Scholar]
- Van Doren CL. Differential effects of load stiffness on matching pinch force, finger span, and effort. Exp Brain Res. 1998;120:487–495. doi: 10.1007/s002210050422. [DOI] [PubMed] [Google Scholar]
- Von Holst E, Mittelstaedt H. The reafference principle. In: Martin R, translator. The Behavioral Physiology of Animals and Man. The Collected Papers of Erich von Holst. Vol. 1. University of Miami Press; Coral Gables, Florida: 1950/1973. pp. 139–173. [Google Scholar]
- Wada M, Kawahara H, Shimada S, Miyazaki T, Baba H. Joint proprioception before and after total knee arthroplasty. Clin Orthop Rel Res. 2002;403:161–167. doi: 10.1097/00003086-200210000-00024. [DOI] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci. 2002;5:598–604. doi: 10.1038/nn0602-858. [DOI] [PubMed] [Google Scholar]
- Wilson TD, Brekke N. Mental contamination and mental correction: unwanted influences on judgments and evaluations. Psychol Bull. 1994;116:117–142. doi: 10.1037/0033-2909.116.1.117. [DOI] [PubMed] [Google Scholar]
- Zwickel J, Grosjean M, Prinz W. Seeing while moving: measuring the online influence of action on perception. Quart J Exp Psychol. 2007;60:1063–1071. doi: 10.1080/17470210701288722. [DOI] [PubMed] [Google Scholar]


