Mechanical Properties of Porcine Brain Tissue In Vivo and Ex Vivo Estimated by MR Elastography

Abstract

The mechanical properties of brain tissue in vivo determine the response of the brain to rapid skull acceleration. These properties are thus of great interest to the developers of mathematical models of traumatic brain injury (TBI) or neurosurgical simulations. Animal models provide valuable insight that can improve TBI modeling. In this study we compare estimates of mechanical properties of the Yucatan mini-pig brain in vivo and ex vivo using magnetic resonance elastography (MRE) at multiple frequencies. MRE allows estimations of properties in soft tissue, either in vivo or ex vivo, by imaging harmonic shear wave propagation. Most direct measurements of brain mechanical properties have been performed using samples of brain tissue ex vivo. It has been observed that direct estimates of brain mechanical properties depend on the frequency and amplitude of loading, as well as the time post-mortem and condition of the sample. Using MRE in the same animals at overlapping frequencies, we observe that porcine brain tissue in vivo appears stiffer than brain tissue samples ex vivo at frequencies of 100 Hz and 125 Hz, but measurements show closer agreement at lower frequencies.

1. Introduction

Traumatic brain injury (TBI) occurs when sudden head acceleration leads to shearing and stretching of brain tissue (Holbourn, 1943; Sierra et al., 2015). It is the leading cause of death in children and young adults (Langlois et al., 2006) and is common among soldiers exposed to explosive blast in combat (Hoge et al., 2008). Computer models can be used to simulate TBI, particularly the mechanics of fast brain deformation. Simulations can be used to improve methods for injury prevention, diagnosis, and treatment. However, computer models of TBI require accurate material properties for brain tissue (Sierra et al., 2015).

The mechanical behavior of the brain remains incompletely characterized (Chatelin et al., 2010). Most mechanical testing of brain tissue is performed using animal tissue ex vivo (Arbogast and Margulies, 1998; Bilston et al., 1997; Brands et al., 2000; Hrapko et al., 2006; Nicolle et al., 2004; Ommaya, 1968; Shen et al., 2006; Thibault and Margulies, 1998; Vappou et al., 2007). However, ex vivo measurements may not necessarily reflect in vivo behavior (Miller et al., 2000; Rashid et al., 2012). In situ and in vivo tests have also been performed using indentation on animals (Gefen and Margulies, 2004; Miller et al., 2000) and magnetic resonance elastography (MRE) on both animals and humans (Clayton et al., 2011; Feng et al., 2013a; Johnson et al., 2016; Papazoglou et al., 2008; Schregel et al., 2012). Substantial differences have been found between estimates of material parameters, likely due to differences in methodology, frequency range, or time scale.

The relationship between in vivo and ex vivo properties of brain tissue remains a topic of active research (Gefen and Margulies, 2004). Bilston et al. (2001) hypothesized that brain tissue properties in vivo would be stiffer than properties ex vivo. Miller et al. (2000) performed one in vivo indentation test on exposed porcine brain and found stiffness measurements on the same order of magnitude as in vitro data. Gefen and Margulies (2004) compared mechanical properties in the porcine brain in vivo to corresponding properties post-mortem, in situ (i.e., after death, but in the intact head), and ex vivo (in the extracted brain), also using indentation. These studies found in vivo shear moduli stiffer than moduli measured post-mortem on preconditioned tissue (either in situ or ex vivo). Although these results offer insight into the relationship between in vivo and ex vivo tissue mechanical properties, the methods have important limitations. Indentation of the intact brain only measures properties near the surface. Also, indentation is sensitive to the detection of contact, and, unless performed at multiple speeds, provides limited information on frequency/strain-rate dependence. Dynamic shear testing of thin tissue samples (Arbogast and Margulies, 1998; Feng et al., 2013b; Hrapko et al., 2006) has been widely used for material characterization. Shear testing assumes flat samples, constant normal force, no slip, and affine deformations; conditions which are rarely satisfied. Furthermore, dynamic shear testing is impractical for in vivo tissue.

MRE is an imaging technique for non-invasively measuring the mechanical properties of soft tissue (Muthupillai et al., 1995). In MRE, shear waves are induced in tissue by harmonic mechanical actuation, and imaged with a modified MR imaging sequence that includes harmonic, motion-sensitizing gradients. The material properties of tissue can be calculated using local wavelength estimation, direct inversion of the viscoelastic shear wave equation, or finite element methods (Manduca et al., 2001). While deformations are typically small (<0.1% strain) the linear, viscoelastic properties that govern behavior in this regime are important and complement parameters that describe large-amplitude, quasi-static response. MRE has been used to characterize tissues like brain, liver, and muscle in vivo and to study changes in stiffness due to aging, disease, or injury (Klatt et al., 2007; Riek et al., 2011; Sack et al., 2011, 2009b; Sinkus et al., 2005). However, estimates of brain properties obtained by MRE (Atay et al., 2008; Johnson et al., 2013; Sack et al., 2009a; Vappou et al., 2008, 2007) tend to differ from estimates of properties measured ex vivo by direct mechanical tests (Feng et al., 2013b; Hrapko et al., 2006; van Dommelen et al., 2010; Vappou et al., 2007). It is not clear whether conflicting estimates arise from differences in methodology or actual properties.

Still lacking are direct comparisons between dynamic mechanical properties estimated throughout the brain by the same method at similar frequencies and amplitudes, both in vivo and ex vivo. In this study, we address this need by performing MRE on porcine brain tissue over a range of frequencies, obtaining stiffness estimates both in vivo and ex vivo within the same tissue volume.

2. Methods

In vivo and ex vivo anatomical MRI and MRE scans were performed on six Yucatan mini-pigs (age range: 4 to 8 months; weight range: 23 to 50 kg). The experimental protocol was approved by the Washington University in St. Louis Animal Studies Committee, and all studies were supervised by veterinary staff.

2.1 In vivo Scanning

All scans were performed on a Siemens Prisma® 3T MRI scanner at Washington University in St. Louis. The mini-pigs were anesthetized with Telazol Ketamine Xylazine (TKX). An IV catheter and endotracheal tube were placed prior to scanning. Anesthesia was maintained with isoflurane via endotracheal tube. Temperature, pulse, respiration, and SPO₂ were monitored. Mini-pigs were scanned in either ventral or dorsal recumbency. For dorsal recumbency (4 animals), the animal was positioned with its back on the scanner table (Figure 1A), and its head was placed in the base of the Siemens Head/Neck 20 coil. A combination of padding and Velcro^™ straps was used to secure the head. For ventral recumbency (2 animals), the animal was positioned with its stomach on the scanner table. Its head was placed under a custom half-dome Plexiglas frame (Figure 1C); a combination of padding and Velcro^™ straps was used to secure the head. The Siemens 18-channel Body Matrix Coil was fastened on the Plexiglas frame and MR table using Velcro^™ straps.

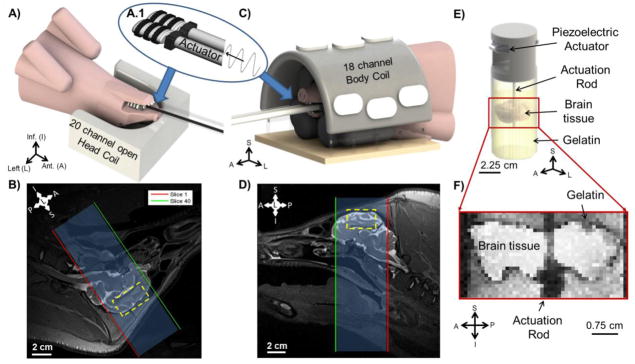
Figure 1.

A–D) Experimental set-up for MRE in vivo. A custom actuator (A.1) driven by the Resoundant^™ system is placed between the back molars of the mini-pig jaw to induce vibrations in the skull and shear waves in brain at 50, 80, 100, and 125 Hz while the mini-pig is positioned in dorsal recumbency or ventral recumbency. A) Mini-pig scanned in dorsal recumbency with its head placed in the lower part of the Seimens Head/Neck20 coil. Padding and Velcro^™ secured the head from excess motion. B) T2-weighted anatomical image (sagittal view, 0.8 mm³ voxels) of the mini-pig in dorsal recumbency, with MRE slices highlighted. Yellow rectangle shows the approximate location of the ex vivo brain tissue disk. C) Mini-pig scanned in ventral recumbency with its head placed under a custom, half-dome, Plexiglas frame which supported the Siemens 18-Channel Body Matrix Coil. Padding and Velcro^™ secured the head from excess motion. D) T2-weighted anatomical image (sagittal view, 0.8 mm³ voxels) of mini-pig in ventral recumbency, with MRE slices highlighted. Yellow rectangle shows approximate location of ex vivo brain tissue disk. E–F) Experimental set-up for MRE ex vivo. E) The cylindrical brain tissue sample is embedded in gelatin and excited by a central actuation rod at 80, 100, 125, 200, and 300 Hz using a piezoelectric actuator. F) Anatomical image (1 mm³ voxels) of the ex vivo brain tissue sample and gelatin, TE = 60 ms and TR = 1000 ms.

A custom multi-directional jaw actuator was designed to transmit harmonic motion from a pneumatic driver into the porcine brain while minimizing dissipation from muscle and fat. The actuator was fabricated from two small, empty plastic bottles (Figure 1A.1). A custom Delrin (Acetal) holder fit around the tube/bottle neck connections of each bottle. Two holes on each side of the Delrin holder secured an elastic Velcro^™ nose strap. Two rubber timing belts encircling each bottle provided traction between the bottles and mini-pig molars (Figure 1A and 1C). After positioning the mini-pig head in the coil, the custom actuator was placed inside the jaw, with the bottles between the rear molars. The nose strap was tightened around the upper and lower jaws to minimize slippage between the teeth and actuator.

T1-weighted (“MP-RAGE”) and T2-weighted MR images were taken at the beginning of every in vivo MR scanning session (Figures 1B, 1D; Figure 2A). Image volumes were acquired at 0.8 mm³ or 0.9 mm³ isotropic resolution for an in-plane field of view of 205 mm x 205 mm (0.8 mm³ res) or 230 mm x 230 mm (0.9 mm³ res). A total of 192 (0.8 mm³ res) or 96 (0.9 mm³ res) slices were taken for each scan. Two averages were done for each image set. The anterior-posterior direction of the image volumes was aligned with the genu-splenium axis of the corpus callosum. The total scan time for the two anatomical acquisitions was 21 minutes.

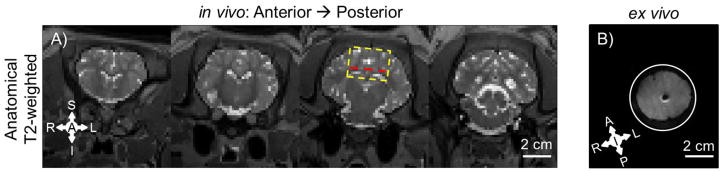
Figure 2.

Comparison of experimental data from the porcine brain in vivo (A) and ex vivo (B). A) T2-weighted MR images of four non-contiguous (7.5 mm spacing) coronal slices of the brain in vivo at 1.5 mm resolution. Yellow rectangle shows approximate location of ex vivo brain tissue disk. Red line denotes approximate slice location pictured in B. B) T2-weighted image of ex vivo cylindrical sample from the same animal at 1 mm resolution.

For MRE, the skull was vibrated at frequencies of 50 Hz, 80 Hz, 100 Hz, or 125 Hz using a commercially available pneumatic driver (Resoundant^™ Rochester, MN) connected to the custom jaw actuator (Table 1). MRE data with 3D displacement components, each encoded by image phase, were acquired with a 2D multi-shot spiral sequence (Johnson et al., 2013) with 1.5 mm isotropic voxels covering a volume of 180 x 180 x 60 mm³. One vibration frequency was used per acquisition. Multiple sinusoidal motion-encoding cycles of gradient strength 30 mT/m were synchronized with motion to induce phase contrast proportional to displacement (2.45 microns/rad at 50 Hz and 100 Hz, 3.91 microns/rad at 80 Hz, and 3.06 microns/rad at 125 Hz) (Atay et al., 2008). Data for each mini-pig were collected over 2–3 scanning sessions using 1–3 actuation frequencies per session.

Table 1.

Numbers of anatomical and MRE scans performed in vivo and ex vivo in the 6 mini-pigs.

	T1/T2	MRE 50 Hz	MRE 80 Hz	MRE 100 Hz	MRE 125 Hz	MRE 200 Hz	MRE 300 Hz
In vivo	19	11	2	10	3	-	-
Ex vivo	6	-	1	5	2	6	6

MRE data were phase-unwrapped using open-source software FSL Prelude (Smith et al., 2004). Voxels in the MRE volume were fitted to a model of rigid-body displacement and these rigid-body effects were removed to isolate displacements due to wave motion (Badachhape et al., 2017).

2.2 Ex vivo Scanning

Ex vivo scanning of tissue from the same six Yucatan mini-pig brains was performed on an Agilent/Varian DirectDrive 4.7T small-bore animal MRI scanner at room temperature (~21°C). Once all in vivo scanning was complete, the mini-pigs (aged 6–9 months) were euthanized by barbiturate overdose. (Note: ages differ from in vivo scans because multiple in vivo scans were performed on each mini-pig over 2–4 months; 0–2 weeks elapsed between the last in vivo scan and the ex vivo scan). The brain was immediately extracted following euthanasia and dissected to expose the inferior section of the corpus callosum. A cylindrical sample containing the corpus callosum and superior gray matter, 42 mm in diameter, was extracted from the brain using a cylindrical punch. The sample was embedded in gelatin made with 2:1:1 glycerol, water, and pre-buffered saline (PBS) in a 45 mm cylindrical container (Schmidt et al., 2016) (Figure 1E). Ex vivo scans began within 2 hours post-mortem.

Ex vivo samples were vibrated at frequencies of 80 Hz, 100 Hz, 125 Hz, 200 Hz, and 300 Hz (Table 1). Shear waves were excited by a central actuation rod of 3 mm diameter that punctured the center of the sample (Figure 1E). This rod was driven harmonically by an MR-compatible piezoelectric actuator (APA150M, Cedrat Technologies, Meylan, France). Anatomical images were taken at 1 mm isotropic resolution with a field of view of 48 x 48 x 25 mm³ (Figure 1F, Figure 2B). Images were obtained at TE of 60 ms. MRE data were acquired with a modified 2D multi-slice spin-echo sequence with 1 mm isotropic voxels, TR = 1000–1200 ms, and TE = 28–40 ms covering a volume of 48 x 48 x 25 mm³ (Figure 1F). Sinusoidal motion-encoding gradients (1–3 cycles) of amplitude 100–120 mT/m were synchronized with motion to induce phase contrast proportional to displacement (7.48 microns/rad at 80 Hz (n=1), 100 Hz (n=2), 200 Hz (n=5), and 300 Hz (n=5) and 9.35 microns/rad at 100 Hz (n=3), 125 Hz (n=2), 200 Hz (n=1), and 300 Hz (n=1)). MRE data were phase-unwrapped and rigid-body motion effects were removed using the methods detailed in section 2.1.

2.3 Local Direct Inversion

Local direct inversion (LDI) was performed on both the in vivo and ex vivo MRE displacement fields to estimate the mean complex shear modulus of the mini-pig brain sample at each of the measured frequencies using the viscoelastic analog to the Navier equation (Okamoto et al., 2011):

$$(G^{\prime }+i{G}^{″}){\nabla }^2\mathit{U}(x,y,z)=-\rho {\omega }^2\mathit{U}(x,y,z),$$ (1)

where the complex vector U(x, y, z) contains the Fourier coefficients of the fundamental harmonic of the 3D displacement field, G′ is the storage modulus, and G″ is the loss modulus. This equation assumes that the material is linear, isotropic, and locally homogeneous.

Estimates of storage and loss moduli were obtained for the entire brain in vivo and the entire sample of ex vivo brain and gelatin. Voxel-wise estimates were averaged over a region of interest (ROI) corresponding to the location and dimensions of the ex vivo brain samples. Storage modulus maps were further eroded using a 7x7x7 kernel to remove the possible effects of neighboring gelatin on the averaged storage modulus estimates in the ex vivo tissue.

3. Results

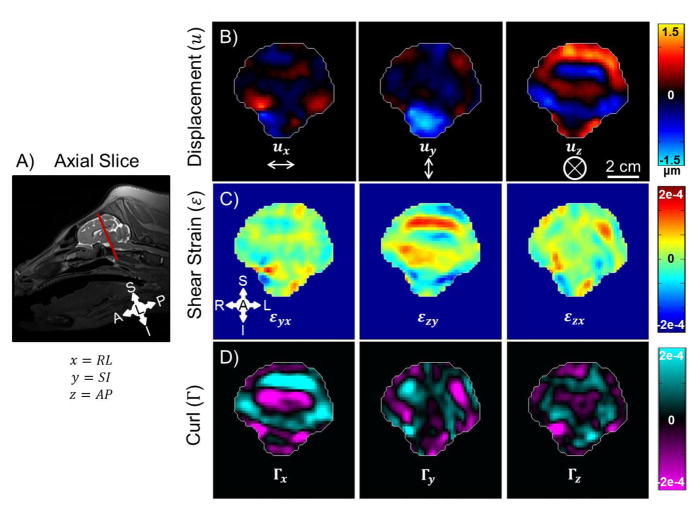
Figure 3 shows examples of wave displacement, shear strain, and curl for one axial slice of the porcine brain in vivo. Although displacement components exist in all three directions, the out-of-plane, anterior-posterior (AP, z) component of motion (u_z) is the dominant component excited by the custom actuator. The displacement amplitude is ~1.5 μm. The curl of the wave field, which isolates the contribution of shear waves, is dominated by the component along the right-left (RL, x) axis, ${\mathrm{\Gamma }}_x=\frac{\partial u_y}{\partial z}-\frac{\partial u_z}{\partial y}$. Shear strain and curl have similar magnitude (~2 × 10⁻⁴); the most prominent component of the strain tensor is ${\mathrm{\epsilon }}_{zy}=\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y}$.

Figure 3.

In vivo MRE results for one axial slice of mini-pig brain at 100 Hz imaged while positioned in dorsal recumbency. A) Image slice location. B) Three components of displacement. C) Three components of shear strain. D) Three components of curl.

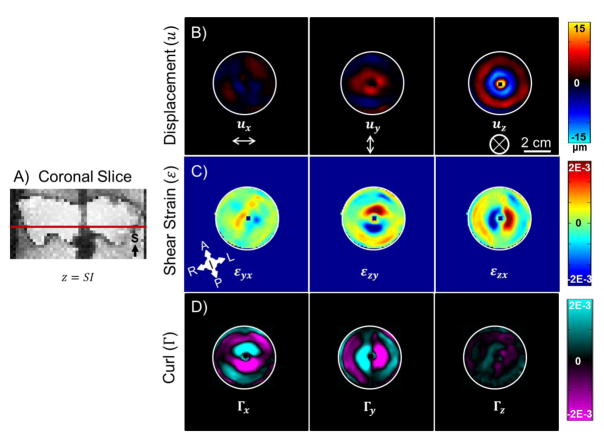
Figure 4 shows examples of displacement, shear strain, and curl maps for one coronal slice of porcine brain tissue ex vivo. The dominant displacement component (~15 μm amplitude) during shear wave propagation is in the out-of-plane (u_z) direction, which is the superior-inferior (SI) direction with respect to the brain. The curl of the wave field shows that the propagation of the waves occurs radially outward in the xy-plane. The largest components of curl and strain are ~2 × 10⁻³ mm/mm, which are well within the small-deformation regime.

Figure 4.

Ex vivo MRE results for one axial slice of brain tissue at 100 Hz. A) Image slice location. Images are from the same mini-pig shown in Figure 3. B) Three components of displacement. C) Three components of shear strain. D) Three components of curl. Note orientations and scale bars are different from Figure 3.

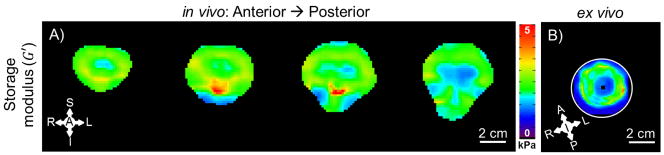
Figure 5 displays storage modulus estimates for four representative in vivo axial slices spaced 7.5 mm apart and one representative ex vivo coronal slice estimated using LDI for the data taken at 100 Hz. The ex vivo sample is surrounded by the gelatin, which is represented by the less stiff (~1 kPa) estimates in the image.

Figure 5.

A) Storage modulus (G′) at 100 Hz in vivo estimated using LDI. The AP component of motion is shown for the same image slices as in Figure 3A and B. G′ was only estimated for voxels where >50% of the 7x7x7 fitting kernel was inside the brain. B) Storage modulus (G′) at 100 Hz ex vivo estimated using LDI. The SI component of motion is shown for the same image slice as in Figure 3C and D. G′ was only estimated for voxels where >50% of the 7x7x7 fitting kernel was inside the sample. Note: Image scales are the same in each panel (scale bars = 2 cm), but image slice orientations differ between panels A and B.

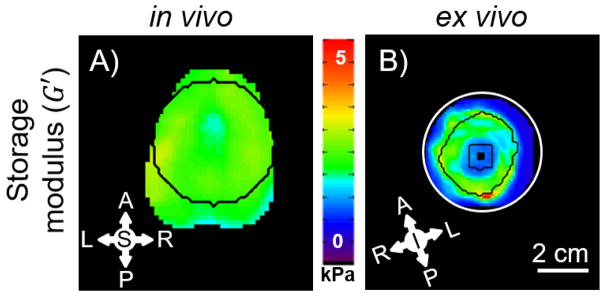
To compare property estimates in vivo and ex vivo, an ROI was defined in the in vivo image volume to match the dissected sample used in ex vivo scanning. The ROI (Figure 6) is a 42 mm cylinder that includes the corpus callosum and superior regions. To remove the effects of the gelatin surrounding the ex vivo sample and the estimates near the actuator rod, the ROI for the ex vivo stiffness data was eroded using the MATLAB imerode command (2014a, MathWorks, Natick, MA) with a 7x7x7 kernel.

Figure 6.

LDI-estimated storage modulus (G′) for one in vivo (A) and one ex vivo (B) mini-pig coronal brain slice using 7x7x7 kernel for LDI. Black outlines denote the area used in the comparison between in vivo and ex vivo samples. The ex vivo sample was eroded using a 7x7x7 kernel to remove the influence of gelatin on G′ estimates.

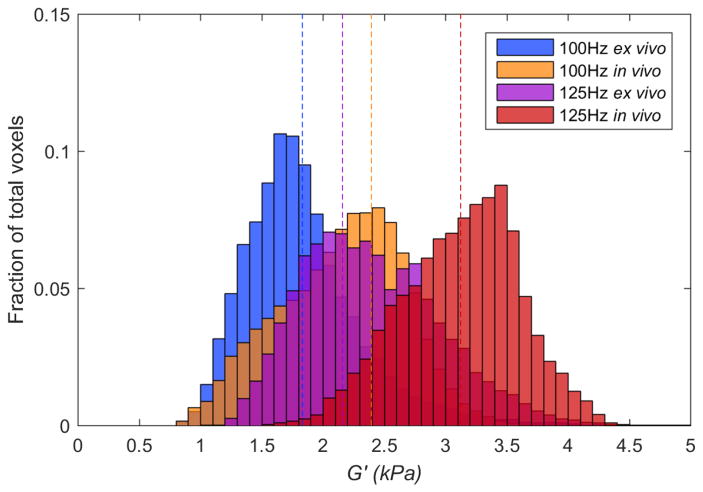
Figure 7 displays histograms of LDI estimates of storage modulus (G′) values for all voxels from the ROI of the in vivo image volume and from the eroded ROI of the ex vivo sample from all scans performed at 100 Hz and 125 Hz. The mean for each data set is depicted by the dashed line. These histograms show (i) higher stiffness at the higher frequency, and (ii) in vivo tissue is stiffer than ex vivo tissue. The effect of orientation (dorsal or ventral) in vivo on brain stiffness was checked, and found to be small (voxelwise mean ± std.: 0.779 ± 0.347 kPa dorsal vs. 0.777 ± 0.468 kPa ventral for 50 Hz; 2.264 ± 0.649 kPa vs. 2.381 ± 0.820 kPa for 100 Hz).

Figure 7.

Histogram of LDI-estimated storage modulus (G′) values of all pixels for in vivo (orange and red) and ex vivo (blue and purple) calculated at 100 and 125 Hz using a 7x7x7 kernel for all of the scanned mini-pigs. Dotted lines represent the mean G′ value. In vivo voxels are from the cylindrical ROI shown in Figure 6A. Ex vivo voxels are from the eroded ROI shown in Figure 6B.

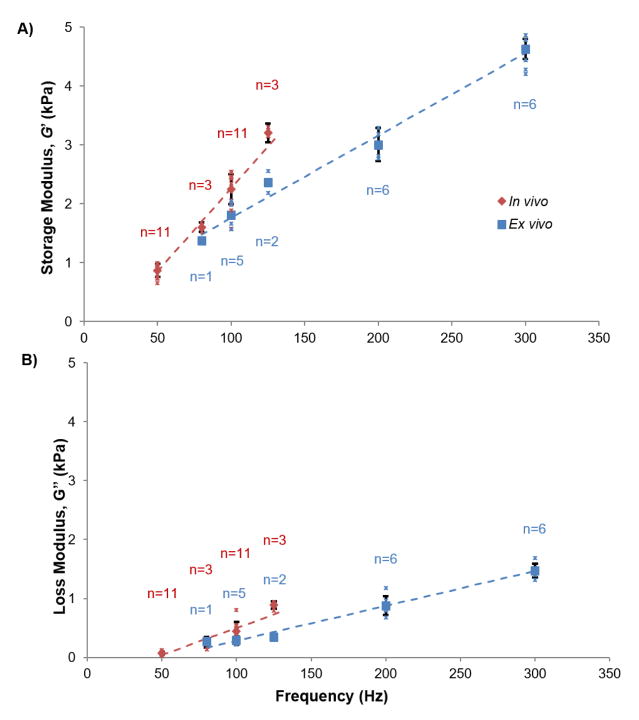
At each frequency, the mean storage and loss moduli from the ROI of the in vivo image volume were estimated, along with the corresponding mean storage and loss moduli in the eroded ROI of the ex vivo image volume. The means and standard deviations of these parameters are plotted versus frequency in Figure 8. Both in vivo and ex vivo estimates of storage modulus increase with frequency. Notably, estimates of storage modulus are higher for the in vivo data than for the ex vivo data at all common frequencies. Multivariate regressions of storage and loss moduli were performed using a linear mixed-effects model with random subject effects. Group (in vivo vs. ex vivo), frequency, and their interaction were the independent predictors (Appendix B). For storage modulus, the slopes between in vivo and ex vivo were significantly different (p < 0.0001) and frequency was a good predictor of the data (p < 0.0001). No significant differences were observed between loss moduli in vivo and ex vivo over this frequency range (p = 0.285). The linear mixed-effects model is included with mean storage and loss modulus estimates, in Figure 8. Storage and loss modulus estimate were also fitted to several candidate rheological models (Appendix C).

Figure 8.

Mean storage modulus (G′) and loss modulus (G″) of in vivo (red) and ex vivo (blue) mini-pig brain tissue estimated by LDI at frequencies from 50–300 Hz for N=6 animals. Each small asterisk (*) represents the mean G′ or G″ for one mini-pig scanned at the specified frequency. Each larger marker (blue □ and red ◇) represents the mean G′ or G″ for all mini-pigs scanned at the specified frequency. Notations above/below markers provide the number of scans represented by the mean value. Standard deviations were only provided for data sets with n≥3. For in vivo data, each marker shows the average modulus estimate in a cylindrical ROI of dimensions matching that of the ex vivo cylindrical sample (Figure 1B). Multivariate linear regressions of G′ and G″ were performed using a linear mixed-effects model with subject as a random effect (dashed lines; see Appendix B). In vivo: G′ = 0.85 + 0.0283 (f − 50); G″ = 0.041 + 0.00916 (f − 50). Ex vivo: G′ = 1.48 + 0.0140 (f − 80); G″ = 0.164 + 0.00592 (f − 80). A) Estimates of G′ increase with frequency due to viscoelasticity. At the common frequencies, 80, 100, and 125 Hz, G′ estimates are higher for brain tissue in vivo than for brain tissue samples ex vivo. B) Estimates of G″ increase with frequency due to viscoelasticity.

4. Discussion

This study provides the first comparison of in vivo and ex vivo material properties throughout a volume of brain tissue in the same large animal using MRE. MRE was performed on brain tissue both in vivo and ex vivo at multiple frequencies, illuminating the viscoelastic behavior of brain tissue under both conditions. MRE estimates of storage modulus suggest that tissue in the intact, living brain is stiffer than in ex vivo samples. Direct comparison was possible at overlapping frequencies of 80 Hz, 100 Hz, and 125 Hz. Estimates in ex vivo tissue at other frequencies (200 Hz, and 300 Hz) support this general observation.

MRE in pigs is quantitatively similar to MRE in humans. In Figure 3 the magnitude of wave displacement in vivo is on the order of 1–2 microns, similar to magnitudes observed in human studies in vivo using a “pillow” actuator (Badachhape et al., 2017) or “paddle” actuator (Clayton et al., 2012). The largest component of wave motion in the current in vivo studies is in the AP direction. Larger amplitudes are achieved in the ex vivo sample since waves are excited by direct vibration of the tissue; the largest component of wave motion is in the SI direction.

Our estimates of storage modulus ex vivo at 80 Hz are within 15% of several estimates from the literature on the porcine brain taken using MRE (Vappou et al., 2007) or oscillatory shear strain at 2.5% (Arbogast and Margulies, 1997; Thibault and Margulies, 1998). At higher frequencies, the current ex vivo estimates of storage modulus are greater than prior estimates in porcine brain and exhibit a steeper dependence on frequency (Arbogast and Margulies, 1997; Thibault and Margulies, 1998; Vappou et al., 2007). Current estimates of loss modulus for ex vivo are lower than prior estimates (Arbogast and Margulies, 1997; Thibault and Margulies, 1998; Vappou et al., 2007).

What might explain the observed mechanical differences between in vivo and ex vivo brain tissue? Ex vivo tissue experiences neither perfusion nor metabolic activity, and any residual stress in ex vivo tissue is relieved by dissection. More comprehensive studies are needed to determine which factors might explain observed stiffness differences.

It is possible that anisotropy of white matter might have contributed to differences between in vivo and ex vivo parameter estimates (Anderson et al., 2016; Schmidt et al., 2016; Tweten et al., 2015). Anderson et al. (2016) found ~20% differences in estimated storage modulus of white matter between areas where displacements were primarily parallel vs. perpendicular to the dominant fiber direction. In the current study, although the dominant tissue motions were in different anatomical directions in vivo and ex vivo, in both cases tissue displacements were perpendicular to the dominant (right-left) fiber direction. Tissue motion in vivo was primarily anterior-posterior (Figure 3) and tissue motion ex vivo was primarily superior-inferior (Figure 4); both are perpendicular to the fiber axis. Also, differences between in vivo and ex vivo estimates diminish at low frequencies. Thus, anisotropy is unlikely to explain the observed differences.

Temperature affects tissue properties. We did not monitor the sample temperature in the current ex vivo studies, but in prior studies with gelatin samples (Okamoto et al., 2011) sample temperature during MRE was ~21°C, which is substantially lower than in vivo (~37°C). However, in viscoelastic tissue lower temperatures are typically associated with higher storage modulus (Hrapko et al., 2008), which would tend to mask observed differences.

The pig brain in vivo is surrounded by CSF and skull; ex vivo tissue was encased in gelatin in a plastic container. Boundaries should have minimal effects in both cases because we analyzed only interior ROIs removed from the boundaries. Also, differences in estimated properties are greater at higher frequencies, at which the effects of boundaries are likely less important, due to shorter wavelengths.

Future studies could investigate ex vivo brain tissue in situ (i.e., in the intact head post mortem) to account for factors related to tissue extraction. However, the logistical challenges of doing in vivo, in situ, and in vitro MRE in the same animal are substantial.

Other limitations exist for both in vivo and ex vivo experiments. Since the porcine brain is small (~100 g), images are at a lower resolution, relative to brain anatomical structures, than typical human scans. Due to differences in actuation and sample geometry, the frequency ranges for in vivo and ex vivo studies did not overlap completely. The mini-pig head in vivo has thick layers of bone, fat and muscle, so that frequencies above 125 Hz dissipated before reaching the brain. In the ex vivo sample, below 80 Hz, insufficient wavelengths were obtained for accurate parameter estimation. Strain amplitudes were higher in ex vivo experiments, though in both in vivo and ex vivo samples strains were < 0.2%, well within the small-strain (linear) regime. Differences between in vivo and ex vivo studies and data characteristics are summarized in Appendix A.

5. Conclusion

This study shows notable differences between material properties estimated by MRE in vivo and ex vivo in similar volumes of brain tissue from the same animal, over multiple frequencies. Although many ex vivo measurements of brain tissue mechanical properties are available, only limited data have been obtained in vivo. Thus, most TBI simulations incorporate material parameters measured ex vivo. The current results thus represent progress toward accurate simulation of TBI in the intact, living brain.

Appendix

A. Error Analysis

The table below summarizes differences between in vivo and ex vivo experiments and their possible effects.

Table A.1.

Error analysis comparing in vivo and ex vivo experiments

Potential error source	Comments	In vivo	Ex vivo
Wave amplitude	Shear modulus is estimated from the wave length. Differences in wave amplitude should not directly affect modulus estimates. In both methods, waves had enough amplitude to produce visible shear waves. In the small-strain regime we do not expect modulus to depend on amplitude.	Wave amplitude ~1.5μm Strain amplitude ~2x10−4	Wave amplitude ~15μm Strain amplitude ~2x10−3
Dominant wave direction	Both methods produced shear wave polarization displacements perpendicular to the dominant fiber direction, oriented right-left, of the corpus callosum. Although the tissue is actuated in different anatomical directions, the tissue is actuated similarly relative to the dominant fiber axis in both situations.	Dominant actuation direction: anterior-posterior (AP)	Dominant actuation direction: superior-inferior (SI)
Temperature	Temperature difference could cause differences in tissue properties. However, cooling of viscoelastic tissue generally leads to stiffening, so the temperature difference is more likely to mask differences in stiffness between the (apparently stiffer) in vivo and softer ex vivo tissue. The fact that a difference is still observed tends to support the paper’s conclusions that in vivo tissue is stiffer.	Body temperature ~37°C	Room temperature ~21°C
Excitation method	Excitation differences created differences in propagation direction. In vivo waves were excited externally and propagated inward from the skull. Ex vivo waves were excited in the center of the tissue and propagated outward (the rod created an internal boundary which was removed through erosion of voxels). The direction of wave propagation should not have an effect since fiber orientation was similar.	External actuation of skull by vibration of jaw	Axial excitation by central rod embedded in tissue
Voxel size	Voxel size affects the physical size of the estimation kernel for LDI, and the size of the eroded regions at boundaries. Kernel size does affect parameter estimates. Estimates converge as kernel size increases; kernel size is limited by sample size. Estimated effect: Results vary 3–7% (ex vivo) and 7–10% (in vivo) between kernel sizes of 5x5x5 to 7x7x7 voxels.	1.5 mm3 isotropic voxels	1 mm3 isotropic voxels
Boundary conditions	Boundary conditions are different, but comparable. The in vivo brain is surrounded by cerebrospinal fluid (CSF) and the skull. The ex vivo brain is surrounded in gelatin/glycerol and a hard plastic case. The boundaries should have only small effects on the conclusions of the study for two reasons: (1) In both cases, we analyzed interior ROIs, removed from the boundaries. All results are based on these interior ROIs. (2) Observed differences in estimated properties are greater at higher frequencies (with short wavelengths) at which the effects of boundaries are less likely to be important than at lower frequencies (longer wavelengths).	Skull and cerebral spinal fluid (CSF)	Gelatin/glycerol and plastic cylinder case

B. Linear Mixed Model

The multivariate regressions of storage modulus (G′) and loss modulus (G″) were performed (Matlab R2017, Statistics Toolbox) using a linear mixed-effects model with random subject effects and fixed effects of group (in vivo vs. ex vivo) and frequency in the form:

$$y_i=a+b_1{x}_{1i}+b_2{x}_{2i}+b_3{x}_{1i}{x}_{2i}.$$ (B.1)

In this model, y_i is G′ or G″, a is the intercept, b₁ is the slope of the group variable, x_1i is the value of the group variable, b₂ is the slope of the frequency variable, x_2i is the value of the frequency variable, and b₃ is the slope of the interaction between group and frequency. The value of the group variable defines whether the tissue is in vivo (x_1i = 1) or ex vivo (x_1i = 0). Tables B.1 and B.2 outline the results of the analysis of G′ and G″, respectively. The slopes between G′ in vivo and ex vivo were significantly different (p < 0.0001) and frequency was a good predictor of the data (p < 0.0001). No significant differences were observed between G″ in vivo and ex vivo over this frequency range (p = 0.285). The linear mixed-effects model is plotted with G′ and G″ estimates in Figure 8.

Table B.1.

Results of multivariate regression of storage modulus (G′) using a linear mixed-effects model with random subject effects

Effect	Variable	Estimate	Standard Error	Alpha (lower, upper)	P
Intercept	a	0.361	0.128	0.05 (0.102, 0.620)	0.007
Group	b1	−0.926	0.178	0.05 (−1.283, −0.568)	<0.0001
Frequency (Hz)	b2	0.0140	0.0007	0.05 (0.0126,0.0154)	<0.0001
Group*Frequency	b3	0.0143	0.0016	0.05 (0.0110,0.0176)	<0.0001

Table B.2.

Results of multivariate regression of loss modulus (G″) using a linear mixed-effects model with random subject effects

Effect	Variable	Estimate	Standard Error	Alpha (lower, upper)	P
Intercept	a	−0.309	0.070	0.05 (−0.448, 0.167)	<0.0001
Group	b1	−0.108	0.100	0.05 (−0.310, −0.093)	0.285
Frequency (Hz)	b2	0.00592	0.00035	0.05 (0.00522,0. 0.00662)	<0.0001
Group*Frequency	b3	0.00324	0.00091	0.05 (0.00140,0.00508)	0.0009

C. Summary of Rheological Model Fitting

Several rheological models were fitted to the complex shear modulus estimates from both in vivo and ex vivo data. Classic rheological models do not fit the estimated moduli well (Table C.1), possibly due to poroelastic behavior (McGarry et al., 2015). However, as noted by Testu et al. (2017), dual power-law models fitted separately to G′ and G″ fit the frequency-dependent shear moduli much better than the classic (springpot) power-law.

Table C.1.

Summary of rheological data fitting.

Model	In vivo		Ex vivo
	Parameters	R2	Parameters	R2
Power law (dual)#  G′ = k1ωα1  G″ = k2ωα2	k1 = 2.88 × 10−4	0.924	k1 = 7.93 × 10−3	0.940
	α1 = 1.39		α1 = 0.840
	k2 = 8.60 × 10−9		k2 = 2.11 × 10−5
	α2 = 2.75		α2 = 1.48
Power law (springpot)†  G* = k(iω)α	k = 0.490	0.168	k = 0.563	0.357
	α = 0.214		α = 0.253
Zener‡   $G^{\ast }=G_{\infty }\frac{1+d(i\omega \tau )}{1+i\omega \tau }$	G∞ = 1.09	0.257	G∞ = 1.93	0.515
	d = 2.38		d = 2.58
	τ = 1.77 × 10−3		τ = 6.61 × 10−4
Fractional Zener‡   $G^{\ast }=G_{\infty }\frac{1+d{(i\omega \tau )}^{0.5}}{1+i\omega \tau }$	G∞ = 0.473	0.178	G∞ = 0.722	0.377
	d = 7.88		d = 10.89
	τ = 9.64 × 10−4		τ = 2.60 × 10−4
Generalized Maxwell§   $G^{\ast }=G_{\infty }+\frac{i\omega {\tau }_1{G}_1}{1+i\omega {\tau }_1}+\frac{i\omega {\tau }_2{G}_2}{1+i\omega {\tau }_2}$	G∞ = 1.09	0.257	G∞ = 1.93	0.515
	G1 = 3.00 × 10−15		G1 = 3.14 × 10−14
	G2 = 1.51		G2 = 3.05
	τ1 = 2.84 × 10−5		τ1 = 3.48 × 10−5
	τ2 = 1.77 × 10−3		τ2 = 6.61 × 10−4

Units: Power law: k, k₁, k₂ (kPa-s^α), α (non-dimensional). Zener, fractional Zener, and generalized Maxwell: G_∞, G₁ G₂ (kPa); d (non-dimensional); τ, τ₁, τ₂ (sec).

^#(Testu et al., 2017);

^†(Koeller et al, 1984);

^‡(Kohandel et al., 2005);

^§(Flugge, 1967)