Considerations for Analysis of Time-to-Event Outcomes Measured with Error: Bias and Correction with SIMEX

Abstract

For time-to-event outcomes, a rich literature exists on the bias introduced by covariate measurement error in regression models, such as the Cox model, and methods of analysis to address this bias. By comparison, less attention has been given to understanding the impact or addressing errors in the failure time outcome. For many diseases, the timing of an event of interest (such as progression-free survival or time to AIDS progression) can be difficult to assess or reliant on self-report and therefore prone to measurement error. For linear models, it is well known that random errors in the outcome variable do not bias regression estimates. With non-linear models, however, even random error or misclassification can introduce bias into estimated parameters. We compare the performance of two common regression models, the Cox and Weibull models, in the setting of measurement error in the failure time outcome. We introduce an extension of the SIMEX method to correct for bias in hazard ratio estimates from the Cox model and discuss other analysis options to address measurement error in the response. A formula to estimate the bias induced into the hazard ratio by classical measurement error in the event time for a log-linear survival model is presented. Detailed numerical studies are presented to examine the performance of the proposed SIMEX method under varying levels and parametric forms of the error in the outcome. We further illustrate the method with observational data on HIV outcomes from the Vanderbilt Comprehensive Care Clinic.

1. Introduction

There are many examples in clinical research where the outcome of interest relies on an imprecisely measured event time. Researchers studying the epidemiology of chronic conditions may enroll subjects some time after an initial diagnosis, and so research questions focused on the timing of events post diagnosis may need to rely on patient recall or chart review of electronic medical records, both of which are subject to error. For example, human biologists and demographers are interested in the variability in the age at menarche (first menstruation) [1]. Oftentimes, subjects are enrolled several years after menarche, and so the event-time is based on retrospective recall and hence subject to error. As Holt et al. [2] observed, studies comparing age at menarche reported retrospectively to those reported in medical records have shown that differences in the two can be attributed to recall error symmetrically distributed around zero. In addition, epidemiological researchers frequently use observational databases, where data accuracy can also be a concern. In observational studies of HIV/AIDS, the event time between antiretroviral therapy (ART) initiation and a disease outcome, such as AIDS-defining illness and associated risk factors, is often of interest. In prior studies using routinely collected health record data, we have observed substantial errors, in as many as 30% of patient records, in the time of ART initiation [3, 4]. Even in studies where a failure time may be measured precisely, such as time to virologic failure defined by an electronically recorded HIV-RNA test exceeding a threshold, the error in the baseline time will create error in the time-to-event outcome. Ignoring these errors can lead to biased estimates of the associations of interest.

There is a rich body of knowledge describing the impact of and methods to correct for covariate measurement error, particularly for time-to-event outcomes [5]. For the Cox model, these methods include approximate methods such as regression calibration [6] and SIMEX [7]. They also include methods that have been shown to be unbiased under certain assumptions; including the parametric corrected score [8], conditional score [9], non-parametric corrected score [10, 11] and likelihood methods [12, 13], to name a few.

Much less has been written about the effect of or methods for errors in the failure time outcome itself. For continuous outcomes and linear regression, it is well known that random outcome error does not introduce bias into the regression coefficients. However, for nonlinear models, simple random error in outcomes can bias the coefficients [5]. This has been well studied in the case of binary outcomes [14, 15] and discrete failure time data [16], where estimates of sensitivity and specificity can be incorporated to adjust estimation for the bias induced by outcome misclassification. Errors in outcome that are correlated with covariates can also be a source of bias in the association between these variables. Some methods, which adjust for covariate-dependent estimates of sensitivity and specificity, have been presented [17, 18, 19].

For uncensored, continuous failure time outcomes, Skinner [20] found that random multiplicative error has little effect on the acceleration parameter estimated by a Weibull regression model, particularly when there is a relatively small measurement error variance. Korn et al. [21] noticed that the bias in estimating the hazard ratio is very small with small random multiplicative measurement error in the failure time. Even with larger random error, the bias was small when the hazard ratio was moderate, as commonly seen in clinical trials. However, Hong et al. [22] noticed in their statistical models for progression-free survival, which involved modeling tumor growth and error-prone detection, that multiplicative error would lead to attenuation of the hazard ratio, with larger measurement error leading to greater attenuation.

The Simulation and Extrapolation method (SIMEX) was developed by Cook and Stefanski [7] to correct additive measurement error in the covariates. SIMEX has been applied to a wide variety of regression models and is generally implemented as an empirical method [5, 23]. It has been shown to be a useful tool for estimation in the presence of unbiased covariate measurement error in regression models for time-to-event outcomes, e.g., see Zhang et al. [24], He et al. [25], and Greene and Cai [26]. We extend the SIMEX approach to address random multiplicative error in the event time and study whether this method can be applied to reduce bias in the regression coefficients.

In this manuscript we will present a detailed numerical study of the impact of non-differential outcome measurement error on association analyses of failure time data. We provide an approximate formula to estimate the bias in the association parameters induced by random multiplicative error in the event time and examine performance of our proposed method to correct for the induced bias. In particular, we will consider two popular regression models for survival data, Cox and Weibull regression, and compare the vulnerability of these two regression frameworks to bias from error in the event time. The Weibull model is both an accelerated failure time (AFT) and proportional hazards (PH) model. Thus, within this modeling framework, we will compare the impact of outcome error on estimation of the hazard ratio and acceleration parameters for different measurement error scenarios.

Section 2 presents the survival time measurement error framework and develops the extended SIMEX method. Then Section 3 presents numerical studies of the bias on the hazard ratio and the acceleration parameter for different measurement error scenarios and the ability of the adapted SIMEX method to ameliorate this bias. We also discuss estimation options when there is a validation subset available with which to estimate the error structure. In Section 4, we apply the SIMEX method in an analysis of HIV outcomes among patients starting ART, where the time-to-event is sometimes recorded incorrectly.

2. Survival Time Model

We consider the Cox proportional hazards model and Weibull parametric regression model to study the effects of random error in survival time T. The Cox model is given by

$$\lambda (t)={\lambda }_0(t)\text{exp }(\mathbf{X}\beta )$$

where λ(t) is the hazard at time t given the p × 1 covariate vector X, λ₀(t) is the baseline hazard, and β is the vector of log hazard ratio parameters. For the Weibull (AFT) model, one has

$$T=\text{exp }({\alpha }_0+X{\alpha }_1+\sigma \epsilon )$$ (1)

where α₀ and α₁ are regression coefficients, σ is a shape parameter, and ε is the error term following an extreme value distribution. The model is also known as a linear transformation model, given by

$$\text{log}(T)={\alpha }_0+X{\alpha }_1+\sigma \epsilon .$$

2.1. Error Framework

We study the case where there is multiplicative error in the uncensored survival time. Let T′ be survival time measured with error such that we observe T′ = T × exp(ν), where ν has mean 0, variance ${\sigma }_{\upsilon }^2$, and is independent of T and X. Then the error prone survival time on the log-scale is given by

$$\text{log}(T\prime )={\alpha }_0+X{\alpha }_1+\sigma \epsilon +\upsilon =\text{log}(T)+\nu .$$ (2)

The performance of the Cox and Weibull models in the presence of outcome error, namely its ability to capture the true association with X, can be directly compared using the fact that the log hazard ratio from the Cox model can also be estimated from the Weibull model with the following relationship

$$\beta =-\frac{{\alpha }_1}{\sigma }.$$

We note that with the linear form for log(T′) above, the extra error term ν that is independent of the covariate X will not induce any bias in the acceleration parameter using a typical linear regression model. We also note that the error equation in (2) has the same mathematical form as a log-linear event time model with an added frailty term, ν. Keiding et al. [27] considered the AFT model for the setting of heterogeneity due to omitted covariates or frailties and observed that there is bias in the Cox model induced by erroneously ignoring an added fraility term ν, whereas there is no expected bias in the acceleration parameter α₁. These authors also derived an approximate formula for the attenuation factor for the hazard ratio parameter in the Cox model, drawing connections between the log-linear model for the uncensored event time and the theoretical linear regression of log(T) on X. For further detail, see Keiding et al. [27]. When adapted to our setting, the bias in β̂_naive, the estimated hazard ratio from naively applying the Cox model in the presence of the error in (2), is given by the approximate attenuation factor

$$\gamma =\frac{1}{\sqrt{1+{\sigma }^{-2}{\sigma }_{\nu }^2}}.$$ (3)

That is, β̂_naive ≈ β × γ.

2.2. SIMEX Method

Given the above framework for the survival model and outcome error, we adapt the SIMEX method to adjust estimation of a regression parameter of interest (e.g. the log hazard ratio β). The SIMEX method was originally developed for additive measurement error in the covariates [7]. We adapt the SIMEX method by working with the log T, which converts the assumed multiplicative error to the additive scale.

We illustrate our method using Figure 1. Similar to the original SIMEX method, we estimate the relationship between the size of the measurement error, ${\sigma }_{\upsilon }^2$, and the bias in the naive estimate of the parameter of interest from an analysis that ignores the error. In the Simulation step, we add additional measurement error to each outcome by drawing ω from $\mathrm{N}(0,\lambda {\sigma }_{\upsilon }^2)$ and adding the value of this random variable to the already error prone variable log T′ and exponentiating to obtain a new $T{\lambda }_b^{\prime }$. This error addition is repeated B times for a range of values of λ ≥ 0. Then for each iteration of λ and b = 1,…, B, we refit the regression model with the new vector of error prone measurement of the survival time $T{\lambda }_b^{\prime }$ to obtain a new naive log hazard ratio estimate β_λb (or other parameter of interest, e.g. acceleration parameter from the AFT). The new total measurement error variance in log $T{\lambda }_b^{\prime }$ is then given by

$${\sigma }_{\nu }^2+\lambda {\sigma }_{\nu }^2=(1+\lambda ){\sigma }_{\nu }^2$$ (4)

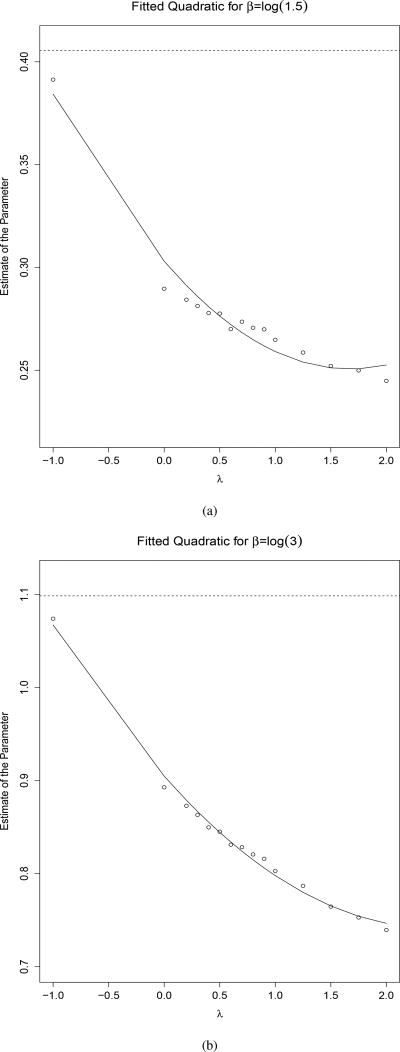
Figure 1.

The quadratic approximations of the β parameters as a function of λ, extrapolated to λ = −1, with the dotted lines denoting the true β for β = log(1.5) (a) and β = log(3) (b)

For illustration, we set B = 1 and $\lambda \in \{\frac{1}{10},\frac{2}{10},\dots ,\frac{9}{10},1\frac{5}{4},\frac{6}{4},\frac{7}{4},2\}$ to estimate new β_λ1, which are shown as small circles in Figure 1, and plot these naive β_λ1 versus λ. In the Extrapolation step, we then fit a curve to the plot of β_λ1 as a function of the λ’s. From this fitted model, we extrapolate back to λ = −1, which given the new total measurement error variance in Equation 4, should approximate the true coefficient value. For the setting with covariate measurement error, Cook and Stefanski recommend a quadratic approximation due to good performance in most cases, but other extrapolation functions such as a linear, loglinear, or nonlinear function are possibilities. We investigated the performance of the quadratic form in our framework using simulations and it outperformed the linear and loglinear approximations. In Figure 1, this extrapolation is shown by extending the curve to λ = −1. Note, in any data application, one could draw a similar figure - increasing the denseness of the vector λ to verify the appropriateness of the chosen extrapolation function (as quadratic or otherwise). This procedure only yields an approximation, since we can only generate curves for which λ ≥ 0, and thus have no estimates on the curve in the region of curve between [−1, 0). To assess the sampling variability of the SIMEX estimates, we utilize the bootstrap to obtain standard errors.

Here, we assume the value of ${\sigma }_{\upsilon }^2$ is known. In some settings, an estimate of ${\sigma }_{\upsilon }^2$ may be available from a validation study. In the case that the true value of the measurement error variance, ${\sigma }_{\upsilon }^2$, is unknown and an estimate is not available, one can apply the method for a variety of possible values for ${\sigma }_{\upsilon }^2$, and examine the sensitivity of the estimated β. In our data example that follows, we will illustrate the method with an estimated ${\sigma }_{\upsilon }^2$ from a validation subsample.

3. Simulations and Results

Through simulation, we examined the bias that results from random multiplicative error in the failure time outcome with different distributions of errors and evaluated the estimators from both the Cox and Weibull models. We then applied the proposed SIMEX method to obtain error-corrected estimates of the log-hazard ratio. These values will be compared to those from the true model, a Cox proportional hazards regression model fit with true times T, and a naive Cox model fit with error prone times T′. We present results for varying values of the log hazard ratio β, assumed error distributions, and error variances. From these experiments, we derived means, biases, standard errors (SE), and mean squared errors (MSE). We also compare our observed bias in the hazard ratio with the expected value given by Equation 3. We estimate the hazard ratio parameter both parametrically using the Weibull model and semi-parametrically using the Cox model. As we will see from our results below, the multiplicative error introduces no bias in the estimated acceleration parameter, as expected, and so we present results for application of the proposed SIMEX method only for the hazard ratio estimated by the commonly applied Cox model approach.

All simulations were run 2000 times using R version 3.2.1 and assumed that the covariate X followed a standard normal distribution. In addition, we set the true parameters to be α₀ = 0 and α₁ = −β for β ∈ {log(1.5), log(3)}. The survival outcome T is generated from a Weibull distribution with shape equal to 1 and scale set to exp (α₀ + Xα₁), as defined in Equation 1. For the error term ν, as defined in Section 2.1, we considered a normal distribution and a shifted gamma distribution with means 0 and variances equal to the varying values of ${\sigma }_{\upsilon }^2$. These are represented by $\mathrm{N}(0,\lambda {\sigma }_{\upsilon }^2)$ and Gamma $(\frac{1}{{\sigma }_{\upsilon }^2},\frac{1}{{\sigma }_{\upsilon }^2})-1$, respectively, using a parametrization such that if X ~ Gamma(α, β), then $E(X)=\frac{\alpha }{\beta }$ and $\text{var}(X)=\frac{\alpha }{{\beta }^2}$. The set of simulations comparing the Cox and Weibull models set the cohort size at n = 1000 and varied the measurement error variance to be ${\sigma }_{\nu }^2\in \{0.25,0.5,1,2\}$. We refer to ${\sigma }_{\nu }^2=0.25$ as small error, ${\sigma }_{\nu }^2=0.5$ moderate error, ${\sigma }_{\nu }^2=1$ large error, and ${\sigma }_{\nu }^2=2$ very large error. For simulations examining the proposed SIMEX method, we set B = 50 and λ ∈ {0, 0.5, 1, 1.5, 2}, following the recommendation by Cook and Stefanski for covariate measurement error. A quadratic function is used in the extrapolation step. These simulations ran 100 bootstrap replications and let the number of subjects be n ∈ {300, 1000}, and set the measurement error variance to be ${\sigma }_{\nu }^2\in \{0.25,0.5,1\}$ to examine the performance of the SIMEX method under different amounts of error.

Supplemental Table 1 presents summary statistics for $\frac{T\prime }{T}$ for different values of ${\sigma }_{\upsilon }^2$ to provide a description of the error in T′ as a function of the ${\sigma }_{\upsilon }^2$ in our simulations. We note that even for our small and normally distributed error, the ratio of $\frac{T\prime }{T}$ could still be quite appreciable. The error-prone time had an average (SD) multiplicative error factor of 1.15(0.61) with an IQR of (0.71, 1.41). For moderate error, the average error (SD) factor was 1.25(0.96) with an IQR of (0.58, 1.59). For large error, average (SD) error factor was 1.69(1.95) with an IQR (0.53, 2.08). As expected for very large error, the error factor was quite large with an average (SD) of 2.55(5.14) and an IQR of (0.38, 2.52). When the error term followed a gamma distribution, we of course observed more extreme skewness in $\frac{T\prime }{T}$ and much larger standard deviation for this factor compared to those of the normal distribution, as seen in Supplemental Table 1.

Table 1 presents the relative performance of the Cox and Weibull models in the presence of multiplicative error, with ν following a normal distribution. Namely, we present the bias, average model standard error (ASE), empirical standard error (ESE), mean-squared error (MSE), and coverage probabilities for the 95% confidence intervals across the simulations. The ASE is calculated as the mean of the model standard errors and the ESE is calculated as the standard deviation of the parameter estimates. As expected, the estimated acceleration parameter (α₁) using both true time and the error-prone time are extremely close, with small bias in the naive estimate for all settings of the measurement error variance and β. We also notice that for all measurement error variance parameter values, the Weibull and Cox estimates for the hazard ratio parameter are biased and reasonably similar, but the bias from the Weibull estimates is consistently slightly smaller. Overall, the naive intercept, shape, and Cox and Weibull hazard ratio parameters remain largely biased through each value of β and the variance of ν. For moderate error, the percent bias magnitude is greater than 16% and the absolute bias is large for the intercept in the Weibull models. For large to very large error, similar results are observed with percent bias magnitude greater than 30% for estimates of β and large absolute bias for the intercept. In addition, these results in Table 1 are consistent with the theoretical amount of attenuation bias in β from Equation 3. The expected attenuation for β is approximately 0.816 for ${\sigma }_{\nu }^2=0.5,0.707$ for ${\sigma }_{\nu }^2=1$, and 0.577 for ${\sigma }_{\nu }^2=2$. For ${\sigma }_{\nu }^2=0.5$, the observed attenuation was 0.799 and 0.797 for true β = log(1.5) and log(3), respectively. Similarly for ${\sigma }_{\nu }^2=1$, the attenuation was 0.689 and 0.687, respectively, and 0.562 and 0.563, respectively, for ${\sigma }_{\nu }^2=2$.

Table 1.

The percent (%) bias (absolute bias for intercept α₀), average model standard error (ASE), empirical standard error (ESE), mean squared error (MSE), and coverage probabilities (CP) are given for 2000 simulated data sets with n = 1000 and a mean zero normal distribution for the error term. For all simulations, the Weibull parameters α₀ = 0, α₁ = −β, and shape equaled 1 (exponential time). Values of β and ${\sigma }_{\upsilon }^2$ are shown below.

		Weibull Model					Cox Model
β	${\sigma }_{\upsilon }^2$		α0	α1	shape	β	β
log(1.5)	0.25	Bias	0.056	0.060	−7.200	−11.84	−15.43
		ASE	0.038	0.038	0.020	0.035	0.033
		ESE	0.039	0.040	0.000	0.036	0.035
		MSE	0.069	0.040	0.072	0.060	0.072
		CP	0.676	0.969	0.000	0.708	0.522
	0.5	Bias	0.108	−0.210	−16.04	−20.34	−24.97
		ASE	0.042	0.044	0.016	0.035	0.033
		ESE	0.042	0.044	0.000	0.036	0.033
		MSE	0.116	0.044	0.160	0.090	0.107
		CP	0.275	0.976	0.000	0.351	0.138
	1	Bias	0.199	−0.070	−32.30	−31.26	−36.35
		ASE	0.049	0.053	0.013	0.037	0.033
		ESE	0.049	0.054	0.000	0.038	0.034
		MSE	0.205	0.054	0.323	0.132	0.151
		CP	0.020	0.976	0.000	0.072	0.006
	2	Bias	0.347	0.700	−42.25	−43.33	−48.19
		ASE	0.060	0.067	0.009	0.038	0.032
		ESE	0.060	0.069	0.000	0.040	0.033
		MSE	0.352	0.069	0.423	0.180	0.198
		CP	0.000	0.974	0.000	0.004	0.000
log(3)	0.25	Bias	0.055	0.050	−11.23	−11.86	−13.69
		ASE	0.038	0.038	0.020	0.040	0.041
		ESE	0.037	0.038	0.000	0.042	0.043
		MSE	0.067	0.038	0.112	0.137	0.156
		CP	0.696	0.972	0.000	0.102	0.056
	0.5	Bias	0.106	0.000	−23.89	−20.17	-22.84
		ASE	0.042	0.044	0.016	0.039	0.039
		ESE	0.041	0.045	0.000	0.043	0.043
		MSE	0.114	0.045	0.239	0.226	0.255
		CP	0.278	0.977	0.000	0.000	0.000
	1	Bias	0.198	0.070	−32.36	−31.22	-34.58
		ASE	0.049	0.053	0.013	0.039	0.037
		ESE	0.049	0.055	0.000	0.043	0.042
		MSE	0.204	0.055	0.324	0.346	0.382
		CP	0.020	0.968	0.000	0.000	0.000
	2	Bias	0.350	0.140	−47.17	−43.83	−47.43
		ASE	0.060	0.067	0.009	0.039	0.035
		ESE	0.059	0.068	0.000	0.042	0.039
		MSE	0.355	0.068	0.472	0.483	0.523
		CP	0.000	0.970	0.000	0.000	0.000

Supplemental Table 2 presents analogous results to Table 1 using the shifted gamma error distribution. Similar results are observed, with the naive intercept, shape, and Cox and Weibull hazard ratio parameters largely biased for each value of ${\sigma }_{\upsilon }^2$ and β.

Table 2 presents the % bias, coverage probabilities (CP), MSE, ESE, average bootstrap standard errors (ASE) for SIMEX estimates, and average model standard errors (ASE) for naive estimates to compare the performance of our SIMEX method for estimating the hazard ratio with the naive method of ignoring the error, which was simulated as normally distributed. We notice that for small error and both values of n and nonzero β, the bias for the SIMEX method is below 5% with coverage close to 95%. The bias for the naive method (14 – 15%) is well over double that of SIMEX, with considerably worse coverage. As ${\sigma }_{\upsilon }^2$ increases, the results tell a similar story. Overall, the bias for both methods increases, but the bias of the naive method continues to be at least double that of the SIMEX method. The coverage for both methods decreases with ${\sigma }_{\upsilon }^2$, with naive methods’ falling off much more rapidly than that of the SIMEX method. For small error, the SIMEX method performs admirably with small % bias and near 95% coverage. For moderate error, SIMEX still works reasonably well with under 10% bias and coverage close to 90%. With large amounts of outcome error, SIMEX is noticeably biased, with close to 20% bias, but still outperforms the naive method.

Table 2.

The percent (%) bias, average bootstrap standard error (ASE) for SIMEX, average model standard error (ASE) for naive, empirical standard error (ESE), mean squared error (MSE), and coverage probabilities (CP) are given for 2000 simulated data sets for the SIMEX and naive methods with exponential time and a mean zero normal distribution for the error term. Type 1 error is shown instead of % bias for β = 0.

β	${\sigma }_{\upsilon }^2$	n	Method	% Bias	ASE	ESE	MSE	CP
log(1.5)	0.25	300	SIMEX	−3.234	0.077	0.076	0.077	0.942
			Naive	−15.05	0.062	0.064	0.089	0.810
		1000	SIMEX	−3.432	0.041	0.041	0.043	0.930
			Naive	−15.25	0.033	0.033	0.070	0.535
	0.5	300	SIMEX	−8.815	0.082	0.082	0.089	0.921
			Naive	−23.72	0.060	0.062	0.114	0.633
		1000	SIMEX	−9.232	0.044	0.044	0.058	0.852
			Naive	−25.05	0.033	0.032	0.107	0.128
	1	300	SIMEX	−18.46	0.087	0.086	0.114	0.852
			Naive	−36.08	0.060	0.063	0.159	0.33
		1000	SIMEX	−18.90	0.046	0.047	0.090	0.615
			Naive	−36.64	0.033	0.035	0.153	0.007
log(3)	0.25	300	SIMEX	−2.100	0.101	0.099	0.101	0.945
			Naive	−13.51	0.075	0.079	0.168	0.466
		1000	SIMEX	−2.172	0.054	0.053	0.058	0.922
			Naive	−13.98	0.041	0.043	0.159	0.049
	0.5	300	SIMEX	−6.780	0.107	0.107	0.130	0.889
			Naive	−22.07	0.072	0.076	0.254	0.112
		1000	SIMEX	−7.037	0.058	0.058	0.097	0.72
			Naive	−22.94	0.039	0.043	0.256	0.000
	1	300	SIMEX	−16.03	0.111	0.112	0.209	0.62
			Naive	−34.03	0.069	0.074	0.381	0.002
		1000	SIMEX	−16.40	0.060	0.061	0.190	0.16
			Naive	−34.53	0.037	0.041	0.382	0.000
β	${\sigma }_{\upsilon }^2$
n	Method	Type 1 Error	ASE	ESE	MSE
0	0.25	300	SIMEX	0.052	0.071	0.071	0.071
		1000	SIMEX	0.043	0.038	0.038	0.038
	0.5	300	SIMEX	0.053	0.076	0.076	0.076
		1000	SIMEX	0.045	0.040	0.040	0.040
	1	300	SIMEX	0.056	0.081	0.081	0.081
		1000	SIMEX	0.047	0.043	0.043	0.043

Table 2 also presents the type 1 error, coverage probability, MSE, ESE, and ASE measurements for the SIMEX method simulated with the true β = 0 with a normal error distribution. For all combinations of ${\sigma }_{\upsilon }^2$ and n, we see that the type 1 error hovers around 0.05.

Table 3 presents similar estimates of relative performance of estimating the hazard ratio, comparing our SIMEX method to the naive method when the error in T′, ν, follows a gamma distribution. In these scenarios, the average multiplicative error and variance for the error in T′ were larger compared to the same scenario for the normally distributed error (Supplemental Table 1), and the SIMEX method performed worse overall than with the normally distributed error for a fixed value of ${\sigma }_{\upsilon }^2$. We notice that for small error and both values of nonzero β and n, the bias for the SIMEX method is 8% or below with coverage close to 95%. The bias for the naive method (16 – 18%) is over double that of SIMEX, with considerably worse coverage. As ${\sigma }_{\upsilon }^2$ increases, the bias for both methods increases, but the bias of the naive method continues to be just under double that of the SIMEX method. As expected, the coverage for both methods decreases with ${\sigma }_{\upsilon }^2$, with naive methods’ decreasing much more rapidly than that of the SIMEX method. Even with dramatically skewed error, for small outcome error, the SIMEX method performs well with reasonably small % bias and decent coverage (76 – 93%). For moderate error, SIMEX performs less well with bias around 16% – 17% and relatively weak coverage with the errors from this skewed distribution becoming quite large. Our most extreme skewed error setting led to upwards of 15-fold multiplicative error factors and SIMEX performing poorly with bias around 30%. In a real data setting, this magnitude of error may actually be detected and corrected by usual out of range data quality assurance methods at the data collection level.

Table 3.

The percent (%) bias, average bootstrap standard error (ASE) for SIMEX, average model standard error (ASE) for naive, empirical standard error (ESE), mean squared error (MSE), and coverage probabilities (CP) are given for 2000 simulated data sets for the SIMEX and naive methods with exponential time and a shifted gamma distribution (mean 0) for the error term. Type 1 error is shown instead of % bias for β = 0.

β	${\sigma }_{\upsilon }^2$	n	Method	% Bias	ASE	ESE	MSE	CP
log(1.5)	0.25	300	SIMEX	−7.270	0.077	0.076	0.082	0.929
			Naive	−17.65	0.061	0.064	0.096	0.766
		1000	SIMEX	−8.025	0.041	0.041	0.053	0.864
			Naive	−18.33	0.033	0.034	0.082	0.379
	0.5	300	SIMEX	−16.98	0.081	0.082	0.107	0.841
			Naive	−30.01	0.060	0.063	0.137	0.483
		1000	SIMEX	−17.87	0.043	0.043	0.084	0.594
			Naive	−29.74	0.033	0.035	0.126	0.055
	1	300	SIMEX	−27.54	0.084	0.083	0.139	0.706
			Naive	−41.07	0.060	0.062	0.178	0.207
		1000	SIMEX	−28.37	0.044	0.045	0.124	0.278
			Naive	−42.45	0.032	0.034	0.176	0.003
log(3)	0.25	300	SIMEX	−5.578	0.105	0.106	0.122	0.898
			Naive	−15.94	0.074	0.084	0.194	0.360
		1000	SIMEX	−6.380	0.057	0.059	0.091	0.758
			Naive	−16.55	0.040	0.047	0.188	0.017
	0.5	300	SIMEX	−15.96	0.113	0.122	0.214	0.636
			Naive	−27.45	0.070	0.089	0.314	0.042
		1000	SIMEX	−17.19	0.062	0.066	0.200	0.146
			Naive	−28.71	0.038	0.049	0.319	0.000
	1	300	SIMEX	−29.28	0.117	0.124	0.345	0.232
			Naive	−41.6	0.066	0.095	0.467	0.000
		1000	SIMEX	−30.91	0.065	0.068	0.346	0.001
			Naive	−42.43	0.035	0.049	0.469	0.000
β	${\sigma }_{\upsilon }^2$	n	Method	Type 1 Error	ASE	ESE	MSE
0	0.25	300	SIMEX	0.049	0.071	0.069	0.069
		1000	SIMEX	0.057	0.037	0.037	0.037
	0.5	300	SIMEX	0.052	0.074	0.074	0.074
		1000	SIMEX	0.049	0.039	0.039	0.039
	1	300	SIMEX	0.037	0.077	0.075	0.075
		1000	SIMEX	0.056	0.040	0.041	0.041

For the proposed SIMEX method, Table 3 also presents analogous type 1 error results to Table 2 using a gamma error distribution. Even for this skewed error, the type 1 error rate was preserved at 0.05 for all ${\sigma }_{\upsilon }^2$ and n.

Supplemental Table 3 presents the performance for the normal error distribution, but with time following a log-normal distribution. In this case, the Weibull model is no longer the correct one even for the true event time. We let ν have variance 1 and let β = log(3). Even for this relatively large β and mis-specified parametric model, we see that the naive acceleration parameter is quite unbiased, as before. However in contrast to the previous results, the Cox and Weibull hazard ratios are quite similar and nearly unbiased, although the bias for the Weibull hazard ratio remains slightly smaller. The naive intercept for the Weibull model continues to display large bias with time distributed log-normally. The lack of bias in the hazard ratio can be attributed to the fact that the naive shape parameter in this model, σ, is estimated without bias, in contrast to all three previous models. These results emphasize that the hazard ratio parameter has unpredictable bias depending on the underlying distribution, but that the acceleration parameter is more robustly estimated in the presence of random multiplicative error in the outcome.

3.1. Censoring

The above simulations were done with no censoring of the event time. To examine the impact of censoring, simulations were run in similar parameter settings as described in the beginning of Section 3 with the addition that the true survival times were randomly censored and error was added to the censored event times. Specifically, we considered β ∈ {log(1.5), log(3)}, ${\sigma }_{\nu }^2\in \{0.5,1\}$, and simulated 25%, 50%, 75%, and 90% censoring. True survival times were again generated exponentially, but with the baseline hazard set to 0.1. After the true survival times were generated, separate random right censoring times were determined for each β to yield the desired % censored event times. The censoring times were generated uniformly with lengths 4, 4, 2, and 1 for each % censored time, respectively, to mimic trials of different lengths. The error-prone times were then generated by adding random multiplicative error to the censored times and the rest of the simulation parameters follow as before. We note that this kind of error, ie. error in the censored event time, is consistent with a time-to-event outcome in the HIV/AIDS setting discussed in the introduction, where there may be error only in the start time of the observation period for an event (e.g. time of ART initiation) but the event time (e.g. virologic failure) is determined precisely. As Table 4 shows, although the SIMEX method does not handle censoring directly, applying our extension to this setting still improves the bias compared to ignoring the error. Of equal interest is that the amount of censoring seems to have an inverse relationship with the percent bias in the log HR. For example with β = log(1.5) and ${\sigma }_{\nu }^2=0.5$, as the percent censored increases from 25 to 50 to 75 to 90, the percent bias decreases from −12.72 to −7.090 to −3.130 and to −1.690, respectively. In addition, we observe that the CP increases with increasing censoring. A similar effect is observed for other combinations of β and ${\sigma }_{\upsilon }^2$ in Table 4. Thus our results suggest that for rare events that are exponentially distributed and randomly censored, the effect of random, multiplicative measurement error in the censored failure time outcome has little effect on the estimates of β. In this case, the risk sets in the Cox partial likelihood score at each failure time remained largely the same. In such scenarios, since the event indicator is correct in this setting, the Cox score defined by the error prone event times would be a sum of similar score contributions over the same individuals as the score defined by the true event times, hence why there is little bias. This seems to reconcile the different conclusions that Korn et al. [21] and Hong et al. [22] came to regarding this setting described in Section 1. Korn et al. considered simulations that approximated data involving outcome error in the evaluation of progression-free survival for breast cancer patients. These authors observed that with the correct hazard ratio and 50% censoring, there is very little bias caused by the random measurement error. In addition, simulating a cancer trial with a very rare event, with 96% censoring, resulted in even less bias. On the other hand, the more appreciable effects of event time error on the estimated hazard ratio that Hong et al. found may be attributed to the studied setting being one where there was a much smaller percentage of censored events (5–25% censoring in simulated tumor progression).

Table 4.

The percent (%) bias, mean squared error (MSE), and coverage probabilities (CP) are given for 2000 simulated data sets for the SIMEX and naive methods with n = 1000, exponential time, baseline hazard of 0.1, a normal distribution for the error term, and 25%, 50%, 75%, and 90% censoring for the true event time.

% Censored	β	${\sigma }_{\upsilon }^2$	Method	% Bias	MSE	CP
25	log(1.5)	0.5	SIMEX	−4.776	0.048	0.931
			Naive	−12.72	0.064	0.712
		1	SIMEX	−9.331	0.059	0.872
			Naive	−18.31	0.084	0.492
	log(3)	0.5	SIMEX	−4.948	0.081	0.836
			Naive	−15.53	0.177	0.054
		1	SIMEX	−10.94	0.135	0.501
			Naive	−23.23	0.260	0.000
50	log(1.5)	0.5	SIMEX	−2.828	0.051	0.939
			Naive	−7.090	0.054	0.902
		1	SIMEX	−5.325	0.056	0.930
			Naive	−10.41	0.063	0.839
	log(3)	0.5	SIMEX	−3.441	0.075	0.904
			Naive	−10.34	0.126	0.408
		1	SIMEX	−7.287	0.105	0.762
			Naive	−15.47	0.179	0.120
75	log(1.5)	0.5	SIMEX	−1.430	0.066	0.948
			Naive	−3.130	0.065	0.939
		1	SIMEX	−2.496	0.068	0.946
			Naive	−4.590	0.067	0.940
	log(3)	0.5	SIMEX	−1.885	0.082	0.947
			Naive	−5.610	0.095	0.848
		1	SIMEX	−3.940	0.093	0.909
			Naive	−8.260	0.117	0.714
90	log(1.5)	0.5	SIMEX	−1.233	0.084	0.956
			Naive	−1.690	0.082	0.946
		1	SIMEX	−1.804	0.085	0.960
			Naive	−2.680	0.084	0.941
	log(3)	0.5	SIMEX	−1.281	0.095	0.950
			Naive	−3.640	0.096	0.918
		1	SIMEX	−2.587	0.101	0.942
			Naive	−5.350	0.106	0.874

Lack of bias in the naive estimates may not always be the case for rare events. For instance, there can be appreciable bias in the naive estimate for the rare event setting when the majority of the censoring happens early in the observation time period, creating observed event times that are close together relative to the size of the measurement error. We simulated this scenario by censoring an exponential event time T, with baseline hazard 0.1 and a log hazard coefficient of 1 for a standard normal covariate X, on the interval (0, 0.15) and generating the error-prone T′ by adding a random, standard normal error term to the censored event time. In this case, there was approximately 90% censoring and −13.55% bias in the naive estimate as Supplemental Table 4 shows. SIMEX in this case provides a modest bias reduction, with a bias of −11.6%. We simulated a second scenario with appreciable bias for rare events, which included multiplicative random error and covariate-dependent censoring. For this setting, we simulated the underlying proportional hazards model, only we censored uniformly on (0,0.15) if X > 0, and otherwise uniformly on (0, .05). Random log-normal multiplicative error with variance 0.5 was added to the censored event time. In this example, there was approximately 90% censoring and the naive estimate had a bias of −14.70%, while the SIMEX estimate had a bias of −7.91% as Supplemental Table 5 shows.

4. Data Example

For the purposes of illustration, we apply the proposed method to electronic health records data from a large HIV clinic, the Vanderbilt Comprehensive Care Clinic (VCCC). The VCCC is an outpatient clinic that provides care to HIV patients and collects clinical data over time, including demographics, laboratory measurements, and pharmacy dispensations. In addition, the VCCC has fully validated all key research variables, which revealed extensive errors in the original data. Thus, this observational cohort is ideal for directly assessing the relative performance of the SIMEX estimators compared to naive estimators. Throughout this example, we considered the estimates from the fully validated dataset to be the “truth”. For a more detailed description of the cohort, see Lemly et al. [28].

We analyzed data on 3996 HIV-positive patients who established care at the VCCC between 1998 and 2013. The event time here is considered to be the time from the start of antiretroviral therapy (ART) to the time at virologic failure, which is defined as an HIV-RNA count greater than or equal to 400 copies/mL. The HIV-RNA assay, and hence time at virologic failure is considered to be free of errors, whereas the time at the start of ART is error-prone. We studied the association between CD4 at enrollment (i.e. at first visit to the VCCC), patient sex, age at enrollment and the defined event time. For each analysis (using validated or unvalidated data), patients were excluded if they had a missing ART start date, did not start ART after enrollment, or had no follow-up after starting ART. In the unvalidated dataset, 3049 patients satisfied the criteria for inclusion whereas 2973 patients satisfied the criteria in the validated dataset. A total of 2923 met the inclusion criteria for the analysis of both the validated and unvalidated datasets and were used in all further analyses to ensure that any differences between estimators are not due to differences in included patients. In this dataset, 28.6% of event times had an error with an average (SD) multiplicative error factor of 2.33(32.06). Of the 2923 subjects, 22 did not reach failure in the unvalidated but did reach failure in the validated and 54 failed in the unvalidated but not in the validated. Thus, the number of subjects who, due to the error-prone ART start time, had an incorrect event indicator was small at 3%. While SIMEX does not directly address this kind of inclusion/exclusion error, we were interested in seeing how SIMEX would perform in this real data scenario. Censoring was 23.4% in the validated data and 22.3% in the unvalidated data.

We utilize the method described in Section 2 and compare the performance of the SIMEX estimator to that of the naive estimator that ignores the error. The univariate and multivariate Cox models were fit and used to calculate the hazard ratios (HR) for a 100-unit increase in CD4, comparing females to males, and a 10-year increase in age. This was done for both the validated and unvalidated datasets. For our SIMEX approach, we set B = 50 and λ = {0, 0.5, 1, 1.5, 2}, as described in Section 2.2. Here, the variance of the error in time is not assumed to be known, but rather estimated from a validation subset. From the 2923 subjects in both datasets, a random subsample of 300 was assumed available and ${\sigma }_{\upsilon }^2$ was estimated. As Supplemental Table 6 shows, the amount of error in $T{\lambda }_b^{\prime }$ compared to T, $\frac{T_{\lambda b}^{\prime }}{T}$, is substantial, as the IQR increases with λ and the standard deviation stays relatively large. Using a quadratic function, we then extrapolate back to λ = −1 and obtain our approximation of the true HR using the full cohort. Standard errors for the SIMEX method were then obtained using a bootstrap method, with bootstrap sampling stratified on the validation subset membership and using 100 bootstrap samples.

The HR’s and their corresponding confidence intervals are shown in Table 5 comparing the true, naive, and SIMEX estimators. The true estimator was calculated using the validated dataset, whereas the naive estimator was calculated using the unvalidated dataset to simulate a scenario in which validated data are not available on any subjects. The SIMEX estimator was also calculated on the unvalidated data, assuming a subset of 300 validated subjects was available to estimate the error variance. For the univariate analyses, the SIMEX estimator appears to slightly improve the bias in the HR compared to the naive estimators for patient sex (−2.39% and −2.66%, respectively) and a 100-unit increase in enrollment CD4 (−0.11% and 0.23%, respectively). However, for a 10 year increase in age at enrollment, the SIMEX estimator does not improve the bias compared to the naive estimator with −1.00% and −0.50% bias, respectively. Overall, there is very little bias in the naive analyses of the unvalidated data. We observe similar results in the multivariate analysis. The SIMEX estimator again appears to slightly improve the bias in the HR compared to the naive estimator for patient sex (−2.10% and −2.58%, respectively) and a 100-unit increase in enrollment CD4 (−0.11% and 0.23%, respectively), but not for a 10 year increase in age at enrollment (−0.82% and −0.20%, respectively). Overall both the SIMEX and naive methods are quite close to the HR from the fully validated data. The performance of our SIMEX extrapolation is presented graphically in Supplemental Figure 1. Note that our SIMEX approach assumes random measurement error in the time-to-event outcomes. To test whether this assumption holds for the VCCC data, logistic regression models were run on the full data (N=2923) to estimate the odds of the unvalidated censored event time being incorrect for the covariates sex (OR=0.971, p-value=0.756), enrollment CD4 (OR=0.880, p-value < 0.001 for a 100 unit increase), and enrollment age(OR=0.995, p-value=0.241 for a 10-year increase). Given the odds ratio and significant p-value for CD4, it appears the measurement error in the outcome is not purely random. However, even under some modest violations of the random error assumption in this data example, the method still performed relatively well.

Table 5.

The hazard ratios (HR) and their corresponding bootstrap 95% confidence intervals for sex, a 100-unit increase in enrollment CD4, and a 10 year increase in age at enrollment for the time at virologic failure post ART.

	Univariate
	Sex	100 × CD4	10 × Age at Enrollment
True	1.128 (1.024,1.243)	0.883 (0.867,0.900)	0.995 (0.955,1.037)
Naive	1.098 (0.997,1.208)	0.885 (0.869,0.901)	0.990 (0.951,1.032)
SIMEX	1.101 (0.988,1.227)	0.882 (0.863,0.902)	0.985 (0.948,1.024)
	Multivariate
	Sex	100 × CD4	10 × Age at Enrollment
True	1.047 (0.950,1.155)	0.883 (0.867,0.900)	0.975 (0.935,1.017)
Naive	1.020 (0.926,1.123)	0.885 (0.869,0.901)	0.973 (0.933,1.014)
SIMEX	1.025 (0.929,1.131)	0.882 (0.862,0.902)	0.967 (0.926,1.010)

In addition, a similar analysis was run with the event time defined to be the time from the start of ART to the time of first opportunistic infection (OI). Here, the time at first OI is also error-prone, resulting in 45.0% error in the event time and an average (SD) multiplicative error factor of 1.84(18.8). Censoring for this endpoint is 79.4% in the validated data and 69.2% in the unvalidated data. We observe similar results in this scenario - the bias in the naive HRs is small to moderate and the SIMEX estimators stay close to those values. More detailed results are shown in Supplemental Table 7. We note that although the average error factor is less than that of the analysis for time to virologic failure, the time at first OI has much greater censoring. This may have contributed to the SIMEX method’s success in estimating HRs very close to those of the validated estimates.

The run time for the mulivariate analysis described above was 1.06 hours on a 64-bit PC with an i7 processor. We also provide code and a simulated dataset in the Supplemental files to further demonstrate the ease of application of our SIMEX method.

4.1. VCCC Data Simulation

We consider a simulation study that mirrors attributes of the VCCC dataset, excluding any covariate-dependent measurement error, to explore the performance of SIMEX under random multiplicative error in this setting. In particular, the true variance of the error in time is estimated from a random subsample of 300 from the VCCC data similar to above. The true beta parameters were obtained by fitting a parametric Weibull regression model to the fully validated data for time to virologic failure, with CD4 count, patient sex, and age at enrollment as covariates. The sample size for the simulated cohort was set at n = 2923 and random right censoring times generated uniformly to average 24% censoring to match those settings of the VCCC data. In addition, all three covariates were generated to be as similar as possible to those observed in the VCCC data. Patient sex was randomly sampled according to the true observed probabilities of males and females. Then stratified on patient sex, we generated bivariate normal distributions for the age at enrollment and the square root of CD4 count, where the square root transformation was applied for normality; the means, SDs, and correlations were matched based on the true covariates. True survival times (T) were generated exponentially using the simulated CD4 count, sex, and age at enrollment variables and censoring applied as described above. For the error-prone T′, we applied random multiplicative error to T and matched the measurement error distribution for ν to that of the VCCC data. Specifically, 71.5% of subjects in the VCCC had no error in the time-to-event and the remaining subjects had highly right-skewed error. Thus, a shifted gamma error with shape and rate both equal to the estimated measurement error variance was applied to 28.5% of the simulated subjects. We additionally varied the distribution of ν to be normal and shifted gamma (applied to all simulated subjects) to test the sensitivity of the results to the shape of the error distribution. Similar to the VCCC data analysis, the SIMEX method estimated the measurement error variance using a validation subsample of 300 simulated subjects and obtained standard errors using 100 bootstrap samples stratified on validation subset membership.

Supplemental Table 8 presents the % bias, CP, and SEs for the simulation described above using the gamma mixture, mean zero normal, or shifted gamma error distributions. First, we note that with the assumed random measurement error, there was a modest amount of bias in the naive estimates (10–17% depending on the coefficient and the error distribution) compared to what we observed in the true data (under 3%). We then observe for our simulation that for all covariates, the SIMEX estimates had at least an 80% reduction in bias over the naive for the gamma mixture, a 60% reduction for normal error, and at least a 40% reduction for the shifted gamma. In addition, the CPs for all covariates are similar or a little higher for SIMEX compared to the naive method for all error distributions and the MSEs are generally similar for the SIMEX and naive methods. Thus, these simulations suggest that the non-random measurement error that seems to be present in the VCCC data counteracted bias that would have been observed in the naive estimates with random, multiplicative error. The random error in our simulation for this setting induces bias in the naive estimates that our SIMEX method is able to correct for a variety of underlying error distributions.

5. Discussion

There is no substitute for carefully and accurately collected data. In the event that an error-free outcome cannot be obtained, then ideally one would be able to do a detailed validation study to obtain data on the structure of the outcome measurement error in a subset so that proper statistical models could be formulated to estimate and adjust estimators for this error structure. Without the availability of a validation subset, it is common practice to simply ignore the errors in the outcome and proceed with the same analysis as if there were no measurement error. In this work, we saw that even simple random error in a survival outcome can bias the hazard ratio estimator for continuous time-to-event outcomes. We propose a few analysis options for this setting involving random multiplicative error.

Regression theory and our simulations demonstrate that the log hazard ratio from the Cox model can be quite biased even for relatively small amounts of random measurement error; whereas, the acceleration parameter of the Weibull model remains unbiased in the presence of random multiplicative measurement error. This is notable, since the addition of the error for the studied settings meant the parametric form for the survival outcome assumed by the Weibull model no longer held for the error prone covariate. The observation also held true in our simulations when the parametric form of the true event time was not Weibull. Given this robustness, and the fact that the AFT model has been advocated as a more intuitive model for treatment effects in clinical settings [29, 30], we recommend consideration of this regression model in place of, or at least performed alongside of, the Cox model, in settings where the censored event time is known to have random error. Due to the Weibull model being both PH and AFT, this is more a change in which summary statistic is chosen for the association between a covariate and outcome, than in the model for how X affects the outcome. Keiding et al. [27] and others [31] made a similar recommendation for AFT models due to their ability to separate out dispersion from regression parameters.

In addition, we described an extension of the SIMEX algorithm to correct the bias in the hazard ratio induced by non-differential multiplicative outcome error for a continuous event time. Although the proposed method is only an approximate method, with some expected bias, simulations demonstrated that our method corrected multiplicative outcome error and performed much better than the common naive method of ignoring the error, maintaining a smaller MSE in a variety of settings. The method does start to break down with large error variance resulting in bias greater than 15%; however, as Supplemental Table 1 illustrates, the amount of multiplicative error that induced large biases was extreme, with the inter-quartile range of the ratio of the error prone to the true outcome ranging from less than half to more than double, and would require analyses beyond that of our approximate method. We also applied the proposed method to a data example where there were both censoring and known associations between the outcome error distribution and important predictors. In this example, SIMEX performed similar to the naive method, and in some cases perhaps made mild improvements. These findings under a non-random error scenario are similar to those of Küchenhoff et al. [23], who studied the use SIMEX for misclassification error in binary response variables and in one simulation assessed effects of differential measurement error. They found that the naive estimates are biased, but in different directions (away from or towards the true parameter). Our results suggest, that like with random error, the hazard may be less subject to bias with moderate systematic error in the outcome when the observed event time is rare. It is of note that the above simulations and data example all involved right-skewed error, with the mean error-prone T′ larger than that of the true T, due to the nature of time-to-event data. We investigated the performance of our method with left-skewed error for a small number of settings and found that SIMEX overestimated the true hazard ratio while still providing similar reduction in the magnitude of the bias for all settings. Detailed results can be found in Supplemental Table 9. Thus, our simulations showed that the SIMEX method under random error was an improvement over the naive estimator for a variety of underlying error distributions.

Because the error model under study was observed to cause appreciable bias in the estimated hazard ratio, but imperceptible bias in the acceleration parameter, we applied our method only to the Cox model. However, it could be similarly applied to other regression models. Limitations of our findings include the need to have a known error variance ${\sigma }_{\upsilon }^2$ or the availability of a validation subset from which to obtain an estimate of this error variance. With a validation subset, our method can incorporate an estimated error variance and the bootstrap can be used to obtain standard error estimates that incorporate the additional uncertainty from the estimated nuisance parameter. It is also noteworthy that all of our simulations were done with independent error terms. Our approximate method is likely not able to easily handle covariate-dependent or differential error in the general setting and correction methods for this error structure is an area for future work. It is also of interest to extend this method to be able to handle data with both outcome and covariate measurement error.

In the setting of random error, SIMEX provides a practical estimation method to adjust the hazard ratio for bias induced by non-differential measurement error in the failure time outcome. Without the availability of a validation subset or known variance for the outcome error, our method provides analysts with a new tool to perform sensitivity analyses that vary assumptions about the underlying measurement error variance, and examine the robustness of results to random error in the event time.