Abstract
Signaling pathways play an important role in the cell’s response to its environment. Signaling pathways are often represented as directed graphs, which are not adequate for modeling reactions such as complex assembly and dissociation, combinatorial regulation, and protein activation/inactivation. More accurate representations such as directed hypergraphs remain underutilized. In this paper, we present an extension of a directed hypergraph that we call a signaling hypergraph. We formulate a problem that asks what proteins and interactions must be involved in order to stimulate a specific response downstream of a signaling pathway. We relate this problem to computing the shortest acyclic B-hyperpath in a signaling hypergraph — an NP-hard problem — and present a mixed integer linear program to solve it. We demonstrate that the shortest hyperpaths computed in signaling hypergraphs are far more informative than shortest paths, Steiner trees, and subnetworks containing many short paths found in corresponding graph representations. Our results illustrate the potential of signaling hypergraphs as an improved representation of signaling pathways and motivate the development of novel hypergraph algorithms.
Index Terms: Hypergraphs, Integer linear programming, Systems biology, Signaling pathways, Wnt signaling
1 Introduction
CELLS respond to signals from their environment through signaling pathways composed of molecular reactions that start at membrane-bound receptors and terminate at transcription factors (TFs) that regulate downstream gene expression. Many types of reactions occur in signaling pathways, e.g., complex assembly and disassembly, activation or deactivation of one protein or complex by another protein or complex, and regulation of reactions by proteins/complexes, etc. Computational methods for reasoning about signaling pathways must be faithful to the complexity of reactions within them. Directed and undirected graphs are the most pervasive representations of the structure of signaling pathways. However, graphs can only model interactions between pairs of molecules; thus they cannot accurately represent the manifold aspects of signaling pathways that involve coordinated activity of assemblages of more than two molecules [1], [2]. Directed hypergraphs and their relatives (reviewed in Section 2) are emerging as attractive alternatives to graphs. Unfortunately, directed hypergraphs continue to remain an underutilized representation for signaling pathways, despite the fact that hypergraph theory has been a well-established area of mathematics since the 1960s [3].
We recently highlighted the potential and power of hypergraphs to address questions such as pathway reconstruction, enrichment, and crosstalk [4]. Until now, methods to solve these problems have represented pathways simply as sets of proteins or as directed or undirected graphs. In previous work, we formally defined the signaling hypergraph as a powerful representation of signaling pathway structure. We used signaling hypergraphs to address two general classes of questions that may be posed on pathways [5]:
Is there a set of reactions that begins at protein A and terminate at protein B?
If we are given a set of reactions annotated to a specific pathway P and a comprehensive signaling network , can we identify un-annotated reactions in that are likely to be in P?
We reduce these problems to that of computing hyperpaths in a signaling hypergraph. We consider B-hyperpaths, which generalize paths in a directed graph by accounting for the fact that a reaction can occur only if all its reactants are present. A B-hyperpath from node s to node t has a natural interpretation in signaling pathways: the hyperpath contains all the intermediate reactants and products needed to “reach” t from s. Unlike shortest paths in graphs, shortest B-hyperpaths may contain cycles (see Section 3). We restrict our attention to acyclic B-hyperpaths in analogy to shortest path and related algorithms (e.g., Steiner trees, which connect a subset of specified nodes using the smallest number of edges) on graphs, which return acyclic networks.
We make four contributions in this paper. First, we describe signaling hypergraphs [5] and B-hyperpaths and provide examples of these concepts. Second, we prove that computing the acyclic B-hyperpath with the smallest number of hyperedges is NP-complete, even in a restricted setting where hypergraphs have a bounded number of possible reactants and products involved in each reaction. Third, we prove that the mixed integer linear program (MILP) [5] returns the shortest acyclic B-hyperpath in a signaling hypergraph. Finally, we find shortest B-hyperpaths in signaling hypergraphs constructed from a signaling pathway database (summarized below). We present results demonstrating that subnetworks from graph representations fail to capture information provided by the computed shortest B-hyperpath. Although notions such as B-hyperpaths have been available since the early 1980s, to the best of our knowledge, this work is the first to modify and apply these ideas to answer very natural questions on signaling pathways.
We compute B-hyperpaths in signaling hypergraphs of varying sizes from the National Cancer Institute’s Pathway Interaction Database (NCI-PID) [6]. We focus on the Wnt signaling pathway, a well-studied pathway involved in development and often perturbed in cancer [7]. Starting with the canonical Wnt signaling pathway, we identify acyclic B-hyperpaths that end in different forms of β-catenin that correspond to the absence and presence of Wnt signaling, answering Question 1 above. We then explore Question 1 on a more comprehensive Wnt signaling pathway by finding acyclic B-hyperpaths that connect membrane-bound complexes to downstream target genes (TCF1 and LEF1). We show that the resulting B-hyperpaths are much more informative than paths, Steiner trees, and subnetworks containing many short paths on corresponding graph representations of the Wnt signaling pathway. Finally, we consider the annotated Wnt signaling pathway in the context of the entire NCI-PID dataset. To answer Question 2, we identify reactions that are not annotated to the Wnt pathway that connect it to the Androgen Receptor pathway.
2 Related Research
We discuss generalizations of signaling pathway graph representations and emphasize their strengths and limitations.
Representing complexes
Compound graphs permit a compound node to contain a set of nodes [8], e.g., a set of proteins in a complex. Similarly, metagraphs support scalable network structure by allowing metanodes to have a nested structure [9]. Compound nodes and metanodes may themselves be connected by edges. Similarly, undirected hypergraphs allow interactions among two or more entities [10]. Software that computes paths, loops, and motifs on compound graphs [11] and visualizes metagraphs [9] have accelerated the adoption of these representations.
Representing pathway directionality
A factor graph [12], [13] is a bipartite graph with partitions corresponding to molecules and to factors, which represent (potentially directed) reactions in a pathway. Factors are connected to the molecules that participate in the reaction. The PARADIGM software [13] uses probabilistic inference on factor graphs to estimate a pathway’s activities from high-throughput data on molecular changes in cancer tissues. A Petri net [14], [15] is a directed bipartite graph with two types of nodes – places and transitions – and tokens on the places. In Petri net models of signaling pathways, places represent proteins, transitions represent reactions among proteins, and the number of tokens in a place represent the concentration of proteins. “Firing” a transition corresponds to redistributing the tokens based on certain rules.
Representing regulation
Influence graphs [16] are graphs where each edge has a sign describing one molecule’s affect on the other. More generally, logic models [16] define logic functions on hyperedges with potentially multiple nodes in the tail but a single node in the head. Multi modal networks [1] are generalizations of hypergraphs that include a single regulator for each hyperedge. Finally, dynamic models (often based on ordinary differential equations) can describe the control mechanisms within signaling pathways faithfully [17].
Limitations of related work
A major limiting factor of compound graphs and metagraphs is that they connect pairs of entities, making interactions consisting of more than two entities (such as complex assembly and disassembly) difficult to model. Factor graphs and Petri nets are not ideal for generalizations of common graph-theoretic operations such as connectivity and paths, which is the focus of this paper. Influence graphs and logic networks represent protein regulation, but they operate only on the “active” forms of proteins. Moreover, it is unclear how they represent complex assembly/disassembly. Finally, the large amounts of experimental data needed by dynamic models in order to fit and tune parameters limits their scalability.
3 Definitions
3.1 Signaling Hypergraphs
Let V be a finite set of nodes. A directed hyperedge e is a pair (T(e), H(e)) where both the tail T(e) and the head H(e) are non-empty subsets of V. A directed hypergraph consists of a finite set V of nodes and a finite set E of directed hyperedges. is a directed graph in the case where |T(e)| = |H(e)| = 1.
At first glance, directed hypergraphs seem sufficient for representing signaling reactions: each hyperedge consists of a set of reactants in the head and a set of products in the tail. However, many signaling reactions involve protein complexes, where a set of proteins act as a single unit in a reaction. Further, directed hypergraphs do not represent molecules that regulate a reaction (e.g., a kinase that phosphorylates, and subsequently activates, a substrate).
To model complexes, we define a hypernode1 as a set of nodes u ⊆ V that act together as a single unit2. A hypernode u may contain a single node, e.g., to represent a protein that acts on its own. We use to denote the set of hypernodes, assuming that each node in V appears in some hypernode in . We define a signaling hyperedge e to be a pair (T(e), H(e)) where both the tail T(e) and the head H(e) are non-empty subsets of , i.e., each member of the tail or the head is a hypernode.
To model positive regulation, we represent each positive regulator as a hypernode. If a hypernode u is a positive regulator for a reaction, we add u to the tail of the signaling hyperedge representing that reaction. Signaling hyperedges can represent the logic of multiple positive regulators, e.g., if all positive regulators must be present for the reaction to occur, we add all the regulators to the tail of the signaling hyperedge. Alternatively, if any of the positive regulators can trigger the reaction, we can make copies of the signaling hyperedge, one for each regulator.
We define a signaling hypergraph , where V is a finite set of nodes, is a set of hypernodes and is a finite set of signaling hyperedges (Figure 1(a)). When it is clear from the context, we will refer to signaling hyperedges and signaling hypergraphs simply as hyperedges and hypergraphs, respectively.
Fig. 1.
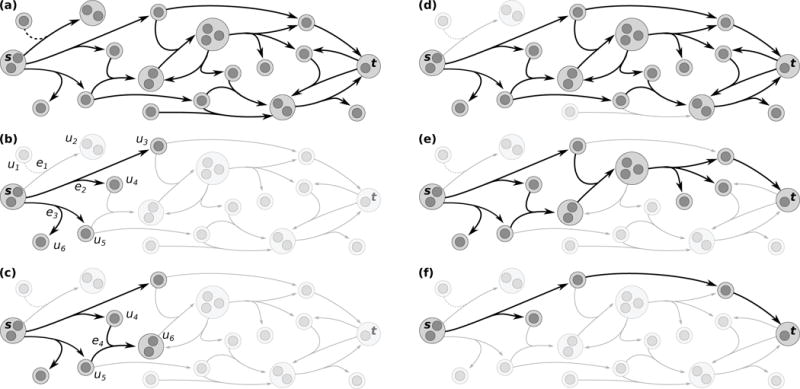
Signaling hypergraph concepts and notation. Dark gray circles represent nodes, and light gray circles represent hypernodes (subsets of nodes). Regulators are denoted by a dashed line for visualization purposes. (a) A signaling hypergraph . (b) Hyperedge e2 establishes that hypernodes u3 and u4 are B-connected to s while hyperedge e3 performs this role for hypernodes u5, and u6. Hypernodes u1 and u2 are not B-connected to s. (c) Hypernode u6 is also B-connected to s because of hyperedge e4. (d) The set of hypernodes that are B-connected to s and the hyperedges that establish these B-connections. (e) An s-t B-hyperpath ∏ (s, t) containing six hyperedges. Note that no hyperedge may be removed from ∏(s, t) and still maintain that t is B-connected to s using only the hyperedges in ∏(s, t). (f) An s-t B-hyperpath ∏(s, t) containing three hyperedges.
Scope of signaling hypergraph representations
Signaling hypergraphs generalize earlier research by simultaneously representing reactions among more than two molecules, complexes, and combinatorial positive regulation. They also model complex rearrangement and post-translational modifications. Signaling hypergraphs do not yet represent negative regulation or more complex regulatory logic.
3.2 B-Hyperpaths
There are numerous ways to define paths in directed hypergraphs [18], [19]. In this section, we describe how to extend these ideas to signaling hypergraphs. One intuitive notion is a straightforward generalization of a path in a directed graph. An s-t path P (s, t) is an alternating sequence of hypernodes and hyperedges starting at hypernode and terminating a hypernode , i.e.,
where s = u1, t = uk, and for every 1 ≤ i ≤ k, ui ∈ T(ei) and ui + 1 ∈ H(ei) [18]. We say that a path P(s, t) is simple if it contains no repeated hypernodes or hyperedges and that P(s, t) is a simple cycle if u1 and uk are both in the tail of e1. We say that is acyclic if it does not contain any simple cycles for any pair of hypernodes s, .
Since simple paths report an alternating sequence of hypernodes and hyperedges, they do not capture all the hypernodes associated with each hyperedge in the path. Thus, they are not useful for representing sequences of signaling reactions that involve multiple reactants and/or products. We use formalisms developed in the hypergraph literature [18], [19] to describe the notion that in order for all products of a signaling reaction to be present, all reactants must be present.
For a hypernode , the backward star BS(u) of u is the set of hyperedges e for which u ∈ H(e). Given a hypergraph and a hypernode we say that hypernode is B-connected to s in if either (i) u = s or (ii) there exists a hyperedge e ∈ BS(u) such that, for all w ∈ T(e), w is B-connected to s. For example, in Figure 1(b), s is B-connected to itself. The backwards star of u3 is {e2}; since the tail of e2 consists of s, then u3 is B-connected to s. In Figure 1(c), u6 is B-connected to s because BS(u6) = {e4}, and each of the hypernodes in the tail of e4 are B-connected to s. We use the notation to denote the set of hypernodes that are B-connected to s in (Figure 1(d)). Note that the inclusion of positive regulators in the tail modifies the definition of B-connectedness as follows: in order for all products of a signaling reaction to be present, all the reactants and all the positive regulators in the tail of the reaction must be present.
A sub-hypergraph of consists of a subset of hypernodes and a subset of hyperedges of , with the property that for every hyperedge , the hypernodes in T(e) and H(e) are members of . Given and two hypernodes s, , an s-t B-hyperpath Π(s, t) is a sub-hypergraph of such that and Π(s, t) is minimal with respect to the deletion of hypernodes and hyperedges (Figure 1(e,f)). Observe that t must be B-connected to s using only the hypernodes and hyperedges in Π(s, t). Further, the set of hypernodes B-connected to s in Π(s, t) are precisely the hypernodes in Π(s, t).
Lemma 1
All hypernodes in B-hyperpath Π(s, t) are B-connected to s, i.e., .
Proof
By the definition of a B-hyperpath, hypernode t is in Π(s, t) and t is B-connected to s in Π(s, t). Suppose there is a hypernode that is not B-connected to s. Hypernode u is not needed to establish that t is B-connected to s, and we can remove u from Π(s, t). However, removing u from Π(s, t) contradicts the fact that Π(s, t) is minimal with respect to the deletion of hypernodes. Thus, all hypernodes are B-connected to s are necessary to establish that t is B-connected to s. □
From this lemma, we see that the hypernodes of any B-hyperpath Π(s, t) must be a subset of all hypernodes B-connected to s.
Corollary 2
If Π(s, t) is a B-hyperpath in , then .
Identifying the set of hypernodes that are B-connected to s can be achieved with a particular hypergraph traversal (Algorithm “B-Visit” in [18]).
3.3 The Shortest Acyclic B-Hyperpath Problem
There may be many s-t B-hyperpaths in a hypergraph . We wish to find a B-hyperpath that represents a minimal set of reactions that lead from s to t (e.g., Figure 1(f)). In other words, we seek to compute a B-hyperpath Π*(s, t) of with the smallest number of hyperedges:
| (1) |
In Equation (1), Π ranges over all sub-hypergraphs with the property that t is B-connected to s in Π. By definition, all s-t B-hyperpaths are considered in this set of sub-hypergraphs. Note that we can assign costs to the hyperedges and compute the B-hyperpath with the smallest cost. In this work, we simply count hyperedges since we construct hypergraphs from manually-curated datasets (Section 4.4).
Finding a B-hyperpath Π*(s, t) that minimizes Equation (1) is NP-hard [18], even when is a directed hypergraph (i.e., each hypernode contains exactly one node). However, since our hypergraphs represent signaling pathways, we can consider a special case of signaling hypergraphs. Reactions in signaling pathways are unlikely to involve a very large number of proteins. Thus, we are interested in computing the shortest B-hyperpath in k-hypergraphs, where each hyperedge has at most k hypernodes in its tail at most k hypernodes in its head.
We say that a B-hyperpath Π(s, t) is acyclic if it contains no simple cycles. Note that B-hyperpaths may be acyclic, even though they are minimal with respect to deletion of hypernodes and hyperedges (Figure 2). These simple cycles may also occur in the shortest B-hyperpath Π*(s, t) of a hypergraph. Thus, we restrict our attention to acyclic B-hyperpaths, in an analogy to computing shortest paths on graphs (which are always acyclic).
Fig. 2.
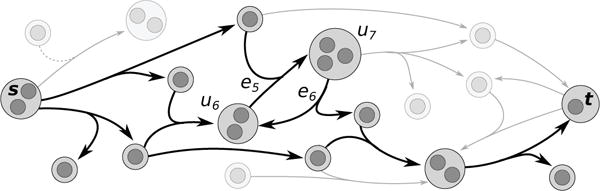
An s-t B-hyperpath with a simple cycle (u6, e5, u7, e6, u6).
We now show that computing the shortest acyclic B-hyperpath in a k-hypergraph is NP-hard. We first prove the NP-completeness of the corresponding decision problem.
Theorem 1
Given a k-hypergraph with k ≥ 3 and s, , finding an acyclic B-hyperpath Π(s, t) with l or fewer hyperedges is NP-complete.
Proof
We prove the theorem by a reduction from Minimum k-Set Cover. Let A = {a1, …, an} be a set of n elements, and let Q = {Q1, …, Qm} be a set of m subsets of A (i.e., Qi ⊆ A) such that |Qi| ≤ k for all subsets Qi ∈ Q and . Given A, Q, and l, a solution to the Minimum k-Set Cover Problem consists of selecting a subset Q′ of Q with cardinality at most l that covers all elements in A (i.e., ).
We first define a k-hypergraph given an instance of Minimum k-Set Cover (A, Q, l) (Figure 3). Let c = ⌈logk n⌉ be the smallest integer such that kc ≥ n. We will first define the hypernode set . Without loss of generality, all hypernodes in are single nodes. consists of five different types of hypernodes (Figure 3):
A source hypernode s and a target hypernode t
n hypernodes denoting the elements A
kc − n “dummy” hypernodes D
“internal” hypernodes B
Fig. 3.
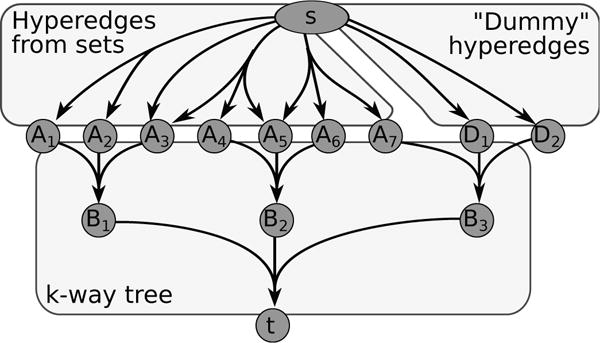
k-hypergraph construction from an instance of Minimum k-Set Cover with seven elements A = {a1, a2, …, a7}, four subsets Q = {{a1, a2}, {a3}, {a3, a4, a5}, {a5, a6, a7}}, and k = 3.
Taken together, {A ∪ D ∪ B ∪ {t}} comprise a perfect k-way tree with leaves {A ∪ D } rooted at t. We define three distinct classes of signaling hyperedges (Figure 3):
Hyperedges from sets. For every set Qi ∈ Q, we connect the source hypernode s to the elements in A that are members of Qi: {({s}, Qi) ∀ Qi ∈ Q}.
“Dummy” hyperedges. We connect s to each of the kc − n “dummy” leaves using a single hyperedge: {({s}, {di},∀ di ∈ D}.
k-way tree hyperedges. We add signaling hyperedges to connect the leaves in the k-way tree to the root t through the internal hypernodes bi ∈ B. Each hyperedge contains exactly k hypernodes in the tail and one hypernode in the head. There are such hyperedges, since the internal hypernodes B and t each have a single incoming hyperedge (Figure 3).
This construction clearly takes polynomial time, producing a k-hypergraph with hypernodes and hyperedges.
We now show that there exists a B-hyperpath Π(s, t) with no more than j hyperedges if and only if there exists a cover Q′ of A whose cardinality is less than or equal to l. First, suppose a cover Q′ of cardinality l exists. Define a sub-hypergraph of that includes all the hypernodes in , all “dummy” hyperedges, all hyperedges in the k-way tree, and the l hyperedges that correspond to the sets in Q′. Each hypernode ai is B-connected to s because, by definition, there is some set in Q′ that covers ai and the corresponding hyperedge in only contains s in the tail. Additionally, each “dummy” hypernode is B-connected to s by means of a “dummy” hyperedge in . Thus, all the leaves of the k-way tree are B-connected to s. By construction, since all the k-way hyperedges are in , t is B-connected to s if all leaves in the k-way tree are B-connected to s. Thus, t is B-connected to s in . All hypernodes in are required to establish B-connectivity; however, there may be some sets in Q′ that are not necessary. We remove the corresponding hyperedges from until there is no hyperedge from the set Q′ that we can remove and still have t be B-connected to s in . Since and is minimal w.r.t. the deletion of hypernodes and hyperedges, and t is B-connected to s in , then must be a B-hyperpath Π(s, t) with at most hyperedges.
For the opposite direction, suppose there exists a B-hyperpath Π(s, t) with j hyperedges from s to t. By the construction of , all n hypernodes representing the elements in A must be in the hyperpath. Thus, for each element ai, there must be a hyperedge in BS(ai) that is in Π(s, t). Define the heads of these hyperedges as the subsets Q′ of s; Q′ covers all elements in A. Since Π(s, t) is minimal, there is no subset in Q′ that could be removed and still cover all elements. Thus, Q′ is a cover of A with hyperedges. □
Since the above decision problem is NP-complete, the corresponding optimization problem is NP-hard.
Corollary 3
Given a k-hypergraph with k ≥ 3 and s, , finding the shortest acyclic B-hyperpath Π*(s, t) is NP-hard.
3.4 Properties of Acyclic B-Hyperpaths
In this section, we state several properties of acyclic B-hyperpaths which we will use in Section 4 to prove the correctness of our algorithm. Given a hypergraph, an ordering of the hypernodes in is function that maps each hypernode in to a real number. We say that o is a valid ordering with respect to , if for every , and for every pair of hypernodes u ∈ T(e) and w ∈ H(e), o(u) < o(w) [20]. An ordering of the hypernodes in is analogous to a topological ordering on a directed acyclic graph. Next, we relate a valid ordering and the acyclicity of a hypergraph .
Lemma 4
Hypergraph has a valid ordering of the hypernodes if and only if it is acyclic.
Proof
We first prove by contradiction that if has a valid ordering of the hypernodes, then it is acyclic. Suppose there is a simple cycle P = (u1, e1, u2, …, uk−1, ek−1, uk) where uk ∈ T(e1). Let w be the hypernode in P with the smallest order value, i.e., . Consider the hyperedge e in P such that w ∈ H(e). Since P is a simple cycle, there must be some hypernode uj in P where uj ∈ T(e). By the definition of a valid ordering, o(uj) < o(w), which contradicts the fact that w minimizes the order function over the hypernodes in P. Therefore, must be acyclic.
Now, we show that if is acyclic, it has a valid ordering with a constructive proof. We build a directed graph , from where is exactly the set of hypernodes in and consists of all pairs of hypernodes in T(e) and H(e) for each hyperedge in , i.e., Since there are no simple cycles in , G is a directed acyclic graph with a topological ordering such that a(u) < a(w) for all (u, w) in . We will prove that a is also a valid ordering of the hypergraph . Suppose there are two hypernodes u and w such that a(u) < a(w) in the topological ordering of G, but there exists a hyperedge where w ∈ T(e) and u ∈ H(e). By construction, (w, u) must be an edge in G, which contradicts the fact that a defines a topological ordering of G. Therefore, a is a valid ordering for . □
The following lemma states that for an acyclic hypergraph , there must be at least one hypernode that does not appear in the head of any hyperedge.
Lemma 5
Given an acyclic hypergraph there exists some hypernode such that BS(u) = ∅.
Proof
Suppose every hypernode is in the head of some hyperedge in , i.e., BS(u) = ∅ for every hypernode . We will establish a contradiction by constructing a simple cycle in . Starting at any hypernode w, we construct a simple path P iteratively as follows. We set w to be a hypernode in P. Since BS(w) = ∅, there must be a hyperedge e such that w ∈ H(e). We prepend e to P. Next, we choose any hypernode y ∈ T(e) and prepend y to P. Since BS(y) = ∅, we can repeat this process with y, thereby alternatively prepending hyperedges and hypernodes to P. Since is finite, this process will result in the addition of a hyperedge f to P such that a hypernode in the tail of f is already in P. At this point, P contains a simple cycle, contradicting the fact that is acyclic. Therefore, there is at least one hypernode in that is not in the head of any hyperedge in . □
The above lemmas concern acyclic hypergraphs; we now turn our attention towards acyclic B-hyperpaths. Since there are no simple cycles in acyclic B-hyperpaths, we can characterize the “beginning” of the B-hyperpath as the set of hypernodes that have an empty backward star. The final claim states that for an acyclic B-hyperpath Π(s, t), s is the only hypernode in Π(s, t) that does not occur in the head of any hyperedge in Π(s, t).
Lemma 6
Given an acyclic B-hyperpath Π(s, t), s is the only hypernode that has an empty backward star (i.e., BS(s) = ∅).
Proof
Since Π(s, t) is a B-hyperpath, all the hypernodes in Π(s, t) are B-connected to s. By definition of a B-connection, all nodes except for s in Π(s, t) must have a hyperedge in the backward star whose tails are B-connected to s, i.e, BS(v) = ∅ for every node v ∈ V except for s (the base case). Since there must be at least one node that has an empty backward star (by Lemma 5), then this node must be s. □
4 Algorithms
We first present the algorithm for computing shortest acyclic B-hyperpaths from previous work [5] and then prove the algorithm’s correctness using the lemmas in Section 3.4. We describe our approach to computing minimum s-t B-hyperpaths in two parts. First, we develop an MILP to compute an acyclic B-connected sub-hypergraph that contains s and t. Although we can compute such a sub-hypergraph in polynomial time [21], we present an MILP so that we can augment it with an objective function in the second part to solve the NP-complete problem of computing shortest B-hyperpaths.
4.1 Computing Acyclic B-Connected Sub-Hypergraphs
Given a hypergraph and two hypernodes s and t in , we seek to compute an acyclic sub-hypergraph that contains s and t such that , i.e. t is B-connected to s in . Note that may not be an s-t B-hyperpath because it is not necessarily minimal.
We introduce binary (0-1) variables αu for every hypernode and αe for every hyperedge The output sub-hypergraph is defined by the values of these variables: the hypernode u (resp., hyperedge e) is in if and only if αu = 1 (resp., αe = 1). Given a setting of the variables in α, we will henceforth refer to the corresponding sub-hypergraph as and to the hypernodes and hyperedges in this sub-hypergraph as and , respectively. The α variables must satisfy the following linear constraints:
| (2) |
| (3) |
| (4) |
| (5) |
These constraints have the following meaning. With the exception of hypernode s, every hypernode u such that αu = 1 has at least one incoming hyperedge e such that αe = 1 (constraint (2). For every hyperedge e such that αe = 1, all hypernodes in the tail (constraint (3)) and the head (constraint (4)) must have α values of one. Finally, we require that t is in (constraint (5)).
Together, constraints (2)–(5) seek to ensure that t is in and that all the hypernodes in are B-connected to s. However, a sub-hypergraph that contains a simple cycle may satisfy these constraints without ensuring that t is not B-connected to s (Figure 4). To address this issue, we introduce a real-valued order variable ou for each . We ensure that o defines a valid ordering with respect to through the following constraint, which ensures that for each edge in , every hypernode in the tail of the edge must have an order value smaller than the order value of every hypernode in the head of the edge:
These constraints apply only to those edges e where αe = 1. Furthermore, linear programs require weak inequalities to define boundary regions. To address both points, we introduce two constants: ε, which takes a very small value and C, which takes a very large value. The following linear constraint applies to all edges in :
| (6) |
Equation (6) is only enforced when αe = 1 for hyperedge e; when αe = 0, the large constant C dominates the right hand side, trivially satisfying the inequality. We relax the strict inequality by requiring that ow is at least ε larger than ou.3
Fig. 4.
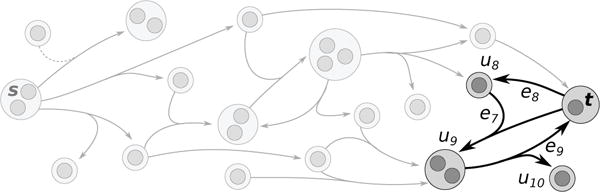
A sub-hypergraph that satisfies constraints (2)–(5) where t is not B-connected to s. Hypernode t is in the solution, and each hypernode in the solution (u8, u9, u10, t) has a hyperedge in its backwards star that is also in the solution (e8, e7, e9, e9).
Given a hypergraph and two hypernodes s and t in , we say that an assignment of α and o variables is feasible if it simultaneously satisfies the constraints in Equations (2)-(6). Given a feasible assignment, we make a number of claims about the resulting sub-hypergraph using the lemmas presented in Section 3.4.
Lemma 7
A feasible assignment of the constraints in Equations (2)-(6) produces a sub-hypergraph with the following properties.
is acyclic.
There exists a hypernode u with an empty backward star, i.e., BS(u) = ∅.
The only hypernode with an empty backward star in is s.
Hypernode s has the smallest value for the order variable in , i.e., .
Proof
We prove the claims in order.
Equation (6) ensures that there is a valid ordering of the hypernodes in ; thus is acyclic by Lemma 4.
Since is acyclic, then there must be some hypernode where BS(u) = ∅ by Lemma 5.
Constraint (2) requires that every hypernode in except for s has at least one hyperedge in its backward star. Thus, the only hypernode with an empty backward star must be s.
For every hypernode , we compute a simple path P by prepending alternate hyperedges in the backward star to the current hypernode and hypernodes in the tail of that hyperedge, starting at u. The path P will terminate at s because is acyclic and s is the only hypernode with an empty backward star. Since every edge in satisfies constraint (6), we see that ou > os for all hypernodes u. Thus, s has the smallest order variable value in . □
From these claims, we prove the following lemma:
Lemma 8
All hypernodes in are B-connected to hypernode s in , i.e., .
Proof
We will use strong induction on the order variables. Without loss of generality, rename the hypernodes in by increasing value of the order variables, so that , for all 1 ≤ i < n, where . Note that s = u1 by Lemma 7. By the definition of B-connected, s is B-connected to itself, establishing the base case. Now consider hypernode u2. Equation (2) requires that u2 must have at least one hyperedge e in its backward star in . Constraint (6) requires that if ui is a hypernode in the tail of e, for some value of i, then . The only possible value of i is 1. Thus, there must exist a hyperedge e such that T(e) = {s} and u2 ∈ H(e), proving that u2 is B-connected to s in .
For the inductive hypothesis, we assume that hypernodes u1, u2, …, uk−2, uk−1 are B-connected to s in . To prove that uk is also B-connected to s in , we must show that there exists a hyperedge such that uk ∈ H(e) and every hypernode W ∈ T(e) is B-connected to s. Constraint (2) requires that there exists some hyperedge that is in the backward star of uk. Now constraint (3) applies to e. Therefore, all hypernodes in T(e) are in . Finally, Equation (6) requires that for any hypernode ui in T(e), , i.e., i < k. Therefore, by the inductive hypothesis, each hypernode in T(e) is B-connected to s. Together, these statements establish that hypernode uk is B-connected to s. □
Observe that t is in because we fix αt to 1 in constraint (5); thus, we will consider t in the inductive proof, leading to the following corollary.
Corollary 9
Hypernode t is B-connected to hypernode s in , i.e., .
From the proof of Lemma 8, we also see that there must be a hyperedge in connecting s to u2 (and possibly other nodes). Thus, there is at least one hyperedge e in such that hypernode s ∈ T(e), which allows us to prove the following lemma.
Lemma 10
contains an acyclic s-t B-hyperpath as a sub-hypergraph.
Proof
Hypernode t is B-connected to hypernode s in by Corollary 9. However, might not be an s-t B-hyperpath because it is not necessarily minimal with respect to the deletion of hypernodes and hyperedges. If this is the case, there must be some hyperedges that can be removed from such that t is still B-connected to s. We can greedily remove such hyperedges from , ensuring after each removal that t is B-connected to hypernode s in the resulting sub-hypergraph. We stop this process when no such hyperedge remains. We also delete any hypernodes that are incident only on the deleted hyperedges. Since is acyclic (by Lemma 7), the resulting sub-hypergraph of is also acyclic. Thus, the final sub-hypergraph produced by this process is an acyclic s-t B-hyperpath. □
The previous lemmas establish that if the MILP has a feasible solution, then is acyclic, contains both s and t, and that all hypernodes in are B-connected to s in . Moreover, contains an acyclic s-t B-hyperpath. The next lemma establishes the inverse property: if the hypergraph contains an acyclic s-t B-hyperpath, then the MILP has a feasible assignment.
Lemma 11
If contains an acyclic B-hyperpath ), then there is a feasible assignment where .
Proof
We construct an assignment that corresponds to Π(s, t). We first define an assignment A of the α variables as follows:
Note that the sub-hypergraph induced by A is exactly Π(s, t). We show that A satisfies constraints (2)-(5). Equation (5) is satisfied because hypernode t is in Π(s, t); thus we have αt = 1. We now satisfy Equations (2)-(4).
The variables αu in assignment A that are 0 trivially satisfy Equation (2); we focus on the variables αu that equal 1 (e.g., ). Every hypernode is B-connected to s in Π(s, t); thus, there is at least one hyperedge in BS(u) that is also in Π(s, t). As a result, if αu = 1 for a hypernode u, then Σe∈BS(u) αe must be at least 1 and Equation (2) is satisfied.
The variables αe in assignment A that are 0 trivially satisfy Equations (3) and (4); we focus on the variables αe that equal 1 (e.g., ). Suppose Equation (3) or (4) is not satisfied for some hyperedge e in Π(s, t). That is, at least one hypernode in the tail or the head of e is not in Π(s, t). The definition of a sub-hypergraph of states that for every hyperedge , all hypernodes in T(e) and H(e) must be in . Since Π(s, t) is a sub-hypergraph of , we have a contradiction, so Equations (3) and (4) must be satisfied.
Finally, we must ensure that there is an assignment of order variables that satisfies Equation (6). We use the fact that a valid ordering of the hypernodes in Π(s, t) exists because it is acyclic (by Lemma 4). Assign the order variables the valid ordering function for ; ou = o(u) for all hypernodes . The values for the other order variables may be arbitrarily set. Equation (6) is trivially satisfied when αe = 0; for the case when αe = 1, the valid ordering ensures that o(u) < o(w) for all (u, w) ∈ {T (e) × H(e)}. Thus, the order variables ou and ow will satisfy Equation (6) for all u ∈ T (e) and w ∈ H (e) for all . □
Lemmas 10 and 11 collectively establish that a feasible assignment of the constraints in Equations (2)-(6) exists if and only if contains an acyclic B-hyperpath Π(s, t).
4.2 Computing Shortest Acyclic B-Hyperpaths
We now augment the MILP developed so far with an objective function in order to compute a shortest acyclic s-t B-hyperpath Π*(s, t), i.e., one that minimizes Equation (1). We compute an assignment of variables that solves the following optimization problem:
| (7) |
The following theorem captures our main result.
Theorem 2
Given a hypergraph and two hypernodes s, , let be the sub-hypergraph of that minimizes the objective function in Equation (7) is a shortest acyclic s-t B-hyperpath Π*(s, t) in .
Proof
It suffices to prove that is acyclic, that , and that is minimal with respect to the deletion of hypernodes and hyperedges. Lemma 7 shows that is acyclic. Hypernode t is B-connected to s in by Corollary 9; thus .
To prove minimality, we begin with hyperedges. Suppose there exists a hyperedge that, when removed, produces a sub-hypergraph of where t remains B-connected to s. The cost of is less than the cost of , which contradicts the fact that is the sub-hypergraph of that minimizes the objective function in (7). Thus, is minimal with respect to the deletion of hyperedges.
We now prove minimality with respect to hypernodes. Hypernodes incident on a hyperedge in cannot be removed due to the definition of a sub-hypergraph. Thus, a hypernode in can only be removed from only if it is not incident on any hyperedges in . Every hypernode other than s in is in the head of at least one edge in ; hence, such a hypernode cannot be present in . Since is acyclic, there must be a hypernode with an empty backward star and it must be s (by Lemma 7), so s cannot be deleted from either. Thus, is minimal with respect to the deletion of hypernodes.
Thus, the sub-hypergraph that minimizes the objective function (7) is indeed an acyclic s-t B-hyperpath Π(s, t). The value of the objective function for Π(s, t) is | Π(s,t)| because αe = 1 for all e ϵ EΠ(s,t). Therefore, Π(s, t) = Π*(s, t) has the smallest number of hyperedges over all acyclic s-t B-hyperpaths in . □
4.3 Conversion to Graph Representations
For the purpose of comparing signaling hypergraphs to graphs, we convert each signaling hypergraph to two different graph representations (Figure 5). First, we build a directed graph with complexes whose nodes are the hypernodes in and where consists of all pairs of hypernodes in the tail and head of each hyperedge in , i.e., . Note each edge in connects exactly two hypernodes (Figure 5B). The graph with complexes is akin to a compound graph, except that it does not explicitly represent the nested structure of complexes. However, it is not difficult to compute this structure from the hypernodes.
Fig. 5.
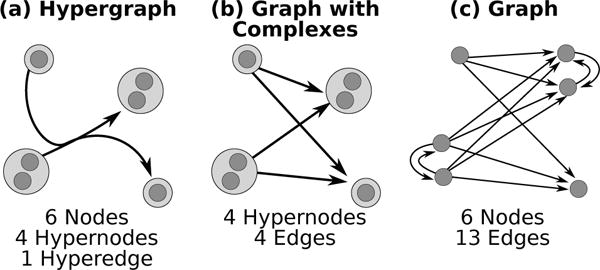
Hypergraph Conversions to Graph Representations. A single hyperedge (a) is converted into a graph with complexes (b) and a graph (c) representations. Note that if the same node appears on in the tail and the head, some edges will be collapsed.
Second, we convert the graph with complexes GC into a graph G = (V, EG) (Figure 5C). The nodes of GC are identical to the set of hypernodes of . The edges in EG are the union of two sets of edges: (a) For each hypernode u in , we connect all pairs of nodes in u by an undirected edge, corresponding to the common practice of representing a complex by a clique in a graph. (b) For each edge (u, v) in GC, we connect every node in the hypernode u to every node in the hypernode v by a directed edge. Finally, we replace every undirected edge by two directed edges.
4.4 NCI-PID Pathways
NCI-PID [6] contains curated human pathways that include biochemical reactions, complex assembly, cellular compartment transport, transcriptional regulation, and regulation of biological processes. We focused on the Wnt signaling pathway, in part due to its central role in development and a number of cancers.
We automatically constructed three signaling hypergraphs by combining different sets of signaling pathways annotated in NCI-PID: a small Wnt signaling pathway, a large Wnt signaling pathway, and the entire set of all NCI-PID pathways. The small Wnt signaling pathway consisted of the union of two NCI-PID pathways: “degradation of β-catenin” and “canonical Wnt signaling”. The large Wnt signaling pathway included four additional NCI-PID pathways: “noncanonical Wnt signaling,” “Wnt signaling network,” “regulation of nuclear β-catenin” and “presenilin action in Notch and Wnt signaling”, which corresponded to non-canonical branches of Wnt signaling. The NCI-PID pathways are freely available in BioPAX format [22], and we processed them using an in-house parser built upon PaxTools [23]. Signaling hypergraphs do not currently support negative regulation; thus negative regulators were ignored (Table 1). NCI-PID represents complexes as sets of unique NCI-PID protein IDs; thus we were able to extract complexes and parse them as hypernodes. Multiple forms of the same protein may be present with attributes such as compartmentalization, activation, and post-translational modifications (PTMs) such as phosphorylation and ubiquitination. We treated each variant as a distinct entity. We used this information to analyze and visualize our results, as the reader can see in the figures in Section 5.
TABLE 1.
Selected Signaling Pathways for Analysis. Negative regulators are ignored in each pathway. “Largest k” denotes the largest number of hypernodes in the tail or head of any hyperedge in the sub-hypergraph, corresponding to the constant k in the k-hypergraph. is the signaling hypergraph, GC is the graph with complexes, and G is the graph representation of each pathway.
| Small Wnt Pathway | Large Wnt Pathway | Full NCI-PID Pathway | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # Pathways | 2 | 6 | 213 | |||||||||
| # Negative Regulators | 6 | 25 | 856 | |||||||||
| Largest k | 3 | 5 | 10 | |||||||||
|
| ||||||||||||
|
|
Gc | G |
|
Gc | G |
|
Gc | G | ||||
|
| ||||||||||||
| # Nodes | 47 | – | 47 | 304 | – | 304 | 6793 | – | 6793 | |||
| # Hypernodes | 57 | 57 | – | 354 | 354 | – | 8779 | 8779 | – | |||
| # Edges | – | 80 | 294 | – | 541 | 1435 | – | 15622 | 40346 | |||
| # Hyperedges | 34 | – | – | 223 | – | – | 7735 | – | – | |||
Table 1 displays statistics on these three sets of pathways when represented as signaling hypergraphs and upon conversion to graphs with complexes GC and graphs G. There are at most ten hypernodes in the tail or head of any hyperedge (“Largest k” row in Table 1), demonstrating that our assumption of k-hypergraphs with a small constant k is reasonable in Theorem 1 and Corollary 3. Note that the nodes in GC are exactly the hypernodes in , and the nodes in G are exactly the nodes in ; however the number of edges vary considerably between representations. For the full NCI-PID database, the number of edges in Gc is twice the number of signaling hyperedges in ; the number of edges in G is about five times as many. These statistics suggest that the information loss incurred upon making these conversions of signaling hypergraphs is accompanied by a significant inflation in the number of edges.
5 Results
Given a signaling hypergraph and two hypernodes s, t ∈ , we wished to compute s-t B-hyperpaths with the smallest number of hyperedges in . We outline the general procedure for computing B-hyperpaths in in Algorithm 1. Corollary 2 states that any B-hyperpath must contain hypernodes that are B-connected to s. Thus, we first computed all hypernodes that were B-connected to s in [18] and the sub-hypergraph of induced by these hypernodes, returning an infeasible solution if t was not B-connected to s (lines 1-5). may be considerably smaller than after this step. We then solved for variables α and o variables in using the MILP that optimizes Equation (7) (Section 4), and stored the optimal objective (lines 6-7). Since there may be many B-hyperpaths with the same number of hyperedges, we iteratively solved the MILP after adding a constraint that forced a new B-hyperpath (line 11). We returned all the B-hyperpaths with the smallest number of hyperedges.
We applied this procedure to signaling hypergraphs as well as their graph-with-complexes and graph counterparts. We acknowledge that the minimal acyclic B-hyperpath path problem can be solved in polynomial time using Dijkstra’s algorithm. However, we continued to use the MILP approach to ensure uniformity of analysis across all inputs.
5.1 Small Wnt Signaling Pathway
The NCI-PID pathway describing the degradation of β-catenin terminates at ubiquitinated β-catenin. The NCI-PID canonical Wnt signaling pathway terminates at nuclear β-catenin, which is a transcriptional co-regulator. To answer Question 1 from the introduction, we asked what reactions terminate at the (a) ubiquitinated form of β-catenin and (b) the nuclear form of β-catenin.
Algorithm 1.
RunMILP(ℋ,s,t)
| Require: ; | |
| 1: | ℬℋ(s) := Set of hypernodes in s that are B-connected to s |
| 2: | ℋ′ := sub-hypergraph of ℋ induced on ℬℋ(s) |
| 3: | if t is not in ℬℋ(s) then |
| 4: | return Infeasible Assignment |
| 5: | end if |
| 6: | α, o := Solve Equation (7) on ℋ′, s, and t |
| 7: | opt := |ℰ(α)| |
| 8: | R := Ø |
| 9: | while |ℰ(α)| = opt do |
| 10: | R := R ∪ ℋ(α) |
| 11: | Add constraint such that . |
| 12: | α, o := Re-solve the MILP on ℋ′, s, and t |
| 13: | end while |
| 14: | return R |
We made the following modifications to the small Wnt signaling pathway before applying the MILP. We introduced a source hypernode s and connected s to 21 hypernodes with an empty backward star. We also connected s to a hypernode representing a complex of APC, Axin1, and β-catenin; this complex is part of a cycle involving cytoplasmic β-catenin, and including the hypernode in the set of sources “breaks” this loop. Finally, we removed one self-loop that contained the same form of β-catenin in the head and the tail. The modified signaling hypergraph consisted of 58 hypernodes, 48 nodes, and 56 hyperedges. All hypernodes and hyperedges were B-connected to s.4 We computed the shortest B-hyperpaths from the source hypernode s (i) to the ubiquitinated form of β-catenin and (ii) to the nuclear form of β-catenin.
5.1.1 Reactions Involved in Ubiquitinated β-catenin
The MILP returned one shortest B-hyperpath with four hyperedges (Figure 6(a)). Since β-catenin is marked for degradation in the absence of Wnt signaling, the absence of Wnt proteins from this B-hyperpath was not surprising. The APC/GSK3/Axin2/β-catenin complex splits to produce two smaller complexes: APC/β-catenin and Axin2/GSK3. The SCF ubitiquitin ligase complex composed of CUL1, SKP1, and an F-box protein then splits the APC/β-catenin complex and ubiquitinates β-catenin, marking it for degradation.
Fig. 6.
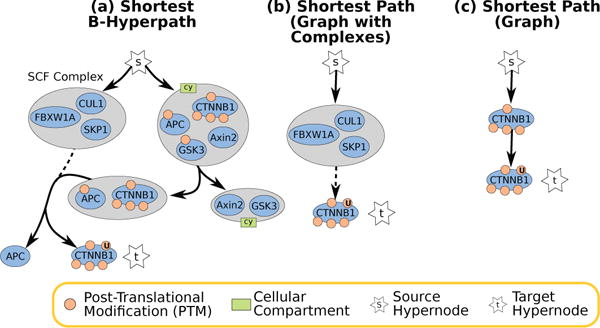
Small Wnt Pathway Solutions to ubiquitinated β-catenin, denoted by a post-translational modification with a ‘U’.
Comparison to Graphs
In the graph-with-complexes representation, there was a single path of length two from s to ubiquitinated β-catenin through the SCF complex (Figure 6(b)). This path corresponded to a simple path in the signaling hypergraph. In the graph representation, there were five paths of length two. Each of the first three paths was a simple path in the signaling hypergraph and contained one of the members of the SCF complex (e.g., the path (s,CUL1,ubiquitinated β-catenin)). However, the other two paths, through APC and through phosphorylated β-catenin, were not simple paths in the signaling hypergraph. The graph representation collapsed the two complexes in the solution for signaling hypergraphs, yielding the path from s to ubiquitinated β-catenin through phosphorylated β-catenin (Figure 6(c)).
5.1.2 Reactions Involved in Nuclear Import of β-catenin
The MILP returns a single shortest B-hyperpath consisting of 11 hyperedges (Figure 7(a)). Here, Wnt signaling is necessary for the formation of the WNT3A/FZD5/LRP6 complex at the cell membrane, which activates a regulator (PP2A-B56α) that dissociates β-catenin from its complex with the destruction box APC/Axin1/GSK35 and dephosphorylates β-catenin, which in turn translocates to the nucleus. The shortest B-hyperpath also contains details about the formation of the APC/GSK3/Axin1/β-catenin complex: first, CK1 family proteins phosphorylate β-catenin in the APC/Axin1/β-catenin complex, and GSK3 then joins the complex and becomes activated.
Fig. 7.
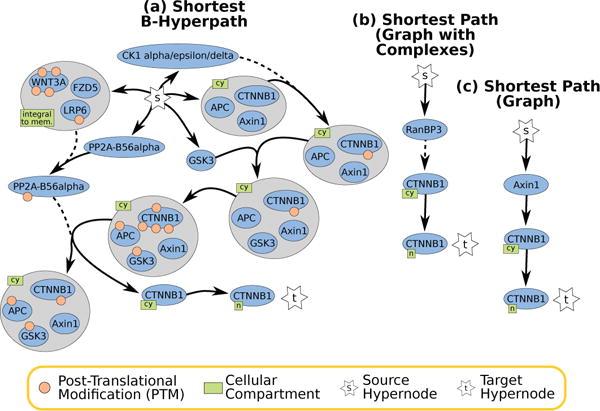
Small Wnt Pathway Solutions to nuclear β-catenin, denoted by a compartment marked ‘n’ for nucleus.
Comparison to Graphs
In the graph-with-complexes representation, there is a single path of length three from s to nuclear β-catenin that contains RanBP3 (Figure 7(b)). RanBP3 is in the Wnt signaling pathway because it aids in the nuclear export of β-catenin back to the cytoplasm [24]; thus, this path is misleading in this context. There are seven paths of length three from s to nuclear β-catenin in the graph representation; the path through RanBP3 is the only one that corresponds to a simple path in the signaling hypergraph. The other paths (through WNT3A, Axin1, GSK3, APC, FZD5, and phosphorylated β-catenin) are all present in multiple complexes that are collapsed in the graph representation. The path through Axin1 is shown in Figure 7(d).
5.2 Large Wnt Signaling Pathway
TCF1 and LEF1, transcription factors involved in Wnt signaling, are also downstream targets of Wnt. To answer Question 1 for the large Wnt signaling pathway, we computed shortest acyclic B-hyperpaths to identify reactions that regulate the transcription of genes tcf1 and lef1.
We introduced a source hypernode s and connected it to 149 hypernodes with an empty backward star. We also connected s to the same hypernode in the cycle involving cytoplasmic β-catenin as for the small Wnt signaling pathway, and removed eight self-loops. The modified signaling hypergraph consisted of 356 hypernodes, 306 nodes, and 374 hyperedges, of which 354 hypernodes and 372 hyperedges were B-connected to s. To identify a series of reactions that regulate both tcf1 and lef1 gene transcription, we added a target hypernode t and a single hyperedge ({TCF1, LEF1},t) to the signaling hypergraph. For t to be B-connected to s, both TCF1 and LEF1 must be B-connected to s.
There were four shortest acyclic B-hyperpaths with 21 hyperedges in the signaling hypergraph (Table 2); one is displayed in Figure 8(a). The four B-hyperpaths shared a majority of the hyperedges, with at most four different hyperedges. A subset of these hyperedges established that nuclear β-catenin is B-connected to s. These hyperedges, denoted in gray in Figure 8(a), were identical to those used to connect nuclear β-catenin to s in the small Wnt pathway in Figure 7(a) with one exception: they included the formation of the WNT3A/FZD5/LRP6 complex. The four B-hyperpaths differed in the complexes containing TLE and TCF family proteins that bind to the promoter regions of LEF1 and TCF genes (Table 2). For example, the transcription factor TCF1E can be replaced by TCF4E in Figure 8 to regulate LEF1 transcription.
TABLE 2.
Shortest B-hyperpaths and paths for the large Wnt signaling pathway.
| Shortest B-Hyperpath/Path from s | #1 | ||
|---|---|---|---|
|
|
(see Figure 8) | 21 | |
| {TLE4,TCF4} replaced by {TLE2,TCF4}2 | 21 | ||
| {TLE2,TCF1E} replaced by {TLE4,TCF4E}2 | 21 | ||
| {TLE2,TCF1E} replaced by {TLE2,TCF4E}, and {CTNNB1,TCF1E} replaced by {CTNNB1,TCF4E}2 | 21 | ||
|
| |||
| Gc | (s, {TLE2,TCF1E }, {CTNNB1,TCF1E },LEF1,t) | 4 | |
| (s,{TLE4,TCF4},{CTNNB1,TCF4},TCF1, t) | 4 | ||
| (s, {TLE4,TCF4E }, {CTNNB1,TCF4E },LEF1, t) | 4 | ||
| (s,PITX2,{CTNNB1,LEF1,PITX2},LEF1, t) | 4 | ||
| (s,{TLE2,TCF4},{CTNNB1,TCF4},TCF1, t) | 4 | ||
|
| |||
| G | (s,LEF1, t) | 2 | |
| (s,TCF1, t) | 2 | ||
Number of hyperedges in optimal solution.
Major differences compared to solution in Figure 8.
Fig. 8.
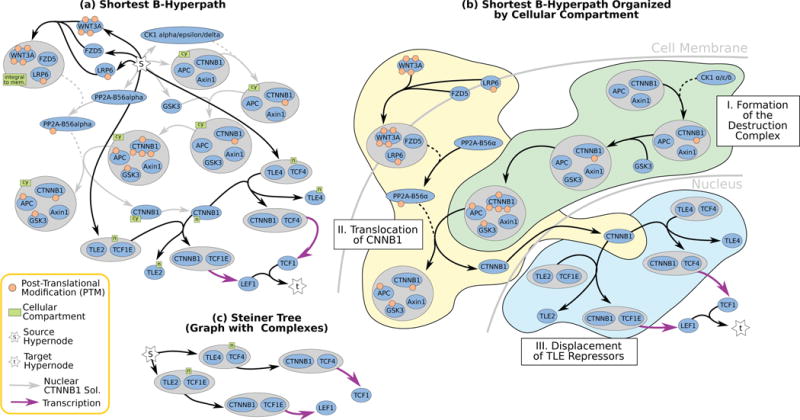
Large Wnt Pathway solutions. (a) The shortest acyclic B-hyperpath in the signaling hypergraph, and (b) the same B-hypergraph organized by cellular compartment (hyperedges from s not shown). (c) The Steiner tree in the graph with complexes connecting s to TCF1 and LEF1 terminals. The Steiner tree was comprised of two of the five shortest paths in the graph with complexes representation (Table 2).
Figure 8(b) shows an alternative layout of the shortest acyclic B-hyperpath according to the hypernodes’ cellular compartment (green boxes in Figure 8(a)). For ease of visualization, we do not show hyperedges from the source s. The shortest acyclic B-hyperpath describes three distinct series of events. First, the destruction complex forms, with a multi-phosphorylated β-catenin bound to the complex (Figure 8(b) Step I). β-catenin is released from the destruction complex by a series of reactions that begin with WNT3A binding to FZD5 and LRP6, which in turn activates phosphatase PP2AB56α. PP2A-B56α subsequently dephosphorylates β-catenin and releases it from the destruction complex (Figure 8(b) Step II). Finally, once β-catenin is in the nucleus, it displaces TLE family proteins which act as transcriptional repressors by binding to TCF family transcription factors. (Figure 8(b) Step III). The other three B-hyperpaths with 21 hyperedges differ from the B-hyperpath shown in Figure 8(b) by replacing the TLE family repressors and TCF family transcription factors in Step III. Thus, in this single shortest acyclic B-hyperpath, we have described a scenario in which both TCF1 and LEF1 may be regulated by Wnt signaling.
5.2.1 Comparison to Graphs
We computed the shortest paths in the graph with complexes GC and the graph G representations of the large Wnt signaling pathway. There were five shortest loopless paths from s to t in GC each containing four edges (Table 2). These paths differed by the TLE repressors and the TCF transcription factors, similar to the different shortest B-hyperpaths. The shortest loopless paths in G connected s to t directly through LEF1 and TCF1, since LEF1 and TCF1 also happen to be members of complexes with empty backward stars (Table 2).
Simply computing the shortest path in these graph representations cannot capture the full complexity of B-hyperpaths. We explored two additional graph-based algorithms – Steiner trees and k shortest paths – to further evaluate the graph decompositions. Steiner trees find a subgraph with the smallest number of edges that span a set of terminal hypernodes in a graph, which are s, LEF1, and TCF1 in our case. We computed the Steiner tree connecting s to TCF1 and to LEF1 in the graph-with-complexes representation.6 The Steiner tree, like all of the shortest paths in the graph-with-complexes representation, did not include the transport of cytoplasmic β-catenin to the nucleus, a crucial component of TCF1 and LEF1 transcriptional activation.
The k shortest paths approach computes a user-defined number of paths in a graph. We used Yen’s algorithm to compute the k = 20,000 shortest paths from source to sink in GC as well as G [26]. Each edge in GC and G was ranked by the length of the first path in which it appeared.
We assessed how well the ranked edges in GC and G corresponded to the shortest acyclic B-hyperpath from the large Wnt pathway. Using the method outlined in Section 4.3, we converted to its corresponding graph representations and G* = (V′, E′) (Table 3). To evaluate the ranked lists, we used and E′ as the “positive” edge sets. All other edges in GC and G were considered “negatives.”
TABLE 3.
Attributes of large Wnt’s shortest B-hyperpath solution and its associated graph decompositions: the graph with complexes solution and the graph solution G*.
|
|
|
G* | |||
|---|---|---|---|---|---|
| # Nodes | 29 | – | 29 | ||
| # Hypernodes | 25 | 25 | – | ||
| # Edges | – | 36 | 107 | ||
| # Hyperedges | 21 | – | – |
We computed precision and recall for the edges ranked with Yen’s algorithm using the positive and negative edge sets for GC and G (Figure 9). As expected, GC recovers the edges that appear in better than G because GC and contain the same set of hypernodes; thus edges in GC will connect hypernodes in . However, neither ranking has precision above 0.4 beyond a recall of 0.25 (Figure 9). Interestingly, neither curve achieves a recall of 1, even though all paths (521 total) from source to sink in GC were generated by the k-shortest paths algorithm. This result implies that there are edges in the solution graph that are not on any path from the source to the sink in GC. This is precisely the case, since a B-hyperpath may include “dangling” hypernodes that become heads of directed edges in (e.g., both TLE2 and TLE4 in Figure 8(a)). This property applies to the edges in the k shortest paths of G as well, even though not all paths from source to sink in G were generated in Figure 9.
Fig. 9.
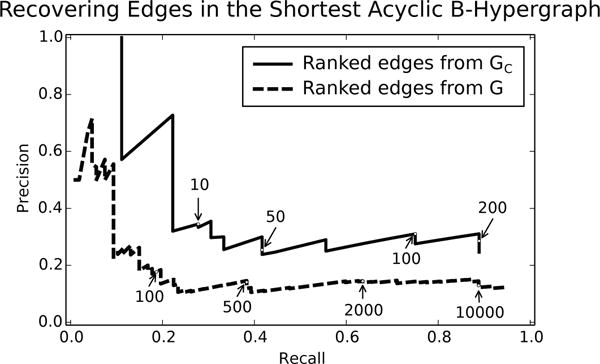
Precision-recall plots for edge recovery of the shortest acyclic B-hyperpath using the k-shortest paths from GC and G from the large Wnt signaling pathway. Labels on the lines represent k, the number of shortest paths used to achieve that exact precision-recall value.
5.3 Full NCI-PID Signaling Pathway
Finally, we analyzed the full NCI-PID signaling pathway to address Question 2 from the introduction. We asked the following complementary two questions:
New Sources to Known Targets: are there reactions currently not annotated to the Wnt pathway that are connected to transcriptional regulators in the Wnt signaling pathway?
Known Sources to New Targets: do reactions in the Wnt pathway connect to transcriptional regulators or factors that are not currently annotated to the Wnt signaling pathway?
These types of questions will not only help improve the manual curation of signaling pathway databases, but will also provide insight into potential means of pathway crosstalk (where the stimulation of one pathway affects the downstream targets of another). To initiate this analysis, we removed self-loops from hypernodes that appeared in the head and the tail of 43 hyperedges.
For the “New Sources to Known Targets” problem, we connected a source hypernode s to 3,065 elements that did not appear in the large Wnt signaling pathway and had an empty backward star. We connected 84 hypernodes from the large Wnt signaling pathway that were located in the nucleus t. The modified signaling hypergraph contained 8,781 hypernodes and 10,876 hyperedges, which reduced to 7,341 hypernodes and 8,569 hyperedges after finding the hypernodes that were B-connected to s.
The shortest B-hyperpath consisted of six hyperedges (s1 to t1 in Figure 10). The nuclear complex containing the Androgen receptor (AR) and the hormone dihydrotestosterone (T-DHT) is present in the Wnt signaling pathway due to a reaction with a complex involving β-catenin [27] (this reaction does not appear in our solution). The shortest B-hyperpath included two upstream biological events: the formation of this complex in the cytosol followed by its translocation of the complex to the nucleus. These upstream events are included in the “Regulation of Androgen receptor activity” NCI-PID pathway.
Fig. 10.
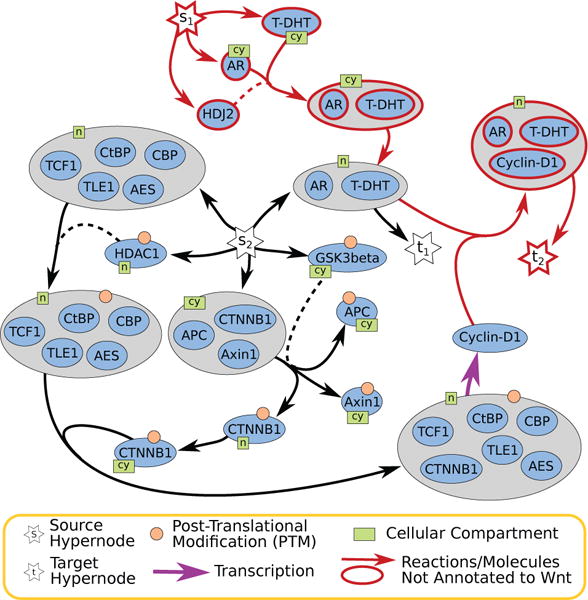
Two B-hyperpaths computed in the full NCI-PID signaling pathway. The B-hyperpath from s1 to t1 is the optimal result for “New Sources to Known Targets”, and the B-hyperpath from s2 to t2 is the optimal result for “Known Sources to New Targets.”
For the “Known Sources to New Targets” problem, we connected s to 143 hypernodes in the large Wnt signaling pathway that had an empty backward star. We connected 939 hypernodes that did not appear in the large Wnt signaling pathway and were located in the nucleus to t. The modified signaling hypergraph contained 8,781 hypernodes and 8,809 hyperedges; this number reduced to 260 hypernodes and 268 hyperedges after finding the hypernodes that are B-connected to s. There were three shortest B-hyperpaths containing three hyperedges; all involve simple paths leading to post-translational modifications of JUN that are not in the Wnt signaling pathway. This result was not surprising, since Jun has many regulators and over 15 different post-translational forms. To find the “next” best B-hyperpath, we removed the hyperedge connecting the Jun proteins to t. In this modified hypergraph, the shortest B-hyperpath contained 12 hyperedges (s2 to t2 in Figure 10). The transcription of Cyclin-D1 (and the events leading up to it) are members of the Wnt signaling pathway; the AR/T-HDT complex is in the pathway as well. Surprisingly, the formation of the AR/T-HDT/Cyclin-D1 complex is not in the Wnt signaling pathway. Cyclin-D1 is a co-repressor of AR [28], and the formation of the AR/T-DHT/Cyclin-D1 complex appears in NCI-PID’s “Coregulation of Androgen receptor activity” pathway. Further, the complex formation is a spontaneous reaction.
On hindsight, the results appear to be unsurprising. One shortest B-hyperpath describes the formation of the AR/T-DHT complex and its transport to the nucleus. The other shortest B-hyperpath culminates in the spontaneous complexing of AR/T-DHT with Cyclin-D1. However, the NCI-PID curators selected to include these complexes and reactions in three different pathways. Manual discovery of these connections is likely to be very difficult. Signaling hypergraph theory offers a facile way to make such discoveries.
5.4 Performance Evaluation
The MILP was implemented in Python version 2.7.3 and CPLEX version 12.6.0.0, and in practice ran in a manner of seconds for all experimental scenarios. For the Wnt signaling pathways, the runtime of the signaling hypergraph representations ranged from 0.1s to 1.29s; comparable to that of graphs with complexes (0.11s to 0.49s) and graphs (0.79s to 1.49s) The runtime of the signaling hypergraph MILP for the full NCI-PID pathway took considerably longer in the “New Sources to Known Targets” scenario (36.57s) compared to the “Known Sources to New Targets” scenario (0.52s), reflecting the large difference in the relative size of the signaling hypergraphs.
6 Conclusions
The limitations of graph-based approaches for signaling pathways analysis have been recognized for years. A number of representations have been developed that involve directed hypergraphs and hypergraph-like notions. We have proposed a related representation called signaling hypergraphs that allow better characterization of reactions that involve multiple complexes and proteins. Signaling hypergraphs produce more informative hyperpaths than corresponding graph representations on NCI-PID curated pathways.
We have described an MILP to compute shortest acyclic B-hyperpaths in signaling hypergraphs. Signaling hypergraphs, as they are defined here, do not yet represent negative regulation or more complex regulatory logic (e.g., allowing B-connectedness with at least one positive regulator, rather than requiring all positive regulators). Further, since the B-hyperpaths we compute are acyclic, we cannot recover feedback loops. Characterizing signaling hypergraphs that handle all forms of regulation and developing algorithms to compute cyclic B-hyperpaths are points of future work. These aspects may require generalizing B-connectedness. Further, other notions of connectedness (including F -connection, which defines connectedness among hypernodes according to the forward star rather than the backward star) are worth considering for signaling pathway analysis [18]. We also note that finding B-hyperpaths that optimize other hyperpath measures, such as hyperpath traversal cost and hyperpath rank, admit polynomial-time solutions [18], [19] and may be useful in the context of signaling pathways. Logic models that contain information about the “state” of a protein or complex are a special case of directed hypergraphs [16]. Incorporating this type of information in signaling hypergraphs may provide a scalable alternative to dynamic models.
We initially chose NCI-PID to interrogate because it contains a balance of manually-curated reactions and annotated signaling pathways that are relatively well-connected. We note that NCI-PID is not longer actively maintained, and we have found minor inconsistencies and ambiguities upon closer inspection of the Wnt signaling pathway. We plan to convert other signaling pathway databases such as Reactome [29] and KEGG [30] to signaling hypergraphs and apply the MILP to these pathways.
We have reported shortest B-hyperpaths in Wnt signaling, both within the annotated pathway as well as in the context of the larger NCI-PID dataset. The corresponding shortest paths found in graph representations miss crucial components of the underlying reactions. Additionally, some of the shortest paths are misleading, as in the case with RanBP3 in the Figure 7(b). We also investigated subnetworks in the graph representations returned by Steiner trees and k-shortest paths approaches, and found that while the subnetworks were much larger than the shortest paths, they failed to fully capture the reactions described by the shortest acyclic B-hyperpath. Through the development of new hypergraph-based algorithms, signaling hypergraphs have the potential to more accurately reflect the complexity of reactions in signaling pathway analysis.
Acknowledgments
National Institute of General Medical Sciences of the National Institutes of Health grant R01-GM095955, National Science Foundation grant DBI-1062380, and Environmental Protection Agency grant EPA-RD-83499801 supported this work.
Biographies

Anna Ritz is a postdoctoral research associate in Dr. T. M. Murali’s group in the Department of Computer Science at Virginia Tech. She received her B.A. degree in Computer Science from Carleton College in Northfield, MN, and her Sc. M. and Ph. D. degrees in computer science from Brown University in Providence, RI. Her research interests include graph and hypergraph algorithms, signaling pathway analysis, computational detection of structural variants in human genomes, and third-generation sequence data

Brendan Avent is an undergraduate at Virginia Tech, pursuing B.S. degrees in computer science, mathematics, and statistics, and a B.A. degree in economics. He is currently an undergraduate research assistant under Dr. T. M. Murali in the Computational Biology and Bioinformatics research group. His research interests include graph and hypergraph theory, algorithm design and analysis, game theory, microeconomics, and machine learning.

T. M. Murali is an associate professor in the Department of Computer Science at Virginia Tech. He co-directs the ICTAS Center for Systems Biology of Engineered Tissues and is the associate director for the Computational Tissue Engineering interdisciplinary graduate education program. Murali’s research group develops phenomenological and predictive models dealing with the function, behaviour, and properties of large-scale molecular interaction networks in the cell. He received his undergraduate degree in computer science from the Indian Institute of Technology, Madras and his Sc. M. and Ph. D. degrees from Brown University in Providence, RI.
Footnotes
Hypernodes may be referred to as undirected hyperedges, compound nodes [8], [11], or metanodes [9] in the literature.
We depart from the standard (uppercase) notation of a set because we consider a hypernode to be a single entity.
To reduce the search space for the MILP, we bound the order variables so that ou ∈ [0, 1] for all hypernodes u ∈ .
We say that a hyperedge is B-connected to s if all hypernodes in its tail are B-connected to s.
This reaction in NCI-PID does have one copy of β-catenin among the reactants and two copies of β-catenin among the products.
We used MSGSteiner [25] to find a prize-collecting Steiner tree that includes all terminals. The resulting Steiner trees contained six edges of edge-disjoint simple paths from s to LEF1 and to TCF1. Figure 8(c) illustrates one of these Steiner trees.
Contributor Information
Anna Ritz, Department of Computer Science, Virginia Tech, Blacksburg, VA, 24061.
Brendan Avent, Department of Computer Science, Virginia Tech, Blacksburg, VA, 24061.
T. M. Murali, Department of Computer Science, Virginia Tech, Blacksburg, VA, 24061 ICTAS Center for Systems Biology of Engineered Tissues, Virginia Tech, Blacksburg, VA, 24061.
References
- 1.Heath LS, Sioson AA. Semantics of multimodal network models. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2009;6(2):271–280. doi: 10.1109/TCBB.2007.70242. [DOI] [PubMed] [Google Scholar]
- 2.Klamt S, Haus U-U, Theis F. Hypergraphs and cellular networks. PLoS Computational Biology. 2009;5(5):e1000385. doi: 10.1371/journal.pcbi.1000385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berge C. Hypergraphs, Volume 45: Combinatorics of Finite Sets. 1st. North Holland; Aug, 1989. [Google Scholar]
- 4.Ritz A, Tegge AN, Kim H, Poirel CL, Murali T. Signaling hypergraphs. Trends in Biotechnology. 2014;32(7):356–362. doi: 10.1016/j.tibtech.2014.04.007. [Online]. Available: http://dx.doi.org/10.1016/j.tibtech.2014.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ritz A, Murali TM. Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics. New York, NY, USA: ACM; 2014. Pathway analysis with signaling hypergraphs; pp. 249–258. (ser BCB ’14). [Online]. Available: http://doi.acm.org/10.1145/2649387.2649450. [Google Scholar]
- 6.Schaefer CF, Anthony K, Krupa S, Buchoff J, Day M, Hannay T, Buetow KH. PID: the Pathway Interaction Database. Nucleic Acids Research. 2009;37:D674–D679. doi: 10.1093/nar/gkn653. Database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Polakis P. Wnt signaling and cancer. Genes Dev. 2000;14(15):1837–51. [PubMed] [Google Scholar]
- 8.Fukuda K, Takagi T. Knowledge representation of signal transduction pathways. Bioinformatics. 2001;17(9):829–837. doi: 10.1093/bioinformatics/17.9.829. [DOI] [PubMed] [Google Scholar]
- 9.Hu Z, Mellor J, Wu J, Kanehisa M, Stuart JM, DeLisi C. Towards zoomable multidimensional maps of the cell. Nature Biotechnology. 2007 May;25(5):547–554. doi: 10.1038/nbt1304. [DOI] [PubMed] [Google Scholar]
- 10.Gallagher SR, Goldberg DS. in Proceedings of the International Conference on Bioinformatics, Computational Biology and Biomedical Informatics. New York, NY, USA: ACM; 2013. Clustering coefficients in protein interaction hypernetworks; pp. 552:552–552:560. (ser BCB’13). [Google Scholar]
- 11.Dogrusoz U, Cetintas A, Demir E, Babur O. Algorithms for effective querying of compound graph-based pathway databases. BMC Bioinformatics. 2009;10(376) doi: 10.1186/1471-2105-10-376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gat-Viks I, Shamir R. Refinement and expansion of signaling pathways: the osmotic response network in yeast. Genome Research. 2007;17(3):358–67. doi: 10.1101/gr.5750507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vaske CJ, Benz SC, Sanborn JZ, Earl D, Szeto C, Zhu J, Haussler D, Stuart JM. Inference of patient-specific pathway activities from multi-dimensional cancer genomics data using PARADIGM. Bioinformatics. 2010;26(12):i237–i245. doi: 10.1093/bioinformatics/btq182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Machado D, Costa RS, Rocha M, Ferreira EC, Tidor B, Rocha I. Modeling formalisms in Systems Biology. AMB Express. 2011 Dec;1(1):45–14. doi: 10.1186/2191-0855-1-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Matsuno H, Tanaka Y, H A, Doi A, Matsui M, Miyano S. Biopathways representation and simulation on hybrid functional petri net. In Silico Biol. 2003;3(3):389–404. [PubMed] [Google Scholar]
- 16.Samaga R, Klamt S. Modeling approaches for qualitative and semi-quantitative analysis of cellular signaling networks. Cell Commun Signal. 2013;11(1):43. doi: 10.1186/1478-811X-11-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Karlebach G, Shamir R. Modelling and analysis of gene regulatory networks. Nature Reviews Molecular Cell Biology. 2008 Sep;9(10):770–780. doi: 10.1038/nrm2503. [DOI] [PubMed] [Google Scholar]
- 18.Ausiello G, Giaccio R, Italiano GF, Nanni U. Optimal traversal of directed hypergraphs. Tech Rep. 1992 [Google Scholar]
- 19.Thakur M, Tripathi R. Linear connectivity problems in directed hypergraphs. Theoretical Computer Science. 2009;410(27):2592–2618. [Google Scholar]
- 20.Cambini R, Gallo G, Scutellà M. Flows on hypergraphs. Mathematical Programming. 1997;78(2):195–217. [Online]. Available: http://dx.doi.org/10.1007/BF02614371. [Google Scholar]
- 21.Gallo G, Longo G, Pallottino S, Nguyen S. Directed hypergraphs and applications. Discrete Applied Mathematics. 1993;42(2–3):177–201. [Google Scholar]
- 22.Demir E, et al. The BioPAX community standard for pathway data sharing. Nature Biotechnology. 2010;28(9):935–942. doi: 10.1038/nbt.1666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Demir E, Babur Ö¨, Rodchenkov I, Aksoy BA, Fukuda KI, Gross B, Sümer OS, Bader GD, Sander C. Using biological pathway data with Paxtools. PLOS Computational Biology. 2013;9(9):e1003194. doi: 10.1371/journal.pcbi.1003194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hendriksen J, Fagotto F, Velde H van der, Schie M van, Noordermeer J, Fornerod M. RanBP3 enhances nuclear export of active (beta)-catenin independently of CRM1. J Cell Biol. 2005 Dec;171(5):785–797. doi: 10.1083/jcb.200502141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bailly-Bechet M, Borgs C, Braunstein A, Chayes J, Dagkessamanskaia A, François JM, Zecchina R. Finding undetected protein associations in cell signaling by belief propagation. Proceedings of the National Academy of Sciences. 2011 Jan;108(2):882–887. doi: 10.1073/pnas.1004751108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yen JY. Finding the k shortest loopless paths in a network. Management Science. 1971;17(11):712–716. [Google Scholar]
- 27.Li H, Kim JH, Koh SS, Stallcup MR. Synergistic effects of coactivators GRIP1 and beta-catenin on gene activation: cross-talk between androgen receptor and Wnt signaling pathways. J Biol Chem. 2004 Feb;279(6):4212–4220. doi: 10.1074/jbc.M311374200. [DOI] [PubMed] [Google Scholar]
- 28.Knudsen KE, Cavenee WK, Arden KC. D-type cyclins complex with the androgen receptor and inhibit its transcriptional transactivation ability. Cancer Res. 1999 May;59(10):2297–2301. [PubMed] [Google Scholar]
- 29.Croft D, O’Kelly G, Wu G, Haw R, Gillespie M, Matthews L, Caudy M, Garapati P, Gopinath G, Jassal B, Jupe S, Kalatskaya I, Mahajan S, May B, Ndegwa N, Schmidt E, Shamovsky V, Yung C, Birney E, Hermjakob H, D’Eustachio P, Stein L. Reactome: a database of reactions, pathways and biological processes. Nucleic Acids Research. 2011 Jan;39:D691–D697. doi: 10.1093/nar/gkq1018. Database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Research. 2012 Jan;40:D109–114. doi: 10.1093/nar/gkr988. Database issue. [DOI] [PMC free article] [PubMed] [Google Scholar]


