Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Feb 13.
Published in final edited form as: Gait Posture. 2016 Jun 24;49:136–143. doi: 10.1016/j.gaitpost.2016.06.031

Predicting Tibiotalar and Subtalar Joint Angles from Skin-Marker Data with Dual-Fluoroscopy as a Reference Standard

Jennifer A Nichols a, Koren E Roach a,b, Niccolo M Fiorentino a, Andrew E Anderson a,b,c,d,*
PMCID: PMC5810542  NIHMSID: NIHMS916506  PMID: 27414041

Abstract

Evidence suggests that the tibiotalar and subtalar joints provide near six degree-of-freedom (DOF) motion. Yet, kinematic models frequently assume one DOF at each of these joints. In this study, we quantified the accuracy of kinematic models to predict joint angles at the tibiotalar and subtalar joints from skin-marker data. Models included 1 or 3 DOF at each joint. Ten asymptomatic subjects, screened for deformities, performed 1.0 m/s treadmill walking and a balanced, single-leg heel-rise. Tibiotalar and subtalar joint angles calculated by inverse kinematics for the 1 and 3 DOF models were compared to those measured directly in vivo using dual-fluoroscopy. Results demonstrated that, for each activity, the average error in tibiotalar joint angles predicted by the 1 DOF model were significantly smaller than those predicted by the DOF model for inversion/eversion and internal/external rotation. In contrast, neither model consistently demonstrated smaller errors when predicting subtalar joint angles. Additionally, neither model could accurately predict discrete angles for the tibiotalar and subtalar joints on a per-subject basis. Differences between model predictions and dual-fluoroscopy measurements were highly variable across subjects, with joint angle errors in at least one rotation direction surpassing 10° for 9 out of 10 subjects. Our results suggest that both the 1 and 3 DOF models can predict trends in tibiotalar joint angles on a limited basis. However, as currently implemented, neither model can predict discrete tibiotalar or subtalar joint angles for individual subjects. Inclusion of subject-specific attributes may improve the accuracy of these models.

Keywords: ankle, hindfoot, dynamic imaging, inverse kinematics, motion capture

1 Introduction

The complex, interrelated motion of the tibiotalar and subtalar joints is a critical component of the foot and ankle. The tibiotalar joint provides the primary means for dorsiflexion/plantarflexion during gait, while the subtalar joint undergoes inversion/eversion, facilitating forward progression of the center of pressure from heel-strike to late stance [1, 2]. Based on these canonical descriptions, biomechanical models frequently assign a single degree-of-freedom (DOF) to each joint, with dorsiflexion/plantarflexion and inversion/eversion defining the tibiotalar and subtalar joints, respectively (e.g., [3–7]). These single DOF models, in combination with inverse kinematics, are widely used. However, investigators rarely estimate independent tibiotalar and subtalar articulation, as reflective skin markers cannot be used to directly measure articulation of these joints in the absence of a suitable marker location for the talus [6, 8]. Instead, articulation of the hindfoot is typically represented as movement of the calcaneus relative to the tibia (e.g., [9–11]). A limitation of this typical representation is that it does not discern how injuries or disease states disproportionately affect articulation of the tibiotalar and subtalar joints. Dynamic imaging techniques, including computed tomography (CT), magnetic resonance imaging, and dual-fluoroscopy have been employed to measure kinematics of the tibiotalar and subtalar joints independently (e.g., [12–16]). However, these methodologies are not widely available and involve time intensive data post-processing, making them less practical than skin-maker motion analysis for studies involving large sample sizes.

Biomechanical models that incorporate multiple DOF at the tibiotalar and subtalar joints may have the ability to predict independent kinematics for these joints using skin-maker data and standard inverse kinematic techniques. However, to our knowledge, prior studies have not assessed the accuracy of joint angle predictions from inverse kinematic simulations using multi6 DOF models versus those using 1 DOF models. Moreover, the accuracy of such predictions has not been previously assessed by direct comparison to in vivo measurements.

The objective of this study was to compare joint angles predicted from inverse kinematic simulations using 1 and 3 DOF models to a reference standard. Here, the 1 DOF model assumed two hinge joints for the tibiotalar and subtalar joints, offering dorsiflexion/plantarflexion and inversion/eversion, respectively, while the 3 DOF model assumed that both joints could undergo rotations about three axes. Joint angle predictions from each model were derived from only skinmarker data, and then compared to joint angles of the same subjects measured in vivo using a validated dual-fluoroscopy system.

2 Methods

2.1 Subjects

Ten control subjects (5 male; age 30.9±7.2 years; height 1.72±0.11 m; weight 70.2±15.9 kg) participated in this study under informed consent and ethics board approval (University of Utah, IRB#65620). Each subject was screened to ensure no history of foot or ankle disorders. Radiographs of both feet were acquired and screened for varus/valgus hindfoot malalignment, osteophytes, and/or osteoarthritis as assessed by Kellgren-Lawrence grades greater than 1. All subjects were included given these criteria.

2.2 Skin-Marker Motion Capture & Dual-Fluoroscopy

Skin-marker motion capture and dual-fluoroscopy data of each subject were collected during 1.0 m/s treadmill walking and a balanced, single-leg heel-rise (Fig. 1A). Walking was selected as a common activity. The heel-rise was chosen to examine a large range of dorsiflexion/plantarflexion. Skin-marker data was spatially and temporally synced to the dual-fluoroscopy data using an external trigger and custom calibration cube [16]. The limited field-of-view (FOV) of the dual-fluoroscopy system could not capture an entire stance phase of gait during treadmill walking [16]. Thus, toe-off and heel-strike were imaged separately and analyzed as distinct activities. One foot (6 right, 4 left) was imaged for each subject. Two trials were collected for each subject and activity (i.e., 2 toe-off, 2 heel-strike, and 2 heel-rise trials). Across all subjects, four trials were excluded (3 heel-rise, 1 toe-off) due to missing data. At least one trial per activity and subject was available for analysis.

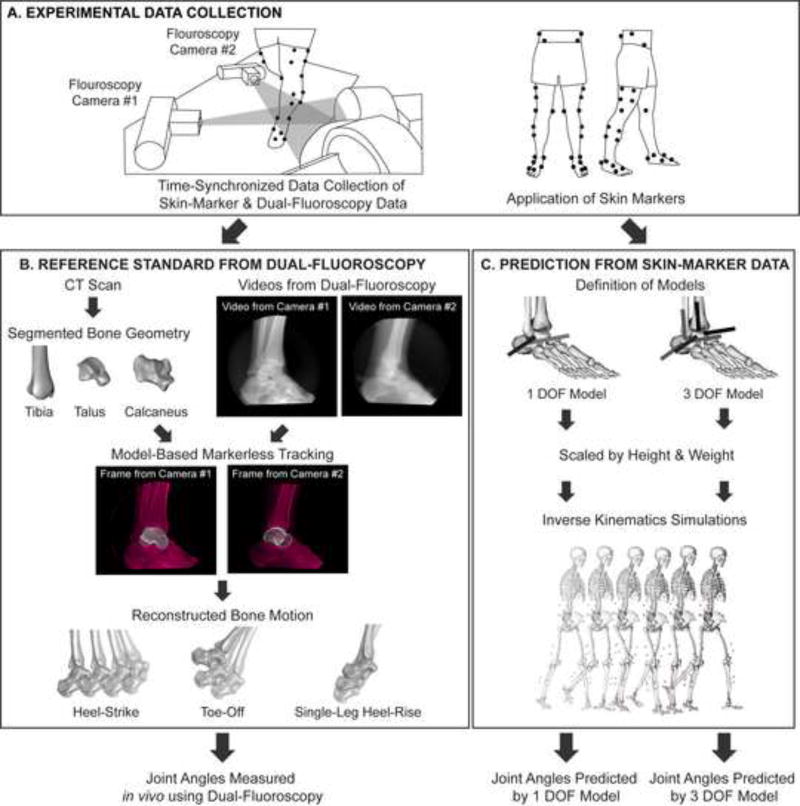
Figure 1.

Figure 1

Open in a new tab

Flowchart of experimental and computational methods. (A) For each subject, experimental skin-marker data and dual-fluoroscopy data were simultaneously collected. Note, at the foot and ankle, the skin-marker set included markers on the medial and lateral malleoli, calcaneal tuberosity, dorsal aspects of the second and fifth phalanxes, dorsal web space between the fourth and fifth metatarsals, and the dorsal-medial aspect of the first metatarsal head. (B) Using only the skin-marker data, tibiotalar and subtalar joint angles were predicted from inverse kinematic simulations using the 1 DOF and 3 DOF models. (C) Independently, tibiotalar and subtalar joint angles were measured using dual-fluoroscopy. The joint angles predicted from skin-marker data were then compared to those measured using dual-fluoroscopy.

Skin-marker motion capture data of both lower extremities was collected at 250–300 Hz using a 10-camera system (Vicon Motion Systems, Oxford, UK). Reflective skin markers were affixed to each subject using a modified Helen-Hayes marker set [17] to track the pelvis, thigh, calf, and foot segments (Fig. 1A). All marker trajectories were processed in Nexus (v. 1.8.5, Vicon Motion Systems, Oxford, UK). Gaps were filled using a spline fitting algorithm. Trajectories were low-pass filtered at 6 Hz.

Dual-fluoroscopy data of the hindfoot were collected as described previously [16]. To enable post-processing of the dual-fluoroscopy data (Fig. 1B), a CT scan (SOMATOM Definition AS, Siemens Medical Solutions, Malvern, PA) was acquired from mid-tibia to toe-tips for each subject at 1.0 mm slice thickness, 366±65.2 mm FOV, 512×512 acquisition matrix, 100 kV, and 16–73 mAs [16]. CT images were segmented using software (Amira 5.5, Visage Imaging, San Diego, CA) to generate 3D bone surfaces [16]. Positions of the tibia, talus, and calcaneus in each dual-fluoroscopy data frame were then determined semi-automatically using model-based markerless tracking (MBT) [18]. The error of MBT for the described dualfluoroscopy system was less than 1 mm [16]. Positions calculated by MBT were smoothed with a fourth-order low-pass Butterworth filter. A residual analysis method [19] was used to select a cutoff frequency of 10 Hz. A landmark-based approach defined coordinate systems for the tibia, talus, and calcaneus [16].

2.3 Inverse Kinematic Models

Both the 1 and 3 DOF models were based on a validated model of the lower limb [3]. The models included only generic bone geometry and joint kinematics (Fig. 1C). In the 1 DOF model, the tibiotalar joint included one axis of rotation defining dorsiflexion/plantarflexion, while the subtalar joint included one axis of rotation defining inversion/eversion. This resulted in 2 DOF across the ankle and hindfoot. Both axes were based on cadaveric experiments [20]. In the 3 DOF model, the ankle and hindfoot were defined as a series of 3 DOF joints. Thus, both the tibiotalar and subtalar joints included three intersecting axes of rotation, which separately defined dorsiflexion/plantarflexion, inversion/eversion, and internal/external rotation. This resulted in 6 DOF across the ankle and hindfoot. The tibiotalar joint axes were parallel to the subtalar joint axes. The orientation of the dorsiflexion/plantarflexion axes and the inversion/eversion axes were defined to be equivalent to those in the 1 DOF model, while the orientation of the internal/external rotation axis was defined as the cross product of the other two axes. These definitions meant that an inverse kinematics problem could theoretically be solved using the exact same rotations about the tibiotalar dorsiflexion/plantarflexion and subtalar inversion/eversion axes in the 1 and 3 DOF models.

2.4 Calculation of Joint Angles

To predict tibiotalar and subtalar joint angles using only skin-marker data, inverse kinematic simulations were performed in OpenSim (v. 3.2, [21]) using the 1 and 3 DOF models scaled to each subject’s height and weight (Fig. 1C). This inverse kinematics approach calculates joint angles by minimizing the weighted least squares error between the modeled and measured skin-marker positions [21]. Simulations were performed separately for each combination of model, subject, activity, and trial (106 simulations in total). Joint angles were calculated from inverse kinematics for the time period where skin marker data were collected, which typically included several seconds of data both before and after dual-fluoroscopy images were acquired. Simulation results were then truncated to analyze only the frames for which dual-fluoroscopy data was also available. The output of each simulation was joint angles defined about the modeled axes of rotation. To enable direct comparison between joint angles about different axes of rotation, all angles were decomposed into components about a standard anatomical reference frame (i.e., dorsiflexion/plantarflexion, inversion/eversion, and internal/external rotation defined as rotations about the medial/lateral, anterior/posterior, and superior/inferior axes, respectively). Note that because the modeled joint axes were not aligned with the anatomical planes (Fig. 1C), decomposing a rotation about any joint axis results in rotations about each anatomical plane.

To define a reference standard independent of the inverse kinematic simulations, tibiotalar and subtalar joint angles were calculated using the dual-fluoroscopy data for each subject, activity, and trial (Fig. 1B). Specifically, using previously described coordinate systems [16] that were modified to match OpenSim sign conventions, homogeneous transformation matrices were defined to describe the motion of the tibia, talus, and calcaneus. Tibiotalar and subtalar joint angles were then defined as roll-pitch-yaw angles derived from the transformation matrices respectively defining the position of the talus relative to the tibia and the calcaneus relative to the talus. Importantly, this method yields joint angles defined relative to the same standard anatomical reference frame as the joint angles predicted using inverse kinematics.

To allow joint angle comparisons across subjects, skin-marker motion capture and dualfluoroscopy data for each trial were normalized based on activity. For walking trials, skin-marker data defined gait events [22]; heel-strike and toe-off of the imaged foot defined 0 and 100 percent of stance, respectively. For heel-rise trials, initial movement, maximum plantarflexion, and final movement of the tibiotalar joint as measured by dual-fluoroscopy defined 0, 50, and 100 percent of heel-rise, respectively. Normalization resulted in joint angle versus percent activity (i.e., percent stance or percent heel-rise) for each trial.

2.5 Data Analysis and Statistics

For all subjects with multiple trials, across trial repeatability was quantified using root mean square (RMS) error. This analysis ensured that each method to calculate joint angles provided consistent results within subjects.

To evaluate the predictive capabilities of the 1 and 3 DOF models, plots of joint angles predicted by the models were assessed qualitatively. Comparisons were made by averaging joint angles from each model and comparing these directly to dual-fluoroscopy results. If the average joint angles predicted by the model were within one standard deviation of the dual-fluoroscopy results, the model was considered to accurately represent in vivo joint motion. Additionally, for each model, the RMS errors between the joint angles predicted by the model and those measured by dual-fluoroscopy were quantified. RMS errors were calculated within each subject and trial, prior to across subject averaging. Paired Student’s t-tests (significance level p<0.05), corrected for multiple comparisons using Holm’s approach [23], determined if the 1 DOF model had a significantly different RMS errors than the 3 DOF model.

To further examine the predictive accuracy of the 1 and 3 DOF models on a per subject basis, joint angles for individual subjects were analyzed using Bland-Altman plots [24]. Here, the mean of the difference defined the average error (or bias), and 1.96 times the standard deviation of the differences defined the 95 percent limits of agreement (i.e., the range in which 95 percent of future measurements are expected to fall). For tibiotalar and subtalar joint angles, we considered limits of agreement less than 5° to be acceptable, as this is within the range of joint angle error that can be measured with a goniometer in the clinical setting [25].

3 Results

The repeatability of the modeling and dual-fluoroscopy methods was similar at the tibiotalar and subtalar joints. Across all activities, directions of motion, and measurement methods, the RMS error (across subject avg. ± st. dev.) between trials ranged from 0.1°±0.1° to 5.6°±2.5° for the tibiotalar joint and 0.6°±0.4° to 4.1°±2.8° for the subtalar joint (Table S1).

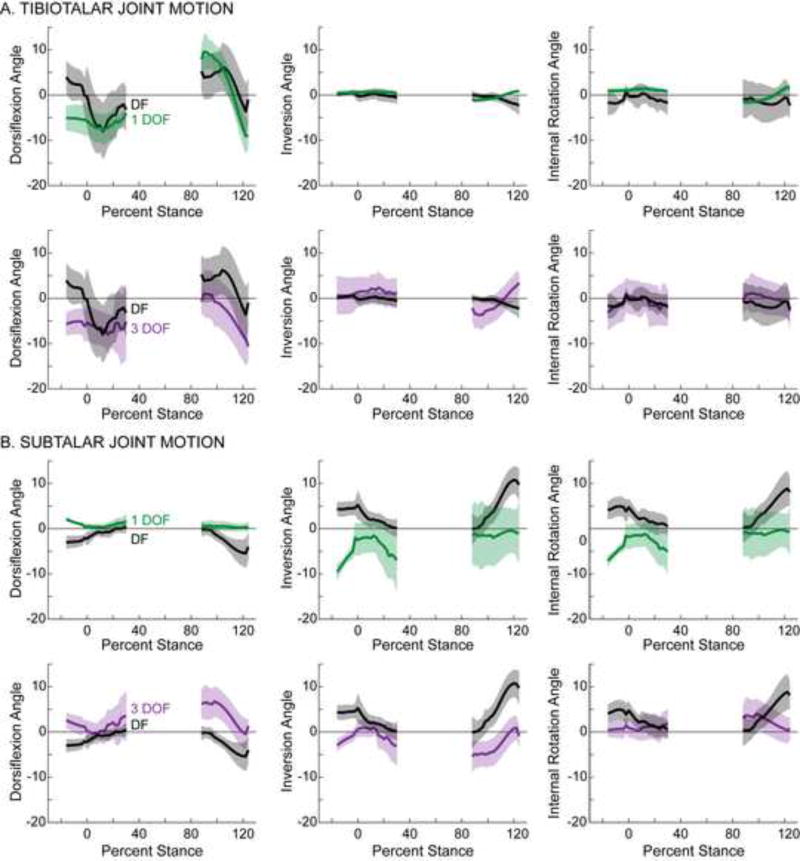
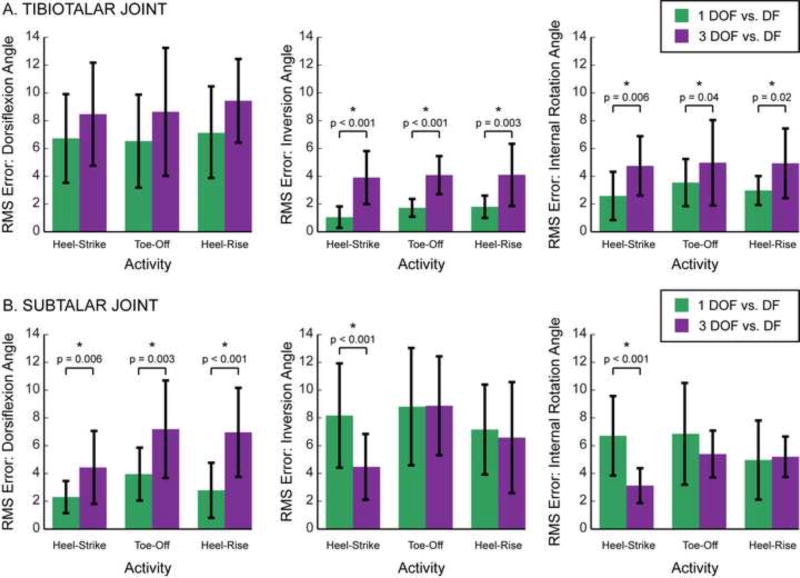
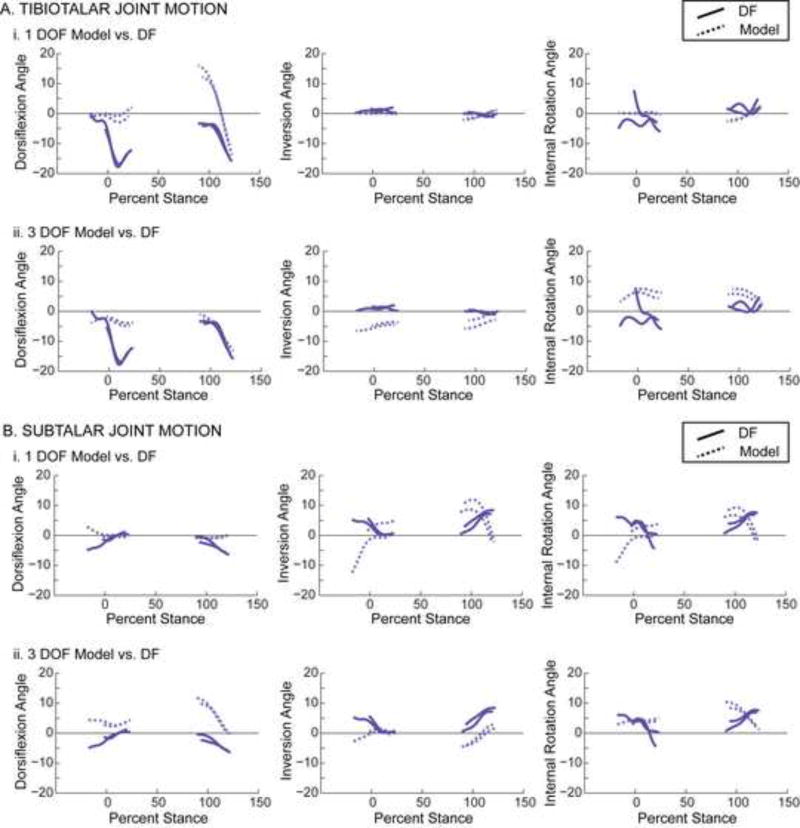
On average, the 1 DOF model represented in vivo tibiotalar joint motion more consistently than the 3 DOF model. During the majority of recorded stance, the average tibiotalar joint angles predicted by the 1 DOF model were within one standard deviation of those measured by dual-fluoroscopy for all rotation directions (Fig. 2A, top). In contrast, the average tibiotalar joint angles predicted by the 3 DOF model were within one standard deviation of those measured by dual-fluoroscopy for only one rotation direction, namely internal/external rotation during the heel-strike and toe-off portions of stance (Fig. 2A, bottom). Similarly, the 1 DOF model also represented tibiotalar joint motion better than the 3 DOF model during heel-rise (Fig. S1A). Across all activities and rotation directions, the RMS errors (across subject avg. ± st. dev.) ranged from 1.1°±0.8° to 7.2°±3.2° for the 1 DOF model and from 3.9°±1.9° to 9.4°±3.0° for the 3 DOF model (Table S2). In terms of RMS error, the 1 DOF model represented in vivo tibiotalar motion more accurately than the 3 DOF model. Here, the RMS errors of the 1 DOF model were significantly smaller than those of the 3 DOF model for both inversion/eversion and internal/external rotation during all activities (Fig. 3A).

Figure 2.

Figure 2

Open in a new tab

Motion of (A) tibiotalar and (B) subtalar joints during the heel-strike and toe-off activities. Joint angles calculated using the 1 DOF model (green) and the 3 DOF model (purple) are plotted separately to facilitate comparison with the joint angles calculated using the experimental dual-fluoroscopy (DF) data (black). Solid lines represent average across subjects. Given that the length of trials varied across subjects, averages were calculated for any region for which data existed for at least 5 subjects. Shaded regions represent one standard deviation. All joint angles are plotted versus the percentage of the stance phase of gait, where 0% represents heel-strike of the imaged foot and 100% represents toe-off of the imaged foot. Dorsiflexion, inversion, and internal rotation are defined as positive.

Figure 3.

Figure 3

Open in a new tab

Root mean square (RMS) errors of the (A) tibiotalar and (B) subtalar joints during each activity. For each model, the RMS errors were calculated between joint angles predicted by the models versus measured experimentally using dual-fluoroscopy. The RMS errors are displayed separately for the 1 DOF (green) and 3 DOF (purple) models. Bars represent average across subjects. Error bars represent one standard deviation, thereby illustrating across subject variability. Asterisks (*) and displayed p-values indicate a significant difference between the RMS errors for the 1 and 3 DOF models.

At the subtalar joint, neither model consistently predicted joint angles measured by dual-fluoroscopy. During stance, the average joint angles predicted by the 1 and 3 DOF models were not within one standard deviation of those measured by dual-fluoroscopy for any rotation direction (Fig. 2B). The 1 DOF model, however, represented average in vivo subtalar motion more accurately than the 3 DOF model during heel-rise, an activity during which very little subtalar motion was observed (Fig. S1B). Across all activities and rotation directions, the RMS errors (across subject avg. ± st. dev.) ranged from 2.3°±1.2° to 8.8°±4.2° for the 1 DOF model and from 3.1°±1.3° to 8.9°±3.6° for the 3 DOF model (Table S2). When examining subtalar motion, the RMS errors associated with the 1 DOF model were significantly less than those of the 3 DOF model for dorsiflexion/plantarflexion during all activities, but significantly greater for inversion/eversion and internal/external rotation during the heel-strike activity (Fig. 3B).

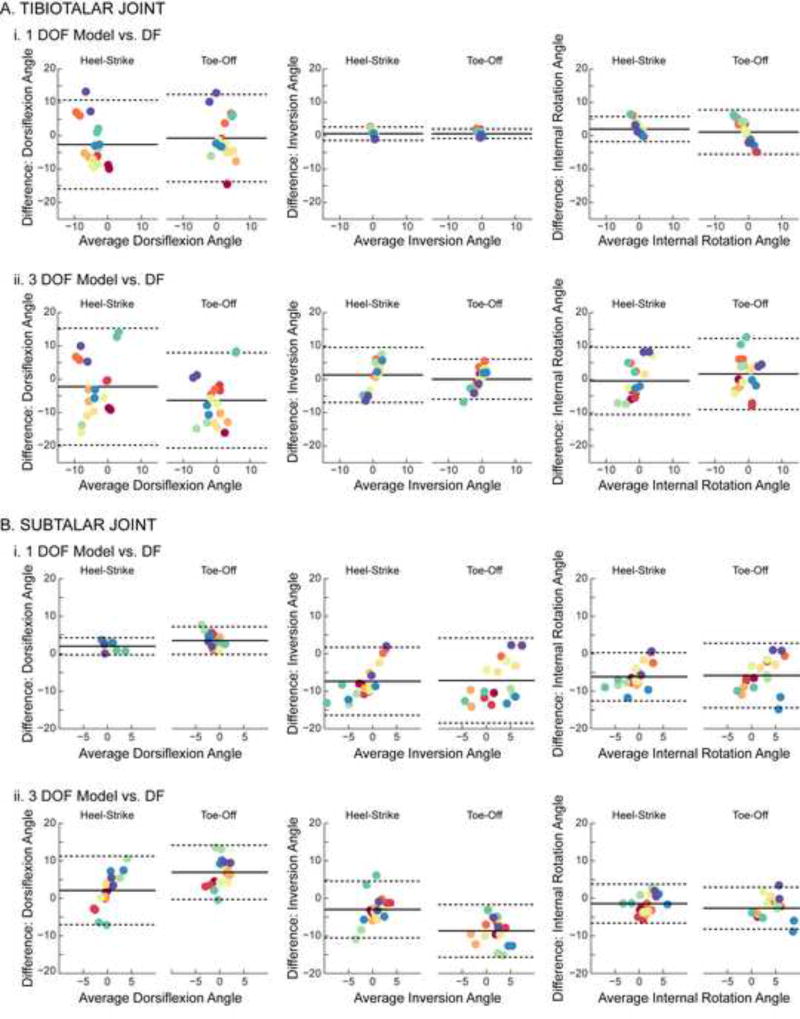
Despite significant differences between RMS errors for the 1 and 3 DOF models, neither model could accurately predict discrete values of joint angles measured by dual-fluoroscopy on a per-subject basis. Specifically, the Bland-Altman analysis indicated that the error between the joint angles estimated by the models and those measured using dual-fluoroscopy exceeded 10° for 9 of 10 subjects during at least one of the activities examined. At the tibiotalar joint, the largest errors for both the 1 and 3 DOF models were observed in the dorsiflexion/plantarflexion angle during heel-strike and toe-off (Fig. 4A) as well as during heel-rise (Fig. S2A), as evidenced by the limits of agreement being widest for these rotation directions. At the subtalar joint, based on a similar assessment of the limits of agreement, the 1 DOF model demonstrated the largest errors for inversion/eversion during heel-strike and toe-off (Fig. 4B-i) as well as during heel-rise (Fig. S2B-i), while the 3 DOF model demonstrated the largest errors for dorsiflexion/plantarflexion during heel-strike and toe-off (Fig. 4B-ii) as well as during heel-rise (Fig. S2B-ii). The fact that the calculated limits of agreement spanned both positive and negative values for heel-strike and toe-off (Table S3) as well as for heel-rise (Table S4) indicated that the 1 and 3 DOF models did not consistently under- or over-estimate the joint angles measured by dual-fluoroscopy. In fact, examination of individual trials demonstrated that the difference between joint angles predicted by the models and measured by dual-fluoroscopy varied substantially in magnitude and direction during heel-strike and toe-off (Fig. 5) as well as during heel-rise (Fig. S3).

Figure 4.

Figure 4

Open in a new tab

Bland-Altman plots of (A) tibiotalar and (B) subtalar joint motion during the heelstrike and toe-off activities. Differences between motions predicted by the models versus measured experimentally using dual-fluoroscopy (DF) are displayed separately for the (i) 1 DOF and (ii) 3 DOF models. Within each trial (unique points) and subject (unique colors), differences were calculated across all collected time points and then averaged. All calculated differences are model minus experimental, thus positive values represent an overestimation by the model. Solid lines represent mean difference (i.e., bias). Dotted lines represent 95% limits of agreement. Dorsiflexion, inversion, and internal rotation are defined as positive.

Figure 5.

Figure 5

Open in a new tab

Motion of (A) tibiotalar and (B) subtalar joints during four separate walking trials (two heel-strike and two toe-off) from a single subject. The displayed subject demonstrated some of the largest tibiotalar joint angle errors, as evidenced in the Bland-Altman analysis (plotted color chosen to be consistent with Bland-Altman plots in Fig. 4). Joint angles calculated using the models (dotted lines) are plotted separately for the (i) 1 DOF and (ii) 3 DOF models to facilitate comparison with the joint angles calculated using the experimental dual-fluoroscopy (DF) data (solid lines). All joint angles are plotted versus the percentage of the stance phase of gait, where 0% represents heel-strike of the imaged foot and 100% represents toe-off of the imaged foot. Dorsiflexion, inversion, and internal rotation are defined as positive.

4 Discussion

This study demonstrates that when using only skin-marker data and inverse kinematic simulations, both 1 and 3 DOF models could predict trends in tibiotalar joint angles measured in vivo on a limited basis. Importantly, neither model was able to predict discrete tibiotalar or subtalar joint angles for individual subjects. Such inaccuracies could negatively influence predictions made by biomechanical models that input joint angles to calculate variables such as joint moments, muscle forces, muscle activations, and joint reaction forces. Overall, our results underscore the importance of selecting kinematic models appropriate for addressing the scientific questions investigated, and motivate additional research to better understand the consequences of assuming simplified kinematic representations for the tibiotalar and subtalar joints.

Our results indicate that the 1 DOF model could predict tibiotalar angles better than the 3 DOF model for the majority of activities and rotation directions analyzed. Thus, incorporation of more DOF at the tibiotalar joint may only serve to decrease predictive accuracy of inverse kinematic models. This conclusion is consistent with studies that describe tibiotalar motion as highly constrained by the bone geometry of and soft tissue surrounding the talar mortise [26–28]. In contrast, neither model was sufficient for representing subtalar motion during gait, an activity with substantial subtalar motion. Some studies have suggested that the subtalar joint offers 6 DOF motion [1, 2, 13]. Thus, a more complex kinematic model that incorporates translational motion may be necessary to eliminate the inaccuracies in predictions of subtalar kinematics. However, further research is necessary to determine whether the kinematic accuracy would actually improve if translations were included. Specifically, skin-marker data alone may not provide the information necessary to predict subtalar translations, as motion of the talus cannot be directly measured by skin markers [6, 8]. Thus, there may be a fine balance between joint model complexity, skin-marker data fidelity, and predictive accuracy.

As currently implemented, utilizing the 1 or 3 DOF models to predict hindfoot motion would require that one accept large errors on a per subject basis. Specifically, the limits of agreement calculated in our study indicate errors of 10° to 20° when estimating tibiotalar and subtalar joint angles for individual subjects, regardless of the model used. Given that the total range of motion for the tibiotalar and subtalar joints measured by dual-fluoroscopy was less than 20° for all rotation directions except tibiotalar dorsiflexion/plantarflexion during heel-rise, such errors would likely be unacceptable for studies aiming to estimate subject-specific hindfoot kinematics. Incorporation of subject-specific parameters, including bone geometry, joint axes of rotation, and coordinate systems, may be a pre-requisite to obtain accurate predictions from inverse kinematic models. Alternatively, categorizing subjects into certain subtypes of hindfoot motion based on natural anatomical variation may be necessary to obtain accurate predictions. These recommendations are supported by previous studies that have suggested that the high variability in reported ankle kinematics may be caused by subject-specific differences in gender, talar tilt, bone morphology, and ligament laxity [29–31], and that anatomical variation in ligament location affects hindfoot motion, thereby creating ankle subtypes requiring careful distinction [32]. In the present study, we did not examine how modeling subject-specific factors influences predictive accuracy. Nevertheless, quantification of the accuracy of 1 and 3 DOF kinematic models, as performed herein, represents an important step toward developing complex hindfoot models that may have increased accuracy.

Supplementary Material

Supplemental

Research Highlights.

  • Tibiotalar and subtalar kinematics were measured in vivo using dual-fluoroscopy

  • 1 and 3 DOF models were used to predict hindfoot kinematics from skin-marker data

  • Joint angles predicted by models were compared directly to dual-fluoroscopy data

  • Both models predicted trends in hindfoot joint angles, but not discrete values

  • Our results underscore the importance of appropriate selection of kinematic models

Acknowledgments

Funding from the National Institutes of Health (R21AR063844, S10RR026565), LS-Peery Discovery Program in Musculoskeletal Restoration, and the American Orthopaedic Foot & Ankle Society (with funding from the Orthopaedic Foot & Ankle Outreach & Education Fund [OEF] and the Orthopaedic Research and Education Foundation [OREF] with designation to the OEF) is gratefully acknowledged. This investigation was also supported by the University of Utah Study Design and Biostatistics Center, with funding in part from the National Center for Research Resources and the National Center for Advancing Translational Sciences, National Institutes of Health, through Grant 5UL1TR001067-02 (formerly 8UL1TR000105 and UL1RR025764). The content is solely the responsibility of the authors and does not necessarily represent the official views of these funding sources. We thank K. Bo Foreman, Justine Goebel, Ashely Kapron, Madeline Singer, Bibo Wang, and Austin West for assistance collecting and processing the experimental data, and Gregory Stoddard for statistical consultation. We also thank Glen Litchwark and Tim Dorn for their open-source OpenSim toolboxes, which were adapted to facilitate batch processing of our computer simulations.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Perry J. Anatomy and biomechanics of the hindfoot. Clinical orthopaedics and related research. 1983 Jul-Aug;:9–15. [PubMed] [Google Scholar]
  • 2.Piazza SJ. Mechanics of the subtalar joint and its function during walking. Foot and ankle clinics. 2005;10:425–42. doi: 10.1016/j.fcl.2005.04.001. [DOI] [PubMed] [Google Scholar]
  • 3.Arnold EM, Ward SR, Lieber RL, Delp SL. A model of the lower limb for analysis of human movement. Annals of biomedical engineering. 2010;38:269–79. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Lewis GS, Piazza SJ, Sommer IHJ. In Vitro Assessment of a Motion-Based Optimization Method for Locating the Talocrural and Subtalar Joint Axes. Journal of Biomechanical Engineering. 2006;128:596–603. doi: 10.1115/1.2205866. [DOI] [PubMed] [Google Scholar]
  • 5.Reinbolt JA, Schutte JF, Fregly BJ, Koh BI, Haftka RT, George AD, et al. Determination of patient-specific multi-joint kinematic models through two-level optimization. Journal of biomechanics. 2005;38:621–6. doi: 10.1016/j.jbiomech.2004.03.031. [DOI] [PubMed] [Google Scholar]
  • 6.Scott SH, Winter DA. Talocrural and talocalcaneal joint kinematics and kinetics during the stance phase of walking. Journal of biomechanics. 1991;24:743–52. doi: 10.1016/0021-9290(91)90338-n. [DOI] [PubMed] [Google Scholar]
  • 7.van den Bogert AJ, Smith GD, Nigg BM. In vivo determination of the anatomical axes of the ankle joint complex: an optimization approach. Journal of biomechanics. 1994;27:1477–88. doi: 10.1016/0021-9290(94)90197-x. [DOI] [PubMed] [Google Scholar]
  • 8.MacWilliams BA, Cowley M, Nicholson DE. Foot kinematics and kinetics during adolescent gait. Gait & posture. 2003;17:214–24. doi: 10.1016/s0966-6362(02)00103-0. [DOI] [PubMed] [Google Scholar]
  • 9.Bruening DA, Cooney KM, Buczek FL. Analysis of a kinetic multi-segment foot model. Part I: Model repeatability and kinematic validity. Gait & posture. 2012;35:529–34. doi: 10.1016/j.gaitpost.2011.10.363. [DOI] [PubMed] [Google Scholar]
  • 10.Kidder SM, Abuzzahab FS, Jr, Harris GF, Johnson JE. A system for the analysis of foot and ankle kinematics during gait. IEEE transactions on rehabilitation engineering : a publication of the IEEE Engineering in Medicine and Biology Society. 1996;4:25–32. doi: 10.1109/86.486054. [DOI] [PubMed] [Google Scholar]
  • 11.Martelli S, Valente G, Viceconti M, Taddei F. Sensitivity of a subject-specific musculoskeletal model to the uncertainties on the joint axes location. Computer methods in biomechanics and biomedical engineering. 2015;18:1555–63. doi: 10.1080/10255842.2014.930134. [DOI] [PubMed] [Google Scholar]
  • 12.Campbell KJ, Wilson KJ, LaPrade RF, Clanton TO. Normative rearfoot motion during barefoot and shod walking using biplane fluoroscopy. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 2014 doi: 10.1007/s00167-014-3084-4. [DOI] [PubMed] [Google Scholar]
  • 13.de Asla RJ, Wan L, Rubash HE, Li G. Six DOF in vivo kinematics of the ankle joint complex: Application of a combined dual-orthogonal fluoroscopic and magnetic resonance imaging technique. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2006;24:1019–27. doi: 10.1002/jor.20142. [DOI] [PubMed] [Google Scholar]
  • 14.Koo S, Lee KM, Cha YJ. Plantar-flexion of the ankle joint complex in terminal stance is initiated by subtalar plantar-flexion: A bi-planar fluoroscopy study. Gait & posture. 2015;42:424–9. doi: 10.1016/j.gaitpost.2015.07.009. [DOI] [PubMed] [Google Scholar]
  • 15.Sheehan FT, Seisler AR, Siegel KL. In vivo talocrural and subtalar kinematics: a noninvasive 3D dynamic MRI study. Foot & ankle international. 2007;28:323–35. doi: 10.3113/FAI.2007.0323. [DOI] [PubMed] [Google Scholar]
  • 16.Wang B, Roach KE, Kapron AL, Fiorentino NM, Saltzman C, Singer M, et al. Accuracy and Feasibility of High-Speed Dual Fluoroscopy and Model-Based Tracking to Measure In Vivo Ankle Arthrokinematics. Gait & posture. 2015;41:888–93. doi: 10.1016/j.gaitpost.2015.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Kadaba MP, Ramakrishnan HK, Wootten ME. Measurement of lower extremity kinematics during level walking. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 1990;8:383–92. doi: 10.1002/jor.1100080310. [DOI] [PubMed] [Google Scholar]
  • 18.Bey MJ, Zauel R, Brock SK, Tashman S. Validation of a new model-based tracking technique for measuring three-dimensional, in vivo glenohumeral joint kinematics. J Biomech Eng. 2006;128:604–9. doi: 10.1115/1.2206199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Winter DA. Biomechanics and Motor Control of Human Movement. 4. Hoboken, New Jersey: John Wiley & Sons, Inc.; 2005. [Google Scholar]
  • 20.Inman VT. The Joints of the Ankle. Baltimore: Williams & Wilkins; 1976. [Google Scholar]
  • 21.Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, et al. OpenSim: opensource software to create and analyze dynamic simulations of movement. IEEE transactions on bio-medical engineering. 2007;54:1940–50. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
  • 22.Roach KE, Wang B, Kapron AL, Fiorentino NM, Saltzman C, Foreman KB, et al. In-vivo Kinematics of the Tibiotalar and Subtalar Joints in Asymptomatic Subjects: A High-Speed Dual Fluoroscopy Study. Journal of Biomechanical Engineering. doi: 10.1115/1.4034263. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
  • 24.Bland JM, Altman DG. Measuring agreement in method comparison studies. Statistical methods in medical research. 1999;8:135–60. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]
  • 25.Rome K, Cowieson F. A reliability study of the universal goniometer, fluid goniometer, and electrogoniometer for the measurement of ankle dorsiflexion. Foot & ankle international. 1996;17:28–32. doi: 10.1177/107110079601700106. [DOI] [PubMed] [Google Scholar]
  • 26.Leardini A, O'Connor JJ, Catani F, Giannini S. A geometric model of the human ankle joint. Journal of biomechanics. 1999;32:585–91. doi: 10.1016/s0021-9290(99)00022-6. [DOI] [PubMed] [Google Scholar]
  • 27.Leardini A, O'Connor JJ, Catani F, Giannini S. Kinematics of the human ankle complex in passive flexion; a single degree of freedom system. Journal of biomechanics. 1999;32:111–8. doi: 10.1016/s0021-9290(98)00157-2. [DOI] [PubMed] [Google Scholar]
  • 28.Watanabe K, Kitaoka HB, Berglund LJ, Zhao KD, Kaufman KR, An KN. The role of ankle ligaments and articular geometry in stabilizing the ankle. Clinical biomechanics. 2012;27:189–95. doi: 10.1016/j.clinbiomech.2011.08.015. [DOI] [PubMed] [Google Scholar]
  • 29.Imhauser CW, Siegler S, Udupa JK, Toy JR. Subject-specific models of the hindfoot reveal a relationship between morphology and passive mechanical properties. Journal of biomechanics. 2008;41:1341–9. doi: 10.1016/j.jbiomech.2007.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Schwarz NA, Kovaleski JE, Heitman RJ, Gurchiek LR, Gubler-Hanna C. Arthrometric measurement of ankle-complex motion: normative values. Journal of athletic training. 2011;46:126–32. doi: 10.4085/1062-6050-46.2.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Wilkerson RD, Mason MA. Differences in men's and women's mean ankle ligamentous laxity. The Iowa orthopaedic journal. 2000;20:46–8. [PMC free article] [PubMed] [Google Scholar]
  • 32.Sarrafian SK. Biomechanics of the subtalar joint complex. Clinical orthopaedics and related research. 1993:17–26. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental
NIHMS916506-supplement-Supplemental.docx (1.2MB, docx)

RESOURCES