Abstract
Chemical exchange saturation transfer (CEST) is a novel contrast mechanism and it is gaining increasing popularity as many promising applications have been proposed and investigated. Fast and quantitative CEST imaging techniques are further needed in order to increase the applicability of CEST for clinical use as well as to derive quantitative physiological and biological information. Steady-state methods for fast CEST imaging have been reported recently. Here, we observe that an extreme case of these methods is a balanced steady-state free precession (bSSFP) sequence. The bSSFP in itself is sensitive to the exchange processes; hence, no additional saturation or preparation is needed for CEST-like data acquisition. The bSSFP experiment can be regarded as observation during saturation, without separate saturation and acquisition modules as used in standard CEST and similar experiments. One of the differences from standard CEST methods is that the bSSFP spectrum is an XY-spectrum not a Z-spectrum. As the first proof-of-principle step, we have implemented the steady state bSSFP sequence for chemical exchange detection (bSSFPX) and verified its feasibility in phantom studies. These studies have shown that bSSFPX can achieve exchange-mediated contrast comparable to the standard CEST experiment. Therefore, the bSSFPX method has a potential for fast and quantitative CEST data acquisition.
Keywords: CEST, Spin-lock, bSSFP, Steady state, T1ρ
Graphical Abstract
1. Introduction
Chemical exchange saturation transfer (CEST) as a new contrast mechanism in MRI is gaining popularity [1, 2]. It employs selective saturation of protons in a specific chemical group which transfers to water via chemical exchange to (i) indirectly visualize the low concentration metabolites which are not observable in conventional MR scans and (ii) indicate quantitative environmental parameters such as pH. Many promising preclinical and clinical applications have been investigated using CEST imaging techniques including but not limited to: brain tumor imaging [3–6], brain ischemia [7], prostate cancer [8], breast cancer [9, 10], kidney pH measurement [11] and cartilage quality assessment [12, 13].
However, a successful translation of CEST into clinical applications is hampered in part by its time-consuming acquisition. Typically, the CEST pulse sequence utilizes a long saturation pulse followed by data acquisition. To correct for the artifacts due to B0 inhomogeneity, and/or to acquire information about multiple exchanging sites, CEST often employs a series of off-resonance saturation pulses to acquire the so-called Z-spectrum. Moreover, exchange rate quantification methods that lead to metabolite distribution maps or pH measurements require several repetitions of the entire experiment with different saturation time or power [14]. Hence, the already time-consuming whole Z-spectrum acquisition becomes even more time-consuming for exchange rate quantification and 3D CEST imaging. Therefore, seeking faster alternative ways for CEST data acquisition is highly desired.
Recently, steady-state methods for fast CEST imaging were reported, where the long saturation irradiation was split into short parts with intermittent acquisition [15, 16]. In steady-state methods, the data acquired first (with shorter saturation time) fills the outer portion of the k-space and the data acquired later (with longer saturation time) fills the center of the k-space. By doing so, the acquisition time is shortened. The extreme case of this approach would be a train of RF pulses with intervals for data acquisition. We observe that this is, in essence, a balanced steady-state free precession (bSSFP or FISP) sequence: a train of RF pulses interleaved with balanced gradients for image acquisition.
At the core of our work is the realization that the bSSFP sequence in itself is sensitive to the exchange processes, hence no additional saturation, preparation or separate detection pulses are needed to create the CEST effect. Here, the bSSFP spectral profile is collected at multiple frequency offsets. The analysis of the resulting profile provides information about the exchanging moieties, similar to CEST or off-resonance T1ρ experiments. This method, using bSSFP sequence for chemical exchange detection shall be dubbed here bSSFPX (bSSFP for eXchange detection). bSSFPX provides a new way for CEST data acquisition: the acquisition is performed during the saturation. Thus, it may speed up the CEST experiment. Also, the bSSFPX method should allow acquisition while the system approaches the steady state, thus providing the data for QUEST-like quantification [14] in a “single-shot”. Notably, in this method we are observing the XY-component of the magnetization and not the Z-component, as is standard in Z-spectroscopy.
Properties of equally spaced pulses have been investigated since the 1960s [17]. Specifically, theory and experiments performed in solid-state NMR had shown that the train of equally spaced pulses creates an effective lock field, similar in its action to the continuous-wave (CW) lock [18–20]. Two cases were thoroughly investigated: with same phase [19] and with 180° phase advance between the pulses [18]. It has been shown that this pulsed spin lock affects the dipolar interaction in the way similar to the application of the CW irradiation.
Since the introduction by Carr in 1958 [21], the basic principles and theory of the steady state signals (FISP or SSFP) generated by the repetitive pulses, has been explored in numerous publications, including the iconic work by Freeman et.al. [22]. Since the introduction of FISP or SSFP imaging combined with balanced gradients (TrueFISP or bSSFP), numerous studies investigated the sequence properties [23–35]. To name a few examples, bSSFP was combined with inversion recovery to continuously acquire data for T1 quantification [26]. The sequence has been used for fast T2 mapping (DESPOT2 [28]). The multicomponent T1 and T2 relaxation in bSSFP has been investigated (mcDESPOT [29]). Miller et.al. investigated asymmetries observed in bSSFP [36]. Bieri and Scheffler have investigated properties of bSSFP to modulate magnetization transfer effects [37]. However, to the best of our knowledge, this is the first time that the spin-locking and off-resonance saturation-transfer properties of the imaging sequence are investigated, thus explicitly realizing and exploring the analogous nature of bSSFP and CEST/T1ρ experiments.
In this paper, we are implementing the bSSFPX method in the steady state. We are demonstrating the ability of bSSFPX to create CEST-like effects by theoretical derivation, simulation and phantom study. We are comparing the results of a bSSFPX experiment with that of the standard pulsed CEST experiment. The comparison demonstrates that the bSSFPX method provides contrast comparable to the standard method. Thus, bSSFPX is a highly promising approach to achieve fast and quantitative CEST imaging.
2. Theory
Here, we present the description of the magnetization dynamics under the influence of the train of RF pulses using effective field formalism, thus bridging bSSFP with CEST/T1ρ. First, the detailed derivation will be given assuming no exchange. Second, the approximation of the exchange contribution will be discussed. The more accurate and quantitative description of exchange influence will be presented in a subsequent publication.
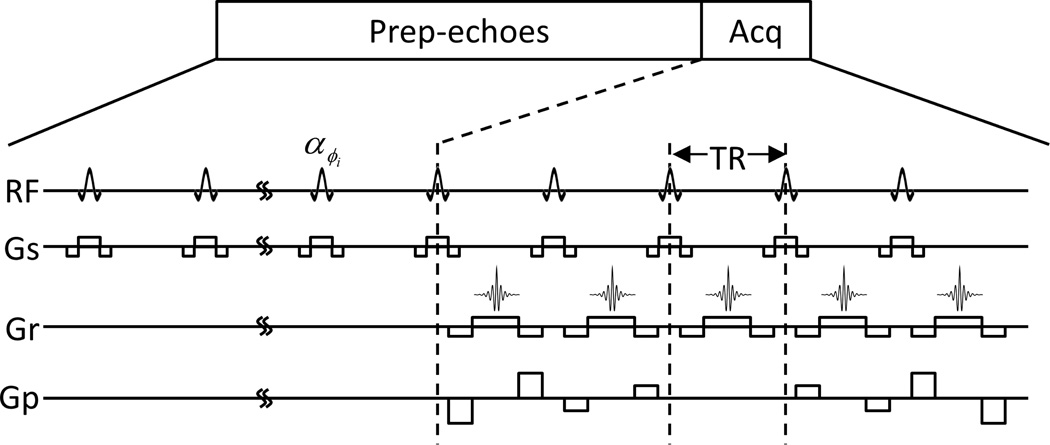
The pulse sequence for 2D steady-state bSSFPX (ss-bSSFPX) imaging is shown in Fig. 1: a large number of prep-echoes followed by a single imaging acquisition. The prep-echoes are to ensure that the observed magnetization is in the steady state. The basic repetitive nth unit of this sequence is [αϕ0+(n−1)Δϕ − TR], where α is the flip angle, ϕ0 is the phase of the first RF and Δϕ is the phase advance between two consecutive RF pulses. In a typical bSSFP experiment, Δϕ = 0 or π. Since the sequence consists of a number of the repeating basic units, the phase advance can be treated as the frequency offset by an amount Δϕ/(2πTR) [38]. In the bSSFP, all the gradients are balanced over one TR. In other words, the net gradient over one TR is 0. Hence, the influence of gradients can be ignored and the evolution of magnetization at the echo times or the end of each unit is governed solely by RF [27]. For simplicity and without loss of generality, the following derivations assume ϕ0 = 0 which makes the basic unit of the bSSFP sequence [α(n−1)Δϕ − TR].
Figure 1.
The schematic for the 2D steady-state bSSFPX pulse sequence. Prep-echoes: preparation echoes needed to reach the steady state. Acq: acquisition.
The signals acquired by a bSSFP sequence are from Mxy. Therefore, the bSSFPX method is observing and analyzing an XY-spectrum for the CEST effect.
2.1. Effective field
First, consider the simplest case in which only one pool is present and TR << T1 & T2 and the influence of relaxation can be ignored. In the absence of relaxation, the propagation of magnetization over one cycle is given by:
| (1) |
where Mn+1 and Mn are the magnetization vectors at the end of n+1 and n cycle. Rz (θ) and Rx (α) are the standard z- and x-rotation matrices respectively. θ = 2πΔwTR − Δϕ is the precession angle, where Δw is the off-resonance [30, 38]. The propagation of the magnetization is given by two consecutive rotations and thus, in accordance with Euler theorem, can be represented by a single rotation. The composite rotation is described by the directionality vector e⃑ and the rotation angle Φ [30]. To be specific, e⃑ represents the axis of rotation about which Mn rotates by the angle Φ. Using Euler parameters, the directionality vector and the rotation angle are:
| (2) |
where is the unit vector in the same direction as e⃑, hence: and . In addition, using Eq. 2, the angle Θ between the effective field and the z-axis can be found:
| (3) |
Thus, the effective field is given by:
| (4) |
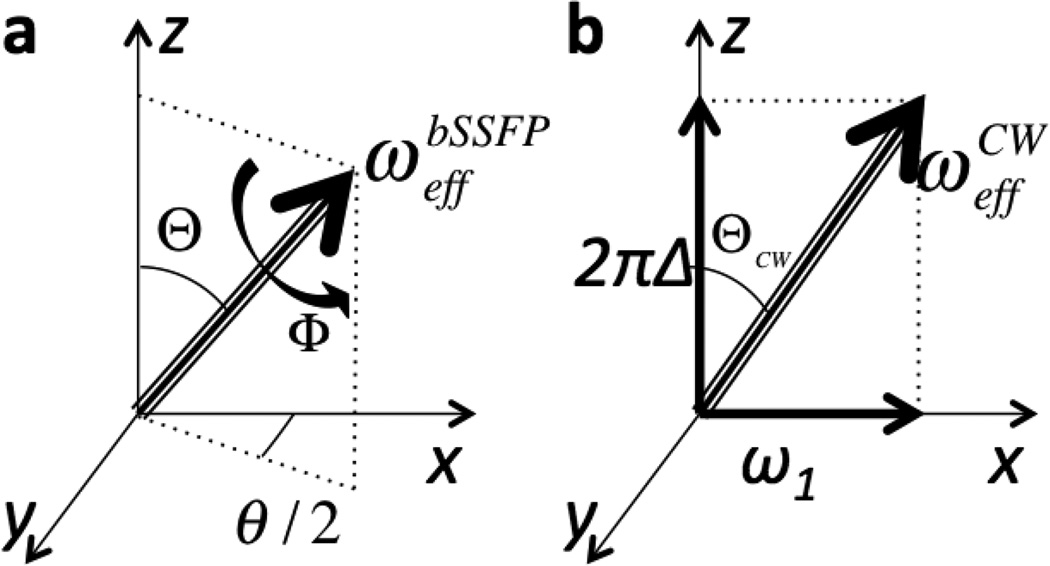
This is illustrated in Fig. 2a. The effective field “strength” (in radians per second) is given by:
| (5) |
i.e. precession over time TR will result in rotation by angle Φ.
Figure 2.
The effective RF fields generated during (a) bSSFP experiment and (b) standard CEST/T1ρ experiment. In CEST/T1ρ the effective field depends on the RF off-resonance value, Δw, and RF intensity, ω1. In bSSFP the effective field can be described by two angles: Θ and Φ, that are functions of the flip angle, TR and off-resonance value used in bSSFP. θ/2 is the angle between the x-axis and the projection of the effective field into the xy-plane.
This effective field governs the magnetization dynamics, in accordance with the Bloch equations. The effective field in the bSSFP sequence can be written in matrix notation as:
| (6) |
where Ix, Iy and Iz are standard 3-dimentional space basis matrices and Ixy = Ix cos (θ/2) + Iy sin (θ/2). An alternative form for Heff using the components of u⃑ is given in Appendix A.
For comparison, in the standard CW spin-lock or saturation-transfer experiment the effective field can be written similar to Eq. 4:
| (7) |
where the effective field strength is given by . In the CW case, the directionality vector is u⃑CW = (sinΘCW cosφ,sinΘCW sinφ,cosΘCW)T, with ΘCW = arctan (ω1/2πΔw) where ω1 is the RF intensity and φ is the RF phase. In the most common case the RF is along x axis with φ = 0, as illustrated in Fig. 2b.
Comparison between Eqs. 4 and 7 demonstrates the complete analogy between bSSFP and CW application (as illustrated in Fig. 2). The key difference is: while in the CW case the effective field strength as a function of off-resonance is a non-periodic function (Eq. 7), in the bSSFP case (Eq. 5) it is cyclic with the period 2π/TR (as can be seen from Φ dependence on α and θ in Eq. 2). Thus, it will lead to RF profile with multiple saturation bands, the known characteristic of bSSFP spectrum.
Assuming small effective field strengths, hence, small Φ, the effective field equation, Eq. 4 can be rewritten as:
| (8) |
In addition, for small flip angle and chemical shifts, the Eq. 8 transforms to:
| (9a) |
| (9b) |
Within a sign, Eqs. 9 agree with the expressions derived for the spin-lock experiment using a train of RF pulses: pulses of same phase in Ref. [19, 20] and alternating 180° phase in Ref. [17, 18, 39].
2.2. Steady-state magnetization, one pool, no exchange, long T1 and T2
Assuming TR << T1 & T2, the relaxation is effectively ignored. In the steady state case1, Mn+1 = Mn = Mss and Mss is aligned with the effective field (as dictated by Eq. 1). In other words, up to an overall constant, Mss is the eigenvector of Re⃑ (Φ) with the eigenvalue equals to one. Thus,
| (10) |
This expression, within a phase in xy plane, agrees with the one derived in Ref. [41].
If the relaxation is ignored, the initial state of magnetization has a crucial influence on the resultant locked magnetization (see Eqs. 1 and 10). The steady-state magnetization magnitude is proportional to the component of the initial magnetization parallel to the effective field. For example, if the initial magnetization is completely aligned with the effective field it will remain unchanged, in magnitude and phase. However, if the initial magnetization is perpendicular to the field at time zero, it will precess indefinitely. Thus, assuming no relaxation, the magnitude of the steady-state magnetization is the component of the initial magnetization parallel to the effective field. For example, assuming that the initial state is equal to equilibrium magnetization, i.e. is aligned with the z-axis, the steady-state magnetization becomes:
| (11) |
The bSSFP signal is determined by the xy-component of Mss. Note, that here, by the definition of Eq. 1, we are discussing the case where the signal is observed immediately before the pulse. If the observation is performed at the time TE during the cycle, an additional phase should be added to the xy-component equal to: e−i2πΔwTE. However, in this paper we will limit the discussion to the magnitude images and, thus, the phase can be ignored.
2.3. Relaxation influence
In the presence of relaxation, the magnetization dynamic becomes more complex. In general, the magnetization equation over one cycle becomes:
| (12) |
where R̃ is standard relaxation matrix [42]. The above equation can be used to assess transient as well as steady-state magnetization. In this publication the treatment will be constrained to the steady state only, while the transient approach to the steady state will be explored in further work. In the steady state, Eq. 12 reduces to:
| (13) |
The analytical solution to Eq. 13 is readily obtainable and is given in Appendix A. However, it is more instructional to observe what happens in the interaction frame, i.e. the frame defined by the eigensystem of the effective RF field, γ B⃑eff. It is also more exact, since in the presence of RF, the standard concepts of R1 and R2 relaxation do not properly describe magnetization dynamics [43]. Instead, it is more appropriate to use the relaxation in the RF interaction frame, which also consists of two components, parallel and perpendicular to the effective field, R‖ or R1ρ and R⊥ or R2ρ respectively [43]. Using analogy with the effective field in the spin-lock experiment, proven earlier, the two relaxation components are:
| (14) |
These expressions are in agreement with the relaxation expressions in bSSFP derived in Ref. [24]. Using these two relaxation components the steady-state magnetization becomes:
| (15) |
where D is the diagonalization matrix of the Heff and is given in Appendix B. Λ is the diagonal matrix:
| (16) |
The detailed derivation from Eq. 15 to 16 can also be found in Appendix B. In the core, Eqs. 15 and 16 describe the transformation to the Heff eigensystem where the steady state is described by the eigenvalues of the effective field 0, ±iΦ / TR (in rad/s) as well as by the two appropriate relaxation components R1ρ and R2ρ.
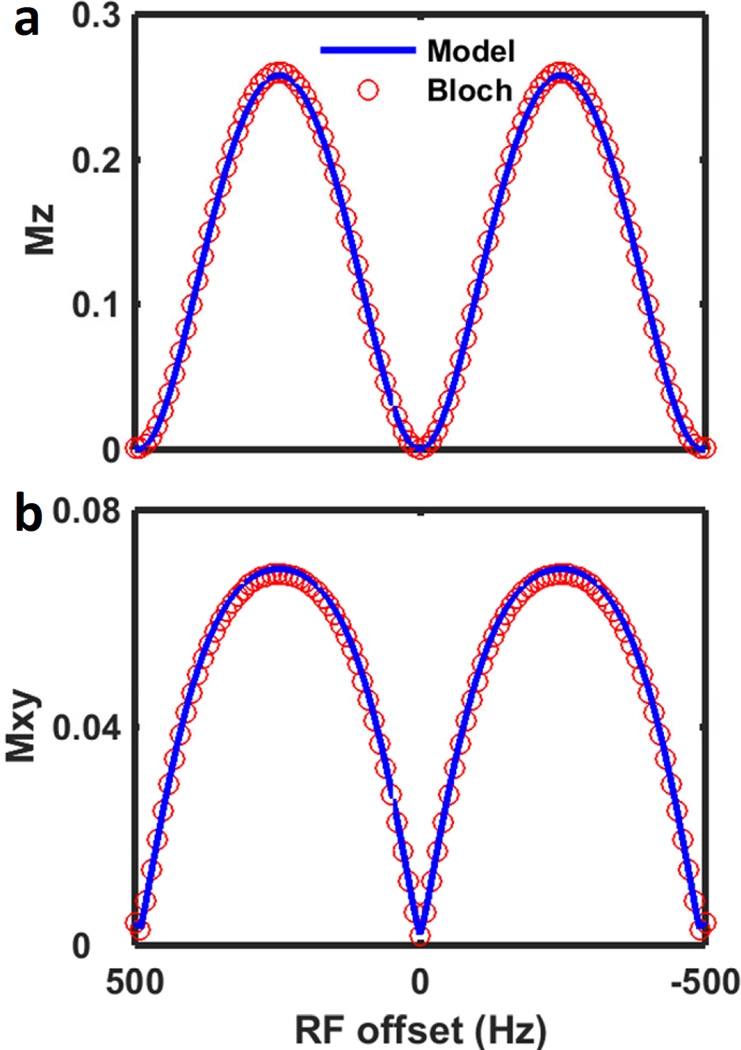
The validity of Eq. 15 is demonstrated in Fig. 3, where it is compared with exact simulation using Bloch equations. The simulation parameters are given in the Methods section. The figure demonstrates high agreement between the numerical simulation and analytical model of Eq. 15.
Figure 3.
(a) Z-spectrum and (b) XY-spectrum obtained using Eq. 15 analytical model (blue) and step-wise simulation using Bloch equation (red circles).
2.4. Two pools without exchange
If more than one non-exchanging pool is present, Eqs. 11, 15 and 16 can easily be extended. If relaxation of the pools is ignored, the overall magnetization is the sum of the individual magnetization vectors, each one aligned with its own effective field depending on the chemical shift of the species, expanding Eq. 11 to:
| (17) |
where index j denotes species “j”. This expression is in agreement with Ref. [41]. Since the flip angle is the same for all the pools, the only factor governing different effective fields is the chemical shift. If relaxation cannot be ignored, Eqs. 15 and 16 are expanded:
| (18) |
| (19) |
In this case each of the pools behaves independently. The effective field strengths as well as diagonalization matrices are dependent on the chemical shifts of the individual pools.
2.5. Two pools with exchange
Next, we shall have a closer look at the exchanging system. We shall confine this discussion to the two-pool system (bulk water pool denoted “w” in subscript and solute pool denoted “s” in subscript) only, at the slow exchange regime, although the generalization to larger number of pools and other exchange regimes is possible. In the presence of two exchanging pools, Eqs. 14, 18 and 19 are expanded to include the contribution of the exchange in the relaxation terms. In the previous sections we have demonstrated the analogy between bSSFP and spin-lock experiment. Thus, the exchange contribution to relaxation rates can be evaluated using expressions derived for the spin-lock experiment [44–46]. Since the water signal is what we are measuring, here we present the Rex term, the contribution of exchange to the relaxation rate for the water pool only. Here, we follow Trott and Palmer’s work [44] for Rex and assume asymmetric population limit (i.e. water pool fraction is much greater than the solute). Other forms for Rex can be evaluated in the future, e.g. the one proposed by Zaiss et.al. [45, 46]. Thus, in the presence of exchange, Eq. 14 becomes:
| (20) |
with
| (21) |
in which is the population fraction of each pool; Δws = δw − δs is the chemical shift difference between the two pools and k = kws + ksw is the exchange rate (ksw and kws are the exchange rates from the solute pool to the water pool and vice-versa, respectively). In Eq. 21 we have used Eq. 4 to express the effective field of the solute pool in terms of the precession angle Φ and the repetition time TR.
Note, that while the form of Rex,w contribution to R1ρ,w in the spin-lock and saturation experiments is widely discussed, the similar contribution to R2ρ,w has not been addressed as thoroughly. To the best of our knowledge, only work by Michaeli, et.al. [47] explicitly discusses the form of Rex,w contribution to R2ρ,w in the presence of adiabatic RF pulses. Hence, in Eq. 20 we assume the same form of Rex,w for both, R1ρ,w and R2ρ,w •.
For bSSFPX, the Eq. 21 predicts that the exchange contribution is maximal when the rotation angle Φs = 0, 2π,…,n2π, making the lock field effectively zero for the solute pool. For small flip angles, α, this translates to the following condition for the solute off-resonance:
| (22) |
This implies that the exchange contribution is maximal when the pulse train is exactly on-resonance with the solute pool or a multiple of 1/TR off-resonance with respect to the water pool. In other words, when the bSSFP saturation is “on-resonance” with the solute, the maximum saturation is achieved. This is indeed similar to the standard CEST case, with the caveat of the repetitive pattern with 1/TR embedded in the bSSFP train.
Higher flip angle α prevents Φ from reaching n2π, as demonstrated in Fig. 7c. However, the condition for general minimum of Rex remains in agreement with Eq. 22, as is evident from Fig. 7a and b. Additional discussion of the influence of the flip angle is conducted in the next sections.
Figure 7.
Two-pool simulation of the bSSFPX spectra dependence on the flip angle α for (a) T2w/T1w~0.83 (T2w = 2.4 s and T1w = 2.9 s) and (b) T2w/T1w~0.025 (T2w = 0.05 s and T1w = 2 s), assuming Δws of 200 Hz. Other simulation parameters are the same as section 3.1. (c) The bSSFPXasym at 200 Hz vs. flip angle for T2w/T1w~0.83 (blue) and T2w/T1w~0.025 (red). (d) The cosine of the effective field precession angle Φs as a function of the flip angle and the precession angle θs=2πΔsTR. (e) The bSSFPXasym at 200 Hz as a function of ksw and the flip angle α. (f) Different snapshot of (e), bSSFPXasym at 200 Hz vs. α for a number of exchange rates. For TR of 2.025 ms, α = 10°, 30°, 45°, 60°, 90° corresponds to B1,field = 0.32, 0.97, 1.45, 1.93, and 2.90 µT, respectively.
As demonstrated in the following, Eqs. 20–22 provide a correct qualitative prediction of the observed behavior of the exchanging system. More detailed, exact quantitative description and evaluation of the exchange contribution is beyond the scope of the current work and will be presented in a subsequent publication.
3. Methods
3.1. Simulation
Numerical simulations were performed in MATLAB 8.4 (The Mathworks, Natick, MA) to (i) validate the theoretical derivations and [44] compare the Z- and XY-spectrum and their corresponding MTRasym of the bSSFPX with that of the standard CW CEST. The simulations were based on a two-pool Bloch-McConnell model [48]. Unless stated differently, the simulation parameters were M0w = 1, T1w = 2 s, T2w = 0.05 s, M0s = 0.05, T1s = 1 s, T2s = 1 s, where M0w/s is the pool concentration. Variety of chemical shift differences and exchange rates was investigated: Δws = 1 to 9 ppm, ksw = 0–4000 Hz. For the bSSFPX sequence, the rectangular pulses with duration τ = 25 µs and initial phase ϕ0 = 0° were used; the interpulse delay was set to 2 ms (TR = 2.025 ms is the sum of the pulse duration and interpulse delay) and the number of prep-echoes was set to 4096. This was equivalent to a 8.2944 second saturation. Range of flip angles was investigated. The flip angle can be translated to B1,field using formula: [36]. For TR ≈ 2 ms used in the simulations and experiments, α = 10°, 30°, 45°, 60°, 90° translates to B1,field = 0.33 µT, 0.98 µT, 1.47 µT, 1.96 µT, 2.94 µT, respectively. No preparation methods were used to smooth the transient-state signals since the magnetization was observed in the steady state. The offset frequencies were from −500 Hz to 500 Hz with 10 Hz increments. A CW CEST sequence comparable to the bSSFPX sequence, with the saturation duration of 8.2944 s and B1,field = 0.97 µT, was also simulated. All the simulations used a field strength of 3 T.
3.2. Phantom preparation
Choline (Sigma-Aldrich, CAS no. 67-48-1), glucose (Research Products International Corporation, CAS no. 50-99-7) and glycogen (Sigma-Aldrich, CAS no. 9005-79-2) water solutions all at the concentration of 100 mM were prepared (phantom I). In addition, choline water solutions with concentrations 10, 25, 50 and 100 mM were prepared (phantom II). These solutions were transferred to glass vials held together in a glass container. The outer glass container was filled with fomblin oil (Ausimont, Thorofare, NJ) to minimize the field inhomogeneity and susceptibility effects.
3.3. MRI experiments and data acquisition
All the MRI data was acquired on a 3 T whole-body human scanner (Ingenia, Philips Healthcare, Best, The Netherlands) at room temperature using a 15-channel headspine coil. The 2D ss-bSSFPX images were acquired using a standard bSSFP sequence with 3500 prep-echoes, α = 40°, TR/TE = 2.2/1.1 ms and linear k-space ordering. This was equivalent to a 7.7 second saturation with B1,field = 1.19 µT. No preparation methods were used to smooth the transient-state signals, since at this proof-of-principle step we were focusing on the steady-state signals. The RF offsets (realized via phase advance [30]) were from −500 Hz to 500 Hz with 10 Hz increments (incrementing Δϕ by 0.02 rad) for increasing frequency sweep and from 500 Hz to −500 Hz with 10 Hz decrements (Δϕ = −0.02 rad) for decreasing frequency sweep. The final profile was the average of the two profiles acquired with reverse frequency sweeps (see section 3.5). Geometric parameters were FOV = 200×200 mm2, voxel size = 3-by-3 mm, slice thickness = 8 mm and reconstructed matrix size = 256. It took 8.0 s per irradiation frequency and 13 min 30 s for a whole profile acquisition. For comparison, the 2D pulsed CEST images were also acquired using the same B1,field as the bSSFPX experiment and the longest saturation time that can be achieved within specific absorption rate (SAR) limitation. The saturation pulse train consisted of 98 hyperbolic secant pulses with duration 50 ms, no interpulse delay and flip angle 909°. To achieve this 100% RF duty cycle, the alternated parallel transmission (pTx) is needed [49]. The total saturation length was 4.9 s and the equivalent CW B1,field was 1.19 µT. A single-shot Turbo SE (TSE) readout with was used for image acquisition. For phantom I, 45 images were acquired from −900 Hz to 900 Hz with 40 Hz increments. For phantom II, 41 images were acquired from −500 Hz to 500 Hz with 25 Hz increments. Geometric parameters were FOV = 200×200 mm2, slice thickness = 8mm, reconstructed matrix size = 256. For phantom I: TR/TE = 5691/5.2 ms, voxel size = 3-by-3 mm, the total Z-spectrum acquisition lasted 4 min 33 s with 5.7 s per irradiation frequency and for phantom II: TR/TE = 5666/4.9 ms and voxel size = 1.5-by-1.5 mm, the total acquisition lasted 4 min 3 s with 5.7 s per irradiation frequency. A reference image was acquired at −200 kHz. The Z-spectrum was corrected for B0 inhomogeneity using the WASSR [50] technique. Additional B0 drift correction is required on our scanner by adding an overall constant value to the B0 maps. The WASSR sequence was essentially the same as the CEST sequence but with shorter and weaker saturation. It contained 2 hyperbolic secant pulses with the same duration and interpulse delay as the CEST sequence but with flip angle 100°. 41 WASSR images were acquired from −200 Hz to 200 Hz with 10 Hz increments using the same geometric parameters and acquisition parameters as the CEST, except TR = 3000 ms and 1522 ms for phantom I and II respectively thus shorter total acquisition times. Second-order shimming was used in all experiments.
3.4. Data processing
All of the data was processed using custom MATLAB codes. The pulsed CEST and the bSSFPX data were analyzed on a pixel-by-pixel basis. The bSSFPX analysis followed the procedures analogous to the common CEST analysis leading to Magnetization Transfer Ratio asymmetry (MTRasym). It also incorporated procedures used in bSSFP processing [36].
First, the bSSFPX profiles were fitted to a single-pool steady-state bSSFP profile [22] to determine the B0 shift. The shift consisted of two parts (i) B0 inhomogeneity and (ii) B0 drift. Phantom susceptibility variation and imperfect shimming caused the former. bSSFP is a sequence with intense gradients. Hence the gradient coil heating up during the scan changes the shimming gradually [51], causing the drift. The profiles were realigned according to the amount of their cumulative B0 shift, following procedure analogous to the one used in Ref. [36].
As mentioned in the earlier sections, the long prep-echo train was to ensure that the image acquisition occurs in the steady state. However, the T1 of the liquid samples is long. As a result, residual transient effects may persist if the preparation length is not sufficiently long and cause asymmetries in the bSSFP profile. Specifically, if the signal at the center k-space originates from both, the transient state and the steady state, the resulting profile is asymmetric; if only the signals in the steady state contributed to the center of k-space, the resulting profile is symmetric [36]. The preparation length was 7.7 s in our experiment, which could not guarantee steady-state for all spins (T1w ≈ 3.0 s). However, the asymmetry caused by transient effects will be “mirrored” upon the reverse of the direction of frequency sweep [36]. Thus, at the next processing step, the profiles acquired at reverse frequency sweeps are averaged to correct for this unwanted asymmetry to some degree.
Lastly, asymmetry of the XY spectra was calculated and normalized to the values at negative frequencies (bSSFPXasym). We use normalization by the negative frequencies not by reference because we observe XY-components here and no reference image can be generated without appropriate RF pulses.
Standard Z-spectra acquired using pulsed saturation were processed using standard methods with WASSR correction for B0 inhomogeneity. Then the Z-spectra were interpolated (shape-preserving piecewise cubic interpolation) for MTRasym calculation. The MTRasym was normalized to the negative frequencies, to be analogous to bSSFPX. Region of interests (ROIs) were manually drawn on the images. Both the bSSFPXasym and MTRasym were averaged across each ROI in the frequency range 100–150 Hz to compare the bSSFPX with the standard pulsed CEST method.
4. Results and discussions
4.1. Simulations
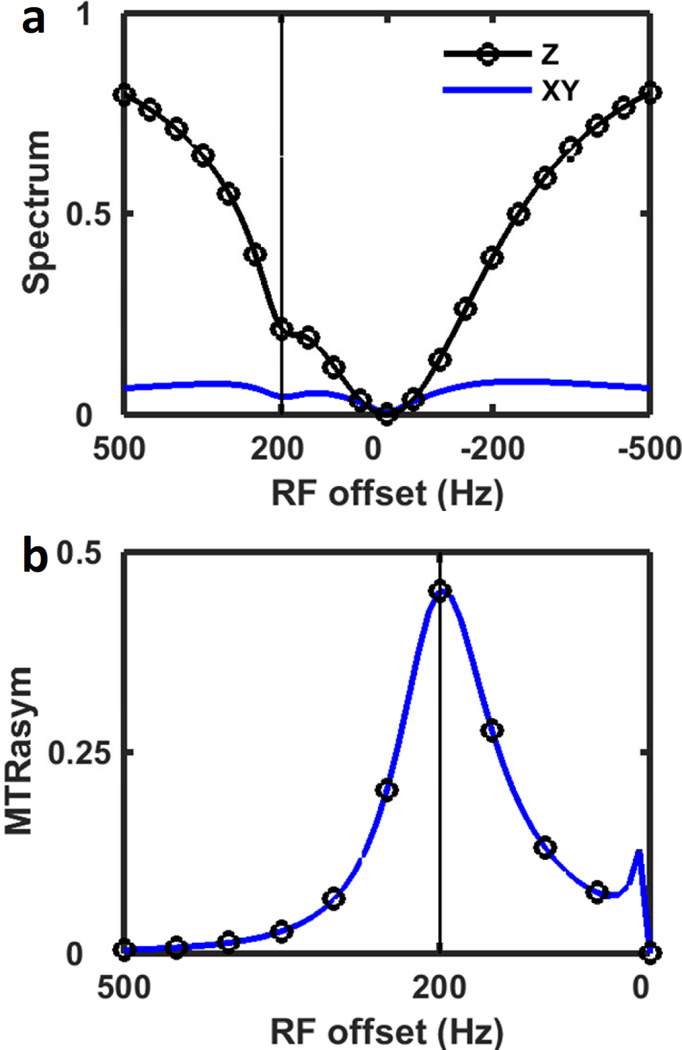
A standard CEST experiment analyzes the z-component of magnetization (the Z-spectrum) for MTR asymmetries. Actually, the MTR asymmetry can also be seen from the transverse magnetization spectrum (XY-spectrum) as shown in Fig. 4a, although the dip in the XY-spectrum is not as pronounced as in the Z-spectrum. Also, the Mxy signal of water gradually approaches 0 as the RF moves further away from water (Fig. 4a blue solid line) while its Mz signal approaches 1 (Fig. 4a black solid line with circle marker). MTRasym for both Z- and XY-spectrum are calculated and normalized with the upfield side of the spectra (Fig. 4b). The resulting Z- and XY-MTRasym are exactly the same, which indicates that the XY-spectrum is equivalent to the Z-spectrum in terms of generating CEST contrast in the absence of noise. However, the XY-MTRaysm is expected to have lower signal-to-noise ratio (SNR) compared with Z-MTRaysm since the XY-spectrum has lower signal intensity. Typically, the MTRasym is normalized with the reference image acquired without saturation irradiation or with RF irradiated far from the water. Yet for the bSSFP sequence, there is no proper reference image either without saturation or with RF irradiated far from the water, since all the images are acquired during “saturation” and the profile will repeat itself every 1/TR cycle. The normalization by upfield side was used before for CEST analysis [12, 52]. This method might better take into account direct water saturation [12]. On the other hand, it is more influenced by the NOE, MT pool asymmetry and lipid artifacts which also appear on the upfield side in vivo [53, 54]. In the future, for the in vivo studies, different normalization and analysis methods could be proposed, potentially incorporating a multi-pool fit [55].
Figure 4.
(a) Two-pool simulation of Z-spectrum (black, circles) and XY-spectrum (blue) using CW saturation. (b) The spectra asymmetries in (a), normalized with the negative side of the spectrum. The Z-MTRaysm and XY-MTRaysm overlap with each other. The vertical line indicates the resonance frequency of the solute pool.
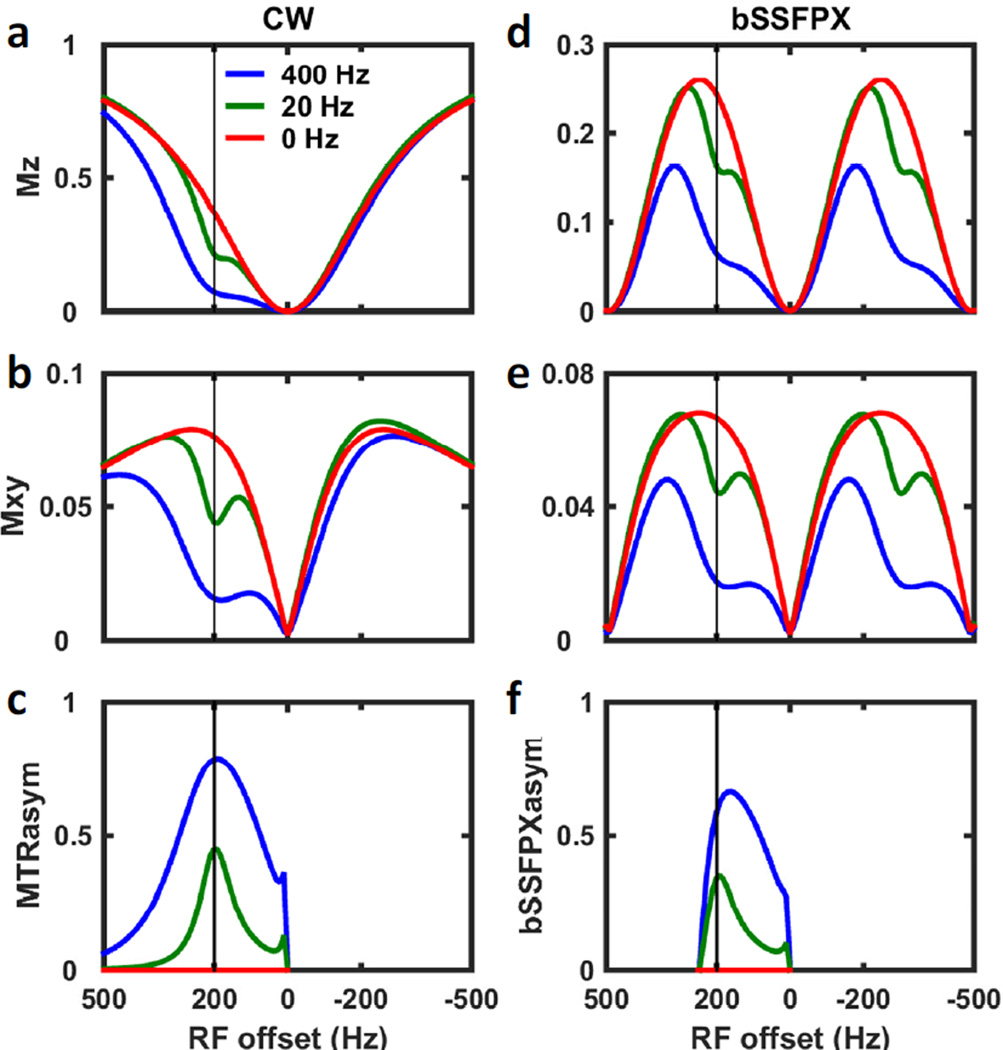
In Fig. 5, two-pool simulations using standard CW (Fig. 5a–c) and bSSFPX (Fig. 5d–f) sequences are shown, displaying representative bSSFPX spectra and comparing the magnetization profiles between the two techniques. Only the signals from the water pool are shown. In the simulations, different exchange rates were investigated. To guarantee that the spins were in the steady state when the spectra were acquired, the total length of the saturation for both sequences was set to 8.2944 s, which is about 4 times longer than the maximum T1 of the two pools. The shallow dips in the spectra (marked by the vertical solid lines) were caused by the CEST effect while the deep dips were caused by direct water saturation. As expected for the zero-degree initial phase these saturation/dark bands or water dips are occurring at n/TR ≈ n*500 Hz (with n an integer, and 1/TR = 1/2.025 ms ≈ 500 Hz). Overall, the profiles for CEST and bSSFP around zero frequency are similar (Fig. 5a,b vs. d,e); however, they start to quickly deviate from each other at higher frequencies, when the repetitive nature of bSSFPX becomes apparent. Despite the differences, it is evident from the figures that bSSFP displays similar behavior to CW. Moreover, there are some similarities with ZAPI [56] experiments or with dual saturation experiments [57, 58].
Figure 5.
Two-pool simulation for (a–c) CW and (d–f) bSSFPX methods assuming different exchange rates: 0 (red), 20 Hz (green) and 400 Hz (blue). (a,d) Z-spectra of the water pool; (b,e) XY-spectra of the water pool; (c) MTRasym and (f) bSSFPXasym. Two periods of the bSSFPX profile are shown. The vertical line indicates the resonance frequency of the solute pool.
The spectra in Fig. 5 with zero exchange rate (i.e. no exchange between the pools), are equivalent to the single water-pool spectra. These spectra are symmetric around the water saturation band at zero frequency. In agreement with the Eqs. 20 and 22, bSSFP pulse train creates saturation of the solute pool when the solute offset is on-resonance with one of the bands: Δw = Δws + Δs ≈ 200 +n500 Hz. Thus, in the cases with nonzero exchange, the asymmetric dips in water magnetization are observed. The dips increase as the exchange rates increase for both, bSSFP and CEST, since higher exchange rate translates to better saturation transfer [48, 59]. The similarities of the spectra between the two sequences imply that the bSSFPX method has the potential to be used as a CEST experiment sequence. We would like to reiterate that in bSSFPX we observe Mxy magnetization (Fig. 5e), and not Mz as in standard CEST experiment (Fig. 5a). Thus, the absolute signal intensity might be lower (Fig. 5a vs. Fig. 5e). At the same time, bSSFP has highest SNR among fast gradient-echo based sequences [60], so when acquisition influence is taken into account, this may not lead to a disadvantage of bSSFPX.
Fig. 5c,f compares the signal asymmetry for both sequences, MTRasym vs. bSSFPXasym. The asymmetry of XY-component is equivalent to the asymmetry of the Z-component: XY-MTRasym = Z-MTRasym and XY-bSSFPXasym = Z-bSSFPXasym (Fig. 4b), hence only XY is shown. For both exchange rates shown here the observed MTRasym is higher than bSSFPXasym (~45% vs. 35% and 79% vs. 59% for ksw of 20 Hz and 400 Hz, respectively). This indicates that the bSSFPXasym is lower than the CW MTRasym, signifying that the CEST contrast obtainable using bSSFPX is lower than the one using CW sequence. It should be noted that CW saturation achieves maximum possible saturation, which is not achievable on many clinical scanners, where pulsed saturations have to be used with duty cycles lower than 100%. Thus, the true decrease in the CEST effects would depend on the specifics of the implementation of the “standard” CEST used for comparison. Here we compare bSSFPX to the maximum CEST scenario, not always achievable in practice.
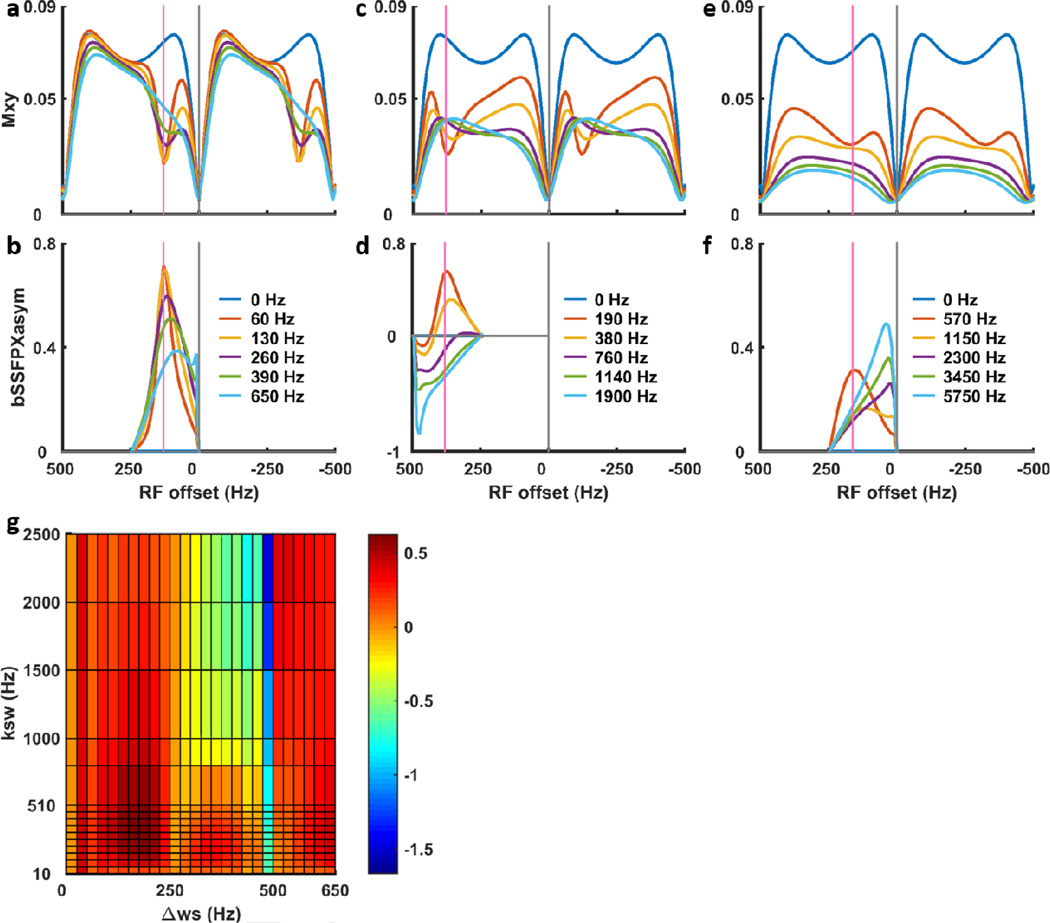
To further investigate the influence of the system parameters (exchange rate and chemical shift difference) and experimental parameters (flip angle and associated B1,field) we have conducted a series of simulations. Fig. 6 shows the representative bSSFPX profiles with different chemical shift differences Δws = 1, 3, 9 ppm and exchange rates from slow to fast exchange regime with ksw = 0.5Δws, Δws, 2Δws, 3Δws, 5Δws. For better illustration, the profiles in Fig. 6 are shown using α = 10° which is translated to B1,field ≈ 0.32 µT assuming TR = 2.025 ms. The flip angle and B1 influences will be discussed in the following. For small chemical shift difference (Fig. 6a), less than 0.5/TR, bSSFPX spectra and asymmetry behaves very similar to the standard CEST. A clear dip in the spectrum can be seen for the slow exchange, and it becomes shallow and shifts toward water/saturation bands at n/TR as exchange rate increases. The trend is also reflected by the bSSFPXasym: it decreases and shifts toward water/saturation bands as exchange rate increase (Fig. 6b). For the fixed B1,field, the asymmetry for certain chemical shifts as a function of the exchange rate increases until reaches a maximum value and starts decreasing (Fig. 6g and Supplement Figs. S1–3).
Figure 6.
Two-pool simulations of bSSFPX profiles (a,c,e) and corresponding bSSFPXasym (b,d,f) for Δws ≈ 1, 3, 9 ppm, exchange rates from slow to fast exchange regime with ksw = 0.5Δws, Δws, 2Δws, 3Δws, 5Δws. For better illustration, the profiles are shown using α = 10° (B1,field ≈ 0.32 µT with TR = 2.025 ms). Additional profiles can be found in Supplement Figs. S1 and S2. Panel (g) shows bSSFPXasym as a function of ksw and Δws for α = 45° (B1,field ≈ 1.45 µT with TR = 2.025 ms).
When the chemical shift difference increases, the overall profile behaves similar to the small shift discussed above. The well-defined peaks at low exchange rates decrease, broaden and shift towards water saturation bands and eventually disappear. This is again, overall similar to the behavior in the standard CEST experiment. However, there are some important differences. First, due to saturation bands, if Δws = n/TR, the CEST dips are not observed at all, since all the magnetization is suppressed, equivalent to the saturating at exactly water frequency in standard experiment (Supplement Fig. S4a). Moreover, our current analysis employs asymmetry, so that when Δws ≥0.5/TR, the analysis underperforms. For example, if the chemical shift difference is exactly Δws = n0.5/TR, the asymmetry analysis leads to complete cancellation of the exchange effects, regardless of the exchange rate (Fig. 6g and Supplement Fig. S4b). Away from these two obviously bad conditions (Δws = n/TR and Δws = n0.5/TR), when the chemical shift increases 0.5/TR < Δws < 1/TR the asymmetry analysis leads to negative asymmetry, as seen in Fig. 6e. Finally, if the chemical shift is larger than 1/TR, the CEST dip will fold back, as is seen in an example in Fig. 6c,f. Thus, if the simplest asymmetry analysis is used, chemical shift difference should be limited to less than 0.5/TR. In the future, more sophisticated analysis methods could be adopted similar to standard CEST, such as multi-peak and Bloch simulation fittings [9, 55]. However, currently, we anticipate that the bSSFPX results will be easiest to interpret for the CEST agents with small chemical shift difference, such as choline, glycine, glycogen or glycosaminoglycan.
Next, we investigated the influence of the flip angle α. From Eqs. 2–3, the angle affects both, the directionality and the strength of the effective field. For the easier comparison with standard CEST, flip angle can be translated to B1,field, by taking TR into the account, as described in the Methods section. The dependence of the bSSFP spectrum intensity on the flip angle, and thus SNR is well investigated [27]. However, in the presence of exchange, the flip angle will also affect asymmetry, and thus CNR. Fig. 7a,b demonstrates the bSSFPX dependence on α. While the exchange parameters are the same for Fig. 7a and 7b, the T2w/T1w ratio is different: 0.83 vs. 0.025 (“large” and “small” in the following). From the SNR perspective, the optimal flip angle is different: ~90° for the “large” T2w/T1w and ~20° for the “small”.
The flip angle will affect the exchange contribution Rex (Eq. 21) via effective field strength and corresponding rotation angle Φs. As was discussed in the theory section, the maximum exchange contribution is obtained when Φs = n2π (effective zero rotation) which translates to the Eq. 22. Fig. 7d illustrates dependence of Φs on α and θ : the figure displays cos(Φ) and maxima correspond to Φs = n2π. The figure demonstrates that while for smaller α almost perfect zero rotation is achieved, for larger α it is unattainable. Thus, the efficiency of saturation may actually decrease with higher flip angles. In addition, higher flip angle translates to higher B1,field and to increased direct saturation, similar to standard CEST. This is further explored in Fig. 7c, where the bSSFPXasym is shown as a function of the flip angle.
The interplay between exchange rates and flip angle is further investigated in Fig. 7e,f (for small chemical shift difference) and Supplements Figs. S1, S2 and S5 (larger chemical shifts). Here too, the analogous nature of the bSSFP and CEST is apparent, when converting flip angle and TR into the B1field. In both methods, optimal B1 exists for each kex [61], and optimal B1 is higher for faster exchange rates (for CEST the condition is 2πB1opt~kex). Both methods are identical for small chemical shifts. Interestingly, for large chemical shift differences, the optimal B1 for bSSFPXasym for intermediate to fast exchange does not increase much and the bSSFPXasym remains about the same when B1,field exceeds certain value (Supplement Fig. S5). This possibly is due to the repetitiveness of the bSSFPX profile. For small chemical shifts the results of the Fig. 7f reiterate previous paragraph conclusion: smaller flip angles α (weaker B1) translate to the most efficient “saturation” and higher asymmetries. Thus, in the phantom experiments that have a large T2w/T1w ratio we have chosen α ≈ 30° – 45° (B1,field ≈ 0.97–1.45 µT) maximizing SNR and CNR.
4.2. Phantom experiments
As was shown in previous sections, the bSSFPX and asymmetry analysis performs best when the chemical shift difference is less than 0.5/TR. The shortest TR attainable on our scanner is about 2 ms. Thus, to ease interpretation we chose model systems where the chemical shift difference between the solute and the solvent is less than 500 Hz: choline, glucose and glycogen solutions in water. Furthermore, in addition to the small chemical shift difference, which is beneficial for the bSSFPX, these molecules have other features making them good models for CEST experiment. Choline is a small molecule with a single hydroxyl group whose exchanging proton resonates at ~1 ppm downfield from water [62, 63]. D-Glucose have several exchanging OH groups with the most prominent CEST effect around 1ppm [64]. Similar, the glycogen molecule possesses several exchanging sites with the maximum CEST around 1ppm [65]. The solutions behavior can be approximated by a two-pool model with their Z-spectra displaying a single prominent dip at ~1ppm in the saturation transfer spectrum. There are no MTC and NOE effects to confound data analysis in our first proof-of-principle step (minor NOE was observed in glycogen). Lastly, a number of recent studies has explored these molecules as interesting markers of cancer metabolism (choline), physiology (glycogen) and infusion agent in cancer (glucose).
Figure S6 in Supplement shows the Z-spectra of the phantoms I and II obtained using the standard pulsed CEST experiment. The maximum CEST effect of choline occurs at ~1 ppm downfield of water. Therefore, we have chosen a frequency window from 0.8 to 1.2 ppm to calculate the MTRasym.
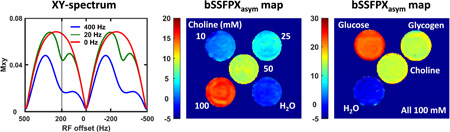
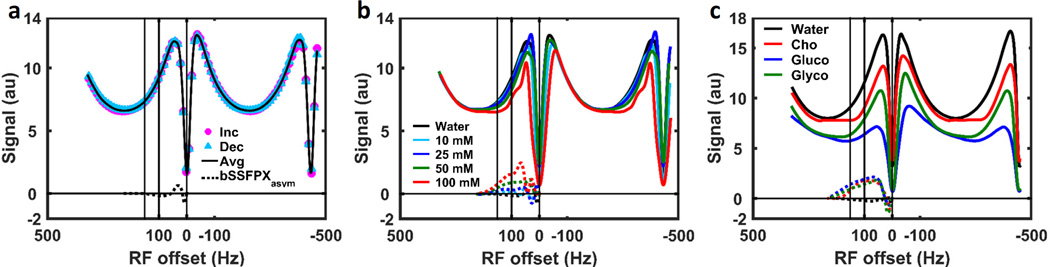
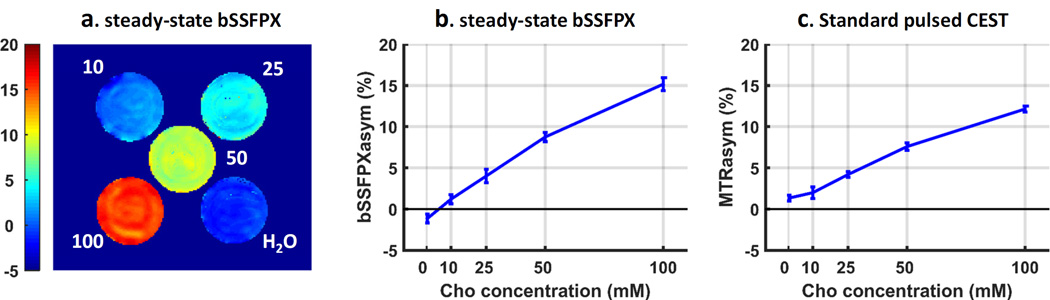
Fig. 8 displays the bSSFPX experimental results: the processing steps shown for the pure water phantom (Fig. 8a), the XY-spectra of the choline solutions of increasing concentrations (Phantom II, Fig. 8b) and the XY-spectra of choline, glucose and glycogen phantoms (Phantom I, Fig. 8c). Since the reference image “without RF” does not exist in bSSFPX, the profiles and bSSFPXasym shown in Fig. 8 were not normalized. As shown in Fig. 8a, asymmetries can be seen in both the increasing (Fig. 8a red dot) and decreasing (Fig. 8a blue dot) frequency sweep profiles. The averaged profile (Fig. 8a black solid line) largely corrects this unwanted asymmetries, however some residual asymmetry still remains close to water. This could be because the 7.7 s saturation time is still not enough to get to a complete steady state for water with T1 of ~3.0 s. As shown in Fig. 8b, the maximum bSSFPXasym effect in choline is observed about 0.8 ppm which is less than 1 ppm observed in the pulsed CEST experiment (Fig. S1). We continued to use the average frequency window determined from the CEST Z-spectra for consistent comparison. From Fig. 8b it is evident that the bSSFPXasym increases with increased choline concentration. Additional asymmetries still observed close to on-resonance and, as in the water case, can be explained by very long T1 in the phantom used.
Figure 8.
Experimental bSSFPX profiles. (a) Acquisition and processing steps demonstrated in water phantom: increasing sweep (purple dots), decreasing sweep (blue dots), their average (black line) and non-normalized bSSFPX profile asymmetry. (b) bSSFPX profiles (average of the increasing and decreasing sweeps) and non-normalized bSSFPX asymmetries for different concentrations of choline solutions in Phantom II: 0 (black), 10 mM (light blue), 25 mM (indigo), 50 mM (green) and 100 mM (red). (c) bSSFPX profiles and non-normalized bSSFPX asymmetries for phantom I: water (black), choline (red), glucose (blue) and glycogen (green), The solid and dotted lines correspond to profiles and asymmetry, respectively. A set of two vertical lines on the downfield side indicates the frequency range 100–150 Hz in which the bSSFPXasym is averaged as shown in Fig. 9a,b.
The bSSFPXasym map for phantom II is shown in Fig. 9a. The map confirms that the bSSFPXasym increases with the increased choline concentration. The bSSFPXasym averaged over the whole ROI and the frequency window is shown in Fig. 9b. The bSSFPXasym increases almost linearly with the concentration, and is equal to −1.1±0.5, 1.2±0.6, 4.0±0.8, 8.7±0.6 and 15.2±0.8% for 0, 10, 25, 50 and 100 mM, respectively. Fig. 9c demonstrates the observed MTRasym. Figs. 9b and c are very similar in overall behavior, except that the bSSFPXasym is about 5% higher than the corresponding MTRasym at highest concentrations. Our simulated results using CW saturation indicated inverse trend (MTRasym higher than bSSFPXasym). However, the experimental pulsed CEST performance may depend on other factors, such as pulse shape and duty cycle, as well as acquisition parameters such as TE and TR, which we do not take into account. Indeed, other metrics, such as average power might be more appropriate for the evaluation of pulsed CEST performance [66]. Despite these quantitative differences, the overall qualitative similarity indicates that the bSSFPX provides CEST contrast comparable to the standard pulsed CEST method.
Figure 9.
(a) bSSFPXasym map, (b) ROI averaged bSSFPXasym for different choline concentrations and (c) ROI averaged MTRasym for different choline concentrations.
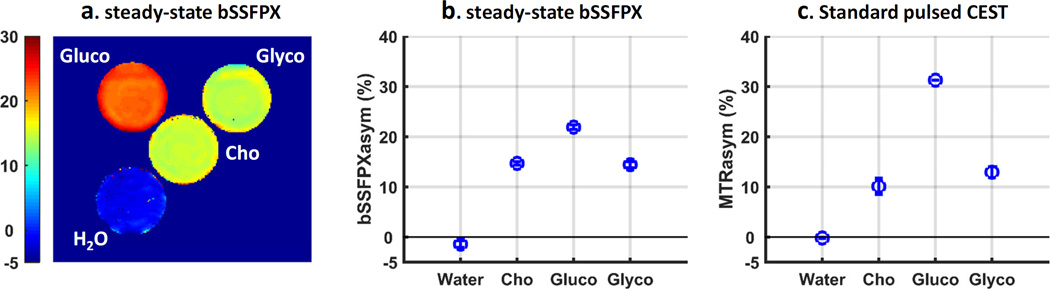
Fig. 10 compares bSSFPXasym and MTRasym for a number of molecules with small chemical shift differences: choline, glucose and glycogen. All three show a very high bSSFPX effect: 14.7±0.3, 21.9±0.5, 14.4±0.6 for choline, glucose and glycogen, respectively (Fig. 10b). Similar to the results in choline, these values are very comparable to the MTRasym observed using standard CEST methods in these molecules (Fig. 10c). Glucose has broader MTRasym and bSSFPXasym than glycogen as shown in both the Z-spectra and bSSFPX profiles (Fig. 8c and Supplement Fig. S6.b), which is also consistent with reported studies [63]. Glucose and glycogen are in the intermediate to fast exchange regime [63]. These results are in agreement with simulations in Fig. 6: bSSFPX performs well for small chemical shift differences in slow to intermediate exchange regimes. This may be not surprising, since bSSFPX shares properties of T1ρ which might be better suited for faster exchange.
Figure 10.
(a) bSSFPXasym map, (b) ROI averaged bSSFPXasym and (c) ROI averaged MTRasym for different molecules (Cho: choline, Gluco: glucose and Glyco: glycogen).
The bSSFPX profile repeats itself every 1/TR. Based on the simulation results, in this proof-of-principle study, we have only investigated molecules with one exchangeable group and small chemical shift difference close to water. As was already discussed in the Simulations results, if the chemical shift difference of the solute pool is greater than the period 1/TR, the dip will fold over in the profile. Such folded profiles might still be analyzable if we know exactly the chemical shift of the solute pool beforehand, otherwise it is hard to tell where the solute pool lies in the spectrum. A solute molecule possessing several exchanging sites, within and outside the 1/TR range will make the analysis more difficult and complicated. The simplest work around is to decrease TR, which is hardware limited and may not be feasible.
At the same time, simulation and experimental results indicate excellent performance of bSSFPX at the small chemical shifts, for a large range of exchange rates (Figs. 6, 7, 9 and 10). Thus, we anticipate that bSSFPX would be most useful for the detection of solutes with a small chemical shift difference from water, such as choline, glycine, and glucose shown here, or glycosaminoglycan and myo-inositole.
The average B1,field attainable with bSSFPX, is generally lower than in standard CEST and is limited by the nature of the experiment. The highest α useful for imaging is 90°. The B1,field may be further increased by shortening TR. In our machine the hardware parameters translated to the highest B1,field of 2.9 µT. However, this is not the limiting factor on the bSSFPX performance, since the simulation and experimental results indicate optimal performance is achieved using smaller flip angles and correspondingly lower average B1. This is perhaps the biggest difference from standard CEST..
It should be noted that the sequence is very straightforward to implement. The only optimization that might be required is in terms of the flip angle, and adjusting TR to the minimum value. Moreover, since Duty Cycle is so low very long saturation times can be achieved effortlessly. The processing is relatively straightforward too, combining elements from bSSFP processing and CEST. Additional advantage of the sequence is that it does not require acquisition of a separate B0 map. In contrast, obtaining reliable CEST and B0 correction data for chemical shifts close to water can be very challenging in standard implementation. This could potentially serve as advantage of bSSFPX in imaging of agents with chemical shift difference close to water.
One more distinctive feature of bSSFPX sequence is the application of the gradients during excitation/saturation pulse. For standard CEST, usually no gradients are used during saturation pulses; hence, the whole volume is saturated. For the single slice bSSFPX, only the spins in the imaging plane are saturated. We used the standard excitation pulses with standard gradients, without any additional refinements. We anticipate that as long as the slice selective excitation pulses perform adequately, the bSSFPX sequence will work and it is not sensitive to the gradients during the excitation pulses.
In the current implementation, the steady-state bSSFPX method was used, with very long phantom T1 requiring long preparation times. Therefore, the time advantage was not seen. However, in the future, we will turn from the steady-state conditions to the transient-state conditions, in which data acquisition is performed during the prep-echoes as well. These images with increasing saturation time will be acquired during the preparation time, and should allow QUEST-like exchange rate quantification [14]. In addition, the sequence is easily expandable to a 3D sequence.
This is first proof-of-the-principle study. Work is in progress to test it in-vivo. Based on our simulation and phantom results we anticipate that the sequence might provide useful addition or alternative into studies using molecules like glucose, glycogen or choline. Although it might be too early to speculate, we anticipate that the sequence will perform well in the studies of glucose infusion into brain tumors. However, it might not be well suited for the APT studies, unless processing method different from the asymmetry analysis is used.
The theory and experiments presented here may also be useful beyond CEST experiments. bSSFP is used in many applications, from fast T1 mapping to fast cardiac imaging and additional understanding of off-resonance and exchange effects would be beneficial. For example, while additional investigation is needed, asymmetries observed in Ref. [36], might contain some contribution from exchange.
5. Conclusion
In this paper, the analogous nature of bSSFP and CEST/T1ρ experiments is realized and explored. We implemented the steady-state bSSFPX method and proved its feasibility for CEST experiments through simulation and phantom studies. The comparison between the bSSFPX and the standard pulsed CEST experiments confirmed that the bSSFPX method could provide comparable CEST contrast to the standard experiment. The data processing methods, possible causes of artifacts and future steps were discussed. Based on results we anticipate that the sequence could be a useful addition or alternative to CEST/T1ρ studies using molecules with small chemical shift differences like glucose, glycogen, choline or glycosaminoglycans. As a new CEST data acquisition method, the bSSFPX experiment holds high promise for fast, quantitative and 3D CEST imaging.
Supplementary Material
Highlights.
Balanced Steady State Free Precession (bSSFP or True FISP) pulse sequence has properties similar to CEST or off-resonance T1ρ experiments.
Effective field is derived for a train of RF pulses and the analogous nature to CW RF saturation is demonstrated.
bSSFP can be used to create contrast based on chemical exchange, analogous to CEST/T1ρ (bSSFPX).
Proof-of-principle steady-state bSSFPX experiments are demonstrated in phantoms containing water solutions of choline, glucose and glycogen at 3T clinical scanner.
Acknowledgments
The authors would like to thank Dr. Shimon Vega (Weizmann Institute of Science) for insightful discussions on relaxation and spin-lock experiments, Dr. Ananth Madhuranthakam (University of Texas Southwestern Medical Center) for valuable discussions of the image artifacts and Drs. Asghar Hajibeigi and Durga Udayakumar (University of Texas Southwestern Medical Center) for phantom preparation. The research was supported by the NIH grant R21EB020245 and by the UTSW Radiology Research fund.
Appendix A
Analytical solution to Eq. 13
According to Eq. 13, Mss = −(Heff − R̃)−1R1M0 in which
| (A1) |
| (A2) |
| (A3) |
where is the water magnetization at thermal equilibrium. Hence,
| (A4) |
with and . The expressions for e0, e1, e2, e3 and Φ are found in Eq. 2. After rearrangement:
| (A5) |
Appendix B
Diagonalization matrix of Heff
D is the diagonalization matrix of Heff, which is composed of eigenvectors of Heff. After diagonalization, Heff = DΛeff D−1. With Λeff diagonal matrix composed of the eigenvalues of Heff:
| (B2) |
The expression for D is:
| (B3) |
with and . The expressions for e0, e1, e2, e3 are found in Eq. 2.
R̃ (the relaxation matrix) can be presented in the eigensystem of the effective field as well:
| (B4) |
Analogous to the effective field in the spin-lock experiment, the off-diagonal values in Eq. B4 are ignored and ΛR becomes:
| (B5) |
where R1ρ and R2ρ are found in Eq. 14. Hence,
| (B6) |
where Λ is found in Eq. 16.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
As a side comment, in fact, this is “pseudo” steady-state: the magnetization is unchanged if observed at the same point in the cycle (the so-called “stroboscopic” observation). However magnetization does evolve, on the same trajectory, between the points, so it is not pure steady-state, defined by “unchanging” magnetization (i.e. here dM/dt ≠ 0) [40] D.C. Alsop, The sensitivity of low flip angle RARE imaging, Magn Reson Med, 37 (1997) 176–184.
References
- 1.Ward K, Aletras A, Balaban R. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST) J. Magn. Reson. 2000;143:79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 2.van Zijl P, Yadav NN. Chemical exchange saturation transfer (CEST): what is in a name and what isn't? Magn. Reson. Med. 2011;65:927–948. doi: 10.1002/mrm.22761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou J, Lal B, Wilson DA, Laterra J, van Zijl P. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn. Reson. Med. 2003;50:1120–1126. doi: 10.1002/mrm.10651. [DOI] [PubMed] [Google Scholar]
- 4.Jones CK, Schlosser MJ, van Zijl P, Pomper MG, Golay X, Zhou J. Amide proton transfer imaging of human brain tumors at 3T. Magn. Reson. Med. 2006;56:585–592. doi: 10.1002/mrm.20989. [DOI] [PubMed] [Google Scholar]
- 5.Zhou J, Tryggestad E, Wen Z, Lal B, Zhou T, Grossman R, Wang S, Yan K, Fu D-X, Ford E. Differentiation between glioma and radiation necrosis using molecular magnetic resonance imaging of endogenous proteins and peptides. Nat. Med. 2011;17:130–134. doi: 10.1038/nm.2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sagiyama K, Mashimo T, Togao O, Vemireddy V, Hatanpaa KJ, Maher EA, Mickey BE, Pan E, Sherry AD, Bachoo RM, Takahashi M. In vivo chemical exchange saturation transfer imaging allows early detection of a therapeutic response in glioblastoma. Proc. Natl. Acad. Sci. U.S.A. 2014;111:4542–4547. doi: 10.1073/pnas.1323855111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhou J, Payen J-F, Wilson DA, Traystman RJ, van Zijl PC. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nat. Med. 2003;9:1085–1090. doi: 10.1038/nm907. [DOI] [PubMed] [Google Scholar]
- 8.Jia G, Abaza R, Williams JD, Zynger DL, Zhou J, Shah ZK, Patel M, Sammet S, Wei L, Bahnson RR. Amide proton transfer MR imaging of prostate cancer: a preliminary study. J. Magn. Reson. Imaging. 2011;33:647–654. doi: 10.1002/jmri.22480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dula AN, Arlinghaus LR, Dortch RD, Dewey BE, Whisenant JG, Ayers GD, Yankeelov TE, Smith SA. Amide proton transfer imaging of the breast at 3 T: establishing reproducibility and possible feasibility assessing chemotherapy response. Magn. Reson. Med. 2013;70:216–224. doi: 10.1002/mrm.24450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schmitt B, Zamecnik P, Zaiss M, Rerich E, Schuster L, Bachert P, Schlemmer HP. A new contrast in MR mammography by means of chemical exchange saturation transfer (CEST) imaging at 3 Tesla: preliminary results. Rofo. 2011;183:1030–1036. doi: 10.1055/s-0031-1281764. [DOI] [PubMed] [Google Scholar]
- 11.Longo DL, Dastrù W, Digilio G, Keupp J, Langereis S, Lanzardo S, Prestigio S, Steinbach O, Terreno E, Uggeri F. Iopamidol as a responsive MRI-chemical exchange saturation transfer contrast agent for pH mapping of kidneys: In vivo studies in mice at 7 T. Magn. Reson. Med. 2011;65:202–211. doi: 10.1002/mrm.22608. [DOI] [PubMed] [Google Scholar]
- 12.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST) Proc. Natl. Acad. Sci. U. S. A. 2008;105:2266–2270. doi: 10.1073/pnas.0707666105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schmitt B, Zbyn S, Stelzeneder D, Jellus V, Paul D, Lauer L, Bachert P, Trattnig S. Cartilage quality assessment by using glycosaminoglycan chemical exchange saturation transfer and (23)Na MR imaging at 7 T. Radiology. 2011;260:257–264. doi: 10.1148/radiol.11101841. [DOI] [PubMed] [Google Scholar]
- 14.McMahon MT, Gilad AA, Zhou J, Sun PZ, Bulte JW, van Zijl P. Quantifying exchange rates in chemical exchange saturation transfer agents using the saturation time and saturation power dependencies of the magnetization transfer effect on the magnetic resonance imaging signal (QUEST and QUESP): Ph calibration for poly-L-lysine and a starburst dendrimer. Magn. Reson. Med. 2006;55:836–847. doi: 10.1002/mrm.20818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jones CK, Polders D, Hua J, Zhu H, Hoogduin HJ, Zhou J, Luijten P, van Zijl P. In vivo three-dimensional whole-brain pulsed steady-state chemical exchange saturation transfer at 7 T. Magn. Reson. Med. 2012;67:1579–1589. doi: 10.1002/mrm.23141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dixon WT, Hancu I, Ratnakar SJ, Sherry AD, Lenkinski RE, Alsop DC. A multislice gradient echo pulse sequence for CEST imaging. Magn. Reson. Med. 2010;63:253–256. doi: 10.1002/mrm.22193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ostroff ED, Waugh JS. Multiple Spin Echoes and Spin Locking in Solids. Phys. Rev. Lett. 1966;16:1097–1098. [Google Scholar]
- 18.Mehring M. Principles of High Resolution NMR in Solids. Heidelberg: Springer-Verlag; 1983. [Google Scholar]
- 19.Rhim W-K, Burum DP, Elleman DD. Multiple-Pulse Spin Locking in Dipolar Solids. Phys. Rev. Lett. 1976;37:1764–1766. [Google Scholar]
- 20.Maricq MM. Application of average Hamiltonian theory to the NMR of solids. Phys. Rev. B: Condens. Matter. 1982;25:6622–6632. [Google Scholar]
- 21.Carr HY. Steady-State Free Precession in Nuclear Magnetic Resonance. Phys. Rev. 1958;112:1693–1701. [Google Scholar]
- 22.Freeman R, Hill HDW. Phase and Intentsity Anomalies in Fourier Transform NMR. J Magn Reson. 1971;4:366–383. [Google Scholar]
- 23.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic Resonance Imaging - Physical Principles and Sequence Design. New York: A John Wiley and Sons, Inc; 1999. [Google Scholar]
- 24.Ganter C. Analytical solution to the transient phase of steady-state free precession sequences. Magn Reson Med. 2009;62:149–164. doi: 10.1002/mrm.21968. [DOI] [PubMed] [Google Scholar]
- 25.Scheffler K, Hennig J. Is TrueFISP a gradient-echo or a spin-echo sequence? Magn Reson Med. 2003;49:395–397. doi: 10.1002/mrm.10351. [DOI] [PubMed] [Google Scholar]
- 26.Scheffler K, Hennig J. T1 quantification with inversion recovery TrueFISP. Magn Reson Med. 2001;45:720–723. doi: 10.1002/mrm.1097. [DOI] [PubMed] [Google Scholar]
- 27.Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Elsevier; 2004. [Google Scholar]
- 28.Deoni SC, Rutt BK, Jones DK. Investigating exchange and multicomponent relaxation in fully-balanced steady-state free precession imaging. J. Magn. Reson. Imaging. 2008;27:1421–1429. doi: 10.1002/jmri.21079. [DOI] [PubMed] [Google Scholar]
- 29.Deoni SC, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn. Reson. Med. 2003;49:515–526. doi: 10.1002/mrm.10407. [DOI] [PubMed] [Google Scholar]
- 30.Zur Y, Stokar S, Bendel P. An analysis of fast imaging sequences with steady-state transverse magnetization refocusing. Magn Reson Med. 1988;6:175–193. doi: 10.1002/mrm.1910060206. [DOI] [PubMed] [Google Scholar]
- 31.Bieri O, Scheffler K. Fundamentals of balanced steady state free precession MRI. J. Magn. Reson. Imaging. 2013;38:2–11. doi: 10.1002/jmri.24163. [DOI] [PubMed] [Google Scholar]
- 32.Hargreaves BA, Vasanawala SS, Pauly JM, Nishimura DG. Characterization and reduction of the transient response in steady-state MR imaging. Magn Reson Med. 2001;46:149–158. doi: 10.1002/mrm.1170. [DOI] [PubMed] [Google Scholar]
- 33.Schmitt P, Griswold MA, Gulani V, Haase A, Flentje M, Jakob PM. A simple geometrical description of the TrueFISP ideal transient and steady-state signal. Magn. Reson. Med. 2006;55:177–186. doi: 10.1002/mrm.20738. [DOI] [PubMed] [Google Scholar]
- 34.Scheffler K, Lehnhardt S. Principles and applications of balanced SSFP techniques. Eur Radiol. 2003;13:2409–2418. doi: 10.1007/s00330-003-1957-x. [DOI] [PubMed] [Google Scholar]
- 35.Oppelt A, Graumann R, Barfuss H, Fischer H, Hartl W, Schajor W. FISP: a new fast MRI sequence Electromedica (Engl Ed) 1986;4:15–18. [Google Scholar]
- 36.Miller KL. Asymmetries of the balanced SSFP profile. Part I: Theory and observation. Magn Reson Med. 2010;63:385–395. doi: 10.1002/mrm.22212. [DOI] [PubMed] [Google Scholar]
- 37.Bieri O, Scheffler K. Optimized balanced steady-state free precession magnetization transfer imaging. Magn Reson Med. 2007;58:511–518. doi: 10.1002/mrm.21326. [DOI] [PubMed] [Google Scholar]
- 38.Hinshaw WS. Image formation by nuclear magnetic resonance: The sensitive-point method. J. Appl. Phys. 1976;47:3709–3721. [Google Scholar]
- 39.Mansfield P, Ware D. Nuclear resonance line narrowing in solids by repeated short pulse r.f. irradiation. Physics Letters. 1966;22:133–135. [Google Scholar]
- 40.Alsop DC. The sensitivity of low flip angle RARE imaging. Magn Reson Med. 1997;37:176–184. doi: 10.1002/mrm.1910370206. [DOI] [PubMed] [Google Scholar]
- 41.Varma G, Wang X, Vinogradov E, Bhatt RS, Sukhatme VP, Seth P, Lenkinski RE, Alsop DC, Grant AK. Selective spectroscopic imaging of hyperpolarized pyruvate and its metabolites using a single-echo variable phase advance method in balanced SSFP. Magn. Reson. Med. 2015 doi: 10.1002/mrm.26004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ernst RR, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions. In: Rowlinson JS, editor. The International Series of Monographs in Chemistry. Oxford: Clarendon Press; 1994. [Google Scholar]
- 43.Abragam A. The principles of nuclear magnetism. Oxford: Clarendon Press; 1961. [Google Scholar]
- 44.Trott O, Palmer AG., III R1ρ Relaxation outside of the Fast-Exchange Limit. J. Magn. Reson. 2002;154:157–160. doi: 10.1006/jmre.2001.2466. [DOI] [PubMed] [Google Scholar]
- 45.Zaiss M, Bachert P. Chemical exchange saturation transfer (CEST) and MR Z-spectroscopy in vivo: a review of theoretical approaches and methods. Phys. Med. Biol. 2013;58:R221. doi: 10.1088/0031-9155/58/22/R221. [DOI] [PubMed] [Google Scholar]
- 46.Zaiss M, Bachert P. Exchange-dependent relaxation in the rotating frame for slow and intermediate exchange–modeling off-resonant spin-lock and chemical exchange saturation transfer. NMR Biomed. 2013;26:507–518. doi: 10.1002/nbm.2887. [DOI] [PubMed] [Google Scholar]
- 47.Michaeli S, Sorce DJ, Idiyatullin D, Ugurbil K, Garwood M. Transverse relaxation in the rotating frame induced by chemical exchange. J. Magn. Reson. 2004;169:293–299. doi: 10.1016/j.jmr.2004.05.010. [DOI] [PubMed] [Google Scholar]
- 48.Zhou J, Wilson DA, Sun PZ, Klaus JA, van Zijl P. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn. Reson. Med. 2004;51:945–952. doi: 10.1002/mrm.20048. [DOI] [PubMed] [Google Scholar]
- 49.Keupp J, Baltes C, Harvey P, Van den Brink J. Parallel RF transmission based MRI technique for highly sensitive detection of amide proton transfer in the human brain. Proceedings of the 19th annual meeting ISMRM. 2011 [Google Scholar]
- 50.Kim M, Gillen J, Landman BA, Zhou J, van Zijl P. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn. Reson. Med. 2009;61:1441–1450. doi: 10.1002/mrm.21873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Foerster BU, Tomasi D, Caparelli EC. Magnetic field shift due to mechanical vibration in functional magnetic resonance imaging. Magn. Reson. Med. 2005;54:1261–1267. doi: 10.1002/mrm.20695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gilad AA, McMahon MT, Walczak P, Winnard PT, Raman V, van Laarhoven HW, Skoglund CM, Bulte JW, van Zijl PC. Artificial reporter gene providing MRI contrast based on proton exchange. Nat. Biotechnol. 2007;25:217–219. doi: 10.1038/nbt1277. [DOI] [PubMed] [Google Scholar]
- 53.Ling W, Eliav U, Navon G, Jerschow A. Chemical Exchange Saturation Transfer by Intermolecular Double-Quantum Coherence. J Magn Reson. 2008;194:29–32. doi: 10.1016/j.jmr.2008.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jones CK, Huang A, Xu J, Edden RA, Schar M, Hua J, Oskolkov N, Zaca D, Zhou J, McMahon MT, Pillai JJ, van Zijl PC. Nuclear Overhauser enhancement (NOE) imaging in the human brain at 7T. Neuroimage. 2013;77:114–124. doi: 10.1016/j.neuroimage.2013.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J. Magn. Reson. 2011;211:149–155. doi: 10.1016/j.jmr.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 56.Narvainen J, Hubbard PL, Kauppinen RA, Morris GA. Z-Spectroscopy with Alternating-Phase Irradiation. J Magn Reson. 2010;207:242–250. doi: 10.1016/j.jmr.2010.09.004. [DOI] [PubMed] [Google Scholar]
- 57.Scheidegger R, Vinogradov E, Alsop D. Amide proton transfer imaging with improved robustness to magnetic field inhomogeneity and magnetization transfer assymetry using Saturation with Frequency ALternating RF Irradiation (SAFARI) Magn. Reson. Med. 2011;66:1275–1285. doi: 10.1002/mrm.22912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lee J-S, Regatte RR, Jerschow A. Separating Chemical Exchange Saturation Transfer Contrast from Magnetization Transfer Asymmetry under Two-Frequency RF Irradiation. J. Magn. Reson. 2012;215:56–63. doi: 10.1016/j.jmr.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn. Reson. Med. 2005;53:790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 60.Hargreaves B. Rapid Gradient-Echo Imaging. Journal of magnetic resonance imaging : JMRI. 2012;36:1300–1313. doi: 10.1002/jmri.23742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Woessner DE, Zhang S, Merrit M, Sherry AD. A numerical solution of the Bloch equations provides insights into the optimal design of PARACEST agents. Magn Reson Med. 2005;53:790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 62.Chan KW, Jiang L, Cheng M, Wijnen JP, Liu G, Huang P, Zijl P, McMahon MT, Glunde K. CEST-MRI detects metabolite levels altered by breast cancer cell aggressiveness and chemotherapy response. NMR Biomed. 2016;29:806–816. doi: 10.1002/nbm.3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lee JS, Xia D, Jerschow A, Regatte RR. In vitro study of endogenous CEST agents at 3T and 7T. Contrast Media and Molecular Imaging. 2016;11:4–14. doi: 10.1002/cmmi.1652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Walker-Samuel S, Ramasawmy R, Torrealdea F, Rega M, Rajkumar V, Johnson SP, Richardson S, Gonçalves M, Parkes HG, Årstad E, Thomas DL, Pedley RB, Lythgoe MF, Golay X. In vivo imaging of glucose uptake and metabolism in tumors. Nature Medicine. 2013;19:1067–1072. doi: 10.1038/nm.3252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.van Zijl PCM, Jones CK, Ren J, Malloy CR, Sherry AD. MRI Detection of Glycogen In Vivo by Using Chemical Exchange Saturation Transfer Imgaing (glycoCEST) Proc. Nat. Acad. Sci. U.S.A. 2007;104:4359–4364. doi: 10.1073/pnas.0700281104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zu Z, Li K, Janve VA, Does MD, Gochberg DF. Optimizing pulsed-chemical exchange saturation transfer imaging sequences. Magn Reson Med. 2011;66:1100–1108. doi: 10.1002/mrm.22884. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.