One (sub-)acinus for all: Fate of inhaled aerosols in heterogeneous pulmonary acinar structures

Abstract

Computational Fluid Dynamics (CFD) have offered an attractive gateway to investigate in silico respiratory flows and aerosol transport in the depths of the lungs. Yet, not only do existing models lack sufficient anatomical realism in capturing the heterogeneity and morphometry of the acinar environment, numerical simulations have been widely restricted to domains capturing a mere few percent of a single acinus. Here, we present to the best of our knowledge the most detailed and comprehensive in silico simulations to date on the fate of aerosols in the acinar depths. Our heterogeneous acinar domains represent complete sub-acinar models (i.e. 1/8th of a full acinus) based on the recent algorithm of Koshiyama & Wada (2015), capturing statistics of human acinar morphometry (Ochs et al. 2004). Our simulations deliver high-resolution, 3D spatial-temporal data on aerosol transport and deposition, emphasizing how variances in acinar heterogeneity only play a minor role in determining general deposition outcomes. With such tools at hand, we revisit whole-lung deposition predictions (i.e. ICRP) based on past 1D lung models. While our findings under quiet breathing substantiate general deposition trends obtained with past predictions in the alveolar regions, we underscore how deposition fractions are anticipated to increase, in particular during deep inhalation. For such inhalation maneuver, our simulations support the notion of significantly augmented deposition for all aerosol sizes (0.005–5.0 μm). Overall, our efforts not only help consolidate our mechanistic understanding of inhaled aerosol transport in the acinar depths but also continue to bridge the gap between “bottom-up” in silico models and regional deposition predictions from whole-lung models. Such quantifications provide what is deemed more accurate deposition predictions in morphometrically-faithful models and are particularly useful in assessing inhalation strategies for deep airway deposition (e.g. systemic delivery).

1. Introduction

In the absence of widely-available in vivo imaging modalities providing both high spatial and temporal resolution (Conway, 2012; Conway et al., 2013; Newman et al., 2012), Computational Fluid Dynamics (CFD) have offered an attractive gateway to explore respiratory airflows and aerosol transport in the depths of the lungs (Sznitman, 2013; Tsuda et al., 2013). These endeavours have been motivated amongst other by a yearning to capture, and ultimately predict, the deposition outcomes of therapeutic aerosols in the alveolar regions (Kleinstreuer and Zhang, 2010; Kleinstreuer et al., 2008), including importantly in the context of systemic drug delivery (Laube, 2014, 2015). In silico approaches provide adaptable platforms to model with some anatomical realism the 3D micro-structure of the deep pulmonary acinar airways; such regions encompass intricate sub-millimeter airspaces that together make up for over 90% of total lung volume. Several recent numerical efforts have revolved around 3D models of pulmonary acinar networks (Hofemeier and Sznitman, 2015; Khajeh-Hosseini-Dalasm and Longest, 2015; Kumar et al., 2009; Sznitman et al., 2009; Tian et al., 2015), where models are assembled from repeating polyhedral-shaped alveolar cavities that attempt to mimic the underlying space-filling acinar morphology (Fung, 1988; Hofemeier and Sznitman, 2014). These generic acinar domains have offered new insight into a broad range of questions surrounding aerosol transport and deposition, including amongst other inhalation therapy (Tenenbaum-Katan et al., 2016) and oxygen transport (Hofemeier et al., 2016) in the developing infant acinar airways, deposition outcomes in diseased emphysematous acini (Oakes et al., 2016), acinar targeting using magnetic particles (Ostrovski et al., 2016), as well as the role of wall asynchrony (Hofemeier et al., 2014) and anisotropic breathing (Hofemeier and Sznitman, 2016) on aerosol transport.

Despite significant progress, some limitations have prevented computational acinar models from coming closer to delivering whole-lung acinar deposition data. Recalling that the human lungs typically hold ~30’000 individual acini where each acinus gathers ~10’000 alveolar cavities (Haefeli-Bleuer and Weibel, 1988; McDonough et al., 2015), existing numerical models have been widely limited in size. These typically feature a mere few hundred alveoli that capture just a few percent of the volume of a single acinus. Such restrictions are most often the consequence of a trade-off between the burden of computational costs and obtaining high-resolution, spatial-temporal 3D data on aerosol transport. Indeed, the prospect of resolving directly in simulations this vast multi-scale flow and transport problem for whole-lung deposition data is overwhelmingly prohibitive and still far beyond reach. Given that the bulk of existing acinar CFD simulations are based on bottom-up approaches that model at best only portions of a single pulmonary acinus in the absence of more proximal (e.g. conductive) airways (Hofemeier and Sznitman, 2016; Tenenbaum-Katan et al., 2016), there is little if any consensus to date on creating a widely-accepted ‘gold standard’ for such reduced acinar models. Yet, a critical step would be to quantify how deposition characteristics correlate with the size of the simulated (sub-)acinar scale, e.g. the number of modelled cavities and acinar generations (Khajeh-Hosseini-Dalasm and Longest, 2015). Such efforts will ultimately help bridge the gap between high-resolution acinar models (i.e. CFD) and whole-lung deposition predictions from semi-empirical models (e.g. ICRP, 1994).

Some efforts have tried to expand polyhedral-based acinar trees into much larger lung models (Tian et al., 2015). However, the intrinsic rigidity of assembling such structures translates into geometries that by definition cannot capture the heterogeneity of the innate acinar environment (Hofemeier and Sznitman, 2015). Moreover, and to the best of our knowledge, most if not all polyhedral-based acinar domains have been based on custom, hand-tailored designs that require significant effort. In other words, each acinar model is laboriously constructed rather than the outcome of an automated algorithm. Thus, creating acinar domains on the scale of an acinus, or even a complete sub-acinus (as is the case presently), becomes rapidly prohibitive. While more recent high-resolution direct 3D acinar imaging data have surfaced (Barré et al., 2014; Kumar et al., 2013; Vasilescu et al., 2012; Xiao et al., 2016), using for example micro-computed tomography (μCT) or scanning transmission X-ray microscopy (STXM), the volumes of the reconstructed acinar models are still restricted (Sera et al., 2014; Sznitman et al., 2010). Moreover, due to technical constraints such data have been confined to small animals rather than human acini. Hence, the shortcomings of imaging-based reconstructions have led to parallel developments. Notably, a mathematical algorithm of a heterogeneous acinus structure composed of alveoli of irregular sizes and shapes was recently proposed (Koshiyama and Wada, 2015), where modelling parameters followed average acinar morphometry for rodents (Mercer and Crapo, 1987). Despite such efforts, there remains an ongoing dearth in our understanding of how morphological heterogeneity at the local acinar scale intertwines with the transport and fate of aerosols in the pulmonary depths.

In the present work, we attempt to shed new light on this latter question and explore how aerosol deposition characteristics correlate with the simulated acinar domain scale. For such purposes, we revisit the recently proposed heterogeneous acinar model of Koshiyama and Wada (2015) and conduct for the first time CFD simulations in high-fidelity acinar models capturing average human morphometry (Ochs et al., 2004). To the best of our knowledge, our efforts represent to date the most detailed numerical simulations across acinar structures that span up to the size of a characteristic sub-acinus (i.e. 1/8 of an acinus) (Haefeli-Bleuer and Weibel, 1988), estimating deposition characteristics for a wide range of aerosols acknowledged to reach the acinar region (d_p = 0.005–5.0 μm) (Sznitman, 2013). With these tools at hand, we showcase how our high-resolution acinar models may be leveraged to estimate acinar deposition outcomes under realistic breathing conditions, including deep inhalation maneuvers for inhalation therapy. In a final step, we explore how in the absence of detailed lung-wide CFD simulations our results may be integrated within whole-lung deposition predictions to revisit semi-empirical models.

2. Methods

2.1. Heterogeneous acinar models

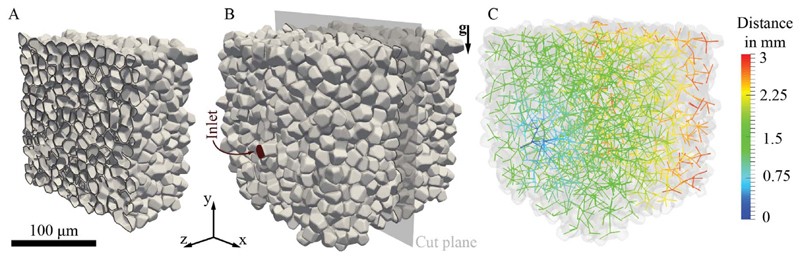
Several morphometric studies have quantified the incredibly complex anatomy of the acinar airspace (Haefeli-Bleuer and Weibel, 1988; McDonough et al., 2015; Ochs et al., 2004; Weibel et al., 2005). Yet, to mimic such intricate 3D geometries in numerical studies remains challenging. As mentioned above, polyhedral-shaped geometries are commonly used as building blocks to assemble acinar ducts and alveolar cavities into networks (Hofemeier and Sznitman, 2015; Khajeh-Hosseini-Dalasm and Longest, 2015; Ma and Darquenne, 2012). More recently, works such as those of Sera et al. (2014) have used reconstructed imaging scans to generate 3D acinar models but approaches are still currently limited to animal data. To circumvent some of these limitations, Koshiyama and Wada (2015) recently proposed a generic heterogeneous acinar model whose principles capture two underlying characteristics of the acinar airspace: its space-filling property and the heterogeneity of alveolar cavities populating the network of bifurcating acinar airways. Briefly, the algorithm can be summarized into three steps (Koshiyama and Wada, 2015): (i) points are first pseudo-randomly distributed in a bounding volume (e.g. cube) such that a minimum distance is preserved between the seed points. These form the center of each airspace, whether they constitute ductal segments or alveolar cavities. Note that as a consequence of such pseudo-randomness, each generated acinar tree is unique. (ii) To expand the random seeds into volumes, Voronoi cells are subsequently created. Finally, (iii) the acinar tree is assembled by connecting individual volumes along a common Voronoi surface. The final acinar tree is constructed using an optimization algorithm that minimizes the total path length, maximizes the number of alveolar cavities and maximizes the cross section or area between two connected volumes. In Fig. 1 (and Supplementary material SM Video 1), we showcase an example of a sub-acinar model highlighting the general structure of the tree and the morphology of the acinar airspace.

Fig. 1.

Heterogeneous pulmonary (sub-)acinar model following Koshiyama and Wada (2015). Characteristic dimensions of the acinar tree and alveolar structures fall within morphometric values of an average human adult (Ochs et al., 2004). The model shown holds over 2000 alveoli across 14 generations, with a net volume of approximately 4.55 × 10⁻³ cm³ (see Table 1). (A) Cross-sectional cut through the acinar structure, highlighting individual alveolar cavities. (B) Whole view of the sub-acinar model, showing domain inlet and cut plane depicted in (A). (C) Color-coded skeleton of the acinar tree structure (colorbar indicates distance in mm from inlet). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To closely match morphometric properties of an average human pulmonary acinus the following anatomical characteristics were adjusted. First, the pulmonary tissue (or inter-alveolar septa) was set to a thickness of 8 μm (Gehr et al., 1978; Mercer et al., 1994). The mean volume of an alveolar cavity was set to 2.1 × 10⁶μ m³ at functional residual capacity (FRC) with a coefficient of variation of 10%, following Ochs et al. (2004). To capture the variance that exists across acinar trees (Haefeli-Bleuer and Weibel, 1988), we aimed to yield a mean of 7 acinar generations for the largest sub-acinar (i.e. 1/8 of an acinus) model, with matching properties for the mean path length (Table 1). In total, we constructed acinar geometries capturing three distinct scales, i.e. ranging from 372 to 2631 alveoli (Table 1). Such strategy was implemented to investigate the role of the acinar domain size on particle transport and deposition outcomes (see Results and discussion 3 section). A view of the distinct scales of the simulated acinar geometries is presented in Fig. 2, relative to the cast of a complete acinus (Haefeli-Bleuer and Weibel, 1988). In particular, to explore the influence of acinar heterogeneity on the fate of aerosols (see Results and discussion 3 section) we constructed a total of 5 different sub-acinar models (Fig. 1), each highlighting a distinct random tree, seed distribution and a unique gravitational orientation. The anatomical variations between such sub-acinar models (n = 5) are captured in the standard deviations of Table 1, where we note that the ratio of surface-to-volume (S/V) for the entire acinar airspace is consistent across all scales investigated with a mean of 332.6 ± 0.7 cm⁻¹ in the complete sub-acinar models. Compared with previous polyhedral-based acinar domains with an S/V of about 240 cm⁻¹ (Hofemeier and Sznitman, 2015), the present heterogeneous structures are more closely in line with morphometric estimations in air-filled excised lungs (Gil et al., 1979), where S/V ranges between about 345 and 400 cm⁻¹ depending on the degree of lung inflation.

Table 1.

Summary of the heterogeneous pulmonary acinar models investigated in simulations, including size and relevant morphological properties.

	1/4 sub-acinus	1/2 sub-acinus	Sub-acinus
No. of models	1	1	5
No. of cavities	512	1184	2631 ± 13
No. of alveoli	372	866	1923 ± 16
Max. generation	8	10	14 ± 1
Mean generation	4.38	5.70	7.28 ± 0.29
Path length in cm	0.102 ± 0.032	0.142 ± 0.044	0.170 ± 0.052
Volume in 10−3cm3	0.93	2.13	4.55 ± 0.01
Surface/volume in cm−1	327.8	329.2	332.6 ± 0.7

Fig. 2.

Transport and deposition of inhaled particles (in the size range of 0.005 μm–5 μm) are numerically simulated across three distinct scales of acinar structures: a 1/4 sub-acinus, a 1/2 sub-acinus and a complete sub-acinus (i.e. 1/8 of a full acinus). Models are shown to scale next to the photograph of a cast of a full acinus (right side).

Source: Reproduced from Haefeli-Bleuer and Weibel (1988).

2.2. Breathing motion

It has long been recognized that local anisotropy at the acinar scale lies at the origin of geometrical hysteresis (Gil and Weibel, 1972; Kojic et al., 2011; Mead et al., 1957), a process observed during lung inflation–deflation maneuvers (Miki et al., 1993) and more recently with advances in imaging modalities (Chang et al., 2015; Kumar et al., 2013; Sera et al., 2013). Despite heterogeneous deformations, the principal mode of pulmonary expansion and contraction motions remains approximately self-similar (Ardila et al., 1974; Gil et al., 1979; Tsuda et al., 1995). In particular, recent simulations in space-filling acinar airways (Hofemeier and Sznitman, 2016) have underlined how the broader range of particles acknowledged to reach the acinar region (d_p = 0.005–5.0 μm) are largely unaffected by the details of anisotropic expansion under quiet breathing conditions. Indeed, anisotropy is anticipated to modulate only slightly the deposition characteristics for a very narrow band of sub-micron particles (d_p ~ 0.5–0.75 μm), where aerosol dynamics are mainly influenced by local convective flows. Yet, across the broader particle size range intrinsic aerosol motion (i.e. diffusion, sedimentation) undermines the role of anisotropic wall expansion.

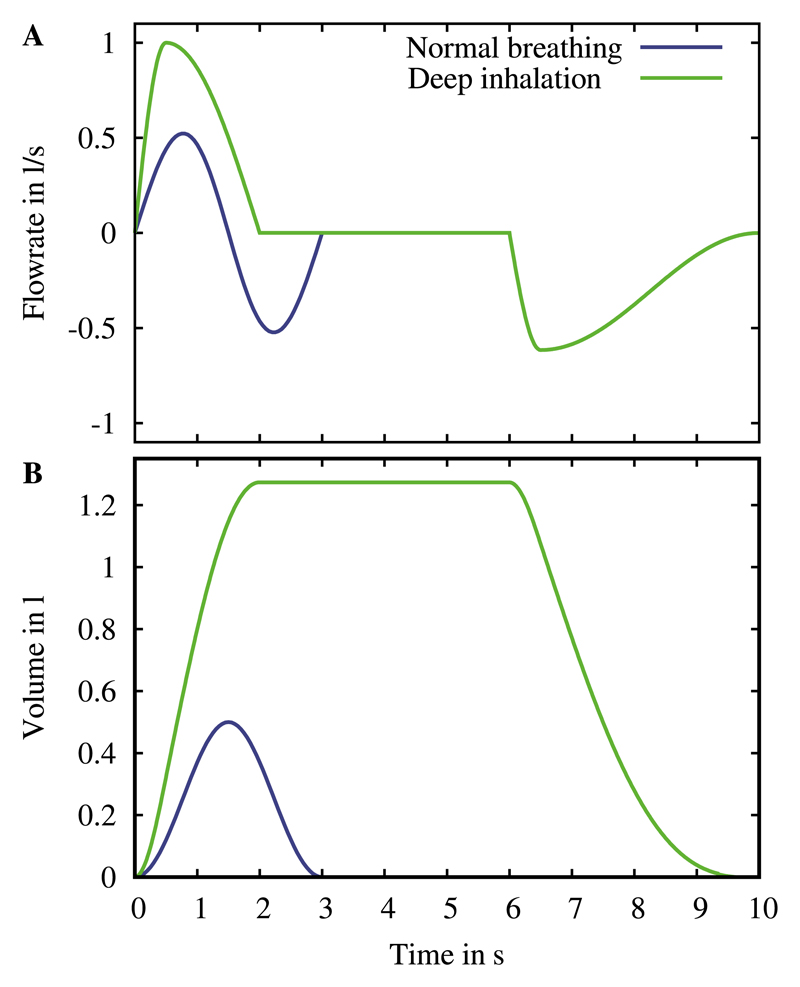
Following such considerations, we focus our analysis on particle deposition outcomes using a self-similar approximation of the acinar expansion. Accordingly, the spatial motion of the domain is governed by a unique length-scale expansion factor β = (1 + V _T/FRC)^1/3 where functional residual capacity (FRC) is about 3 L and V _T is the tidal volume (Sznitman et al., 2009; Tsuda et al., 1995). Specifically, we model two distinct breathing scenarios: quiet breathing (V _T = 500 mL) and a deep inspiratory maneuver (V _T = 2500 mL), as detailed previously (Hofemeier and Sznitman, 2015; Khajeh-Hosseini-Dalasm and Longest, 2015). Quiet breathing is approximated as an ideal sinusoidal function (Hofemeier and Sznitman, 2015; Khajeh-Hosseini-Dalasm and Longest, 2015; Tenenbaum-Katan et al., 2016), governed by the oscillatory breathing period T =1/f (f is the breathing frequency) set to T = 3 s. In contrast, the deep inhalation maneuver is comprised of three distinct sequences in time: (i) an inhalation phase, where we adopt a sine-cosine function (Khajeh-Hosseini-Dalasm and Longest, 2015) to mimic rapid inhalation (T_in = 2 s), (ii) a breath hold fixed at a constant volume for T_BH = 4 s and (iii) an exhalation phase, where we use a similar function to that during inhalation. The overall breathing period for the deep inhalation is set to T = 10 s. The time-dependent breathing waveforms (i.e. flow rate and volume) imposed respectively for quiet (normal) breathing and a deep inhalation with breath hold are recapitulated in Fig. 3.

Fig. 3.

Breathing waveforms imposed for quiet (normal) breathing and a deep inhalation with breath hold in an average human adult: (A) flow rate and (B) corresponding volume expansion.

2.3. Numerical simulations

In the deep acinar regions, respiratory airflows may be modelled as a continuum by numerically solving the incompressible Navier-Stokes equations for a Newtonian, single-phase fluid (i.e. air) (Sznitman, 2013). To account for the dynamic oscillatory motion of the acinar walls during breathing (see above), the momentum and continuity equations are solved in an arbitrary Lagrangian-Eulerian (ALE) framework (Duarte et al., 2004; Jasak and Rusche, 2009). Simulations are performed using a custom-built solver in the open source C++ library OpenFOAM (Open Source Field Operation and Manipulation, version 2.1.1). As discussed in detail elsewhere (Hofemeier and Sznitman, 2015), second-order temporal and spatial discretization schemes are used to ensure high accuracy. A zero (relative) pressure boundary condition is implemented at the inlet, while at the acinar surface a no-slip condition is imposed.

To ensure sufficient spatial discretization, a mesh convergence study was first thoroughly conducted. At peak inhalation (i.e. quiet breathing), 14 distinct locations along the acinar tree were monitored such that velocities and velocity gradients were compared. A total of 5 different domain sizes were simulated ranging from 7 M to 52 M tetrahedral cells. We found that 18 M cells are sufficient to capture adequately the ensuing flows with an average of < 3% in velocity magnitude compared to the reference computational mesh with 52 M cells. Additionally, we note that despite the complexity of the numerical domain the continuity equation was fulfilled throughout the simulations such that leakage did not occur. In particular, no collateral ventilation was present between neighbouring alveoli as their walls do not directly communicate given the finite septal thickness (see Heterogeneous acinar models 2.1 section).

In the present simulations we explore the dynamics of spherical particles (ρ_p = 1000 kg/m³) spanning the size range of d_p = 0.005–5.0 μm in diameter as this broad window of particles has the ability to enter the acinar region (Hinds, 1999; Sznitman, 2013). Following recent methodologies (Hofemeier and Sznitman, 2016; Oakes et al., 2016; Tenenbaum-Katan et al., 2016), we account for the bolus transit time to cross over the anatomical dead space of an average human adult (~150 ml). In turn, aerosols are continuously injected from t ~ 0.2T (depending on quiet vs. deep inhalation) until the end of inhalation and proportionally to the local inlet velocity, thus mimicking a constant aerosol concentration entering the acinar domain (Oakes et al., 2014). Depending on the inhalation scenario, a total of ~210k to 320k particles are injected with a log-uniform size distribution and simulated for a full breathing cycle where the overwhelming majority ( > 99.99%) of injected aerosols either deposit upon wall contact or exit the domain.

We model the three leading forces acting on the transport and deposition of aerosols, namely gravitational sedimentation, viscous drag (convection) and Brownian diffusion (Hofemeier and Sznitman, 2015). Other forces such as hygroscopic growth and electrostatic effects are effectively neglected. Since particle concentration in the acinar regions is anticipated to be low (Sznitman, 2013), a one-way fluid-particle coupling is implemented. Both fluid and particle solvers have been recently validated using established analytical models (Hofemeier and Sznitman, 2014, 2015) as well as in recent microfluidic in vitro experiments of true-scale alveolated airway models (Fishler et al., 2015, 2017).

3. Results and discussion

In the present manuscript we have set out to quantify in detail and discuss below the fate of inhaled aerosols in the acinar depths of human lungs using novel numerical models of heterogeneous acinar structures (Koshiyama and Wada, 2015). We have hence deliberately omitted for the sake of brevity an in depth discussion of the respiratory acinar flow patterns characteristic of such structures. Indeed, this latter topic has been thoroughly elaborated in a number of available reviews (Sznitman, 2013; Tsuda et al., 2013) and original research contributions, both in experiments (Fishler et al., 2015, 2013, 2017; Tsuda et al., 2002) and simulations (Hofemeier and Sznitman, 2015; Kumar et al., 2009; Oakes et al., 2016; Sznitman et al., 2009; Tsuda et al., 1995). Regardless of the anatomical geometry chosen to model the acinar environment and in particular an alveolar cavity (e.g. spherical, polyhedral, cylindrical) and its position relative to an alveolar duct, the underlying flow properties of such low-Reynolds-number cavity flows have been shown to be overwhelmingly similar both in topology and magnitude (Hofemeier and Sznitman, 2014).

Here, we note that the peak Reynolds number at the entrance of the complete sub-acinar domains reaches about 4 and 12, respectively under quiet breathing and a deep inhalation maneuver (corresponding values of the Womersley number capturing the influence of unsteady acceleration are 0.05 and 0.09, respectively, underlining quasi-steady flow phenomena (Sznitman, 2013)). From thereon, such low-Reynolds-number flow magnitudes rapidly decay with each successive acinar bifurcation as a result of mass conservation along the tree. The present heterogeneous acinar models hence give rise to analogous flow structures discussed in earlier studies (not shown here for brevity), whereby a range of complex recirculating alveolar flows coexist in the proximal generations with a gradual cross-over to radial-like alveolar streamlines in distal generations of the bifurcating tree structures. Such flows arise as a consequence of the interplay between weakening ductal flows shearing across the alveolar cavity openings and the intrinsic wall motion during oscillatory breathing that leads to a net change of alveolar volume (Sznitman, 2013); a point to which we return to in the Role of acinar domain size 3.4 section.

3.1. Transport dynamics & general deposition patterns

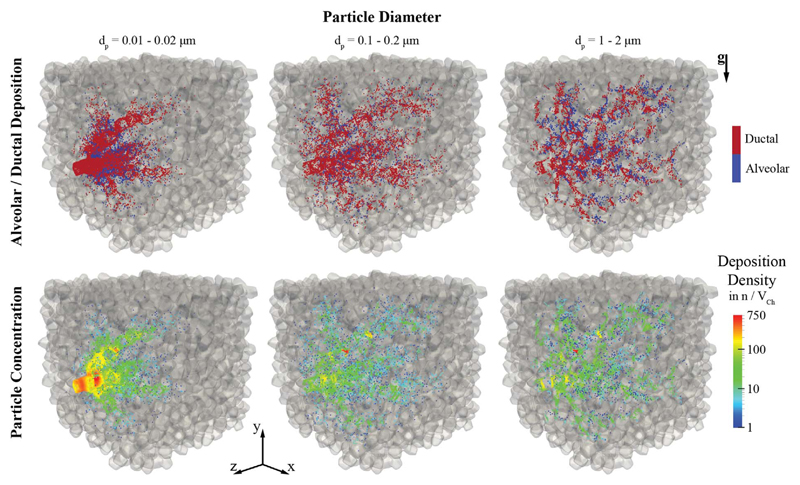
To gain some initial qualitative insight into the deposition outcomes of inhaled aerosols in heterogeneous acinar structures we begin by showcasing deposition patterns in one sub-acinar model resembling closest average deposition statistics (n = 5) under quiet breathing conditions. Fig. 4 highlights alveolar (blue) and ductal (red) deposition patterns (top row) as well as the corresponding concentration maps (bottom row) of deposited particles for three representative particle size groups spanning two orders of magnitude in diameter. Such particle sizes underline characteristic transport dynamics influenced by increasing diffusion (0.01–0.02 μm), bulk convection (0.1–0.2 μm) and gravitational sedimentation (1–2 μm), respectively (Hofemeier and Sznitman, 2015, 2016). A rendering of the transport dynamics of the complete aerosol bolus (d_p = 0.005–5.0 μm) during a breathing cycle is provided in SM Video 2.

Fig. 4.

Deposition patterns in a heterogeneous sub-acinus under quiet breathing for particle size bins covering two orders of magnitude and highlighting diffusive (left column), convective (middle column) and gravitational transport (right column). Top row: alveolar versus ductal deposition. Bottom row: Map of deposition density; color-coding indicates the number of particles (n) depositing within a radius of 50 μm with respect to each individual particle forming the control volume V _Ch. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Discriminating between deposition in acinar ducts and alveolar cavities is physiologically pertinent when assessing the spatial deposition patterns of inhaled particulate matter (Tsuda et al., 2013). Moreover, it may underscore for example the relative success of aerosol targeting for systemic delivery (Laube, 2015; Patton and Byron, 2007), where inhaled therapeutics should be delivered near the alveolar capillaries embedded within the inter-alveolar septa (Muehlfeld et al., 2010). Previous simulations under quiet breathing (Darquenne and Paiva, 1996; Hofemeier and Sznitman, 2015, 2016; Tsuda et al., 1994) have hinted at how aerosol deposition is biased towards acinar ducts and alveolar rings, as also observed in vivo (Zeltner et al., 1991). Our results in heterogeneous acinar structures (Fig. 4, top row) corroborate such findings where deposition is highly confined within the ducts, although some differences arise when looking at the distinct particle size groups; e.g. in Fig. 4 (right column), the largest particle group has the highest potential to reach into the acinar space with 10% of inhaled particles depositing inside alveolar cavities. Overall, however, particles visit only a small fraction of the sub-acinar volume under quiet breathing and hence few alveolar cavities. This largely results from the limited depth of the convective tidal front that reaches into the acinar space (Hofemeier and Sznitman, 2015); a point we will return to when considering deep inhalation maneuver.

We turn our attention to the existence of deposition “hotspots” that may be linked to inflammation or increased tissue damage as a result of highly localized deposition (Bermudez et al., 2004; Pinkerton et al., 2000). Here, we have quantified spatial deposition patterns according to deposition densities or concentrations (Fig. 4, bottom row), where the number of neighbouring particles deposited within a specified radius of any given particle is counted; i.e. this radius was chosen as 50 μm, representative of the characteristic length scale of an alveolar volume. In practice, our methodology is based on counting particles within a defined sphere (or characteristic volume V _Ch). As recently noted in simulations for polyhedral-based acinar networks (Hofemeier and Sznitman, 2015), the smallest group of nanometer-sized particles (Fig. 4, first column) deposits in high concentrations near the domain inlet; an outcome of strong Brownian motion leading to deposition within short time scales (i.e. < 0.1T upon entering the acinar domain). Larger particles do not exhibit such localized deposition at the domain entrance (Fig. 4, middle and last columns). Rather, particles are somewhat more evenly distributed in the acinar space, either as a result of bulk convection or gravitational sedimentation. Yet, deposition sites remain broadly confined along the skeleton of the tree (i.e. acinar ducts), as highlighted above.

3.2. Spatial deposition characteristics

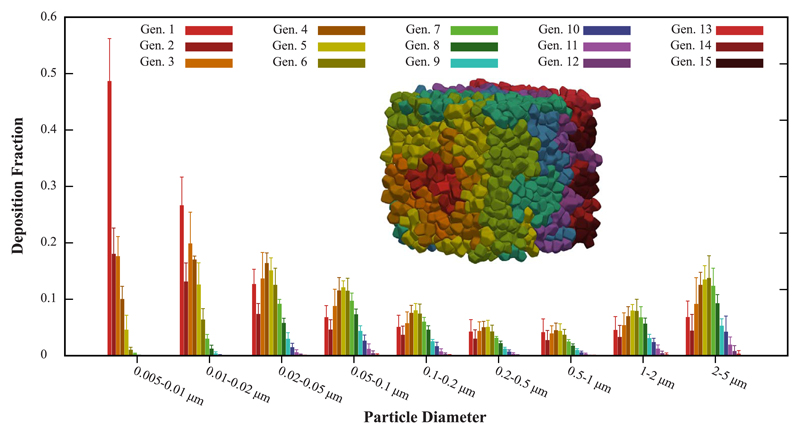
Following these initial observations, we next quantify the ensemble statistics of the spatial deposition patterns across all sub-acinar models. Fig. 5 presents for each particle size bin (x-axis) the normalized deposition fraction (mean ± SD) extracted according to acinar penetration depth, where color-coding corresponds to the acinar generation. As discussed for space-filling models of asymmetrically bifurcating alveolated airways (Khajeh-Hosseini-Dalasm and Longest, 2015), a single gravity orientation is sufficient to adequately predict acinar deposition outcomes. In turn, the error bars of Fig. 5 capture foremost the variances in deposition due to heterogeneity across the n = 5 sub-acinar models. When comparing the relative magnitude of the SDs to the normalized distributions for each particle size bin, our simulations suggest that penetration depth is mainly affected by particle size. While we find that average deposition fractions range between 28% (d_p = 0.5–1.0 μm) and 100% (d_p < 0.02 μm), the maximum SD is 5% of the mean for aerosols in the window 1.0–2.0 μm, as these particles are subject to increased sedimentation.

Fig. 5.

Deposition fractions (mean ± SD) in sub-acinar models (n = 5) under quiet breathing. For each particle size bin (x-axis), the normalized deposition fraction is presented according to penetration depth in the acinar model, i.e. color-coding indicates the acinar generation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Under tidal breathing, the overarching characteristics of spatial deposition patterns in heterogeneous sub-acinar structures may be summarized as follows. For highly-diffusive aerosols ( < 0.02 μm) we observe high deposition fractions where sites are almost entirely confined within the proximal acinar generations. In contrast, aerosols in the broad size range 0.1–1 μm that are principally advected by bulk acinar flow (in the absence of significant intrinsic motion) yield decreased deposition fractions; yet, such particles have the ability to visit in very small fractions some of the deeper acinar generations. As the role of gravity gradually dominates, deposition fractions of larger particles ( > 1 μm) increase with a slight shift towards deeper generations, since aerosols may reach into the acinar space following gravitational orientation, in particular near flow reversal (Sznitman et al., 2009). A common feature for all aerosol size groups is the relatively elevated deposition observed in the first acinar generation. This somewhat biased result is partly caused by a longer pathway in the entrance region; a necessary compromise in adjusting for the domain inlet of the heterogeneous models that is not driven by anatomy. Overall, deposition remains largely restricted to proximal generations. Recalling that half of the alveolar surface is located in the last acinar generation (Sznitman, 2013; Weibel et al., 2005), an inhalation strategy based on quiet breathing is thus not particularly attractive for delivery to the deep acinar regions.

Qualitatively, the observed deposition trends are consistent with past simulations covering the particle size range 0.005–5.0 μm in space-filling acinar trees assembled from polyhedral-shaped alveoli (Hofemeier and Sznitman, 2015, 2016). Indeed, the underlying physics of unsteady particle transport in branching alveolated tree structures under slow oscillatory flow (i.e. low Womersley number, low Reynolds number) remain analogous. In the absence of inertial impaction in the acinar regions (Sznitman, 2013), inhaled aerosols are thus subject to viscous drag (i.e. convection), diffusion and sedimentation. However, past acinar models following polyhedral geometries come short of capturing faithfully average morphometries of the acinar space and have been frequently limited to much smaller acinar domains (i.e. by an order of magnitude). In turn, quantitative deposition predictions in these domains are not anticipated to be sufficiently accurate. Despite a lack of in vivo acinar deposition data for validation purposes, the fidelity of the heterogeneous models to acinar anatomy gives reason to suppose that the present deposition predictions are a significant step closer to those anticipated in vivo.

3.3. Total deposition fractions

Deposition results from semi-empirical models and in vivo data are most commonly summarized as total deposition fractions in different lung regions (e.g. extrathoracic, tracheo-bronchial, alveolar) (Heyder, 2004; ICRP, 1994; Stahlhofen et al., 1989). Accordingly, Fig. 6A summarizes total deposition fractions in the heterogeneous acinar models as a function of particle size (bins); ensemble results (mean ± SD) are shown for the heterogeneous sub-acinar models under quiet breathing (blue curve). We begin by noting again that acinar heterogeneity has only a minor influence on total deposition outcomes. The maximum SD extracted is 10% of the mean and only observed for particles in the specific size bin 0.5–1.0 μm; an anticipated result since such particles are overwhelmingly influenced by convective acinar flows (Hofemeier and Sznitman, 2016; Sznitman, 2013), whereby these may locally vary between each unique acinar tree (n = 5). For most other particle sizes, SDs are otherwise well below 5% of the mean (i.e. ≪1%).

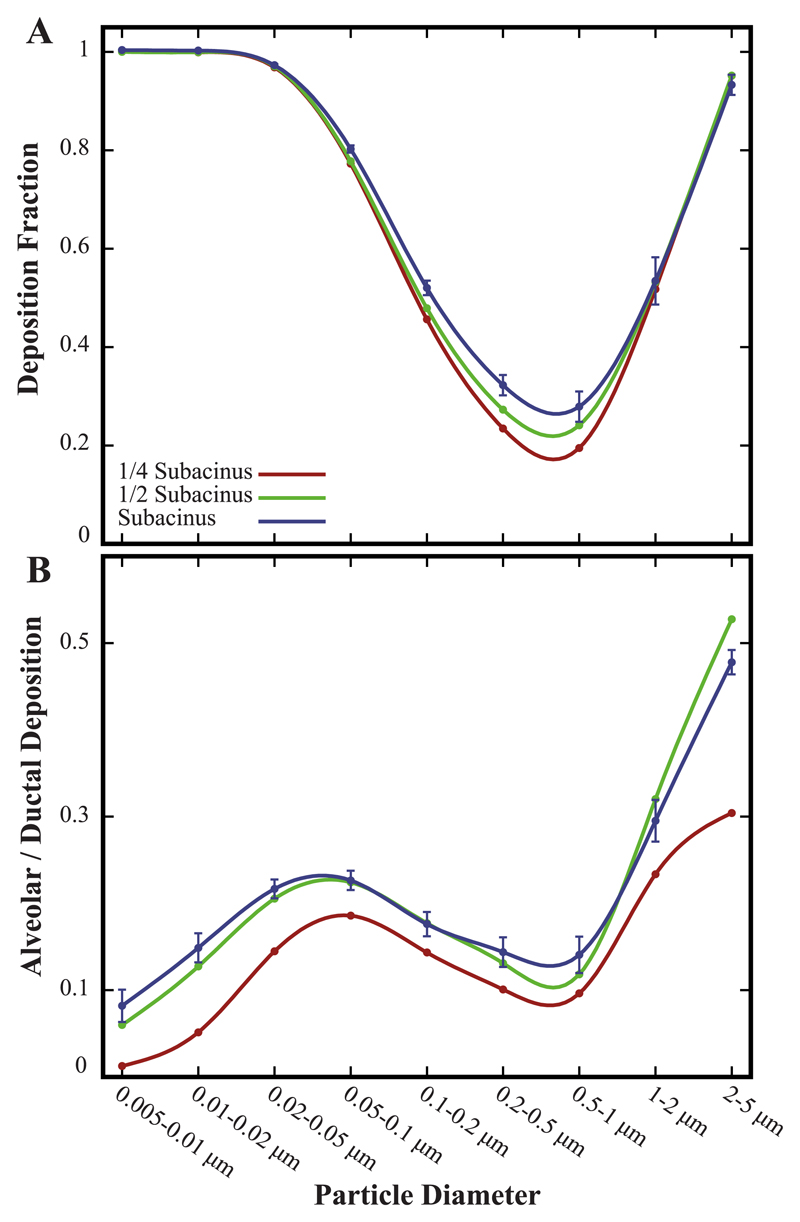
Fig. 6.

General deposition statistics in sub-acinar structures under quiet breathing. (A) Total deposition fraction and (B) ratio of alveolar to ductal deposition as a function of particle size for various acinar domain sizes (see legend). Note that for the largest sub-acinar models, data represent mean ± SD (n = 5).

We recall that the present simulations follow a bottom-up approach and thereby do not account for filtration or deposition in airways proximal to the acinar network nor the re-entry of particles into the acinar space over multiple breathing cycles (Tenenbaum-Katan et al., 2016). In turn, deposition outcomes reflect the fate of particles assumed to have effectively entered the sub-acinar space. Despite such limitations, our simulations recover deposition trends foreseen in the alveolar regions of the lungs for particles in the size range 0.005–5.0 μm (Heyder, 2004; Hinds, 1999; ICRP, 1994). Namely, acinar deposition efficiency may be identified according to the three principal transport mechanisms (Hofemeier and Sznitman, 2015, 2016). For particles below ~0.1 μm, deposition fraction rapidly converges to unity as a consequence of significant Brownian motion. Yet, few ultrafine aerosols ( < 100 nm) are anticipated in reality to deposit altogether in the acinar regions during inhalation; rather, these would deposit in more proximal airway generations of the conductive region (Hinds, 1999; ICRP, 1994). On the opposing end of the spectrum (Fig. 6A), larger particles (≥1 μm) yield deposition fractions that approach unity as sedimentation becomes prevalent. In accordance with our discussion above, the range of sub-micron particles dominated by bulk convection (i.e. 0.1–1.0 μm) exhibits the lowest deposition fractions (i.e. 30%–50%) as they lack sufficient intrinsic motion (e.g. diffusion, sedimentation) to effectively cross between streamlines and deposit at the walls (Fishler et al., 2017).

3.4. Role of acinar domain size

We next investigate how the size of the acinar domain correlates with deposition efficiency. We recall that our simulations are bounded by acinar structures capturing at most a sub-acinus (i.e. 1/8 of a full acinus) (Haefeli-Bleuer and Weibel, 1988) where we have thus modelled smaller acinar domains (Fig. 2). Since acinar heterogeneity is anticipated to play a minor role in predicting both spatial deposition patterns (Fig. 5) and total deposition efficiency (Fig. 6A), we may limit our simulations to a single model both for a 1/4 and 1/2 sub-acinar domain. Our results underscore how deposition efficiency retains its characteristic “U-shaped” curve across all models (Fig. 6A). In particular, for both diffusion- ( < 0.1 μm) and sedimentation-driven ( > 1 μm) deposition, all curves closely collapse. Differences in deposition efficiency are hence only observed for particles in the range of 0.1–1.0 μm, where maximum differences in deposition efficiency are seen for aerosols least affected by intrinsic motion (i.e. ~500 nm).

Our results highlight how smaller acinar volumes yield lower deposition efficiency (Fig. 6A). This follows as acinar domain size (i.e. number of alveolar cavities and acinar generation depth) governs the magnitude of the ensuing convective flows carried along the acinar ducts; a direct consequence of Q = dV/dt during oscillatory wall motion, where Q(t) is the flow rate and V (t) is the time-dependent volume of the acinar domain (Sznitman, 2013; Sznitman et al., 2009). In turn, we may speculate that for a complete acinus the overall deposition trends will be closely preserved but the total deposition efficiency for 0.1–1.0 μm particles will be incrementally higher due to a net increase in the bulk convective flow in the larger domain.

Quantitative outcomes for the alveolar to ductal deposition ratio are presented as a function of particle size bin in Fig. 6B. In line with our qualitative observations (Fig. 4, top row), this ratio remains well below 0.5 across the majority of particle sizes ( < 2 μm). We observe that the influence of acinar heterogeneity is overall negligible: SDs are ≤5% of the mean within the largest sub-acinar structures (blue curve). As recently discussed in the context of anisotropic breathing motions (Hofemeier and Sznitman, 2016), our findings support the idea that results for the ratio of alveolar to ductal deposition reflect by and large the underlying geometric properties of the innate acinar topology, rather than variances between acinar models. Indeed, transport and deposition of aerosols occurs in sub-millimeter networks where alveolar cavities are densely arranged around acinar ducts and adjacent alveoli are separated by inter-alveolar septa (Gehr et al., 1978; Weibel et al., 2005). Hence, heterogeneity by itself does not modulate the basic underlying structure of the acinar anatomy, where we recall that delivering aerosols directly into the acinar cavity depths (i.e. high ratio of alveolar to ductal deposition) remains challenging under quiet breathing (Fig. 4, bottom row).

We may expand on the above argument by attempting to compare deposition results in the heterogeneous structures with those obtained in previous polyhedral-based models. We revisit here available deposition data from a recent CFD study (Tenenbaum-Katan et al., 2016) for an adult acinar model comprising polyhedral structures with approximately the same number of alveolar cavities (i.e. 277) as the present 1/4 sub-acinus model (see Table 1). Note that in the work of Tenenbaum-Katan et al. (2016), only particles in the size range 0.1 to 5 μm were investigated and thus we restrict our direct comparison to such particle size window. Not surprisingly, we find that overall deposition efficiency is consistent between the two models, i.e. deposition fractions are almost identical with a characteristic “U-shaped” curve as seen in Fig. 6A (not shown here for brevity). In contrast however, alveolar deposition in the polyhedral-based model is about twice that seen in the heterogeneous one for aerosols > 1 μm; we recall that such particles experience increasing gravitational sedimentation. This discrepancy may be due to the fact that the entrance pathway in the heterogeneous domain is relatively large; a point raised earlier. Hence, heavier particles may not have the opportunity to visit more distal generations. Overall, such comparison supports further the notion that the specific acinar geometry (e.g. polyhedral vs. heterogeneous) does not dictate ‘macroscopic’ deposition outcomes (e.g. total deposition efficiency) as previously discussed in a study comparing deposition for various geometrical models of alveolar cavities (Hofemeier et al., 2014). Rather, intrinsic particle dynamics govern first and foremost variations in deposition outcomes, a critical point underlined in our most recent work (Hofemeier and Sznitman, 2016). Nevertheless, the local deposition patterns of particles are sensitive to the acinar topology (i.e. model). Not only do we thus anticipate the heterogeneous acinar models to deliver more accurate descriptions in contrast to existing polyhedral-based models, they provide an opportunity to explore in simulations scales of acinar domains approaching a complete (sub-) acinus.

We finally note that unlike the clear pattern observed in total deposition fractions as a function of acinar domain size (Fig. 6A), trends are not as striking when interpreting the influence of the acinar domain size on the ratio of alveolar to ductal deposition (Fig. 6B). Our results suggest nevertheless that under quiet breathing conditions this ratio will remain low (≤0.5) but may possibly increase slightly with a larger acinar domain (e.g. full acinus).

3.5. Deposition outcomes under deep inhalation

By and large, the bulk of acinar simulations to date have focused on aerosol transport under quiet breathing. Few CFD attempts have been made to map deposition outcomes in the alveolar regions under more realistic inhalation maneuvers for inhalation therapy to the deep lungs (Laube, 2014, 2015). In particular, recent efforts have been limited to polyhedral-based acinar networks (Khajeh-Hosseini-Dalasm and Longest, 2015; Tian et al., 2015) and hence, still do not mimic accurately enough the alveolar environment and importantly its morphometry. We have thus leveraged our heterogeneous sub-acinar models to revisit this question in simulations. To gain some insight into the transport of inhaled aerosols during deep inhalation with a breath hold, SM Video 3 compares the ensuing dynamics of the complete aerosol bolus (d_p = 0.005–5.0 μm) with that under quiet breathing.

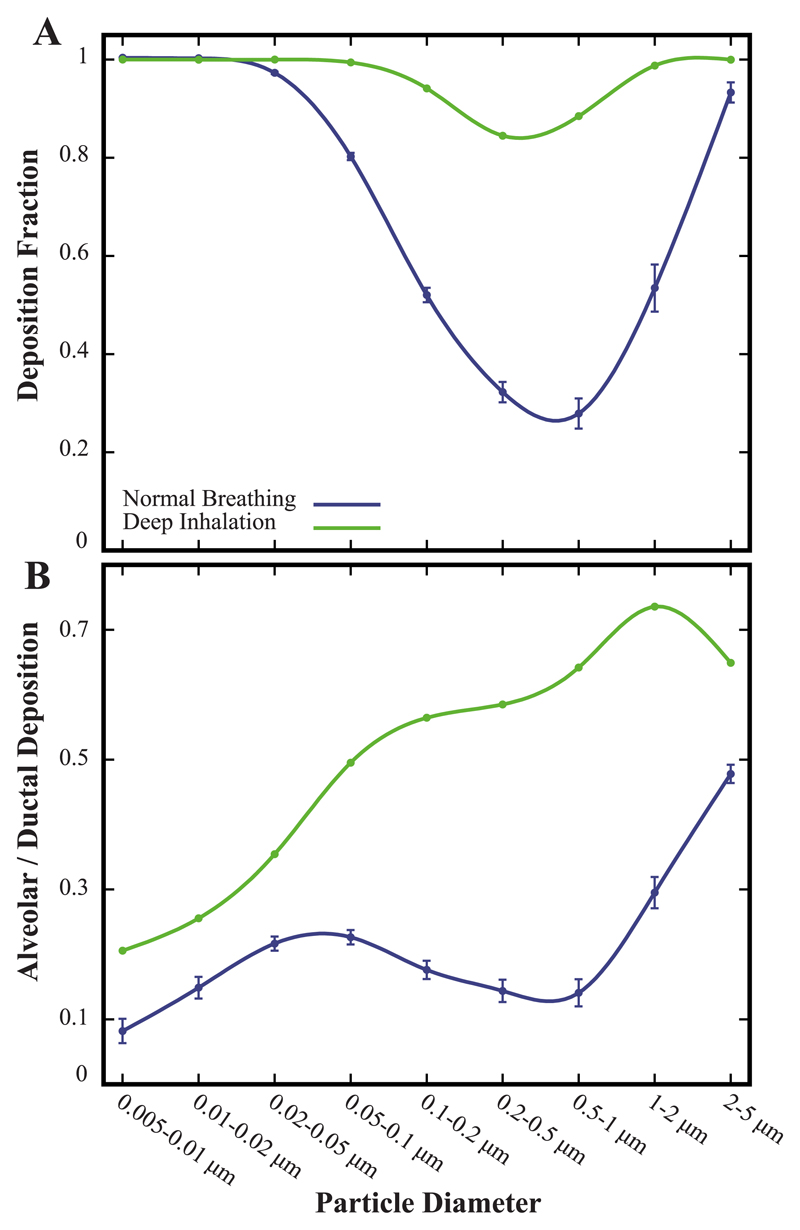
Fig. 7A recapitulates total deposition fractions between the breathing scenarios in the full sub-acinar models: deposition outcomes are dramatically affected under deep inhalation followed by a breath hold. Recalling that our results pertain only to aerosols effectively entering the computational domain, nearly all aerosol sizes are now witnessed to deposit. Importantly, aerosols least affected by intrinsic motion (0.1–1.0 μm) now yield deposition fractions > 80%. In other words, few aerosols escape during the exhalation phase. For such range of particle sizes, stronger convective flows during deep inhalation (i.e. tidal volume is increased by a factor of 5 relative to quiet breathing) bolster aerosols to reach deeper into the acinar volume. Moreover, a breath hold sustains longer time scales for deposition to occur during flow reversal as a result of either diffusion or sedimentation. We recall that following our earlier results (Fig. 6A), we have simulated a single sub-acinar domain capturing average morphometric statistics of the ensemble (n = 5). We hence anticipate that SDs due to heterogeneity may be marginally increased with stronger convective flows without, however, affecting the general trends observed.

Fig. 7.

Comparing deposition statistics between a deep inhalation maneuver (with breath hold) and quiet breathing in a sub-acinar model. (A) Total deposition fraction and (B) ratio of alveolar to ductal deposition as a function of particle size. Note that for quiet breathing, data for the full sub-acinar models represent mean ± SD (n = 5).

We find that a deep inhalation strategy is attractive to significantly augment the ratio of alveolar to ductal deposition (Fig. 7B). Although small diffusing aerosols ( < 0.1 μm) still rapidly deposit and thus benefit little from convective flow enhancement, larger particles that undergo either convective- or sedimentation-driven transport experience heightened deposition into the alveolar cavities (with an alveolar to-ductal ratio between 0.5 and 0.7 for particles > 0.1 μm). It has long been advocated that a deep inhalation with a breath hold delivers a simple yet potent strategy to effectively increase deposition in the deep airways (Heyder, 2004; Khajeh-Hosseini-Dalasm and Longest, 2015). Our present simulations provide an attractive tool to quantify for the first time changes in such outcomes.

3.6. Revisiting whole-lung deposition predictions

As reviewed by Longest and Holbrook (2012), regional lung deposition (e.g. alveolar) is often predicted using whole-lung one-dimensional (1D) models (Asgharian et al., 2001; Koblinger and Hofmann, 1990). These models typically implement analytic approximations of the various particle transport mechanisms to predict deposition at the level of individual airways and bifurcations, and subsequently extrapolate results for the entire respiratory tree (Isaacs et al., 2005). In particular, correlations used for alveolar deposition are frequently based on aerosol sedimentation in a fixed inclined tube during steady flow (Finlay, 2001) that exhibit some agreement with in vivo data as determined from slow clearance measurements (24 h) in the lungs (Hofmann and Koblinger, 1992; Koblinger and Hofmann, 1990). Yet, such modelling approaches are known to omit a number of significant flow and transport related factors to accurately capture alveolar deposition, as discussed earlier in our results (e.g. acinar structure, flow reversal, breathing wall displacements). This has also been previously highlighted by Kojic and Tsuda (2004) who showed the importance of considering oscillatory breathing flow in determining gravitational sedimentation in a simple pipe model. In addition, Kim (2009) and Choi and Kim (2007) have demonstrated how airway wall motion is important to accurately match alveolar deposition data in vivo with 1D model predictions.

Following the acknowledged limitations of 1D models for whole lung deposition predictions, we thus find merit in attempting to narrow, or even close, the gap between high-fidelity bottom-up CFD approaches and whole lung deposition predictions. As acinar deposition is anticipated to increase in a full acinus (see Section 3.4), we have conservatively estimated deposition fractions in the alveolar regions by utilizing our deposition data from the heterogeneous sub-acinar models. To integrate our in silico results within whole-lung deposition predictions (Hinds, 1999; ICRP, 1994), the following assumptions were made: aerosol deposition in the conductive airways occurs during inhalation or flow reversal only (Hofemeier and Sznitman, 2015); all remaining airborne particles may reach the respiratory (i.e. alveolar) region during inhalation. This latter assumption is deemed reasonable for inhalation therapy since particle concentrations are extremely high at the onset of inhalation and accordingly, the bolus is carried with the tidal front deep into the acinar region. However, as such, our assumptions have the tendency to overestimate particle entry into the acinar region. Bearing these limitations in mind, our total deposition fractions are estimated by subtracting particles depositing in the conductive regions (i.e. extrathoracic, tracheo-bronchial), as previously reported (Hinds, 1999; ICRP, 1994), from the particles injected into the acinar model.

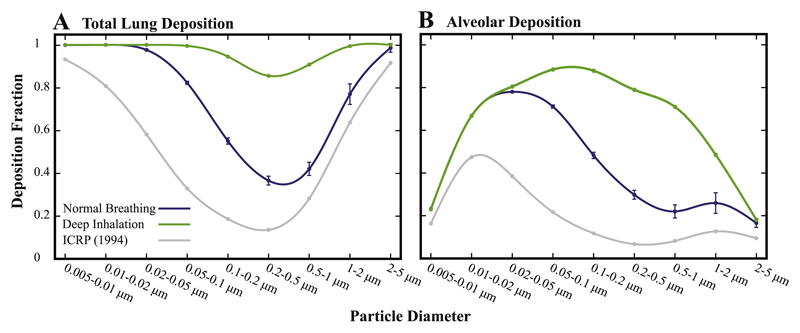
We compare acinar deposition fractions from 1D models with our new findings under both quiet breathing and a deep inhalation maneuver (Fig. 8). Our results recover the overall deposition trends established in the classic ICRP report (Hinds, 1999; ICRP, 1994), where we find that alveolar deposition exhibits local maxima for two distinct aerosol diameters (i.e. ~0.02 μm and ~1.0 μm). In contrast, however, we find significantly elevated deposition fractions relative to semi-empirical predictions, even under quiet breathing. Accordingly, total lung deposition (Fig. 8A, blue curve) exhibits increased deposition for all particle sizes, while retaining the same overall trend with that of the ICRP predictions; the most noticeable difference is observed in the deposition of particles < 0.1 μm.

Fig. 8.

Predicted deposition fractions following deposition data in the sub-acinar models (see text for methodology); data for the full sub-acini represent mean ± SD (n = 5). (A) Total lung deposition fractions in the extra-thoracic and conducting airways and (B) alveolar deposition fraction compared to semi-empirical predictions (ICRP, 1994). Note that our predictions assume that particle deposition in extra-thoracic and conductive airways are taken from the ICRP (1994) study, assuming that deposition solely occurs during inhalation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Looking at changes under deep inhalation, we showcase drastic changes compared to the ICRP study. Total lung deposition now yields unity (i.e. 100%) across almost the entire particle size range (Fig. 8A, green curve). That is, only aerosols in the narrow region near 0.5 μm are effectively able to escape due to the leading role of convection during exhalation. In Fig. 8B, the augmented trend in acinar deposition is further highlighted, where a single peak now emerges in the deposition fraction (near ~0.1 μm). Recalling the aforementioned assumptions, our exercise nevertheless emphasizes how under deep inhalation aerosols in the broad range 0.01–1.0 μm may potentially reach and deposit in the acinar region with more than 50% chance. Our findings support the hypothesis that in combination with a deep inhalation maneuver sub-micron particles are conceivably attractive carrier sizes for pulmonary acinar delivery.

We finish on a final note pertaining to the numerical model itself and its limitations. In the wide absence of high-spatial resolution human in vivo 3D morphological data pertinent to the acinar environment, the heterogeneous acinar structures represent a tangible step forward in circumventing ongoing hurdles to quantitatively predict the fate of inhaled aerosols in the acinus with high fidelity. Yet, it is important to bear in mind that these algorithmic structures still come short of faithfully mimicking the intrinsic acinar environment. Notably, beyond the restrictions of simulating a complete sub-acinus but not beyond, the topology of the structure remains bound within a rectangular (or cubic) bounding box given the framework of the algorithm. No random (sub-)acinus sample in the lungs will ever adopt such shape in nature. Furthermore, the space-filling nature of the lungs is such that with each deeper acinar generation the average size (i.e. diameter) of alveolar cavities grows (Haefeli-Bleuer and Weibel, 1988), an anatomical feature that is not captured at present. While the macroscopic deposition characteristics (e.g. deposition fractions of Figs. 6A, 7A and 8) are not anticipated to vary significantly, the aforementioned limitations may infer local changes in spatial deposition properties (e.g. Fig. 5 and alveolar to ductal ratio).

4. Conclusions

In the present work, we have described what is to the best of our knowledge the most detailed and comprehensive in silico simulations on the unsteady transport and deposition of aerosols acknowledged to enter the alveolar regions of the lungs. While computational costs have limited the extent of the acinar models to a full sub-acinus, these are to date the largest domains to have ever been simulated. Moreover, our heterogeneous models capture faithfully the statistics of acinar morphometry and thus help circumvent the ongoing lack of image-reconstructed data on human pulmonary acini. Our results emphasize that by and large, the variances in the details of the heterogeneous acinar structure play a minor role in determining general deposition outcomes, whereby particle size determines principally the fate of acinar deposition. That is, to a first yet reasonable approximation, any arbitrary heterogeneous sub-acinar structure will capture the overarching deposition outcomes anticipated. Such findings not only help consolidate our mechanistic understanding of inhaled aerosol transport in the acinar depths but also provide what is deemed to be more accurate deposition predictions using morphometrically-faithful models, compared with previous approaches using geometrically-inspired repeating structures.

With such tools at hand, we have revisited whole lung deposition statistics and integrated our high-fidelity 3D simulations into previous semi-empirical deposition predictions (Hinds, 1999; ICRP, 1994). While our findings under quiet breathing substantiate the general deposition trends obtained with past 1D models for the alveolar regions, we underscore how deposition fractions are anticipated to be increased, in particular during deep inhalation. For such latter inhalation maneuver, our simulations support the notion of significantly augmented deposition for all particle sizes. In particular, aerosols in the size range near 0.5 μm exhibit a peak in acinar deposition; an aerosol size traditionally associated with the lowest deposition efficiencies. While the present simulations have pertained to domains representative of adult acinar structures under health, the versatility of our heterogeneous models provides a tangible opportunity to explore for example acinar deposition outcomes following changes in acinar morphology due to disease (e.g. emphysema) or growth (e.g. infants).

Overall, our efforts continue to lay the foundations in bridging the gap between bottom-up in silico approaches and regional deposition predictions from whole-lung models. In the ongoing absence of available image-reconstructed human pulmonary acinar data, it must be noted that the path towards a straightforward comparison between in silico and in vivo experiments remains to be tackled, in particular for lung deposition in humans. In this context, one alternative would be to return to rodent-based heterogeneous models as originally discussed in the algorithm of Koshiyama and Wada (2015) and in parallel conduct in vivo inhalation experiments in animals (e.g. rodents). Subsequently imaging-based measurements and/or histology could be leveraged to investigate deposition characteristics on a sub-acinar scale (pending on the limited spatial resolution of the imaging modality). This could help corroborate in silico deposition predictions. A somewhat similar approach was recently conducted (Oakes et al., 2016), where flow waveforms of ventilated rodents and particle properties were implemented to match experimental MRI data and explore in silico the deposition properties of 1 μm particles in emphysematous acini using polyhedral-based acinar models. While some encouraging agreement with experimental data was met, nevertheless such studies still fall short of a one-to-one comparison between experiments and numerics, and importantly do not go as far as translating directly to lung deposition in humans.

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.ejps.2017.09.033.